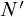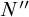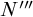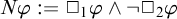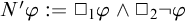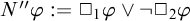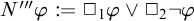1 Introduction
Recent years have witnessed extensive logical studies on bundled operators. Bundled operators are a kind of modal operators that pack several notions together. Where
$\varphi (p_1,\dots ,p_n)$
is any formula of a logical language
$\mathcal {L}$
constructed using at most the propositional variables
$p_1,\dots ,p_n$
, we write
$\varphi (\psi _1,\dots ,\psi _n)$
to denote the result of replacing every occurrence of each
$p_i$
in
$\varphi (p_1,\dots ,p_n)$
by
$\psi _i$
. Define an n-place operator
$O_{\varphi }(\psi _1,\dots ,\psi _n)=\varphi (\psi _1,\dots ,\psi _n)$
, for all
$\psi _1,\dots ,\psi _n\in \mathcal {L}$
. We call
$O_\varphi $
the bundled operator determined by the formula
$\varphi $
(i.e., by
$\varphi (p_1,\dots ,p_n)$
). For example, if
$\varphi (p)$
is the formula
$\Box p\vee \Box \neg p$
, then
$O_\varphi $
is the non-contingency operator usually written as
$\Delta $
(e.g., [Reference Montgomery and Routley33]); if
$\varphi (p,q)$
is the formula
$\Box (p\to q)$
, then
$O_\varphi $
is the strict implication operator usually written as
$\prec $
; if
$\varphi (p,q)$
is the formula
$\Diamond p\land (\Box (p\to q)\vee \Box (p\to \neg q))$
, then
$O_\varphi $
is the (possibility-based) dyadic non-contingency operator
$\boldsymbol { \Delta }$
[Reference Fan16, Reference Pizzi36]; if
$\varphi (p)$
is the formula
$\exists x\Box p$
, then
$O_\varphi $
is the operator
$\Box ^x$
(e.g., [Reference Wang and Lang42]). A bundled operator is simply the bundled operator determined by some formula.Footnote
1
There are a lot of bundled operators in the literature, for instance, the non-contingency operator
$\Delta \varphi :=\Box \varphi \vee \Box \neg \varphi $
studied in [Reference Fan, Wang and van Ditmarsch19, Reference Fan, Wang and van Ditmarsch20, Reference Humberstone26, Reference Kuhn30, Reference Montgomery and Routley33, Reference Zolin46], the accident operator
$\bullet \varphi :=\varphi \land \neg \Box \varphi $
studied in [Reference Fan9, Reference Marcos32, Reference Steinsvold39], the ‘false belief’ operator
$W\varphi :=\Box \varphi \land \neg \varphi $
studied in [Reference Fan15, Reference Fan18, Reference Gilbert and Venturi24, Reference Steinsvold40, Reference Witczak43], the ‘strong accident’ operator
$\odot\phi:=\varphi \land \Box \neg \varphi $
studied in [Reference Pan and Yang34], the ‘disjunctive ignorance’ operator
$\nabla \varphi \vee \bullet \varphi $
studied in [Reference Fan12], the ‘strong non-contingency’ operator
$\blacktriangle \varphi :=(\varphi \to \Box \varphi )\land (\neg \varphi \to \Box \neg \varphi )$
studied in [Reference Balbiani and Fan4, Reference Fan11], the ‘von Wright’s deontic necessity’ operator
$\boxplus \varphi :=\Box \varphi \land \Diamond \varphi $
studied in [Reference Bezerra and Venturi5, Reference Fan14], the ‘true belief’ operator
$\boxdot \varphi :=\Box \varphi \land \varphi $
studied in [Reference Chagrov and Zakharyaschev7, lemma 3.86] (also see [Reference Yang45]), and the (possibility-based) dyadic non-contingency operator
$\boldsymbol { \Delta }(\varphi ,\psi )=\Diamond \varphi \land (\Box (\varphi \to \psi )\vee \Box (\varphi \to \neg \psi ))$
studied in [Reference Fan16, Reference Pizzi36], just to name a few. They characterize important notions in philosophy and philosophical logic. Despite being definable with other operators, studying them as first-class citizens has some advantages. First, the logical properties of the bundled operators can be seen more clearly. Second, the bundled operators are more succinctly expressed directly than by unpacking their occurrence into the conventional vocabulary by using the proposed definition (see, e.g., [Reference van Ditmarsch, Fan, van der Hoek and Iliev8]).
However, given the fact that most of the bundled operators are non-normal, a known difficulty of such studies is how to axiomatize this kind of operators, when an operator of this kind is taken as primitive and even more particularly, is taken as the sole non-Boolean primitive. For instance, although the problem of axiomatizing non-contingency logic has been considered since 1960s [Reference Montgomery and Routley33], its axiomatization over symmetric frames has not been solved until [Reference Fan, Wang and van Ditmarsch19]. One main reason for this is that the desired core axiom is hard to find due to its complexity, and the other one is that the completeness proof needs novel strategy. As another example, despite much work on the axiomatization of the logic of false belief, the problem of axiomatizing this logic over transitive frames has been thought of as a difficult issue (see [Reference Steinsvold40, sec. 5] and [Reference Gilbert and Venturi24, sec. 2.4]), where the author(s) spend a whole section on discussing the issue.
In this paper, we introduce a uniform approach to axiomatizing bundled operators.Footnote
2
The approach is called ‘the method based on almost-definability schemas’ (MBADS for short). The term almost-definability schema can be traced back to [Reference Fan, Wang and van Ditmarsch19], where it is shown that although the necessity operator
$\Box $
is not definable with the non-contingency operator
$\Delta $
in general,
$\Box $
is almost definable in terms of
$\Delta $
, in that given a contingent proposition,
$\Box $
is definable with
$\Delta $
; in more detail,
$\neg \Delta \psi \to (\Box \varphi \leftrightarrow (\Delta \varphi \land \Delta (\psi \to \varphi )))$
is a validity. With the help of the almost-definability schema, in addition to other contributions (e.g., the proposal of a suitable bisimulation notion for non-contingency logic), the desired core axiom for symmetric contingency logic is found, and a suitable definition of canonical model is proposed, which helps to uniformly handle completeness proofs of various axiomatizations for this logic.
The approach MBADS can be sketched as follows. Roughly speaking, given any tuples of operators
$\langle O_1,\dots ,O_m \rangle $
and
$\langle O_1',\dots ,O^{\prime }_n \rangle $
, where
$O_1,\dots ,O_m$
constitute the primitive modalities of a familiar language L,
$O_1',\dots ,O_n'$
constitute the primitive modalities of a relatively unfamiliar language
$L'$
,Footnote
3
and every
$O_i$
differs from every
$O_j'$
, if given certain conditions, for every
$i=1,\dots ,m$
,
$O_i$
is definable with
$O_1',\dots ,O_n'$
, then we say
$O_i$
is almost definable in terms of
$O_1',\dots ,O_n'$
(see Definition 1 for the formal definition). We call the so-obtained (frame) validity/validities ‘almost-definability schema(s)’. Based on the schema(s), one can find suitable canonical relation and desired core axioms for the special systems. This is why we call the approach ‘the MBADS’. Compared to other approaches, this approach has incomparable advantages in axiomatizing bundled operators, including seeking out the suitable canonical relation and the desired core axioms and inference rules.
The approach has been applied to many other logics. In addition to the above-mentioned non-contingency logic, examples include the bimodal logic with contingency and accident [Reference Fan10], the logic for disjunctive ignorance [Reference Fan12], the logic of von Wright’s deontic necessity [Reference Fan14], the logic of temporal contingency [Reference Fan17], and the logic of false belief [Reference Fan18]. The almost-definability schemas involved in these logics are all valid. In this paper, we systematically propose this approach and extend it to the schemas that are valid on a class of frames, which is not necessarily the class of all frames. The core idea of this approach lies in the definability of familiar operators in terms of relatively unfamiliar ones given certain premises, thus one can ‘reduce’ the latter operators to the former ones in some way. To illustrate this approach, we choose four operators, among which one is the operator N of purely physical necessity introduced in [Reference Bacon3], one is the operator
$N'$
called ‘All
$_1$
and Only
$_2$
’ in [Reference Humberstone25], and another two are
$N"$
and
$N"'$
proposed in [Reference Humberstone28]. The choice is mainly based on two reasons: firstly, the operators are interesting in their own right, where some open questions are raised; secondly, some existing bundled operators can be seen as their special instances, thus their axiomatizations can be obtained easily.
The remainder of the paper is structured as follows. In §2, we introduce the MBADS in a general way. §3 axiomatizes the operator N of purely physical necessity proposed by Bacon in [Reference Bacon3] over various frames via MBADS. Among other results, we also axiomatize N over
$\mathbf { S4}$
-frames, thereby partly answering an open question raised by Bacon. Through proper transformation, we also obtain the almost-definability schemas in terms of
$N"$
, and then we can also axiomatize
$N"$
over various frame classes via MBADS. As the accident operator in the literature can be seen as a special instance of N, we also obtain some alternative axiomatizations of the logic of accident that are deductively equivalent to the existing ones in the literature. §4 axiomatizes the operator
$N'$
of ‘All
$_1$
and Only
$_2$
’. Among other results, we give a finite minimal axiomatization for
$N'$
, which is absent in the literature concerning the logic of
$N'$
; moreover, we gain a lot of canonicity results, including the transitive axiomatization of the logic of false belief, which has been left open in the literature. §5 axiomatizes the operator
$N"$
proposed in the literature via MBADS, whereas
$N"$
amounts to
$\neg N$
, we only illustrate this with the minimal logic of
$N"$
. §6 axiomatizes the operator
$N"'$
proposed in the literature, which has connections with the operator of accident and the operator of non-contingency, and thus gives alternative axiomatizations of the logic concerning the two operators, which are deductively equivalent to the existing ones in the literature. §7 concludes with some remarks.
It is worth noting that the completeness results of §3–§6 immediately yield axiomatizations of various unimodal fragments of extensions of the bimodal logic
$\mathbf {K}_2$
given by the operators N,
$N'$
,
$N"$
,
$N"'$
defined as
$$\begin{align*}\begin{array}{lll} N\varphi & := & \Box_1\varphi\land \neg\Box_2\varphi, \\ N'\varphi & := & \Box_1\varphi\land\Box_2\neg\varphi,\\ N"\varphi & := & \Box_1\varphi\vee \neg\Box_2\varphi,\\ N"'\varphi & := & \Box_1\varphi\vee\Box_2\neg\varphi,\\ \end{array} \end{align*}$$
where
$\Box _1,\Box _2$
are the two operators of
$\mathbf {K}_2$
(see, e.g., [Reference Gabbay, Kurucz, Wolter and Zakharyaschev22, pp. 20–22]). Moreover, the finite model property and decidability are known for many developing systems of
$\mathcal {L}(\Box _1,\Box _2)$
, where
$\mathcal {L}(\Box _1,\Box _2)$
extends the language of propositional logic with
$\Box _1$
and
$\Box _2$
as primitive modalities (see, e.g., [Reference Gabbay, Kurucz, Wolter and Zakharyaschev22]). These properties are inherited by the considered fragments which has N (
$N'$
,
$N"$
,
$N"'$
, resp.) as the sole primitive modality.
2 The method based on almost-definability schemas
Given any unary operators
$O_1,\dots ,O_m$
and
$O_1',\dots ,O^{\prime }_n$
with some semantics, where
$O_1,\dots ,O_m$
constitute the primitive modalities of a familiar language L,
$O_1',\dots ,O_n'$
constitute the primitive modalities of a relatively unfamiliar language
$L'$
, and every
$O_i$
differs from every
$O_j'$
, if given certain conditions, for every
$i=1,\dots ,m$
,
$O_i$
is definable with
$O_1',\dots , O_n'$
, then we say
$O_i$
is almost definable in terms of
$O_1',\dots ,O_n'$
. More specifically, we have the following.
Definition 1. Let
$i\in \{1,\dots ,m\}$
. For a nonempty class
$F=\langle W,R_1,\dots ,R_m \rangle $
of L-frames and each L-modality
$O_i$
that is interpreted with
$R_i$
, we say that
$O_i$
is almost definable in terms of
$O_1',\dots ,O^{\prime }_n$
over F, if there are
$L'$
-formulas
$FOR_i(\psi )$
and
$FOR_i'(\varphi ,\psi )$
as described below, for which we have:Footnote
4
for all
$\varphi ,\psi \in L'$
,
$$ \begin{align*}F\vDash FOR_i(\psi)\to (O_i\varphi\leftrightarrow FOR^{\prime}_i(\varphi,\psi)).\end{align*} $$
Here
$FOR_i(\psi )$
and
$FOR_i'(\varphi ,\psi )$
are
$L'$
-formulas which are constructed from
$\psi $
and from
$\varphi ,\psi $
, respectively, using the Boolean connectives and modal operators
$O_1',\dots ,O_n'$
. If the relevant class F of frames is clear from the context (for example, as the class of all L-frames), we simply say that
$O_i$
is almost definable in terms of
$O_1', \dots , O_n'$
, when
$O_i$
is almost definable in terms of
$O_1, \dots , O_n$
over F.
As we will illustrate, the almost definability schemas are very useful in our axiomatizations. First, they help us find core axioms for special frames; second, they help us define suitable canonical relations in the canonical model, which can handle the completeness proofs of more proof systems than those in the literature.
In more detail, once we find the almost definability schemas of
$O_i$
in
$L'$
, we can construct the canonical model for the minimal logic of
$L'$
, where the canonical relations (denoted
$R^c_i$
for all
$i=1,\dots ,m$
) can be defined as follows, which is inspired by the almost definability schemas.
-
• If
$FOR_i(\psi )\in w$
for no
$\psi $
, then
$wR^c_iu$
iff
$w=u$
. -
• If
$FOR_i(\psi )\in w$
for some
$\psi $
, then
$wR^c_iu$
is defined as in the canonical model for the minimal logic of L except that
$O_i\varphi $
is replaced by
$FOR^{\prime }_i(\varphi ,\psi )$
.
Note that the choice of
$\psi $
in the above second case is inessential to
$R^c$
, and it matters that the
$\psi $
in
$FOR_i'(\varphi ,\psi )$
is required to be the same as that in
$FOR_i(\psi )$
. It is also worth noting that the second case of
$R^c$
is inspired by Almost Definability Schema in Definition 1. Specifically, given
$FOR_i(\psi )\in w$
for some
$\psi $
, we replace
$O_i\varphi $
with
$FOR_i'(\varphi ,\psi )$
; otherwise, w can and only can access itself.
It is note remarking that instead of using the second item (denoted
$(\ast )$
) of the above definition of
$R^c_i$
, we can also use the following condition (denoted
$(\ast \ast )$
):
-
• Otherwise, for every
$\psi $
, if
$FOR_i(\psi )\in w$
, then
$wR^c_iu$
is defined as in the canonical model for the minimal logic of L except that
$O_i\varphi $
is replaced by
$FOR^{\prime }_i(\varphi ,\psi )$
.
This is because
$(\ast )$
and
$(\ast \ast )$
are equivalent. The implication from
$(\ast \ast )$
to
$(\ast )$
is immediate, and the converse also holds since the
$\psi $
in
$FOR_i'(\varphi ,\psi )$
is the same as that in
$FOR_i(\psi )$
. We prefer using
$(\ast )$
due to its simplicity.
Then we can obtain the axioms and inference rules of the minimal system for
$L'$
, according to the need of showing that the truth lemma holds and that the canonical model belongs to F in the completeness proof.Footnote
5
3 The operator of purely physical necessity
In [Reference Burks6], Arthur Burks establishes a bimodal system of logical necessity and physical necessity (or “causal necessity”, as he calls it). According to this system, logical necessity implies physical necessity (in symbols,
$\Box \varphi \to \boxed {\mathrm{c}}\varphi $
, where
$\Box $
and
$\boxed {\mathrm{c}}$
are operators of logical necessity and physical necessity, respectively), but not vice versa, and both
$\Box $
and
$\boxed {\mathrm{c}}$
are T necessity operators (namely, satisfy the conditions of K-axiom (namely,
$\Box (\varphi \to \psi )\to (\Box \varphi \to \Box \psi )$
and
$\boxed {\mathrm{c}}(\varphi \to \psi )\to (\boxed {\mathrm{c}}\varphi \to \boxed {\mathrm{c}}\psi )$
) and T-axiom (namely,
$\Box \varphi \to \varphi $
and
$\boxed {\mathrm{c}}\varphi \to \varphi $
) and necessitation rule). Kripke semantics for such bimodal systems have been given in the literature (e.g., [Reference Fitting21, Reference Rennie37]).
Partly inspired by this, and partly inspired by Armstrong’s idea that the laws of nature are logically contingent [Reference Armstrong2, p. 79], Bacon [Reference Bacon3] proposed a notion of purely physical necessity, expressed by the operator N. According to his definition, a proposition is a law of nature in the sense of logical contingency, if it is physical but not logically necessary; in symbols,
$N\varphi :=\boxed {\mathrm{c}}\varphi \land \neg \Box \varphi $
. Then Bacon axiomatizes the logic which has purely physical necessity as the sole modality over the class of bi-relational frames with two accessibility relations R and S, R for logical necessity and S for physical necessity, such that
$S\subseteq R$
, and
$\Box $
and
$\boxed {\mathrm{c}}$
are interpreted in terms of R and S in the usual way. Following Burks’s idea, Bacon also assumes that R and S are reflexive, and axiomatizes this notion of necessity over such bi-relational frames. As Bacon noted, since N incorporates aspects of both logical and physical necessity, the axiomatization becomes tricky; in particular, he mentioned the difficulty of guaranteeing the transitivity of R in the completeness proof [Reference Bacon3, p. 140]. As an open question, Bacon wonders what the S4- and S5-like extensions of the logic are.
The applications of
$\boxed {\mathrm{c}}\varphi \land \neg \Box \varphi $
to deontic logic are suggested in Jones and Pörn [Reference Jones and Pörn29] and Åqvist [Reference Åqvist1]. In [Reference Jones and Pörn29], to block various monotonicity-related paradoxes of deontic logic and implement the idea that genuine obligations are inherently susceptible of being violated, an Ought operator is introduced, defined as
$\text {Ought}~\varphi :=O\varphi \land \neg O'\varphi $
, where O and
$O'$
amount to the above
$\boxed {\mathrm{c}}$
and
$\Box $
, respectively, with different semantic restrictions to R and S.Footnote
6
In [Reference Åqvist1], a notion of supererogation is proposed, defined as
$\text {Sup}\varphi :=\text {Om-1}\varphi \land \neg \text {O1}\varphi $
, where
$\text {Om-1}\varphi $
and
$\text {O1}\varphi $
, respectively, mean that
$\varphi $
is true at all best worlds and that
$\varphi $
is true at all morally permissible worlds, so that “it is supererogatory that
$\varphi $
” means that
$\varphi $
is true at all best worlds but not at all morally permissible worlds.
3.1 Syntax and semantics
Throughout the paper, we assume
$\textbf {Prop}$
to be a nonempty set of propositional variables. We introduce the language of Bacon’s logic of purely physical necessity. For the sake of references, we also introduce the language of the bimodal logic of logical necessity and physical necessity.
Definition 2. The language
$\mathcal {L}(\Box ,\boxed {\mathrm{c}},N)$
is defined recursively as follows:
$$\begin{align*}\begin{array}{ll} \varphi::= & p\mid \neg p\mid (\varphi\land\varphi)\mid \Box\varphi\mid \boxed{\mathrm{c}}\varphi\mid N\varphi, \\ \end{array} \end{align*}$$
where
$p\in \textbf {Prop}$
.
Without the modal construct
$N\varphi $
, we obtain the language
$\mathcal {L}(\Box ,\boxed {\mathrm{c}})$
of the bimodal logic of logical necessity and physical necessity, which is a fragment of Burks’s logic of causal propositions without first-order quantifiers in [Reference Burks6]; with the modal construct
$N\varphi $
only, we obtain the language
$\mathcal {L}(N)$
of Bacon’s purely physical necessity logic. In what follows, we will mainly focus on
$\mathcal {L}(N)$
.
The language
$\mathcal {L}(\Box ,\boxed {\mathrm{c}},N)$
is interpreted on models. A model is a tuple
$\mathcal {M}=\langle W, S,R,V \rangle $
, where W is a nonempty set of possible worlds, S and R are, respectively, physical and logical accessibility relations, and
$V:\textbf {Prop}\to \mathcal {P}(W)$
is a valuation. Given
$w\in W$
,
$S(w)=\{u\in W\mid wSu\}$
and
$R(w)=\{u\in W\mid wRu\}$
. A frame is a model without valuations. A pointed model is a pair consisting of a model and a world within it. We say that
$\mathcal {M}$
is a P-model if both S and R have the property P. We say that a frame
$\mathcal {F}$
is a P-frame if all models based on that frame are P-models. In particular, throughout the paper, we use
$\mathbf {T}$
,
$\mathbf {4}$
, and
$\mathbf {S4}$
for the class of reflexive frames, the class of transitive frames, and the class of reflexive and transitive frames, respectively.
Note that, unlike Bacon, we do not assume that S and R are reflexive. This is because it is debatable which first-order properties the two accessibility relations should possess. For instance, despite following Burks’s idea that both relations are reflexive (and
$S\subseteq R$
) without further restrictions, Bacon himself thinks that S and R are better to have
$\mathbf {T}$
and
$\mathbf {S5}$
structures, which means that S is reflexive and R is an equivalence relation. Moreover, as noted on page 228 of [Reference Humberstone28], the reflexivity of accessibility relation S for physical necessity (or ‘nomic necessity’, as Humberstone calls it), is disputable in the literature (see also Remark 4.2.1, p. 217 and Note 177, p. 219 and the references thereof). Rather, we will only assume that S is a subset of R. This is quite natural, given that logical necessity implies physical necessity; in other words, whatever is physically possible is also logically possible.
Definition 3. Given a model
$\mathcal {M}=\langle W,S,R,V \rangle $
and a world
$w\in W$
, the semantics of
$\mathcal {L}(\Box ,\boxed {\mathrm{c}},N)$
is defined recursively as follows:
$$\begin{align*}\begin{array}{lll} \mathcal{M},w\vDash p & \Longleftrightarrow & w\in V(p) \\ \mathcal{M},w\vDash \neg\varphi & \Longleftrightarrow & \mathcal{M},w\nvDash \varphi\\ \mathcal{M},w\vDash \varphi\land\psi & \Longleftrightarrow & \mathcal{M},w\vDash\varphi\textrm{ and }\mathcal{M},w\vDash\psi\\ \mathcal{M},w\vDash \Box\varphi & \Longleftrightarrow & R(w)\vDash\varphi\\ \mathcal{M},w\vDash \boxed{\mathrm{c}}\varphi & \Longleftrightarrow & S(w)\vDash\varphi\\ \mathcal{M},w\vDash N\varphi & \Longleftrightarrow & S(w)\vDash\varphi \textrm{ and }R(w)\nvDash\varphi,\\ \end{array} \end{align*}$$
where
$R(w)\vDash \varphi $
means that for all
$u\in R(w)$
,
$\mathcal {M},u\vDash \varphi $
, whereas
$R(w)\nvDash \varphi $
means that it is not the case that
$R(w)\vDash \varphi $
; similarly for
$S(w)\vDash \varphi $
and
$S(w)\nvDash \varphi $
.
If
$\mathcal {M},w\vDash \varphi $
, we say that
$\varphi $
is true in
$(\mathcal {M},w)$
; if for all
$w\in W$
we have
$\mathcal {M},w\vDash \varphi $
, we say that
$\varphi $
is valid on
$\mathcal {M}$
and write
$\mathcal {M}\vDash \varphi $
; if for all models
$\mathcal {M}$
based on a frame
$\mathcal {F}$
we have
$\mathcal {M}\vDash \varphi $
, we say that
$\varphi $
is valid on
$\mathcal {F}$
and write
$\mathcal {F}\vDash \varphi $
; if for all frames
$\mathcal {F}$
in a class of frames F we have
$\mathcal {F}\vDash \varphi $
, we say
$\varphi $
is valid over F and write
$F\vDash \varphi $
, when F is the class of all frames, we say
$\varphi $
is valid and write
$\vDash \varphi $
.
Observe that there are two almost definability schemas—one for
$\boxed {\mathrm{c}}$
, and the other for
$\Box $
—in terms of N. Intuitively, they say that both physical necessity and logical necessity are definable with purely physical necessity, provided that there is a purely physically necessary proposition. They guide us to propose the desired canonical model later:
$$\begin{align*}\begin{array}{ll} N\psi\to (\boxed{\mathrm{c}}\varphi\leftrightarrow N(\varphi\land\psi))& (\textbf{NAD1}) \\ N\psi\to (\Box\varphi\leftrightarrow \neg N\varphi\land N(\varphi\land\psi)) & (\textbf{NAD2}).\\ \end{array} \end{align*}$$
The following result shows that the two schemas are indeed valid (over the class of bi-relational frames). Note that the proof of (1) does not need any semantic restriction of accessibility relations, whereas (2) only uses
$S\subseteq R$
.
Proposition 4. Let
$\mathcal {F}=\langle W,S,R \rangle $
such that
$S\subseteq R$
.
-
(1)
$\vDash N\psi \to (\boxed {\mathrm{c}}\varphi \leftrightarrow N(\varphi \land \psi ))$
. -
(2)
$\mathcal {F}\vDash N\psi \to (\Box \varphi \leftrightarrow \neg N\varphi \land N(\varphi \land \psi ))$
.
Proof. Let
$\mathcal {M}=\langle W,S,R,V \rangle $
be a model and
$w\in W$
.
For (1), suppose that
$\mathcal {M},w\vDash N\psi $
, to show that
$\mathcal {M},w\vDash \boxed {\mathrm{c}}\varphi \leftrightarrow N(\varphi \land \psi )$
. By semantics, it is straightforward to see that
$\vDash N(\varphi \land \psi )\to \boxed {\mathrm{c}}\varphi $
. It remains only to show that
$\mathcal {M},w\vDash \boxed {\mathrm{c}}\varphi \to N(\varphi \land \psi )$
. For this, assume that
$\mathcal {M},w\vDash \boxed {\mathrm{c}}\varphi $
. Then
$S(w)\vDash \varphi $
. By supposition, we have
$S(w)\vDash \psi $
and
$R(w)\nvDash \psi $
. This entails that
$S(w)\vDash \varphi \land \psi $
and
$R(w)\nvDash \varphi \land \psi $
, and therefore
$\mathcal {M},w\vDash N(\varphi \land \psi )$
.
For (2), assume that
$\mathcal {M},w\vDash N\psi $
, to prove that
$\mathcal {M},w\vDash \Box \varphi \leftrightarrow \neg N\varphi \land N(\varphi \land \psi )$
. First, suppose that
$\mathcal {M},w\vDash \neg N\varphi $
and
$\mathcal {M},w\vDash N(\varphi \land \psi )$
. From the latter it follows that
$S(w)\vDash \varphi \land \psi $
, and then
$S(w)\vDash \varphi $
. This plus
$\mathcal {M},w\vDash \neg N\varphi $
implies that
$R(w)\vDash \varphi $
, and thus
$\mathcal {M},w\vDash \Box \varphi $
. Conversely, suppose that
$\mathcal {M},w\vDash \Box \varphi $
, then
$R(w)\vDash \varphi $
, thus
$\mathcal {M},w\vDash \neg N\varphi $
. Since
$S\subseteq R$
, it follows that
$S(w)\vDash \varphi $
. Then similarly to the proof of (1), we can show that
$\mathcal {M},w\vDash N(\varphi \land \psi )$
, as desired.
Remark 5. In [Reference Humberstone28, p. 229], Humberstone also proposes several variations of N, namely
$N'$
,
$N"$
,
$N"'$
. Among these variations,
$N"\varphi $
is defined as
$\Box _1\varphi \vee \neg \Box _2\varphi $
. Semantically, given a model
$\mathcal {M}=\langle W,R_1,R_2,V \rangle $
and
$w\in W$
,
$$\begin{align*}\begin{array}{lll} \mathcal{M},w\vDash N"\varphi & \Longleftrightarrow & R_1(w)\vDash\varphi\text{ or }R_2(w)\nvDash\varphi. \\ \end{array} \end{align*}$$
Thus
$\neg N"\varphi :=\Box _2\varphi \land \neg \Box _1\varphi $
. If we think as
$\Box _2$
and
$\Box _1$
as
$\boxed {\mathrm{c}}$
and
$\Box $
, respectively, then
$\neg N"$
amounts to N. Based on this observation, we can obtain two almost definability schemas in terms of
$N"$
, one for
$\Box _2$
and the other for
$\Box _1$
:
$$\begin{align*}\begin{array}{ll} \neg N"\psi\to (\Box_1\varphi\leftrightarrow (N"\varphi\land \neg N"(\varphi\land\psi)))& (\textbf{N}"\textbf{AD1}) \\ \neg N"\psi\to (\Box_2\varphi\leftrightarrow\neg N"(\varphi\land\psi)) & (\textbf{N}"\textbf{AD2}).\\ \end{array} \end{align*}$$
And we can show the following:
-
(1) Let
$\mathcal {F}=\langle W,R_1,R_2 \rangle $
such that
$R_2\subseteq R_1$
. Then
$$ \begin{align*}\mathcal{F}\vDash \neg N"\psi\to (\Box_1\varphi\leftrightarrow (N"\varphi\land \neg N"(\varphi\land\psi))).\end{align*} $$
-
(2)
$\vDash \neg N"\psi \to (\Box _2\varphi \leftrightarrow \neg N"(\varphi \land \psi ))$
.
Then we can also axiomatize
$N"$
over various frame classes via MBADS. We will illustrate this by axiomatizing the minimal logic of
$N"$
in §5.
3.2 Bacon’s proof system
First, we review Bacon’s proof system in [Reference Bacon3, p. 136] (also see [Reference Humberstone28, p. 228]), named TN,Footnote 7 which consists of the following axioms and inference rules:Footnote 8
$$\begin{align*}\begin{array}{ll} \text{PC} & \text{All instances of propositional tautologies} \\ \text{N1} & N\varphi\to\varphi \\ \text{N2} & N\varphi\land N\psi\to N(\varphi\land\psi)\\ \text{N3} & N((\varphi\to\psi)\to\psi)\to N((\psi\to\varphi)\to\varphi)\\ \text{N4} & \neg N(\varphi\to \psi)\land N\psi\to (N\chi\to N((\varphi\to\psi)\to\chi))\\ \text{MP} & \text{From }\varphi\text{ and }\varphi\to\psi\text{ infer }\psi \\ \text{N5} & \text{From }\varphi\text{ infer }\neg N\varphi\\ \text{N6} & \text{From }\varphi\to\psi\text{ infer }N(\chi\to\psi)\to (N\varphi\to N\psi).\\ \end{array} \end{align*}$$
As mentioned before, axiom N1 is disputable. In a footnote appended to N3 [Reference Bacon3, fn. 1, p. 136], Bacon says: “I suspect that N3 may be redundant.” As Humberstone [Reference Humberstone28, p. 228] noted, this axiom would be redundant if one has a ‘rule of congruentiality’ for N, denoted as T3 by Bacon and as (NCong) by Humberstone, namely
$\dfrac {\varphi \leftrightarrow \psi }{N\varphi \leftrightarrow N\psi }$
, which is derivable without use of N3, since then N3 can be simplified to
$N(\varphi \vee \psi )\to N(\psi \vee \varphi )$
, which follows easily from the rule of congruentiality. However, as Bacon shows, the derivation of T3 does make use of N3.
Bacon then shows that TN is sound and strongly complete with respect to the class of all frames with the requirement that
$S\subseteq R$
and S be reflexive (thus R be reflexive as well). The proof is via the Henkin-style canonical model method. However, it is not very clear what the canonical relations are. This was not done until Humberstone [Reference Humberstone28, p. 232], where purely physical necessity is also called ‘purely nomic necessity’, and
$\boxed {\mathrm{c}}$
and
$\Box $
are replaced with
$\Box _1$
and
$\Box _2$
, respectively. Based on Bacon’s proof, Humberstone [Reference Humberstone28, p. 232] explicitly defines the canonical relations
$S^c$
and
$R^c$
as follows, where
$x,y$
are maximal consistent sets:
-
•
$wS^cu$
iff for all
$\varphi $
, if
$N\varphi \in w$
, then
$\varphi \in u$
; -
•
$wR^cu$
iff for all
$\varphi ,\psi $
, if
$\neg N(\varphi \vee \psi )\land N\psi \in w$
, then
$\varphi \vee \psi \in u$
.
Nevertheless, it is still unclear how
$S^c$
and
$R^c$
come about. Moreover, it is difficult to obtain the S4 extension of TN, given that
$S^c$
is not transitive, which, in turn, is due to the fact that
$N\varphi \to NN\varphi $
is not valid over the class of S4-frames. Furthermore, to the best of our knowledge, the open question raised by Bacon, that is, what the S4- and S5-like extensions of TN are, has not been solved yet. In what follows, in addition to our new proof systems, we will also give different definitions for
$S^c$
and for
$R^c$
, which are inspired by the aforementioned two almost definability schemas (NAD1) and (NAD2). The new definitions can also handle the S4-extension of TN.
3.3 Our systems
3.3.1 Minimal system and soundness
Definition 6. The minimal system of
$\mathcal {L}(N)$
, denoted
$\mathbf {K^N}$
, consists of the following axioms and inference rules:
$$\begin{align*}\begin{array}{ll} \text{PC} & \text{All instances of propositional tautologies} \\ \text{A1} & N\varphi\land N\psi\to N(\varphi\land\psi) \\ \text{A2} & N(\varphi\land\psi)\to N\varphi\vee N\psi\\ \text{MP} & \text{From }\varphi\text{ and }\varphi\to\psi\text{ infer }\psi \\ \text{R1} & \text{From }\varphi\text{ infer }\neg N\varphi\\ \text{R2} & \text{From }\varphi\to\psi\text{ and }\psi\to\chi\text{ infer }(N\varphi\land N\chi)\to N\psi.\\ \end{array} \end{align*}$$
The above axioms and inference rules are obtained based on the need of showing that the truth lemma (Lemma 13) holds and that the canonical model is as desired. One may check that our
$\mathbf {K^N}$
is simpler than Bacon’s TN. Also, we do not have the debatable axiom N1. The rule R2 says that the operator N has an important property called ‘Convexity’ in [Reference Humberstone27, p. 548] and ‘Interpolation’ in [Reference Xiong and Agotnes44, prop. 27].
Notions of derivation and theorems are defined as usual. The following proposition is important in the proof later.
Proposition 7.
-
(1) If
$\vdash \varphi \to \chi $
, then
$\vdash N(\varphi \land \psi )\land N\chi \to N\varphi $
. -
(2) If
$\vdash \varphi \to \chi $
, then
$\vdash N(\varphi \land \psi )\land N\psi \to N(\chi \land \psi )$
. -
(3) If
$\vdash \varphi \to \chi $
, then
$\vdash \neg N\varphi \land N(\varphi \land \psi )\to N(\chi \land \psi )$
. -
(4) If
$\vdash \varphi \leftrightarrow \psi $
, then
$\vdash N\varphi \leftrightarrow N\psi $
.
Proof. (1) Suppose that
$\vdash \varphi \to \chi $
. By axiom PC,
$\vdash \varphi \land \psi \to \varphi $
. Then using rule R2, we infer that
$\vdash N(\varphi \land \psi )\land N\chi \to N\varphi $
.
(2) Suppose that
$\vdash \varphi \to \chi $
. Then
$\vdash \varphi \land \psi \to \chi \land \psi $
. By axiom PC,
$\vdash \chi \land \psi \to \psi $
. Now using rule R2, we derive that
$\vdash N(\varphi \land \psi )\land N\psi \to N(\chi \land \psi )$
.
(3) Assume that
$\vdash \varphi \to \chi $
. By (2),
$\vdash N(\varphi \land \psi )\land N\psi \to N(\chi \land \psi )$
. Then by axiom A2,
$\vdash N(\varphi \land \psi )\land \neg N\varphi \to N\psi $
. Therefore,
$\vdash \neg N\varphi \land N(\varphi \land \psi )\to N(\chi \land \psi )$
.
(4) Suppose that
$\vdash \varphi \leftrightarrow \psi $
. Then
$\vdash \varphi \to \psi $
and
$\vdash \psi \to \varphi $
. Then by R2,
$\vdash N\varphi \land N\varphi \to N\psi $
, that is,
$\vdash N\varphi \to N\psi $
. Similarly, we can show that
$\vdash N\psi \to N\varphi $
. Therefore,
$\vdash N\varphi \leftrightarrow N\psi $
.
Proposition 8.
$\mathbf {K^N}$
is sound with respect to the class of all frames.
Proof. We only show the validity of axioms A1 and A2 and the validity-preserving of rules R1 and R2, since others are straightforward. Let
$\mathcal {M}=\langle W,S,R,V \rangle $
be a model and
$w\in W$
.
For A1: suppose that
$\mathcal {M},w\vDash N\varphi $
and
$\mathcal {M},w\vDash N\psi $
. Then
$S(w)\vDash \varphi $
and
$R(w)\nvDash \varphi $
, and
$S(w)\vDash \psi $
. This implies that
$S(w)\vDash \varphi \land \psi $
and
$R(w)\nvDash \varphi \land \psi $
. Therefore,
$\mathcal {M},w\vDash N(\varphi \land \psi )$
.
For A2: assume that
$\mathcal {M},w\vDash N(\varphi \land \psi )$
. Then
$S(w)\vDash \varphi \land \psi $
and
$R(w)\nvDash \varphi \land \psi $
. This entails that
$S(w)\vDash \varphi $
and
$S(w)\vDash \psi $
, and either
$R(w)\nvDash \varphi $
or
$R(w)\nvDash \psi $
. Therefore,
$\mathcal {M},w\vDash N\varphi \vee N\psi $
.
For R1: suppose that
$\vDash \varphi $
, then for all models
$\mathcal {M}=\langle W,S,R,V \rangle $
and
$w\in W$
, we have
$R(w)\vDash \varphi $
, which implies that
$\mathcal {M},w\vDash \neg N\varphi $
. Thus
$\vDash \neg N\varphi $
.
For R2: assume that
$\vDash \varphi \to \psi $
and
$\vDash \psi \to \chi $
. Suppose that
$\mathcal {M},w\vDash N\varphi \land N\chi $
, to show that
$\mathcal {M},w\vDash N\psi $
. From the supposition, it follows that
$S(w)\vDash \varphi $
and
$R(w)\nvDash \chi $
. Then by assumption, we get
$S(w)\vDash \psi $
and
$R(w)\nvDash \psi $
. Thus
$\mathcal {M},w\vDash N\psi $
, as desired.
3.3.2 Completeness
We proceed with the completeness of
$\mathbf {K^N}$
. This is shown via a construction of the canonical model, in which the crucial part is the definition of the canonical relations.
Definition 9. The canonical model for
$\mathbf {K^N}$
is a tuple
$\mathcal {M}^c=\langle W^c,S^c,R^c,V^c \rangle $
, where
-
•
$W^c=\{w\mid w\text { is a maximal consistent set for }\mathbf {K^N}\}$
; -
• if
$N\psi \in w$
for no
$\psi $
, then
$wS^cu$
iff
$w=u$
, and
$wR^cu$
iff
$w=u$
; -
• if
$N\psi \in w$
for some
$\psi $
, then
$wS^cu$
iff for all
$\varphi $
, if
$N(\varphi \land \psi )\in w$
, then
$\varphi \in u$
, and
$wR^cu$
iff for all
$\varphi $
, if
$\neg N\varphi \land N(\varphi \land \psi )\in w$
, then
$\varphi \in u$
; -
•
$V^c(p)=\{w\in W^c\mid p\in w\}$
.
It is required that the
$\psi $
in
$N(\varphi \land \psi )\in w$
and
$\neg N\varphi \land N(\varphi \land \psi )\in w$
be the same as that in
$N\psi \in w$
. Note that the choice of
$\psi $
in the above second case of the canonical relations is inessential to
$S^c$
and
$R^c$
(see Remark 10 below). It is also noteworthy that
$S^c$
and
$R^c$
are inspired by almost definability schemas (NAD1) and (
$\textbf {NAD2}$
), respectively, based on the analysis of §2. Recall that in the construction of the canonical model for the minimal logic of
$\mathcal {L}(\Box ,\boxed {\mathrm{c}})$
, the canonical relations
$S^c$
and
$R^c$
are defined as, respectively,
$wS^cu$
iff for all
$\varphi $
, if
$\boxed {\mathrm{c}}\varphi \in w$
then
$\varphi \in u$
, and
$wR^cu$
iff for all
$\varphi $
, if
$\Box \varphi \in w$
then
$\varphi \in u$
.Footnote
9
Now according to (NAD1), given a precondition that
$N\psi \in w$
for some
$\psi $
,
$\boxed {\mathrm{c}}\varphi \in w$
can be replaced with
$N(\varphi \land \psi )\in w$
, and according to (NAD2),
$\Box \varphi \in w$
can be replaced with
$\neg N\varphi \land N(\varphi \land \psi )\in w$
; otherwise, we let w access and only access itself.
Remark 10. We noted that the choice of
$\psi $
in the above second case of the canonical relations is inessential to
$S^c$
and
$R^c$
. This means that, if
$N\psi _1\in w$
and
$N\psi _2\in w$
, then it does not matter whether we choose
$\psi =\psi _1$
or
$\psi =\psi _2$
. This is because
$N\psi \land N(\varphi \land \chi )\to N(\varphi \land \psi )$
is derivable in
$\mathbf {K^N}$
. To see the derivability, note that by axiom A1,
$\vdash N\psi \land N(\varphi \land \chi )\to N(\varphi \land \psi \land \chi )$
. Since
$\vdash \varphi \land \psi \land \chi \to \varphi \land \psi $
and
$\vdash \varphi \land \psi \to \psi $
, by rule R2,
$\vdash N(\varphi \land \psi \land \chi )\land N\psi \to N(\varphi \land \psi )$
. Therefore,
$\vdash N\psi \land N(\varphi \land \chi )\to N(\varphi \land \psi )$
. Given the precondition that
$N\psi \in w$
for some
$\psi $
, the above second case for
$wS^cu$
is given by the following (denoted (1)):
$$ \begin{align*} \text{for all } \varphi, \text{ if } N(\varphi\land\psi)\in w, \text{ then } \varphi\in u. \end{align*} $$
Now assume that for some
$\psi _1,\psi _2$
we have
$N\psi _1,N\psi _2\in w$
, and (1) holds for the case
$\psi =\psi _1$
. Using the derivable formula in question, we can show that (1) also holds for the case
$\psi =\psi _2$
. The converse is similarly shown. This shows that
$S^c$
does not depend on the instance of
$\psi $
.
To see that
$R^c$
does not depend on the instance of
$\psi $
either, note that from the derivable formula in question, we can derive that
$\vdash \neg N\varphi \land N\psi \land N(\varphi \land \chi )\to \neg N\varphi \land N(\varphi \land \psi )$
. Then the proof goes as in the case of
$S^c$
.
Propositions 11 and 12 list the logical properties of the functions
$\lambda _1$
and
$\lambda _2$
, respectively. They are important in the proof of Lemma 13 below.
Proposition 11. Let
$w\in W^c$
such that
$N\psi \in w$
. Define
$\lambda _1(w)=\{\chi \mid N(\chi \land \psi )\in w\}$
. Then
-
(1)
$\lambda _1(w)\neq \emptyset $
. -
(2) If
$\varphi ,\chi \in \lambda _1(w)$
, then
$\varphi \land \chi \in \lambda _1(w)$
. -
(3) If
$\varphi \in \lambda _1(w)$
and
$\vdash \varphi \to \chi $
, then
$\chi \in \lambda _1(w)$
.
Proof. Suppose that
$N\psi \in w$
, where
$w\in W^c$
.
-
(1) By supposition and Proposition 7(4), we have
$N(\top \land \psi )\in w$
, thus
$\top \in \lambda _1(w)$
. Hence
$\lambda _1(w)\neq \emptyset $
. -
(2) Assume that
$\varphi \in \lambda _1(w)$
and
$\chi \in \lambda _1(w)$
, to show that
$\varphi \land \chi \in \lambda _1(w)$
. By assumption,
$N(\varphi \land \psi )\in w$
and
$N(\chi \land \psi )\in w$
. Then using axiom A1 and Proposition 7(4), we infer that
$N(\varphi \land \chi \land \psi )\in w$
. Therefore,
$\varphi \land \chi \in \lambda _1(w)$
. -
(3) Suppose that
$\varphi \in \lambda _1(w)$
and
$\vdash \varphi \to \chi $
. From
$\varphi \in \lambda _1(w)$
, it follows that
$N(\varphi \land \psi )\in w$
. Then using supposition and Proposition 7(2), we derive that
$N(\chi \land \psi )\in w$
, and therefore
$\chi \in \lambda _1(w)$
.
Proposition 12. Let
$w\in W^c$
such that
$N\varphi \in w$
. Define
$\lambda _2(w)=\{\chi \mid \neg N\chi \land N(\chi \land \varphi )\in w\}$
. Then
-
(1)
$\lambda _2(w)\neq \emptyset $
. -
(2) If
$\psi ,\chi \in \lambda _2(w)$
, then
$\psi \land \chi \in \lambda _2(w)$
. -
(3) If
$\psi \in \lambda _2(w)$
and
$\vdash \psi \to \chi $
, then
$\chi \in \lambda _2(w)$
.
Proof. Assume that
$N\varphi \in w$
, where
$w\in W^c$
.
-
(1) We claim that
$\top \in \lambda _2(w)$
. Since
$\vdash \top $
, by rule R1,
$\vdash \neg N\top $
, thus
$\neg N\top \in w$
; moreover, from the assumption, it follows that
$N(\top \land \varphi )\in w$
. Therefore,
$\neg N\top \land N(\top \land \varphi )\in w$
. -
(2) Suppose that
$\psi \in \lambda _2(w)$
and
$\chi \in \lambda _2(w)$
. Then
$\neg N\psi \land N(\psi \land \varphi )\in w$
and
$\neg N\chi \land N(\chi \land \varphi )\in w$
. From
$\neg N\psi \in w$
and
$\neg N\chi \in w$
and axiom A2, it follows that
$\neg N(\psi \land \chi )\in w$
; from
$N(\psi \land \varphi )\in w$
and
$N(\chi \land \varphi )\in w$
and axiom A1, it follows that
$N(\psi \land \chi \land \varphi )\in w$
. Therefore,
$\neg N(\psi \land \chi )\land N(\psi \land \chi \land \varphi )\in w$
, thus
$\psi \land \chi \in \lambda _2(w)$
. -
(3) Suppose that
$\psi \in \lambda _2(w)$
and
$\vdash \psi \to \chi $
. Then
$\neg N\psi \land N(\psi \land \varphi )\in w$
. By Proposition 7(1), we infer that
$\neg N\chi \in w$
; by Proposition 7(3), we derive that
$N(\chi \land \varphi )\in w$
, and therefore
$\chi \in \lambda _2(w)$
.
Lemma 13. For all
$\varphi \in \mathcal {L}(N)$
, for all
$w\in W^c$
, we have
$$ \begin{align*}\mathcal{M}^c,w\vDash\varphi\Longleftrightarrow \varphi\in w.\end{align*} $$
Proof. By induction on
$\varphi $
. The nontrivial case is
$N\varphi $
.
Suppose that
$N\varphi \in w$
, to show that
$\mathcal {M}^c,w\vDash N\varphi $
, that is,
$S^c(w)\vDash \varphi $
and
$R^c(w)\nvDash \varphi $
. Let
$u\in W^c$
such that
$wS^cu$
. By supposition and Proposition 7(4),
$N(\varphi \land \varphi )\in w$
. Then by definition of
$S^c$
, we obtain that
$\varphi \in u$
. By induction hypothesis,
$\mathcal {M}^c,u\vDash \varphi $
. This establishes that
$S^c(w)\vDash \varphi $
. We need to show that there exists
$v\in W^c$
such that
$wR^cv$
and
$\mathcal {M}^c,v\nvDash \varphi $
. Define
$\lambda _2(w)=\{\chi \mid \neg N\chi \land N(\chi \land \varphi )\in w\}$
. By induction hypothesis and Lindenbaum’s Lemma, it remains only to show (
$\star $
):
$\lambda _2(w)\cup \{\neg \varphi \}$
is consistent.
By Proposition 12(1),
$\lambda _2(w)\neq \emptyset $
. If
$(\star )$
fails, then there exist
$\chi _1,\ldots ,\chi _n\in \lambda _2(w)$
such that
$\vdash \chi _1\land \cdots \land \chi _n\to \varphi $
. By items (2) and (3) of Proposition 12, we can obtain that
$\varphi \in \lambda _2(w)$
, thus
$\neg N\varphi \in w$
, which is contrary to the supposition and consistency of w.
Conversely, assume that
$N\varphi \notin w$
, to prove that
$\mathcal {M}^c,w\nvDash N\varphi $
, that is,
$S^c(w)\nvDash \varphi $
or
$R^c(w)\vDash \varphi $
. For this, we suppose that
$R^c(w)\nvDash \varphi $
, to demonstrate that
$S^c(w)\nvDash \varphi $
. By induction hypothesis, it suffices to find a
$u\in W^c$
such that
$wS^cu$
and
$\neg \varphi \in u$
. By supposition, there exists
$v\in W^c$
such that
$wR^cv$
and
$\varphi \notin v$
. We consider two cases.
-
•
$N\psi \in w$
for no
$\psi $
. Then according to the definition of
$R^c$
, by
$wR^cv$
we have
$w=v$
. Now using the definition of
$S^c$
,
$wS^cv$
. As
$\varphi \notin v$
,
$\neg \varphi \in v$
. -
•
$N\psi \in w$
for some
$\psi $
. In this case, from
$wR^cv$
and
$\varphi \notin v$
, it follows that
$\neg N\varphi \land N(\varphi \land \psi )\notin w$
. By assumption,
$\neg N\varphi \in w$
. This gives us that
$N(\varphi \land \psi )\notin w$
. Define
$\lambda _1(w)=\{\chi \mid N(\chi \land \psi )\in w\}$
. In the sequel, we show that
$\lambda _1(w)\cup \{\neg \varphi \}$
is consistent. The item (1) of Proposition 11 provides the nonemptiness of
$\lambda _1(w)$
. If
$\lambda _1(w)\cup \{\neg \varphi \}$
is not consistent, then there are
$\chi _1,\ldots ,\chi _n\in \lambda _1(w)$
such that
$\vdash \chi _1\land \cdots \land \chi _n\to \varphi $
. By items (2) and (3) of Proposition 11, we can get that
$\varphi \in \lambda _1(w)$
, that is,
$N(\varphi \land \psi )\in w$
: a contradiction. We have now shown that
$\lambda _1(w)\cup \{\neg \varphi \}$
is consistent. By Lindenbaum’s Lemma, there is a
$u\in W^c$
such that
$wS^cu$
and
$\neg \varphi \in u$
, as desired.
By Proposition 8 and Lemma 13, we have the following result.
Theorem 14.
$\mathbf {K^N}$
is sound and strongly complete with respect to the class of all frames.
Theorem 15.
$\mathbf {K^N}$
is sound and strongly complete with respect to the class of all frames
$\langle W,S,R \rangle $
where
$S\subseteq R$
.
Proof. By Theorem 14, it remains only to show that
$S^c\subseteq R^c$
. This is straightforward by definitions of
$S^c$
and
$R^c$
.
We can show that all axioms and rules in TN (except for N1, which needs the reflexivity of S) are derivable in our
$\mathbf { K^N}$
, from a pure proof-theoretic perspective. According to the previous analysis, axiom N3 is immediate from Proposition 7(4). It remains only to consider axiom N4 and rule N6.
Proposition 16. (N4) is provable in the proof system
$\mathbf {K^N}$
. That is,
$\vdash (\neg N(\varphi \to \psi )\land N\psi )\to (N\chi \to N((\varphi \to \psi )\to \chi ))$
.
Proof. We have the following proof sequence in
$\mathbf {K^N}$
:
$$\begin{align*}\begin{array}{@{}lll} (1) & (\psi\land\chi)\to ((\varphi\to\psi)\to\chi)\land(\varphi\to\psi) & \text{PC} \\ (2) & ((\varphi\to\psi)\to\chi)\land(\varphi\to\psi)\to\chi & \text{PC} \\ (3) & N(\psi\land\chi)\land N\chi\to N(((\varphi\to\psi)\to\chi)\land(\varphi\to\psi)) & (1),(2),\text{R2}\\ (4) & N\psi\land N\chi\to N(\psi\land\chi)\land N\chi & \text{A1}\\ (5) & N(((\varphi\to\psi)\to\chi)\land(\varphi\to\psi))\to N((\varphi\to\psi)\to\chi)\vee N(\varphi\to\psi) & \text{A2}\\ (6) & N\psi\land N\chi\to N((\varphi\to\psi)\to\chi)\vee N(\varphi\to\psi) & (3)\text{--}(5)\\ (7) & (\neg N(\varphi\to\psi)\land N\psi)\to (N\chi\to N((\varphi\to\psi)\to\chi)) & (6).\\ \end{array} \end{align*}$$
Proposition 17. (N6) is derivable in
$\mathbf {K^N}$
. That is, if
$\vdash \varphi \to \psi $
, then
$\vdash N(\chi \to \psi )\to (N\varphi \to N\psi )$
.
Proof. Suppose that
$\vdash \varphi \to \psi $
. By axiom PC,
$\vdash \psi \to (\chi \to \psi )$
. Now using rule R2, we get
$\vdash N\varphi \land N(\chi \to \psi )\to N\psi $
, and thus
$\vdash N(\chi \to \psi )\to (N\varphi \to N\psi )$
.
3.4 Extensions
3.4.1 Serial logic
Define
$\mathbf {D^N}$
to be the extension of
$\mathbf {K^N}$
with the axiom
$\neg N\bot $
(denoted ND). We recall that the relation S on W is serial, if for all
$w\in W$
, there is a
$u\in W$
such that
$wSu$
.
Theorem 18.
$\mathbf {D^N}$
is sound and strongly complete with respect to the class of all frames
$\langle W,S,R \rangle $
where S is serial.
Proof. For soundness, by Proposition 8, it suffices to show the validity of ND over serial frames. Suppose not, then there exists a serial model
$\mathcal {M}=\langle W,S,R,V \rangle $
and
$w\in W$
such that
$\mathcal {M},w\vDash N\bot $
. Then
$S(w)\vDash \bot $
. Since S is serial, there exists
$u\in W$
such that
$wSu$
and
$\mathcal {M},y\vDash \bot $
: a contradiction.
For completeness, define
$\mathcal {M}^c$
w.r.t.
$\mathbf {D^N}$
as in Definition 9. By Theorem 14, it remains only to show that
$S^c$
is serial.
For this, let
$w\in W^c$
. If
$N\psi \in w$
for no
$\psi $
, then as
$w=w$
, we have
$wS^cw$
. If
$N\psi \in w$
for some
$\psi $
, then define
$\lambda _1(w)$
as in Proposition 11. It suffices to show that
$\lambda _1(w)$
is consistent. If not, then there are
$\chi _1,\ldots ,\chi _n\in \lambda _1(w)$
such that
$\vdash \chi _1\land \cdots \land \chi _n\to \bot $
. Then by items (2) and (3) of Proposition 11, we can get
$\bot \in \lambda _1(w)$
, that is,
$N(\bot \land \psi )\in w$
. By Proposition 7(4),
$N\bot \in w$
. However, by axiom ND,
$\neg N\bot \in w$
, which is contrary to the consistency of w.
Thus
$\lambda _1(x)$
is consistent. By Lindenbaum’s Lemma, there exists
$u\in W^c$
such that
$\lambda _1(w)\subseteq u$
. By definition of
$S^c$
,
$wS^cu$
. This establishes that
$S^c$
is serial.
As
$S^c\subseteq R^c$
(Theorem 15), we have more characterization results.
Theorem 19.
$\mathbf {D^N}$
is sound and strongly complete with respect to the class of all frames
$\langle W,S,R \rangle $
where S is serial and
$S\subseteq R$
(thus R is serial).
Theorem 20.
$\mathbf {D^N}$
is sound and strongly complete with respect to the class of serial frames.
3.4.2 Serial–reflexive logic
Define
$\mathbf {DT^N}$
to be the extension of
$\mathbf {K^N}$
with the axiom ND and the axiom
$\neg N\varphi \land N(\varphi \land \psi )\to \varphi $
(denoted wNT).
Theorem 21.
$\mathbf {DT^N}$
is sound and strongly complete with respect to the class of all frames
$\langle W,S,R \rangle $
where S is serial and R is reflexive.
Proof. For soundness, by Theorem 18, it suffices to show the validity of axiom wNT. Let
$\mathcal {M}=\langle W,S,R,V \rangle $
be a model such that S is serial and R is reflexive and
$w\in W$
. Suppose that
$\mathcal {M},w\vDash \neg N\varphi \land N(\varphi \land \psi )$
, then
$S(w)\nvDash \varphi $
or
$R(w)\vDash \varphi $
, and
$S(w)\vDash \varphi \land \psi $
. Thus
$R(w)\vDash \varphi $
. Since R is reflexive,
$w\in R(w)$
, and hence
$\mathcal {M},w\vDash \varphi $
.
For completeness, define
$\mathcal {M}^c$
w.r.t.
$\mathbf {DT^N}$
as in Definition 9. By Theorem 18, it remains only to prove that
$R^c$
is reflexive. Let
$w\in W^c$
. If
$N\psi \in w$
for no
$\psi $
, then as
$w=w$
,
$wR^cw$
; otherwise, for all
$\varphi $
, if
$\neg N\varphi \land N(\varphi \land \psi )\in w$
, then by axiom wNT, we infer that
$\varphi \in w$
, which implies that
$wR^cw$
again.
Again, since
$S^c\subseteq R^c$
(Theorem 15), we have the following.
Theorem 22.
$\mathbf {DT^N}$
is sound and strongly complete with respect to the class of all frames
$\langle W,S,R \rangle $
where S is serial and R is reflexive and
$S\subseteq R$
.
3.4.3 Reflexive logic
Define
$\mathbf {T^N}$
to be the extension of
$\mathbf {K^N}$
with the axiom
$N(\varphi \land \psi )\to \varphi $
(denoted NT).
Theorem 23.
$\mathbf {T^N}$
is sound and strongly complete with respect to the class of all frames
$\langle W,S,R \rangle $
where S is reflexive.
Proof. For soundness, by Proposition 8, it remains only to show that axiom NT is valid over reflexive frames. Let
$\mathcal {M}=\langle W,S,R,V \rangle $
be a reflexive model and
$w\in W$
. Suppose that
$\mathcal {M},w\vDash N(\varphi \land \psi )$
, then
$S(w)\vDash \varphi \land \psi $
. Since S is reflexive,
$wSw$
. Thus
$\mathcal {M},w\vDash \varphi \land \psi $
, and hence
$\mathcal {M},w\vDash \varphi $
.
For completeness, define
$\mathcal {M}^c$
w.r.t.
$\mathbf {T^N}$
as in Definition 9. By Theorem 14, it suffices to show that
$S^c$
is reflexive.
For this, let
$w\in W^c$
. If
$N\psi \in w$
for no
$\psi $
, then as
$w=w$
, we have
$wS^cw$
. If
$N\psi \in w$
for some
$\psi $
, then for all
$\varphi $
, if
$N(\varphi \land \psi )\in w$
, by axiom NT,
$\varphi \in w$
. Thus again
$wS^cw$
. This completes the proof that
$S^c$
is reflexive, as desired.
Again, as
$S^c\subseteq R^c$
(Theorem 15), we have more characterization results.
Theorem 24.
$\mathbf {T^N}$
is sound and strongly complete with respect to the class of all frames
$\langle W,S,R \rangle $
where S is reflexive and
$S\subseteq R$
(thus R is reflexive).
Theorem 25.
$\mathbf {T^N}$
is sound and strongly complete with respect to the class of reflexive frames.
We close this part with the following result, which will be used in §3.5.
Proposition 26.
$N\psi \to (\varphi \leftrightarrow N(\varphi \land \psi ))$
is not derivable from
$\mathbf {T^N}$
.
Proof. We show that
$\varphi \land N\psi \to N(\varphi \land \psi )$
is not derivable from
$\mathbf {T^N}$
. Consider the following reflexive model
$\mathcal {M}=\langle W,S,R,V \rangle $
, where for sake of simplicity we skip the reflexive arrows (the valuation of p at u is inessential):
Since
$S(w)=\{w,v\}$
and q is true at both w and v, we have
$S(w)\vDash q$
; as
$wRu$
and
$\mathcal {M},u\nvDash q$
, we infer that
$R(w)\nvDash q$
. This implies that
$\mathcal {M},w\vDash Nq$
, and thus
$\mathcal {M},w\vDash p\land Nq$
. However, since
$wSv$
and
$\mathcal {M},v\nvDash p\land q$
, we derive that
$S(w)\nvDash p\land q$
, and thus
$\mathcal {M},w\nvDash N(p\land q)$
. Therefore,
$p\land Nq\to N(p\land q)$
is not valid over reflexive frames. By the soundness of
$\mathbf {T^N}$
w.r.t. the class of reflexive frames (Theorem 25),
$p\land Nq\to N(p\land q)$
is not derivable in
$\mathbf {T^N}$
, and hence
$\varphi \land N\psi \to N(\varphi \land \psi )$
is not derivable in
$\mathbf {T^N}$
.
3.4.4 Transitive logic
Define
$\mathbf {K4^N}$
to be the extension of
$\mathbf {K^N}$
with the following axioms:Footnote
10
$$\begin{align*}\begin{array}{ll} \text{A4-1} & N\psi\land N(\varphi\land \psi)\to N((N\psi'\to N(\varphi\land\psi'))\land\psi) \\ \text{A4-2} & N\psi\land\neg N\varphi\land N(\varphi\land\psi)\to \neg N(N\psi'\to\neg N\varphi\land N(\varphi\land\psi'))\land\\ & ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\land N((N\psi'\to \neg N\varphi\land N(\varphi\land\psi'))\land\psi).\\ \end{array} \end{align*}$$
Although the two axioms are complicated, there is an explanation for how they get here. They are obtained from the transitive axioms for
$\boxed {\mathrm{c}}$
and
$\Box $
, via a translation induced by almost definability schemas (NAD1) and (NAD2), respectively:
$$\begin{align*}\begin{array}{lll} & N\psi\to (\boxed{\mathrm{c}}\varphi\to \boxed{\mathrm{c}}(N\psi'\to\boxed{\mathrm{c}}\varphi)) & (1) \\\Longleftrightarrow & N\psi\to (\boxed{\mathrm{c}}\varphi\to \boxed{\mathrm{c}}(N\psi'\to N(\varphi\land\psi'))) & (2)\\\Longleftrightarrow & N\psi\to (N(\varphi\land\psi)\to N((N\psi'\to N(\varphi\land\psi'))\land \psi)) & (3)\\\Longleftrightarrow & N\psi\land N(\varphi\land\psi) \to N((N\psi'\to N(\varphi\land\psi'))\land\psi) & (4).\\\end{array}\end{align*}$$
Here we write (1) rather than
$\boxed {\mathrm{c}}\varphi \to \boxed {\mathrm{c}}~\boxed {\mathrm{c}}\varphi $
, since according to (NAD1),
$\boxed {\mathrm{c}}$
is definable with N under the condition
$N\psi $
for some
$\psi $
. The above transitions from (1) to (2) and then to (3) follow from Proposition 4(1). Then using simple propositional reasoning, we obtain the desired axiom (4), namely A4-1.
$$\begin{align*}\begin{array}{lll} & N\psi\to [\Box\varphi\to \Box(N\psi'\to \Box\varphi)] & (1') \\ \Longleftrightarrow & N\psi\to [\Box\varphi\to \Box(N\psi'\to \neg N\varphi\land N(\varphi\land\psi'))] & (2')\\ \Longleftrightarrow & N\psi\to [\neg N\varphi\land N(\varphi\land\psi)\to \neg N(N\psi'\to \neg N\varphi\land N(\varphi\land\psi'))\land\\ &~~~~~~~N((N\psi'\to \neg N\varphi\land N(\varphi\land\psi'))\land\psi)] & (3')\\ \Longleftrightarrow & N\psi\land\neg N\varphi\land N(\varphi\land \psi)\to \neg N(N\psi'\to \neg N\varphi\land N(\varphi\land\psi'))\land \\ &~~~~~~~N((N\psi'\to\neg N\varphi\land N(\varphi\land\psi'))\land \psi) & (4').\\ \end{array} \end{align*}$$
Similarly, here we write
$(1')$
rather than
$\Box \varphi \to \Box \Box \varphi $
, because according to (NAD2),
$\Box $
is definable with N given
$N\psi $
for some
$\psi $
. The above transitions from
$(1')$
to
$(2')$
and then to
$(3')$
are due to Proposition 4(2). Then using simple propositional reasoning, we get the desired axiom
$(4')$
, viz. A4-2.
Proposition 27.
$\mathbf {K4^N}$
is sound with respect to the class of transitive frames
$\langle W,S,R \rangle $
where
$S\subseteq R$
.
Proof. By Proposition 8, it remains only to show the validity of A4-1 and A4-2 over transitive frames
$\langle W,S,R \rangle $
where
$S\subseteq R$
. Let
$\mathcal {M}=\langle W,S,R,V \rangle $
be a model based on such a frame, and
$w\in W$
.
For A4-1: suppose that
$\mathcal {M},w\vDash N\psi $
and
$\mathcal {M},w\vDash N(\varphi \land \psi )$
, to show that
$\mathcal {M},w\vDash N((N\psi '\to N(\varphi \land \psi '))\land \psi )$
. Assume not, then by
$\mathcal {M},w\vDash N\psi $
, we infer that
$R(w)\nvDash \psi $
, thus
$R(w)\nvDash (N\psi '\to N(\varphi \land \psi '))\land \psi $
. Then by assumption,
$S(w)\nvDash (N\psi '\to N(\varphi \land \psi '))\land \psi $
. Moreover,
$S(w)\vDash \psi $
. This implies that
$S(w)\nvDash N\psi '\to N(\varphi \land \psi ')$
. Hence there exists
$u\in W$
such that
$wSu$
and
$\mathcal {M},u\nvDash N\psi '\to N(\varphi \land \psi ')$
, namely
$\mathcal {M},u\vDash N\psi '$
and
$\mathcal {M},u\nvDash N(\varphi \land \psi ')$
. From
$\mathcal {M},u\vDash N\psi '$
it follows that
$R(u)\nvDash \psi '$
, and then
$R(u)\nvDash \varphi \land \psi '$
. Then using
$\mathcal {M},u\nvDash N(\varphi \land \psi ')$
, we derive that
$S(u)\nvDash \varphi \land \psi '$
. However, we have also
$S(u)\vDash \varphi \land \psi '$
: firstly, as
$wSu$
and S is transitive,
$S(u)\subseteq S(w)$
. By
$\mathcal {M},w\vDash N(\varphi \land \psi )$
, we have
$S(w)\vDash \varphi \land \psi $
, thus
$S(w)\vDash \varphi $
, and hence
$S(u)\vDash \varphi $
. Secondly, by
$\mathcal {M},u\vDash N\psi '$
, we get
$S(u)\vDash \psi '$
. Thus
$S(u)\vDash \varphi \land \psi '$
. So far we arrive at a contradiction. This establishes that
$\mathcal {M},w\vDash N((N\psi '\to N(\varphi \land \psi '))\land \psi )$
.
For A4-2: assume that
$\mathcal {M},w\vDash N\psi \land \neg N\varphi \land N(\varphi \land \psi )$
, to show that
$\mathcal {M},w\vDash \neg N(N\psi '\to \neg N\varphi \land N(\varphi \land \psi '))$
and
$\mathcal {M},w\vDash N((N\psi '\to \neg N\varphi \land N(\varphi \land \psi '))\land \psi )$
. By
$\mathcal {M},w\vDash \neg N\varphi $
, we infer that either
$S(x)\nvDash \varphi $
or
$R(w)\vDash \varphi $
. By
$\mathcal {M},w\vDash N(\varphi \land \psi )$
, we derive that
$S(w)\vDash \varphi \land \psi $
, thus
$S(w)\vDash \varphi $
. This entails that
$R(w)\vDash \varphi $
.
First, we show that
$\mathcal {M},w\vDash \neg N(N\psi '\to \neg N\varphi \land N(\varphi \land \psi '))$
. Suppose not, that is,
$\mathcal {M},w\vDash N(N\psi '\to \neg N\varphi \land N(\varphi \land \psi '))$
, then there exists a u such that
$wRu$
and
$\mathcal {M},u\nvDash N\psi '\to \neg N\varphi \land N(\varphi \land \psi ')$
, thus
$\mathcal {M},u\vDash N\psi '$
and
$\mathcal {M},u\nvDash \neg N\varphi \land N(\varphi \land \psi ')$
, and hence
$\mathcal {M},u\vDash N\varphi \vee \neg N(\varphi \land \psi ')$
. We consider two cases.
-
•
$\mathcal {M},u\vDash N\varphi $
. Then there exists v such that
$uRv$
and
$\mathcal {M},v\nvDash \varphi $
. By
$wRu$
and
$uRv$
and the transitivity of R, we obtain that
$wRv$
. Now from
$R(w)\vDash \varphi $
, it follows that
$\mathcal {M},v\vDash \varphi $
. A contradiction. -
•
$\mathcal {M},u\vDash \neg N(\varphi \land \psi ')$
. Then either
$S(u)\nvDash \varphi \land \psi '$
or
$R(u)\vDash \varphi \land \psi '$
. If the former is the case, then there exists v such that
$uSv$
and
$\mathcal {M},v\nvDash \varphi \land \psi '$
. Since
$\mathcal {M},u\vDash N\psi '$
, it follows that
$S(u)\vDash \psi '$
, thus
$\mathcal {M},v\vDash \psi '$
, and hence
$\mathcal {M},v\nvDash \varphi $
. Since
$S\subseteq R$
, we have
$uRv$
, and then
$wRv$
due to
$wRu$
and the transitivity of R. Now using
$R(w)\vDash \varphi $
again, we derive that
$\mathcal {M},v\vDash \varphi $
. A contradiction again.
This completes the proof of
$\mathcal {M},w\vDash \neg N(N\psi '\to \neg N\varphi \land N(\varphi \land \psi '))$
.
Second, we prove that
$\mathcal {M},w\vDash N((N\psi '\to \neg N\varphi \land N(\varphi \land \psi '))\land \psi )$
. Suppose not, then either
$S(w)\nvDash (N\psi '\to \neg N\varphi \land N(\varphi \land \psi '))\land \psi $
or
$R(w)\vDash (N\psi '\to \neg N\varphi \land N(\varphi \land \psi '))\land \psi $
. By
$\mathcal {M},w\vDash N\psi $
, it follows that
$S(w)\vDash \psi $
and
$R(w)\nvDash \psi $
. This would give us that
$S(w)\nvDash N\psi '\to \neg N\varphi \land N(\varphi \land \psi ')$
. Because
$S\subseteq R$
, this implies that
$R(w)\nvDash N\psi '\to \neg N\varphi \land N(\varphi \land \psi ')$
. Then similarly to the above proof, we can arrive a contradiction. This finishes the proof of
$\mathcal {M},w\vDash N((N\psi '\to \neg N\varphi \land N(\varphi \land \psi '))\land \psi )$
, as desired.
We proceed with the completeness proof of
$\mathbf {K4^N}$
. For this, define
$\mathcal {M}^c$
w.r.t.
$\mathbf {K4^N}$
as in Definition 9. By Theorem 15, it remains only to show that both
$S^c$
and
$R^c$
are transitive.
Lemma 28.
$S^c$
is transitive.
Proof. Let
$w,u,v\in W^c$
. Suppose that
$wS^cu$
and
$uS^cv$
, to show that
$wS^cv$
. According to the definition of
$S^c$
, we consider the following cases:
-
•
$N\psi \in w$
for no
$\psi $
. In this case, by
$wS^cu$
we have
$w=u$
. Then as
$uS^cv$
, we derive that
$wS^cv$
. -
•
$N\psi \in u$
for no
$\psi $
. In this case, from
$uS^cv$
we infer that
$u=v$
. Then since
$wS^cu$
, it follows that
$wS^cv$
. -
•
$N\psi \in w$
for some
$\psi $
, and
$N\psi '\in u$
for some
$\psi '$
. In this case, assume for any
$\varphi $
that
$N(\varphi \land \psi )\in w$
, we hope to derive that
$\varphi \in v$
. By
$N\psi \in w$
,
$N(\varphi \land \psi )\in w$
and axiom A4-1, we obtain that
$N((N\psi '\to N(\varphi \land \psi '))\land \psi )\in w$
. Then using
$wS^cu$
we infer that
$N\psi '\to N(\varphi \land \psi ')\in u$
, thus
$N(\varphi \land \psi ')\in u$
. Thanks to
$N\psi '\in u$
and
$uS^cv$
, we conclude that
$\varphi \in v$
, as desired.
Lemma 29.
$R^c$
is transitive.
Proof. Let
$w,u,v\in W^c$
. Assume that
$wR^cu$
and
$uR^cv$
, to prove that
$wR^cv$
. Based on the definition of
$R^c$
, we consider the following cases:
-
•
$N\psi \in w$
for no
$\psi $
. By
$wR^cu$
we get
$w=u$
. Then with
$uR^cv$
we derive that
$wR^cv$
. -
•
$N\psi \in u$
for no
$\psi $
. From
$uR^cv$
it follows that
$u=v$
. Then due to
$wR^cu$
, we infer that
$wR^cv$
. -
•
$N\psi \in w$
for some
$\psi $
, and
$N\psi '\in u$
for some
$\psi '$
. Suppose for any
$\varphi $
that
$\neg N\varphi \land N(\varphi \land \psi )\in w$
, we hope to infer that
$\varphi \in v$
. By supposition and
$N\psi \in w$
and axiom A4-2, we derive that
$\neg N(N\psi '\to \neg N\varphi \land N(\varphi \land \psi '))\in w$
and
$N((N\psi '\to \neg N\varphi \land N(\varphi \land \psi '))\land \psi )\in w$
. Then as
$wR^cu$
,
$N\psi '\to \neg N\varphi \land N(\varphi \land \psi ')\in u$
, thus
$\neg N\varphi \land N(\varphi \land \psi ')\in u$
. Now using
$uR^cv$
, we conclude that
$\varphi \in v$
, as required.
Based on the previous analysis, we have the following result.
Theorem 30.
$\mathbf {K4^N}$
is sound and strongly complete with respect to the class of transitive frames
$\langle W,S,R \rangle ,$
where
$S\subseteq R$
.
3.4.5 S4 logic
Let
$\mathbf {S4^N}$
be the extension of
$\mathbf {K4^N}$
with the axiom NT.
Theorem 31.
$\mathbf {S4^N}$
is sound and strongly complete with respect to the class of
$\mathbf {S4}$
-frames
$\langle W,S,R \rangle ,$
where
$S\subseteq R$
.
This partly answers open questions raised in [Reference Bacon3].
3.5 Connection with the logic of accidental truths
If S is the identity relation and R is reflexive, then N becomes the accident operator
$\bullet $
, and the language
$\mathcal {L}(N)$
becomes
$\mathcal {L}(\bullet )$
. That is,
$$\begin{align*}\begin{array}{lll} \mathcal{M},w\vDash N\varphi & \Longleftrightarrow & \mathcal{M},w\vDash\varphi\text{ and }R(w)\nvDash\varphi. \\ \end{array} \end{align*}$$
Moreover,
$\boxed {\mathrm{c}}\varphi $
becomes
$\varphi $
. That is,
$$\begin{align*}\begin{array}{lll} \mathcal{M},w\vDash\boxed{\mathrm{c}}\varphi & \Longleftrightarrow & \mathcal{M},w\vDash\varphi. \\ & \end{array} \end{align*}$$
Then (NAD1) and (NAD2) become the following almost definability schemas:
$$\begin{align*}\begin{array}{lll} N\psi\to (\varphi\leftrightarrow N(\varphi\land\psi)) & & (\textbf{NAD1}')\\ N\psi\to (\Box\varphi\leftrightarrow\neg{N\varphi}\land N(\varphi\land\psi)) & & (\textbf{NAD2}). \\ \end{array} \end{align*}$$
One may easily verify that according to the simplified semantics (where S is identity),
$(\textbf {N}\textbf {AD1}')$
is valid over the class of all frames, whereas
$(\textbf {N}\textbf {AD2})$
is valid over the class of (R-)reflexive frames. This contrasts with the fact that
$(\textbf {N}\textbf {AD1}')$
is not valid under the original semantics, where S is not the identity relation (see the proofs of Proposition 26). To provide the completeness, we need to establish a proof system from which
$(\textbf {N}\textbf {AD1}')$
is derivable. However, recall from Proposition 26 that the schema is not derivable from
$\mathbf {T^{N}}$
, so
$\mathbf {T^{N}}$
is not a desired system. As we shall see, the extension of
$\mathbf {T^N}$
with the formula
$\varphi \land N\psi \to N(\varphi \land \psi )$
is a desired minimal logic of accidental truths. We denote the formula as
$\text {A1}'$
and the extension as
$\mathbf {T1^N}$
.Footnote
11
We can see that the schema
$(\textbf {NAD1}')$
is derivable from
$\mathbf {T1^N}$
because of axioms
$\text {A1}'$
and NT.
Based on the schemas
$(\textbf {NAD1}')$
and
$\textbf {NAD2}$
, the canonical model for
$\mathbf {T^N}$
can be simplified as follows.
Definition 32. The canonical model for
$\mathbf {T1^N}$
is a tuple
$\mathcal {M}^c=\langle W^c,S^c,R^c,V^c \rangle $
, where the only change is
$N(\varphi \land \psi )\in w$
in the definition of
$S^c$
is now becoming
$\varphi \in w$
, due to the derivable schema (NAD1
$'$
). In other words,
-
•
$W^c=\{w\mid w\text { is a maximal consistent set for }\mathbf {T1^N}\}$
; -
• if
$N\psi \in w$
for no
$\psi $
, then
$wS^cu$
iff
$w=u$
, and
$wR^cu$
iff
$w=u$
; -
• if
$N\psi \in w$
for some
$\psi $
, then
$wS^cu$
iff for all
$\varphi $
, if
$\varphi \in w$
, then
$\varphi \in u$
, and
$wR^cu$
iff for all
$\varphi $
, if
$\neg N\varphi \land N(\varphi \land \psi )\in w$
, then
$\varphi \in u$
; -
•
$V^c(p)=\{w\in W^c\mid p\in w\}$
.
Proposition 33.
$S^c$
is the identity relation, and
$R^c$
is reflexive. Consequently,
$S^c\subseteq R^c$
.
Proof. According to the definitions of
$S^c$
and
$R^c$
, we consider two cases. Let
$w,u\in W^c$
.
-
•
$N\psi \in w$
for no
$\psi $
. Then
$wS^cu$
iff
$w=u$
, and
$wR^cu$
iff
$w=u$
. -
•
$N\psi \in w$
for some
$\psi $
. First, we show that
$wS^cu$
iff
$w=u$
. It follows from the fact that
$wS^cu$
iff
$w\subseteq u$
(thus iff
$w=u$
).Second, we prove that
$wR^cw$
. Suppose for any
$\varphi $
that
$\neg N\varphi \land N(\varphi \land \psi )\in w$
, then since
$\vdash N(\varphi \land \psi )\to \varphi $
, we infer that
$\varphi \in w$
. Therefore,
$wR^cw$
.
Therefore,
$S^c$
is the identity relation, and
$R^c$
is reflexive.
Recall that in §3.4.3, axiom NT is shown to be valid over reflexive frames, where the reflexivity of S is used. Since now S is the identity relation, S is automatically reflexive. So here NT is valid over the class of all frames, without need of the reflexivity of R. This gives us axiomatizations of
$\mathcal {L}(\bullet )$
over various frames.
Theorem 34.
-
(1) Where
$\mathbf {T}\subseteq X$
,
$\mathbf {T1^N}$
is sound and strongly complete with respect to the class of X. -
(2) Where
$\mathbf {S4}\subseteq X\subseteq \mathbf {4}$
and
$\mathbf {S41^N}$
extends
$\mathbf {S4^N}$
with axiom
$\text {A1}'$
,
$\mathbf {S41^N}$
is sound and strongly complete with respect to X.
Proof. It remains to show the truth lemma for
$\mathbf {T1^{N}}$
. That is to show, for all
$\varphi \in \mathcal {L}(N)$
, for all
$w\in W^c$
, we have
$$ \begin{align*}\mathcal{M}^c,w\vDash\varphi\text{ iff }\varphi\in w.\end{align*} $$
We proceed by induction on
$\varphi $
. The nontrivial case is
$N\varphi $
.
Suppose that
$N\varphi \in w$
, to show that
$\mathcal {M}^c,w\vDash N\varphi $
. By supposition and Proposition 7(4), we infer that
$N(\varphi \land \varphi )\in w$
. Then by axiom NT, we derive that
$\varphi \in w$
, which by induction hypothesis implies that
$\mathcal {M}^c,w\vDash \varphi $
. It suffices to show that
$R^c(w)\nvDash \varphi $
. For this, we show that
$\lambda _2(w)\cup \{\neg \varphi \}$
is consistent, where
$\lambda _2(w)=\{\chi \mid \neg N\chi \land N(\chi \land \varphi )\in w\}$
. By Proposition 12(1),
$\lambda _2(w)\neq \emptyset $
.
If
$\lambda _2(w)\cup \{\neg \varphi \}$
is not consistent, then there are
$\chi _1,\dots ,\chi _n\in \lambda _2(w)$
such that
$$ \begin{align*}\vdash \chi_1\land\cdots\land\chi_n\to \varphi.\end{align*} $$
By Proposition 12(2) and (3), we have
$\varphi \in \lambda _2(w)$
, thus
$\neg N\varphi \in w$
, which contradicts the supposition and the consistency of w.
We have shown that
$\lambda _2(w)\cup \{\neg \varphi \}$
is consistent. Then by Lindenbaum’s Lemma, there exists
$u\in W^c$
such that
$wR^cu$
and
$\neg \varphi \in u$
, thus
$\varphi \notin u$
. By induction hypothesis, we conclude that
$R^c(w)\nvDash \varphi $
.
Conversely, assume that
$N\varphi \notin w$
, to prove that
$\mathcal {M}^c,w\nvDash N\varphi $
. If
$\mathcal {M}^c,w\nvDash \varphi $
, then
$\mathcal {M}^c,w\nvDash N\varphi $
. In what follows, we only consider the case that
$\mathcal {M}^c,w\vDash \varphi $
, in which case
$\varphi \in w$
. It suffices to show that
$R^c(w)\vDash \varphi $
. Let
$u\in R^c(w)$
. According to the definition of
$R^c$
, we consider two cases.
-
•
$N\psi \in w$
for no
$\psi $
. Then
$w=u$
, and thus
$\varphi \in u$
. -
•
$N\psi \in w$
for some
$\psi $
. In this case, from
$\varphi \in w$
and axiom
$\text {A1}'$
, it follows that
$N(\varphi \land \psi )\in w$
. Then by
$wR^cu$
, we obtain that
$\varphi \in u$
.
Both cases imply that
$\varphi \in u$
. By induction hypothesis,
$\mathcal {M}^c,u\vDash \varphi $
. Hence,
$R^c(w)\vDash \varphi $
, as desired.
Recall that the minimal logic of accident is proposed in the literature (see, e.g., [Reference Fan9, Reference Marcos32, Reference Steinsvold38]). Here we choose the system
$\mathbf {K}^\circ $
in [Reference Fan9] due to its simplicity, which consists of the following axioms and inference rules, where for the sake of reference, we write N for
$\bullet $
and
$\neg N$
for
$\circ $
(namely, the negation of
$\bullet $
):
$$\begin{align*}\begin{array}{ll} \text{TAUT} & \text{All instances of propositional tautologies} \\ \circ\top & \neg N\top \\ \circ\neg & \neg\varphi\to\neg N\varphi\\ \circ\land & \neg N\varphi\land\neg N\psi\to \neg N(\varphi\land\psi)\\ \text{MP} & \text{From }\varphi\text{ and }\varphi\to\psi\text{ infer }\psi \\ \text{R} & \text{From }\varphi\to\psi\text{ infer }\neg N\varphi\land\varphi\to \neg N\psi. \\ \end{array} \end{align*}$$
In what follows, we will show that the systems
$\mathbf {T1^N}$
and
$\mathbf {K}^\circ $
are deductively equivalent, from a pure proof-theoretic perspective.
Proposition 35. All axioms and inference rules in
$\mathbf {K}^\circ $
are derivable in
$\mathbf {T1^N}$
.
Proof. Axiom
$\circ \top $
is an immediate consequence of
$\text {PC}$
and
$\text {R1}$
, axiom
$\circ \neg $
can be easily obtained from
$\text {NT}$
, and axiom
$\circ \land $
is an equivalent transformation of
$\text {A2}$
. For the rule
$\text {R}$
, suppose that
$\vdash \varphi \to \psi $
, it remains only to show that
$\vdash N\psi \land \varphi \to N\varphi $
. By axiom
$\text {A1}'$
, we only need to show that
$\vdash N\psi \land N(\varphi \land \psi )\to N\varphi $
. This follows from Proposition 7(1).
Proposition 36. All axioms and inference rules in
$\mathbf {T1^N}$
are derivable in
$\mathbf {K}^\circ $
.
Proof. The proof of axiom
$\text {A1}'$
. By TAUT,
$\vdash \varphi \land \psi \to \psi $
. Then using rule R, we infer that
$\vdash \neg N(\varphi \land \psi )\land (\varphi \land \psi )\to \neg N\psi $
. By propositional reasoning, we have
$\vdash N\psi \land (\varphi \land \psi )\to N(\varphi \land \psi )$
. Then by axiom
$\circ \neg $
,
$\vdash N\psi \to \psi $
. Therefore,
$\vdash \varphi \land N\psi \to N(\varphi \land \psi )$
.
Axiom
$\text {A2}$
is a direct consequence of
$\circ \land $
.
The proof of rule R1. Assume that
$\vdash \varphi $
. Then
$\vdash \top \to \varphi $
. Using
$\text {R}$
, we infer that
$\vdash \neg N\top \land \top \to \neg N\varphi $
. By
$\circ \top $
, it follows that
$\vdash \neg N\top $
. Hence,
$\vdash \neg N\varphi $
.
The proof of rule R2. Suppose that
$\vdash \varphi \to \psi $
and
$\vdash \psi \to \chi $
, to prove that
$\vdash (N\varphi \land N\chi )\to N\psi $
. By
$\vdash \psi \to \chi $
and
$\text {R}$
, we derive that
$\vdash \neg N\psi \land \psi \to \neg N\chi $
, that is,
$\vdash N\chi \land \psi \to N\psi $
. Since
$\vdash \varphi \to \psi $
, it follows that
$\vdash N\chi \land \varphi \to N\psi $
. Moreover, by
$\circ \neg $
, we get
$\vdash N\varphi \to \varphi $
. Hence,
$\vdash (N\varphi \land N\chi )\to N\psi $
.
The proof of axiom
$\text {NT}$
. By
$\circ \neg $
, it follows that
$\vdash N(\varphi \land \psi )\to (\varphi \land \psi )$
. Moreover, by
$\text {TAUT}$
,
$\vdash (\varphi \land \psi )\to \varphi $
. Therefore,
$\vdash N(\varphi \land \psi )\to \varphi $
.
The proof of axiom
$\text {A1}$
. By axiom
$\circ \neg $
, we have
$\vdash N\varphi \to \varphi $
. Then using
$\text {A1}'$
, we conclude that
$\vdash N\varphi \land N\psi \to N(\varphi \land \psi )$
.
As a corollary, we give an alternative proof for the completeness of
$\mathbf {K}^\circ $
.
Theorem 37. Where
$\mathbf {T}\subseteq X$
,
$\mathbf {K}^\circ $
is sound and strongly complete with respect to the class of X.
Finally, since the operator
$\boxdot $
of true belief is interdefinable with the accident operator of
$\bullet $
, since
$\vDash \boxdot \varphi \leftrightarrow (\varphi \land \neg {\bullet \varphi })$
and
$\vDash \bullet \varphi \leftrightarrow \neg (\varphi \to \boxdot \varphi )$
[Reference Yang45, sec. 5.1], we can also obtain the axiomatizations of the logic of true belief over various frames.
4 The operator of ‘All
$_1$
and Only
$_2$
’
In [Reference Humberstone28, p. 229], a variation of N, denoted
$N'$
, is proposed, with the following semantics. Given an arbitrary model
$\mathcal {M}=\langle W,R_1,R_2,V \rangle $
and
$w\in W$
, where
$R_1$
and
$R_2$
are arbitrary,
$$\begin{align*}\begin{array}{lll} \mathcal{M},w\vDash N'\varphi&\Longleftrightarrow&R_1(w)\vDash\varphi\text{ and }R_2(w)\vDash\neg\varphi,\\ \end{array} \end{align*}$$
where for
$i\in \{1,2\}$
,
$R_i(w)\vDash \varphi $
means that for all
$u\in R_i(w)$
,
$\mathcal {M},u\vDash \varphi $
.
Since
$R_2$
is arbitrary, so is its complement (in symbols,
$\overline {R_2}=(W\times W)\backslash R_2$
). Thus we can also adopt the following equivalent semantics of
$N'$
, called ‘[All
$_1$
-
$\&$
-Only
$_2$
] semantics’ in [Reference Humberstone25, p. 181]:
$$\begin{align*}\begin{array}{lll} \mathcal{M},w\vDash N'\varphi&\Longleftrightarrow&R_1(w)\vDash\varphi\text{ and }\overline{R_2}(w)\vDash\neg\varphi.\\ \end{array} \end{align*}$$
In this sense, we call
$N'$
the operator of ‘All
$_1$
and Only
$_2$
’, for want of a better name.Footnote
12
In what follows, we still adopt the first semantics of
$N'$
.
A proof system AO is then proposed and shown to be determined by the class of all frames (on the [All
$_1$
-
$\&$
-Only
$_2$
] semantics). However, AO is an infinitary system which extends propositional calculus with the following schema for infinitely many finitary rules:Footnote
13
where
$m,n\in \mathbb {N}$
,
$$\begin{align*}\begin{array}{ll} \text{[AO]} & \dfrac{(\psi_1\land\cdots\land \psi_m)\to \chi~~~~~~\chi\to (\varphi_1\vee\cdots\vee \varphi_n)}{(N'\varphi_1\land \cdots\land N'\varphi_n\land N'\psi_1\land \cdots\land N'\psi_m)\to N' \chi}. \\ \end{array} \end{align*}$$
To our knowledge, it is still unknown whether AO has an alternative finite axiomatization. In what follows, we will provide a finite minimal axiomatization for
$N'$
using our approach.
Define a language with
$N'$
and
$\Box _1$
and
$\Box _2$
as primitive modalities, and denote the language with
$N'$
as the sole primitive modality as
$\mathcal {L}(N')$
. The semantics of
$\Box _1$
and
$\Box _2$
are defined as
$\mathcal {M},w\vDash \Box _i\varphi $
iff
$R_i(w)\vDash \varphi $
, where
$i\in \{1,2\}$
.
First, we observe two almost definability schemas—one for
$\Box _1$
and the other for
$\Box _2$
—in terms of
$N'$
. Intuitively, they say that both necessity operators are definable with
$N'$
, provided that there is a truth of the form
$N'\psi $
. They guide us to propose the desired canonical model later:
$$\begin{align*}\begin{array}{lr} N'\psi\to (\Box_1\varphi\leftrightarrow N'(\psi\land\varphi))& (\textbf{N}'\textbf{AD1}) \\ N'\psi\to (\Box_2\varphi\leftrightarrow N'(\psi\lor\neg\varphi)) & (\textbf{N}'\textbf{AD2}).\\ \end{array} \end{align*}$$
Notions of truth, frame validity, and validity are defined as before. The following result states that the above two schemas are indeed valid.
Proposition 38.
-
(1)
$\vDash N'\psi \to (\Box _1\varphi \leftrightarrow N'(\psi \land \varphi ))$
. -
(2)
$\vDash N'\psi \to (\Box _2\varphi \leftrightarrow N'(\psi \vee \neg \varphi ))$
.
Proof. Let
$\mathcal {M}=\langle W,R_1,R_2,V \rangle $
be a model and
$w\in W$
. Suppose that
$\mathcal {M},w\vDash N'\psi $
, then
$R_1(w)\vDash \psi $
and
$R_2(w)\vDash \neg \psi $
, thus
$R_1(w)\vDash \psi \vee \neg \varphi $
and
$R_2(w)\vDash \neg (\psi \land \varphi )$
.
-
(1) Assume that
$\mathcal {M},w\vDash \Box _1\varphi $
. Then
$R_1(w)\vDash \varphi $
. It then follows that
$R_1(w)\vDash \psi \land \varphi $
. Hence
$\mathcal {M},w\vDash N'(\psi \land \varphi )$
.Conversely, assume that
$\mathcal {M},w\vDash N'(\psi \land \varphi )$
. Then
$R_1(w)\vDash \psi \land \varphi $
, and thus
$R_1(w)\vDash \varphi $
. Hence
$\mathcal {M},w\vDash \Box _1\varphi $
, as desired. -
(2) Suppose that
$\mathcal {M},w\vDash \Box _2\varphi $
. Then
$R_2(w)\vDash \varphi $
, and thus
$R_2(w)\vDash \neg (\psi \vee \neg \varphi )$
. Hence
$\mathcal {M},w\vDash N'(\psi \vee \neg \varphi )$
.Conversely, assume that
$\mathcal {M},w\vDash N'(\psi \vee \neg \varphi )$
, then
$R_2(w)\vDash \neg (\psi \vee \neg \varphi )$
, thus
$R_2(w)\vDash \varphi $
. Hence
$\mathcal {M},w\vDash \Box _2\varphi $
, as desired.
Note that in the above result, there is no restriction to
$R_1$
or
$R_2$
. One may impose certain conditions on these two accessibility relations. For instance, if
$R_2\subseteq R_1$
, then we get the semantics of
$\Box $
in [Reference Vander Nat41], which has an equivalent semantics with non-normal possible worlds; if
$R_2$
is the complement of
$R_1$
(relative to
$W\times W$
), we get the operator of ‘all and only’ in [Reference Humberstone25]; if
$R_2$
is the identity relation, then we obtain the operator W of false belief [Reference Fan18, Reference Gilbert, Kubyshkina, Petrolo and Venturi23, Reference Gilbert and Venturi24, Reference Steinsvold40].
4.1 Minimal system and soundness
Definition 39. The minimal system of
$\mathcal {L}(N')$
, denoted
$\mathbf {K^{N'}}$
, consists of the following axioms and inference rules:
$$\begin{align*}\begin{array}{ll} \text{PC} & \text{All instances of propositional tautologies} \\ \text{B1} & N'\varphi\land N'\psi\to N'(\varphi\land\psi)\\ \text{B2} & N'\varphi\land N'\psi\to N'(\varphi\lor\psi)\\ \text{MP} & \text{From }\varphi\text{ and }\varphi\to\psi\text{ infer }\psi\\ \text{N}'\text{R} & \text{From }\varphi\to \psi\text{ and }\psi\to\chi \text{ infer }(N'\varphi\land N'\chi)\to N'\psi.\\ \end{array}\end{align*}$$
The above axioms and inference rules are obtained based on the need of showing the truth lemma (Lemma 44). Notions of derivation and theorems are defined as usual. The following proposition is important in the proof later.
Proposition 40.
-
(1) If
$\vdash \varphi \leftrightarrow \psi $
, then
$\vdash N'\varphi \leftrightarrow N'\psi $
. -
(2)
$\vdash N'(\psi \land \varphi )\land N'(\chi \vee \varphi )\to N'\varphi $
. -
(3) If
$\vdash \varphi \to \chi $
, then
$\vdash (N'(\psi \land \varphi )\land N'\psi )\to N'(\psi \land \chi )$
. -
(4) If
$\vdash \varphi \to \chi $
, then
$\vdash (N'\psi \land N'(\psi \vee \neg \varphi ))\to N'(\psi \vee \neg \chi )$
.
Proof. Item (1) can be shown as Proposition 7(4), and (2) is immediate from the rule N
$'$
R. (3) Suppose that
$\vdash \varphi \to \chi $
, then
$\vdash \psi \land \varphi \to \psi \land \chi $
. Moreover,
$\vdash \psi \land \chi \to \psi $
. Now using the rule
$\text {N}'\text {R}$
,
$\vdash (N'(\psi \land \varphi )\land N'\psi )\to N'(\psi \land \chi )$
. (4) Assume that
$\vdash \varphi \to \chi $
, then
$\vdash \neg \chi \to \neg \varphi $
, thus
$\vdash \psi \vee \neg \chi \to \psi \vee \neg \varphi $
. Also,
$\vdash \psi \to \psi \vee \neg \chi $
. Using the rule
$\text {N}'\text {R}$
, we derive that
$\vdash (N'\psi \land N'(\psi \vee \neg \varphi ))\to N'(\psi \vee \neg \chi )$
.
Proposition 41.
$\mathbf {K^{N'}}$
is sound with respect to the class of all frames.
Proof. We only show the soundness of axioms B1, B2 and rule
$\text {N}'\text {R}$
. Let
$\mathcal {M}=\langle W,R_1,R_2,V \rangle $
be a frame and
$w\in W$
.
For B1 and B2. Suppose that
$\mathcal {M},w\vDash N'\varphi $
and
$\mathcal {M},w\vDash N'\psi $
. Then
$R_1(w)\vDash \varphi $
and
$R_2(w)\vDash \neg \varphi $
, and
$R_1(w)\vDash \psi $
and
$R_2(w)\vDash \neg \psi $
, which implies that
$R_1(w)\vDash \varphi \land \psi $
and
$R_2(w)\vDash \neg (\varphi \land \psi )$
. Hence,
$\mathcal {M},w\vDash N'(\varphi \land \psi )$
. Moreover, we have also
$R_1(w)\vDash \varphi \vee \psi $
and
$R_2(w)\vDash \neg (\varphi \vee \psi )$
. Hence,
$\mathcal {M},w\vDash N'(\varphi \vee \psi )$
.
For
$\text {N}'\text {R}$
. Assume that
$\vDash \varphi \to \psi $
and
$\vDash \psi \to \chi $
, to show that
$\vDash N'\varphi \land N'\chi \to N'\psi $
. For this, suppose that
$\mathcal {M},w\vDash N'\varphi \land N'\chi $
, then
$R_1(w)\vDash \varphi $
and
$R_2(w)\vDash \neg \chi $
. By assumption, we infer that
$R_1(w)\vDash \psi $
and
$R_2(w)\vDash \neg \psi $
. Therefore,
$\mathcal {M},w\vDash N'\psi $
, as desired.
4.2 Completeness
For completeness, we construct the canonical model for
$\mathbf {K^{N'}}$
.
Definition 42. The canonical model for
$\mathbf {K^{N'}}$
is a tuple
$\mathcal {M}=\langle W^c,R_1^c,R_2^c,V^c \rangle $
, where
-
•
$W^c=\{w\mid w\text { is a maximal consistent set for }\mathbf {K^{N'}}\}$
; -
• if
$N'\psi \in w$
for no
$\psi $
, then
$wR_1^cu$
iff
$w=u$
, and
$wR_2^cu$
iff
$w=u$
; -
• if
$N'\psi \in w$
for some
$\psi $
, then
$wR^c_1u$
iff for every
$\varphi $
, if
$N'(\psi \land \varphi )\in w$
, then
$\varphi \in u$
, and
$wR^c_2u$
iff for every
$\varphi $
, if
$N'(\psi \vee \neg \varphi )\in w$
, then
$\varphi \in u$
; -
•
$V^c(p)=\{w\in W^c\mid p\in w\}$
.
It is required that the
$\psi $
in
$N'(\psi \land \varphi )\in w$
and
$N'(\psi \lor \neg \varphi )\in w$
be the same as that in
$N'\psi \in w$
. Note that the choice of
$\psi $
in the above second case of the canonical relations is inessential to
$R_1^c$
and
$R_2^c$
, as shown in Remark 10. It is also noteworthy that
$R_1^c$
and
$R_2^c$
in the above definition are inspired by almost definability schemas (
$\textbf {N}'\textbf {AD1}$
) and (
$\textbf {N}'\textbf {AD2}$
), respectively, based on the analysis of §2. Recall that in the construction of the canonical model for the minimal logic of
$\mathcal {L}(\Box _1,\Box _2)$
, the canonical relations
$R_1^c$
and
$R^c_2$
are defined as, respectively,
$wR^c_1u$
iff for all
$\varphi $
, if
$\Box _1\varphi \in w$
then
$\varphi \in u$
, and
$wR^c_2u$
iff for all
$\varphi $
, if
$\Box _2\varphi \in w$
then
$\varphi \in u$
. Now given a precondition that
$N'\psi \in w$
for some
$\psi $
, according to
$(\textbf {N}'\textbf {AD1})$
,
$\Box _1\varphi \in w$
can be replaced with
$N'(\psi \land \varphi )\in w$
, and according to
$(\textbf {N}'\textbf {AD2})$
,
$\Box _2\varphi \in w$
can be replaced with
$ N'(\psi \lor \neg \varphi )\in w$
; otherwise, we let w access and only access itself.
Proposition 43 lists some logical properties of
$\Gamma _1$
and
$\Gamma _2$
. They are important in the proof of Lemma 44 below.
Proposition 43. Let
$w\in W^c$
such that
$N'\psi \in w$
. Define
$\Gamma _1(w)=\{\chi \mid N'(\psi \land \chi )\in w\}$
and
$\Gamma _2(w)=\{\chi \mid N'(\psi \vee \neg \chi )\in w\}$
. Then for any
$i\in \{1,2\}$
,
-
(1)
$\Gamma _i(w)\neq \emptyset $
. -
(2) If
$\varphi ,\chi \in \Gamma _i(w)$
, then
$\varphi \land \chi \in \Gamma _i(w)$
. -
(3) If
$\varphi \in \Gamma _i(w)$
and
$\vdash \varphi \to \chi $
, then
$\chi \in \Gamma _i(w)$
. -
(4) If
$\varphi \in \Gamma _1(w)$
and
$\neg \varphi \in \Gamma _2(w)$
, then
$N'\varphi \in w$
.
Proof. Suppose that
$N'\psi \in w$
.
-
(1) By supposition and Proposition 40(1), we have
$N'(\psi \land \top )\in w$
and
$N'(\psi \vee \neg \top )\in w$
, thus
$\top \in \Gamma _1(w)$
and
$\top \in \Gamma _2(w)$
. Thus
$\Gamma _1(w)\neq \emptyset $
and
$\Gamma _2(w)\neq \emptyset $
. -
(2) Assume that
$\varphi \in \Gamma _1(w)$
and
$\chi \in \Gamma _1(w)$
. Then
$N'(\psi \land \varphi )\in w$
and
$N'(\psi \land \chi )\in w$
. By axiom B1 and Proposition 40(1), we infer that
$N'(\psi \land (\varphi \land \chi ))\in w$
, which implies that
$\varphi \land \chi \in \Gamma _1(w)$
.Assume that
$\varphi \in \Gamma _2(w)$
and
$\chi \in \Gamma _2(w)$
. Then
$N'(\psi \vee \neg \varphi )\in w$
and
$N'(\psi \vee \neg \chi )\in w$
. By axiom B2 and Proposition 40(1), we derive that
$N'(\psi \vee \neg (\varphi \land \chi ))\in w$
, which entails that
$\varphi \land \chi \in \Gamma _2(w)$
. -
(3) Assume that
$\varphi \in \Gamma _1(w)$
and
$\vdash \varphi \to \chi $
. Then
$N'(\psi \land \varphi )\in w$
. Then using the supposition and Proposition 40(3), we get
$N'(\psi \land \chi )\in w$
, which implies that
$\chi \in \Gamma _1(w)$
.Assume that
$\varphi \in \Gamma _2(w)$
and
$\vdash \varphi \to \chi $
. Then
$N'(\psi \vee \neg \varphi )\in w$
. Now using the supposition and Proposition 40(4), we have
$N'(\psi \vee \neg \chi )\in w$
, which entails that
$\chi \in \Gamma _2(w)$
. -
(4) Assume that
$\varphi \in \Gamma _1(w)$
and
$\neg \varphi \in \Gamma _2(w)$
. Then
$N'(\psi \land \varphi )\in w$
and
$N'(\psi \vee \neg \neg \varphi )\in w$
(that is,
$N'(\psi \vee \varphi )\in w$
). By Proposition 40(2),
$N'\varphi \in w$
.
Lemma 44. For all
$w\in W^c$
, for all
$\varphi \in \mathcal {L}(N')$
, we have
$$ \begin{align*}\mathcal{M}^c,w\vDash\varphi\text{ iff }\varphi\in w.\end{align*} $$
Proof. By induction on
$\varphi $
. The nontrivial case is
$N'\varphi $
.
Suppose that
$N'\varphi \in w$
, to show that
$\mathcal {M}^c,w\vDash N'\varphi $
, that is,
$R^c_1(w)\vDash \varphi $
and
$R_2^c(w)\vDash \neg \varphi $
. By supposition and Proposition 40(1),
$N'(\varphi \land \varphi )\in w$
and
$N'(\varphi \vee \neg \neg \varphi )\in w$
. Then given any
$u\in W^c$
such that
$wR^c_1u$
,
$\varphi \in u$
; given any
$u\in W^c$
such that
$wR^c_2u$
,
$\neg \varphi \in u$
. By induction hypothesis,
$R^c_1(w)\vDash \varphi $
and
$R^c_2(w)\vDash \neg \varphi $
.
Conversely, assume that
$N'\varphi \notin w$
, to show that
$\mathcal {M}^c,w\nvDash N'\varphi $
, that is,
$R^c_1(w)\nvDash \varphi $
or
$R_2^c(w)\nvDash \neg \varphi $
. If
$N'\psi \in w$
for no
$\psi $
, then
$R^c_1(w)=R^c_2(w)=\{w\}$
, then we are done. In what follows, we consider the case that
$N'\psi \in w$
for some
$\psi $
. Let
$\Gamma _1(w)=\{\chi \mid N'(\psi \land \chi )\in w\}$
and
$\Gamma _2(w)=\{\chi \mid N'(\psi \vee \neg \chi )\in w\}$
. By induction hypothesis and Lindenbaum’s Lemma, it remains only to show that
$\Gamma _1(w)\cup \{\neg \varphi \}$
is consistent or
$\Gamma _2(w)\cup \{\varphi \}$
is consistent. Note that by Proposition 43(1),
$\Gamma _1(w)$
and
$\Gamma _2(w)$
are nonempty.
If not, then there are
$\chi _1,\ldots ,\chi _n\in \Gamma _1(w)$
such that
$$ \begin{align*}\vdash \chi_1\land\cdots\land\chi_n\to\varphi,\end{align*} $$
and there are
$\delta _1,\ldots ,\delta _m\in \Gamma _2(w)$
such that
$$ \begin{align*}\vdash \delta_1\land\cdots\land\delta_n\to\neg\varphi.\end{align*} $$
By Proposition 43(2), we infer that
$\chi _1\land \cdots \land \chi _n\in \Gamma _1(w)$
. Then by Proposition 43(3), we derive that
$\varphi \in \Gamma _1(w)$
. Similarly, we can show that
$\neg \varphi \in \Gamma _2(w)$
. Then by Proposition 43(4),
$N'\varphi \in w$
, contradicting the assumption.
Theorem 45.
$\mathbf {K^{N'}}$
is strongly complete with respect to the class of all frames.
Based on the previous analysis, we obtain the completeness of
$\mathbf {K^{N'}}$
with respect to the class of all frames (on the [All
$_1$
-
$\&$
-Only
$_2$
] semantics). Thus we have given a finite minimal axiomatization for the operator ‘All
$_1$
and Only
$_2$
’. This may also help find a finite axiomatization for the operator ‘all and only’, which is a special case of
$N'$
when
$R_2$
is the complement of
$R_1$
in the semantic structure.
4.3 Extensions
In this section, we consider extensions of
$\mathbf {K^{N'}}$
over various classes of frames. Although
$\mathcal {L}(N')$
is not a normal modal logic, we can also define what it means by a formula in it being canonical for a frame property, just as the case for normal modal logics.
Let
$\varphi $
be a formula, and P be a frame property. We say that
$\varphi $
is canonical for P, if the canonical frame for any extension of
$\mathbf {K^{N'}}$
containing
$\varphi $
has property P, and
$\varphi $
is valid on any class of frames with property P. The following table summarizes that the formulas in the middle column are canonical for the frame properties in the right column.Footnote
14
$$\begin{align*}\begin{array}{@{}l@{\hskip4pt}l@{\hskip4pt}l} \hline \text{Notation} & \text{Axiom schemas} & \text{Frame properties} \\ \text{N}'\text{D1} & \neg N'\bot & R_1\text{ serial}\\ \text{N}'\text{D2} & \neg N'\top & R_2\text{ serial}\\ \text{N}'\text{T1} & N'(\varphi\land\psi)\to\psi & R_1\text{ reflexive}\\ \text{N}'\text{T2} & N'(\varphi\lor\neg\psi)\to\psi & R_2\text{ reflexive}\\ \text{N}'\text{41} & N'\psi\land N'(\psi\land\varphi)\to N'(\psi\land (N'\chi\to N'(\chi\land\varphi))) & R_1\text{ transitive}\\ \text{N}'\text{42} & N'\psi\land N'(\psi\vee\neg\varphi)\to N'(\psi\vee\neg (N'\chi\to N'(\chi\vee\neg\varphi))) & R_2\text{ transitive}\\ \text{MIX1}& N'\psi\to N'(\psi\land\varphi) & R_1\subseteq R_2\\ \text{MIX2} & N'\psi\to N'(\psi\lor\neg\varphi) & R_2\subseteq R_1\\ \text{N}'\text{ID1}&N'\psi\to (\varphi\leftrightarrow N'(\psi\land\varphi))&R_1\text{ identity}\\ \text{N}'\text{ID2}& N'\psi\to (\varphi\leftrightarrow N'(\psi\vee\neg\varphi))&R_2\text{ identity}\\ \hline \end{array} \end{align*}$$
Theorem 46.
-
(1)
$\text {N}'\text {D1}$
is canonical for the seriality of
$R_1$
. -
(2)
$\text {N}'\text {D2}$
is canonical for the seriality of
$R_2$
. -
(3)
$\text {N}'\text {T1}$
is canonical for the reflexivity of
$R_1$
. -
(4)
$\text {N}'\text {T2}$
is canonical for the reflexivity of
$R_2$
. -
(5)
$\text {N}'\text {41}$
is canonical for the transitivity of
$R_1$
. -
(6)
$\text {N}'\text {42}$
is canonical for the transitivity of
$R_2$
. -
(7) MIX1 is canonical for
$R_1\subseteq R_2$
. -
(8) MIX2 is canonical for
$R_2\subseteq R_1$
. -
(9)
$\text {N}'\text {ID1}$
is canonical for
$R_1$
being identity. -
(10)
$\text {N}'\text {ID2}$
is canonical for
$R_2$
being identity.
Proof.
-
(1) Suppose, for reductio, that there is a model
$\mathcal {M}=\langle W,R_1,R_2,V \rangle $
with
$R_1$
serial and a world
$w\in W$
such that
$\mathcal {M},w\vDash N'\bot $
. Then
$R_1(w)\vDash \bot $
. Since
$R_1$
is serial, there is a
$u\in W$
such that
$wR_1u$
and
$\mathcal {M},u\vDash \bot $
: a contradiction.Define the canonical frame
$\mathcal {F}^c=\langle S^c,R^c_1,R^c_2 \rangle $
as in Definition 42. Let
${w\in W^c}$
. We consider two cases.-
–
$N'\psi \in w$
for no
$\psi $
. Then according to the definition of
$R^c_1$
,
$wR^c_1w$
. -
–
$N'\psi \in w$
for some
$\psi $
. Then define
$\Gamma _1(w)=\{\chi \mid N'(\psi \land \chi )\in w\}$
. According to the definition of
$R^c_1$
, we only need to show that
$\Gamma _1(w)$
is consistent. If not, then there are
$\chi _1,\ldots ,\chi _n\in \Gamma _1(w)$
such that
${\vdash \chi _1\land \cdots \land \chi _n\to \bot }$
. By items (2) and (3) of Proposition 43, we infer that
$\bot \in \Gamma _1(w)$
, and thus
$N'(\psi \land \bot )\in w$
, that is,
$N'\bot \in w$
. However, by axiom N
$'$
D1,
$\neg N'\bot \in w$
: a contradiction.
This shows that
$R^c_1$
is serial. -
-
(2) Assume, for a contradiction, that there is a model
$\mathcal {M}=\langle W,R_1,R_2,V \rangle $
with
$R_2$
serial and a world
$w\in W$
such that
$\mathcal {M},w\vDash N'\top $
. Then
$R_2(w)\vDash \neg \top $
. Since
$R_2$
is serial, there exists
$v\in W$
such that
$wR_2v$
and
$\mathcal {M},v\vDash \neg \top $
: a contradiction.Define the canonical frame
$\mathcal {F}^c=\langle W^c,R_1^c,R_2^c \rangle $
as in Definition 42. Let
$w\in W^c$
. We consider two cases.-
–
$N'\psi \in w$
for no
$\psi $
. Then according to the definition of
$R^c_2$
, we have
$wR^c_2w$
. -
–
$N'\psi \in w$
for some
$\psi $
. Then define
$\Gamma _2(w)=\{\chi \mid N'(\psi \vee \neg \chi )\in w\}$
. According to the definition of
$R^c_2$
, we only need to show that
$\Gamma _2(w)$
is consistent. If not, then there are
$\chi _1,\ldots ,\chi _n\in \Gamma _2(w)$
such that
$\vdash \chi _1\land \cdots \land \chi _n\to \bot $
. By items (2) and (3) of Proposition 43, we infer that
$\bot \in \Gamma _2(w)$
, and thus
$N'(\psi \lor \neg \bot )\in w$
, that is,
$N'\top \in w$
. However, by axiom N
$'$
D2,
$\neg N'\top \in w$
: a contradiction.
This shows that
$R^c_2$
is serial. -
-
(3) Let
$\mathcal {M}=\langle W,R_1,R_2,V \rangle $
be a model with
$R_1$
reflexive, and
$w\in W$
. Assume that
$\mathcal {M},w\vDash N'(\varphi \land \psi )$
. Then
$R_1(w)\vDash \varphi \land \psi $
. By reflexivity of
$R_1$
,
$wR_1w$
. Then
$\mathcal {M},w\vDash \psi $
.Define the canonical frame
$\mathcal {F}^c=\langle W^c,R_1^c,R_2^c \rangle $
as in Definition 42. Let
$w\in W^c$
. We consider two cases.-
–
$N'\psi \in w$
for no
$\psi $
. Then according to the definition of
$R^c_1$
,
$wR^c_1w$
. -
–
$N'\psi \in w$
for some
$\psi $
. Then define
$\Gamma _1(w)=\{\chi \mid N'(\psi \land \chi )\in w\}$
. According to the definition of
$R^c_1$
, we only need to show that
$\Gamma _1(w)\subseteq w$
. For this, suppose for any
$\chi $
that
$\chi \in \Gamma _1(w)$
, that is,
$N'(\psi \land \chi )\in w$
. By axiom N
$'$
T1, we obtain that
$\chi \in w$
.
This shows that
$R^c_1$
is reflexive. -
-
(4) Let
$\mathcal {M}=\langle W,R_1,R_2,V \rangle $
be a model with
$R_2$
reflexive, and
$w\in W$
. Suppose that
$\mathcal {M},w\vDash N'(\varphi \vee \neg \psi )$
. Then
$R_2(w)\vDash \neg (\varphi \vee \neg \psi )$
. By reflexivity of
$R_2$
,
$wR_2w$
. Then
$\mathcal {M},w\vDash \psi $
. Define the canonical frame
$\mathcal {F}^c=\langle W^c,R_1^c,R_2^c \rangle $
as in Definition 42. Let
$w\in W^c$
. We consider two cases.-
–
$N'\psi \in w$
for no
$\psi $
. Then according to the definition of
$R^c_2$
,
$wR^c_2w$
. -
–
$N'\psi \in w$
for some
$\psi $
. Then define
$\Gamma _2(w)=\{\chi \mid N'(\psi \lor \neg \chi )\in w\}$
. According to the definition of
$R^c_2$
, we only need to show that
$\Gamma _2(w)\subseteq w$
. For this, suppose for any
$\chi $
that
$\chi \in \Gamma _2(w)$
, that is,
$N'(\psi \lor \neg \chi )\in w$
. By axiom N
$'$
T2, we obtain that
$\chi \in w$
.
This shows that
$R^c_2$
is reflexive. -
-
(5) Let
$\mathcal {M}=\langle W,R_1,R_2,V \rangle $
be a model with
$R_1$
transitive, and
$w\in W$
. Suppose, for reductio, that
$\mathcal {M},w\vDash N'\psi \land N'(\psi \land \varphi )$
, and
$\mathcal {M},w\nvDash N'(\psi \land (N'\chi \to N'(\chi \land \varphi )))$
. From
$\mathcal {M},w\vDash N'\psi $
, it follows that
$R_2(w)\vDash \neg \psi $
. Thus there exists
$u\in W$
such that
$wR_1u$
and
$\mathcal {M},u\nvDash \psi \land (N'\chi \to N'(\chi \land \varphi ))$
. We have also
$R_1(w)\vDash \psi $
. This implies that
$\mathcal {M},u\nvDash N'\chi \to N'(\chi \land \varphi )$
, thus
$\mathcal {M},u\vDash N'\chi $
and
$\mathcal {M},u\nvDash N'(\chi \land \varphi )$
. From the former, it follows that
$R_1(u)\vDash \chi $
and
$R_2(u)\vDash \neg \chi $
; from the latter, it follows that either
$R_1(u)\nvDash \chi \land \varphi $
or
$R_2(u)\nvDash \neg (\chi \land \varphi )$
. Thus
$R_1(u)\nvDash \chi \land \varphi $
. However, by
$wR_1u$
and transitivity of
$R_1$
,
$R_1(u)\subseteq R_1(w)$
. Now using
$\mathcal {M},w\vDash N'(\psi \land \varphi )$
, we obtain that
$R_1(w)\vDash \varphi $
and thus
$R_1(u)\vDash \varphi $
, and hence
$R_1(u)\vDash \chi \land \varphi $
: a contradiction.Define the canonical frame
$\mathcal {F}^c=\langle W^c,R^c_1,R^c_2 \rangle $
as in Definition 42. Let
$w,u,v\in W^c$
. Assume that
$wR^c_1u$
and
$uR^c_1v$
, to show that
$wR^c_1v$
. We consider the following cases.-
–
$N'\psi \in w$
for no
$\psi $
. Then by
$wR^c_1u$
we infer that
$w=u$
. As
$uR^c_1v$
, we derive that
$wR^c_1v$
. -
–
$N'\psi \in u$
for no
$\psi $
. From
$uR^c_1v$
it follows that
$u=v$
. This plus
$wR^c_1u$
entails that
$wR^c_1v$
. -
–
$N'\psi \in w$
and
$N'\chi \in u$
for some
$\psi $
and
$\chi $
. Suppose for any
$\varphi $
that
$N'(\psi \land \varphi )\in w$
, it remains only to show that
$\varphi \in v$
. By axiom N
$'$
41,
$N'(\psi \land (N'\chi \to N'(\chi \land \varphi )))\in w$
. Due to
$wR^c_1u$
, we have
$N'\chi \to N'(\chi \land \varphi )\in u$
, thus
$N'(\chi \land \varphi )\in u$
. Then using
$uR^c_1v$
, we get
$\varphi \in v$
, as desired.
This shows that
$R^c_1$
is transitive. -
-
(6) Let
$\mathcal {M}=\langle W,R_1,R_2 \rangle $
be a model with
$R_2$
transitive, and
$w\in W$
. Assume, for a contradiction, that
$\mathcal {M},w\vDash N'\psi \land N'(\psi \vee \neg \varphi )$
and
$\mathcal {M},w\nvDash N'(\psi \vee \neg (N'\chi \to N'(\chi \vee \neg \varphi )))$
. By
$\mathcal {M},w\vDash N'\psi $
, we have
$R_1(w)\vDash \psi $
. Then by
$\mathcal {M},w\nvDash N'(\psi \vee \neg (N'\chi \to N'(\chi \vee \neg \varphi )))$
, we infer that
$R_2(w)\nvDash \neg (\psi \vee \neg (N'\chi \to N'(\chi \vee \neg \varphi )))$
; in other words, there is a
$u\in W$
such that
$wR_2u$
and
$\mathcal {M},u\vDash \psi \vee \neg (N'\chi \to N'(\chi \vee \neg \varphi ))$
. We have also
$R_2(w)\vDash \neg \psi $
. Thus
$\mathcal {M},u\vDash \neg (N'\chi \to N'(\chi \vee \neg \varphi ))$
, that is,
$\mathcal {M},u\vDash N'\chi $
and
$\mathcal {M},u\nvDash N'(\chi \vee \neg \varphi )$
. From the former, it follows that
$R_1(u)\vDash \chi $
and
$R_2(u)\vDash \neg \chi $
; from the latter, it follows that either
$R_1(u)\nvDash \chi \vee \neg \varphi $
or
$R_2(u)\nvDash \neg (\chi \vee \neg \varphi )$
. This implies that
$R_2(u)\nvDash \neg (\chi \vee \neg \varphi )$
. However, as
$\mathcal {M},w\vDash N'(\psi \vee \neg \varphi )$
, we derive that
$R_2(w)\vDash \varphi $
. By
$wR_2u$
and transitivity of
$R_2$
,
$R_2(u)\subseteq R_2(w)$
, thus
$R_2(u)\vDash \varphi $
, and hence
$R_2(u)\vDash \neg (\chi \vee \neg \varphi )$
. A contradiction.Define the canonical frame
$\mathcal {F}^c=\langle W^c,R^c_1,R^c_2 \rangle $
as in Definition 42. Let
$w,u,v\in W^c$
. Suppose that
$wR^c_2u$
and
$uR^c_2v$
, to prove that
$wR^c_2v$
. We consider the following cases:-
–
$N'\psi \in w$
for no
$\psi $
. Then by
$wR^c_2u$
we obtain that
$w=u$
. This plus
$uR^c_2v$
implies that
$wR^c_2v$
. -
–
$N'\psi \in u$
for no
$\psi $
. By
$uR^c_2v$
we infer that
$u=v$
. Then using
$wR^c_2u$
we derive that
$wR^c_2v$
. -
–
$N'\psi \in w$
and
$N'\chi \in u$
for some
$\psi $
and
$\chi $
. Assume for any
$\varphi $
that
$N'(\psi \vee \neg \varphi )\in w$
, to show that
$\varphi \in v$
. By axiom N
$'$
42,
$N'(\psi \vee \neg (N'\chi \to N'(\chi \vee \neg \varphi )))\in w$
. Then using
$wR^c_2u$
, we get
$N'\chi \to N'(\chi \vee \neg \varphi )\in u$
, thus
$N'(\chi \vee \neg \varphi )\in u$
. Now due to
$uR^c_2v$
, we conclude that
$\varphi \in v$
, as desired.
This shows that
$R^c_2$
is transitive. -
-
(7) Let
$\mathcal {M}=\langle W,R_1,R_2,V \rangle $
be a model with
$R_1\subseteq R_2$
, and
$w\in W$
. Suppose, for reductio, that
$\mathcal {M},w\vDash N'\psi $
and
$\mathcal {M},w\nvDash N'(\psi \land \varphi )$
. Then either
$R_1(w)\nvDash \psi \land \varphi $
or
$R_2(w)\nvDash \neg (\psi \land \varphi )$
. By
$\mathcal {M},w\vDash N'\psi $
,
$R_2(w)\vDash \neg \psi $
, thus
$R_2(w)\vDash \neg (\psi \land \varphi )$
, and hence
$R_1(w)\nvDash \psi \land \varphi $
. So there exists
$u\in W$
such that
$wR_1u$
and
$\mathcal {M},u\nvDash \psi \land \varphi $
. Using
$\mathcal {M},w\vDash N'\psi $
again, we derive that
$R_1(w)\vDash \psi $
, thus
$\mathcal {M},u\vDash \psi $
. Moreover,
$R_2(w)\vDash \neg \psi $
and
$R_1(w)\subseteq R_2(w)$
implies that
$R_1(w)\vDash \neg \psi $
, and thus
$\mathcal {M},u\vDash \neg \psi $
. A contradiction.Define the canonical frame
$\mathcal {F}^c=\langle W^c,R^c_1,R^c_2 \rangle $
as in Definition 42. Let
$w,u\in W^c$
. Assume that
$wR^c_1u$
, to show that
$wR^c_2u$
. We consider two cases.-
–
$N'\psi \in w$
for no
$\psi $
. Then from
$wR^c_1u$
it follows that
$w=u$
. Then
$wR^c_2u$
. -
–
$N'\psi \in w$
for some
$\psi $
. Suppose for any
$\varphi $
that
$N'(\psi \vee \neg \varphi )\in w$
, to prove that
$\varphi \in u$
. By
$N'\psi \in w$
and axiom MIX1, we have
$N'(\psi \land \varphi )\in w$
. Now using
$wR^c_1u$
, we derive that
$\varphi \in u$
, as desired.
This shows that
$R^c_1\subseteq R^c_2$
. -
-
(8) Let
$\mathcal {M}=\langle W,R_1,R_2,V \rangle $
be a model with
$R_2\subseteq R_1$
, and
$w\in W$
. Assume, for a contradiction, that
$\mathcal {M},w\vDash N'\psi $
and
$\mathcal {M},w\nvDash N'(\psi \vee \neg \varphi )$
. Then either
$R_1(w)\nvDash \psi \vee \neg \varphi $
or
$R_2(w)\nvDash \neg (\psi \vee \neg \varphi )$
. By
$\mathcal {M},w\vDash N'\psi $
, it follows that
$R_1(w)\vDash \psi $
, thus
$R_1(w)\vDash \psi \vee \neg \varphi $
. Hence
$R_2(w)\nvDash \neg (\psi \vee \neg \varphi )$
. Thus there exists
$u\in W$
such that
$wR_2u$
and
$\mathcal {M},u\vDash \psi \vee \neg \varphi $
. Using
$\mathcal {M},w\vDash N'\psi $
again, we derive that
$R_2(w)\vDash \neg \psi $
, thus
$\mathcal {M},u\vDash \neg \psi $
. Further,
$R_1(w)\vDash \psi $
and
$R_2(w)\subseteq R_1(w)$
entails that
$R_2(w)\vDash \psi $
, thus
$\mathcal {M},u\vDash \psi $
. A contradiction.Define the canonical frame
$\mathcal {F}^c=\langle W^c,R^c_1,R^c_2 \rangle $
as in Definition 42. Let
$w,u\in W^c$
. Suppose that
$wR^c_2u$
, to prove that
$wR^c_1u$
. We consider two cases.-
–
$N'\psi \in w$
for no
$\psi $
. Then from
$wR^c_2u$
it follows that
$w=u$
. Then
$wR^c_1u$
. -
–
$N'\psi \in w$
for some
$\psi $
. Assume for any
$\varphi $
that
$N'(\psi \land \varphi )\in w$
, to show that
$\varphi \in u$
. By
$N'\psi \in w$
and axiom MIX2, we infer that
$N'(\psi \vee \neg \varphi )\in w$
. Now using
$wR^c_2u$
we conclude that
$\varphi \in u$
, as desired.
This shows that
$R^c_2\subseteq R^c_1$
. -
-
(9) Let
$\mathcal {M}=\langle W,R_1,R_2,V \rangle $
be a model with the identity relation
$R_1$
, and
$w\in W$
. Assume that
$\mathcal {M},w\vDash N'\psi $
, to show that
$\mathcal {M},w\vDash \varphi \leftrightarrow N'(\psi \land \varphi )$
. By assumption,
$R_1(w)\vDash \psi $
and
$R_2(w)\vDash \neg \psi $
. Thus
$R_2(w)\vDash \neg (\psi \land \varphi )$
. Moreover, due to
$R_1(w)=\{w\}$
,
$\mathcal {M},w\vDash \psi $
.Suppose that
$\mathcal {M},w\vDash \varphi $
. Then
$\mathcal {M},w\vDash \psi \land \varphi $
. Since
$R_1(w)=\{w\}$
,
$R_1(w)\vDash \psi \land \varphi $
, and thus
$\mathcal {M},w\vDash N'(\psi \land \varphi )$
.Conversely, suppose that
$\mathcal {M},w\vDash N'(\psi \land \varphi )$
, then
$R_1(w)\vDash \psi \land \varphi $
. Since
$R_1(w)=\{w\}$
, we derive that
$\mathcal {M},w\vDash \psi \land \varphi $
, and thus
$\mathcal {M},w\vDash \varphi $
.Define the canonical frame
$\mathcal {F}^c=\langle W^c,R^c_1,R^c_2 \rangle $
as in Definition 42. In what follows, we show that
$R^c_1=\{(w,w)\mid w\in W^c\}$
; equivalently, for all
$w,u\in W^c$
,
$wR^c_1u$
iff
$w=u$
.Let
$w,u\in W^c$
. Assume that
$wR^c_1u$
, to show that
$w=u$
, it suffices to show that
$w\subseteq u$
. If
$N'\psi \in w$
for no
$\psi $
, then clearly, from the assumption it follows that
$w=u$
. If
$N'\psi \in w$
for some
$\psi $
. If
$\varphi \in w$
, then by axiom N
$'$
ID1, we infer that
$N'(\psi \land \varphi )\in w$
. This plus the assumption implies that
$\varphi \in u$
.Conversely, suppose that
$w=u$
, to prove that
$wR^c_1u$
. If
$N'\psi \in w$
for no
$\psi $
, then by supposition, it is obvious that
$wR^c_1u$
. If
$N'\psi \in w$
for some
$\psi $
, then for any
$\varphi $
, if
$N'(\psi \land \varphi )\in w$
, then by axiom N
$'$
ID1, we derive that
$\varphi \in w$
, thus
$\varphi \in u$
, and therefore
$wR^c_1u$
, as desired. -
(10) Let
$\mathcal {M}=\langle W,R_1,R_2,V \rangle $
be a model with the identity relation
$R_2$
, and
$w\in W$
. Suppose that
$\mathcal {M},w\vDash N'\psi $
, to show that
$\mathcal {M},w\vDash \varphi \leftrightarrow N'(\psi \vee \neg \varphi )$
. By supposition,
$R_1(w)\vDash \psi $
and
$R_2(w)\vDash \neg \psi $
. Thus
$R_1(w)\vDash \psi \vee \neg \varphi $
. Moreover, due to
$R_2(w)=\{w\}$
,
$\mathcal {M},w\vDash \neg \psi $
.Assume that
$\mathcal {M},w\vDash \varphi $
. If
$\mathcal {M},w\nvDash N'(\psi \vee \neg \varphi )$
, then either
$R_1(w)\nvDash \psi \vee \neg \varphi $
or
$R_2(w)\nvDash \neg (\psi \vee \neg \varphi )$
. The first case contradicts
$R_1(w)\vDash \psi \vee \neg \varphi $
. If the second case holds, due to
$R_2(w)=\{w\}$
, then
$\mathcal {M},w\nvDash \neg (\psi \vee \neg \varphi )$
, equivalently,
$\mathcal {M},w\nvDash \neg \psi \land \varphi $
. This contradicts
$\mathcal {M},w\vDash \neg \psi $
and the assumption. Hence,
$\mathcal {M},w\vDash N'(\psi \vee \neg \varphi )$
.Conversely, assume that
$\mathcal {M},w\vDash N'(\psi \vee \neg \varphi )$
, to show that
$\mathcal {M},w\vDash \varphi $
. By assumption,
$R_2(w)\vDash \neg (\psi \vee \neg \varphi )$
. As
$R_2(w)=\{w\}$
, we infer that
$\mathcal {M},w\vDash \neg (\psi \vee \neg \varphi )$
, and thus
$\mathcal {M},w\vDash \varphi $
.Define the canonical frame
$\mathcal {F}^c=\langle W^c,R^c_1,R^c_2 \rangle $
as in Definition 42. In what follows, we show that
$R^c_2=\{(w,w)\mid w\in W^c\}$
; equivalently, for all
$w,u\in W^c$
,
$wR^c_2u$
iff
$w=u$
.Let
$w,u\in W^c$
. Suppose that
$wR^c_2u$
, to show that
$w=u$
, it suffices to show that
$w\subseteq u$
. If
$N'\psi \in w$
for no
$\psi $
, then clearly, from supposition it follows that
$w=u$
. If
$N'\psi \in w$
for some
$\psi $
. If
$\varphi \in w$
, then by axiom N
$'$
ID2, we infer that
$N'(\psi \vee \neg \varphi )\in w$
. This plus the supposition implies that
$\varphi \in u$
.Conversely, assume that
$w=u$
, to prove that
$wR^c_2u$
. If
$N'\psi \in w$
for no
$\psi $
, then by assumption, it is obvious that
$wR^c_2u$
. If
$N'\psi \in w$
for some
$\psi $
, then for any
$\varphi $
, if
$N'(\psi \vee \neg \varphi )\in w$
, then by axiom N
$'$
ID2, we derive that
$\varphi \in w$
, thus
$\varphi \in u$
, and therefore
$wR^c_2u$
, as desired.
Note that the above theorem gives us a lot of axiomatizations. In particular, from (10), we know that
$\mathbf {K^{\mathbf { N'}}}+\text {N}'\text {ID2}$
is a minimal axiomatization of the logic
$\mathcal {L}(W)$
of false beliefs which has W as the sole modality. With (5) as well, we get that
$\mathbf {K^{\mathbf {N'}}}+\text {N}'\text {ID2}+\text {N}'\text {41}$
is the transitive axiomatization of
$\mathcal {L}(W)$
, which solves an open question raised in the literature of the logic of false beliefs (see, for instance, [Reference Gilbert and Venturi24, Reference Steinsvold40]). From (9), we obtain the minimal axiomatization of the logic of weak essence and strong accident [Reference Pan and Yang34]. Moreover, from (7) and (8), it follows that
$\mathbf {K^{N'}}+\text {MIX1}+\text {MIX2}$
is the minimal axiomatization of the logic of belief inconsistency.
5 The operator
$N"$
In [Reference Humberstone28, p. 229], Humberstone also proposes another variation of N, denoted
$N"$
, which is defined as
$N"\varphi :=\Box _1\varphi \vee \neg \Box _2\varphi $
. Syntactically, by extending the language of propositional logic with the sole modality
$N"$
, we obtain the language
$\mathcal {L}(N")$
. Semantically, given a model
$\mathcal {M}=\langle W,R_1,R_2,V \rangle $
and
$w\in W$
,
$\Box _1$
and
$\Box _2$
are interpreted as before, and
$$\begin{align*}\begin{array}{lll} \mathcal{M},w\vDash N"\varphi & \Longleftrightarrow & R_1(w)\vDash\varphi\text{ or }R_2(w)\nvDash\varphi. \\ \end{array} \end{align*}$$
We observe the following almost-definability schemas, which guides us to propose the desired canonical model later:
$$\begin{align*}\begin{array}{ll} \neg N"\psi\to (\Box_1\varphi\leftrightarrow (N"\varphi\land \neg N"(\varphi\land\psi)))& (\textbf{N}"\textbf{AD1}) \\ \neg N"\psi\to (\Box_2\varphi\leftrightarrow\neg N"(\varphi\land\psi)) & (\textbf{N}"\textbf{AD2}).\\ \end{array} \end{align*}$$
Proposition 47. Let
$\mathcal {F}=\langle W,R_1,R_2 \rangle $
such that
$R_2\subseteq R_1$
. Then
-
(1)
$\mathcal {F}\vDash \neg N"\psi \to (\Box _1\varphi \leftrightarrow (N"\varphi \land \neg N"(\varphi \land \psi ))).$
-
(2)
$\vDash \neg N"\psi \to (\Box _2\varphi \leftrightarrow \neg N"(\varphi \land \psi ))$
.
Proof. Let
$\mathcal {M}=\langle W,R_1,R_2,V \rangle $
be a model such that
$R_2\subseteq R_1$
and
$w\in W$
. Suppose that
$\mathcal {M},w\vDash \neg N"\psi $
, then
$R_1(w)\nvDash \psi $
and
$R_2(w)\vDash \psi $
.
-
(1) It remains only to show that
$\mathcal {M},w\vDash \Box _1\varphi \leftrightarrow (N"\varphi \land \neg N"(\varphi \land \psi ))$
.Assume that
$\mathcal {M},w\vDash \Box _1\varphi $
. Then
$R_1(w)\vDash \varphi $
, and thus
$\mathcal {M},w\vDash N"\varphi $
. From
$R_1(w)\nvDash \psi $
, it follows that
$R_1(w)\nvDash \varphi \land \psi $
; moreover, since
$R_1(w)\vDash \varphi $
and
$R_2\subseteq R_1$
, we obtain
$R_2(w)\vDash \varphi $
, and thus
$R_2(w)\vDash \varphi \land \psi $
. This implies that
$\mathcal {M},w\vDash \neg N"(\varphi \land \psi )$
. Therefore,
$\mathcal {M},w\vDash N"\varphi \land \neg N"(\varphi \land \psi )$
.Conversely, assume that
$\mathcal {M},w\vDash N"\varphi \land \neg N"(\varphi \land \psi )$
. Then from
$\mathcal {M},w\vDash N"\varphi $
, it follows that
$R_1(w)\vDash \varphi $
or
$R_2(w)\nvDash \varphi $
; from
$\mathcal {M},w\vDash \neg N"(\varphi \land \psi )$
, it follows that
$R_2(w)\vDash \varphi \land \psi $
, thus
$R_2(w)\vDash \varphi $
. Therefore,
$R_1(w)\vDash \varphi $
, which entails that
$\mathcal {M},w\vDash \Box _1\varphi $
. -
(2) It suffices to prove that
$\mathcal {M},w\vDash \Box _2\varphi \leftrightarrow \neg N"(\varphi \land \psi )$
.Assume that
$\mathcal {M},w\vDash \Box _2\varphi $
. Then
$R_2(w)\vDash \varphi $
. Since
$R_2(w)\vDash \psi $
, it follows that
$R_2(w)\vDash \varphi \land \psi $
. Moreover, as
$R_1(w)\nvDash \psi $
, we infer that
$R_1(w)\nvDash \varphi \land \psi $
. Hence,
$\mathcal {M},w\vDash \neg N"(\varphi \land \psi )$
.Conversely, assume that
$\mathcal {M},w\vDash \neg N"(\varphi \land \psi )$
. Then
$R_2(w)\vDash \varphi \land \psi $
, thus
$R_2(w)\vDash \varphi $
, and hence
$\mathcal {M},w\vDash \Box _2\varphi $
.
Note that the proof of (2) does not need any semantic restriction of accessibility relations, whereas (1) only uses
$R_2\subseteq R_1$
.
Unlike N and
$N'$
, the operator
$N"$
does not have the property of convexity. In other words, the transition from
$\varphi \to \psi $
and
$\psi \to \chi $
to
$(N"\varphi \land N"\chi )\to N"\psi $
does not preserve validity.
Proposition 48.
$\dfrac {\varphi \to \psi ~~~\psi \to \chi }{(N"\varphi \land N"\chi )\to N"\psi }$
is not validity-preserving.
Proof. Since
$\vDash p\land q\to q$
and
$\vDash q\to q\lor r$
, it remains only to show that
$\nvDash N"(p\land q)\land N"(q\vee r)\to N"q$
. Consider the following model
$\mathcal {M}$
(other valuations are inessential):
Since
$wR_2v$
and
$\mathcal {M},v\nvDash p\land q$
, we have
$R_2(w)\nvDash p\land q$
, thus
$\mathcal {M},w\vDash N"(p\land q)$
. Moreover, as
$R_1(w)=\{u\}$
and
$\mathcal {M},u\vDash q\vee r$
, we infer that
$R_1(w)\vDash q\vee r$
, thus
$\mathcal {M},w\vDash N"(q\vee r)$
. However,
$R_1(w)\nvDash q$
and
$R_2(w)\vDash q$
, hence
$\mathcal {M},w\nvDash N"q$
. Therefore,
$\nvDash N"(p\land q)\land N"(q\vee r)\to N"q$
.
Despite this,
$N"$
has a property called ‘coconvexity’.Footnote
15
That is, the transition from
$\varphi \to \psi $
and
$\psi \to \chi $
to
$N"\psi \to (N"\varphi \lor N"\chi )$
preserves validity.
Proposition 49.
$\dfrac {\varphi \to \psi ~~~\psi \to \chi }{N"\psi \to (N"\varphi \lor N"\chi )}$
is validity-preserving.
Proof. Suppose that
$\vDash \varphi \to \psi $
and
$\vDash \psi \to \chi $
, to show that
$\vDash N"\psi \to (N"\varphi \vee N"\chi )$
. Let
$\mathcal {M}=\langle W,R_1,R_2,V \rangle $
be a model and
$w\in W$
. Assume that
$\mathcal {M},w\vDash N"\psi $
. Then
$R_1(w)\vDash \psi $
or
$R_2(w)\nvDash \psi $
. If the former holds, then from
$\vDash \psi \to \chi $
, it follows that
$R_1(w)\vDash \chi $
, and thus
$\mathcal {M},w\vDash N"\chi $
; if the latter holds, then from
$\vDash \varphi \to \psi $
, it follows that
$R_2(w)\nvDash \varphi $
, and thus
$\mathcal {M},w\vDash N"\varphi $
. Therefore,
$\mathcal {M},w\vDash N"\varphi \vee N"\chi $
, as desired.
5.1 Axiomatization
As commented in Remark 5, we can axiomatize
$\mathcal {L}(N")$
over various frames. Due to space limitation, we illustrate this with the minimal logic.
5.1.1 Minimal system and soundness
Definition 50. The minimal system of
$\mathcal {L}(N")$
, denoted
$\mathbf {K^{N"}}$
, consists of the following axioms and inference rules:
$$\begin{align*}\begin{array}{ll} \text{PC} & \text{All instances of propositional tautologies} \\ \text{C1} & N"\varphi\land N"\psi\to N"(\varphi\land\psi)\\\text{C2} & N"(\varphi\land\psi)\to N"\varphi\lor N"\psi\\ \text{MP} & \text{From }\varphi\text{ and }\varphi\to\psi\text{ infer }\psi\\ \text{N}"\text{R1} & \text{From }\varphi\text{ infer }N"\varphi \\ \text{N}"\text{R2} & \text{From }\varphi\to\psi\text{ and }\psi\to\chi\text{ infer }N"\psi\to (N"\varphi\vee N"\chi).\\ \end{array} \end{align*}$$
Notions of derivation and theorems are defined as usual. The following proposition is important in the proof later.
Proposition 51.
-
(1) If
$\vdash \varphi \to \chi $
, then
$\vdash N"\varphi \to N"(\varphi \land \psi )\vee N"\chi $
. -
(2) If
$\vdash \varphi \to \chi $
, then
$\vdash N"(\chi \land \psi )\to N"(\varphi \land \psi )\vee N"\psi $
. -
(3) If
$\vdash \varphi \to \chi $
, then
$\vdash N"(\chi \land \psi )\land N"\varphi \to N"(\varphi \land \psi )$
. -
(4) If
$\vdash \varphi \leftrightarrow \psi $
, then
$\vdash N"\varphi \leftrightarrow N"\psi $
.
Proof.
-
(1) Suppose that
$\vdash \varphi \to \chi $
. Since
$\vdash \varphi \land \psi \to \varphi $
, by rule
$\text {N}"\text {R2}$
, we infer that
$\vdash N"\varphi \to N"(\varphi \land \psi )\vee N"\chi $
. -
(2) Assume that
$\vdash \varphi \to \chi $
. Then
$\vdash \varphi \land \psi \to \chi \land \psi $
. Moreover,
$\vdash \chi \land \psi \to \psi $
. Now using
$\text {N}"\text {R2}$
, we derive that
$\vdash N"(\chi \land \psi )\to N"(\varphi \land \psi )\vee N"\psi $
. -
(3) Suppose that
$\vdash \varphi \to \chi $
. By (2),
$\vdash N"(\chi \land \psi )\to N"(\varphi \land \psi )\vee N"\psi $
. Then by axiom C1, we obtain that
$\vdash N"\varphi \land N"\psi \to N"(\varphi \land \psi )$
. Therefore,
$\vdash N"(\chi \land \psi )\land N"\varphi \to N"(\varphi \land \psi )$
. -
(4) Assume that
$\vdash \varphi \leftrightarrow \psi $
. Then
$\vdash \varphi \to \psi $
and
$\vdash \psi \to \varphi $
. Using rule
$\text {N}"\text {R2}$
, we get that
$\vdash N"\psi \to (N"\varphi \vee N"\varphi )$
, and thus
$\vdash N"\psi \to N"\varphi $
. Similarly, we can show that
$\vdash N"\varphi \to N"\psi $
. Therefore,
$\vdash N"\varphi \leftrightarrow N"\psi $
.
Proposition 52.
$\mathbf {K^{N"}}$
is sound with respect to the class of all frames.
Proof. We only need to show the validity of axioms C1 and C2, since the validity-preserving of
$\text {N}"\text {R2}$
has been shown in Proposition 49, and other axiom and inference rules are straightforward. Let
$\mathcal {M}=\langle W,R_1,R_2,V \rangle $
be a model and
$w\in W$
.
For C1, suppose that
$\mathcal {M},w\vDash N"\varphi $
and
$\mathcal {M},w\vDash N"\psi $
. Then
$R_1(w)\vDash \varphi $
or
$R_2(w)\nvDash \varphi $
, and
$R_1(w)\vDash \psi $
or
$R_2(w)\nvDash \psi $
. If
$R_2(w)\nvDash \varphi $
or
$R_2(w)\nvDash \psi $
, then
$R_2(w)\nvDash \varphi \land \psi $
, and thus
$\mathcal {M},w\vDash N"(\varphi \land \psi )$
. Otherwise, that is, if
$R_1(w)\vDash \varphi $
and
$R_1(w)\vDash \psi $
, then
$R_1(w)\vDash \varphi \land \psi $
, and thus again
$\mathcal {M},w\vDash N"(\varphi \land \psi )$
. Therefore,
$\mathcal {M},w\vDash N"(\varphi \land \psi )$
.
For C2, assume that
$\mathcal {M},w\vDash N"(\varphi \land \psi )$
, then
$R_1(w)\vDash \varphi \land \psi $
or
$R_2(w)\nvDash \varphi \land \psi $
. If the former is the case, then
$R_1(w)\vDash \varphi $
and
$R_1(w)\vDash \psi $
, which implies that
$\mathcal {M},w\vDash N"\varphi $
and
$\mathcal {M},w\vDash N"\psi $
; if the latter is the case, then
$R_2(w)\nvDash \varphi $
or
$R_2(w)\nvDash \psi $
, which implies that
$\mathcal {M},w\vDash N"\varphi $
or
$\mathcal {M},w\vDash N"\psi $
. Therefore,
$\mathcal {M},w\vDash N"\varphi \vee N"\psi $
, as desired.
5.1.2 Completeness
We continue with the completeness of
$\mathbf {K^{N"}}$
. This is shown via a construction of the canonical model, where again, the crucial part is the definition of canonical relations.
Definition 53. The canonical model for
$\mathbf {K^{N"}}$
is the tuple
$\mathcal {M}^c=\langle W^c,R^c_1,R^c_2,V^c \rangle $
, where
-
•
$W^c=\{w\mid w\text { is a maximal consistent set for }\mathbf {K^{N"}}\}$
; -
• if
$\neg N"\psi \in w$
for no
$\psi $
, then
$wR^c_1u$
iff
$w=u$
, and
$wR^c_2u$
iff
$w=u$
; -
• if
$\neg N"\psi \in w$
for some
$\psi $
, then
$wR^c_1u$
iff for all
$\varphi $
, if
$N"\varphi \land \neg N"(\varphi \land \psi )\in w$
, then
$\varphi \in u$
, and
$wR^c_2u$
iff for all
$\varphi $
, if
$\neg N"(\varphi \land \psi )\in w$
, then
$\varphi \in u$
; -
•
$V^c(p)=\{w\in W^c\mid p\in w\}$
.
It is required that the
$\psi $
in
$N"\varphi \land \neg N"(\varphi \land \psi )\in w$
and
$\neg N"(\varphi \land \psi )\in w$
be the same as that in
$\neg N"\psi \in w$
. Note that the choice of
$\psi $
in the above second case of the canonical relations is inessential to
$R_1^c$
and
$R_2^c$
, as shown in Remark 10. It is also worth noting that
$R_1^c$
and
$R^c_2$
are inspired by the almost-definability schemas
$(\textbf {N}"\textbf {AD1})$
and
$(\textbf {N}"\textbf {AD2})$
, respectively, based on the analysis of §2. Recall that in the construction of the canonical model for the minimal logic of
$\mathcal {L}(\Box _1,\Box _2)$
, the canonical relations
$R_1^c$
and
$R^c_2$
are defined as, respectively,
$wR^c_1u$
iff for all
$\varphi $
, if
$\Box _1\varphi \in w$
then
$\varphi \in u$
, and
$wR^c_2u$
iff for all
$\varphi $
, if
$\Box _2\varphi \in w$
then
$\varphi \in u$
. Now given a precondition that
$\neg N"\psi \in w$
for some
$\psi $
, according to
$(\textbf {N}"\textbf {AD1})$
,
$\Box _1\varphi \in w$
can be replaced with
$N"\varphi \land \neg N"(\varphi \land \psi )\in w$
, and according to
$(\textbf {N}"\textbf {AD2})$
,
$\Box _2\varphi \in w$
can be replaced with
$\neg N"(\varphi \land \psi )\in w$
; otherwise, we let w access and only access itself.
Propositions 54 and 55 list some logical properties of
$\mu _1$
and
$\mu _2$
, respectively. They are important in the proof of Lemma 56 below.
Proposition 54. Let
$w\in W^c$
such that
$\neg N"\varphi \in w$
. Define
$\mu _1(w)=\{\chi \mid N"\chi \land \neg N"(\chi \land \varphi )\in w\}$
. Then
-
(1)
$\mu _1(w)\neq \emptyset $
. -
(2) If
$\psi ,\chi \in \mu _1(w)$
, then
$\psi \land \chi \in \mu _1(w)$
. -
(3) If
$\psi \in \mu _1(w)$
and
$\vdash \psi \to \chi $
, then
$\chi \in \mu _1(w)$
.
Proof. Suppose
$w\in W^c$
such that
$\neg N"\varphi \in w$
.
-
(1) By axiom PC and rule
$\text {N}"\text {R1}$
,
$N"\top \in w$
; by supposition and Proposition 51(4),
$\neg N"(\top \land \varphi )\in w$
. Thus
$N"\top \land \neg N"(\top \land \varphi )\in w$
, and hence
$\top \in \mu _1(w)$
. This entails that
$\mu _1(w)\neq \emptyset $
. -
(2) Assume that
$\psi ,\chi \in \mu _1(w)$
. Then
$N"\psi \land \neg N"(\psi \land \varphi )\in w$
and
$N"\chi \land \neg N"(\chi \land \varphi )\in w$
. By axiom C1,
$N"(\psi \land \chi )\in w$
; by axioms C2, PC and Proposition 51(4), we can show that
$\neg N"((\psi \land \chi )\land \varphi )\in w$
. Thus
$N"(\psi \land \chi )\land \neg N"((\psi \land \chi )\land \varphi )\in w$
, and hence
$\psi \land \chi \in \mu _1(w)$
. -
(3) Assume that
$\psi \in \mu _1(w)$
and
$\vdash \psi \to \chi $
. Then
$N"\psi \land \neg N"(\psi \land \varphi )\in w$
. By Proposition 51(1),
$N"\chi \in w$
; by Proposition 51(3),
$\neg N"(\chi \land \varphi )\in w$
. Thus
$N"\chi \land \neg N"(\chi \land \varphi )\in w$
, and hence
$\chi \in \mu _1(w)$
.
Proposition 55. Let
$w\in W^c$
such that
$\neg N"\psi \in w$
. Define
$\mu _2(w)=\{\chi \mid \neg N"(\chi \land \psi )\in w\}$
. Then
-
(1)
$\mu _2(w)\neq \emptyset $
. -
(2) If
$\varphi ,\chi \in \mu _2(w)$
, then
$\varphi \land \chi \in \mu _2(w)$
. -
(3) If
$\varphi \in \mu _2(w)$
and
$\vdash \varphi \to \chi $
, then
$\chi \in \mu _2(w)$
.
Proof. Suppose that
$w\in W^c$
such that
$\neg N"\psi \in w$
.
-
(1) By supposition and axiom PC and Proposition 51(4), we have
$\neg N"(\top \land \psi )\in w$
, and thus
$\top \in \mu _2(w)$
. -
(2) Assume that
$\varphi ,\chi \in \mu _2(w)$
. Then
$\neg N"(\varphi \land \psi )\in w$
and
$\neg N"(\chi \land \psi )\in w$
. Then by axioms C2 and PC and Proposition 51(4), it follows that
$\neg N"((\varphi \land \chi )\land \psi )\in w$
, and thus
$\varphi \land \chi \in \mu _2(w)$
. -
(3) Assume that
$\varphi \in \mu _2(w)$
and
$\vdash \varphi \to \chi $
. Then
$\neg N"(\varphi \land \psi )\in w$
. By
$\vdash \varphi \to \chi $
and Proposition 51(2), it follows that
$\neg N"(\chi \land \psi )\in w$
, and thus
$\chi \in \mu _2(w)$
.
Lemma 56. For all
$w\in W^c$
, for all
$\varphi \in \mathcal {L}(N")$
, we have
$$ \begin{align*}\mathcal{M}^c,w\vDash\varphi\text{ iff }\varphi\in w.\end{align*} $$
Proof. By induction on
$\varphi $
, where the nontrivial case is
$N"\varphi $
.
Suppose that
$N"\varphi \in w$
, to show that
$\mathcal {M}^c,w\vDash N"\varphi $
. If
$R^c_1(w)\vDash \varphi $
, then we immediately have
$\mathcal {M}^c,w\vDash N"\varphi $
. Otherwise, that is,
$R^c_1(w)\nvDash \varphi $
, it remains only to show that
$R^c_2(w)\nvDash \varphi $
. It follows by induction hypothesis that there exists
$u\in W^c$
such that
$wR^c_1u$
and
$\varphi \notin u$
. According to the definition of
$R^c_1$
and
$R^c_2$
, we distinguish two cases.
-
•
$\neg N"\psi \in w$
for no
$\psi $
. Then as
$wR^c_1u$
, we have
$w=u$
, and thus
$\varphi \notin w$
, which by induction hypothesis implies that
$\mathcal {M}^c,w\nvDash \varphi $
. Since
$w=w$
, we infer that
$wR^c_2w$
, and thus
$R^c_2(w)\nvDash \varphi $
. -
•
$\neg N"\psi \in w$
for some
$\psi $
. In this case, from
$wR^c_1u$
and
$\varphi \notin u$
and
$N"\varphi \in w$
, it follows that
$\neg N"(\varphi \land \psi )\notin w$
, that is,
$N"(\varphi \land \psi )\in w$
. To show that
$R^c_2(w)\nvDash \varphi $
, by Lindenbaum’s Lemma and induction hypothesis, it suffices to show that
$\mu _2(w)\cup \{\neg \varphi \}$
is consistent, where
$\mu _2(w)=\{\chi \mid \neg N"(\chi \land \psi )\in w\}$
. By Lemma 55(1),
$\mu _2(w)\neq \emptyset $
.If
$\mu _2(w) \cup \{\neg \varphi \}$
is inconsistent, then there are
$\chi _1,\dots ,\chi _n\in \mu _2(w)$
such that
$$ \begin{align*}\vdash\chi_1\land\cdots\land \chi_n\to\varphi.\end{align*} $$
By Lemma 55(2) and (3), we obtain that
$\varphi \in \mu _2(w)$
, thus
$\neg N"(\varphi \land \psi )\in w$
: a contradiction. Thus
$\mu _2(w)\cup \{\neg \varphi \}$
is consistent, as desired.
Conversely, assume that
$N"\varphi \notin w$
, to prove that
$\mathcal {M}^c,w\nvDash N"\varphi $
, that is,
$R^c_1(w)\nvDash \varphi $
and
$R^c_2(w)\vDash \varphi $
. By assumption,
$\neg N"\varphi \in w$
. Using axiom PC and Proposition 51(4), we derive that
$\neg N"(\varphi \land \varphi )\in w$
. Then for all
$u\in W^c$
such that
$wR^c_2u$
, we have
$\varphi \in u$
, which by induction hypothesis entails that
$\mathcal {M}^c,u\vDash \varphi $
. This means that
$R^c_2(w)\vDash \varphi $
. By Lindenbaum’s Lemma and induction hypothesis, it remains only to show that
$\mu _1(w)\cup \{\neg \varphi \}$
is consistent, where
$\mu _1(w)=\{\chi \mid N"\chi \land \neg N"(\chi \land \varphi )\in w\}$
. By Lemma 54(1),
$\mu _1(w)\neq \emptyset $
.
If
$\mu _1(w)\cup \{\neg \varphi \}$
is inconsistent, then there are
$\chi _1,\dots ,\chi _n\in \mu _1(w)$
such that
$$ \begin{align*}\vdash \chi_1\land\cdots\land\chi_n\to\varphi.\end{align*} $$
By Lemma 54(2) and (3), we derive that
$\varphi \in \mu _1(w)$
, and thus
$N"\varphi \in w$
, which contradicts the assumption.
Theorem 57.
$\mathbf {K^{N"}}$
is sound and strongly complete with respect to the class of all frames.
Theorem 58.
$\mathbf {K^{N"}}$
is sound and strongly complete with respect to the class of all frames
$\langle W,R_1,R_2 \rangle ,$
where
$R_2\subseteq R_1$
.
Proof. By Theorem 57, it remains only to show that
$R^c_2\subseteq R^c_1$
. This is straightforward by definitions of
$R^c_1$
and
$R^c_2$
.
We can also axiomatize
$N"$
over special frames, like the case for the operator N, with the only change that all occurrences of N are replaced with
$\neg N"$
. The reason is that, as observed in Remark 5,
$\neg N"\varphi $
is equivalent to
$\Box _2\varphi \land \neg \Box _1\varphi $
, and if we think of
$\Box _2$
and
$\Box _1$
as
$\boxed {\mathrm{c}}$
and
$\Box $
, respectively, then
$\neg N"$
amounts to N.
6 The operator
$N"'$
Another variation of N, namely
$N"'$
, is also proposed in [Reference Humberstone28, p. 229], where
$N"'\varphi :=\Box _1\varphi \vee \Box _2\neg \varphi $
. Syntactically, by enriching the language of propositional logic with the sole modality
$N"'$
, we obtain the language
$\mathcal {L}(N"')$
. Semantically, as before, given a model
$\mathcal {M}=\langle W,R_1,R_2,V \rangle $
and
$w\in W$
,
$\Box _1$
and
$\Box _2$
are interpreted as before, and
$$\begin{align*}\begin{array}{lll} \mathcal{M},w\vDash N"'\varphi & \Longleftrightarrow & R_1(w)\vDash\varphi \text{ or }R_2(w)\vDash\neg\varphi. \\ \end{array} \end{align*}$$
This is exactly the semantics of the operator
$\boxplus $
in [Reference Fan13]. First, we observe the following almost-definability schemas, which guide us to propose the desired canonical model later:
$$\begin{align*}\begin{array}{lcr} \neg N"'\psi\to (\Box_1\varphi\leftrightarrow N"'\varphi\land N"'(\varphi\vee\psi)) & & (\textbf{N}"'\textbf{AD1}) \\ \neg N"'\psi\to (\Box_2\varphi\leftrightarrow N"'\neg\varphi\land N"'(\varphi\vee\psi)) & & (\textbf{N}"'\textbf{AD2}). \\ \end{array} \end{align*}$$
Proposition 59. Let
$\mathcal {F}=\langle W,R_1,R_2 \rangle $
such that
$R_1\subseteq R_2$
. Then
-
(1)
$\mathcal {F}\vDash \neg N"'\psi \to (\Box _1\varphi \leftrightarrow N"'\varphi \land N"'(\varphi \vee \psi ))$
. -
(2)
$\mathcal {F}\vDash \neg N"'\psi \to (\Box _2\varphi \leftrightarrow N"'\neg \varphi \land N"'(\varphi \vee \psi ))$
.
Proof. Let
$\mathcal {M}=\langle W,R_1,R_2,V \rangle $
be a model such that
$R_1\subseteq R_2$
and
$w\in W$
. Suppose that
$\mathcal {M},w\vDash \neg N"'\psi $
, then
$R_1(w)\nvDash \psi $
and
$R_2(w)\nvDash \neg \psi $
(thus
$R_2(w)\nvDash \neg (\varphi \vee \psi )$
).
-
(1) It suffices to show that
$\mathcal {M},w\vDash \Box _1\varphi \leftrightarrow N"'\varphi \land N"'(\varphi \vee \psi )$
.Firstly, assume that
$\mathcal {M},w\vDash \Box _1\varphi $
, then
$R_1(w)\vDash \varphi $
. Thus
$R_1(w)\vDash \varphi \vee \psi $
. It then follows that
$\mathcal {M},w\vDash N"'\varphi $
and
$\mathcal {M},w\vDash N"'(\varphi \vee \psi )$
.Conversely, assume, for a contradiction, that
$\mathcal {M},w\vDash N"'\varphi $
and
$\mathcal {M},w\vDash N"'(\varphi \vee \psi )$
but
$\mathcal {M},w\nvDash \Box _1\varphi $
. By
$\mathcal {M},w\nvDash \Box _1\varphi $
, we have
$R_1(w)\nvDash \varphi $
, and then due to
$\mathcal {M},w\vDash N"'\varphi $
, we infer that
$R_2(w)\vDash \neg \varphi $
. Moreover, by
$\mathcal {M},w\vDash N"'(\varphi \vee \psi )$
, we derive that
$R_1(w)\vDash \varphi \vee \psi $
or
$R_2(w)\vDash \neg (\varphi \vee \psi )$
, and thus
$R_1(w)\vDash \varphi \vee \psi $
. This entails that
$R_1(w)\nvDash \neg \varphi $
: otherwise, we would have
$R_1(w)\vDash \psi $
, a contradiction. Since
$R_1\subseteq R_2$
, it follows that
$R_2(w)\nvDash \neg \varphi $
: a contradiction. -
(2) It remains only to prove that
$\mathcal {M},w\vDash \Box _2\varphi \leftrightarrow N"'\neg \varphi \land N"'(\varphi \vee \psi )$
.Firstly, assume that
$\mathcal {M},w\vDash \Box _2\varphi $
, then
$R_2(w)\vDash \varphi $
. It follows immediately that
$\mathcal {M},w\vDash N"'\neg \varphi $
. If
$\mathcal {M},w\nvDash N"'(\varphi \vee \psi )$
, then
$R_1(w)\nvDash \varphi \vee \psi $
. As
$R_1\subseteq R_2$
,
$R_2(w)\nvDash \varphi \vee \psi $
, and thus
$R_2(w)\nvDash \varphi $
: a contradiction. Hence
$\mathcal {M},w\vDash N"'(\varphi \vee \psi )$
.Conversely, assume towards contradiction that
$\mathcal {M},w\vDash N"'\neg \varphi $
and
$\mathcal {M},w\vDash N"'(\varphi \vee \psi )$
, but
$\mathcal {M},w\nvDash \Box _2\varphi $
. From
$\mathcal {M},w\vDash N"'\neg \varphi $
, it follows that
$R_1(w)\vDash \neg \varphi $
or
$R_2(w)\vDash \varphi $
; from
$\mathcal {M},w\nvDash \Box _2\varphi $
, it follows that
$R_2(w)\nvDash \varphi $
. This entails that
$R_1(w)\vDash \neg \varphi $
. By
$\mathcal {M},w\vDash N"'(\varphi \vee \psi )$
, we obtain
$R_1(w)\vDash \varphi \vee \psi $
or
$R_2(w)\vDash \neg (\varphi \vee \psi )$
. If
$R_1(w)\vDash \varphi \vee \psi $
, then since
$R_1(w)\vDash \neg \varphi $
, it follows that
$R_1(w)\vDash \psi $
: a contradiction; if
$R_2(w)\vDash \neg (\varphi \vee \psi )$
, then
$R_2(w)\vDash \neg \psi $
: a contradiction again.
Unlike N and
$N'$
but like
$N"$
, the operator
$N"'$
does not have the property of convexity. In other words, the transition from
$\varphi \to \psi $
and
$\psi \to \chi $
to
$(N"'\varphi \land N"'\chi )\to N"'\psi $
does not preserve validity. Here we introduce some notation. We say that a frame (model) with accessibility relations
$R_1$
and
$R_2$
is a
$\subseteq $
-frame (
$\subseteq $
-model, resp.), if
$R_1\subseteq R_2$
.
Proposition 60.
$\dfrac {\varphi \to \psi ~~~\psi \to \chi }{(N"'\varphi \land N"'\chi )\to N"'\psi }$
is not validity-preserving (even on
$\subseteq $
-frames).
Proof. Since
$\vDash p\land q\to q$
and
$\vDash q\to q\vee r$
, it remains only to show that
$\nvDash N"'(p\land q)\land N"'(q\vee r)\to N"'q$
. Consider the following model
$\mathcal {M}$
:
One may check that
$\mathcal {M}$
is a
$\subseteq $
-model. Moreover,
$R_2(w)\vDash \neg (p\land q)$
, thus
$\mathcal {M},w\vDash N"'(p\land q)$
;
$R_1(w)\vDash q\vee r$
, thus
$\mathcal {M},w\vDash N"'(q\vee r)$
. However,
$R_1(w)\nvDash q$
and
$R_2(w)\nvDash \neg q$
, thus
$\mathcal {M},w\nvDash N"'q$
. Therefore,
$\mathcal {M},w\nvDash N"'(p\land q)\land N"'(q\vee r)\to N"'q$
, as desired.
Despite this, like
$N"$
,
$N"'$
has the property of coconvexity. That is, the transition from
$\varphi \to \psi $
and
$\psi \to \chi $
to
$N"'\psi \to (N"'\varphi \lor N"'\chi )$
preserves validity.
Proposition 61.
$\dfrac {\varphi \to \psi ~~~\psi \to \chi }{N"'\psi \to (N"'\varphi \lor N"'\chi )}$
is validity-preserving.
Proof. Suppose that
$\vDash \varphi \to \psi $
and
$\vDash \psi \to \chi $
, to show that
$\vDash N"'\psi \to (N"'\varphi \lor N"'\chi )$
. For this, assume that there is a model
$\mathcal {M}=\langle W,R_1,R_2,V \rangle $
and
$w\in W$
such that
$\mathcal {M},w\vDash N"'\psi $
. By
$\mathcal {M},w\vDash N"'\psi $
, we have
$R_1(w)\vDash \psi $
or
$R_2(w)\vDash \neg \psi $
. If the former is the case, then by
$\vDash \psi \to \chi $
, we infer that
$R_1(w)\vDash \chi $
, which implies that
$\mathcal {M},w\vDash N"'\chi $
; if the latter is the case, then by
$\vDash \varphi \to \psi $
, we derive that
$R_2(w)\vDash \neg \varphi $
, which entails that
$\mathcal {M},w\vDash N"'\varphi $
. Either case gives us
$\mathcal {M},w\vDash N"'\varphi \vee N"'\chi $
, as desired.
6.1 Axiomatizations
In this part, we axiomatize
$\mathcal {L}(N"')$
over various frames. We start with the minimal logic.
6.1.1 Minimal logic and soundness
Definition 62. The minimal system of
$\mathcal {L}(N"')$
, denoted
$\mathbf {K^{N"'}}$
, consists of the following axioms and inference rules:
$$\begin{align*}\begin{array}{ll} \text{PC} & \text{All instances of propositional tautologies} \\\text{D1} & N"'\top\\\text{D2} & N"'\bot\\\text{D3} & N"'\varphi\land N"'\psi\to N"'(\varphi\land\psi)\\\text{D4} & N"'\varphi\land N"'\psi\to N"'(\varphi\lor\psi)\\\text{D5} & N"'\varphi\to N"'(\varphi\vee\psi)\vee N"'(\neg\varphi\vee\chi)\\\text{D6} & \neg N"'\psi\land N"'\neg\varphi\land N"'(\varphi\vee\psi)\to N"'\varphi\\\end{array} \end{align*}$$
$$\begin{align*}\begin{array}{ll}\text{MP} & \text{From }\varphi\text{ and }\varphi\to\psi\text{ infer }\psi\\\text{N}"'\text{R1} & \text{From }\varphi\to\psi\text{ and }\psi\to\chi\text{ infer }N"'\psi\to (N"'\varphi\vee N"'\chi)\\\text{N}"'\text{R2} & \text{From }\psi\to\chi\text{ infer }\neg N"'\varphi\land N"'\psi\land N"'(\psi\vee\varphi)\to N"'\chi\\\text{N}"'\text{R3} & \text{From }\psi\to\neg\chi\text{ infer }\neg N"'\varphi\land N"'\neg\psi\land N"'(\psi\vee\varphi)\to N"'\chi.\\ \end{array} \end{align*}$$
As before, all these axioms and inference rules can be obtained according to the need of showing that the truth lemma (Lemma 68) holds and that the canonical model is as desired. Axiom D6 plays the core role in guaranteeing the canonical model below to be a
$\subseteq $
-model. The following result is derivable from
$\text {N}"'\text {R1}$
and
$\text {N}"'\text {R2}$
.
Proposition 63.
-
(1) If
$\vdash \varphi \leftrightarrow \psi $
, then
$\vdash N"'\varphi \leftrightarrow N"'\psi $
. -
(2) If
$\vdash \psi \to \chi $
, then
$\vdash \neg N"'\varphi \land N"'(\psi \vee \varphi )\to N"'(\chi \vee \varphi )$
.
Proposition 64.
$\mathbf {K^{N"'}}$
is sound with respect to the class of all
$\subseteq $
-frames.
Proof. The soundness of
$\text {N}"'\text {R1}$
has been shown in Proposition 61. The verifications for D1 and D2 are straightforward. Let
$\mathcal {M}=\langle W,R_1,R_2,V \rangle $
be a model such that
$R_1\subseteq R_2$
and
$w\in W$
.
For D3. Assume that
$\mathcal {M},w\vDash N"'\varphi $
and
$\mathcal {M},w\vDash N"'\psi $
, to show that
$\mathcal {M},w\vDash N"'(\varphi \land \psi )$
. By assumption,
$R_1(w)\vDash \varphi $
or
$R_2(w)\vDash \neg \varphi $
, and
$R_1(w)\vDash \psi $
or
$R_2(w)\vDash \neg \psi $
. If
$R_2(w)\vDash \neg \varphi $
or
$R_2(w)\vDash \neg \psi $
, then
$R_2(w)\vDash \neg (\varphi \land \psi )$
, and thus
$\mathcal {M},w\vDash N"'(\varphi \land \psi )$
; otherwise, then
$R_1(w)\vDash \varphi $
and
$R_1(w)\vDash \psi $
, and thus
$R_1(w)\vDash \varphi \land \psi $
, and we also have
$\mathcal {M},w\vDash N"'(\varphi \land \psi )$
.
For D4. Suppose that
$\mathcal {M},w\vDash N"'\varphi $
and
$\mathcal {M},w\vDash N"'\psi $
, to prove that
$\mathcal {M},w\vDash N"'(\varphi \vee \psi )$
. By supposition,
$R_1(w)\vDash \varphi $
or
$R_2(w)\vDash \neg \varphi $
, and
$R_1(w)\vDash \psi $
or
$R_2(w)\vDash \neg \psi $
. If
$R_1(w)\vDash \varphi $
or
$R_1(w)\vDash \psi $
, then
$R_1(w)\vDash \varphi \vee \psi $
, and thus
$\mathcal {M},w\vDash N"'(\varphi \vee \psi )$
; otherwise, we would have
$R_2(w)\vDash \neg \varphi $
and
$R_2(w)\vDash \neg \psi $
, which implies that
$R_2(w)\vDash \neg (\varphi \vee \psi )$
, and hence
$\mathcal {M},w\vDash N"'(\varphi \vee \psi )$
again. Therefore
$\mathcal {M},w\vDash N"'(\varphi \vee \psi )$
.
For D5. Assume that
$\mathcal {M},w\vDash N"'\varphi $
. Then
$R_1(w)\vDash \varphi $
or
$R_2(w)\vDash \neg \varphi $
. The first case implies that
$R_1(w)\vDash \varphi \vee \psi $
, thus
$\mathcal {M},w\vDash N"'(\varphi \vee \psi )$
. The second case implies that
$R_2(w)\vDash \neg \varphi \vee \chi $
. Since
$R_1\subseteq R_2$
, it follows that
$R_1(w)\vDash \neg \varphi \vee \chi $
, hence
$\mathcal {M},w\vDash N"'(\neg \varphi \vee \chi )$
. Therefore,
$\mathcal {M},w\vDash N"'(\varphi \vee \psi )\vee N"'(\neg \varphi \vee \chi )$
.
For D6. Suppose that
$\mathcal {M},w\vDash \neg N"'\psi $
and
$\mathcal {M},w\vDash N"'\neg \varphi $
and
$\mathcal {M},w\vDash N"'(\varphi \vee \psi )$
, to prove that
$\mathcal {M},w\vDash N"'\varphi $
. By
$\mathcal {M},w\vDash \neg N"'\psi $
, we infer that
$R_1(w)\nvDash \psi $
and
$R_2(w)\nvDash \neg \psi $
. By
$\mathcal {M},w\vDash N"'\neg \varphi $
, we derive that
$R_1(w)\vDash \neg \varphi $
or
$R_2(w)\vDash \varphi $
. By
$\mathcal {M},w\vDash N"'(\varphi \vee \psi )$
, we obtain that
$R_1(w)\vDash \varphi \vee \psi $
or
$R_2(w)\vDash \neg (\varphi \vee \psi )$
. If
$R_2(w)\vDash \neg (\varphi \vee \psi )$
, then
$R_2(w)\vDash \neg \psi $
: a contradiction, and thus
$R_1(w)\vDash \varphi \vee \psi $
. From
$R_1(w)\nvDash \psi $
, it follows that
$R_1(w)\nvDash \neg \varphi $
, thus
$R_2(w)\vDash \varphi $
. Since
$R_1\subseteq R_2$
, we have
$R_1(w)\vDash \varphi $
, and therefore
$\mathcal {M},w\vDash N"'\varphi $
.
For
$\text {N}"'\text {R2}$
. Assume that
$\vDash \psi \to \chi $
and
$\mathcal {M},w\vDash \neg N"'\varphi \land N"'\psi \land N"'(\psi \vee \varphi )$
, to show that
$\mathcal {M},w\vDash N"'\chi $
. By
$\mathcal {M},w\vDash \neg N"'\varphi $
,
$R_1(w)\nvDash \varphi $
and
$R_2(w)\nvDash \neg \varphi $
. By
$\mathcal {M},w\vDash N"'\psi $
, it follows that
$R_1(w)\vDash \psi $
or
$R_2(w)\vDash \neg \psi $
. By
$\mathcal {M},w\vDash N"'(\psi \vee \varphi )$
,
$R_1(w)\vDash \psi \vee \varphi $
or
$R_2(w)\vDash \neg (\psi \vee \varphi )$
. Since
$R_2(w)\nvDash \neg \varphi $
, we have
$R_2(w)\nvDash \neg (\psi \vee \varphi )$
, and thus
$R_1(w)\vDash \psi \vee \varphi $
. Moreover, it is impossible that
$R_2(w)\vDash \neg \psi $
: otherwise, as
$R_1\subseteq R_2$
, we get
$R_1(w)\vDash \neg \psi $
, and then
$R_1(w)\vDash \varphi $
, a contradiction. This shows that
$R_1(w)\vDash \psi $
. Then by assumption, we infer that
$R_1(w)\vDash \chi $
, and thus
$\mathcal {M},w\vDash N"'\chi $
.
For
$\text {N}"'\text {R3}$
. Suppose that
$\vDash \psi \to \neg \chi $
and
$\mathcal {M},w\vDash \neg N"'\varphi \land N"'\neg \psi \land N"'(\psi \vee \varphi )$
, to prove that
$\mathcal {M},w\vDash N"'\chi $
. Since
$\mathcal {M},w\vDash \neg N"'\varphi $
, it follows that
$R_1(w)\nvDash \varphi $
and
$R_2(w)\nvDash \neg \varphi $
. By
$\mathcal {M},w\vDash N"'(\psi \vee \varphi )$
, we obtain that
$R_1(w)\vDash \psi \vee \varphi $
or
$R_2(w)\vDash \neg (\psi \vee \varphi )$
. If the latter is the case,
$R_2(w)\vDash \neg \varphi $
, a contradiction, and thus
$R_1(w)\vDash \psi \vee \varphi $
. By
$\mathcal {M},w\vDash N"'\neg \psi $
, it follows that
$R_1(w)\vDash \neg \psi $
or
$R_2(w)\vDash \psi $
. If
$R_1(w)\vDash \neg \psi $
, then
$R_1(w)\vDash \varphi $
, a contradiction. Thus
$R_2(w)\vDash \psi $
, and hence using the supposition, we derive that
$R_2(w)\vDash \neg \chi $
, which implies that
$\mathcal {M},w\vDash N"'\chi $
.
6.1.2 Completeness
For completeness, we construct the canonical model for
$\mathbf {K^{N"'}}$
.
Definition 65. The canonical model for
$\mathbf {K^{N"'}}$
is a tuple
$\mathcal {M}^c=\langle W^c,R^c_1,R^c_2,V^c \rangle $
, where
-
•
$W^c=\{w\mid w\text { is a maximal consistent set for }\mathbf {K^{N"'}}\}$
; -
• if
$\neg N"'\psi \in w$
for no
$\psi $
, then
$wR^c_1u$
iff
$w=u$
, and
$wR^c_2u$
iff
$w=u$
; -
• if
$\neg N"'\psi \in s$
for some
$\psi $
, then
$wR_1^cu$
iff for every
$\varphi $
, if
$N"'\varphi \land N"'(\varphi \vee \psi )\in w$
, then
$\varphi \in u$
, and
$wR^c_2u$
iff for every
$\varphi $
, if
$N"'\neg \varphi \land N"'(\varphi \vee \psi )\in w$
, then
$\varphi \in u$
; -
•
$V^c(p)=\{w\in W^c\mid p\in w\}$
.
As before, it is required that the
$\psi $
in
$N"'\varphi \land N"'(\varphi \lor \psi )\in w$
and
$N"'\neg \varphi \land N"'(\varphi \vee \psi )\in w$
be the same as that in
$\neg N"'\psi \in w$
. Note that the choice of
$\psi $
in the above second case of the canonical relations is inessential to
$R_1^c$
and
$R_2^c$
, as shown in Remark 10. It is also worth noting that
$R_1^c$
and
$R_2^c$
in the above definition are inspired by almost definability schemas (
$\textbf {N}"'\textbf {AD1}$
) and (
$\textbf {N}"'\textbf {AD2}$
), respectively, based on the analysis of §2. Recall that in the construction of the canonical model for the minimal logic of
$\mathcal {L}(\Box _1,\Box _2)$
, the canonical relations
$R_1^c$
and
$R^c_2$
are defined as, respectively,
$wR^c_1u$
iff for all
$\varphi $
, if
$\Box _1\varphi \in w$
then
$\varphi \in u$
, and
$wR^c_2u$
iff for all
$\varphi $
, if
$\Box _2\varphi \in w$
then
$\varphi \in u$
. Now given a precondition that
$\neg N"'\psi \in w$
for some
$\psi $
, according to
$(\textbf {N}"'\textbf {AD1})$
,
$\Box _1\varphi \in w$
can be replaced with
$N"'\varphi \land N"'(\varphi \lor \psi )\in w$
, and according to
$(\textbf {N}"'\textbf {AD2})$
,
$\Box _2\varphi \in w$
can be replaced with
$N"'\neg \varphi \land N"'(\varphi \lor \psi )\in w$
; otherwise, we let w access and only access itself.
Proposition 66 lists some logical properties of
$\Sigma _1$
and
$\Sigma _2$
, respectively. They are important in the proof of Lemma 68 below.
Proposition 66. Let
$w\in W^c$
and
$\neg N"'\varphi \in w$
. Define
$\Sigma _1(w)=\{\chi \mid N"'\chi \land N"'(\chi \vee \varphi )\in w\}$
and
$\Sigma _2(w)=\{\chi \mid N"'\neg \chi \land N"'(\chi \vee \varphi )\in w\}$
. Then for
$i\in \{1,2\}$
,
-
(1)
$\Sigma _i(w)\neq \emptyset $
. -
(2) If
$\psi ,\chi \in \Sigma _i(w)$
, then
$\psi \land \chi \in \Sigma _i(w)$
. -
(3) If
$\psi \in \Sigma _1(w)$
and
$\vdash \psi \to \chi $
, then
$\chi \in \Sigma _1(w)$
. -
(4) If
$\psi \in \Sigma _2(w)$
and
$\vdash \psi \to \neg \chi $
, then
$N"'\chi \in w$
.
Proof. Let
$\neg N"'\varphi \in w$
, where
$w\in W^c$
.
-
(1) By axioms D1 and D2.
-
(2) Suppose that
$\psi \in \Sigma _1(w)$
and
$\chi \in \Sigma _1(w)$
. Then
$N"'\psi \land N"'(\psi \vee \varphi )\in w$
and
$N"'\chi \land N"'(\chi \vee \varphi )\in w$
. By axiom D3 and Proposition 63(1), we obtain that
$N"'(\psi \land \chi )\in w$
and
$N"'((\psi \land \chi )\vee \varphi )\in w$
. Therefore,
$\psi \land \chi \in \Sigma _1(w)$
.Assume that
$\psi \in \Sigma _2(w)$
and
$\chi \in \Sigma _2(w)$
. Then
$N"'\neg \psi \land N"'(\psi \vee \varphi )\in w$
, and
$N"'\neg \chi \land N"'(\chi \vee \varphi )\in w$
. Then by axiom D4,
$N"'(\neg \psi \vee \neg \chi )\in w$
, equivalently,
$N"'\neg (\psi \land \chi )\in w$
; by axiom D3 and Proposition 63(1),
$N"'((\psi \land \chi )\vee \varphi )\in w$
. Therefore,
$\psi \land \chi \in \Sigma _2(w)$
. -
(3) Suppose that
$\psi \in \Sigma _1(w)$
and
$\vdash \psi \to \chi $
. Then
$N"'\psi \land N"'(\psi \vee \varphi )\in w$
. Since
$\neg N"'\varphi \in w$
, by rule
$\text {N}"'\text {R2}$
and Proposition 63(2), it follows that
$N"'\chi \land N"'(\chi \vee \varphi )\in w$
, and therefore,
$\chi \in \Sigma _1(w)$
. -
(4) Assume that
$\psi \in \Sigma _2(w)$
and
$\vdash \psi \to \neg \chi $
. Then
$N"'\neg \psi \land N"'(\psi \vee \varphi )\in w$
. Since
$\neg N"'\varphi \in w$
, by rule
$\text {N}"'\text {R3}$
, it follows that
$N"'\chi \in w$
.
Proposition 67.
$\mathcal {M}^c$
is indeed a
$\subseteq $
-model. That is,
$R_1^c\subseteq R_2^c$
.
Proof. This is provided by axiom D6.
Lemma 68. For all
$w\in W^c$
, for all
$\varphi \in \mathcal {L}(N"')$
, we have
$$ \begin{align*}\mathcal{M}^c,w\vDash\varphi\text{~iff~}\varphi\in w.\end{align*} $$
Proof. By induction on
$\varphi $
. The nontrivial case is
$N"'\varphi $
.
Suppose that
$N"'\varphi \in w$
(equivalently,
$N"'\neg \neg \varphi \in w$
), to show that
$\mathcal {M}^c,s\vDash N"'\varphi $
. Assume not, then
$R^c_1(w)\nvDash \varphi $
and
$R^c_2(w)\nvDash \neg \varphi $
. By induction hypothesis, this means that (1) there exists
$u\in W^c$
such that
$wR^c_1u$
and
$\varphi \notin u$
and (2) there exists
$v\in W^c$
such that
$wR^c_2v$
and
$\neg \varphi \notin v$
(thus
$\varphi \in v$
). According to the definition of
$R^c_1$
and
$R^c_2$
, we consider two cases.
-
•
$\neg N"'\psi \in w$
for no
$\psi $
. Then
$w=u$
and
$w=v$
, thus
$u=v$
: a contradiction. -
•
$\neg N"'\psi \in w$
for some
$\psi $
. In this case, by (1), we infer that
$N"'\varphi \land N"'(\varphi \vee \psi )\notin w$
, thus
$N"'(\varphi \vee \psi )\notin w$
; by (2), we derive that
$N"'\neg \neg \varphi \land N"'(\neg \varphi \vee \psi )\notin w$
, thus
$N"'(\neg \varphi \vee \psi )\notin w$
. By axiom D5,
$N"'\varphi \notin w$
, which contradicts the supposition.Conversely, suppose that
$N"'\varphi \notin w$
, then
$\neg N"'\varphi \in w$
. To prove that
$\mathcal {M},w\nvDash N"'\varphi $
, by induction hypothesis, it remains only to show (1) and (2). Define
$\Sigma _1$
and
$\Sigma _2$
as in Proposition 66. According to the definition of
$R^c_1$
and
$R^c_2$
and Lindenbaum’s Lemma, it suffices to show that both
$\Sigma _1(w)\cup \{\neg \varphi \}$
and
$\Sigma _2(w)\cup \{\varphi \}$
are consistent. By Proposition 66(1),
$\Sigma _1(w)$
and
$\Sigma _2(w)$
are both nonempty.If
$\Sigma _1(w)\cup \{\neg \varphi \}$
is inconsistent, then there are
$\varphi _1,\dots ,\varphi _n\in \Sigma _1(w)$
and
$$ \begin{align*}\vdash \varphi_1\land\cdots\land \varphi_n\to \varphi.\end{align*} $$
Then by items (2) and (3) of Proposition 66, we derive that
$N"'\varphi \in w$
: a contradiction. Therefore,
$\Sigma _1(w)\cup \{\neg \varphi \}$
is consistent.If
$\Sigma _2(w)\cup \{\varphi \}$
is inconsistent, then there exist
$\chi _1,\ldots ,\chi _m\in \Sigma _2(w)$
and
$$ \begin{align*}\vdash \chi_1\land\cdots\land\chi_m\to\neg\varphi.\end{align*} $$
Now using items (2) and (4) of Proposition 66, we derive that
$N"'\varphi \in w$
: a contradiction. Therefore,
$\Sigma _2(w)\cup \{\varphi \}$
is consistent.
Theorem 69.
$\mathbf {K^{N"'}}$
is sound and strongly complete with respect to the class of
$\subseteq $
-frames.
6.2 Extensions
6.2.1 Serial logic
Theorem 70.
$\mathbf {K^{N"'}}$
is sound and strongly complete with respect to the class of serial
$\subseteq $
-frames.
Proof. By Theorem 69, we only need to show the completeness. Define
$\mathcal {M}^c$
as in Definition 65. It remains only to show the seriality of
$R^c_1$
. Let
$w\in W^c$
.
If
$\neg N"'\psi \in w$
for no
$\psi $
, then as
$w=w$
, we have
$wR^c_1w$
. If
$\neg N"'\psi \in w$
for some
$\psi $
, define
$\Sigma _1(w)$
as in Proposition 66, it suffices to prove that
$\Sigma _1(w)$
is consistent. The item (1) of Proposition 66 provides the nonemptiness of
$\Sigma _1(w)$
. Suppose that
$\Sigma _1(w)$
is not consistent, then there are
$\chi _1,\dots ,\chi _n\in \Sigma _1(w)$
such that
$\vdash \chi _1\land \cdots \land \chi _n\to \bot $
. By items (2) and (3) of Proposition 66, we infer that
$\bot \in \Sigma _1(w)$
, and thus
$N"'(\bot \vee \psi )\in w$
, equivalently,
$N"'\psi \in w$
: a contradicition.
6.2.2 Reflexive logic
Extending
$\mathbf {K^{N"'}}$
with the following axiom (denoted
$\text {N}"'\text {T}$
), we obtain the system
$\mathbf {T^{N"'}}$
:
$$ \begin{align*}\neg N"'\psi\land N"'\varphi\land N"'(\varphi\vee\psi)\to\varphi.\end{align*} $$
Theorem 71.
$\mathbf {T^{N"'}}$
is sound and strongly complete with respect to the class of reflexive
$\subseteq $
-frames.
Proof. For soundness, by Theorem 69, it remains only to show the validity of
$\text {N}"'\text {T}$
. Let
$\mathcal {M}=\langle W,R_1,R_2,V \rangle $
be a reflexive
$\subseteq $
-model and
$w\in W$
. Suppose that
$\mathcal {M},w\vDash \neg N"'\psi \land N"'\varphi \land N"'(\varphi \vee \psi )$
, to show that
$\mathcal {M},w\vDash \varphi $
. Since
$\mathcal {M},w\vDash \neg N"'\psi $
, we have
$R_1(w)\nvDash \psi $
and
$R_2(w)\nvDash \neg \psi $
, thus
$R_2(w)\nvDash \neg (\varphi \vee \psi )$
. Due to
$\mathcal {M},w\vDash N"'(\varphi \vee \psi )$
, we get
$R_1(w)\vDash \varphi \vee \psi $
or
$R_2(w)\vDash \neg (\varphi \vee \psi )$
, and then
$R_1(w)\vDash \varphi \vee \psi $
. Plus
$R_1(w)\nvDash \psi $
, this implies that
$R_1(w)\nvDash \neg \varphi $
. Since
$R_1\subseteq R_2$
, it follows that
$R_2(w)\nvDash \neg \varphi $
. Now using
$\mathcal {M},w\vDash N"'\varphi $
, we derive that
$R_1(w)\vDash \varphi $
, from which and the reflexivity of
$R_1$
, it follows that
$\mathcal {M},w\vDash \varphi $
.
For completeness, define
$\mathcal {M}^c$
w.r.t.
$\mathbf {T^{N"'}}$
as in Definition 65. By Theorem 69, it suffices to prove that
$R^c_1$
is reflexive.
Let
$w\in W^c$
. If
$\neg N"'\psi \in w$
for no
$\psi $
, then as
$w=w$
, we immediately have
$wR^c_1w$
. If
$\neg N"'\psi \in w$
for some
$\psi $
, assume for any
$\varphi $
that
$N"'\varphi \land N"'(\varphi \vee \psi )\in w$
. By axiom
$\text {N}"'\text {T}$
,
$\varphi \in w$
. Thus
$wR^c_1w$
again.
We conclude this part with two unprovable results which will be used in §6.3.
Proposition 72.
$\neg N"'\psi \to (\varphi \leftrightarrow N"'\varphi \land N"'(\varphi \vee \psi ))$
is not derivable from
$\mathbf {T^{N"'}}$
.
Proof. We only show that
$\neg N"'\psi \land \varphi \to N"'(\varphi \lor \psi )$
is not derivable from
$\mathbf {T^{N"'}}$
. For this, consider the following reflexive
$\subseteq $
-model
$\mathcal {M}=\langle W,R_1,R_2,V \rangle $
, where we omit all reflexive arrows for sake of simplicity:
One may verify that
$\mathcal {M},w\vDash \neg N"'q$
(since
$wR_1u$
and
$u\nvDash q$
and
$wR_2v$
and
$v\vDash q$
) and
$\mathcal {M},w\vDash p$
, whereas
$\mathcal {M},w\nvDash N"'(p\vee q)$
(because
$u\nvDash p\vee q$
and
$v\vDash p\vee q$
). Thus,
$\mathcal {M},w\nvDash \neg N"'q\land p\to N"'(p\vee q)$
, and hence
$\mathcal {M},w\nvDash \neg N"'\psi \land \varphi \to N"'(\varphi \vee \psi )$
and therefore
$\mathcal {M}\nvDash \neg N"'\psi \land \varphi \to N"'(\varphi \vee \psi )$
. By soundness of
$\mathbf { T^{N"'}}$
(Theorem 71),
$\neg N"'\psi \land \varphi \to N"'(\varphi \vee \psi )$
is not derivable from
$\mathbf { T^{N"'}}$
.
Proposition 73.
$\neg N"'\psi \to (\varphi \leftrightarrow N"'(\varphi \vee \psi ))$
is not derivable from
$\mathbf {T^{N"'}}$
.
Proof. We only show that
$\neg N"'\psi \land N"'(\varphi \lor \psi )\to \varphi $
is not derivable from
$\mathbf {T^{N"'}}$
. For this, consider the following reflexive
$\subseteq $
-model
$\mathcal {M}=\langle W,R_1,R_2,V \rangle $
, where we omit all reflexive arrows for sake of simplicity:
One may verify that
$\mathcal {M},w\vDash \neg N"'q$
(since
$wR_1u$
and
$u\nvDash q$
and
$wR_2v$
and
$v\vDash q$
) and
$\mathcal {M},w\vDash N"'(p\vee q)$
(because
$R_1(w)=\{w,u\}\vDash p\vee q$
), whereas
$\mathcal {M},w\nvDash p$
. Thus,
$\mathcal {M},w\nvDash \neg N"'q\land N"'(p\vee q)\to p$
, and hence
$\mathcal {M},w\nvDash \neg N"'\psi \land N"'(\varphi \vee \psi )\to \varphi $
and therefore
$\mathcal {M}\nvDash \neg N"'\psi \land N"'(\varphi \vee \psi )\to \varphi $
. By soundness of
$\mathbf {T^{N"'}}$
(Theorem 71),
$\neg N"'\psi \land N"'(\varphi \vee \psi )\to \varphi $
is not derivable from
$\mathbf {T^{N"'}}$
.
6.2.3 Transitive logic
Extending
$\mathbf {K^{N"'}}$
with the following axioms, we obtain the system
$\mathbf {K4^{N"'}}$
:
$$\begin{align*}\begin{array}{ll} \text{N}"'\text{4-1} & \neg N"'\psi\land N"'\varphi\land N"'(\varphi\vee\psi)\to N"'(\neg N"'\psi'\to N"'\varphi\land N"'(\varphi\vee\psi'))\land\\&N"'((\neg N"'\psi'\to N"'\varphi\land N"'(\varphi\vee\psi'))\vee\psi) \\\text{N}"'\text{4-2} & \neg N"'\psi\land N"'\neg\varphi\land N"'(\varphi\vee\psi)\to N"'\neg(\neg N"'\psi'\to N"'\neg\varphi\land \\& N"'(\varphi\vee\psi'))\land N"'((\neg N"'\psi'\to N"'\neg\varphi\land N"'(\varphi\vee\psi'))\vee\psi).\\ \end{array} \end{align*}$$
Similar to axioms A4-1 and A4-2 in §3.4.4, axioms
$\text {N}"'\text {4-1}$
and
$\text {N}"'\text {4-2}$
are obtained from the transitive axioms for
$\Box _1$
and
$\Box _2$
via a translation induced by almost definability schemas
$(\textbf {N}"'\textbf {AD1})$
and
$(\textbf {N}"'\textbf {AD2})$
, respectively.
Theorem 74.
$\mathbf {K4^{N"'}}$
is sound and strongly complete with respect to the class of transitive
$\subseteq $
-frames.
Proof. For soundness, by Theorem 69, it suffices to show the validity of axioms
$\text {N}"'\text {4-1}$
and
$\text {N}"'\text {4-2}$
. To see this, just notice that in the transformation of the two axioms starting from the schemas
$(\textbf {N}"'\textbf {AD1})$
and
$(\textbf {N}"'\textbf {AD2})$
, every step is equivalent, and that the proof of the validity of the two schemas only uses
$R_1\subseteq R_2$
(see Proposition 59).
For completeness, define
$\mathcal {M}^c$
w.r.t.
$\mathbf {K4^{N"'}}$
as in Definition 65. By Theorem 69, it remains only to show that both
$R^c_1$
and
$R^c_2$
are transitive. For this, let
$w,u,v\in W^c$
.
Suppose that
$wR^c_1u$
and
$uR^c_1v$
, to show that
$wR^c_1v$
. We consider the following cases:
-
•
$\neg N"'\psi \in w$
for no
$\psi $
. In this case,
$w=u$
, and thus
$wR^c_1v$
. -
•
$\neg N"'\psi '\in u$
for no
$\psi '$
. In this case,
$u=v$
, and hence
$wR^c_1v$
. -
•
$\neg N"'\psi \in w$
for some
$\psi $
and
$\neg N"'\psi '\in u$
for some
$\psi '$
. Assume for any
$\varphi $
that
$N"'\varphi \land N"'(\varphi \vee \psi )\in w$
, to prove that
$\varphi \in v$
. By axiom
$\text {N}"'\text {4-1}$
,
$N"'(\neg N"'\psi '\to N"'\varphi \land N"'(\varphi \vee \psi '))\land N"'((\neg N"'\psi '\to N"'\varphi \land N"'(\varphi \vee \psi '))\vee \psi )\in w$
. From
$wR^c_1u$
, it follows that
$\neg N"'\psi '\to N"'\varphi \land N"'(\varphi \vee \psi ')\in u$
, thus
$N"'\varphi \land N"'(\varphi \vee \psi ')\in u$
. Now using
$uR^c_1v$
, we derive that
$\varphi \in v$
, as desired.
Now suppose that
$wR^c_2u$
and
$uR^c_2v$
, to prove that
$wR^c_2v$
. Again, we consider the following cases:
-
•
$\neg N"'\psi \in w$
for no
$\psi $
. In this case,
$w=u$
, and thus
$wR^c_2v$
. -
•
$\neg N"'\psi '\in u$
for no
$\psi '$
. In this case,
$u=v$
, and hence
$wR^c_2v$
. -
•
$\neg N"'\psi \in w$
for some
$\psi $
and
$\neg N"'\psi '\in u$
for some
$\psi '$
. Assume for any
$\varphi $
that
$N"'\neg \varphi \land N"'(\varphi \vee \psi )\in w$
, to show that
$\varphi \in v$
. By axiom
$\text {N}"'\text {4-2}$
,
$N"'\neg (\neg N"'\psi ' {\kern2.8pt}\to{\kern2.8pt} N"'\neg \varphi {\kern2.8pt}\land{\kern2.8pt} N"'(\varphi {\kern2.8pt}\vee{\kern2.8pt} \psi ')){\kern2.8pt}\land{\kern2.8pt} N"'((\neg N"'\psi '{\kern2.8pt}\to{\kern2.8pt} N"'\neg \varphi{\kern2.8pt} \land N"'(\varphi \vee \psi '))\vee \psi )\in w$
. From
$wR^c_2u$
, it follows that
$\neg N"'\psi '\to N"'\neg \varphi \land N"'(\varphi \vee \psi ')\in u$
, thus
$N"'\neg \varphi \land N"'(\varphi \vee \psi ')\in u$
. Then using
$uR^c_2v$
, we infer that
$\varphi \in v$
, as desired.
6.2.4
$\mathbf {S4}$
-logic
Define
$\mathbf {S4^{N"'}}$
to be the extension of
$\mathbf {K4^{N"'}}$
with axiom
$\text {N}"'\text {T}$
. By Theorems 71 and 74, we have the following result.
Theorem 75.
$\mathbf {S4^{N"'}}$
is sound and strongly complete with respect to the class of
$\mathbf {S4} \subseteq $
-frames.
6.3 Connection with the logic of accidental truths
Let
$R_1$
be the identity relation and
$R_2$
be reflexive. Of course,
$R_1\subseteq R_2$
. Then
$N"'\varphi $
becomes
$\varphi \vee \Box _2\neg \varphi $
, equivalently,
$\neg \varphi \to \Box _2\neg \varphi $
. This is exactly
$\circ \neg \varphi $
, where the essential operator
$\circ $
is the negation of the accident operator
$\bullet $
. That is,
$$\begin{align*}\begin{array}{lll} \mathcal{M},w\vDash N"'\varphi & \Longleftrightarrow & \mathcal{M},w\vDash\varphi\text{ or }R_2(w)\vDash\neg\varphi. \\ \end{array} \end{align*}$$
Moreover,
$\Box _1\varphi $
becomes
$\varphi $
. That is,
$$\begin{align*}\begin{array}{lll} \mathcal{M},w\vDash\Box_1\varphi & \Longleftrightarrow & \mathcal{M},w\vDash\varphi. \\ \end{array} \end{align*}$$
Then
$(\textbf {N}"'\textbf {AD1})$
and
$(\textbf {N}"'\textbf {AD2})$
become the following almost-definability schemas:
$$\begin{align*}\begin{array}{lcr} \neg N"'\psi\to (\varphi\leftrightarrow N"'\varphi\land N"'(\varphi\vee\psi)) & & (\textbf{N}"'\textbf{AD1}') \\ \neg N"'\psi\to (\Box_2\varphi\leftrightarrow N"'\neg\varphi\land N"'(\varphi\vee\psi)) & & (\textbf{N}"'\textbf{AD2}). \\ \end{array} \end{align*}$$
As a matter of fact,
$(\textbf {N}"'\textbf {AD1}')$
can be simplified as
$$\begin{align*}\begin{array}{lcr} \neg N"'\psi\to (\varphi\leftrightarrow N"'(\varphi\vee\psi)) & & (\textbf{N}"'\textbf{AD1}"). \\ \end{array} \end{align*}$$
One may easily verify that according to this simplified semantics (that is,
$R_1$
being identity),
$(\textbf {N}"'\textbf {AD1}')$
and
$(\textbf {N}"'\textbf {AD1}")$
are valid over the class of all frames, whereas
$(\textbf {N}"'\textbf {AD2})$
is valid over the class of (
$R_2$
-)reflexive frames. This contrasts with the fact that
$(\textbf {N}"'\textbf {AD1}')$
and
$(\textbf {N}"'\textbf {AD1}")$
are not valid under the original semantics, where
$R_1$
is not the identity relation (see the proofs of Propositions 72 and 73). To provide the completeness, we need to establish a proof system from which
$(\textbf {N}"'\textbf {AD1}')$
and
$(\textbf {N}"'\textbf {AD1}")$
are derivable. However, recall from Propositions 72 and 73 that the two schemas are not derivable from
$\mathbf { T^{N"'}}$
, so
$\mathbf {T^{N"'}}$
is not a desired system. We will show that the extension of
$\mathbf {T^{N"'}}$
with
$\varphi \to N"'\varphi $
and
$\neg N"'\psi \land N"'(\varphi \vee \psi )\to \varphi $
is a desired minimal logic of accidental truths. We denote the formulas as
$\text {A1}"'$
and
$\text {A2}"'$
and the extension as
$\mathbf {T1^{N"'}}$
. We can see that the schemas
$(\textbf {N}"'\textbf {AD1}')$
and
$(\textbf {N}"'\textbf {AD1}")$
are derivable from
$\mathbf {T1^{N"'}}$
because of axioms
$\text {A1}"'$
and
$\text {A2}"'$
.
Based on the schemas
$(\textbf {N}"'\textbf {AD1}')$
and
$(\textbf {N}"'\textbf {AD2}')$
, the canonical model for
$\mathbf {T^{N"'}}$
can be simplified as follows.
Definition 76. The canonical model for
$\mathbf {T1^{N"'}}$
is a tuple
$\mathcal {M}^c=\langle W^c,R_1^c,R^c_2,V^c \rangle $
, where the only change is that
$N"'\varphi \land N"'(\varphi \vee \psi )\in w$
in the definition of
$R^c_1$
in Definition 65 now becomes
$\phi\in w $
, due to the derivable schema
$(\textbf {N}"'\textbf {AD1}')$
. In other words,
-
•
$W^c=\{w\mid w\text { is a maximal consistent set for }\mathbf {T1^{N"'}}\}$
; -
• if
$\neg N"'\psi \in w$
for no
$\psi $
, then
$wR^c_1u$
iff
$w=u$
, and
$wR^c_2u$
iff
$w=u$
; -
• if
$\neg N"'\psi \in w$
for some
$\psi $
, then
$wR_1^cu$
iff for every
$\varphi $
, if
$\varphi \in w$
, then
$\varphi \in u$
, and
$wR^c_2u$
iff for every
$\varphi $
, if
$N"'\neg \varphi \land N"'(\varphi \vee \psi )\in w$
, then
$\varphi \in u$
; -
•
$V^c(p)=\{w\in W^c\mid p\in w\}$
.
Proposition 77.
$R^c_1$
is the identity relation, and
$R^c_2$
is reflexive. Consequently,
$R^c_1\subseteq R^c_2$
.
Proof. The proof of the case
$R^c_1$
is the same as the case of
$S^c$
in Proposition 33.
For the case
$R^c_2$
. Let
$w\in W^c$
. If
$\neg N"'\psi \in w$
for no
$\psi $
, then as
$w=w$
,
$wR^c_2w$
. If
$\neg N"'\psi \in w$
for some
$\psi $
, if
$N"'\neg \varphi \land N"'(\varphi \vee \psi )\in w$
, then by axiom D6 and axiom
$\text {N}"'\text {T}$
, we derive that
$\varphi \in w$
, and thus
$wR^c_2w$
.
Recall that in Theorem 71, axiom
$\text {N}"'\text {T}$
is shown to be valid over reflexive
$\subseteq $
-frames, where the reflexivity of
$R_1$
and
$R_1\subseteq R_2$
are used. Since now
$R_1$
is the identity relation and
$R_2$
is reflexive, the reflexivity of
$R_1$
and
$R_1\subseteq R_2$
are automatic. In fact, one may show that NT is valid over the class of all frames (due to the validity of the schema
$\textbf {N}"'\textbf {AD1}'$
), without need of the reflexivity of
$R_2$
. This gives us axiomatizations of
$\mathcal {L}(\bullet )$
over various frames.
Theorem 78.
-
(1) Where
$\mathbf {T}\subseteq X$
,
$\mathbf {T1^{N"'}}$
is sound and strongly complete with respect to the class of X. -
(2) Where
$\mathbf {S4}\subseteq X\subseteq \mathbf {4}$
and
$\mathbf {S41^{N"'}}$
extends
$\mathbf {S4^{N"'}}$
with
$\text {A1}"'$
and
$\text {A2}"'$
,
$\mathbf {S41^{N"'}}$
is sound and strongly complete with respect to X.
Proof. It remains to show the truth lemma for
$\mathbf {T1^{N"'}}$
. That is, for all
$\varphi \in \mathcal {L}(N"')$
, for all
$w\in W^c$
, we have
$$ \begin{align*}\mathcal{M}^c,w\vDash\varphi\text{~iff~}\varphi\in w.\end{align*} $$
The proof proceeds by induction on
$\varphi $
. The nontrivial case is
$N"'\varphi $
.
Suppose, for reductio, that
$N"'\varphi \in w$
but
$\mathcal {M}^c,w\nvDash N"'\varphi $
. Then
$\mathcal {M}^c,w\nvDash \varphi $
and
$R_2^c(w)\nvDash \neg \varphi $
. By induction hypothesis,
$\varphi \notin w$
(thus
$\neg \varphi \in w$
) and there exists
$u\in W^c$
such that
$wR^c_2u$
and
$\neg \varphi \notin u$
. Since
$w\neq u$
, by definition of
$R^c_2$
, it must be the case that
$\neg N"'\psi \in w$
for some
$\psi $
. Thus
$N"'\neg \neg \varphi \land N"'(\neg \varphi \vee \psi )\notin w$
. By supposition and Proposition 63(1), we infer that
$N"'\neg \neg \varphi \in w$
, and thus
$N"'(\neg \varphi \vee \psi )\notin w$
. From
$\neg \varphi \in w$
, it follows that
$\neg \varphi \vee \psi \in w$
, then by axiom
$\text {A1}"'$
, we derive that
$N"'(\neg \varphi \vee \psi )\in w$
: a contradiction.
Conversely, assume that
$N"'\varphi \notin w$
(thus
$\neg N"'\varphi \in w$
), to show that
$\mathcal {M}^c,w\nvDash N"'\varphi $
. By induction hypothesis, it remains only to prove that
$\varphi \notin w$
and there exists
$u\in W^c$
such that
$wR^c_2u$
and
$\neg \varphi \notin u$
. By assumption and axiom
$\text {A1}"'$
,
$\varphi \notin w$
. Moreover, we show that
$\Sigma _2(w)\cup \{\varphi \}$
is consistent, where
$\Sigma _2(w)=\{\chi \mid N"'\neg \chi \land N"'(\chi \vee \varphi )\in w\}$
. By Lemma 66(1),
$\Sigma _2(w)\neq \emptyset $
.
If not, then there are
$\psi _1,\dots ,\psi _n\in \Sigma _2(w)$
such that
$$ \begin{align*}\vdash \psi_1\land\cdots\land\psi_n\to\neg\varphi.\end{align*} $$
Using Lemma 66(2) and (4), we derive that
$N"'\varphi \in w$
: a contradiction.
We have shown that
$\Sigma _2(w)\cup \{\varphi \}$
is consistent. By Lindenbaum’s Lemma, there exists
$u\in W^c$
such that
$\Sigma _2(w)\cup \{\varphi \}\subseteq u$
. By definition of
$R^c_2$
,
$wR^c_2u$
and
$\varphi \in u$
, thus
$\neg \varphi \notin u$
, as desired.
6.4 Connection with the logic of contingency
Let
$R_1=R_2=R$
. Then
$N"'$
becomes the non-contingency operator
$\Delta $
. That is,
$$\begin{align*}\begin{array}{lll} \mathcal{M},w\vDash N"'\varphi & \Longleftrightarrow & R(w)\vDash\varphi\text{ or }R(w)\vDash \neg\varphi. \\ \end{array} \end{align*}$$
It is easy to see that
$\vDash N"'\varphi \leftrightarrow N"'\neg \varphi $
. Then
$(\textbf {N}"'\textbf {AD1})$
and
$(\textbf {N}"'\textbf {AD2})$
become the following:
$$\begin{align*}\begin{array}{lcr} \neg N"'\psi\to (\Box_1\varphi\leftrightarrow N"'\varphi\land N"'(\varphi\vee\psi)) & & (\textbf{N}"'\textbf{AD1}') \\ \neg N"'\psi\to (\Box_2\varphi\leftrightarrow N"'\varphi\land N"'(\varphi\vee\psi)) & & (\textbf{N}"'\textbf{AD2}'). \\ \end{array} \end{align*}$$
In this case, as
$\vDash N"'\top \leftrightarrow N"'\bot $
and
$\vDash N"'\varphi \leftrightarrow N"'\neg \varphi $
,
$\mathbf {K^{N"'}}$
can be replaced by the following simpler proof system (denoted
$\mathbf {K1^{N"'}}$
), where we omit axiom PC and the inference rule MP:
$$\begin{align*}\begin{array}{ll} \text{D1} & N"'\top \\ \text{D2}' & N"'\varphi\leftrightarrow N"'\neg\varphi \\ \text{D3} & N"'\varphi\land N"'\psi\to N"'(\varphi\land\psi)\\ \text{D5} & N"'\varphi\to N"'(\varphi\vee\psi)\vee N"'(\neg\varphi\vee\chi)\\ \text{N}"'\text{R2} & \text{From }\psi\to\chi\text{ infer }\neg N"'\varphi\land N"'\psi\land N"'(\psi\vee\varphi)\to N"'\chi.\\ \end{array}\end{align*}$$
Notice that
$\mathbf {K1^{N"'}}$
extends
$\mathbf {K^{N"'}}$
with axiom
$\text {D2}'$
. To see that
$\mathbf {K1^{N"'}}$
extends
$\mathbf { K^{N"'}}$
, we only need to consider the rule
$\text {N}"'\text {R1}$
, since the other axioms and rules are easy to show.
Proposition 79.
$\text {N}"'\text {R1}$
, namely
$\dfrac {\varphi \to \psi ~~~\psi \to \chi }{N"'\psi \to (N"'\varphi \vee N"'\chi )}$
, is derivable in
$\mathbf { K1^{N"'}}$
.
Proof. We have the proof sequence in
$\mathbf {K^{N"'}}$
:
$$\begin{align*}\begin{array}{lll} (1) & \psi\to\chi & \text{premise}\\ (2) & \neg N"'\chi\land N"'\psi\land N"'(\psi\vee\chi)\to N"'\chi & (1),\text{N}"'\text{R2}\\ (3) & N"'\psi\land N"'(\psi\vee\chi)\to N"'\chi & (2)\\ (4) & \varphi\to\psi & \text{premise} \\ (5) & \neg\psi\to\neg\varphi & (4)\\ (6) & N"'\neg\psi\land N"'(\neg\psi\vee\neg \varphi)\to N"'\neg\varphi & (5),\text{ similar to }(1)\text{--}(3)\\ (7) & N"'\psi\land N"'(\neg\psi\vee\neg\varphi)\to N"'\varphi & (6),\text{D2}'\\ (8) & N"'\psi\to N"'(\psi\vee\chi)\vee N"'(\neg\psi\vee\neg\varphi) & \text{D5}\\ (9) & N"'\psi\to (N"'\varphi\vee N"'\chi) & (3),(7),(8).\\ \end{array} \end{align*}$$
Moreover, the canonical model for
$\mathbf {K^{N"'}}$
becomes the following.
Definition 80. The canonical model for
$\mathbf {K1^{N"'}}$
is a tuple
$\mathcal {M}^c=\langle W^c,R^c_1,R^c_2,V^c \rangle $
, where
-
•
$W^c=\{w\mid w\text { is a maximal consistent set for }\mathbf {K1^{N"'}}\}$
; -
• if
$\neg N"'\psi \in w$
for no
$\psi $
, then
$wR^c_1u$
iff
$w=u$
, and
$wR^c_2u$
iff
$w=u$
; -
• if
$\neg N"'\psi \in s$
for some
$\psi $
, then
$sR_1^ct$
iff for every
$\varphi $
, if
$N"'\varphi \land N"'(\varphi \vee \psi )\in w$
, then
$\varphi \in u$
, and
$wR^c_2u$
iff for every
$\varphi $
, if
$N"'\varphi \land N"'(\varphi \vee \psi )\in w$
, then
$\varphi \in u$
; -
•
$V^c(p)=\{w\in W^c\mid p\in w\}$
.
One may easily verify that
$R^c_1=R^c_2$
.
Then along with the completeness proof of
$\mathbf {K^{N"'}}$
in §6.1.2, we can finally show the following.
Theorem 81.
$\mathbf {K1^{N"'}}$
is sound and strongly complete with respect to the class of all frames.
This gives an alternative axiomatization of contingency logic
$\mathcal {L}(\Delta )$
over the class of all frames. Then we can also axiomatize
$N"'$
(
$=\Delta $
) over various classes of special frames, as in [Reference Fan, Wang and van Ditmarsch19, Reference Fan, Wang and van Ditmarsch20].
Recall that various axiomatizations of
$\mathcal {L}(\Delta )$
are proposed in the literature (see, for instance, [Reference Fan, Wang and van Ditmarsch19, Reference Fan, Wang and van Ditmarsch20, Reference Humberstone26, Reference Kuhn30, Reference Montgomery and Routley33, Reference Zolin46]). We may show that our systems are equivalent to the corresponding ones from a proof-theoretic perspective. For the sake of simplicity, we illustrate with the minimal logics. We choose the minimal logic given in [Reference Kuhn30], denoted
$\boldsymbol {K\Delta }$
here.Footnote
16
The system
$\boldsymbol {K\Delta }$
consists of the following axioms and inference rules, where we write
$N"'$
for
$\Delta $
for convenience:
$$\begin{align*}\begin{array}{ll} \textbf{PL} & \text{All substitution instances of tautologies} \\ \textbf{A1} & N"'\neg\varphi\to N"'\varphi\\ \textbf{A2} & N"'\varphi\land\neg N"'(\varphi\land\psi)\to \neg N"'\psi\\ \textbf{A3} & N"'\varphi\land \neg N"'(\varphi\lor\psi)\to N"'(\neg\varphi\vee\chi)\\ \textbf{R}\Delta & \text{From }\varphi\text{ infer }N"'\varphi\\ \textbf{RE}\Delta & \text{From }\varphi\leftrightarrow \psi\text{ infer }N"'\varphi\leftrightarrow N"'\psi\\ \textbf{MP} & \text{From }\varphi \text{ and }\varphi\to \psi\text{ infer }\psi.\\ \end{array} \end{align*}$$
In what follows, we show that our system
$\mathbf {K1^{N"'}}$
is equivalent to
$\boldsymbol {K\Delta }$
.
Proposition 82. All axioms and inference rules in
$\boldsymbol {K\Delta }$
are derivable in
$\mathbf {K1^{N"'}}$
.
Proof. Axiom
$\textbf {A1}$
is direct from
$\text {D2}'$
. Axioms
$\textbf {A2}$
and
$\textbf {A3}$
are equivalent transformations of D3 and D5, respectively. Rule
$\mathbf {RE}\Delta $
can be shown from
$\text {N}"'\text {R1}$
, which is derivable in
$\mathbf {K1^{N"'}}$
(Proposition 79). In details, the proof of
$\mathbf {RE}\Delta $
is as follows. Suppose that
$\vdash \varphi \leftrightarrow \psi $
, then
$\vdash \varphi \to \psi $
and
$\vdash \psi \to \varphi $
. By
$\text {N}"'\text {R1}$
, we infer that
$\vdash N"'\psi \to N"'\varphi \vee N"'\varphi $
, equivalently,
$\vdash N"'\psi \to N"'\varphi $
. Similarly, we can show that
$\vdash N"'\varphi \to N"'\psi $
. Therefore,
$\vdash N"'\varphi \leftrightarrow N"'\psi $
. The proof of
$\mathbf {R}\Delta $
is the following. Assume that
$\vdash \varphi $
, then
$\vdash \varphi \leftrightarrow \top $
. By
$\mathbf {RE}\Delta $
,
$\vdash N"'\varphi \leftrightarrow N"'\top $
. Then using D1 (namely
$\vdash N"'\top $
), we derive that
$\vdash N"'\varphi $
.
Proposition 83. All axioms and inference rules in
$\mathbf {K1^{N"'}}$
are derivable in
$\boldsymbol {K\Delta }$
.
Proof. Axiom D1 is immediate by
$\textbf {PL}$
and
$\mathbf {R}\Delta $
. Axiom
$\text {D2}'$
can be easily shown from
$\textbf {A1}$
and
$\textbf {RE}\Delta $
. Axioms
$\text {D3}$
and
$\text {D5}$
are equivalent transformations of
$\textbf {A2}$
and
$\textbf {A3}$
, respectively.
The proof of
$\text {N}"'\text {R2}$
is as follows. Suppose that
$\vdash \psi \to \chi $
. By
$\textbf {R}\Delta $
,
$\vdash N"'(\psi \to \chi )$
. By
$\textbf {A2}$
,
$\vdash N"'(\psi \to \chi )\land N"'(\psi \vee \chi )\to N"'((\psi \to \chi )\land (\psi \vee \chi ))$
. By
$\textbf {PL}$
and
$\textbf {RE}\Delta $
, we can show that
$\vdash N"'((\psi \to \chi )\land (\psi \vee \chi ))\leftrightarrow N"'\chi $
. Thus
$\vdash N"'(\psi \to \chi )\land N"'(\psi \vee \chi )\to N"'\chi $
, thus
$\vdash N"'(\psi \vee \chi )\to N"'\chi $
. By axiom
$\textbf {A2}$
again,
$\vdash \neg N"'\varphi \land N"'(\psi \vee \varphi )\to \neg N"'(\neg \psi \vee \varphi )$
. Moreover, by axiom
$\textbf {A3}$
,
$\vdash N"'\psi \land \neg N"'(\neg \psi \vee \varphi )\to N"'(\psi \vee \chi )$
. Therefore,
$\vdash \neg N"'\varphi \land N"'\psi \land N"'(\psi \vee \varphi )\to N"'\chi $
, as desired.
7 Conclusion
In this paper, we proposed a uniform approach to axiomatizing bundled operators, called the ‘MBADS’. The core idea lies in the definability of familiar operators in terms of relatively unfamiliar ones given some certain premises, thus one can ‘reduce’ the latter operators to the former ones in some way. This approach extends the cases where the schemas are valid to those that are valid on a class of frames, which is not necessarily the class of all frames. We illustrated this approach with several bundled operators such as the operator of purely physical necessity N, the operator
$N'$
called ‘All
$_1$
and Only
$_2$
’, the operator
$N"$
, and the operator
$N"'$
in the literature. With the aid of this approach, among other contributions, we answered several open questions, including
$\mathbf { S4}$
-like logic of
$\mathcal {L}(N)$
, a finite minimal axiomatization for the operator ‘All
$_1$
and Only
$_2$
’, the transitive axiomatization of the logic of false belief; also, we obtained various alternative axiomatizations, which are shown to be deductively equivalent to the existing ones in the literature.
For us, the most difficult part of this approach is finding the desired almost-definability schema(s). Once we find the desired almost-definability schemas, the axiomatization can be done step by step: first, according to the almost-definability schema(s), define the canonical relation(s), and thus the canonical model. Second, in the completeness proof, show that the truth lemma holds and that the canonical model is the desired one. Third, in the process of the second step, find out which axioms and inference rules are needed.
In comparison with other approaches, this approach is useful in finding axioms and inference rules, and in defining suitable canonical relation(s), thus in the completeness proof of logical systems. In these aspects, our approach MBADS seems to be incomparable with other approaches. This is, hopefully, good news for modal logicians who are interested in axiomatizing bundled operators. When we deal with the axiomatizations of the bundled operators, we can consider to use this approach.
Although this paper focuses solely on relational semantics, we believe that this approach can be generalized to other semantics as well. We have already extended this approach to neighborhood semantics, whose details will be presented in a separate paper.
Acknowledgments
The author thanks the two anonymous reviewers for their insightful comments and constructive suggestions, and is particularly indebted to Lloyd Humberstone for his invaluable discussions and Yanjing Wang for providing some key references.
Funding
This article is supported by the Key Project of National Social Science Fund of China (no. 24AZX019).
