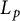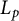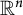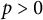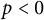1 Introduction
The well-known Minkowski problem in convex geometry originated from the seminal works of Minkowski [Reference Minkowski16, Reference Minkowski17], and was developed by Aleksandrov [Reference Aleksandrov2, Reference Aleksandrov3] and Fenchel–Jessen [Reference Fenchel and Jessen6]. The classical Minkowski problem asks: Given a finite Borel measure on the unit sphere
$\mathbb {S}^{n-1}$
. Does there exist a convex body in
$\mathbb {R}^n$
whose surface area measure equals the given measure? Here, a convex body denotes a compact convex subset with nonempty interior. Since the influential work [Reference Lutwak14], this problem has attracted increasing attention over the past decades, and many significant contributions can be found in the literatures (see, e.g., [Reference Haberl, Lutwak, Yang and Zhang7, Reference Huang, Lutwak, Yang and Zhang9–Reference Huang, Yang and Zhang11, Reference Lutwak, Xi, Yang and Zhang15, Reference Zou and Xiong28]).
Böröczky et al. [Reference Böröczky, Lutwak, Yang, Zhang and Zhao4] introduced a significant generalization – the Gauss image problem – which concerns the existence of a convex body so that two given spherical Borel measures satisfy a prescribed relationship via the Gauss image map. For more detailed explanations, see the introduction in [Reference Böröczky, Lutwak, Yang, Zhang and Zhao4]. Böröczky and coauthors obtained the necessary and sufficient conditions for the existence of solutions, as well as their uniqueness. Subsequently, Chen et al. [Reference Chen, Wu and Xiang5] proved the existence of smooth solutions, and Semenov [Reference Semenov24] studied the existence under a weak assumption, where one measure is discrete and the other is absolutely continuous. For Musielak–Orlicz functions, a generalized Gauss image problem has been comprehensively analyzed in [Reference Huang, Xing, Ye and Zhu8, Reference Li, Sheng, Ye and Yi13].
In recent years, the Brunn–Minkowski theory for convex bodies [Reference Schneider18] has been generalized to the noncompact setting, for instance, the Minkowski problems [Reference Li, Ye and Zhu12, Reference Schneider19, Reference Schneider20] and the Brunn–Minkowski inequality [Reference Yang, Ye and Zhu26]. In this work, we advance this direction by studying the
$L_p$
Gauss image problem for unbounded closed convex sets. Before stating our main results, we recall necessary definitions.
Let C denote a pointed closed convex cone in
$\mathbb {R}^n$
with vertex at the origin and having nonempty interior, and let
$C^\circ :=\{x\in \mathbb {R}^n:x\cdot y\leq 0\ \text {for all}\ y\in C\}$
be its dual cone, where
$x\cdot y$
is the standard inner product of x and y. Denote
$\Omega _C:=\mathrm {int}C\cap \mathbb {S}^{n-1}$
and
$\Omega _{C^\circ }:=\mathrm {int}C^\circ \cap \mathbb {S}^{n-1}$
, where
$\mathrm {int}C$
(resp.
$\mathrm {int}C^\circ $
) denotes the interior of C (resp.
$C^\circ $
).
Let K denote a nonempty closed convex set not containing the origin. If
$tK\subset K$
for any
$t\geq 1$
, we say that K is a pseudo-cone. If
$\{z\in \mathbb {R}^n:K+z\subset K\}=C$
, or equivalently, C is the recession cone of K, then K is called a C-pseudo-cone.
Let
$\lambda $
be a nonzero finite measure on the Lebesgue-measurable subsets of
$\mathrm {cl}\Omega _{C^\circ }$
. The Gauss image measure
$\lambda (K,\cdot )$
of
$\lambda $
, associated with a C-pseudo-cone K, is defined by [Reference Schneider22]
$\lambda (K,\eta ):=\lambda (\boldsymbol {\alpha }_K(\eta ))$
, for any Borel set
$\eta \subset \Omega _C$
, where
$\boldsymbol {\alpha }_K(\eta )$
denotes the radial Gauss image of
$\eta $
. Based on this, we prove a variational formula related to the Wulff shape and hence induce a new Borel measure, the
$L_p$
Gauss image measure, denoted as
$\lambda _p(K,\cdot )$
. Specifically, for
$p\in \mathbb {R}$
, the
$L_p$
Gauss image measure is defined by
$$ \begin{align} \lambda_p(K,\cdot) =\rho_K^p\lambda(K,\cdot)\ \text{on}\ \eta, \end{align} $$
where
$\rho _K$
is the radial function of K. Moreover, we study the following problem.
The
$L_p$
Gauss image problem for
${C}$
-pseudo-cones. Let
$\lambda $
be a nonzero finite measure on the Lebesgue measurable subsets of
$\mathrm {cl}\Omega _{C^\circ }$
, and
$\mu $
be a Borel measure on
$\Omega _C$
. What are the necessary and sufficient conditions on
$\lambda $
and
$\mu $
, such that there is a C-pseudo-cone K satisfying
$\mu =\lambda _p(K,\cdot )$
on the Borel subsets of
$\Omega _C$
?
When
$\lambda $
is the spherical Lebesgue measure,
$L_p$
Gauss image problem becomes the
$L_p$
Alexandrov problem [Reference Ai, Yang and Ye1]. Recently, Xu et al. [Reference Xu, Li and Leng25] and Schneider [Reference Schneider21] studied the pseudo-cones. Schneider [Reference Schneider22, Reference Schneider23] introduced the Gauss image problem for pseudo-cones and interpreted it from the measure transportation viewpoint. It is worth emphasizing that the
$L_p$
Gauss image problem for
${C}$
-pseudo-cones is considerably more intricate than the case
$p =0$
, necessitating the development of new techniques.
To address the problem, we first prove an existence result for
$p>0$
.
Theorem 1 Let
$\lambda $
be a nonzero finite measure on the Lebesgue measurable subsets of
$\mathrm {cl}\Omega _{C^\circ }$
which vanishes on Borel sets of Hausdorff dimension
$(n-2)$
. If
$\mu $
is a finite Borel measure on
$\Omega _C$
and
$p>0$
, there exists a
${C}$
-pseudo-cone K such that
$\mu =\lambda _p(K,\cdot )$
.
Next, we consider the restricted C-pseudo-cones, in the sense that their outer unit normal vectors belong to
$\Omega _{C^\circ }$
, and we establish a uniqueness characterization for the
$L_p$
Gauss image measure for
$p<0$
as follows.
Theorem 2 Let
$p<0$
and
$K,L$
be two restricted C-pseudo-cones. If
$\lambda $
is strictly positive on open sets in
$\Omega _{C^\circ }$
and
$\lambda _p(K,\cdot )=\lambda _p(L,\cdot )$
, then
$K=L$
.
In this article, we first study a new optimization problem for
$p\neq 0$
, and we establish the existence of solutions for a Borel measure on compact subsets. Then, the general existence shown in Theorem 1 can be proved via a limiting argument. To characterize the uniqueness, we shall decompose
$\Omega _C$
and employ a proof by contradiction to prove Theorem 2. The existence and uniqueness of solutions are nontrivial and have not been completely solved. We have established the existence of solutions for
$p>0$
and the uniqueness for
$p<0$
. However, the methods employed here may not apply to the remaining cases, which will be investigated in future work.
This article is organized as follows. In Section 2, we recall some necessary notions and lemmas for the
${C}$
-pseudo-cones. In Section 3, we prove a variational formula and introduce the
$L_p$
Gauss image measure as well as its weak convergence. In Section 4, Theorems 1 and 2 will be proved.
2 Preliminaries
In this section, we recall known results from the Brunn–Minkowski theory of pseudo-cones, for more details, we refer to [Reference Li, Ye and Zhu12, Reference Schneider19–Reference Schneider22]. Throughout the article, the pseudo-cone C and its dual cone
$C^\circ $
share analogous properties; thus we may interchange their roles. We use the same notations regardless of whether the sets are in C or
$C^\circ $
.
2.1 Support function, radial function, and the copolar set
A pseudo-cone K with recession cone C is called a C-pseudo-cone. It is internal if vectors of
$\Omega _{C^\circ }$
occur as outer unit normals of K only at points in
$\mathrm {int}C$
. We use
${ps}(C)$
and
${psi}(C)$
to denote the set of all C-pseudo-cones and that of all internal C-pseudo-cones, respectively.
Let
$K\in {ps}(C)$
. The support function
$h_K:C^\circ \rightarrow \mathbb {R}$
of K is defined by
$$ \begin{align*} h_K(x)=\sup\{x\cdot y:y\in K\}\ \text{for}\ x\in C^\circ. \end{align*} $$
Here,
$\sup $
can be replaced by
$\max $
if
$x\in \mathrm {int}C^\circ $
. As
$h_K\le 0$
, we also write
$\bar {h}_K=-h_K$
. The radial function
$\rho _K:\Omega _C\rightarrow \mathbb {R}$
of K is defined by
$$ \begin{align*}\nonumber \rho_K(v)=\min\{\lambda\in\mathbb{R}:\lambda v\in K\}\ \text{for}\ v\in\Omega_C. \end{align*} $$
The support and radial functions can, respectively, determine a pseudo-cone, and they are related by
$$ \begin{align} \bar{h}_{K^\circ}(v)=\frac{1}{\rho_K(v)}\ \text{for}\ v\in\Omega_C, \end{align} $$
where
$K^\circ :=\{x\in \mathbb {R}^n:x\cdot y\leq -1\ \text {for all}\ y\in K\}$
denotes the copolar set of K. In fact, it follows from Lemma 4 of [Reference Schneider21] that
$K^\circ $
is a
$C^\circ $
-pseudo-cone.
Let
$\omega \subset C^\circ $
be nonempty and compact. A C-pseudo-cone K is C-determined by
$\omega $
if
$K=C\cap \bigcap _{u\in \omega }H_K^-(u)$
, where
$H_K^-(u)$
is the supporting halfspace of K with outer normal u. The set of all C-pseudo-cones which are C-determined by
$\omega $
is denoted by
${\mathcal K}(C,\omega )$
.
Let
$\eta \subset \Omega _C$
be a nonempty compact subset and
$f:\eta \rightarrow (0,\infty )$
be a continuous function. Then, one can define the Wulff shape
$[f]$
associated with
$(C^\circ , \eta , f)$
by
$$ \begin{align*}\nonumber [f]: =C^\circ\cap\bigcap_{v\in\eta}\{x\in\mathbb{R}^n:x\cdot v\leq-f(v)\}, \end{align*} $$
and one has
$[f]\in {\mathcal K}(C^\circ ,\eta )$
.
Analogously, one can define the convexification
$\langle f\rangle $
associated with
$(C, \eta , f)$
by
$$ \begin{align} \langle f\rangle =\bigcap\Big\{K\in{ps}(C):f(v)v\in K\ \text{for any}\ v\in\eta\}. \end{align} $$
Clearly,
$\langle f\rangle $
is a C-pseudo-cone and
$\langle sf\rangle =s\langle f\rangle $
for
$s>0$
. Notice that
$\langle f\rangle $
is contained in
$\mathrm {int}C$
, thus we have
$\langle f\rangle \in {psi}(C)$
. It follows from definition (2.2) that
$$ \begin{align} \rho_{\langle f\rangle}(v)\leq f(v)\ \text{on}\ \eta. \end{align} $$
The C-pseudo-cone K is called C-defined by
$\eta $
if
$K=\langle {\rho _K{|_\eta }}\rangle $
, where
$\rho _K{|_\eta }$
is the restriction of the function
$\rho _K$
to
$\eta $
. The set of all C-pseudo-cones that are C-defined by
$\eta $
is denoted by
${\mathcal K}^*(C,\eta )$
. It turns out that
$K\in {\mathcal K}^*(C,\eta )$
if and only if
$K^\circ \in {\mathcal K}(C^\circ ,\eta )$
(see page 8 of [Reference Schneider22]).
The convergence of C-pseudo-cones is defined via Hausdorff convergence of compact sections: write
$K_i\rightarrow K_0$
if
$K_i\cap t\mathbb {B}_2^n\rightarrow K_0\cap t\mathbb {B}_2^n$
for each
$t\ge t_0$
. Here,
$\mathbb {B}_2^n$
is the standard unit ball in
$\mathbb {R}^n$
. It follows from (2.1) that
$$ \begin{align*}K_i\rightarrow K_0\Leftrightarrow K_i^\circ\rightarrow K_0^\circ. \end{align*} $$
Let
$\eta \subset \Omega _C$
be a nonempty compact subset and
${\mathcal {C}}^+(\eta )$
be the set of all positive continuous functions on
$\eta $
. If
$f\in {\mathcal {C}}^+(\eta )$
, then
$$ \begin{align} [f]=\langle1/f\rangle^\circ\ \text{and}\ [f]^\circ=\langle1/f\rangle. \end{align} $$
Moreover, the C-pseudo-cones satisfy the continuity properties and selection theorem as follows.
Lemma 1 (cf. Lemma 2 of [Reference Schneider22])
If
$\{f_i\}_{i\in \mathbb {N}_0}\subset {\mathcal {C}}^+(\eta )$
, and
$\{f_i\}_{i\in \mathbb {N}}$
converges uniformly on
$\eta $
to
$f_0$
as
$i\rightarrow \infty $
, then
$[f_i]\rightarrow [f_0]$
and
$\langle f_i\rangle \rightarrow \langle f_0\rangle $
as
$i\rightarrow \infty $
.
Lemma 2 (cf. Lemma 1 of [Reference Schneider21])
Every sequence of C-pseudo-cones whose distances from the origin are bounded and bounded away from
$0$
has a subsequence that converges to a C-pseudo-cone.
2.2 Some maps for pseudo-cones
Huang et al. [Reference Huang, Lutwak, Yang and Zhang9] introduced some critical maps for convex bodies, including the spherical image map, the reverse spherical image map, the radial map, the radial Gauss map, and the reverse radial Gauss map. In this section, we review these maps for pseudo-cones.
Let
$K\in {ps}(C)$
with boundary
$\partial K$
. The spherical image of
$\sigma \subset \partial K$
is defined by
$$ \begin{align*}\nonumber \boldsymbol{\nu}_K(\sigma) =\{u\in\Omega_{C^\circ}:x\in H_K(u)\ \text{for some}\ x\in\sigma\}. \end{align*} $$
The spherical image map
$\nu _K(x):\partial K\backslash \sigma _K\rightarrow \Omega _{C^\circ }$
is defined by
$\nu _K(x)=\boldsymbol {\nu }_K(\{x\})$
, where
$\sigma _K$
is the set of all
$x\in \partial K$
for which the set
$\boldsymbol {\nu }_K(\{x\})$
contains more than a single element. The reverse spherical image of
$\omega \subset \Omega _{C^\circ }$
is defined by
$$ \begin{align*}\nonumber \boldsymbol{x}_K(\omega) =\{x\in\partial K:x\in H_K(u)\ \text{for some}\ u\in\omega\}, \end{align*} $$
and the reverse spherical image map
$x_K:\Omega _{C^\circ }\backslash \omega _K\rightarrow \partial K$
is defined by
$x_K(u)=\boldsymbol {x}_K(\{u\})$
, where
$\omega _K$
is the set of all
$u\in \Omega _{C^\circ }$
for which the set
$\boldsymbol {x}_K(\{u\})$
contains more than one element.
The radial Gauss image of
$\eta \subset \Omega _C$
is defined by
$$ \begin{align*}\nonumber \boldsymbol{\alpha}_K(\eta)=\boldsymbol{\nu}_K(r_K(\eta)), \end{align*} $$
and the radial Gauss map
$\alpha _K:\Omega _C\backslash \eta _K\rightarrow \Omega _{C^\circ }$
is defined by
$\alpha _K=\nu _K\circ r_K$
, where
${r_K:\Omega _C\rightarrow \partial K}$
is the radial map defined by
$r_K(v)=\rho _K(v)v$
for
$v\in \Omega _C$
, and
${\eta _K=r_K^{-1}(\sigma _K)}$
. Here, the radial map and the radial Gauss map are only defined on
$\Omega _C$
, not on its closure.
For
$K\in {psi}(C)$
, the reverse radial Gauss image of
$\omega \subset \Omega _{C^\circ }$
is defined by
$$ \begin{align*}\nonumber \boldsymbol{\alpha}_K^*(\omega)=r_K^{-1}(\boldsymbol{x}_K(\omega)), \end{align*} $$
and the reverse radial Gauss map
$\alpha _K^*:\Omega _{C^\circ }\backslash \omega _K\rightarrow \Omega _C$
is defined by
$\alpha _K^*=r_K^{-1}\circ x_K$
. Here, we have restricted this map to
${psi}(C)$
to ensure that for
$u\in \Omega _{C^\circ }\backslash \omega _K$
, the vector
$r_K^{-1}\circ x_K(u)$
belongs to
$\Omega _C$
. Two maps
$\alpha _K$
and
$\alpha _K^*$
are all continuous, and moreover,
$$ \begin{align} \alpha_K^*(u)=\alpha_{K^\circ}(u),\ \text{for any}\ u\in\Omega_{C^\circ}\backslash\omega_K. \end{align} $$
Let
$K\in {ps}(C)$
, and
$\lambda $
be a nonzero finite measure on the Lebesgue measurable subsets of
$\mathrm {cl}\Omega _{C^\circ }$
which vanishes on Borel sets of Hausdorff dimension
$(n-2)$
. Then,
$$ \begin{align} \lambda(\omega_K)=0. \end{align} $$
3 The variational formula
Let
$\lambda $
be a nonzero finite measure on the Lebesgue measurable subsets of
$\mathrm {cl}\Omega _{C^\circ }$
which vanishes on Borel sets of Hausdorff dimension
$(n-2)$
, unless specified otherwise. Then, for
$K\in {ps}(C^\circ )$
, we introduce the dual entropy functional associated with
$\lambda $
as follows:
$$ \begin{align} E_\lambda(K):=\int_{\Omega_{C^\circ}}\log\rho_K(u)d\lambda(u). \end{align} $$
When
$\lambda $
is the spherical Lebesgue measure, this definition is due to [Reference Li, Ye and Zhu12]. In the remaining part of this section, we use the dual entropy functional to prove a variational formula related to the Wulff shape, which induces the
$L_p$
Gauss image measure. We begin with two preliminary lemmas needed for the proof.
To state the first lemma of this section, we let
$\eta \subset \Omega _C$
be a nonempty compact subset and
$f:\eta \rightarrow \mathbb {R}$
be continuous. Let
$\delta>0$
be small enough and for
$t\in (-\delta ,\delta )$
. We define a continuous function
$h_t:\eta \rightarrow (0,\infty )$
by
$$ \begin{align} \log h_t(v)=\log h_0(v)+tf(v)+o(t,v),\ \text{for any}\ v\in\eta, \end{align} $$
where
$o(t,\cdot ):\eta \rightarrow \mathbb {R}$
is continuous, and
$\lim \limits _{t\rightarrow 0}o(t,\cdot )/t=0$
uniformly on
$\eta $
.
By adapting the arguments in [Reference Huang, Lutwak, Yang and Zhang9] and interchanging the roles of C and
$C^\circ $
in Lemma 5.4 of [Reference Li, Ye and Zhu12], we can prove the following lemma.
Lemma 3 Let
$\eta \subset \Omega _C$
be a nonempty compact subset and
$f:\eta \rightarrow \mathbb {R}$
be continuous. If
$[h_t]$
is the Wulff shape associated with
$(C^\circ ,\eta ,h_t)$
, where
$h_t$
is given by (3.2), then for almost all
$u\in \Omega _{C^\circ }$
,
$$ \begin{align*}\nonumber \lim\limits_{t\rightarrow0} \frac{\log\rho_{[h_t]}(u)-\log\rho_{[h_0]}(u)}{t} =f(\alpha_{[h_0]}(u)). \end{align*} $$
Moreover, there exist two constants
$\delta _0>0$
and
$M>0$
such that
$$ \begin{align*}\nonumber |\log\rho_{[h_t]}(u)-\log\rho_{[h_0]}(u)|\leq M|t|, \end{align*} $$
for all
$u\in \Omega _{C^\circ }$
and
$t\in (-\delta _0,\delta _0)$
.
Furthermore, we apply Lemma 3 to obtain the following result.
Lemma 4 Let
$\eta \subset \Omega _C$
be a nonempty compact subset and
$f:\eta \rightarrow \mathbb {R}$
be continuous. If
$[h_t]$
is the Wulff shape associated with
$(C^\circ ,\eta ,h_t)$
, where
$h_t$
is given by (3.2), then for
$t\in (-\delta ,\delta )$
, we have
$$ \begin{align} \frac{d}{dt}E_\lambda([h_t])\Big|_{t=0} =\int_\eta f(v)d\lambda([h_0]^\circ,v). \end{align} $$
Proof Note that
$\langle 1/h_0\rangle \in {psi}(C)$
. It follows from (2.4) and (2.5) that
$$ \begin{align*}\nonumber \alpha_{[h_0]}(u) =\alpha_{\langle1/h_0\rangle^\circ}(u) =\alpha^*_{\langle1/h_0\rangle}(u) =\alpha^*_{[h_0]^\circ}(u)\ \text{for any}\ u\in\Omega_{C^\circ}\backslash\omega_{\langle1/h_0\rangle}. \end{align*} $$
Then, by definition (3.1), Lemma 3, the dominated convergence theorem, and (2.6), we have
$$ \begin{align*}\nonumber \frac{d}{dt}E_\lambda([h_t])\Big|_{t=0} &=\lim\limits_{t\rightarrow0}\int_{\Omega_{C^\circ}} \frac{\log\rho_{[h_t]}(u)-\log\rho_{[h_0]}(u)}{t}d\lambda(u)\\ &=\int_{\Omega_{C^\circ}}f(\alpha_{[h_0]}(u))d\lambda(u)\\ &=\int_{\Omega_{C^\circ}}f(\alpha^*_{[h_0]^\circ}(u))d\lambda(u). \end{align*} $$
Consequently, the desired (3.3) immediately follows from Lemma 4 of [Reference Schneider22]. Here, we have extended the function f to
$\Omega _C$
by taking
$f=0$
outside
$\eta $
.
We are now in the position to prove a variational formula related to the Wulff shape.
Lemma 5 Let
$\eta \subset \Omega _C$
be a nonempty compact subset and
$K,L\in {ps}(C)$
, and let
$[h_{t,p}]$
be the Wulff shape associated with
$(C^\circ ,\eta ,h_{t,p})$
. If
$p\neq 0$
and
$h_{t,p}(v)=(\bar {h}_{K^\circ }^p(v)+t\bar {h}_{L^\circ }^p(v))^{1/p}$
for any
$v\in \eta $
, then
$$ \begin{align} \frac{d}{dt}E_\lambda([h_{t,p}])\Big|_{t=0} =\frac{1}{p}\int_\eta\rho_L^{-p}(v)\rho_K^p(v) d\lambda(\langle\rho_K|_\eta\rangle,v). \end{align} $$
If
$p=0$
and
$h_{t,0}(v)=\bar {h}_{K^\circ }(v)\bar {h}_{L^\circ }^t(v)$
for any
$v\in \eta $
, then
$$ \begin{align} \frac{d}{dt}E_\lambda([h_{t,0}])\Big|_{t=0} =-\int_\eta\log\rho_L(v)d\lambda(\langle\rho_K|_\eta\rangle,v). \end{align} $$
Proof We first prove the case of
$p\neq 0$
. As
$h_{t,p}(v)=(\bar {h}_{K^\circ }^p(v)+t\bar {h}_{L^\circ }^p(v))^{1/p}$
for any
$v\in \eta $
, it follows that
$$ \begin{align*}\log h_{t,p} =\log\bar{h}_{K^\circ}+\frac{1}{p} \left(\frac{\bar{h}_{L^\circ}}{\bar{h}_{K^\circ}}\right)^pt+o_p(t,\cdot), \end{align*} $$
where
$o_p(t,\cdot ):\eta \rightarrow \mathbb {R}$
is continuous, and
$\lim \limits _{t\rightarrow 0}o_p(t,\cdot )/t=0$
uniformly on
$\eta $
. Then, from Lemma 4 and (2.1), and noting that
$[\bar {h}_{K^\circ }]^\circ =[1/\rho _K]^\circ =\langle \rho _K|_\eta \rangle $
, we obtain the desired (3.4) immediately.
Analogously, to deal with the case of
$p=0$
, we note that
$$ \begin{align*}\log h_{t,0}=\log\bar{h}_{K^\circ}+t\log\bar{h}_{L^\circ}\ \text{on}\ \eta. \end{align*} $$
Then, by the arguments similar to those for the case of
$p\neq 0$
, we can easily verify (3.5).
For a
${C}$
-pseudo-cone K, the variational formula (3.4) induces an important geometric measure
$\rho _K^p\lambda (K,\cdot )$
. We call it the
$L_p$
Gauss image measure and denote it by
$\lambda _p(K,\cdot )$
. Since the Gauss image measure
$\lambda (K,\cdot )$
introduced by Schneider [Reference Schneider22] is a Borel measure, and the radial function
$\rho _K$
is positive and continuous, the
$L_p$
Gauss image measure
$\lambda _p(K,\cdot )$
remains a Borel measure. In the following, we further prove its weak convergence.
Lemma 6 Let
$\eta \subset \Omega _C$
be a nonempty compact subset,
$K_i\in {psi}(C)$
for
$i\in \mathbb {N}_0$
and
$p\neq 0$
. If
$K_i\rightarrow K_0$
as
$i\rightarrow \infty $
, then
$\lambda _p(K_i,\cdot )$
converges to
$\lambda _p(K_0,\cdot )$
weakly on
$\eta $
.
Proof As
$K_i\rightarrow K_0$
as
$i\rightarrow \infty $
, it follows that
$\rho _{K_i}$
converges to
$\rho _{K_0}$
uniformly on
$\eta $
. Note that
$\rho _{K_0}$
is positive, and
$\rho _{K_i}$
are uniformly bounded on
$\eta $
. Thus, we conclude that
$\rho _{K_i}^p$
converges to
$\rho _{K_0}^p$
uniformly, and
$g\rho _{K_i}^p$
converges to
$g\rho _{K_0}^p$
uniformly as well, where g denotes a continuous function on
$\eta $
.
Furthermore, it follows from Lemma 5 of [Reference Schneider22] that restriction of the measure
$\lambda (K_i,\cdot )$
to
$\eta $
is weakly convergent. That is, 
converges to 
weakly as
$i\rightarrow \infty $
. Therefore, we have
$$ \begin{align*}\nonumber \lim\limits_{i\rightarrow\infty} \int_\eta g(v)\rho_{K_i}^p(v)d\lambda(K_i,v) =\int_\eta g(v)\rho_{K_0}^p(v)d\lambda(K_0,v). \end{align*} $$
Equivalently,
$$ \begin{align*}\nonumber \lim\limits_{i\rightarrow\infty} \int_\eta g(v)d\lambda_p(K_i,v) =\int_\eta g(v)d\lambda_p(K_0,v), \end{align*} $$
and the desired weak convergence follows.
4 Proofs of the main results
This section is dedicated to proving our existence and uniqueness theorems. To complete the proof of the former, we first recall a necessary lemma in [Reference Schneider22], and we establish an existence result under the additional assumption that measure
$\mu $
is defined on the nonempty compact set. We shall begin with stating the following lemma.
Lemma 7 (cf. Lemma 9 of [Reference Schneider22])
Let
$\lambda $
be a nonzero finite measure on the Lebesgue measurable subsets of
$\mathrm {cl}\Omega _{C^\circ }$
which vanishes on Borel sets of Hausdorff dimension
${(n-2)}$
. Let
$\eta \subset \Omega _C$
be a nonempty compact subset,
$g:\eta \rightarrow \mathbb {R}$
be continuous, and
$K\in {ps}(C)$
. If
$\langle f_t\rangle $
is the convexification associated with
$(C, \eta , f_t)$
, where
$$ \begin{align*}\nonumber \log f_t(v)=\log\rho_K(v)+tg(v)\ \text{for}\ v\in\eta, \end{align*} $$
then
$$ \begin{align} \frac{d}{dt}\int_{\Omega_{C^\circ}} \log\rho_{\langle f_t\rangle^\circ}(u)d\lambda(u)\Big|_{t=0} =-\int_\eta g(v)d\lambda(\langle f_0\rangle,v). \end{align} $$
To prove the existence of solutions for a finite Borel measure
$\mu $
on the nonempty compact subset, we study a critical optimization problem that differs from the one considered in [Reference Schneider22]. Then, we use Lemma 7 to obtain the following existence result.
Lemma 8 Let
$\lambda $
be a nonzero finite measure on the Lebesgue measurable subsets of
$\mathrm {cl}\Omega _{C^\circ }$
which vanishes on Borel sets of Hausdorff dimension
$(n-2)$
. If
$\mu $
is a finite Borel measure on the nonempty compact subset
$\eta \subset \Omega _C$
and
$p\neq 0$
, there exists a
${C}$
-pseudo-cone
$K\in {\mathcal K}^*(C,\eta )$
such that
$\mu =\lambda _p(K,\cdot )$
.
Proof Let
$|\lambda |=\lambda (\Omega _{C^\circ })$
. Recall that
${\mathcal {C}}^+(\eta )$
denotes the set of all positive continuous functions on
$\eta $
. Then, for
$p\neq 0$
, we construct a functional
$\Phi _{\lambda ,\mu ,p}$
on
${\mathcal {C}}^+(\eta )$
as follows:
$$ \begin{align*}\nonumber \Phi_{\lambda,\mu,p}(f) =-\frac{1}{p}\log\left(\frac{1}{\mu(\eta)} \int_\eta f^{-p}(v)d\mu(v)\right) +\frac{1}{|\lambda|} \int_{\Omega_{C^\circ}}\log\rho_{{\langle f\rangle}^\circ}(u)d\lambda(u), \end{align*} $$
where
$f\in \mathcal {C}^+{(\eta )}$
. Obviously, Lemma 1 shows that functional
$\Phi _{\lambda ,\mu ,p}$
is continuous on
${\mathcal {C}}^+(\eta )$
. Moreover, we verify
$\Phi _{\lambda ,\mu ,p}(sf)=\Phi _{\lambda ,\mu ,p}(f)$
for
$s>0$
. That is, functional
$\Phi _{\lambda ,\mu ,p}$
is homogeneous of degree
$0$
. Next, we consider a minimization problem
$$ \begin{align} \inf\big\{\Phi_{\lambda,\mu,p}(f):f\in\mathcal{C}^+(\eta)\big\}, \end{align} $$
and we prove that problem (4.2) is indeed solvable.
For any
$f\in \mathcal {C}^+(\eta )$
, it follows from (2.3) that
$\rho _{\langle f\rangle }\leq f$
on
$\eta $
, and
$\langle \rho _{\langle f\rangle }{|_\eta }\rangle =\langle f\rangle \in {psi}(C)$
. Then, we obtain
$\Phi _{\lambda ,\mu ,p}(\rho _{\langle f\rangle }{|_\eta }) \leq \Phi _{\lambda ,\mu ,p}(f)$
. Now, we focus on the set of all radial functions of pseudo-cones in
${psi}(C)$
. Thus, the problem (4.2) can be equivalently transformed into the problem
$$ \begin{align} \inf\big\{\Phi_{\lambda,\mu,p}(\rho_K{|_\eta}):K\in{psi}(C)\big\}. \end{align} $$
In fact, we can verify that
$K\in {psi}(C)$
is a solution to the problem (4.3) if and only if
$\rho _K{|_\eta }$
is a solution to the problem (4.2).
In the following, we further have the following Claim.
Claim. The infimum in (4.3) can be attained by some C-pseudo-cone in
${psi}(C)$
.
To verify the Claim, we take a minimizing sequence
$\{K_i\}$
of pseudo-cones in
${psi}(C)$
, such that
$$ \begin{align*}\nonumber \lim\limits_{i\rightarrow+\infty} \Phi_{\lambda,\mu,p}(\rho_{K_i}{|_\eta}) =\inf\big\{\Phi_{\lambda,\mu,p}(\rho_K{|_\eta}) :K\in{psi}(C)\big\}. \end{align*} $$
Since the functional
$\Phi _{\lambda ,\mu ,p}$
is homogeneous of degree
$0$
, we assume that each
$K_i$
has distance
$1$
from the origin. Then, by Lemma 2, we conclude that sequence
$\{K_i\}$
has a subsequence, still denoted by
$\{K_i\}$
, convergent to some C-pseudo-cone
$K_0$
as
$i\rightarrow \infty $
. Consequently, from the continuity of functional
$\Phi _{\lambda ,\mu ,p}$
, we can verify the assertion of Claim.
To continue with the proof of Lemma 8, we take a sufficiently small
$\delta>0$
. For each
$t\in (-\delta ,\delta )$
, we define a function
$\rho _t$
on
$\eta $
by
$\rho _t:=\rho _{K_0}e^{tg}$
, where
$g\in {\mathcal {C}}^+(\eta )$
.
For any
$s\in (-1,1)$
, we have the inequality
$|e^s-1-s|\leq es^2$
. Taking
$s=-ptg(v)$
, then for any
$|t|<\min \{\frac {1}{|p|\max \{g(v):v\in \eta \}},\delta \}$
, we have
$$ \begin{align*}\nonumber \Big|\frac{e^{-ptg(v)}-1}{t}+pg(v)\Big|\leq ep^2|t|g^2(v),\ \text{for}\ v\in\eta. \end{align*} $$
Furthermore, we conclude that, as
$t\rightarrow 0$
,
$$ \begin{align*}\nonumber \frac{\rho_t^{-p}-\rho_0^{-p}}{t} =\rho_{K_0}^{-p}\frac{e^{-ptg}-1}{t}\rightarrow-\rho_{K_0}^{-p}pg,\ \text{uniformly on}\ \eta. \end{align*} $$
Then, we have the following calculation:
$$ \begin{align} \begin{aligned} &\frac{d}{dt}\log\left(\frac{1}{\mu(\eta)} \int_\eta\rho_t^{-p}(v)d\mu(v)\right)\bigg|_{t=0}\\ =&\frac{1}{\int_\eta\rho_{K_0}^{-p}(v)d\mu(v)} \frac{d}{dt}\int_\eta\rho_t^{-p}(v)d\mu(v)\bigg|_{t=0}\\ =&\frac{1}{\int_\eta\rho_{K_0}^{-p}(v)d\mu(v)} \lim\limits_{t\rightarrow0} \int_\eta\frac{\rho_t^{-p}(v)-\rho_0^{-p}(v)}{t}d\mu(v)\bigg|_{t=0}\\ =&-\frac{p}{\int_\eta\rho_{K_0}^{-p}(v)d\mu(v)} \int_\eta\rho_{K_0}^{-p}(v)g(v)d\mu(v). \end{aligned} \end{align} $$
It follows from Lemma 7 that
$\Phi _{\lambda ,\mu ,p}(\rho _t)$
is differentiable at
$t=0$
. As
$\rho _{K_0}|_\eta $
is a solution to the problem (4.2), we obtain that
$$ \begin{align*}\nonumber \frac{d}{dt}\Phi_{\lambda,\mu,p}(\rho_t)\Big|_{t=0}=0. \end{align*} $$
This, together with (4.1) and (4.4), gives that
$$ \begin{align} \frac{1}{\int_\eta\rho_{K_0}^{-p}(v)d\mu(v)} \int_\eta\rho_{K_0}^{-p}(v)g(v)d\mu(v) -\frac{1}{|\lambda|}\int_\eta g(v)d\lambda(\langle\rho_{K_0}|_\eta\rangle,v)=0. \end{align} $$
Then, from (4.5) and the Riesz representation theorem, we employ (1.1) to obtain
$$ \begin{align} \mu =\frac{\int_\eta\rho_{K_0}^{-p}(v)d\mu(v)}{|\lambda|} \lambda_p(\langle\rho_{K_0}|_\eta\rangle,\cdot). \end{align} $$
Since the right-hand side of (4.6) is invariant under any dilations of
$K_0$
, we can rescale
$K_0$
to obtain the desired equality.
Lemma 8 is an essential step toward the general existence theorem. We now remove the assumption of compactness condition, and then we adopt the approximation method to prove our existence theorem.
Proof of Theorem 1
Let
$\mu $
be a Borel measure on
$\Omega _C$
, and let
$\{\eta _j\}_{j\in \mathbb {N}}$
be a sequence of compact sets in
$\Omega _C$
such that
$$ \begin{align*}\nonumber \mu(\eta_1)>0,\ \eta_j\subset\eta_{j+1}\ \text{for}\ j\in\mathbb{N},\ \bigcup\limits_{j\in\mathbb{N}}\eta_j=\Omega_C. \end{align*} $$
Define 
; that is,
$\mu _j(\beta )=\mu (\beta \cap \eta _j)$
for any Borel set
$\beta $
in
$\Omega _C$
. Thus,
$\mu _j$
is a finite Borel measure on
$\eta _j$
. Then, for each j, the proof of Lemma 8 shows that there exists a
${C}$
-pseudo-cone
$K_j\in {\mathcal K}^*(C,\eta _j)$
with
$\mu _j=c_j\lambda _p(K_j,\cdot )$
on
$\eta _j$
, where
$$ \begin{align*}\nonumber c_j=\frac{1}{|\lambda|}\int_{\eta_j}\rho_{K_j}^{-p}d\mu_j =\frac{1}{|\lambda|}\int_{\Omega_C}\rho_{K_j}^{-p}\chi_{\eta_j}d\mu, \end{align*} $$
where
$\chi _{\eta _j}$
is the characteristic function of
$\eta _j$
.
As
$\lambda (K_j,\cdot )$
is positively homogeneous of degree
$0$
, we assume that
$K_j$
has distance
$1$
from the origin. Then, we apply Lemma 2 again to obtain that sequence
$\{K_j\}$
has a subsequence, still denoted by
$\{K_j\}$
, converging to C-pseudo-cone K as
$j\rightarrow \infty $
. Moreover, we obtain that
$\rho _{K_j}^{-p}\le 1$
due to
$p>0$
. It follows that
$$ \begin{align*}\nonumber c_j\rightarrow\frac{1}{|\lambda|}\int_{\Omega_C}\rho_K^{-p}d\mu =:c>0\ \text{as}\ j\rightarrow\infty. \end{align*} $$
Fix
$k\in \mathbb {N}$
, then for any Borel set
$\beta \subseteq \eta _k$
and
$j\geq k$
,
$\mu (\beta )=\mu _j(\beta )=c_j\lambda _p(K_j,\beta )$
, and the restrictions to
$\eta _k$
satisfy
Taking
$j\rightarrow \infty $
and applying Lemma 6 on
$\eta _k$
, we conclude that
$\mu (\beta )=c\lambda _p(K,\beta )$
for
$\beta \subseteq \eta _k$
. As
$k\in \mathbb {N}$
is arbitrary and
$\bigcup \limits _{k\in \mathbb {N}}\eta _k=\Omega _C$
, we have
$\mu =c\lambda _p(K,\cdot )$
on
$\Omega _C$
. Finally, by rescaling K, we can obtain the desired equality.
Recall that Böröczky et al. [Reference Böröczky, Lutwak, Yang, Zhang and Zhao4] adopted the method in [Reference Zhao27] to prove a uniqueness lemma, and Schneider [Reference Schneider22] has recently carried over that proof to pseudo-cones. In the following, we prove that uniqueness remains valid in the
$L_p$
setting for
$p<0$
. Our proof technique follows from [Reference Schneider22].
Proof of Theorem 2
Let
$p<0$
. Suppose
$\lambda _p(K,\cdot )=\lambda _p(L,\cdot )$
, but
$K\neq L$
. This implies that there exists some
$v_0\in \Omega _C$
so that
$r_K(v_0)$
and
$r_L(v_0)$
are regular points, and the support hyperplane of K at
$r_K(v_0)$
and that of L at
$r_L(v_0)$
have distinct normal vectors. Without loss of generality, we assume that
$r_K(v_0)$
is closer to the origin than
$r_L(v_0)$
, then we rescale K and denote by
$K^{\prime }=cK$
, where
$c=:r_L(v_0)/r_K(v_0)\ge 1$
.
We now define a disjoint decomposition
$\Omega _C=\eta ^{\prime }\cup \eta _0\cup \eta $
as follows:
$$ \begin{align*}\nonumber \begin{aligned} \eta^{\prime} =\{v\in\Omega_C:\rho_{K^{\prime}}(v)<\rho_L(v)\},\\ \eta_0 =\{v\in\Omega_C:\rho_{K^{\prime}}(v)=\rho_L(v)\},\\ \eta =\{v\in\Omega_C:\rho_{K^{\prime}}(v)>\rho_L(v)\}. \end{aligned} \end{align*} $$
If
$v\in \eta ^{\prime }$
and
$H_L$
is a support hyperplane of L at
$r_L(v)$
, then pseudo-cone
$K^{\prime }$
has a parallel support hyperplane
$H_{K^\prime }$
at some
$r_{K^\prime }(v^{\prime })$
with
$v^{\prime }\in \eta ^{\prime }$
. Moreover, we have
$$ \begin{align} \boldsymbol{\alpha}_L(\eta^{\prime}) \subseteq\boldsymbol{\alpha}_{K^\prime}(\eta^{\prime}) =\boldsymbol{\alpha}_K(\eta^{\prime}). \end{align} $$
Note that
$\eta ^{\prime }\cup \eta _0$
and
$\eta \cup \eta _0$
are closed sets. It follows that
$\boldsymbol {\alpha }_L(\eta ^{\prime }\cup \eta _0)$
and
${\boldsymbol {\alpha }_{K^\prime }(\eta \cup \eta _0)}$
are two closed subsets in
$\Omega _{C^\circ }$
. Consequently,
$\Omega _{C^\circ }\backslash \boldsymbol {\alpha }_L(\eta ^{\prime }\cup \eta _0)$
and
$\Omega _{C^\circ }\backslash \boldsymbol {\alpha }_{K^\prime }(\eta \cup \eta _0)$
are open sets, and moreover, we can easily verify that
$$ \begin{align*}\nonumber \Omega_{C^\circ}\backslash\boldsymbol{\alpha}_{K^\prime}(\eta\cup\eta_0) \subset\boldsymbol{\alpha}_{K^\prime}(\eta^{\prime})\ \text{and}\ (\Omega_{C^\circ}\backslash\boldsymbol{\alpha}_L(\eta^{\prime}\cup\eta_0)) \cap\boldsymbol{\alpha}_L(\eta^{\prime})=\emptyset. \end{align*} $$
Taking an open set
$\beta =(\Omega _{C^\circ }\backslash \boldsymbol {\alpha }_{K^\prime }(\eta \cup \eta _0)) \cap (\Omega _{C^\circ }\backslash \boldsymbol {\alpha }_L(\eta ^{\prime }\cup \eta _0)), $
we shall prove that
$$ \begin{align*}\nonumber v_1 :=(\alpha_K(v_0)+\alpha_L(v_0))/|\alpha_K(v_0)+\alpha_L(v_0)|\in\beta. \end{align*} $$
We first verify that
$v_1\notin \boldsymbol {\alpha }_{K^\prime }(\eta \cup \eta _0)$
. Let
$H_{K^\prime }(v_1)$
be a support hyperplane of
$K^\prime $
with unit normal
$v_1$
. Then, for
$r_{K^\prime }(v)\in H_{K^\prime }(v_1)$
, there exist a
$x^\prime \in P$
and
$s>0$
so that
$r_{K^\prime }(v)=x^\prime +sv_1$
, where P is a hyperplane passing through
$x_0:=r_{K^\prime }(v_0)$
with
$v_1$
as its normal vector. Since
$$ \begin{align*}\nonumber x_0\cdot\alpha_{K^\prime}(v_0) =h_{K^\prime}(\alpha_{K^\prime}(v_0)) \ge x^\prime\cdot\alpha_{K^\prime}(v_0) +sv_1\cdot\alpha_{K^\prime}(v_0), \end{align*} $$
and
$v_1\cdot \alpha _{K^\prime }(v_0)>0$
, we obtain that
$x_0\cdot \alpha _{K^\prime }(v_0)>x^\prime \cdot \alpha _{K^\prime }(v_0)$
. Then, from
$x^\prime \cdot v_1=x_0\cdot v_1,$
we conclude
$x^\prime \cdot \alpha _L(v_0)>x_0\cdot \alpha _L(v_0)$
. It follows from
$v_1\cdot \alpha _L(v_0)>0$
that
$$ \begin{align*}\nonumber r_{K^\prime}(v)\cdot\alpha_L(v_0)>x^\prime\cdot\alpha_L(v_0) >x_0\cdot\alpha_L(v_0) =h_L(\alpha_L(v_0)). \end{align*} $$
This shows that
$r_{K^\prime }(v)\notin L$
. Thus, we obtain
$v\in \eta ^{\prime }$
, and
$v_1\notin \boldsymbol {\alpha }_{K^\prime }(\eta \cup \eta _0)$
.
Similarly, we can verify that
$v_1\notin \boldsymbol {\alpha }_L(\eta ^\prime \cup \eta _0)$
. Therefore,
$\beta $
is a nonempty open set in
$\Omega _{C^\circ }$
.
As
$\beta \subset \boldsymbol {\alpha }_{K^\prime }(\eta ^{\prime })$
and
$\beta \cap \boldsymbol {\alpha }_L(\eta ^{\prime })=\emptyset $
, by (4.7), we obtain
$\boldsymbol {\alpha }_L(\eta ^{\prime }) =\boldsymbol {\alpha }_L(\eta ^{\prime })\backslash \beta \subseteq \boldsymbol {\alpha }_{K^\prime }(\eta ^{\prime })\backslash \beta .$
Consequently,
$\lambda (\boldsymbol {\alpha }_L(\eta ^{\prime })) <\lambda (\boldsymbol {\alpha }_{K^\prime }(\eta ^{\prime }))$
due to that
$\lambda (\beta )>0$
, and
$$ \begin{align*}\nonumber \lambda_p(L,\eta^{\prime}) &=\int_{\eta^{\prime}}\rho_L^p(v)d\lambda(\alpha_L(v)) <\int_{\eta^{\prime}}\rho_{K^\prime}^p(v)d\lambda(\alpha_{K^\prime}(v))\\& \le\int_{\eta^{\prime}}\rho_K^p(v)d\lambda(\alpha_K(v)) =\lambda_p(K,\eta^{\prime}). \end{align*} $$
This contradicts our assumption; hence,
$K=L$
.
Acknowledgments
The authors are greatly indebted to the referees for many valuable suggestions and comments, which greatly improve the quality and presentation of the present article.
