1 Introduction
The thesis of Philippe Delsarte [Reference Delsarte8] was a landmark in coding theory and combinatorial design theory. Employing the language of association schemes, Delsarte’s approach was one of the first to cast combinatorial questions in a linear algebraic framework where tools from matrix theory, orthogonal polynomials, and optimization could be applied. In particular, Delsarte [Reference Delsarte8, Theorems 4.4 and 4.7] characterized orthogonal arrays and block designs as 01-vectors orthogonal to specific eigenspaces of the Hamming scheme and Johnson scheme, respectively. It is natural, then, to look at analogous substructures in the q-analogs of these families of association schemes and other classical families of Q-polynomial distance-regular graphs [Reference Brouwer, Cohen and Neumaier6]. The following decades brought more examples, more applications, and more connections to other parts of mathematics.
Association schemes are ubiquitous in combinatorics. For many problems, the vertex set of an association scheme is the natural “ambient space” in which to search for subsets with desired structure. Schurian association schemes are fundamental to the study of group actions. Dual polar spaces and sesquilinear forms schemes play key roles in finite geometry. And, of course, various extremal codes and designs themselves form interesting association schemes.
The generic definition of a Delsarte design in an association scheme – a subset or weighted subsetFootnote 1 of the vertex set whose characteristic vector is orthogonal to some specified set of eigenspaces of (the Bose–Mesner algebra of) that scheme – is again and again found to coincide with interesting and important combinatorial substructures. In [Reference Ernst and Schmidt11, Reference Martin and Sagan17], orthogonality to natural collections of eigenspaces translates exactly to transitivity properties of a subset of a symmetric group or finite general linear group. In [Reference Bamberg, Giudici, Lansdown and Royle2], Delsarte designs play a key role in the study of synchronization. In recent years, we have seen many Erdős–Ko–Rado results [Reference Godsil and Meagher12] for various families of association schemes and the extremal subsets in most cases are Delsarte designs.
It is crucial, therefore, to further develop Delsarte’s theory in the case of general (commutative) association schemes and beyond. While the Hamming and Johnson schemes, etc., have only integer eigenvalues, most association schemes have irrational eigenvalues. The most obvious situation where restriction to a subfield of the splitting field is necessary is that in which one applies Delsarte’s linear programming bound [Reference Delsarte8, Section 3.2] to problems in non-symmetric association schemes: here, the splitting field is not contained in
![]() $\mathbb {R}$
so one moves to the symmetrization to obtain a scheme with only real eigenvalues. But one can go further: since codes and designs, even weighted versions with rational weights, are represented by vectors with rational entries, we benefit by moving to rational vector spaces of matrices and, in the best scenario, work instead with a subalgebra of the Bose–Mesner which itself is a Bose–Mesner algebra having only rational eigenvalues.
$\mathbb {R}$
so one moves to the symmetrization to obtain a scheme with only real eigenvalues. But one can go further: since codes and designs, even weighted versions with rational weights, are represented by vectors with rational entries, we benefit by moving to rational vector spaces of matrices and, in the best scenario, work instead with a subalgebra of the Bose–Mesner which itself is a Bose–Mesner algebra having only rational eigenvalues.
To this end, we explore the set of minimal rational idempotents in a Bose–Mesner algebra and their relation to the Galois group of the splitting field of the association scheme. In this article, all association schemes are commutative; so a Bose–Mesner algebra of dimension
![]() $d+1$
contains exactly
$d+1$
contains exactly
![]() $2^{d+1}$
matrix idempotents. The complex vector space spanned by any subset of these summing to I is closed under both the conjugate transpose operation and matrix multiplication. (We will assume that our collection always includes a scalar multiple of the all ones matrix, J.) A fusion scheme arises when such a vector space is also closed under the Schur (entrywise) product. We are particularly interested in which subfields
$2^{d+1}$
matrix idempotents. The complex vector space spanned by any subset of these summing to I is closed under both the conjugate transpose operation and matrix multiplication. (We will assume that our collection always includes a scalar multiple of the all ones matrix, J.) A fusion scheme arises when such a vector space is also closed under the Schur (entrywise) product. We are particularly interested in which subfields
![]() $\mathbb {K}$
of the splitting field
$\mathbb {K}$
of the splitting field
![]() $\mathbb {F}$
have the property that the matrix idempotents having entries in
$\mathbb {F}$
have the property that the matrix idempotents having entries in
![]() $\mathbb {K}$
produce a fusion scheme in this way.
$\mathbb {K}$
produce a fusion scheme in this way.
The most important case for Delsarte theory, of course, is
![]() $\mathbb {K}=\mathbb {Q}$
. The matrix idempotents with rational entries are obtained by summing (or merging) primitive idempotents over orbits of the full Galois group
$\mathbb {K}=\mathbb {Q}$
. The matrix idempotents with rational entries are obtained by summing (or merging) primitive idempotents over orbits of the full Galois group
![]() ${\mathsf {Gal}}(\mathbb {F}/\mathbb {Q})$
. These idempotents are fundamental to our understanding of T-designs in association schemes with irrational eigenvalues. Our main tool is based on a simple observation. Suppose
${\mathsf {Gal}}(\mathbb {F}/\mathbb {Q})$
. These idempotents are fundamental to our understanding of T-designs in association schemes with irrational eigenvalues. Our main tool is based on a simple observation. Suppose
![]() $(X,{\mathcal R})$
is a d-class association scheme with basis
$(X,{\mathcal R})$
is a d-class association scheme with basis
![]() $\{E_0,\ldots ,E_d\}$
of primitive idempotents over its splitting field
$\{E_0,\ldots ,E_d\}$
of primitive idempotents over its splitting field
![]() $\mathbb {F}$
. If a subset
$\mathbb {F}$
. If a subset
![]() $C\subset X$
is a T-design for some subset T of
$C\subset X$
is a T-design for some subset T of
![]() $\{1,\ldots ,d\}$
with
$\{1,\ldots ,d\}$
with
![]() $j\in T$
and
$j\in T$
and
![]() $E_j^{\boldsymbol {\sigma }}=E_\ell $
for
$E_j^{\boldsymbol {\sigma }}=E_\ell $
for
![]() $\boldsymbol {\sigma } \in {\mathsf {Gal}}(\mathbb {F}/\mathbb {Q})$
, then C is also a
$\boldsymbol {\sigma } \in {\mathsf {Gal}}(\mathbb {F}/\mathbb {Q})$
, then C is also a
![]() $\left (T \cup \{\ell \}\right )$
-design.
$\left (T \cup \{\ell \}\right )$
-design.
This leads us to study the span of all idempotent matrices in our Bose–Mesner algebra having all entries in a specified subfield
![]() $\mathbb {K}$
of the splitting field
$\mathbb {K}$
of the splitting field
![]() $\mathbb {F}$
. We show, in Theorem 4.1, how this can greatly reduce the size of a search space or optimization problem. When the process of merging idempotents over orbits of
$\mathbb {F}$
. We show, in Theorem 4.1, how this can greatly reduce the size of a search space or optimization problem. When the process of merging idempotents over orbits of
![]() ${\mathsf {Gal}}(\mathbb {F}/\mathbb {K})$
results in another association scheme (see Lemmas 2.2(v) and 3.5), the Delsarte T-designs in the original scheme are precisely the Delsarte
${\mathsf {Gal}}(\mathbb {F}/\mathbb {K})$
results in another association scheme (see Lemmas 2.2(v) and 3.5), the Delsarte T-designs in the original scheme are precisely the Delsarte
![]() $T'$
-design in this fusion scheme for a particular
$T'$
-design in this fusion scheme for a particular
![]() $T'$
depending on T (Theorem 4.3), and this has powerful implications for the collections of T-designs in two association schemes which happen to have isomorphic rational fusions (Theorem 4.5).
$T'$
depending on T (Theorem 4.3), and this has powerful implications for the collections of T-designs in two association schemes which happen to have isomorphic rational fusions (Theorem 4.5).
An important family of association schemes to consider are the conjugacy class schemes (or “group schemes”) of finite groups. These have the property that a fusion scheme is obtained by merging conjugacy classes in a way that respects the Galois group (over
![]() $\mathbb {Q}$
). We provide a proof of this result along with some basic background material for the sake of exposition, including a natural method for obtaining a basis of eigenvectors for the Bose–Mesner algebra.
$\mathbb {Q}$
). We provide a proof of this result along with some basic background material for the sake of exposition, including a natural method for obtaining a basis of eigenvectors for the Bose–Mesner algebra.
We finish with an illustration of how these three themes – Delsarte theory, Galois groups, and conjugacy class schemes – come together. In the final section of the article, we apply the tools of Sections 3 and 4 to look at the inner distributions and MacWilliams transforms of all subgroups of the dicyclic groups
![]() ${\mathsf {Dic}}_n$
(n odd).
${\mathsf {Dic}}_n$
(n odd).
2 Association schemes, Bose–Mesner algebras, and matrices over subfields
Our notation and terminology generally follow [Reference Brouwer, Cohen and Neumaier6] but see also [Reference Bannai and Ito4, Reference Godsil13]. In this article, all association schemes are commutative. An association scheme (or, more simply, scheme) is an ordered pair
![]() $\mathscr {X}=(X,{\mathcal R}),$
where X is a nonempty finite set and
$\mathscr {X}=(X,{\mathcal R}),$
where X is a nonempty finite set and
![]() ${{\mathcal R}=\{R_0,\ldots , R_d\}}$
is a partition of
${{\mathcal R}=\{R_0,\ldots , R_d\}}$
is a partition of
![]() $X\times X$
satisfying:
$X\times X$
satisfying:
-
(i)
 $R_0= \mathrm {id}_X$
, the identity relation;
$R_0= \mathrm {id}_X$
, the identity relation; -
(ii) for each i,
 $0\le i\le d$
, there is an
$0\le i\le d$
, there is an
 $i'$
for which
$i'$
for which
 $R_{i'}=R_i^\top = \{ (b,a) \mid (a,b)\in R_i\}$
;
$R_{i'}=R_i^\top = \{ (b,a) \mid (a,b)\in R_i\}$
; -
(iii) there exist
 $p_{ij}^k$
(
$p_{ij}^k$
(
 $0\le i,j,k\le d$
) such that
$0\le i,j,k\le d$
) such that
 $\left | \{ c\in X \mid (a,c)\in R_i, \ (c,b)\in R_j\} \right | =p_{ij}^k$
for any
$\left | \{ c\in X \mid (a,c)\in R_i, \ (c,b)\in R_j\} \right | =p_{ij}^k$
for any
 $(a,b)\in R_k$
;
$(a,b)\in R_k$
; -
(iv)
 $p_{ij}^k=p_{ji}^k$
for all i, j, and k.
$p_{ij}^k=p_{ji}^k$
for all i, j, and k.
We may view the pair
![]() $(X,R_i)$
as a digraph on the vertex set X. We write
$(X,R_i)$
as a digraph on the vertex set X. We write
![]() $R_i(x) = \{ y\in X | (x,y) \in R_i\}$
. Condition (iii) is then
$R_i(x) = \{ y\in X | (x,y) \in R_i\}$
. Condition (iii) is then
![]() $\left | R_i(a) \cap R_{j'}(b) \right | = p_{ij}^k$
whenever
$\left | R_i(a) \cap R_{j'}(b) \right | = p_{ij}^k$
whenever
![]() $b\in R_k(a)$
. We typically deal with these directed graphs via their adjacency matrices.
$b\in R_k(a)$
. We typically deal with these directed graphs via their adjacency matrices.
For a nonempty finite set X and a field
![]() $\mathbb {K}$
, we denote by
$\mathbb {K}$
, we denote by
![]() $\mathsf {Mat}_X(\mathbb {K})$
the algebra of matrices with rows and columns indexed by the elements of X having entries in
$\mathsf {Mat}_X(\mathbb {K})$
the algebra of matrices with rows and columns indexed by the elements of X having entries in
![]() $\mathbb {K}$
. For
$\mathbb {K}$
. For
![]() $x,y\in X$
and
$x,y\in X$
and
![]() $A \in \mathsf {Mat}_X(\mathbb {K})$
, the entry in row x, column y of A is denoted
$A \in \mathsf {Mat}_X(\mathbb {K})$
, the entry in row x, column y of A is denoted
![]() $A_{xy}$
. For
$A_{xy}$
. For
![]() $[m]=\{1,\ldots ,m\}$
, we will simply write
$[m]=\{1,\ldots ,m\}$
, we will simply write
![]() $\mathsf {Mat}_m(\mathbb {K})$
for
$\mathsf {Mat}_m(\mathbb {K})$
for
![]() $\mathsf {Mat}_{[m]}(\mathbb {K})$
. For an association scheme
$\mathsf {Mat}_{[m]}(\mathbb {K})$
. For an association scheme
![]() $\mathscr {X}=(X,{\mathcal R})$
as above, the
$\mathscr {X}=(X,{\mathcal R})$
as above, the
![]() $i^{\mathrm {th}}$
adjacency matrix or
$i^{\mathrm {th}}$
adjacency matrix or
![]() $i^{\mathrm {th}}$
Schur idempotent
Footnote
2
$i^{\mathrm {th}}$
Schur idempotent
Footnote
2
![]() $A_i$
is the matrix in
$A_i$
is the matrix in
![]() $\mathsf {Mat}_X(\mathbb {Q})$
with
$\mathsf {Mat}_X(\mathbb {Q})$
with
![]() $(a,b)$
-entry equal to one if
$(a,b)$
-entry equal to one if
![]() $(a,b)\in R_i$
and a zero otherwise. The fact that the
$(a,b)\in R_i$
and a zero otherwise. The fact that the
![]() $R_i$
partition
$R_i$
partition
![]() $X\times X$
means
$X\times X$
means
![]() $\sum _i A_i =J$
, the all ones matrix,
$\sum _i A_i =J$
, the all ones matrix,
![]() $A_i\circ A_j = 0$
for
$A_i\circ A_j = 0$
for
![]() $i\neq j$
, and
$i\neq j$
, and
![]() $A_i\circ A_i =A_i \neq 0$
. Conditions (i)–(iv) are then rephrased as:
$A_i\circ A_i =A_i \neq 0$
. Conditions (i)–(iv) are then rephrased as:
-
(i’)
 $A_0= I$
;
$A_0= I$
; -
(ii’) for each i,
 $A_i^\top \in \{A_0,\ldots ,A_d\}$
;
$A_i^\top \in \{A_0,\ldots ,A_d\}$
; -
(iii’)
 $A_i A_j = \sum _{k=0}^d p_{ij}^k A_k$
;
$A_i A_j = \sum _{k=0}^d p_{ij}^k A_k$
; -
(iv’)
 $A_i A_j = A_j A_i$
.
$A_i A_j = A_j A_i$
.
We use
![]() ${\mathcal R}=\{R_0,\ldots ,R_d\}$
and
${\mathcal R}=\{R_0,\ldots ,R_d\}$
and
![]() $\mathcal {A}=\{A_0,\ldots ,A_d\}$
interchangeably. Note that, in this article, a Bose–Mesner algebra
$\mathcal {A}=\{A_0,\ldots ,A_d\}$
interchangeably. Note that, in this article, a Bose–Mesner algebra
![]() $\mathbb {A}= \mathbb {C}[\mathcal {A}] = \operatorname {\mathrm {span}}_{\mathbb {C}}\{A_0,\ldots ,A_d\}$
is always defined over
$\mathbb {A}= \mathbb {C}[\mathcal {A}] = \operatorname {\mathrm {span}}_{\mathbb {C}}\{A_0,\ldots ,A_d\}$
is always defined over
![]() $\mathbb {C}$
, by extension of scalars, if necessary.
$\mathbb {C}$
, by extension of scalars, if necessary.
The commuting normal matrices
![]() $A_0,\ldots ,A_d$
are simultaneously diagonalizable over
$A_0,\ldots ,A_d$
are simultaneously diagonalizable over
![]() $\mathbb {C}$
, and we have a second canonical basis of primitive idempotents
$\mathbb {C}$
, and we have a second canonical basis of primitive idempotents
![]() $\{ E_0,E_1,\ldots ,E_d\}$
for
$\{ E_0,E_1,\ldots ,E_d\}$
for
![]() $\mathbb {A}$
satisfying
$\mathbb {A}$
satisfying
![]() $E_i E_j = \delta _{ij} E_i$
and
$E_i E_j = \delta _{ij} E_i$
and
![]() $\sum _j E_j = I$
(see, e.g., [Reference Bannai, Bannai, Ito and Tanaka5, Lemma 2.18]). By convention,
$\sum _j E_j = I$
(see, e.g., [Reference Bannai, Bannai, Ito and Tanaka5, Lemma 2.18]). By convention,
![]() $E_0=\frac {1}{|X|} J$
. For
$E_0=\frac {1}{|X|} J$
. For
![]() $0\le j\le d$
, there is a
$0\le j\le d$
, there is a
![]() $j^*$
such that
$j^*$
such that
![]() $E_{j^*} = E_j^\dagger $
, the Hermitian transpose of
$E_{j^*} = E_j^\dagger $
, the Hermitian transpose of
![]() $E_j$
. The splitting field of
$E_j$
. The splitting field of
![]() $\mathscr {X}$
(or of
$\mathscr {X}$
(or of
![]() $\mathbb {A}$
) is the subfield of
$\mathbb {A}$
) is the subfield of
![]() $\mathbb {C}$
obtained from
$\mathbb {C}$
obtained from
![]() $\mathbb {Q}$
by adjoining all eigenvalues of
$\mathbb {Q}$
by adjoining all eigenvalues of
![]() $A_1,\ldots ,A_d$
.
$A_1,\ldots ,A_d$
.
For a field
![]() $\mathbb {K}\subseteq \mathbb {C}$
and a set of matrices
$\mathbb {K}\subseteq \mathbb {C}$
and a set of matrices
![]() ${\mathcal E} \subset \mathsf {Mat}_X(\mathbb {K})$
, we will write
${\mathcal E} \subset \mathsf {Mat}_X(\mathbb {K})$
, we will write
![]() $\mathbb {K}[{\mathcal E}]= \operatorname {\mathrm {span}}_{\mathbb {K}}({\mathcal E})$
the
$\mathbb {K}[{\mathcal E}]= \operatorname {\mathrm {span}}_{\mathbb {K}}({\mathcal E})$
the
![]() $\mathbb {K}$
-span of
$\mathbb {K}$
-span of
![]() ${\mathcal E}$
. Assuming
${\mathcal E}$
. Assuming
![]() $\mathcal {A}$
is the basis of Schur idempotents of some association scheme,
$\mathcal {A}$
is the basis of Schur idempotents of some association scheme,
![]() $\mathbb {K}[\mathcal {A}]$
is always closed and commutative under both ordinary and Schur multiplication. Under these conditions,
$\mathbb {K}[\mathcal {A}]$
is always closed and commutative under both ordinary and Schur multiplication. Under these conditions,
![]() $\mathbb {K}[\mathcal {A}]$
is also closed under taking transpose and contains both I and J. While the set
$\mathbb {K}[\mathcal {A}]$
is also closed under taking transpose and contains both I and J. While the set
![]() $\mathbb {K}[\mathcal {A}]$
is diagonalizable over
$\mathbb {K}[\mathcal {A}]$
is diagonalizable over
![]() $\mathbb {C}$
, it is not diagonalizable over
$\mathbb {C}$
, it is not diagonalizable over
![]() $\mathbb {K}$
in general. Among the
$\mathbb {K}$
in general. Among the
![]() $2^{d+1}$
idempotents in
$2^{d+1}$
idempotents in
![]() $\mathbb {C}[\mathcal {A}]$
, we consider those with entries in subfield
$\mathbb {C}[\mathcal {A}]$
, we consider those with entries in subfield
![]() $\mathbb {K}$
:
$\mathbb {K}$
:
 $$ \begin{align} {\mathcal E}_{\mathbb{K}} = \left\{ F=\sum_{j=0}^d c_j E_j \middle| c_0,\ldots,c_d\in \{0,1\}, \ F\in \mathsf{Mat}_X(\mathbb{K}) \right\}. \end{align} $$
$$ \begin{align} {\mathcal E}_{\mathbb{K}} = \left\{ F=\sum_{j=0}^d c_j E_j \middle| c_0,\ldots,c_d\in \{0,1\}, \ F\in \mathsf{Mat}_X(\mathbb{K}) \right\}. \end{align} $$
Example 2.1 Consider the conjugacy class scheme of
![]() $\mathbb {Z}_{12}$
with splitting field
$\mathbb {Z}_{12}$
with splitting field
![]() $\mathbb {Q}(\sqrt {3},i)$
. Let
$\mathbb {Q}(\sqrt {3},i)$
. Let
![]() $\zeta =e^{\pi i/6}$
and index the primitive idempotents
$\zeta =e^{\pi i/6}$
and index the primitive idempotents
![]() $E_0,\ldots ,E_{11}$
so that
$E_0,\ldots ,E_{11}$
so that
![]() ${E_j = \frac {1}{12} u_j u_j^\dagger }$
, where
${E_j = \frac {1}{12} u_j u_j^\dagger }$
, where
![]() $\left ( u_j \right )_\ell = \zeta ^{j\ell }$
. For
$\left ( u_j \right )_\ell = \zeta ^{j\ell }$
. For
![]() $\mathbb {K}=\mathbb {Q}(\sqrt {-3})$
,
$\mathbb {K}=\mathbb {Q}(\sqrt {-3})$
,
![]() ${\mathcal E}_{\mathbb {K}} = \left \{ \sum _{j=0}^{11} c_j E_j \middle | c_j \in \{0,1\}, c_1=c_7, \ c_3=c_9, \ c_5=c_{11} \right \}$
and similar expressions can be derived for the subfields
${\mathcal E}_{\mathbb {K}} = \left \{ \sum _{j=0}^{11} c_j E_j \middle | c_j \in \{0,1\}, c_1=c_7, \ c_3=c_9, \ c_5=c_{11} \right \}$
and similar expressions can be derived for the subfields
![]() $\mathbb {Q}$
,
$\mathbb {Q}$
,
![]() $\mathbb {Q}(i)$
, and
$\mathbb {Q}(i)$
, and
![]() $\mathbb {Q}(\sqrt {3})$
.
$\mathbb {Q}(\sqrt {3})$
.
Lemma 2.2 Let
![]() $\mathscr {X}=(X,\mathcal {A})$
be an association scheme with Bose–Mesner algebra
$\mathscr {X}=(X,\mathcal {A})$
be an association scheme with Bose–Mesner algebra
![]() ${\mathbb {A}=\mathbb {C}[\mathcal {A}]}$
having basis
${\mathbb {A}=\mathbb {C}[\mathcal {A}]}$
having basis
![]() $\{E_0,\ldots ,E_d\}$
of primitive idempotents. Let
$\{E_0,\ldots ,E_d\}$
of primitive idempotents. Let
![]() $\mathbb {Q} \subseteq \mathbb {K}$
and
$\mathbb {Q} \subseteq \mathbb {K}$
and
![]() $\mathbb {E} \subseteq \mathbb {C}$
. Then,
$\mathbb {E} \subseteq \mathbb {C}$
. Then,
-
(i) the vector space
 $\mathbb {K}[{\mathcal E}_{\mathbb {K}}]$
is closed under both conjugate transpose and ordinary matrix multiplication and contains I and J;
$\mathbb {K}[{\mathcal E}_{\mathbb {K}}]$
is closed under both conjugate transpose and ordinary matrix multiplication and contains I and J; -
(ii) if
 $\mathbb {K}\subseteq \mathbb {E}$
, then
$\mathbb {K}\subseteq \mathbb {E}$
, then
 ${\mathcal E}_{\mathbb {K}}\subseteq {\mathcal E}_{\mathbb {E}}$
and
${\mathcal E}_{\mathbb {K}}\subseteq {\mathcal E}_{\mathbb {E}}$
and
 $\mathbb {C}\left [{\mathcal E}_{\mathbb {K}}\right ] \subseteq \mathbb {C} \left [{\mathcal E}_{\mathbb {E}}\right ]$
;
$\mathbb {C}\left [{\mathcal E}_{\mathbb {K}}\right ] \subseteq \mathbb {C} \left [{\mathcal E}_{\mathbb {E}}\right ]$
; -
(iii)
 ${\mathcal E}_{\mathbb {E}} \cap {\mathcal E}_{\mathbb {K}} = {\mathcal E}_{\mathbb {E}\cap \mathbb {K}}$
;
${\mathcal E}_{\mathbb {E}} \cap {\mathcal E}_{\mathbb {K}} = {\mathcal E}_{\mathbb {E}\cap \mathbb {K}}$
; -
(iv)
 ${\mathcal E}_{\mathbb {K}}\ = {\mathcal E}_{\mathbb {C}}$
if and only if
${\mathcal E}_{\mathbb {K}}\ = {\mathcal E}_{\mathbb {C}}$
if and only if
 $\mathbb {K}$
contains the splitting field of
$\mathbb {K}$
contains the splitting field of
 $\mathscr {X}$
;
$\mathscr {X}$
; -
(v) the complexification
 $\mathbb {C}[{\mathcal E}_{\mathbb {K}}]$
is the Bose–Mesner algebra of an association scheme if and only if
$\mathbb {C}[{\mathcal E}_{\mathbb {K}}]$
is the Bose–Mesner algebra of an association scheme if and only if
 $\mathbb {K}[{\mathcal E}_{\mathbb {K}}]$
is closed under Schur multiplication.
$\mathbb {K}[{\mathcal E}_{\mathbb {K}}]$
is closed under Schur multiplication.
Proof (i) Each
![]() $E\in {\mathcal E}_{\mathbb {K}}$
is Hermitian and those satisfying
$E\in {\mathcal E}_{\mathbb {K}}$
is Hermitian and those satisfying
![]() $EF=c_F E$
(some
$EF=c_F E$
(some
![]() $c_F$
) for all
$c_F$
) for all
![]() $F\in {\mathcal E}_{\mathbb {K}}$
form a basis of pairwise orthogonal idempotents. So we have closure under ordinary multiplication.
$F\in {\mathcal E}_{\mathbb {K}}$
form a basis of pairwise orthogonal idempotents. So we have closure under ordinary multiplication.
(ii)–(iv) are straightforward.
(v) By the Bose–Mesner Theorem [Reference Bannai, Bannai, Ito and Tanaka5, Proposition 2.15], [Reference Brouwer, Cohen and Neumaier6, Theorem 2.6.1], a vector space
![]() $\mathbf {A}\subseteq \mathsf {Mat}_X(\mathbb {C})$
is the Bose–Mesner algebra of an association scheme if and only if it is closed under transposition, matrix multiplication, and Schur multiplication and contains I and J. Since
$\mathbf {A}\subseteq \mathsf {Mat}_X(\mathbb {C})$
is the Bose–Mesner algebra of an association scheme if and only if it is closed under transposition, matrix multiplication, and Schur multiplication and contains I and J. Since
![]() $\mathbb {K}[{\mathcal E}_{\mathbb {K}}]$
is closed under the conjugate transpose operation, its Schur closure is closed under taking transposes.
$\mathbb {K}[{\mathcal E}_{\mathbb {K}}]$
is closed under the conjugate transpose operation, its Schur closure is closed under taking transposes.
We now introduce terminology for the case where condition (v) holds.
Definition 2.1 Let
![]() $\mathscr {X}=(X,{\mathcal R})$
be an association scheme with Bose–Mesner algebra
$\mathscr {X}=(X,{\mathcal R})$
be an association scheme with Bose–Mesner algebra
![]() $\mathbb {A}$
having primitive idempotents
$\mathbb {A}$
having primitive idempotents
![]() $E_0,\ldots ,E_d$
. For a subfield
$E_0,\ldots ,E_d$
. For a subfield
![]() $\mathbb {K} \subseteq \mathbb {C}$
, we say
$\mathbb {K} \subseteq \mathbb {C}$
, we say
![]() $\mathscr {X}$
(likewise
$\mathscr {X}$
(likewise
![]() $\mathbb {A}$
) has Property
$\mathbb {A}$
) has Property
![]() $\Phi _{\mathbb {K}}$
if
$\Phi _{\mathbb {K}}$
if
![]() $\mathbb {K}[{\mathcal E}_{\mathbb {K}}]$
, where
$\mathbb {K}[{\mathcal E}_{\mathbb {K}}]$
, where
![]() ${\mathcal E}_{\mathbb {K}}$
is as defined in (2.1), is closed under Schur multiplication. This occurs precisely when condition (v) of Lemma 2.2 holds. We denote the Bose–Mesner algebra
${\mathcal E}_{\mathbb {K}}$
is as defined in (2.1), is closed under Schur multiplication. This occurs precisely when condition (v) of Lemma 2.2 holds. We denote the Bose–Mesner algebra
![]() $\mathbb {C}[{\mathcal E}_{\mathbb {K}}]$
by
$\mathbb {C}[{\mathcal E}_{\mathbb {K}}]$
by
![]() $\mathbb {A}_{\downarrow _{\mathbb {K}}}$
. (Note that we use the notation
$\mathbb {A}_{\downarrow _{\mathbb {K}}}$
. (Note that we use the notation
![]() $\mathbb {A}_{\downarrow _{{\mathbb {K}}}}$
only when
$\mathbb {A}_{\downarrow _{{\mathbb {K}}}}$
only when
![]() $\mathbb {A}$
has Property
$\mathbb {A}$
has Property
![]() $\Phi _{\mathbb {K}}$
.)
$\Phi _{\mathbb {K}}$
.)
The two standard bases
![]() $\{A_0,\ldots ,A_d\}$
and
$\{A_0,\ldots ,A_d\}$
and
![]() $\{E_0,\ldots ,E_d\}$
for the Bose–Mesner algebra
$\{E_0,\ldots ,E_d\}$
for the Bose–Mesner algebra
![]() $\mathbb {A}$
of
$\mathbb {A}$
of
![]() $\mathscr {X}$
are related by the first and second eigenmatricesFootnote
3
P and Q by
$\mathscr {X}$
are related by the first and second eigenmatricesFootnote
3
P and Q by
 $$ \begin{align} \hfill A_i = \sum_{j=0}^d P_{ji} E_j, \hspace{1in} E_j = \frac{1}{|X|} \sum_{i=0}^d Q_{ij} A_i. \hfill \end{align} $$
$$ \begin{align} \hfill A_i = \sum_{j=0}^d P_{ji} E_j, \hspace{1in} E_j = \frac{1}{|X|} \sum_{i=0}^d Q_{ij} A_i. \hfill \end{align} $$
So the matrices
![]() $P=\left [ P_{ji} \right ]_{j,i=0}^d$
and
$P=\left [ P_{ji} \right ]_{j,i=0}^d$
and
![]() $Q=\left [ Q_{ij} \right ]_{i,j=0}^d$
are, up to scalar multiple, inverses of one another. However, each may be obtained from the other in another way. Each digraph
$Q=\left [ Q_{ij} \right ]_{i,j=0}^d$
are, up to scalar multiple, inverses of one another. However, each may be obtained from the other in another way. Each digraph
![]() $(X,R_i)$
is regular,
$(X,R_i)$
is regular, ![]() for
for
![]() $v_i=P_{0i}$
. Set
$v_i=P_{0i}$
. Set
![]() $\Delta _v$
as the
$\Delta _v$
as the
![]() $(d+1)\times (d+1)$
diagonal matrix with
$(d+1)\times (d+1)$
diagonal matrix with
![]() $(i,i)$
-entry
$(i,i)$
-entry
![]() $v_i$
and
$v_i$
and
![]() $\Delta _m$
the
$\Delta _m$
the
![]() $(d+1)\times (d+1)$
diagonal matrix with
$(d+1)\times (d+1)$
diagonal matrix with
![]() $(j,j)$
-entry
$(j,j)$
-entry
![]() $m_j=\operatorname {\mathrm {rk}} E_j$
. Then, P and Q satisfy both the first and second orthogonality relations [Reference Bannai and Ito4, Theorem II.3.5], [Reference Brouwer, Cohen and Neumaier6, Section 2.2] for association schemes,
$m_j=\operatorname {\mathrm {rk}} E_j$
. Then, P and Q satisfy both the first and second orthogonality relations [Reference Bannai and Ito4, Theorem II.3.5], [Reference Brouwer, Cohen and Neumaier6, Section 2.2] for association schemes,
The Krein parameters of X are those scalars
![]() $q_{ij}^k$
(
$q_{ij}^k$
(
![]() $0\le i,j,k\le d$
) for which
$0\le i,j,k\le d$
) for which
![]() $E_i \circ E_j = \frac {1}{|X|} \sum _{k=0}^d q_{ij}^k E_k$
, and these also satisfy
$E_i \circ E_j = \frac {1}{|X|} \sum _{k=0}^d q_{ij}^k E_k$
, and these also satisfy
![]() $Q_{hi}Q_{hj} = \sum _{k=0}^d q_{ij}^k Q_{hk}$
for each
$Q_{hi}Q_{hj} = \sum _{k=0}^d q_{ij}^k Q_{hk}$
for each
![]() $0\le h\le d$
. The Krein conditions (e.g., [Reference Brouwer, Cohen and Neumaier6, Theorem 2.3.2]) state that, for each
$0\le h\le d$
. The Krein conditions (e.g., [Reference Brouwer, Cohen and Neumaier6, Theorem 2.3.2]) state that, for each
![]() $i,j,k$
,
$i,j,k$
,
![]() $q_{ij}^k \ge 0$
. We will refer to the extension of
$q_{ij}^k \ge 0$
. We will refer to the extension of
![]() $\mathbb {Q}$
by all
$\mathbb {Q}$
by all
![]() $q_{ij}^k$
as the Krein field of
$q_{ij}^k$
as the Krein field of
![]() $\mathscr {X}$
. In some cases, this is a proper subfield of the splitting field; in particular, it is contained in
$\mathscr {X}$
. In some cases, this is a proper subfield of the splitting field; in particular, it is contained in
![]() $\mathbb {R}$
even when some
$\mathbb {R}$
even when some
![]() $A_i$
is not symmetric. This holds because each
$A_i$
is not symmetric. This holds because each
![]() $E_i$
is a Hermitian matrix as is
$E_i$
is a Hermitian matrix as is
![]() $E_i \circ E_j$
.
$E_i \circ E_j$
.
3 Fusion schemes and the Galois group
Let X be a finite nonempty set and let
![]() $\mathscr {X}=(X,\{R_0,R_1,\ldots ,R_d\})$
and
$\mathscr {X}=(X,\{R_0,R_1,\ldots ,R_d\})$
and
![]() $\mathscr {F}=(X,\{R^{\prime }_0, R^{\prime }_1,\ldots $
,
$\mathscr {F}=(X,\{R^{\prime }_0, R^{\prime }_1,\ldots $
,
![]() $R^{\prime }_e\})$
be association schemes on X. We say that
$R^{\prime }_e\})$
be association schemes on X. We say that
![]() $\mathscr {F}$
is a fusion (scheme) of
$\mathscr {F}$
is a fusion (scheme) of
![]() $\mathscr {X}$
if each
$\mathscr {X}$
if each
![]() $R_i$
is contained in some
$R_i$
is contained in some
![]() $R^{\prime }_j$
; that is, each relation
$R^{\prime }_j$
; that is, each relation
![]() $R^{\prime }_j$
is expressible as a union of basis relations (or by fusing or merging basis relations) in
$R^{\prime }_j$
is expressible as a union of basis relations (or by fusing or merging basis relations) in
![]() $\{R_0,\ldots ,R_d\}$
. Some authors also refer to
$\{R_0,\ldots ,R_d\}$
. Some authors also refer to
![]() $\mathscr {X}$
as a fission scheme with respect to
$\mathscr {X}$
as a fission scheme with respect to
![]() $\mathscr {F}$
while Godsil [Reference Godsil14, Chapter 5], for example, uses the term “subscheme” for what we call a fusion scheme to highlight the relationship between the corresponding Bose–Mesner algebras.
$\mathscr {F}$
while Godsil [Reference Godsil14, Chapter 5], for example, uses the term “subscheme” for what we call a fusion scheme to highlight the relationship between the corresponding Bose–Mesner algebras.
Example 3.1 Fusion schemes play key roles in several examples of and constructions for association schemes. Several of the examples we list here are fusions of product schemes. For
![]() $\mathscr {X}=(X,\mathcal {A})$
and
$\mathscr {X}=(X,\mathcal {A})$
and
![]() $\mathscr {Y}=(Y,\mathcal {B})$
, the product scheme
$\mathscr {Y}=(Y,\mathcal {B})$
, the product scheme
![]() $\mathscr {X}\times \mathscr {Y}$
has vertex set
$\mathscr {X}\times \mathscr {Y}$
has vertex set
![]() $X\times Y$
and adjacency matrices
$X\times Y$
and adjacency matrices
![]() $\{ A\otimes B \mid A\in \mathcal {A}, \, B\in \mathcal {B}\}$
, and this obviously generalizes to any number of components.
$\{ A\otimes B \mid A\in \mathcal {A}, \, B\in \mathcal {B}\}$
, and this obviously generalizes to any number of components.
-
• If
 $\Gamma $
and
$\Gamma $
and
 $\Delta $
are distance-regular graphs whose Cartesian product
$\Delta $
are distance-regular graphs whose Cartesian product
 $\Gamma \, \square \, \Delta $
is also distance-regular, then each of these gives us an association scheme whose relations are determined by distance in the respective graphs. In this setting, the association scheme generated in this manner by
$\Gamma \, \square \, \Delta $
is also distance-regular, then each of these gives us an association scheme whose relations are determined by distance in the respective graphs. In this setting, the association scheme generated in this manner by
 $\Gamma \, \square \, \Delta $
is a fusion of the product of the two association schemes generated by
$\Gamma \, \square \, \Delta $
is a fusion of the product of the two association schemes generated by
 $\Gamma $
and
$\Gamma $
and
 $\Delta $
. (See [Reference Bailey and Cameron1] for other interesting fusions of product schemes.)
$\Delta $
. (See [Reference Bailey and Cameron1] for other interesting fusions of product schemes.) -
• Some distance-regular graphs are obtained by fusing classes in the association schemes of other distance-regular graphs [Reference Brouwer, Cohen and Neumaier6, Section 4.2F]. For example, the Ustimenko graphs [Reference Brouwer, Cohen and Neumaier6, Section 9.1] can be constructed by fusing distances one and two in the symplectic forms dual polar space graphs.
-
• The m-fold extension of an association scheme
 $\mathscr {X}$
[Reference Delsarte8, Section 2.5] is a fusion of the m-fold product of
$\mathscr {X}$
[Reference Delsarte8, Section 2.5] is a fusion of the m-fold product of
 $\mathscr {X}$
.
$\mathscr {X}$
. -
• Every imprimitive association scheme contains a fusion scheme which restricts to a trivial scheme on each cell of the imprimitivity partition (this is a product of the corresponding quotient scheme with a trivial scheme) [Reference Brouwer, Cohen and Neumaier6, Section 2.4] (see also [Reference van Dam, Martin and Muzychuk10, Section 2.3] where the term “Bose–Mesner subalgebra” is used).
-
• Every translation association scheme [Reference Brouwer, Cohen and Neumaier6, Section 2.10] is a fusion scheme of the conjugacy class scheme (with all valencies one) of the underlying abelian group [Reference Brouwer, Cohen and Neumaier6, p. 52].
-
• An amorphic association scheme is an association scheme enjoying the property that every possible merging of relations yields a fusion scheme. Provided
 $d>2$
, each basis relation is the adjacency relation of some strongly regular graph.
$d>2$
, each basis relation is the adjacency relation of some strongly regular graph.
The fusion schemes of a given association scheme form a meet semilattice. We now list this and some other basic facts about fusions.
Proposition 3.2 Let
![]() $\mathscr {X}=(X,\{R_0,\ldots ,R_d\})$
be an association scheme with Bose–Mesner algebra
$\mathscr {X}=(X,\{R_0,\ldots ,R_d\})$
be an association scheme with Bose–Mesner algebra
![]() $\mathbb {A}$
and let
$\mathbb {A}$
and let
![]() $\mathscr {F}_1$
,
$\mathscr {F}_1$
,
![]() $\mathscr {F}_2$
denote fusion schemes of
$\mathscr {F}_2$
denote fusion schemes of
![]() $\mathscr {X}$
with Bose–Mesner algebras
$\mathscr {X}$
with Bose–Mesner algebras
![]() $\mathbb {B}_1$
and
$\mathbb {B}_1$
and
![]() $\mathbb {B}_2$
:
$\mathbb {B}_2$
:
-
(i)
 $\mathscr {X}$
has two trivial fusions,
$\mathscr {X}$
has two trivial fusions,
 $\mathscr {X}$
and its minimal fusion, the complete graph
$\mathscr {X}$
and its minimal fusion, the complete graph
 $(X,\{R_0, R_1\cup \cdots \cup R_d\})$
;
$(X,\{R_0, R_1\cup \cdots \cup R_d\})$
; -
(ii) any fusion scheme of
 $\mathscr {F}_1$
is also a fusion scheme of
$\mathscr {F}_1$
is also a fusion scheme of
 $\mathscr {X}$
;
$\mathscr {X}$
; -
(iii) if
 $\mathscr {F}_1$
and
$\mathscr {F}_1$
and
 $\mathscr {F}_2$
are both fusions of
$\mathscr {F}_2$
are both fusions of
 $\mathscr {X}$
, then
$\mathscr {X}$
, then
 $\mathbb {B}_1 \cap \mathbb {B}_2$
is the Bose–Mesner algebra of some fusion scheme of
$\mathbb {B}_1 \cap \mathbb {B}_2$
is the Bose–Mesner algebra of some fusion scheme of
 $\mathscr {X}$
, the unique maximal common fusion of
$\mathscr {X}$
, the unique maximal common fusion of
 $\mathscr {F}_1$
and
$\mathscr {F}_1$
and
 $\mathscr {F}_2$
;
$\mathscr {F}_2$
; -
(iv) the splitting field of
 $\mathscr {F}_1$
is a subfield of the splitting field of
$\mathscr {F}_1$
is a subfield of the splitting field of
 $\mathscr {X}$
.
$\mathscr {X}$
.
Given an association scheme
![]() $\mathscr {X}=(X,\mathcal {A})$
with Bose–Mesner algebra
$\mathscr {X}=(X,\mathcal {A})$
with Bose–Mesner algebra
![]() $\mathbb {A}$
and primitive idempotents
$\mathbb {A}$
and primitive idempotents
![]() $\{E_0,\ldots ,E_d\}$
, any partition
$\{E_0,\ldots ,E_d\}$
, any partition
![]() $\{{\mathcal O}_0,{\mathcal O}_1,\ldots ,{\mathcal O}_e\}$
of
$\{{\mathcal O}_0,{\mathcal O}_1,\ldots ,{\mathcal O}_e\}$
of
![]() $\{0,1,\ldots ,d\}$
gives us a Schur-closed vector subspace of
$\{0,1,\ldots ,d\}$
gives us a Schur-closed vector subspace of
![]() $\mathbb {A}$
by merging classes, namely,
$\mathbb {A}$
by merging classes, namely,
![]() $\mathbb {C}\left [ \left \{ \sum _{i\in {\mathcal O}_j} A_i \middle | 0\le j\le e\right \}\right ]$
. Dually, the subspace
$\mathbb {C}\left [ \left \{ \sum _{i\in {\mathcal O}_j} A_i \middle | 0\le j\le e\right \}\right ]$
. Dually, the subspace
![]() $\mathbb {C}\left [ \left \{ \sum _{i\in {\mathcal O}_j} E_i \middle | 0\le j\le e\right \}\right ]$
is always closed under ordinary matrix multiplication. We next discuss how to check whether one of these subspaces is a Bose–Mesner algebra.
$\mathbb {C}\left [ \left \{ \sum _{i\in {\mathcal O}_j} E_i \middle | 0\le j\le e\right \}\right ]$
is always closed under ordinary matrix multiplication. We next discuss how to check whether one of these subspaces is a Bose–Mesner algebra.
The Bannai–Muzychuk criterion is the fundamental computational tool in testing for fusion schemes of an association scheme with known parameters. It comes in two forms.
Proposition 3.3 (Bannai–Muzychuk Criterion [Reference Bannai3, Reference Muzychuk20])
Let
![]() $\mathscr {X}=(X,\{R_0,\ldots ,R_d\})$
be an association scheme with eigenmatrices P and Q. Let
$\mathscr {X}=(X,\{R_0,\ldots ,R_d\})$
be an association scheme with eigenmatrices P and Q. Let
![]() $\{{\mathcal O}_0,{\mathcal O}_1,\ldots ,{\mathcal O}_e\}$
be a partition of
$\{{\mathcal O}_0,{\mathcal O}_1,\ldots ,{\mathcal O}_e\}$
be a partition of
![]() $\{0,1,\ldots ,d\}$
with
$\{0,1,\ldots ,d\}$
with
![]() ${\mathcal O}_0=\{0\}$
, and define the
${\mathcal O}_0=\{0\}$
, and define the
![]() $(d+1)\times (e+1)$
partition matrix O by
$(d+1)\times (e+1)$
partition matrix O by
![]() $O_{ij}=1$
if
$O_{ij}=1$
if
![]() $i \in {\mathcal O}_j$
and
$i \in {\mathcal O}_j$
and
![]() $O_{ij}=0$
otherwise.
$O_{ij}=0$
otherwise.
-
(i) The matrix
 $PO$
has at least
$PO$
has at least
 $e+1$
distinct rows; equality holds if and only if the set
$e+1$
distinct rows; equality holds if and only if the set
 $\left \{ \cup _{i\in {\mathcal O}_j} R_i \middle | 0\le j\le e\right \}$
is the set of relations of a fusion scheme of
$\left \{ \cup _{i\in {\mathcal O}_j} R_i \middle | 0\le j\le e\right \}$
is the set of relations of a fusion scheme of
 $\mathscr {X}$
.
$\mathscr {X}$
. -
(ii) The matrix
 $QO$
has at least
$QO$
has at least
 $e+1$
distinct rows; equality holds if and only if the set
$e+1$
distinct rows; equality holds if and only if the set
 $\left \{ \sum _{i\in {\mathcal O}_j} E_i \middle | 0\le j\le e\right \}$
is the set of minimal idempotents of the Bose–Mesner algebra of a fusion scheme of
$\left \{ \sum _{i\in {\mathcal O}_j} E_i \middle | 0\le j\le e\right \}$
is the set of minimal idempotents of the Bose–Mesner algebra of a fusion scheme of
 $\mathscr {X}$
.
$\mathscr {X}$
.
Suppose
![]() $\mathscr {F}=(X,\{A_0',\ldots ,A_e'\})$
is a fusion scheme of
$\mathscr {F}=(X,\{A_0',\ldots ,A_e'\})$
is a fusion scheme of
![]() $\mathscr {X}=(X,\{A_0,\ldots ,A_d\})$
with
$\mathscr {X}=(X,\{A_0,\ldots ,A_d\})$
with
![]() $A^{\prime }_j = \sum _{i\in {\mathcal O}_j} A_i$
(
$A^{\prime }_j = \sum _{i\in {\mathcal O}_j} A_i$
(
![]() $0\le j\le e$
) as in the proposition above. The partition
$0\le j\le e$
) as in the proposition above. The partition
![]() $\{{\mathcal O}_0,\ldots ,{\mathcal O}_e\}$
of
$\{{\mathcal O}_0,\ldots ,{\mathcal O}_e\}$
of
![]() $\{0,1,\ldots ,d\}$
induces a partition
$\{0,1,\ldots ,d\}$
induces a partition
![]() $\{ {\mathcal S}_0,\ldots ,{\mathcal S}_e\}$
of the rows of P as follows [Reference Godsil13, Section 5.2]: the
$\{ {\mathcal S}_0,\ldots ,{\mathcal S}_e\}$
of the rows of P as follows [Reference Godsil13, Section 5.2]: the
![]() $(e+1)\times (d+1)$
matrix S with
$(e+1)\times (d+1)$
matrix S with
![]() $S_{ij}=1$
if
$S_{ij}=1$
if
![]() $j\in {\mathcal S}_i$
and
$j\in {\mathcal S}_i$
and
![]() $S_{ij}=0$
otherwise satisfies
$S_{ij}=0$
otherwise satisfies
![]() $PO=S P_{\mathscr {F}}$
for some
$PO=S P_{\mathscr {F}}$
for some
![]() $(e+1)\times (e+1)$
matrix
$(e+1)\times (e+1)$
matrix
![]() $P_{\mathscr {F}}$
which, according to the theorem of Bannai and Muzychuk, is the first eigenmatrix of the corresponding fusion scheme. As
$P_{\mathscr {F}}$
which, according to the theorem of Bannai and Muzychuk, is the first eigenmatrix of the corresponding fusion scheme. As
![]() $QP=|X|I$
, we then have
$QP=|X|I$
, we then have
![]() $O=\frac {1}{|X|}QS P_{\mathscr {F}}$
, or
$O=\frac {1}{|X|}QS P_{\mathscr {F}}$
, or
![]() $QS=OQ_{\mathscr {F}}$
, where
$QS=OQ_{\mathscr {F}}$
, where
![]() $Q_{\mathscr {F}}$
is the second eigenmatrix of
$Q_{\mathscr {F}}$
is the second eigenmatrix of
![]() $\mathscr {F}$
.
$\mathscr {F}$
.
Our primary interest in fusion schemes of
![]() $\mathscr {X}$
is their connection to subfields of the splitting field of
$\mathscr {X}$
is their connection to subfields of the splitting field of
![]() $\mathscr {X}$
.
$\mathscr {X}$
.
Example 3.4 Consider the association scheme
![]() $C_n=(\mathbb {Z}_n,{\mathcal R})$
of the n-cycle, a commutative d-class scheme for
$C_n=(\mathbb {Z}_n,{\mathcal R})$
of the n-cycle, a commutative d-class scheme for
![]() $d=\lfloor n/2\rfloor $
with vertex set
$d=\lfloor n/2\rfloor $
with vertex set
![]() $\mathbb {Z}_n$
. We have relations
$\mathbb {Z}_n$
. We have relations
![]() ${\mathcal R}=\{R_0,\ldots , R_d\}$
defined by
${\mathcal R}=\{R_0,\ldots , R_d\}$
defined by
![]() $(x,y)\in R_i$
if
$(x,y)\in R_i$
if
![]() $y=x\pm i$
in
$y=x\pm i$
in
![]() $\mathbb {Z}_n$
. Set
$\mathbb {Z}_n$
. Set
![]() $R^{\prime }_0=R_0$
and, for each divisor e of n, define
$R^{\prime }_0=R_0$
and, for each divisor e of n, define
![]() $R^{\prime }_e = {\bigcup _{\gcd (i,n)=e} R_i}$
. Then, we obtain a fusion scheme
$R^{\prime }_e = {\bigcup _{\gcd (i,n)=e} R_i}$
. Then, we obtain a fusion scheme
![]() $\left (\mathbb {Z}_n,\left \{ R^{\prime }_0,\ldots ,R_{\nu (n)} \right \} \right )$
of the scheme of the n-cycle, where
$\left (\mathbb {Z}_n,\left \{ R^{\prime }_0,\ldots ,R_{\nu (n)} \right \} \right )$
of the scheme of the n-cycle, where
![]() $\nu (n)$
is the number of positive divisors of n. We will see later that all eigenvalues of this “gcd scheme” are rational. All fusion schemes of this latter scheme were classified by Muzychuk [Reference Muzychuk21].
$\nu (n)$
is the number of positive divisors of n. We will see later that all eigenvalues of this “gcd scheme” are rational. All fusion schemes of this latter scheme were classified by Muzychuk [Reference Muzychuk21].
3.1 The Galois group of an association scheme
To our knowledge, the Galois group of (the splitting field of) an association scheme
![]() $\mathscr {X}=(X,\mathcal {A})$
was first studied by Munemasa in [Reference Munemasa19]. We defined this above as the extension of the rationals by all eigenvalues of the scheme; alternatively, if Q is the second eigenmatrix of
$\mathscr {X}=(X,\mathcal {A})$
was first studied by Munemasa in [Reference Munemasa19]. We defined this above as the extension of the rationals by all eigenvalues of the scheme; alternatively, if Q is the second eigenmatrix of
![]() $\mathscr {X}$
, the splitting field is defined as
$\mathscr {X}$
, the splitting field is defined as
![]() $\mathbb {Q}(\{Q_{ij} : i,j=1,\ldots ,d\})$
and will be henceforth denoted by
$\mathbb {Q}(\{Q_{ij} : i,j=1,\ldots ,d\})$
and will be henceforth denoted by
![]() $\mathbb {F}$
. Munemasa proved that, for any subfield
$\mathbb {F}$
. Munemasa proved that, for any subfield
![]() $\mathbb {K}$
of
$\mathbb {K}$
of
![]() $\mathbb {F}$
containing all the Krein parameters of
$\mathbb {F}$
containing all the Krein parameters of
![]() $\mathscr {X}$
,
$\mathscr {X}$
,
![]() ${\mathsf {Gal}}(\mathbb {F}/\mathbb {K})$
is contained in the center of
${\mathsf {Gal}}(\mathbb {F}/\mathbb {K})$
is contained in the center of
![]() ${\mathsf {Gal}}(\mathbb {F}/\mathbb {Q})$
.
${\mathsf {Gal}}(\mathbb {F}/\mathbb {Q})$
.
As each
![]() $A_i$
is rational, each
$A_i$
is rational, each
![]() $\boldsymbol {\sigma }$
in the Galois group
$\boldsymbol {\sigma }$
in the Galois group
![]() ${\mathsf {Gal}}(\mathbb {F}/\mathbb {Q})$
maps each
${\mathsf {Gal}}(\mathbb {F}/\mathbb {Q})$
maps each
![]() $A_i$
to itself. On the other hand, the Galois group acts faithfully on the set
$A_i$
to itself. On the other hand, the Galois group acts faithfully on the set
![]() $\{E_0,E_1,\ldots ,E_d\}$
[Reference Martin and Williford18, Theorem 2.1].
$\{E_0,E_1,\ldots ,E_d\}$
[Reference Martin and Williford18, Theorem 2.1].
Definition 3.1 Let
![]() $(X,\mathcal {A})$
be an association scheme with splitting field
$(X,\mathcal {A})$
be an association scheme with splitting field
![]() $\mathbb {F}$
and primitive idempotents
$\mathbb {F}$
and primitive idempotents
![]() $E_0,\ldots ,E_d$
and let
$E_0,\ldots ,E_d$
and let
![]() $\mathbb {Q} \subseteq \mathbb {K} \subseteq \mathbb {F}$
. Write
$\mathbb {Q} \subseteq \mathbb {K} \subseteq \mathbb {F}$
. Write
![]() $M^{\boldsymbol {\sigma }}$
for the matrix obtained by applying
$M^{\boldsymbol {\sigma }}$
for the matrix obtained by applying
![]() $\boldsymbol {\sigma }$
to M entrywise. For each
$\boldsymbol {\sigma }$
to M entrywise. For each
![]() $\boldsymbol {\sigma } \in {\mathsf {Gal}}(\mathbb {F}/\mathbb {K})$
, there is a permutation
$\boldsymbol {\sigma } \in {\mathsf {Gal}}(\mathbb {F}/\mathbb {K})$
, there is a permutation
![]() ${\sigma \in \operatorname {\mathrm {Sym}}(\{0,\ldots ,d\})}$
defined by
${\sigma \in \operatorname {\mathrm {Sym}}(\{0,\ldots ,d\})}$
defined by
![]() $E_{j^\sigma }=\left ( E_j\right )^{\boldsymbol {\sigma }}$
. We define the corresponding permutation group
$E_{j^\sigma }=\left ( E_j\right )^{\boldsymbol {\sigma }}$
. We define the corresponding permutation group
Since the action of
![]() $\Sigma _{\mathbb {Q}}$
is faithful, so too is the action of
$\Sigma _{\mathbb {Q}}$
is faithful, so too is the action of
![]() $\Sigma _{\mathbb {K}}$
, as
$\Sigma _{\mathbb {K}}$
, as
![]() ${\mathsf {Gal}}(\mathbb {F}/\mathbb {K}) \leq {\mathsf {Gal}}(\mathbb {F}/\mathbb {Q})$
for any
${\mathsf {Gal}}(\mathbb {F}/\mathbb {K}) \leq {\mathsf {Gal}}(\mathbb {F}/\mathbb {Q})$
for any
![]() $\mathbb {Q} \subseteq \mathbb {K} \subseteq \mathbb {F}$
. One consequence of this is that, for distinct subfields
$\mathbb {Q} \subseteq \mathbb {K} \subseteq \mathbb {F}$
. One consequence of this is that, for distinct subfields
![]() $\mathbb {K}$
and
$\mathbb {K}$
and
![]() $\mathbb {L}$
of the splitting field
$\mathbb {L}$
of the splitting field
![]() $\mathbb {F}$
,
$\mathbb {F}$
,
![]() ${\mathcal E}_{\mathbb {K}} \neq {\mathcal E}_{\mathbb {L}}$
. In the case where all Krein parameters are rational, we also have an action on the columns of matrix P [Reference Bannai and Ito4, Theorem II.7.3] by the subgroup of
${\mathcal E}_{\mathbb {K}} \neq {\mathcal E}_{\mathbb {L}}$
. In the case where all Krein parameters are rational, we also have an action on the columns of matrix P [Reference Bannai and Ito4, Theorem II.7.3] by the subgroup of
![]() ${\mathsf {Gal}}(\mathbb {F}/\mathbb {Q})$
centralizing complex conjugation. Note that, for computational purposes, one uses the fact that
${\mathsf {Gal}}(\mathbb {F}/\mathbb {Q})$
centralizing complex conjugation. Note that, for computational purposes, one uses the fact that
![]() $\Sigma _{\mathbb {K}}$
is also the permutation action of
$\Sigma _{\mathbb {K}}$
is also the permutation action of
![]() ${\mathsf {Gal}}(\mathbb {F}/\mathbb {K})$
on the columns of the second eigenmatrix Q.
${\mathsf {Gal}}(\mathbb {F}/\mathbb {K})$
on the columns of the second eigenmatrix Q.
Lemma 3.5 Let
![]() ${\mathcal Q}_0=\{0\},{\mathcal Q}_1,\ldots ,{\mathcal Q}_e$
be the orbits of the action of
${\mathcal Q}_0=\{0\},{\mathcal Q}_1,\ldots ,{\mathcal Q}_e$
be the orbits of the action of
![]() $\Sigma _{\mathbb {K}}$
on
$\Sigma _{\mathbb {K}}$
on
![]() $\{0,1,\ldots ,d\}$
and, for
$\{0,1,\ldots ,d\}$
and, for
![]() $0\le \ell \le e$
, define
$0\le \ell \le e$
, define
Then, the minimal elements of
![]() ${\mathcal E}_{\mathbb {K}}$
are precisely
${\mathcal E}_{\mathbb {K}}$
are precisely
![]() $\{F_0, F_1, \ldots , F_e\}$
; that is,
$\{F_0, F_1, \ldots , F_e\}$
; that is,
![]() $E\in {\mathcal E}_{\mathbb {K}}$
if and only if E is expressible as a sum of some subset of
$E\in {\mathcal E}_{\mathbb {K}}$
if and only if E is expressible as a sum of some subset of
![]() $\{F_0, F_1, \ldots , F_e\}$
.
$\{F_0, F_1, \ldots , F_e\}$
.
Proof It is clear that each
![]() $F_\ell $
has all entries in
$F_\ell $
has all entries in
![]() $\mathbb {K}$
as
$\mathbb {K}$
as
![]() $F_\ell ^{\boldsymbol {\sigma }}=F_\ell $
for each
$F_\ell ^{\boldsymbol {\sigma }}=F_\ell $
for each
![]() $\boldsymbol {\sigma }\in {\mathsf {Gal}}(\mathbb {F}/\mathbb {K})$
. Conversely, if
$\boldsymbol {\sigma }\in {\mathsf {Gal}}(\mathbb {F}/\mathbb {K})$
. Conversely, if
![]() $E\in {\mathcal E}_{\mathbb {K}}$
with
$E\in {\mathcal E}_{\mathbb {K}}$
with
![]() $E=\sum _{j=0}^d c_j E_j$
with each
$E=\sum _{j=0}^d c_j E_j$
with each
![]() $c_j\in \{0,1\}$
, then
$c_j\in \{0,1\}$
, then
![]() $c_{j^\sigma }=c_j$
for each j and each
$c_{j^\sigma }=c_j$
for each j and each
![]() $\sigma \in \Sigma _{\mathbb {K}}$
so that
$\sigma \in \Sigma _{\mathbb {K}}$
so that
![]() $EF_\ell = c_j F_\ell $
for any
$EF_\ell = c_j F_\ell $
for any
![]() $j\in {\mathcal Q}_\ell $
.
$j\in {\mathcal Q}_\ell $
.
Recall that
![]() $\mathscr {X}$
is said to have Property
$\mathscr {X}$
is said to have Property
![]() $\Phi _{\mathbb {K}}$
if
$\Phi _{\mathbb {K}}$
if
![]() ${\mathcal E}_{\mathbb {K}}$
is closed under Schur multiplication. That is, Property
${\mathcal E}_{\mathbb {K}}$
is closed under Schur multiplication. That is, Property
![]() $\Phi _{\mathbb {K}}$
holds for
$\Phi _{\mathbb {K}}$
holds for
![]() $\mathscr {X}$
when
$\mathscr {X}$
when
![]() $\mathbb {C}[{\mathcal E}_{\mathbb {K}}]$
is a Bose–Mesner algebra, denoted by
$\mathbb {C}[{\mathcal E}_{\mathbb {K}}]$
is a Bose–Mesner algebra, denoted by
![]() $\mathbb {A}_{\downarrow _{\mathbb {K}}}$
. This occurs precisely when there is a corresponding fusion of
$\mathbb {A}_{\downarrow _{\mathbb {K}}}$
. This occurs precisely when there is a corresponding fusion of
![]() $\mathscr {X}$
. In particular, this fusion can be determined by applying the Bannai–Muzychuk criterion (Proposition 3.3) with the partition determined by the orbits
$\mathscr {X}$
. In particular, this fusion can be determined by applying the Bannai–Muzychuk criterion (Proposition 3.3) with the partition determined by the orbits
![]() ${\mathcal Q}_\ell $
of
${\mathcal Q}_\ell $
of
![]() $\Sigma _{\mathbb {K}}$
on the minimal idempotents defined in Lemma 3.5. (Indeed, if
$\Sigma _{\mathbb {K}}$
on the minimal idempotents defined in Lemma 3.5. (Indeed, if
![]() $QO$
has exactly r distinct rows, then the Schur closure of
$QO$
has exactly r distinct rows, then the Schur closure of
![]() $\mathbb {C}\left [ {\mathcal E}_{\mathbb {K}} \right ]$
has dimension r.)
$\mathbb {C}\left [ {\mathcal E}_{\mathbb {K}} \right ]$
has dimension r.)
Definition 3.2 Let
![]() $\mathscr {X}=(X,{\mathcal R})$
be an association scheme satisfying Property
$\mathscr {X}=(X,{\mathcal R})$
be an association scheme satisfying Property
![]() $\Phi _{\mathbb {K}}$
. We denote by
$\Phi _{\mathbb {K}}$
. We denote by
![]() $\mathscr {X}_{\downarrow _{{\mathbb {K}}}}$
the fusion scheme which has Bose–Mesner algebra
$\mathscr {X}_{\downarrow _{{\mathbb {K}}}}$
the fusion scheme which has Bose–Mesner algebra
![]() $\mathbb {A}_{\downarrow _{{\mathbb {K}}}}$
. We shall call
$\mathbb {A}_{\downarrow _{{\mathbb {K}}}}$
. We shall call
![]() $\mathscr {X}_{\downarrow _{{\mathbb {K}}}}$
the Galois fusion of
$\mathscr {X}_{\downarrow _{{\mathbb {K}}}}$
the Galois fusion of
![]() $\mathscr {X}$
with respect to
$\mathscr {X}$
with respect to
![]() $\mathbb {K}$
in light of Lemma 3.5 and the Bannai–Muzychuk criterion. We shall refer to
$\mathbb {K}$
in light of Lemma 3.5 and the Bannai–Muzychuk criterion. We shall refer to
![]() $\mathscr {X}_{\downarrow _{{\mathbb {Q}}}}$
simply as the Galois fusion of
$\mathscr {X}_{\downarrow _{{\mathbb {Q}}}}$
simply as the Galois fusion of
![]() $\mathscr {X}$
. (Note that we use the notation
$\mathscr {X}$
. (Note that we use the notation
![]() $\mathscr {X}_{\downarrow _{{\mathbb {K}}}}$
only when
$\mathscr {X}_{\downarrow _{{\mathbb {K}}}}$
only when
![]() $\mathscr {X}$
has Property
$\mathscr {X}$
has Property
![]() $\Phi _{\mathbb {K}}$
.)
$\Phi _{\mathbb {K}}$
.)
The following is also well known.
Proposition 3.6 A commutative association scheme has only real eigenvalues if and only if it is symmetric. Given any non-symmetric commutative scheme
![]() $(X,{\mathcal R})$
with splitting field
$(X,{\mathcal R})$
with splitting field
![]() $\mathbb {F}$
, the Galois group
$\mathbb {F}$
, the Galois group
![]() ${\mathsf {Gal}}\left (\mathbb {F}/(\mathbb {F} \cap \mathbb {R}) \right )$
has complex conjugation as its sole non-identity element and the relative Galois fusion of our non-symmetric scheme with respect to this subgroup of its Galois group is simply the symmetrization of
${\mathsf {Gal}}\left (\mathbb {F}/(\mathbb {F} \cap \mathbb {R}) \right )$
has complex conjugation as its sole non-identity element and the relative Galois fusion of our non-symmetric scheme with respect to this subgroup of its Galois group is simply the symmetrization of
![]() $(X,{\mathcal R})$
.
$(X,{\mathcal R})$
.
Remark 3.7 This is a special case of a much more general phenomenon: stratifiability of a homogeneous coherent configuration.
Proposition 3.8 Let
![]() $\mathbb {K}_1$
and
$\mathbb {K}_1$
and
![]() $\mathbb {K}_2$
be subfields of the splitting field of
$\mathbb {K}_2$
be subfields of the splitting field of
![]() $\mathscr {X}$
. If
$\mathscr {X}$
. If
![]() $\mathscr {X}$
satisfies Property
$\mathscr {X}$
satisfies Property
![]() $\Phi _{\mathbb {K}_1}$
and Property
$\Phi _{\mathbb {K}_1}$
and Property
![]() $\Phi _{\mathbb {K}_2}$
, then
$\Phi _{\mathbb {K}_2}$
, then
![]() $\mathscr {X}$
satisfies Property
$\mathscr {X}$
satisfies Property
![]() $\Phi _{{\mathbb {K}_1 \cap \mathbb {K}_2}}$
.
$\Phi _{{\mathbb {K}_1 \cap \mathbb {K}_2}}$
.
Proof By Lemma 2.2(iii),
![]() $\mathbb {C} \left [ {\mathcal E}_{\mathbb {K}_1 \cap \mathbb {K}_2} \right ] =\mathbb {C} \left [ {\mathcal E}_{\mathbb {K}_1} \cap {\mathcal E}_{\mathbb {K}_2} \right ] =\mathbb {C} \left [ {\mathcal E}_{\mathbb {K}_1} \right ] \cap \mathbb {C} \left [ {\mathcal E}_{\mathbb {K}_2} \right ]$
is a Bose–Mesner algebra.
$\mathbb {C} \left [ {\mathcal E}_{\mathbb {K}_1 \cap \mathbb {K}_2} \right ] =\mathbb {C} \left [ {\mathcal E}_{\mathbb {K}_1} \cap {\mathcal E}_{\mathbb {K}_2} \right ] =\mathbb {C} \left [ {\mathcal E}_{\mathbb {K}_1} \right ] \cap \mathbb {C} \left [ {\mathcal E}_{\mathbb {K}_2} \right ]$
is a Bose–Mesner algebra.
We now introduce some additional notation which will be useful in discussing Galois fusions and will also be used in the following sections.
Definition 3.3 Let
![]() ${\mathcal Q}_0=\{0\},{\mathcal Q}_1,\ldots ,{\mathcal Q}_e$
be the orbits of the action of
${\mathcal Q}_0=\{0\},{\mathcal Q}_1,\ldots ,{\mathcal Q}_e$
be the orbits of the action of
![]() $\Sigma _{\mathbb {K}}$
on
$\Sigma _{\mathbb {K}}$
on
![]() $\{0,1,\ldots ,d\}$
. We define a map
$\{0,1,\ldots ,d\}$
. We define a map
![]() $\iota :\{0, \ldots , d\} \to \{0, \ldots , e\}$
by
$\iota :\{0, \ldots , d\} \to \{0, \ldots , e\}$
by
![]() $\iota (i) = j$
for
$\iota (i) = j$
for
![]() $i \in \mathcal {Q}_j$
. Given this partition of
$i \in \mathcal {Q}_j$
. Given this partition of
![]() $\{0,\ldots ,d\}$
, we shall set
$\{0,\ldots ,d\}$
, we shall set
![]() $\overline {Q}=QO,$
where O is the
$\overline {Q}=QO,$
where O is the
![]() $(d+1)\times (e+1)$
matrix with
$(d+1)\times (e+1)$
matrix with
![]() $(i,j)$
-entry equal to one if
$(i,j)$
-entry equal to one if
![]() $i\in {\mathcal Q}_j$
and zero otherwise. Note that we will use
$i\in {\mathcal Q}_j$
and zero otherwise. Note that we will use
![]() $\iota _{\mathscr {X}}$
and
$\iota _{\mathscr {X}}$
and
![]() $\overline {Q}_{\mathscr {X}}$
when such a clarification is needed.
$\overline {Q}_{\mathscr {X}}$
when such a clarification is needed.
The map
![]() $\iota $
is clearly surjective with
$\iota $
is clearly surjective with
![]() $\iota ^{-1}(j) = \mathcal {Q}_j$
. It is injective precisely when
$\iota ^{-1}(j) = \mathcal {Q}_j$
. It is injective precisely when
![]() $\mathbb {F}=\mathbb {K}$
. Henceforth, we shall restrict
$\mathbb {F}=\mathbb {K}$
. Henceforth, we shall restrict
![]() $F_j$
to not simply any sums of the minimal idempotents, but to those arising from the Galois orbits with respect to some subfield
$F_j$
to not simply any sums of the minimal idempotents, but to those arising from the Galois orbits with respect to some subfield
![]() $\mathbb {K}$
; henceforth,
$\mathbb {K}$
; henceforth,
Example 3.9 Consider the scheme
![]() $\mathscr {X}$
built from Cayley graphs on
$\mathscr {X}$
built from Cayley graphs on
![]() $\mathbb {Z}_4 \times \mathbb {Z}_2$
specified by its relation matrix
$\mathbb {Z}_4 \times \mathbb {Z}_2$
specified by its relation matrix
![]() $\sum i A_i$
and the relation matrix of its Galois fusion
$\sum i A_i$
and the relation matrix of its Galois fusion
![]() $\mathscr {X}_{\downarrow _{\mathbb {Q}}}$
together with their corresponding second eigenmatrices
$\mathscr {X}_{\downarrow _{\mathbb {Q}}}$
together with their corresponding second eigenmatrices
![]() $Q_{\mathscr {X}}$
and
$Q_{\mathscr {X}}$
and
![]() $Q_{\mathscr {X}_{\downarrow _{\mathbb {Q}}}}$
. Here, we see this last matrix is obtained from
$Q_{\mathscr {X}_{\downarrow _{\mathbb {Q}}}}$
. Here, we see this last matrix is obtained from
![]() $\overline {Q}_{\mathscr {X}}$
by the removal of repeated rows:
$\overline {Q}_{\mathscr {X}}$
by the removal of repeated rows:
 $$\begin{align*}\mathscr{X}: \begin{bmatrix} 0 & 1 & 2 & 3 & 4 & 4 & 4 & 4 \\ 1 & 0 & 3 & 2 & 4 & 4 & 4 & 4 \\ 3 & 2 & 0 & 1 & 4 & 4 & 4 & 4 \\ 2 & 3 & 1 & 0 & 4 & 4 & 4 & 4 \\ 4 & 4 & 4 & 4 & 0 & 1 & 2 & 3 \\ 4 & 4 & 4 & 4 & 1 & 0 & 3 & 2 \\ 4 & 4 & 4 & 4 & 3 & 2 & 0 & 1 \\ 4 & 4 & 4 & 4 & 2 & 3 & 1 & 0 \end{bmatrix}, \quad \mathscr{X}_{\downarrow\mathbb{Q}}: \begin{bmatrix} 0 & 1 & 2 & 2 & 3 & 3 & 3 & 3 \\ 1 & 0 & 2 & 2 & 3 & 3 & 3 & 3 \\ 2 & 2 & 0 & 1 & 3 & 3 & 3 & 3 \\ 2 & 2 & 1 & 0 & 3 & 3 & 3 & 3 \\ 3 & 3 & 3 & 3 & 0 & 1 & 2 & 2 \\ 3 & 3 & 3 & 3 & 1 & 0 & 2 & 2 \\ 3 & 3 & 3 & 3 & 2 & 2 & 0 & 1 \\ 3 & 3 & 3 & 3 & 2 & 2 & 1 & 0 \end{bmatrix} \end{align*}$$
$$\begin{align*}\mathscr{X}: \begin{bmatrix} 0 & 1 & 2 & 3 & 4 & 4 & 4 & 4 \\ 1 & 0 & 3 & 2 & 4 & 4 & 4 & 4 \\ 3 & 2 & 0 & 1 & 4 & 4 & 4 & 4 \\ 2 & 3 & 1 & 0 & 4 & 4 & 4 & 4 \\ 4 & 4 & 4 & 4 & 0 & 1 & 2 & 3 \\ 4 & 4 & 4 & 4 & 1 & 0 & 3 & 2 \\ 4 & 4 & 4 & 4 & 3 & 2 & 0 & 1 \\ 4 & 4 & 4 & 4 & 2 & 3 & 1 & 0 \end{bmatrix}, \quad \mathscr{X}_{\downarrow\mathbb{Q}}: \begin{bmatrix} 0 & 1 & 2 & 2 & 3 & 3 & 3 & 3 \\ 1 & 0 & 2 & 2 & 3 & 3 & 3 & 3 \\ 2 & 2 & 0 & 1 & 3 & 3 & 3 & 3 \\ 2 & 2 & 1 & 0 & 3 & 3 & 3 & 3 \\ 3 & 3 & 3 & 3 & 0 & 1 & 2 & 2 \\ 3 & 3 & 3 & 3 & 1 & 0 & 2 & 2 \\ 3 & 3 & 3 & 3 & 2 & 2 & 0 & 1 \\ 3 & 3 & 3 & 3 & 2 & 2 & 1 & 0 \end{bmatrix} \end{align*}$$
 $$\begin{align*}Q_{\mathscr{X}}= \left[ \begin{array}{@{}crrrr@{}} 1 & 1 & 2 & 2 & 2 \\ 1 & 1 & -2 & -2 & 2 \\ 1 & 1 & -2i & 2i & -2 \\ 1 & 1 & 2i & -2i & -2 \\ 1 & \!\!-1 & 0 & 0 & 0 \end{array} \right], \ \overline{Q}_{\mathscr{X}}= \left[ \begin{array}{@{}rrrr@{}} 1 & 1 & 4 & 2 \\ 1 & 1 & \!-4 & 2 \\ 1 & 1 & 0 & \!-2 \\ 1 & 1 & 0 & \!-2 \\ 1 & \!-1 & 0 & 0 \end{array} \right], \ Q_{\mathscr{X}_{\downarrow_{\mathbb{Q}}}}= \left[ \begin{array}{@{}rrrr@{}} 1& 1& 2& 4 \\ 1& \!\!-1& 0& 0 \\ 1& 1& \!\!-2& 0 \\ 1& 1& 2& \!\!-4 \end{array}\right]. \end{align*}$$
$$\begin{align*}Q_{\mathscr{X}}= \left[ \begin{array}{@{}crrrr@{}} 1 & 1 & 2 & 2 & 2 \\ 1 & 1 & -2 & -2 & 2 \\ 1 & 1 & -2i & 2i & -2 \\ 1 & 1 & 2i & -2i & -2 \\ 1 & \!\!-1 & 0 & 0 & 0 \end{array} \right], \ \overline{Q}_{\mathscr{X}}= \left[ \begin{array}{@{}rrrr@{}} 1 & 1 & 4 & 2 \\ 1 & 1 & \!-4 & 2 \\ 1 & 1 & 0 & \!-2 \\ 1 & 1 & 0 & \!-2 \\ 1 & \!-1 & 0 & 0 \end{array} \right], \ Q_{\mathscr{X}_{\downarrow_{\mathbb{Q}}}}= \left[ \begin{array}{@{}rrrr@{}} 1& 1& 2& 4 \\ 1& \!\!-1& 0& 0 \\ 1& 1& \!\!-2& 0 \\ 1& 1& 2& \!\!-4 \end{array}\right]. \end{align*}$$
The splitting field of
![]() $\mathscr {X}$
is
$\mathscr {X}$
is
![]() $\mathbb {Q}(i)$
and the permutation action of
$\mathbb {Q}(i)$
and the permutation action of
![]() ${\mathsf {Gal}}(\mathbb {Q}(i)/\mathbb {Q})$
on the idempotents gives
${\mathsf {Gal}}(\mathbb {Q}(i)/\mathbb {Q})$
on the idempotents gives
![]() $\langle (2,3) \rangle $
. Hence,
$\langle (2,3) \rangle $
. Hence,
![]() $F_0 = E_0$
,
$F_0 = E_0$
,
![]() $F_1 = E_1$
,
$F_1 = E_1$
,
![]() $F_2 = E_2 + E_3$
,
$F_2 = E_2 + E_3$
,
![]() $F_3 = E_4$
, and
$F_3 = E_4$
, and
![]() $\iota : \{0, 1, 2, 3, 4\} \to \{0, 1, 2, 3\}$
by
$\iota : \{0, 1, 2, 3, 4\} \to \{0, 1, 2, 3\}$
by
![]() $\iota (0) = 0$
,
$\iota (0) = 0$
,
![]() $\iota (1) = 1$
,
$\iota (1) = 1$
,
![]() $\iota (2) = 2$
,
$\iota (2) = 2$
,
![]() $\iota (3) = 2,$
and
$\iota (3) = 2,$
and
![]() $\iota (4) = 3$
. This is described by
$\iota (4) = 3$
. This is described by
![]() $\overline {Q}$
, where columns 2 and 3 of Q have been replaced by their sum. Repeated rows indicate that relations 2 and 3 fuse, and by the Bannai–Muzychuk criterion, we have a valid fusion
$\overline {Q}$
, where columns 2 and 3 of Q have been replaced by their sum. Repeated rows indicate that relations 2 and 3 fuse, and by the Bannai–Muzychuk criterion, we have a valid fusion
![]() $\mathscr {X}_{\downarrow _{\mathbb {Q}}}$
with second eigenmatrix
$\mathscr {X}_{\downarrow _{\mathbb {Q}}}$
with second eigenmatrix
![]() $Q_{\mathscr {X}_{\downarrow _{\mathbb {Q}}}}$
.
$Q_{\mathscr {X}_{\downarrow _{\mathbb {Q}}}}$
.
Note that not every scheme has property
![]() $\Phi _{\mathbb {Q}}$
as the following example shows.
$\Phi _{\mathbb {Q}}$
as the following example shows.
Example 3.10 The Coxeter graph (considered as a metric association scheme) has second eigenmatrix Q, below, and corresponding matrix
![]() $\overline {Q}$
:
$\overline {Q}$
:
 $$\begin{align*}Q = \begin{bmatrix} 1 & 8 & 6 & 7 & 6 \\ 1 & 16/3 & -2+2\sqrt{2} & -7/3 & -2-2\sqrt{2} \\ 1 & 4/3 & -2\sqrt{2} & -7/3 & 2\sqrt{2} \\ 1 & -4/3 & -1 & 7/3 & -1\\ 1 & -8/3 & 2+\sqrt{2} & -7/3 & 2-\sqrt{2} \end{bmatrix}, \quad \overline{Q} = \begin{bmatrix} 1 & 8 & 12 & 7 \\ 1 & 16/3 & -4 & -7/3 \\ 1 & \phantom{-}4/3 & \phantom{-}0 & -7/3 \\ 1 & -4/3 & -2 & \phantom{-}7/3 \\ 1 & -8/3 & \phantom{-}4 & -7/3 \end{bmatrix}. \end{align*}$$
$$\begin{align*}Q = \begin{bmatrix} 1 & 8 & 6 & 7 & 6 \\ 1 & 16/3 & -2+2\sqrt{2} & -7/3 & -2-2\sqrt{2} \\ 1 & 4/3 & -2\sqrt{2} & -7/3 & 2\sqrt{2} \\ 1 & -4/3 & -1 & 7/3 & -1\\ 1 & -8/3 & 2+\sqrt{2} & -7/3 & 2-\sqrt{2} \end{bmatrix}, \quad \overline{Q} = \begin{bmatrix} 1 & 8 & 12 & 7 \\ 1 & 16/3 & -4 & -7/3 \\ 1 & \phantom{-}4/3 & \phantom{-}0 & -7/3 \\ 1 & -4/3 & -2 & \phantom{-}7/3 \\ 1 & -8/3 & \phantom{-}4 & -7/3 \end{bmatrix}. \end{align*}$$
That is, we have summed the columns of Q according to the Galois orbits to obtain
![]() $\overline {Q}$
, which clearly fails the Bannai–Muzychuk criterion. Hence, the Coxeter graph does not satisfy property
$\overline {Q}$
, which clearly fails the Bannai–Muzychuk criterion. Hence, the Coxeter graph does not satisfy property
![]() $\Phi _{\mathbb {Q}}$
. This means that the Coxeter graph does not have a Galois fusion over any proper subfield.
$\Phi _{\mathbb {Q}}$
. This means that the Coxeter graph does not have a Galois fusion over any proper subfield.
Problem 3.11 For any association scheme
![]() $\mathscr {X}$
, when does Property
$\mathscr {X}$
, when does Property
![]() $\Phi _{\mathbb {K}}$
hold for
$\Phi _{\mathbb {K}}$
hold for
![]() $\mathbb {Q} \subseteq \mathbb {K} \subseteq \mathbb {F}$
? In particular, when does Property
$\mathbb {Q} \subseteq \mathbb {K} \subseteq \mathbb {F}$
? In particular, when does Property
![]() $\Phi _{\mathbb {Q}}$
hold? That is, what are the Galois fusions of
$\Phi _{\mathbb {Q}}$
hold? That is, what are the Galois fusions of
![]() $\mathscr {X}$
with respect to subfields of
$\mathscr {X}$
with respect to subfields of
![]() $\mathbb {F}$
?
$\mathbb {F}$
?
4 Delsarte designs and irrational eigenvalues
We continue with the notation used in Sections 2 and 3.
For
![]() $T\subseteq \{1,\ldots ,d\},$
a subset
$T\subseteq \{1,\ldots ,d\},$
a subset
![]() $\emptyset \subset C \subseteq X$
is a Delsarte T-design if the characteristic vector
$\emptyset \subset C \subseteq X$
is a Delsarte T-design if the characteristic vector
![]() ${\mathbf x}={\mathbf x}_C$
of C (with
${\mathbf x}={\mathbf x}_C$
of C (with
![]() ${\mathbf x}_a=1$
if
${\mathbf x}_a=1$
if
![]() $a\in C$
and
$a\in C$
and
![]() ${\mathbf x}_a=0$
otherwise) satisfies
${\mathbf x}_a=0$
otherwise) satisfies
![]() $E_j {\mathbf x} = 0$
for all
$E_j {\mathbf x} = 0$
for all
![]() $j\in T$
. Given C, the largest set of indices for which C is a design is
$j\in T$
. Given C, the largest set of indices for which C is a design is
![]() $T(C)=\{ j \mid E_j{\mathbf x}=0\}$
. The inner distribution
$T(C)=\{ j \mid E_j{\mathbf x}=0\}$
. The inner distribution
![]() $a=a(C)=[a_0,\ldots ,a_d]$
and dual distribution (or MacWilliams transform)
$a=a(C)=[a_0,\ldots ,a_d]$
and dual distribution (or MacWilliams transform)
![]() $b=b(C)=[b_0,\ldots ,b_d]$
defined by
$b=b(C)=[b_0,\ldots ,b_d]$
defined by
are related by
![]() $b=aQ$
, and we know that
$b=aQ$
, and we know that
![]() $a\ge 0$
and
$a\ge 0$
and
![]() $b\ge 0$
(see, e.g., [Reference Brouwer, Cohen and Neumaier6, Section 2.5]). Evidently,
$b\ge 0$
(see, e.g., [Reference Brouwer, Cohen and Neumaier6, Section 2.5]). Evidently,
![]() $j\in T(C) \Leftrightarrow b_j=0$
.
$j\in T(C) \Leftrightarrow b_j=0$
.
We may also consider weighted Delsarte T-designs where each vertex in C is assigned a weight in
![]() $\mathbb {Q}$
; we call such a function on the vertex set a rational Delsarte design. If the weights are in
$\mathbb {Q}$
; we call such a function on the vertex set a rational Delsarte design. If the weights are in
![]() $\mathbb {Z}_+$
then they may be considered as “repeated points” or as a multiset. Any rationally weighted Delsarte T-design corresponds to a vector
$\mathbb {Z}_+$
then they may be considered as “repeated points” or as a multiset. Any rationally weighted Delsarte T-design corresponds to a vector
![]() ${\mathbf x}$
with rational entries. As for non-weighted Delsarte T-designs, we have the same properties for
${\mathbf x}$
with rational entries. As for non-weighted Delsarte T-designs, we have the same properties for
![]() $T(C)$
and the MacWilliams transform, after suitably adjusting the inner distribution to
$T(C)$
and the MacWilliams transform, after suitably adjusting the inner distribution to
We are typically interested in 01-characteristic vectors. However, even when considering weighted Delsarte designs, the characteristic vector has rational entries. This means that we have
![]() ${\mathbf x}_C = \sum _{j \not \in T(C)} E_j {\mathbf x}_C$
in
${\mathbf x}_C = \sum _{j \not \in T(C)} E_j {\mathbf x}_C$
in
![]() $\mathbb {Q}^{X}$
. Hence, if
$\mathbb {Q}^{X}$
. Hence, if
![]() $F_0, \ldots , F_e$
are the minimal elements of
$F_0, \ldots , F_e$
are the minimal elements of
![]() $\mathcal {E}_{\mathbb {Q}}$
, then
$\mathcal {E}_{\mathbb {Q}}$
, then
![]() ${\mathbf x}_C$
must be expressible as
${\mathbf x}_C$
must be expressible as
![]() ${\mathbf x}_C = \sum _{j \in S} F_j{\mathbf x}_C$
for some
${\mathbf x}_C = \sum _{j \in S} F_j{\mathbf x}_C$
for some
![]() $S \subseteq \{0, \ldots , e\}$
. We will develop this idea in what follows, so we restrict ourselves to
$S \subseteq \{0, \ldots , e\}$
. We will develop this idea in what follows, so we restrict ourselves to
![]() $\mathbb {K}=\mathbb {Q}$
. We note, however, that the results generalize to other choices of
$\mathbb {K}=\mathbb {Q}$
. We note, however, that the results generalize to other choices of
![]() $\mathbb {K}$
.
$\mathbb {K}$
.
Theorem 4.1 Let
![]() $(X,{\mathcal R})$
be an association scheme and let
$(X,{\mathcal R})$
be an association scheme and let
![]() $C\subseteq X$
be a nonempty (possibly weighted) subset of the vertices with inner distribution a and characteristic vector
$C\subseteq X$
be a nonempty (possibly weighted) subset of the vertices with inner distribution a and characteristic vector
![]() ${\mathbf x}$
.
${\mathbf x}$
.
-
(i) If
 $j\in T(C)$
and
$j\in T(C)$
and
 $\sigma \in \Sigma _{\mathbb {Q}}$
, then
$\sigma \in \Sigma _{\mathbb {Q}}$
, then
 $j^\sigma \in T(C)$
. Hence,
$j^\sigma \in T(C)$
. Hence,
 $T(C)$
is a union of orbits
$T(C)$
is a union of orbits
 ${\mathcal Q}_j \in \{ {\mathcal Q}_1,\ldots , {\mathcal Q}_e\}$
.
${\mathcal Q}_j \in \{ {\mathcal Q}_1,\ldots , {\mathcal Q}_e\}$
. -
(ii) Let
 $\iota (i)=\iota (j)$
. If
$\iota (i)=\iota (j)$
. If
 $aQ_i = 0$
, then
$aQ_i = 0$
, then
 $aQ_j = 0$
. Equivalently, if
$aQ_j = 0$
. Equivalently, if
 $E_i {\mathbf x} = 0$
, then
$E_i {\mathbf x} = 0$
, then
 $E_j {\mathbf x} = 0$
.
$E_j {\mathbf x} = 0$
. -
(iii) If
 $aQ_i = 0$
, then
$aQ_i = 0$
, then
 $a\overline {Q}_{\iota (i)}=0$
. Equivalently, if
$a\overline {Q}_{\iota (i)}=0$
. Equivalently, if
 $E_i {\mathbf x} = 0$
, then
$E_i {\mathbf x} = 0$
, then
 $F_{\iota (i)} {\mathbf x} = 0$
.
$F_{\iota (i)} {\mathbf x} = 0$
.
Proof (i) For
![]() $\boldsymbol {\sigma } \in {\mathsf {Gal}}(\mathbb {F}/\mathbb {Q})$
and corresponding
$\boldsymbol {\sigma } \in {\mathsf {Gal}}(\mathbb {F}/\mathbb {Q})$
and corresponding
![]() $\sigma \in \Sigma _{\mathbb {Q}} \subseteq \operatorname {\mathrm {Sym}}(\{0,\ldots ,d\})$
, we have
$\sigma \in \Sigma _{\mathbb {Q}} \subseteq \operatorname {\mathrm {Sym}}(\{0,\ldots ,d\})$
, we have
so that
![]() $b_j=0$
if and only if
$b_j=0$
if and only if
![]() $b_{j'}=0$
for all
$b_{j'}=0$
for all
![]() $j'$
in the orbit
$j'$
in the orbit
![]() ${\mathcal Q}_\ell $
containing j. Parts (ii) and (iii) follow immediately.
${\mathcal Q}_\ell $
containing j. Parts (ii) and (iii) follow immediately.
Theorem 4.1 has important implications in practice, since it means that the study of Delsarte designs in an association scheme with irrational eigenvalues is essentially equivalent to the study of subsets satisfying
![]() $F_j {\mathbf x}=0$
for all j in some reduced set
$F_j {\mathbf x}=0$
for all j in some reduced set
![]() ${T' \subseteq \{1,\ldots ,e\}}$
. In many cases, this greatly reduces the complexity of a search, for example, when using linear programming.
${T' \subseteq \{1,\ldots ,e\}}$
. In many cases, this greatly reduces the complexity of a search, for example, when using linear programming.
Example 4.2 Recall the Coxeter graph from Example 3.10. It can be viewed as being obtained from the Odd graph
![]() $O_4$
by deleting the vertices of a Fano plane. The Galois merging of idempotents for the Coxeter graph is given by
$O_4$
by deleting the vertices of a Fano plane. The Galois merging of idempotents for the Coxeter graph is given by
![]() $\iota :\{0,1,2,3,4\} \to \{0,1,2,3\},$
where
$\iota :\{0,1,2,3,4\} \to \{0,1,2,3\},$
where
![]() $\iota (0)=0$
,
$\iota (0)=0$
,
![]() $\iota (1)=1$
,
$\iota (1)=1$
,
![]() $\iota (2)=2$
,
$\iota (2)=2$
,
![]() $\iota (3)=3$
, and
$\iota (3)=3$
, and
![]() $\iota (4)=2$
. Hence, for example, any
$\iota (4)=2$
. Hence, for example, any
![]() $\{1,2\}$
-design or
$\{1,2\}$
-design or
![]() $\{1,4\}$
-design of
$\{1,4\}$
-design of
![]() $\mathscr {X}$
is in fact a
$\mathscr {X}$
is in fact a
![]() $\{1,2,4\}$
-design, since
$\{1,2,4\}$
-design, since
![]() $\iota (\{1,2,4\}) = \iota (\{1,2\})= \iota (\{1,4\}) = \{1,2\}$
. For instance, a second Fano plane taken from the remaining vertices gives a
$\iota (\{1,2,4\}) = \iota (\{1,2\})= \iota (\{1,4\}) = \{1,2\}$
. For instance, a second Fano plane taken from the remaining vertices gives a
![]() $\{1, 2, 4\}$
-design with inner distribution
$\{1, 2, 4\}$
-design with inner distribution
![]() $a = [1, 0, 0, 6, 0]$
. Note that
$a = [1, 0, 0, 6, 0]$
. Note that
![]() $aQ = [7, 0, 0, 21, 0 ]$
and
$aQ = [7, 0, 0, 21, 0 ]$
and
![]() $a\overline {Q} =[7, 0, 0, 21]$
.
$a\overline {Q} =[7, 0, 0, 21]$
.
We have a stronger result than Theorem 4.1 when property
![]() $\Phi _{\mathbb {Q}}$
holds.
$\Phi _{\mathbb {Q}}$
holds.
Theorem 4.3 Let
![]() $\mathscr {X}$
be a d-class scheme satisfying property
$\mathscr {X}$
be a d-class scheme satisfying property
![]() $\Phi _{\mathbb {Q}}$
and let
$\Phi _{\mathbb {Q}}$
and let
![]() $T \subset \{1, \ldots , d\}$
. Then,
$T \subset \{1, \ldots , d\}$
. Then,
![]() $C \subset X$
is a T-design of
$C \subset X$
is a T-design of
![]() $\mathscr {X}$
if and only if it is a
$\mathscr {X}$
if and only if it is a
![]() $\iota (T)$
-design of
$\iota (T)$
-design of
![]() $\mathscr {X}_{\downarrow _{\mathbb {Q}}}$
.
$\mathscr {X}_{\downarrow _{\mathbb {Q}}}$
.
This says in essence that it is sufficient to consider the T-designs of the
![]() $\mathscr {X}_{\downarrow _{\mathbb {Q}}}$
when studying T-designs of
$\mathscr {X}_{\downarrow _{\mathbb {Q}}}$
when studying T-designs of
![]() $\mathscr {X}$
. This is helpful in particular when showing non-existence or when classifying T-designs. Note, however, that they may have different combinatorial properties. This is essentially used in an ad hoc manner in [Reference Bamberg, Giudici, Lansdown and Royle2].
$\mathscr {X}$
. This is helpful in particular when showing non-existence or when classifying T-designs. Note, however, that they may have different combinatorial properties. This is essentially used in an ad hoc manner in [Reference Bamberg, Giudici, Lansdown and Royle2].
Example 4.4 Recall
![]() $\mathscr {X}$
and
$\mathscr {X}$
and
![]() $\mathscr {X}_{\downarrow _{\mathbb {Q}}}$
from Example 3.9. Let
$\mathscr {X}_{\downarrow _{\mathbb {Q}}}$
from Example 3.9. Let
![]() $C = \{ 1, 2, 5, 6 \} \subset X = \{1, \ldots , 8\}$
. Now, C is a
$C = \{ 1, 2, 5, 6 \} \subset X = \{1, \ldots , 8\}$
. Now, C is a
![]() $\{1, 2, 3\}$
-design in
$\{1, 2, 3\}$
-design in
![]() $\mathscr {X}$
with inner distribution
$\mathscr {X}$
with inner distribution
![]() $[1, 1, 0, 0, 2]$
. Moreover, C is a
$[1, 1, 0, 0, 2]$
. Moreover, C is a
![]() $\{\iota (1), \iota (2), \iota (3)\} = \{1, 2\}$
-design in
$\{\iota (1), \iota (2), \iota (3)\} = \{1, 2\}$
-design in
![]() $\mathscr {X}_{\downarrow _{\mathbb {Q}}}$
. With respect to
$\mathscr {X}_{\downarrow _{\mathbb {Q}}}$
. With respect to
![]() $\mathscr {X}_{\downarrow _{\mathbb {Q}}}$
, the inner distribution of C is
$\mathscr {X}_{\downarrow _{\mathbb {Q}}}$
, the inner distribution of C is
![]() $[ 1, 1, 0, 2 ]$
. We note that equivalently
$[ 1, 1, 0, 2 ]$
. We note that equivalently
![]() $[1, 1, 0, 0, 2]\overline {Q}_{\mathscr {X}} = [ 1, 1, 0, 2 ] Q_{\mathscr {X}_{\downarrow _{\mathbb {Q}}}}$
.
$[1, 1, 0, 0, 2]\overline {Q}_{\mathscr {X}} = [ 1, 1, 0, 2 ] Q_{\mathscr {X}_{\downarrow _{\mathbb {Q}}}}$
.
Theorem 4.3 establishes a correspondence between the designs of
![]() $\mathscr {X}$
and those of
$\mathscr {X}$
and those of
![]() $\mathscr {X}_{\downarrow _{\mathbb {Q}}}$
, which has curious implications for pairs of non-isomorphic schemes having isomorphic Galois fusions. We call
$\mathscr {X}_{\downarrow _{\mathbb {Q}}}$
, which has curious implications for pairs of non-isomorphic schemes having isomorphic Galois fusions. We call
![]() $\mathscr {X} =(X, \mathcal {R})$
isomorphic to
$\mathscr {X} =(X, \mathcal {R})$
isomorphic to
![]() $\mathscr {Y}=(Y, \mathcal {S})$
,
$\mathscr {Y}=(Y, \mathcal {S})$
,
![]() ${\mathcal S}=\{S_0,\ldots ,S_e\}$
, if there is a bijection
${\mathcal S}=\{S_0,\ldots ,S_e\}$
, if there is a bijection
![]() $\sigma _1$
from X to Y and a bijection
$\sigma _1$
from X to Y and a bijection
![]() $\sigma _2$
from
$\sigma _2$
from
![]() $\{0, \ldots , d\}$
to
$\{0, \ldots , d\}$
to
![]() $\{0, \ldots , e\}$
such that
$\{0, \ldots , e\}$
such that
![]() $\{\left (\sigma _1(x), \sigma _1(y)\right ) \mid (x,y) \in R_i\} = S_{\sigma _2(i)}$
in which case we write
$\{\left (\sigma _1(x), \sigma _1(y)\right ) \mid (x,y) \in R_i\} = S_{\sigma _2(i)}$
in which case we write
![]() $\mathscr {X\kern3pt}^{(\sigma _1, \sigma _2)} = \mathscr {Y}$
. For some
$\mathscr {X\kern3pt}^{(\sigma _1, \sigma _2)} = \mathscr {Y}$
. For some
![]() $T \subseteq \{1, \ldots , d\},$
we define
$T \subseteq \{1, \ldots , d\},$
we define
![]() $\mathfrak{D}_T(\mathscr {X\kern3pt}) = \{ C \subset X : C \text { is a} T\text {-Design of } \mathscr {X\kern3pt}\}$
, that is,
$\mathfrak{D}_T(\mathscr {X\kern3pt}) = \{ C \subset X : C \text { is a} T\text {-Design of } \mathscr {X\kern3pt}\}$
, that is,
![]() $\mathfrak{D}_T(\mathscr {X\kern3pt})$
is the collection of all T-designs of
$\mathfrak{D}_T(\mathscr {X\kern3pt})$
is the collection of all T-designs of
![]() $\mathscr {X}$
.
$\mathscr {X}$
.
Theorem 4.5 Let
![]() $\mathscr {X}$
and
$\mathscr {X}$
and
![]() $\mathscr {Y}$
, respectively, be d-class and e-class schemes that satisfy property
$\mathscr {Y}$
, respectively, be d-class and e-class schemes that satisfy property
![]() $\Phi _{\mathbb {Q}}$
, and let
$\Phi _{\mathbb {Q}}$
, and let
![]() $T \subset \{1, \ldots , d\}$
and
$T \subset \{1, \ldots , d\}$
and
![]() $T' \subset \{1, \ldots , e\}$
. If
$T' \subset \{1, \ldots , e\}$
. If
![]() $\mathscr {X\kern3pt}_{\downarrow _{\mathbb {Q}}}^{(\sigma _1, \sigma _2)} = \mathscr {Y}_{\downarrow _{\mathbb {Q}}}$
and
$\mathscr {X\kern3pt}_{\downarrow _{\mathbb {Q}}}^{(\sigma _1, \sigma _2)} = \mathscr {Y}_{\downarrow _{\mathbb {Q}}}$
and
![]() $\iota _{\mathscr {X\kern3pt}}(T) = \iota _{\mathscr {Y\kern1.5pt}}(T')$
, then
$\iota _{\mathscr {X\kern3pt}}(T) = \iota _{\mathscr {Y\kern1.5pt}}(T')$
, then
![]() $C \mapsto C^{\sigma _1}$
is a bijection from
$C \mapsto C^{\sigma _1}$
is a bijection from
![]() $\mathfrak{D}_T(\mathscr {X\kern3pt})$
to
$\mathfrak{D}_T(\mathscr {X\kern3pt})$
to
![]() $\mathfrak{D}_{T'}(\mathscr {Y\kern3pt})$
.
$\mathfrak{D}_{T'}(\mathscr {Y\kern3pt})$
.
Example 4.6 Let
![]() $\mathscr {X}$
be as in Example 3.9 and let
$\mathscr {X}$
be as in Example 3.9 and let
![]() $\mathscr {Y\kern3pt}$
be the association scheme on the same vertex set
$\mathscr {Y\kern3pt}$
be the association scheme on the same vertex set
![]() $\mathbb {Z}_4\times \mathbb {Z}_2$
defined by the following relation matrix
$\mathbb {Z}_4\times \mathbb {Z}_2$
defined by the following relation matrix
![]() $\sum i A_i$
and having second eigenmatrix
$\sum i A_i$
and having second eigenmatrix
![]() $Q_{\mathscr {Y}}$
as follows:
$Q_{\mathscr {Y}}$
as follows:
 $$\begin{align*}\mathscr{Y}: \begin{bmatrix} 0 & 1 & 2 & 2 & 3 & 3 & 4 & 4 \\ 1 & 0 & 2 & 2 & 3 & 3 & 4 & 4 \\ 2 & 2 & 0 & 1 & 4 & 4 & 3 & 3 \\ 2 & 2 & 1 & 0 & 4 & 4 & 3 & 3 \\ 4 & 4 & 3 & 3 & 0 & 1 & 2 & 2 \\ 4 & 4 & 3 & 3 & 1 & 0 & 2 & 2 \\ 3 & 3 & 4 & 4 & 2 & 2 & 0 & 1 \\ 3 & 3 & 4 & 4 & 2 & 2 & 1 & 0 \end{bmatrix}, \quad Q_{\mathscr{Y}}= \left[ \begin{array}{rrrrr} 1 & 1 & 1 & 1 & 4 \\ 1 & 1 & 1 & 1 & \!\!-4 \\ 1 & \!\!-1 & \!\!-1 & 1 & 0 \\ 1 & \!\!-i & i & \!\!-1 & 0 \\ 1 & i & \!\!-i & \!\!-1 & 0 \end{array} \right]. \end{align*}$$
$$\begin{align*}\mathscr{Y}: \begin{bmatrix} 0 & 1 & 2 & 2 & 3 & 3 & 4 & 4 \\ 1 & 0 & 2 & 2 & 3 & 3 & 4 & 4 \\ 2 & 2 & 0 & 1 & 4 & 4 & 3 & 3 \\ 2 & 2 & 1 & 0 & 4 & 4 & 3 & 3 \\ 4 & 4 & 3 & 3 & 0 & 1 & 2 & 2 \\ 4 & 4 & 3 & 3 & 1 & 0 & 2 & 2 \\ 3 & 3 & 4 & 4 & 2 & 2 & 0 & 1 \\ 3 & 3 & 4 & 4 & 2 & 2 & 1 & 0 \end{bmatrix}, \quad Q_{\mathscr{Y}}= \left[ \begin{array}{rrrrr} 1 & 1 & 1 & 1 & 4 \\ 1 & 1 & 1 & 1 & \!\!-4 \\ 1 & \!\!-1 & \!\!-1 & 1 & 0 \\ 1 & \!\!-i & i & \!\!-1 & 0 \\ 1 & i & \!\!-i & \!\!-1 & 0 \end{array} \right]. \end{align*}$$
Then,
![]() $\mathscr {X}$
and
$\mathscr {X}$
and
![]() $\mathscr {Y}$
are non-isomorphic but
$\mathscr {Y}$
are non-isomorphic but
![]() $\mathscr {X}_{\downarrow _{\mathbb {Q}}} = \mathscr {Y}_{\downarrow _{\mathbb {Q}}}$
. Now,
$\mathscr {X}_{\downarrow _{\mathbb {Q}}} = \mathscr {Y}_{\downarrow _{\mathbb {Q}}}$
. Now,
![]() $\iota _{\mathscr {Y}}:\{0,1,2,3,4\} \to \{0,1,2,3\}$
by
$\iota _{\mathscr {Y}}:\{0,1,2,3,4\} \to \{0,1,2,3\}$
by
![]() $\iota _{\mathscr {Y\kern1.5pt}}(0)=0$
,
$\iota _{\mathscr {Y\kern1.5pt}}(0)=0$
,
![]() $\iota _{\mathscr {Y\kern1.5pt}}(1)=1$
,
$\iota _{\mathscr {Y\kern1.5pt}}(1)=1$
,
![]() $\iota _{\mathscr {Y\kern1.5pt}}(2)=1$
,
$\iota _{\mathscr {Y\kern1.5pt}}(2)=1$
,
![]() $\iota _{\mathscr {Y\kern1.5pt}}(3)=2$
, and
$\iota _{\mathscr {Y\kern1.5pt}}(3)=2$
, and
![]() $\iota _{\mathscr {Y\kern1.5pt}}(4)=3$
. Consider C from Example 4.4, which is a
$\iota _{\mathscr {Y\kern1.5pt}}(4)=3$
. Consider C from Example 4.4, which is a
![]() $\{1,2,3\}$
-design in
$\{1,2,3\}$
-design in
![]() $\mathscr {X}$
and a
$\mathscr {X}$
and a
![]() $\{1, 2\}$
-design in
$\{1, 2\}$
-design in
![]() $\mathscr {X}_{\downarrow _{\mathbb {Q}}} = \mathscr {Y}_{\downarrow _{\mathbb {Q}}}$
. So C is a
$\mathscr {X}_{\downarrow _{\mathbb {Q}}} = \mathscr {Y}_{\downarrow _{\mathbb {Q}}}$
. So C is a
![]() $\iota _{\mathscr {Y}}^{-1}(1) \cup \iota _{\mathscr {Y}}^{-1}(2) = \{3, 4\}$
-design of
$\iota _{\mathscr {Y}}^{-1}(1) \cup \iota _{\mathscr {Y}}^{-1}(2) = \{3, 4\}$
-design of
![]() $\mathscr {Y}$
. Note that
$\mathscr {Y}$
. Note that
![]() $\mathscr {X}_{\downarrow _{\mathbb {Q}}}$
and
$\mathscr {X}_{\downarrow _{\mathbb {Q}}}$
and
![]() $\mathscr {Y}_{\downarrow _{\mathbb {Q}}}$
are equal and not just isomorphic, so no permutation of the vertices needs to be applied to C for it to be a design of
$\mathscr {Y}_{\downarrow _{\mathbb {Q}}}$
are equal and not just isomorphic, so no permutation of the vertices needs to be applied to C for it to be a design of
![]() $\mathscr {Y}$
. It is not hard for the interested reader to completely enumerate all T-designs for both
$\mathscr {Y}$
. It is not hard for the interested reader to completely enumerate all T-designs for both
![]() $\mathscr {X}$
and
$\mathscr {X}$
and
![]() $\mathscr {Y\kern3pt}$
by computer. Indeed, in light of Theorem 4.5, one need only enumerate them for
$\mathscr {Y\kern3pt}$
by computer. Indeed, in light of Theorem 4.5, one need only enumerate them for
![]() $\mathscr {X}_{\downarrow _{\mathbb {Q}}}$
.
$\mathscr {X}_{\downarrow _{\mathbb {Q}}}$
.
5 Conjugacy class association schemes
We begin this section with a brisk review of the general theory of conjugacy class association schemes. These are well-studied and serve as fundamental examples in some standard texts; see [Reference Bannai and Ito4, p. 54], [Reference Godsil13, pp. 230–231, p. 264], [Reference Bannai, Bannai, Ito and Tanaka5, p. 51], but also [Reference Bannai and Ito4, pp. 19–21] and [Reference Brouwer, Cohen and Neumaier6, Section 2.9].
Let G be a finite group with decomposition
![]() $G = \mathcal {C}_0\cup \mathcal {C}_1 \cup \cdots \cup \mathcal {C}_d$
into conjugacy classes where
$G = \mathcal {C}_0\cup \mathcal {C}_1 \cup \cdots \cup \mathcal {C}_d$
into conjugacy classes where
![]() $\mathcal {C}_0=\{1\}$
. We build matrices in
$\mathcal {C}_0=\{1\}$
. We build matrices in
![]() $\mathsf {Mat}_G(\mathbb {C})$
as follows. For
$\mathsf {Mat}_G(\mathbb {C})$
as follows. For
![]() $0\le i\le d$
, define
$0\le i\le d$
, define
![]() $A_i$
, the
$A_i$
, the
![]() $i^{\mathrm {th}}$
adjacency matrix, as the 01-matrix in
$i^{\mathrm {th}}$
adjacency matrix, as the 01-matrix in
![]() $\mathsf {Mat}_G(\mathbb {C})$
having a one in position
$\mathsf {Mat}_G(\mathbb {C})$
having a one in position
![]() $(g,h)$
if
$(g,h)$
if
![]() $g^{-1}h\in \mathcal {C}_i$
. This is the adjacency matrix of the digraph with vertex set G and arc set
$g^{-1}h\in \mathcal {C}_i$
. This is the adjacency matrix of the digraph with vertex set G and arc set
![]() $R_i = \left \{ (g,ga) \middle | g\in G, \ a\in \mathcal {C}_i \right \}$
. The Bose–Mesner algebra
$R_i = \left \{ (g,ga) \middle | g\in G, \ a\in \mathcal {C}_i \right \}$
. The Bose–Mesner algebra
![]() $\mathbb {A}$
, defined above as the vector space span of
$\mathbb {A}$
, defined above as the vector space span of
![]() $\{A_0,\ldots ,A_d\}$
, is also the center of the group algebra
$\{A_0,\ldots ,A_d\}$
, is also the center of the group algebra
![]() $\mathbb {C} [\hat {G}],$
where
$\mathbb {C} [\hat {G}],$
where
![]() $\hat {G}$
is the group of
$\hat {G}$
is the group of
![]() $v=|G|$
permutation matrices in
$v=|G|$
permutation matrices in
![]() $\mathsf {Mat}_G(\mathbb {C})$
given by the right regular representation
$\mathsf {Mat}_G(\mathbb {C})$
given by the right regular representation
![]() $g\cdot x=xg^{-1}$
; the permutation matrix
$g\cdot x=xg^{-1}$
; the permutation matrix
![]() $P_g \in \hat {G}$
has a one in position
$P_g \in \hat {G}$
has a one in position
![]() $(x,xg^{-1})$
for
$(x,xg^{-1})$
for
![]() $x\in G$
and
$x\in G$
and
![]() $P_g {\mathbf e}_x = {\mathbf e}_{xg}$
, where
$P_g {\mathbf e}_x = {\mathbf e}_{xg}$
, where
![]() ${\mathbf e}_{x} \in \mathbb {C}^G$
is the standard basis vector corresponding to
${\mathbf e}_{x} \in \mathbb {C}^G$
is the standard basis vector corresponding to
![]() $x\in G$
.
$x\in G$
.
We have a partition
![]() ${\mathcal R}=\{R_0,\ldots ,R_d\}$
of
${\mathcal R}=\{R_0,\ldots ,R_d\}$
of
![]() $G\times G$
into binary relations. It is well-known that
$G\times G$
into binary relations. It is well-known that
![]() $(G,{\mathcal R})$
is a commutative association scheme [Reference Bannai and Ito4, p. 20]; the scheme is symmetric precisely when all conjugacy classes are inverse-closed. Each normal subgroup of G determines an imprimitivity system of this association scheme; if
$(G,{\mathcal R})$
is a commutative association scheme [Reference Bannai and Ito4, p. 20]; the scheme is symmetric precisely when all conjugacy classes are inverse-closed. Each normal subgroup of G determines an imprimitivity system of this association scheme; if
![]() ${N \unlhd G}$
, then N is expressible as a union of conjugacy classes,
${N \unlhd G}$
, then N is expressible as a union of conjugacy classes,
![]() $\mathcal {C}_0\cup \cdots \cup \mathcal {C}_s$
say, and
$\mathcal {C}_0\cup \cdots \cup \mathcal {C}_s$
say, and
![]() $(X,R_1\cup \cdots \cup R_s)$
is a disjoint union of
$(X,R_1\cup \cdots \cup R_s)$
is a disjoint union of
![]() $|G:N|$
complete graphs of size
$|G:N|$
complete graphs of size
![]() $|N|$
. Moreover, every imprimitivity system of a conjugacy class scheme arises in this way: the component of the disconnected graph containing the identity is a union of conjugacy classes closed under multiplication.
$|N|$
. Moreover, every imprimitivity system of a conjugacy class scheme arises in this way: the component of the disconnected graph containing the identity is a union of conjugacy classes closed under multiplication.
There are exactly
![]() $d+1$
irreducible characters of
$d+1$
irreducible characters of
![]() $G,$
including the trivial character
$G,$
including the trivial character
![]() $\chi _0:G \rightarrow \{1\}$
. The character table
$\chi _0:G \rightarrow \{1\}$
. The character table
![]() ${\mathsf {T}}$
of G has one row for each irreducible character and one column for each conjugacy class; in row j, column i, the value is
${\mathsf {T}}$
of G has one row for each irreducible character and one column for each conjugacy class; in row j, column i, the value is
![]() $\chi _j(g)$
for
$\chi _j(g)$
for
![]() $g\in \mathcal {C}_i$
. We denote the basis of primitive idempotents of the Bose–Mesner algebra
$g\in \mathcal {C}_i$
. We denote the basis of primitive idempotents of the Bose–Mesner algebra
![]() $\mathbb {A}$
by
$\mathbb {A}$
by
![]() $\{E_0,\ldots ,E_d\}$
and define the first and second eigenmatrices P and Q by the equations (2.2) as usual.
$\{E_0,\ldots ,E_d\}$
and define the first and second eigenmatrices P and Q by the equations (2.2) as usual.
Though it is well-known, we will show below using eigenvectors of the
![]() $A_i$
that for the conjugacy class scheme of a finite group G, we have
$A_i$
that for the conjugacy class scheme of a finite group G, we have
![]() $Q_{ij} = \chi _j(1) \, \overline {\chi _j(g)}$
and
$Q_{ij} = \chi _j(1) \, \overline {\chi _j(g)}$
and
![]() ${P_{ji} = |\mathcal {C}_i|\chi _j(g)/\chi _j(1)}$
(
${P_{ji} = |\mathcal {C}_i|\chi _j(g)/\chi _j(1)}$
(
![]() $g\in \mathcal {C}_i$
).Footnote
4
Denoting the corresponding irreducible representations by
$g\in \mathcal {C}_i$
).Footnote
4
Denoting the corresponding irreducible representations by
![]() $\rho _0,\ldots ,\rho _d$
, we have
$\rho _0,\ldots ,\rho _d$
, we have
![]() $\chi _j(g)=\mathsf {tr} \rho _j(g)$
and the right regular representation
$\chi _j(g)=\mathsf {tr} \rho _j(g)$
and the right regular representation
![]() $\rho :G\rightarrow \hat {G}$
can be block diagonalized as a direct sum of irreducible representations [Reference Dummit and Foote9, Theorem 18.10]; in the notation of Bannai and Ito [Reference Bannai and Ito4, p. 17], we have
$\rho :G\rightarrow \hat {G}$
can be block diagonalized as a direct sum of irreducible representations [Reference Dummit and Foote9, Theorem 18.10]; in the notation of Bannai and Ito [Reference Bannai and Ito4, p. 17], we have
where, in the block diagonalization of the right regular representation
![]() $\rho $
, the
$\rho $
, the
![]() $j^{\mathrm {th}}$
irreducible representation
$j^{\mathrm {th}}$
irreducible representation
![]() $\rho _j$
appears with multiplicity equal to its degree
$\rho _j$
appears with multiplicity equal to its degree
![]() $f_j$
.
$f_j$
.
Our final goal in this section is to diagonalize the Bose–Mesner algebra of a conjugacy class association scheme.
For
![]() $0\le j\le d$
, fix a choice of representation
$0\le j\le d$
, fix a choice of representation
![]() $\rho _j:G\rightarrow \mathsf {Mat}_{f_j}(\mathbb {C})$
with
$\rho _j:G\rightarrow \mathsf {Mat}_{f_j}(\mathbb {C})$
with
![]() $\mathsf {tr} \rho _j(g)=\chi _j(g)$
for each
$\mathsf {tr} \rho _j(g)=\chi _j(g)$
for each
![]() $g\in G$
. With
$g\in G$
. With
![]() $f=f_j$
, consider the bijection
$f=f_j$
, consider the bijection
![]() $\upsilon :[f]\times [f] \rightarrow [f^2]$
, vectorizing each matrix
$\upsilon :[f]\times [f] \rightarrow [f^2]$
, vectorizing each matrix
![]() $R=[r_{ij}] \in \mathsf {Mat}_f(\mathbb {C})$
into
$R=[r_{ij}] \in \mathsf {Mat}_f(\mathbb {C})$
into
![]() $[r_{11},r_{12},\ldots ,r_{ff}]$
. Construct a
$[r_{11},r_{12},\ldots ,r_{ff}]$
. Construct a
![]() $|G|\times f^2$
matrix
$|G|\times f^2$
matrix
![]() $U_j$
with row g equal to
$U_j$
with row g equal to
![]() $u_g:=\upsilon \left ( \rho (g)\right )$
.
$u_g:=\upsilon \left ( \rho (g)\right )$
.
Theorem 5.1 (Cf. [Reference Godsil and Meagher12, Lemma 11.12.1])
The representations
![]() $\rho _0,\ldots ,\rho _d$
give us
$\rho _0,\ldots ,\rho _d$
give us
![]() $|G|$
linearly independent eigenvectors for
$|G|$
linearly independent eigenvectors for
![]() $\mathbb {A}$
. More precisely, the
$\mathbb {A}$
. More precisely, the
![]() $\sum _{j=0}^d f_j^2$
columns of the partitioned matrix
$\sum _{j=0}^d f_j^2$
columns of the partitioned matrix
![]() $\left [ U_0 | U_1 | \cdots | U_d \right ]$
form a basis for
$\left [ U_0 | U_1 | \cdots | U_d \right ]$
form a basis for
![]() $\mathbb {C}^G$
, where every basis vector is a common eigenvector for
$\mathbb {C}^G$
, where every basis vector is a common eigenvector for
![]() $A_0,\ldots ,A_d$
.
$A_0,\ldots ,A_d$
.
Proof Let j be given,
![]() $0\le j\le d$
, and write simply
$0\le j\le d$
, and write simply
![]() $U=U_j$
as constructed above and write
$U=U_j$
as constructed above and write
![]() $\rho=\rho_j$
. We will show that, for each i,
$\rho=\rho_j$
. We will show that, for each i,
![]() $0\le i\le d$
,
$0\le i\le d$
,
 $$ \begin{align*}A_i U = \frac{ |\mathcal{C}_i| \chi_j(g_i)}{f_j} U,\end{align*} $$
$$ \begin{align*}A_i U = \frac{ |\mathcal{C}_i| \chi_j(g_i)}{f_j} U,\end{align*} $$
where
![]() $g_i\in \mathcal {C}_i$
. Let
$g_i\in \mathcal {C}_i$
. Let
![]() $C = \sum _{x\in \mathcal {C}_i} \rho (x)$
. Then, for any
$C = \sum _{x\in \mathcal {C}_i} \rho (x)$
. Then, for any
![]() $g\in G$
,
$g\in G$
,
![]() $\rho (g)^{-1} C\rho (g) = C$
so that
$\rho (g)^{-1} C\rho (g) = C$
so that
![]() $C\rho (g) = \rho (g) C$
. By Schur’s Lemma [Reference Serre23, Proposition 4, 2.2], [Reference Ledermann16, Theorem 1.4],
$C\rho (g) = \rho (g) C$
. By Schur’s Lemma [Reference Serre23, Proposition 4, 2.2], [Reference Ledermann16, Theorem 1.4],
![]() $C=\theta I_{f_j}$
for some
$C=\theta I_{f_j}$
for some
![]() $\theta $
. Thus,
$\theta $
. Thus,
![]() $\sum _{x\in \mathcal {C}_i} \rho (gx)= \rho (g) C = \theta \rho (g)$
, and the row g of
$\sum _{x\in \mathcal {C}_i} \rho (gx)= \rho (g) C = \theta \rho (g)$
, and the row g of
![]() $A_iU$
is
$A_iU$
is
 $$\begin{align*}\sum_{x\in \mathcal{C}_i} u_{gx} =\upsilon\left( \sum_{x\in \mathcal{C}_i} \rho({gx}) \right) = \theta u_g. \end{align*}$$
$$\begin{align*}\sum_{x\in \mathcal{C}_i} u_{gx} =\upsilon\left( \sum_{x\in \mathcal{C}_i} \rho({gx}) \right) = \theta u_g. \end{align*}$$
In other words,
![]() $A_iU=\theta U$
for some
$A_iU=\theta U$
for some
![]() $\theta \in \mathbb {C}$
. Taking the trace of both sides of the equation
$\theta \in \mathbb {C}$
. Taking the trace of both sides of the equation
![]() $\sum _{x\in \mathcal {C}_i} \rho (x) = \theta I$
, we find
$\sum _{x\in \mathcal {C}_i} \rho (x) = \theta I$
, we find
![]() $ |\mathcal {C}_i| \chi _j(g_i) = \theta f_j$
.
$ |\mathcal {C}_i| \chi _j(g_i) = \theta f_j$
.
By Wedderburn’s structure theorem for semisimple algebras (see also [Reference Serre23, p. 48]), the image
![]() $\{ \rho (g) \mid g\in G\}$
is full-dimensional in
$\{ \rho (g) \mid g\in G\}$
is full-dimensional in
![]() $\mathsf {Mat}_f(\mathbb {C})$
. In fact, extending
$\mathsf {Mat}_f(\mathbb {C})$
. In fact, extending
![]() $\rho $
linearly to the full group algebra, we have that
$\rho $
linearly to the full group algebra, we have that
![]() $\rho : \mathbb {C}[G] \rightarrow \mathsf {Mat}_{f_j}(\mathbb {C})$
is surjective. So the
$\rho : \mathbb {C}[G] \rightarrow \mathsf {Mat}_{f_j}(\mathbb {C})$
is surjective. So the
![]() $f_j^2$
columns of U are linearly independent. Distinct irreducible representations
$f_j^2$
columns of U are linearly independent. Distinct irreducible representations
![]() $\rho _j,\rho _k$
of G correspond to orthogonal columns of the matrix Q, so these
$\rho _j,\rho _k$
of G correspond to orthogonal columns of the matrix Q, so these
![]() $f_j^2$
vectors are orthogonal to the eigenvectors obtained in this same manner from the remaining d irreducible representations of G. So we have
$f_j^2$
vectors are orthogonal to the eigenvectors obtained in this same manner from the remaining d irreducible representations of G. So we have
![]() $\sum _{j=0}^d f_j^2$
linearly independent eigenvectors for the Bose–Mesner algebra. We then use the standard identity
$\sum _{j=0}^d f_j^2$
linearly independent eigenvectors for the Bose–Mesner algebra. We then use the standard identity
![]() $\sum _{j=0}^d f_j^2=|G|$
(see, e.g., [Reference Dummit and Foote9, Theorem 18.10(3)]) to finish the proof.
$\sum _{j=0}^d f_j^2=|G|$
(see, e.g., [Reference Dummit and Foote9, Theorem 18.10(3)]) to finish the proof.
The first and second eigenmatrices of the conjugacy class association scheme
![]() $P=[P_{ji}]$
and
$P=[P_{ji}]$
and
![]() $Q=[Q_{ij}]$
defined by (2.2) above satisfy the standard first and second orthogonality relations for association schemes (2.3), where
$Q=[Q_{ij}]$
defined by (2.2) above satisfy the standard first and second orthogonality relations for association schemes (2.3), where
![]() $v_i=|\mathcal {C}_i|$
, but in this case, of course, these reduce to the classical orthogonality relations for group characters [Reference Bannai and Ito4, Theorems I.4.4 and I.4.9], [Reference Serre23, Section 2.3]. Our construction of the matrix U above shows
$v_i=|\mathcal {C}_i|$
, but in this case, of course, these reduce to the classical orthogonality relations for group characters [Reference Bannai and Ito4, Theorems I.4.4 and I.4.9], [Reference Serre23, Section 2.3]. Our construction of the matrix U above shows
![]() $m_j=f_j^2$
. So the second orthogonality relation gives us
$m_j=f_j^2$
. So the second orthogonality relation gives us
![]() $Q_{ij} = f_j \overline {\chi _j(x_i)}$
. In summary (cf. [Reference Bannai and Ito4, Theorem II.7.2], with
$Q_{ij} = f_j \overline {\chi _j(x_i)}$
. In summary (cf. [Reference Bannai and Ito4, Theorem II.7.2], with
![]() $g_i$
a representative of
$g_i$
a representative of
![]() $\mathcal {C}_i$
,
$\mathcal {C}_i$
,
The Krein parameters of the conjugacy class scheme are closely related to the decomposition of Kronecker products of irreducible representations into irreducibles. If
![]() $f_i$
denotes the degree of
$f_i$
denotes the degree of
![]() $\rho _i$
and
$\rho _i$
and
then
![]() $\chi _i \circ \chi _j = \sum _{k=0}^d r_{ij}^k \chi _k$
and, after scaling each column by its degree and using [Reference Brouwer, Cohen and Neumaier6, Lemma 2.3.1(vii)], we find
$\chi _i \circ \chi _j = \sum _{k=0}^d r_{ij}^k \chi _k$
and, after scaling each column by its degree and using [Reference Brouwer, Cohen and Neumaier6, Lemma 2.3.1(vii)], we find
![]() $q_{ij}^k = \frac {f_if_j}{f_k} r_{ij}^k$
.
$q_{ij}^k = \frac {f_if_j}{f_k} r_{ij}^k$
.
The conjugacy classes of size one are precisely
![]() $\left \{ \{a\} \middle | a\in Z(G) \right \}$
and the eigenspaces of dimension one correspond to the elements of the abelianization
$\left \{ \{a\} \middle | a\in Z(G) \right \}$
and the eigenspaces of dimension one correspond to the elements of the abelianization
![]() ${G'=G/[G,G]}$
of G.
${G'=G/[G,G]}$
of G.
The intersection numbers
![]() $p_{ij}^k$
are given by
$p_{ij}^k$
are given by
where
![]() $z \in \mathcal {C}_k$
and
$z \in \mathcal {C}_k$
and
![]() $\mathcal {C}_j^{-1} = \{ h^{-1} \mid h\in \mathcal {C}_j\}$
. To see this, consider any
$\mathcal {C}_j^{-1} = \{ h^{-1} \mid h\in \mathcal {C}_j\}$
. To see this, consider any
![]() $x,y\in G$
with
$x,y\in G$
with
![]() ${x^{-1}y\in \mathcal {C}_k}$
; find
${x^{-1}y\in \mathcal {C}_k}$
; find
![]() $g\in G$
with
$g\in G$
with
![]() $g^{-1} x^{-1} y g = z$
so that
$g^{-1} x^{-1} y g = z$
so that
![]() $xg^{-1} \left ( \mathcal {C}_i \cap R_{j'}(z) \right ) g = R_i(x) \cap R_{j'}(y)$
.
$xg^{-1} \left ( \mathcal {C}_i \cap R_{j'}(z) \right ) g = R_i(x) \cap R_{j'}(y)$
.
5.1 Galois group and rational fusions
From here forward, let
![]() $\zeta _\ell $
denote a primitive (complex)
$\zeta _\ell $
denote a primitive (complex)
![]() $\ell ^{\mathrm {th}}$
root of unity.
$\ell ^{\mathrm {th}}$
root of unity.
The splitting field of the finite group G is defined to be the extension of
![]() $\mathbb {Q}$
by the entries of its character table. This then agrees with the concept of the splitting field [Reference Munemasa19] of the conjugacy class association scheme by (5.1). Let
$\mathbb {Q}$
by the entries of its character table. This then agrees with the concept of the splitting field [Reference Munemasa19] of the conjugacy class association scheme by (5.1). Let
![]() $\mathbb {F}$
denote the splitting field of the conjugacy class scheme of G. As discussed in Section 3.1, each
$\mathbb {F}$
denote the splitting field of the conjugacy class scheme of G. As discussed in Section 3.1, each
![]() $\boldsymbol {\sigma }\in {\mathsf {Gal}}(\mathbb {F}/\mathbb {Q})$
acts on the set of primitive idempotents
$\boldsymbol {\sigma }\in {\mathsf {Gal}}(\mathbb {F}/\mathbb {Q})$
acts on the set of primitive idempotents
![]() $\{E_0,\ldots ,E_d\}$
; to
$\{E_0,\ldots ,E_d\}$
; to
![]() $\boldsymbol {\sigma }$
, associate the permutation
$\boldsymbol {\sigma }$
, associate the permutation
![]() $\sigma \in \Sigma _{\mathbb {Q}}$
defined by
$\sigma \in \Sigma _{\mathbb {Q}}$
defined by
![]() $E_{j^\sigma }=\left ( E_j\right )^{\boldsymbol {\sigma }}$
, where the action of
$E_{j^\sigma }=\left ( E_j\right )^{\boldsymbol {\sigma }}$
, where the action of
![]() $\boldsymbol {\sigma }$
on matrices is entrywise.
$\boldsymbol {\sigma }$
on matrices is entrywise.
Recall that
![]() $x,y\in G$
are rationally conjugate if
$x,y\in G$
are rationally conjugate if
![]() $g\langle x\rangle g^{-1} = \langle y \rangle $
for some
$g\langle x\rangle g^{-1} = \langle y \rangle $
for some
![]() $g\in G$
. Clearly, if x and y are conjugate in G, then x and y are rationally conjugate; any equivalence class
$g\in G$
. Clearly, if x and y are conjugate in G, then x and y are rationally conjugate; any equivalence class
![]() $\mathcal {C}$
of this “rationally conjugate” relation is a union of conjugacy classes of G and so
$\mathcal {C}$
of this “rationally conjugate” relation is a union of conjugacy classes of G and so
![]() $R_{\mathcal {C}}=\{ (x,y) \mid x^{-1}y\in \mathcal {C} \}$
is expressible as a union of basis relations of the conjugacy class scheme.
$R_{\mathcal {C}}=\{ (x,y) \mid x^{-1}y\in \mathcal {C} \}$
is expressible as a union of basis relations of the conjugacy class scheme.
The exponent of finite group G, i.e., the smallest positive integer k such that
![]() $g^k=1$
for all
$g^k=1$
for all
![]() $g\in G$
, divides
$g\in G$
, divides
![]() $n=|G|$
. If G has exponent k, then, in any representation
$n=|G|$
. If G has exponent k, then, in any representation
![]() $\rho :G\rightarrow {\mathsf {GL}}_m(\mathbb {C})$
,
$\rho :G\rightarrow {\mathsf {GL}}_m(\mathbb {C})$
,
![]() $\rho (g)^k=I$
for each
$\rho (g)^k=I$
for each
![]() $g\in G$
, and so the eigenvalues of
$g\in G$
, and so the eigenvalues of
![]() $\rho (g)$
are
$\rho (g)$
are
![]() $k^{\mathrm {th}}$
roots of unity. Hence, the trace
$k^{\mathrm {th}}$
roots of unity. Hence, the trace
![]() $\chi (g) =\mathsf {tr} \rho (g)$
belongs to the cyclotomic extension
$\chi (g) =\mathsf {tr} \rho (g)$
belongs to the cyclotomic extension
![]() $\mathbb {Q}( \zeta _k)$
, and this is contained in
$\mathbb {Q}( \zeta _k)$
, and this is contained in
![]() $\mathbb {Q}( \zeta _n)$
. In some cases (e.g., whenever all conjugacy classes are inverse-closed and the eigenvalues are all real), the splitting field of G can be a proper subfield of
$\mathbb {Q}( \zeta _n)$
. In some cases (e.g., whenever all conjugacy classes are inverse-closed and the eigenvalues are all real), the splitting field of G can be a proper subfield of
![]() $\mathbb {Q}( \zeta _k)$
. Motivated by this important class of examples, Simon Norton asked whether the splitting field of any commutative association scheme is contained in some cyclotomic extension of the rational numbers [Reference Bannai and Ito4, p. 183].
$\mathbb {Q}( \zeta _k)$
. Motivated by this important class of examples, Simon Norton asked whether the splitting field of any commutative association scheme is contained in some cyclotomic extension of the rational numbers [Reference Bannai and Ito4, p. 183].
While we choose here to cite a reference dealing directly with Schur rings, the connection between rational characters and rational conjugacy classes of G is well studied (indeed, this connection is the origin of the term “rational conjugacy class”). For instance, the fact that there are equally many rational conjugacy classes of G as orbits of the full Galois group can be found in Serre [Reference Serre23, Chapter 13].
Theorem 5.2 (Muzychuk et al. [Reference Muzychuk, Ponomarenko and Chen22])
The conjugacy class association scheme
![]() $(G,{\mathcal R})$
of any finite group G satisfies Property
$(G,{\mathcal R})$
of any finite group G satisfies Property
![]() $\Phi _{\mathbb {Q}}$
. The basis relations of the corresponding fusion scheme are the relations
$\Phi _{\mathbb {Q}}$
. The basis relations of the corresponding fusion scheme are the relations
![]() $R_{\mathcal {C}}$
as
$R_{\mathcal {C}}$
as
![]() $\mathcal {C}$
ranges over the rational conjugacy classes of G as defined above.
$\mathcal {C}$
ranges over the rational conjugacy classes of G as defined above.
Proof An idempotent
![]() $\sum _{j=0}^d c_jE_j$
belongs to
$\sum _{j=0}^d c_jE_j$
belongs to
![]() ${\mathcal E}_{\mathbb {Q}}$
if and only if the corresponding character
${\mathcal E}_{\mathbb {Q}}$
if and only if the corresponding character
![]() $\psi (g) = \sum _{j=0}^d c_j \chi _j(g)$
is rational for each
$\psi (g) = \sum _{j=0}^d c_j \chi _j(g)$
is rational for each
![]() $g\in G$
.
$g\in G$
.
As shown above in our discussion of the exponent, the splitting field
![]() $\mathbb {F}$
is contained in a cyclotomic extension
$\mathbb {F}$
is contained in a cyclotomic extension
![]() $\mathbb {Q}(\zeta _n)$
and, for each m with
$\mathbb {Q}(\zeta _n)$
and, for each m with
![]() $\gcd (m,n)=1$
, there is a Galois automorphism
$\gcd (m,n)=1$
, there is a Galois automorphism
![]() $\boldsymbol {\sigma }\in {\mathsf {Gal}}(\mathbb {Q}(\zeta _n)/\mathbb {Q})$
with
$\boldsymbol {\sigma }\in {\mathsf {Gal}}(\mathbb {Q}(\zeta _n)/\mathbb {Q})$
with
![]() $\zeta _n^{\boldsymbol {\sigma }}=\zeta _n^m$
.
$\zeta _n^{\boldsymbol {\sigma }}=\zeta _n^m$
.
Now suppose
![]() $\langle x\rangle = \langle y\rangle $
. Then,
$\langle x\rangle = \langle y\rangle $
. Then,
![]() $y=x^m$
for some m with
$y=x^m$
for some m with
![]() $\gcd (m,n)=1$
. If
$\gcd (m,n)=1$
. If
![]() $\psi $
is a rational character of G, say
$\psi $
is a rational character of G, say
![]() $\psi (g) = \mathsf {tr} \rho (g)$
for some complex representation
$\psi (g) = \mathsf {tr} \rho (g)$
for some complex representation
![]() $\rho :G \rightarrow {\mathsf {GL}}_f(\mathbb {C})$
, then
$\rho :G \rightarrow {\mathsf {GL}}_f(\mathbb {C})$
, then
![]() $\psi (x) = \mathsf {tr} \rho (x) = \sum _{j=1}^f \omega _j$
for some
$\psi (x) = \mathsf {tr} \rho (x) = \sum _{j=1}^f \omega _j$
for some
![]() $n^{\mathrm {th}}$
roots of unity
$n^{\mathrm {th}}$
roots of unity
![]() $\omega _1,\ldots ,\omega _f$
. We then have
$\omega _1,\ldots ,\omega _f$
. We then have
 $$ \begin{align*}\psi(y) = \mathsf{tr} \, \rho\left( x^m \right) = \mathsf{tr} \, \rho\left( x\right)^m = \sum_{j=1}^f \omega_j^m =\sum_{j=1}^f \omega_j^{\boldsymbol{\sigma}} =\left( \sum_{j=1}^f \omega_j \right)^{\boldsymbol{\sigma}} = \psi(x)^{\boldsymbol{\sigma}} = \psi(x),\end{align*} $$
$$ \begin{align*}\psi(y) = \mathsf{tr} \, \rho\left( x^m \right) = \mathsf{tr} \, \rho\left( x\right)^m = \sum_{j=1}^f \omega_j^m =\sum_{j=1}^f \omega_j^{\boldsymbol{\sigma}} =\left( \sum_{j=1}^f \omega_j \right)^{\boldsymbol{\sigma}} = \psi(x)^{\boldsymbol{\sigma}} = \psi(x),\end{align*} $$
since
![]() $\psi $
is rational. Now, if y is instead conjugate to some
$\psi $
is rational. Now, if y is instead conjugate to some
![]() $x^m$
with
$x^m$
with
![]() $\langle x^m\rangle = \langle x \rangle $
, then
$\langle x^m\rangle = \langle x \rangle $
, then
![]() $\psi (y) = \psi \left (x^m\right )=\psi (x)$
. This tells us that the adjacency matrix of the relation
$\psi (y) = \psi \left (x^m\right )=\psi (x)$
. This tells us that the adjacency matrix of the relation
![]() $R_{\mathcal {C}}$
,
$R_{\mathcal {C}}$
,
![]() $A=\displaystyle {\sum _{\mathcal {C}_i\subseteq \mathcal {C}}} A_i$
, satisfies
$A=\displaystyle {\sum _{\mathcal {C}_i\subseteq \mathcal {C}}} A_i$
, satisfies
![]() $A\circ E= \alpha _E A$
(some
$A\circ E= \alpha _E A$
(some
![]() $\alpha _E$
) for each
$\alpha _E$
) for each
![]() $E\in {\mathcal E}_{\mathbb {Q}}$
, so A belongs to the Schur closure of
$E\in {\mathcal E}_{\mathbb {Q}}$
, so A belongs to the Schur closure of
![]() $\mathbb {C}[{\mathcal E}_{\mathbb {Q}}]$
. Equivalently, collapsing over orbits of
$\mathbb {C}[{\mathcal E}_{\mathbb {Q}}]$
. Equivalently, collapsing over orbits of
![]() ${\mathsf {Gal}}(\mathbb {F}/\mathbb {Q})$
, we find that the rows i and j of
${\mathsf {Gal}}(\mathbb {F}/\mathbb {Q})$
, we find that the rows i and j of
![]() $\overline {Q} =QO$
are equal whenever
$\overline {Q} =QO$
are equal whenever
![]() $\mathcal {C}_i$
and
$\mathcal {C}_i$
and
![]() $\mathcal {C}_j$
are contained in the same rational conjugacy class. So the number
$\mathcal {C}_j$
are contained in the same rational conjugacy class. So the number
![]() $e+1$
of Galois orbits
$e+1$
of Galois orbits
![]() ${\mathcal Q}_j$
is at most the number of rational conjugacy classes. Going in the other direction, the adjacency matrix A of any relation
${\mathcal Q}_j$
is at most the number of rational conjugacy classes. Going in the other direction, the adjacency matrix A of any relation
![]() $R_{\mathcal {C}}$
belongs to the full Bose–Mesner algebra and has only rational eigenvalues, so A belongs to
$R_{\mathcal {C}}$
belongs to the full Bose–Mesner algebra and has only rational eigenvalues, so A belongs to
![]() $\mathbb {Q}[{\mathcal E}_{\mathbb {Q}}]$
.
$\mathbb {Q}[{\mathcal E}_{\mathbb {Q}}]$
.
Example 5.3 The “gcd scheme” for
![]() $\mathbb {Z}_n$
described in Example 3.4 is precisely the rational fusion of the conjugacy class scheme of
$\mathbb {Z}_n$
described in Example 3.4 is precisely the rational fusion of the conjugacy class scheme of
![]() $\mathbb {Z}_n$
.
$\mathbb {Z}_n$
.
Example 5.4 The alternating group
![]() $A_4$
has character table and eigenmatrices
$A_4$
has character table and eigenmatrices
 $$ \begin{align*}{\mathsf{T}}=\left[ \begin{array}{crcc} 1 & 1 & 1 & 1 \\ 1 & 1 & \zeta\ & \zeta^2 \\ 1 & 1 & \zeta^2 & \zeta\ \\ 3 &\!\!-1 & 0 & 0 \end{array} \right], \quad Q =\left[ \begin{array}{cccr} 1 & 1 & 1 & 9 \\ 1 & 1 & 1 & \!\!-3 \\ 1 & \zeta & \zeta^2 & 0 \\ 1 & \zeta^2 & \zeta & 0 \end{array} \right], \quad P =\left[ \begin{array}{crcc} 1 & 3 & 4 & 4 \\ 1 & 3 & 4 \zeta & 4\zeta^2 \\ 1 & 3 & 4 \zeta^2 & 4\zeta \\ 1 &\!\!-1 & 0 & 0 \end{array} \right],\end{align*} $$
$$ \begin{align*}{\mathsf{T}}=\left[ \begin{array}{crcc} 1 & 1 & 1 & 1 \\ 1 & 1 & \zeta\ & \zeta^2 \\ 1 & 1 & \zeta^2 & \zeta\ \\ 3 &\!\!-1 & 0 & 0 \end{array} \right], \quad Q =\left[ \begin{array}{cccr} 1 & 1 & 1 & 9 \\ 1 & 1 & 1 & \!\!-3 \\ 1 & \zeta & \zeta^2 & 0 \\ 1 & \zeta^2 & \zeta & 0 \end{array} \right], \quad P =\left[ \begin{array}{crcc} 1 & 3 & 4 & 4 \\ 1 & 3 & 4 \zeta & 4\zeta^2 \\ 1 & 3 & 4 \zeta^2 & 4\zeta \\ 1 &\!\!-1 & 0 & 0 \end{array} \right],\end{align*} $$
where
![]() $\zeta $
is a primitive cube root of unity. We fuse the conjugate pair of eigenspaces to find
$\zeta $
is a primitive cube root of unity. We fuse the conjugate pair of eigenspaces to find
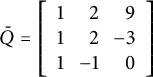 $\bar {Q} = \left [ \begin {array}{crr} 1 & 2 & 9 \\ 1 & 2 & \!\!-3 \\ 1 &\!\!-1& 0 \end {array} \right ]$
and
$\bar {Q} = \left [ \begin {array}{crr} 1 & 2 & 9 \\ 1 & 2 & \!\!-3 \\ 1 &\!\!-1& 0 \end {array} \right ]$
and
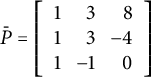 $\bar {P} = \left [ \begin {array}{crr} 1 & 3 & 8 \\ 1 & 3 & \!\!-4 \\ 1 &\!\!-1& 0 \end {array} \right ]$
; the Galois fusion is the association scheme of the complete multipartite graph
$\bar {P} = \left [ \begin {array}{crr} 1 & 3 & 8 \\ 1 & 3 & \!\!-4 \\ 1 &\!\!-1& 0 \end {array} \right ]$
; the Galois fusion is the association scheme of the complete multipartite graph
![]() $\overline {3K_4}$
.
$\overline {3K_4}$
.
Observe that, as a consequence, Theorems 4.3 and 4.5 are always applicable for conjugacy class schemes.
Problem 5.5 Does there exist a finite group G whose rational fusion is a primitive 2-class association scheme? Note that some graphs with Paley parameters, e.g.,
![]() $\mathsf {Paley}(q^2)$
but also
$\mathsf {Paley}(q^2)$
but also
![]() $\mathrm {srg}(225,112,55,56)$
, have rational eigenvalues.
$\mathrm {srg}(225,112,55,56)$
, have rational eigenvalues.
Problem 5.6 Suppose
![]() $\mathbb {E}$
and
$\mathbb {E}$
and
![]() $\mathbb {K}$
are subfields of the splitting field of the conjugacy class scheme
$\mathbb {K}$
are subfields of the splitting field of the conjugacy class scheme
![]() $(G,{\mathcal R})$
. Is there a simple relationship between
$(G,{\mathcal R})$
. Is there a simple relationship between
![]() $\mathbb {E}$
and
$\mathbb {E}$
and
![]() $\mathbb {K}$
such that, whenever
$\mathbb {K}$
such that, whenever
![]() $(G,{\mathcal R})$
satisfies Property
$(G,{\mathcal R})$
satisfies Property
![]() $\Phi _{\mathbb {E}}$
, it must also satisfy Property
$\Phi _{\mathbb {E}}$
, it must also satisfy Property
![]() $\Phi _{\mathbb {K}}$
?
$\Phi _{\mathbb {K}}$
?
6 Case study: Dicyclic groups
The dicyclic group
![]() ${\mathsf {Dic}}_n$
is the group of order
${\mathsf {Dic}}_n$
is the group of order
![]() $4n$
with presentation
$4n$
with presentation
For n even, this group has the same character table as the dihedral group
![]() $D_{2n}$
of the same order. In fact, the two association schemes are isomorphic. Since the dihedral case is studied elsewhere, we will focus on the case where n is odd.
$D_{2n}$
of the same order. In fact, the two association schemes are isomorphic. Since the dihedral case is studied elsewhere, we will focus on the case where n is odd.
Multiplication and conjugation (using
![]() $y^{-1}=yx^n$
) are given by
$y^{-1}=yx^n$
) are given by
 $$ \begin{align*} \begin{array}{l|ll} g\cdot h & \phantom{y}x^\ell & yx^\ell \\ \hline \phantom{y}x^k & \phantom{y}x^{k+\ell} & yx^{\ell-k} \\ {y}x^k & {y}x^{k+\ell} & \phantom{y}x^{n+\ell-k} \end{array}\qquad\qquad \begin{array}{l|ll} h^g & \phantom{y}x^\ell & yx^\ell \\ \hline \phantom{y}x^k & \phantom{y}x^{\ell} & yx^{\ell+2k} \\ {y}x^k & \phantom{y}x^{-\ell} & {y}x^{2k-\ell} \end{array}. \hfill \phantom{.} \end{align*} $$
$$ \begin{align*} \begin{array}{l|ll} g\cdot h & \phantom{y}x^\ell & yx^\ell \\ \hline \phantom{y}x^k & \phantom{y}x^{k+\ell} & yx^{\ell-k} \\ {y}x^k & {y}x^{k+\ell} & \phantom{y}x^{n+\ell-k} \end{array}\qquad\qquad \begin{array}{l|ll} h^g & \phantom{y}x^\ell & yx^\ell \\ \hline \phantom{y}x^k & \phantom{y}x^{\ell} & yx^{\ell+2k} \\ {y}x^k & \phantom{y}x^{-\ell} & {y}x^{2k-\ell} \end{array}. \hfill \phantom{.} \end{align*} $$
The
![]() $n+2$
nontrivial conjugacy classes are
$n+2$
nontrivial conjugacy classes are
![]() $\mathcal {C}_k=\{x^k,x^{2n-k} \}$
,
$\mathcal {C}_k=\{x^k,x^{2n-k} \}$
,
![]() $1\le k< n$
,
$1\le k< n$
,
![]() $\mathcal {C}_n=\{x^n\}$
,
$\mathcal {C}_n=\{x^n\}$
,
where
![]() $\mathcal {C}_{n+2} = \mathcal {C}_{n+1}^{(-1)}$
since n is assumed odd.
$\mathcal {C}_{n+2} = \mathcal {C}_{n+1}^{(-1)}$
since n is assumed odd.
The conjugacy class association scheme contains two vertex-disjoint subschemes (or induced schemes) isomorphic to the association scheme of the
![]() $2n$
-gon: one induced on the cyclic subgroup
$2n$
-gon: one induced on the cyclic subgroup
![]() $\langle x\rangle $
and the other on
$\langle x\rangle $
and the other on
![]() $y\langle x\rangle $
. In both the association scheme of the dihedral group
$y\langle x\rangle $
. In both the association scheme of the dihedral group
![]() $D_{2n}$
and this association scheme, the remaining pairs are partitioned into two relations
$D_{2n}$
and this association scheme, the remaining pairs are partitioned into two relations
![]() $R_{n+1}\cup R_{n+2} = \left ( \langle x\rangle \times y\langle x\rangle \right ) \cup \left ( y\langle x\rangle \times \langle x\rangle \right )$
. Whereas, in the dihedral case, these two relations are both isomorphic to two copies of the complete bipartite graph
$R_{n+1}\cup R_{n+2} = \left ( \langle x\rangle \times y\langle x\rangle \right ) \cup \left ( y\langle x\rangle \times \langle x\rangle \right )$
. Whereas, in the dihedral case, these two relations are both isomorphic to two copies of the complete bipartite graph
![]() $K_{n,n}$
, in the dicyclic case, the relations
$K_{n,n}$
, in the dicyclic case, the relations
![]() $R_{n+1}$
and
$R_{n+1}$
and
![]() $R_{n+2}$
are orientations of
$R_{n+2}$
are orientations of
![]() $K_{2n,2n}$
. More precisely, pairs in
$K_{2n,2n}$
. More precisely, pairs in
![]() $R_{n+1}$
incident to
$R_{n+1}$
incident to
![]() $x^k \in {\mathsf {Dic}}_n$
are
$x^k \in {\mathsf {Dic}}_n$
are
![]() $(x^k,yx^{k+2\ell })$
and
$(x^k,yx^{k+2\ell })$
and
![]() $(yx^{n-k+2\ell },x^k)$
(
$(yx^{n-k+2\ell },x^k)$
(
![]() $0\le \ell < n$
).
$0\le \ell < n$
).
The (transpose of the) eigenmatrix for the association scheme of the cycle
![]() $C_{2n}$
appears as a submatrix of our character table. The splitting field of
$C_{2n}$
appears as a submatrix of our character table. The splitting field of
![]() $C_{2n}$
is well-known to be the real part of a cyclotomic extension,
$C_{2n}$
is well-known to be the real part of a cyclotomic extension,
![]() $\mathbb {Q}(\zeta _{2n}) \cap \mathbb {R}$
, and we extend this by the square root of
$\mathbb {Q}(\zeta _{2n}) \cap \mathbb {R}$
, and we extend this by the square root of
![]() $-1$
to get our splitting field
$-1$
to get our splitting field
![]() $\mathbb {F} = \left ( \mathbb {Q}(\zeta _{2n}) \cap \mathbb {R} \right ) (i) = \mathbb {Q}(\zeta _{2n}+\zeta _{2n}^{-1}, i)$
.
$\mathbb {F} = \left ( \mathbb {Q}(\zeta _{2n}) \cap \mathbb {R} \right ) (i) = \mathbb {Q}(\zeta _{2n}+\zeta _{2n}^{-1}, i)$
.

The cyclotomic extension
![]() $\mathbb {Q}(\zeta _m)$
has Galois group
$\mathbb {Q}(\zeta _m)$
has Galois group
![]() $\left ( \mathbb {Z}_m\right )^\times $
[Reference Dummit and Foote9, Section 14.6]; the Galois automorphism corresponding to
$\left ( \mathbb {Z}_m\right )^\times $
[Reference Dummit and Foote9, Section 14.6]; the Galois automorphism corresponding to
![]() $k\in \mathbb {Z}_m$
with
$k\in \mathbb {Z}_m$
with
![]() $\gcd (k,m)=1$
is given by
$\gcd (k,m)=1$
is given by
![]() ${\zeta _m\mapsto \zeta _m^k}$
. (See also [Reference Conrad7] for a nice exposition.) We have Galois group
${\zeta _m\mapsto \zeta _m^k}$
. (See also [Reference Conrad7] for a nice exposition.) We have Galois group
![]() ${\mathsf {Gal}}(\mathbb {F}/\mathbb {Q})$
where our splitting field
${\mathsf {Gal}}(\mathbb {F}/\mathbb {Q})$
where our splitting field
![]() $\mathbb {F}$
is a subfield of
$\mathbb {F}$
is a subfield of
![]() $\mathbb {Q}(\zeta _{4n})$
whose Galois group is
$\mathbb {Q}(\zeta _{4n})$
whose Galois group is
![]() $\left ( \mathbb {Z}_{4n}\right )^\times $
. Since all subgroups are normal, all intermediate fields
$\left ( \mathbb {Z}_{4n}\right )^\times $
. Since all subgroups are normal, all intermediate fields
![]() $\mathbb {Q} \subset \mathbb {K} \subseteq \mathbb {Q}(\zeta _{4n})$
are Galois extensions. So
$\mathbb {Q} \subset \mathbb {K} \subseteq \mathbb {Q}(\zeta _{4n})$
are Galois extensions. So
![]() $[\mathbb {F}:\mathbb {Q}]=[\mathbb {Q}(\zeta _{2n}):\mathbb {Q}]= \phi (2n)$
, the Euler totient function. Since n is assumed to be odd,
$[\mathbb {F}:\mathbb {Q}]=[\mathbb {Q}(\zeta _{2n}):\mathbb {Q}]= \phi (2n)$
, the Euler totient function. Since n is assumed to be odd,
![]() $\mathbb {F}$
is a degree
$\mathbb {F}$
is a degree
![]() $\phi (n)$
extension of the rationals. By [Reference Dummit and Foote9, Proposition 14.19],
$\phi (n)$
extension of the rationals. By [Reference Dummit and Foote9, Proposition 14.19],
![]() ${\mathsf {Gal}}(\mathbb {F}/\mathbb {Q}(i))\cong {\mathsf {Gal}}( \mathbb {Q}(\zeta _{2n}+\zeta _{2n}^{-1})/\mathbb {Q})$
, the Galois group of the splitting field of the
${\mathsf {Gal}}(\mathbb {F}/\mathbb {Q}(i))\cong {\mathsf {Gal}}( \mathbb {Q}(\zeta _{2n}+\zeta _{2n}^{-1})/\mathbb {Q})$
, the Galois group of the splitting field of the
![]() $2n$
-cycle, and
$2n$
-cycle, and
![]() ${\mathsf {Gal}}(\mathbb {F}/\mathbb {Q}(\zeta _{2n}+\zeta _{2n}^{-1})) \cong \mathbb {Z}_2$
. Moreover, writing
${\mathsf {Gal}}(\mathbb {F}/\mathbb {Q}(\zeta _{2n}+\zeta _{2n}^{-1})) \cong \mathbb {Z}_2$
. Moreover, writing
![]() $\zeta =\zeta _{4n}$
now, the subgroup of
$\zeta =\zeta _{4n}$
now, the subgroup of
![]() ${\mathsf {Gal}}\left ( \mathbb {Q}(\zeta )/\mathbb {Q} \right )$
that stabilizes
${\mathsf {Gal}}\left ( \mathbb {Q}(\zeta )/\mathbb {Q} \right )$
that stabilizes
![]() $\mathbb {F}$
is
$\mathbb {F}$
is
![]() $N=\langle \zeta \mapsto \zeta ^{2n-1} \rangle $
, since
$N=\langle \zeta \mapsto \zeta ^{2n-1} \rangle $
, since
![]() $k=1$
and
$k=1$
and
![]() ${k=2n-1}$
are the only exponents with
${k=2n-1}$
are the only exponents with
![]() $\zeta ^{nk}=\zeta ^n$
and
$\zeta ^{nk}=\zeta ^n$
and
![]() $\zeta ^{2k}+\zeta ^{-2k}=\zeta ^2+\zeta ^{-2}$
. We now have
$\zeta ^{2k}+\zeta ^{-2k}=\zeta ^2+\zeta ^{-2}$
. We now have
![]() ${\mathsf {Gal}}(\mathbb {F}/\mathbb {Q}) \cong \left ( \mathbb {Z}_{4n}\right )^\times / \langle 2n-1\rangle $
. So, for
${\mathsf {Gal}}(\mathbb {F}/\mathbb {Q}) \cong \left ( \mathbb {Z}_{4n}\right )^\times / \langle 2n-1\rangle $
. So, for
![]() $1\le k\le 4n-1$
with
$1\le k\le 4n-1$
with
![]() $\gcd (k,4n)=1$
,
$\gcd (k,4n)=1$
,
![]() $\zeta \mapsto \zeta ^k$
and
$\zeta \mapsto \zeta ^k$
and
![]() $\zeta \mapsto \zeta ^{2n-k}$
act identically on
$\zeta \mapsto \zeta ^{2n-k}$
act identically on
![]() $\mathbb {F}$
, and we need only consider
$\mathbb {F}$
, and we need only consider
![]() $0<k<n$
and
$0<k<n$
and
![]() $3n<k<4n$
or
$3n<k<4n$
or
![]() $-n<k<n$
with
$-n<k<n$
with
![]() $\gcd (k,2n)=1$
.
$\gcd (k,2n)=1$
.
With this notation for elements of
![]() ${\mathsf {Gal}}(\mathbb {F}/\mathbb {Q})$
, let us see how
${\mathsf {Gal}}(\mathbb {F}/\mathbb {Q})$
, let us see how
![]() $\boldsymbol {\theta }_k:\zeta \mapsto \zeta ^k$
acts on the columns of matrix Q, i.e., on the rows of the character table. The character table for
$\boldsymbol {\theta }_k:\zeta \mapsto \zeta ^k$
acts on the columns of matrix Q, i.e., on the rows of the character table. The character table for
![]() ${\mathsf {Dic}}_n$
takes the following general form. Let
${\mathsf {Dic}}_n$
takes the following general form. Let
![]() $\kappa ^{(r)} = \zeta ^{2r}+\zeta ^{-2r}=2\cos \left ( \frac {\pi r}{n} \right )$
to save space.
$\kappa ^{(r)} = \zeta ^{2r}+\zeta ^{-2r}=2\cos \left ( \frac {\pi r}{n} \right )$
to save space.
 $$ \begin{align*} \begin{array}{c|ccccccc|rr} \mathcal{C} & \mathcal{C}_0 & \mathcal{C}_1 & \mathcal{C}_2 & \cdots & \mathcal{C}_k & \cdots & \mathcal{C}_n & \mathcal{C}_{n+1} & \mathcal{C}_{n+2} \\ |\mathcal{C}| & 1 & 2 & 2 & \cdots & 2 & \cdots & 1 & n & n \\ \hline \chi_{0} & 1 & 1 & 1 & \cdots & 1 & \cdots & 1 & 1 & 1 \\ \chi_{1} & 1 & 1 & 1 & \cdots & 1 & \cdots & 1 & -1 & -1 \\ \chi_{2} & 1 & \!\!\!\!-1 & 1 & \cdots & (-1)^k & \cdots & (-1)^n & i & -i \\ \chi_{3} & 1 & \!\!\!\!-1 & 1 & \cdots & (-1)^k & \cdots & (-1)^n & -i & i \\ \hline \psi_{1} & 2 & \kappa^{(1)} & \kappa^{(2)} & \cdots & \kappa^{(k)} & \cdots & \!\!\!\!-2 & 0 & 0 \\ \psi_{2} & 2 & \kappa^{(2)} & \kappa^{(4)} & \cdots & \kappa^{(2k)} & \cdots & 2 & 0 & 0 \\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots & \ddots & \vdots & \vdots & \vdots \\ \psi_{n-1} & 2 & \kappa^{(n-1)} & \kappa^{(2n-2)} & \cdots & \kappa^{(nk-k)} & \cdots & (-1)^{n-1}2 & 0 & 0 \\ \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{c|ccccccc|rr} \mathcal{C} & \mathcal{C}_0 & \mathcal{C}_1 & \mathcal{C}_2 & \cdots & \mathcal{C}_k & \cdots & \mathcal{C}_n & \mathcal{C}_{n+1} & \mathcal{C}_{n+2} \\ |\mathcal{C}| & 1 & 2 & 2 & \cdots & 2 & \cdots & 1 & n & n \\ \hline \chi_{0} & 1 & 1 & 1 & \cdots & 1 & \cdots & 1 & 1 & 1 \\ \chi_{1} & 1 & 1 & 1 & \cdots & 1 & \cdots & 1 & -1 & -1 \\ \chi_{2} & 1 & \!\!\!\!-1 & 1 & \cdots & (-1)^k & \cdots & (-1)^n & i & -i \\ \chi_{3} & 1 & \!\!\!\!-1 & 1 & \cdots & (-1)^k & \cdots & (-1)^n & -i & i \\ \hline \psi_{1} & 2 & \kappa^{(1)} & \kappa^{(2)} & \cdots & \kappa^{(k)} & \cdots & \!\!\!\!-2 & 0 & 0 \\ \psi_{2} & 2 & \kappa^{(2)} & \kappa^{(4)} & \cdots & \kappa^{(2k)} & \cdots & 2 & 0 & 0 \\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots & \ddots & \vdots & \vdots & \vdots \\ \psi_{n-1} & 2 & \kappa^{(n-1)} & \kappa^{(2n-2)} & \cdots & \kappa^{(nk-k)} & \cdots & (-1)^{n-1}2 & 0 & 0 \\ \end{array} \end{align*} $$
We compute
![]() $\boldsymbol {\theta }_k\left ( \kappa ^{(r)}\right ) = \boldsymbol {\theta }_k \left ( \zeta ^{2r}+\zeta ^{-2r}\right )= \zeta ^{2kr}+\zeta ^{-2kr}= \kappa ^{(kr)}$
when
$\boldsymbol {\theta }_k\left ( \kappa ^{(r)}\right ) = \boldsymbol {\theta }_k \left ( \zeta ^{2r}+\zeta ^{-2r}\right )= \zeta ^{2kr}+\zeta ^{-2kr}= \kappa ^{(kr)}$
when
![]() $kr<n$
. As this suggests,
$kr<n$
. As this suggests,
![]() $\boldsymbol {\theta }_k$
and
$\boldsymbol {\theta }_k$
and
![]() $\boldsymbol {\theta }_{-k}$
have the same action on
$\boldsymbol {\theta }_{-k}$
have the same action on
![]() $\kappa ^{(1)},\ldots ,\kappa ^{(n-1)}$
, but one fixes
$\kappa ^{(1)},\ldots ,\kappa ^{(n-1)}$
, but one fixes
![]() $\pm i,$
while the other swaps them, namely, the one among
$\pm i,$
while the other swaps them, namely, the one among
![]() $\pm k$
that is three modulo four.
$\pm k$
that is three modulo four.
If, for integers
![]() $k,m$
with
$k,m$
with
![]() $m>1$
, we write
$m>1$
, we write
![]() $k \ {\scriptscriptstyle \mathrm {{MOD}}} \ m = k'$
for that unique
$k \ {\scriptscriptstyle \mathrm {{MOD}}} \ m = k'$
for that unique
![]() $k' \equiv k \pmod {m}$
in the range
$k' \equiv k \pmod {m}$
in the range
![]() $-\frac {m}{2} < k' \le \frac {m}{2}$
, then we have
$-\frac {m}{2} < k' \le \frac {m}{2}$
, then we have
So each permutation
![]() $\theta _k \in \Sigma _{\mathbb {F}}$
defined by
$\theta _k \in \Sigma _{\mathbb {F}}$
defined by
![]() $E_\ell ^{\boldsymbol {\theta }_k} = E_{\ell ^{\theta _k}}$
fixes
$E_\ell ^{\boldsymbol {\theta }_k} = E_{\ell ^{\theta _k}}$
fixes
![]() $0$
and
$0$
and
![]() $1$
, fixes (resp., swaps)
$1$
, fixes (resp., swaps)
![]() $2$
and
$2$
and
![]() $3$
if
$3$
if
![]() $k\equiv 1\ \pmod {4}$
(resp.,
$k\equiv 1\ \pmod {4}$
(resp.,
![]() $k\equiv 3\ \pmod {4}$
), and for
$k\equiv 3\ \pmod {4}$
), and for
![]() $E_{j+3}$
corresponding to
$E_{j+3}$
corresponding to
![]() $\psi _{j}$
,
$\psi _{j}$
,
![]() $\theta _k(j+3)= |kj \ {\scriptscriptstyle \mathrm {{MOD}}} \ 2n|+3$
.
$\theta _k(j+3)= |kj \ {\scriptscriptstyle \mathrm {{MOD}}} \ 2n|+3$
.
We can simplify things significantly if we merely wish to work out the orbits of
![]() $\Sigma _{\mathbb {Q}}$
on
$\Sigma _{\mathbb {Q}}$
on
![]() $\{0,1,\ldots ,d\}$
. We have orbits
$\{0,1,\ldots ,d\}$
. We have orbits
![]() ${\mathcal Q}_0=\{0\}$
,
${\mathcal Q}_0=\{0\}$
,
![]() ${\mathcal Q}_1=\{1\}$
, and
${\mathcal Q}_1=\{1\}$
, and
![]() ${\mathcal Q}_2=\{2,3\}$
and the remaining orbits are precisely the orbits of the Galois group of the
${\mathcal Q}_2=\{2,3\}$
and the remaining orbits are precisely the orbits of the Galois group of the
![]() $2n$
-cycle acting on
$2n$
-cycle acting on
![]() $\{ \psi _1,\ldots , \psi _{n-1}\}$
as the transpose of the eigenmatrix of this (self-dual) scheme appears among the first
$\{ \psi _1,\ldots , \psi _{n-1}\}$
as the transpose of the eigenmatrix of this (self-dual) scheme appears among the first
![]() $n+1$
columns of
$n+1$
columns of
![]() ${\mathsf {T}}$
after deleting repeated rows.
${\mathsf {T}}$
after deleting repeated rows.
So our rational decomposition tool gives the following result in this case.
Corollary 6.1 Let
![]() $({\mathsf {Dic}}_n,{\mathcal R})$
be the conjugacy class scheme of the dicyclic group
$({\mathsf {Dic}}_n,{\mathcal R})$
be the conjugacy class scheme of the dicyclic group
![]() ${\mathsf {Dic}}_n$
with primitive idempotents indexed
${\mathsf {Dic}}_n$
with primitive idempotents indexed
![]() $\{E_{\chi _0}, E_{\chi _1},E_{\chi _2},E_{\chi _3},E_{\psi _1},\ldots ,E_{\psi _{n-1}}\}$
as above. Let
$\{E_{\chi _0}, E_{\chi _1},E_{\chi _2},E_{\chi _3},E_{\psi _1},\ldots ,E_{\psi _{n-1}}\}$
as above. Let
![]() $C\subset {\mathsf {Dic}}_n$
be a Delsarte T-design for
$C\subset {\mathsf {Dic}}_n$
be a Delsarte T-design for
![]() $T=T(C)$
. Then
$T=T(C)$
. Then
![]() $\chi _2\in T$
if and only if
$\chi _2\in T$
if and only if
![]() $\chi _3\in T$
and, for
$\chi _3\in T$
and, for
![]() $1\le r,k<n$
with
$1\le r,k<n$
with
![]() $\gcd (k,n)=1$
,
$\gcd (k,n)=1$
,
![]() $\psi _\ell \in T$
if and only if
$\psi _\ell \in T$
if and only if
![]() $\psi _{|k\ell \ {\scriptscriptstyle \mathrm {{MOD}}} \ 2n|}\in T$
for each
$\psi _{|k\ell \ {\scriptscriptstyle \mathrm {{MOD}}} \ 2n|}\in T$
for each
![]() $-n<k<n$
with
$-n<k<n$
with
![]() $\gcd (k,2n)=1$
.
$\gcd (k,2n)=1$
.
Note that, since
![]() $\gcd ( \ell ^{\theta _k},2n)$
is divisible by
$\gcd ( \ell ^{\theta _k},2n)$
is divisible by
![]() $\gcd (\ell ,2n)$
, the set
$\gcd (\ell ,2n)$
, the set
![]() $\psi _\ell , \psi _{2\ell },\psi _{3\ell },\ldots $
is a union of Galois orbits.
$\psi _\ell , \psi _{2\ell },\psi _{3\ell },\ldots $
is a union of Galois orbits.
Every subgroup of
![]() ${\mathsf {Dic}}_n$
is either cyclic or dicyclic. Since we are restricting to the case where n is odd, k is even if and only if
${\mathsf {Dic}}_n$
is either cyclic or dicyclic. Since we are restricting to the case where n is odd, k is even if and only if
![]() $2n/k$
is odd. For
$2n/k$
is odd. For
![]() ${H=\langle x^k\rangle }$
, we have
${H=\langle x^k\rangle }$
, we have
![]() $|H|= 2n/k$
and
$|H|= 2n/k$
and
![]() $H \unlhd {\mathsf {Dic}}_n$
with inner distribution of the form
$H \unlhd {\mathsf {Dic}}_n$
with inner distribution of the form
![]() ${a = [1,0,\ldots ,0,2,0,\ldots ,0,2,0,\ldots \ldots , 0,0],}$
where
${a = [1,0,\ldots ,0,2,0,\ldots ,0,2,0,\ldots \ldots , 0,0],}$
where
![]() $a_0=1$
,
$a_0=1$
,
![]() $a_i=2$
if
$a_i=2$
if
![]() $k|i$
and
$k|i$
and
![]() $i<n$
, and
$i<n$
, and
![]() $a_n=0$
or
$a_n=0$
or
![]() $1$
depending on whether k is even or odd, respectively. (The remaining entries of a are zero.) The dual distribution
$1$
depending on whether k is even or odd, respectively. (The remaining entries of a are zero.) The dual distribution
![]() $b=aQ$
has entries naturally indexed by
$b=aQ$
has entries naturally indexed by
![]() $\chi _0,\chi _1,\chi _2,\chi _3,\psi _1,\ldots ,\psi _{n-1}$
with values
$\chi _0,\chi _1,\chi _2,\chi _3,\psi _1,\ldots ,\psi _{n-1}$
with values
 $$ \begin{align*} \begin{array}{|c|cc|cc|c|l|} \hline \ell=2n/k & \chi_0,& \chi_1 & \chi_2,&\chi_3 & \psi_{\ell i} (1\le i \le \lfloor (k-1)/2 \rfloor) & \psi_j (\text{otherwise}) \\ \hline |H|=\ell \text{ even} & \ell & \ell & 0 & 0 & 4\ell & 0 \\ |H|=\ell \ \text{ odd} & \ell & \ell & \ell & \ell & 4\ell & 0 \\ \hline \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{|c|cc|cc|c|l|} \hline \ell=2n/k & \chi_0,& \chi_1 & \chi_2,&\chi_3 & \psi_{\ell i} (1\le i \le \lfloor (k-1)/2 \rfloor) & \psi_j (\text{otherwise}) \\ \hline |H|=\ell \text{ even} & \ell & \ell & 0 & 0 & 4\ell & 0 \\ |H|=\ell \ \text{ odd} & \ell & \ell & \ell & \ell & 4\ell & 0 \\ \hline \end{array} \end{align*} $$
So the idempotents outside
![]() $T(H)$
are either
$T(H)$
are either
![]() $\{E_{\chi _0}, E_{\chi _1},E_{\psi _\ell },E_{\psi _{2\ell }},E_{\psi _{3\ell }},\ldots \}$
or
$\{E_{\chi _0}, E_{\chi _1},E_{\psi _\ell },E_{\psi _{2\ell }},E_{\psi _{3\ell }},\ldots \}$
or
![]() $\{E_{\chi _0}, E_{\chi _1}$
,
$\{E_{\chi _0}, E_{\chi _1}$
,
![]() $E_{\chi _2}$
,
$E_{\chi _2}$
,
![]() $E_{\chi _3},E_{\psi _\ell },E_{\psi _{2\ell }},E_{\psi _{3\ell }},\ldots \}$
.
$E_{\chi _3},E_{\psi _\ell },E_{\psi _{2\ell }},E_{\psi _{3\ell }},\ldots \}$
.
The case where H is dicyclic is almost identical. Here, the cyclic subgroup
![]() $H \cap \langle x\rangle $
behaves as above and
$H \cap \langle x\rangle $
behaves as above and
![]() $H \setminus \langle x\rangle $
contributes either
$H \setminus \langle x\rangle $
contributes either
![]() $a_{d-1}=|H|/2=2n/k$
when k is even or
$a_{d-1}=|H|/2=2n/k$
when k is even or
![]() $a_{d-1}=a_d=|H|/4=n/k$
when k is odd. In the first case, the first few entries of the MacWilliams transform are
$a_{d-1}=a_d=|H|/4=n/k$
when k is odd. In the first case, the first few entries of the MacWilliams transform are
![]() $aQ = \left [ \begin {array}{@{}ccccc@{}} \frac {4n}{k} & 0 & 0 & 0 & \cdots \end {array} \right ]$
and, in the second case,
$aQ = \left [ \begin {array}{@{}ccccc@{}} \frac {4n}{k} & 0 & 0 & 0 & \cdots \end {array} \right ]$
and, in the second case,
![]() $aQ = \left [ \begin {array}{@{}ccccc@{}} \frac {4n}{k} & 0 & \frac {4n}{k} & \frac {4n}{k} & \cdots \end {array} \right ]$
; in both cases, the entries of
$aQ = \left [ \begin {array}{@{}ccccc@{}} \frac {4n}{k} & 0 & \frac {4n}{k} & \frac {4n}{k} & \cdots \end {array} \right ]$
; in both cases, the entries of
![]() $aQ$
indexed by
$aQ$
indexed by
![]() $\psi _1,\ldots ,\psi _{n-1}$
are exactly as in the table above for the cyclic subgroups.
$\psi _1,\ldots ,\psi _{n-1}$
are exactly as in the table above for the cyclic subgroups.
Acknowledgments
The major part of this work was carried out while W.J.M. was visiting the University of Canterbury generously supported by an Erskine Fellowship; he thanks the School of Mathematics and Statistics, University of Canterbury, for their hospitality during this stay. The authors thank the referee for their careful review of the manuscript. The second author thanks Sycamore Herlihy for helpful conversations.
Note added in proof. In the final days of editing, the authors learned of the preprint [Reference Godsil and Zhang15] of Godsil and Zhang which also addresses fusions of group schemes in the context of continuous time quantum walks on Cayley graphs. Whereas the present article considers the span of the idempotents in
![]() $\mathbb {A} \cap \mathsf {Mat}_X(\mathbb {K})$
, the approach in [Reference Godsil and Zhang15] considers the matrices in
$\mathbb {A} \cap \mathsf {Mat}_X(\mathbb {K})$
, the approach in [Reference Godsil and Zhang15] considers the matrices in
![]() $\mathbb {A} \cap \mathsf {Mat}_X(\mathbb {K})$
whose eigenvalues also lie in
$\mathbb {A} \cap \mathsf {Mat}_X(\mathbb {K})$
whose eigenvalues also lie in
![]() $\mathbb {K}$
.
$\mathbb {K}$
.




