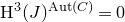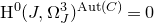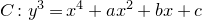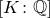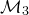1. Introduction
Let k be an algebraically closed field and C a smooth, projective, and connected curve over k of genus
![]() $g \geqslant 2$
with Jacobian variety J. Let e be a degree-1 divisor of C and let
$g \geqslant 2$
with Jacobian variety J. Let e be a degree-1 divisor of C and let
![]() $\iota_e \colon C \hookrightarrow J$
be the Abel–Jacobi map based at e. We study the torsion behaviour of the Ceresa cycle
$\iota_e \colon C \hookrightarrow J$
be the Abel–Jacobi map based at e. We study the torsion behaviour of the Ceresa cycle
in the Chow group modulo rational equivalence. If
![]() $\kappa_{C,e}$
is torsion, then
$\kappa_{C,e}$
is torsion, then
![]() $(2g-2)e= K_C$
in
$(2g-2)e= K_C$
in
![]() $\mathrm{CH}_0(C)\otimes \mathrm{\mathbb{Q}}$
, where
$\mathrm{CH}_0(C)\otimes \mathrm{\mathbb{Q}}$
, where
![]() $K_C$
is the canonical divisor class. Moreover, if
$K_C$
is the canonical divisor class. Moreover, if
![]() $(2g-2)e$
is canonical, then the image of
$(2g-2)e$
is canonical, then the image of
![]() $\kappa_{C,e}$
in
$\kappa_{C,e}$
in
![]() $\mathrm{CH}_1(J)\otimes{\mathrm{\mathbb{Q}}}$
is independent of e and we denote it by
$\mathrm{CH}_1(J)\otimes{\mathrm{\mathbb{Q}}}$
is independent of e and we denote it by
![]() $\kappa(C)$
; see § 2.7 for these claims. Thus, the class
$\kappa(C)$
; see § 2.7 for these claims. Thus, the class
![]() $\kappa(C)$
vanishes if and only if
$\kappa(C)$
vanishes if and only if
![]() $\kappa_{C,e}$
is torsion for some degree-1 divisor e.
$\kappa_{C,e}$
is torsion for some degree-1 divisor e.
We also consider the image
![]() $\bar{\kappa}(C)$
of
$\bar{\kappa}(C)$
of
![]() $\kappa(C)$
in the Griffiths group
$\kappa(C)$
in the Griffiths group
![]() $\mathrm{Gr}_1(J)\otimes \mathrm{\mathbb{Q}}$
of homologically trivial 1-cycles modulo algebraic equivalence. When
$\mathrm{Gr}_1(J)\otimes \mathrm{\mathbb{Q}}$
of homologically trivial 1-cycles modulo algebraic equivalence. When
![]() $g = 2$
, or more generally when C is hyperelliptic, it is easy to see that
$g = 2$
, or more generally when C is hyperelliptic, it is easy to see that
![]() $\kappa(C) = 0$
. On the other hand, Ceresa famously showed that
$\kappa(C) = 0$
. On the other hand, Ceresa famously showed that
![]() $\bar{\kappa}(C) \neq 0$
for a very general curve C over C of genus
$\bar{\kappa}(C) \neq 0$
for a very general curve C over C of genus
![]() $g \geqslant 3$
[Reference CeresaCer83].
$g \geqslant 3$
[Reference CeresaCer83].
The vanishing of the Ceresa cycle is of interest for various reasons. For example,
![]() $\kappa(C) = 0$
if and only if the Chow motive
$\kappa(C) = 0$
if and only if the Chow motive
![]() ${\frak{h}}(C)$
has a multiplicative Chow–Künneth decomposition (by [Reference Fu, Laterveer and VialFLV21, Proposition 3.1] and Proposition 11). Moreover,
${\frak{h}}(C)$
has a multiplicative Chow–Künneth decomposition (by [Reference Fu, Laterveer and VialFLV21, Proposition 3.1] and Proposition 11). Moreover,
![]() $\bar{\kappa}(C)=0$
if and only if the tautological subring modulo algebraic equivalence is generated by a theta divisor (by [Reference BeauvilleBea04, Corollary 3.4]), in which case Poincaré’s formula
$\bar{\kappa}(C)=0$
if and only if the tautological subring modulo algebraic equivalence is generated by a theta divisor (by [Reference BeauvilleBea04, Corollary 3.4]), in which case Poincaré’s formula
![]() $[C] = {\Theta^{g-1}}/{(g-1)!}$
holds modulo algebraic equivalence. More generally, the Ceresa cycle over
$[C] = {\Theta^{g-1}}/{(g-1)!}$
holds modulo algebraic equivalence. More generally, the Ceresa cycle over
![]() $\mathcal{M}_g$
serves as a testing ground for the study of homologically trivial algebraic cycles in codimension greater than 1.
$\mathcal{M}_g$
serves as a testing ground for the study of homologically trivial algebraic cycles in codimension greater than 1.
1.1 Vanishing criteria
We prove cohomological vanishing criteria for Ceresa cycles of curves with non-trivial automorphisms. Let
![]() $\mathrm{H}^*(-)$
be a Weil cohomology functor, such as
$\mathrm{H}^*(-)$
be a Weil cohomology functor, such as
![]() $\ell$
-adic cohomology with
$\ell$
-adic cohomology with
![]() $\ell \neq \mathrm{char \hspace{1mm}}(k)$
or singular cohomology when
$\ell \neq \mathrm{char \hspace{1mm}}(k)$
or singular cohomology when
![]() $k = \mathrm{\mathbb{C}}$
. Note that the finite group
$k = \mathrm{\mathbb{C}}$
. Note that the finite group
![]() $\mathrm{Aut}(C)$
acts on
$\mathrm{Aut}(C)$
acts on
![]() $\mathrm{H}^*(J)$
, by functoriality. Cupping with the principal polarization gives an injection
$\mathrm{H}^*(J)$
, by functoriality. Cupping with the principal polarization gives an injection
![]() $\mathrm{H}^1(J)(-1) \hookrightarrow \mathrm{H}^3(J)$
, allowing us to define the primitive cohomology
$\mathrm{H}^1(J)(-1) \hookrightarrow \mathrm{H}^3(J)$
, allowing us to define the primitive cohomology
![]() $\mathrm{H}^3(J)_{\mathrm{prim}} := \mathrm{H}^3(J)/\mathrm{H}^1(J)(-1)$
.
$\mathrm{H}^3(J)_{\mathrm{prim}} := \mathrm{H}^3(J)/\mathrm{H}^1(J)(-1)$
.
Theorem A.
If
![]() $\mathrm{H}^3(J)_{\mathrm{prim}}^{\mathrm{Aut}(C)} = 0$
, then
$\mathrm{H}^3(J)_{\mathrm{prim}}^{\mathrm{Aut}(C)} = 0$
, then
![]() $\kappa(C) = 0$
.
$\kappa(C) = 0$
.
This improves on a recent result of Qiu and Zhang stating that if
![]() $(\mathrm{H}^1(C)^{\otimes 3})^{\mathrm{Aut}(C)} = 0$
, then
$(\mathrm{H}^1(C)^{\otimes 3})^{\mathrm{Aut}(C)} = 0$
, then
![]() $\kappa(C) = 0$
[Reference Qiu and ZhangQZ24].Footnote
1
By contrast, Theorem A requires only the weaker condition that the subrepresentation
$\kappa(C) = 0$
[Reference Qiu and ZhangQZ24].Footnote
1
By contrast, Theorem A requires only the weaker condition that the subrepresentation
![]() $\mathrm{H}^3(J)_{\mathrm{prim}} \subset \mathrm{H}^3(J) \simeq \bigwedge^3 \mathrm{H}^1(C) \subset \mathrm{H}^1(C)^{\otimes 3}$
has no non-trivial
$\mathrm{H}^3(J)_{\mathrm{prim}} \subset \mathrm{H}^3(J) \simeq \bigwedge^3 \mathrm{H}^1(C) \subset \mathrm{H}^1(C)^{\otimes 3}$
has no non-trivial
![]() $\mathrm{Aut}(C)$
-fixed points. If the quotient
$\mathrm{Aut}(C)$
-fixed points. If the quotient
![]() $C/\mathrm{Aut}(C)$
has genus 0, then our hypothesis is equivalent to
$C/\mathrm{Aut}(C)$
has genus 0, then our hypothesis is equivalent to
![]() $\mathrm{H}^3(J)^{\mathrm{Aut}(C)} = 0$
.
$\mathrm{H}^3(J)^{\mathrm{Aut}(C)} = 0$
.
Our proof of Theorem A is inspired by Beauville’s proof that for the curve
![]() $y^3 = x^4 + x$
, the image of
$y^3 = x^4 + x$
, the image of
![]() $\kappa(C)$
under the complex Abel–Jacobi map vanishes [Reference BeauvilleBea21]. To achieve a vanishing result in the Chow group, we work directly with the rational Chow motive
$\kappa(C)$
under the complex Abel–Jacobi map vanishes [Reference BeauvilleBea21]. To achieve a vanishing result in the Chow group, we work directly with the rational Chow motive
![]() ${\frak{h}}^3(J)$
and make crucial use of the finite-dimensionality results of Kimura [Reference KimuraKim05].
${\frak{h}}^3(J)$
and make crucial use of the finite-dimensionality results of Kimura [Reference KimuraKim05].
Our second result is a vanishing criterion for
![]() $\overline{\kappa}(C)$
; however, the result is conditional on the Hodge conjecture. In particular, we assume for the rest of this introduction that k has characteristic 0.
$\overline{\kappa}(C)$
; however, the result is conditional on the Hodge conjecture. In particular, we assume for the rest of this introduction that k has characteristic 0.
Theorem B.
Assume the Hodge conjecture for abelian varieties. If
![]() $\mathrm{H}^0(J, \Omega_J^3)^{\mathrm{Aut}(C)} = 0$
, then
$\mathrm{H}^0(J, \Omega_J^3)^{\mathrm{Aut}(C)} = 0$
, then
![]() $\bar{\kappa}(C) = 0$
.
$\bar{\kappa}(C) = 0$
.
More precisely, we require the Hodge conjecture for
![]() $J\times A$
, where A is the abelian variety described in Proposition 3.3. Note that
$J\times A$
, where A is the abelian variety described in Proposition 3.3. Note that
![]() $\mathrm{H}^0(J, \Omega_J^3) \simeq \bigwedge^3\mathrm{H}^0(C, \Omega_C^1)$
, so the conditions of Theorems A and B both depend only on the abstract representation
$\mathrm{H}^0(J, \Omega_J^3) \simeq \bigwedge^3\mathrm{H}^0(C, \Omega_C^1)$
, so the conditions of Theorems A and B both depend only on the abstract representation
![]() $(G,V) = (\mathrm{Aut}(C), \mathrm{H}^0(C, \Omega_C^1))$
.
$(G,V) = (\mathrm{Aut}(C), \mathrm{H}^0(C, \Omega_C^1))$
.
The proof of Theorem B is in the same spirit as that of Theorem A. The Hodge conjecture is used to show that the motive
![]() ${\frak{h}}^3(J)^{\mathrm{Aut}(C)}$
is isomorphic to
${\frak{h}}^3(J)^{\mathrm{Aut}(C)}$
is isomorphic to
![]() ${\frak{h}}^1(A)(-1)$
, from which the algebraic triviality of
${\frak{h}}^1(A)(-1)$
, from which the algebraic triviality of
![]() $\kappa(C)$
follows.
$\kappa(C)$
follows.
1.2 Picard curves
The condition
![]() $\mathrm{H}^3(J)_{\mathrm{prim}}^{\mathrm{Aut}(C)} = 0$
in Theorem A is only rarely satisfied; for example, it holds for exactly two plane quartic curves over C (see Theorem E below). The condition
$\mathrm{H}^3(J)_{\mathrm{prim}}^{\mathrm{Aut}(C)} = 0$
in Theorem A is only rarely satisfied; for example, it holds for exactly two plane quartic curves over C (see Theorem E below). The condition
![]() $\mathrm{H}^0(J, \Omega_J^3)^{\mathrm{Aut}(C)}=0$
of Theorem B is satisfied more often; for example, it holds for all Picard curves
$\mathrm{H}^0(J, \Omega_J^3)^{\mathrm{Aut}(C)}=0$
of Theorem B is satisfied more often; for example, it holds for all Picard curves
![]() $y^3 = x^4 + ax^2 + bx + c$
. 4-fold is algebraic. Fortunately, Schoen has proved the Hodge conjecture in our specific situation [Reference SchoenSch98]. (See also recent work of Markman [Reference MarkmanMar23, Reference MarkmanMar25].) This leads to an unconditional proof of the vanishing of
$y^3 = x^4 + ax^2 + bx + c$
. 4-fold is algebraic. Fortunately, Schoen has proved the Hodge conjecture in our specific situation [Reference SchoenSch98]. (See also recent work of Markman [Reference MarkmanMar23, Reference MarkmanMar25].) This leads to an unconditional proof of the vanishing of
![]() $\bar{\kappa}(C)$
. By further analysing
$\bar{\kappa}(C)$
. By further analysing
![]() $\kappa(C)$
, we prove the following precise characterization of the vanishing of
$\kappa(C)$
, we prove the following precise characterization of the vanishing of
![]() $\kappa(C)$
in the Picard family.
$\kappa(C)$
in the Picard family.
Theorem C. thm: Picard main Let
![]() $C_f$
be a smooth projective Picard curve with model
$C_f$
be a smooth projective Picard curve with model
for some
![]() $a,b,c\in k$
. Consider the point
$a,b,c\in k$
. Consider the point
![]() $P_f= (a^2+12c,72ac-2a^3-27b^2)$
on the elliptic curve
$P_f= (a^2+12c,72ac-2a^3-27b^2)$
on the elliptic curve
Then
![]() $\bar{\kappa}(C_f)=0$
, and
$\bar{\kappa}(C_f)=0$
, and
![]() $\kappa(C_f)=0$
if and only if
$\kappa(C_f)=0$
if and only if
![]() $P_f \in E_f(k)$
is torsion.
$P_f \in E_f(k)$
is torsion.
Here,
![]() $\mathrm{disc}(f)$
is the discriminant of f and the coordinates of
$\mathrm{disc}(f)$
is the discriminant of f and the coordinates of
![]() $P_f$
are the usual I- and J-invariants of the binary quartic form
$P_f$
are the usual I- and J-invariants of the binary quartic form
![]() $z^4 f(x/z)$
; see § 4.1. The fact that
$z^4 f(x/z)$
; see § 4.1. The fact that
![]() $P_f$
defines a point on
$P_f$
defines a point on
![]() $E_f$
follows from a classical relation between the invariants of a binary quartic. Picard curves have a unique point
$E_f$
follows from a classical relation between the invariants of a binary quartic. Picard curves have a unique point
![]() $\infty$
at infinity, for which
$\infty$
at infinity, for which
![]() $(2g-2)\infty = 4\infty$
is canonical. For a more precise version of Theorem C relating the torsion orders of
$(2g-2)\infty = 4\infty$
is canonical. For a more precise version of Theorem C relating the torsion orders of
![]() $\kappa_{C_f,\infty}$
and
$\kappa_{C_f,\infty}$
and
![]() $P_f$
, see § 4.2.
$P_f$
, see § 4.2.
Theorem C generalizes the results of [Reference Laga and ShnidmanLS25] concerning bielliptic Picard curves, that is, those with
![]() $b=0$
in (1.2). There we exploited the explicit geometry of the bielliptic cover to characterize the vanishing locus of
$b=0$
in (1.2). There we exploited the explicit geometry of the bielliptic cover to characterize the vanishing locus of
![]() $\kappa(C)$
. Here we must proceed more indirectly: using Schoen’s work on the Hodge conjecture, we first show that the vanishing of
$\kappa(C)$
. Here we must proceed more indirectly: using Schoen’s work on the Hodge conjecture, we first show that the vanishing of
![]() $\kappa(C)$
is equivalent to the vanishing of its Abel–Jacobi image in the intermediate Jacobian. Using the Shioda–Tate formula and considerations of isotrivial families of elliptic curves, we are able to bootstrap the calculations of [Reference Laga and ShnidmanLS25] to determine the Abel–Jacobi image up to a multiple and obtain the characterization of Theorem C.
$\kappa(C)$
is equivalent to the vanishing of its Abel–Jacobi image in the intermediate Jacobian. Using the Shioda–Tate formula and considerations of isotrivial families of elliptic curves, we are able to bootstrap the calculations of [Reference Laga and ShnidmanLS25] to determine the Abel–Jacobi image up to a multiple and obtain the characterization of Theorem C.
In § 3, we give several examples of higher-genus families of curves
![]() $\mathcal{C} \rightarrow B$
for which Theorem B applies. It would be interesting to completely characterize the vanishing of
$\mathcal{C} \rightarrow B$
for which Theorem B applies. It would be interesting to completely characterize the vanishing of
![]() $\kappa(C)$
in these families as well, and to find more such families. The general proof strategy would follow that of Theorem C: using the Hodge conjecture, one shows that the vanishing of
$\kappa(C)$
in these families as well, and to find more such families. The general proof strategy would follow that of Theorem C: using the Hodge conjecture, one shows that the vanishing of
![]() $\kappa(\mathcal{C}_b)$
is equivalent to the vanishing of
$\kappa(\mathcal{C}_b)$
is equivalent to the vanishing of
![]() $\sigma(b)$
, where
$\sigma(b)$
, where
![]() $\sigma$
is a section of a certain abelian scheme
$\sigma$
is a section of a certain abelian scheme
![]() $\mathcal{A} \rightarrow B$
. (The analytification of
$\mathcal{A} \rightarrow B$
. (The analytification of
![]() $\sigma$
is the normal function associated to the Ceresa cycle over B, which lands in the
$\sigma$
is the normal function associated to the Ceresa cycle over B, which lands in the
![]() $\mathrm{Aut}(C)$
-fixed points of the intermediate Jacobian.) One then tries to identify
$\mathrm{Aut}(C)$
-fixed points of the intermediate Jacobian.) One then tries to identify
![]() $\mathcal{A} \rightarrow B$
and
$\mathcal{A} \rightarrow B$
and
![]() $\sigma$
explicitly.
$\sigma$
explicitly.
1.3 Vanishing loci in genus 3
Let
![]() $\mathcal{M}_g$
be the coarse moduli space of genus-g curves C, seen as a variety over Q. Let
$\mathcal{M}_g$
be the coarse moduli space of genus-g curves C, seen as a variety over Q. Let
![]() $V_g^{\mathrm{rat}}\subset \mathcal{M}_g$
be the locus of curves with
$V_g^{\mathrm{rat}}\subset \mathcal{M}_g$
be the locus of curves with
![]() $\kappa(C) = 0$
. Let
$\kappa(C) = 0$
. Let
![]() $V_g^{\mathrm{alg}}\subset \mathcal{M}_g$
be the analogous subset for
$V_g^{\mathrm{alg}}\subset \mathcal{M}_g$
be the analogous subset for
![]() $\bar{\kappa}(C)$
. The subsets
$\bar{\kappa}(C)$
. The subsets
![]() $V_g^{\mathrm{rat}}$
and
$V_g^{\mathrm{rat}}$
and
![]() $V_g^{\mathrm{alg}}$
are each a countable union of closed algebraic subvarieties (Lemma 5.1). We have
$V_g^{\mathrm{alg}}$
are each a countable union of closed algebraic subvarieties (Lemma 5.1). We have
![]() $V_g^{\mathrm{rat}}\subset V_g^{\mathrm{alg}}$
, and Ceresa’s result [Reference CeresaCer83] shows that
$V_g^{\mathrm{rat}}\subset V_g^{\mathrm{alg}}$
, and Ceresa’s result [Reference CeresaCer83] shows that
![]() $V_g^{\mathrm{alg}} \neq \mathcal{M}_g$
for all
$V_g^{\mathrm{alg}} \neq \mathcal{M}_g$
for all
![]() $g\geqslant 3$
. What can be said about the irreducible components of
$g\geqslant 3$
. What can be said about the irreducible components of
![]() $V_g^{\mathrm{rat}}$
and
$V_g^{\mathrm{rat}}$
and
![]() $V_g^{\mathrm{alg}}$
and their dimensions? For a fixed g, are there only finitely many components? Collino and Pirola showed that
$V_g^{\mathrm{alg}}$
and their dimensions? For a fixed g, are there only finitely many components? Collino and Pirola showed that
![]() $V_3^{\mathrm{rat}}$
does not contain subvarieties of dimension at least 4 that are not themselves contained in the hyperelliptic locus [Reference Collino and PirolaCP95, Corollary 4.3.4]. On the other hand, Theorem C shows that
$V_3^{\mathrm{rat}}$
does not contain subvarieties of dimension at least 4 that are not themselves contained in the hyperelliptic locus [Reference Collino and PirolaCP95, Corollary 4.3.4]. On the other hand, Theorem C shows that
![]() $V_3^{\mathrm{alg}}$
contains the two-dimensional Picard locus. Turning to
$V_3^{\mathrm{alg}}$
contains the two-dimensional Picard locus. Turning to
![]() $V_3^{\mathrm{rat}}$
, we answer several open question about its geometry and arithmetic by analysing the torsion locus of the section
$V_3^{\mathrm{rat}}$
, we answer several open question about its geometry and arithmetic by analysing the torsion locus of the section
![]() $P_f$
of
$P_f$
of
![]() $E_f$
.
$E_f$
.
Theorem D.
Let
![]() $X\subset \mathcal{M}_3$
be the Picard locus.
$X\subset \mathcal{M}_3$
be the Picard locus.
-
(i) The base change
 $(X\cap V_3^{\mathrm{rat}})\times_{\mathrm{\mathbb{Q}}} \mathbb{C}$
is a countably infinite disjoint union of rational curves. In particular, there exist one-parameter families of plane quartic curves in
$(X\cap V_3^{\mathrm{rat}})\times_{\mathrm{\mathbb{Q}}} \mathbb{C}$
is a countably infinite disjoint union of rational curves. In particular, there exist one-parameter families of plane quartic curves in
 $V_3^{\mathrm{rat}}$
, and
$V_3^{\mathrm{rat}}$
, and
 $V_3^{\mathrm{rat}}$
contains infinitely many positive-dimensional components.
$V_3^{\mathrm{rat}}$
contains infinitely many positive-dimensional components. -
(ii) If K is a number field and
 $C \in (X \cap V_3^{\mathrm{rat}})(K)$
, then the order of
$C \in (X \cap V_3^{\mathrm{rat}})(K)$
, then the order of
 $\kappa_{C,\infty}$
in
$\kappa_{C,\infty}$
in
 $\mathrm{CH}_1(J)$
is bounded above by a quantity depending only on
$\mathrm{CH}_1(J)$
is bounded above by a quantity depending only on
 $[K\colon \mathrm{\mathbb{Q}}]$
.
$[K\colon \mathrm{\mathbb{Q}}]$
.
An example of a one-parameter family as in (i) is the family
![]() $C_t \colon y^3 = x^4 -12x^2 + tx -12$
. Note that we have previously shown in [Reference Laga and ShnidmanLS25, Theorem 1.3] that the torsion orders of the classes
$C_t \colon y^3 = x^4 -12x^2 + tx -12$
. Note that we have previously shown in [Reference Laga and ShnidmanLS25, Theorem 1.3] that the torsion orders of the classes
![]() $\kappa_{C,e}$
, where C has genus 3 and
$\kappa_{C,e}$
, where C has genus 3 and
![]() $4e= K_C$
, are unbounded.
$4e= K_C$
, are unbounded.
Recall that there is a stratification of the non-hyperelliptic locus of
![]() $\mathcal{M}_3$
by locally closed subvarieties
$\mathcal{M}_3$
by locally closed subvarieties
![]() $X_G$
, indexed by certain finite groups G, with the property that a non-hyperelliptic curve
$X_G$
, indexed by certain finite groups G, with the property that a non-hyperelliptic curve
![]() $[C]\in \mathcal{M}_3(\mathrm{\mathbb{C}})$
lies in
$[C]\in \mathcal{M}_3(\mathrm{\mathbb{C}})$
lies in
![]() $X_G$
if and only if
$X_G$
if and only if
![]() $\mathrm{Aut}(C)\simeq G$
. It turns out that the isomorphism class of the
$\mathrm{Aut}(C)\simeq G$
. It turns out that the isomorphism class of the
![]() $\mathrm{Aut}(C)$
-representation
$\mathrm{Aut}(C)$
-representation
![]() $\mathrm{H}^0(C, \Omega_C^1)$
does not depend on the choice of curve [C] in
$\mathrm{H}^0(C, \Omega_C^1)$
does not depend on the choice of curve [C] in
![]() $X_G(\mathrm{\mathbb{C}})$
. Our final theorem determines exactly which
$X_G(\mathrm{\mathbb{C}})$
. Our final theorem determines exactly which
![]() $X_G$
are contained in
$X_G$
are contained in
![]() $V_3^{\mathrm{rat}}$
or
$V_3^{\mathrm{rat}}$
or
![]() $V_3^{\mathrm{alg}}$
.
$V_3^{\mathrm{alg}}$
.
Theorem E. Let G be a finite group isomorphic to the automorphism group of a plane quartic. Then
![]() $X_G\subset V_3^{\mathrm{rat}}$
if and only if
$X_G\subset V_3^{\mathrm{rat}}$
if and only if
![]() $G=C_9$
or
$G=C_9$
or
![]() $G_{48}$
, and
$G_{48}$
, and
![]() $X_G\subset V_3^{\mathrm{alg}}$
if and only if
$X_G\subset V_3^{\mathrm{alg}}$
if and only if
![]() $X_G$
is contained in the Picard locus, in other words if and only if
$X_G$
is contained in the Picard locus, in other words if and only if
![]() $G= C_3,C_6,C_9$
or
$G= C_3,C_6,C_9$
or
![]() $G_{48}$
.
$G_{48}$
.
Here,
![]() $G_{48}$
is the group with GAP label (48,33). The strata
$G_{48}$
is the group with GAP label (48,33). The strata
![]() $X_{C_{9}}$
and
$X_{C_{9}}$
and
![]() $X_{G_{48}}$
are single closed points, represented by the curves
$X_{G_{48}}$
are single closed points, represented by the curves
![]() $y^3= x^4+x$
and
$y^3= x^4+x$
and
![]() $y^3 = x^4+1$
, respectively.
$y^3 = x^4+1$
, respectively.
Theorem E shows that
![]() $X_G\subset V_3^{\mathrm{rat}}$
if and only if
$X_G\subset V_3^{\mathrm{rat}}$
if and only if
![]() $\mathrm{H}^3(J)^G=0$
for every (equivalently, some) curve in
$\mathrm{H}^3(J)^G=0$
for every (equivalently, some) curve in
![]() $X_G$
, and that
$X_G$
, and that
![]() $X_G\subset V_3^{\mathrm{alg}}$
if and only if
$X_G\subset V_3^{\mathrm{alg}}$
if and only if
![]() $\mathrm{H}^0(J, \Omega_J^3)^G=0$
for every curve in
$\mathrm{H}^0(J, \Omega_J^3)^G=0$
for every curve in
![]() $X_G$
. Thus, for
$X_G$
. Thus, for
![]() $g = 3$
, the criteria of Theorems A and B exactly single out the strata
$g = 3$
, the criteria of Theorems A and B exactly single out the strata
![]() $X_G$
where
$X_G$
where
![]() $\kappa(C)$
or
$\kappa(C)$
or
![]() $\bar{\kappa}(C)$
identically vanishes. Does this continue to hold in higher genera? Are there non-hyperelliptic curves of arbitrarily large genus for which Theorem A or B applies?
$\bar{\kappa}(C)$
identically vanishes. Does this continue to hold in higher genera? Are there non-hyperelliptic curves of arbitrarily large genus for which Theorem A or B applies?
We also use Theorem B to find the first examples of positive-dimensional components of
![]() $V_g^{\mathrm{alg}}$
with generic point satisfying
$V_g^{\mathrm{alg}}$
with generic point satisfying
![]() $\mathrm{Aut}(C) = \{1\}$
.Footnote
2
This uses the following fact: if C dominates another curve D, then
$\mathrm{Aut}(C) = \{1\}$
.Footnote
2
This uses the following fact: if C dominates another curve D, then
![]() $\overline{\kappa}(C)=0$
implies
$\overline{\kappa}(C)=0$
implies
![]() $\overline{\kappa}(D) = 0$
. For example, the genus 6 family
$\overline{\kappa}(D) = 0$
. For example, the genus 6 family
admits a
![]() $D_9$
-action and lies in
$D_9$
-action and lies in
![]() $V_6^{\mathrm{alg}}$
(conditional on the Hodge conjecture). The quotient by the involution
$V_6^{\mathrm{alg}}$
(conditional on the Hodge conjecture). The quotient by the involution
![]() $(x,y) \mapsto (-x,y^{-1})$
is the genus-3 family
$(x,y) \mapsto (-x,y^{-1})$
is the genus-3 family
where
![]() $u = (t-1)/(t+1)$
, which lies in
$u = (t-1)/(t+1)$
, which lies in
![]() $V_3^{\mathrm{alg}}$
by the fact above, and satisfies
$V_3^{\mathrm{alg}}$
by the fact above, and satisfies
![]() $\mathrm{Aut}(X_u) = \{1\}$
generically. A similar construction gives a one-dimensional component of
$\mathrm{Aut}(X_u) = \{1\}$
generically. A similar construction gives a one-dimensional component of
![]() $V_4^{\mathrm{alg}}$
(again conditional on the Hodge conjecture) with trivial generic automorphism group; see Theorem 3.12. Thus, even in genus 3, the implications of Theorems A and B are not yet fully understood, since it is hard to know which curves admit high-genus covers that satisfy our vanishing criteria. We should remark that, as far as we know, there are no known examples of curves C with
$V_4^{\mathrm{alg}}$
(again conditional on the Hodge conjecture) with trivial generic automorphism group; see Theorem 3.12. Thus, even in genus 3, the implications of Theorems A and B are not yet fully understood, since it is hard to know which curves admit high-genus covers that satisfy our vanishing criteria. We should remark that, as far as we know, there are no known examples of curves C with
![]() $\overline{\kappa}(C) = 0$
,
$\overline{\kappa}(C) = 0$
,
![]() $\mathrm{Aut}(C) = \{1\}$
, and
$\mathrm{Aut}(C) = \{1\}$
, and
![]() $\mathrm{End}(J) = \mathrm{\mathbb{Z}}$
; see [Reference Ellenberg, Logan and SrinivasanELS24] for data confirming this for many quartic plane curves. The curves
$\mathrm{End}(J) = \mathrm{\mathbb{Z}}$
; see [Reference Ellenberg, Logan and SrinivasanELS24] for data confirming this for many quartic plane curves. The curves
![]() $X_u$
are no exceptions as generically we have
$X_u$
are no exceptions as generically we have
![]() $\mathrm{End}^0(\mathrm{Jac}(X_u)) = \mathrm{\mathbb{Q}}(\zeta_9 + \zeta_9^{-1})$
by Remark 3.13.
$\mathrm{End}^0(\mathrm{Jac}(X_u)) = \mathrm{\mathbb{Q}}(\zeta_9 + \zeta_9^{-1})$
by Remark 3.13.
Finally, Gao and Zhang have recently proven a Northcott property for the Beilinson–Bloch height of the Ceresa cycle on J and (equivalently) the modified diagonal cycle
![]() $\Delta(C)$
on
$\Delta(C)$
on
![]() $C^3$
[Reference Gao and ZhangGZ24]. More precisely, for each
$C^3$
[Reference Gao and ZhangGZ24]. More precisely, for each
![]() $g \geqslant 3$
, there exists an open dense subset
$g \geqslant 3$
, there exists an open dense subset
![]() $U_g \subset \mathcal{M}_g$
such that for any
$U_g \subset \mathcal{M}_g$
such that for any
![]() $X \in \mathrm{\mathbb{R}}$
and
$X \in \mathrm{\mathbb{R}}$
and
![]() $d \in \mathrm{\mathbb{N}}$
, the number of
$d \in \mathrm{\mathbb{N}}$
, the number of
![]() $C \in U_g(\bar{\mathrm{\mathbb{Q}}})$
defined over a number field of degree at most d and with
$C \in U_g(\bar{\mathrm{\mathbb{Q}}})$
defined over a number field of degree at most d and with
![]() $\langle \Delta(C), \Delta(C)\rangle < X$
is finite. In order to better understand Ceresa vanishing loci in families of curves, it is of great interest to try to identify the largest such open dense set
$\langle \Delta(C), \Delta(C)\rangle < X$
is finite. In order to better understand Ceresa vanishing loci in families of curves, it is of great interest to try to identify the largest such open dense set
![]() $U_g$
, or equivalently, its complement
$U_g$
, or equivalently, its complement
![]() $Z_g^{\mathrm{slim}} := \mathcal{M}_g \setminus U_g$
. The Northcott property implies that any positive-dimensional component of
$Z_g^{\mathrm{slim}} := \mathcal{M}_g \setminus U_g$
. The Northcott property implies that any positive-dimensional component of
![]() $V_g^{\mathrm{rat}}$
is contained in
$V_g^{\mathrm{rat}}$
is contained in
![]() $Z_g^{\mathrm{slim}}$
, but
$Z_g^{\mathrm{slim}}$
, but
![]() $Z_g^{\mathrm{slim}}$
may be strictly larger than the union of the positive-dimensional components of
$Z_g^{\mathrm{slim}}$
may be strictly larger than the union of the positive-dimensional components of
![]() $V_g^{\mathrm{rat}}$
. Indeed, Theorem D shows that
$V_g^{\mathrm{rat}}$
. Indeed, Theorem D shows that
![]() $X_{C_3} \subset Z_3^{\mathrm{slim}}$
, even though
$X_{C_3} \subset Z_3^{\mathrm{slim}}$
, even though
![]() $X_{C_3} \not\subset V_3^{\mathrm{rat}}$
.
$X_{C_3} \not\subset V_3^{\mathrm{rat}}$
.
1.4 Structure of paper
In § 2 we collect some standard results on Chow groups, Chow motives and Ceresa cycles. In § 3 we prove the cohomological vanishing criteria (Theorems A and B) and give some examples. In § 4 we study the family of Picard curves in detail and prove Theorems C and D. Finally, in § 5 we introduce the Ceresa vanishing loci
![]() $V_g^{\mathrm{rat}},V_g^{\mathrm{alg}}\subset \mathcal{M}_g$
, prove Theorem D and determine which automorphism strata they contain in genus 3, proving Theorem E.
$V_g^{\mathrm{rat}},V_g^{\mathrm{alg}}\subset \mathcal{M}_g$
, prove Theorem D and determine which automorphism strata they contain in genus 3, proving Theorem E.
2. Notation and background
2.1 Chow groups
Let k be a field. A variety is by definition a separated scheme of finite type over k. We say a variety is nice if it is smooth, projective and geometrically integral. If X is a smooth and geometrically integral variety and
![]() $p\in \{0,\dots,\dim X\}$
, let
$p\in \{0,\dots,\dim X\}$
, let
![]() $\mathrm{CH}^p(X)$
denote the Chow group (with Z-coefficients) of codimension p cycles modulo rational equivalence. If
$\mathrm{CH}^p(X)$
denote the Chow group (with Z-coefficients) of codimension p cycles modulo rational equivalence. If
![]() $Z\subset X$
is a closed subscheme of codimension p, we denote its class in
$Z\subset X$
is a closed subscheme of codimension p, we denote its class in
![]() $\mathrm{CH}^p(X)$
by [Z] (using [Sta18, Tag 02QS] if Z is not integral).
$\mathrm{CH}^p(X)$
by [Z] (using [Sta18, Tag 02QS] if Z is not integral).
If X is additionally projective, then
![]() $\mathrm{CH}^p(X)$
has a filtration by subgroups
$\mathrm{CH}^p(X)$
has a filtration by subgroups
where
![]() $\mathrm{CH}^p(X)_{\mathrm{alg}}$
is the subgroup of algebraically trivial cycles (in the sense of [Reference Achter, Casalaina-Martin and VialACMV19b, § 3.1]) and
$\mathrm{CH}^p(X)_{\mathrm{alg}}$
is the subgroup of algebraically trivial cycles (in the sense of [Reference Achter, Casalaina-Martin and VialACMV19b, § 3.1]) and
![]() $\mathrm{CH}^p(X)_{\mathrm{hom}}$
the subgroup of homologically trivial cycles (with respect to a fixed Weil cohomology theory for nice varieties over k). The Griffiths group is by definition
$\mathrm{CH}^p(X)_{\mathrm{hom}}$
the subgroup of homologically trivial cycles (with respect to a fixed Weil cohomology theory for nice varieties over k). The Griffiths group is by definition
![]() $\mathrm{Gr}^p(X) = \mathrm{CH}^p(X)_{\mathrm{hom}}/\mathrm{CH}^p(X)_{\mathrm{alg}}$
. We occasionally write
$\mathrm{Gr}^p(X) = \mathrm{CH}^p(X)_{\mathrm{hom}}/\mathrm{CH}^p(X)_{\mathrm{alg}}$
. We occasionally write
![]() $\mathrm{CH}_p(X) = \mathrm{CH}^{\dim X -p}(X)$
and
$\mathrm{CH}_p(X) = \mathrm{CH}^{\dim X -p}(X)$
and
![]() $\mathrm{Gr}_p(X) = \mathrm{Gr}^{\dim X -p}(X)$
. If R is a ring, we write
$\mathrm{Gr}_p(X) = \mathrm{Gr}^{\dim X -p}(X)$
. If R is a ring, we write
![]() $\mathrm{CH}^p(X)_R= \mathrm{CH}^p(X)\otimes_{\mathrm{\mathbb{Z}}} R$
and
$\mathrm{CH}^p(X)_R= \mathrm{CH}^p(X)\otimes_{\mathrm{\mathbb{Z}}} R$
and
![]() $\mathrm{Gr}^p(X)_R = \mathrm{Gr}^p(X)\otimes_{\mathrm{\mathbb{Z}}} R$
.
$\mathrm{Gr}^p(X)_R = \mathrm{Gr}^p(X)\otimes_{\mathrm{\mathbb{Z}}} R$
.
2.2 Base change, specialization and families
We state three lemmas concerning operations on cycles. These seem to be standard, but we could not locate proofs in the literature.
Lemma 2.1. Let
![]() $X/k$
be a nice variety and
$X/k$
be a nice variety and
![]() $K/k$
a (not necessarily finite) extension of fields.
$K/k$
a (not necessarily finite) extension of fields.
-
(i)The base-change maps
 $\mathrm{CH}^p(X)_\mathrm{\mathbb{Q}} \rightarrow \mathrm{CH}^p(X_K)_\mathrm{\mathbb{Q}}$
and
$\mathrm{CH}^p(X)_\mathrm{\mathbb{Q}} \rightarrow \mathrm{CH}^p(X_K)_\mathrm{\mathbb{Q}}$
and
 $\mathrm{Gr}^p(X)_\mathrm{\mathbb{Q}}\rightarrow \mathrm{Gr}^p(X_K)_\mathrm{\mathbb{Q}}$
are injective.
$\mathrm{Gr}^p(X)_\mathrm{\mathbb{Q}}\rightarrow \mathrm{Gr}^p(X_K)_\mathrm{\mathbb{Q}}$
are injective.
-
(ii)If in addition k is algebraically closed, the base-change maps
 $\mathrm{CH}^p(X) \rightarrow \mathrm{CH}^p(X_K)$
and
$\mathrm{CH}^p(X) \rightarrow \mathrm{CH}^p(X_K)$
and
 $\mathrm{Gr}^p(X)\rightarrow \mathrm{Gr}^p(X_K)$
are injective.
$\mathrm{Gr}^p(X)\rightarrow \mathrm{Gr}^p(X_K)$
are injective.
Proof. The proof is an adaptation of [Reference BlochBlo10, Lemma 1A.3, p.22]. We first prove (ii) for
![]() $\mathrm{CH}^p(X)\rightarrow \mathrm{CH}^p(X_K)$
. Suppose
$\mathrm{CH}^p(X)\rightarrow \mathrm{CH}^p(X_K)$
. Suppose
![]() $\alpha\in \mathrm{CH}^p(X)$
has trivial image in
$\alpha\in \mathrm{CH}^p(X)$
has trivial image in
![]() $\mathrm{CH}^p(X_K)$
. Then
$\mathrm{CH}^p(X_K)$
. Then
![]() $\alpha$
already has trivial image in
$\alpha$
already has trivial image in
![]() $\mathrm{CH}^p(X_{K'})$
, where
$\mathrm{CH}^p(X_{K'})$
, where
![]() $K'\subset K$
is a subfield that is finitely generated over k, since the data witnessing triviality in
$K'\subset K$
is a subfield that is finitely generated over k, since the data witnessing triviality in
![]() $\mathrm{CH}^p(X_K)$
can be defined over such a subfield. By spreading out, we can find a smooth integral variety
$\mathrm{CH}^p(X_K)$
can be defined over such a subfield. By spreading out, we can find a smooth integral variety
![]() $U/k$
with function field K’ such that
$U/k$
with function field K’ such that
![]() $\alpha$
has trivial image in
$\alpha$
has trivial image in
![]() $\mathrm{CH}^p(X\times_k U)$
. Since k is algebraically closed, there exists a k-point
$\mathrm{CH}^p(X\times_k U)$
. Since k is algebraically closed, there exists a k-point
![]() $u\in U(k)$
. Pulling back along u defines a left-inverse
$u\in U(k)$
. Pulling back along u defines a left-inverse
![]() $\mathrm{CH}^p(X\times_k U) \rightarrow \mathrm{CH}^p(X)$
to the map
$\mathrm{CH}^p(X\times_k U) \rightarrow \mathrm{CH}^p(X)$
to the map
![]() $\mathrm{CH}^p(X) \rightarrow \mathrm{CH}^p(X\times_k U)$
. It follows that
$\mathrm{CH}^p(X) \rightarrow \mathrm{CH}^p(X\times_k U)$
. It follows that
![]() $\alpha$
is trivial in
$\alpha$
is trivial in
![]() $\mathrm{CH}^p(X)$
, as desired. The argument for
$\mathrm{CH}^p(X)$
, as desired. The argument for
![]() $\mathrm{Gr}^p(X)$
is identical and omitted.
$\mathrm{Gr}^p(X)$
is identical and omitted.
We now prove (i) for
![]() $\mathrm{CH}^p(X)_{\mathrm{\mathbb{Q}}}\rightarrow \mathrm{CH}^p(X_K)_{\mathrm{\mathbb{Q}}}$
. There exists a field L containing both K and an algebraic closure
$\mathrm{CH}^p(X)_{\mathrm{\mathbb{Q}}}\rightarrow \mathrm{CH}^p(X_K)_{\mathrm{\mathbb{Q}}}$
. There exists a field L containing both K and an algebraic closure
![]() $\bar{k}$
of k. It therefore suffices to prove the two base-change maps
$\bar{k}$
of k. It therefore suffices to prove the two base-change maps
![]() $\mathrm{CH}^p(X)_\mathrm{\mathbb{Q}} \rightarrow \mathrm{CH}^p(X_{\bar{k}})_\mathrm{\mathbb{Q}} \rightarrow \mathrm{CH}^p(X_L)_{\mathrm{\mathbb{Q}}}$
are both injective. The first one follows from the fact that for a finite extension
$\mathrm{CH}^p(X)_\mathrm{\mathbb{Q}} \rightarrow \mathrm{CH}^p(X_{\bar{k}})_\mathrm{\mathbb{Q}} \rightarrow \mathrm{CH}^p(X_L)_{\mathrm{\mathbb{Q}}}$
are both injective. The first one follows from the fact that for a finite extension
![]() $k'/k$
the pushforward map
$k'/k$
the pushforward map
![]() $\mathrm{CH}^p(X_{k'}) \rightarrow \mathrm{CH}^p(X)$
, when precomposed with the base-change map, is multiplication by
$\mathrm{CH}^p(X_{k'}) \rightarrow \mathrm{CH}^p(X)$
, when precomposed with the base-change map, is multiplication by
![]() $[k':k]$
. The second follows from (ii). The case of
$[k':k]$
. The second follows from (ii). The case of
![]() $\mathrm{Gr}^p(X)_{\mathrm{\mathbb{Q}}}$
is again analogous.
$\mathrm{Gr}^p(X)_{\mathrm{\mathbb{Q}}}$
is again analogous.
To discuss specialization in the next lemma, let R be a discrete valuation ring with fraction field K and residue field k. Let
![]() $X\rightarrow \mathrm{Spec} (R)$
be a smooth, projective morphism with geometrically integral fibres, so the generic and special fibres
$X\rightarrow \mathrm{Spec} (R)$
be a smooth, projective morphism with geometrically integral fibres, so the generic and special fibres
![]() $X_K$
and
$X_K$
and
![]() $X_k$
are nice varieties over K and k, respectively. In this setting, Fulton [Reference FultonFul98, § 20.3] has defined a specialization morphism
$X_k$
are nice varieties over K and k, respectively. In this setting, Fulton [Reference FultonFul98, § 20.3] has defined a specialization morphism
![]() $\mathrm{sp}\colon \mathrm{CH}^p(X_K) \rightarrow \mathrm{CH}^p(X_k)$
for every
$\mathrm{sp}\colon \mathrm{CH}^p(X_K) \rightarrow \mathrm{CH}^p(X_k)$
for every
![]() $0\leqslant p\leqslant \dim(X_K)$
. It has the property that if
$0\leqslant p\leqslant \dim(X_K)$
. It has the property that if
![]() $Z\subset X$
is a closed integral subscheme of codimension p, flat over R, then
$Z\subset X$
is a closed integral subscheme of codimension p, flat over R, then
![]() $\mathrm{sp}([Z_K]) = [Z_k]$
.
$\mathrm{sp}([Z_K]) = [Z_k]$
.
Lemma 2.2.
In the above notation, sp sends
![]() $\mathrm{CH}^p(X_K)_{\mathrm{alg}}\otimes \mathrm{\mathbb{Q}}$
to
$\mathrm{CH}^p(X_K)_{\mathrm{alg}}\otimes \mathrm{\mathbb{Q}}$
to
![]() $\mathrm{CH}^p(X_k)_{\mathrm{alg}}\otimes \mathrm{\mathbb{Q}}$
.
$\mathrm{CH}^p(X_k)_{\mathrm{alg}}\otimes \mathrm{\mathbb{Q}}$
.
Proof. Let
![]() $C/K$
be a nice curve with K-points
$C/K$
be a nice curve with K-points
![]() $t_0, t_1\in C(K)$
and let
$t_0, t_1\in C(K)$
and let
![]() $Z\subset (X_K)\times_K C$
be an integral closed subscheme of codimension p, flat over C. By [Reference Achter, Casalaina-Martin and VialACMV19b, Theorem 1] and the remarks thereafter, it suffices to prove that
$Z\subset (X_K)\times_K C$
be an integral closed subscheme of codimension p, flat over C. By [Reference Achter, Casalaina-Martin and VialACMV19b, Theorem 1] and the remarks thereafter, it suffices to prove that
![]() $\mathrm{sp}([Z_{t_0}] - [Z_{t_1}]) \in \mathrm{CH}^p(X_k)_{\mathrm{alg}} \otimes \mathrm{\mathbb{Q}}$
for each such tuple
$\mathrm{sp}([Z_{t_0}] - [Z_{t_1}]) \in \mathrm{CH}^p(X_k)_{\mathrm{alg}} \otimes \mathrm{\mathbb{Q}}$
for each such tuple
![]() $(C, t_0,t_1, Z)$
.
$(C, t_0,t_1, Z)$
.
Let
![]() $\mathcal{C}\rightarrow \mathrm{Spec}(R)$
be an integral, projective, flat, proper and regular model of C, which exists by [Reference LiuLiu02, Proposition 10.1.8]. Let
$\mathcal{C}\rightarrow \mathrm{Spec}(R)$
be an integral, projective, flat, proper and regular model of C, which exists by [Reference LiuLiu02, Proposition 10.1.8]. Let
![]() $\mathrm{Hilb}_{X/R}\rightarrow \mathrm{Spec}(R)$
be the Hilbert scheme of the projective morphism
$\mathrm{Hilb}_{X/R}\rightarrow \mathrm{Spec}(R)$
be the Hilbert scheme of the projective morphism
![]() $X\rightarrow \mathrm{Spec}(R)$
. The closed subscheme Z determines a K-morphism
$X\rightarrow \mathrm{Spec}(R)$
. The closed subscheme Z determines a K-morphism
![]() $\alpha\colon C\rightarrow \mathrm{Hilb}_{X/R}$
. Since C is connected, the image of
$\alpha\colon C\rightarrow \mathrm{Hilb}_{X/R}$
. Since C is connected, the image of
![]() $\alpha$
is contained in an open and closed subscheme
$\alpha$
is contained in an open and closed subscheme
![]() $\mathrm{Hilb}_{X/R}^{\phi}$
with fixed Hilbert polynomial. The surface
$\mathrm{Hilb}_{X/R}^{\phi}$
with fixed Hilbert polynomial. The surface
![]() $\mathcal{C}$
is regular,
$\mathcal{C}$
is regular,
![]() $\mathrm{Hilb}^{\phi}_{X/R}\rightarrow \mathrm{Spec}(R)$
is projective [Reference Altman and KleimanAK80, Corollary (2.8)] and we may view
$\mathrm{Hilb}^{\phi}_{X/R}\rightarrow \mathrm{Spec}(R)$
is projective [Reference Altman and KleimanAK80, Corollary (2.8)] and we may view
![]() $\alpha$
as a rational map
$\alpha$
as a rational map
![]() $\mathcal{C}\dashrightarrow \mathrm{Hilb}_{X/R}^{\phi}$
. Therefore, by [Reference LiuLiu02, Theorem 9.2.7], there exists a birational map
$\mathcal{C}\dashrightarrow \mathrm{Hilb}_{X/R}^{\phi}$
. Therefore, by [Reference LiuLiu02, Theorem 9.2.7], there exists a birational map
![]() $\widetilde{\mathcal{C}} \rightarrow \mathcal{C}$
, obtained by successively blowing up closed points in the special fibre, and an R-morphism
$\widetilde{\mathcal{C}} \rightarrow \mathcal{C}$
, obtained by successively blowing up closed points in the special fibre, and an R-morphism
![]() $\tilde{\alpha}\colon \widetilde{\mathcal{C}} \rightarrow \mathrm{Hilb}^{\phi}_{X/R}$
with generic fibre
$\tilde{\alpha}\colon \widetilde{\mathcal{C}} \rightarrow \mathrm{Hilb}^{\phi}_{X/R}$
with generic fibre
![]() $\alpha$
. In other words, there exists a closed subscheme
$\alpha$
. In other words, there exists a closed subscheme
![]() $\mathcal{Z} \subset \widetilde{\mathcal{C}} \times_R X$
, flat over
$\mathcal{Z} \subset \widetilde{\mathcal{C}} \times_R X$
, flat over
![]() $\widetilde{\mathcal{C}}$
, whose generic fibre equals Z.
$\widetilde{\mathcal{C}}$
, whose generic fibre equals Z.
The K-points
![]() $t_i\in C(K)$
extend to R-points
$t_i\in C(K)$
extend to R-points
![]() $\tilde{t}_i\colon \mathrm{Spec}(R) \rightarrow \widetilde{\mathcal{C}}$
whose reductions
$\tilde{t}_i\colon \mathrm{Spec}(R) \rightarrow \widetilde{\mathcal{C}}$
whose reductions
![]() $\bar{t}_i\in \widetilde{\mathcal{C}}_k(k)$
land in the smooth locus of
$\bar{t}_i\in \widetilde{\mathcal{C}}_k(k)$
land in the smooth locus of
![]() $\widetilde{\mathcal{C}}_k$
. The closed subschemes
$\widetilde{\mathcal{C}}_k$
. The closed subschemes
![]() $\mathcal{Z}_{\tilde{t}_i}\subset X$
are flat over R. Therefore,
$\mathcal{Z}_{\tilde{t}_i}\subset X$
are flat over R. Therefore,
![]() $\mathrm{sp}([Z_{t_0}]-[Z_{t_1}]) = [\mathcal{Z}_{\bar{t}_0}] - [\mathcal{Z}_{\bar{t}_1}]$
.
$\mathrm{sp}([Z_{t_0}]-[Z_{t_1}]) = [\mathcal{Z}_{\bar{t}_0}] - [\mathcal{Z}_{\bar{t}_1}]$
.
By the Zariski connectedness theorem, the special fibre
![]() $\widetilde{\mathcal{C}}_k$
is connected. Consequently, by resolving irreducible components of
$\widetilde{\mathcal{C}}_k$
is connected. Consequently, by resolving irreducible components of
![]() $\widetilde{\mathcal{C}}_k$
, we can connect
$\widetilde{\mathcal{C}}_k$
, we can connect
![]() $\bar{t}_0$
to
$\bar{t}_0$
to
![]() $\bar{t}_1$
by a sequence of nice curves: there exist a finite extension
$\bar{t}_1$
by a sequence of nice curves: there exist a finite extension
![]() $k'/k$
, a collection of nice curves
$k'/k$
, a collection of nice curves
![]() $D_1, \dots,D_n$
over k’, and for each
$D_1, \dots,D_n$
over k’, and for each
![]() $1\leqslant i \leqslant n$
a pair of points
$1\leqslant i \leqslant n$
a pair of points
![]() $s_{i,1}, s_{i,2}\in D_i(k')$
and a morphism
$s_{i,1}, s_{i,2}\in D_i(k')$
and a morphism
![]() $\varphi_i\colon D_i \rightarrow \mathcal{C}_{k'}$
such that
$\varphi_i\colon D_i \rightarrow \mathcal{C}_{k'}$
such that
![]() $\varphi_1(s_{1,1}) = \bar{t}_1$
,
$\varphi_1(s_{1,1}) = \bar{t}_1$
,
![]() $\varphi_i(s_{i,2}) = \varphi_{i+1}(s_{i+1,1})$
for all
$\varphi_i(s_{i,2}) = \varphi_{i+1}(s_{i+1,1})$
for all
![]() $1\leqslant i\leqslant n-1$
, and
$1\leqslant i\leqslant n-1$
, and
![]() $\varphi_{n}(s_{n,2}) = \bar{t}_2$
. Letting
$\varphi_{n}(s_{n,2}) = \bar{t}_2$
. Letting
![]() $W^{(i)}$
be the pullback of
$W^{(i)}$
be the pullback of
![]() $\mathcal{Z}_k$
along
$\mathcal{Z}_k$
along
![]() $\varphi_i$
, we have
$\varphi_i$
, we have
Since each term
![]() $([W^{(i)}_{s_{i,1}}]- [W^{(i)}_{s_{i,2}}])$
lies in
$([W^{(i)}_{s_{i,1}}]- [W^{(i)}_{s_{i,2}}])$
lies in
![]() $\mathrm{CH}^p(X_{k'})_{\mathrm{alg}}\otimes \mathrm{\mathbb{Q}}$
by definition of algebraic triviality, the same is true for their sum. Taking the pushforward along
$\mathrm{CH}^p(X_{k'})_{\mathrm{alg}}\otimes \mathrm{\mathbb{Q}}$
by definition of algebraic triviality, the same is true for their sum. Taking the pushforward along
![]() $X_{k'} \rightarrow X_k$
, we see that
$X_{k'} \rightarrow X_k$
, we see that
![]() $[k':k] \cdot \mathrm{sp}([Z_{t_0}]-[Z_{t_1}]) \in \mathrm{CH}^p(X_k)_{\mathrm{alg}}$
, as desired.
$[k':k] \cdot \mathrm{sp}([Z_{t_0}]-[Z_{t_1}]) \in \mathrm{CH}^p(X_k)_{\mathrm{alg}}$
, as desired.
Remark 2.3. The proof shows that if K is perfect and k is algebraically closed, then sp even sends
![]() $\mathrm{CH}^p(X_K)_{\mathrm{alg}}$
to
$\mathrm{CH}^p(X_K)_{\mathrm{alg}}$
to
![]() $\mathrm{CH}^p(X_k)_{\mathrm{alg}}$
.
$\mathrm{CH}^p(X_k)_{\mathrm{alg}}$
.
Lemma 2.4. Let
![]() $X\rightarrow S$
be a smooth proper morphism of smooth varieties over a field k. Let
$X\rightarrow S$
be a smooth proper morphism of smooth varieties over a field k. Let
![]() $\alpha$
be a codimension-p cycle on X. Then the locus of points
$\alpha$
be a codimension-p cycle on X. Then the locus of points
![]() $s\in S$
such that the (Gysin) fibre
$s\in S$
such that the (Gysin) fibre
![]() $\alpha_s\in \mathrm{CH}^p(X_s)_{\mathrm{\mathbb{Q}}}$
is zero (respectively, lies in
$\alpha_s\in \mathrm{CH}^p(X_s)_{\mathrm{\mathbb{Q}}}$
is zero (respectively, lies in
![]() $\mathrm{CH}^p(X_s)_{\mathrm{alg}, \mathrm{\mathbb{Q}}}$
) is a countable union of closed algebraic subvarieties of S.
$\mathrm{CH}^p(X_s)_{\mathrm{alg}, \mathrm{\mathbb{Q}}}$
) is a countable union of closed algebraic subvarieties of S.
Proof. There exist a countable subfield
![]() $k_0\subset k$
, a smooth proper morphism
$k_0\subset k$
, a smooth proper morphism
![]() $X_0\rightarrow S_0$
of varieties over
$X_0\rightarrow S_0$
of varieties over
![]() $k_0$
and a cycle
$k_0$
and a cycle
![]() $\alpha_0$
on
$\alpha_0$
on
![]() $X_0$
whose base change to k are
$X_0$
whose base change to k are
![]() $X\rightarrow S$
and
$X\rightarrow S$
and
![]() $\alpha$
, respectively. Since
$\alpha$
, respectively. Since
![]() $k_0$
is countable,
$k_0$
is countable,
![]() $S_0$
has only countably many closed subschemes. Let
$S_0$
has only countably many closed subschemes. Let
![]() $\mathcal{F}$
be the collection of integral closed subschemes
$\mathcal{F}$
be the collection of integral closed subschemes
![]() $Z\subset S_0$
such that
$Z\subset S_0$
such that
![]() $\alpha_0$
is zero in
$\alpha_0$
is zero in
![]() $\mathrm{CH}^p(X_{0,\eta(Z)})_{\mathrm{\mathbb{Q}}}$
, where
$\mathrm{CH}^p(X_{0,\eta(Z)})_{\mathrm{\mathbb{Q}}}$
, where
![]() $\eta(Z)\in S_0$
denotes the generic point of Z. Then we claim that the locus of
$\eta(Z)\in S_0$
denotes the generic point of Z. Then we claim that the locus of
![]() $s\in S$
for which
$s\in S$
for which
![]() $\alpha_s\in \mathrm{CH}^p(X_s)_{\mathrm{\mathbb{Q}}}$
is zero is exactly the union
$\alpha_s\in \mathrm{CH}^p(X_s)_{\mathrm{\mathbb{Q}}}$
is zero is exactly the union
![]() $\bigcup_{Z\in \mathcal{F}} Z_k \subset S$
. This follows from Lemmas 2.1 and properties of the specialization map; we omit the details, and the similar argument for algebraic triviality.
$\bigcup_{Z\in \mathcal{F}} Z_k \subset S$
. This follows from Lemmas 2.1 and properties of the specialization map; we omit the details, and the similar argument for algebraic triviality.
2.3 Chow motives
We recall a few relevant facts about the category
![]() $\mathsf{Mot}(k)$
of (pure, contravariant) Chow motives M over k with Q-coefficients; see [Reference SchollSch94] or [Reference Murre, Nagel and PetersMNP13, § 2] for basic definitions.
$\mathsf{Mot}(k)$
of (pure, contravariant) Chow motives M over k with Q-coefficients; see [Reference SchollSch94] or [Reference Murre, Nagel and PetersMNP13, § 2] for basic definitions.
Denote the Lefschetz motive by
![]() $\mathbb{L}$
, its nth tensor power by
$\mathbb{L}$
, its nth tensor power by
![]() $\mathbb{L}^n$
, and write
$\mathbb{L}^n$
, and write
![]() $M(n) = M\otimes \mathbb{L}^n$
. Following [Reference Murre, Nagel and PetersMNP13, § 2.5], the Chow group in codimension p of M is by definition
$M(n) = M\otimes \mathbb{L}^n$
. Following [Reference Murre, Nagel and PetersMNP13, § 2.5], the Chow group in codimension p of M is by definition
![]() $\mathrm{CH}^p(M) = \mathrm{Hom}_{\mathsf{Mot}(k)}(\mathbb{L}^{p}, M)$
. If
$\mathrm{CH}^p(M) = \mathrm{Hom}_{\mathsf{Mot}(k)}(\mathbb{L}^{p}, M)$
. If
![]() $M = {\frak{h}}(X)$
, where X is smooth projective over k, then
$M = {\frak{h}}(X)$
, where X is smooth projective over k, then
![]() $\mathrm{CH}^p(M) = \mathrm{CH}^p(X)_{\mathrm{\mathbb{Q}}}$
. (Beware that we need to take Q-coefficients on the right-hand side.) If C is a nice curve over k, a morphism
$\mathrm{CH}^p(M) = \mathrm{CH}^p(X)_{\mathrm{\mathbb{Q}}}$
. (Beware that we need to take Q-coefficients on the right-hand side.) If C is a nice curve over k, a morphism
![]() $\varphi\colon {\frak{h}}(C)\rightarrow M(p-1)$
in
$\varphi\colon {\frak{h}}(C)\rightarrow M(p-1)$
in
![]() $\mathsf{Mot}(k)$
induces a homomorphism of abelian groups
$\mathsf{Mot}(k)$
induces a homomorphism of abelian groups
![]() $\mathrm{CH}^1(\varphi)\colon \mathrm{CH}^1(C)_{\mathrm{alg},\mathrm{\mathbb{Q}}} \rightarrow \mathrm{CH}^p(M)$
. We define
$\mathrm{CH}^1(\varphi)\colon \mathrm{CH}^1(C)_{\mathrm{alg},\mathrm{\mathbb{Q}}} \rightarrow \mathrm{CH}^p(M)$
. We define
![]() $\mathrm{CH}^p(M)_{\mathrm{alg}}$
to be the union of the images of
$\mathrm{CH}^p(M)_{\mathrm{alg}}$
to be the union of the images of
![]() $\mathrm{CH}^1(\varphi)$
ranging over all pairs
$\mathrm{CH}^1(\varphi)$
ranging over all pairs
![]() $(C, \varphi)$
as above. This coincides with
$(C, \varphi)$
as above. This coincides with
![]() $\mathrm{CH}^p(X)_{\mathrm{alg}} \otimes \mathrm{\mathbb{Q}}$
when
$\mathrm{CH}^p(X)_{\mathrm{alg}} \otimes \mathrm{\mathbb{Q}}$
when
![]() $M = {\frak{h}}(X)$
; see [Reference Achter, Casalaina-Martin and VialACMV19b, Corollary 4.13].
$M = {\frak{h}}(X)$
; see [Reference Achter, Casalaina-Martin and VialACMV19b, Corollary 4.13].
Finally, we define motives of fixed points. If G is a finite group acting on a motive M, write
![]() $M^G$
for the submotive cut out by the idempotent
$M^G$
for the submotive cut out by the idempotent
![]() $({1}/{\#G})\sum_{g \in G} g_* \in \mathrm{End}(M)$
. We have
$({1}/{\#G})\sum_{g \in G} g_* \in \mathrm{End}(M)$
. We have
![]() $\mathrm{CH}^p(M^G) = \mathrm{CH}^p(M)^G$
. If G acts on a nice variety X, then G acts on
$\mathrm{CH}^p(M^G) = \mathrm{CH}^p(M)^G$
. If G acts on a nice variety X, then G acts on
![]() ${\frak{h}}(X)$
and
${\frak{h}}(X)$
and
![]() $\mathrm{CH}^p(X)$
, and
$\mathrm{CH}^p(X)$
, and
![]() $\mathrm{CH}^p({\frak{h}}(X)^G) = \mathrm{CH}^p(X)^G\otimes {\mathrm{\mathbb{Q}}}$
.
$\mathrm{CH}^p({\frak{h}}(X)^G) = \mathrm{CH}^p(X)^G\otimes {\mathrm{\mathbb{Q}}}$
.
2.4 Chow–Künneth decomposition for abelian varieties
Let
![]() $A/k$
be a g-dimensional abelian variety. Deninger and Murre [Reference Deninger and MurreDM91, § 3] have constructed a canonical Chow–Künneth decomposition
$A/k$
be a g-dimensional abelian variety. Deninger and Murre [Reference Deninger and MurreDM91, § 3] have constructed a canonical Chow–Künneth decomposition
 \begin{align}{\frak{h}}(A) = \bigoplus_{i = 0}^{2g}{\frak{h}}^i(A),\end{align}
\begin{align}{\frak{h}}(A) = \bigoplus_{i = 0}^{2g}{\frak{h}}^i(A),\end{align}
uniquely characterized by the following property: if
![]() $(n)\colon A\rightarrow A$
denotes multiplication by n, then
$(n)\colon A\rightarrow A$
denotes multiplication by n, then
![]() $(n)^*$
acts on
$(n)^*$
acts on
![]() ${\frak{h}}^i(A)$
via
${\frak{h}}^i(A)$
via
![]() $n^i$
for every integer n. On the other hand, Beauville [Reference BeauvilleBea86] has shown that there exists a direct sum decomposition
$n^i$
for every integer n. On the other hand, Beauville [Reference BeauvilleBea86] has shown that there exists a direct sum decomposition
![]() $\mathrm{CH}^p(A)_\mathrm{\mathbb{Q}} = \bigoplus_{s = p-g}^p \mathrm{CH}^p_{(s)}(A)$
, where
$\mathrm{CH}^p(A)_\mathrm{\mathbb{Q}} = \bigoplus_{s = p-g}^p \mathrm{CH}^p_{(s)}(A)$
, where
The two decompositions are linked by the formula
![]() $\mathrm{CH}^p({\frak{h}}^i(A)) = \mathrm{CH}^p_{(2p-i)}(A)$
. Beauville conjectured that
$\mathrm{CH}^p({\frak{h}}^i(A)) = \mathrm{CH}^p_{(2p-i)}(A)$
. Beauville conjectured that
![]() $\mathrm{CH}^p_{(s)}(A) = 0$
when
$\mathrm{CH}^p_{(s)}(A) = 0$
when
![]() $s<0$
, and he proved it when
$s<0$
, and he proved it when
![]() $p \in \{0,1,g-2,g-1,g\}$
[Reference BeauvilleBea86, Proposition 3(a)].
$p \in \{0,1,g-2,g-1,g\}$
[Reference BeauvilleBea86, Proposition 3(a)].
Example 2.5. For
![]() $p = 1$
, the Beauville decomposition
$p = 1$
, the Beauville decomposition
![]() $\mathrm{CH}^1(A)_\mathrm{\mathbb{Q}} = \mathrm{CH}^1_{(0)}(A) \bigoplus \mathrm{CH}^1_{(1)}(A)$
is the decomposition of a divisor class into symmetric and anti-symmetric classes.
$\mathrm{CH}^1(A)_\mathrm{\mathbb{Q}} = \mathrm{CH}^1_{(0)}(A) \bigoplus \mathrm{CH}^1_{(1)}(A)$
is the decomposition of a divisor class into symmetric and anti-symmetric classes.
Lemma 2.6.
If
![]() $A/k$
is an abelian variety, then
$A/k$
is an abelian variety, then
![]() $\mathrm{CH}^p({\frak{h}}^1(A))_{\mathrm{alg}} = \mathrm{CH}^p({\frak{h}}^1(A))$
for all
$\mathrm{CH}^p({\frak{h}}^1(A))_{\mathrm{alg}} = \mathrm{CH}^p({\frak{h}}^1(A))$
for all
![]() $p\geqslant 0$
.
$p\geqslant 0$
.
Proof. By Lemma 2.1(1), we may assume k is algebraically closed. The only non-zero Chow group of
![]() ${\frak{h}}^1(A)$
is
${\frak{h}}^1(A)$
is
![]() $\mathrm{CH}^1({\frak{h}}^1(A)) = \mathrm{CH}^1_{(1)}(A)$
, the set of anti-symmetric elements of
$\mathrm{CH}^1({\frak{h}}^1(A)) = \mathrm{CH}^1_{(1)}(A)$
, the set of anti-symmetric elements of
![]() $\mathrm{CH}^1(A)_{\mathrm{\mathbb{Q}}}$
. The lemma follows from the fact that
$\mathrm{CH}^1(A)_{\mathrm{\mathbb{Q}}}$
. The lemma follows from the fact that
![]() $\mathrm{CH}^1_{(1)}(A) = \mathrm{CH}^1(A)_{\mathrm{hom}}\otimes \mathrm{\mathbb{Q}}$
and that homological and algebraic equivalence coincide for codimension-1 cycles.
$\mathrm{CH}^1_{(1)}(A) = \mathrm{CH}^1(A)_{\mathrm{hom}}\otimes \mathrm{\mathbb{Q}}$
and that homological and algebraic equivalence coincide for codimension-1 cycles.
2.5 The Lefschetz decomposition for abelian varieties
Let
![]() $A/k$
be an abelian variety with polarization
$A/k$
be an abelian variety with polarization
![]() $\lambda\colon A \rightarrow A^{\vee}$
. Let
$\lambda\colon A \rightarrow A^{\vee}$
. Let
![]() $\ell \in \mathrm{CH}^1_{(0)}(A)$
be the unique class satisfying
$\ell \in \mathrm{CH}^1_{(0)}(A)$
be the unique class satisfying
![]() $2\ell = (1, \lambda)^* \mathcal{P}$
, where
$2\ell = (1, \lambda)^* \mathcal{P}$
, where
![]() $\mathcal{P}\in \mathrm{Pic}(A\times A^{\vee})$
is the Poincaré bundle. Künnemann has shown [Kün93, Theorem 5.2] that intersecting with
$\mathcal{P}\in \mathrm{Pic}(A\times A^{\vee})$
is the Poincaré bundle. Künnemann has shown [Kün93, Theorem 5.2] that intersecting with
![]() $\ell^{g-i}$
induces an isomorphism
$\ell^{g-i}$
induces an isomorphism
![]() ${\frak{h}}^i(A) \rightarrow {\frak{h}}^{2g-i}(A)(g-i)$
for all
${\frak{h}}^i(A) \rightarrow {\frak{h}}^{2g-i}(A)(g-i)$
for all
![]() $0\leqslant i \leqslant g$
. This induces a Lefschetz decomposition of the Chow–Künneth components
$0\leqslant i \leqslant g$
. This induces a Lefschetz decomposition of the Chow–Künneth components
![]() ${\frak{h}}^i(A)$
; see [Kün93, Theorem 5.1]. We are chiefly interested in the components
${\frak{h}}^i(A)$
; see [Kün93, Theorem 5.1]. We are chiefly interested in the components
![]() ${\frak{h}}^3(A)$
and
${\frak{h}}^3(A)$
and
![]() ${\frak{h}}^{2g-3}(A)$
when
${\frak{h}}^{2g-3}(A)$
when
![]() $g\geqslant 2$
; in that case the Lefschetz decomposition has the form
$g\geqslant 2$
; in that case the Lefschetz decomposition has the form
![]() ${\frak{h}}^3(A) = {\frak{h}}^3_{\mathrm{prim}}(A) \bigoplus \ell \cdot {\frak{h}}^1(A)$
and
${\frak{h}}^3(A) = {\frak{h}}^3_{\mathrm{prim}}(A) \bigoplus \ell \cdot {\frak{h}}^1(A)$
and
![]() ${\frak{h}}^{2g-3}(A) = {\frak{h}}^{2g-3}_{\mathrm{prim}}(A) \bigoplus \ell^{g-2}\cdot {\frak{h}}^1(A)$
. It has the property that the isomorphism
${\frak{h}}^{2g-3}(A) = {\frak{h}}^{2g-3}_{\mathrm{prim}}(A) \bigoplus \ell^{g-2}\cdot {\frak{h}}^1(A)$
. It has the property that the isomorphism
![]() $\ell^{g-3}\colon {\frak{h}}^3(A) \rightarrow {\frak{h}}^{2g-3}(A)(g-3)$
is a direct sum of isomorphisms
$\ell^{g-3}\colon {\frak{h}}^3(A) \rightarrow {\frak{h}}^{2g-3}(A)(g-3)$
is a direct sum of isomorphisms
![]() ${\frak{h}}^3_{\mathrm{prim}}(A) \rightarrow {\frak{h}}^{2g-3}_{\mathrm{prim}}(A)$
and
${\frak{h}}^3_{\mathrm{prim}}(A) \rightarrow {\frak{h}}^{2g-3}_{\mathrm{prim}}(A)$
and
![]() $\ell\cdot {\frak{h}}^1(A) \rightarrow \ell^{g-2} {\frak{h}}^1(A)$
. Taking Chow groups, we get a decomposition
$\ell\cdot {\frak{h}}^1(A) \rightarrow \ell^{g-2} {\frak{h}}^1(A)$
. Taking Chow groups, we get a decomposition
![]() $\mathrm{CH}^{g-1}({\frak{h}}^{2g-3}(A)) = \mathrm{CH}^{g-1}({\frak{h}}_{\mathrm{prim}}^{2g-3}(A))\bigoplus \mathrm{CH}^{g-1}(\ell^{g-2} \cdot {\frak{h}}^1(A))$
.
$\mathrm{CH}^{g-1}({\frak{h}}^{2g-3}(A)) = \mathrm{CH}^{g-1}({\frak{h}}_{\mathrm{prim}}^{2g-3}(A))\bigoplus \mathrm{CH}^{g-1}(\ell^{g-2} \cdot {\frak{h}}^1(A))$
.
2.6 Beauville components of C
Consider a nice curve C of genus
![]() $g\geqslant 2$
over k with Jacobian J. Let e be a degree-1 divisor on C and embed C in J using the Abel–Jacobi map based at e, sending
$g\geqslant 2$
over k with Jacobian J. Let e be a degree-1 divisor on C and embed C in J using the Abel–Jacobi map based at e, sending
![]() $x\in C$
to the divisor class of
$x\in C$
to the divisor class of
![]() $x-e$
. Decompose
$x-e$
. Decompose
![]() $[C] = [C]_0 + \cdots + [C]_{g-1}$
with
$[C] = [C]_0 + \cdots + [C]_{g-1}$
with
![]() $[C]_s \in \mathrm{CH}_{(s)}^{g-1}(J)$
. In this subsection we analyse the component
$[C]_s \in \mathrm{CH}_{(s)}^{g-1}(J)$
. In this subsection we analyse the component
![]() $[C]_1$
more closely, whose vanishing is equivalent to the vanishing of
$[C]_1$
more closely, whose vanishing is equivalent to the vanishing of
![]() $\kappa(C)$
. Proposition 2.7 can be viewed as a determination of the ‘imprimitive part’ of
$\kappa(C)$
. Proposition 2.7 can be viewed as a determination of the ‘imprimitive part’ of
![]() $[C]_1$
.
$[C]_1$
.
For
![]() $\alpha \in \mathrm{CH}_p(J)$
and
$\alpha \in \mathrm{CH}_p(J)$
and
![]() $\beta \in \mathrm{CH}_q(J)$
, the Pontryagin product
$\beta \in \mathrm{CH}_q(J)$
, the Pontryagin product
![]() $\alpha\star \beta$
is the pushforward of
$\alpha\star \beta$
is the pushforward of
![]() $\alpha\times \beta$
under the addition map
$\alpha\times \beta$
under the addition map
![]() $J\times J\rightarrow J$
. If n is a positive integer, let
$J\times J\rightarrow J$
. If n is a positive integer, let
![]() $\alpha^{\star n}$
be the n-fold Pontryagin product of
$\alpha^{\star n}$
be the n-fold Pontryagin product of
![]() $\alpha$
with itself. Let
$\alpha$
with itself. Let
![]() $K_C\in \mathrm{CH}_0(C)$
denote the canonical divisor class and let
$K_C\in \mathrm{CH}_0(C)$
denote the canonical divisor class and let
![]() $x_e\in J(k)$
be the point corresponding to the degree-0 divisor class
$x_e\in J(k)$
be the point corresponding to the degree-0 divisor class
![]() $[(2g-2)e]-K_C$
.
$[(2g-2)e]-K_C$
.
Proposition 2.7.
We have an equality in
![]() $\mathrm{CH}_{(1)}^1(J)$
:
$\mathrm{CH}_{(1)}^1(J)$
:
Here we view
![]() $[0]-[x_e]$
as an element of
$[0]-[x_e]$
as an element of
![]() $\mathrm{CH}_0(J)$
.
$\mathrm{CH}_0(J)$
.
Proof. If D is a degree-(
![]() $g-1$
) divisor class on C, let
$g-1$
) divisor class on C, let
![]() $\Theta_{D}$
be the image of the map
$\Theta_{D}$
be the image of the map
![]() $\mathrm{Sym}^{g-1}(C) \rightarrow J$
defined by
$\mathrm{Sym}^{g-1}(C) \rightarrow J$
defined by
![]() $x\mapsto [x]-D$
. Then
$x\mapsto [x]-D$
. Then
![]() $[C]^{\star (g-1)} = (g-1)![\Theta_{(g-1)e}]$
. By Riemann–Roch,
$[C]^{\star (g-1)} = (g-1)![\Theta_{(g-1)e}]$
. By Riemann–Roch,
Combining the last two sentences shows that
![]() $(-1)_*([C]^{\star (g-1)}) = [x_e]\star [C]^{\star(g-1)}$
.
$(-1)_*([C]^{\star (g-1)}) = [x_e]\star [C]^{\star(g-1)}$
.
Since the Pontryagin product sends
![]() $\mathrm{CH}^{g-p}_{(s)}(J) \times \mathrm{CH}^{g-q}_{(t)}(J)$
to
$\mathrm{CH}^{g-p}_{(s)}(J) \times \mathrm{CH}^{g-q}_{(t)}(J)$
to
![]() $\mathrm{CH}^{g-p-q}_{(s+t)}(J)$
and since
$\mathrm{CH}^{g-p-q}_{(s+t)}(J)$
and since
![]() $\mathrm{CH}^1_{(s)}(J)\neq 0$
only if
$\mathrm{CH}^1_{(s)}(J)\neq 0$
only if
![]() $s\in\{0,1\}$
, we calculate that
$s\in\{0,1\}$
, we calculate that
![]() $[C]^{\star(g-1)} = [C]_0^{\star(g-1)} + (g-1) \cdot [C]_0^{\star(g-2)} \star [C]_1$
. Applying
$[C]^{\star(g-1)} = [C]_0^{\star(g-1)} + (g-1) \cdot [C]_0^{\star(g-2)} \star [C]_1$
. Applying
![]() $(-1)_*$
and
$(-1)_*$
and
![]() $[x_e]\star$
to the previous identity, we obtain
$[x_e]\star$
to the previous identity, we obtain
 \begin{align*} (-1)_*[C]^{\star(g-1)} &= [C]_0^{\star(g-1)} - (g-1) \cdot [C]_0^{\star(g-2)} \star [C]_1, \\ [x_e]\star [C]^{\star(g-1)} &= [x_e]\star [C]_0^{\star(g-1)} + (g-1) \cdot [C]_0^{\star(g-2)} \star [C]_1. \end{align*}
\begin{align*} (-1)_*[C]^{\star(g-1)} &= [C]_0^{\star(g-1)} - (g-1) \cdot [C]_0^{\star(g-2)} \star [C]_1, \\ [x_e]\star [C]^{\star(g-1)} &= [x_e]\star [C]_0^{\star(g-1)} + (g-1) \cdot [C]_0^{\star(g-2)} \star [C]_1. \end{align*}
Note that
![]() $[x_e]\star$
acts trivially on
$[x_e]\star$
acts trivially on
![]() $\mathrm{CH}^1_{(1)}(J)$
since
$\mathrm{CH}^1_{(1)}(J)$
since
![]() $([x_e]-[0])\in \bigoplus_{s\geqslant 1} \mathrm{CH}^g_{(s)}(J)$
by the explicit description of the Beauville decomposition for 0-cycles [Reference BeauvilleBea86, bottom of p.649]. Equating the right-hand sides of the two centred equations proves that
$([x_e]-[0])\in \bigoplus_{s\geqslant 1} \mathrm{CH}^g_{(s)}(J)$
by the explicit description of the Beauville decomposition for 0-cycles [Reference BeauvilleBea86, bottom of p.649]. Equating the right-hand sides of the two centred equations proves that
![]() $(2g-2) \cdot [C]_0^{\star(g-2)} \star [C]_1 = [C]_0^{\star(g-1)} \star ([0]-[x_e])$
. Since
$(2g-2) \cdot [C]_0^{\star(g-2)} \star [C]_1 = [C]_0^{\star(g-1)} \star ([0]-[x_e])$
. Since
![]() $[C]_s^{\star(g-1)} \star ([0]-[x_e]) \in \bigoplus_{t\geqslant s+1} \mathrm{CH}^1_{(t)}(J) = \{0\}$
for all
$[C]_s^{\star(g-1)} \star ([0]-[x_e]) \in \bigoplus_{t\geqslant s+1} \mathrm{CH}^1_{(t)}(J) = \{0\}$
for all
![]() $s\geqslant 1$
, it follows that
$s\geqslant 1$
, it follows that
![]() $[C]_0^{\star(g-1)} \star ([0]-[x_e]) = [C]^{\star(g-1)} \star ([0]-[x_e])$
, concluding the proof.
$[C]_0^{\star(g-1)} \star ([0]-[x_e]) = [C]^{\star(g-1)} \star ([0]-[x_e])$
, concluding the proof.
Corollary 2.8.
Suppose that
![]() $[C]_1=0$
in
$[C]_1=0$
in
![]() $\mathrm{CH}_1(J)_{\mathrm{\mathbb{Q}}}$
. Then
$\mathrm{CH}_1(J)_{\mathrm{\mathbb{Q}}}$
. Then
![]() $(2g-2)e=K_C$
in
$(2g-2)e=K_C$
in
![]() $\mathrm{CH}_0(C)_{\mathrm{\mathbb{Q}}}$
.
$\mathrm{CH}_0(C)_{\mathrm{\mathbb{Q}}}$
.
Proof. If
![]() $[C]_1=0$
, then
$[C]_1=0$
, then
![]() $[C]^{\star(g-1)} \star([0]-[x_e])=0$
by (2.3). On the other hand,
$[C]^{\star(g-1)} \star([0]-[x_e])=0$
by (2.3). On the other hand,
![]() $[C]^{\star (g-1)} = (g-1)![\Theta_{(g-1)e}]$
is multiple of a theta divisor, in the notation of the proof of Proposition 2.7. Since
$[C]^{\star (g-1)} = (g-1)![\Theta_{(g-1)e}]$
is multiple of a theta divisor, in the notation of the proof of Proposition 2.7. Since
![]() $\Theta_{(g-1)e}$
defines a principal polarization, the map
$\Theta_{(g-1)e}$
defines a principal polarization, the map
![]() $x\mapsto [\Theta_{(g-1)e + x}] - [\Theta_{(g-1 )e}] = [\Theta_{(g-1)e}]\star ([x]-[0])$
induces an isomorphism
$x\mapsto [\Theta_{(g-1)e + x}] - [\Theta_{(g-1 )e}] = [\Theta_{(g-1)e}]\star ([x]-[0])$
induces an isomorphism
![]() $\varphi\colon J(k)\rightarrow \mathrm{CH}^1(J)_{\hom}$
. Since
$\varphi\colon J(k)\rightarrow \mathrm{CH}^1(J)_{\hom}$
. Since
![]() $\varphi(x_e)$
is torsion, it follows that
$\varphi(x_e)$
is torsion, it follows that
![]() $x_e\in J(k)$
is itself torsion, as desired.
$x_e\in J(k)$
is itself torsion, as desired.
The principal polarization defines an ample class
![]() $\ell\in \mathrm{CH}_{(0)}^1(J)$
, which induces a Lefschetz decomposition
$\ell\in \mathrm{CH}_{(0)}^1(J)$
, which induces a Lefschetz decomposition
![]() ${\frak{h}}^{2g-3}(J) = {\frak{h}}^{2g-3}_{\mathrm{prim}}(J) \bigoplus \ell^{g-2}\cdot {\frak{h}}^1(J)$
as in § 2.5.
${\frak{h}}^{2g-3}(J) = {\frak{h}}^{2g-3}_{\mathrm{prim}}(J) \bigoplus \ell^{g-2}\cdot {\frak{h}}^1(J)$
as in § 2.5.
Corollary 2.9.
Suppose that
![]() $(2g-2)e = K_C$
in
$(2g-2)e = K_C$
in
![]() $\mathrm{CH}_0(C)_{\mathrm{\mathbb{Q}}}$
. Then
$\mathrm{CH}_0(C)_{\mathrm{\mathbb{Q}}}$
. Then
![]() $[C]_1 \in \mathrm{CH}^{g-1}({\frak{h}}^{2g-3}_{\mathrm{prim}}(J))$
.
$[C]_1 \in \mathrm{CH}^{g-1}({\frak{h}}^{2g-3}_{\mathrm{prim}}(J))$
.
Proof. By definition and the discussion in § 2.4,
![]() $[C]_1\in \mathrm{CH}_{(1)}^{g-1}(J) = \mathrm{CH}^{g-1}({\frak{h}}^{2g-3}(J))$
. Since
$[C]_1\in \mathrm{CH}_{(1)}^{g-1}(J) = \mathrm{CH}^{g-1}({\frak{h}}^{2g-3}(J))$
. Since
![]() $x_e$
is torsion,
$x_e$
is torsion,
![]() $(n)_*([0]-[x_e]) =0$
for some integer
$(n)_*([0]-[x_e]) =0$
for some integer
![]() $n\geqslant 1$
. The decomposition (2.2) implies that
$n\geqslant 1$
. The decomposition (2.2) implies that
![]() $[0] = [x_e]$
in
$[0] = [x_e]$
in
![]() $\mathrm{CH}_0(J)_{\mathrm{\mathbb{Q}}}$
. Therefore, (2.3) shows that
$\mathrm{CH}_0(J)_{\mathrm{\mathbb{Q}}}$
. Therefore, (2.3) shows that
![]() $[C]_0^{\star(g-2)} \star [C]_1=0$
. Using properties of the
$[C]_0^{\star(g-2)} \star [C]_1=0$
. Using properties of the
![]() $\mathfrak{sl}_2$
-action on
$\mathfrak{sl}_2$
-action on
![]() $\mathrm{CH}^*(J)_{\mathrm{\mathbb{Q}}}$
(in the sense of [Reference MoonenMoo09, § 1.3]), this implies that
$\mathrm{CH}^*(J)_{\mathrm{\mathbb{Q}}}$
(in the sense of [Reference MoonenMoo09, § 1.3]), this implies that
![]() $\ell \cdot [C]_1 = 0$
. Since
$\ell \cdot [C]_1 = 0$
. Since
![]() $\mathrm{CH}^{g-1}({\frak{h}}^{2g-3}_{\mathrm{prim}}(J))$
equals the kernel of
$\mathrm{CH}^{g-1}({\frak{h}}^{2g-3}_{\mathrm{prim}}(J))$
equals the kernel of
![]() $\ell \cdot (-) \colon \mathrm{CH}^{g-1}({\frak{h}}^{2g-3}(J)) \rightarrow \mathrm{CH}^{g-1}({\frak{h}}^{2g-1}(J)(1))$
, the corollary follows.
$\ell \cdot (-) \colon \mathrm{CH}^{g-1}({\frak{h}}^{2g-3}(J)) \rightarrow \mathrm{CH}^{g-1}({\frak{h}}^{2g-1}(J)(1))$
, the corollary follows.
2.7 Ceresa cycles
Let
![]() $C/k$
be a nice curve of genus
$C/k$
be a nice curve of genus
![]() $g\geqslant 2$
with Jacobian J. Let e be a degree-1 divisor on C and let
$g\geqslant 2$
with Jacobian J. Let e be a degree-1 divisor on C and let
![]() $\iota_e\colon C\rightarrow J$
be the Abel–Jacobi map based at e. We define
$\iota_e\colon C\rightarrow J$
be the Abel–Jacobi map based at e. We define
![]() $\kappa_{C,e}\in \mathrm{CH}_1(J)$
using formula (1.1). Using the Beauville decomposition (2.2) to write
$\kappa_{C,e}\in \mathrm{CH}_1(J)$
using formula (1.1). Using the Beauville decomposition (2.2) to write
![]() $[C] = [\iota_e(C)] = \sum_{s=0}^{g-1} [C]_s$
with
$[C] = [\iota_e(C)] = \sum_{s=0}^{g-1} [C]_s$
with
![]() $[C]_s\in \mathrm{CH}^{g-1}_{(s)}(J)$
, we calculate that
$[C]_s\in \mathrm{CH}^{g-1}_{(s)}(J)$
, we calculate that
in
![]() $\mathrm{CH}_1(J)_{\mathrm{\mathbb{Q}}}$
.
$\mathrm{CH}_1(J)_{\mathrm{\mathbb{Q}}}$
.
Lemma 2.10.
If
![]() $\kappa_{C,e}$
is torsion, then
$\kappa_{C,e}$
is torsion, then
![]() $(2g-2)e-K_C$
is torsion.
$(2g-2)e-K_C$
is torsion.
Lemma 2.11.
If
![]() $e,e'\in \mathrm{CH}_0(C)$
are degree-1 divisors such that
$e,e'\in \mathrm{CH}_0(C)$
are degree-1 divisors such that
![]() $e-e'$
is torsion, then
$e-e'$
is torsion, then
![]() $[\iota_e(C)] = [\iota_{e'}(C)]$
and
$[\iota_e(C)] = [\iota_{e'}(C)]$
and
![]() $\kappa_{C,e} = \kappa_{C,e'}$
in
$\kappa_{C,e} = \kappa_{C,e'}$
in
![]() $\mathrm{CH}_1(J)_{\mathrm{\mathbb{Q}}}$
.
$\mathrm{CH}_1(J)_{\mathrm{\mathbb{Q}}}$
.
Proof. Suppose
![]() $e-e'$
has order n in
$e-e'$
has order n in
![]() $\mathrm{CH}_0(C)$
. Then
$\mathrm{CH}_0(C)$
. Then
![]() $(n)\circ \iota_e = (n) \circ \iota_{e'}$
, hence
$(n)\circ \iota_e = (n) \circ \iota_{e'}$
, hence
![]() $(n)_*([\iota_e(C)] - [\iota_{e'}(C)]) = 0$
in
$(n)_*([\iota_e(C)] - [\iota_{e'}(C)]) = 0$
in
![]() $\mathrm{CH}_1(J)$
. On the other hand, the decomposition (2.2) shows that
$\mathrm{CH}_1(J)$
. On the other hand, the decomposition (2.2) shows that
![]() $(n)_*\colon \mathrm{CH}_1(J)_{\mathrm{\mathbb{Q}}} \rightarrow \mathrm{CH}_1(J)_{\mathrm{\mathbb{Q}}}$
is an isomorphism. Therefore,
$(n)_*\colon \mathrm{CH}_1(J)_{\mathrm{\mathbb{Q}}} \rightarrow \mathrm{CH}_1(J)_{\mathrm{\mathbb{Q}}}$
is an isomorphism. Therefore,
![]() $[\iota_e(C)] - [\iota_{e'}(C)]$
is torsion. Hence,
$[\iota_e(C)] - [\iota_{e'}(C)]$
is torsion. Hence,
![]() $\kappa_{C,e}- \kappa_{C,e'}$
is torsion too.
$\kappa_{C,e}- \kappa_{C,e'}$
is torsion too.
Let
![]() $\kappa(C)$
be the image of
$\kappa(C)$
be the image of
![]() $\kappa_{C,e}$
in
$\kappa_{C,e}$
in
![]() $\mathrm{CH}_1(J)_\mathrm{\mathbb{Q}}$
for any choice of degree-1 divisor e on C such that
$\mathrm{CH}_1(J)_\mathrm{\mathbb{Q}}$
for any choice of degree-1 divisor e on C such that
![]() $(2g-2)e = K_C$
in
$(2g-2)e = K_C$
in
![]() $\mathrm{CH}_0(C)_{\mathrm{\mathbb{Q}}}$
. Lemma 2.11 shows that this class is independent of the choice of e. (If no such e exists over k and if k has characteristic not dividing
$\mathrm{CH}_0(C)_{\mathrm{\mathbb{Q}}}$
. Lemma 2.11 shows that this class is independent of the choice of e. (If no such e exists over k and if k has characteristic not dividing
![]() $2g-2$
, then there exists a unique class
$2g-2$
, then there exists a unique class
![]() $\kappa(C)\in \mathrm{CH}_1(J)_{\mathrm{\mathbb{Q}}}$
such that
$\kappa(C)\in \mathrm{CH}_1(J)_{\mathrm{\mathbb{Q}}}$
such that
![]() $\kappa(C)_{\bar{k}} = \kappa(C_{\bar{k}})$
in
$\kappa(C)_{\bar{k}} = \kappa(C_{\bar{k}})$
in
![]() $\mathrm{CH}_1(J_{\bar{k}})_{\mathrm{\mathbb{Q}}}$
, since Chow groups with Q-coefficients satisfy Galois descent.) We let
$\mathrm{CH}_1(J_{\bar{k}})_{\mathrm{\mathbb{Q}}}$
, since Chow groups with Q-coefficients satisfy Galois descent.) We let
![]() $\bar{\kappa}(C)$
be the image of
$\bar{\kappa}(C)$
be the image of
![]() $\kappa(C)$
in
$\kappa(C)$
in
![]() $\mathrm{Gr}_1(J)_{\mathrm{\mathbb{Q}}}$
. Since all degree-1 divisors e on C are algebraically equivalent,
$\mathrm{Gr}_1(J)_{\mathrm{\mathbb{Q}}}$
. Since all degree-1 divisors e on C are algebraically equivalent,
![]() $\bar{\kappa}(C)$
is also the image of
$\bar{\kappa}(C)$
is also the image of
![]() $\kappa_{e}(C)$
in
$\kappa_{e}(C)$
in
![]() $\mathrm{Gr}_1(J)_\mathrm{\mathbb{Q}}$
for any degree-1 divisor, not necessarily with the property that
$\mathrm{Gr}_1(J)_\mathrm{\mathbb{Q}}$
for any degree-1 divisor, not necessarily with the property that
![]() $(2g-2)e = K_C$
in
$(2g-2)e = K_C$
in
![]() $\mathrm{CH}_0(C)_{\mathrm{\mathbb{Q}}}$
.
$\mathrm{CH}_0(C)_{\mathrm{\mathbb{Q}}}$
.
Suppose now that
![]() $(2g-2)e= K_C$
in
$(2g-2)e= K_C$
in
![]() $\mathrm{CH}_0(C)_{\mathrm{\mathbb{Q}}}$
. Since
$\mathrm{CH}_0(C)_{\mathrm{\mathbb{Q}}}$
. Since
![]() $[\iota_e(C)]\in \mathrm{CH}_1(J)_{\mathrm{\mathbb{Q}}}$
is independent of the choice of e, the same is true for the classes
$[\iota_e(C)]\in \mathrm{CH}_1(J)_{\mathrm{\mathbb{Q}}}$
is independent of the choice of e, the same is true for the classes
![]() $[C]_{s}$
. In particular, they are
$[C]_{s}$
. In particular, they are
![]() $\mathrm{Aut}(C)$
-invariant. The following result, due to Zhang [Reference ZhangZha10, Theorem 1.5.5], shows that the vanishing of
$\mathrm{Aut}(C)$
-invariant. The following result, due to Zhang [Reference ZhangZha10, Theorem 1.5.5], shows that the vanishing of
![]() $\kappa(C)$
is equivalent to the vanishing of
$\kappa(C)$
is equivalent to the vanishing of
![]() $[C]_1$
.
$[C]_1$
.
Proposition 2.12 (S.-W.Zhang). In the above notation,
![]() $\kappa(C)=0$
in
$\kappa(C)=0$
in
![]() $\mathrm{CH}_1(J)_{\mathrm{\mathbb{Q}}}$
if and only if
$\mathrm{CH}_1(J)_{\mathrm{\mathbb{Q}}}$
if and only if
![]() $[C]_1=0$
in
$[C]_1=0$
in
![]() $\mathrm{CH}_1(J)_{\mathrm{\mathbb{Q}}}$
if and only if
$\mathrm{CH}_1(J)_{\mathrm{\mathbb{Q}}}$
if and only if
![]() $[C]_s=0$
for all
$[C]_s=0$
for all
![]() $s\geqslant 1$
. Moreover,
$s\geqslant 1$
. Moreover,
![]() $\bar{\kappa}(C) =0$
in
$\bar{\kappa}(C) =0$
in
![]() $\mathrm{Gr}_1(J)_{\mathrm{\mathbb{Q}}}$
if and only if
$\mathrm{Gr}_1(J)_{\mathrm{\mathbb{Q}}}$
if and only if
![]() $[C]_1 \in \mathrm{Gr}_1(J)_{\mathrm{\mathbb{Q}}}$
if and only if
$[C]_1 \in \mathrm{Gr}_1(J)_{\mathrm{\mathbb{Q}}}$
if and only if
![]() $[C]_s=0$
in
$[C]_s=0$
in
![]() $\mathrm{Gr}_1(J)_{\mathrm{\mathbb{Q}}}$
for all
$\mathrm{Gr}_1(J)_{\mathrm{\mathbb{Q}}}$
for all
![]() $s\geqslant 1$
.
$s\geqslant 1$
.
Proof. Using expression (2.4), it suffices to prove
![]() $[C]_1 = 0$
implies
$[C]_1 = 0$
implies
![]() $[C]_s=0$
for all
$[C]_s=0$
for all
![]() $s\geqslant 1$
. This follows from the third centred equation of [Reference ZhangZha10, Theorem 1.5.5]. The proof for
$s\geqslant 1$
. This follows from the third centred equation of [Reference ZhangZha10, Theorem 1.5.5]. The proof for
![]() $\bar{\kappa}(C)$
is identical.
$\bar{\kappa}(C)$
is identical.
The next lemma isolates a summand of the Chow group that contains
![]() $[C]_1$
. Recall that if M is a direct summand of
$[C]_1$
. Recall that if M is a direct summand of
![]() ${\frak{h}}(J)$
, then
${\frak{h}}(J)$
, then
![]() $\mathrm{CH}^p(M)$
is naturally a summand of
$\mathrm{CH}^p(M)$
is naturally a summand of
![]() $\mathrm{CH}^p({\frak{h}}(J)) = \mathrm{CH}^p(J)_{\mathrm{\mathbb{Q}}}$
.
$\mathrm{CH}^p({\frak{h}}(J)) = \mathrm{CH}^p(J)_{\mathrm{\mathbb{Q}}}$
.
Proposition 2.13.
In the above notation,
![]() $[C]_1\in \mathrm{CH}^{g-1}({\frak{h}}^{2g-3}_{\mathrm{prim}}(J)^{\mathrm{Aut}(C)})\subset \mathrm{CH}_1(J)_{\mathrm{\mathbb{Q}}}$
.
$[C]_1\in \mathrm{CH}^{g-1}({\frak{h}}^{2g-3}_{\mathrm{prim}}(J)^{\mathrm{Aut}(C)})\subset \mathrm{CH}_1(J)_{\mathrm{\mathbb{Q}}}$
.
Proof. Combine Corollary 2.9 and the fact that
![]() $[C]_1$
is
$[C]_1$
is
![]() $\mathrm{Aut}(C)$
-invariant.
$\mathrm{Aut}(C)$
-invariant.
3. Vanishing criteria in the Chow and Griffiths groups
The proof of Theorem A is quite short, but uses Kimura’s notion of finite-dimensional Chow motives in a crucial way [Reference KimuraKim05].
Proof of Theorem A. We use the definitions and notations of §§ 2.3 and 2.7. Choose a degree-1 divisor e such that
![]() $(2g-2)e=K_C$
in
$(2g-2)e=K_C$
in
![]() $\mathrm{CH}_0(C)_{\mathrm{\mathbb{Q}}}$
and decompose
$\mathrm{CH}_0(C)_{\mathrm{\mathbb{Q}}}$
and decompose
![]() $[\iota_e(C)] = \sum_{s=0}^{g-1} [C]_s$
with
$[\iota_e(C)] = \sum_{s=0}^{g-1} [C]_s$
with
![]() $[C]_s \in \mathrm{CH}^{g-1}_{(s)}(J)$
. Let
$[C]_s \in \mathrm{CH}^{g-1}_{(s)}(J)$
. Let
![]() $G = \mathrm{Aut}(C)$
. Proposition 2.13 shows that
$G = \mathrm{Aut}(C)$
. Proposition 2.13 shows that
![]() $[C]_1\in \mathrm{CH}^{g-1}({\frak{h}}^{2g-3}_{\mathrm{prim}}(J)^{G})$
.
$[C]_1\in \mathrm{CH}^{g-1}({\frak{h}}^{2g-3}_{\mathrm{prim}}(J)^{G})$
.
By the hypothesis and the Lefschetz isomorphism,
![]() $\mathrm{H}^*({\frak{h}}_{\mathrm{prim}}^{2g-3}(J)^{G}) = \mathrm{H}^{2g-3}_{\mathrm{prim}}(J)^G=0$
. Since any summand of the motive of an abelian variety is finite-dimensional in the sense of Kimura [Reference KimuraKim05, Example 9.1], it follows from [Reference KimuraKim05, Corollary 7.3] that
$\mathrm{H}^*({\frak{h}}_{\mathrm{prim}}^{2g-3}(J)^{G}) = \mathrm{H}^{2g-3}_{\mathrm{prim}}(J)^G=0$
. Since any summand of the motive of an abelian variety is finite-dimensional in the sense of Kimura [Reference KimuraKim05, Example 9.1], it follows from [Reference KimuraKim05, Corollary 7.3] that
![]() ${\frak{h}}^{2g-3}_{\mathrm{prim}}(J)^{G} = 0$
and hence
${\frak{h}}^{2g-3}_{\mathrm{prim}}(J)^{G} = 0$
and hence
![]() $[C]_1 = 0$
in
$[C]_1 = 0$
in
![]() $\mathrm{CH}^{g-1}(J)_{\mathrm{\mathbb{Q}}}$
. By Proposition 2.12, we conclude that
$\mathrm{CH}^{g-1}(J)_{\mathrm{\mathbb{Q}}}$
. By Proposition 2.12, we conclude that
![]() $\kappa(C)=0$
.
$\kappa(C)=0$
.
Example 3.1. There is exactly one non-hyperelliptic genus-3 curve over C for which the criterion of [Reference Qiu and ZhangQZ24] applies, namely the curve
![]() $y^3 = x^4 + 1$
. The curve
$y^3 = x^4 + 1$
. The curve
![]() $y^3 = x^4 + x$
satisfies the weaker hypothesis of Theorem A (as was observed in [Reference BeauvilleBea21]), so we deduce that
$y^3 = x^4 + x$
satisfies the weaker hypothesis of Theorem A (as was observed in [Reference BeauvilleBea21]), so we deduce that
![]() $\kappa(C) = 0$
for this curve as well. Beauville and Schoen studied the specific geometry of this curve and showed that
$\kappa(C) = 0$
for this curve as well. Beauville and Schoen studied the specific geometry of this curve and showed that
![]() $\bar{\kappa}(C) = 0$
[Reference Beauville and SchoenBS23].
$\bar{\kappa}(C) = 0$
[Reference Beauville and SchoenBS23].
Example 3.2. The genus-4 curve
![]() $y^3 = x^5 + 1$
satisfies
$y^3 = x^5 + 1$
satisfies
![]() $\mathrm{H}^3(J)^{\mathrm{Aut}(C)} = 0$
[Reference Lilienfeldt and ShnidmanLS23b, proof of Theorem 3.3], so
$\mathrm{H}^3(J)^{\mathrm{Aut}(C)} = 0$
[Reference Lilienfeldt and ShnidmanLS23b, proof of Theorem 3.3], so
![]() $\kappa(C)=0$
.
$\kappa(C)=0$
.
Theorem B will follow from the next proposition. In that proposition and its proof, if X is a nice variety over C we write
![]() $\mathrm{H}^*(X)$
for the singular cohomology of
$\mathrm{H}^*(X)$
for the singular cohomology of
![]() $X(\mathrm{\mathbb{C}})$
with Q-coefficients, seen as an object in the category of Hodge structures.
$X(\mathrm{\mathbb{C}})$
with Q-coefficients, seen as an object in the category of Hodge structures.
Proposition 3.3. Let C be a smooth, projective, integral curve over C with Jacobian J and let
![]() $G\subset \mathrm{Aut}(C)$
be a subgroup with
$G\subset \mathrm{Aut}(C)$
be a subgroup with
![]() $\mathrm{H}^0(J, \Omega_J^3)^{G}=0$
. Then there exists an abelian variety
$\mathrm{H}^0(J, \Omega_J^3)^{G}=0$
. Then there exists an abelian variety
![]() $A/\mathrm{\mathbb{C}}$
such that
$A/\mathrm{\mathbb{C}}$
such that
![]() $\mathrm{H}^3(J)^{G} \simeq \mathrm{H}^1(A)(-1)$
. If the Hodge conjecture holds for
$\mathrm{H}^3(J)^{G} \simeq \mathrm{H}^1(A)(-1)$
. If the Hodge conjecture holds for
![]() $J\times A$
, then
$J\times A$
, then
![]() ${\frak{h}}^3(J)^{G}\simeq {\frak{h}}^1(A)(-1)$
and
${\frak{h}}^3(J)^{G}\simeq {\frak{h}}^1(A)(-1)$
and
![]() $\bar{\kappa}(C)=0$
.
$\bar{\kappa}(C)=0$
.
Proof. Let
![]() $N^1\mathrm{H}^3(J)$
be the largest sub-Hodge structure of
$N^1\mathrm{H}^3(J)$
be the largest sub-Hodge structure of
![]() $\mathrm{H}^3(J)$
of type
$\mathrm{H}^3(J)$
of type
![]() $(1,2)+(2,1)$
. The polarization on
$(1,2)+(2,1)$
. The polarization on
![]() $\mathrm{H}^1(J)$
induces a polarization on
$\mathrm{H}^1(J)$
induces a polarization on
![]() $N^1\mathrm{H}^3(J)$
and so
$N^1\mathrm{H}^3(J)$
and so
![]() $N^1\mathrm{H}^3(J) \simeq \mathrm{H}^1(B)(-1)$
for some abelian variety
$N^1\mathrm{H}^3(J) \simeq \mathrm{H}^1(B)(-1)$
for some abelian variety
![]() $B/\mathrm{\mathbb{C}}$
. The assumptions and the Hodge decomposition imply that
$B/\mathrm{\mathbb{C}}$
. The assumptions and the Hodge decomposition imply that
![]() $\mathrm{H}^3(J)^G$
is a Hodge structure of type
$\mathrm{H}^3(J)^G$
is a Hodge structure of type
![]() $(1,2) + (2,1)$
. It follows that
$(1,2) + (2,1)$
. It follows that
![]() $\mathrm{H}^3(J)^G \subset N^1\mathrm{H}^3(J)$
, so there exists an abelian subvariety
$\mathrm{H}^3(J)^G \subset N^1\mathrm{H}^3(J)$
, so there exists an abelian subvariety
![]() $A\subset B$
with
$A\subset B$
with
![]() $\mathrm{H}^3(J)^G \simeq \mathrm{H}^1(A)(-1)$
.
$\mathrm{H}^3(J)^G \simeq \mathrm{H}^1(A)(-1)$
.
We now show that the Hodge conjecture for
![]() $J\times A$
implies the claims of the final sentence. Fix mutually inverse isomorphisms of Hodge structures
$J\times A$
implies the claims of the final sentence. Fix mutually inverse isomorphisms of Hodge structures
![]() $\phi\colon \mathrm{H}^3(J)^G\rightarrow \mathrm{H}^1(A)(-1)$
and
$\phi\colon \mathrm{H}^3(J)^G\rightarrow \mathrm{H}^1(A)(-1)$
and
![]() $\psi\colon \mathrm{H}^1(A)(-1)\rightarrow \mathrm{H}^3(J)^G$
. By the Hodge conjecture, there exist morphisms of motives
$\psi\colon \mathrm{H}^1(A)(-1)\rightarrow \mathrm{H}^3(J)^G$
. By the Hodge conjecture, there exist morphisms of motives
![]() $\Phi\colon {\frak{h}}^3(J)^G \rightarrow {\frak{h}}^1(A)(-1)$
and
$\Phi\colon {\frak{h}}^3(J)^G \rightarrow {\frak{h}}^1(A)(-1)$
and
![]() $\Psi \colon {\frak{h}}^1(A)(-1) \rightarrow {\frak{h}}^3(J)^G$
(in other words, cycles on
$\Psi \colon {\frak{h}}^1(A)(-1) \rightarrow {\frak{h}}^3(J)^G$
(in other words, cycles on
![]() $J\times A$
with certain properties) with
$J\times A$
with certain properties) with
![]() $\mathrm{H}^*(\Phi) = \phi$
and
$\mathrm{H}^*(\Phi) = \phi$
and
![]() $\mathrm{H}^*(\Psi) = \psi$
. Since
$\mathrm{H}^*(\Psi) = \psi$
. Since
![]() ${\frak{h}}^1(A)(-1)$
and
${\frak{h}}^1(A)(-1)$
and
![]() ${\frak{h}}^3(J)^G$
are Kimura finite-dimensional [Reference KimuraKim05, Example 9.1] and
${\frak{h}}^3(J)^G$
are Kimura finite-dimensional [Reference KimuraKim05, Example 9.1] and
![]() $\mathrm{H}^*(\Phi) \circ \mathrm{H}^*(\Psi)$
and
$\mathrm{H}^*(\Phi) \circ \mathrm{H}^*(\Psi)$
and
![]() $\mathrm{H}^*(\Psi) \circ \mathrm{H}^*(\Phi)$
are the identity, it follows from [Reference KimuraKim05, Proposition 7.2(ii)] (see also [Reference AndréAnd05, Corollaire 3.16]) that
$\mathrm{H}^*(\Psi) \circ \mathrm{H}^*(\Phi)$
are the identity, it follows from [Reference KimuraKim05, Proposition 7.2(ii)] (see also [Reference AndréAnd05, Corollaire 3.16]) that
![]() $\Psi\circ \Phi$
and
$\Psi\circ \Phi$
and
![]() $\Phi\circ \Psi$
are themselves isomorphisms. Hence,
$\Phi\circ \Psi$
are themselves isomorphisms. Hence,
![]() $\Phi$
and
$\Phi$
and
![]() $\Psi$
are isomorphisms too and we conclude that
$\Psi$
are isomorphisms too and we conclude that
![]() ${\frak{h}}^3(J)^G \simeq {\frak{h}}^1(A)(-1)$
.
${\frak{h}}^3(J)^G \simeq {\frak{h}}^1(A)(-1)$
.
Using the Lefschetz isomorphism
![]() ${\frak{h}}^{2g-3}(J) \simeq {\frak{h}}^3(J)(-g+3)$
of [Kün93, Theorem 5.2], we obtain an isomorphism
${\frak{h}}^{2g-3}(J) \simeq {\frak{h}}^3(J)(-g+3)$
of [Kün93, Theorem 5.2], we obtain an isomorphism
![]() ${\frak{h}}^{2g-3}(J)^G\simeq {\frak{h}}^1(A)(-g+2)$
. Similarly to the proof of Theorem A, we decompose
${\frak{h}}^{2g-3}(J)^G\simeq {\frak{h}}^1(A)(-g+2)$
. Similarly to the proof of Theorem A, we decompose
![]() $[\iota_e(C)] = \sum_{s=0}^{g-1} [C]_s$
with
$[\iota_e(C)] = \sum_{s=0}^{g-1} [C]_s$
with
![]() $[C]_s \in \mathrm{CH}^{g-1}_{(s)}(J)$
and observe that the class
$[C]_s \in \mathrm{CH}^{g-1}_{(s)}(J)$
and observe that the class
![]() $[C]_1$
lies in
$[C]_1$
lies in
![]() $\mathrm{CH}_{(1)}^{g-1}(J)^G = \mathrm{CH}^{g-1}({\frak{h}}^{2g-3}(J)^G)$
. Lemma 2.6 combined with the isomorphism
$\mathrm{CH}_{(1)}^{g-1}(J)^G = \mathrm{CH}^{g-1}({\frak{h}}^{2g-3}(J)^G)$
. Lemma 2.6 combined with the isomorphism
![]() ${\frak{h}}^{2g-3}(J)^G\simeq {\frak{h}}^1(A)(-g+2)$
shows that
${\frak{h}}^{2g-3}(J)^G\simeq {\frak{h}}^1(A)(-g+2)$
shows that
![]() $\mathrm{CH}^{g-1}({\frak{h}}^{2g-3}(J)^G) = \mathrm{CH}^{g-1}({\frak{h}}^{2g-3}(J)^G)_{\mathrm{alg}}$
, hence every element of
$\mathrm{CH}^{g-1}({\frak{h}}^{2g-3}(J)^G) = \mathrm{CH}^{g-1}({\frak{h}}^{2g-3}(J)^G)_{\mathrm{alg}}$
, hence every element of
![]() $\mathrm{CH}^{g-1}_{(1)}(J)^G$
lies in
$\mathrm{CH}^{g-1}_{(1)}(J)^G$
lies in
![]() $\mathrm{CH}^{g-1}(J)_{\mathrm{alg},\mathrm{\mathbb{Q}}}$
. Therefore,
$\mathrm{CH}^{g-1}(J)_{\mathrm{alg},\mathrm{\mathbb{Q}}}$
. Therefore,
![]() $[C]_1\in \mathrm{CH}^{g-1}(J)_{\mathrm{alg},\mathrm{\mathbb{Q}}}$
, hence the image of
$[C]_1\in \mathrm{CH}^{g-1}(J)_{\mathrm{alg},\mathrm{\mathbb{Q}}}$
, hence the image of
![]() $[C]_1$
in
$[C]_1$
in
![]() $\mathrm{Gr}_1(J)_{\mathrm{\mathbb{Q}}}$
vanishes. Proposition 2.12 then implies that
$\mathrm{Gr}_1(J)_{\mathrm{\mathbb{Q}}}$
vanishes. Proposition 2.12 then implies that
![]() $\bar{\kappa}(C)$
vanishes too.
$\bar{\kappa}(C)$
vanishes too.
Proof of Theorem B.Since C can be defined over a countable field and since such a field can be embedded in C, Lemma 2.1 shows that we may assume
![]() $k=\mathrm{\mathbb{C}}$
. We conclude by Proposition 3.3 applied to
$k=\mathrm{\mathbb{C}}$
. We conclude by Proposition 3.3 applied to
![]() $G = \mathrm{Aut}(C)$
.
$G = \mathrm{Aut}(C)$
.
We now describe some families of curves for which the criterion of Theorem B applies. If
![]() $C/k$
is a curve we write
$C/k$
is a curve we write
![]() $V(C) = \mathrm{H}^0(C, \Omega_C)$
, which we think of as an
$V(C) = \mathrm{H}^0(C, \Omega_C)$
, which we think of as an
![]() $\mathrm{Aut}(C)$
-representation. Recall that it is
$\mathrm{Aut}(C)$
-representation. Recall that it is
![]() $\bigwedge^3 V(C) \simeq \mathrm{H}^0(J, \Omega_J^3)$
that appears in Theorem B.
$\bigwedge^3 V(C) \simeq \mathrm{H}^0(J, \Omega_J^3)$
that appears in Theorem B.
Example 3.4. Let
![]() $C \colon y^3 = x^4 + ax^2 + bx + c$
be a Picard curve. Then
$C \colon y^3 = x^4 + ax^2 + bx + c$
be a Picard curve. Then
![]() $V(C) \simeq \chi \bigoplus \chi \bigoplus \chi^2$
as
$V(C) \simeq \chi \bigoplus \chi \bigoplus \chi^2$
as
![]() $C_3$
-representations, where
$C_3$
-representations, where
![]() $\chi$
is a character of order 3. It follows that
$\chi$
is a character of order 3. It follows that
![]() $(\bigwedge^3V(C))^{\mathrm{Aut}(C)} = 0$
, so that the condition of Theorem B is satisfied. We consider these curves in detail in the next section.
$(\bigwedge^3V(C))^{\mathrm{Aut}(C)} = 0$
, so that the condition of Theorem B is satisfied. We consider these curves in detail in the next section.
Example 3.5. The general
![]() $\mu_3$
-cover of
$\mu_3$
-cover of
![]() $\mathrm{\mathbb{P}}^1$
with equation
$\mathrm{\mathbb{P}}^1$
with equation
has genus 4 and by [Reference MoonenMoo10, Lemma 2.7] we have
![]() $V(C) \simeq \chi \bigoplus \chi \bigoplus \chi^2 \bigoplus \chi^2$
as
$V(C) \simeq \chi \bigoplus \chi \bigoplus \chi^2 \bigoplus \chi^2$
as
![]() $C_3$
-representations. It follows that
$C_3$
-representations. It follows that
![]() $(\bigwedge^3V(C))^{C_3} = 0$
and the abelian variety A from Proposition 13 is four-dimensional. If the Hodge conjecture holds for the eight-dimensional
$(\bigwedge^3V(C))^{C_3} = 0$
and the abelian variety A from Proposition 13 is four-dimensional. If the Hodge conjecture holds for the eight-dimensional
![]() $J \times A$
, then
$J \times A$
, then
![]() $\bar{\kappa}(C) = 0$
.
$\bar{\kappa}(C) = 0$
.
For our next class of examples, we consider one-parameter families of smooth projective curves with affine model of the form
for integers m,a, and b satisfying
![]() $0 < a < b < m/2$
and
$0 < a < b < m/2$
and
![]() $\gcd(m,a,b) = 1$
. If
$\gcd(m,a,b) = 1$
. If
![]() $t\neq 0,\pm 1$
, then
$t\neq 0,\pm 1$
, then
![]() $C_t$
is smooth projective of genus
$C_t$
is smooth projective of genus
which we will assume below is at least 3. These curves admit an action by the dihedral group
![]() $D_m$
, generated by the automorphisms
$D_m$
, generated by the automorphisms
![]() $(x,y) \mapsto (x,\zeta_m y)$
and
$(x,y) \mapsto (x,\zeta_m y)$
and
![]() $\tau(x,y) = (-x, y^{-1})$
.
$\tau(x,y) = (-x, y^{-1})$
.
Lemma 3.6.
The induced action of
![]() $\mu_m \subset D_m$
on
$\mu_m \subset D_m$
on
![]() $V(C_t)$
has character
$V(C_t)$
has character
![]() $\sum_{n = 1}^{m-1} \epsilon(n) \chi^n$
, where
$\sum_{n = 1}^{m-1} \epsilon(n) \chi^n$
, where
![]() $\chi^n$
is the one-dimensional representation of
$\chi^n$
is the one-dimensional representation of
![]() $\mu_m$
on which
$\mu_m$
on which
![]() $\zeta \in \mu_m$
acts by
$\zeta \in \mu_m$
acts by
![]() $\zeta^n$
and
$\zeta^n$
and
 \[ \epsilon(n) = \begin{cases} 1 & \mbox{if neither $m\nmid na$ nor $m \nmid nb$,}\\ 0 & \mbox{otherwise.} \end{cases} \]
\[ \epsilon(n) = \begin{cases} 1 & \mbox{if neither $m\nmid na$ nor $m \nmid nb$,}\\ 0 & \mbox{otherwise.} \end{cases} \]
Proof. This follows from [Reference MoonenMoo10, Lemma 2.7].
Corollary 3.7.
The space
![]() $\bigwedge^3 V(C_t)$
has a non-trivial
$\bigwedge^3 V(C_t)$
has a non-trivial
![]() $D_m$
-invariant subspace if and only if there exists a triple of integers
$D_m$
-invariant subspace if and only if there exists a triple of integers
![]() $0 < n_1 < n_2 < n_3 < m$
such that for all
$0 < n_1 < n_2 < n_3 < m$
such that for all
![]() $i \in \{1,2,3\}$
neither
$i \in \{1,2,3\}$
neither
![]() $m\mid n_ia$
nor
$m\mid n_ia$
nor
![]() $m \mid n_i b$
, and such that
$m \mid n_i b$
, and such that
![]() $n_1 + n_2 + n_3 = m$
.
$n_1 + n_2 + n_3 = m$
.
Proof. By the lemma, a
![]() $\mu_m$
-invariant subspace exists if and only if there exists a triple with the above divisibility properties and such that
$\mu_m$
-invariant subspace exists if and only if there exists a triple with the above divisibility properties and such that
![]() $n_1 +n_2 + n_3 \in \{m, 2m\}$
. However, if there exists such a triple summing to 2m then the triple
$n_1 +n_2 + n_3 \in \{m, 2m\}$
. However, if there exists such a triple summing to 2m then the triple
![]() $m-n_3,m-n_2,m-n_1$
is another such triple whose sum is m. Finally, observe that
$m-n_3,m-n_2,m-n_1$
is another such triple whose sum is m. Finally, observe that
![]() $\tau$
swaps the
$\tau$
swaps the
![]() $\chi^n$
-isotypic component of
$\chi^n$
-isotypic component of
![]() $V(C_t)$
with the
$V(C_t)$
with the
![]() $\chi^{-n}$
-isotypic component. It follows that
$\chi^{-n}$
-isotypic component. It follows that
![]() $(\bigwedge^3V(C_t))^{\mu_m} = 0$
if and only if
$(\bigwedge^3V(C_t))^{\mu_m} = 0$
if and only if
![]() $(\bigwedge^3V(C_t))^{D_m} = 0$
.
$(\bigwedge^3V(C_t))^{D_m} = 0$
.
Below, we determine the triples
![]() $a < b < m/2$
such that
$a < b < m/2$
such that
![]() $C_t$
satisfies the hypotheses of Theorem B.
$C_t$
satisfies the hypotheses of Theorem B.
Example 3.8. Suppose
![]() $\gcd(m,6) = 1$
. As long as
$\gcd(m,6) = 1$
. As long as
![]() $m \geqslant 7$
, the triple
$m \geqslant 7$
, the triple
![]() $1 < 2 < m-3$
corresponds to an invariant subspace of
$1 < 2 < m-3$
corresponds to an invariant subspace of
![]() $\bigwedge^3V(C_t)$
, so that Theorem B does not apply. However, when
$\bigwedge^3V(C_t)$
, so that Theorem B does not apply. However, when
![]() $m = 5$
, the sum of any three non-zero elements of
$m = 5$
, the sum of any three non-zero elements of
![]() $\mathrm{\mathbb{Z}}/5\mathrm{\mathbb{Z}}$
is non-zero and so we find a genus-4 family which does satisfy the criteria of Theorem B, namely,
$\mathrm{\mathbb{Z}}/5\mathrm{\mathbb{Z}}$
is non-zero and so we find a genus-4 family which does satisfy the criteria of Theorem B, namely,
One checks that
![]() $\mathrm{H}^3(J)^{\mu_5} \simeq \mathrm{H}^1(A)(-1)$
, for some abelian surface A (using Proposition 3.3).
$\mathrm{H}^3(J)^{\mu_5} \simeq \mathrm{H}^1(A)(-1)$
, for some abelian surface A (using Proposition 3.3).
Lemma 3.9.
The 4-fold
![]() $\mathrm{Jac}(C_t)$
is isogenous to the square of
$\mathrm{Jac}(C_t)$
is isogenous to the square of
![]() $\mathrm{Jac}(C_t/\tau)$
.
$\mathrm{Jac}(C_t/\tau)$
.
Proof. The group
![]() $D_5 \subset \mathrm{Aut}(C_t)$
is the union of its six non-trivial proper subgroups, with all pairwise intersections being trivial. Moreover,
$D_5 \subset \mathrm{Aut}(C_t)$
is the union of its six non-trivial proper subgroups, with all pairwise intersections being trivial. Moreover,
![]() $C_t/\tau \simeq C_t/\sigma$
for any other involution
$C_t/\tau \simeq C_t/\sigma$
for any other involution
![]() $\sigma \in D_5$
, since all involutions are conjugate. Applying [Reference Kani and RosenKR89, Theorem B], we conclude that
$\sigma \in D_5$
, since all involutions are conjugate. Applying [Reference Kani and RosenKR89, Theorem B], we conclude that
![]() $\mathrm{Jac}(C_t)^5 \sim \mathrm{Jac}(C_t/\tau)^{10}$
(note that
$\mathrm{Jac}(C_t)^5 \sim \mathrm{Jac}(C_t/\tau)^{10}$
(note that
![]() $C_t/D_5$
and
$C_t/D_5$
and
![]() $C_t/C_5$
have genus 0). Thus
$C_t/C_5$
have genus 0). Thus
![]() $\mathrm{Jac}(C_t)\sim \mathrm{Jac}(C_t/\tau)^2$
.
$\mathrm{Jac}(C_t)\sim \mathrm{Jac}(C_t/\tau)^2$
.
The Hodge conjecture is known for products of abelian surfaces [Reference Ramón MarRM08, Theorem 3.15], so Proposition 3.3 implies that
![]() $\bar{\kappa}(C_t) = 0$
.
$\bar{\kappa}(C_t) = 0$
.
Example 3.10. If m is even, then proceeding in a manner similar to the previous example, one checks that
![]() $(\bigwedge^3 V(C_t))^{D_m} = 0$
implies that
$(\bigwedge^3 V(C_t))^{D_m} = 0$
implies that
![]() $m = 6$
(giving a subfamily of Example 3.5) or
$m = 6$
(giving a subfamily of Example 3.5) or
![]() $m = 12$
. In the latter case, we find the family of genus-6 curves
$m = 12$
. In the latter case, we find the family of genus-6 curves
which indeed satisfies the hypotheses of Theorem B.
Example 3.11. In the remaining case where m is an odd multiple of 3, we check that the condition
![]() $(\bigwedge^3 V(C_t))^{D_m} = 0$
implies that
$(\bigwedge^3 V(C_t))^{D_m} = 0$
implies that
![]() $m = 9$
or
$m = 9$
or
![]() $m = 15$
and moreover that one of a or b is
$m = 15$
and moreover that one of a or b is
![]() $m/3$
. These correspond to the genus-6 family
$m/3$
. These correspond to the genus-6 family
and the genus-8 family
which again satisfy the hypotheses of Theorem B.
One can check (by specializing) that the families above are generically non-hyperelliptic, so these are genuinely interesting curves satisfying
![]() $\overline{\kappa}(C) = 0$
(in some cases, conditional on the Hodge conjecture). Quotienting by the involution
$\overline{\kappa}(C) = 0$
(in some cases, conditional on the Hodge conjecture). Quotienting by the involution
![]() $\tau$
, we also recover the first known examples of families of curves C with
$\tau$
, we also recover the first known examples of families of curves C with
![]() $\overline{\kappa}(C) = 0$
and
$\overline{\kappa}(C) = 0$
and
![]() $\mathrm{Aut}(C) = 0$
:
$\mathrm{Aut}(C) = 0$
:
Theorem 3.12. Assuming the Hodge conjecture, there exist, for
![]() $g \in \{3,4\}$
, non-trivial one-parameter families
$g \in \{3,4\}$
, non-trivial one-parameter families
![]() $\{X_u\}$
of genus-g curves over C with
$\{X_u\}$
of genus-g curves over C with
![]() $\bar{\kappa}(X_u) = 0$
and which generically satisfy
$\bar{\kappa}(X_u) = 0$
and which generically satisfy
![]() $\mathrm{Aut}(X_u) = \{1\}$
.
$\mathrm{Aut}(X_u) = \{1\}$
.
Proof. Consider the family
![]() $C_t$
in (3.1), which satisfies the hypotheses of Theorem B. The quotient
$C_t$
in (3.1), which satisfies the hypotheses of Theorem B. The quotient
![]() $Y_t = C_t/\tau$
is a family of genus-3 curves. Since we assume the Hodge conjecture, Theorem B implies that
$Y_t = C_t/\tau$
is a family of genus-3 curves. Since we assume the Hodge conjecture, Theorem B implies that
![]() $\overline{\kappa}(C_t) = 0$
and hence
$\overline{\kappa}(C_t) = 0$
and hence
![]() $\overline{\kappa}(Y_t) = 0$
as well. Computing in Magma [Reference Bosma, Cannon and PlayoustBCP97], we find that
$\overline{\kappa}(Y_t) = 0$
as well. Computing in Magma [Reference Bosma, Cannon and PlayoustBCP97], we find that
![]() $Y_t$
is isomorphic to the curve
$Y_t$
is isomorphic to the curve
where
![]() $u = (t-1)/(t+1)$
. Specializing to
$u = (t-1)/(t+1)$
. Specializing to
![]() $u = 2$
, we check in Magma that the automorphism group is trivial and hence
$u = 2$
, we check in Magma that the automorphism group is trivial and hence
![]() $\mathrm{Aut}(X_u) = \{1\}$
generically.
$\mathrm{Aut}(X_u) = \{1\}$
generically.
The proof when
![]() $g = 4$
is similar, using the involution on the genus-8 family (3.2).
$g = 4$
is similar, using the involution on the genus-8 family (3.2).
Remark 3.13. Edgar Costa has verified for us, using [Reference Costa, Mascot, Sijsling and VoightCMSV19], that the generic endomorphism algebra of
![]() $\mathrm{Jac}(X_u)$
is contained in
$\mathrm{Jac}(X_u)$
is contained in
![]() $K = \mathrm{\mathbb{Q}}(\zeta_9 + \zeta_9^{-1})$
; by [Reference EllenbergEll01,§ 3], this inclusion is an equality. Similarly, in the genus-4 family, the algebra
$K = \mathrm{\mathbb{Q}}(\zeta_9 + \zeta_9^{-1})$
; by [Reference EllenbergEll01,§ 3], this inclusion is an equality. Similarly, in the genus-4 family, the algebra
![]() $\mathrm{End}^0(\mathrm{Jac}(X_u))$
contains
$\mathrm{End}^0(\mathrm{Jac}(X_u))$
contains
![]() $\mathrm{\mathbb{Q}}(\zeta_{15} + \zeta_{15}^{-1})$
.
$\mathrm{\mathbb{Q}}(\zeta_{15} + \zeta_{15}^{-1})$
.
It would be interesting to study the families in Examples 3.5, 3.8, 3.10 and 3.11 in more detail, and in particular to try to prove the relevant case of the Hodge conjecture and determine the locus where the Ceresa class vanishes in the Chow group (and not just the Griffiths group). We do this for the family of Picard curves in the next section.
4 Picard curves
4.1 Generalities
Let k be a field of characteristic 0. A Picard curve over k is by definition a nice curve with an affine model
![]() $y^3 = f(x) = x^4+ax^2+bx+c$
for some
$y^3 = f(x) = x^4+ax^2+bx+c$
for some
![]() $a,b,c\in k$
. Conversely, given such a polynomial
$a,b,c\in k$
. Conversely, given such a polynomial
![]() $f(x) \in k[x]$
of non-zero discriminant, the projective closure of
$f(x) \in k[x]$
of non-zero discriminant, the projective closure of
![]() $y^3= f(x)$
in
$y^3= f(x)$
in
![]() $\mathrm{\mathbb{P}}^2_k$
is a nice curve denoted by
$\mathrm{\mathbb{P}}^2_k$
is a nice curve denoted by
![]() $C_f$
. It has a unique point at infinity
$C_f$
. It has a unique point at infinity
![]() $P_{\infty}$
, which is k-rational.
$P_{\infty}$
, which is k-rational.
For every third root of unity
![]() $\omega \in \bar{k}$
, the map
$\omega \in \bar{k}$
, the map
![]() $(x,y)\mapsto (x,\omega y)$
defines an automorphism of
$(x,y)\mapsto (x,\omega y)$
defines an automorphism of
![]() $C_{f,\bar{k}}$
. We view
$C_{f,\bar{k}}$
. We view
![]() $\mu_3$
as a subgroup of
$\mu_3$
as a subgroup of
![]() $\mathrm{Aut}(C_{f,\bar{k}})$
in this way. Then
$\mathrm{Aut}(C_{f,\bar{k}})$
in this way. Then
![]() $\mu_3$
also acts on the Jacobian
$\mu_3$
also acts on the Jacobian
![]() $J_{f,\bar{k}}$
by taking images of divisors.
$J_{f,\bar{k}}$
by taking images of divisors.
The discriminant of f has the following expression:
We view f as the dehomogenization F(x,1) of the quartic form
![]() $F(X,Z) = X^4+aX^2Z^2+bXZ^3+cZ^4$
, and we define I(f) and J(f) to be the usual I- and J-invariants attached to F, as in [Reference Bhargava and ShankarBS15, § 2]. Their explicit formulae in our case are
$F(X,Z) = X^4+aX^2Z^2+bXZ^3+cZ^4$
, and we define I(f) and J(f) to be the usual I- and J-invariants attached to F, as in [Reference Bhargava and ShankarBS15, § 2]. Their explicit formulae in our case are
The nineteenth-century invariant theorists observed the identity
![]() $J(f)^2 = 4I(f)^3 - 27\cdot \mathrm{disc}(f)$
, which can be verified by direct computation. Therefore,
$J(f)^2 = 4I(f)^3 - 27\cdot \mathrm{disc}(f)$
, which can be verified by direct computation. Therefore,
![]() $P_f:=(I(f),J(f))$
is a k-point on the elliptic curve
$P_f:=(I(f),J(f))$
is a k-point on the elliptic curve
4.2 Ceresa vanishing criteria
Since
![]() $(2g-2)P_{\infty}=4P_{\infty}$
is canonical, we may use
$(2g-2)P_{\infty}=4P_{\infty}$
is canonical, we may use
![]() $P_{\infty}$
to embed
$P_{\infty}$
to embed
![]() $C_f$
in its Jacobian
$C_f$
in its Jacobian
![]() $J_f$
and define the Ceresa cycle
$J_f$
and define the Ceresa cycle
![]() $\kappa_{C_f, P_{\infty}}\in \mathrm{CH}_1(J_f)$
as in the introduction; we denote it by
$\kappa_{C_f, P_{\infty}}\in \mathrm{CH}_1(J_f)$
as in the introduction; we denote it by
![]() $\kappa_f$
for simplicity. Recall that
$\kappa_f$
for simplicity. Recall that
![]() $\kappa(C_f)$
denotes the image of
$\kappa(C_f)$
denotes the image of
![]() $\kappa_f$
in
$\kappa_f$
in
![]() $\mathrm{CH}_1(J_f)_{\mathrm{\mathbb{Q}}}$
and
$\mathrm{CH}_1(J_f)_{\mathrm{\mathbb{Q}}}$
and
![]() $\bar{\kappa}(C_f)$
its image in
$\bar{\kappa}(C_f)$
its image in
![]() $\mathrm{Gr}_1(J_f)_{\mathrm{\mathbb{Q}}}$
. Theorem C follows from the following slightly stronger theorems, whose proofs will take up the rest of this section.
$\mathrm{Gr}_1(J_f)_{\mathrm{\mathbb{Q}}}$
. Theorem C follows from the following slightly stronger theorems, whose proofs will take up the rest of this section.
Theorem 4.1. There exists an integer
![]() $N\geqslant 1$
(depending neither on f nor on k) such that
$N\geqslant 1$
(depending neither on f nor on k) such that
![]() $N\cdot \kappa_f\in \mathrm{CH}^2(J_f)_{\mathrm{alg}}$
for every Picard curve
$N\cdot \kappa_f\in \mathrm{CH}^2(J_f)_{\mathrm{alg}}$
for every Picard curve
![]() $C_f$
over every algebraically closed field k (of characteristic 0).
$C_f$
over every algebraically closed field k (of characteristic 0).
Theorem 4.2. The Ceresa cycle
![]() $\kappa_f\in \mathrm{CH}_1(J)$
is torsion if and only if
$\kappa_f\in \mathrm{CH}_1(J)$
is torsion if and only if
![]() $P_f\in E_f(k)$
is torsion. Moreover, if k is algebraically closed, then there exists an integer
$P_f\in E_f(k)$
is torsion. Moreover, if k is algebraically closed, then there exists an integer
![]() $M\geqslant 1$
with the following property: if
$M\geqslant 1$
with the following property: if
![]() $C_f$
is a Picard curve and
$C_f$
is a Picard curve and
![]() $\kappa_f$
is torsion, then
$\kappa_f$
is torsion, then
![]() ${\rm ord}(\kappa_f)$
divides
${\rm ord}(\kappa_f)$
divides
![]() $M\cdot {\rm ord}(P_f)$
and
$M\cdot {\rm ord}(P_f)$
and
![]() ${\rm ord}(P_f)$
divides
${\rm ord}(P_f)$
divides
![]() $M\cdot {\rm ord}(\kappa_f)$
.
$M\cdot {\rm ord}(\kappa_f)$
.
Theorem 4.1 will be proven in § 4.4, and Theorem 4.2 will be proven in § 4.7. A standard argument using Lemma 2.1 shows that we may assume
![]() $k=\mathrm{\mathbb{C}}$
. So in the remainder of § 4, all varieties will be over C, and cohomology will be singular cohomology.
$k=\mathrm{\mathbb{C}}$
. So in the remainder of § 4, all varieties will be over C, and cohomology will be singular cohomology.
Remark 4.3. Theorem 4.2 generalizes [Reference Laga and ShnidmanLS25, Theorem 5.16], which considered the special case where
![]() $b = 0$
. There, we exploited the bielliptic cover to show that the Ceresa cycle maps via a correspondence to a multiple of the point
$b = 0$
. There, we exploited the bielliptic cover to show that the Ceresa cycle maps via a correspondence to a multiple of the point
![]() $Q_f = (a^2 -4c,a(a^2 -4c))$
on the elliptic curve
$Q_f = (a^2 -4c,a(a^2 -4c))$
on the elliptic curve
![]() $E_f' \colon y^2 = x^3 +16 \cdot \mathrm{disc}(f)$
. This is compatible with the general case since there is a 3-isogeny
$E_f' \colon y^2 = x^3 +16 \cdot \mathrm{disc}(f)$
. This is compatible with the general case since there is a 3-isogeny
![]() $\phi_f \colon E'_f \rightarrow E_f$
, and one checks using the explicit formula for
$\phi_f \colon E'_f \rightarrow E_f$
, and one checks using the explicit formula for
![]() $\phi_f$
[Reference Bhargava, Elkies and ShnidmanBES20, equation (2)] that
$\phi_f$
[Reference Bhargava, Elkies and ShnidmanBES20, equation (2)] that
![]() $\phi_f(Q_f) = P_f$
.
$\phi_f(Q_f) = P_f$
.
Remark 4.4. Is it always the case that
![]() $\kappa_f \neq 0$
? (Recall that
$\kappa_f \neq 0$
? (Recall that
![]() $\kappa_f$
lies in the Chow group with Z-coefficients.) We cannot conclude this from our proof of Theorem 20 below since we have worked with Q-coefficients, and we make use of various isogenies whose degrees we do not control.
$\kappa_f$
lies in the Chow group with Z-coefficients.) We cannot conclude this from our proof of Theorem 20 below since we have worked with Q-coefficients, and we make use of various isogenies whose degrees we do not control.
4.3 Multilinear algebra
Our first goal (Proposition 4.7) is to explicitly identify the abelian variety A of Proposition 3.3 for Picard curves.
Write
![]() $\mathcal{O} = \mathrm{\mathbb{Z}}[\omega]$
for the ring of Eisenstein integers with
$\mathcal{O} = \mathrm{\mathbb{Z}}[\omega]$
for the ring of Eisenstein integers with
![]() $\omega^2+ \omega +1=0$
and let
$\omega^2+ \omega +1=0$
and let
![]() $K=\mathrm{\mathbb{Q}}(\sqrt{-3})$
be its fraction field. Let C be a Picard curve over C with Jacobian variety J. The
$K=\mathrm{\mathbb{Q}}(\sqrt{-3})$
be its fraction field. Let C be a Picard curve over C with Jacobian variety J. The
![]() $\mu_3$
-action on C extends to an embedding
$\mu_3$
-action on C extends to an embedding
![]() $\mathcal{O} \subset \mathrm{End}(J)$
. Using this action, the singular cohomology group
$\mathcal{O} \subset \mathrm{End}(J)$
. Using this action, the singular cohomology group
![]() $\mathrm{H}^1(J;\mathrm{\mathbb{Z}})$
is a free
$\mathrm{H}^1(J;\mathrm{\mathbb{Z}})$
is a free
![]() $\mathcal{O}$
-module of rank 3, and
$\mathcal{O}$
-module of rank 3, and
![]() $\mathrm{H}^1(J;\mathrm{\mathbb{Q}})$
is a three-dimensional K-vector space. The next lemma says that the criterion of Theorem B is always satisfied for Picard curves.
$\mathrm{H}^1(J;\mathrm{\mathbb{Q}})$
is a three-dimensional K-vector space. The next lemma says that the criterion of Theorem B is always satisfied for Picard curves.
Lemma 4.5.
![]() $\mathrm{H}^0(J, \Omega_J^3)^{\mu_3} = 0$
and the Hodge structure
$\mathrm{H}^0(J, \Omega_J^3)^{\mu_3} = 0$
and the Hodge structure
![]() $\mathrm{H}^3(J;\mathrm{\mathbb{Q}})^{\mu_3}$
is of type
$\mathrm{H}^3(J;\mathrm{\mathbb{Q}})^{\mu_3}$
is of type
![]() $(1,2) +(2,1)$
.
$(1,2) +(2,1)$
.
Proof. Since
![]() $\mathrm{H}^0(J, \Omega_J^3) \simeq \bigwedge^3 \mathrm{H}^0(C, \Omega_C^1)$
, the first claim follows from a calculation with differentials (Example 3.4). The second claim follows from the Hodge decomposition for
$\mathrm{H}^0(J, \Omega_J^3) \simeq \bigwedge^3 \mathrm{H}^0(C, \Omega_C^1)$
, the first claim follows from a calculation with differentials (Example 3.4). The second claim follows from the Hodge decomposition for
![]() $\mathrm{H}^3(J;\mathrm{\mathbb{Q}})$
.
$\mathrm{H}^3(J;\mathrm{\mathbb{Q}})$
.
We may view
![]() $\mathrm{H}^1(J;\mathrm{\mathbb{Q}})$
either as a K-vector space or Q-vector space; when we perform tensor operations, we will add the subscript K when we view it as a K-vector space, and add no subscript otherwise. For example, the cup product induces an isomorphism
$\mathrm{H}^1(J;\mathrm{\mathbb{Q}})$
either as a K-vector space or Q-vector space; when we perform tensor operations, we will add the subscript K when we view it as a K-vector space, and add no subscript otherwise. For example, the cup product induces an isomorphism
![]() $\bigwedge^3 \mathrm{H}^1(J;\mathrm{\mathbb{Q}}) \simeq \mathrm{H}^3(J;\mathrm{\mathbb{Q}})$
, and we will use this identification without further mention.
$\bigwedge^3 \mathrm{H}^1(J;\mathrm{\mathbb{Q}}) \simeq \mathrm{H}^3(J;\mathrm{\mathbb{Q}})$
, and we will use this identification without further mention.
The universal property of exterior powers induces a canonical Q-linear surjection
![]() $\bigwedge^3 \mathrm{H}^1(J;\mathrm{\mathbb{Q}}) \rightarrow \bigwedge^3_K \mathrm{H}^1(J;\mathrm{\mathbb{Q}})$
. It is well known (see [Reference Moonen and ZarhinMZ98, Lemma 12(i)] or [Reference DeligneDel82, Lemma 4.3]) that this map admits a canonical splitting, which we use to view
$\bigwedge^3 \mathrm{H}^1(J;\mathrm{\mathbb{Q}}) \rightarrow \bigwedge^3_K \mathrm{H}^1(J;\mathrm{\mathbb{Q}})$
. It is well known (see [Reference Moonen and ZarhinMZ98, Lemma 12(i)] or [Reference DeligneDel82, Lemma 4.3]) that this map admits a canonical splitting, which we use to view
![]() $\bigwedge_K^3 \mathrm{H}^1(J;\mathrm{\mathbb{Q}})$
as a direct summand of
$\bigwedge_K^3 \mathrm{H}^1(J;\mathrm{\mathbb{Q}})$
as a direct summand of
![]() $\mathrm{H}^3(J;\mathrm{\mathbb{Q}})$
.
$\mathrm{H}^3(J;\mathrm{\mathbb{Q}})$
.
Lemma 4.6.
We have
![]() $\mathrm{H}^3(J;\mathrm{\mathbb{Q}})^{\mu_3}= \bigwedge_K^3 \mathrm{H}^1(J;\mathrm{\mathbb{Q}})$
inside
$\mathrm{H}^3(J;\mathrm{\mathbb{Q}})^{\mu_3}= \bigwedge_K^3 \mathrm{H}^1(J;\mathrm{\mathbb{Q}})$
inside
![]() $\mathrm{H}^3(J;\mathrm{\mathbb{Q}})$
. Moreover,
$\mathrm{H}^3(J;\mathrm{\mathbb{Q}})$
. Moreover,
![]() $\dim_{\mathrm{\mathbb{Q}}} \mathrm{H}^3(J;\mathrm{\mathbb{Q}})^{\mu_3}=2$
.
$\dim_{\mathrm{\mathbb{Q}}} \mathrm{H}^3(J;\mathrm{\mathbb{Q}})^{\mu_3}=2$
.
Proof. View
![]() $\mathrm{H}^3(J;\mathrm{\mathbb{Q}})$
as the space of trilinear skew-symmetric forms on
$\mathrm{H}^3(J;\mathrm{\mathbb{Q}})$
as the space of trilinear skew-symmetric forms on
![]() $\mathrm{H}_1(J; \mathrm{\mathbb{Q}})$
. Then
$\mathrm{H}_1(J; \mathrm{\mathbb{Q}})$
. Then
![]() $\bigwedge^3_K \mathrm{H}_1(J; \mathrm{\mathbb{Q}})$
is the two-dimensional subspace
$\bigwedge^3_K \mathrm{H}_1(J; \mathrm{\mathbb{Q}})$
is the two-dimensional subspace
![]() $\{ \mathrm{Tr}_{K/\mathrm{\mathbb{Q}}} \circ \phi\}$
where
$\{ \mathrm{Tr}_{K/\mathrm{\mathbb{Q}}} \circ \phi\}$
where
![]() $\phi$
is a K-trilinear skew-symmetric form. Since
$\phi$
is a K-trilinear skew-symmetric form. Since
![]() $\phi(\omega x,\omega y,\omega z) = \phi(x,y,z)$
, we see that
$\phi(\omega x,\omega y,\omega z) = \phi(x,y,z)$
, we see that
![]() $\bigwedge^3_K \mathrm{H}_1(J; \mathrm{\mathbb{Q}}) \subset \mathrm{H}^3(J, \mathrm{\mathbb{Q}})^{\mu_3}$
, and it is enough to show that
$\bigwedge^3_K \mathrm{H}_1(J; \mathrm{\mathbb{Q}}) \subset \mathrm{H}^3(J, \mathrm{\mathbb{Q}})^{\mu_3}$
, and it is enough to show that
![]() $\dim_\mathrm{\mathbb{Q}} \mathrm{H}^3(J, \mathrm{\mathbb{Q}})^{\mu_3} = 2$
. It suffices to prove this after tensoring with C. Let
$\dim_\mathrm{\mathbb{Q}} \mathrm{H}^3(J, \mathrm{\mathbb{Q}})^{\mu_3} = 2$
. It suffices to prove this after tensoring with C. Let
![]() $g\in \mu_3$
be non-trivial. The action of g on
$g\in \mu_3$
be non-trivial. The action of g on
![]() $\mathrm{H}^1(J;\mathrm{\mathbb{Q}})$
has eigenvalues
$\mathrm{H}^1(J;\mathrm{\mathbb{Q}})$
has eigenvalues
![]() $\omega, \omega, \omega, \omega^2, \omega^2, \omega^2$
, so we can write
$\omega, \omega, \omega, \omega^2, \omega^2, \omega^2$
, so we can write
![]() $\mathrm{H}^1(J;\mathrm{\mathbb{C}}) = V_1 \bigoplus V_2$
where
$\mathrm{H}^1(J;\mathrm{\mathbb{C}}) = V_1 \bigoplus V_2$
where
![]() $V_i$
is the three-dimensional
$V_i$
is the three-dimensional
![]() $\omega^i$
-eigenspace. Since a three-element subset of these eigenvalues have product 1 if and only if they are all equal,
$\omega^i$
-eigenspace. Since a three-element subset of these eigenvalues have product 1 if and only if they are all equal,
![]() $\mathrm{H}^3(J;\mathrm{\mathbb{C}})^{\mu_3} = (\bigwedge^3 V_1) \bigoplus (\bigwedge^3 V_2)$
, which is two-dimensional.
$\mathrm{H}^3(J;\mathrm{\mathbb{C}})^{\mu_3} = (\bigwedge^3 V_1) \bigoplus (\bigwedge^3 V_2)$
, which is two-dimensional.
Let E be the elliptic curve with Weierstrass equation
![]() $y^2 =x^3+1$
.
$y^2 =x^3+1$
.
Proposition 4.7.
There is an isomorphism of Hodge structures
![]() $\mathrm{H}^3(J;\mathrm{\mathbb{Q}})^{\mu_3} \simeq \mathrm{H}^1(E,\mathrm{\mathbb{Q}})(-1)$
.
$\mathrm{H}^3(J;\mathrm{\mathbb{Q}})^{\mu_3} \simeq \mathrm{H}^1(E,\mathrm{\mathbb{Q}})(-1)$
.
Proof. Since there exists a unique elliptic curve up to isogeny with endomorphism algebra K, there exists a unique Hodge structure of dimension 2, type
![]() $(0,1)+(1,0)$
and carrying an action of K. Since both
$(0,1)+(1,0)$
and carrying an action of K. Since both
![]() $\mathrm{H}^3(J;\mathrm{\mathbb{Q}})^{\mu_3}$
and
$\mathrm{H}^3(J;\mathrm{\mathbb{Q}})^{\mu_3}$
and
![]() $\mathrm{H}^1(E;\mathrm{\mathbb{Q}})$
have these properties (the former by Lemma 4.6), they must be isomorphic, and we conclude using Lemma 4.6.
$\mathrm{H}^1(E;\mathrm{\mathbb{Q}})$
have these properties (the former by Lemma 4.6), they must be isomorphic, and we conclude using Lemma 4.6.
4.4 Weil classes and Schoen’s theorem
Our next goal is to upgrade the isomorphism of Proposition 4.7 to an isomorphism in the category of Chow motives, and hence deduce (using Proposition 3.3) the vanishing of
![]() $\bar{\kappa}(C)$
in the Griffiths group. We use the following special case of a result of Schoen, which crucially uses the assumption that the endomorphism algebra of
$\bar{\kappa}(C)$
in the Griffiths group. We use the following special case of a result of Schoen, which crucially uses the assumption that the endomorphism algebra of
![]() $J\times E$
contains
$J\times E$
contains
![]() $K=\mathrm{\mathbb{Q}}(\omega)$
.
$K=\mathrm{\mathbb{Q}}(\omega)$
.
Theorem 4.8 (Schoen). The Hodge conjecture holds for
![]() $J\times E$
.
$J\times E$
.
Proof. Since
![]() $J\times E$
is four-dimensional, it suffices to prove that Hodge classes in
$J\times E$
is four-dimensional, it suffices to prove that Hodge classes in
![]() $\mathrm{H}^4(J\times E;\mathrm{\mathbb{Q}})$
are algebraic. By [Reference Moonen and ZarhinMZ99, Theorem (0.1), parts (i) and (iv)], such Hodge classes are sums of products of divisor classes (which are algebraic) and Weil classes
$\mathrm{H}^4(J\times E;\mathrm{\mathbb{Q}})$
are algebraic. By [Reference Moonen and ZarhinMZ99, Theorem (0.1), parts (i) and (iv)], such Hodge classes are sums of products of divisor classes (which are algebraic) and Weil classes
![]() $W_K := \bigwedge^4_K \mathrm{H}^4(J\times E;\mathrm{\mathbb{Q}}) \subset \mathrm{H}^4(J\times E;\mathrm{\mathbb{Q}})$
. Since
$W_K := \bigwedge^4_K \mathrm{H}^4(J\times E;\mathrm{\mathbb{Q}}) \subset \mathrm{H}^4(J\times E;\mathrm{\mathbb{Q}})$
. Since
![]() $K= \mathrm{\mathbb{Q}}(\omega)$
and the embedding
$K= \mathrm{\mathbb{Q}}(\omega)$
and the embedding
![]() $K\subset \mathrm{End}(J\times E)\otimes \mathrm{\mathbb{Q}}$
can be chosen to have signature (2,2), Schoen has shown in [Reference SchoenSch98] that the classes in
$K\subset \mathrm{End}(J\times E)\otimes \mathrm{\mathbb{Q}}$
can be chosen to have signature (2,2), Schoen has shown in [Reference SchoenSch98] that the classes in
![]() $W_K$
are algebraic, concluding that all Hodge classes of
$W_K$
are algebraic, concluding that all Hodge classes of
![]() $\mathrm{H}^4(J\times E;\mathrm{\mathbb{Q}})$
are algebraic.
$\mathrm{H}^4(J\times E;\mathrm{\mathbb{Q}})$
are algebraic.
Recall from § 2.3 our conventions on motives, the canonical Chow–Künneth components
![]() ${\frak{h}}^i(J)$
and
${\frak{h}}^i(J)$
and
![]() ${\frak{h}}^j(E)$
, and the motive of fixed points of a finite group action.
${\frak{h}}^j(E)$
, and the motive of fixed points of a finite group action.
Corollary 4.9.
There is an isomorphism
![]() ${\frak{h}}^3(J)^{\mu_3} \simeq {\frak{h}}^1(E)(-1)$
.
${\frak{h}}^3(J)^{\mu_3} \simeq {\frak{h}}^1(E)(-1)$
.
Corollary 4.10.
If C is a Picard curve over C, then
![]() $\bar{\kappa}(C)=0$
.
$\bar{\kappa}(C)=0$
.
Proof of Theorem 4.1. Consider the parameter space
![]() $S_0 = \{(a,b,c) \mid \mathrm{disc}(f)\neq 0\} \subset \mathrm{\mathbb{A}}^3_{\mathrm{\mathbb{Q}}}$
of Picard curves. Let
$S_0 = \{(a,b,c) \mid \mathrm{disc}(f)\neq 0\} \subset \mathrm{\mathbb{A}}^3_{\mathrm{\mathbb{Q}}}$
of Picard curves. Let
![]() $\eta$
be the generic point of
$\eta$
be the generic point of
![]() $S_0$
with function field
$S_0$
with function field
![]() $k(\eta)= \mathrm{\mathbb{Q}}(a,b,c)$
, let
$k(\eta)= \mathrm{\mathbb{Q}}(a,b,c)$
, let
![]() $C_{\eta}$
be the generic Picard curve over
$C_{\eta}$
be the generic Picard curve over
![]() $k(\eta)$
with Jacobian
$k(\eta)$
with Jacobian
![]() $J_{\eta}$
, and let
$J_{\eta}$
, and let
![]() $\kappa_{C_{\eta}}\in \mathrm{CH}_1(J_{\eta})$
be the Ceresa cycle of
$\kappa_{C_{\eta}}\in \mathrm{CH}_1(J_{\eta})$
be the Ceresa cycle of
![]() $C_{\eta}$
based at the point at infinity. Fix an embedding
$C_{\eta}$
based at the point at infinity. Fix an embedding
![]() $j\colon k(\eta) \rightarrow \mathrm{\mathbb{C}}$
. By Corollary 4.10, the base change of
$j\colon k(\eta) \rightarrow \mathrm{\mathbb{C}}$
. By Corollary 4.10, the base change of
![]() $\kappa_{C{\eta}}$
along j is torsion in the Griffiths group. By Lemma 2.1, this implies
$\kappa_{C{\eta}}$
along j is torsion in the Griffiths group. By Lemma 2.1, this implies
![]() $\kappa_{C_{\eta}}$
is itself torsion in
$\kappa_{C_{\eta}}$
is itself torsion in
![]() $\mathrm{Gr}_1(J_{\eta})$
. Let
$\mathrm{Gr}_1(J_{\eta})$
. Let
![]() $N_0$
be the finite order of
$N_0$
be the finite order of
![]() $\kappa_{C_{\eta}}$
in
$\kappa_{C_{\eta}}$
in
![]() $\mathrm{Gr}_1(J_{\eta})$
. By spreading out, it follows that
$\mathrm{Gr}_1(J_{\eta})$
. By spreading out, it follows that
![]() $\kappa_{C_f}$
is
$\kappa_{C_f}$
is
![]() $N_0$
-torsion in
$N_0$
-torsion in
![]() $\mathrm{Gr}_1(J_f)$
for all f in an open dense subset
$\mathrm{Gr}_1(J_f)$
for all f in an open dense subset
![]() $U_0\subset S_0$
. By applying the same argument to the generic points of the irreducible components of
$U_0\subset S_0$
. By applying the same argument to the generic points of the irreducible components of
![]() $S_0\setminus U_0$
, there exists an open dense
$S_0\setminus U_0$
, there exists an open dense
![]() $U_1\subset S_0$
containing
$U_1\subset S_0$
containing
![]() $U_0$
and those generic points such that
$U_0$
and those generic points such that
![]() $\kappa_{C_f}$
is
$\kappa_{C_f}$
is
![]() $N_1$
-torsion in
$N_1$
-torsion in
![]() $\mathrm{Gr}_1(J_f)$
for all f in
$\mathrm{Gr}_1(J_f)$
for all f in
![]() $U_1$
. Repeating this process, we obtain a sequence of open subsets
$U_1$
. Repeating this process, we obtain a sequence of open subsets
![]() $U_0\subset U_1\subset \cdots \subset S_0$
whose complements have strictly decreasing codimension. Therefore, this sequence must terminate after finitely many steps; hence, there exists an integer
$U_0\subset U_1\subset \cdots \subset S_0$
whose complements have strictly decreasing codimension. Therefore, this sequence must terminate after finitely many steps; hence, there exists an integer
![]() $N\geqslant 1$
such that
$N\geqslant 1$
such that
![]() $\kappa_{C_f}$
is N-torsion in
$\kappa_{C_f}$
is N-torsion in
![]() $\mathrm{Gr}_1(J_f)$
for all
$\mathrm{Gr}_1(J_f)$
for all
![]() $f\in S_0(k)$
over every algebraically closed field of characteristic 0.
$f\in S_0(k)$
over every algebraically closed field of characteristic 0.
The remainder of the section is devoted to proving Theorem 4.2. To this end, we will analyse the Abel–Jacobi image of
![]() $\kappa_f$
(the ‘normal function’ associated to
$\kappa_f$
(the ‘normal function’ associated to
![]() $\kappa_f$
) in the next two subsections.
$\kappa_f$
) in the next two subsections.
4.5 The Abel–Jacobi map
If X is a smooth variety over C, we will use the notion of an integral (respectively, rational) variation of (pure) Hodge structures over the complex manifold
![]() $X(\mathrm{\mathbb{C}})$
, called a Z-VHS (respectively, Q-VHS) for short; see [Reference VoisinVoi07, § 5.3.1] for definitions. If V is a Hodge structure of odd weight
$X(\mathrm{\mathbb{C}})$
, called a Z-VHS (respectively, Q-VHS) for short; see [Reference VoisinVoi07, § 5.3.1] for definitions. If V is a Hodge structure of odd weight
![]() $2k-1$
, its intermediate Jacobian
$2k-1$
, its intermediate Jacobian
![]() $\mathrm{J}(V)$
is the complex torus
$\mathrm{J}(V)$
is the complex torus
where
![]() $F^k\subset V\otimes_{\mathrm{\mathbb{Z}}} \mathrm{\mathbb{C}}$
is a part of the descending Hodge filtration and
$F^k\subset V\otimes_{\mathrm{\mathbb{Z}}} \mathrm{\mathbb{C}}$
is a part of the descending Hodge filtration and
![]() $V_{\tau}$
denotes the quotient of V by its torsion subgroup. More generally, if
$V_{\tau}$
denotes the quotient of V by its torsion subgroup. More generally, if
![]() $\mathbb{V}$
is a Z-VHS of weight
$\mathbb{V}$
is a Z-VHS of weight
![]() $2k-1$
over
$2k-1$
over
![]() $X(\mathrm{\mathbb{C}})$
, we can define its intermediate Jacobian
$X(\mathrm{\mathbb{C}})$
, we can define its intermediate Jacobian
![]() $\mathrm{J}(\mathbb{V})\rightarrow X(\mathrm{\mathbb{C}})$
, a relative complex torus whose fibres over points
$\mathrm{J}(\mathbb{V})\rightarrow X(\mathrm{\mathbb{C}})$
, a relative complex torus whose fibres over points
![]() $x\in X(\mathrm{\mathbb{C}})$
are the classical intermediate Jacobians
$x\in X(\mathrm{\mathbb{C}})$
are the classical intermediate Jacobians
![]() $\mathrm{J}(\mathbb{V}_x)$
; see [Reference VoisinVoi07, § 7.1.1]. If
$\mathrm{J}(\mathbb{V}_x)$
; see [Reference VoisinVoi07, § 7.1.1]. If
![]() $\mathbb{V}, \mathbb{W}$
are two Z-VHSs of odd weight, then
$\mathbb{V}, \mathbb{W}$
are two Z-VHSs of odd weight, then
![]() $\mathrm{J}(\mathbb{V}(p)) = \mathrm{J}(\mathbb{V})$
for all
$\mathrm{J}(\mathbb{V}(p)) = \mathrm{J}(\mathbb{V})$
for all
![]() $p \in \mathrm{\mathbb{Z}}$
and a morphism
$p \in \mathrm{\mathbb{Z}}$
and a morphism
![]() $\mathbb{V} \rightarrow \mathbb{W}$
of Z-VHSs induces a homomorphism of (relative) complex tori
$\mathbb{V} \rightarrow \mathbb{W}$
of Z-VHSs induces a homomorphism of (relative) complex tori
![]() $\mathrm{J}(\mathbb{V}) \rightarrow \mathrm{J}(\mathbb{W})$
.
$\mathrm{J}(\mathbb{V}) \rightarrow \mathrm{J}(\mathbb{W})$
.
If
![]() $X/\mathrm{\mathbb{C}}$
is a nice variety and
$X/\mathrm{\mathbb{C}}$
is a nice variety and
![]() $0\leqslant p\leqslant \dim(X)$
, we write
$0\leqslant p\leqslant \dim(X)$
, we write
![]() $\mathrm{J}^p(X) = \mathrm{J}(\mathrm{H}^{2p-1}(X(\mathrm{\mathbb{C}});\mathrm{\mathbb{Z}}))$
. In this situation there is an Abel–Jacobi map
$\mathrm{J}^p(X) = \mathrm{J}(\mathrm{H}^{2p-1}(X(\mathrm{\mathbb{C}});\mathrm{\mathbb{Z}}))$
. In this situation there is an Abel–Jacobi map
defined in [Reference VoisinVoi07, § 7.2.1]. Moreover, if
![]() $S/\mathrm{\mathbb{C}}$
is a smooth variety,
$S/\mathrm{\mathbb{C}}$
is a smooth variety,
![]() $\pi\colon X\rightarrow S$
a smooth projective morphism with geometrically integral fibres and
$\pi\colon X\rightarrow S$
a smooth projective morphism with geometrically integral fibres and
![]() $p \in \mathrm{\mathbb{Z}}_{\geqslant 0}$
, then
$p \in \mathrm{\mathbb{Z}}_{\geqslant 0}$
, then
![]() $R^p \pi_*\mathrm{\mathbb{Z}}$
(pushforward of the constant sheaf in the analytic topology) has the structure of a Z-VHS over
$R^p \pi_*\mathrm{\mathbb{Z}}$
(pushforward of the constant sheaf in the analytic topology) has the structure of a Z-VHS over
![]() $S(\mathrm{\mathbb{C}})$
. If Z is a codimension p cycle on X all of whose components are flat over S, and such that
$S(\mathrm{\mathbb{C}})$
. If Z is a codimension p cycle on X all of whose components are flat over S, and such that
![]() $Z_s \in \mathrm{CH}^p(X_s)_{\hom}$
for every
$Z_s \in \mathrm{CH}^p(X_s)_{\hom}$
for every
![]() $s\in S(\mathrm{\mathbb{C}})$
, then Griffiths has shown that there exists a holomorphic section
$s\in S(\mathrm{\mathbb{C}})$
, then Griffiths has shown that there exists a holomorphic section
![]() $\mathrm{AJ}(Z)$
of the relative complex torus
$\mathrm{AJ}(Z)$
of the relative complex torus
![]() $\mathrm{J}(R^p\pi_* \mathrm{\mathbb{Z}}) \rightarrow S(\mathrm{\mathbb{C}})$
with the property that
$\mathrm{J}(R^p\pi_* \mathrm{\mathbb{Z}}) \rightarrow S(\mathrm{\mathbb{C}})$
with the property that
![]() $\mathrm{AJ}(Z)_s = \mathrm{AJ}_X^p(Z_s)$
for all
$\mathrm{AJ}(Z)_s = \mathrm{AJ}_X^p(Z_s)$
for all
![]() $s\in S(\mathrm{\mathbb{C}})$
; this is called the normal function associated to Z.
$s\in S(\mathrm{\mathbb{C}})$
; this is called the normal function associated to Z.
We record the fact that Abel–Jacobi maps are compatible with correspondences. Let X,Y be nice varieties over C and let
![]() $\gamma \in\mathrm{CH}^{r+\dim(X)}(X\times Y)$
be a correspondence of degree r. This induces for every
$\gamma \in\mathrm{CH}^{r+\dim(X)}(X\times Y)$
be a correspondence of degree r. This induces for every
![]() $p\geqslant 0$
a homomorphism
$p\geqslant 0$
a homomorphism
![]() $\gamma_* \colon \mathrm{CH}^p(X) \rightarrow \mathrm{CH}^{p+r}(Y)$
via the formula
$\gamma_* \colon \mathrm{CH}^p(X) \rightarrow \mathrm{CH}^{p+r}(Y)$
via the formula
![]() $\alpha \mapsto \pi_{Y,*}(\pi_{X}^*(\alpha) \cdot \gamma)$
, where
$\alpha \mapsto \pi_{Y,*}(\pi_{X}^*(\alpha) \cdot \gamma)$
, where
![]() $\pi_X\colon X\times Y\rightarrow X$
and
$\pi_X\colon X\times Y\rightarrow X$
and
![]() $\pi_Y\colon X\times Y\rightarrow Y$
denote the projections. The same formula defines morphism of Hodge structures
$\pi_Y\colon X\times Y\rightarrow Y$
denote the projections. The same formula defines morphism of Hodge structures
![]() $\mathrm{H}^p(X;\mathrm{\mathbb{Z}}) \rightarrow \mathrm{H}^{p+2r}(Y)(r)$
for every p, hence a homomorphism of complex tori
$\mathrm{H}^p(X;\mathrm{\mathbb{Z}}) \rightarrow \mathrm{H}^{p+2r}(Y)(r)$
for every p, hence a homomorphism of complex tori
![]() $\gamma_*\colon \mathrm{J}^p(X) \rightarrow \mathrm{J}^{p+r}(Y)$
.
$\gamma_*\colon \mathrm{J}^p(X) \rightarrow \mathrm{J}^{p+r}(Y)$
.
Lemma 4.11.
In the above notation,
![]() $\gamma_*$
sends
$\gamma_*$
sends
![]() $\mathrm{CH}^p(X)_{\hom}$
to
$\mathrm{CH}^p(X)_{\hom}$
to
![]() $\mathrm{CH}^{p+r}(Y)_{\hom}$
. Moreover, for every
$\mathrm{CH}^{p+r}(Y)_{\hom}$
. Moreover, for every
![]() $\alpha \in \mathrm{CH}^p(X)_{\hom}$
,
$\alpha \in \mathrm{CH}^p(X)_{\hom}$
,
![]() $\gamma_*(\mathrm{AJ}_X^p(\alpha)) = \mathrm{AJ}_Y^{p+r}(\gamma_*(\alpha))$
.
$\gamma_*(\mathrm{AJ}_X^p(\alpha)) = \mathrm{AJ}_Y^{p+r}(\gamma_*(\alpha))$
.
Proof. The first sentence follows from the compatibility of the cycle class map with correspondences [Reference VoisinVoi07, Proposition 9.21]. To prove the compatibility of the Abel–Jacobi map with correspondences, it suffices to prove the compatibility with pullbacks, pushforwards and intersection product. The pullback case is elementary, using the definition of
![]() $\mathrm{AJ}^p_X$
in terms of extensions of Hodge structures; see [Reference CharlesCha10, § 2.2]. The pushforward case follows from the pullback case and Poincaré duality. Finally, compatibility with the intersection product follows from [Reference VoisinVoi07, Proposition 9.23].
$\mathrm{AJ}^p_X$
in terms of extensions of Hodge structures; see [Reference CharlesCha10, § 2.2]. The pushforward case follows from the pullback case and Poincaré duality. Finally, compatibility with the intersection product follows from [Reference VoisinVoi07, Proposition 9.23].
Let
![]() $S = \{(a,b,c) \mid \mathrm{disc}(f) \neq 0\}\subset \mathrm{\mathbb{A}}^3_{\mathrm{\mathbb{C}}}$
be the parameter space of Picard curves over C. We will identify C-valued points of S with polynomials
$S = \{(a,b,c) \mid \mathrm{disc}(f) \neq 0\}\subset \mathrm{\mathbb{A}}^3_{\mathrm{\mathbb{C}}}$
be the parameter space of Picard curves over C. We will identify C-valued points of S with polynomials
![]() $f = x^4+ax^2+bx+c \in \mathrm{\mathbb{C}}[x]$
of non-zero discriminant. Let
$f = x^4+ax^2+bx+c \in \mathrm{\mathbb{C}}[x]$
of non-zero discriminant. Let
![]() $\mathcal{C}\rightarrow S$
be the universal Picard curve, and let
$\mathcal{C}\rightarrow S$
be the universal Picard curve, and let
![]() $\pi\colon \mathcal{J}\rightarrow S$
its relative Jacobian variety. The point at infinity defines a section
$\pi\colon \mathcal{J}\rightarrow S$
its relative Jacobian variety. The point at infinity defines a section
![]() $P_{\infty}$
of
$P_{\infty}$
of
![]() $\mathcal{C}$
. Let
$\mathcal{C}$
. Let
![]() $\kappa_{\mathcal{C}} \in \mathrm{CH}_1(\mathcal{J})$
be the universal Ceresa cycle with respect to this section. (Comparing with our earlier notation, we have
$\kappa_{\mathcal{C}} \in \mathrm{CH}_1(\mathcal{J})$
be the universal Ceresa cycle with respect to this section. (Comparing with our earlier notation, we have
![]() $\mathcal{C}_f = C_f$
and
$\mathcal{C}_f = C_f$
and
![]() $\kappa_{\mathcal{C},f} = \kappa_f$
for every
$\kappa_{\mathcal{C},f} = \kappa_f$
for every
![]() $f \in S(\mathrm{\mathbb{C}})$
.)
$f \in S(\mathrm{\mathbb{C}})$
.)
Let
![]() $\mathbb{V} = R^3 \pi_* \mathrm{\mathbb{Z}}$
be the Z-VHS on
$\mathbb{V} = R^3 \pi_* \mathrm{\mathbb{Z}}$
be the Z-VHS on
![]() $S(\mathrm{\mathbb{C}})$
such that
$S(\mathrm{\mathbb{C}})$
such that
![]() $\mathbb{V}_f \simeq \mathrm{H}^3(\mathcal{J}_f;\mathrm{\mathbb{Z}})$
for
$\mathbb{V}_f \simeq \mathrm{H}^3(\mathcal{J}_f;\mathrm{\mathbb{Z}})$
for
![]() $f\in S(\mathrm{\mathbb{C}})$
. Then the normal function
$f\in S(\mathrm{\mathbb{C}})$
. Then the normal function
![]() $\mathrm{AJ}(\kappa_{\mathcal{C}})$
is a section of
$\mathrm{AJ}(\kappa_{\mathcal{C}})$
is a section of
![]() $\mathrm{J}(\mathbb{V}) {\rightarrow}S(\mathrm{\mathbb{C}})$
interpolating
$\mathrm{J}(\mathbb{V}) {\rightarrow}S(\mathrm{\mathbb{C}})$
interpolating
![]() $\mathrm{AJ}_{J_f}^2(\kappa_f)$
.
$\mathrm{AJ}_{J_f}^2(\kappa_f)$
.
Proposition 4.12.
For
![]() $f\in S(\mathrm{\mathbb{C}})$
, the class
$f\in S(\mathrm{\mathbb{C}})$
, the class
![]() $\kappa_f\in \mathrm{CH}^2(J_f)_{\mathrm{hom}}$
is torsion if and only if
$\kappa_f\in \mathrm{CH}^2(J_f)_{\mathrm{hom}}$
is torsion if and only if
![]() $\mathrm{AJ}_{J_f}^2(\kappa_f)\in \mathrm{J}^2(J_f)$
is torsion. The torsion order of
$\mathrm{AJ}_{J_f}^2(\kappa_f)\in \mathrm{J}^2(J_f)$
is torsion. The torsion order of
![]() $\kappa_f$
, if finite, equals the torsion order of
$\kappa_f$
, if finite, equals the torsion order of
![]() $\mathrm{AJ}_{J_f}^2(\kappa_f)$
.
$\mathrm{AJ}_{J_f}^2(\kappa_f)$
.
Proof. Let E be the elliptic curve
![]() $y^2 = x^3+1$
. Corollary 4.9 shows that there exists a correspondence
$y^2 = x^3+1$
. Corollary 4.9 shows that there exists a correspondence
![]() $\gamma \in \mathrm{CH}^2(E\times J)$
such that
$\gamma \in \mathrm{CH}^2(E\times J)$
such that
![]() $\gamma_*$
induces isomorphisms
$\gamma_*$
induces isomorphisms
![]() $\mathrm{CH}^1(E)_{\hom, \mathrm{\mathbb{Q}}} \rightarrow \mathrm{CH}^2_{(1)}(J)^{\mu_3}$
and
$\mathrm{CH}^1(E)_{\hom, \mathrm{\mathbb{Q}}} \rightarrow \mathrm{CH}^2_{(1)}(J)^{\mu_3}$
and
![]() $\mathrm{H}^1(E;\mathrm{\mathbb{Q}}) \rightarrow \mathrm{H}^3(J;\mathrm{\mathbb{Q}})^{\mu_3}(1)$
. Let
$\mathrm{H}^1(E;\mathrm{\mathbb{Q}}) \rightarrow \mathrm{H}^3(J;\mathrm{\mathbb{Q}})^{\mu_3}(1)$
. Let
![]() $\varphi$
be the restriction of
$\varphi$
be the restriction of
![]() $\mathrm{AJ}_{J_f}^2\otimes \mathrm{\mathbb{Q}}$
to
$\mathrm{AJ}_{J_f}^2\otimes \mathrm{\mathbb{Q}}$
to
![]() $\mathrm{CH}_{(1)}^2(J_f)^{\mu_3}$
. By Lemma 4.11 these form a commutative diagram.
$\mathrm{CH}_{(1)}^2(J_f)^{\mu_3}$
. By Lemma 4.11 these form a commutative diagram.

All arrows except
![]() $\varphi$
are isomorphisms of abelian groups. Therefore,
$\varphi$
are isomorphisms of abelian groups. Therefore,
![]() $\varphi$
is an isomorphism too. Since the image of
$\varphi$
is an isomorphism too. Since the image of
![]() $\kappa_f$
in
$\kappa_f$
in
![]() $\mathrm{CH}^2(J_f)_{\mathrm{\mathbb{Q}}}$
lies in
$\mathrm{CH}^2(J_f)_{\mathrm{\mathbb{Q}}}$
lies in
![]() $\mathrm{CH}^2_{(1)}(J_f)^{\mu_3}$
by (2.4), we conclude that
$\mathrm{CH}^2_{(1)}(J_f)^{\mu_3}$
by (2.4), we conclude that
![]() $\kappa_f$
is torsion if and only if
$\kappa_f$
is torsion if and only if
![]() $\mathrm{AJ}_{J_f}^2(\kappa_f)$
is. The claim about torsion orders follows from the fact that
$\mathrm{AJ}_{J_f}^2(\kappa_f)$
is. The claim about torsion orders follows from the fact that
![]() $\mathrm{AJ}^2_{J_f}$
is injective on torsion subgroups by a result of Murre [Reference MurreMur85, Theorem 10.3].
$\mathrm{AJ}^2_{J_f}$
is injective on torsion subgroups by a result of Murre [Reference MurreMur85, Theorem 10.3].
4.6 Identifying the complex torus
 $\mathrm{J}(\mathbb{V}^{\mu_3})$
$\mathrm{J}(\mathbb{V}^{\mu_3})$
The
![]() $\mu_3$
-action on
$\mu_3$
-action on
![]() $\mathcal{C}$
induces, via functoriality, a
$\mathcal{C}$
induces, via functoriality, a
![]() $\mu_3$
-action on
$\mu_3$
-action on
![]() $\mathcal{J}$
,
$\mathcal{J}$
,
![]() $\mathbb{V}$
and
$\mathbb{V}$
and
![]() $\mathrm{J}(\mathbb{V})$
. The subsheaf of fixed points
$\mathrm{J}(\mathbb{V})$
. The subsheaf of fixed points
![]() $\mathbb{V}^{\mu_3}$
has the structure of a Z-VHS. The connected component of the identity
$\mathbb{V}^{\mu_3}$
has the structure of a Z-VHS. The connected component of the identity
![]() $\mathrm{J}(\mathbb{V})^{\mu_3,\circ}$
of
$\mathrm{J}(\mathbb{V})^{\mu_3,\circ}$
of
![]() $\mathrm{J}(\mathbb{V})^{\mu_3}$
is a relative complex torus over
$\mathrm{J}(\mathbb{V})^{\mu_3}$
is a relative complex torus over
![]() $S(\mathrm{\mathbb{C}})$
. Moreover, the natural homomorphism
$S(\mathrm{\mathbb{C}})$
. Moreover, the natural homomorphism
![]() $\mathrm{J}(\mathbb{V}^{\mu_3}) \rightarrow \mathrm{J}(\mathbb{V})$
induces an isomorphism onto
$\mathrm{J}(\mathbb{V}^{\mu_3}) \rightarrow \mathrm{J}(\mathbb{V})$
induces an isomorphism onto
![]() $\mathrm{J}(\mathbb{V})^{\mu_3,\circ}$
.
$\mathrm{J}(\mathbb{V})^{\mu_3,\circ}$
.
Lemma 4.13.
The multiple
![]() $3 \cdot \mathrm{AJ}(\kappa_{\mathcal{C}})$
lands in
$3 \cdot \mathrm{AJ}(\kappa_{\mathcal{C}})$
lands in
![]() $\mathrm{J}(\mathbb{V})^{\mu_3,\circ}$
.
$\mathrm{J}(\mathbb{V})^{\mu_3,\circ}$
.
Proof. Since the Ceresa cycle
![]() $\kappa_{\mathcal{C}}$
is
$\kappa_{\mathcal{C}}$
is
![]() $\mu_3$
-invariant,
$\mu_3$
-invariant,
![]() $\mathrm{AJ}(\kappa_{\mathcal{C}})$
lands in
$\mathrm{AJ}(\kappa_{\mathcal{C}})$
lands in
![]() $\mathrm{J}(\mathbb{V})^{\mu_3}$
. The norm map
$\mathrm{J}(\mathbb{V})^{\mu_3}$
. The norm map
![]() $\mathrm{N}\colon \mathrm{J}(\mathbb{V}) \rightarrow \mathrm{J}(\mathbb{V})$
, defined by
$\mathrm{N}\colon \mathrm{J}(\mathbb{V}) \rightarrow \mathrm{J}(\mathbb{V})$
, defined by
![]() $x\mapsto x+ \omega \cdot x + \omega^2 \cdot x$
, lands in
$x\mapsto x+ \omega \cdot x + \omega^2 \cdot x$
, lands in
![]() $\mathrm{J}(\mathbb{V})^{\mu_3,\circ}$
, since the image must be connected and
$\mathrm{J}(\mathbb{V})^{\mu_3,\circ}$
, since the image must be connected and
![]() $\mu_3$
-invariant. We conclude that
$\mu_3$
-invariant. We conclude that
![]() $\mathrm{N}(\mathrm{AJ}(\kappa_{\mathcal{C}})) = 3\cdot \mathrm{AJ}(\kappa_{\mathcal{C}})$
lands in
$\mathrm{N}(\mathrm{AJ}(\kappa_{\mathcal{C}})) = 3\cdot \mathrm{AJ}(\kappa_{\mathcal{C}})$
lands in
![]() $\mathrm{J}(\mathbb{V})^{\mu_3,\circ}$
.
$\mathrm{J}(\mathbb{V})^{\mu_3,\circ}$
.
Therefore,
![]() $3\cdot \mathrm{AJ}(\kappa_{\mathcal{C}})$
defines a section of
$3\cdot \mathrm{AJ}(\kappa_{\mathcal{C}})$
defines a section of
![]() $\mathrm{J}(\mathbb{V})^{\mu_3,\circ}$
, hence we may view it as a section of the complex torus
$\mathrm{J}(\mathbb{V})^{\mu_3,\circ}$
, hence we may view it as a section of the complex torus
![]() $\mathrm{J}(\mathbb{V}^{\mu_3}) \rightarrow S(\mathrm{\mathbb{C}})$
in what follows. We study this relative complex torus (up to isogeny) in the next two propositions.
$\mathrm{J}(\mathbb{V}^{\mu_3}) \rightarrow S(\mathrm{\mathbb{C}})$
in what follows. We study this relative complex torus (up to isogeny) in the next two propositions.
Proposition 4.14. Let
![]() $\mathcal{E} \rightarrow S$
be the relative elliptic curve with Weierstrass equation
$\mathcal{E} \rightarrow S$
be the relative elliptic curve with Weierstrass equation
Then the relative complex torus
![]() $\mathrm{J}(\mathbb{V}^{\mu_3})\rightarrow S$
is isogenous to the relative complex torus
$\mathrm{J}(\mathbb{V}^{\mu_3})\rightarrow S$
is isogenous to the relative complex torus
![]() $\mathcal{E}(\mathrm{\mathbb{C}}) \rightarrow S(\mathrm{\mathbb{C}})$
.
$\mathcal{E}(\mathrm{\mathbb{C}}) \rightarrow S(\mathrm{\mathbb{C}})$
.
Proof. Recall from § 4.3 that we write
![]() $\mathcal{O} = \mathrm{\mathbb{Z}}[\omega]$
and
$\mathcal{O} = \mathrm{\mathbb{Z}}[\omega]$
and
![]() $K = \mathrm{\mathbb{Q}}(\omega)$
. The Z-VHS
$K = \mathrm{\mathbb{Q}}(\omega)$
. The Z-VHS
![]() $R^1 \pi_* \mathrm{\mathbb{Z}}$
whose fibres are the cohomology groups
$R^1 \pi_* \mathrm{\mathbb{Z}}$
whose fibres are the cohomology groups
![]() $\mathrm{H}^1(\mathcal{J}_f;\mathrm{\mathbb{Z}})$
comes equipped with an action of
$\mathrm{H}^1(\mathcal{J}_f;\mathrm{\mathbb{Z}})$
comes equipped with an action of
![]() $\mathcal{O}$
, and the cup product induces an isomorphism
$\mathcal{O}$
, and the cup product induces an isomorphism
![]() $\bigwedge^3 R^1 \pi_* \mathrm{\mathbb{Z}} \simeq R^3 \pi_* \mathrm{\mathbb{Z}} = \mathbb{V}$
. Let
$\bigwedge^3 R^1 \pi_* \mathrm{\mathbb{Z}} \simeq R^3 \pi_* \mathrm{\mathbb{Z}} = \mathbb{V}$
. Let
![]() $\mathbb{W} = \bigwedge^3_{\mathcal{O}} R^1\pi_* \mathrm{\mathbb{Z}}$
(the third exterior product of
$\mathbb{W} = \bigwedge^3_{\mathcal{O}} R^1\pi_* \mathrm{\mathbb{Z}}$
(the third exterior product of
![]() $R^1\pi_*\mathrm{\mathbb{Z}}$
, viewed as a sheaf of
$R^1\pi_*\mathrm{\mathbb{Z}}$
, viewed as a sheaf of
![]() $\mathcal{O}$
-modules), a Z-VHS with an
$\mathcal{O}$
-modules), a Z-VHS with an
![]() $\mathcal{O}$
-action. Lemma 4.6 shows that
$\mathcal{O}$
-action. Lemma 4.6 shows that
![]() $\mathbb{W} \otimes \mathrm{\mathbb{Q}} \simeq \mathbb{V}^{\mu_3} \otimes \mathrm{\mathbb{Q}}$
, so
$\mathbb{W} \otimes \mathrm{\mathbb{Q}} \simeq \mathbb{V}^{\mu_3} \otimes \mathrm{\mathbb{Q}}$
, so
![]() $\mathrm{J}(\mathbb{W})$
and
$\mathrm{J}(\mathbb{W})$
and
![]() $\mathrm{J}(\mathbb{V}^{\mu_3})$
are isogenous.
$\mathrm{J}(\mathbb{V}^{\mu_3})$
are isogenous.
To analyse
![]() $\mathrm{J}(\mathbb{W})$
, we analyse the Z-VHS
$\mathrm{J}(\mathbb{W})$
, we analyse the Z-VHS
![]() $\mathbb{W}(1)$
more closely. It has an
$\mathbb{W}(1)$
more closely. It has an
![]() $\mathcal{O}$
-action by construction, Lemma 4.6 shows that it has constant rank 2, and Lemma 4.5 shows that it has type
$\mathcal{O}$
-action by construction, Lemma 4.6 shows that it has constant rank 2, and Lemma 4.5 shows that it has type
![]() $(1,0)+(0,1)$
. Since
$(1,0)+(0,1)$
. Since
![]() $\mathcal{O}$
has class number 1, there exists a unique Z-Hodge structure with these properties, hence
$\mathcal{O}$
has class number 1, there exists a unique Z-Hodge structure with these properties, hence
![]() $\mathbb{W}_f(1) \simeq \mathrm{H}^1(E;\mathrm{\mathbb{Z}})$
for every
$\mathbb{W}_f(1) \simeq \mathrm{H}^1(E;\mathrm{\mathbb{Z}})$
for every
![]() $f\in S(\mathrm{\mathbb{C}})$
, where E is the elliptic curve with Weierstrass equation
$f\in S(\mathrm{\mathbb{C}})$
, where E is the elliptic curve with Weierstrass equation
![]() $y^2 = x^3+1$
.
$y^2 = x^3+1$
.
Therefore,
![]() $\mathrm{J}(\mathbb{W}) \rightarrow S(\mathrm{\mathbb{C}})$
is an isotrivial family of elliptic curves: analytically locally on
$\mathrm{J}(\mathbb{W}) \rightarrow S(\mathrm{\mathbb{C}})$
is an isotrivial family of elliptic curves: analytically locally on
![]() $S(\mathrm{\mathbb{C}})$
, it is isomorphic to
$S(\mathrm{\mathbb{C}})$
, it is isomorphic to
![]() $E(\mathrm{\mathbb{C}}) \times S(\mathrm{\mathbb{C}}) \rightarrow S(\mathrm{\mathbb{C}})$
. It follows that the sheaf of local isomorphisms between
$E(\mathrm{\mathbb{C}}) \times S(\mathrm{\mathbb{C}}) \rightarrow S(\mathrm{\mathbb{C}})$
. It follows that the sheaf of local isomorphisms between
![]() $\mathrm{J}(\mathbb{W})$
and
$\mathrm{J}(\mathbb{W})$
and
![]() $E(\mathrm{\mathbb{C}}) \times S(\mathrm{\mathbb{C}})$
is an
$E(\mathrm{\mathbb{C}}) \times S(\mathrm{\mathbb{C}})$
is an
![]() $\mathrm{Aut}(E)$
-torsor in the analytic topology on
$\mathrm{Aut}(E)$
-torsor in the analytic topology on
![]() $S(\mathrm{\mathbb{C}})$
. Since
$S(\mathrm{\mathbb{C}})$
. Since
![]() $\mathrm{Aut}(E) \simeq \mu_6$
is finite, this torsor is the analytification of an étale
$\mathrm{Aut}(E) \simeq \mu_6$
is finite, this torsor is the analytification of an étale
![]() $\mu_6$
-torsor on S.
$\mu_6$
-torsor on S.
To analyse étale
![]() $\mu_6$
-torsors on S, consider the following exact sequence induced by the Kummer exact sequence in étale cohomology:
$\mu_6$
-torsors on S, consider the following exact sequence induced by the Kummer exact sequence in étale cohomology:
The Picard group
![]() $\mathrm{Pic}(S)$
vanishes, being a quotient of
$\mathrm{Pic}(S)$
vanishes, being a quotient of
![]() $\mathrm{Pic}(\mathrm{\mathbb{A}}^3_{\mathrm{\mathbb{C}}})$
, hence the outer term in the sequence vanishes. We claim that
$\mathrm{Pic}(\mathrm{\mathbb{A}}^3_{\mathrm{\mathbb{C}}})$
, hence the outer term in the sequence vanishes. We claim that
![]() $\mathrm{disc} \in \mathrm{\mathbb{C}}[a,b,c]$
is irreducible. Indeed, let
$\mathrm{disc} \in \mathrm{\mathbb{C}}[a,b,c]$
is irreducible. Indeed, let
be the ring extension given by adjoining the roots of the universal quartic
![]() $x^4 + ax^2+ bx + c \in \mathrm{\mathbb{C}}[a,b,c][x]$
. The symmetric group
$x^4 + ax^2+ bx + c \in \mathrm{\mathbb{C}}[a,b,c][x]$
. The symmetric group
![]() $S_4$
acts on
$S_4$
acts on
![]() $\{\omega_i\}$
hence on R by ring automorphisms. By the fundamental theorem of symmetric functions, the subring of
$\{\omega_i\}$
hence on R by ring automorphisms. By the fundamental theorem of symmetric functions, the subring of
![]() $S_4$
-fixed points of R is
$S_4$
-fixed points of R is
![]() $\mathrm{\mathbb{C}}[a,b,c]$
. There is a factorization
$\mathrm{\mathbb{C}}[a,b,c]$
. There is a factorization
![]() $\mathrm{disc} = \prod_{i\neq j} (\omega_i - \omega_j)$
in R, and
$\mathrm{disc} = \prod_{i\neq j} (\omega_i - \omega_j)$
in R, and
![]() $S_4$
acts transitively on the linear factors in this factorization. So disc is indeed irreducible in
$S_4$
acts transitively on the linear factors in this factorization. So disc is indeed irreducible in
![]() $\mathrm{\mathbb{C}}[a,b,c]$
. Second, we claim that
$\mathrm{\mathbb{C}}[a,b,c]$
. Second, we claim that
![]() $\mathrm{\mathbb{G}}_m(S)=\mathrm{H}^0(S,\mathcal{O}_S)^{\times} = \{ c\cdot \mathrm{disc}^n \mid c\in \mathrm{\mathbb{C}}^{\times},\, n \in \mathrm{\mathbb{Z}}\}$
. Indeed, every
$\mathrm{\mathbb{G}}_m(S)=\mathrm{H}^0(S,\mathcal{O}_S)^{\times} = \{ c\cdot \mathrm{disc}^n \mid c\in \mathrm{\mathbb{C}}^{\times},\, n \in \mathrm{\mathbb{Z}}\}$
. Indeed, every
![]() $c\cdot \mathrm{disc}^n$
is clearly a unit in
$c\cdot \mathrm{disc}^n$
is clearly a unit in
![]() $\mathrm{H}^0(S, \mathcal{O}_S)$
. Conversely, given a unit
$\mathrm{H}^0(S, \mathcal{O}_S)$
. Conversely, given a unit
![]() $f\in \mathrm{H}^0(S, \mathcal{O}_S)$
, seen as a rational function on
$f\in \mathrm{H}^0(S, \mathcal{O}_S)$
, seen as a rational function on
![]() $\mathrm{\mathbb{A}}^3_{\mathrm{\mathbb{C}}}$
, its divisor
$\mathrm{\mathbb{A}}^3_{\mathrm{\mathbb{C}}}$
, its divisor
![]() $\mathrm{div}(f)$
of zeros and poles must be supported on the zero locus of disc. Since
$\mathrm{div}(f)$
of zeros and poles must be supported on the zero locus of disc. Since
![]() $\mathrm{disc}\in \mathrm{\mathbb{C}}[a,b,c]$
is irreducible,
$\mathrm{disc}\in \mathrm{\mathbb{C}}[a,b,c]$
is irreducible,
![]() $\mathrm{div}(f) = n\cdot [\{\mathrm{disc}=0\}]$
for some
$\mathrm{div}(f) = n\cdot [\{\mathrm{disc}=0\}]$
for some
![]() $n\in \mathrm{\mathbb{Z}}$
. Then
$n\in \mathrm{\mathbb{Z}}$
. Then
![]() $\mathrm{div}(f/\mathrm{disc}^n) = 0$
as a rational function on
$\mathrm{div}(f/\mathrm{disc}^n) = 0$
as a rational function on
![]() $\mathrm{\mathbb{A}}^3_{\mathrm{\mathbb{C}}}$
, hence
$\mathrm{\mathbb{A}}^3_{\mathrm{\mathbb{C}}}$
, hence
![]() $f/\mathrm{disc}^n$
is a unit in
$f/\mathrm{disc}^n$
is a unit in
![]() $\mathrm{\mathbb{C}}[a,b,c]$
, hence
$\mathrm{\mathbb{C}}[a,b,c]$
, hence
![]() $f/\mathrm{disc}^n \in \mathrm{\mathbb{C}}^{\times}$
, proving the claim. We conclude that the group
$f/\mathrm{disc}^n \in \mathrm{\mathbb{C}}^{\times}$
, proving the claim. We conclude that the group
![]() $\mathrm{H}^1_{\mathrm{et}}(S,\mu_6)$
classifying
$\mathrm{H}^1_{\mathrm{et}}(S,\mu_6)$
classifying
![]() $\mu_6$
-torsors is generated by the image of disc.
$\mu_6$
-torsors is generated by the image of disc.
Let
![]() $\mathcal{E}_i\rightarrow S$
be the relative elliptic curve with equation
$\mathcal{E}_i\rightarrow S$
be the relative elliptic curve with equation
![]() $y^2 = x^3 + \mathrm{disc}(f)^i$
. The previous paragraph shows that
$y^2 = x^3 + \mathrm{disc}(f)^i$
. The previous paragraph shows that
![]() $\mathrm{J}(\mathbb{W})$
is isomorphic to
$\mathrm{J}(\mathbb{W})$
is isomorphic to
![]() $\mathcal{E}_i(\mathrm{\mathbb{C}})$
for some
$\mathcal{E}_i(\mathrm{\mathbb{C}})$
for some
![]() $i\in \{0,1,2,3,4,5\}$
. We show that
$i\in \{0,1,2,3,4,5\}$
. We show that
![]() $i=1$
, using our previous results on bielliptic Picard curves in [Reference Laga and ShnidmanLS25]. Let
$i=1$
, using our previous results on bielliptic Picard curves in [Reference Laga and ShnidmanLS25]. Let
![]() $T\subset S$
be the closed subscheme where
$T\subset S$
be the closed subscheme where
![]() $b=0$
, parametrizing even quartic polynomials
$b=0$
, parametrizing even quartic polynomials
![]() $f = x^4+ ax^2+c$
. For
$f = x^4+ ax^2+c$
. For
![]() $f\in T(\mathrm{\mathbb{C}})$
, the
$f\in T(\mathrm{\mathbb{C}})$
, the
![]() $\mu_3$
-action on
$\mu_3$
-action on
![]() $\mathcal{C}_f$
extends to a
$\mathcal{C}_f$
extends to a
![]() $\mu_6$
-action. A calculation shows
$\mu_6$
-action. A calculation shows
![]() $\mathrm{disc}|_T = 16 c (-a^2 + 4 c)^2$
. Applying the singular cohomology realization functor to [Reference Laga and ShnidmanLS25, Theorem 5.1], the relative complex torus
$\mathrm{disc}|_T = 16 c (-a^2 + 4 c)^2$
. Applying the singular cohomology realization functor to [Reference Laga and ShnidmanLS25, Theorem 5.1], the relative complex torus
![]() $\mathrm{J}((\mathbb{V}|_{T(\mathrm{\mathbb{C}})})^{\mu_6})\rightarrow T(\mathrm{\mathbb{C}})$
is isogenous to
$\mathrm{J}((\mathbb{V}|_{T(\mathrm{\mathbb{C}})})^{\mu_6})\rightarrow T(\mathrm{\mathbb{C}})$
is isogenous to
![]() $\mathcal{E}_1(\mathrm{\mathbb{C}})|_{T(\mathrm{\mathbb{C}})}\rightarrow T(\mathrm{\mathbb{C}})$
. Since
$\mathcal{E}_1(\mathrm{\mathbb{C}})|_{T(\mathrm{\mathbb{C}})}\rightarrow T(\mathrm{\mathbb{C}})$
. Since
![]() $\mathrm{J}((\mathbb{V}|_{T(\mathrm{\mathbb{C}})})^{\mu_6})$
is a subtorus of
$\mathrm{J}((\mathbb{V}|_{T(\mathrm{\mathbb{C}})})^{\mu_6})$
is a subtorus of
![]() $\mathrm{J}((\mathbb{V}|_{T(\mathrm{\mathbb{C}})})^{\mu_3})$
of the same dimension, they must be equal, hence
$\mathrm{J}((\mathbb{V}|_{T(\mathrm{\mathbb{C}})})^{\mu_3})$
of the same dimension, they must be equal, hence
![]() $\mathrm{J}(\mathbb{W})|_{T(\mathrm{\mathbb{C}})}$
is isogenous to
$\mathrm{J}(\mathbb{W})|_{T(\mathrm{\mathbb{C}})}$
is isogenous to
![]() $\mathcal{E}_1(\mathrm{\mathbb{C}})|_{T(\mathrm{\mathbb{C}})}$
over
$\mathcal{E}_1(\mathrm{\mathbb{C}})|_{T(\mathrm{\mathbb{C}})}$
over
![]() $T(\mathrm{\mathbb{C}})$
. On the other hand, let
$T(\mathrm{\mathbb{C}})$
. On the other hand, let
![]() $i\in \{0,1,2,3,4,5\}$
be such that
$i\in \{0,1,2,3,4,5\}$
be such that
![]() $\mathrm{J}(\mathbb{W})\simeq \mathcal{E}_i(\mathrm{\mathbb{C}})$
. Then
$\mathrm{J}(\mathbb{W})\simeq \mathcal{E}_i(\mathrm{\mathbb{C}})$
. Then
![]() $\mathrm{J}(\mathbb{W})|_{T(\mathrm{\mathbb{C}})}\simeq \mathcal{E}_i(\mathrm{\mathbb{C}})|_{T(\mathrm{\mathbb{C}})}$
, hence
$\mathrm{J}(\mathbb{W})|_{T(\mathrm{\mathbb{C}})}\simeq \mathcal{E}_i(\mathrm{\mathbb{C}})|_{T(\mathrm{\mathbb{C}})}$
, hence
![]() $\mathcal{E}_1(\mathrm{\mathbb{C}})|_{T(\mathrm{\mathbb{C}})}$
is isogenous to
$\mathcal{E}_1(\mathrm{\mathbb{C}})|_{T(\mathrm{\mathbb{C}})}$
is isogenous to
![]() $\mathcal{E}_i(\mathrm{\mathbb{C}})|_{T(\mathrm{\mathbb{C}})}$
.
$\mathcal{E}_i(\mathrm{\mathbb{C}})|_{T(\mathrm{\mathbb{C}})}$
.
We show that the latter can happen only if
![]() $i=1$
. Indeed, let
$i=1$
. Indeed, let
![]() $\varphi\colon \mathcal{E}_1(\mathrm{\mathbb{C}})|_{T(\mathrm{\mathbb{C}})} \rightarrow \mathcal{E}_i(\mathrm{\mathbb{C}})|_{T(\mathrm{\mathbb{C}})}$
be an isogeny. Since the domain and target of
$\varphi\colon \mathcal{E}_1(\mathrm{\mathbb{C}})|_{T(\mathrm{\mathbb{C}})} \rightarrow \mathcal{E}_i(\mathrm{\mathbb{C}})|_{T(\mathrm{\mathbb{C}})}$
be an isogeny. Since the domain and target of
![]() $\varphi$
are isotrivial relative elliptic curves with
$\varphi$
are isotrivial relative elliptic curves with
![]() $\mathcal{O}$
-multiplication,
$\mathcal{O}$
-multiplication,
![]() $\varphi$
factors as
$\varphi$
factors as
![]() $\psi\circ \gamma$
, where
$\psi\circ \gamma$
, where
![]() $\gamma$
is an endomorphism of
$\gamma$
is an endomorphism of
![]() $\mathcal{E}_1(\mathrm{\mathbb{C}})|_{T(\mathrm{\mathbb{C}})}$
and
$\mathcal{E}_1(\mathrm{\mathbb{C}})|_{T(\mathrm{\mathbb{C}})}$
and
![]() $\psi$
an isomorphism. Therefore,
$\psi$
an isomorphism. Therefore,
![]() $\mathcal{E}_1(\mathrm{\mathbb{C}})|_{T(\mathrm{\mathbb{C}})}$
and
$\mathcal{E}_1(\mathrm{\mathbb{C}})|_{T(\mathrm{\mathbb{C}})}$
and
![]() $\mathcal{E}_i(\mathrm{\mathbb{C}})|_{T(\mathrm{\mathbb{C}})}$
are isomorphic. Since the monodromy representations of
$\mathcal{E}_i(\mathrm{\mathbb{C}})|_{T(\mathrm{\mathbb{C}})}$
are isomorphic. Since the monodromy representations of
![]() $\mathcal{E}_1(\mathrm{\mathbb{C}})|_{T(\mathrm{\mathbb{C}})}$
and
$\mathcal{E}_1(\mathrm{\mathbb{C}})|_{T(\mathrm{\mathbb{C}})}$
and
![]() $\mathcal{E}_i(\mathrm{\mathbb{C}})|_{T(\mathrm{\mathbb{C}})}$
are non-isomorphic when
$\mathcal{E}_i(\mathrm{\mathbb{C}})|_{T(\mathrm{\mathbb{C}})}$
are non-isomorphic when
![]() $i\neq 1$
, we conclude that
$i\neq 1$
, we conclude that
![]() $i=1$
and that
$i=1$
and that
![]() $\mathrm{J}(\mathbb{W})$
is isogenous to
$\mathrm{J}(\mathbb{W})$
is isogenous to
![]() $\mathcal{E}_1(\mathrm{\mathbb{C}})$
over
$\mathcal{E}_1(\mathrm{\mathbb{C}})$
over
![]() $S(\mathrm{\mathbb{C}})$
.
$S(\mathrm{\mathbb{C}})$
.
In summary, we have shown that
![]() $\mathrm{J}(\mathbb{V}^{\mu_3})$
,
$\mathrm{J}(\mathbb{V}^{\mu_3})$
,
![]() $\mathrm{J}(\mathbb{W})$
and
$\mathrm{J}(\mathbb{W})$
and
![]() $\mathcal{E}_1(\mathrm{\mathbb{C}})$
are isogenous. Since
$\mathcal{E}_1(\mathrm{\mathbb{C}})$
are isogenous. Since
![]() $\mathcal{E}_1(\mathrm{\mathbb{C}})$
is isomorphic to
$\mathcal{E}_1(\mathrm{\mathbb{C}})$
is isomorphic to
![]() $\mathcal{E}(\mathrm{\mathbb{C}})$
, we conclude the proof.
$\mathcal{E}(\mathrm{\mathbb{C}})$
, we conclude the proof.
Proposition 4.15.
The group of (algebraic) sections of
![]() $\mathcal{E} \rightarrow S$
is free of rank 1 over
$\mathcal{E} \rightarrow S$
is free of rank 1 over
![]() $\mathcal{O} = \mathrm{\mathbb{Z}}[\omega]$
, and contains the
$\mathcal{O} = \mathrm{\mathbb{Z}}[\omega]$
, and contains the
![]() $\mathcal{O}$
-span of
$\mathcal{O}$
-span of
![]() $P := (a^2+12c,72ac-2a^3-27b^2)$
as a finite-index subgroup.
$P := (a^2+12c,72ac-2a^3-27b^2)$
as a finite-index subgroup.
Proof. Given
![]() $s = (a,b,c) \in S(\mathrm{\mathbb{C}})$
, consider the closed subscheme
$s = (a,b,c) \in S(\mathrm{\mathbb{C}})$
, consider the closed subscheme
![]() $T = \{ (at,bt,ct^2) \colon t\in \mathrm{\mathbb{A}}^1_{\mathrm{\mathbb{C}}}\} \cap S$
of S and the restriction
$T = \{ (at,bt,ct^2) \colon t\in \mathrm{\mathbb{A}}^1_{\mathrm{\mathbb{C}}}\} \cap S$
of S and the restriction
![]() $\pi\colon \mathcal{E}|_T\rightarrow T$
. The variety
$\pi\colon \mathcal{E}|_T\rightarrow T$
. The variety
![]() $\mathcal{E}|_T$
is an open subscheme of an elliptic surface with Weierstrass equation
$\mathcal{E}|_T$
is an open subscheme of an elliptic surface with Weierstrass equation
![]() $y^2 = x^3+t^4g(t)$
, where
$y^2 = x^3+t^4g(t)$
, where
![]() $g(t) \in \mathrm{\mathbb{C}}[t]$
has degree less than or equal to 2, using formula (4.1). There exists a dense open
$g(t) \in \mathrm{\mathbb{C}}[t]$
has degree less than or equal to 2, using formula (4.1). There exists a dense open
![]() $U\subset S$
such that for all
$U\subset S$
such that for all
![]() $s\in U(\mathrm{\mathbb{C}})$
, g(t) has two distinct non-zero roots. Let
$s\in U(\mathrm{\mathbb{C}})$
, g(t) has two distinct non-zero roots. Let
![]() $s\in U(\mathrm{\mathbb{C}})$
. Using Tate’s algorithm [Reference Schütt and ShiodaSS10, Section 4.5, Table 1], we see that the elliptic surface has a singular fibre above
$s\in U(\mathrm{\mathbb{C}})$
. Using Tate’s algorithm [Reference Schütt and ShiodaSS10, Section 4.5, Table 1], we see that the elliptic surface has a singular fibre above
![]() $t=0$
of Kodaira type
$t=0$
of Kodaira type
![]() $\mathrm{IV}^*$
, singular fibres above the roots of g(t) of Kodaira type II, and is smooth above
$\mathrm{IV}^*$
, singular fibres above the roots of g(t) of Kodaira type II, and is smooth above
![]() $t=\infty$
. The presence of a fibre of type II implies that
$t=\infty$
. The presence of a fibre of type II implies that
![]() $\mathcal{E}|_T\rightarrow T$
has no torsion sections [Reference Schütt and ShiodaSS10, Lemma 7.8]. Moreover, the Shioda–Tate formula [Reference Schütt and ShiodaSS10, Theorem 6.3, Proposition 6.6 and § 8.8] shows that the group of sections of
$\mathcal{E}|_T\rightarrow T$
has no torsion sections [Reference Schütt and ShiodaSS10, Lemma 7.8]. Moreover, the Shioda–Tate formula [Reference Schütt and ShiodaSS10, Theorem 6.3, Proposition 6.6 and § 8.8] shows that the group of sections of
![]() $\mathcal{E}|_T\rightarrow T$
is free of rank 2. Since
$\mathcal{E}|_T\rightarrow T$
is free of rank 2. Since
![]() $\mathcal{E}|_T$
receives an
$\mathcal{E}|_T$
receives an
![]() $\mathcal{O}$
-action, its group of sections is free of rank 1 over
$\mathcal{O}$
-action, its group of sections is free of rank 1 over
![]() $\mathcal{O}$
. We will now show that these facts can be used to prove the claims of the proposition by varying s in
$\mathcal{O}$
. We will now show that these facts can be used to prove the claims of the proposition by varying s in
![]() $U(\mathrm{\mathbb{C}})$
.
$U(\mathrm{\mathbb{C}})$
.
We first show that
![]() $\mathcal{E}(S)$
is torsion-free. Suppose
$\mathcal{E}(S)$
is torsion-free. Suppose
![]() $Q \in \mathcal{E}(S)$
is a torsion section. Then
$Q \in \mathcal{E}(S)$
is a torsion section. Then
![]() $N\cdot Q =0$
for some
$N\cdot Q =0$
for some
![]() $N\geqslant 1$
. Hence,
$N\geqslant 1$
. Hence,
![]() $N\cdot Q|_{T}=0$
for every
$N\cdot Q|_{T}=0$
for every
![]() $s\in U(\mathrm{\mathbb{C}})$
. Since the group of sections of
$s\in U(\mathrm{\mathbb{C}})$
. Since the group of sections of
![]() $\mathcal{E}|_T\rightarrow T$
is torsion-free,
$\mathcal{E}|_T\rightarrow T$
is torsion-free,
![]() $Q|_T=0$
for every
$Q|_T=0$
for every
![]() $s\in U(\mathrm{\mathbb{C}})$
. Hence,
$s\in U(\mathrm{\mathbb{C}})$
. Hence,
![]() $Q|_U = 0$
. Since U is dense in S, we must have
$Q|_U = 0$
. Since U is dense in S, we must have
![]() $Q = 0$
, as desired.
$Q = 0$
, as desired.
The fact that P defines a section of
![]() $\mathcal{E}\rightarrow S$
can be verified by direct computation (see § 4.1). Let
$\mathcal{E}\rightarrow S$
can be verified by direct computation (see § 4.1). Let
![]() $L = \mathrm{\mathbb{Z}}\langle P, \omega\cdot P\rangle $
be the
$L = \mathrm{\mathbb{Z}}\langle P, \omega\cdot P\rangle $
be the
![]() $\mathcal{O}$
-span of P, which is a subgroup of the group of sections
$\mathcal{O}$
-span of P, which is a subgroup of the group of sections
![]() $\mathcal{E}(S)$
of
$\mathcal{E}(S)$
of
![]() $\mathcal{E}\rightarrow S$
. The previous paragraph shows that L is free of rank 1 over
$\mathcal{E}\rightarrow S$
. The previous paragraph shows that L is free of rank 1 over
![]() $\mathcal{O}$
. It remains to show that it has finite index in
$\mathcal{O}$
. It remains to show that it has finite index in
![]() $\mathcal{E}(S)$
. Suppose for the sake of contradiction that there exists a third section
$\mathcal{E}(S)$
. Suppose for the sake of contradiction that there exists a third section
![]() $Q \in \mathcal{E}(S)$
which is not in
$Q \in \mathcal{E}(S)$
which is not in
![]() $L\otimes \mathrm{\mathbb{Q}}$
. Then the locus
$L\otimes \mathrm{\mathbb{Q}}$
. Then the locus
![]() $S_{\mathrm{dep}}$
of
$S_{\mathrm{dep}}$
of
![]() $s\in S(\mathrm{\mathbb{C}})$
where
$s\in S(\mathrm{\mathbb{C}})$
where
![]() $P_{s}, \omega\cdot P_{s}$
and
$P_{s}, \omega\cdot P_{s}$
and
![]() $Q_s$
are linearly dependent is a countable union of closed proper algebraic subvarieties. For every
$Q_s$
are linearly dependent is a countable union of closed proper algebraic subvarieties. For every
![]() $s\in U(\mathrm{\mathbb{C}})$
, the group of sections of
$s\in U(\mathrm{\mathbb{C}})$
, the group of sections of
![]() $\mathcal{E}|_T\rightarrow T$
is free of rank 1 over
$\mathcal{E}|_T\rightarrow T$
is free of rank 1 over
![]() $\mathcal{O}$
. There exists a possibly smaller dense open
$\mathcal{O}$
. There exists a possibly smaller dense open
![]() $V\subset U$
such that if
$V\subset U$
such that if
![]() $s\in V(\mathrm{\mathbb{C}})$
then
$s\in V(\mathrm{\mathbb{C}})$
then
![]() $P_{s}$
is non-zero, hence
$P_{s}$
is non-zero, hence
![]() $\langle P_{s}, \omega \cdot P_s \rangle$
is a finite-index subgroup of
$\langle P_{s}, \omega \cdot P_s \rangle$
is a finite-index subgroup of
![]() $\mathcal{E}(T)$
. Therefore,
$\mathcal{E}(T)$
. Therefore,
![]() $Q_t, P_{1,t}, P_{2,t}$
are linearly dependent for all
$Q_t, P_{1,t}, P_{2,t}$
are linearly dependent for all
![]() $s\in V(\mathrm{\mathbb{C}})$
. Since
$s\in V(\mathrm{\mathbb{C}})$
. Since
![]() $V(\mathrm{\mathbb{C}})\setminus S_{\mathrm{dep}}$
is non-empty, we obtain a contradiction.
$V(\mathrm{\mathbb{C}})\setminus S_{\mathrm{dep}}$
is non-empty, we obtain a contradiction.
4.7 Proof of the vanishing criterion in the Chow group
Proof of Theorem 4.2. We may assume (using Lemma 2.1) that
![]() $k=\mathrm{\mathbb{C}}$
. Recall that
$k=\mathrm{\mathbb{C}}$
. Recall that
![]() $3\cdot \mathrm{AJ}(\kappa_{\mathcal{C}})$
defines a holomorphic section of
$3\cdot \mathrm{AJ}(\kappa_{\mathcal{C}})$
defines a holomorphic section of
![]() $\mathrm{J}(\mathbb{V}^{\mu_3})\rightarrow S(\mathrm{\mathbb{C}})$
. Choose an isogeny of complex tori
$\mathrm{J}(\mathbb{V}^{\mu_3})\rightarrow S(\mathrm{\mathbb{C}})$
. Choose an isogeny of complex tori
![]() $\mathrm{J}(\mathbb{V}^{\mu_3})\rightarrow \mathcal{E}(\mathrm{\mathbb{C}})$
using Proposition 4.14 and let
$\mathrm{J}(\mathbb{V}^{\mu_3})\rightarrow \mathcal{E}(\mathrm{\mathbb{C}})$
using Proposition 4.14 and let
![]() $\sigma$
be the image of
$\sigma$
be the image of
![]() $3\cdot \mathrm{AJ}(\kappa_{\mathcal{C}})$
under this isogeny. This is a holomorphic section of
$3\cdot \mathrm{AJ}(\kappa_{\mathcal{C}})$
under this isogeny. This is a holomorphic section of
![]() $\mathcal{E}(\mathrm{\mathbb{C}}) \rightarrow S(\mathrm{\mathbb{C}})$
.
$\mathcal{E}(\mathrm{\mathbb{C}}) \rightarrow S(\mathrm{\mathbb{C}})$
.
We claim that
![]() $\sigma$
is not a torsion section. If it were torsion, then
$\sigma$
is not a torsion section. If it were torsion, then
![]() $\mathrm{AJ}(\kappa_{\mathcal{C}})$
would be a torsion section of
$\mathrm{AJ}(\kappa_{\mathcal{C}})$
would be a torsion section of
![]() $\mathrm{J}(\mathbb{V}^{\mu_3})$
, hence, by Proposition 4.12,
$\mathrm{J}(\mathbb{V}^{\mu_3})$
, hence, by Proposition 4.12,
![]() $\kappa_f$
would be torsion for every
$\kappa_f$
would be torsion for every
![]() $f\in S(\mathrm{\mathbb{C}})$
. This is not the case, since
$f\in S(\mathrm{\mathbb{C}})$
. This is not the case, since
![]() $\kappa_f$
is of infinite order if
$\kappa_f$
is of infinite order if
![]() $f = x^4+x^2+1$
by [Reference Laga and ShnidmanLS25, Corollary 2.9]. We conclude that
$f = x^4+x^2+1$
by [Reference Laga and ShnidmanLS25, Corollary 2.9]. We conclude that
![]() $\sigma$
is not a torsion section.
$\sigma$
is not a torsion section.
Next we claim that
![]() $\sigma$
is the analytification of an algebraic section of
$\sigma$
is the analytification of an algebraic section of
![]() $\mathcal{E}\rightarrow S$
. Let
$\mathcal{E}\rightarrow S$
. Let
![]() $N\geqslant 1$
be an integer such that
$N\geqslant 1$
be an integer such that
![]() $N\cdot \kappa_f$
is algebraically trivial for every Picard curve
$N\cdot \kappa_f$
is algebraically trivial for every Picard curve
![]() $f\in S(\mathrm{\mathbb{C}})$
(such an integer exists by Theorem 4.1). By the algebraicity of the Abel–Jacobi map for algebraically trivial cycles ([Reference Achter, Casalaina-Martin and VialACMV19a, Theorem 1]), there exists a relative algebraic subtorus
$f\in S(\mathrm{\mathbb{C}})$
(such an integer exists by Theorem 4.1). By the algebraicity of the Abel–Jacobi map for algebraically trivial cycles ([Reference Achter, Casalaina-Martin and VialACMV19a, Theorem 1]), there exists a relative algebraic subtorus
![]() $\mathrm{J}_a(\mathbb{V})\subset \mathrm{J}(\mathbb{V})$
with the following property: the section
$\mathrm{J}_a(\mathbb{V})\subset \mathrm{J}(\mathbb{V})$
with the following property: the section
![]() $\mathrm{AJ}(3N\cdot \kappa_{\mathcal{C}})$
lands in
$\mathrm{AJ}(3N\cdot \kappa_{\mathcal{C}})$
lands in
![]() $\mathrm{J}_a(\mathbb{V})$
and the corresponding holomorphic map
$\mathrm{J}_a(\mathbb{V})$
and the corresponding holomorphic map
![]() $S(\mathrm{\mathbb{C}}) \rightarrow \mathrm{J}_a(\mathbb{V})$
is algebraic. On the other hand,
$S(\mathrm{\mathbb{C}}) \rightarrow \mathrm{J}_a(\mathbb{V})$
is algebraic. On the other hand,
![]() $\mathrm{AJ}(3N\cdot \kappa_{\mathcal{C}})$
also lands in
$\mathrm{AJ}(3N\cdot \kappa_{\mathcal{C}})$
also lands in
![]() $\mathrm{J}(\mathbb{V}^{\mu_3})$
, is not a torsion section by the previous paragraph, and
$\mathrm{J}(\mathbb{V}^{\mu_3})$
, is not a torsion section by the previous paragraph, and
![]() $\mathrm{J}(\mathbb{V}^{\mu_3})$
has relative dimension 1 over
$\mathrm{J}(\mathbb{V}^{\mu_3})$
has relative dimension 1 over
![]() $S(\mathrm{\mathbb{C}})$
. Therefore,
$S(\mathrm{\mathbb{C}})$
. Therefore,
![]() $\mathrm{J}(\mathbb{V}^{\mu_3})$
is the smallest relative subtorus of
$\mathrm{J}(\mathbb{V}^{\mu_3})$
is the smallest relative subtorus of
![]() $\mathrm{J}(\mathbb{V})$
containing the image of
$\mathrm{J}(\mathbb{V})$
containing the image of
![]() $\mathrm{AJ}(3N \cdot \kappa_{\mathcal{C}})$
. Hence,
$\mathrm{AJ}(3N \cdot \kappa_{\mathcal{C}})$
. Hence,
![]() $\mathrm{J}(\mathbb{V}^{\mu_3})\subset \mathrm{J}_a(\mathbb{V})$
. We conclude that
$\mathrm{J}(\mathbb{V}^{\mu_3})\subset \mathrm{J}_a(\mathbb{V})$
. We conclude that
![]() $\mathrm{AJ}(3N \cdot\kappa_{\mathcal{C}}) \colon S(\mathrm{\mathbb{C}}) \rightarrow \mathrm{J}(\mathbb{V}^{\mu_3})$
is algebraic, so
$\mathrm{AJ}(3N \cdot\kappa_{\mathcal{C}}) \colon S(\mathrm{\mathbb{C}}) \rightarrow \mathrm{J}(\mathbb{V}^{\mu_3})$
is algebraic, so
![]() $\mathrm{AJ}(3\cdot \kappa_{\mathcal{C}})$
is algebraic, so
$\mathrm{AJ}(3\cdot \kappa_{\mathcal{C}})$
is algebraic, so
![]() $\sigma$
is algebraic.
$\sigma$
is algebraic.
Since
![]() $\sigma$
is an algebraic section of
$\sigma$
is an algebraic section of
![]() $\mathcal{E}\rightarrow S$
, Proposition 33 shows that there exist an integer
$\mathcal{E}\rightarrow S$
, Proposition 33 shows that there exist an integer
![]() $M\geqslant 1$
and an element
$M\geqslant 1$
and an element
![]() $\gamma \in \mathcal{O}$
such that
$\gamma \in \mathcal{O}$
such that
![]() $M \cdot \sigma = \gamma \cdot P$
. Since
$M \cdot \sigma = \gamma \cdot P$
. Since
![]() $\sigma$
is not a torsion section,
$\sigma$
is not a torsion section,
![]() $\gamma \neq 0$
.
$\gamma \neq 0$
.
Putting everything together, we have for
![]() $f\in S(\mathrm{\mathbb{C}})$
that
$f\in S(\mathrm{\mathbb{C}})$
that
![]() $\kappa_f$
is torsion if and only if
$\kappa_f$
is torsion if and only if
![]() $\mathrm{AJ}_{J_f}^2(\kappa_f)$
torsion (by Proposition 4.12), if and only if
$\mathrm{AJ}_{J_f}^2(\kappa_f)$
torsion (by Proposition 4.12), if and only if
![]() $\mathrm{AJ}(\kappa_{\mathcal{C}})_f \in \mathrm{J}(\mathbb{V}^{\mu_3})_f$
torsion, if and only if
$\mathrm{AJ}(\kappa_{\mathcal{C}})_f \in \mathrm{J}(\mathbb{V}^{\mu_3})_f$
torsion, if and only if
![]() $\sigma_f \in \mathcal{E}_f(\mathrm{\mathbb{C}})$
torsion, if and only if
$\sigma_f \in \mathcal{E}_f(\mathrm{\mathbb{C}})$
torsion, if and only if
![]() $P_f$
torsion. Tracing through the equivalences, the quotient of the torsion orders
$P_f$
torsion. Tracing through the equivalences, the quotient of the torsion orders
![]() ${\rm ord}(\kappa_f)/{\rm ord}(P_f)$
(if defined) takes only finitely many values as f ranges in
${\rm ord}(\kappa_f)/{\rm ord}(P_f)$
(if defined) takes only finitely many values as f ranges in
![]() $S(\mathrm{\mathbb{C}})$
.
$S(\mathrm{\mathbb{C}})$
.
4.8 Analysing the torsion locus of P
Theorem 4.2 shows that there are infinitely many plane quartic curves over Q with torsion Ceresa cycle, since we may take
![]() $a = c = -12$
. In fact, we can find explicit families of torsion Ceresa cycles over
$a = c = -12$
. In fact, we can find explicit families of torsion Ceresa cycles over
![]() $\overline{\mathrm{\mathbb{Q}}}$
of arbitrarily large order by explicitly computing the torsion locus of the section P of
$\overline{\mathrm{\mathbb{Q}}}$
of arbitrarily large order by explicitly computing the torsion locus of the section P of
![]() $\mathcal{E}\rightarrow S$
.
$\mathcal{E}\rightarrow S$
.
Recall that
![]() $S\subset \mathrm{\mathbb{A}}^3_{\mathrm{\mathbb{C}}}$
is the parameter space of polynomials
$S\subset \mathrm{\mathbb{A}}^3_{\mathrm{\mathbb{C}}}$
is the parameter space of polynomials
![]() $f(x) = x^4 + ax^2 + bx+c$
of non-zero discriminant. For
$f(x) = x^4 + ax^2 + bx+c$
of non-zero discriminant. For
![]() $(I,J) \in \mathbb{C}^2$
such that
$(I,J) \in \mathbb{C}^2$
such that
![]() $4I^3- J^2 \neq 0$
, let
$4I^3- J^2 \neq 0$
, let
![]() $X_{I,J}\subset S$
be the closed subscheme of elements f satisfying
$X_{I,J}\subset S$
be the closed subscheme of elements f satisfying
![]() $(I(f), J(f)) = (I,J)$
, and let
$(I(f), J(f)) = (I,J)$
, and let
![]() $E_{I,J}$
be the elliptic curve
$E_{I,J}$
be the elliptic curve
![]() $y^2 = x^3- Ix /3 - J /27$
. Let
$y^2 = x^3- Ix /3 - J /27$
. Let
![]() $E_{I,J}^{\circ}\subset E_{I,J}$
be the complement of the origin.
$E_{I,J}^{\circ}\subset E_{I,J}$
be the complement of the origin.
Lemma 4.16.
For
![]() $(I,J)\in \mathrm{\mathbb{C}}^2$
such that
$(I,J)\in \mathrm{\mathbb{C}}^2$
such that
![]() $4I^3 -J^2 \neq 0$
, the map
$4I^3 -J^2 \neq 0$
, the map
![]() $f\mapsto (-2a/3,b)$
is an isomorphism
$f\mapsto (-2a/3,b)$
is an isomorphism
![]() $X_{I,J} \simeq E_{I,J}^{\circ}$
.
$X_{I,J} \simeq E_{I,J}^{\circ}$
.
Proof. Indeed, a calculation shows that an inverse is given by
We now describe the locus of
![]() $f\in S$
where the specialization
$f\in S$
where the specialization
![]() $P_f = (I(f), J(f))$
of the section P of
$P_f = (I(f), J(f))$
of the section P of
![]() $\mathcal{E}\rightarrow S$
is torsion. First we consider the restriction of this locus to the closed subscheme
$\mathcal{E}\rightarrow S$
is torsion. First we consider the restriction of this locus to the closed subscheme
![]() $S_1\subset S$
where
$S_1\subset S$
where
![]() $\mathrm{disc}(f) =1$
, so that
$\mathrm{disc}(f) =1$
, so that
![]() $\mathcal{E}\rightarrow S$
restricts to the trivial family with fibre the elliptic curve
$\mathcal{E}\rightarrow S$
restricts to the trivial family with fibre the elliptic curve
![]() $E_0\colon y^2 = 4x^3-27$
. Let
$E_0\colon y^2 = 4x^3-27$
. Let
![]() $E_0^{\circ}\subset E_0$
be the complement of the origin. If
$E_0^{\circ}\subset E_0$
be the complement of the origin. If
![]() $(I,J) \in E_0^{\circ}(\mathrm{\mathbb{C}})$
, then
$(I,J) \in E_0^{\circ}(\mathrm{\mathbb{C}})$
, then
![]() $X_{I,J}$
is a closed subscheme of
$X_{I,J}$
is a closed subscheme of
![]() $S_1$
. For G a group, write
$S_1$
. For G a group, write
![]() $G_{\mathrm{tors}}\subset G$
for the subset of torsion elements. Then we tautologically have
$G_{\mathrm{tors}}\subset G$
for the subset of torsion elements. Then we tautologically have
Define a
![]() $\mathrm{\mathbb{G}}_m$
-action on S via the formula
$\mathrm{\mathbb{G}}_m$
-action on S via the formula
![]() $\lambda \cdot (a,b,c) = (\lambda^2a,\lambda^3 b, \lambda^4 c)$
. The polynomials I(f), J(f) and
$\lambda \cdot (a,b,c) = (\lambda^2a,\lambda^3 b, \lambda^4 c)$
. The polynomials I(f), J(f) and
![]() $\mathrm{disc}(f)$
are then homogeneous of degree 4,6,12. Using the
$\mathrm{disc}(f)$
are then homogeneous of degree 4,6,12. Using the
![]() $\mathrm{\mathbb{G}}_m$
-action on S, we can form the (coarse) quotient
$\mathrm{\mathbb{G}}_m$
-action on S, we can form the (coarse) quotient
![]() $\mathcal{M}_{\mathrm{Pic}} = S/\mathrm{\mathbb{G}}_m$
, an open subscheme of weighted projective space
$\mathcal{M}_{\mathrm{Pic}} = S/\mathrm{\mathbb{G}}_m$
, an open subscheme of weighted projective space
![]() $\mathbb{P}(2,3,4)$
.
$\mathbb{P}(2,3,4)$
.
Lemma 4.17. The variety
![]() $\mathcal{M}_{\mathrm{Pic}}$
is the coarse moduli space of Picard curves over C.
$\mathcal{M}_{\mathrm{Pic}}$
is the coarse moduli space of Picard curves over C.
Proof. See [Reference HolzapfelHol95, p. 15, Proposition 2.3].
The inclusion
![]() $S_1\subset S$
determines an isomorphism
$S_1\subset S$
determines an isomorphism
![]() $S_1/\mu_{12}\simeq \mathcal{M}_{\mathrm{Pic}}$
, where
$S_1/\mu_{12}\simeq \mathcal{M}_{\mathrm{Pic}}$
, where
![]() $\mu_{12}\subset \mathrm{\mathbb{G}}_m$
acts via restriction on
$\mu_{12}\subset \mathrm{\mathbb{G}}_m$
acts via restriction on
![]() $S_1$
. Write
$S_1$
. Write
![]() $\pi\colon S\rightarrow \mathcal{M}_{\mathrm{Pic}}$
and
$\pi\colon S\rightarrow \mathcal{M}_{\mathrm{Pic}}$
and
![]() $\pi_1\colon S_1\rightarrow \mathcal{M}_{\mathrm{Pic}}$
for the quotient maps.
$\pi_1\colon S_1\rightarrow \mathcal{M}_{\mathrm{Pic}}$
for the quotient maps.
Let
![]() $V\subset \mathcal{M}_{\mathrm{Pic}}$
be the image of the torsion locus in S of the section P of
$V\subset \mathcal{M}_{\mathrm{Pic}}$
be the image of the torsion locus in S of the section P of
![]() $\mathcal{E}\rightarrow S$
. Since this torsion locus is
$\mathcal{E}\rightarrow S$
. Since this torsion locus is
![]() $\mathrm{\mathbb{G}}_m$
-invariant, V also equals the image of the torsion locus of
$\mathrm{\mathbb{G}}_m$
-invariant, V also equals the image of the torsion locus of
![]() $P_f \in E_0$
under
$P_f \in E_0$
under
![]() $\pi_1$
. Therefore, V equals
$\pi_1$
. Therefore, V equals
![]() $\cup \pi_1(X_{I,J})$
, where (I,J) ranges over torsion points of
$\cup \pi_1(X_{I,J})$
, where (I,J) ranges over torsion points of
![]() $E_{0}^{\circ}$
. If
$E_{0}^{\circ}$
. If
![]() $\zeta\in \mu_{12}$
, then
$\zeta\in \mu_{12}$
, then
![]() $\zeta\cdot X_{I,J} = X_{\zeta^4 I , \zeta^6 J}$
, so
$\zeta\cdot X_{I,J} = X_{\zeta^4 I , \zeta^6 J}$
, so
![]() $\mu_2\subset \mu_{12}$
preserves
$\mu_2\subset \mu_{12}$
preserves
![]() $X_{I,J}$
. Under the bijection
$X_{I,J}$
. Under the bijection
![]() $X_{I,J}\simeq E_{I,J}^{\circ}$
,
$X_{I,J}\simeq E_{I,J}^{\circ}$
,
![]() $-1$
acts as
$-1$
acts as
![]() $(\alpha, \beta)\mapsto (\alpha, -\beta)$
on
$(\alpha, \beta)\mapsto (\alpha, -\beta)$
on
![]() $E_{I,J}^{\circ}$
. Therefore, the quotient
$E_{I,J}^{\circ}$
. Therefore, the quotient
![]() $X_{I,J}/\mu_2$
is isomorphic, via the a-coordinate, to
$X_{I,J}/\mu_2$
is isomorphic, via the a-coordinate, to
![]() $\mathrm{\mathbb{A}}^1$
. It follows that for each torsion point (I,J), the restriction
$\mathrm{\mathbb{A}}^1$
. It follows that for each torsion point (I,J), the restriction
![]() $X_{I,J}\hookrightarrow S_1 \rightarrow \mathcal{M}_{\mathrm{Pic}}$
factors through a map
$X_{I,J}\hookrightarrow S_1 \rightarrow \mathcal{M}_{\mathrm{Pic}}$
factors through a map
![]() $\varphi_{(I,J)}\colon X_{I,J}/\mu_2 =\mathrm{\mathbb{A}}^1 \rightarrow \mathcal{M}_{\mathrm{Pic}}$
, and V is the union of the images of
$\varphi_{(I,J)}\colon X_{I,J}/\mu_2 =\mathrm{\mathbb{A}}^1 \rightarrow \mathcal{M}_{\mathrm{Pic}}$
, and V is the union of the images of
![]() $\varphi_{(I,J)}$
. If
$\varphi_{(I,J)}$
. If
![]() $(I,J) = (\zeta^4 I',\zeta^6 J')$
for some
$(I,J) = (\zeta^4 I',\zeta^6 J')$
for some
![]() $\zeta \in \mu_{12}$
, then the images of
$\zeta \in \mu_{12}$
, then the images of
![]() $\varphi_{(I,J)}$
are equal. Otherwise, they are disjoint. We conclude the following result.
$\varphi_{(I,J)}$
are equal. Otherwise, they are disjoint. We conclude the following result.
Proposition 4.18. We have
The images of two maps
![]() $\varphi_{(I,J)}$
are either equal or disjoint. The maps
$\varphi_{(I,J)}$
are either equal or disjoint. The maps
![]() $\varphi_{(I,J)}$
are quasi-finite.
$\varphi_{(I,J)}$
are quasi-finite.
We can identify
![]() $\varphi_{(I,J)}(t)$
explicitly, at least when
$\varphi_{(I,J)}(t)$
explicitly, at least when
![]() $b\neq 0$
. For
$b\neq 0$
. For
![]() $t\in \mathrm{\mathbb{C}}$
, let
$t\in \mathrm{\mathbb{C}}$
, let
![]() $g_{(I,J)}(t)= t^3 - It/3 -J/27$
, let
$g_{(I,J)}(t)= t^3 - It/3 -J/27$
, let
![]() $(\alpha_t, \beta_t) = (t g_{(I,J)}(t), g_{(I,J)}(t)^2)$
and let
$(\alpha_t, \beta_t) = (t g_{(I,J)}(t), g_{(I,J)}(t)^2)$
and let
![]() $f_{(I,J),t}(x) = x^4 - 3\alpha_t x^2/2 + \beta_t x + (I/12 - 3\alpha_t^2/16)$
.
$f_{(I,J),t}(x) = x^4 - 3\alpha_t x^2/2 + \beta_t x + (I/12 - 3\alpha_t^2/16)$
.
Proposition 4.19.
In the above notation, assume
![]() $g_{(I,J)}(t)\neq 0$
. Then
$g_{(I,J)}(t)\neq 0$
. Then
![]() $\varphi_{(I,J)}(t) = \pi(f_{(I,J),t})$
.
$\varphi_{(I,J)}(t) = \pi(f_{(I,J),t})$
.
Proof. Let
![]() $\tilde{f}$
be an element of
$\tilde{f}$
be an element of
![]() $X_{I,J}$
which under the isomorphism
$X_{I,J}$
which under the isomorphism
![]() $X_{I,J}\simeq E_{I,J}^{\circ}$
corresponds to an element
$X_{I,J}\simeq E_{I,J}^{\circ}$
corresponds to an element
![]() $(\tilde{\alpha}, \tilde{\beta})$
with
$(\tilde{\alpha}, \tilde{\beta})$
with
![]() $\tilde{\alpha} = t$
. By definition,
$\tilde{\alpha} = t$
. By definition,
![]() $\varphi_{(I,J)}(t) = \pi_1(\tilde{f})$
. We have
$\varphi_{(I,J)}(t) = \pi_1(\tilde{f})$
. We have
![]() $\tilde{\beta}^2 = g_{(I,J)}(t)\neq 0$
. A calculation shows that
$\tilde{\beta}^2 = g_{(I,J)}(t)\neq 0$
. A calculation shows that
![]() $f_{(I,J),t} = \tilde{\beta}\cdot \tilde{f}$
, so
$f_{(I,J),t} = \tilde{\beta}\cdot \tilde{f}$
, so
![]() $f_{(I,J), t}$
and
$f_{(I,J), t}$
and
![]() $\tilde{f}$
have the same image in
$\tilde{f}$
have the same image in
![]() $\mathcal{M}_{\mathrm{Pic}}$
, as claimed.
$\mathcal{M}_{\mathrm{Pic}}$
, as claimed.
Proposition 4.19 gives explicit one-parameter families of Picard curves with equation
![]() $C_t\colon y^3 = f_{(I,J),t}(x)$
whose Ceresa cycle is torsion. The explicit description shows that when
$C_t\colon y^3 = f_{(I,J),t}(x)$
whose Ceresa cycle is torsion. The explicit description shows that when
![]() $(I,J)\in k^2$
, where k is a subfield of
$(I,J)\in k^2$
, where k is a subfield of
![]() $\mathbb{C}$
, the family
$\mathbb{C}$
, the family
![]() $C_t$
is defined over k. Since all torsion points of
$C_t$
is defined over k. Since all torsion points of
![]() $E_0$
are defined over Q, so are the families
$E_0$
are defined over Q, so are the families
![]() $C_t$
.
$C_t$
.
We can now prove Theorem D.
Proof of Theorem D.Part (i) follows from Theorems 4.2 and Proposition 4.18.
We now turn to (ii). For every
![]() $d \geqslant 1$
, there exists
$d \geqslant 1$
, there exists
![]() $N = N(d) \geqslant 1$
such that for every Picard curve
$N = N(d) \geqslant 1$
such that for every Picard curve
![]() $C_f$
over a number field k of degree d, the order of
$C_f$
over a number field k of degree d, the order of
![]() $\kappa_f$
in
$\kappa_f$
in
![]() $\mathrm{CH}_1(J_{f,\bar{k}})$
is either infinite or less than N. Indeed, this follows from Theorem 4.2 and the uniform bound (depending only on d) on the order of a k-rational torsion point on an elliptic curve
$\mathrm{CH}_1(J_{f,\bar{k}})$
is either infinite or less than N. Indeed, this follows from Theorem 4.2 and the uniform bound (depending only on d) on the order of a k-rational torsion point on an elliptic curve
![]() $y^2 = x^3 + D$
over any number field k of degree d.
$y^2 = x^3 + D$
over any number field k of degree d.
5. Ceresa vanishing loci in genus 3
Fix
![]() $g\geqslant 3$
and let
$g\geqslant 3$
and let
![]() $\mathcal{M}_g$
be the (coarse) moduli space of genus-g curves, seen as a variety over Q. Let
$\mathcal{M}_g$
be the (coarse) moduli space of genus-g curves, seen as a variety over Q. Let
![]() $V_g^{\mathrm{rat}}\subset \mathcal{M}_g$
be the subset of curves [C] for which
$V_g^{\mathrm{rat}}\subset \mathcal{M}_g$
be the subset of curves [C] for which
![]() $\kappa(C)$
vanishes in
$\kappa(C)$
vanishes in
![]() $\mathrm{CH}_1(\mathrm{Jac}(C))_{\mathrm{\mathbb{Q}}}$
, in the notation of § 2.7. Since the vanishing of
$\mathrm{CH}_1(\mathrm{Jac}(C))_{\mathrm{\mathbb{Q}}}$
, in the notation of § 2.7. Since the vanishing of
![]() $\kappa(C)$
only depends on the geometric isomorphism class of C (by Lemma 2.1), this locus is well defined. Similarly define the locus
$\kappa(C)$
only depends on the geometric isomorphism class of C (by Lemma 2.1), this locus is well defined. Similarly define the locus
![]() $V_g^{\mathrm{alg}} \subset \mathcal{M}_g$
where
$V_g^{\mathrm{alg}} \subset \mathcal{M}_g$
where
![]() $\bar{\kappa}(C) \in \mathrm{Gr}_1(\mathrm{Jac}(C))_{\mathrm{\mathbb{Q}}}$
vanishes.
$\bar{\kappa}(C) \in \mathrm{Gr}_1(\mathrm{Jac}(C))_{\mathrm{\mathbb{Q}}}$
vanishes.
Lemma 5.1. The subsets
![]() $V_g^{\mathrm{rat}}, V_g^{\mathrm{alg}}\subset \mathcal{M}_g$
are countable unions of proper closed algebraic subvarieties.
$V_g^{\mathrm{rat}}, V_g^{\mathrm{alg}}\subset \mathcal{M}_g$
are countable unions of proper closed algebraic subvarieties.
Proof. Let
![]() $\widetilde{\mathcal{M}}_g$
be the fine moduli space parametrizing genus-g curves C with full symplectic level-5 structure and a degree-1 divisor class
$\widetilde{\mathcal{M}}_g$
be the fine moduli space parametrizing genus-g curves C with full symplectic level-5 structure and a degree-1 divisor class
![]() $e\in \mathrm{CH}_0(C)$
such that
$e\in \mathrm{CH}_0(C)$
such that
![]() $(2g-2)e$
is canonical. Considering the universal curve over it together with its degree-1 divisor, we can define a universal Ceresa cycle on the universal Jacobian over
$(2g-2)e$
is canonical. Considering the universal curve over it together with its degree-1 divisor, we can define a universal Ceresa cycle on the universal Jacobian over
![]() $\widetilde{\mathcal{M}}_g$
; Lemma 2.4 then implies that the locus in
$\widetilde{\mathcal{M}}_g$
; Lemma 2.4 then implies that the locus in
![]() $\widetilde{\mathcal{M}}_g$
where this Ceresa cycle vanishes (with Q-coefficients) is a countable union of closed algebraic subvarieties. Since the forgetful map
$\widetilde{\mathcal{M}}_g$
where this Ceresa cycle vanishes (with Q-coefficients) is a countable union of closed algebraic subvarieties. Since the forgetful map
![]() $\widetilde{\mathcal{M}}_g\rightarrow \mathcal{M}_g$
is proper, the same is true for the image of this locus, which is exactly
$\widetilde{\mathcal{M}}_g\rightarrow \mathcal{M}_g$
is proper, the same is true for the image of this locus, which is exactly
![]() $V_g^{\mathrm{rat}}$
. The proof for
$V_g^{\mathrm{rat}}$
. The proof for
![]() $V_g^{\mathrm{alg}}$
is identical.
$V_g^{\mathrm{alg}}$
is identical.
These vanishing loci have the following basic properties:
![]() $V_g^{\mathrm{rat}}\subset V_g^{\mathrm{alg}}\subset \mathcal{M}_g$
; the hyperelliptic locus is contained in
$V_g^{\mathrm{rat}}\subset V_g^{\mathrm{alg}}\subset \mathcal{M}_g$
; the hyperelliptic locus is contained in
![]() $V_g^{\mathrm{rat}}$
; and
$V_g^{\mathrm{rat}}$
; and
![]() $V_g^{\mathrm{alg}} \neq \mathcal{M}_g$
by Ceresa’s famous result [Reference CeresaCer83]. It would be interesting to obtain further information about the components of
$V_g^{\mathrm{alg}} \neq \mathcal{M}_g$
by Ceresa’s famous result [Reference CeresaCer83]. It would be interesting to obtain further information about the components of
![]() $V_g^{\mathrm{rat}}$
and
$V_g^{\mathrm{rat}}$
and
![]() $V_g^{\mathrm{alg}}$
. We end our paper by determining the automorphism group strata in
$V_g^{\mathrm{alg}}$
. We end our paper by determining the automorphism group strata in
![]() $\mathcal{M}_3$
that are contained in
$\mathcal{M}_3$
that are contained in
![]() $V_3^{\mathrm{rat}}$
or
$V_3^{\mathrm{rat}}$
or
![]() $V_3^{\mathrm{alg}}$
. So let
$V_3^{\mathrm{alg}}$
. So let
![]() $g=3$
and consider the open subscheme
$g=3$
and consider the open subscheme
![]() $\mathcal{M}_3^{\mathrm{nh}}\subset \mathcal{M}_3$
of non-hyperelliptic curves. There is a stratification
$\mathcal{M}_3^{\mathrm{nh}}\subset \mathcal{M}_3$
of non-hyperelliptic curves. There is a stratification
![]() $\mathcal{M}_3^{\mathrm{nh}} = \bigsqcup X_G$
into locally closed subvarieties such that a non-hyperelliptic curve C over C belongs to
$\mathcal{M}_3^{\mathrm{nh}} = \bigsqcup X_G$
into locally closed subvarieties such that a non-hyperelliptic curve C over C belongs to
![]() $X_G$
if and only if
$X_G$
if and only if
![]() $\mathrm{Aut}(C) \simeq G$
. It turns out that
$\mathrm{Aut}(C) \simeq G$
. It turns out that
![]() $X_G$
is irreducible and the closure of
$X_G$
is irreducible and the closure of
![]() $X_G$
is a union of other strata. We refer to [Reference Lombardo, Lorenzo Garca, Ritzenthaler and SijslingLLGRS23, § 2.2] and references therein for a complete description of the loci
$X_G$
is a union of other strata. We refer to [Reference Lombardo, Lorenzo Garca, Ritzenthaler and SijslingLLGRS23, § 2.2] and references therein for a complete description of the loci
![]() $X_G$
and the closure relations between them. We reproduce here a diagram capturing these closure relations.
$X_G$
and the closure relations between them. We reproduce here a diagram capturing these closure relations.

For
![]() $n\in \{16,48, 96\}$
, the symbol
$n\in \{16,48, 96\}$
, the symbol
![]() $G_n$
denotes the group of order n and GAP label (16,13), (48, 33), and (96,64), respectively [GAP24]. See [Reference Lombardo, Lorenzo Garca, Ritzenthaler and SijslingLLGRS23, Table 2] for models for a generic plane quartic in
$G_n$
denotes the group of order n and GAP label (16,13), (48, 33), and (96,64), respectively [GAP24]. See [Reference Lombardo, Lorenzo Garca, Ritzenthaler and SijslingLLGRS23, Table 2] for models for a generic plane quartic in
![]() $X_G$
. We make explicit the strata that are relevant for us:
$X_G$
. We make explicit the strata that are relevant for us:
![]() $\overline{X_{C_3}}$
is the locus of Picard curves studied in § 4;
$\overline{X_{C_3}}$
is the locus of Picard curves studied in § 4;
![]() $\overline{X_{C_6}}$
is the locus of bielliptic Picard curves studied in [Reference Laga and ShnidmanLS23a]; and the zero-dimensional strata each consist of a single automorphism-maximal curve with equation
$\overline{X_{C_6}}$
is the locus of bielliptic Picard curves studied in [Reference Laga and ShnidmanLS23a]; and the zero-dimensional strata each consist of a single automorphism-maximal curve with equation
 \begin{align*}\begin{cases} y^3z = x^4+xz^3 & \text{ if }G = C_9, \\ y^3z = x^4+z^4 & \text{ if }G = G_{48,}\\ x^4+y^4+z^4=0 & \text{ if }G = G_{96},\\ x^3y+y^3z+z^3x=0 & \text{ if }G = \mathrm{GL}_3(\mathrm{\mathbb{F}}_2).\end{cases}\end{align*}
\begin{align*}\begin{cases} y^3z = x^4+xz^3 & \text{ if }G = C_9, \\ y^3z = x^4+z^4 & \text{ if }G = G_{48,}\\ x^4+y^4+z^4=0 & \text{ if }G = G_{96},\\ x^3y+y^3z+z^3x=0 & \text{ if }G = \mathrm{GL}_3(\mathrm{\mathbb{F}}_2).\end{cases}\end{align*}
If C is a non-hyperelliptic genus-3 curve over a field k, we say that C is a generic curve for
![]() $X_G$
if the classifying map
$X_G$
if the classifying map
![]() $\mathrm{Spec}(k) \rightarrow \mathcal{M}_3$
maps to the generic point of
$\mathrm{Spec}(k) \rightarrow \mathcal{M}_3$
maps to the generic point of
![]() $X_G$
. If X is an integral variety over C, we say that a property holds for a very general
$X_G$
. If X is an integral variety over C, we say that a property holds for a very general
![]() $x\in X(\mathrm{\mathbb{C}})$
if it holds true outside a countable union of proper closed subvarieties of X.
$x\in X(\mathrm{\mathbb{C}})$
if it holds true outside a countable union of proper closed subvarieties of X.
Lemma 5.2. For a group G in the above diagram, the following assertions are equivalent:
-
(i)
 $\kappa(C)\neq 0$
for some generic curve C for
$\kappa(C)\neq 0$
for some generic curve C for
 $X_G$
;
$X_G$
; -
(ii)
 $\kappa(C)\neq 0$
for a very general C in
$\kappa(C)\neq 0$
for a very general C in
 $X_G(\mathrm{\mathbb{C}})$
;
$X_G(\mathrm{\mathbb{C}})$
; -
(iii)
 $\kappa(C)\neq 0$
for some C in
$\kappa(C)\neq 0$
for some C in
 $X_G$
;
$X_G$
; -
(iv)
 $X_G\not \subset V_3^{\mathrm{rat}}$
;
$X_G\not \subset V_3^{\mathrm{rat}}$
; -
(v)
 $\overline{X_G}\not\subset V_3^{\mathrm{rat}}$
.
$\overline{X_G}\not\subset V_3^{\mathrm{rat}}$
.
Moreover, the analogous equivalences hold for
![]() $\bar{\kappa}(C)\in \mathrm{Gr}_1(J)_\mathrm{\mathbb{Q}}$
and
$\bar{\kappa}(C)\in \mathrm{Gr}_1(J)_\mathrm{\mathbb{Q}}$
and
![]() $V_3^{\mathrm{alg}}$
.
$V_3^{\mathrm{alg}}$
.
Proof. The lemma follows immediately from Lemma 5.1.
We end with the proof of Theorem E, which we restate for convenience.
Proposition 5.3. Let G be a group in the diagram. Then:
-
(i)
 $X_G\subset V_3^{\mathrm{alg}}$
if and only if
$X_G\subset V_3^{\mathrm{alg}}$
if and only if
 $G=C_3,C_6,C_9, G_{48}$
;
$G=C_3,C_6,C_9, G_{48}$
; -
(ii)
 $X_G \subset V_3^{\mathrm{rat}}$
if and only if
$X_G \subset V_3^{\mathrm{rat}}$
if and only if
 $G = C_9, G_{48}$
.
$G = C_9, G_{48}$
.
Proof. (i) The equivalence between (iv) and (v) of Lemma 5.2 implies that if
![]() $X_H\subset \overline{X_G}$
and
$X_H\subset \overline{X_G}$
and
![]() $X_G\subset V_3^{\mathrm{rat}}$
, then
$X_G\subset V_3^{\mathrm{rat}}$
, then
![]() $X_H\subset V_3^{\mathrm{rat}}$
; we will use this observation in the remainder of the proof.
$X_H\subset V_3^{\mathrm{rat}}$
; we will use this observation in the remainder of the proof.
Our analysis of Picard curves (Theorem C) shows that
![]() $X_{C_3}\subset V_3^{\mathrm{rat}}$
, so
$X_{C_3}\subset V_3^{\mathrm{rat}}$
, so
![]() $X_G\subset V_3^{\mathrm{rat}}$
for
$X_G\subset V_3^{\mathrm{rat}}$
for
![]() $G= C_6, C_9$
and
$G= C_6, C_9$
and
![]() $G_{48}$
as well. On the other hand, the Ceresa cycle of the Fermat quartic and Klein quartic are known to be of infinite order in the Griffiths group; see [Reference BlochBlo84, Theorem (4.1)] for the former and [Reference KimuraKim00, § 4] for the latter. By our observation, this means that
$G_{48}$
as well. On the other hand, the Ceresa cycle of the Fermat quartic and Klein quartic are known to be of infinite order in the Griffiths group; see [Reference BlochBlo84, Theorem (4.1)] for the former and [Reference KimuraKim00, § 4] for the latter. By our observation, this means that
![]() $X_G\not\subset V_3^{\mathrm{rat}}$
for every stratum whose closure contains one of these curves. Since every stratum not contained in
$X_G\not\subset V_3^{\mathrm{rat}}$
for every stratum whose closure contains one of these curves. Since every stratum not contained in
![]() $\overline{X_{C_3}}$
has this property, we conclude the proof.
$\overline{X_{C_3}}$
has this property, we conclude the proof.
(ii) Since
![]() $V_3^{\mathrm{rat}}\subset V_3^{\mathrm{alg}}$
, part (i) implies that
$V_3^{\mathrm{rat}}\subset V_3^{\mathrm{alg}}$
, part (i) implies that
![]() $X_G\subset V_3^{\mathrm{rat}}$
only if
$X_G\subset V_3^{\mathrm{rat}}$
only if
![]() $G = C_3,C_6,C_9$
or
$G = C_3,C_6,C_9$
or
![]() $G_{48}$
. The criterion of Theorem A applies to the curves in
$G_{48}$
. The criterion of Theorem A applies to the curves in
![]() $X_{C_9}$
and
$X_{C_9}$
and
![]() $X_{G_{48}}$
(see Example 3.1), so
$X_{G_{48}}$
(see Example 3.1), so
![]() $V_3^{\mathrm{rat}}$
contains these strata. On the other hand, there exist curves in
$V_3^{\mathrm{rat}}$
contains these strata. On the other hand, there exist curves in
![]() $X_{C_6}$
with non-vanishing
$X_{C_6}$
with non-vanishing
![]() $\kappa(C)$
, by [Reference Laga and ShnidmanLS25, Corollary 1.2]. So
$\kappa(C)$
, by [Reference Laga and ShnidmanLS25, Corollary 1.2]. So
![]() $X_{C_6}\not\subset V_3^{\mathrm{rat}}$
and
$X_{C_6}\not\subset V_3^{\mathrm{rat}}$
and
![]() $X_{C_3}\not\subset V_3^{\mathrm{rat}}$
.
$X_{C_3}\not\subset V_3^{\mathrm{rat}}$
.
Acknowledgements
We thank Jeffrey Achter, Irene Bouw, Edgar Costa, Ben Moonen, Burt Totaro and Congling Qiu for helpful conversations. We also thank the referee for their careful reading of the paper and suggesting the clean proof of Lemma 4.6.
Conflicts of interest
None.
Financial support
This research was carried out while the first author was a research fellow at St John’s College, University of Cambridge. The second author was funded by the European Research Council (ERC, CurveArithmetic, grant no. 101078157).
Journal information
Compositio Mathematica is owned by the Foundation Compositio Mathematica and published by the London Mathematical Society in partnership with Cambridge University Press. All surplus income from the publication of Compositio Mathematica is returned to mathematics and higher education through the charitable activities of the Foundation, the London Mathematical Society and Cambridge University Press.