1. Introduction and main results
The classes of Muckenhoupt Ap weights play a central role in harmonic and geometric analysis, and in potential theory both in ![]() ${\mathbb R}^n$ and in metric measure spaces. Among other relevant properties, they characterize the weights w for which the Hardy-Littlewood maximal function defines a bounded operator between the appropriate weighted Lp-spaces. Also, provided the underlying measure supports a
${\mathbb R}^n$ and in metric measure spaces. Among other relevant properties, they characterize the weights w for which the Hardy-Littlewood maximal function defines a bounded operator between the appropriate weighted Lp-spaces. Also, provided the underlying measure supports a ![]() $(1,1)$-Poincaré inequality and the weight w belongs to the Ap class, then the corresponding w-weighted
$(1,1)$-Poincaré inequality and the weight w belongs to the Ap class, then the corresponding w-weighted ![]() $(1,p)$-Poincaré inequality holds true; see e.g. [Reference Björn4]. Moreover, they are crucial in understanding the structure of the functions of bounded mean oscillation and the classes of quasiconformal mappings. For background about the theory of Ap weights and related issues in harmonic analysis and potential theory in Euclidean and in metric measure spaces, we refer to the monographs by A. Björn and J. Björn [Reference Björn and Björn2], Heinonen, Kilpeläinen, and Martio [Reference Heinonen, Kilpeläinen and Martio11], Kinnunen, Lehrbäck, and Vähäkangas [Reference Kinnunen, Lehrbäck and Vähäkangas14], and Strömberg and Torchinsky [Reference Strömberg and Torchinsky19].
$(1,p)$-Poincaré inequality holds true; see e.g. [Reference Björn4]. Moreover, they are crucial in understanding the structure of the functions of bounded mean oscillation and the classes of quasiconformal mappings. For background about the theory of Ap weights and related issues in harmonic analysis and potential theory in Euclidean and in metric measure spaces, we refer to the monographs by A. Björn and J. Björn [Reference Björn and Björn2], Heinonen, Kilpeläinen, and Martio [Reference Heinonen, Kilpeläinen and Martio11], Kinnunen, Lehrbäck, and Vähäkangas [Reference Kinnunen, Lehrbäck and Vähäkangas14], and Strömberg and Torchinsky [Reference Strömberg and Torchinsky19].
Our framework will be a complete metric space (X, d) equipped with a doubling Borel regular measure ![]() $\mu.$ We are interested in the Ap-properties of the weights of the form
$\mu.$ We are interested in the Ap-properties of the weights of the form ![]() $w_{\alpha,E}(x) = \operatorname{dist}(x,E)^{-\alpha},$
$w_{\alpha,E}(x) = \operatorname{dist}(x,E)^{-\alpha},$ ![]() $x\in X,$ for subsets E of
$x\in X,$ for subsets E of ![]() $X.$ The fundamental starting point for the results in this paper is our recent work [Reference Anderson, Lehrbäck, Mudarra and Vähäkangas1]. There, we considered the class of weakly porous sets in
$X.$ The fundamental starting point for the results in this paper is our recent work [Reference Anderson, Lehrbäck, Mudarra and Vähäkangas1]. There, we considered the class of weakly porous sets in ![]() ${\mathbb R}^n$ equipped with the Lebesgue measure, and proved that this is precisely the class of sets E for which
${\mathbb R}^n$ equipped with the Lebesgue measure, and proved that this is precisely the class of sets E for which ![]() $w_{\alpha,E}\in A_1({\mathbb R}^n)$ for some α > 0. Moreover, we introduced the concept of Muckenhoupt exponent for a set E, which permitted us to quantify the range of those α for which
$w_{\alpha,E}\in A_1({\mathbb R}^n)$ for some α > 0. Moreover, we introduced the concept of Muckenhoupt exponent for a set E, which permitted us to quantify the range of those α for which ![]() $w_{\alpha,E}\in A_1({\mathbb R}^n).$ Furthermore, in [Reference Anderson, Lehrbäck, Mudarra and Vähäkangas1] we constructed examples of sets E for which
$w_{\alpha,E}\in A_1({\mathbb R}^n).$ Furthermore, in [Reference Anderson, Lehrbäck, Mudarra and Vähäkangas1] we constructed examples of sets E for which ![]() $\operatorname{dist}(\cdot,E)^{-\alpha} \in A_p \setminus A_1$ for every α > 0 and p > 1.
$\operatorname{dist}(\cdot,E)^{-\alpha} \in A_p \setminus A_1$ for every α > 0 and p > 1.
Previously, Vasin [Reference Vasin20] obtained the corresponding A 1-characterization for subsets E contained in the one-dimensional torus ![]() $\mathbb{T}$. Also, in [Reference Dyda, Ihnatsyeva, Lehrbäck, Tuominen and Vähäkangas6], Dyda, Ihnatsyeva, Lehrbäck, Tuominen, and Vähäkangas studied the Ap-properties of distance functions to porous sets, and applied their results to obtain certain weighted Hardy-Sobolev inequalities. See also Semmes’ work [Reference Semmes18] (in Section 4) for results on the strong
$\mathbb{T}$. Also, in [Reference Dyda, Ihnatsyeva, Lehrbäck, Tuominen and Vähäkangas6], Dyda, Ihnatsyeva, Lehrbäck, Tuominen, and Vähäkangas studied the Ap-properties of distance functions to porous sets, and applied their results to obtain certain weighted Hardy-Sobolev inequalities. See also Semmes’ work [Reference Semmes18] (in Section 4) for results on the strong ![]() $A_\infty$ condition of some weights given by distance functions to uniformly disconnected sets. A detailed study of the Minkowski and Hausdorff dimensions of porous and locally porous sets can be found in the paper of Salli [Reference Salli17]. For results concerning the Assouad dimension and spectrum of porous and/or fractals sets, and their distorsion under quasiconformal maps, we refer, for instance, to the papers of Chrontsios-Garitsis and Tyson [Reference Garitsis and Tyson10], Luukkainen [Reference Luukkainen16], and Fraser and Yu [Reference Fraser and Yu9], and the references therein. Finally, see the monograph [Reference Falconer7] by Falconer, for a thorough exposition of fractal geometry and their applications.
$A_\infty$ condition of some weights given by distance functions to uniformly disconnected sets. A detailed study of the Minkowski and Hausdorff dimensions of porous and locally porous sets can be found in the paper of Salli [Reference Salli17]. For results concerning the Assouad dimension and spectrum of porous and/or fractals sets, and their distorsion under quasiconformal maps, we refer, for instance, to the papers of Chrontsios-Garitsis and Tyson [Reference Garitsis and Tyson10], Luukkainen [Reference Luukkainen16], and Fraser and Yu [Reference Fraser and Yu9], and the references therein. Finally, see the monograph [Reference Falconer7] by Falconer, for a thorough exposition of fractal geometry and their applications.
The Muckenhoupt ![]() $A_1(X)$ class of weights is the smallest among all the classes
$A_1(X)$ class of weights is the smallest among all the classes ![]() $A_p(X)$, with
$A_p(X)$, with ![]() $p \geq 1.$ We recall that a weight w (a nonnegative locally integrable function in X) belongs to
$p \geq 1.$ We recall that a weight w (a nonnegative locally integrable function in X) belongs to ![]() $A_1(X)$ if there exists some constant C > 0 for which
$A_1(X)$ if there exists some constant C > 0 for which
 \begin{equation*}
{\int{\kern-10.5pt}-}_{\hskip-3.7pt B}\hskip1.5pt w(x) \, d \mu(x) \leq C\ \mathop{\mathrm{ess\, inf}}\limits_{x\in B} w(x), \quad \text{for every ball} \quad B \subset X.
\end{equation*}
\begin{equation*}
{\int{\kern-10.5pt}-}_{\hskip-3.7pt B}\hskip1.5pt w(x) \, d \mu(x) \leq C\ \mathop{\mathrm{ess\, inf}}\limits_{x\in B} w(x), \quad \text{for every ball} \quad B \subset X.
\end{equation*} This A 1-condition characterizes the weights w for which the maximal function M defines a bounded operator between the weighted spaces ![]() $M: L^1(X, w \, d \mu) \to L^{1,\infty}(X, w \, d \mu).$
$M: L^1(X, w \, d \mu) \to L^{1,\infty}(X, w \, d \mu).$
The main goal of this paper is to obtain characterizations of the property ![]() $w_{\alpha,E}\in A_1(X)$ for some α > 0 similar to those in [Reference Anderson, Lehrbäck, Mudarra and Vähäkangas1], when the underlying space is a metric space
$w_{\alpha,E}\in A_1(X)$ for some α > 0 similar to those in [Reference Anderson, Lehrbäck, Mudarra and Vähäkangas1], when the underlying space is a metric space ![]() $(X,d,\mu)$ with a doubling measure. In order to solve this problem, we consider the following size of the maximal E-free holes, namely, if
$(X,d,\mu)$ with a doubling measure. In order to solve this problem, we consider the following size of the maximal E-free holes, namely, if ![]() $B=B(x,R)$, we set
$B=B(x,R)$, we set
Then we define the weakly porous sets of X as those ![]() $E \subset X$ for which there are two constants
$E \subset X$ for which there are two constants ![]() $c, \delta \in (0,1)$ such that every open ball
$c, \delta \in (0,1)$ such that every open ball ![]() $B=B(x,R) \subset X$ contains finitely many non-overlapping open balls
$B=B(x,R) \subset X$ contains finitely many non-overlapping open balls ![]() $\lbrace B_i=B(x_i,r_i) \rbrace_{i=1}^N $ containing no point of E with
$\lbrace B_i=B(x_i,r_i) \rbrace_{i=1}^N $ containing no point of E with
 \begin{equation*}
\delta h_E(B) \leq r_i \leq 2R, \quad i=1,\ldots,N, \quad \text{and} \quad \sum_{i=1}^N \mu(B_i) \geq c \mu(B).
\end{equation*}
\begin{equation*}
\delta h_E(B) \leq r_i \leq 2R, \quad i=1,\ldots,N, \quad \text{and} \quad \sum_{i=1}^N \mu(B_i) \geq c \mu(B).
\end{equation*} Unlike in the case where ![]() $X={\mathbb R}^n,$ the weak porosity does not provide a characterization by itself, and certain doubling-type behavior for the quantity hE is needed, that is,
$X={\mathbb R}^n,$ the weak porosity does not provide a characterization by itself, and certain doubling-type behavior for the quantity hE is needed, that is, ![]() $h_E(2B) \lesssim h_E(B)$ for all balls
$h_E(2B) \lesssim h_E(B)$ for all balls ![]() $B.$ Along with this doubling property, the condition of weak porosity provides a complete characterization, and our first main result is the following.
$B.$ Along with this doubling property, the condition of weak porosity provides a complete characterization, and our first main result is the following.
Theorem 1.1. Let ![]() $E\subset X$ be a subset. Then, the following statements are equivalent:
$E\subset X$ be a subset. Then, the following statements are equivalent:
(A)
 $E$ is weakly porous and
$E$ is weakly porous and  $h_E$ satisfies the doubling condition.
$h_E$ satisfies the doubling condition.(B) There exists α > 0 for which
 $\operatorname{dist}(\cdot, E)^{-\alpha} \in A_1(X)$.
$\operatorname{dist}(\cdot, E)^{-\alpha} \in A_1(X)$.
The proof of this theorem is given in Section 6. Notice that, for positive powers ![]() $\beta \gt 0,$ the weight
$\beta \gt 0,$ the weight ![]() $v=\operatorname{dist}(\cdot, E)^{\beta} $ belongs to
$v=\operatorname{dist}(\cdot, E)^{\beta} $ belongs to ![]() $A_1(X)$ only when E is dense in X, i.e., when v is identically zero. The definitions of a weakly porous set and the doubling condition for hE are restated in Definitions 3.1 and 3.4 below.
$A_1(X)$ only when E is dense in X, i.e., when v is identically zero. The definitions of a weakly porous set and the doubling condition for hE are restated in Definitions 3.1 and 3.4 below.
When ![]() $X={\mathbb R}^n$ is equipped with the Lebesgue measure, we proved in [Reference Anderson, Lehrbäck, Mudarra and Vähäkangas1] that hE always satisfies the doubling condition for weakly porous sets E, and thus the second assumption in Theorem 1.1(A) is unnecessary in this setting. However, there are connected metric spaces with doubling measure containing subsets E that are weakly porous and yet hE is not doubling. This will be shown in this paper via Example 8.1 in Section 8, where we further prove that for such weakly porous set
$X={\mathbb R}^n$ is equipped with the Lebesgue measure, we proved in [Reference Anderson, Lehrbäck, Mudarra and Vähäkangas1] that hE always satisfies the doubling condition for weakly porous sets E, and thus the second assumption in Theorem 1.1(A) is unnecessary in this setting. However, there are connected metric spaces with doubling measure containing subsets E that are weakly porous and yet hE is not doubling. This will be shown in this paper via Example 8.1 in Section 8, where we further prove that for such weakly porous set ![]() $E,$ the functions
$E,$ the functions ![]() $\operatorname{dist}(\cdot,E)^{-\alpha}$,
$\operatorname{dist}(\cdot,E)^{-\alpha}$, ![]() $\alpha \gt 0,$ do not even define doubling weights.
$\alpha \gt 0,$ do not even define doubling weights.
In addition, we give an example of a set ![]() $E \subset {\mathbb R}$ for which all the functions of the form
$E \subset {\mathbb R}$ for which all the functions of the form ![]() $\operatorname{dist}(\cdot,E)^{-\alpha},$ with
$\operatorname{dist}(\cdot,E)^{-\alpha},$ with ![]() $\alpha \lt 1,$ define weights in
$\alpha \lt 1,$ define weights in ![]() ${\mathbb R},$ the maximal E-free hole hE is doubling, and still E is not weakly porous. Thus we show that the properties of weak porosity and doubling maximal holes are independent of each other in the general setting. Remarkably, this set E is so that, for all
${\mathbb R},$ the maximal E-free hole hE is doubling, and still E is not weakly porous. Thus we show that the properties of weak porosity and doubling maximal holes are independent of each other in the general setting. Remarkably, this set E is so that, for all ![]() $\alpha \lt 1,$
$\alpha \lt 1,$ ![]() $\alpha \neq 0,$
$\alpha \neq 0,$ ![]() $\operatorname{dist}(\cdot,E)^{-\alpha}$ defines a doubling weight that does not belong to any
$\operatorname{dist}(\cdot,E)^{-\alpha}$ defines a doubling weight that does not belong to any ![]() $A_p({\mathbb R})$ class, thus providing a new family of doubling weight functions that are not in
$A_p({\mathbb R})$ class, thus providing a new family of doubling weight functions that are not in ![]() $A_\infty({\mathbb R})$. The first example of such weights was by Fefferman and Muckenhoupt [Reference Fefferman and Muckenhoupt8].
$A_\infty({\mathbb R})$. The first example of such weights was by Fefferman and Muckenhoupt [Reference Fefferman and Muckenhoupt8].
Theorem 1.2. Endow ![]() ${\mathbb R}$ with the usual distance and the Lebesgue measure. Then there exists
${\mathbb R}$ with the usual distance and the Lebesgue measure. Then there exists ![]() $E \subset {\mathbb R}$ with doubling maximal holes
$E \subset {\mathbb R}$ with doubling maximal holes ![]() $h_E$, and so that, for all
$h_E$, and so that, for all ![]() $ \alpha \lt 1,$
$ \alpha \lt 1,$ ![]() $\alpha \neq 0,$ the function
$\alpha \neq 0,$ the function ![]() $w_\alpha:=\operatorname{dist}(\cdot, E)^{-\alpha} $ is a doubling weight in
$w_\alpha:=\operatorname{dist}(\cdot, E)^{-\alpha} $ is a doubling weight in ![]() ${\mathbb R}$ that does not belong to
${\mathbb R}$ that does not belong to ![]() $A_\infty({\mathbb R})$.
$A_\infty({\mathbb R})$.
In particular, ![]() $E$ is not weakly porous.
$E$ is not weakly porous.
The proof of this theorem is given in Section 8.2. This theorem has an obvious generalization to ![]() ${\mathbb R}^n,$ by replacing
${\mathbb R}^n,$ by replacing ![]() $E \subset {\mathbb R}$ with
$E \subset {\mathbb R}$ with ![]() $ E \times {\mathbb R}^{n-1} \subset {\mathbb R}^n$; see Remark 8.5.
$ E \times {\mathbb R}^{n-1} \subset {\mathbb R}^n$; see Remark 8.5.
We will reformulate Theorem 1.2 with more details in Example 8.3, but here we offer a brief description of the set ![]() $E.$ We begin with the two-point set
$E.$ We begin with the two-point set ![]() $E_0= \lbrace 0, 1 \rbrace,$ and define E 1 by chaining, from left to right, the set
$E_0= \lbrace 0, 1 \rbrace,$ and define E 1 by chaining, from left to right, the set ![]() $E_{0},$ a
$E_{0},$ a ![]() $1/2$-contraction of a copy of E 0, and finally another copy of
$1/2$-contraction of a copy of E 0, and finally another copy of ![]() $E_{0}.$ With the same procedure we define recursively
$E_{0}.$ With the same procedure we define recursively ![]() $E_2,E_3,\ldots,$ and let
$E_2,E_3,\ldots,$ and let ![]() $E^+$ be the union of all the En’s. It is precisely this palindromic distribution of the various copies of E 0 which allows to show the doubling properties of the theorem. The desired set E is merely the symmetrization of
$E^+$ be the union of all the En’s. It is precisely this palindromic distribution of the various copies of E 0 which allows to show the doubling properties of the theorem. The desired set E is merely the symmetrization of ![]() $E^+$ about the origin.
$E^+$ about the origin.
It is also worth noticing the beautiful example by Wik [Reference Wik21, p. 253] of a doubling weight w in ![]() ${\mathbb R}$ with
${\mathbb R}$ with ![]() $w \notin A_\infty({\mathbb R}).$ Wik’s example can be seen as a distance function to a set F constructed by chaining bounded sets
$w \notin A_\infty({\mathbb R}).$ Wik’s example can be seen as a distance function to a set F constructed by chaining bounded sets ![]() $\lbrace F_n \rbrace_n$, where each Fn contains in turn infinitely many copies of (arbitrarily) small
$\lbrace F_n \rbrace_n$, where each Fn contains in turn infinitely many copies of (arbitrarily) small ![]() $2^{-k}$-contractions of the previous
$2^{-k}$-contractions of the previous ![]() $F_{n-1}.$ The initial set F 0 is also a two-point set. As in our construction, these sets are conveniently chained in a symmetric way. The set E in Theorem 1.2 is, perhaps, simpler, as each of the main blocks En of our construction is a finite set whose smallest gap has size
$F_{n-1}.$ The initial set F 0 is also a two-point set. As in our construction, these sets are conveniently chained in a symmetric way. The set E in Theorem 1.2 is, perhaps, simpler, as each of the main blocks En of our construction is a finite set whose smallest gap has size ![]() $2^{-n}.$ Also, the advantage of our Theorem 1.2 is that, besides showing that hE is doubling, it tells us that all the powers
$2^{-n}.$ Also, the advantage of our Theorem 1.2 is that, besides showing that hE is doubling, it tells us that all the powers ![]() $ \lbrace \operatorname{dist}(\cdot, E)^{-\alpha} \rbrace_{\alpha \in (-\infty,1) \setminus \lbrace 0 \rbrace },$ are doubling weights outside the
$ \lbrace \operatorname{dist}(\cdot, E)^{-\alpha} \rbrace_{\alpha \in (-\infty,1) \setminus \lbrace 0 \rbrace },$ are doubling weights outside the ![]() $A_\infty({\mathbb R})$ class.
$A_\infty({\mathbb R})$ class.
Going back to the general setting, if our metric measure space ![]() $(X,d,\mu)$ additionally satisfies a weak version of the standard annular decay property (29), the situation changes and the doubling condition for hE is a consequence of the weak porosity of E. The resulting A 1-characterization is therefore as clean as in
$(X,d,\mu)$ additionally satisfies a weak version of the standard annular decay property (29), the situation changes and the doubling condition for hE is a consequence of the weak porosity of E. The resulting A 1-characterization is therefore as clean as in ![]() ${\mathbb R}^n.$
${\mathbb R}^n.$
Theorem 1.3. Assume that ![]() $(X,d,\mu)$ satisfies the annular decay property (29), and let
$(X,d,\mu)$ satisfies the annular decay property (29), and let ![]() $E \subset X$ be a subset. Then, the following statements are equivalent:
$E \subset X$ be a subset. Then, the following statements are equivalent:
(A’)
 $E$ is weakly porous.
$E$ is weakly porous.(B’) There exists α > 0 for which
 $\operatorname{dist}(\cdot, E)^{-\alpha} \in A_1(X)$.
$\operatorname{dist}(\cdot, E)^{-\alpha} \in A_1(X)$.
For the proof of our results, we will formulate a condition of dyadic weak porosity for subsets of X; see Definition 3.3. This formulation is given in terms of a system of adjacent dyadic grids in doubling metric spaces, which provide partitions of the space at all scales, into sets that enjoy many of the good properties of the usual dyadic grids of cubes in ![]() ${\mathbb R}^n.$ They have proven to be instrumental in harmonic and geometric analysis in metric spaces; as shown, for instance, by the classical and recent works of Christ [Reference Christ5], Hytönen and Kairema [Reference Hytönen and Kairema12], and Käenmäki, Rajala and Suomala [Reference Käenmäki, Rajala and Suomala13]. We additionally prove some estimates for the measures of the ɛ-boundaries of dyadic sets. These estimates were obtained by Christ [Reference Christ5] for the corresponding Christ’s (open) cubes, as well as by Hytönen and Kairema [Reference Hytönen and Kairema12] for the half-open cubes in a probabilistic form.
${\mathbb R}^n.$ They have proven to be instrumental in harmonic and geometric analysis in metric spaces; as shown, for instance, by the classical and recent works of Christ [Reference Christ5], Hytönen and Kairema [Reference Hytönen and Kairema12], and Käenmäki, Rajala and Suomala [Reference Käenmäki, Rajala and Suomala13]. We additionally prove some estimates for the measures of the ɛ-boundaries of dyadic sets. These estimates were obtained by Christ [Reference Christ5] for the corresponding Christ’s (open) cubes, as well as by Hytönen and Kairema [Reference Hytönen and Kairema12] for the half-open cubes in a probabilistic form.
Using this dyadic formulation of weak porosity, the idea of proof of Theorem 1.1 is inspired by that in the Euclidean setting from [Reference Anderson, Lehrbäck, Mudarra and Vähäkangas1]. We decompose each dyadic set into carefully chosen E-free descendants that conveniently depend on the parameters of weak porosity of the set E. By means of a dyadic iteration and employing the assumption that the maximal E-free holes hE is doubling, we obtain a discrete and quantitative lower estimate for the sizes of the maximal holes in terms of the maximal holes of those dyadic descendants; see Lemma 5.3. Finally, we prove the A 1-estimates over every dyadic set of the systems, making use of the mentioned estimates for the measures of the ɛ-boundaries.
Dealing with systems of dyadic sets in our proofs will lead us to several technicalities. However, there are two main reasons for wanting to use them. 1) There is a suitable partial order between the dyadic sets that allows to derive many properties for the size of the largest (dyadic) E-free holes, as well as the key discrete lower estimate for the maximal holes of a dyadic set in terms of the ones of its descendants. 2) Even if we were able to obtain such a key estimate for some balls at various scales, it would not be possible to estimate integrals of the type  ${\int{\kern-9.5pt}-}_B \operatorname{dist}(\cdot, E)^{-\gamma}$ in terms of
${\int{\kern-9.5pt}-}_B \operatorname{dist}(\cdot, E)^{-\gamma}$ in terms of ![]() $\textrm{rad}(B)^{-\gamma}$, e.g., when B is close to
$\textrm{rad}(B)^{-\gamma}$, e.g., when B is close to ![]() $E.$ This is mainly due to the fact that there is no control on the measure of an ɛ-neighborhood of
$E.$ This is mainly due to the fact that there is no control on the measure of an ɛ-neighborhood of ![]() $\partial B$ within
$\partial B$ within ![]() $B,$ as the measure of a ball may be concentrated near the boundary in arbitrary metric spaces with doubling measure. However, the same integral averages replacing balls B with a dyadic set Q can be estimated from above by a power of the length of
$B,$ as the measure of a ball may be concentrated near the boundary in arbitrary metric spaces with doubling measure. However, the same integral averages replacing balls B with a dyadic set Q can be estimated from above by a power of the length of ![]() $Q,$ if one uses conveniently the quantitative (with power-type rate) estimates we will prove for the measure of the ɛ-boundaries of the dyadic sets of the systems; see Sections 6.2 and 6.3.
$Q,$ if one uses conveniently the quantitative (with power-type rate) estimates we will prove for the measure of the ɛ-boundaries of the dyadic sets of the systems; see Sections 6.2 and 6.3.
As concerns the proof of Theorem 1.3, we first show a lemma of rescaling (Lemma 7.1) that essentially allows us to utilize E-free admissible balls with very small radii in the definition of weak porosity. Together with the assumption (29), this enables us to obtain certain absolute continuity of the maximal E-free holes of balls with respect to their radii, and this leads us to the doubling property for ![]() $h_E;$ see Lemma 7.2. Then, Theorem 1.3 follows as a consequence of Theorem 1.1.
$h_E;$ see Lemma 7.2. Then, Theorem 1.3 follows as a consequence of Theorem 1.1.
The structure of the paper is as follows. In Section 2, we collect some basic properties of Muckenhoupt weights and also explain and prove the properties of the systems of dyadic sets we will be using. In Section 3, we define the concepts of weak porosity and dyadic weak porosity, along with the doubling conditions for the size of the largest free holes associated with a set, and prove the relevant relationships. In Section 4, we give the proof of the implication (A)![]() $\implies$(B) in Theorem 1.1. Sections 5 and 6 are devoted to the proof of the converse implication of Theorem 1.1, Lemma 5.3 being one of the key ingredients. Then, in Section 6, we prove the desired A 1-estimates for the weight
$\implies$(B) in Theorem 1.1. Sections 5 and 6 are devoted to the proof of the converse implication of Theorem 1.1, Lemma 5.3 being one of the key ingredients. Then, in Section 6, we prove the desired A 1-estimates for the weight ![]() $\operatorname{dist}(\cdot,E)^{-\alpha}$. In Section 7, we prove Theorem 1.3, and we also show how a variant of the dyadic weak porosity condition, called absolute dyadic weak porosity, provides another characterization of the sets E for which
$\operatorname{dist}(\cdot,E)^{-\alpha}$. In Section 7, we prove Theorem 1.3, and we also show how a variant of the dyadic weak porosity condition, called absolute dyadic weak porosity, provides another characterization of the sets E for which ![]() $\operatorname{dist}(\cdot,E)^{-\alpha} \in A_1(X)$ in the general setting; see Corollary 7.4. In Section 8, we give two examples that prove that the properties of weak porosity and doubling maximal free holes do not imply each other, and also construct new doubling weights that are not in
$\operatorname{dist}(\cdot,E)^{-\alpha} \in A_1(X)$ in the general setting; see Corollary 7.4. In Section 8, we give two examples that prove that the properties of weak porosity and doubling maximal free holes do not imply each other, and also construct new doubling weights that are not in ![]() $A_\infty({\mathbb R}),$ thus proving Theorem 1.2. Finally, in Section 9, we define the Muckenhoupt exponent associated with a set and we use it to determine the exponents α for which
$A_\infty({\mathbb R}),$ thus proving Theorem 1.2. Finally, in Section 9, we define the Muckenhoupt exponent associated with a set and we use it to determine the exponents α for which ![]() $\operatorname{dist}(\cdot, E)^{-\alpha} \in A_p$, for a given
$\operatorname{dist}(\cdot, E)^{-\alpha} \in A_p$, for a given ![]() $1\leq p \lt \infty.$
$1\leq p \lt \infty.$
2. Preliminary concepts and systems of dyadic sets
The underlying space we will be working on is a complete metric space ![]() $(X,d).$ For every
$(X,d).$ For every ![]() $x\in X$ and
$x\in X$ and ![]() $r \gt 0,$ the open ball centered at x and with radius r > 0 is denoted by
$r \gt 0,$ the open ball centered at x and with radius r > 0 is denoted by
We will denote the distance between any two subsets ![]() $E,F \subset X$ by
$E,F \subset X$ by ![]() $\operatorname{dist}(E,F):= \inf\lbrace d(x,y) \, : \, x\in E,\,y\in F \rbrace,$ and the distance from a point
$\operatorname{dist}(E,F):= \inf\lbrace d(x,y) \, : \, x\in E,\,y\in F \rbrace,$ and the distance from a point ![]() $p\in X$ to a subset E by
$p\in X$ to a subset E by ![]() $\operatorname{dist}(p,E):=\inf\lbrace d(p,x) \, : \, x\in E \rbrace.$
$\operatorname{dist}(p,E):=\inf\lbrace d(p,x) \, : \, x\in E \rbrace.$
In addition, we endow (X, d) with a complete Borel regular measure ![]() $\mu,$ satisfying the following standard doubling condition: the existence of a constant
$\mu,$ satisfying the following standard doubling condition: the existence of a constant ![]() $C_\mu \gt 0$ for which
$C_\mu \gt 0$ for which
Notice that then ![]() $0 \lt \mu(B) \lt \infty$ for every ball
$0 \lt \mu(B) \lt \infty$ for every ball ![]() $B.$ Condition (1) implies that X is separable, and also proper, meaning that every closed and bounded set is compact.
$B.$ Condition (1) implies that X is separable, and also proper, meaning that every closed and bounded set is compact.
Since our metric space (X, d) supports a doubling measure (1) µ, the space (X, d) is geometrically doubling, meaning that there exists ![]() $N\in {\mathbb N}$ so that for every
$N\in {\mathbb N}$ so that for every ![]() $x\in X$ and
$x\in X$ and ![]() $r \gt 0,$ the ball
$r \gt 0,$ the ball ![]() $B(x,r)$ can be covered by at most N balls
$B(x,r)$ can be covered by at most N balls ![]() $B(x_1, r/2), \ldots, B(x_N, r/2).$ The smallest of those
$B(x_1, r/2), \ldots, B(x_N, r/2).$ The smallest of those ![]() $N\in {\mathbb N}$ is called the geometric doubling constant, and is related to our constant
$N\in {\mathbb N}$ is called the geometric doubling constant, and is related to our constant ![]() $C_\mu.$
$C_\mu.$
We will also use the notation
 \begin{equation*}
{\int{\kern-10.5pt}-}_{\hskip-3.7pt F}\hskip1.5pt w \, d \mu = \frac 1 {\mu( F)} \int_F w(x) \, d\mu(x),
\end{equation*}
\begin{equation*}
{\int{\kern-10.5pt}-}_{\hskip-3.7pt F}\hskip1.5pt w \, d \mu = \frac 1 {\mu( F)} \int_F w(x) \, d\mu(x),
\end{equation*} for the mean value integral over a measurable set ![]() $F\subset X$ with
$F\subset X$ with ![]() $0 \lt \mu(F) \lt \infty$. Also, in some cases we will denote by w(F) the integral
$0 \lt \mu(F) \lt \infty$. Also, in some cases we will denote by w(F) the integral  $\int_F w \, d \mu,$ for any weight w and
$\int_F w \, d \mu,$ for any weight w and ![]() $F\subset X$ a measurable subset.
$F\subset X$ a measurable subset.
A weight w in X is any nonnegative and locally integrable function of ![]() $X.$ We next remind the reader the definition of an Ap weight, for
$X.$ We next remind the reader the definition of an Ap weight, for ![]() $1\leq p \lt \infty.$
$1\leq p \lt \infty.$
Definition 2.1. A weight ![]() $w$ in
$w$ in ![]() $X$ belongs to the Muckenhoupt class
$X$ belongs to the Muckenhoupt class ![]() $A_1$ if there exists a constant
$A_1$ if there exists a constant ![]() $C \geq 0$ such that
$C \geq 0$ such that
 \begin{equation}
{\int{\kern-10.5pt}-}_{\hskip-3.7pt B}\hskip-1.5pt w \, d\mu \le C\, \mathop{\mathrm{ess\, inf}}\limits_{x\in B} w(x),
\end{equation}
\begin{equation}
{\int{\kern-10.5pt}-}_{\hskip-3.7pt B}\hskip-1.5pt w \, d\mu \le C\, \mathop{\mathrm{ess\, inf}}\limits_{x\in B} w(x),
\end{equation} for every ball ![]() $B \subset X$. The smallest possible constant C in (2) is called the
$B \subset X$. The smallest possible constant C in (2) is called the ![]() $A_1$ constant of
$A_1$ constant of ![]() $w$, and it is denoted by
$w$, and it is denoted by ![]() $[w]_{A_1}$.
$[w]_{A_1}$.
Also, for ![]() $1 \lt p \lt \infty,$ a weight belongs to the Muckenhoupt class
$1 \lt p \lt \infty,$ a weight belongs to the Muckenhoupt class ![]() $A_p(X)$ if
$A_p(X)$ if
 \begin{equation}
[w]_{A_p}:=\sup_{B \subset X} \left( {\int{\kern-10.5pt}-}_{\hskip-3.5pt B}\hskip1.5pt w \, d\mu \right) \biggl({\int{\kern-10.5pt}-}_{\hskip-3.5pt B}\hskip1.5pt w^{\frac{1}{1-p}}\, d\mu\biggr)^{p-1} \lt \infty,
\end{equation}
\begin{equation}
[w]_{A_p}:=\sup_{B \subset X} \left( {\int{\kern-10.5pt}-}_{\hskip-3.5pt B}\hskip1.5pt w \, d\mu \right) \biggl({\int{\kern-10.5pt}-}_{\hskip-3.5pt B}\hskip1.5pt w^{\frac{1}{1-p}}\, d\mu\biggr)^{p-1} \lt \infty,
\end{equation} where the supremum is taken over all balls ![]() $B$ of
$B$ of ![]() $X.$
$X.$
The inclusions ![]() $A_p(X) \subset A_q(X)$ hold for any
$A_p(X) \subset A_q(X)$ hold for any ![]() $1\leq p \leq q \lt \infty.$
$1\leq p \leq q \lt \infty.$
A straightforward consequence of the Hölder inequality in combination with (1) is that a weight w belonging to any of these Ap-classes satisfies the following doubling property:
This fact will be used in Section 8. A less elementary property of Ap weights is their well-known self-improvement; see [Reference Kurki and Mudarra15, Lemma 2.12] in combination with [Reference Strömberg and Torchinsky19, Theorem I.15]. We state it together with an additional property involving powers of Muckenhoupt weights, the proof of which is identical to that of [Reference Anderson, Lehrbäck, Mudarra and Vähäkangas1, Lemma 2.3].
Proposition 2.2. The following two properties hold.
(1) If
 $w\in A_p(X)$ for
$w\in A_p(X)$ for  $1\leq p \lt \infty,$ there exists
$1\leq p \lt \infty,$ there exists  $s=s(p,[w]_{A_p},C_\mu) \gt 1$ so that
$s=s(p,[w]_{A_p},C_\mu) \gt 1$ so that  $w^s\in A_p(X).$
$w^s\in A_p(X).$(2) If
 $w\in A_1(X),$ and
$w\in A_1(X),$ and  $s\geq 0$ is so that
$s\geq 0$ is so that  $w^s \in \bigcup_{p \gt 1} A_p(X),$ then
$w^s \in \bigcup_{p \gt 1} A_p(X),$ then  $w^s\in A_1(X)$ as well.
$w^s\in A_1(X)$ as well.
A fundamental tool in the proof of our results is the systems of adjacent dyadic sets. These systems can be constructed in any geometrically doubling metric (or even quasi-metric) space. They provide partitions of the space X into mutually disjoint sets at every scale, and enjoy very similar properties to those of the dyadic cubes in ![]() ${\mathbb R}^n.$ The Christ’s construction [Reference Christ5] provided an almost everywhere-covering of
${\mathbb R}^n.$ The Christ’s construction [Reference Christ5] provided an almost everywhere-covering of ![]() $X,$ via open sets satisfying these properties. More recent developments of this technique provided a finite collection of systems of dyadic half-open sets, with the additional properties that their union cover all points of X, and every ball of radius r is contained in a dyadic set of one of these systems that has length approximately
$X,$ via open sets satisfying these properties. More recent developments of this technique provided a finite collection of systems of dyadic half-open sets, with the additional properties that their union cover all points of X, and every ball of radius r is contained in a dyadic set of one of these systems that has length approximately ![]() $r.$ Our main reference here will be the paper by Hytönen and Kairema [Reference Hytönen and Kairema12], where a probabilistic approach is used to obtain further properties for this construction that lead to sharp weighted norm inequalities for the maximal function operator. It is also worth mentioning the work by Käenmäki, Rajala, and Suomala [Reference Käenmäki, Rajala and Suomala13, Theorem 2.1], where similar constructions of dyadic sets were developed and applied to prove the existence of doubling measures in geometrically-doubling metric spaces.
$r.$ Our main reference here will be the paper by Hytönen and Kairema [Reference Hytönen and Kairema12], where a probabilistic approach is used to obtain further properties for this construction that lead to sharp weighted norm inequalities for the maximal function operator. It is also worth mentioning the work by Käenmäki, Rajala, and Suomala [Reference Käenmäki, Rajala and Suomala13, Theorem 2.1], where similar constructions of dyadic sets were developed and applied to prove the existence of doubling measures in geometrically-doubling metric spaces.
The following result is contained in [Reference Hytönen and Kairema12, Theorem 4.1–Remark 4.13] for the more general setting of (geometrically) doubling quasi-metric spaces.
Proposition 2.3. Fix ![]() $0 \lt \theta \lt 1/1000$. For every
$0 \lt \theta \lt 1/1000$. For every ![]() $k\in {\mathbb Z}$ and
$k\in {\mathbb Z}$ and ![]() $t=1,\ldots,T=T(\theta, C_\mu) \in {\mathbb N},$ there exist a countable set of points
$t=1,\ldots,T=T(\theta, C_\mu) \in {\mathbb N},$ there exist a countable set of points ![]() $\{z_\alpha^{k,t}\mathbin{:}\alpha\in\mathcal{A}_k\} \subset X,$ and a collection
$\{z_\alpha^{k,t}\mathbin{:}\alpha\in\mathcal{A}_k\} \subset X,$ and a collection ![]() $\mathcal{D}_t = \{Q_\alpha^{k,t}\mathbin{:} \alpha\in \mathcal{A}_k\}$ of Borel subsets of
$\mathcal{D}_t = \{Q_\alpha^{k,t}\mathbin{:} \alpha\in \mathcal{A}_k\}$ of Borel subsets of ![]() $X$ such that
$X$ such that
(1)
 $X = \biguplus_{\alpha\in \mathcal{A}_k}Q_\alpha^{k,t}$ for every
$X = \biguplus_{\alpha\in \mathcal{A}_k}Q_\alpha^{k,t}$ for every  $k\in {\mathbb Z}$ and every
$k\in {\mathbb Z}$ and every  $t=1\,\ldots,T$;
$t=1\,\ldots,T$;(2) If
 $Q_{\alpha}^{k,t}, Q_\beta^{l,t} \in \mathcal{D}_t$ and
$Q_{\alpha}^{k,t}, Q_\beta^{l,t} \in \mathcal{D}_t$ and  $l \geq k,$ then
$l \geq k,$ then
 \begin{equation*}
\textit{either} \: Q_\beta^{l,t} \subset Q_\alpha^{k,t} \: \text{or} \: Q_{\alpha}^{k,t} \cap Q_\beta^{l,t} =\emptyset,
\end{equation*}
\begin{equation*}
\textit{either} \: Q_\beta^{l,t} \subset Q_\alpha^{k,t} \: \text{or} \: Q_{\alpha}^{k,t} \cap Q_\beta^{l,t} =\emptyset,
\end{equation*}for every
 $t=1,\ldots,T$;
$t=1,\ldots,T$;(3) for every
 $Q_\alpha^{k,t}\in\mathcal{D}_t$ we have
$Q_\alpha^{k,t}\in\mathcal{D}_t$ we have
 \begin{equation*} B(z_\alpha^{k,t}, a \theta^k) \subset Q_\alpha^{k,t} \subset B(z_\alpha^{k,t},A\theta^k),\end{equation*}
\begin{equation*} B(z_\alpha^{k,t}, a \theta^k) \subset Q_\alpha^{k,t} \subset B(z_\alpha^{k,t},A\theta^k),\end{equation*}where
 $0 \lt a \lt A \lt \infty$ are absolute constants;
$0 \lt a \lt A \lt \infty$ are absolute constants;(4) for every ball
 $B=B(x,r)$ there exists a cube
$B=B(x,r)$ there exists a cube  $Q\in \mathcal{D}:=\bigcup_{t=1}^T \mathcal{D}_t $ such that
$Q\in \mathcal{D}:=\bigcup_{t=1}^T \mathcal{D}_t $ such that  $B\subset Q $ and
$B\subset Q $ and  $Q = Q_\alpha^{k, t}$ for some indices α and
$Q = Q_\alpha^{k, t}$ for some indices α and  $t$, and
$t$, and  $k$ being the unique integer such that
$k$ being the unique integer such that  $\theta^{k+2} \lt r\leq\theta^{k+1}$.
$\theta^{k+2} \lt r\leq\theta^{k+1}$.
To each of the collections ![]() $\mathcal{D}_t$ we will refer as a grid or dyadic grid of
$\mathcal{D}_t$ we will refer as a grid or dyadic grid of ![]() $\mathcal{D}.$ And each set
$\mathcal{D}.$ And each set ![]() $Q_\alpha^{k,t}$ of these collections will be called a dyadic cube or a dyadic set.
$Q_\alpha^{k,t}$ of these collections will be called a dyadic cube or a dyadic set.
If ![]() $Q \in \mathcal{D},$ then
$Q \in \mathcal{D},$ then ![]() $Q=Q_\alpha^{k,t}$ for some
$Q=Q_\alpha^{k,t}$ for some ![]() $k\in {\mathbb Z}$,
$k\in {\mathbb Z}$, ![]() $\alpha \in \mathcal{A}_k$,
$\alpha \in \mathcal{A}_k$, ![]() $t\in \lbrace 1,\ldots, T\rbrace.$ We will say that the generation of Q is
$t\in \lbrace 1,\ldots, T\rbrace.$ We will say that the generation of Q is ![]() $g(Q)=k,$ and that
$g(Q)=k,$ and that ![]() $z=z_\alpha^{k,t}$ is the reference point of
$z=z_\alpha^{k,t}$ is the reference point of ![]() $Q=Q_\alpha^{k,t}.$
$Q=Q_\alpha^{k,t}.$
It may occur that two cubes ![]() $Q, Q' \in \mathcal{D}$ belong to different grids
$Q, Q' \in \mathcal{D}$ belong to different grids ![]() $\mathcal{D}_t,$
$\mathcal{D}_t,$ ![]() $\mathcal{D}_{t'}$ and still
$\mathcal{D}_{t'}$ and still ![]() $Q=Q'$ as sets of points. In this case, Q and Qʹ are considered different cubes. Whenever we are given a cube
$Q=Q'$ as sets of points. In this case, Q and Qʹ are considered different cubes. Whenever we are given a cube ![]() $Q \in \mathcal{D},$ we understand that Q is in a fixed grid
$Q \in \mathcal{D},$ we understand that Q is in a fixed grid ![]() $\mathcal{D}_t,$ and so its reference point and its generation are taken with respect to the grid
$\mathcal{D}_t,$ and so its reference point and its generation are taken with respect to the grid ![]() $\mathcal{D}_t.$
$\mathcal{D}_t.$
If ![]() $Q_0 \in \mathcal{D},$ then
$Q_0 \in \mathcal{D},$ then ![]() $Q_0\in \mathcal{D}_t$ for some
$Q_0\in \mathcal{D}_t$ for some ![]() $t,$ and by
$t,$ and by ![]() $\mathcal{D}(Q_0)$ we denote the family of all the cubes Q in the same grid
$\mathcal{D}(Q_0)$ we denote the family of all the cubes Q in the same grid ![]() $\mathcal{D}_t$ that are contained in Q 0 and such that
$\mathcal{D}_t$ that are contained in Q 0 and such that ![]() $g(Q) \geq g(Q_0).$ Thus we can informally say that
$g(Q) \geq g(Q_0).$ Thus we can informally say that ![]() $\mathcal{D}(Q_0)$ is the collection of all the dyadic descendants of
$\mathcal{D}(Q_0)$ is the collection of all the dyadic descendants of ![]() $Q_0.$ Also, note that if
$Q_0.$ Also, note that if ![]() $Q \in \mathcal{D}(Q_0),$ then
$Q \in \mathcal{D}(Q_0),$ then ![]() $\mathcal{D}(Q) \subset \mathcal{D}(Q_0)$. We include the lower bound
$\mathcal{D}(Q) \subset \mathcal{D}(Q_0)$. We include the lower bound ![]() $g(Q) \geq g(Q_0)$ in the definition of
$g(Q) \geq g(Q_0)$ in the definition of ![]() $\mathcal{D}(Q_0)$, because in certain metric spaces X, (e.g., when X is bounded), a dyadic set Q 0 may very well coincide with all its ancestors, leading us to generations unbounded from below. By the properties of the dyadic systems we have
$\mathcal{D}(Q_0)$, because in certain metric spaces X, (e.g., when X is bounded), a dyadic set Q 0 may very well coincide with all its ancestors, leading us to generations unbounded from below. By the properties of the dyadic systems we have
 \begin{equation*}
Q_0=\bigcup \lbrace Q \in \mathcal{D}(Q_0) \, : \, g(Q)=g(Q_0)+l \rbrace \quad \text{for every} \quad l\in {\mathbb N},
\end{equation*}
\begin{equation*}
Q_0=\bigcup \lbrace Q \in \mathcal{D}(Q_0) \, : \, g(Q)=g(Q_0)+l \rbrace \quad \text{for every} \quad l\in {\mathbb N},
\end{equation*} and the union is disjoint, for each ![]() $Q_0\in \mathcal{D}.$
$Q_0\in \mathcal{D}.$
It is important to notice that, even when two cubes Q, Qʹ in a common grid ![]() $\mathcal{D}_t$ are equal as sets of points, their generations may differ. The generation function is monotonic only when the inclusions between the cubes are proper. This is clarified in the following remark. We also include an additional basic property that we will take into account in several arguments in the paper.
$\mathcal{D}_t$ are equal as sets of points, their generations may differ. The generation function is monotonic only when the inclusions between the cubes are proper. This is clarified in the following remark. We also include an additional basic property that we will take into account in several arguments in the paper.
Lemma 2.4. Let ![]() $P,P'\in \mathcal{D}_t$ be cubes in the same grid
$P,P'\in \mathcal{D}_t$ be cubes in the same grid ![]() $\mathcal{D}_t.$ The following holds
$\mathcal{D}_t.$ The following holds
(i) If
 $P \subsetneq P',$ then
$P \subsetneq P',$ then  $g(P') \lt g(P).$
$g(P') \lt g(P).$(ii) If
 $g(P)=g(P')$ and
$g(P)=g(P')$ and  $P\cap P' \neq \emptyset$, then they are exactly the same cube, meaning that, not only
$P\cap P' \neq \emptyset$, then they are exactly the same cube, meaning that, not only  $P=P'$ as sets, but also their labels
$P=P'$ as sets, but also their labels  $(\alpha, g(P))$ and
$(\alpha, g(P))$ and  $(\beta, g(P'))$ coincide.
$(\beta, g(P'))$ coincide.(iii) If
 $P \in \mathcal{D}(P')$ and
$P \in \mathcal{D}(P')$ and  $l=g(P)-g(P') \geq 1,$ then there exists a (unique) chain of cubes
$l=g(P)-g(P') \geq 1,$ then there exists a (unique) chain of cubes  $P=Q_0 \subset Q_1 \subset \cdots \subset Q_{l-1} \subset Q_l=P'$ so that
$P=Q_0 \subset Q_1 \subset \cdots \subset Q_{l-1} \subset Q_l=P'$ so that  $Q_{i-1} \in \mathcal{D}(Q_{i})$ and
$Q_{i-1} \in \mathcal{D}(Q_{i})$ and  $g(Q_i)=g(Q_{i-1})-1$ for each
$g(Q_i)=g(Q_{i-1})-1$ for each  $i=1,\ldots,l.$
$i=1,\ldots,l.$
Proof. (i) If ![]() $P=Q_\alpha^{k,t},$
$P=Q_\alpha^{k,t},$  $P'=Q_\beta^{l,t},$ and
$P'=Q_\beta^{l,t},$ and ![]() $l \geq k,$ then either
$l \geq k,$ then either  $Q_{\alpha}^{k,t} \cap Q_\beta^{l,t} =\emptyset$ or
$Q_{\alpha}^{k,t} \cap Q_\beta^{l,t} =\emptyset$ or  $Q_\beta^{l,t} \subset Q_\alpha^{k,t}$ by Proposition 2.3(2). Because
$Q_\beta^{l,t} \subset Q_\alpha^{k,t}$ by Proposition 2.3(2). Because ![]() $P \subsetneq P',$ this is a contradiction. Consequently,
$P \subsetneq P',$ this is a contradiction. Consequently, ![]() $l \lt k.$
$l \lt k.$
(ii) Let ![]() $P=Q_\alpha^{k,t},$
$P=Q_\alpha^{k,t},$  $P'=Q_\beta^{k,t}$. By Proposition 2.3,
$P'=Q_\beta^{k,t}$. By Proposition 2.3, ![]() $Q_\alpha^{k,t}$ and
$Q_\alpha^{k,t}$ and  $Q_\beta^{k,t}$ coincide as sets of points. Now, if
$Q_\beta^{k,t}$ coincide as sets of points. Now, if ![]() $\alpha \neq \beta,$ then
$\alpha \neq \beta,$ then  $Q_\beta^{k,t} \subset X \setminus B(z_\alpha^{k,t}, a \theta^k)$; see [Reference Hytönen and Kairema12, Lemma 3.6]. This contradicts the inclusion
$Q_\beta^{k,t} \subset X \setminus B(z_\alpha^{k,t}, a \theta^k)$; see [Reference Hytönen and Kairema12, Lemma 3.6]. This contradicts the inclusion ![]() $Q_\alpha^{k,t} \supset B(z_\alpha^{k,t}, a \theta^k).$
$Q_\alpha^{k,t} \supset B(z_\alpha^{k,t}, a \theta^k).$
(iii) By the comments subsequent to Proposition 2.3, Pʹ can be written as a disjoint union of cubes ![]() $Q \in \mathcal{D}(P')$ with
$Q \in \mathcal{D}(P')$ with ![]() $g(Q)=g(P)-1.$ And, by Proposition 2.3, the cube P must be contained in one (and only one) of these cubes, say
$g(Q)=g(P)-1.$ And, by Proposition 2.3, the cube P must be contained in one (and only one) of these cubes, say ![]() $Q_1.$ If
$Q_1.$ If ![]() $l=1,$ then
$l=1,$ then ![]() $g(Q_1)=g(P') $ and by (ii), Q 1 and Pʹ are the same cube, and thus we obtain the desired chain of cubes. If
$g(Q_1)=g(P') $ and by (ii), Q 1 and Pʹ are the same cube, and thus we obtain the desired chain of cubes. If ![]() $l \gt 1,$ we write Pʹ as the disjoint union of cubes
$l \gt 1,$ we write Pʹ as the disjoint union of cubes ![]() $Q \in \mathcal{D}(P')=$ with
$Q \in \mathcal{D}(P')=$ with ![]() $g(Q)=g(Q_1)-1,$ where one (and only one) of these cubes, say Q 2, must contain
$g(Q)=g(Q_1)-1,$ where one (and only one) of these cubes, say Q 2, must contain ![]() $Q_1.$ Repeating this procedure, we obtain the chain
$Q_1.$ Repeating this procedure, we obtain the chain ![]() $P=:Q_0 \subset Q_1 \subset \cdots \subset Q_{l-1} \subset Q_l:=P',$ with the desired properties.
$P=:Q_0 \subset Q_1 \subset \cdots \subset Q_{l-1} \subset Q_l:=P',$ with the desired properties.
The following result gives a quantitative (with power-type rate) estimate for the measure of the ɛ-boundary of our dyadic cubes, and it is crucial for our purposes. This property was proved by Christ [Reference Christ5, Theorem 11] for the corresponding open cubes. Also, Hytönen and Kairema [Reference Hytönen and Kairema12] stated and proved a probabilistic version for the cubes of Proposition 2.3. Because the cubes we are using in this paper are those from [Reference Hytönen and Kairema12], which are larger than the ones from [Reference Christ5], the desired estimates do not immediately follow from [Reference Christ5, Theorem 11], and so, for the sake of completeness, we provide the proof for all the cubes of the systems.
Proposition 2.5. For the cubes of the collection ![]() $\mathcal{D},$ the following property holds. There exist constants
$\mathcal{D},$ the following property holds. There exist constants ![]() $C, \eta \gt 0$ depending only on θ and Cµ so that
$C, \eta \gt 0$ depending only on θ and Cµ so that
 \begin{equation}
\mu \left( \lbrace x\in \overline{Q} \: : \: \operatorname{dist}(x, X \setminus Q) \leq \lambda \theta^{g(Q)} \rbrace \right) \leq C \lambda^{\eta} \mu(Q), \quad \text{for all} \quad \lambda \gt 0, \, Q\in \mathcal{D}.
\end{equation}
\begin{equation}
\mu \left( \lbrace x\in \overline{Q} \: : \: \operatorname{dist}(x, X \setminus Q) \leq \lambda \theta^{g(Q)} \rbrace \right) \leq C \lambda^{\eta} \mu(Q), \quad \text{for all} \quad \lambda \gt 0, \, Q\in \mathcal{D}.
\end{equation} In the proof of the above proposition, we follow the strategy from [Reference Christ5, Theorem 11], adapted to these collections of half-open cubes. Let us briefly describe how the cubes ![]() $\lbrace Q_\alpha^k \rbrace_{k,\alpha}$ of a fixed dyadic grid are constructed, as we will employ some of their specific properties. For fixed constants
$\lbrace Q_\alpha^k \rbrace_{k,\alpha}$ of a fixed dyadic grid are constructed, as we will employ some of their specific properties. For fixed constants ![]() $0 \lt c_0 \leq C_0 \lt \infty,$ and for every
$0 \lt c_0 \leq C_0 \lt \infty,$ and for every ![]() $k\in {\mathbb Z},$ let
$k\in {\mathbb Z},$ let ![]() $\lbrace z_\alpha^k \rbrace_{\alpha\in \mathcal{A}_k}$ be a set of points in X for which
$\lbrace z_\alpha^k \rbrace_{\alpha\in \mathcal{A}_k}$ be a set of points in X for which
 \begin{equation*}
d(z_\alpha^k,z_\beta^k)\geq c_0 \theta^k \quad \text{if} \quad \alpha \neq \beta, \quad \text{and} \quad \min_\alpha d(x,z_\alpha^k) \lt C_0 \theta^k \quad \text{for every} \quad x\in X.
\end{equation*}
\begin{equation*}
d(z_\alpha^k,z_\beta^k)\geq c_0 \theta^k \quad \text{if} \quad \alpha \neq \beta, \quad \text{and} \quad \min_\alpha d(x,z_\alpha^k) \lt C_0 \theta^k \quad \text{for every} \quad x\in X.
\end{equation*} There exists a partial order ![]() $\preceq$ in the set of all labels
$\preceq$ in the set of all labels ![]() $ \lbrace (k,\alpha) \, : \, k\in {\mathbb Z}, \, \alpha\in \mathcal{A}_k \rbrace$ with the following properties:
$ \lbrace (k,\alpha) \, : \, k\in {\mathbb Z}, \, \alpha\in \mathcal{A}_k \rbrace$ with the following properties:
 \begin{equation*}
d(z_\beta^{k+1}, z_\alpha^k) \lt \frac{c_0}{2} \theta^k \implies (k+1,\beta) \preceq (k,\alpha);
\end{equation*}
\begin{equation*}
d(z_\beta^{k+1}, z_\alpha^k) \lt \frac{c_0}{2} \theta^k \implies (k+1,\beta) \preceq (k,\alpha);
\end{equation*} \begin{equation*}
(k+1,\beta) \preceq (k,\alpha) \implies d(z_\beta^{k+1},z_\alpha^k) \lt c_0 \theta^k;
\end{equation*}
\begin{equation*}
(k+1,\beta) \preceq (k,\alpha) \implies d(z_\beta^{k+1},z_\alpha^k) \lt c_0 \theta^k;
\end{equation*} \begin{align*}
(l,\beta) \preceq (k,\alpha) \iff & l \geq k\; \text{and exist}\;\gamma_k=\alpha, \gamma_{k+1}, \ldots, \gamma_{l-1}, \gamma_l =\beta, \\
& \text{with}\, (j+1, \gamma_{j+1}) \preceq (j,\gamma_j) \,\text{for}\;j=k,\ldots,l-1.
\end{align*}
\begin{align*}
(l,\beta) \preceq (k,\alpha) \iff & l \geq k\; \text{and exist}\;\gamma_k=\alpha, \gamma_{k+1}, \ldots, \gamma_{l-1}, \gamma_l =\beta, \\
& \text{with}\, (j+1, \gamma_{j+1}) \preceq (j,\gamma_j) \,\text{for}\;j=k,\ldots,l-1.
\end{align*} Here ![]() $M\in {\mathbb N}$ is a constant only depending on the geometric doubling constant of
$M\in {\mathbb N}$ is a constant only depending on the geometric doubling constant of ![]() $X,$ and thereby only depending on our constant Cµ from (1).
$X,$ and thereby only depending on our constant Cµ from (1).
The closed and open cubes  $\overline{Q}_\alpha^k$,
$\overline{Q}_\alpha^k$,  $\widetilde{Q}_\alpha^k$ are defined by
$\widetilde{Q}_\alpha^k$ are defined by
 \begin{equation*}
\overline{Q}_\alpha^k= \overline{\bigcup_{(l,\beta) \preceq (k,\alpha)} \lbrace z_\beta^l \rbrace}, \quad \widetilde{Q}_\alpha^k: =X \setminus \bigcup_{\beta \in \mathcal{A}_k,\, \beta \neq \alpha} \overline{Q}_\beta^k.
\end{equation*}
\begin{equation*}
\overline{Q}_\alpha^k= \overline{\bigcup_{(l,\beta) \preceq (k,\alpha)} \lbrace z_\beta^l \rbrace}, \quad \widetilde{Q}_\alpha^k: =X \setminus \bigcup_{\beta \in \mathcal{A}_k,\, \beta \neq \alpha} \overline{Q}_\beta^k.
\end{equation*} The cubes  $\overline{Q}_\alpha^k$ and
$\overline{Q}_\alpha^k$ and  $\widetilde{Q}_\alpha^k$ are respectively closed and open subsets of
$\widetilde{Q}_\alpha^k$ are respectively closed and open subsets of ![]() $X.$ The formula defining the half-open cubes
$X.$ The formula defining the half-open cubes ![]() $Q_\alpha^k$ is more intricate, and we do not recall it here; see [Reference Hytönen and Kairema12, Lemma 2.18]. For these three types of cubes, the following properties hold.
$Q_\alpha^k$ is more intricate, and we do not recall it here; see [Reference Hytönen and Kairema12, Lemma 2.18]. For these three types of cubes, the following properties hold.
 \begin{equation*}
B(z_\alpha^k, a \theta^k) \subset \widetilde{Q}_\alpha^k \subset Q_\alpha^k \subset \overline{Q}_\alpha^k \subset B(z_\alpha^k, A \theta^k), \quad \text{for all} \quad k\in {\mathbb Z}, \, \alpha\in \mathcal{A}_k;
\end{equation*}
\begin{equation*}
B(z_\alpha^k, a \theta^k) \subset \widetilde{Q}_\alpha^k \subset Q_\alpha^k \subset \overline{Q}_\alpha^k \subset B(z_\alpha^k, A \theta^k), \quad \text{for all} \quad k\in {\mathbb Z}, \, \alpha\in \mathcal{A}_k;
\end{equation*} \begin{equation*}
\textrm{int}(\overline{Q}_\alpha^k) = \widetilde{Q}_\alpha^k \quad \text{and} \quad \overline{\widetilde{Q}_\alpha^k} = \overline{Q}_\alpha^k, \quad \text{for all} \quad k\in {\mathbb Z}, \, \alpha\in \mathcal{A}_k;
\end{equation*}
\begin{equation*}
\textrm{int}(\overline{Q}_\alpha^k) = \widetilde{Q}_\alpha^k \quad \text{and} \quad \overline{\widetilde{Q}_\alpha^k} = \overline{Q}_\alpha^k, \quad \text{for all} \quad k\in {\mathbb Z}, \, \alpha\in \mathcal{A}_k;
\end{equation*} \begin{equation*}
\overline{Q}_\alpha^k= \bigcup_{\beta\in \mathcal{A}_l, \, (l,\beta) \preceq (k,\alpha)} \overline{Q}_\beta^l,\quad \text{for all} \quad l, k\in {\mathbb Z}, \, l \geq k, \, \alpha\in \mathcal{A}_k;
\end{equation*}
\begin{equation*}
\overline{Q}_\alpha^k= \bigcup_{\beta\in \mathcal{A}_l, \, (l,\beta) \preceq (k,\alpha)} \overline{Q}_\beta^l,\quad \text{for all} \quad l, k\in {\mathbb Z}, \, l \geq k, \, \alpha\in \mathcal{A}_k;
\end{equation*} \begin{align*}
\widetilde{Q}_\beta^l \subset \widetilde{Q}_\alpha^k\; \text{if}\; (l,\beta) \preceq (k,\alpha)\; \text{and}\; \widetilde{Q}_\beta^l \cap \overline{Q}_\alpha^k= \overline{Q}_\beta^l \cap \widetilde{Q}_\alpha^k& = \emptyset\; \text{otherwise}; \,\nonumber\\ l, k\in {\mathbb Z}, \, l \geq k, \alpha\in \mathcal{A}_k;
\end{align*}
\begin{align*}
\widetilde{Q}_\beta^l \subset \widetilde{Q}_\alpha^k\; \text{if}\; (l,\beta) \preceq (k,\alpha)\; \text{and}\; \widetilde{Q}_\beta^l \cap \overline{Q}_\alpha^k= \overline{Q}_\beta^l \cap \widetilde{Q}_\alpha^k& = \emptyset\; \text{otherwise}; \,\nonumber\\ l, k\in {\mathbb Z}, \, l \geq k, \alpha\in \mathcal{A}_k;
\end{align*} \begin{equation*}X=\bigcup_{\alpha\in{\mathcal A}_k}\overline Q_\alpha^k=\bigcup_{\alpha\in{\mathcal A}_k}Q_\alpha^k,\;\;\text{with the latter union disjoint,}\;\text{for all}\, k\in\mathbb{Z}.\end{equation*}
\begin{equation*}X=\bigcup_{\alpha\in{\mathcal A}_k}\overline Q_\alpha^k=\bigcup_{\alpha\in{\mathcal A}_k}Q_\alpha^k,\;\;\text{with the latter union disjoint,}\;\text{for all}\, k\in\mathbb{Z}.\end{equation*} See [Reference Hytönen and Kairema12] for a proof of all the above properties. The constants ![]() $0 \lt a \lt A \lt \infty$ depend on the initial choice of c 0 and
$0 \lt a \lt A \lt \infty$ depend on the initial choice of c 0 and ![]() $C_0,$ but being θ so small (
$C_0,$ but being θ so small (![]() $\theta \lt 1/1000$), all these constants can be considered to be absolute.
$\theta \lt 1/1000$), all these constants can be considered to be absolute.
Notice that, because  $\textrm{int}(Q_\alpha^k)=\widetilde{Q}_\alpha^k,$ one can replace the term
$\textrm{int}(Q_\alpha^k)=\widetilde{Q}_\alpha^k,$ one can replace the term ![]() $\operatorname{dist}(\cdot, X \setminus Q)$ with
$\operatorname{dist}(\cdot, X \setminus Q)$ with  $\operatorname{dist}(\cdot, X \setminus \widetilde{Q})$ in the estimate (4). To prove Proposition 2.5, we first need a qualitative version of (4). The following key proposition corresponds to [Reference Hytönen and Kairema12, Lemma 5.12].
$\operatorname{dist}(\cdot, X \setminus \widetilde{Q})$ in the estimate (4). To prove Proposition 2.5, we first need a qualitative version of (4). The following key proposition corresponds to [Reference Hytönen and Kairema12, Lemma 5.12].
Proposition 2.6. ([Reference Hytönen and Kairema12, Lemma 5.12])
If parameters ![]() $N\in {\mathbb N} \cup \lbrace 0 \rbrace,$ and λ > 0 are so that
$N\in {\mathbb N} \cup \lbrace 0 \rbrace,$ and λ > 0 are so that ![]() $12\lambda \leq c_0 \theta^N,$ and
$12\lambda \leq c_0 \theta^N,$ and ![]() $(k,\alpha)$ is a label so that
$(k,\alpha)$ is a label so that  $x\in \overline{Q}_\alpha^k$ with
$x\in \overline{Q}_\alpha^k$ with  $\operatorname{dist}(x, X \setminus \widetilde{Q}_\alpha^k) \lt \lambda \theta^k,$ then for any chain of labels
$\operatorname{dist}(x, X \setminus \widetilde{Q}_\alpha^k) \lt \lambda \theta^k,$ then for any chain of labels
with  $x\in \overline{Q}_{\sigma}^{k+N},$ one has
$x\in \overline{Q}_{\sigma}^{k+N},$ one has  $d(z_{\sigma_j}^j, z_{\sigma_i}^i) \geq \varepsilon_1\theta^j$ for all
$d(z_{\sigma_j}^j, z_{\sigma_i}^i) \geq \varepsilon_1\theta^j$ for all ![]() $k \leq j \lt i \leq k+N;$ where
$k \leq j \lt i \leq k+N;$ where ![]() $\varepsilon_1= c_0/12.$
$\varepsilon_1= c_0/12.$
Proposition 2.7. For every ![]() $\varepsilon$ > 0 there exists
$\varepsilon$ > 0 there exists ![]() $\lambda \in (0,1]$ so that
$\lambda \in (0,1]$ so that
 \begin{equation*}
\mu\left(\lbrace x\in \overline{Q}_\alpha^k \, : \, \operatorname{dist}(x, X\setminus \widetilde{Q}_\alpha^k) \leq \lambda \theta^k \rbrace \right) \lt \varepsilon \mu(Q_\alpha^k), \quad \text{for all} \quad \alpha\in \mathcal{A}_k, \, k \in {\mathbb Z}.
\end{equation*}
\begin{equation*}
\mu\left(\lbrace x\in \overline{Q}_\alpha^k \, : \, \operatorname{dist}(x, X\setminus \widetilde{Q}_\alpha^k) \leq \lambda \theta^k \rbrace \right) \lt \varepsilon \mu(Q_\alpha^k), \quad \text{for all} \quad \alpha\in \mathcal{A}_k, \, k \in {\mathbb Z}.
\end{equation*}Proof. Fix a cube  $\overline{Q}_\alpha^k$ and denote
$\overline{Q}_\alpha^k$ and denote  $E_\lambda=\lbrace x\in \overline{Q}_\alpha^k \, : \, \operatorname{dist}(x, X\setminus \widetilde{Q}_\alpha^k) \leq \lambda \theta^k \rbrace$ for λ > 0. Given a natural
$E_\lambda=\lbrace x\in \overline{Q}_\alpha^k \, : \, \operatorname{dist}(x, X\setminus \widetilde{Q}_\alpha^k) \leq \lambda \theta^k \rbrace$ for λ > 0. Given a natural ![]() $N\in {\mathbb N},$ let
$N\in {\mathbb N},$ let  $\lambda \in (0, \frac{c_0}{12}\theta^N)$, and define, for
$\lambda \in (0, \frac{c_0}{12}\theta^N)$, and define, for ![]() $x\in E_\lambda$, the set of indices
$x\in E_\lambda$, the set of indices
 \begin{equation*}
\mathcal{I}_{k+N}(x) =\lbrace \sigma \in \mathcal{A}_{k+N} \, : \, (k+N, \sigma) \preceq (k,\alpha) \,\text{and}\, x\in \overline{Q}_\sigma^{k+N} \rbrace.
\end{equation*}
\begin{equation*}
\mathcal{I}_{k+N}(x) =\lbrace \sigma \in \mathcal{A}_{k+N} \, : \, (k+N, \sigma) \preceq (k,\alpha) \,\text{and}\, x\in \overline{Q}_\sigma^{k+N} \rbrace.
\end{equation*} Notice that ![]() $\mathcal{I}_{k+N}(x)$ is non-empty, since
$\mathcal{I}_{k+N}(x)$ is non-empty, since  $\overline{Q}_\alpha^k = \bigcup_{\lbrace \sigma \in \mathcal{A}_{k+N}\, : \, (k+N, \sigma ) \preceq (k,\alpha) \rbrace} \overline{Q}_\sigma^{k+N}.$ Also, for
$\overline{Q}_\alpha^k = \bigcup_{\lbrace \sigma \in \mathcal{A}_{k+N}\, : \, (k+N, \sigma ) \preceq (k,\alpha) \rbrace} \overline{Q}_\sigma^{k+N}.$ Also, for ![]() $x\in E_\lambda,$ and
$x\in E_\lambda,$ and ![]() $k \leq j \leq k+N,$ we define
$k \leq j \leq k+N,$ we define
 \begin{align*}
\mathcal{I}_j^\lambda=\lbrace \gamma \in \mathcal{A}_j \, : \, \text{there are}\, x\in E_\lambda \,\text{and}\, (k+N,\sigma) \preceq \cdots \preceq (j,\gamma) \preceq \cdots &\preceq (k,\alpha) \,\text{with}\nonumber\\ &\sigma \in \mathcal{I}_{k+N}(x) \rbrace.
\end{align*}
\begin{align*}
\mathcal{I}_j^\lambda=\lbrace \gamma \in \mathcal{A}_j \, : \, \text{there are}\, x\in E_\lambda \,\text{and}\, (k+N,\sigma) \preceq \cdots \preceq (j,\gamma) \preceq \cdots &\preceq (k,\alpha) \,\text{with}\nonumber\\ &\sigma \in \mathcal{I}_{k+N}(x) \rbrace.
\end{align*} We now make the following claim: there exists ![]() $0 \lt \varepsilon_2 \leq \min\lbrace a, \varepsilon_1, c_0/2 \rbrace$ so that
$0 \lt \varepsilon_2 \leq \min\lbrace a, \varepsilon_1, c_0/2 \rbrace$ so that
 \begin{equation}
\text{the family of balls} \: \lbrace B(z_\gamma^j, \varepsilon_2 \theta^j) \, : \, \gamma \in \mathcal{I}_j^\lambda, \: k \leq j \leq k+N \rbrace \:\ \text{is disjointed}.
\end{equation}
\begin{equation}
\text{the family of balls} \: \lbrace B(z_\gamma^j, \varepsilon_2 \theta^j) \, : \, \gamma \in \mathcal{I}_j^\lambda, \: k \leq j \leq k+N \rbrace \:\ \text{is disjointed}.
\end{equation} Indeed, for every two different indices  $\gamma \in \mathcal{I}_j^\lambda,$
$\gamma \in \mathcal{I}_j^\lambda,$ ![]() $\beta \in \mathcal{I}_i^\lambda$ with
$\beta \in \mathcal{I}_i^\lambda$ with ![]() $k \leq j \leq i \leq k+N,$ let us show that
$k \leq j \leq i \leq k+N,$ let us show that  $B(z_\gamma^j, \varepsilon_2 \theta^j) $ and
$B(z_\gamma^j, \varepsilon_2 \theta^j) $ and  $B(z_\beta^i, \varepsilon_2 \theta^j)$ are disjoint, for a constant
$B(z_\beta^i, \varepsilon_2 \theta^j)$ are disjoint, for a constant ![]() $\varepsilon_2 \gt 0$. In the case
$\varepsilon_2 \gt 0$. In the case ![]() $i=j,$ because
$i=j,$ because ![]() $\gamma \neq \beta,$ the points are
$\gamma \neq \beta,$ the points are ![]() $z_\gamma^j$ and
$z_\gamma^j$ and ![]() $z_\beta^j$ are
$z_\beta^j$ are ![]() $c_0 \theta^j$-separated, and the claim follows if
$c_0 \theta^j$-separated, and the claim follows if ![]() $\varepsilon_2 \leq c_0/2.$ Now, if
$\varepsilon_2 \leq c_0/2.$ Now, if ![]() $i \gt j,$ let us denote
$i \gt j,$ let us denote ![]() $\gamma_j= \gamma$ and
$\gamma_j= \gamma$ and ![]() $\beta_i=\beta.$ Let
$\beta_i=\beta.$ Let ![]() $x,y\in E_\lambda$ be so that
$x,y\in E_\lambda$ be so that ![]() $(j,\gamma_j)$ belongs to a chain
$(j,\gamma_j)$ belongs to a chain ![]() $(k+N,\gamma_{k+N}) \preceq \cdots \preceq (k,\gamma_N)=(k,\alpha)$ with
$(k+N,\gamma_{k+N}) \preceq \cdots \preceq (k,\gamma_N)=(k,\alpha)$ with ![]() $\gamma_{k+N}\in \mathcal{I}_{k+N}(x)$, and so that
$\gamma_{k+N}\in \mathcal{I}_{k+N}(x)$, and so that ![]() $(i, \beta_i)$ belongs to a chain
$(i, \beta_i)$ belongs to a chain ![]() $(k+N,\beta_{k+N}) \preceq \cdots \preceq (k,\beta_N)=(k,\alpha)$ with
$(k+N,\beta_{k+N}) \preceq \cdots \preceq (k,\beta_N)=(k,\alpha)$ with ![]() $\beta_{k+N}\in \mathcal{I}_{k+N}(y).$ Because
$\beta_{k+N}\in \mathcal{I}_{k+N}(y).$ Because  $x\in E_\lambda \cap \overline{Q}_{\gamma_{k+N}}^{k+N},$
$x\in E_\lambda \cap \overline{Q}_{\gamma_{k+N}}^{k+N},$  $y\in E_\lambda \cap \overline{Q}_{\beta_{k+N}}^{k+N}$ and
$y\in E_\lambda \cap \overline{Q}_{\beta_{k+N}}^{k+N}$ and  $\lambda \lt \frac{c_0 \theta^N}{12},$ Proposition 2.6 can be applied to obtain
$\lambda \lt \frac{c_0 \theta^N}{12},$ Proposition 2.6 can be applied to obtain
 \begin{equation*}
d(z_{\gamma_j}^j, z_{\gamma_i}^i) \geq \varepsilon_1 \theta^j \quad \text{and} \quad d(z_{\beta_j}^j, z_{\beta_i}^i) \geq \varepsilon_1 \theta^j.
\end{equation*}
\begin{equation*}
d(z_{\gamma_j}^j, z_{\gamma_i}^i) \geq \varepsilon_1 \theta^j \quad \text{and} \quad d(z_{\beta_j}^j, z_{\beta_i}^i) \geq \varepsilon_1 \theta^j.
\end{equation*} If ![]() $\beta_j = \gamma_j$, then we immediately get
$\beta_j = \gamma_j$, then we immediately get  $d(z_{\gamma_j}^j, z_{\beta_i}^i) = d(z_{\beta_j}^j, z_{\beta_i}^i) \geq \varepsilon_1 \theta^j.$ In the other case,
$d(z_{\gamma_j}^j, z_{\beta_i}^i) = d(z_{\beta_j}^j, z_{\beta_i}^i) \geq \varepsilon_1 \theta^j.$ In the other case, ![]() $\beta_j \neq \gamma_j$, and since
$\beta_j \neq \gamma_j$, and since ![]() $(i,\beta_i) \preceq (j,\beta_j),$ then
$(i,\beta_i) \preceq (j,\beta_j),$ then ![]() $(i,\beta_i) \not\preceq (j,\gamma_j)$. The properties of the cubes
$(i,\beta_i) \not\preceq (j,\gamma_j)$. The properties of the cubes ![]() $\widetilde{Q}, \overline{Q}$ imply
$\widetilde{Q}, \overline{Q}$ imply  $\widetilde{Q}_{\beta_i}^i \cap \overline{Q}_{\gamma_j}^j = \emptyset,$ and so the balls
$\widetilde{Q}_{\beta_i}^i \cap \overline{Q}_{\gamma_j}^j = \emptyset,$ and so the balls  $B(z_{\beta_i}^i,a \theta^i)$ and
$B(z_{\beta_i}^i,a \theta^i)$ and  $B(z_{\gamma_j}^j,a \theta^j)$ are disjoint too. In either case we see that there is
$B(z_{\gamma_j}^j,a \theta^j)$ are disjoint too. In either case we see that there is ![]() $\varepsilon_2 \gt 0$ so that
$\varepsilon_2 \gt 0$ so that  $B(z_\beta^i, \varepsilon_2 \theta^j) \cap B(z_\gamma^j, \varepsilon_2 \theta^j) = \emptyset,$ proving claim (5).
$B(z_\beta^i, \varepsilon_2 \theta^j) \cap B(z_\gamma^j, \varepsilon_2 \theta^j) = \emptyset,$ proving claim (5).
Before starting with the desired estimates for the measures, observe that  $\mathcal{I}_{k+N}^\lambda$ can be written as
$\mathcal{I}_{k+N}^\lambda$ can be written as
 \begin{equation*}
\mathcal{I}_{k+N}^\lambda=\lbrace \sigma \in \mathcal{A}_{k+N} \, : \, (k+N, \sigma) \preceq (k,\alpha) \,\text{and}\, x\in \overline{Q}_\sigma^{k+N} \text{for some}\, x\in E_\lambda \rbrace,
\end{equation*}
\begin{equation*}
\mathcal{I}_{k+N}^\lambda=\lbrace \sigma \in \mathcal{A}_{k+N} \, : \, (k+N, \sigma) \preceq (k,\alpha) \,\text{and}\, x\in \overline{Q}_\sigma^{k+N} \text{for some}\, x\in E_\lambda \rbrace,
\end{equation*}and thus
 \begin{equation*}
E_\lambda \subset \bigcup_{\sigma \in \mathcal{I}_{k+N}^\lambda} \overline{Q}_\sigma^{k+N} \subset \bigcup_{\sigma \in \mathcal{I}_{k+N}^\lambda} B(z_\sigma^{k+N}, A\theta^{k+N}).
\end{equation*}
\begin{equation*}
E_\lambda \subset \bigcup_{\sigma \in \mathcal{I}_{k+N}^\lambda} \overline{Q}_\sigma^{k+N} \subset \bigcup_{\sigma \in \mathcal{I}_{k+N}^\lambda} B(z_\sigma^{k+N}, A\theta^{k+N}).
\end{equation*} In addition,  $\mathcal{I}_{k+N}^\lambda \subset \bigcup_{\gamma \in \mathcal{I}_j^\lambda} \lbrace \sigma \in \mathcal{A}_{k+N} \, : \, (k+N,\sigma) \preceq (j,\gamma) \rbrace$ for every
$\mathcal{I}_{k+N}^\lambda \subset \bigcup_{\gamma \in \mathcal{I}_j^\lambda} \lbrace \sigma \in \mathcal{A}_{k+N} \, : \, (k+N,\sigma) \preceq (j,\gamma) \rbrace$ for every ![]() $k \leq j \leq k+N.$ We will also take into account that for every
$k \leq j \leq k+N.$ We will also take into account that for every ![]() $k \leq l \leq k+N,$ and
$k \leq l \leq k+N,$ and ![]() $\beta \in \mathcal{I}_l^\lambda,$ the ball
$\beta \in \mathcal{I}_l^\lambda,$ the ball  $B(z_\beta^l, \varepsilon_2 \theta^l)$ is contained in
$B(z_\beta^l, \varepsilon_2 \theta^l)$ is contained in  $\widetilde{Q}_\beta^l$, and thereby contained in
$\widetilde{Q}_\beta^l$, and thereby contained in ![]() $\widetilde{Q}_\gamma^j$ whenever
$\widetilde{Q}_\gamma^j$ whenever ![]() $(l,\beta) \preceq (j,\gamma).$ All these observations lead us to
$(l,\beta) \preceq (j,\gamma).$ All these observations lead us to
 \begin{align*}
\mu(E_\lambda) & \leq \sum_{\sigma \in \mathcal{I}_{k+N}^\lambda} \mu\left( B(z_\sigma^{k+N}, A \theta^{k+N}) \right)\\ & \leq C(C_\mu,A,\theta,\varepsilon_2) \sum_{\sigma \in \mathcal{I}_{k+N}^\lambda} \mu\left( B(z_\sigma^{k+N}, \varepsilon_2 \theta^{k+N}) \right) \\
& \leq C \sum_{\gamma\in \mathcal{I}_j^\lambda}\sum_{\substack{\sigma \in \mathcal{A}_{k+N} \\ (k+N,\sigma)\preceq (j,\gamma)}} \mu\left( B(z_\sigma^{k+N}, \varepsilon_2 \theta^{k+N}) \right) \leq C \sum_{\gamma\in \mathcal{I}_j^\lambda} \mu( \widetilde{Q}_\gamma^j ) \\
& \leq C \sum_{\gamma\in \mathcal{I}_j^\lambda} \mu( B(z_\gamma^j, A \theta^j) ) \leq C^2 \sum_{\gamma\in \mathcal{I}_j^\lambda} \mu( B(z_\gamma^j, \varepsilon_2 \theta^j) ).
\end{align*}
\begin{align*}
\mu(E_\lambda) & \leq \sum_{\sigma \in \mathcal{I}_{k+N}^\lambda} \mu\left( B(z_\sigma^{k+N}, A \theta^{k+N}) \right)\\ & \leq C(C_\mu,A,\theta,\varepsilon_2) \sum_{\sigma \in \mathcal{I}_{k+N}^\lambda} \mu\left( B(z_\sigma^{k+N}, \varepsilon_2 \theta^{k+N}) \right) \\
& \leq C \sum_{\gamma\in \mathcal{I}_j^\lambda}\sum_{\substack{\sigma \in \mathcal{A}_{k+N} \\ (k+N,\sigma)\preceq (j,\gamma)}} \mu\left( B(z_\sigma^{k+N}, \varepsilon_2 \theta^{k+N}) \right) \leq C \sum_{\gamma\in \mathcal{I}_j^\lambda} \mu( \widetilde{Q}_\gamma^j ) \\
& \leq C \sum_{\gamma\in \mathcal{I}_j^\lambda} \mu( B(z_\gamma^j, A \theta^j) ) \leq C^2 \sum_{\gamma\in \mathcal{I}_j^\lambda} \mu( B(z_\gamma^j, \varepsilon_2 \theta^j) ).
\end{align*}These estimates, along with (5), permit to write
 \begin{align*}
(N +1) \mu(E_\lambda) &\leq C^2 \sum_{j=k}^{k+N} \sum_{\gamma\in \mathcal{I}_j^\lambda} \mu( B(z_\gamma^j, \varepsilon_2 \theta^j) )\\
&= C^2 \mu \left( \bigcup_{k \leq j \leq k+N} \bigcup_{\gamma\in \mathcal{I}_j^\lambda} B(z_\gamma^j, \varepsilon_2 \theta^j) \right) \leq C^2 \mu(Q_\alpha^k),
\end{align*}
\begin{align*}
(N +1) \mu(E_\lambda) &\leq C^2 \sum_{j=k}^{k+N} \sum_{\gamma\in \mathcal{I}_j^\lambda} \mu( B(z_\gamma^j, \varepsilon_2 \theta^j) )\\
&= C^2 \mu \left( \bigcup_{k \leq j \leq k+N} \bigcup_{\gamma\in \mathcal{I}_j^\lambda} B(z_\gamma^j, \varepsilon_2 \theta^j) \right) \leq C^2 \mu(Q_\alpha^k),
\end{align*} which holds for every ![]() $\alpha,k$ whenever
$\alpha,k$ whenever  $\lambda \in (0, \frac{c_0}{12} \theta^N).$ In the last inequality we have used the fact that all the balls
$\lambda \in (0, \frac{c_0}{12} \theta^N).$ In the last inequality we have used the fact that all the balls  $B(z_\gamma^j, \varepsilon_2 \theta^j) $ are contained in
$B(z_\gamma^j, \varepsilon_2 \theta^j) $ are contained in ![]() $\widetilde{Q}_\gamma^j$, and so, in
$\widetilde{Q}_\gamma^j$, and so, in  $\widetilde{Q}_\alpha^k$ as well because
$\widetilde{Q}_\alpha^k$ as well because ![]() $(j,\gamma) \preceq (k,\alpha)$.
$(j,\gamma) \preceq (k,\alpha)$.
Using the technique from [Reference Christ5], where a version of Proposition 2.7 for the open cubes is combined with an iterative argument, we next show Proposition 2.5.
Proof of Proposition 2.5
Denote  $E_\lambda(\overline{Q}_\alpha^k)= \lbrace x\in \overline{Q}_\alpha^k \, : \, \operatorname{dist}(x, X\setminus \widetilde{Q}_\alpha^k) \leq \lambda \theta^k \rbrace.$ The desired estimate in the case
$E_\lambda(\overline{Q}_\alpha^k)= \lbrace x\in \overline{Q}_\alpha^k \, : \, \operatorname{dist}(x, X\setminus \widetilde{Q}_\alpha^k) \leq \lambda \theta^k \rbrace.$ The desired estimate in the case ![]() $\lambda \geq \theta$ is true because in this case we can simply estimate by
$\lambda \geq \theta$ is true because in this case we can simply estimate by
 \begin{equation*}
\mu(E_\lambda(\overline{Q}_\alpha^k)) \leq \mu(\overline{Q}_\alpha^k) \leq C(C_\mu) \mu(Q_\alpha^k) \leq C(C_\mu) \theta^{-\eta} \lambda^\eta\mu(Q_\alpha^k),
\end{equation*}
\begin{equation*}
\mu(E_\lambda(\overline{Q}_\alpha^k)) \leq \mu(\overline{Q}_\alpha^k) \leq C(C_\mu) \mu(Q_\alpha^k) \leq C(C_\mu) \theta^{-\eta} \lambda^\eta\mu(Q_\alpha^k),
\end{equation*} using any η > 0. So let us assume ![]() $\lambda \in (0,\theta)$ in the rest of the proof. Define for every
$\lambda \in (0,\theta)$ in the rest of the proof. Define for every ![]() $j \in {\mathbb N}\cup \lbrace 0 \rbrace,$ the set of labels
$j \in {\mathbb N}\cup \lbrace 0 \rbrace,$ the set of labels
 \begin{equation*}
\mathcal{I}_j(\overline{Q}_\alpha^k) := \lbrace (k+j,\beta) \preceq (k,\alpha) \, : \, \operatorname{dist}( \overline{Q}_\beta^{k+j}, X \setminus \widetilde{Q}_\alpha^k) \leq \theta^{k+j} \rbrace,
\end{equation*}
\begin{equation*}
\mathcal{I}_j(\overline{Q}_\alpha^k) := \lbrace (k+j,\beta) \preceq (k,\alpha) \, : \, \operatorname{dist}( \overline{Q}_\beta^{k+j}, X \setminus \widetilde{Q}_\alpha^k) \leq \theta^{k+j} \rbrace,
\end{equation*} together with the corresponding sets of points  $S_j(\overline{Q}_\alpha^k) := \bigcup_{(k+j,\beta)\in \mathcal{I}_j(\overline{Q}_\alpha^k)} \overline{Q}_\beta^{k+j}.$ We claim the following.
$S_j(\overline{Q}_\alpha^k) := \bigcup_{(k+j,\beta)\in \mathcal{I}_j(\overline{Q}_\alpha^k)} \overline{Q}_\beta^{k+j}.$ We claim the following.
Claim 2.8.
There exist constants ![]() $C, \eta \gt 0$ depending on θ and Cµ so that
$C, \eta \gt 0$ depending on θ and Cµ so that  $\mu(S_j(\overline{Q}_\alpha^k)) \leq C \theta^{j \eta} \mu(Q_\alpha^k)$ for every
$\mu(S_j(\overline{Q}_\alpha^k)) \leq C \theta^{j \eta} \mu(Q_\alpha^k)$ for every ![]() $j\in {\mathbb N},$ and every
$j\in {\mathbb N},$ and every ![]() $\alpha, k.$
$\alpha, k.$
Before proving this claim, let us explain why this would imply Proposition 2.5. Assume for the moment that Claim 2.8 is true. For any ![]() $\lambda \in (0,\theta)$, let
$\lambda \in (0,\theta)$, let ![]() $j \in {\mathbb N} \cup \lbrace 0 \rbrace$ be so that
$j \in {\mathbb N} \cup \lbrace 0 \rbrace$ be so that ![]() $ \theta^{j+1} \lt \lambda \leq \theta^j.$ If
$ \theta^{j+1} \lt \lambda \leq \theta^j.$ If  $x\in \overline{Q}_\alpha^k$ is so that
$x\in \overline{Q}_\alpha^k$ is so that  $\operatorname{dist}(x, X \setminus \widetilde{Q}_\alpha^k) \leq \lambda \theta^k,$ and β so that
$\operatorname{dist}(x, X \setminus \widetilde{Q}_\alpha^k) \leq \lambda \theta^k,$ and β so that ![]() $(k+j,\beta) \preceq (k,\alpha)$ and
$(k+j,\beta) \preceq (k,\alpha)$ and  $x\in \overline{Q}_\beta^{k+j},$ then
$x\in \overline{Q}_\beta^{k+j},$ then  $(k+j,\beta) \in \mathcal{I}_j(\overline{Q}_\alpha^k),$ showing that
$(k+j,\beta) \in \mathcal{I}_j(\overline{Q}_\alpha^k),$ showing that  $E_\lambda(\overline{Q}_\alpha^k) \subset S_j(\overline{Q}_\alpha^k).$ This yields
$E_\lambda(\overline{Q}_\alpha^k) \subset S_j(\overline{Q}_\alpha^k).$ This yields
 \begin{equation*}
\mu(E_\lambda(\overline{Q}_\alpha^k)) \leq \mu( S_j(\overline{Q}_\alpha^k)) \leq C \theta^{j\eta}\mu(Q_\alpha^k) \leq \theta^{-\eta} C \lambda^\eta \mu(Q_\alpha^k).
\end{equation*}
\begin{equation*}
\mu(E_\lambda(\overline{Q}_\alpha^k)) \leq \mu( S_j(\overline{Q}_\alpha^k)) \leq C \theta^{j\eta}\mu(Q_\alpha^k) \leq \theta^{-\eta} C \lambda^\eta \mu(Q_\alpha^k).
\end{equation*} Let us now prove Claim 2.8. The triangle inequality and the fact that  $\overline{Q}_\gamma^l \subset B(z_\gamma^l, A \theta^l)$ for all
$\overline{Q}_\gamma^l \subset B(z_\gamma^l, A \theta^l)$ for all ![]() $(l,\gamma)$ give
$(l,\gamma)$ give
 \begin{equation*}
\mu( S_j(\overline{Q}_\alpha^k)) \leq \mu \left( \lbrace x\in \overline{Q}_\alpha^k \, : \, \operatorname{dist}(x, X\setminus \widetilde{Q}_\alpha^k) \leq (2A+1) \theta^j \theta^{k} \rbrace \right).
\end{equation*}
\begin{equation*}
\mu( S_j(\overline{Q}_\alpha^k)) \leq \mu \left( \lbrace x\in \overline{Q}_\alpha^k \, : \, \operatorname{dist}(x, X\setminus \widetilde{Q}_\alpha^k) \leq (2A+1) \theta^j \theta^{k} \rbrace \right).
\end{equation*} Hence, according to Proposition 2.7, we can find ![]() $J\in {\mathbb N}$ with the property that
$J\in {\mathbb N}$ with the property that
 \begin{equation}
\mu( S_J(\overline{Q}_\alpha^k) ) \leq \frac{1}{2} \mu(Q_\alpha^k), \quad \text{for all} \, \alpha \in \mathcal{A}_k,\, k \in {\mathbb Z}.
\end{equation}
\begin{equation}
\mu( S_J(\overline{Q}_\alpha^k) ) \leq \frac{1}{2} \mu(Q_\alpha^k), \quad \text{for all} \, \alpha \in \mathcal{A}_k,\, k \in {\mathbb Z}.
\end{equation} We define new subfamilies of labels obtained from the previous ![]() $(\mathcal{I}_j)_j:$
$(\mathcal{I}_j)_j:$
 \begin{equation*}
\widehat{\mathcal{I}}_1(\overline{Q}_\alpha^k):=\mathcal{I}_J(\overline{Q}_\alpha^k), \quad \widehat{\mathcal{I}}_{n+1}(\overline{Q}_\alpha^k):= \bigcup_{(k+nJ,\beta) \in \widehat{\mathcal{I}}_n(\overline{Q}_\alpha^k)} \mathcal{I}_J(\overline{Q}_\beta^{k+nJ}), \quad n \geq 1.
\end{equation*}
\begin{equation*}
\widehat{\mathcal{I}}_1(\overline{Q}_\alpha^k):=\mathcal{I}_J(\overline{Q}_\alpha^k), \quad \widehat{\mathcal{I}}_{n+1}(\overline{Q}_\alpha^k):= \bigcup_{(k+nJ,\beta) \in \widehat{\mathcal{I}}_n(\overline{Q}_\alpha^k)} \mathcal{I}_J(\overline{Q}_\beta^{k+nJ}), \quad n \geq 1.
\end{equation*} The corresponding sets of points are defined as  $ \widehat{S}_n(\overline{Q}_\alpha^k) := \bigcup_{(k+nJ,\beta)\in \widehat{\mathcal{I}}_n(\overline{Q}_\alpha^k)} \overline{Q}_\beta^{k+nJ}.$
$ \widehat{S}_n(\overline{Q}_\alpha^k) := \bigcup_{(k+nJ,\beta)\in \widehat{\mathcal{I}}_n(\overline{Q}_\alpha^k)} \overline{Q}_\beta^{k+nJ}.$
Let us prove by induction on n that  $\mathcal{I}_{nJ}(\overline{Q}_\alpha^k) \subset \widehat{\mathcal{I}}_n(\overline{Q}_\alpha^k).$ If
$\mathcal{I}_{nJ}(\overline{Q}_\alpha^k) \subset \widehat{\mathcal{I}}_n(\overline{Q}_\alpha^k).$ If ![]() $n=1, $ the inclusion is actually an identity and it follows from the definitions. Now assume that the inclusion holds for some natural n and let us show the corresponding inclusion for n + 1. Given
$n=1, $ the inclusion is actually an identity and it follows from the definitions. Now assume that the inclusion holds for some natural n and let us show the corresponding inclusion for n + 1. Given  $(k+(n+1)J, \beta) \in \mathcal{I}_{(n+1)J}(\overline{Q}_\alpha^k)$ there exists (a unique)
$(k+(n+1)J, \beta) \in \mathcal{I}_{(n+1)J}(\overline{Q}_\alpha^k)$ there exists (a unique) ![]() $(k+nJ, \gamma)$ with
$(k+nJ, \gamma)$ with ![]() $(k+(n+1)J, \beta) \preceq (k+nJ, \gamma) \preceq (k,\alpha).$ The index
$(k+(n+1)J, \beta) \preceq (k+nJ, \gamma) \preceq (k,\alpha).$ The index ![]() $(k+(n+1)J, \beta)$ belongs to
$(k+(n+1)J, \beta)$ belongs to  $\mathcal{I}_J(\overline{Q}_\gamma^{k+nJ}) $, because
$\mathcal{I}_J(\overline{Q}_\gamma^{k+nJ}) $, because  $\widetilde{Q}_\gamma^{k+nJ} \subset \widetilde{Q}_\alpha^k$ and
$\widetilde{Q}_\gamma^{k+nJ} \subset \widetilde{Q}_\alpha^k$ and
 \begin{equation*}
\operatorname{dist}(\overline{Q}_\beta^{k+(n+1)J}, X \setminus \widetilde{Q}_\gamma^{k+nJ}) \leq \operatorname{dist}(\overline{Q}_\beta^{k+(n+1)J}, X \setminus \widetilde{Q}_\alpha^{k}) \leq \theta^{k+(n+1)J}=\theta^{(k+nJ)+J}.
\end{equation*}
\begin{equation*}
\operatorname{dist}(\overline{Q}_\beta^{k+(n+1)J}, X \setminus \widetilde{Q}_\gamma^{k+nJ}) \leq \operatorname{dist}(\overline{Q}_\beta^{k+(n+1)J}, X \setminus \widetilde{Q}_\alpha^{k}) \leq \theta^{k+(n+1)J}=\theta^{(k+nJ)+J}.
\end{equation*} On the other hand,  $\overline{Q}_\beta^{k+(n+1)J} \subset \overline{Q}_\gamma^{k+nJ}$ and then clearly
$\overline{Q}_\beta^{k+(n+1)J} \subset \overline{Q}_\gamma^{k+nJ}$ and then clearly
 \begin{equation*}
\operatorname{dist}(\overline{Q}_\gamma^{k+nJ}, X \setminus \widetilde{Q}_\alpha^{k}) \leq \operatorname{dist}(\overline{Q}_\beta^{k+(n+1)J}, X \setminus \widetilde{Q}_\alpha^{k}) \leq \theta^{k+(n+1)J} \leq \theta^{k+nJ}.
\end{equation*}
\begin{equation*}
\operatorname{dist}(\overline{Q}_\gamma^{k+nJ}, X \setminus \widetilde{Q}_\alpha^{k}) \leq \operatorname{dist}(\overline{Q}_\beta^{k+(n+1)J}, X \setminus \widetilde{Q}_\alpha^{k}) \leq \theta^{k+(n+1)J} \leq \theta^{k+nJ}.
\end{equation*} This tells us that  $(k+nJ,\gamma) \in \mathcal{I}_{nJ}(\overline{Q}_\alpha^k),$ and therefore
$(k+nJ,\gamma) \in \mathcal{I}_{nJ}(\overline{Q}_\alpha^k),$ and therefore  $(k+nJ,\gamma) \in \widehat{\mathcal{I}}_n(\overline{Q}_\alpha^k)$ by the induction hypothesis. Together with the already proven fact that
$(k+nJ,\gamma) \in \widehat{\mathcal{I}}_n(\overline{Q}_\alpha^k)$ by the induction hypothesis. Together with the already proven fact that  $(k+(n+1)J, \beta)\in \mathcal{I}_J(\overline{Q}_\gamma^{k+nJ}), $ we may conclude
$(k+(n+1)J, \beta)\in \mathcal{I}_J(\overline{Q}_\gamma^{k+nJ}), $ we may conclude  $(k+(n+1)J, \beta) \in \widehat{\mathcal{I}}_{n+1}(\overline{Q}_\alpha^k).$
$(k+(n+1)J, \beta) \in \widehat{\mathcal{I}}_{n+1}(\overline{Q}_\alpha^k).$
We summarize the key inclusions here:
 \begin{equation}
\mathcal{I}_{nJ}(\overline{Q}_\alpha^k) \subset \widehat{\mathcal{I}}_n(\overline{Q}_\alpha^k), \quad S_{nJ}(\overline{Q}_\alpha^k) \subset \widehat{S}_{n}(\overline{Q}_\alpha^k), \quad n \geq 2.
\end{equation}
\begin{equation}
\mathcal{I}_{nJ}(\overline{Q}_\alpha^k) \subset \widehat{\mathcal{I}}_n(\overline{Q}_\alpha^k), \quad S_{nJ}(\overline{Q}_\alpha^k) \subset \widehat{S}_{n}(\overline{Q}_\alpha^k), \quad n \geq 2.
\end{equation} Observing that  $\widehat{S}_{n}(\overline{Q}_\alpha^k) \subset \bigcup_{(k+(n-1)J,\beta) \in \widehat{\mathcal{I}}_{n-1}(\overline{Q}_\alpha^k)} S_J(\overline{Q}_\beta^{k+(n-1)J})$ for
$\widehat{S}_{n}(\overline{Q}_\alpha^k) \subset \bigcup_{(k+(n-1)J,\beta) \in \widehat{\mathcal{I}}_{n-1}(\overline{Q}_\alpha^k)} S_J(\overline{Q}_\beta^{k+(n-1)J})$ for ![]() $n\geq 2,$ and employing (6), we can write
$n\geq 2,$ and employing (6), we can write
 \begin{align*}
\mu\left( \widehat{S}_{n}(\overline{Q}_\alpha^k) \right) & \leq \sum_{(k+(n-1)J,\beta) \in \widehat{\mathcal{I}}_{n-1}(\overline{Q}_\alpha^k)} \mu(S_J(\overline{Q}_\beta^{k+(n-1)J}))\\ & \leq \frac{1}{2} \sum_{(k+(n-1)J,\beta) \in \widehat{\mathcal{I}}_{n-1}(\overline{Q}_\alpha^k)} \mu( Q_\beta^{k+(n-1)J}) \\
& = \frac{1}{2} \mu \Big ( \bigcup_{(k+(n-1)J,\beta) \in \widehat{\mathcal{I}}_{n-1}(\overline{Q}_\alpha^k)} Q_\beta^{k+(n-1)J} \Big ) \leq \frac{1}{2}\mu(\widehat{S}_{n-1}(\overline{Q}_\alpha^k)) \\
& \leq \cdots \leq \frac{1}{2^{n-1}} \mu(\widehat{S}_1(\overline{Q}_\alpha^k)) =\frac{1}{2^{n-1}} \mu(S_J( \overline{Q}_\alpha^k)) \leq \frac{1}{2^{n}} \mu( Q_\alpha^k),\, \text{for every}\\ & \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad\qquad\qquad n \geq 1.
\end{align*}
\begin{align*}
\mu\left( \widehat{S}_{n}(\overline{Q}_\alpha^k) \right) & \leq \sum_{(k+(n-1)J,\beta) \in \widehat{\mathcal{I}}_{n-1}(\overline{Q}_\alpha^k)} \mu(S_J(\overline{Q}_\beta^{k+(n-1)J}))\\ & \leq \frac{1}{2} \sum_{(k+(n-1)J,\beta) \in \widehat{\mathcal{I}}_{n-1}(\overline{Q}_\alpha^k)} \mu( Q_\beta^{k+(n-1)J}) \\
& = \frac{1}{2} \mu \Big ( \bigcup_{(k+(n-1)J,\beta) \in \widehat{\mathcal{I}}_{n-1}(\overline{Q}_\alpha^k)} Q_\beta^{k+(n-1)J} \Big ) \leq \frac{1}{2}\mu(\widehat{S}_{n-1}(\overline{Q}_\alpha^k)) \\
& \leq \cdots \leq \frac{1}{2^{n-1}} \mu(\widehat{S}_1(\overline{Q}_\alpha^k)) =\frac{1}{2^{n-1}} \mu(S_J( \overline{Q}_\alpha^k)) \leq \frac{1}{2^{n}} \mu( Q_\alpha^k),\, \text{for every}\\ & \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad\qquad\qquad n \geq 1.
\end{align*} Then (7) leads us to  $\mu\left( S_{nJ}(\overline{Q}_\alpha^k) \right) \leq \mu\left( \widehat{S}_{n}(\overline{Q}_\alpha^k) \right) \leq 2^{-n} \mu(Q_\alpha^k)$ for each
$\mu\left( S_{nJ}(\overline{Q}_\alpha^k) \right) \leq \mu\left( \widehat{S}_{n}(\overline{Q}_\alpha^k) \right) \leq 2^{-n} \mu(Q_\alpha^k)$ for each ![]() $n\in {\mathbb N}.$ Taking η > 0 so that
$n\in {\mathbb N}.$ Taking η > 0 so that ![]() $\theta^{J \eta}=1/2,$ we obtain Claim 2.8 when j is a multiple of
$\theta^{J \eta}=1/2,$ we obtain Claim 2.8 when j is a multiple of ![]() $J,$ and with the constant C = 1. When
$J,$ and with the constant C = 1. When ![]() $j\in {\mathbb N}$ is arbitrary with
$j\in {\mathbb N}$ is arbitrary with ![]() $j \geq J,$ we find
$j \geq J,$ we find ![]() $m\in {\mathbb N}$ with
$m\in {\mathbb N}$ with ![]() $mJ \leq j \lt (m+1)J$ and observe that
$mJ \leq j \lt (m+1)J$ and observe that  $S_j(\overline{Q}_\alpha^k) \subset S_{mJ}(\overline{Q}_\alpha^k).$ Then the result for the multiples of J gives the estimate
$S_j(\overline{Q}_\alpha^k) \subset S_{mJ}(\overline{Q}_\alpha^k).$ Then the result for the multiples of J gives the estimate  $\mu( S_j(\overline{Q}_\alpha^k)) \leq (\theta^{mJ})^\eta\mu(Q_\alpha^k),$ and this term is bounded above by
$\mu( S_j(\overline{Q}_\alpha^k)) \leq (\theta^{mJ})^\eta\mu(Q_\alpha^k),$ and this term is bounded above by ![]() $\theta^{-J\eta} (\theta^j)^\eta \mu(Q_\alpha^k).$ And when
$\theta^{-J\eta} (\theta^j)^\eta \mu(Q_\alpha^k).$ And when ![]() $j \lt J,$ we simply write
$j \lt J,$ we simply write
 \begin{equation*}
\mu(S_j(\overline{Q}_\alpha^k)) \leq \mu(\overline{Q}_\alpha^k) \leq C(C_\mu) \mu(Q_\alpha^k) \leq C(C_\mu) \theta^{-J\eta} \theta^{j\eta} \mu(Q_\alpha^k).
\end{equation*}
\begin{equation*}
\mu(S_j(\overline{Q}_\alpha^k)) \leq \mu(\overline{Q}_\alpha^k) \leq C(C_\mu) \mu(Q_\alpha^k) \leq C(C_\mu) \theta^{-J\eta} \theta^{j\eta} \mu(Q_\alpha^k).
\end{equation*}This completes the proof of Claim 2.8, and hence Proposition 2.5.
3. Weakly porous sets and dyadic weakly porous sets
We begin by defining the maximal E-free hole for a ball ![]() $B=B(x,R)\subset X$:
$B=B(x,R)\subset X$:
If for a ball ![]() $B=B(x,R)$ there is no ball
$B=B(x,R)$ there is no ball ![]() $B(y,r) \subset B(x,R) \setminus E,$ we understand
$B(y,r) \subset B(x,R) \setminus E,$ we understand ![]() $h_E(B)=0.$ Notice that, even if two balls
$h_E(B)=0.$ Notice that, even if two balls ![]() $B(x,R)$ and
$B(x,R)$ and ![]() $B(x',R')$ define the same set of points, their maximal E-free holes
$B(x',R')$ define the same set of points, their maximal E-free holes ![]() $h_E(B(x,R))$ and
$h_E(B(x,R))$ and ![]() $h_E(B(x',R'))$ may be distinct.
$h_E(B(x',R'))$ may be distinct.
The upper bound ![]() $r \leq 2R$ for the radii in the supremum prevents
$r \leq 2R$ for the radii in the supremum prevents ![]() $h_E(B)$ from being equal to
$h_E(B)$ from being equal to ![]() $\infty,$ which may otherwise occur, e.g., when X is a bounded space. This bound is also motivated by the fact that if two balls satisfy
$\infty,$ which may otherwise occur, e.g., when X is a bounded space. This bound is also motivated by the fact that if two balls satisfy ![]() $B(y,r) \subset B(x,R)$ for r arbitrary, then the ball
$B(y,r) \subset B(x,R)$ for r arbitrary, then the ball ![]() $B(y,t)$, with
$B(y,t)$, with ![]() $t=\min\lbrace r,2R \rbrace$, defines the same set of points as
$t=\min\lbrace r,2R \rbrace$, defines the same set of points as ![]() $B(y,r)$, and has radius t bounded above by
$B(y,r)$, and has radius t bounded above by ![]() $2R.$
$2R.$
Let us now give the definition of a weakly porous set.
Definition 3.1. (Weak porosity)
We say that a set ![]() $E \subset X$ is weakly porous if there are two constants
$E \subset X$ is weakly porous if there are two constants ![]() $c, \delta \in (0,1)$ such that for every open ball
$c, \delta \in (0,1)$ such that for every open ball ![]() $B=B(x,R) \subset X$ there exists a finite collection of mutually disjoint open balls
$B=B(x,R) \subset X$ there exists a finite collection of mutually disjoint open balls ![]() $\lbrace B_i=B(x_i,r_i) \rbrace_{i=1}^N $ contained in
$\lbrace B_i=B(x_i,r_i) \rbrace_{i=1}^N $ contained in ![]() $B\setminus E$, with:
$B\setminus E$, with:
(a)
 $r_i \leq 2R$ for every
$r_i \leq 2R$ for every  $i=1,\ldots,N$;
$i=1,\ldots,N$;(b)
 $r_i \geq \delta h_E(B)$ for every
$r_i \geq \delta h_E(B)$ for every  $i=1,\ldots,N$;
$i=1,\ldots,N$;(c)
 $ \sum_{i=1}^N \mu(B_i) \geq c \mu(B). $
$ \sum_{i=1}^N \mu(B_i) \geq c \mu(B). $
We immediately observe that if E is weakly porous, then ![]() $h_E(B) \gt 0$ for every ball
$h_E(B) \gt 0$ for every ball ![]() $B \subset X.$ Moreover, as a consequence of the Lebesgue differentiation theorem, every weakly porous set E satisfies
$B \subset X.$ Moreover, as a consequence of the Lebesgue differentiation theorem, every weakly porous set E satisfies ![]() $\mu(E)=0.$ We also notice that, since the balls we consider are open sets, a set E is weakly porous if and only if its closure
$\mu(E)=0.$ We also notice that, since the balls we consider are open sets, a set E is weakly porous if and only if its closure ![]() $\overline{E}$ is weakly porous, and with the exact same constants
$\overline{E}$ is weakly porous, and with the exact same constants ![]() $c,\delta.$
$c,\delta.$
It is worth comparing with the (much stronger) classical porous sets: a set E is porous if there is a constant ![]() $c \in (0,1)$ so that every ball
$c \in (0,1)$ so that every ball ![]() $B(x,R)$ contains another ball Bʹ with radius at least cR and
$B(x,R)$ contains another ball Bʹ with radius at least cR and ![]() $B' \cap E = \emptyset.$ Then, by the doubling property of the measure (1), this implies that every porous set is weakly porous. The converse is false; it suffices to equip
$B' \cap E = \emptyset.$ Then, by the doubling property of the measure (1), this implies that every porous set is weakly porous. The converse is false; it suffices to equip ![]() $X={\mathbb R}$ with the usual metric and the Lebesgue measure, and consider
$X={\mathbb R}$ with the usual metric and the Lebesgue measure, and consider ![]() $E= \mathbb{Z}$ or
$E= \mathbb{Z}$ or ![]() $E= \lbrace \pm j^{-\gamma} \, : \, j\in {\mathbb N} \rbrace \cup \lbrace 0 \rbrace$, γ > 0. A detailed study of the A 1 properties of distances to these sets can be found in [Reference Anderson, Lehrbäck, Mudarra and Vähäkangas1, Theorem 7.1].
$E= \lbrace \pm j^{-\gamma} \, : \, j\in {\mathbb N} \rbrace \cup \lbrace 0 \rbrace$, γ > 0. A detailed study of the A 1 properties of distances to these sets can be found in [Reference Anderson, Lehrbäck, Mudarra and Vähäkangas1, Theorem 7.1].
Remark 3.2. Definition 3.1 of weak porosity can be re-formulated in terms of admissible E-free balls that are not necessarily mutually disjoint: there are two constants ![]() $c, \delta \in (0,1)$ such that for every open ball
$c, \delta \in (0,1)$ such that for every open ball ![]() $B=B(x,R) \subset X$ there exists a finite collection of open balls
$B=B(x,R) \subset X$ there exists a finite collection of open balls ![]() $\lbrace B_i=B(x_i,r_i) \rbrace_{i=1}^N $ contained in
$\lbrace B_i=B(x_i,r_i) \rbrace_{i=1}^N $ contained in ![]() $B\setminus E$, with:
$B\setminus E$, with:
(a’)
 $r_i \leq 2R$ for every
$r_i \leq 2R$ for every  $i=1,\ldots,N$;
$i=1,\ldots,N$;(b’)
 $r_i \geq \delta h_E(B)$ for every
$r_i \geq \delta h_E(B)$ for every  $i=1,\ldots,N$;
$i=1,\ldots,N$;(c’)
 $ \mu\left( \bigcup_{i=1}^N B_i \right) \geq c \mu(B). $
$ \mu\left( \bigcup_{i=1}^N B_i \right) \geq c \mu(B). $
Indeed, if ![]() $E \subset X,$
$E \subset X,$ ![]() $c,\delta \in (0,1)$, B and
$c,\delta \in (0,1)$, B and ![]() $\lbrace B_i \rbrace_i$ are as above, the radii of the balls
$\lbrace B_i \rbrace_i$ are as above, the radii of the balls ![]() $\lbrace B_i \rbrace_i$ are uniformly bounded by 2R and the 5-covering lemma (see e.g., [Reference Björn and Björn2, p. 5]) can be applied to obtain a subcollection
$\lbrace B_i \rbrace_i$ are uniformly bounded by 2R and the 5-covering lemma (see e.g., [Reference Björn and Björn2, p. 5]) can be applied to obtain a subcollection ![]() $\lbrace B_j \rbrace_j$ of
$\lbrace B_j \rbrace_j$ of ![]() $\lbrace B_i \rbrace_i$ of mutually disjoint balls with
$\lbrace B_i \rbrace_i$ of mutually disjoint balls with  $\bigcup_i B_i \subset \bigcup_j 5 B_j$. Using that
$\bigcup_i B_i \subset \bigcup_j 5 B_j$. Using that  $\mu(5B_j) \leq C_\mu^3 \, \mu(B_j),$ it is easy to see that the family
$\mu(5B_j) \leq C_\mu^3 \, \mu(B_j),$ it is easy to see that the family ![]() $\lbrace B_j \rbrace_j$ satisfies the properties (a), (b), (c) of Definition 3.1 with constants
$\lbrace B_j \rbrace_j$ satisfies the properties (a), (b), (c) of Definition 3.1 with constants  $(C_\mu^{-3} c, \delta)$ instead of
$(C_\mu^{-3} c, \delta)$ instead of ![]() $(c,\delta).$
$(c,\delta).$
For the reasons explained in the introduction, we also need a formulation of weak porosity in terms of the dyadic structures from Section 2. From now on, we fix a parameter ![]() $0 \lt \theta \lt 1/1000$ and consider the associated dyadic systems
$0 \lt \theta \lt 1/1000$ and consider the associated dyadic systems ![]() $\mathcal{D}=\lbrace \mathcal{D}_t \rbrace_{t=1}^T$ from Proposition 2.3.
$\mathcal{D}=\lbrace \mathcal{D}_t \rbrace_{t=1}^T$ from Proposition 2.3.
Given a cube Q 0 in a dyadic grid ![]() $\mathcal{D}_t,$ the dyadic version of the maximal E-free hole for Q 0 is defined by the formula
$\mathcal{D}_t,$ the dyadic version of the maximal E-free hole for Q 0 is defined by the formula
In the trivial case where every ![]() $Q\in \mathcal{D}(Q_0)$ intersects
$Q\in \mathcal{D}(Q_0)$ intersects ![]() $E,$ we understand
$E,$ we understand ![]() $g_E(Q_0)=+\infty,$ and
$g_E(Q_0)=+\infty,$ and ![]() $\theta^{g_E(Q_0)}=0.$ Note that
$\theta^{g_E(Q_0)}=0.$ Note that ![]() $g_E(Q_0) \geq g(Q_0)$ for every
$g_E(Q_0) \geq g(Q_0)$ for every ![]() $Q_0.$ Equipped with this definition, we introduce the dyadic weakly porous sets in a metric measure space
$Q_0.$ Equipped with this definition, we introduce the dyadic weakly porous sets in a metric measure space ![]() $(X,d,\mu).$
$(X,d,\mu).$
Definition 3.3. (Dyadic weak porosity)
We say that a set ![]() $E \subset X$ is dyadic weakly porous if there exist constants
$E \subset X$ is dyadic weakly porous if there exist constants ![]() $c \in (0,1)$ and
$c \in (0,1)$ and ![]() $M\in {\mathbb N}$ such that for every cube
$M\in {\mathbb N}$ such that for every cube ![]() $Q_0 \in \mathcal{D}$ of X, there exists a finite collection of mutually disjoint cubes
$Q_0 \in \mathcal{D}$ of X, there exists a finite collection of mutually disjoint cubes ![]() $Q_1, \ldots, Q_N \in \mathcal{D}(Q_0)$ that are contained in
$Q_1, \ldots, Q_N \in \mathcal{D}(Q_0)$ that are contained in ![]() $Q_0\setminus E$, with
$Q_0\setminus E$, with ![]() $g(Q_i) \leq M + g_E(Q_0)$ for every
$g(Q_i) \leq M + g_E(Q_0)$ for every ![]() $i=1,\ldots,N$, and
$i=1,\ldots,N$, and  $\sum_{i=1}^N \mu(Q_i) \geq c \mu(Q_0)$.
$\sum_{i=1}^N \mu(Q_i) \geq c \mu(Q_0)$.
We next define the doubling properties for the size of maximal E-free holes, both in terms of balls and dyadic sets.
Definition 3.4. Let ![]() $E \subset X$ be a subset.
$E \subset X$ be a subset.
• We say that hE is doubling if there exists
 $C$ > 0 for which
$C$ > 0 for which
 \begin{equation*}
h_E(B(x,2R)) \leq C h_E(B(x,R)), \quad \text{for all} \quad x\in X, \, R \gt 0.
\end{equation*}
\begin{equation*}
h_E(B(x,2R)) \leq C h_E(B(x,R)), \quad \text{for all} \quad x\in X, \, R \gt 0.
\end{equation*}• We say that gE is doubling if there exists
 $m\in {\mathbb N}$ for which
$m\in {\mathbb N}$ for which
 \begin{equation*}
g_E(Q) \leq m + g_E(Q^*), \quad \text{whenever} \: Q \in \mathcal{D}(Q^*), \, g(Q)=1+g(Q^*), \, Q^* \in \mathcal{D}.
\end{equation*}
\begin{equation*}
g_E(Q) \leq m + g_E(Q^*), \quad \text{whenever} \: Q \in \mathcal{D}(Q^*), \, g(Q)=1+g(Q^*), \, Q^* \in \mathcal{D}.
\end{equation*}
First notice that ![]() $h_E=h_{\overline{E}}$ since the balls we consider are all open.
$h_E=h_{\overline{E}}$ since the balls we consider are all open.
Also observe that if gE is doubling with constant ![]() $m\in {\mathbb N}$, then for every two cubes
$m\in {\mathbb N}$, then for every two cubes ![]() $Q, Q^*$ with
$Q, Q^*$ with ![]() $Q \in \mathcal{D}(Q^*),$ we have, as a consequence of Lemma 2.4(iii),
$Q \in \mathcal{D}(Q^*),$ we have, as a consequence of Lemma 2.4(iii),
The rest of this section is devoted to proving that the two formulations of weak porosity and doubling conditions are equivalent. More precisely, a weakly porous set E whose maximal hole function hE is doubling is dyadic weakly porous with gE doubling as well, and vice-versa. We begin with the following lemma, which we will invoke several times in the paper.
Lemma 3.5. (Large cubes inside balls)
Let ![]() $B=B(x,r)$ be a ball, and
$B=B(x,r)$ be a ball, and ![]() $Q$ a cube in some grid
$Q$ a cube in some grid ![]() $\mathcal{D}_t$ with
$\mathcal{D}_t$ with ![]() $B \subsetneq Q$. Then there exists a cube
$B \subsetneq Q$. Then there exists a cube  $\widehat{Q} \in \mathcal{D}(Q)$ with
$\widehat{Q} \in \mathcal{D}(Q)$ with  $x\in \widehat{Q} \subset B$ and
$x\in \widehat{Q} \subset B$ and  $r\leq \frac{2A}{\theta} \theta^{g(\widehat{Q})}.$
$r\leq \frac{2A}{\theta} \theta^{g(\widehat{Q})}.$
Proof. Consider the set of integers
Let us first explain why this set is non-empty. The cube Q can be written as the union of cubes of ![]() $\mathcal{D}(Q)$, all of them with generation equal to
$\mathcal{D}(Q)$, all of them with generation equal to ![]() $l,$ where
$l,$ where ![]() $l \geq g(Q)$ is so that
$l \geq g(Q)$ is so that ![]() $2A \theta^l \lt r.$ Because
$2A \theta^l \lt r.$ Because ![]() $B(x,r)$ is contained in
$B(x,r)$ is contained in ![]() $Q,$ one of these cubes, say Qʹ, must contain the point
$Q,$ one of these cubes, say Qʹ, must contain the point ![]() $x.$ Denoting by zʹ the reference point of
$x.$ Denoting by zʹ the reference point of ![]() $Q',$ the ball
$Q',$ the ball ![]() $B(z',A \theta^{l})$ contains Qʹ and then every point
$B(z',A \theta^{l})$ contains Qʹ and then every point ![]() $y \in Q'$ satisfies
$y \in Q'$ satisfies ![]() $d(x,y) \lt 2A \theta^{l} \lt r.$ This implies that
$d(x,y) \lt 2A \theta^{l} \lt r.$ This implies that ![]() $x\in Q' \subset B(x,r),$ showing that the set in (11) is nonempty. Also, this set is bounded below by
$x\in Q' \subset B(x,r),$ showing that the set in (11) is nonempty. Also, this set is bounded below by ![]() $g(Q)\in {\mathbb Z},$ by the definition of
$g(Q)\in {\mathbb Z},$ by the definition of ![]() $\mathcal{D}(Q)$. Therefore, the minimum of the set (11) is well-defined and there exists a cube
$\mathcal{D}(Q)$. Therefore, the minimum of the set (11) is well-defined and there exists a cube  $\widehat{Q} \in \mathcal{D}(Q)$ with
$\widehat{Q} \in \mathcal{D}(Q)$ with  $x\in \widehat{Q} \subset B$ with
$x\in \widehat{Q} \subset B$ with  $g(\widehat{Q})$ equal to the minimum of (11). Since
$g(\widehat{Q})$ equal to the minimum of (11). Since ![]() $B \subsetneq Q,$ we must have
$B \subsetneq Q,$ we must have  $g(\widehat{Q}) \gt g(Q),$ as otherwise the equality
$g(\widehat{Q}) \gt g(Q),$ as otherwise the equality  $g(\widehat{Q})=g(Q)$ would lead us to
$g(\widehat{Q})=g(Q)$ would lead us to  $Q= \widehat{Q}$ by virtue of Lemma 2.4, and thus implying
$Q= \widehat{Q}$ by virtue of Lemma 2.4, and thus implying ![]() $B=Q,$ a contradiction. Consequently,
$B=Q,$ a contradiction. Consequently,  $g(\widehat{Q})$ is strictly larger than g(Q) and hence there exists another cube
$g(\widehat{Q})$ is strictly larger than g(Q) and hence there exists another cube ![]() $Q^* \in \mathcal{D}(Q)$ with
$Q^* \in \mathcal{D}(Q)$ with  $\widehat{Q} \subset Q^*$ and
$\widehat{Q} \subset Q^*$ and  $g(Q^*)=g(\widehat{Q})-1.$ By the minimality of
$g(Q^*)=g(\widehat{Q})-1.$ By the minimality of  $g(\widehat{Q}),$ the cube
$g(\widehat{Q}),$ the cube ![]() $Q^*$ cannot be contained in
$Q^*$ cannot be contained in ![]() $B,$ and then
$B,$ and then ![]() $d(p,x) \geq r$ for some
$d(p,x) \geq r$ for some ![]() $p\in Q^*.$ Denoting by
$p\in Q^*.$ Denoting by ![]() $z^*$ the reference point of
$z^*$ the reference point of ![]() $Q^*,$ the ball
$Q^*,$ the ball ![]() $B(z^*,A \theta^{g(Q^*)})$ contains
$B(z^*,A \theta^{g(Q^*)})$ contains ![]() $Q^*$ and, because
$Q^*$ and, because ![]() $x\in Q^*$, we have
$x\in Q^*$, we have
 \begin{equation*}
r \leq d(p,x) \leq \operatorname{diam}(Q^*) \leq \operatorname{diam} \left( B(z^*,A \theta^{g(Q^*)}) \right) \leq 2A \theta^{g(Q^*)} = \frac{2A}{\theta} \theta^{g(\widehat{Q})}.
\end{equation*}
\begin{equation*}
r \leq d(p,x) \leq \operatorname{diam}(Q^*) \leq \operatorname{diam} \left( B(z^*,A \theta^{g(Q^*)}) \right) \leq 2A \theta^{g(Q^*)} = \frac{2A}{\theta} \theta^{g(\widehat{Q})}.
\end{equation*}This proves the assertion.
Remark 3.6. Among other properties, Lemma 3.5 permits to show that a set E is dyadic weakly porous if and only if its closure ![]() $\overline{E}$ is, though possibly with different parameters
$\overline{E}$ is, though possibly with different parameters ![]() $M,c.$
$M,c.$
Indeed, assume first that E is dyadic weakly porous with constants ![]() $M\in {\mathbb N}$ and
$M\in {\mathbb N}$ and ![]() $c\in(0,1).$ If
$c\in(0,1).$ If ![]() $Q_0 \in \mathcal{D}$ is a cube and
$Q_0 \in \mathcal{D}$ is a cube and ![]() $Q \in \mathcal{D}(Q_0)$ with
$Q \in \mathcal{D}(Q_0)$ with ![]() $Q \subset Q_0 \setminus E,$ then Q contains the open ball
$Q \subset Q_0 \setminus E,$ then Q contains the open ball ![]() $B:=B(z, a \theta^{g(Q)}),$ where we denote by z the reference point of
$B:=B(z, a \theta^{g(Q)}),$ where we denote by z the reference point of ![]() $Q.$ If Q = B as sets of points, then Q is an open set and thus we have
$Q.$ If Q = B as sets of points, then Q is an open set and thus we have ![]() $Q \subset Q_0 \setminus \overline{E}.$ If
$Q \subset Q_0 \setminus \overline{E}.$ If ![]() $B \subsetneq Q,$ Lemma 3.5 gives some
$B \subsetneq Q,$ Lemma 3.5 gives some  $\widehat{Q} \in \mathcal{D}(Q) \subset \mathcal{D}(Q_0) $ so that
$\widehat{Q} \in \mathcal{D}(Q) \subset \mathcal{D}(Q_0) $ so that  $\widehat{Q} \subset B$ and
$\widehat{Q} \subset B$ and  $a\theta^{g(Q)} \leq \frac{2A}{\theta} \theta^{g(\widehat{Q})}$. We deduce
$a\theta^{g(Q)} \leq \frac{2A}{\theta} \theta^{g(\widehat{Q})}$. We deduce  $g(\widehat{Q}) \leq n + g(Q)$ for some natural n depending only on
$g(\widehat{Q}) \leq n + g(Q)$ for some natural n depending only on ![]() $\theta,$ and also that
$\theta,$ and also that  $\widehat{Q} \subset Q_0 \setminus \overline{E}$ because B is open. Also, denoting by
$\widehat{Q} \subset Q_0 \setminus \overline{E}$ because B is open. Also, denoting by ![]() $\widehat{z}$ the reference point of
$\widehat{z}$ the reference point of ![]() $\widehat{Q},$ the inclusions
$\widehat{Q},$ the inclusions
 \begin{equation*}
B(\widehat{z}, a \theta^{g(\widehat{Q})}) \subset \widehat{Q} \subset Q \subset B(z, A \theta^{g(Q)})
\end{equation*}
\begin{equation*}
B(\widehat{z}, a \theta^{g(\widehat{Q})}) \subset \widehat{Q} \subset Q \subset B(z, A \theta^{g(Q)})
\end{equation*} together with (1), imply  $\mu(\widehat{Q}) \geq c(\theta,C_\mu) \mu(Q).$ We have shown that given cubes
$\mu(\widehat{Q}) \geq c(\theta,C_\mu) \mu(Q).$ We have shown that given cubes ![]() $Q_1, \ldots, Q_N \in \mathcal{D}(Q_0)$ that are admissible for the definition of dyadic weak porosity with constants M,c, one can find pairwise disjoint cubes
$Q_1, \ldots, Q_N \in \mathcal{D}(Q_0)$ that are admissible for the definition of dyadic weak porosity with constants M,c, one can find pairwise disjoint cubes  $\widehat{Q}_1, \ldots, \widehat{Q}_N \in \mathcal{D}(Q_0)$ so that
$\widehat{Q}_1, \ldots, \widehat{Q}_N \in \mathcal{D}(Q_0)$ so that  $\widehat{Q}_i \subset Q_0 \setminus \overline{E}$,
$\widehat{Q}_i \subset Q_0 \setminus \overline{E}$,
 \begin{equation*}
g(\widehat{Q}_i) \leq n+ g(Q_i) \leq n+M +g_E(Q_0) \leq n+M +g_{\overline{E}}(Q_0),
\end{equation*}
\begin{equation*}
g(\widehat{Q}_i) \leq n+ g(Q_i) \leq n+M +g_E(Q_0) \leq n+M +g_{\overline{E}}(Q_0),
\end{equation*} and  $\sum_{i=1}^N \mu(\widehat{Q}_i) \geq c(\theta,C_\mu) \sum_{i=1}^N\mu(Q_i) \geq c(\theta,C_\mu) \, c \mu(Q_0).$
$\sum_{i=1}^N \mu(\widehat{Q}_i) \geq c(\theta,C_\mu) \sum_{i=1}^N\mu(Q_i) \geq c(\theta,C_\mu) \, c \mu(Q_0).$
Conversely, if ![]() $\overline{E}$ is dyadic weakly porous with parameters
$\overline{E}$ is dyadic weakly porous with parameters ![]() $M\in {\mathbb N},$
$M\in {\mathbb N},$ ![]() $c\in(0,1),$ one can use the same argument as above involving Lemma 3.5 to show that
$c\in(0,1),$ one can use the same argument as above involving Lemma 3.5 to show that ![]() $g_{\overline{E}}(Q_0) \leq n + g_E(Q_0)$ for
$g_{\overline{E}}(Q_0) \leq n + g_E(Q_0)$ for ![]() $n=n(\theta) \in {\mathbb N}$. Thus, every collection of admissible cubes
$n=n(\theta) \in {\mathbb N}$. Thus, every collection of admissible cubes ![]() $Q_1, \ldots , Q_N \in \mathcal{D}(Q_0)$ for the definition of dyadic weak porosity of
$Q_1, \ldots , Q_N \in \mathcal{D}(Q_0)$ for the definition of dyadic weak porosity of ![]() $\overline{E}$ on Q 0 is also admissible for dyadic weak porosity of E, with parameters
$\overline{E}$ on Q 0 is also admissible for dyadic weak porosity of E, with parameters ![]() $M+n\in {\mathbb N}$ and
$M+n\in {\mathbb N}$ and ![]() $c\in(0,1).$
$c\in(0,1).$
Lemma 3.7. Assume that ![]() $g_E$ is doubling. Then the following holds.
$g_E$ is doubling. Then the following holds.
(i)
 $h_E$ is doubling.
$h_E$ is doubling.(ii) If, in addition,
 $E$ is dyadic weakly porous, then
$E$ is dyadic weakly porous, then  $E$ is weakly porous.
$E$ is weakly porous.
Proof. (i) Fix the balls ![]() $B_0=B(x_0,R_0),$
$B_0=B(x_0,R_0),$ ![]() $2B_0=B(x_0, 2 R_0) .$ If
$2B_0=B(x_0, 2 R_0) .$ If ![]() $B(x_0,R_0) \cap E = \emptyset$, then
$B(x_0,R_0) \cap E = \emptyset$, then
and the doubling property for hE holds.
Now suppose that ![]() $B(x_0,R_0) \,\cap\, E \neq \emptyset.$ We may also assume that
$B(x_0,R_0) \,\cap\, E \neq \emptyset.$ We may also assume that ![]() $B_0 \subsetneq 2B_0$ because in the case where
$B_0 \subsetneq 2B_0$ because in the case where ![]() $B_0=2B_0$ (as sets of points), for every ball
$B_0=2B_0$ (as sets of points), for every ball ![]() $B(y,r) \subset 2B_0 \setminus E$ with
$B(y,r) \subset 2B_0 \setminus E$ with ![]() $0 \lt r\leq 4R_0$, the concentric ball
$0 \lt r\leq 4R_0$, the concentric ball ![]() $B(y,r/2)$ is contained in
$B(y,r/2)$ is contained in ![]() $B_0 \setminus E$ and
$B_0 \setminus E$ and ![]() $0 \lt r/2\leq 2R_0,$ from which we would obtain
$0 \lt r/2\leq 2R_0,$ from which we would obtain ![]() $h_E(2B_0) \leq 2 h_E(B_0).$
$h_E(2B_0) \leq 2 h_E(B_0).$
By Proposition 2.3, there exist t and ![]() $Q_0^* \in \mathcal{D}_t$ with
$Q_0^* \in \mathcal{D}_t$ with ![]() $2B_0 \subset Q_0^*,$ and
$2B_0 \subset Q_0^*,$ and ![]() $\theta^{g(Q_0^*)+2} \lt 2 R_0 \leq \theta^{g(Q_0^*)+1}.$ If
$\theta^{g(Q_0^*)+2} \lt 2 R_0 \leq \theta^{g(Q_0^*)+1}.$ If ![]() $B=B(y,r) \subset 2B_0 \setminus E$, then
$B=B(y,r) \subset 2B_0 \setminus E$, then ![]() $B \subsetneq 2B_0^*$ since
$B \subsetneq 2B_0^*$ since ![]() $B_0 \cap E \neq \emptyset,$ and thereby
$B_0 \cap E \neq \emptyset,$ and thereby ![]() $B \subsetneq Q_0^*.$ Lemma 3.5 provides us with a cube
$B \subsetneq Q_0^*.$ Lemma 3.5 provides us with a cube ![]() $Q \in \mathcal{D}(Q_0^*)$ with
$Q \in \mathcal{D}(Q_0^*)$ with ![]() $Q \subset B$ and
$Q \subset B$ and  $r \leq \frac{2A}{\theta} \theta^{g(Q)}.$ Because
$r \leq \frac{2A}{\theta} \theta^{g(Q)}.$ Because ![]() $Q \cap E= \emptyset$, this implies
$Q \cap E= \emptyset$, this implies
 \begin{equation*}
h_E(2 B_0) \leq \frac{2A}{\theta} \theta^{g_E(Q_0^*)}.
\end{equation*}
\begin{equation*}
h_E(2 B_0) \leq \frac{2A}{\theta} \theta^{g_E(Q_0^*)}.
\end{equation*} Since ![]() $B_0 \subsetneq 2B_0 \subset Q_0^*$ we can apply Lemma 3.5 to obtain a cube
$B_0 \subsetneq 2B_0 \subset Q_0^*$ we can apply Lemma 3.5 to obtain a cube ![]() $Q_0 \in \mathcal{D}(Q_0^*)$ with
$Q_0 \in \mathcal{D}(Q_0^*)$ with ![]() $Q_0 \subset B_0$ and
$Q_0 \subset B_0$ and  $R_0\leq \frac{2A}{\theta} \theta^{g(Q_0)}$. Then the inequality
$R_0\leq \frac{2A}{\theta} \theta^{g(Q_0)}$. Then the inequality ![]() $\theta^{g(Q_0^*)+2} \lt 2R_0$ tells us that
$\theta^{g(Q_0^*)+2} \lt 2R_0$ tells us that ![]() $g(Q_0)$ and
$g(Q_0)$ and ![]() $g(Q_0^*)$ are comparable, meaning that
$g(Q_0^*)$ are comparable, meaning that ![]() $g(Q_0)\leq n + g(Q_0^*)$ for some
$g(Q_0)\leq n + g(Q_0^*)$ for some ![]() $n=n(\theta) \in {\mathbb N}.$ Using the doubling property of gE (more precisely, the estimates (10)) for the cubes Q 0 and
$n=n(\theta) \in {\mathbb N}.$ Using the doubling property of gE (more precisely, the estimates (10)) for the cubes Q 0 and ![]() $Q_0^*$, we get
$Q_0^*$, we get
 \begin{equation*}
\theta^{g_E(Q_0^*)} \leq C(\theta,m) \theta^{g_E(Q_0)};
\end{equation*}
\begin{equation*}
\theta^{g_E(Q_0^*)} \leq C(\theta,m) \theta^{g_E(Q_0)};
\end{equation*} where ![]() $m \in {\mathbb N}$ is as in Definition 3.4. Given a cube
$m \in {\mathbb N}$ is as in Definition 3.4. Given a cube ![]() $Q \in \mathcal{D}(Q_0)$ with reference point z and
$Q \in \mathcal{D}(Q_0)$ with reference point z and ![]() $Q \cap E= \emptyset,$ the
$Q \cap E= \emptyset,$ the ![]() $B(z, a \theta^{g(Q)})$ is contained in
$B(z, a \theta^{g(Q)})$ is contained in ![]() $B_0 \setminus E,$ with
$B_0 \setminus E,$ with
 \begin{equation*}
\theta^{g(Q)} \leq \theta^{g(Q_0)} \leq \theta^{g(Q_0^*)} \lt \frac{2R_0}{\theta^2}.
\end{equation*}
\begin{equation*}
\theta^{g(Q)} \leq \theta^{g(Q_0)} \leq \theta^{g(Q_0^*)} \lt \frac{2R_0}{\theta^2}.
\end{equation*} Thus, the θ 2-contraction of ![]() $B(z, a \theta^{g(Q)})$ is a ball inside
$B(z, a \theta^{g(Q)})$ is a ball inside ![]() $B_0 \setminus E$ that is admissible for the definition of
$B_0 \setminus E$ that is admissible for the definition of ![]() $h_E(B_0),$ and so
$h_E(B_0),$ and so
Therefore  $\theta^{g_E(Q_0)} \leq \frac{1}{a \theta^2} h_E(B_0),$ and gathering all the estimates, we conclude
$\theta^{g_E(Q_0)} \leq \frac{1}{a \theta^2} h_E(B_0),$ and gathering all the estimates, we conclude ![]() $h_E(2 B_0) \leq C(m,\theta) h_E(B_0).$ This shows that hE is doubling.
$h_E(2 B_0) \leq C(m,\theta) h_E(B_0).$ This shows that hE is doubling.
(ii) Let ![]() $B_0=B(x_0,R_0)$ be a fixed ball with
$B_0=B(x_0,R_0)$ be a fixed ball with ![]() $B_0 \cap E \neq \emptyset$. By Proposition 2.3, we can find
$B_0 \cap E \neq \emptyset$. By Proposition 2.3, we can find ![]() $Q_0\in \mathcal{D}$ with
$Q_0\in \mathcal{D}$ with ![]() $B_0 \subset Q_0$ and
$B_0 \subset Q_0$ and ![]() $\theta^{g(Q_0)+2} \lt R_0 \leq \theta^{g(Q_0)+1}.$
$\theta^{g(Q_0)+2} \lt R_0 \leq \theta^{g(Q_0)+1}.$
Let us fit a cube  $\widehat{Q}_0 \in \mathcal{D}(Q_0)$ in B 0 of length
$\widehat{Q}_0 \in \mathcal{D}(Q_0)$ in B 0 of length ![]() $\theta^{g(\widehat{Q}_0)}$ comparable to
$\theta^{g(\widehat{Q}_0)}$ comparable to ![]() $R_0.$ If
$R_0.$ If ![]() $B_0=Q_0$ (as sets of points), then we simply take
$B_0=Q_0$ (as sets of points), then we simply take ![]() $\widehat{Q}_0$ as
$\widehat{Q}_0$ as ![]() $Q_0.$ If
$Q_0.$ If ![]() $B_0 \subsetneq Q_0,$ by Lemma 3.5 we get a cube
$B_0 \subsetneq Q_0,$ by Lemma 3.5 we get a cube  $\widehat{Q}_0 \in \mathcal{D}(Q_0)$ with
$\widehat{Q}_0 \in \mathcal{D}(Q_0)$ with ![]() $Q_0 \subset B_0$ and
$Q_0 \subset B_0$ and  $R_0 \leq \frac{2A}{\theta} \theta^{g(\widehat{Q}_0)}.$ In any case, we have the relation
$R_0 \leq \frac{2A}{\theta} \theta^{g(\widehat{Q}_0)}.$ In any case, we have the relation
 \begin{equation}
\theta^{g(Q_0)+2} \lt R_0 \leq \frac{2A}{\theta} \theta^{g(\widehat{Q}_0)}.
\end{equation}
\begin{equation}
\theta^{g(Q_0)+2} \lt R_0 \leq \frac{2A}{\theta} \theta^{g(\widehat{Q}_0)}.
\end{equation} Also, denoting the reference points of Q 0, ![]() $\widehat{Q}_0$ respectively by
$\widehat{Q}_0$ respectively by ![]() $z_0,$
$z_0,$ ![]() $\widehat{z}_0$ we have the inclusions,
$\widehat{z}_0$ we have the inclusions,
 \begin{align*}
B(\widehat{z}_0,a \theta^{g({\widehat{Q}_0})}) \subset \widehat{Q}_0 \subset B_0 \subset Q_0 \subset B(z_0,A \theta^{g(Q_0)}) & \subset B(\widehat{z}_0,3A \theta^{g(Q_0)})\nonumber\\ & \quad\quad \subset B(\widehat{z}_0,6A^2 \theta^{-3} \theta^{g({\widehat{Q}_0})});
\end{align*}
\begin{align*}
B(\widehat{z}_0,a \theta^{g({\widehat{Q}_0})}) \subset \widehat{Q}_0 \subset B_0 \subset Q_0 \subset B(z_0,A \theta^{g(Q_0)}) & \subset B(\widehat{z}_0,3A \theta^{g(Q_0)})\nonumber\\ & \quad\quad \subset B(\widehat{z}_0,6A^2 \theta^{-3} \theta^{g({\widehat{Q}_0})});
\end{align*}from which the doubling condition (1) for µ leads us to
 \begin{equation}
\mu(\widehat{Q}_0)\geq C_\mu^{-1-\left\lfloor \log_2(6A^2a^{-1} \theta^{-3}) \right\rfloor} \mu(B_0).
\end{equation}
\begin{equation}
\mu(\widehat{Q}_0)\geq C_\mu^{-1-\left\lfloor \log_2(6A^2a^{-1} \theta^{-3}) \right\rfloor} \mu(B_0).
\end{equation} Because E is dyadic weakly porous, there exist E-free and pairwise disjoint cubes ![]() $Q_1, \ldots, Q_N$ of
$Q_1, \ldots, Q_N$ of  $\mathcal{D}(\widehat{Q}_0)$ with
$\mathcal{D}(\widehat{Q}_0)$ with
 \begin{equation}
g(Q_i) \leq M + g_E(\widehat{Q}_0), \:\: i=1,\ldots,N, \quad \text{and} \quad \sum_{i=1}^N \mu(Q_i) \geq c \mu(\widehat{Q}_0).
\end{equation}
\begin{equation}
g(Q_i) \leq M + g_E(\widehat{Q}_0), \:\: i=1,\ldots,N, \quad \text{and} \quad \sum_{i=1}^N \mu(Q_i) \geq c \mu(\widehat{Q}_0).
\end{equation} If zi denotes the reference point of Qi define the ball ![]() $B_i=B ( z_i, r_i ),$ with
$B_i=B ( z_i, r_i ),$ with ![]() $r_i:=a \theta^2 \theta^{g(Q_i)}.$ By Proposition 2.3, each Bi is contained in
$r_i:=a \theta^2 \theta^{g(Q_i)}.$ By Proposition 2.3, each Bi is contained in ![]() $Q_i,$ implying that the collection
$Q_i,$ implying that the collection ![]() $\lbrace B_i \rbrace_i$ is disjoint, and that
$\lbrace B_i \rbrace_i$ is disjoint, and that  $B_i \subset \widehat{Q}_0 \setminus E \subset B_0 \setminus E.$ Let us verify the properties (a), (b) and (c) from Definition 3.1 for the collection
$B_i \subset \widehat{Q}_0 \setminus E \subset B_0 \setminus E.$ Let us verify the properties (a), (b) and (c) from Definition 3.1 for the collection ![]() $\lbrace B_i \rbrace_i$.
$\lbrace B_i \rbrace_i$.
Notice that ![]() $r_i \leq a \theta^{g(Q_0)+2} \lt R_0,$ and so property (a) holds.
$r_i \leq a \theta^{g(Q_0)+2} \lt R_0,$ and so property (a) holds.
To prove (b), observe that for each ball ![]() $B=B(p,r) \subset B_0 \setminus E$ with
$B=B(p,r) \subset B_0 \setminus E$ with ![]() $0 \lt r \leq 2 R_0,$ we have
$0 \lt r \leq 2 R_0,$ we have ![]() $B \subsetneq B_0 \subset Q_0$, and Lemma 3.5 can be applied to obtain
$B \subsetneq B_0 \subset Q_0$, and Lemma 3.5 can be applied to obtain ![]() $Q \in \mathcal{D}(Q_0) $ with
$Q \in \mathcal{D}(Q_0) $ with ![]() $Q \subset B$ and
$Q \subset B$ and  $r\leq \frac{2A}{\theta}\theta^{g(Q)}.$ Since
$r\leq \frac{2A}{\theta}\theta^{g(Q)}.$ Since ![]() $Q \cap E = \emptyset,$ this proves
$Q \cap E = \emptyset,$ this proves  $h_E(B_0) \leq \frac{2A}{\theta} \theta^{g_E(Q_0)}.$ The radius ri of the ball Bi satisfies
$h_E(B_0) \leq \frac{2A}{\theta} \theta^{g_E(Q_0)}.$ The radius ri of the ball Bi satisfies  $r_i \geq a \theta^{M+2} \theta^{g_E(\widehat{Q}_0)},$ and using first that gE is doubling and then (12), we get
$r_i \geq a \theta^{M+2} \theta^{g_E(\widehat{Q}_0)},$ and using first that gE is doubling and then (12), we get
 \begin{align*}
r_i \geq a \theta^{M+2} \theta^{g_E(\widehat{Q}_0)} \geq a \theta^{M+2} \theta^{m (g(\widehat{Q}_0)-g(Q_0))} \theta^{g_E( Q_0)} & \geq a \theta^{M+2} \left( \frac{\theta^3}{2A} \right)^m \theta^{g_E( Q_0)}\\ & \qquad\qquad\qquad\quad\geq \delta h_E(B_0);
\end{align*}
\begin{align*}
r_i \geq a \theta^{M+2} \theta^{g_E(\widehat{Q}_0)} \geq a \theta^{M+2} \theta^{m (g(\widehat{Q}_0)-g(Q_0))} \theta^{g_E( Q_0)} & \geq a \theta^{M+2} \left( \frac{\theta^3}{2A} \right)^m \theta^{g_E( Q_0)}\\ & \qquad\qquad\qquad\quad\geq \delta h_E(B_0);
\end{align*} where  $\delta= a\theta^{3} \frac{\theta^{M+3m}}{(2A)^{m+1}}.$
$\delta= a\theta^{3} \frac{\theta^{M+3m}}{(2A)^{m+1}}.$
As concerns property (c), we use that ![]() $B_i=B(z_i, a \theta^2 \theta^{g(Q_i)}) \subset Q_i \subset B ( z_i, A \theta^{g(Q_i)}),$ and the doubling condition (1) on the measure µ to obtain
$B_i=B(z_i, a \theta^2 \theta^{g(Q_i)}) \subset Q_i \subset B ( z_i, A \theta^{g(Q_i)}),$ and the doubling condition (1) on the measure µ to obtain
 \begin{equation*}
\mu(Q_i) \leq C_\mu^{1+\left\lfloor \log_2( a^{-1} \theta^{-2 }A) \right\rfloor} \mu(B_i).
\end{equation*}
\begin{equation*}
\mu(Q_i) \leq C_\mu^{1+\left\lfloor \log_2( a^{-1} \theta^{-2 }A) \right\rfloor} \mu(B_i).
\end{equation*}Combining this estimate with (14) and (13), we obtain
 \begin{equation*}
\sum_{i=1}^N \mu(B_i) \geq c_0(\theta,C_\mu) \, c \, \mu(B_0).
\end{equation*}
\begin{equation*}
\sum_{i=1}^N \mu(B_i) \geq c_0(\theta,C_\mu) \, c \, \mu(B_0).
\end{equation*} for some constant ![]() $c_0(\theta,C_\mu) \gt 0$ depending only on θ and
$c_0(\theta,C_\mu) \gt 0$ depending only on θ and ![]() $C_\mu.$
$C_\mu.$
Now we show that the formulation with balls implies the dyadic formulation.
Lemma 3.8. Assume that ![]() $h_E$ is doubling with constant
$h_E$ is doubling with constant ![]() $C.$ Then the following holds.
$C.$ Then the following holds.
(i)
 $g_E$ is doubling with constant
$g_E$ is doubling with constant  $m=m(\theta,C) \in {\mathbb N}.$
$m=m(\theta,C) \in {\mathbb N}.$(ii) If, in addition,
 $E$ is weakly porous with constants
$E$ is weakly porous with constants  $(c,\delta)$, then
$(c,\delta)$, then  $E$ is dyadic weakly porous with constants
$E$ is dyadic weakly porous with constants  $c'=c'(\theta,C_\mu,c)$ and
$c'=c'(\theta,C_\mu,c)$ and  $M=M(\theta,\delta,C).$
$M=M(\theta,\delta,C).$
Proof. (i) Let ![]() $Q_0,$
$Q_0,$ ![]() $Q_0^*$ be two cubes in a common grid, with
$Q_0^*$ be two cubes in a common grid, with ![]() $Q _0 \in \mathcal{D}( Q_0^*)$ and
$Q _0 \in \mathcal{D}( Q_0^*)$ and ![]() $g(Q_0^*)=g(Q_0)-1.$ If z 0,
$g(Q_0^*)=g(Q_0)-1.$ If z 0, ![]() $z_0^*$ are respectively the reference points of Q 0 and
$z_0^*$ are respectively the reference points of Q 0 and ![]() $Q_0^*,$ define
$Q_0^*,$ define ![]() $B_0=B(z_0,a\theta^{g(Q_0)})$ and
$B_0=B(z_0,a\theta^{g(Q_0)})$ and ![]() $B_0^*=B(z_0^*, A \theta^{g(Q_0^*)}).$ By Proposition 2.3,
$B_0^*=B(z_0^*, A \theta^{g(Q_0^*)}).$ By Proposition 2.3, ![]() $B_0 \subset Q_0$ and
$B_0 \subset Q_0$ and ![]() $Q_0^* \subset B_0^*.$ Also observe that
$Q_0^* \subset B_0^*.$ Also observe that  $B_0^* \subset B(z_0,\frac{2A}{\theta} \theta^{g(Q_0)}),$ and this implies, by virtue of the doubling condition for hE,
$B_0^* \subset B(z_0,\frac{2A}{\theta} \theta^{g(Q_0)}),$ and this implies, by virtue of the doubling condition for hE,
 \begin{equation}
h_E(B_0^*) \leq C^{1+\lfloor \log_2\left(\frac{2A}{a \theta}\right) \rfloor } h_E(B_0);
\end{equation}
\begin{equation}
h_E(B_0^*) \leq C^{1+\lfloor \log_2\left(\frac{2A}{a \theta}\right) \rfloor } h_E(B_0);
\end{equation}where C > 0 is that of Definition 3.4.
Let us now verify that ![]() $ \theta^{g_E(Q_0^*)} \lesssim h_E(B_0^*)$ and
$ \theta^{g_E(Q_0^*)} \lesssim h_E(B_0^*)$ and ![]() $h_E(B_0) \lesssim \theta^{g_E(Q_0)}.$
$h_E(B_0) \lesssim \theta^{g_E(Q_0)}.$
If ![]() $Q \in \mathcal{D}(Q_0^*)$ is such that
$Q \in \mathcal{D}(Q_0^*)$ is such that ![]() $Q \cap E =\emptyset$ and has reference point
$Q \cap E =\emptyset$ and has reference point ![]() $z,$ then the ball
$z,$ then the ball ![]() $B(z, a \theta^{g(Q)})$ is contained in
$B(z, a \theta^{g(Q)})$ is contained in ![]() $B_0^* \setminus E$ and its radius
$B_0^* \setminus E$ and its radius ![]() $a \theta^{g(Q)}$ is smaller than
$a \theta^{g(Q)}$ is smaller than ![]() $A \theta^{g(Q_0^*)}$. By the definition of
$A \theta^{g(Q_0^*)}$. By the definition of ![]() $h_E(B_0^*)$ and
$h_E(B_0^*)$ and ![]() $g_E(Q_0^*)$ (8)–(9), we get
$g_E(Q_0^*)$ (8)–(9), we get ![]() $a\theta^{g_E(Q_0^*)} \leq h_E(B_0^*).$ In the case where
$a\theta^{g_E(Q_0^*)} \leq h_E(B_0^*).$ In the case where ![]() $Q \cap E \neq \emptyset$ for all
$Q \cap E \neq \emptyset$ for all ![]() $Q\in \mathcal{D}(Q_0^*),$ we have
$Q\in \mathcal{D}(Q_0^*),$ we have ![]() $g_E(Q_0^*)=+\infty$ and
$g_E(Q_0^*)=+\infty$ and ![]() $\theta^{g_E(Q_0^*)}=0,$ and the estimate
$\theta^{g_E(Q_0^*)}=0,$ and the estimate ![]() $\theta^{g_E(Q_0^*)} \lesssim h_E(B_0^*)$ is true as well.
$\theta^{g_E(Q_0^*)} \lesssim h_E(B_0^*)$ is true as well.
For the other estimate ![]() $h_E(B_0) \lesssim \theta^{g_E(Q_0)}$, suppose first that
$h_E(B_0) \lesssim \theta^{g_E(Q_0)}$, suppose first that ![]() $Q_0 \cap E = \emptyset.$ Then
$Q_0 \cap E = \emptyset.$ Then ![]() $g_E(Q_0)=g(Q_0)$ and
$g_E(Q_0)=g(Q_0)$ and ![]() $h_E(B_0) \leq 2a \theta^{g(Q_0)}=2a \theta^{g_E(Q_0)}$. Now, if
$h_E(B_0) \leq 2a \theta^{g(Q_0)}=2a \theta^{g_E(Q_0)}$. Now, if ![]() $Q_0 \cap E \neq \emptyset,$ let
$Q_0 \cap E \neq \emptyset,$ let ![]() $B=B(x,r)$ be a ball contained in
$B=B(x,r)$ be a ball contained in ![]() $B_0\setminus E$ (If such ball does not exist, then
$B_0\setminus E$ (If such ball does not exist, then ![]() $h_E(B_0)=0$ and the desired estimate follows immediately). Because of the strict inclusion
$h_E(B_0)=0$ and the desired estimate follows immediately). Because of the strict inclusion ![]() $B \subsetneq Q_0$ (as B does not intersect E), we can apply Lemma 3.5 in order to obtain a cube
$B \subsetneq Q_0$ (as B does not intersect E), we can apply Lemma 3.5 in order to obtain a cube ![]() $Q \in \mathcal{D}(Q_0)$ with
$Q \in \mathcal{D}(Q_0)$ with ![]() $Q \subset B$ and
$Q \subset B$ and  $r \leq \frac{2A}{\theta} \theta^{g(Q)}.$ Because
$r \leq \frac{2A}{\theta} \theta^{g(Q)}.$ Because ![]() $Q \cap E = \emptyset,$ we may conclude
$Q \cap E = \emptyset,$ we may conclude  $h_E(B_0) \leq \frac{2A}{\theta} \theta^{g_E(Q_0)}.$
$h_E(B_0) \leq \frac{2A}{\theta} \theta^{g_E(Q_0)}.$
These estimates together with (15) give ![]() $\theta^{g_E(Q_0^*)} \leq \kappa(\theta,C) \theta^{g_E(Q_0)},$ showing that gE is doubling.
$\theta^{g_E(Q_0^*)} \leq \kappa(\theta,C) \theta^{g_E(Q_0)},$ showing that gE is doubling.
(ii) Let Q 0 a cube of some dyadic grid ![]() $\mathcal{D}_t,$ with reference point
$\mathcal{D}_t,$ with reference point ![]() $z_0.$ We may assume that
$z_0.$ We may assume that ![]() $Q_0 \cap E \neq \emptyset,$ as otherwise the dyadic weak porosity property holds for
$Q_0 \cap E \neq \emptyset,$ as otherwise the dyadic weak porosity property holds for ![]() $Q_0.$ Defining
$Q_0.$ Defining ![]() $B_0:=B(z_0, a\theta^{g(Q_0)})$ and
$B_0:=B(z_0, a\theta^{g(Q_0)})$ and ![]() $B_0^*:= B(z_0, A\theta^{g(Q_0)}),$ we have the inclusions
$B_0^*:= B(z_0, A\theta^{g(Q_0)}),$ we have the inclusions ![]() $B_0 \subset Q_0 \subset B_0^*,$ and so
$B_0 \subset Q_0 \subset B_0^*,$ and so ![]() $\mu(B_0) \geq \kappa(C_\mu) \mu(Q_0)$ by virtue of the doubling condition for
$\mu(B_0) \geq \kappa(C_\mu) \mu(Q_0)$ by virtue of the doubling condition for ![]() $\mu.$
$\mu.$
We first claim that ![]() $\theta^{g_E(Q_0)} \leq \kappa(\theta,C) h_E(B_0)$ where C is the constant of Definition 3.4 for
$\theta^{g_E(Q_0)} \leq \kappa(\theta,C) h_E(B_0)$ where C is the constant of Definition 3.4 for ![]() $h_E.$ Indeed, if
$h_E.$ Indeed, if ![]() $Q\in \mathcal{D}(Q_0) $ with
$Q\in \mathcal{D}(Q_0) $ with ![]() $Q \cap E =\emptyset,$ and Q has reference point
$Q \cap E =\emptyset,$ and Q has reference point ![]() $z,$ then the ball
$z,$ then the ball ![]() $B(z,a \theta^{g(Q)})$ is contained in
$B(z,a \theta^{g(Q)})$ is contained in ![]() $ B_0^* \setminus E,$ and obviously
$ B_0^* \setminus E,$ and obviously ![]() $ a \theta^{g(Q)} \leq A \theta^{g(Q_0)}.$ This argument implies that
$ a \theta^{g(Q)} \leq A \theta^{g(Q_0)}.$ This argument implies that ![]() $a \theta^{g_E(Q_0)} \leq h_E( B_0^*).$ Because hE is doubling, we have
$a \theta^{g_E(Q_0)} \leq h_E( B_0^*).$ Because hE is doubling, we have
 \begin{equation}
a \theta^{g_E(Q_0)} \leq h_E( B_0^*) \leq \kappa(C) h_E(B_0),
\end{equation}
\begin{equation}
a \theta^{g_E(Q_0)} \leq h_E( B_0^*) \leq \kappa(C) h_E(B_0),
\end{equation}which proves our claim.
Now, we apply the weak porosity condition for E to the ball B 0, obtaining disjoint balls ![]() $\lbrace B_i=B(x_i,r_i) \rbrace_{i=1}^N$ contained in
$\lbrace B_i=B(x_i,r_i) \rbrace_{i=1}^N$ contained in ![]() $B_0 \setminus E$ as in Definition 3.1, with constants
$B_0 \setminus E$ as in Definition 3.1, with constants ![]() $c, \delta \in (0,1).$ Since
$c, \delta \in (0,1).$ Since ![]() $B_i \subsetneq Q_0,$ Lemma 3.5 gives a cube
$B_i \subsetneq Q_0,$ Lemma 3.5 gives a cube ![]() $Q_i \in \mathcal{D}(Q_0)$ with
$Q_i \in \mathcal{D}(Q_0)$ with ![]() $Q_i \subset B_i$ and
$Q_i \subset B_i$ and  $r_i \leq \frac{2A}{\theta} \theta^{g(Q_i)}.$ In particular,
$r_i \leq \frac{2A}{\theta} \theta^{g(Q_i)}.$ In particular, ![]() $Q_i \cap E = \emptyset$ for each
$Q_i \cap E = \emptyset$ for each ![]() $i,$ and the cubes
$i,$ and the cubes ![]() $\lbrace Q_i \rbrace_i$ are mutually disjoint.
$\lbrace Q_i \rbrace_i$ are mutually disjoint.
On the other hand, ![]() $2 A \theta^{-1} \theta^{g(Q_i)} \geq r_i \geq \delta h_E(B_0)$, and by (16) this yields
$2 A \theta^{-1} \theta^{g(Q_i)} \geq r_i \geq \delta h_E(B_0)$, and by (16) this yields ![]() $\theta^{g(Q_i)} \geq \kappa(\theta,\delta,C) \theta^{g_E(Q_0)} .$ Thus, there exists
$\theta^{g(Q_i)} \geq \kappa(\theta,\delta,C) \theta^{g_E(Q_0)} .$ Thus, there exists ![]() $ M(\delta,C, \theta) \in {\mathbb N}$ so that
$ M(\delta,C, \theta) \in {\mathbb N}$ so that
Also, if zi denotes the reference point of ![]() $Q_i,$ the following inclusions hold
$Q_i,$ the following inclusions hold
Then, the doubling property of µ implies that  $ \mu(B_i) \leq C_\mu^{1+ \left\lfloor \log_2(4A \theta^{-1} a^{-1}) \right\rfloor} \mu(Q_i).$ So, the cubes
$ \mu(B_i) \leq C_\mu^{1+ \left\lfloor \log_2(4A \theta^{-1} a^{-1}) \right\rfloor} \mu(Q_i).$ So, the cubes ![]() $\lbrace Q_i \rbrace_i$ are disjoint E-free cubes in
$\lbrace Q_i \rbrace_i$ are disjoint E-free cubes in ![]() $\mathcal{D}(Q_0)$ with
$\mathcal{D}(Q_0)$ with
 \begin{equation*}
\kappa(\theta,C_\mu)\sum_{i=1}^N \mu(Q_i) \geq \sum_{i=1}^N \mu(B_i) \geq c \, \mu(B_0) \geq \kappa(C_\mu) \, c \, \mu(Q_0),
\end{equation*}
\begin{equation*}
\kappa(\theta,C_\mu)\sum_{i=1}^N \mu(Q_i) \geq \sum_{i=1}^N \mu(B_i) \geq c \, \mu(B_0) \geq \kappa(C_\mu) \, c \, \mu(Q_0),
\end{equation*} and then we get  $\sum_{i=1}^N \mu(Q_i) \geq \kappa(\theta,C_\mu) \, c \, \mu(Q_0),$ for certain constant
$\sum_{i=1}^N \mu(Q_i) \geq \kappa(\theta,C_\mu) \, c \, \mu(Q_0),$ for certain constant ![]() $\kappa(\theta,C_\mu) \gt 0.$
$\kappa(\theta,C_\mu) \gt 0.$
4. Implications of the A 1-condition
The purpose of this section is to prove the implication (A)![]() $\implies$(B) of Theorem 1.1. In order to do so, we start by proving that if
$\implies$(B) of Theorem 1.1. In order to do so, we start by proving that if ![]() $\operatorname{dist}( \cdot, E)^{-\alpha} \in A_1(X)$ for some
$\operatorname{dist}( \cdot, E)^{-\alpha} \in A_1(X)$ for some ![]() $\alpha \gt 0,$ then the set E is dyadic weakly porous, and gE is doubling; see Definitions 3.3 and 3.4. We will use the fact that a weight
$\alpha \gt 0,$ then the set E is dyadic weakly porous, and gE is doubling; see Definitions 3.3 and 3.4. We will use the fact that a weight ![]() $w\in A_1(X)$ (see (2.1)) if and only if the same A 1-estimates hold when replacing all balls with all cubes
$w\in A_1(X)$ (see (2.1)) if and only if the same A 1-estimates hold when replacing all balls with all cubes ![]() $Q\in \mathcal{D},$ i.e, there exists a constant
$Q\in \mathcal{D},$ i.e, there exists a constant ![]() $C \gt \infty$ so that
$C \gt \infty$ so that
 \begin{equation*}
{\int{\kern-10.5pt}-}_{\hskip-3.5pt Q}\hskip1.5pt w \, d\mu \leq C\ \mathop{\mathrm{ess\, inf}}\limits_{Q} w, \quad \text{for all} \quad Q\in \mathcal{D}.
\end{equation*}
\begin{equation*}
{\int{\kern-10.5pt}-}_{\hskip-3.5pt Q}\hskip1.5pt w \, d\mu \leq C\ \mathop{\mathrm{ess\, inf}}\limits_{Q} w, \quad \text{for all} \quad Q\in \mathcal{D}.
\end{equation*} This can be easily proved using properties (3) and (4) of Proposition 2.3, together with the doubling condition (1) for the measure ![]() $\mu.$
$\mu.$
Lemma 4.1. If ![]() $E \subset X$ is a subset, and
$E \subset X$ is a subset, and ![]() $w= \operatorname{dist}( \cdot, E)^{-\alpha} \in A_1(X)$ with
$w= \operatorname{dist}( \cdot, E)^{-\alpha} \in A_1(X)$ with ![]() $\alpha \gt 0,$ the following holds.
$\alpha \gt 0,$ the following holds.
(i) For every
 $c\in (0,1),$ there exists
$c\in (0,1),$ there exists  $M=M(c,\alpha,[w]_1,\theta,C_\mu) \in {\mathbb N}$ such that, for every dyadic cube
$M=M(c,\alpha,[w]_1,\theta,C_\mu) \in {\mathbb N}$ such that, for every dyadic cube  $Q_0 \subset X,$ there are mutually disjoint cubes
$Q_0 \subset X,$ there are mutually disjoint cubes  $Q_1,\ldots,Q_N \in \mathcal{D}(Q_0)$ containing no point of
$Q_1,\ldots,Q_N \in \mathcal{D}(Q_0)$ containing no point of  $E,$ such that
$E,$ such that  $g(Q_i) \leq M + g_E(Q_0)$ for every
$g(Q_i) \leq M + g_E(Q_0)$ for every  $i,$ and
$i,$ and  $\sum_{i=1}^N \mu(Q_i) \geq c \mu(Q_0).$ In particular,
$\sum_{i=1}^N \mu(Q_i) \geq c \mu(Q_0).$ In particular,  $E$ is dyadic weakly porous.
$E$ is dyadic weakly porous.(ii) There exists
 $m=m(\alpha,[w]_1,\theta,C_\mu) \in {\mathbb N}$ such that, for every two cubes
$m=m(\alpha,[w]_1,\theta,C_\mu) \in {\mathbb N}$ such that, for every two cubes  $Q_0, Q_0^*$ in a same grid with
$Q_0, Q_0^*$ in a same grid with  $Q_0 \in \mathcal{D}(Q_0^*)$ and
$Q_0 \in \mathcal{D}(Q_0^*)$ and  $g(Q_0)=g(Q_0^*)+1,$ we have
$g(Q_0)=g(Q_0^*)+1,$ we have
 \begin{equation*}
g_E(Q_0) \leq m + g_E(Q_0^*).
\end{equation*}
\begin{equation*}
g_E(Q_0) \leq m + g_E(Q_0^*).
\end{equation*}In other words, gE is doubling with constant m.
Proof. First of all, notice that ![]() $\mu(E)=0$ since
$\mu(E)=0$ since ![]() $w:=\operatorname{dist}(\cdot,E)^{-\alpha} $ is locally integrable in
$w:=\operatorname{dist}(\cdot,E)^{-\alpha} $ is locally integrable in ![]() $X.$
$X.$
(i) Thanks to Remark 3.6, we may assume that E is closed. Fix a cube Q 0 in some system ![]() $\mathcal{D}_t$ and assume that
$\mathcal{D}_t$ and assume that ![]() $Q_0 \cap E \neq \emptyset.$ Let
$Q_0 \cap E \neq \emptyset.$ Let ![]() $M\in {\mathbb N}$ be a number to be chosen later, and consider
$M\in {\mathbb N}$ be a number to be chosen later, and consider
 \begin{equation*}
\mathcal{A}_M= \bigcup \lbrace Q \in \mathcal{D}(Q_0) \, : \, Q \cap E = \emptyset \, \,\text{and}\, \, g(Q) \leq M+ g_E(Q_0) \rbrace.
\end{equation*}
\begin{equation*}
\mathcal{A}_M= \bigcup \lbrace Q \in \mathcal{D}(Q_0) \, : \, Q \cap E = \emptyset \, \,\text{and}\, \, g(Q) \leq M+ g_E(Q_0) \rbrace.
\end{equation*} Now, for ![]() $x\in \left( Q_0 \setminus E \right) \setminus \mathcal{A}_M,$ define
$x\in \left( Q_0 \setminus E \right) \setminus \mathcal{A}_M,$ define
Because E is closed, we have that ![]() $\operatorname{dist}(x,E) \gt 0,$ and then an argument similar to the one in the beginning of the proof of Lemma 3.5 shows that gx is well-defined. Let
$\operatorname{dist}(x,E) \gt 0,$ and then an argument similar to the one in the beginning of the proof of Lemma 3.5 shows that gx is well-defined. Let ![]() $Q_x \in \mathcal{D}(Q_0)$ be so that
$Q_x \in \mathcal{D}(Q_0)$ be so that ![]() $x\in Q_x$,
$x\in Q_x$, ![]() $Q_x \cap E= \emptyset,$ and
$Q_x \cap E= \emptyset,$ and ![]() $g(Q_x)=g_x.$ Observe that
$g(Q_x)=g_x.$ Observe that ![]() $g_x \gt M + g_E(Q_0)$ since
$g_x \gt M + g_E(Q_0)$ since ![]() $x\notin \mathcal{A}_M.$ Also, if
$x\notin \mathcal{A}_M.$ Also, if ![]() $Q_x^*$ is a cube in
$Q_x^*$ is a cube in ![]() $\mathcal{D}(Q_0)$ with
$\mathcal{D}(Q_0)$ with ![]() $Q_x \in \mathcal{D}( Q_x^*)$ and
$Q_x \in \mathcal{D}( Q_x^*)$ and ![]() $g(Q_x^*)= g(Q_x)-1$ (such cube exists because
$g(Q_x^*)= g(Q_x)-1$ (such cube exists because ![]() $Q_0 \cap E \neq \emptyset$), we must have
$Q_0 \cap E \neq \emptyset$), we must have ![]() $Q_x^* \cap E \neq \emptyset.$ Denoting by
$Q_x^* \cap E \neq \emptyset.$ Denoting by ![]() $z^*$ the reference point of
$z^*$ the reference point of ![]() $Q_x^*$, the inclusion
$Q_x^*$, the inclusion  $Q_x^* \subset B \left( z^*, A \theta^{g(Q_x^*)} \right)$ holds and thus
$Q_x^* \subset B \left( z^*, A \theta^{g(Q_x^*)} \right)$ holds and thus
 \begin{equation*}
\operatorname{dist}(x,E) \leq \operatorname{diam}\left( B \left( z^*, A \theta^{g(Q_x^*)} \right) \right) \leq \frac{2A}{\theta} \theta^{g_x} \leq \frac{2A}{\theta} \theta^{M} \theta^{g_E(Q_0)}.
\end{equation*}
\begin{equation*}
\operatorname{dist}(x,E) \leq \operatorname{diam}\left( B \left( z^*, A \theta^{g(Q_x^*)} \right) \right) \leq \frac{2A}{\theta} \theta^{g_x} \leq \frac{2A}{\theta} \theta^{M} \theta^{g_E(Q_0)}.
\end{equation*}Employing this inequality, we have
 \begin{align}
\mu \left( Q_0 \setminus \mathcal{A}_M \right) & \leq \left( \frac{2A}{\theta} \theta^{M} \theta^{g_E(Q_0)} \right)^{\alpha} \int_{\left( Q_0 \setminus E \right) \setminus \mathcal{A}_M } \operatorname{dist}(x,E)^{-\alpha} \, d\mu(x) \nonumber \\
& \leq \left( \frac{2A}{\theta} \theta^{M} \theta^{g_E(Q_0)} \right)^{\alpha} \mu (Q_0) [w]_{A_1}\ \mathrm{ess\, inf}_{Q_0} \operatorname{dist}(\cdot,E)^{-\alpha}.
\end{align}
\begin{align}
\mu \left( Q_0 \setminus \mathcal{A}_M \right) & \leq \left( \frac{2A}{\theta} \theta^{M} \theta^{g_E(Q_0)} \right)^{\alpha} \int_{\left( Q_0 \setminus E \right) \setminus \mathcal{A}_M } \operatorname{dist}(x,E)^{-\alpha} \, d\mu(x) \nonumber \\
& \leq \left( \frac{2A}{\theta} \theta^{M} \theta^{g_E(Q_0)} \right)^{\alpha} \mu (Q_0) [w]_{A_1}\ \mathrm{ess\, inf}_{Q_0} \operatorname{dist}(\cdot,E)^{-\alpha}.
\end{align} Now, let ![]() $Q_{E} \in \mathcal{D}(Q_0)$ with
$Q_{E} \in \mathcal{D}(Q_0)$ with ![]() $Q_E \cap E = \emptyset$ and
$Q_E \cap E = \emptyset$ and ![]() $g(Q_E)=g_E(Q_0)$, and let z be its reference point. Because
$g(Q_E)=g_E(Q_0)$, and let z be its reference point. Because  $B \left( z, a \theta^{g_E(Q_0)} \right) \subset Q_E,$ we have
$B \left( z, a \theta^{g_E(Q_0)} \right) \subset Q_E,$ we have ![]() $d(z,E) \gt a \theta^{g_E(Q_0)},$ and therefore, continuing from (17) we derive
$d(z,E) \gt a \theta^{g_E(Q_0)},$ and therefore, continuing from (17) we derive
 \begin{align}
\mu \left( Q_0 \setminus \mathcal{A}_M \right) & \leq \left( \frac{2A}{\theta} \theta^{M} \theta^{g_E(Q_0)} \right)^{\alpha} \mu (Q_0) [w]_{A_1} \operatorname{dist}(z,E)^{-\alpha}\nonumber \\
& \leq \left( \frac{2A}{\theta} \theta^{M} \theta^{g_E(Q_0)} \right)^{\alpha} \mu (Q_0) [w]_{A_1} \left( a \theta^{g_E(Q_0)} \right)^{-\alpha}\nonumber \\ & = \left( \frac{2A}{a \theta} \theta^{M} \right)^{\alpha} [w]_{A_1} \mu (Q_0).
\end{align}
\begin{align}
\mu \left( Q_0 \setminus \mathcal{A}_M \right) & \leq \left( \frac{2A}{\theta} \theta^{M} \theta^{g_E(Q_0)} \right)^{\alpha} \mu (Q_0) [w]_{A_1} \operatorname{dist}(z,E)^{-\alpha}\nonumber \\
& \leq \left( \frac{2A}{\theta} \theta^{M} \theta^{g_E(Q_0)} \right)^{\alpha} \mu (Q_0) [w]_{A_1} \left( a \theta^{g_E(Q_0)} \right)^{-\alpha}\nonumber \\ & = \left( \frac{2A}{a \theta} \theta^{M} \right)^{\alpha} [w]_{A_1} \mu (Q_0).
\end{align} For every ![]() $c\in (0,1),$ we can find
$c\in (0,1),$ we can find ![]() $M=M(\theta, [w]_{A_1}, \alpha,c) \in {\mathbb N}$ large enough so that
$M=M(\theta, [w]_{A_1}, \alpha,c) \in {\mathbb N}$ large enough so that  $\left( \frac{2A}{a \theta} \theta^{M} \right)^{\alpha} [w]_{A_1} \lt 1-c,$ obtaining
$\left( \frac{2A}{a \theta} \theta^{M} \right)^{\alpha} [w]_{A_1} \lt 1-c,$ obtaining
The family of cubes  $\widehat{\mathcal{F}}_M(Q_0)=\lbrace Q \in \mathcal{D}(Q_0) \, : \, Q \cap E = \emptyset \, \text{and} \, g(Q) \leq M+ g_E(Q_0) \rbrace$ is not necessarily disjoint, but we can make it disjoint by taking a maximal subcollection of
$\widehat{\mathcal{F}}_M(Q_0)=\lbrace Q \in \mathcal{D}(Q_0) \, : \, Q \cap E = \emptyset \, \text{and} \, g(Q) \leq M+ g_E(Q_0) \rbrace$ is not necessarily disjoint, but we can make it disjoint by taking a maximal subcollection of  $\widehat{\mathcal{F}}_M(Q_0).$ Indeed, given
$\widehat{\mathcal{F}}_M(Q_0).$ Indeed, given  $Q\in \widehat{\mathcal{F}}_M(Q_0),$ let
$Q\in \widehat{\mathcal{F}}_M(Q_0),$ let  $Q^\sharp \in \widehat{\mathcal{F}}_M(Q_0)$ be a cube with
$Q^\sharp \in \widehat{\mathcal{F}}_M(Q_0)$ be a cube with ![]() $Q \subset Q^\sharp$ such that
$Q \subset Q^\sharp$ such that
 \begin{equation*}
g(Q^\sharp)=\min\lbrace g(Q') \, : \, Q \subset Q' \text{and} Q'\in \widehat{\mathcal{F}}_M(Q_0) \rbrace.
\end{equation*}
\begin{equation*}
g(Q^\sharp)=\min\lbrace g(Q') \, : \, Q \subset Q' \text{and} Q'\in \widehat{\mathcal{F}}_M(Q_0) \rbrace.
\end{equation*} Notice that ![]() $Q \in \mathcal{D}(Q^\sharp)$ for every
$Q \in \mathcal{D}(Q^\sharp)$ for every  $Q\in \widehat{\mathcal{F}}_M(Q_0).$ If we define
$Q\in \widehat{\mathcal{F}}_M(Q_0).$ If we define  $\mathcal{F}_M(Q_0)=\lbrace Q^\sharp \, : \, Q \in \widehat{\mathcal{F}}_M(Q_0) \rbrace,$ for any two cubes
$\mathcal{F}_M(Q_0)=\lbrace Q^\sharp \, : \, Q \in \widehat{\mathcal{F}}_M(Q_0) \rbrace,$ for any two cubes ![]() $P, P' \in \mathcal{F}_M(Q_0)$ with non-empty intersection, one has that P and Pʹ are the same cube. Indeed, if
$P, P' \in \mathcal{F}_M(Q_0)$ with non-empty intersection, one has that P and Pʹ are the same cube. Indeed, if ![]() $P \subsetneq P',$ then
$P \subsetneq P',$ then ![]() $g(P') \lt g(P)$ by virtue of Lemma 2.4. But
$g(P') \lt g(P)$ by virtue of Lemma 2.4. But ![]() $P=Q^\sharp$ for some
$P=Q^\sharp$ for some  $Q \in \widehat{\mathcal{F}}_M$ and since Pʹ also contains Q, the minimality of g(P) would lead us to
$Q \in \widehat{\mathcal{F}}_M$ and since Pʹ also contains Q, the minimality of g(P) would lead us to ![]() $g(P') \geq g(P),$ a contradiction. Similarly, one can prove that
$g(P') \geq g(P),$ a contradiction. Similarly, one can prove that ![]() $P' \subsetneq P$ is impossible, and the properties of the dyadic cubes tell us that
$P' \subsetneq P$ is impossible, and the properties of the dyadic cubes tell us that ![]() $P=P'$ as sets. Moreover, by the minimality of their generations, one has
$P=P'$ as sets. Moreover, by the minimality of their generations, one has ![]() $g(P)=g(P').$ According to Lemma 2.4, P and Pʹ define the exact same cube. Therefore, the cubes of the family
$g(P)=g(P').$ According to Lemma 2.4, P and Pʹ define the exact same cube. Therefore, the cubes of the family ![]() $\mathcal{F}_M(Q_0)$ are mutually disjoint.
$\mathcal{F}_M(Q_0)$ are mutually disjoint.
Clearly  $\mathcal{A}_M= \bigcup \widehat{\mathcal{F}}_M(Q_0)=\bigcup \mathcal{F}_M(Q_0).$ Also, every cube
$\mathcal{A}_M= \bigcup \widehat{\mathcal{F}}_M(Q_0)=\bigcup \mathcal{F}_M(Q_0).$ Also, every cube ![]() $Q \in \mathcal{F}_M $ contains the ball
$Q \in \mathcal{F}_M $ contains the ball ![]() $B_Q:=B\left( z_Q, r \right),$ with
$B_Q:=B\left( z_Q, r \right),$ with ![]() $r=a \theta^{M+g_E(Q_0)}$ and zQ being the reference point of
$r=a \theta^{M+g_E(Q_0)}$ and zQ being the reference point of ![]() $Q.$ The balls of the family
$Q.$ The balls of the family ![]() $\lbrace B_Q \rbrace_{Q \in \mathcal{F}_M(Q_0)}$ are disjoint and contained in Q 0. Because Q 0 is in turn contained in a ball B 0 of radius
$\lbrace B_Q \rbrace_{Q \in \mathcal{F}_M(Q_0)}$ are disjoint and contained in Q 0. Because Q 0 is in turn contained in a ball B 0 of radius ![]() $R_0= A \theta^{g(Q_0)},$ then
$R_0= A \theta^{g(Q_0)},$ then ![]() $B_0 \subset B(z_Q, 2R_0)$ for each
$B_0 \subset B(z_Q, 2R_0)$ for each ![]() $Q \in \mathcal{F}_M(Q_0)$. The doubling condition (1) for µ gives the estimates
$Q \in \mathcal{F}_M(Q_0)$. The doubling condition (1) for µ gives the estimates ![]() $\mu(B_0) \leq C(C_\mu, R_0/r) \mu (B_Q)$ for all
$\mu(B_0) \leq C(C_\mu, R_0/r) \mu (B_Q)$ for all ![]() $Q \in \mathcal{F}_M(Q_0).$ Thus
$Q \in \mathcal{F}_M(Q_0).$ Thus ![]() $ \mathcal{F}_M(Q_0)$ must be a finite collection. This concludes the proof of the dyadic weak porosity of
$ \mathcal{F}_M(Q_0)$ must be a finite collection. This concludes the proof of the dyadic weak porosity of ![]() $E,$ since
$E,$ since
 \begin{equation*}
\sum_{Q\in \mathcal{F}_M(Q_0)} \mu(Q) =\mu\left( \bigcup\mathcal{F}_M(Q_0) \right)= \mu(\mathcal{A}_M) \geq c \mu(Q_0).
\end{equation*}
\begin{equation*}
\sum_{Q\in \mathcal{F}_M(Q_0)} \mu(Q) =\mu\left( \bigcup\mathcal{F}_M(Q_0) \right)= \mu(\mathcal{A}_M) \geq c \mu(Q_0).
\end{equation*} (ii) Let ![]() $Q_0, Q_0^*\in \mathcal{D}$ be cubes in the same grid with
$Q_0, Q_0^*\in \mathcal{D}$ be cubes in the same grid with ![]() $Q_0 \in \mathcal{D}(Q_0^*)$ with
$Q_0 \in \mathcal{D}(Q_0^*)$ with ![]() $g(Q_0^*)=g(Q_0)-1.$ In the case where
$g(Q_0^*)=g(Q_0)-1.$ In the case where ![]() $Q_0 \cap E = \emptyset$, then
$Q_0 \cap E = \emptyset$, then ![]() $g_E(Q_0)=g(Q_0)$ and, because we always have the estimate
$g_E(Q_0)=g(Q_0)$ and, because we always have the estimate ![]() $g(Q_0^*) \leq g_E(Q_0^*),$ we can write
$g(Q_0^*) \leq g_E(Q_0^*),$ we can write
Suppose now that ![]() $Q_0 \cap E \neq \emptyset$. If
$Q_0 \cap E \neq \emptyset$. If ![]() $x\in Q_0$, there exists
$x\in Q_0$, there exists ![]() $Q \in \mathcal{D}(Q_0)$ with
$Q \in \mathcal{D}(Q_0)$ with ![]() $x\in Q $ and
$x\in Q $ and ![]() $g(Q)=g_E(Q_0).$ Also, by the assumption, there is
$g(Q)=g_E(Q_0).$ Also, by the assumption, there is ![]() $Q^* \in\mathcal{D}(Q_0)$ so that
$Q^* \in\mathcal{D}(Q_0)$ so that ![]() $Q \in \mathcal{D}(Q^*)$ and
$Q \in \mathcal{D}(Q^*)$ and ![]() $g(Q^*)=g(Q)-1.$ Due to the minimality of
$g(Q^*)=g(Q)-1.$ Due to the minimality of ![]() $g_E(Q_0),$ the cube
$g_E(Q_0),$ the cube ![]() $Q^*$ must intersects
$Q^*$ must intersects ![]() $E,$ and so
$E,$ and so
 \begin{equation*}
d(x,E) \leq \operatorname{diam}(Q^*) \leq \operatorname{diam} \left( B(z^*,A \theta^{g(Q^*)}) \right) \leq 2A \theta^{g(Q)-1} = \frac{2A}{\theta} \theta^{g_E(Q_0)};
\end{equation*}
\begin{equation*}
d(x,E) \leq \operatorname{diam}(Q^*) \leq \operatorname{diam} \left( B(z^*,A \theta^{g(Q^*)}) \right) \leq 2A \theta^{g(Q)-1} = \frac{2A}{\theta} \theta^{g_E(Q_0)};
\end{equation*} where ![]() $z^*$ denotes the reference point of
$z^*$ denotes the reference point of ![]() $Q^*.$ This argument permits to write
$Q^*.$ This argument permits to write
 \begin{align}
\mu(Q_0) \left( \frac{2A}{\theta} \theta^{g_E(Q_0)} \right)^{-\alpha} & \leq \int_{Q_0} \operatorname{dist}(x,E)^{-\alpha}\, d\mu(x)\leq \int_{Q_0^*} \operatorname{dist}(x,E)^{-\alpha}\, d\mu(x) \nonumber \\
& \leq \mu(Q_0^*) [w]_{A_1}\ \mathrm{ess\, inf}_{Q_0^*} \operatorname{dist}(\cdot, E)^{-\alpha}\nonumber\\ & \leq \mu (Q_0^*) [w]_{A_1} \left( a \theta^{g_E(Q_0^*)} \right)^{-\alpha};
\end{align}
\begin{align}
\mu(Q_0) \left( \frac{2A}{\theta} \theta^{g_E(Q_0)} \right)^{-\alpha} & \leq \int_{Q_0} \operatorname{dist}(x,E)^{-\alpha}\, d\mu(x)\leq \int_{Q_0^*} \operatorname{dist}(x,E)^{-\alpha}\, d\mu(x) \nonumber \\
& \leq \mu(Q_0^*) [w]_{A_1}\ \mathrm{ess\, inf}_{Q_0^*} \operatorname{dist}(\cdot, E)^{-\alpha}\nonumber\\ & \leq \mu (Q_0^*) [w]_{A_1} \left( a \theta^{g_E(Q_0^*)} \right)^{-\alpha};
\end{align} where we argued as in (17)-(18) to obtain the last inequality. Also, denoting by z 0 and ![]() $z_0^*$ the reference points of Q 0 and
$z_0^*$ the reference points of Q 0 and ![]() $Q_0^*$, we have the inclusions
$Q_0^*$, we have the inclusions
 \begin{equation*}
B(z_0, a \theta^{g(Q_0)} ) \subset Q_0 \subset Q_0^* \subset B(z_0^*, A \theta^{g(Q_0^*)} )\subset B(z_0, 3 A \theta^{g(Q_0^*)} ).
\end{equation*}
\begin{equation*}
B(z_0, a \theta^{g(Q_0)} ) \subset Q_0 \subset Q_0^* \subset B(z_0^*, A \theta^{g(Q_0^*)} )\subset B(z_0, 3 A \theta^{g(Q_0^*)} ).
\end{equation*} The doubling condition on the measure gives  $\mu(Q_0^*) \leq C(\theta,C_\mu) \mu(\widehat{Q}_0).$ Using this estimate in (19) and reorganizing the terms we conclude
$\mu(Q_0^*) \leq C(\theta,C_\mu) \mu(\widehat{Q}_0).$ Using this estimate in (19) and reorganizing the terms we conclude
 \begin{equation}
g_E(\widehat{Q}_0) \leq m+ g_E(Q_0) ,
\end{equation}
\begin{equation}
g_E(\widehat{Q}_0) \leq m+ g_E(Q_0) ,
\end{equation} for some ![]() $m=m( \alpha,[w]_{A_1},\theta,C_\mu) \in {\mathbb N}.$
$m=m( \alpha,[w]_{A_1},\theta,C_\mu) \in {\mathbb N}.$
As a consequence of the previous lemma, we obtain the implication (B)![]() $\implies$(A) of Theorem 1.1.
$\implies$(A) of Theorem 1.1.
Lemma 4.2. If ![]() $E \subset X$ is a subset and
$E \subset X$ is a subset and ![]() $w= \operatorname{dist}( \cdot, E)^{-\alpha} \in A_1(X)$ with
$w= \operatorname{dist}( \cdot, E)^{-\alpha} \in A_1(X)$ with ![]() $\alpha \gt 0,$ then
$\alpha \gt 0,$ then ![]() $E$ is weakly porous and
$E$ is weakly porous and ![]() $h_E$ is doubling.
$h_E$ is doubling.
5. E-free dyadic decompositions and a key discrete inequality
In this section, we begin with the proof of the implication (A)![]() $\implies$(B) in Theorem 1.1. Suppose that E is weakly porous and that hE is doubling. By the subsequent comments to Definitions 3.1 and 3.4, the same properties hold for
$\implies$(B) in Theorem 1.1. Suppose that E is weakly porous and that hE is doubling. By the subsequent comments to Definitions 3.1 and 3.4, the same properties hold for ![]() $\overline{E}$ as well. Since our goal is to prove that
$\overline{E}$ as well. Since our goal is to prove that ![]() $\operatorname{dist}(\cdot, E)^{-\alpha}$ for some
$\operatorname{dist}(\cdot, E)^{-\alpha}$ for some ![]() $\alpha \gt 0,$ and
$\alpha \gt 0,$ and ![]() $\operatorname{dist}(\cdot, E) = \operatorname{dist}(\cdot, \overline{E})$, we may and do assume that E is closed throughout the Sections 5 and 6.
$\operatorname{dist}(\cdot, E) = \operatorname{dist}(\cdot, \overline{E})$, we may and do assume that E is closed throughout the Sections 5 and 6.
By Lemma 3.8, E is dyadic weakly porous, and gE is doubling (Definitions 3.3 and 3.4).
Let ![]() $M, m \in {\mathbb N}$,
$M, m \in {\mathbb N}$, ![]() $c\in (0,1)$ be the constants from Definitions 3.3 and 3.4 for the set
$c\in (0,1)$ be the constants from Definitions 3.3 and 3.4 for the set ![]() $E.$ Because E is (dyadic) weakly porous, for every
$E.$ Because E is (dyadic) weakly porous, for every ![]() $P \in \mathcal{D}$ there exists a cube
$P \in \mathcal{D}$ there exists a cube ![]() $Q\in \mathcal{D}(P)$ with
$Q\in \mathcal{D}(P)$ with ![]() $Q \cap E= \emptyset.$ Thus, the number
$Q \cap E= \emptyset.$ Thus, the number ![]() $g_E(P)$ is well-defined; see formula (9).
$g_E(P)$ is well-defined; see formula (9).
Now, given ![]() $P \in \mathcal{D},$ we define the families of cubes
$P \in \mathcal{D},$ we define the families of cubes
 \begin{equation*}
\widehat{\mathcal{F}}_M(P)=\lbrace Q \in \mathcal{D}(P) \: : \: Q \cap E = \emptyset, \: g(Q) \leq M +g_E(P) \rbrace;
\end{equation*}
\begin{equation*}
\widehat{\mathcal{F}}_M(P)=\lbrace Q \in \mathcal{D}(P) \: : \: Q \cap E = \emptyset, \: g(Q) \leq M +g_E(P) \rbrace;
\end{equation*} \begin{equation*}
\widehat{\mathcal{G}}_M(P)=\lbrace Q \in \mathcal{D}(P) \: : \: Q \subset P \setminus \bigcup_{R \in \widehat{\mathcal{F}}_M(P)} R \rbrace.
\end{equation*}
\begin{equation*}
\widehat{\mathcal{G}}_M(P)=\lbrace Q \in \mathcal{D}(P) \: : \: Q \subset P \setminus \bigcup_{R \in \widehat{\mathcal{F}}_M(P)} R \rbrace.
\end{equation*} Let us construct maximal subfamilies of  $\widehat{\mathcal{F}}_M(P)$ and
$\widehat{\mathcal{F}}_M(P)$ and  $\widehat{\mathcal{G}}_M(P).$ Given
$\widehat{\mathcal{G}}_M(P).$ Given  $Q\in \widehat{\mathcal{F}}_M(P),$ let
$Q\in \widehat{\mathcal{F}}_M(P),$ let  $Q^\sharp \in \widehat{\mathcal{F}}_M(P)$ and
$Q^\sharp \in \widehat{\mathcal{F}}_M(P)$ and  $Q^\flat \in \widehat{\mathcal{G}}_M(P)$ be cubes with
$Q^\flat \in \widehat{\mathcal{G}}_M(P)$ be cubes with ![]() $Q \subset Q^\sharp, Q^\flat$ such that
$Q \subset Q^\sharp, Q^\flat$ such that
 \begin{equation*}
g(Q^\sharp)=\min\lbrace g(Q') \, : \, Q \subset Q' \,\text{and}\, Q'\in \widehat{\mathcal{F}}_M(P) \rbrace,
\end{equation*}
\begin{equation*}
g(Q^\sharp)=\min\lbrace g(Q') \, : \, Q \subset Q' \,\text{and}\, Q'\in \widehat{\mathcal{F}}_M(P) \rbrace,
\end{equation*} \begin{equation*}
g(Q^\flat)=\min\lbrace g(Q') \, : \, Q \subset Q' \,\text{and}\, Q'\in \widehat{\mathcal{G}}_M(P) \rbrace.
\end{equation*}
\begin{equation*}
g(Q^\flat)=\min\lbrace g(Q') \, : \, Q \subset Q' \,\text{and}\, Q'\in \widehat{\mathcal{G}}_M(P) \rbrace.
\end{equation*}We define
 \begin{equation*}
\mathcal{F}_M(P):= \lbrace Q^\sharp \, : \, Q \in \widehat{\mathcal{F}}_M(P) \rbrace, \quad \mathcal{G}_M(P)=\lbrace Q^\flat \, : \, Q \in \widehat{\mathcal{G}}_M(P) \rbrace.
\end{equation*}
\begin{equation*}
\mathcal{F}_M(P):= \lbrace Q^\sharp \, : \, Q \in \widehat{\mathcal{F}}_M(P) \rbrace, \quad \mathcal{G}_M(P)=\lbrace Q^\flat \, : \, Q \in \widehat{\mathcal{G}}_M(P) \rbrace.
\end{equation*} It is important to notice that, by the minimality of their generations, any two cubes ![]() $R, R'$ of
$R, R'$ of ![]() $\mathcal{F}_M(P)$ (or
$\mathcal{F}_M(P)$ (or ![]() $\mathcal{G}_M(P)$) defining the same set of points must have the same generation. We remind that this implies that R and Rʹ have exactly the same label within the system
$\mathcal{G}_M(P)$) defining the same set of points must have the same generation. We remind that this implies that R and Rʹ have exactly the same label within the system ![]() $\mathcal{D}_t$ to which P belongs, according to Lemma 2.4. This guarantees that the families
$\mathcal{D}_t$ to which P belongs, according to Lemma 2.4. This guarantees that the families ![]() $\mathcal{F}_M(P)$ and
$\mathcal{F}_M(P)$ and ![]() $\mathcal{G}_M(P)$ consist of non-duplicate cubes.
$\mathcal{G}_M(P)$ consist of non-duplicate cubes.
Let us make several remarks and clarifications concerning the families ![]() $\mathcal{F}_M$ and
$\mathcal{F}_M$ and ![]() $\mathcal{G}_M.$
$\mathcal{G}_M.$
Remark 5.1. If ![]() $P \in \mathcal{D},$ the families
$P \in \mathcal{D},$ the families ![]() $\mathcal{F}_M(P)$ and
$\mathcal{F}_M(P)$ and ![]() $\mathcal{G}_M(P)$ satisfy the following.
$\mathcal{G}_M(P)$ satisfy the following.
(a)
 $\mathcal{F}_M(P) \subset \widehat{\mathcal{F}}_M(P)$,
$\mathcal{F}_M(P) \subset \widehat{\mathcal{F}}_M(P)$,  $\mathcal{G}_M(P) \subset \widehat{\mathcal{G}}_M(P)$, and
$\mathcal{G}_M(P) \subset \widehat{\mathcal{G}}_M(P)$, and  $\bigcup \mathcal{F}_M(P) = \bigcup \widehat{\mathcal{F}}_M(P)$,
$\bigcup \mathcal{F}_M(P) = \bigcup \widehat{\mathcal{F}}_M(P)$,  $\bigcup \mathcal{G}_M(P) = \bigcup \widehat{\mathcal{G}}_M(P)$. Moreover, P is the disjoint union of
$\bigcup \mathcal{G}_M(P) = \bigcup \widehat{\mathcal{G}}_M(P)$. Moreover, P is the disjoint union of  $\bigcup \mathcal{F}_M(P) $ and
$\bigcup \mathcal{F}_M(P) $ and  $\bigcup \mathcal{G}_M(P) $.
$\bigcup \mathcal{G}_M(P) $.(b)
 $\mathcal{F}_M(P) \neq \emptyset$ always, and
$\mathcal{F}_M(P) \neq \emptyset$ always, and  $\mathcal{F}_M(P)=\lbrace P \rbrace$ (or equivalently
$\mathcal{F}_M(P)=\lbrace P \rbrace$ (or equivalently  $P\notin \mathcal{F}_M(P)$) if and only if
$P\notin \mathcal{F}_M(P)$) if and only if  $P \cap E = \emptyset.$ Also,
$P \cap E = \emptyset.$ Also,  $\mathcal{G}_M(P) \neq \emptyset $ if and only if
$\mathcal{G}_M(P) \neq \emptyset $ if and only if  $P \cap E \neq \emptyset.$
$P \cap E \neq \emptyset.$(c) If
 $R, R' \in \mathcal{F}_M(P)$ (or
$R, R' \in \mathcal{F}_M(P)$ (or  $R,R'\in \mathcal{G}_M(P)$), then either
$R,R'\in \mathcal{G}_M(P)$), then either  $R \cap R' = \emptyset$; or else R and Rʹ are the same cube, meaning that they define the same set of points and
$R \cap R' = \emptyset$; or else R and Rʹ are the same cube, meaning that they define the same set of points and  $g(R)=g(R').$
$g(R)=g(R').$(d) If
 $R \in \mathcal{G}_M(P),$ and
$R \in \mathcal{G}_M(P),$ and  $R^* \in \mathcal{D}(P)$ is so that
$R^* \in \mathcal{D}(P)$ is so that  $R \subset R^*$ and
$R \subset R^*$ and  $g(R^*)=g(R)-1,$ then
$g(R^*)=g(R)-1,$ then  $R^*$ intersects some
$R^*$ intersects some  $Q \in \mathcal{F}_M(P).$
$Q \in \mathcal{F}_M(P).$(e) If
 $R \in \mathcal{F}_M(P),$ then
$R \in \mathcal{F}_M(P),$ then  $R \cap E = \emptyset.$ And if
$R \cap E = \emptyset.$ And if  $R \in \mathcal{G}_M(P),$ then
$R \in \mathcal{G}_M(P),$ then  $g(R) \leq M + g_E(P)$ and
$g(R) \leq M + g_E(P)$ and  $R \cap E \neq \emptyset.$
$R \cap E \neq \emptyset.$(f)
 $\mu\left( \bigcup_{Q \in \mathcal{F}_M(P)} Q \right)= \sum_{Q \in \mathcal{F}_M(P)} \mu(Q) \geq c \mu(P).$
$\mu\left( \bigcup_{Q \in \mathcal{F}_M(P)} Q \right)= \sum_{Q \in \mathcal{F}_M(P)} \mu(Q) \geq c \mu(P).$
Proof. The first part of (a) is immediate from the definitions of ![]() $Q^\sharp$ and
$Q^\sharp$ and ![]() $Q^\flat.$ For the second part, observe that for any two cubes
$Q^\flat.$ For the second part, observe that for any two cubes ![]() $R\in \mathcal{F}_M(P)$ and
$R\in \mathcal{F}_M(P)$ and ![]() $R' \in \mathcal{G}_M(P)$. Then also
$R' \in \mathcal{G}_M(P)$. Then also  $R \in \widehat{\mathcal{F}}_M(P)$ and
$R \in \widehat{\mathcal{F}}_M(P)$ and  $R' \in \widehat{\mathcal{G}}_M(P)$ and the definition of
$R' \in \widehat{\mathcal{G}}_M(P)$ and the definition of  $\widehat{\mathcal{G}}_M(P)$ implies
$\widehat{\mathcal{G}}_M(P)$ implies  $R' \subset P \setminus \bigcup \widehat{\mathcal{F}}_M(P) \subset P \setminus R.$
$R' \subset P \setminus \bigcup \widehat{\mathcal{F}}_M(P) \subset P \setminus R.$
The statement (b): ![]() $\mathcal{F}_M(P) \neq \emptyset$ for every
$\mathcal{F}_M(P) \neq \emptyset$ for every ![]() $P \in \mathcal{D}$ thanks to the (dyadic) weak porosity of
$P \in \mathcal{D}$ thanks to the (dyadic) weak porosity of ![]() $E.$ Now, if
$E.$ Now, if ![]() $P \cap E \neq \emptyset,$ then
$P \cap E \neq \emptyset,$ then  $P \notin \widehat{\mathcal{F}}_M(P),$ and therefore
$P \notin \widehat{\mathcal{F}}_M(P),$ and therefore ![]() $\mathcal{F}_M(P) \neq \lbrace P \rbrace.$ Also,
$\mathcal{F}_M(P) \neq \lbrace P \rbrace.$ Also,  $\bigcup_{R\in \widehat{\mathcal{F}}(P)} R \subsetneq P$ because
$\bigcup_{R\in \widehat{\mathcal{F}}(P)} R \subsetneq P$ because ![]() $P \cap E \neq \emptyset,$ and since all the cubes of
$P \cap E \neq \emptyset,$ and since all the cubes of  $\widehat{\mathcal{F}}_M(P)$ have generation at least
$\widehat{\mathcal{F}}_M(P)$ have generation at least ![]() $M+g_E(P),$ there must exist
$M+g_E(P),$ there must exist ![]() $Q \in \mathcal{D}(P)$ with
$Q \in \mathcal{D}(P)$ with ![]() $Q \subset P \setminus E.$ Thus
$Q \subset P \setminus E.$ Thus  $Q \in\bigcup_{R\in \widehat{\mathcal{F}}(P)} R ,$ and therefore
$Q \in\bigcup_{R\in \widehat{\mathcal{F}}(P)} R ,$ and therefore  $Q \in \widehat{\mathcal{G}}_M(P),$ and
$Q \in \widehat{\mathcal{G}}_M(P),$ and ![]() $ \mathcal{G}_M(P) \neq \emptyset .$ And if
$ \mathcal{G}_M(P) \neq \emptyset .$ And if ![]() $P \cap E =\emptyset,$ then, by the minimality of the generations of the cubes in
$P \cap E =\emptyset,$ then, by the minimality of the generations of the cubes in ![]() $\mathcal{F}_M(P),$ we must have
$\mathcal{F}_M(P),$ we must have ![]() $\mathcal{F}_M(P) =\lbrace P \rbrace$ and so
$\mathcal{F}_M(P) =\lbrace P \rbrace$ and so ![]() $\mathcal{G}_M(P) = \emptyset.$
$\mathcal{G}_M(P) = \emptyset.$
For property (c), suppose that ![]() $R,R'\in \mathcal{F}_M(P)$ with
$R,R'\in \mathcal{F}_M(P)$ with ![]() $R \cap R' \neq \emptyset.$ Because R and Rʹ are in the same grid
$R \cap R' \neq \emptyset.$ Because R and Rʹ are in the same grid ![]() $\mathcal{D}_t,$ we have
$\mathcal{D}_t,$ we have ![]() $R \subset R'$ or
$R \subset R'$ or ![]() $R' \subset R.$ Assume for example
$R' \subset R.$ Assume for example ![]() $R\subset R'.$ Now write
$R\subset R'.$ Now write ![]() $R=Q^\sharp$ and
$R=Q^\sharp$ and ![]() $R'=(Q')^\sharp$, with
$R'=(Q')^\sharp$, with  $Q, Q' \in \widehat{\mathcal{F}}_M(P)$. Because
$Q, Q' \in \widehat{\mathcal{F}}_M(P)$. Because ![]() $Q \subset R \subset R',$ by the definition of
$Q \subset R \subset R',$ by the definition of ![]() $Q^\sharp,$ we must have
$Q^\sharp,$ we must have ![]() $g(R) \leq g(R').$ This implies
$g(R) \leq g(R').$ This implies ![]() $R=R'$ as otherwise we would have
$R=R'$ as otherwise we would have ![]() $R \subsetneq R'$ and so, by Lemma 2.4,
$R \subsetneq R'$ and so, by Lemma 2.4, ![]() $g(R) \gt g(R') ,$ a contradiction. So,
$g(R) \gt g(R') ,$ a contradiction. So, ![]() $R=R',$ and because
$R=R',$ and because ![]() $Q' \subset R' =R,$ the definition of
$Q' \subset R' =R,$ the definition of ![]() $(Q')^\sharp$ gives the reverse inequality
$(Q')^\sharp$ gives the reverse inequality ![]() $g(R') \leq g(R)$. Lemma 2.4 implies that R and Rʹ are the same cube. The proof for cubes
$g(R') \leq g(R)$. Lemma 2.4 implies that R and Rʹ are the same cube. The proof for cubes ![]() $R,R'\in \mathcal{G}_M(P)$ is identical.
$R,R'\in \mathcal{G}_M(P)$ is identical.
To prove (d), observe that if  $R^* \subset P \setminus \bigcup_{Q\in \mathcal{F}_M(P)} Q,$ then
$R^* \subset P \setminus \bigcup_{Q\in \mathcal{F}_M(P)} Q,$ then  $R^* \in \widehat{\mathcal{G}}_M(P)$, contradicting the minimality of g(R).
$R^* \in \widehat{\mathcal{G}}_M(P)$, contradicting the minimality of g(R).
Let us prove (e). If ![]() $R \in \mathcal{F}_M(P),$ then
$R \in \mathcal{F}_M(P),$ then  $R \in \widehat{\mathcal{F}}_M(P)$ as well, and so
$R \in \widehat{\mathcal{F}}_M(P)$ as well, and so ![]() $R \cap E = \emptyset.$ Now assume that
$R \cap E = \emptyset.$ Now assume that ![]() $R \in \mathcal{G}_M(P).$ By (b) this implies
$R \in \mathcal{G}_M(P).$ By (b) this implies ![]() $P \cap E \neq \emptyset,$ and so
$P \cap E \neq \emptyset,$ and so ![]() $R \subset P \setminus \bigcup \mathcal{F}_M(P) \subsetneq P,$ which in turn yields
$R \subset P \setminus \bigcup \mathcal{F}_M(P) \subsetneq P,$ which in turn yields ![]() $g(R) \gt g(P)$ thanks to Lemma 2.4. Thus, we can find
$g(R) \gt g(P)$ thanks to Lemma 2.4. Thus, we can find ![]() $R^*\in \mathcal{D}(P)$ with
$R^*\in \mathcal{D}(P)$ with ![]() $R \subset R^*$ and
$R \subset R^*$ and ![]() $g(R^*)=g(R)-1.$ By property (d),
$g(R^*)=g(R)-1.$ By property (d), ![]() $R^*$ intersects some cube
$R^*$ intersects some cube ![]() $Q\in \mathcal{F}_M(P),$ and hence either
$Q\in \mathcal{F}_M(P),$ and hence either ![]() $R^* \subseteq Q$ or
$R^* \subseteq Q$ or ![]() $Q \subsetneq R^*.$ Since
$Q \subsetneq R^*.$ Since ![]() $R \cap Q = \emptyset$ and
$R \cap Q = \emptyset$ and ![]() $R \subset R^*,$ the first case is impossible. Therefore, we must have
$R \subset R^*,$ the first case is impossible. Therefore, we must have ![]() $Q \subsetneq R^*,$ yielding
$Q \subsetneq R^*,$ yielding
Thus ![]() $g(R) \leq M+ g_E(P).$ Now, because
$g(R) \leq M+ g_E(P).$ Now, because ![]() $R \subset P \setminus \bigcup \mathcal{F}_M(P) ,$ the cube
$R \subset P \setminus \bigcup \mathcal{F}_M(P) ,$ the cube ![]() $R \in \mathcal{D}(P)$ is not in
$R \in \mathcal{D}(P)$ is not in  $\widehat{\mathcal{F}}_M(P),$ and because g(R) satisfies the estimate
$\widehat{\mathcal{F}}_M(P),$ and because g(R) satisfies the estimate ![]() $g(R) \leq M+ g_E(P),$ we must necessarily have
$g(R) \leq M+ g_E(P),$ we must necessarily have ![]() $R \cap E \neq \emptyset.$
$R \cap E \neq \emptyset.$
Finally, let us show (f). By the dyadic weak porosity of E, there are pairwise disjoint cubes ![]() $Q_1, \ldots, Q_N \in \mathcal{D}(P)$ belonging to
$Q_1, \ldots, Q_N \in \mathcal{D}(P)$ belonging to  $\widehat{\mathcal{F}}_M(P)$ and satisfying
$\widehat{\mathcal{F}}_M(P)$ and satisfying  $\sum_{j=1}^N \mu(Q_j) \geq c \mu(P).$ Each of these cubes Qj is contained in some cube of the disjointed family
$\sum_{j=1}^N \mu(Q_j) \geq c \mu(P).$ Each of these cubes Qj is contained in some cube of the disjointed family ![]() $\mathcal{F}_M(P),$ and we can write
$\mathcal{F}_M(P),$ and we can write
 \begin{equation*}
\sum_{Q \in \mathcal{F}_M(P)} \mu(Q) =\mu ( \bigcup_{Q\in \mathcal{F}_M(P)} Q ) \geq \mu \left( \bigcup_{j=1}^N Q_j \right) = \sum_{j=1}^N \mu(Q_j) \geq c \mu(P).
\end{equation*}
\begin{equation*}
\sum_{Q \in \mathcal{F}_M(P)} \mu(Q) =\mu ( \bigcup_{Q\in \mathcal{F}_M(P)} Q ) \geq \mu \left( \bigcup_{j=1}^N Q_j \right) = \sum_{j=1}^N \mu(Q_j) \geq c \mu(P).
\end{equation*} We continue defining new families of cubes. Fix ![]() $P \in \mathcal{D},$ and define
$P \in \mathcal{D},$ and define ![]() $\mathcal{G}_M^0(P)=\{P \}$,
$\mathcal{G}_M^0(P)=\{P \}$, ![]() $\mathcal{F}_M^1(P)=\mathcal{F}_M(P)$,
$\mathcal{F}_M^1(P)=\mathcal{F}_M(P)$, ![]() $\mathcal{G}_M^1(P)=\mathcal{G}_M(P)$, and in general, for
$\mathcal{G}_M^1(P)=\mathcal{G}_M(P)$, and in general, for ![]() $k=2,3,4,\ldots$, we define
$k=2,3,4,\ldots$, we define
 \begin{equation}
\mathcal{F}_M^k(P)=\bigcup_{R\in\mathcal{G}_M^{k-1}(P)} \mathcal{F}_M(R),\,\qquad \mathcal{G}_M^k(P)=\bigcup_{R\in\mathcal{G}_M^{k-1}(P)}\mathcal{G}_M(R).
\end{equation}
\begin{equation}
\mathcal{F}_M^k(P)=\bigcup_{R\in\mathcal{G}_M^{k-1}(P)} \mathcal{F}_M(R),\,\qquad \mathcal{G}_M^k(P)=\bigcup_{R\in\mathcal{G}_M^{k-1}(P)}\mathcal{G}_M(R).
\end{equation} We now prove that the cubes of the families ![]() $\lbrace \mathcal{F}_M^k(P) \rbrace_k$ cover the complement of E in
$\lbrace \mathcal{F}_M^k(P) \rbrace_k$ cover the complement of E in ![]() $P.$
$P.$
Lemma 5.2. For every ![]() $P \in \mathcal{D},$ we have
$P \in \mathcal{D},$ we have  $P\setminus E= \bigcup_{k=1}^\infty \bigcup_{Q \in \mathcal{F}_M^k(P)} Q.$
$P\setminus E= \bigcup_{k=1}^\infty \bigcup_{Q \in \mathcal{F}_M^k(P)} Q.$
Proof. For every ![]() $Q \in \mathcal{F}_M^k(P),$ with
$Q \in \mathcal{F}_M^k(P),$ with ![]() $k \in {\mathbb N},$ we have that
$k \in {\mathbb N},$ we have that ![]() $Q \in \mathcal{F}_M(R),$ for some
$Q \in \mathcal{F}_M(R),$ for some  $R\in \mathcal{G}_M^{k-1}(P).$ In particular,
$R\in \mathcal{G}_M^{k-1}(P).$ In particular, ![]() $Q \cap E =\emptyset$ (see Remark 5.1(e)), showing the inclusion
$Q \cap E =\emptyset$ (see Remark 5.1(e)), showing the inclusion ![]() $\bigcup_{k=1}^\infty \bigcup \mathcal{F}_M^k(P) \subset P \setminus E.$
$\bigcup_{k=1}^\infty \bigcup \mathcal{F}_M^k(P) \subset P \setminus E.$
To prove the reverse inclusion, we may assume that ![]() $P \cap E \neq \emptyset,$ as otherwise
$P \cap E \neq \emptyset,$ as otherwise ![]() $P \setminus E=P,$
$P \setminus E=P,$ ![]() $\mathcal{F}_M^1(P) =\lbrace P \rbrace$ and
$\mathcal{F}_M^1(P) =\lbrace P \rbrace$ and ![]() $\mathcal{F}_M^k(P) = \emptyset$ for every
$\mathcal{F}_M^k(P) = \emptyset$ for every ![]() $k \geq 2.$ Now, let
$k \geq 2.$ Now, let ![]() $x\in P \setminus E,$ and let
$x\in P \setminus E,$ and let ![]() $Q \in \mathcal{D}(P)$ be a cube with
$Q \in \mathcal{D}(P)$ be a cube with ![]() $x\in Q$ and
$x\in Q$ and ![]() $Q \cap E= \emptyset.$ Notice that such cube Q exists because E is closed, and for every
$Q \cap E= \emptyset.$ Notice that such cube Q exists because E is closed, and for every ![]() $l\in {\mathbb Z}$ with
$l\in {\mathbb Z}$ with ![]() $l \geq g(P),$ P can be written as union of dyadic subcubes of P with diameter at most
$l \geq g(P),$ P can be written as union of dyadic subcubes of P with diameter at most ![]() $2A \theta^l.$
$2A \theta^l.$
We will next show that ![]() $Q \subset \bigcup_{k=1}^\infty \bigcup \mathcal{F}_M^k(P).$ Suppose, for the sake of contradiction, that
$Q \subset \bigcup_{k=1}^\infty \bigcup \mathcal{F}_M^k(P).$ Suppose, for the sake of contradiction, that ![]() $Q \not \subset \bigcup_{k=1}^\infty \bigcup \mathcal{F}_M^k(P).$ In particular,
$Q \not \subset \bigcup_{k=1}^\infty \bigcup \mathcal{F}_M^k(P).$ In particular, ![]() $Q \not \subset \bigcup \mathcal{F}_M^1(P).$ By Remark 5.1(a), there must exist some cube
$Q \not \subset \bigcup \mathcal{F}_M^1(P).$ By Remark 5.1(a), there must exist some cube ![]() $R_1\in \mathcal{G}_M^1(P)$ intersecting Q. And this actually implies that
$R_1\in \mathcal{G}_M^1(P)$ intersecting Q. And this actually implies that ![]() $Q \subsetneq R_1,$ because if
$Q \subsetneq R_1,$ because if ![]() $R_1 \subseteq Q$ the facts that
$R_1 \subseteq Q$ the facts that ![]() $R_1 \cap E \neq \emptyset$ (see Remark 5.1(e)) and
$R_1 \cap E \neq \emptyset$ (see Remark 5.1(e)) and ![]() $Q \cap E = \emptyset$ lead us to contradiction. Therefore Q is entirely and strictly contained in
$Q \cap E = \emptyset$ lead us to contradiction. Therefore Q is entirely and strictly contained in ![]() $R_1.$ But now
$R_1.$ But now  $Q \not \subset \bigcup \mathcal{F}_M^2(P) = \bigcup_{R \in \mathcal{G}_M^1(P)}\bigcup \mathcal{F}_M(R)$, and so
$Q \not \subset \bigcup \mathcal{F}_M^2(P) = \bigcup_{R \in \mathcal{G}_M^1(P)}\bigcup \mathcal{F}_M(R)$, and so ![]() $Q \not \subset \bigcup \mathcal{F}_M(R_1)$. Using the same argument as above, the cube Q must be strictly contained in some
$Q \not \subset \bigcup \mathcal{F}_M(R_1)$. Using the same argument as above, the cube Q must be strictly contained in some ![]() $R_2 \in \mathcal{G}_M(R_1) \subset \mathcal{G}_M^2(P) .$ And since
$R_2 \in \mathcal{G}_M(R_1) \subset \mathcal{G}_M^2(P) .$ And since  $Q \not \subset \bigcup \mathcal{F}_M^3= \bigcup_{R \in \mathcal{G}_M^2(P)} \bigcup \mathcal{F}_M(R)$, we have
$Q \not \subset \bigcup \mathcal{F}_M^3= \bigcup_{R \in \mathcal{G}_M^2(P)} \bigcup \mathcal{F}_M(R)$, we have ![]() $Q \not \subset \bigcup \mathcal{F}_M(R_2).$ Repeating this procedure up to any natural number
$Q \not \subset \bigcup \mathcal{F}_M(R_2).$ Repeating this procedure up to any natural number ![]() $k,$ we obtain cubes
$k,$ we obtain cubes
with ![]() $Q \not \subset \bigcup \mathcal{F}_M(R_k)$ and
$Q \not \subset \bigcup \mathcal{F}_M(R_k)$ and ![]() $R_j \in \mathcal{G}_M(R_{j-1})$ for every
$R_j \in \mathcal{G}_M(R_{j-1})$ for every ![]() $j=2,\ldots,k.$ Because Q is strictly contained in
$j=2,\ldots,k.$ Because Q is strictly contained in ![]() $R_k,$ then
$R_k,$ then ![]() $g(Q) \gt g(R_k),$ by Lemma 2.4, and we can say that
$g(Q) \gt g(R_k),$ by Lemma 2.4, and we can say that ![]() $Q \in \mathcal{D}(R_k).$ Moreover, Q is not contained in any
$Q \in \mathcal{D}(R_k).$ Moreover, Q is not contained in any ![]() $R\in \mathcal{F}_M(R_k)$, and
$R\in \mathcal{F}_M(R_k)$, and ![]() $Q\in \mathcal{D}(R_k)$,
$Q\in \mathcal{D}(R_k)$, ![]() $Q \cap E = \emptyset.$ According to the definition of
$Q \cap E = \emptyset.$ According to the definition of ![]() $\mathcal{F}_M(R_k),$ this tells us that
$\mathcal{F}_M(R_k),$ this tells us that ![]() $g(Q) \gt M + g_E(R_k).$ On the other hand, each Rj is strictly contained in
$g(Q) \gt M + g_E(R_k).$ On the other hand, each Rj is strictly contained in ![]() $R_{j-1}$ because
$R_{j-1}$ because ![]() $R_j \subset R_{j-1} \setminus \bigcup \mathcal{F}_M(R_{j-1}),$ and
$R_j \subset R_{j-1} \setminus \bigcup \mathcal{F}_M(R_{j-1}),$ and ![]() $\mathcal{F}_M(R_{j-1}) \neq \emptyset$. Thus
$\mathcal{F}_M(R_{j-1}) \neq \emptyset$. Thus ![]() $g(R_j) \geq g(R_{j-1}) +1$ for every
$g(R_j) \geq g(R_{j-1}) +1$ for every ![]() $j,$ and all these observations lead us to
$j,$ and all these observations lead us to
Since k is arbitrary, we get a contradiction, showing that ![]() $Q \subset \bigcup_{k=1}^\infty \bigcup \mathcal{F}_M^k(P).$
$Q \subset \bigcup_{k=1}^\infty \bigcup \mathcal{F}_M^k(P).$
Lemma 5.3. There exists a constant ![]() $\beta=\beta(\theta,c,m,M)\in (0,1)$ depending on
$\beta=\beta(\theta,c,m,M)\in (0,1)$ depending on ![]() $\theta, c,m,M$ such that
$\theta, c,m,M$ such that
 \begin{equation*}
\sum_{k=1}^\infty \sum_{Q\in\mathcal{F}_M^k(Q_0) } \theta^{- g(Q) \gamma} \mu( Q)
\leq \frac{2}{c} \, \theta^{- g_E(Q_0) \gamma} \mu( Q_0).
\end{equation*}
\begin{equation*}
\sum_{k=1}^\infty \sum_{Q\in\mathcal{F}_M^k(Q_0) } \theta^{- g(Q) \gamma} \mu( Q)
\leq \frac{2}{c} \, \theta^{- g_E(Q_0) \gamma} \mu( Q_0).
\end{equation*} for every cube ![]() $Q_0 \in \mathcal{D} $ and every
$Q_0 \in \mathcal{D} $ and every ![]() $\gamma \in (0,\beta].$
$\gamma \in (0,\beta].$
Proof. Let ![]() $\beta \in (0,1)$ be a constant whose value will be specified later. Fix a cube
$\beta \in (0,1)$ be a constant whose value will be specified later. Fix a cube ![]() $Q_0 \in \mathcal{D}.$ We will need the following claim.
$Q_0 \in \mathcal{D}.$ We will need the following claim.
Claim 5.4.
For every natural ![]() $k \in {\mathbb N},$ we have
$k \in {\mathbb N},$ we have
 \begin{equation*}
\sum_{R \in \mathcal{G}_M^{k-1}(Q_0)} \theta^{-g_E(R)\beta} \mu(R)\leq \left( (\theta^{m+M} )^{-\beta} (1-c) \right)^{k-1} \theta^{-g_E(Q_0)\beta} \mu(Q_0).
\end{equation*}
\begin{equation*}
\sum_{R \in \mathcal{G}_M^{k-1}(Q_0)} \theta^{-g_E(R)\beta} \mu(R)\leq \left( (\theta^{m+M} )^{-\beta} (1-c) \right)^{k-1} \theta^{-g_E(Q_0)\beta} \mu(Q_0).
\end{equation*}Proof of Claim 5.4
For ![]() $k=1,$ we have
$k=1,$ we have  $\mathcal{G}_M^{k-1}(Q_0)=\lbrace Q_0 \rbrace,$ and the estimate trivially holds. Now, suppose that the inequality holds for
$\mathcal{G}_M^{k-1}(Q_0)=\lbrace Q_0 \rbrace,$ and the estimate trivially holds. Now, suppose that the inequality holds for ![]() $k,$ and let us estimate from above the term
$k,$ and let us estimate from above the term 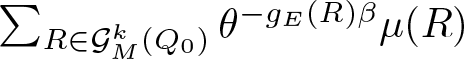 $\sum_{R \in \mathcal{G}_M^{k}(Q_0)} \theta^{-g_E(R)\beta} \mu(R)$. Each
$\sum_{R \in \mathcal{G}_M^{k}(Q_0)} \theta^{-g_E(R)\beta} \mu(R)$. Each ![]() $R\in \mathcal{G}_M^k(Q_0)$ belongs to
$R\in \mathcal{G}_M^k(Q_0)$ belongs to ![]() $\mathcal{G}_M(P)$ for some
$\mathcal{G}_M(P)$ for some  $P\in \mathcal{G}_M^{k-1}(Q_0).$ In particular
$P\in \mathcal{G}_M^{k-1}(Q_0).$ In particular ![]() $R\in \mathcal{D}(P),$ and if
$R\in \mathcal{D}(P),$ and if ![]() $R^* \in \mathcal{D}(P)$ with
$R^* \in \mathcal{D}(P)$ with ![]() $R \subset R^*$ and
$R \subset R^*$ and ![]() $g(R^*)=g(R)-1,$ then
$g(R^*)=g(R)-1,$ then ![]() $R^* \cap Q \neq \emptyset,$ for some
$R^* \cap Q \neq \emptyset,$ for some ![]() $Q\in \mathcal{F}_M(P)$ by Remark 5.1(d). If
$Q\in \mathcal{F}_M(P)$ by Remark 5.1(d). If ![]() $R^* \subseteq Q,$ then we have
$R^* \subseteq Q,$ then we have  $R \subset R^* \subset \bigcup_{Q' \in \mathcal{F}_M(P)} Q',$ which contradicts the fact that R belongs to
$R \subset R^* \subset \bigcup_{Q' \in \mathcal{F}_M(P)} Q',$ which contradicts the fact that R belongs to ![]() $\mathcal{G}_M(P).$ Thus, we necessarily have
$\mathcal{G}_M(P).$ Thus, we necessarily have ![]() $Q \subsetneq R^*.$ We remind that this implies
$Q \subsetneq R^*.$ We remind that this implies ![]() $g(Q) \gt g(R^*)$ by Lemma 2.4, and so
$g(Q) \gt g(R^*)$ by Lemma 2.4, and so ![]() $Q \in \mathcal{D}(R^*)$. In particular
$Q \in \mathcal{D}(R^*)$. In particular ![]() $g_E(R^*) \leq g(Q)$ because
$g_E(R^*) \leq g(Q)$ because ![]() $Q \cap E =\emptyset.$ Using that gE is doubling (see Definition 3.4) and the fact
$Q \cap E =\emptyset.$ Using that gE is doubling (see Definition 3.4) and the fact ![]() $Q\in \mathcal{F}_M(P)$, we obtain the estimates
$Q\in \mathcal{F}_M(P)$, we obtain the estimates
On the other hand, the weak porosity condition together with Remark 5.1(a) give
 \begin{equation}
\sum_{R \in \mathcal{G}_M(P)} \mu(R) = \mu (P) - \sum_{R \in \mathcal{F}_M(P)} \mu(R) \leq (1-c) \mu(P).
\end{equation}
\begin{equation}
\sum_{R \in \mathcal{G}_M(P)} \mu(R) = \mu (P) - \sum_{R \in \mathcal{F}_M(P)} \mu(R) \leq (1-c) \mu(P).
\end{equation}Using first (22), then (23), and finally the induction hypothesis, we derive
 \begin{align*}
\sum_{R \in \mathcal{G}_M^{k}(Q_0)} \theta^{-g_E(R)\beta} \mu(R) & = \sum_{P \in \mathcal{G}_M^{k-1}(Q_0)} \sum_{R\in \mathcal{G}_M(P)} \theta^{-g_E(R)\beta} \mu(R) \\
& \leq (\theta^{m+M} )^{-\beta} \sum_{P \in \mathcal{G}_M^{k-1}(Q_0)} \theta^{-g_E(P)\beta} \sum_{R\in \mathcal{G}_M(P)} \mu(R) \\
& \leq (\theta^{m+M} )^{-\beta} (1-c) \sum_{P \in \mathcal{G}_M^{k-1}(Q_0)} \theta^{-g_E(P)\beta} \mu(P) \\
& \leq (\theta^{m+M} )^{-\beta} (1-c) \left( (\theta^{m+M} )^{-\beta} (1-c) \right)^{k-1} \theta^{-g_E(Q_0)\beta} \mu(Q_0) \\
& = \left( (\theta^{m+M} )^{-\beta} (1-c) \right)^{k}\theta^{-g_E(Q_0)\beta} \mu(Q_0).
\end{align*}
\begin{align*}
\sum_{R \in \mathcal{G}_M^{k}(Q_0)} \theta^{-g_E(R)\beta} \mu(R) & = \sum_{P \in \mathcal{G}_M^{k-1}(Q_0)} \sum_{R\in \mathcal{G}_M(P)} \theta^{-g_E(R)\beta} \mu(R) \\
& \leq (\theta^{m+M} )^{-\beta} \sum_{P \in \mathcal{G}_M^{k-1}(Q_0)} \theta^{-g_E(P)\beta} \sum_{R\in \mathcal{G}_M(P)} \mu(R) \\
& \leq (\theta^{m+M} )^{-\beta} (1-c) \sum_{P \in \mathcal{G}_M^{k-1}(Q_0)} \theta^{-g_E(P)\beta} \mu(P) \\
& \leq (\theta^{m+M} )^{-\beta} (1-c) \left( (\theta^{m+M} )^{-\beta} (1-c) \right)^{k-1} \theta^{-g_E(Q_0)\beta} \mu(Q_0) \\
& = \left( (\theta^{m+M} )^{-\beta} (1-c) \right)^{k}\theta^{-g_E(Q_0)\beta} \mu(Q_0).
\end{align*}This shows that the desired estimate holds for k + 1 as well, and the proof of Claim 5.4 is complete.
Now we continue with the proof of Lemma 5.3. For every ![]() $k\in {\mathbb N},$ we can write
$k\in {\mathbb N},$ we can write
 \begin{align*}
\sum_{Q\in\mathcal{F}_M^k(Q_0) } \theta^{-g(Q) \beta} \mu( Q) & = \sum_{R\in\mathcal{G}_M^{k-1} (Q_0) } \sum_{Q\in \mathcal{F}_M(R)} \theta^{- g(Q) \beta} \mu( Q) \\
& \leq \sum_{R\in\mathcal{G}_M^{k-1}(Q_0) }\theta^{-M\beta} \theta^{- g_E(R) \beta} \sum_{Q\in \mathcal{F}_M(R)} \mu( Q) \\
& \leq \theta^{-M\beta} \sum_{R\in\mathcal{G}_M^{k-1}(Q_0) }\theta^{- g_E(R) \beta} \mu( R),
\end{align*}
\begin{align*}
\sum_{Q\in\mathcal{F}_M^k(Q_0) } \theta^{-g(Q) \beta} \mu( Q) & = \sum_{R\in\mathcal{G}_M^{k-1} (Q_0) } \sum_{Q\in \mathcal{F}_M(R)} \theta^{- g(Q) \beta} \mu( Q) \\
& \leq \sum_{R\in\mathcal{G}_M^{k-1}(Q_0) }\theta^{-M\beta} \theta^{- g_E(R) \beta} \sum_{Q\in \mathcal{F}_M(R)} \mu( Q) \\
& \leq \theta^{-M\beta} \sum_{R\in\mathcal{G}_M^{k-1}(Q_0) }\theta^{- g_E(R) \beta} \mu( R),
\end{align*} where in the last inequality we used the fact that the cubes of ![]() $\mathcal{F}_M(R)$ are disjoint. Applying Claim 5.4 to the last term, we obtain
$\mathcal{F}_M(R)$ are disjoint. Applying Claim 5.4 to the last term, we obtain
 \begin{align*}
\sum_{k=1}^\infty\sum_{Q\in\mathcal{F}_M^k (Q_0) } \theta^{-g(Q) \beta} \mu( Q) & \leq \theta^{-M\beta} \sum_{k=1}^\infty \sum_{R\in\mathcal{G}_M^{k-1}(Q_0) } \theta^{- g_E(R) \beta} \mu( R) \\
& \leq \theta^{-M\beta} \theta^{-g_E(Q_0)\beta} \mu(Q_0) \sum_{k=1}^\infty \left( (\theta^{m+M} )^{-\beta} (1-c) \right)^{k-1}.
\end{align*}
\begin{align*}
\sum_{k=1}^\infty\sum_{Q\in\mathcal{F}_M^k (Q_0) } \theta^{-g(Q) \beta} \mu( Q) & \leq \theta^{-M\beta} \sum_{k=1}^\infty \sum_{R\in\mathcal{G}_M^{k-1}(Q_0) } \theta^{- g_E(R) \beta} \mu( R) \\
& \leq \theta^{-M\beta} \theta^{-g_E(Q_0)\beta} \mu(Q_0) \sum_{k=1}^\infty \left( (\theta^{m+M} )^{-\beta} (1-c) \right)^{k-1}.
\end{align*} If the parameter β > 0 is small enough, then ![]() $(\theta^{m+M} )^{-\beta} (1-c) \lt 1$ and the constant multiplying
$(\theta^{m+M} )^{-\beta} (1-c) \lt 1$ and the constant multiplying ![]() $\theta^{-g_E(Q_0)\beta} \mu(Q_0)$ becomes
$\theta^{-g_E(Q_0)\beta} \mu(Q_0)$ becomes  $\theta^{-M\beta} \left( 1- (\theta^{m+M} )^{-\beta} (1-c) \right)^{-1}.$ For sufficiently small β this term is bounded by
$\theta^{-M\beta} \left( 1- (\theta^{m+M} )^{-\beta} (1-c) \right)^{-1}.$ For sufficiently small β this term is bounded by ![]() $2/c.$
$2/c.$
6. Proof of Theorem 1.1
In this section we prove the implication (A)![]() $\implies$(B) of Theorem 1.1. Let E be a weakly porous set such that hE is doubling. As pointed out in Section 5, Lemma 3.8 then implies that E is dyadic weakly porous and gE is doubling, which allows us to use Lemma 5.3. Also, E can be assumed to be closed, as we explained in the beginning of Section 5.
$\implies$(B) of Theorem 1.1. Let E be a weakly porous set such that hE is doubling. As pointed out in Section 5, Lemma 3.8 then implies that E is dyadic weakly porous and gE is doubling, which allows us to use Lemma 5.3. Also, E can be assumed to be closed, as we explained in the beginning of Section 5.
In the next three subsections, we are going to prove the A 1-estimate (2) for the weight ![]() $\operatorname{dist}(\cdot,E)^{-\gamma}$ for suitable
$\operatorname{dist}(\cdot,E)^{-\gamma}$ for suitable ![]() $\gamma \gt 0,$ for all the cubes of the systems
$\gamma \gt 0,$ for all the cubes of the systems ![]() $\mathcal{D}$ instead of balls. Then, a simple argument will allow us to deduce (2) for every ball of
$\mathcal{D}$ instead of balls. Then, a simple argument will allow us to deduce (2) for every ball of ![]() $X.$
$X.$
6.1. E-free cubes that are far from E
Let ![]() $Q_0 \in \mathcal{D}$ such that
$Q_0 \in \mathcal{D}$ such that ![]() $Q_0 \cap E= \emptyset,$ and
$Q_0 \cap E= \emptyset,$ and ![]() $\operatorname{dist}(Q_0,E) \geq 2 \operatorname{diam}(Q_0).$ Observe that, for every
$\operatorname{dist}(Q_0,E) \geq 2 \operatorname{diam}(Q_0).$ Observe that, for every ![]() $x,y\in Q_0,$ we have
$x,y\in Q_0,$ we have ![]() $\operatorname{dist}(y,E) \leq 2 \operatorname{dist}(x,E)$. Also, if z 0 denotes the reference point of
$\operatorname{dist}(y,E) \leq 2 \operatorname{dist}(x,E)$. Also, if z 0 denotes the reference point of ![]() $Q_0,$ because
$Q_0,$ because ![]() $Q_0 \cap E = \emptyset,$ the ball
$Q_0 \cap E = \emptyset,$ the ball ![]() $B(z_0, a \theta^{g(Q_0)})$ does not contain any point of
$B(z_0, a \theta^{g(Q_0)})$ does not contain any point of ![]() $E,$ and so
$E,$ and so ![]() $\operatorname{dist}(z_0, E) \geq a\theta^{g(Q_0)}.$ These observations lead us to the estimates
$\operatorname{dist}(z_0, E) \geq a\theta^{g(Q_0)}.$ These observations lead us to the estimates
 \begin{align}
{\int{\kern-10.5pt}-}_{{\hskip-3.5pt Q_0}} \operatorname{dist}(x, E)^{-\gamma}\, d\mu \leq 2^\gamma\ \mathrm{ess\, inf}_{y\in Q_0} \operatorname{dist}(y, E)^{-\gamma} & \leq 2^\gamma \operatorname{dist}(z_0,E)^{-\gamma}\nonumber\\ & \quad\quad \leq (2/a)^\gamma \theta^{-g(Q_0) \gamma},
\end{align}
\begin{align}
{\int{\kern-10.5pt}-}_{{\hskip-3.5pt Q_0}} \operatorname{dist}(x, E)^{-\gamma}\, d\mu \leq 2^\gamma\ \mathrm{ess\, inf}_{y\in Q_0} \operatorname{dist}(y, E)^{-\gamma} & \leq 2^\gamma \operatorname{dist}(z_0,E)^{-\gamma}\nonumber\\ & \quad\quad \leq (2/a)^\gamma \theta^{-g(Q_0) \gamma},
\end{align}for every γ > 0.
6.2. E-free cubes that are close to E
Let ![]() $Q_0 \in \mathcal{D}$ such that
$Q_0 \in \mathcal{D}$ such that ![]() $Q_0 \cap E= \emptyset,$
$Q_0 \cap E= \emptyset,$ ![]() $\operatorname{dist}(Q_0,E) \lt 2 \operatorname{diam}(Q_0).$ Notice that, since E is closed,
$\operatorname{dist}(Q_0,E) \lt 2 \operatorname{diam}(Q_0).$ Notice that, since E is closed, ![]() $\operatorname{dist}(x,E) \gt 0$ for every
$\operatorname{dist}(x,E) \gt 0$ for every ![]() $x\in Q_0.$ Also, we have that
$x\in Q_0.$ Also, we have that ![]() $E \subset X \setminus Q_0,$ and, if
$E \subset X \setminus Q_0,$ and, if ![]() $x\in Q_0$,
$x\in Q_0$,
Now we define the sets ![]() $A_j=\lbrace x\in Q_0 \, : \, 6 A\theta^{j+1} \lt \operatorname{dist}(x, E) \leq 6 A\theta^j \rbrace$, for every
$A_j=\lbrace x\in Q_0 \, : \, 6 A\theta^{j+1} \lt \operatorname{dist}(x, E) \leq 6 A\theta^j \rbrace$, for every ![]() $j \in {\mathbb Z}$ with
$j \in {\mathbb Z}$ with ![]() $j \geq g(Q_0)$. By the preceding remarks,
$j \geq g(Q_0)$. By the preceding remarks,  $Q_0 = \bigcup_{j \geq g(Q_0)} A_j$, and the union is of course disjoint. Also, employing the estimate (4) from Proposition 2.5 with
$Q_0 = \bigcup_{j \geq g(Q_0)} A_j$, and the union is of course disjoint. Also, employing the estimate (4) from Proposition 2.5 with ![]() $t=6 A \theta^{j-g(Q_0)}$, we get positive constants C and η depending only on Cµ and θ so that
$t=6 A \theta^{j-g(Q_0)}$, we get positive constants C and η depending only on Cµ and θ so that
 \begin{equation*}
\mu(A_j) \leq \mu \left( \lbrace x\in Q_0 \, : \, \operatorname{dist}(x, X \setminus Q_0) \leq 6 A\theta^j \rbrace \right) \leq C(6A)^\eta \theta^{(j-g(Q_0)) \eta} \mu(Q_0).
\end{equation*}
\begin{equation*}
\mu(A_j) \leq \mu \left( \lbrace x\in Q_0 \, : \, \operatorname{dist}(x, X \setminus Q_0) \leq 6 A\theta^j \rbrace \right) \leq C(6A)^\eta \theta^{(j-g(Q_0)) \eta} \mu(Q_0).
\end{equation*}We momentarily use C to denote this constant, which should not be confused with any of the previously used C’s in the doubling condition for hE. All these properties lead us to
 \begin{align*}
\int_{Q_0} \operatorname{dist}(x, E)^{-\gamma} \, d\mu & =\sum_{j=g(Q_0)}^\infty \int_{A_j} \operatorname{dist}(x, E)^{-\gamma} \, d\mu \leq \sum_{j=g(Q_0)}^\infty (6A \theta^{j+1})^{-\gamma} \mu(A_j)\\
& \leq C (6A)^\eta (6A\theta)^{-\gamma} \theta^{-g(Q_0) \eta} \mu(Q_0) \sum_{j=g(Q_0)}^\infty \theta^{j(\eta-\gamma)}.
\end{align*}
\begin{align*}
\int_{Q_0} \operatorname{dist}(x, E)^{-\gamma} \, d\mu & =\sum_{j=g(Q_0)}^\infty \int_{A_j} \operatorname{dist}(x, E)^{-\gamma} \, d\mu \leq \sum_{j=g(Q_0)}^\infty (6A \theta^{j+1})^{-\gamma} \mu(A_j)\\
& \leq C (6A)^\eta (6A\theta)^{-\gamma} \theta^{-g(Q_0) \eta} \mu(Q_0) \sum_{j=g(Q_0)}^\infty \theta^{j(\eta-\gamma)}.
\end{align*} Assuming ![]() $\gamma \lt \eta$, the series converges and we obtain the estimate
$\gamma \lt \eta$, the series converges and we obtain the estimate
 \begin{equation}
\int_{Q_0} \operatorname{dist}(x, E)^{-\gamma} \, d\mu \leq \kappa(\theta, C_\mu,\gamma) \theta^{-g(Q_0)\gamma} \mu(Q_0).
\end{equation}
\begin{equation}
\int_{Q_0} \operatorname{dist}(x, E)^{-\gamma} \, d\mu \leq \kappa(\theta, C_\mu,\gamma) \theta^{-g(Q_0)\gamma} \mu(Q_0).
\end{equation} Since ![]() $\operatorname{dist}(Q_0,E) \lt 2 \operatorname{diam}(Q_0),$ we have that
$\operatorname{dist}(Q_0,E) \lt 2 \operatorname{diam}(Q_0),$ we have that ![]() $\operatorname{dist}(x,E) \leq 3 \operatorname{diam}(Q_0)$ for every
$\operatorname{dist}(x,E) \leq 3 \operatorname{diam}(Q_0)$ for every ![]() $x \in Q_0,$ and so
$x \in Q_0,$ and so
 \begin{equation*}
\mathrm{ess\, inf}_{Q_0} \operatorname{dist}(\cdot,E)^{-\gamma} \geq (3 \operatorname{diam}(Q_0))^{-\gamma} \geq (6A \theta^{g(Q_0)})^{-\gamma}.
\end{equation*}
\begin{equation*}
\mathrm{ess\, inf}_{Q_0} \operatorname{dist}(\cdot,E)^{-\gamma} \geq (3 \operatorname{diam}(Q_0))^{-\gamma} \geq (6A \theta^{g(Q_0)})^{-\gamma}.
\end{equation*}Combining this estimate with (25), we conclude
 \begin{equation}
{\int{\kern-10.5pt}-}_{{\hskip-3.5pt Q_0}} \operatorname{dist}(x, E)^{-\gamma} \, d\mu \leq \kappa(\theta, C_\mu,\gamma)\ \mathrm{ess\, inf}_{Q_0} \operatorname{dist}(\cdot,E)^{-\gamma}.
\end{equation}
\begin{equation}
{\int{\kern-10.5pt}-}_{{\hskip-3.5pt Q_0}} \operatorname{dist}(x, E)^{-\gamma} \, d\mu \leq \kappa(\theta, C_\mu,\gamma)\ \mathrm{ess\, inf}_{Q_0} \operatorname{dist}(\cdot,E)^{-\gamma}.
\end{equation}6.3. Non-E-free cubes
Fix ![]() $Q_0 \in \mathcal{D}$ with
$Q_0 \in \mathcal{D}$ with ![]() $Q_0 \cap E \neq \emptyset$. Given
$Q_0 \cap E \neq \emptyset$. Given ![]() $x\in Q_0 \setminus E,$ we have that
$x\in Q_0 \setminus E,$ we have that ![]() $\operatorname{dist}(x,E) \gt 0$ because E is closed. For
$\operatorname{dist}(x,E) \gt 0$ because E is closed. For ![]() $l\in {\mathbb Z}$,
$l\in {\mathbb Z}$, ![]() $l\geq g(Q_0)$ so that
$l\geq g(Q_0)$ so that ![]() $2 A \theta^l \lt \operatorname{dist}(x,E),$ we can write Q 0 as union of subcubes
$2 A \theta^l \lt \operatorname{dist}(x,E),$ we can write Q 0 as union of subcubes ![]() $Q \in \mathcal{D}(Q_0)$ with
$Q \in \mathcal{D}(Q_0)$ with ![]() $g(Q) = l.$ The point x must be contained in some of these cubes, say
$g(Q) = l.$ The point x must be contained in some of these cubes, say ![]() $Q,$ and because
$Q,$ and because ![]() $\operatorname{diam}(Q) \leq 2A \theta^l,$ we have
$\operatorname{diam}(Q) \leq 2A \theta^l,$ we have ![]() $Q \cap E = \emptyset.$
$Q \cap E = \emptyset.$
This allows us to find ![]() $Q_x\in \mathcal{D}(Q_0)$ with
$Q_x\in \mathcal{D}(Q_0)$ with ![]() $x\in Q_x,$
$x\in Q_x,$ ![]() $ Q_x \cap E= \emptyset$, and
$ Q_x \cap E= \emptyset$, and
Notice that ![]() $g(Q_x) \geq g_E(Q_0).$ Also, because
$g(Q_x) \geq g_E(Q_0).$ Also, because ![]() $Q_x \subsetneq Q_0$ (since
$Q_x \subsetneq Q_0$ (since ![]() $Q_0 \cap E \neq \emptyset= Q_x \cap E$), we can find
$Q_0 \cap E \neq \emptyset= Q_x \cap E$), we can find ![]() $Q_x^*\in \mathcal{D}(Q_0)$ with
$Q_x^*\in \mathcal{D}(Q_0)$ with ![]() $Q_x \subset Q_x^*$ and
$Q_x \subset Q_x^*$ and ![]() $g(Q_x^*)= g(Q_x)-1.$ By the minimality of
$g(Q_x^*)= g(Q_x)-1.$ By the minimality of ![]() $g(Q_x),$ the cube
$g(Q_x),$ the cube ![]() $Q_x^*$ must intersect
$Q_x^*$ must intersect ![]() $E.$ Then, if
$E.$ Then, if ![]() $z^*$ is the reference point of
$z^*$ is the reference point of ![]() $Q_x^*$, the containing ball
$Q_x^*$, the containing ball  $B \left( z^*, A \theta^{g(Q_x^*)} \right)$ of
$B \left( z^*, A \theta^{g(Q_x^*)} \right)$ of ![]() $Q_x^*$ also intersects
$Q_x^*$ also intersects ![]() $E,$ and we derive
$E,$ and we derive
 \begin{equation*}
\operatorname{dist}(x,E) \leq \operatorname{diam}\left( B \left( z^*, A \theta^{g(Q_x^*)} \right) \right) \leq \frac{2A}{\theta} \theta^{g(Q_x)} \leq \frac{2A}{\theta} \theta^{g_E(Q_0)}.
\end{equation*}
\begin{equation*}
\operatorname{dist}(x,E) \leq \operatorname{diam}\left( B \left( z^*, A \theta^{g(Q_x^*)} \right) \right) \leq \frac{2A}{\theta} \theta^{g(Q_x)} \leq \frac{2A}{\theta} \theta^{g_E(Q_0)}.
\end{equation*}Consequently, the following estimate holds:
 \begin{equation}
\mathrm{ess\, inf}_{x\in Q_0} \operatorname{dist}(x,E)^{-\gamma} \geq \left( \frac{\theta}{2A} \right)^\gamma \theta^{-g_E(Q_0) \gamma}.
\end{equation}
\begin{equation}
\mathrm{ess\, inf}_{x\in Q_0} \operatorname{dist}(x,E)^{-\gamma} \geq \left( \frac{\theta}{2A} \right)^\gamma \theta^{-g_E(Q_0) \gamma}.
\end{equation} On the other hand, using Lemma 5.2 and the fact that all the cubes in the family ![]() $\lbrace Q \, : \, Q \in \mathcal{F}_M^k(Q_0), \, k\in {\mathbb N} \rbrace$ are mutually disjoint, we can write
$\lbrace Q \, : \, Q \in \mathcal{F}_M^k(Q_0), \, k\in {\mathbb N} \rbrace$ are mutually disjoint, we can write
 \begin{equation*}
\int_{Q_0 \setminus E} \operatorname{dist}(x,E)^{-\gamma} \, d\mu = \sum_{k=1}^\infty \sum_{Q \in \mathcal{F}_M^k(Q_0)} \int_{Q}\operatorname{dist}(x,E)^{-\gamma} \, d\mu .
\end{equation*}
\begin{equation*}
\int_{Q_0 \setminus E} \operatorname{dist}(x,E)^{-\gamma} \, d\mu = \sum_{k=1}^\infty \sum_{Q \in \mathcal{F}_M^k(Q_0)} \int_{Q}\operatorname{dist}(x,E)^{-\gamma} \, d\mu .
\end{equation*} Now, each cube ![]() $Q \in \mathcal{F}_M^k(Q_0)$ does not intersect
$Q \in \mathcal{F}_M^k(Q_0)$ does not intersect ![]() $E;$ see the definition of this families in (21) together with Remark 5.1(e). Thus, we can estimate from above each of the integrals in the previous series, by applying either (24) or (25) depending on whether the cube
$E;$ see the definition of this families in (21) together with Remark 5.1(e). Thus, we can estimate from above each of the integrals in the previous series, by applying either (24) or (25) depending on whether the cube ![]() $Q \in \mathcal{F}_M^k(Q_0)$ satisfies the assumption of Subsections 6.1 or 6.2. Notice that (24) holds for any positive
$Q \in \mathcal{F}_M^k(Q_0)$ satisfies the assumption of Subsections 6.1 or 6.2. Notice that (24) holds for any positive ![]() $\gamma,$ whereas (25) holds if
$\gamma,$ whereas (25) holds if ![]() $\gamma \lt \eta.$ Hence, taking
$\gamma \lt \eta.$ Hence, taking ![]() $\gamma \lt \eta,$ the preceding series can be estimated from above by
$\gamma \lt \eta,$ the preceding series can be estimated from above by
 \begin{equation*}
\sum_{k=1}^\infty \sum_{Q \in \mathcal{F}_M^k(Q_0)} \kappa(\theta,C_\mu,\gamma) \theta^{-g(Q)\gamma} \mu(Q).
\end{equation*}
\begin{equation*}
\sum_{k=1}^\infty \sum_{Q \in \mathcal{F}_M^k(Q_0)} \kappa(\theta,C_\mu,\gamma) \theta^{-g(Q)\gamma} \mu(Q).
\end{equation*} Now, if ![]() $\beta=\beta(\theta,c,m,M) \gt 0$ is the number from Lemma 5.3, we take further
$\beta=\beta(\theta,c,m,M) \gt 0$ is the number from Lemma 5.3, we take further ![]() $\gamma \lt \beta,$ and the same lemma gives the estimate
$\gamma \lt \beta,$ and the same lemma gives the estimate
 \begin{equation*}
\sum_{k=1}^\infty \sum_{Q \in \mathcal{F}_M^k(Q_0)} \kappa(\theta,C_\mu,\gamma) \theta^{-g(Q)\gamma} \mu(Q) \leq \kappa(\theta,C_\mu, \gamma,c)\theta^{-g_E(Q_0) \gamma} \mu( Q_0).
\end{equation*}
\begin{equation*}
\sum_{k=1}^\infty \sum_{Q \in \mathcal{F}_M^k(Q_0)} \kappa(\theta,C_\mu,\gamma) \theta^{-g(Q)\gamma} \mu(Q) \leq \kappa(\theta,C_\mu, \gamma,c)\theta^{-g_E(Q_0) \gamma} \mu( Q_0).
\end{equation*} Recall that ![]() $M,c$ are the constants of dyadic weak porosity of
$M,c$ are the constants of dyadic weak porosity of ![]() $E,$ and that m is the doubling constant for
$E,$ and that m is the doubling constant for ![]() $g_E.$ Together with (27), these estimates yield
$g_E.$ Together with (27), these estimates yield
 \begin{equation}
{\int{\kern-10.5pt}-}_{\hskip-3.5pt {Q_0}} \operatorname{dist}(x,E)^{-\gamma} \, d\mu \leq \kappa(\theta,C_\mu,\gamma,c)\ \mathrm{ess\, inf}_{x\in Q_0} \operatorname{dist}(x,E)^{-\gamma}.
\end{equation}
\begin{equation}
{\int{\kern-10.5pt}-}_{\hskip-3.5pt {Q_0}} \operatorname{dist}(x,E)^{-\gamma} \, d\mu \leq \kappa(\theta,C_\mu,\gamma,c)\ \mathrm{ess\, inf}_{x\in Q_0} \operatorname{dist}(x,E)^{-\gamma}.
\end{equation} Notice that we have used the fact that ![]() $\mu(E)=0,$ which follows from the weak porosity condition for
$\mu(E)=0,$ which follows from the weak porosity condition for ![]() $E;$ see Definition 3.1 and the subsequent comment.
$E;$ see Definition 3.1 and the subsequent comment.
6.4. The A 1-estimate for all balls of X
Collecting the estimates from the three previous subsections, we obtain the following theorem, which is the implication (A)![]() $\implies$(B) in Theorem 1.1.
$\implies$(B) in Theorem 1.1.
Theorem 6.1. Let ![]() $E$ be a weakly porous set with constants
$E$ be a weakly porous set with constants ![]() $c,\delta$ and so that
$c,\delta$ and so that ![]() $h_E$ is doubling with constant
$h_E$ is doubling with constant ![]() $C.$ Then there exists
$C.$ Then there exists ![]() $\gamma=\gamma(\theta,C_\mu,c,\delta,C) \gt 0$ so that
$\gamma=\gamma(\theta,C_\mu,c,\delta,C) \gt 0$ so that ![]() $\operatorname{dist}(\cdot, E)^{-\gamma} \in A_1(X).$ The
$\operatorname{dist}(\cdot, E)^{-\gamma} \in A_1(X).$ The ![]() $A_1$-constant of the weight
$A_1$-constant of the weight ![]() $\operatorname{dist}(\cdot, E)^{-\gamma}$ depends on
$\operatorname{dist}(\cdot, E)^{-\gamma}$ depends on ![]() $\theta,C_\mu,\gamma,c.$
$\theta,C_\mu,\gamma,c.$
Proof. By Lemma 3.8, E is dyadic weakly porous with some new constants ![]() $c'=c'(\theta,C_\mu,c)$ and
$c'=c'(\theta,C_\mu,c)$ and ![]() $M=M(\theta,\delta,C)$, and gE is doubling with constant
$M=M(\theta,\delta,C)$, and gE is doubling with constant ![]() $m=m(\theta,C) \in {\mathbb N}.$
$m=m(\theta,C) \in {\mathbb N}.$
We combine the conclusions of Subsections 6.1, 6.2, and 6.3, i.e., (24), (26) and (28). We deduce that, for ![]() $\gamma=\gamma(\theta,C_\mu,c',M,m) \gt 0$ small enough, and for every cube
$\gamma=\gamma(\theta,C_\mu,c',M,m) \gt 0$ small enough, and for every cube ![]() $Q\in \mathcal{D},$ the estimate
$Q\in \mathcal{D},$ the estimate
 \begin{equation*}
{\int{\kern-10.5pt}-}_{\hskip-3.5pt Q} \operatorname{dist}( \cdot, E)^{-\gamma} \, d\mu \leq \kappa(\theta,C_\mu,\gamma,c')\ \mathrm{ess\, inf}_Q \operatorname{dist}(\cdot, E)^{-\gamma}
\end{equation*}
\begin{equation*}
{\int{\kern-10.5pt}-}_{\hskip-3.5pt Q} \operatorname{dist}( \cdot, E)^{-\gamma} \, d\mu \leq \kappa(\theta,C_\mu,\gamma,c')\ \mathrm{ess\, inf}_Q \operatorname{dist}(\cdot, E)^{-\gamma}
\end{equation*} holds true. Now, given any open ball ![]() $B=B(x,R) \subset X,$ Proposition 2.3 provides a cube
$B=B(x,R) \subset X,$ Proposition 2.3 provides a cube ![]() $Q\in \mathcal{D}$ with
$Q\in \mathcal{D}$ with ![]() $B \subset Q$ and
$B \subset Q$ and ![]() $\theta^{g(Q)+2} \lt R \leq \theta^{g(Q)+1}.$ If z denotes the reference point of
$\theta^{g(Q)+2} \lt R \leq \theta^{g(Q)+1}.$ If z denotes the reference point of ![]() $Q,$ we have the inclusion
$Q,$ we have the inclusion ![]() $Q \subset B(z, A \theta^{g(Q)}) $. Because x is contained in this ball and
$Q \subset B(z, A \theta^{g(Q)}) $. Because x is contained in this ball and ![]() $\theta^{g(Q)+2} \lt R,$ the triangle inequality gives
$\theta^{g(Q)+2} \lt R,$ the triangle inequality gives ![]() $B(z,A \theta^{g(Q)}) \subset B(x, 2 A \theta^{-2} R).$ Hence, the doubling condition for µ yields
$B(z,A \theta^{g(Q)}) \subset B(x, 2 A \theta^{-2} R).$ Hence, the doubling condition for µ yields ![]() $\mu(Q) \leq C(\theta, C_\mu) \mu(B).$ These observations permit to write
$\mu(Q) \leq C(\theta, C_\mu) \mu(B).$ These observations permit to write
 \begin{align*}
{\int{\kern-10.5pt}-}_{\hskip-3.5pt B}\hskip1.5pt \operatorname{dist}( \cdot, E)^{-\gamma} \, d\mu & \leq \kappa(\theta, C_\mu) {\int{\kern-10.5pt}-}_Q \operatorname{dist}( \cdot, E)^{-\gamma} \, d\mu \\
& \leq \kappa(\theta,C_\mu,\gamma,c')\ \mathrm{ess\, inf}_Q \operatorname{dist}(\cdot, E)^{-\gamma} \\ &\leq \kappa(\theta,C_\mu,\gamma,c)\ \mathrm{ess\, inf}_B\nonumber \operatorname{dist}(\cdot, E)^{-\gamma} .
\end{align*}
\begin{align*}
{\int{\kern-10.5pt}-}_{\hskip-3.5pt B}\hskip1.5pt \operatorname{dist}( \cdot, E)^{-\gamma} \, d\mu & \leq \kappa(\theta, C_\mu) {\int{\kern-10.5pt}-}_Q \operatorname{dist}( \cdot, E)^{-\gamma} \, d\mu \\
& \leq \kappa(\theta,C_\mu,\gamma,c')\ \mathrm{ess\, inf}_Q \operatorname{dist}(\cdot, E)^{-\gamma} \\ &\leq \kappa(\theta,C_\mu,\gamma,c)\ \mathrm{ess\, inf}_B\nonumber \operatorname{dist}(\cdot, E)^{-\gamma} .
\end{align*}Proof of Theorem 1.1
It now suffices to combine Lemma 4.2 and Theorem 6.1
7. Proof of Theorem 1.3 and a bonus characterization
We now prove that in spaces with a slightly weaker variant of the standard annular decay property, the weak porosity condition implies the doubling property of the maximal holes. This permits to complete the proof of Theorem 1.3. Then, without the assumption of the variant of the annular decay property, we give a sufficient condition for a dyadic weakly porous set E to imply the doubling property for its dyadic maximal free holes ![]() $g_E,$ and this will lead us to another characterization of the property
$g_E,$ and this will lead us to another characterization of the property ![]() $\operatorname{dist}(\cdot,E)^{-\alpha}\in A_1(X)$ for some α > 0.
$\operatorname{dist}(\cdot,E)^{-\alpha}\in A_1(X)$ for some α > 0.
7.1. Admissible balls with small radii
The following lemma of rescaling for the parameter δ in the definition of weak porosity is valid in any metric space with a doubling measure. It essentially tells us that one can replace the parameters ![]() $(c,\delta)$ in the definition of weak porosity with
$(c,\delta)$ in the definition of weak porosity with  $(c \, C_\mu^{-2}, \delta')$ for
$(c \, C_\mu^{-2}, \delta')$ for ![]() $\delta'$ as small as desired, and so that the admissible balls have arbitrarily small radii.
$\delta'$ as small as desired, and so that the admissible balls have arbitrarily small radii.
Lemma 7.1. Suppose ![]() $E$ is weakly porous with constants
$E$ is weakly porous with constants ![]() $c, \delta \in (0,1).$ Then, for every
$c, \delta \in (0,1).$ Then, for every ![]() $\tau \in (0,1/2),$ there exists
$\tau \in (0,1/2),$ there exists ![]() $\delta_\tau \in (0,1)$ depending on δ and
$\delta_\tau \in (0,1)$ depending on δ and ![]() $\tau,$ for which the following holds.
$\tau,$ for which the following holds.
Given a ball ![]() $B_0=B(x_0,R_0) \subset X,$ there exists a finite collection of disjoint balls
$B_0=B(x_0,R_0) \subset X,$ there exists a finite collection of disjoint balls ![]() $\lbrace B(z_n,s_n) \rbrace_n$ contained in
$\lbrace B(z_n,s_n) \rbrace_n$ contained in ![]() $B_0 \setminus E,$ with
$B_0 \setminus E,$ with
 \begin{equation*}
\tau R_0 \geq s_n \geq \delta_\tau h_E(B_0) \quad \text{and} \quad \sum_n \mu( B(z_n,s_n) ) \geq c \, C_\mu^{-2} \mu(B_0).
\end{equation*}
\begin{equation*}
\tau R_0 \geq s_n \geq \delta_\tau h_E(B_0) \quad \text{and} \quad \sum_n \mu( B(z_n,s_n) ) \geq c \, C_\mu^{-2} \mu(B_0).
\end{equation*}Proof. Let ![]() $\lbrace B(x_j,r_j) \rbrace_j$ be a collection of disjoint balls as in Definition 3.1 for the ball
$\lbrace B(x_j,r_j) \rbrace_j$ be a collection of disjoint balls as in Definition 3.1 for the ball ![]() $B_0.$ For every
$B_0.$ For every ![]() $j,$ let
$j,$ let  $\lbrace z_j^i \rbrace_i$ be a finite
$\lbrace z_j^i \rbrace_i$ be a finite ![]() $\tau r_j$-maximal net of the relatively compact set
$\tau r_j$-maximal net of the relatively compact set ![]() $B(x_j,(1-\tau) r_j).$ This means that
$B(x_j,(1-\tau) r_j).$ This means that  $z_j^i \in B(x_j,(1-\tau) r_j)$ for every
$z_j^i \in B(x_j,(1-\tau) r_j)$ for every ![]() $i,j$; that
$i,j$; that  $B(x_j,(1-\tau) r_j) \subset \bigcup_i B(z_j^i, \tau r_j)$ for every j; and the balls
$B(x_j,(1-\tau) r_j) \subset \bigcup_i B(z_j^i, \tau r_j)$ for every j; and the balls  $\lbrace B(z_j^i, \frac{\tau r_j}{2}) \rbrace_i$ are pairwise disjoint. In addition, the triangle inequality gives
$\lbrace B(z_j^i, \frac{\tau r_j}{2}) \rbrace_i$ are pairwise disjoint. In addition, the triangle inequality gives  $\bigcup_i B(z_j^i, \tau r_j) \subset B(x_j,r_j)$ for every
$\bigcup_i B(z_j^i, \tau r_j) \subset B(x_j,r_j)$ for every ![]() $j.$ Define
$j.$ Define ![]() $s_j=\frac{\tau r_j}{2}$ and
$s_j=\frac{\tau r_j}{2}$ and  $\delta_\tau=\frac{\tau \delta}{2}.$ Since the balls of the collection
$\delta_\tau=\frac{\tau \delta}{2}.$ Since the balls of the collection ![]() $\lbrace B(x_j,r_j) \rbrace_j$ are pairwise disjoint and are contained in
$\lbrace B(x_j,r_j) \rbrace_j$ are pairwise disjoint and are contained in ![]() $B_0 \setminus E,$ the new family
$B_0 \setminus E,$ the new family  $\lbrace B(z_j^i, s_j) \rbrace_{i,j}$ satisfies these two properties as well. Also, their radii sj satisfy
$\lbrace B(z_j^i, s_j) \rbrace_{i,j}$ satisfies these two properties as well. Also, their radii sj satisfy
 \begin{equation*}
\tau R_0 \geq s_j \geq \frac{\tau \delta}{2} h_E(B_0) = \delta_\tau h_E(B_0),
\end{equation*}
\begin{equation*}
\tau R_0 \geq s_j \geq \frac{\tau \delta}{2} h_E(B_0) = \delta_\tau h_E(B_0),
\end{equation*}and the first claim is proven. As concerns the estimate for the measures, we write
 \begin{align*}
c \mu(B_0) & \leq \sum_j \mu(B(x_j,r_j)) \leq C_\mu \sum_j \mu(B(x_j,(1-\tau)r_j)) \\
& \leq C_\mu \sum_j \sum_i \mu(B(z_j^i, \tau r_j)) \leq C_\mu^2 \sum_{j,i} \mu(B(z_j^i, s_j)).
\end{align*}
\begin{align*}
c \mu(B_0) & \leq \sum_j \mu(B(x_j,r_j)) \leq C_\mu \sum_j \mu(B(x_j,(1-\tau)r_j)) \\
& \leq C_\mu \sum_j \sum_i \mu(B(z_j^i, \tau r_j)) \leq C_\mu^2 \sum_{j,i} \mu(B(z_j^i, s_j)).
\end{align*} Dividing by ![]() $C_\mu^2$ in both sides, we get the desired inequality.
$C_\mu^2$ in both sides, we get the desired inequality.
7.2. Measures with annular decay properties
Assume that the space ![]() $(X, d, \mu)$ satisfies the following annular decay property: for every
$(X, d, \mu)$ satisfies the following annular decay property: for every ![]() $\eta \gt 0,$ there exists
$\eta \gt 0,$ there exists ![]() $\varepsilon \in (0,1)$ such that
$\varepsilon \in (0,1)$ such that
 \begin{equation}
\sup_{x\in X,\, 0 \lt t\leq s, \, 1- \frac{t}{s}\leq \varepsilon} \frac{\mu\left( B(x,s) \setminus B(x,t) \right)}{\mu(B(x,s))} \lt \eta.
\end{equation}
\begin{equation}
\sup_{x\in X,\, 0 \lt t\leq s, \, 1- \frac{t}{s}\leq \varepsilon} \frac{\mu\left( B(x,s) \setminus B(x,t) \right)}{\mu(B(x,s))} \lt \eta.
\end{equation}The standard annular decay property with power-type rate of decay (see e.g., [Reference Björn, Björn and Lehrbäck3, Definition 1.1]) is slightly stronger than (29). In this setting, if E is weakly porous, then hE is doubling.
Lemma 7.2. Let ![]() $E \subset X$ be a weakly porous set, with constants
$E \subset X$ be a weakly porous set, with constants ![]() $c, \delta \in (0,1).$
$c, \delta \in (0,1).$
(i) There exist constants
 $\lambda^* \in (1,2)$ and
$\lambda^* \in (1,2)$ and  $\delta^* \in (0,1)$ depending on
$\delta^* \in (0,1)$ depending on  $c,\delta,C_\mu$ and the parameters from (29), for which
$c,\delta,C_\mu$ and the parameters from (29), for which  $h_E(B(x_0,R_0)) \geq \delta^* h_E(B(x_0, \lambda^* R_0))$ for all
$h_E(B(x_0,R_0)) \geq \delta^* h_E(B(x_0, \lambda^* R_0))$ for all  $x_0 \in X,$
$x_0 \in X,$  $R_0 \gt 0.$
$R_0 \gt 0.$(ii) There are positive constants
 $b=b(\delta^*)$ and
$b=b(\delta^*)$ and  $d=d(\delta^*, \lambda^*)$ such that, for every
$d=d(\delta^*, \lambda^*)$ such that, for every  $x_0\in X$,
$x_0\in X$,  $R_0 \gt 0,$ and
$R_0 \gt 0,$ and  $L\geq 1,$ we have
$L\geq 1,$ we have
 \begin{equation*}
h_E(B(x_0, L R_0)) \leq b L^d h_E(B(x_0,R_0)).
\end{equation*}
\begin{equation*}
h_E(B(x_0, L R_0)) \leq b L^d h_E(B(x_0,R_0)).
\end{equation*}In particular,
 $h_E$ is doubling.
$h_E$ is doubling.
Proof. Let us prove (i). For  $ \eta= c \, C_\mu^{-2},$ let
$ \eta= c \, C_\mu^{-2},$ let ![]() $\varepsilon \in (0,1)$ be as in (29). Now, let parameters
$\varepsilon \in (0,1)$ be as in (29). Now, let parameters ![]() $\lambda \in (1,2)$,
$\lambda \in (1,2)$, ![]() $\tau \in (0,1/4)$ be so that
$\tau \in (0,1/4)$ be so that ![]() $\lambda \in (1,2)$ with
$\lambda \in (1,2)$ with  $ \lambda^{-1}=1- \frac{\varepsilon}{2}$ and
$ \lambda^{-1}=1- \frac{\varepsilon}{2}$ and ![]() $\tau=\varepsilon/4.$ The desired constants
$\tau=\varepsilon/4.$ The desired constants ![]() $\lambda^*$ and
$\lambda^*$ and ![]() $\delta^*$ are respectively defined as λ and
$\delta^*$ are respectively defined as λ and ![]() $\delta_\tau,$ where δτ is the one associated with τ from Lemma 7.1.
$\delta_\tau,$ where δτ is the one associated with τ from Lemma 7.1.
Now, for a fixed ball ![]() $B_0=B(x_0,R_0),$ we will denote
$B_0=B(x_0,R_0),$ we will denote ![]() $K B_0=B(x_0,K R_0)$ for any K > 0. If
$K B_0=B(x_0,K R_0)$ for any K > 0. If ![]() $s=\lambda^* R_0$ and
$s=\lambda^* R_0$ and ![]() $t= (1-2 \tau \lambda^*) R_0,$ we have that
$t= (1-2 \tau \lambda^*) R_0,$ we have that ![]() $1- \frac{t}{s} = \varepsilon,$ and so (29) yields
$1- \frac{t}{s} = \varepsilon,$ and so (29) yields
 \begin{equation}
\mu\left( \lambda^* B_0 \setminus (1-2\tau \lambda^*)B_0 \right) \lt c \, C_\mu^{-2}\mu(\lambda^* B_0).
\end{equation}
\begin{equation}
\mu\left( \lambda^* B_0 \setminus (1-2\tau \lambda^*)B_0 \right) \lt c \, C_\mu^{-2}\mu(\lambda^* B_0).
\end{equation} Suppose for the sake of contradiction, that ![]() $h_E(B_0) \lt \delta^* h_E(\lambda^* B_0).$
$h_E(B_0) \lt \delta^* h_E(\lambda^* B_0).$
Let ![]() $B=B(y,r) \subset \lambda^* B_0 \setminus E$ be a ball with
$B=B(y,r) \subset \lambda^* B_0 \setminus E$ be a ball with ![]() $ \tau \lambda^* R_0 \geq r \geq \delta^* h_E(\lambda^* B_0).$ We claim that the center y of the ball B does not belong to
$ \tau \lambda^* R_0 \geq r \geq \delta^* h_E(\lambda^* B_0).$ We claim that the center y of the ball B does not belong to ![]() $(1- \tau \lambda^*)B_0.$ Indeed, otherwise
$(1- \tau \lambda^*)B_0.$ Indeed, otherwise ![]() $d(x_0,y) \lt (1- \tau\lambda^*) R_0,$ and the ball
$d(x_0,y) \lt (1- \tau\lambda^*) R_0,$ and the ball ![]() $B(y,r)$ is contained in
$B(y,r)$ is contained in ![]() $B_0 \setminus E,$ with
$B_0 \setminus E,$ with ![]() $r \leq \tau \lambda^* R_0 \lt 2R_0$ and
$r \leq \tau \lambda^* R_0 \lt 2R_0$ and ![]() $r \geq \delta^* h_E(\lambda^* B_0) \gt h_E(B_0),$ contradicting the definition of
$r \geq \delta^* h_E(\lambda^* B_0) \gt h_E(B_0),$ contradicting the definition of ![]() $h_E(B_0).$ Thus, the point y does not belong to
$h_E(B_0).$ Thus, the point y does not belong to ![]() $(1-\tau \lambda^*)B_0,$ and because
$(1-\tau \lambda^*)B_0,$ and because ![]() $r\leq \tau \lambda^* R_0,$ the ball
$r\leq \tau \lambda^* R_0,$ the ball ![]() $B(y,r)$ does not contain any point of
$B(y,r)$ does not contain any point of ![]() $(1-2\tau \lambda^*)B_0,$ by virtue of the triangle inequality. Therefore
$(1-2\tau \lambda^*)B_0,$ by virtue of the triangle inequality. Therefore ![]() $B \subset \lambda^* B_0 \setminus (1-2\tau \lambda^*)B_0.$
$B \subset \lambda^* B_0 \setminus (1-2\tau \lambda^*)B_0.$
Now, let ![]() $B_1,\ldots, B_N$ be pairwise disjoint balls contained in
$B_1,\ldots, B_N$ be pairwise disjoint balls contained in ![]() $\lambda^* B_0 \setminus E,$ satisfying the conclusion of Lemma 7.1 for the ball
$\lambda^* B_0 \setminus E,$ satisfying the conclusion of Lemma 7.1 for the ball ![]() $\lambda^* B_0$ and τ as above. By the previous argument, all these balls are contained in
$\lambda^* B_0$ and τ as above. By the previous argument, all these balls are contained in ![]() $\lambda^* B_0 \setminus (1-2\tau \lambda^*)B_0,$ and so we have the estimates
$\lambda^* B_0 \setminus (1-2\tau \lambda^*)B_0,$ and so we have the estimates
 \begin{equation*}
\mu\left( \lambda^* B_0 \setminus (1-2\tau \lambda^*)B_0 \right) \geq \sum_{i=1}^N \mu(B_i) \geq c \, C_\mu^{-2} \mu(\lambda^* B_0) .
\end{equation*}
\begin{equation*}
\mu\left( \lambda^* B_0 \setminus (1-2\tau \lambda^*)B_0 \right) \geq \sum_{i=1}^N \mu(B_i) \geq c \, C_\mu^{-2} \mu(\lambda^* B_0) .
\end{equation*} But this contradicts (30). We conclude ![]() $h_E(B_0) \geq \delta^* h_E(\lambda^* B_0)$.
$h_E(B_0) \geq \delta^* h_E(\lambda^* B_0)$.
Next, we show (ii). Given ![]() $L \gt 1,$ let
$L \gt 1,$ let ![]() $n\in {\mathbb N}$ be so that
$n\in {\mathbb N}$ be so that  $n-1 \lt \frac{\log L}{\log(\lambda^*)} \leq n$, where
$n-1 \lt \frac{\log L}{\log(\lambda^*)} \leq n$, where ![]() $\lambda^*$ is the constant from (i). Then
$\lambda^*$ is the constant from (i). Then ![]() $ L \leq (\lambda^*)^n$ and we can apply repeatedly (i) to obtain
$ L \leq (\lambda^*)^n$ and we can apply repeatedly (i) to obtain
 \begin{align*}
h_E( L B_0) & \leq h_E((\lambda^*)^{n} B_0) \leq (\delta^*)^{-1} h_E((\lambda^*)^{n-1} B_0) \leq \cdots \\
& \leq (\delta^*)^{-n} h_E( B_0) \leq (\delta^*)^{-1} L^{\frac{\log(1/\delta^*)}{\log(\lambda^*)}} h_E(B_0).
\end{align*}
\begin{align*}
h_E( L B_0) & \leq h_E((\lambda^*)^{n} B_0) \leq (\delta^*)^{-1} h_E((\lambda^*)^{n-1} B_0) \leq \cdots \\
& \leq (\delta^*)^{-n} h_E( B_0) \leq (\delta^*)^{-1} L^{\frac{\log(1/\delta^*)}{\log(\lambda^*)}} h_E(B_0).
\end{align*} We conclude from Lemma 7.2 that in a metric measure space ![]() $(X,d,\mu)$ with the property (29), the statements (A) of Theorem 1.3 and (A) of Theorem 1.1 are equivalent. Theorem 1.3 is then a consequence of Theorem 1.1 in this class of spaces.
$(X,d,\mu)$ with the property (29), the statements (A) of Theorem 1.3 and (A) of Theorem 1.1 are equivalent. Theorem 1.3 is then a consequence of Theorem 1.1 in this class of spaces.
7.3. Absolute dyadic weak porosity
In this subsection, we only assume that ![]() $(X,d,\mu)$ is a metric space with doubling measure. The following lemma shows that if we can cover a sufficiently large portion of the measure of all the dyadic cubes Q 0 using the E-free dyadic subcubes of Q 0 that are admissible for the definition of dyadic weak porosity, then the maximal dyadic hole is doubling.
$(X,d,\mu)$ is a metric space with doubling measure. The following lemma shows that if we can cover a sufficiently large portion of the measure of all the dyadic cubes Q 0 using the E-free dyadic subcubes of Q 0 that are admissible for the definition of dyadic weak porosity, then the maximal dyadic hole is doubling.
Lemma 7.3. Let ![]() $E$ be dyadic weakly porous set with constants
$E$ be dyadic weakly porous set with constants ![]() $M\in {\mathbb N},$ and
$M\in {\mathbb N},$ and ![]() $c\in (0,1).$ If
$c\in (0,1).$ If  $c \geq 1- C_\mu^{-1-\left\lfloor \log_2 \left( \frac{2A}{a \theta} \right) \right\rfloor},$ then
$c \geq 1- C_\mu^{-1-\left\lfloor \log_2 \left( \frac{2A}{a \theta} \right) \right\rfloor},$ then ![]() $g_E$ is doubling with number
$g_E$ is doubling with number ![]() $M.$
$M.$
Proof. Let ![]() $Q_0, Q_0^* \in \mathcal{D}$ be two cubes of the same grid with
$Q_0, Q_0^* \in \mathcal{D}$ be two cubes of the same grid with ![]() $Q_0 \in \mathcal{D}(Q_0^*),$
$Q_0 \in \mathcal{D}(Q_0^*),$ ![]() $g(Q_0^*)=g(Q_0)-1,$ and
$g(Q_0^*)=g(Q_0)-1,$ and ![]() $Q_0 \cap E \neq \emptyset.$ Suppose for the sake of contradiction, that
$Q_0 \cap E \neq \emptyset.$ Suppose for the sake of contradiction, that ![]() $g_E(Q_0) \gt M+g_E(Q_0^*).$ Let
$g_E(Q_0) \gt M+g_E(Q_0^*).$ Let ![]() $P_1,\ldots,P_N \in \mathcal{D}(Q_0^*)$ be E-free and mutually disjoint cubes with
$P_1,\ldots,P_N \in \mathcal{D}(Q_0^*)$ be E-free and mutually disjoint cubes with ![]() $g(P_i) \leq M + g_E(Q_0^*),$ and
$g(P_i) \leq M + g_E(Q_0^*),$ and  $\sum_{i=1}^N \mu(P_i) \geq c \mu(Q_0^*).$ Suppose that one of these cubes Pi intersects
$\sum_{i=1}^N \mu(P_i) \geq c \mu(Q_0^*).$ Suppose that one of these cubes Pi intersects ![]() $Q_0.$ Then either
$Q_0.$ Then either ![]() $Q_0 \subseteq P_i$ or
$Q_0 \subseteq P_i$ or ![]() $P_i \subsetneq Q_0.$ The first case is impossible, because
$P_i \subsetneq Q_0.$ The first case is impossible, because ![]() $Q_0 \cap E \neq \emptyset = P_i \cap E.$ The second one would imply, by Lemma 2.4, that
$Q_0 \cap E \neq \emptyset = P_i \cap E.$ The second one would imply, by Lemma 2.4, that ![]() $P_i \in \mathcal{D}(Q_0),$ with
$P_i \in \mathcal{D}(Q_0),$ with ![]() $P_i \cap E =\emptyset,$ and so
$P_i \cap E =\emptyset,$ and so ![]() $g_E(Q_0) \leq g(P_i) \leq M + g_E(Q_0^*),$ contradicting the assumption. Consequently, we must have
$g_E(Q_0) \leq g(P_i) \leq M + g_E(Q_0^*),$ contradicting the assumption. Consequently, we must have ![]() $Q_0 \cap P_i = \emptyset$ for every
$Q_0 \cap P_i = \emptyset$ for every ![]() $i=1,\ldots, N,$ and thus we obtain
$i=1,\ldots, N,$ and thus we obtain
 \begin{equation*}
\mu(Q_0^*\setminus Q_0) \geq \sum_{i=1}^N \mu(P_i) \geq c \mu(Q_0^*).
\end{equation*}
\begin{equation*}
\mu(Q_0^*\setminus Q_0) \geq \sum_{i=1}^N \mu(P_i) \geq c \mu(Q_0^*).
\end{equation*} Then  $\mu(Q_0) \leq (1-c) \mu(Q^*_0) \leq C_\mu^{-1-\left\lfloor \log_2 \left( \frac{2A}{a \theta} \right) \right\rfloor} \mu(Q_0^*).$ But denoting z 0 and
$\mu(Q_0) \leq (1-c) \mu(Q^*_0) \leq C_\mu^{-1-\left\lfloor \log_2 \left( \frac{2A}{a \theta} \right) \right\rfloor} \mu(Q_0^*).$ But denoting z 0 and ![]() $z_0^*$ respectively the reference points of Q 0 and
$z_0^*$ respectively the reference points of Q 0 and ![]() $Q_0^*,$ the chain of inclusions
$Q_0^*,$ the chain of inclusions
 \begin{equation*}
B(z_0,a \theta^{g(Q_0)}) \subset Q_0 \subset Q_0^* \subset B(z_0^*,A\theta^{g(Q_0^*)}) \subset B(z_0, 2A \theta^{-1} \theta^{g(Q_0)}),
\end{equation*}
\begin{equation*}
B(z_0,a \theta^{g(Q_0)}) \subset Q_0 \subset Q_0^* \subset B(z_0^*,A\theta^{g(Q_0^*)}) \subset B(z_0, 2A \theta^{-1} \theta^{g(Q_0)}),
\end{equation*} together with the doubling property for ![]() $\mu,$ lead us to a contradiction. We conclude
$\mu,$ lead us to a contradiction. We conclude ![]() $g_E(Q_0) \leq M+g_E(Q_0^*).$ On the other hand, in the case where
$g_E(Q_0) \leq M+g_E(Q_0^*).$ On the other hand, in the case where ![]() $Q_0 \cap E= \emptyset,$ one has
$Q_0 \cap E= \emptyset,$ one has ![]() $g_E(Q_0)=g(Q_0)=g(Q_0^*)+1 \leq g_E(Q_0^*)+1,$ and the result follows as well.
$g_E(Q_0)=g(Q_0)=g(Q_0^*)+1 \leq g_E(Q_0^*)+1,$ and the result follows as well.
Define  $b_\mu:=1- C_\mu^{-1-\left\lfloor \log_2 \left( \frac{2A}{a \theta} \right) \right\rfloor},$ the lower bound from Lemma 7.3. We say that E has absolute dyadic weak porosity when E is dyadic weakly porous with some constants
$b_\mu:=1- C_\mu^{-1-\left\lfloor \log_2 \left( \frac{2A}{a \theta} \right) \right\rfloor},$ the lower bound from Lemma 7.3. We say that E has absolute dyadic weak porosity when E is dyadic weakly porous with some constants ![]() $M\in {\mathbb N}$ and
$M\in {\mathbb N}$ and ![]() $c\in [ b_\mu,1).$
$c\in [ b_\mu,1).$
Lemma 7.3 has the following consequence: for a set E with absolute dyadic weak porosity, gE is doubling. Therefore, we obtain that ![]() $\operatorname{dist}(\cdot , E)^{-\alpha} \in A_1(X)$ for some
$\operatorname{dist}(\cdot , E)^{-\alpha} \in A_1(X)$ for some ![]() $\alpha \gt 0,$ e.g., using the implication (A)
$\alpha \gt 0,$ e.g., using the implication (A)![]() $\implies$(B) in Theorem 1.1 together with Lemma 3.7. On the other hand, in Lemma 4.1(i) we showed that the A 1 condition for
$\implies$(B) in Theorem 1.1 together with Lemma 3.7. On the other hand, in Lemma 4.1(i) we showed that the A 1 condition for ![]() $ \operatorname{dist}(\cdot , E)^{-\alpha} $ implies that E satisfies the condition of dyadic weak porosity with constant c as close to 1 as desired. This observation leads us to the following corollary.
$ \operatorname{dist}(\cdot , E)^{-\alpha} $ implies that E satisfies the condition of dyadic weak porosity with constant c as close to 1 as desired. This observation leads us to the following corollary.
Corollary 7.4. Let ![]() $(X,d,\mu)$ be a metric space with doubling measure, and
$(X,d,\mu)$ be a metric space with doubling measure, and ![]() $E \subset X$ a subset. The following statements are equivalent:
$E \subset X$ a subset. The following statements are equivalent:
(1)
 $E$ has absolute dyadic weak porosity.
$E$ has absolute dyadic weak porosity.(2) There exists α > 0 for which
 $\operatorname{dist}(\cdot, E)^{-\alpha} \in A_1(X)$.
$\operatorname{dist}(\cdot, E)^{-\alpha} \in A_1(X)$.
8. Weak porosity and doubling maximal free holes are unrelated
The purpose of this section is to show that the conditions of weak porosity and of doubling maximal E-free holes hE for a set E are, in general, independent of each other. To do this, we present two examples in the following subsections, the latter of which is Theorem 1.2.
8.1. Weak porosity does not imply doubling maximal holes
The following example tells us that not for every weakly porous set E the maximal hole hE is doubling. Combining Lemmas 4.1 and 3.7, this implies that not every weakly porous set E has the property that ![]() $\operatorname{dist}(\cdot, E)^{-\alpha} \in A_1(X)$ for some α > 0. Furthermore, we can actually prove that the weights of the form
$\operatorname{dist}(\cdot, E)^{-\alpha} \in A_1(X)$ for some α > 0. Furthermore, we can actually prove that the weights of the form ![]() $\operatorname{dist}(\cdot, E)^{-\alpha}$, with α > 0, are not doubling.
$\operatorname{dist}(\cdot, E)^{-\alpha}$, with α > 0, are not doubling.
Example 8.1. Consider the space ![]() $X= \lbrace (x_1,x_2) \in {\mathbb R}^2 \, : \, x_1 x_2=0, \: x_1 \geq 0,\, x_2 \geq 0 \rbrace,$ equipped with the distance
$X= \lbrace (x_1,x_2) \in {\mathbb R}^2 \, : \, x_1 x_2=0, \: x_1 \geq 0,\, x_2 \geq 0 \rbrace,$ equipped with the distance ![]() $d:=\ell_\infty \! \! \! \upharpoonright_X$, and with the measure
$d:=\ell_\infty \! \! \! \upharpoonright_X$, and with the measure ![]() $\mu:=\mathcal{H}^1$. Then
$\mu:=\mathcal{H}^1$. Then ![]() $(X, d,\mu)$ is a connected metric space with doubling measure. In addition, it can be easily checked that every open ball
$(X, d,\mu)$ is a connected metric space with doubling measure. In addition, it can be easily checked that every open ball ![]() $B \subset X$ has unique center and radius. The set
$B \subset X$ has unique center and radius. The set ![]() $E= ({\mathbb N} \cup \lbrace 0 \rbrace) \times \lbrace 0 \rbrace \subset X$ satisfies the following properties.
$E= ({\mathbb N} \cup \lbrace 0 \rbrace) \times \lbrace 0 \rbrace \subset X$ satisfies the following properties.
(1) E is weakly porous with constants
 $c=1/3$ and
$c=1/3$ and  $\delta=1/2.$
$\delta=1/2.$(2) hE is not doubling.
(3) For every
 $\alpha \in (0,1),$ the weight
$\alpha \in (0,1),$ the weight  $w=\operatorname{dist}(\cdot, E)^{-\alpha}$ is not doubling. Consequently,
$w=\operatorname{dist}(\cdot, E)^{-\alpha}$ is not doubling. Consequently,  $\operatorname{dist}(\cdot, E)^{-\alpha} \notin A_p(X)$ for all α > 0 and
$\operatorname{dist}(\cdot, E)^{-\alpha} \notin A_p(X)$ for all α > 0 and  $p\geq 1;$ see the comment subsequent to Definition 2.1.
$p\geq 1;$ see the comment subsequent to Definition 2.1.(4) If
 $c \gt 1/3,$ then for every
$c \gt 1/3,$ then for every  $\delta \in (0,1)$ there exists an open ball
$\delta \in (0,1)$ there exists an open ball  $B_0 \subset X,$ such that for any finite collection of open balls
$B_0 \subset X,$ such that for any finite collection of open balls  $\lbrace B_i=B(p_i,r_i) \rbrace_i$ contained in
$\lbrace B_i=B(p_i,r_i) \rbrace_i$ contained in  $B_0 \setminus E$ with
$B_0 \setminus E$ with  $r_i \geq \delta h_E(B_0),$ we have
$r_i \geq \delta h_E(B_0),$ we have  $\mu \left( \bigcup_i B_i \right) \lt c \mu(B_0).$ Therefore, if
$\mu \left( \bigcup_i B_i \right) \lt c \mu(B_0).$ Therefore, if  $c \gt 1/3,$ for no
$c \gt 1/3,$ for no  $\delta \in (0,1)$ the set E is weakly porous with constants
$\delta \in (0,1)$ the set E is weakly porous with constants  $(c,\delta). $
$(c,\delta). $
(1) There are two types of open balls
 $B_0=B(p,R_0) \subset X,$
$B_0=B(p,R_0) \subset X,$  $p=(p_1,p_2)\in X,$
$p=(p_1,p_2)\in X,$  $R_0 \gt 0$ to be checked.
$R_0 \gt 0$ to be checked.(I)
 $(0,0) \notin B_0.$ This is equivalent to saying that
$(0,0) \notin B_0.$ This is equivalent to saying that  $R_0 \leq \max \lbrace p_1,p_2 \rbrace.$ If
$R_0 \leq \max \lbrace p_1,p_2 \rbrace.$ If  $p_1=0,$ then
$p_1=0,$ then  $B_0 \subset \lbrace x_1=0 \rbrace,$
$B_0 \subset \lbrace x_1=0 \rbrace,$  $B_0 \cap E =\emptyset,$ and the condition of weak porosity trivially holds. If
$B_0 \cap E =\emptyset,$ and the condition of weak porosity trivially holds. If  $p_2=0,$ then
$p_2=0,$ then  $B_0 \subset \lbrace x_2=0 \rbrace$, and the condition of weak porosity with constants
$B_0 \subset \lbrace x_2=0 \rbrace$, and the condition of weak porosity with constants  $c=1/3$ and
$c=1/3$ and  $\delta =1/2$ for B 0 follows by easy computations.
$\delta =1/2$ for B 0 follows by easy computations.(II)
 $(0,0) \in B_0.$ Then
$(0,0) \in B_0.$ Then  $R_0 \gt \max\lbrace p_1,p_2 \rbrace,$ and B 0 can be written as
$R_0 \gt \max\lbrace p_1,p_2 \rbrace,$ and B 0 can be written as
 \begin{equation*}
B_0=\left\lbrace
\begin{array}{lccl}
\left( (0, p_1+R_0) \times \lbrace 0 \rbrace \right) \cup \left(\lbrace 0 \rbrace \times (0,R_0) \right) \cup \lbrace (0,0) \rbrace & \mbox{if } &\: p_2=0 & \\
\left( (0, R_0) \times \lbrace 0 \rbrace \right) \cup \left(\lbrace 0 \rbrace \times (0,p_2+R_0) \right) \cup \lbrace (0,0) \rbrace & \mbox{if } &\: p_1 = 0, &
\end{array}
\right.
\end{equation*}
\begin{equation*}
B_0=\left\lbrace
\begin{array}{lccl}
\left( (0, p_1+R_0) \times \lbrace 0 \rbrace \right) \cup \left(\lbrace 0 \rbrace \times (0,R_0) \right) \cup \lbrace (0,0) \rbrace & \mbox{if } &\: p_2=0 & \\
\left( (0, R_0) \times \lbrace 0 \rbrace \right) \cup \left(\lbrace 0 \rbrace \times (0,p_2+R_0) \right) \cup \lbrace (0,0) \rbrace & \mbox{if } &\: p_1 = 0, &
\end{array}
\right.
\end{equation*}where the unions are disjoint.
In the case where
 $p_2=0,$ the ball
$p_2=0,$ the ball  $B^*=\lbrace 0 \rbrace \times (0,R_0) \subset B_0 \setminus E $ has radius equal to
$B^*=\lbrace 0 \rbrace \times (0,R_0) \subset B_0 \setminus E $ has radius equal to  $R_0/2$ and
$R_0/2$ and  $\mu(B^*) =R_0 \geq \mu(B_0)/3.$ The value of
$\mu(B^*) =R_0 \geq \mu(B_0)/3.$ The value of  $h_E(B_0)$ is
$h_E(B_0)$ is  $h_E(B_0)=\frac{1}{2}\max\lbrace R_0, \min\lbrace 1, p_1+R_0 \rbrace \rbrace$, and because
$h_E(B_0)=\frac{1}{2}\max\lbrace R_0, \min\lbrace 1, p_1+R_0 \rbrace \rbrace$, and because  $p_1 \lt R_0,$ for any value of
$p_1 \lt R_0,$ for any value of  $h_E(B_0)$ we have that the radius
$h_E(B_0)$ we have that the radius  $R_0/2$ of
$R_0/2$ of  $B^*$ satisfies
$B^*$ satisfies  $R_0/2 \geq h_E(B_0)/2.$ Thus, for the balls B 0 in this subcase where
$R_0/2 \geq h_E(B_0)/2.$ Thus, for the balls B 0 in this subcase where  $p_2=0,$ the weak porosity for B 0 is true with
$p_2=0,$ the weak porosity for B 0 is true with  $c=1/3$ and
$c=1/3$ and  $\delta=1/2.$
$\delta=1/2.$Now, when
 $p_1=0,$ the ball
$p_1=0,$ the ball  $B^*=\lbrace 0 \rbrace \times (0,p_2+R_0) \subset B_0 \setminus E$ has radius equal to
$B^*=\lbrace 0 \rbrace \times (0,p_2+R_0) \subset B_0 \setminus E$ has radius equal to  $(p_2+R_0)/2$ and
$(p_2+R_0)/2$ and  $\mu(B^*)=p_2+R_0 \geq \mu(B_0)/2.$ In this subcase, we have
$\mu(B^*)=p_2+R_0 \geq \mu(B_0)/2.$ In this subcase, we have  $h_E(B_0)=(p_2+R_0)/2,$ so the condition of weak porosity for B 0 is true with constants
$h_E(B_0)=(p_2+R_0)/2,$ so the condition of weak porosity for B 0 is true with constants  $c=\delta=1/2$
$c=\delta=1/2$
(2) For every
 $n\in {\mathbb N},$ consider the open balls
$n\in {\mathbb N},$ consider the open balls  $B_n=B((n,0),n)$ and
$B_n=B((n,0),n)$ and  $2B_n=B((n,0),2n)$ of X centered at
$2B_n=B((n,0),2n)$ of X centered at  $(n,0)$ and with radius n and 2n respectively. Then
$(n,0)$ and with radius n and 2n respectively. Then  $B_n = (0,2n) \times \lbrace 0 \rbrace$ and
$B_n = (0,2n) \times \lbrace 0 \rbrace$ and  $2B_n= \left( (0,3n) \times \lbrace 0 \rbrace \right) \cup \left( \lbrace 0 \rbrace \times (0, 2n) \right) \cup \lbrace (0,0) \rbrace$. Clearly,
$2B_n= \left( (0,3n) \times \lbrace 0 \rbrace \right) \cup \left( \lbrace 0 \rbrace \times (0, 2n) \right) \cup \lbrace (0,0) \rbrace$. Clearly,  $h_E(B_n)= 1/2,$ but the open ball
$h_E(B_n)= 1/2,$ but the open ball  $\widehat{B}_n=\lbrace 0 \rbrace \times (0,2n)$ is contained in
$\widehat{B}_n=\lbrace 0 \rbrace \times (0,2n)$ is contained in  $2B_n \setminus E$ and has radius equal to
$2B_n \setminus E$ and has radius equal to  $n.$ Therefore
$n.$ Therefore  $h_E(2B_n) \geq n,$ and so
$h_E(2B_n) \geq n,$ and so
 \begin{equation*}
\lim_n \frac{h_E(2B_n)}{h_E(B_n)} = \infty.
\end{equation*}
\begin{equation*}
\lim_n \frac{h_E(2B_n)}{h_E(B_n)} = \infty.
\end{equation*}According to Definition 3.4, hE is not doubling.
(3) Fix
 $\alpha \in (0,1),$ and set
$\alpha \in (0,1),$ and set  $w=\operatorname{dist}(\cdot,E)^{-\alpha}.$ For the balls
$w=\operatorname{dist}(\cdot,E)^{-\alpha}.$ For the balls  $B_n=B((0,n),n)= \lbrace 0 \rbrace \times (0, 2n)$ and
$B_n=B((0,n),n)= \lbrace 0 \rbrace \times (0, 2n)$ and  $2B_n=B((0,n),2n)= \left( \lbrace 0 \rbrace \times (0, 3n) \right) \cup \left( (0,2n) \times \lbrace 0 \rbrace \right) \cup \lbrace (0,0) \rbrace,$ we have
$2B_n=B((0,n),2n)= \left( \lbrace 0 \rbrace \times (0, 3n) \right) \cup \left( (0,2n) \times \lbrace 0 \rbrace \right) \cup \lbrace (0,0) \rbrace,$ we have
 \begin{equation*}
w(B_n)=\int_0^{2n} t^{-\alpha} \, d t = \frac{(2n)^{1-\alpha}}{1-\alpha},
\end{equation*}
\begin{equation*}
w(B_n)=\int_0^{2n} t^{-\alpha} \, d t = \frac{(2n)^{1-\alpha}}{1-\alpha},
\end{equation*}whereas
 \begin{equation*}
w(2B_n) \geq \int_{ (0,2n) \times \lbrace 0 \rbrace } w\, d \mu = \sum_{k=1}^{2n} \int_{k-1}^{k} \operatorname{dist} \left( t, \lbrace k-1,k \rbrace \right)^{-\alpha} \, d t= c(\alpha) 2n.
\end{equation*}
\begin{equation*}
w(2B_n) \geq \int_{ (0,2n) \times \lbrace 0 \rbrace } w\, d \mu = \sum_{k=1}^{2n} \int_{k-1}^{k} \operatorname{dist} \left( t, \lbrace k-1,k \rbrace \right)^{-\alpha} \, d t= c(\alpha) 2n.
\end{equation*}Here
 $c(\alpha) \gt 0$ is a constant depending only on
$c(\alpha) \gt 0$ is a constant depending only on  $\alpha.$ Because
$\alpha.$ Because  $\alpha \gt 0,$
$\alpha \gt 0,$  $\lim_n \frac{w(2B_n)}{w(B_n)} = \infty,$ and hence w is not a doubling weight. On the other hand, if
$\lim_n \frac{w(2B_n)}{w(B_n)} = \infty,$ and hence w is not a doubling weight. On the other hand, if  $\alpha \geq 1,$
$\alpha \geq 1,$  $w=\operatorname{dist}(\cdot, E)^{-\alpha}$ is not locally integrable (e.g., over balls centered at
$w=\operatorname{dist}(\cdot, E)^{-\alpha}$ is not locally integrable (e.g., over balls centered at  $(0,0)$) and thus w does not even define a weight function.
$(0,0)$) and thus w does not even define a weight function.(4) Fix the parameters
 $c \gt 1/3$ and
$c \gt 1/3$ and  $\delta\in (0,1).$ Let λ > 1 be close enough to 1 so that
$\delta\in (0,1).$ Let λ > 1 be close enough to 1 so that  $\frac{\lambda}{1+2\lambda} \lt c,$ and
$\frac{\lambda}{1+2\lambda} \lt c,$ and  $n\in {\mathbb N}$ be so that
$n\in {\mathbb N}$ be so that  $ \lambda \delta n \gt 2.$ For the ball
$ \lambda \delta n \gt 2.$ For the ball  $B_0=B( (n,0), \lambda n),$ we have
$B_0=B( (n,0), \lambda n),$ we have  $h_E(B_0)=\frac{\lambda n}{2}$, and every ball
$h_E(B_0)=\frac{\lambda n}{2}$, and every ball  $B(p,r)$ contained in
$B(p,r)$ contained in  $B_0 \setminus E $ with the property that
$B_0 \setminus E $ with the property that  $r \geq \delta h_E(B_0)$ must be contained in
$r \geq \delta h_E(B_0)$ must be contained in  $B^*_0=\lbrace 0 \rbrace \times (0, \lambda n)$. Therefore, for any finite collection of balls
$B^*_0=\lbrace 0 \rbrace \times (0, \lambda n)$. Therefore, for any finite collection of balls  $B_1, \ldots, B_N $ contained in
$B_1, \ldots, B_N $ contained in  $B_0 \setminus E$ and with radius at least
$B_0 \setminus E$ and with radius at least  $\delta h_E(B_0),$ one has
$\delta h_E(B_0),$ one has
 \begin{equation*}
\mu \Big ( \bigcup_i B_i \Big ) \leq \mu(B_0^*) = \lambda n \lt c (1+2\lambda) n = c \mu(B_0).
\end{equation*}
\begin{equation*}
\mu \Big ( \bigcup_i B_i \Big ) \leq \mu(B_0^*) = \lambda n \lt c (1+2\lambda) n = c \mu(B_0).
\end{equation*}
Notice that property (4) in Example 8.1 shows that the condition of weak porosity of E is, in general, not self-improving in the sense of enlarging the parameter ![]() $c.$
$c.$
Remark 8.2. It is not difficult to adapt Example 8.1 to a bounded space ![]() $X.$ Indeed, it suffices to consider
$X.$ Indeed, it suffices to consider ![]() $X = [0,1] \times [0,1],$ with the same metric and measure as above, and the set
$X = [0,1] \times [0,1],$ with the same metric and measure as above, and the set ![]() $E = \lbrace (0,0) \rbrace \cup \left( \lbrace 1/n \, : \, n \in {\mathbb N} \rbrace \times \lbrace 0 \rbrace \right).$ Then hE does not satisfy the doubling property for balls Bn centered at
$E = \lbrace (0,0) \rbrace \cup \left( \lbrace 1/n \, : \, n \in {\mathbb N} \rbrace \times \lbrace 0 \rbrace \right).$ Then hE does not satisfy the doubling property for balls Bn centered at ![]() $(1/(2n), 0)$ and with radius
$(1/(2n), 0)$ and with radius ![]() $1/(2n),$ because
$1/(2n),$ because ![]() $h_E(2B_n) = 1/n$ and
$h_E(2B_n) = 1/n$ and ![]() $h_E(B_n) \approx 1/n^2.$ And with similar arguments to those in Example 8.1(1), one can show that E is weakly porous. Indeed, the proof differs only in the case where
$h_E(B_n) \approx 1/n^2.$ And with similar arguments to those in Example 8.1(1), one can show that E is weakly porous. Indeed, the proof differs only in the case where ![]() $(0,0) \notin B_0=B(p,R_0)$ where
$(0,0) \notin B_0=B(p,R_0)$ where ![]() $p=(p_1,0),$ so that
$p=(p_1,0),$ so that ![]() $p_1\geq R_0$ and
$p_1\geq R_0$ and ![]() $B_0 = (0, \min\lbrace 1, p_1 + R_0 \rbrace) \times \lbrace 0 \rbrace.$ The set E satisfies the weak porosity condition for B 0 for the same reason that the set
$B_0 = (0, \min\lbrace 1, p_1 + R_0 \rbrace) \times \lbrace 0 \rbrace.$ The set E satisfies the weak porosity condition for B 0 for the same reason that the set ![]() $\lbrace 1/n \rbrace_n$ satisfies the weak porosity for any interval
$\lbrace 1/n \rbrace_n$ satisfies the weak porosity for any interval ![]() $(0,a),$ a > 0. The easy proof of this fact is left to the reader.
$(0,a),$ a > 0. The easy proof of this fact is left to the reader.
8.2. A non-weakly porous set with doubling maximal holes
We will now prove Theorem 1.2, where we obtain a non-weakly porous set ![]() $E \subset {\mathbb R}$ whose maximal free holes are doubling. As a matter of fact, although the functions
$E \subset {\mathbb R}$ whose maximal free holes are doubling. As a matter of fact, although the functions ![]() $\operatorname{dist}(\cdot,E)^{-\alpha}$, with
$\operatorname{dist}(\cdot,E)^{-\alpha}$, with ![]() $\alpha \in (-\infty,1)\setminus \lbrace 0 \rbrace,$ define doubling weights, they do not belong to any class
$\alpha \in (-\infty,1)\setminus \lbrace 0 \rbrace,$ define doubling weights, they do not belong to any class ![]() $A_p({\mathbb R})$,
$A_p({\mathbb R})$, ![]() $p \geq 1.$ The following example is a more precise formulation of the theorem.
$p \geq 1.$ The following example is a more precise formulation of the theorem.
Example 8.3. We endow ![]() ${\mathbb R}$ with the usual distance and the Lebesgue measure. There exists a set
${\mathbb R}$ with the usual distance and the Lebesgue measure. There exists a set ![]() $E \subset {\mathbb R}$ such that:
$E \subset {\mathbb R}$ such that:
(1)
 $w_{\alpha}:=\operatorname{dist}(\cdot,E)^{-\alpha} \in L_{\textrm{loc}}^1({\mathbb R})$ for
$w_{\alpha}:=\operatorname{dist}(\cdot,E)^{-\alpha} \in L_{\textrm{loc}}^1({\mathbb R})$ for  $\alpha \lt 1, $ i.e., wα defines a weight function.
$\alpha \lt 1, $ i.e., wα defines a weight function.(2)
 $E$ is not weakly porous. In fact,
$E$ is not weakly porous. In fact,  $w_{\alpha}\notin \bigcup_{p \geq 1} A_p({\mathbb R})$ for every α ≠ 0.
$w_{\alpha}\notin \bigcup_{p \geq 1} A_p({\mathbb R})$ for every α ≠ 0.(3) hE is doubling with constant 16.
(4) wα defines a doubling weight in
 ${\mathbb R}$ for all α < 1; meaning that
${\mathbb R}$ for all α < 1; meaning that  $w_\alpha(K) \leq C w_\alpha(J)$ whenever
$w_\alpha(K) \leq C w_\alpha(J)$ whenever  $J \subset K \subset {\mathbb R}$ are intervals with
$J \subset K \subset {\mathbb R}$ are intervals with  $|K| \leq 2 |J|.$
$|K| \leq 2 |J|.$
Proof. We construct E as in [Reference Anderson, Lehrbäck, Mudarra and Vähäkangas1, Section 8], but here all the dilations will be equal to ![]() $1/2.$ Define
$1/2.$ Define ![]() $E_0:=\lbrace 0,1 \rbrace$ and
$E_0:=\lbrace 0,1 \rbrace$ and ![]() $E_n:=E_{n-1} \cup E_{n-1}^1 \cup E_{n-1}^2,$ for every
$E_n:=E_{n-1} \cup E_{n-1}^1 \cup E_{n-1}^2,$ for every ![]() $n\in {\mathbb N},$ where:
$n\in {\mathbb N},$ where:
•
 $E_{n-1}^1$ is a translation of
$E_{n-1}^1$ is a translation of  $E_{n-1}$ dilated by
$E_{n-1}$ dilated by  $1/2$ and whose first point is the last point of
$1/2$ and whose first point is the last point of  $E_{n-1},$
$E_{n-1},$•
 $E_{n-1}^2$ is a translation of
$E_{n-1}^2$ is a translation of  $E_{n-1}$ whose first point is the last point of
$E_{n-1}$ whose first point is the last point of  $E_{n-1}^1.$
$E_{n-1}^1.$
Finally, we define ![]() $E^+= \bigcup_{n=0}^\infty E_n$ and
$E^+= \bigcup_{n=0}^\infty E_n$ and ![]() $E= E^+ \cup \left( - E^+ \right).$ Here
$E= E^+ \cup \left( - E^+ \right).$ Here ![]() $-E^+$ is the reflection of
$-E^+$ is the reflection of ![]() $E^+$ with respect to the origin. We let
$E^+$ with respect to the origin. We let ![]() $\mathcal{I}_n,$
$\mathcal{I}_n,$ ![]() $\mathcal{I}_n^1,$ and
$\mathcal{I}_n^1,$ and ![]() $\mathcal{I}_n^2$ denote the smallest closed intervals containing En,
$\mathcal{I}_n^2$ denote the smallest closed intervals containing En, ![]() $E_n^1,$ and
$E_n^1,$ and ![]() $E_n^2$ respectively, for every
$E_n^2$ respectively, for every ![]() $n\in {\mathbb N} \cup \lbrace 0 \rbrace.$ A closed interval I whose endpoints are two consecutive points of E is called an edge of E. In particular,
$n\in {\mathbb N} \cup \lbrace 0 \rbrace.$ A closed interval I whose endpoints are two consecutive points of E is called an edge of E. In particular, ![]() $\textrm{int}(I) \cap E = \emptyset$ if I is an edge of
$\textrm{int}(I) \cap E = \emptyset$ if I is an edge of ![]() $E.$ The main properties of E are:
$E.$ The main properties of E are:
• For every
 $n\in {\mathbb N} \cup \lbrace 0 \rbrace$ and
$n\in {\mathbb N} \cup \lbrace 0 \rbrace$ and  $k\in \lbrace 0,\ldots, n\rbrace,$ the interval
$k\in \lbrace 0,\ldots, n\rbrace,$ the interval  $\mathcal{I}_n$ contains exactly
$\mathcal{I}_n$ contains exactly  $\binom{n}{k} 2^{n-k}$ edges of E of length equal to
$\binom{n}{k} 2^{n-k}$ edges of E of length equal to  $2^{-k}.$ In particular, each of the intervals
$2^{-k}.$ In particular, each of the intervals  $\mathcal{I}_n,$
$\mathcal{I}_n,$  $\mathcal{I}_n^1,$ and
$\mathcal{I}_n^1,$ and  $\mathcal{I}_n^2$ has exactly 3n edges of
$\mathcal{I}_n^2$ has exactly 3n edges of  $E.$
$E.$• Each of the intervals
 $\mathcal{I}_n$ and
$\mathcal{I}_n$ and  $\mathcal{I}_n^2$ contains translated copies of the intervals
$\mathcal{I}_n^2$ contains translated copies of the intervals  $\mathcal{I}_0, \ldots, \mathcal{I}_{n-1}$ distributed in a palindromic manner: both
$\mathcal{I}_0, \ldots, \mathcal{I}_{n-1}$ distributed in a palindromic manner: both  $\mathcal{I}_n$ and
$\mathcal{I}_n$ and  $\mathcal{I}_n^2$ contain from left to right as well as from right to left intervals
$\mathcal{I}_n^2$ contain from left to right as well as from right to left intervals  $\mathcal{I}_0^* \subset \mathcal{I}_1^* \subset \cdots \subset \mathcal{I}_{n-1}^*$ that are translated copies of
$\mathcal{I}_0^* \subset \mathcal{I}_1^* \subset \cdots \subset \mathcal{I}_{n-1}^*$ that are translated copies of  $\mathcal{I}_0 \subset \mathcal{I}_1 \subset \cdots \subset \mathcal{I}_{n-1}$, respectively.
$\mathcal{I}_0 \subset \mathcal{I}_1 \subset \cdots \subset \mathcal{I}_{n-1}$, respectively.• Each interval
 $\mathcal{I}_n^1$ contains from left to right as well as from right to left intervals
$\mathcal{I}_n^1$ contains from left to right as well as from right to left intervals  $(1/2) \mathcal{I}_0^* \subset (1/2) \mathcal{I}_1^* \subset \cdots \subset (1/2) \mathcal{I}_{n-1}^*$ that are translated copies of
$(1/2) \mathcal{I}_0^* \subset (1/2) \mathcal{I}_1^* \subset \cdots \subset (1/2) \mathcal{I}_{n-1}^*$ that are translated copies of  $\mathcal{I}_0 \subset \mathcal{I}_1 \subset \cdots \subset \mathcal{I}_{n-1}$ dilated by
$\mathcal{I}_0 \subset \mathcal{I}_1 \subset \cdots \subset \mathcal{I}_{n-1}$ dilated by  $1/2.$
$1/2.$•
 $\operatorname{dist}(\cdot,E)= \operatorname{dist}(\cdot,E_n)$ on
$\operatorname{dist}(\cdot,E)= \operatorname{dist}(\cdot,E_n)$ on  $\mathcal{I}_n$ for every
$\mathcal{I}_n$ for every  $n\in {\mathbb N} \cup \lbrace 0 \rbrace.$
$n\in {\mathbb N} \cup \lbrace 0 \rbrace.$•
 $\lvert \mathcal{I}_n \rvert = (5/2)^n$ for every
$\lvert \mathcal{I}_n \rvert = (5/2)^n$ for every  $n\in {\mathbb N} \cup \lbrace 0 \rbrace.$
$n\in {\mathbb N} \cup \lbrace 0 \rbrace.$
Let us prove properties (1)–(4).
(1) For every ![]() $n\in {\mathbb N},$ the construction of
$n\in {\mathbb N},$ the construction of ![]() $\mathcal{I}_n$ yields
$\mathcal{I}_n$ yields
 \begin{align*}
\int_{\mathcal{I}_n} \!\!\operatorname{dist}(\cdot,E)^{-\alpha} & =\int_{\mathcal{I}_{n-1}} \!\!\!\!\operatorname{dist}(\cdot,E_{n-1})^{-\alpha} + \int_{\mathcal{I}_{n-1}^1}\!\! \!\!\operatorname{dist}(\cdot,E_{n-1}^1)^{-\alpha} + \int_{\mathcal{I}_{n-1}^2} \!\!\!\!\operatorname{dist}(\cdot,E_{n-1}^2)^{-\alpha} \\
& = (2+2^{\alpha-1}) \int_{\mathcal{I}_{n-1}}\!\!\!\! \operatorname{dist}(\cdot,E_{n-1})^{-\alpha} = (2+2^{\alpha-1})^n \int_{\mathcal{I}_0}\!\! \operatorname{dist}(\cdot,\lbrace 0,1 \rbrace)^{-\alpha} .
\end{align*}
\begin{align*}
\int_{\mathcal{I}_n} \!\!\operatorname{dist}(\cdot,E)^{-\alpha} & =\int_{\mathcal{I}_{n-1}} \!\!\!\!\operatorname{dist}(\cdot,E_{n-1})^{-\alpha} + \int_{\mathcal{I}_{n-1}^1}\!\! \!\!\operatorname{dist}(\cdot,E_{n-1}^1)^{-\alpha} + \int_{\mathcal{I}_{n-1}^2} \!\!\!\!\operatorname{dist}(\cdot,E_{n-1}^2)^{-\alpha} \\
& = (2+2^{\alpha-1}) \int_{\mathcal{I}_{n-1}}\!\!\!\! \operatorname{dist}(\cdot,E_{n-1})^{-\alpha} = (2+2^{\alpha-1})^n \int_{\mathcal{I}_0}\!\! \operatorname{dist}(\cdot,\lbrace 0,1 \rbrace)^{-\alpha} .
\end{align*} Because ![]() $\mathcal{I}_0=[0,1]$ and
$\mathcal{I}_0=[0,1]$ and ![]() $\alpha \lt 1 ,$ the last integral is finite, and this shows that
$\alpha \lt 1 ,$ the last integral is finite, and this shows that ![]() $\operatorname{dist}(\cdot,E)^{-\alpha}$ is integrable at every interval contained in
$\operatorname{dist}(\cdot,E)^{-\alpha}$ is integrable at every interval contained in ![]() $[0, +\infty).$ By the symmetry of E around the origin, the same property holds for intervals contained in
$[0, +\infty).$ By the symmetry of E around the origin, the same property holds for intervals contained in ![]() $(-\infty, 0].$
$(-\infty, 0].$
(2) For the sake of contradiction, suppose E is weakly porous with constants ![]() $\delta,c\in (0,1).$ Fix
$\delta,c\in (0,1).$ Fix ![]() $n_0=n_0(\delta)\in {\mathbb N}$ so that
$n_0=n_0(\delta)\in {\mathbb N}$ so that ![]() $\delta \geq 2^{-n_0}.$ For
$\delta \geq 2^{-n_0}.$ For ![]() $n \in {\mathbb N}$ with
$n \in {\mathbb N}$ with ![]() $n \gt n_0,$ one has
$n \gt n_0,$ one has ![]() $h_E(\mathcal{I}_n)= 1/2$ and so any edge J of E contained in
$h_E(\mathcal{I}_n)= 1/2$ and so any edge J of E contained in ![]() $\mathcal{I}_n$ with radius at least
$\mathcal{I}_n$ with radius at least ![]() $\delta h_E(\mathcal{I}_n)$ must satisfy
$\delta h_E(\mathcal{I}_n)$ must satisfy ![]() $|J| \geq 2^{-n_0}.$ The interval
$|J| \geq 2^{-n_0}.$ The interval ![]() $\mathcal{I}_n$ contains exactly
$\mathcal{I}_n$ contains exactly  $\binom{n}{k} 2^{n-k}$ edges of E with length
$\binom{n}{k} 2^{n-k}$ edges of E with length ![]() $2^{-k},$ for
$2^{-k},$ for ![]() $k=0,\ldots,n.$ Denote by Fn the union of all the edges of E that are contained in
$k=0,\ldots,n.$ Denote by Fn the union of all the edges of E that are contained in ![]() $\mathcal{I}_n$ and have radius at least
$\mathcal{I}_n$ and have radius at least ![]() $\delta h_E(\mathcal{I}_n).$ By the assumption of weak porosity for E, we must have
$\delta h_E(\mathcal{I}_n).$ By the assumption of weak porosity for E, we must have ![]() $|F_n| \geq c |\mathcal{I}_n|$ for every
$|F_n| \geq c |\mathcal{I}_n|$ for every ![]() $n \gt n_0.$ However, the previous observations permit to write the estimates
$n \gt n_0.$ However, the previous observations permit to write the estimates
 \begin{align*}
|F_n | & \leq \sum_{k=0}^{n_0} \binom{n}{k} 2^{n-k} 2^{-k} = 2^{n-n_0} \sum_{k=0}^{n_0} \binom{n}{k} 2^{n_0-k} 2^{-k} \\
& \leq 2^{n-n_0} \sum_{k=0}^{n_0} \binom{n}{n_0} \binom{n_0}{k} 2^{n_0-k} 2^{-k} \leq \frac{2^{n-n_0} n^{n_0}}{n_0!} \sum_{k=0}^{n_0} \binom{n_0}{k} 2^{n_0-k} 2^{-k}\nonumber\\
& = C(n_0) 2^n n^{n_0}.
\end{align*}
\begin{align*}
|F_n | & \leq \sum_{k=0}^{n_0} \binom{n}{k} 2^{n-k} 2^{-k} = 2^{n-n_0} \sum_{k=0}^{n_0} \binom{n}{k} 2^{n_0-k} 2^{-k} \\
& \leq 2^{n-n_0} \sum_{k=0}^{n_0} \binom{n}{n_0} \binom{n_0}{k} 2^{n_0-k} 2^{-k} \leq \frac{2^{n-n_0} n^{n_0}}{n_0!} \sum_{k=0}^{n_0} \binom{n_0}{k} 2^{n_0-k} 2^{-k}\nonumber\\
& = C(n_0) 2^n n^{n_0}.
\end{align*} Together with ![]() $|\mathcal{I}_n|=(5/2)^n,$ this implies
$|\mathcal{I}_n|=(5/2)^n,$ this implies
 \begin{equation*}
\frac{|F_n|}{|\mathcal{I}_n|}\leq C(n_0) (4/5)^n n^{n_0}, \quad \text{for every} \quad n \gt n_0,
\end{equation*}
\begin{equation*}
\frac{|F_n|}{|\mathcal{I}_n|}\leq C(n_0) (4/5)^n n^{n_0}, \quad \text{for every} \quad n \gt n_0,
\end{equation*} contradicting that ![]() $|F_n| \geq c |\mathcal{I}_n|$ for every
$|F_n| \geq c |\mathcal{I}_n|$ for every ![]() $n\in {\mathbb N}.$
$n\in {\mathbb N}.$
Let us mention that the first part of (2) can also be proven via Theorem 1.3. Indeed, for this set E, a computation similar to the one in (1) permits to prove that ![]() $\operatorname{dist}(\cdot, E)^{-\alpha} \notin A_1({\mathbb R}^n)$ for
$\operatorname{dist}(\cdot, E)^{-\alpha} \notin A_1({\mathbb R}^n)$ for ![]() $\alpha \in (0,1],$ and so Theorem 1.3 implies that E is not weakly porous. In fact, using similar computations as in (1), we next show the second part of (2). Let us fix p > 1 and
$\alpha \in (0,1],$ and so Theorem 1.3 implies that E is not weakly porous. In fact, using similar computations as in (1), we next show the second part of (2). Let us fix p > 1 and ![]() $\alpha \in (0,1).$ For our purposes, we can assume further p > 2, thanks to the inclusions
$\alpha \in (0,1).$ For our purposes, we can assume further p > 2, thanks to the inclusions ![]() $A_r({\mathbb R}) \subset A_s({\mathbb R})$ for
$A_r({\mathbb R}) \subset A_s({\mathbb R})$ for ![]() $r \leq s.$ For any
$r \leq s.$ For any ![]() $\beta \gt -1,$ those computations lead to
$\beta \gt -1,$ those computations lead to
 \begin{equation*}
\int_{\mathcal{I}_n} \!\!\operatorname{dist}(\cdot,E)^{\beta} = (2+2^{-1-\beta})^n \int_{\mathcal{I}_0}\!\! \operatorname{dist}(\cdot,\lbrace 0,1 \rbrace)^{\beta}, \quad n\in {\mathbb N}.
\end{equation*}
\begin{equation*}
\int_{\mathcal{I}_n} \!\!\operatorname{dist}(\cdot,E)^{\beta} = (2+2^{-1-\beta})^n \int_{\mathcal{I}_0}\!\! \operatorname{dist}(\cdot,\lbrace 0,1 \rbrace)^{\beta}, \quad n\in {\mathbb N}.
\end{equation*} Applying this equality with  $\beta= -\alpha, \, \frac{\alpha}{p-1}, $ and using that
$\beta= -\alpha, \, \frac{\alpha}{p-1}, $ and using that ![]() $|\mathcal{I}_n|= (5/2)^n,$ we obtain
$|\mathcal{I}_n|= (5/2)^n,$ we obtain
 \begin{equation}
{\int{\kern-10.5pt}-}_{{\hskip-3.5pt \mathcal{I}_n}} \!\!\operatorname{dist}(\cdot,E)^{-\alpha} \left( {\int{\kern-10.5pt}-}_{{\hskip-3.5pt \mathcal{I}_n}} \!\!\operatorname{dist}(\cdot,E)^{\frac{\alpha}{p-1}} \right)^{p-1} = C(\alpha,p) \left( \frac{(2+2^{\alpha-1})(2+2^{-\frac{\alpha}{p-1}-1})^{p-1}}{(5/2)^p} \right)^n,
\end{equation}
\begin{equation}
{\int{\kern-10.5pt}-}_{{\hskip-3.5pt \mathcal{I}_n}} \!\!\operatorname{dist}(\cdot,E)^{-\alpha} \left( {\int{\kern-10.5pt}-}_{{\hskip-3.5pt \mathcal{I}_n}} \!\!\operatorname{dist}(\cdot,E)^{\frac{\alpha}{p-1}} \right)^{p-1} = C(\alpha,p) \left( \frac{(2+2^{\alpha-1})(2+2^{-\frac{\alpha}{p-1}-1})^{p-1}}{(5/2)^p} \right)^n,
\end{equation} for every ![]() $n\in {\mathbb N}.$ Defining the function
$n\in {\mathbb N}.$ Defining the function  $h(t)=(2+2^{t-1})(2+2^{-\frac{t}{p-1}-1})^{p-1},$
$h(t)=(2+2^{t-1})(2+2^{-\frac{t}{p-1}-1})^{p-1},$ ![]() $t \in [0,1)$, and using that
$t \in [0,1)$, and using that ![]() $p \gt 2,$ a computation shows that
$p \gt 2,$ a computation shows that ![]() $h' \gt 0$ on
$h' \gt 0$ on ![]() $(0,1)$, and thus
$(0,1)$, and thus ![]() $h(\alpha) \gt h(0)=(5/2)^p$ for all
$h(\alpha) \gt h(0)=(5/2)^p$ for all ![]() $\alpha \in (0,1).$ Therefore, for every
$\alpha \in (0,1).$ Therefore, for every ![]() $\alpha \in (0,1)$ and
$\alpha \in (0,1)$ and ![]() $p \gt 2,$ the right-hand side term of (31) goes to
$p \gt 2,$ the right-hand side term of (31) goes to ![]() $\infty$ as
$\infty$ as ![]() $n \to \infty.$ We conclude that
$n \to \infty.$ We conclude that ![]() $\operatorname{dist}(\cdot, E)^{-\alpha} \notin A_p({\mathbb R})$ for every
$\operatorname{dist}(\cdot, E)^{-\alpha} \notin A_p({\mathbb R})$ for every ![]() $\alpha \in (0,1)$ and p > 1. For negative values of
$\alpha \in (0,1)$ and p > 1. For negative values of ![]() $\alpha,$ it suffices to note that if we had
$\alpha,$ it suffices to note that if we had ![]() $w_{\alpha} \in A_p({\mathbb R})$, for some
$w_{\alpha} \in A_p({\mathbb R})$, for some ![]() $p \gt 1,$ then also
$p \gt 1,$ then also  $w_{\frac{\alpha}{1-p}} \in A_{p'}({\mathbb R}),$ where
$w_{\frac{\alpha}{1-p}} \in A_{p'}({\mathbb R}),$ where ![]() $\alpha/(1-p) \gt 0$, and this is impossible by what we have just proved.
$\alpha/(1-p) \gt 0$, and this is impossible by what we have just proved.
(3) The verification of this property requires more work. We first show the doubling estimates for hE over intervals that are contained in ![]() $[0,+\infty).$
$[0,+\infty).$
Lemma 8.4. We have ![]() $h_E(K) \leq 16 h_E(J)$ for any two intervals
$h_E(K) \leq 16 h_E(J)$ for any two intervals ![]() $J \subset K \subset [0,+ \infty)$ with
$J \subset K \subset [0,+ \infty)$ with  $\lvert J \rvert \geq \frac{1}{2}\lvert K \rvert.$
$\lvert J \rvert \geq \frac{1}{2}\lvert K \rvert.$
Proof of Lemma 8.4
In the case where J is contained in the union of three consecutive edges ![]() $J_1, J_2, J_3$ of
$J_1, J_2, J_3$ of ![]() $E,$ the result easily follows by observing that
$E,$ the result easily follows by observing that
 \begin{equation*}
2 h_E(J) = \max_{1 \leq j \leq 3} \lvert J \cap J_j \rvert \geq \frac{1}{3} \sum_{j=1}^3 \lvert J \cap J_j \rvert = \frac{1}{3}\lvert J \rvert \geq \frac{1}{6}\lvert K \rvert \geq \frac{1}{3} h_E(K) .
\end{equation*}
\begin{equation*}
2 h_E(J) = \max_{1 \leq j \leq 3} \lvert J \cap J_j \rvert \geq \frac{1}{3} \sum_{j=1}^3 \lvert J \cap J_j \rvert = \frac{1}{3}\lvert J \rvert \geq \frac{1}{6}\lvert K \rvert \geq \frac{1}{3} h_E(K) .
\end{equation*} Now, we prove by induction on N the desired estimate for every interval ![]() $K \subset \mathcal{I}_N.$ The cases
$K \subset \mathcal{I}_N.$ The cases ![]() $N=0,1$ are covered by the preceding argument, so let us assume that the estimate holds true for
$N=0,1$ are covered by the preceding argument, so let us assume that the estimate holds true for ![]() $n=1, \ldots, N-1,$ and let us verify the property for intervals K contained in
$n=1, \ldots, N-1,$ and let us verify the property for intervals K contained in ![]() $\mathcal{I}_N.$
$\mathcal{I}_N.$
We may and do assume that K is not contained in ![]() $\mathcal{I}_{N-1},$ as otherwise we can simply apply the induction hypothesis. Moreover, let us suppose first that K is entirely contained in one of the intervals
$\mathcal{I}_{N-1},$ as otherwise we can simply apply the induction hypothesis. Moreover, let us suppose first that K is entirely contained in one of the intervals ![]() $\mathcal{I}_{N-1}^1$,
$\mathcal{I}_{N-1}^1$, ![]() $\mathcal{I}_{N-1}^2.$ In the first case, it is clear that there are translations
$\mathcal{I}_{N-1}^2.$ In the first case, it is clear that there are translations ![]() $J^*$ and
$J^*$ and ![]() $K^*$ dilated by 2 of the intervals J and K respectively, and such that
$K^*$ dilated by 2 of the intervals J and K respectively, and such that ![]() $J^*\subset K^* \subset \mathcal{I}_{N-1},$
$J^*\subset K^* \subset \mathcal{I}_{N-1},$  $\lvert J^* \rvert \geq \frac{1}{2}\lvert K^*\rvert,$
$\lvert J^* \rvert \geq \frac{1}{2}\lvert K^*\rvert,$ ![]() $ h_E(J^*)=2h_E(J)$ and
$ h_E(J^*)=2h_E(J)$ and ![]() $h_E(K^*)=2h_E(K).$ The induction hypothesis tells us that
$h_E(K^*)=2h_E(K).$ The induction hypothesis tells us that ![]() $h_E(K^*)\leq 16 h_E(J^*),$ and so
$h_E(K^*)\leq 16 h_E(J^*),$ and so ![]() $h_E(K)\leq 16 h_E(J)$ as well. In the latter case,
$h_E(K)\leq 16 h_E(J)$ as well. In the latter case, ![]() $K \subset \mathcal{I}_{N-1}^2,$ we consider translations
$K \subset \mathcal{I}_{N-1}^2,$ we consider translations ![]() $J^*\subset K^* \subset \mathcal{I}_{N-1}$ of
$J^*\subset K^* \subset \mathcal{I}_{N-1}$ of ![]() $J \subset K$ and apply the induction hypothesis.
$J \subset K$ and apply the induction hypothesis.
Thus, from now on we will assume that K intersects both intervals of one of the couples ![]() $\lbrace \mathcal{I}_{N-1}, \mathcal{I}_{N-1}^1 \rbrace,$
$\lbrace \mathcal{I}_{N-1}, \mathcal{I}_{N-1}^1 \rbrace,$ ![]() $\lbrace \mathcal{I}_{N-1}^1, \mathcal{I}_{N-1}^2 \rbrace.$ We will only study the situation where K intersects both of
$\lbrace \mathcal{I}_{N-1}^1, \mathcal{I}_{N-1}^2 \rbrace.$ We will only study the situation where K intersects both of ![]() $\lbrace \mathcal{I}_{N-1}, \mathcal{I}_{N-1}^1 \rbrace,$ as the proof in the other situation is identical, thanks to the properties of symmetry of
$\lbrace \mathcal{I}_{N-1}, \mathcal{I}_{N-1}^1 \rbrace,$ as the proof in the other situation is identical, thanks to the properties of symmetry of ![]() $\mathcal{I}_N.$
$\mathcal{I}_N.$
![]() $\textbf{Case 1.}$ J is contained in
$\textbf{Case 1.}$ J is contained in ![]() $\mathcal{I}_{N-1}.$ Denote
$\mathcal{I}_{N-1}.$ Denote ![]() $K^0=K \cap \mathcal{I}_{N-1},$
$K^0=K \cap \mathcal{I}_{N-1},$ ![]() $K^1=K \cap \mathcal{I}_{N-1}^1$ and
$K^1=K \cap \mathcal{I}_{N-1}^1$ and ![]() $K^2=K \cap \mathcal{I}_{N-1}^2.$ The fact that K intersects
$K^2=K \cap \mathcal{I}_{N-1}^2.$ The fact that K intersects ![]() $\mathcal{I}_{N-1}^1$ yields the identities
$\mathcal{I}_{N-1}^1$ yields the identities ![]() $2h_E(K^0)=\min\lbrace 1, \lvert K^0 \rvert \rbrace,$
$2h_E(K^0)=\min\lbrace 1, \lvert K^0 \rvert \rbrace,$ ![]() $2h_E(K^1)=\min\lbrace 1/2, \lvert K^1 \rvert \rbrace,$ and
$2h_E(K^1)=\min\lbrace 1/2, \lvert K^1 \rvert \rbrace,$ and ![]() $2h_E(K^2)=\min\lbrace 1, \lvert K^2 \rvert \rbrace$. And, because K 0 contains
$2h_E(K^2)=\min\lbrace 1, \lvert K^2 \rvert \rbrace$. And, because K 0 contains ![]() $J,$ and
$J,$ and  $\lvert J \rvert \geq \frac{1}{2} \lvert K \rvert,$ it is clear that
$\lvert J \rvert \geq \frac{1}{2} \lvert K \rvert,$ it is clear that ![]() $\lvert K^1 \rvert, \lvert K^2 \rvert \leq \lvert K^0 \rvert.$ This implies
$\lvert K^1 \rvert, \lvert K^2 \rvert \leq \lvert K^0 \rvert.$ This implies
But K 0 is a cube in ![]() $\mathcal{I}_{N-1}$ containing J with
$\mathcal{I}_{N-1}$ containing J with  $\lvert J \rvert \geq \frac{1}{2} \lvert K^0 \rvert$ and so, the induction hypothesis gives
$\lvert J \rvert \geq \frac{1}{2} \lvert K^0 \rvert$ and so, the induction hypothesis gives ![]() $h_E(K)\leq h_E(K^0) \leq 16 h_E( J).$
$h_E(K)\leq h_E(K^0) \leq 16 h_E( J).$
![]() $\textbf{Case 2.}$ J is contained in
$\textbf{Case 2.}$ J is contained in ![]() $\mathcal{I}_{N-1}^1.$ Consider the cube
$\mathcal{I}_{N-1}^1.$ Consider the cube ![]() $K^1=K \cap \mathcal{I}_{N-1}^1.$ If K 1 intersects at most three edges of E within
$K^1=K \cap \mathcal{I}_{N-1}^1.$ If K 1 intersects at most three edges of E within ![]() $\mathcal{I}_{N-1}^1,$ then the same property holds for
$\mathcal{I}_{N-1}^1,$ then the same property holds for ![]() $J,$ and the argument from the beginning of the proof shows that
$J,$ and the argument from the beginning of the proof shows that ![]() $h_E(K) \leq 6 h_E(J).$
$h_E(K) \leq 6 h_E(J).$
Now, suppose K 1 intersects more than three edges of E within ![]() $\mathcal{I}_{N-1}^1.$ By the properties of
$\mathcal{I}_{N-1}^1.$ By the properties of ![]() $\mathcal{I}_{N-1}^1,$ and because K intersects
$\mathcal{I}_{N-1}^1,$ and because K intersects ![]() $\mathcal{I}_{N-1},$ there must exist
$\mathcal{I}_{N-1},$ there must exist ![]() $ 1\leq m \leq N-2$ such that
$ 1\leq m \leq N-2$ such that  $(1/2) \mathcal{I}_m^* \subset K^1 \subset (1/2) \mathcal{I}_{m+1}^*,$ where
$(1/2) \mathcal{I}_m^* \subset K^1 \subset (1/2) \mathcal{I}_{m+1}^*,$ where ![]() $(1/2) \mathcal{I}_m^*$ and
$(1/2) \mathcal{I}_m^*$ and ![]() $(1/2) \mathcal{I}_{m+1}^*$ are translations of
$(1/2) \mathcal{I}_{m+1}^*$ are translations of ![]() $\mathcal{I}_m$ and
$\mathcal{I}_m$ and ![]() $\mathcal{I}_{m+1}$ dilated by
$\mathcal{I}_{m+1}$ dilated by ![]() $1/2.$ Notice that
$1/2.$ Notice that ![]() $(1/2) \mathcal{I}_{m+1}^*$ can be regarded as the union of three intervals
$(1/2) \mathcal{I}_{m+1}^*$ can be regarded as the union of three intervals ![]() $(1/2) \mathcal{I}_{m}^*$,
$(1/2) \mathcal{I}_{m}^*$,  $(1/2) \left( \mathcal{I}_{m}^1 \right)^*$,
$(1/2) \left( \mathcal{I}_{m}^1 \right)^*$,  $(1/2) \left( \mathcal{I}_{m}^2\right)^*,$ where
$(1/2) \left( \mathcal{I}_{m}^2\right)^*,$ where  $\left( \mathcal{I}_{m}^1 \right)^*$ and
$\left( \mathcal{I}_{m}^1 \right)^*$ and  $\left( \mathcal{I}_{m}^2 \right)^*$ are translations of
$\left( \mathcal{I}_{m}^2 \right)^*$ are translations of ![]() $\mathcal{I}_m^1$ and
$\mathcal{I}_m^1$ and ![]() $\mathcal{I}_m^2.$ Furthermore, each of the intervals
$\mathcal{I}_m^2.$ Furthermore, each of the intervals  $\mathcal{I}_m^*, \left( \mathcal{I}_{m}^1 \right)^*, \left( \mathcal{I}_{m}^2 \right)^*$ can be in turn subdivided into three intervals in the following manner. Denoting by
$\mathcal{I}_m^*, \left( \mathcal{I}_{m}^1 \right)^*, \left( \mathcal{I}_{m}^2 \right)^*$ can be in turn subdivided into three intervals in the following manner. Denoting by ![]() $\mathcal{I}_{m-1}^*$,
$\mathcal{I}_{m-1}^*$,  $\left( \mathcal{I}_{m-1}^1 \right)^*,$
$\left( \mathcal{I}_{m-1}^1 \right)^*,$  $\left( \mathcal{I}_{m-1}^2 \right)^*$ various translated copies of
$\left( \mathcal{I}_{m-1}^2 \right)^*$ various translated copies of ![]() $\mathcal{I}_{m-1}$,
$\mathcal{I}_{m-1}$, ![]() $\mathcal{I}_{m-1}^1$,
$\mathcal{I}_{m-1}^1$, ![]() $\mathcal{I}_{m-1}^2$, both
$\mathcal{I}_{m-1}^2$, both ![]() $\mathcal{I}_m^*$ and
$\mathcal{I}_m^*$ and  $\left( \mathcal{I}_m^2 \right)^*$ are the union of the intervals
$\left( \mathcal{I}_m^2 \right)^*$ are the union of the intervals ![]() $\mathcal{I}_{m-1}^*$,
$\mathcal{I}_{m-1}^*$,  $\left( \mathcal{I}_{m-1}^1 \right)^*,$
$\left( \mathcal{I}_{m-1}^1 \right)^*,$  $\left( \mathcal{I}_{m-1}^2 \right)^*$; and
$\left( \mathcal{I}_{m-1}^2 \right)^*$; and  $\left( \mathcal{I}_{m}^1 \right)^*$ is the union of
$\left( \mathcal{I}_{m}^1 \right)^*$ is the union of ![]() $(1/2)\mathcal{I}_{m-1}^*$,
$(1/2)\mathcal{I}_{m-1}^*$,  $(1/2) \left( \mathcal{I}_{m-1}^1 \right)^*,$
$(1/2) \left( \mathcal{I}_{m-1}^1 \right)^*,$  $(1/2)\left( \mathcal{I}_{m-1}^2 \right)^*.$ Therefore
$(1/2)\left( \mathcal{I}_{m-1}^2 \right)^*.$ Therefore ![]() $(1/2)\mathcal{I}_{m+1}^*$ is the union of 9 intervals, the largest of which has length equal to
$(1/2)\mathcal{I}_{m+1}^*$ is the union of 9 intervals, the largest of which has length equal to ![]() $(1/2) \lvert \mathcal{I}_{m-1} \rvert$. Because
$(1/2) \lvert \mathcal{I}_{m-1} \rvert$. Because ![]() $K^1 \supset (1/2) \mathcal{I}_m^*,$ we have that
$K^1 \supset (1/2) \mathcal{I}_m^*,$ we have that
 \begin{equation*}
\lvert J \rvert \geq \frac{1}{2} \lvert K^1 \rvert \geq \frac{1}{4} \lvert \mathcal{I}_m^* \rvert = \frac{1}{4} \lvert \mathcal{I}_m \rvert = \frac{5}{8} \lvert \mathcal{I}_{m-1} \rvert \gt \frac{1}{2} \lvert \mathcal{I}_{m-1} \rvert.
\end{equation*}
\begin{equation*}
\lvert J \rvert \geq \frac{1}{2} \lvert K^1 \rvert \geq \frac{1}{4} \lvert \mathcal{I}_m^* \rvert = \frac{1}{4} \lvert \mathcal{I}_m \rvert = \frac{5}{8} \lvert \mathcal{I}_{m-1} \rvert \gt \frac{1}{2} \lvert \mathcal{I}_{m-1} \rvert.
\end{equation*} This shows that J must contain either the first half or the second half of one of those 9 intervals. By the construction of the ![]() $\mathcal{I}_j$’s, the first and the last edges of E within each of those 9 intervals have length equal to
$\mathcal{I}_j$’s, the first and the last edges of E within each of those 9 intervals have length equal to ![]() $1/2,$
$1/2,$ ![]() $1/4$ or
$1/4$ or ![]() $1/8.$ Therefore,
$1/8.$ Therefore,
 \begin{equation*}
2h_E(J) \geq \frac{1}{16} \geq \frac{1}{8} h_E(K).
\end{equation*}
\begin{equation*}
2h_E(J) \geq \frac{1}{16} \geq \frac{1}{8} h_E(K).
\end{equation*} ![]() $\textbf{Case 3.}$ J is contained in
$\textbf{Case 3.}$ J is contained in ![]() $\mathcal{I}_{N-1}^2.$ This case is identical to
$\mathcal{I}_{N-1}^2.$ This case is identical to ![]() $\textbf{Case 1}$.
$\textbf{Case 1}$.
![]() $\textbf{Case 4.}$ J intersects both
$\textbf{Case 4.}$ J intersects both ![]() $\mathcal{I}_{N-1}$ and
$\mathcal{I}_{N-1}$ and ![]() $\mathcal{I}_{N-1}^1.$ If J contains the last edge of E within
$\mathcal{I}_{N-1}^1.$ If J contains the last edge of E within ![]() $\mathcal{I}_{N-1}$ or the first edge of E within
$\mathcal{I}_{N-1}$ or the first edge of E within ![]() $\mathcal{I}_{N-1}^1,$ then
$\mathcal{I}_{N-1}^1,$ then ![]() $2h_E(J) \geq 1/2 \geq h_E(K).$ Otherwise, we have
$2h_E(J) \geq 1/2 \geq h_E(K).$ Otherwise, we have
 \begin{equation*}
2h_E(J)=\max \lbrace \lvert J \cap \mathcal{I}_{N-1} \rvert, \lvert J \cap \mathcal{I}_{N-1}^1 \rvert \rbrace \geq \frac{1}{2}\lvert J \rvert \geq \frac{1}{4}\lvert K \rvert \geq \frac{1}{2} h_E(K).
\end{equation*}
\begin{equation*}
2h_E(J)=\max \lbrace \lvert J \cap \mathcal{I}_{N-1} \rvert, \lvert J \cap \mathcal{I}_{N-1}^1 \rvert \rbrace \geq \frac{1}{2}\lvert J \rvert \geq \frac{1}{4}\lvert K \rvert \geq \frac{1}{2} h_E(K).
\end{equation*} ![]() $\textbf{Case 5.}$ J intersects both
$\textbf{Case 5.}$ J intersects both ![]() $\mathcal{I}_{N-1}^1$ and
$\mathcal{I}_{N-1}^1$ and ![]() $\mathcal{I}_{N-1}^2. $ This case is identical to
$\mathcal{I}_{N-1}^2. $ This case is identical to ![]() $\textbf{Case 4}$.
$\textbf{Case 4}$.
Now, using Lemma 8.4, we can prove property (3) of Example 8.3. Let ![]() $J \subset K \subset {\mathbb R}$ with
$J \subset K \subset {\mathbb R}$ with  $\lvert J \rvert \geq \frac{1}{2}\lvert K \rvert.$ By Lemma 8.4 and the symmetry of E about the origin, we may assume that K intersects both
$\lvert J \rvert \geq \frac{1}{2}\lvert K \rvert.$ By Lemma 8.4 and the symmetry of E about the origin, we may assume that K intersects both ![]() $(-\infty, 0]$ and
$(-\infty, 0]$ and ![]() $[0, +\infty).$ Let us distinguish three cases.
$[0, +\infty).$ Let us distinguish three cases.
![]() $\textbf{Case 1.}$ J is contained in
$\textbf{Case 1.}$ J is contained in ![]() $[0,+\infty).$ Denote
$[0,+\infty).$ Denote ![]() $K^+=K \cap [0,+\infty)$ and
$K^+=K \cap [0,+\infty)$ and ![]() $K^-=K \cap (-\infty, 0].$ Because
$K^-=K \cap (-\infty, 0].$ Because ![]() $J \subset K^+,$ we may apply Lemma 8.4 to obtain
$J \subset K^+,$ we may apply Lemma 8.4 to obtain ![]() $h_E(K^+) \leq 16 h_E(J).$ Also, notice that
$h_E(K^+) \leq 16 h_E(J).$ Also, notice that ![]() $\lvert K^- \vert \leq \lvert K^+ \rvert$ as
$\lvert K^- \vert \leq \lvert K^+ \rvert$ as ![]() $K^+$ contains no less than half of the measure of
$K^+$ contains no less than half of the measure of ![]() $K.$ This fact and the symmetry of E about the origin leads us to
$K.$ This fact and the symmetry of E about the origin leads us to
Consequently, ![]() $h_E(K)=\max \lbrace h_E(K^-), h_E(K^+) \rbrace \leq 16 h_E(J).$
$h_E(K)=\max \lbrace h_E(K^-), h_E(K^+) \rbrace \leq 16 h_E(J).$
![]() $\textbf{Case 2.}$ J is contained in
$\textbf{Case 2.}$ J is contained in ![]() $(-\infty,0].$ This is identical to
$(-\infty,0].$ This is identical to ![]() $\textbf{Case 1}$, due to the symmetry of E about the origin.
$\textbf{Case 1}$, due to the symmetry of E about the origin.
![]() $\textbf{Case 3.}$ J intersects both
$\textbf{Case 3.}$ J intersects both ![]() $(-\infty, 0]$ and
$(-\infty, 0]$ and ![]() $[0, +\infty).$ If J contains a subinterval of E of length equal to
$[0, +\infty).$ If J contains a subinterval of E of length equal to ![]() $1,$ then
$1,$ then ![]() $h_E(J)=1$ and the result follows immediately. Otherwise, denoting
$h_E(J)=1$ and the result follows immediately. Otherwise, denoting ![]() $J^+=J \cap [0,+\infty)$ and
$J^+=J \cap [0,+\infty)$ and ![]() $J^-=J \cap (-\infty, 0],$ we have
$J^-=J \cap (-\infty, 0],$ we have
 \begin{equation*}
2h_E(J)= \max \lbrace \lvert J^- \rvert, \lvert J^+ \rvert \rbrace \geq \frac{1}{2}\lvert J \rvert \geq \frac{1}{4}\lvert K \rvert \geq \frac{1}{2} h_E(K).
\end{equation*}
\begin{equation*}
2h_E(J)= \max \lbrace \lvert J^- \rvert, \lvert J^+ \rvert \rbrace \geq \frac{1}{2}\lvert J \rvert \geq \frac{1}{4}\lvert K \rvert \geq \frac{1}{2} h_E(K).
\end{equation*} (4) Fix α < 1 and denote ![]() $w=w_\alpha.$ It is clear that if we find constants
$w=w_\alpha.$ It is clear that if we find constants ![]() $\varepsilon= \varepsilon(\alpha) \in (0,1)$ and
$\varepsilon= \varepsilon(\alpha) \in (0,1)$ and ![]() $C=C(\varepsilon,\alpha) \gt 0$ so that, for any two intervals
$C=C(\varepsilon,\alpha) \gt 0$ so that, for any two intervals ![]() $J \subset K \subset {\mathbb R}$,
$J \subset K \subset {\mathbb R}$, ![]() $|J| \geq (1-\varepsilon) |K|$ implies
$|J| \geq (1-\varepsilon) |K|$ implies ![]() $w(K) \leq C w(J),$ then also
$w(K) \leq C w(J),$ then also  $|J| \geq \frac{1}{2}|K|$ implies
$|J| \geq \frac{1}{2}|K|$ implies ![]() $w(K) \leq C w(J)$ for a new constant
$w(K) \leq C w(J)$ for a new constant ![]() $C,$ and all intervals
$C,$ and all intervals ![]() $J \subset K.$ Moreover, we will only prove the estimates when
$J \subset K.$ Moreover, we will only prove the estimates when ![]() $J \subset K \subset [0, + \infty),$ as the general case can be deduced using the symmetry of E about the origin, and arguments similar to those at the end of the proof of (3).
$J \subset K \subset [0, + \infty),$ as the general case can be deduced using the symmetry of E about the origin, and arguments similar to those at the end of the proof of (3).
To prove the existence of such ɛ and ![]() $C,$ we first observe that, by the construction of
$C,$ we first observe that, by the construction of ![]() $E,$ for any two consecutive edges of
$E,$ for any two consecutive edges of ![]() $E,$ say
$E,$ say ![]() $R_1, R_2,$ one has
$R_1, R_2,$ one has
 \begin{equation}
\frac{1}{2}|R_2| \leq |R_1| \leq 2 |R_2|.
\end{equation}
\begin{equation}
\frac{1}{2}|R_2| \leq |R_1| \leq 2 |R_2|.
\end{equation}This takes care of the first (and non-trivial) case.
Case 0. Suppose that J contains at most 1 point of ![]() $E.$ Then
$E.$ Then ![]() $J \subset I_1 \cup I_2$, where I 1 and I 2 are two consecutive edges of
$J \subset I_1 \cup I_2$, where I 1 and I 2 are two consecutive edges of ![]() $E.$ We claim that if
$E.$ We claim that if ![]() $J \subset K$ and
$J \subset K$ and ![]() $|J| \geq (1-\varepsilon) |K|,$ then
$|J| \geq (1-\varepsilon) |K|,$ then ![]() $K \subset I_0 \cup I_1 \cup I_2 \cup I_3,$ where these Ij are consecutive edges of E ordered from left to right. Indeed, suppose that, for instance, there is another edge of E lying in the left of I 0 and intersecting
$K \subset I_0 \cup I_1 \cup I_2 \cup I_3,$ where these Ij are consecutive edges of E ordered from left to right. Indeed, suppose that, for instance, there is another edge of E lying in the left of I 0 and intersecting ![]() $K.$ Then,
$K.$ Then,  $\frac{1}{2}|J| \leq \max \lbrace |I_1|, |I_2| \rbrace,$ and the relation (32) gives
$\frac{1}{2}|J| \leq \max \lbrace |I_1|, |I_2| \rbrace,$ and the relation (32) gives
 \begin{equation*}
|K| \geq |I_0|+ |J| \geq \max\left\lbrace \frac{1}{2} |I_1|, \frac{1}{4} |I_2| \right\rbrace + |J| \geq \frac{9}{8} |J|.
\end{equation*}
\begin{equation*}
|K| \geq |I_0|+ |J| \geq \max\left\lbrace \frac{1}{2} |I_1|, \frac{1}{4} |I_2| \right\rbrace + |J| \geq \frac{9}{8} |J|.
\end{equation*} If ![]() $\varepsilon \in (0,1)$ is small enough, the above contradicts
$\varepsilon \in (0,1)$ is small enough, the above contradicts ![]() $|J| \geq (1-\varepsilon) |K|.$ Therefore K is contained in the union of (at most) 4 consecutive edges of
$|J| \geq (1-\varepsilon) |K|.$ Therefore K is contained in the union of (at most) 4 consecutive edges of ![]() $E,$ and the estimate
$E,$ and the estimate ![]() $ w(K) \leq C_0 w(J)$ holds for some constant C 0 depending only on ɛ and
$ w(K) \leq C_0 w(J)$ holds for some constant C 0 depending only on ɛ and ![]() $\alpha.$
$\alpha.$
Thus, from now on, we assume that J contains at least two points of ![]() $E.$
$E.$
Case 1. ![]() $K \subset \mathcal{I}_1.$ Clearly,
$K \subset \mathcal{I}_1.$ Clearly, ![]() $|J| \geq (1-\varepsilon) |K|$ implies
$|J| \geq (1-\varepsilon) |K|$ implies ![]() $w(K) \leq C w(J)$ for some constant
$w(K) \leq C w(J)$ for some constant ![]() $C=C(\varepsilon,\alpha).$
$C=C(\varepsilon,\alpha).$
Now suppose that for some ![]() $N \geq 2$, and all
$N \geq 2$, and all ![]() $J \subset K $ with
$J \subset K $ with ![]() $K \subset \mathcal{I}_{N-1}$,
$K \subset \mathcal{I}_{N-1}$, ![]() $|J| \geq (1-\varepsilon) |K|$ implies
$|J| \geq (1-\varepsilon) |K|$ implies ![]() $w(K) \leq C w(J)$ for some constant
$w(K) \leq C w(J)$ for some constant ![]() $C=C(\varepsilon,\alpha).$ We next show that the same holds for
$C=C(\varepsilon,\alpha).$ We next show that the same holds for ![]() $\mathcal{I}_N,$ of course, without increasing the constant C in the iteration. We will see how large the constant C should be during the proof, but it will be independent of
$\mathcal{I}_N,$ of course, without increasing the constant C in the iteration. We will see how large the constant C should be during the proof, but it will be independent of ![]() $N.$ The induction hypothesis will be used only in Case 2 and Case 3 below.
$N.$ The induction hypothesis will be used only in Case 2 and Case 3 below.
From now on, we also assume that ![]() $K \subset \mathcal{I}_N,$ and
$K \subset \mathcal{I}_N,$ and ![]() $K \not \subset \mathcal{I}_{N-1}$.
$K \not \subset \mathcal{I}_{N-1}$.
Case 2. ![]() $K \subset \mathcal{I}_{N-1}^2.$ Up to a translation, one can assume that both J and K are contained in
$K \subset \mathcal{I}_{N-1}^2.$ Up to a translation, one can assume that both J and K are contained in ![]() $\mathcal{I}_{N-1},$ and then apply the induction hypothesis.
$\mathcal{I}_{N-1},$ and then apply the induction hypothesis.
Case 3. ![]() $K \subset \mathcal{I}_{N-1}^1.$ Then there are intervals
$K \subset \mathcal{I}_{N-1}^1.$ Then there are intervals ![]() $K^*$ and
$K^*$ and ![]() $J^*$ contained in
$J^*$ contained in ![]() $\mathcal{I}_{N-1}$ so that K (resp. J) is a translation of
$\mathcal{I}_{N-1}$ so that K (resp. J) is a translation of ![]() $K^*$ (resp.
$K^*$ (resp. ![]() $J^*$) dilated by the factor
$J^*$) dilated by the factor ![]() $1/2.$ Since
$1/2.$ Since ![]() $|J^*| \geq (1-\varepsilon) |K^*|,$ by the induction hypothesis, one has
$|J^*| \geq (1-\varepsilon) |K^*|,$ by the induction hypothesis, one has
Case 4. ![]() $\mathcal{I}_{N-1}^1 \subset J.$ In this case, we simply estimate by
$\mathcal{I}_{N-1}^1 \subset J.$ In this case, we simply estimate by
 \begin{equation*}
w(K) \leq w(\mathcal{I}_N) = \left( 1+2^{2-\alpha} \right) w(\mathcal{I}_{N-1}^1) \leq \left( 1+2^{2-\alpha} \right) w(J).
\end{equation*}
\begin{equation*}
w(K) \leq w(\mathcal{I}_N) = \left( 1+2^{2-\alpha} \right) w(\mathcal{I}_{N-1}^1) \leq \left( 1+2^{2-\alpha} \right) w(J).
\end{equation*} Case 5. ![]() $J \cap \mathcal{I}_{N-1} \neq \emptyset \neq J \cap \mathcal{I}_{N-1}^1,$
$J \cap \mathcal{I}_{N-1} \neq \emptyset \neq J \cap \mathcal{I}_{N-1}^1,$ ![]() $ J \cap \mathcal{I}_{N-1}^2 = \emptyset.$ By the construction of
$ J \cap \mathcal{I}_{N-1}^2 = \emptyset.$ By the construction of ![]() $E,$ there are integers
$E,$ there are integers ![]() $n_0, n_1, m_0, m_1, m_2 \geq -1$ and translated copies
$n_0, n_1, m_0, m_1, m_2 \geq -1$ and translated copies ![]() $\mathcal{I}_{j}^*$ of
$\mathcal{I}_{j}^*$ of ![]() $\mathcal{I}_j$, for
$\mathcal{I}_j$, for ![]() $j\in \lbrace n_0, n_1, m_0, m_1, m_2 \rbrace$, so that
$j\in \lbrace n_0, n_1, m_0, m_1, m_2 \rbrace$, so that
 \begin{equation*}
\mathcal{I}_{n_0}^* \subset J \cap \mathcal{I}_{N-1} \subset \mathcal{I}_{n_0+1}^*, \qquad \frac{1}{2}\mathcal{I}_{n_1}^* \subset J \cap \mathcal{I}_{N-1}^1 \subset \frac{1}{2}\mathcal{I}_{n_1+1}^*,
\end{equation*}
\begin{equation*}
\mathcal{I}_{n_0}^* \subset J \cap \mathcal{I}_{N-1} \subset \mathcal{I}_{n_0+1}^*, \qquad \frac{1}{2}\mathcal{I}_{n_1}^* \subset J \cap \mathcal{I}_{N-1}^1 \subset \frac{1}{2}\mathcal{I}_{n_1+1}^*,
\end{equation*} \begin{equation*}
\mathcal{I}_{m_0}^* \subset K \cap \mathcal{I}_{N-1} \subset \mathcal{I}_{m_0+1}^*, \quad \frac{1}{2}\mathcal{I}_{m_1}^* \subset K \cap \mathcal{I}_{N-1}^1 \subset \frac{1}{2}\mathcal{I}_{m_1+1}^*, \quad \mathcal{I}_{m_2}^* \subset K \cap \mathcal{I}_{N-1}^2 \subset \mathcal{I}_{m_2+1}^*.
\end{equation*}
\begin{equation*}
\mathcal{I}_{m_0}^* \subset K \cap \mathcal{I}_{N-1} \subset \mathcal{I}_{m_0+1}^*, \quad \frac{1}{2}\mathcal{I}_{m_1}^* \subset K \cap \mathcal{I}_{N-1}^1 \subset \frac{1}{2}\mathcal{I}_{m_1+1}^*, \quad \mathcal{I}_{m_2}^* \subset K \cap \mathcal{I}_{N-1}^2 \subset \mathcal{I}_{m_2+1}^*.
\end{equation*} We understand ![]() $\mathcal{I}_j= \emptyset$ whenever
$\mathcal{I}_j= \emptyset$ whenever ![]() $j=-1.$ Define
$j=-1.$ Define ![]() $n= \max\lbrace n_0, n_1 \rbrace$ and
$n= \max\lbrace n_0, n_1 \rbrace$ and ![]() $m=\max\lbrace m_0,m_1,m_2 \rbrace.$ Since we are assuming that J contains at least two points of
$m=\max\lbrace m_0,m_1,m_2 \rbrace.$ Since we are assuming that J contains at least two points of ![]() $E,$ we must have
$E,$ we must have ![]() $m \geq n \geq 0.$ Let us first see that m and n are comparable. We clearly have
$m \geq n \geq 0.$ Let us first see that m and n are comparable. We clearly have
an so
where c denotes various constants depending only on ![]() $\alpha.$ This shows that
$\alpha.$ This shows that ![]() $m \leq n + C,$ for a constant
$m \leq n + C,$ for a constant ![]() $C=C(\alpha,\varepsilon) \gt 0.$ We can now estimate w(K) by
$C=C(\alpha,\varepsilon) \gt 0.$ We can now estimate w(K) by
 \begin{align*}
w(K) & = w(K \cap \mathcal{I}_{N-1})+ w(K \cap \mathcal{I}_{N-1}^1) + w(K \cap \mathcal{I}_{N-1}^2) \leq C(\alpha) w(\mathcal{I}_m) \\
& \leq C(\alpha,\varepsilon) w(\mathcal{I}_n) \leq C(\alpha,\varepsilon) \max\lbrace w(J \cap \mathcal{I}_{N-1}) , 2^{1-\alpha} w(J \cap \mathcal{I}_{N-1}^1) \rbrace\nonumber\\
& \quad\leq C(\alpha,\varepsilon) w(J).
\end{align*}
\begin{align*}
w(K) & = w(K \cap \mathcal{I}_{N-1})+ w(K \cap \mathcal{I}_{N-1}^1) + w(K \cap \mathcal{I}_{N-1}^2) \leq C(\alpha) w(\mathcal{I}_m) \\
& \leq C(\alpha,\varepsilon) w(\mathcal{I}_n) \leq C(\alpha,\varepsilon) \max\lbrace w(J \cap \mathcal{I}_{N-1}) , 2^{1-\alpha} w(J \cap \mathcal{I}_{N-1}^1) \rbrace\nonumber\\
& \quad\leq C(\alpha,\varepsilon) w(J).
\end{align*} Case 6. ![]() $\mathcal{I}_{N-1}^1 \cap J \neq \emptyset \neq J \cap \mathcal{I}_{N-1}^2,$
$\mathcal{I}_{N-1}^1 \cap J \neq \emptyset \neq J \cap \mathcal{I}_{N-1}^2,$ ![]() $ J \cap \mathcal{I}_{N-1} = \emptyset.$ This case is identical to Case 5, due to the palindromic distribution of the edges of
$ J \cap \mathcal{I}_{N-1} = \emptyset.$ This case is identical to Case 5, due to the palindromic distribution of the edges of ![]() $E.$
$E.$
Case 7. ![]() $J \subset \mathcal{I}_{N-1},$ and
$J \subset \mathcal{I}_{N-1},$ and ![]() $K \not \subset \mathcal{I}_{N-1}.$ Let us first see that
$K \not \subset \mathcal{I}_{N-1}.$ Let us first see that ![]() $K \cap \mathcal{I}_{N-1}^2 = \emptyset.$ Indeed, otherwise, K contains both
$K \cap \mathcal{I}_{N-1}^2 = \emptyset.$ Indeed, otherwise, K contains both ![]() $\mathcal{I}_{N-1}^1$ and J, and so
$\mathcal{I}_{N-1}^1$ and J, and so
 \begin{equation*}
|K| \geq |J| + |\mathcal{I}_{N-1}^1| = |J| + \frac{1}{2} |\mathcal{I}_{N-1}| \geq |J| + \frac{1}{2}|J| = \frac{3}{2}|J|.
\end{equation*}
\begin{equation*}
|K| \geq |J| + |\mathcal{I}_{N-1}^1| = |J| + \frac{1}{2} |\mathcal{I}_{N-1}| \geq |J| + \frac{1}{2}|J| = \frac{3}{2}|J|.
\end{equation*} If ɛ is chosen small enough from the beginning, the above contradicts that ![]() $|J| \geq (1-\varepsilon) |K|.$ Thus
$|J| \geq (1-\varepsilon) |K|.$ Thus ![]() $K \subset \mathcal{I}_{N-1} \cup \mathcal{I}_{N-1}^1$. Again, let
$K \subset \mathcal{I}_{N-1} \cup \mathcal{I}_{N-1}^1$. Again, let ![]() $m_0, m_1 \geq -1$ be integers so that
$m_0, m_1 \geq -1$ be integers so that
 \begin{equation*}
\mathcal{I}_{m_0}^* \subset K \cap \mathcal{I}_{N-1} \subset \mathcal{I}_{m_0+1}^* \quad \text{and} \quad \frac{1}{2}\mathcal{I}_{m_1}^* \subset K \cap \mathcal{I}_{N-1}^1 \subset \frac{1}{2}\mathcal{I}_{m_1+1}^*;
\end{equation*}
\begin{equation*}
\mathcal{I}_{m_0}^* \subset K \cap \mathcal{I}_{N-1} \subset \mathcal{I}_{m_0+1}^* \quad \text{and} \quad \frac{1}{2}\mathcal{I}_{m_1}^* \subset K \cap \mathcal{I}_{N-1}^1 \subset \frac{1}{2}\mathcal{I}_{m_1+1}^*;
\end{equation*} where ![]() $\mathcal{I}_{m_0}^*$ and
$\mathcal{I}_{m_0}^*$ and ![]() $\mathcal{I}_{m_1}^*$ are translated copies of
$\mathcal{I}_{m_1}^*$ are translated copies of ![]() $\mathcal{I}_{m_0}$ and
$\mathcal{I}_{m_0}$ and ![]() $\mathcal{I}_{m_1},$ and understanding that
$\mathcal{I}_{m_1},$ and understanding that ![]() $\mathcal{I}_{-1}= \emptyset.$ Either m 0 or m 1 must be nonnegative, since K contains at least two points of
$\mathcal{I}_{-1}= \emptyset.$ Either m 0 or m 1 must be nonnegative, since K contains at least two points of ![]() $E.$ Also,
$E.$ Also,
 \begin{equation*}
| \mathcal{I}_{m_1} | \leq 2 |K \cap \mathcal{I}_{N-1}^1| \leq 2 | K \setminus J| \leq \frac{2\varepsilon}{1-\varepsilon} |J| \leq \frac{2\varepsilon}{1-\varepsilon} |\mathcal{I}_{m_0+1}^*| = \frac{2\varepsilon}{1-\varepsilon} |\mathcal{I}_{m_0+1}|.
\end{equation*}
\begin{equation*}
| \mathcal{I}_{m_1} | \leq 2 |K \cap \mathcal{I}_{N-1}^1| \leq 2 | K \setminus J| \leq \frac{2\varepsilon}{1-\varepsilon} |J| \leq \frac{2\varepsilon}{1-\varepsilon} |\mathcal{I}_{m_0+1}^*| = \frac{2\varepsilon}{1-\varepsilon} |\mathcal{I}_{m_0+1}|.
\end{equation*} Thus, for ɛ small enough (but depending only on α), we necessarily have ![]() $m_0 \gt m_1.$ In particular
$m_0 \gt m_1.$ In particular ![]() $m_0 \geq 0,$ and
$m_0 \geq 0,$ and
In the case where ![]() $m_0=0,$ then
$m_0=0,$ then ![]() $|J| \geq (1-\varepsilon) |\mathcal{I}_{0}^*|$ and J is contained in
$|J| \geq (1-\varepsilon) |\mathcal{I}_{0}^*|$ and J is contained in ![]() $\mathcal{I}_{1}^*$. So, after translating J,
$\mathcal{I}_{1}^*$. So, after translating J, ![]() $I_0^*$ and
$I_0^*$ and ![]() $I_1^*,$ it is clear, e.g., by Case 1, that
$I_1^*,$ it is clear, e.g., by Case 1, that ![]() $w(\mathcal{I}_{m_0}) \leq C(\alpha,\varepsilon) w(J).$ And if
$w(\mathcal{I}_{m_0}) \leq C(\alpha,\varepsilon) w(J).$ And if ![]() $m_0 \geq 1,$ then J contains a translated copy of
$m_0 \geq 1,$ then J contains a translated copy of ![]() $\mathcal{I}_{m_0-1}$ or
$\mathcal{I}_{m_0-1}$ or  $\frac{1}{2} \mathcal{I}_{m_0-1}$ due to the fact that
$\frac{1}{2} \mathcal{I}_{m_0-1}$ due to the fact that ![]() $|J| \geq (1-\varepsilon) |\mathcal{I}_{m_0}|$ (and choosing ɛ small enough). This yields
$|J| \geq (1-\varepsilon) |\mathcal{I}_{m_0}|$ (and choosing ɛ small enough). This yields
Case 8. ![]() $J \subset \mathcal{I}_{N-1}^1 \not \supset K,$ or
$J \subset \mathcal{I}_{N-1}^1 \not \supset K,$ or ![]() $J \subset \mathcal{I}_{N-1}^2 \not \supset K.$ Due to the relationship between
$J \subset \mathcal{I}_{N-1}^2 \not \supset K.$ Due to the relationship between ![]() $\mathcal{I}_{N-1} ,$
$\mathcal{I}_{N-1} ,$ ![]() $ \mathcal{I}_{N-1}^1$ and
$ \mathcal{I}_{N-1}^1$ and ![]() $\mathcal{I}_{N-1}^2,$ we can repeat the arguments of Case 7 above.
$\mathcal{I}_{N-1}^2,$ we can repeat the arguments of Case 7 above.
Remark 8.5. A set ![]() $F \subset {\mathbb R}^n$ with properties similar to those of E from Example 8.3 can be constructed, for example, by setting
$F \subset {\mathbb R}^n$ with properties similar to those of E from Example 8.3 can be constructed, for example, by setting ![]() $F: = E \times {\mathbb R}^{n-1} \subset {\mathbb R}^n.$ Indeed, it suffices to note that
$F: = E \times {\mathbb R}^{n-1} \subset {\mathbb R}^n.$ Indeed, it suffices to note that
and that  $\widetilde{h_F}([a,b)^n) = h_E([a,b))$ for all
$\widetilde{h_F}([a,b)^n) = h_E([a,b))$ for all ![]() $a,b\in {\mathbb R},$
$a,b\in {\mathbb R},$ ![]() $a \lt b,$ where
$a \lt b,$ where
 \begin{equation*}
\widetilde{h_F}([a,b)^n) : = \sup \lbrace r \gt 0 \: : \: \text{there exists } t\in {\mathbb R}\; \text{with } [t-r,t+r]^n \subset [a,b]^n \setminus F \rbrace.
\end{equation*}
\begin{equation*}
\widetilde{h_F}([a,b)^n) : = \sup \lbrace r \gt 0 \: : \: \text{there exists } t\in {\mathbb R}\; \text{with } [t-r,t+r]^n \subset [a,b]^n \setminus F \rbrace.
\end{equation*} Comparing ![]() $\widetilde{h_F}$ with hF from (8), we see that if
$\widetilde{h_F}$ with hF from (8), we see that if ![]() $Q, B \subset {\mathbb R}^n$ are respectively a cube and a Euclidean ball with
$Q, B \subset {\mathbb R}^n$ are respectively a cube and a Euclidean ball with ![]() $Q \subset B$ (resp.
$Q \subset B$ (resp. ![]() $B \subset Q$), then
$B \subset Q$), then  $ \widetilde{h_F} (Q) \lesssim h_F(B)$ (resp.
$ \widetilde{h_F} (Q) \lesssim h_F(B)$ (resp.  $h_F(B) \lesssim \widetilde{h_F}(Q)$). These remarks show that F satisfies the following properties:
$h_F(B) \lesssim \widetilde{h_F}(Q)$). These remarks show that F satisfies the following properties:
•
 $w_{\alpha}:=\operatorname{dist}(\cdot,F)^{-\alpha} \in L_{\textrm{loc}}^1({\mathbb R}^n)$ for
$w_{\alpha}:=\operatorname{dist}(\cdot,F)^{-\alpha} \in L_{\textrm{loc}}^1({\mathbb R}^n)$ for  $\alpha \lt 1, $ i.e., wα defines a weight function.
$\alpha \lt 1, $ i.e., wα defines a weight function.• F is not weakly porous. In fact,
 $w_{\alpha}\notin \bigcup_{p \geq 1} A_p({\mathbb R}^n)$ for every α ≠ 0.
$w_{\alpha}\notin \bigcup_{p \geq 1} A_p({\mathbb R}^n)$ for every α ≠ 0.• wα defines a doubling weight in
 ${\mathbb R}^n$ for all α < 1.
${\mathbb R}^n$ for all α < 1.• hF is doubling (recall the Definition 3.4).
The first three properties follow from (33), Fubini’s Theorem, and Example 8.3 (1),(2),(4). The fourth one is a consequence of the previous remarks on ![]() $\widetilde{h_F}$ and Example 8.3 (3).
$\widetilde{h_F}$ and Example 8.3 (3).
9. Muckenhoupt exponents and A 1 conditions
The purpose of this section is to give a precise quantification for the range of those ![]() $\alpha \in {\mathbb R}$ such that
$\alpha \in {\mathbb R}$ such that ![]() $\operatorname{dist}(\cdot, E)^{-\alpha} $ belongs to the
$\operatorname{dist}(\cdot, E)^{-\alpha} $ belongs to the ![]() $A_p(X)$ class for a given
$A_p(X)$ class for a given ![]() $1\leq p \lt \infty.$ Previous results on this direction were obtained in [Reference Anderson, Lehrbäck, Mudarra and Vähäkangas1, Reference Dyda, Ihnatsyeva, Lehrbäck, Tuominen and Vähäkangas6] in the Euclidean setting. Moreover, the concept of Muckenhoupt exponent introduced in [Reference Anderson, Lehrbäck, Mudarra and Vähäkangas1] for subsets E of
$1\leq p \lt \infty.$ Previous results on this direction were obtained in [Reference Anderson, Lehrbäck, Mudarra and Vähäkangas1, Reference Dyda, Ihnatsyeva, Lehrbäck, Tuominen and Vähäkangas6] in the Euclidean setting. Moreover, the concept of Muckenhoupt exponent introduced in [Reference Anderson, Lehrbäck, Mudarra and Vähäkangas1] for subsets E of ![]() ${\mathbb R}^n $ allowed us to determine the mentioned range of exponents, provided E is a weakly porous set in
${\mathbb R}^n $ allowed us to determine the mentioned range of exponents, provided E is a weakly porous set in ![]() ${\mathbb R}^n$. Here we extend these results to metric spaces with doubling measure
${\mathbb R}^n$. Here we extend these results to metric spaces with doubling measure ![]() $(X,d,\mu).$
$(X,d,\mu).$
Definition 9.1. (Muckenhoupt exponent of a set)
Let ![]() $E\subset X$. If
$E\subset X$. If ![]() $h_E(B(x,R)) \gt 0$ for every
$h_E(B(x,R)) \gt 0$ for every ![]() $x\in E$ and
$x\in E$ and ![]() $R \gt 0$, then the Muckenhoupt exponent
$R \gt 0$, then the Muckenhoupt exponent ![]() $\operatorname{{Mu}}(E)$ is the supremum of the numbers
$\operatorname{{Mu}}(E)$ is the supremum of the numbers ![]() $\alpha\in {\mathbb R}$ for which there exists a constant
$\alpha\in {\mathbb R}$ for which there exists a constant ![]() $C$ such that
$C$ such that
 \begin{equation}
\frac{\mu (E_r\cap B(x,R))}{\mu( B(x,R) )} \le C\biggl(\frac {h_E(B(x,R))}{r}\biggr)^{-\alpha}
\end{equation}
\begin{equation}
\frac{\mu (E_r\cap B(x,R))}{\mu( B(x,R) )} \le C\biggl(\frac {h_E(B(x,R))}{r}\biggr)^{-\alpha}
\end{equation} for every ![]() $x\in E$ and
$x\in E$ and ![]() $0 \lt r \lt h_E(B(x,R)) \le 2R$. If
$0 \lt r \lt h_E(B(x,R)) \le 2R$. If ![]() $h_E(B(x,R))=0$ for some
$h_E(B(x,R))=0$ for some ![]() $x\in E$ and
$x\in E$ and ![]() $R \gt 0$, then we set
$R \gt 0$, then we set ![]() $\operatorname{{Mu}}(E)=0$.
$\operatorname{{Mu}}(E)=0$.
Here and below, we denote ![]() $E_r:=\lbrace y\in X \, : \, \operatorname{dist}(y,E) \lt r \rbrace, $ for every r > 0. The first goal of this section is to prove, for any nonempty subset
$E_r:=\lbrace y\in X \, : \, \operatorname{dist}(y,E) \lt r \rbrace, $ for every r > 0. The first goal of this section is to prove, for any nonempty subset ![]() $E\subset X$, that for
$E\subset X$, that for ![]() $\alpha \gt 0,$
$\alpha \gt 0,$
This is precisely Theorem 9.4 below, a consequence of the next two lemmas. We will only give a sketch of the proofs, because they are almost identical to the proofs of the corresponding results in ![]() ${\mathbb R}^n$ from [Reference Anderson, Lehrbäck, Mudarra and Vähäkangas1], if one uses the doubling condition (1) for the measure µ at the appropriate points.
${\mathbb R}^n$ from [Reference Anderson, Lehrbäck, Mudarra and Vähäkangas1], if one uses the doubling condition (1) for the measure µ at the appropriate points.
Lemma 9.2. Let ![]() $E\subset X$ be a nonempty set and let
$E\subset X$ be a nonempty set and let ![]() $\alpha \geq 0$ be such that
$\alpha \geq 0$ be such that ![]() $\operatorname{dist}(\cdot,E)^{-\alpha}\in A_1(X)$. Then
$\operatorname{dist}(\cdot,E)^{-\alpha}\in A_1(X)$. Then ![]() $0\le \alpha\le \operatorname{{Mu}}(E)$.
$0\le \alpha\le \operatorname{{Mu}}(E)$.
Proof. The claim holds if α = 0, and so we may assume that α > 0. Then ![]() $h_E(B(x,R)) \gt 0$ for every
$h_E(B(x,R)) \gt 0$ for every ![]() $x\in E$ and R > 0, and if
$x\in E$ and R > 0, and if ![]() $0 \lt r \lt h_E(B(x,R))\le 2R$, we have
$0 \lt r \lt h_E(B(x,R))\le 2R$, we have
 \begin{align*}
\mu \left( E_r \cap B(x,R) \right) &\leq r^\alpha \int_{ B(x,R)} \operatorname{dist}(\cdot,E)^{-\alpha} \, d \mu \\ & \leq [w]_{A_1} r^\alpha \mu \left( B(x,R) \right)\ \mathrm{ess\, inf}_{B(x,R)}\nonumber\operatorname{dist}(\cdot,E)^{-\alpha};
\end{align*}
\begin{align*}
\mu \left( E_r \cap B(x,R) \right) &\leq r^\alpha \int_{ B(x,R)} \operatorname{dist}(\cdot,E)^{-\alpha} \, d \mu \\ & \leq [w]_{A_1} r^\alpha \mu \left( B(x,R) \right)\ \mathrm{ess\, inf}_{B(x,R)}\nonumber\operatorname{dist}(\cdot,E)^{-\alpha};
\end{align*} where ![]() $w=\operatorname{dist}(\cdot,E)^{-\alpha}.$ On the other hand, taking
$w=\operatorname{dist}(\cdot,E)^{-\alpha}.$ On the other hand, taking ![]() $y\in X$ and s > 0 so that
$y\in X$ and s > 0 so that  $h_E(B(x,R)) \geq s \geq \frac{1}{2} h_E(B(x,R))$ and
$h_E(B(x,R)) \geq s \geq \frac{1}{2} h_E(B(x,R))$ and ![]() $B(y,s) \subset B(x,R) \setminus E,$ we obtain
$B(y,s) \subset B(x,R) \setminus E,$ we obtain
The two inequalities lead us to ![]() $\operatorname{{Mu}}(E) \gt \alpha.$
$\operatorname{{Mu}}(E) \gt \alpha.$
Lemma 9.3. Let ![]() $E\subset X$ be a nonempty set and assume that
$E\subset X$ be a nonempty set and assume that ![]() $0\le \alpha \lt \operatorname{{Mu}}(E)$. Then
$0\le \alpha \lt \operatorname{{Mu}}(E)$. Then ![]() $\operatorname{dist}(\cdot,E)^{-\alpha}\in A_1(X)$.
$\operatorname{dist}(\cdot,E)^{-\alpha}\in A_1(X)$.
Proof. We follow the arguments from the proof in the Euclidean setting [Reference Anderson, Lehrbäck, Mudarra and Vähäkangas1, Theorem 6.5]. We first prove the A 1-estimate (2.1) for balls ![]() $B(x,r)$ centered at points
$B(x,r)$ centered at points ![]() $x\in E:$
$x\in E:$
 \begin{equation}
{\int{\kern-10.5pt}-}_{{\hskip-3.5pt B(x,r)}} \operatorname{dist}(y,E)^{-\alpha}\, d \mu(y)
\le C_0(C_\mu,\lambda,\alpha,E)\ \mathrm{ess\, inf}_{y\in B(x,r)}\operatorname{dist}(y,E)^{-\alpha}.
\end{equation}
\begin{equation}
{\int{\kern-10.5pt}-}_{{\hskip-3.5pt B(x,r)}} \operatorname{dist}(y,E)^{-\alpha}\, d \mu(y)
\le C_0(C_\mu,\lambda,\alpha,E)\ \mathrm{ess\, inf}_{y\in B(x,r)}\operatorname{dist}(y,E)^{-\alpha}.
\end{equation} Let λ > 0 with ![]() $\operatorname{{Mu}}(E) \gt \lambda \gt \alpha$, and let
$\operatorname{{Mu}}(E) \gt \lambda \gt \alpha$, and let ![]() $x\in E$ and r > 0. Observe from inequality
$x\in E$ and r > 0. Observe from inequality ![]() $\operatorname{{Mu}}(E) \gt 0$ that
$\operatorname{{Mu}}(E) \gt 0$ that ![]() $0 \lt h_E(B(x,2r))\le 4r$. Hence, there is
$0 \lt h_E(B(x,2r))\le 4r$. Hence, there is ![]() $j_0\in {\mathbb Z}, j_0 \geq -1$ such that
$j_0\in {\mathbb Z}, j_0 \geq -1$ such that
Define ![]() $F_j=\{y\in B(x,r) : \operatorname{dist}(y,E) \le 2^{1-j}r \}$ and
$F_j=\{y\in B(x,r) : \operatorname{dist}(y,E) \le 2^{1-j}r \}$ and ![]() $ A_{j}=F_{j}\setminus F_{j+1},$ for
$ A_{j}=F_{j}\setminus F_{j+1},$ for ![]() $j\ge j_0$. Reasoning as in the proof of [Reference Anderson, Lehrbäck, Mudarra and Vähäkangas1, Theorem 6.5] and using that
$j\ge j_0$. Reasoning as in the proof of [Reference Anderson, Lehrbäck, Mudarra and Vähäkangas1, Theorem 6.5] and using that ![]() $\mu(B(x,2r)) \leq C_\mu\, \mu(B(x,r)),$ we obtain a constant
$\mu(B(x,2r)) \leq C_\mu\, \mu(B(x,r)),$ we obtain a constant ![]() $C_1=C_1(E,\lambda,C_\mu)$ such that
$C_1=C_1(E,\lambda,C_\mu)$ such that
 \begin{equation}
\begin{split}
\frac {\mu\left( F_{j} \right)}{\mu \left( B(x,r) \right)} \leq C_\mu \frac {\mu\left( E_{2^{2-j}r} \cap B(x,2r) \right)}{\mu \left( B(x,2r) \right)} \leq
C_1 2^{-j\lambda}\biggl(\frac {h_E(B(x,2r))}{r}\biggr)^{-\lambda}.
\end{split}
\end{equation}
\begin{equation}
\begin{split}
\frac {\mu\left( F_{j} \right)}{\mu \left( B(x,r) \right)} \leq C_\mu \frac {\mu\left( E_{2^{2-j}r} \cap B(x,2r) \right)}{\mu \left( B(x,2r) \right)} \leq
C_1 2^{-j\lambda}\biggl(\frac {h_E(B(x,2r))}{r}\biggr)^{-\lambda}.
\end{split}
\end{equation} We then deduce that ![]() $\mu( E ) =0$. The union of the sets Aj with
$\mu( E ) =0$. The union of the sets Aj with ![]() $j\ge j_0$ cover
$j\ge j_0$ cover ![]() $B(x,r)$ up to the zero-measure set
$B(x,r)$ up to the zero-measure set ![]() $\overline{E}\cap B(x,r)$. Integrating over these annuli
$\overline{E}\cap B(x,r)$. Integrating over these annuli ![]() $\lbrace A_j\rbrace_{j \geq j_0}$ as in [Reference Anderson, Lehrbäck, Mudarra and Vähäkangas1, Theorem 6.5] and using (36), we obtain (35), for the points
$\lbrace A_j\rbrace_{j \geq j_0}$ as in [Reference Anderson, Lehrbäck, Mudarra and Vähäkangas1, Theorem 6.5] and using (36), we obtain (35), for the points ![]() $x\in E.$
$x\in E.$
Now, if ![]() $B=B(x,R)$ is an arbitrary ball in X, suppose first that
$B=B(x,R)$ is an arbitrary ball in X, suppose first that ![]() $\operatorname{dist}(B,E) \lt 2 \operatorname{diam}(B).$ Let
$\operatorname{dist}(B,E) \lt 2 \operatorname{diam}(B).$ Let ![]() $p\in E$ be so that
$p\in E$ be so that
It is clear that ![]() $d(p,x) \leq \operatorname{diam}(B) + \operatorname{dist}(p,B) \leq 5 \operatorname{diam}(B) \leq 10R,$ implying
$d(p,x) \leq \operatorname{diam}(B) + \operatorname{dist}(p,B) \leq 5 \operatorname{diam}(B) \leq 10R,$ implying ![]() $B(x,R) \subset B(p, 11 R) \subset B(x, 21 R).$ Because (35) holds for
$B(x,R) \subset B(p, 11 R) \subset B(x, 21 R).$ Because (35) holds for ![]() $B(p,11R),$ we have
$B(p,11R),$ we have
 \begin{align*}
{\int{\kern-10.5pt}-}_{{\hskip-3.5pt B(x,R)}} \operatorname{dist}(\cdot,E)^{-\alpha}\, d \mu & \le C(C_\mu,C_0) {\int{\kern-10.5pt}-}_{{\hskip-3.5pt B(p,11 R)}} \operatorname{dist}(\cdot,E)^{-\alpha} \, d \mu \\
& \leq C(C_\mu,C_0) \ \mathrm{ess\, inf}_{y\in B(p,11R)}\operatorname{dist}(y,E)^{-\alpha}\nonumber\\ & \leq C(C_\mu,C_0) \mathrm{ess\, inf}_{y\in B(x,R)}\operatorname{dist}(y,E)^{-\alpha} .
\end{align*}
\begin{align*}
{\int{\kern-10.5pt}-}_{{\hskip-3.5pt B(x,R)}} \operatorname{dist}(\cdot,E)^{-\alpha}\, d \mu & \le C(C_\mu,C_0) {\int{\kern-10.5pt}-}_{{\hskip-3.5pt B(p,11 R)}} \operatorname{dist}(\cdot,E)^{-\alpha} \, d \mu \\
& \leq C(C_\mu,C_0) \ \mathrm{ess\, inf}_{y\in B(p,11R)}\operatorname{dist}(y,E)^{-\alpha}\nonumber\\ & \leq C(C_\mu,C_0) \mathrm{ess\, inf}_{y\in B(x,R)}\operatorname{dist}(y,E)^{-\alpha} .
\end{align*} And in the case where ![]() $\operatorname{dist}(B,E) \geq 2 \operatorname{diam}(B),$ the triangle inequality gives
$\operatorname{dist}(B,E) \geq 2 \operatorname{diam}(B),$ the triangle inequality gives ![]() $\operatorname{dist}(y,E) \leq 2 \operatorname{dist}(z,E)$ for any
$\operatorname{dist}(y,E) \leq 2 \operatorname{dist}(z,E)$ for any ![]() $y,z\in E,$ and so the A 1 estimate trivially holds over
$y,z\in E,$ and so the A 1 estimate trivially holds over ![]() $B.$
$B.$
Theorem 9.4. Let α > 0 and let ![]() $E\subset X$ be a nonempty set. Then
$E\subset X$ be a nonempty set. Then ![]() $\operatorname{dist}(\cdot,E)^{-\alpha}\in A_1(X)$ if and only if
$\operatorname{dist}(\cdot,E)^{-\alpha}\in A_1(X)$ if and only if ![]() $\operatorname{{Mu}}(E) \gt \alpha$.
$\operatorname{{Mu}}(E) \gt \alpha$.
Proof. If ![]() $\operatorname{{Mu}}(E) \gt \alpha,$ then
$\operatorname{{Mu}}(E) \gt \alpha,$ then ![]() $\operatorname{dist}(\cdot,E)^{-\alpha}\in A_1(X)$ by Lemma 9.3. For the reverse implication, we use the self-improvement of A 1 weights (see Proposition 2.2(1)) and Lemma 9.2.
$\operatorname{dist}(\cdot,E)^{-\alpha}\in A_1(X)$ by Lemma 9.3. For the reverse implication, we use the self-improvement of A 1 weights (see Proposition 2.2(1)) and Lemma 9.2.
Theorem 9.5. Assume that E is weakly porous and hE is doubling. Let ![]() $\alpha\in{\mathbb R}$ and define
$\alpha\in{\mathbb R}$ and define ![]() $w(x)=\operatorname{dist}(x,E)^{-\alpha}$ for every
$w(x)=\operatorname{dist}(x,E)^{-\alpha}$ for every ![]() $x\in X$. Then
$x\in X$. Then
(i)
 $w\in A_1(X)$ if and only if
$w\in A_1(X)$ if and only if  $0\le \alpha \lt \operatorname{{Mu}}(E)$.
$0\le \alpha \lt \operatorname{{Mu}}(E)$.(ii)
 $w\in A_p(X)$, for
$w\in A_p(X)$, for  $1 \lt p \lt \infty$, if and only if
$1 \lt p \lt \infty$, if and only if
 \begin{equation*}
(1-p)\operatorname{{Mu}}(E) \lt \alpha \lt \operatorname{{Mu}}(E).
\end{equation*}
\begin{equation*}
(1-p)\operatorname{{Mu}}(E) \lt \alpha \lt \operatorname{{Mu}}(E).
\end{equation*}
Proof. By Theorem 1.1, there exists α > 0 for which ![]() $\operatorname{dist}(\cdot,E)^{-\alpha} \in A_1(X).$ Taking into account the self-improvement properties of Proposition 2.2, the proof is identical to the one for the corresponding result in
$\operatorname{dist}(\cdot,E)^{-\alpha} \in A_1(X).$ Taking into account the self-improvement properties of Proposition 2.2, the proof is identical to the one for the corresponding result in ![]() ${\mathbb R}^n$ from [Reference Anderson, Lehrbäck, Mudarra and Vähäkangas1, Theorem 1.2].
${\mathbb R}^n$ from [Reference Anderson, Lehrbäck, Mudarra and Vähäkangas1, Theorem 1.2].
Finally, if X satisfies the annular decay property (29), the assumption that hE is doubling can be done away with in Theorem 9.5.
Corollary 9.6. Suppose that ![]() $(X,d,\mu)$ satisfies (29), and let
$(X,d,\mu)$ satisfies (29), and let ![]() $E \subset X$ be weakly porous. Let
$E \subset X$ be weakly porous. Let ![]() $\alpha\in{\mathbb R}$ and define
$\alpha\in{\mathbb R}$ and define ![]() $w(x)=\operatorname{dist}(x,E)^{-\alpha}$ for every
$w(x)=\operatorname{dist}(x,E)^{-\alpha}$ for every ![]() $x\in X$. Then
$x\in X$. Then
(i)
 $w\in A_1(X)$ if and only if
$w\in A_1(X)$ if and only if  $0\le \alpha \lt \operatorname{{Mu}}(E)$.
$0\le \alpha \lt \operatorname{{Mu}}(E)$.(ii)
 $w\in A_p(X)$, for
$w\in A_p(X)$, for  $1 \lt p \lt \infty$, if and only if
$1 \lt p \lt \infty$, if and only if
 \begin{equation*}
(1-p)\operatorname{{Mu}}(E) \lt \alpha \lt \operatorname{{Mu}}(E).
\end{equation*}
\begin{equation*}
(1-p)\operatorname{{Mu}}(E) \lt \alpha \lt \operatorname{{Mu}}(E).
\end{equation*}
Proof. Since ![]() $(X,d,\mu)$ satisfies (29), for every weakly porous set E, the maximal E-free hole function hE is doubling by virtue of Lemma 7.2. Now, it suffices to apply Theorem 9.5.
$(X,d,\mu)$ satisfies (29), for every weakly porous set E, the maximal E-free hole function hE is doubling by virtue of Lemma 7.2. Now, it suffices to apply Theorem 9.5.
Acknowledgements
I am very grateful to Juha Lehrbäck and Antti Vähäkangas for their valuable comments and suggestions on earlier versions of this manuscript. I also thank the referees for several suggestions that improved the exposition of the paper. Finally, I acknowledge financial support from the Academy of Finland via the project “Geometric Analysis” (grant No. 323960) and from the Research Council of Norway via the project “Fourier Methods and Multiplicative Analysis” (grant no. 334466).































