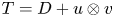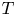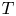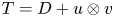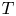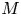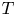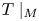1. Introduction and preliminaries
Let $H$![]() denote an infinite-dimensional separable complex Hilbert space and $\mathcal {L}(H)$
denote an infinite-dimensional separable complex Hilbert space and $\mathcal {L}(H)$![]() the Banach algebra of all bounded linear operators on $H$
the Banach algebra of all bounded linear operators on $H$![]() . An operator $T\in \mathcal {L}(H)$
. An operator $T\in \mathcal {L}(H)$![]() is reductive if every closed invariant subspace $M$
is reductive if every closed invariant subspace $M$![]() of $T$
of $T$![]() reduces $T$
reduces $T$![]() or is a so-called reducing subspace; namely $M$
or is a so-called reducing subspace; namely $M$![]() is invariant under both $T$
is invariant under both $T$![]() and its adjoint $T^{\star }$
and its adjoint $T^{\star }$![]() (equivalently, both subspaces $M$
(equivalently, both subspaces $M$![]() and its orthogonal complement $M^{\perp }$
and its orthogonal complement $M^{\perp }$![]() are invariant under $T$
are invariant under $T$![]() ). A well-known unsolved problem in the context of bounded linear operators acting on $H$
). A well-known unsolved problem in the context of bounded linear operators acting on $H$![]() is if every reductive operator must be a normal operator. Indeed, the answer is affirmative if we restrict ourselves to the class of compact operators [Reference Andô1] or polynomially compact operators [Reference Rosenthal36, Reference Saito37]. In the general context $\mathcal {L}(H)$
is if every reductive operator must be a normal operator. Indeed, the answer is affirmative if we restrict ourselves to the class of compact operators [Reference Andô1] or polynomially compact operators [Reference Rosenthal36, Reference Saito37]. In the general context $\mathcal {L}(H)$![]() , such a problem is equivalent to the existence of non-trivial closed invariant subspaces and hence equivalent to provide a positive answer to the Invariant Subspace Problem in the frame of infinite-dimensional separable complex Hilbert spaces [Reference Dyer, Pedersen and Porcelli15].
, such a problem is equivalent to the existence of non-trivial closed invariant subspaces and hence equivalent to provide a positive answer to the Invariant Subspace Problem in the frame of infinite-dimensional separable complex Hilbert spaces [Reference Dyer, Pedersen and Porcelli15].
The Invariant Subspace Problem is, by now, a long-standing open question which have called the attention of many operator theorists since 1940s, producing approaching strategies leading to deep theorems and intricate examples. Within the most remarkable theorems, we mention Lomonosov theorem [Reference Lomonosov30], while among the most relevant examples, one may find the constructions by Enflo [Reference Enflo16] and Read [Reference Read34, Reference Read35] of bounded linear operators acting on infinite-dimensional complex Banach spaces lacking non-trivial closed invariant subspaces (or even non-trivial closed invariant subsets). Recently, in [Reference Gallardo-Gutiérrez and Read21] the authors exhibit a bounded linear operator $T$![]() acting on $\ell ^{1}$
acting on $\ell ^{1}$![]() such that $f(T)$
such that $f(T)$![]() has no non-trivial closed invariant subspaces for every non-constant analytic germ $f$
has no non-trivial closed invariant subspaces for every non-constant analytic germ $f$![]() . We refer to the classical monograph by Radjavi and Rosenthal [Reference Radjavi and Rosenthal32] and the recent one by Chalendar and Partington [Reference Chalendar and Partington9] for more on the subject.
. We refer to the classical monograph by Radjavi and Rosenthal [Reference Radjavi and Rosenthal32] and the recent one by Chalendar and Partington [Reference Chalendar and Partington9] for more on the subject.
Regarding the different aforementioned approaching strategies, there is one coming from the analysis of the behaviour of operators acting on finite-dimensional subspaces which led to the concept of quasitriangular operators. Recall that a bounded linear operator $T$![]() acting on $H$
acting on $H$![]() is said to be quasitriangular if there exists an increasing sequence $(P_n)_{n=1}^{\infty }$
is said to be quasitriangular if there exists an increasing sequence $(P_n)_{n=1}^{\infty }$![]() of finite rank projections converging to the identity $I$
of finite rank projections converging to the identity $I$![]() strongly as $n\to \infty$
strongly as $n\to \infty$![]() such that
such that
Clearly, given any triangular operator in $H$![]() , that is, a bounded linear operator which admits a representation as an upper triangular matrix with respect to a suitable orthonormal basis, there exists an increasing sequence $(P_n)_{n=1}^{\infty }$
, that is, a bounded linear operator which admits a representation as an upper triangular matrix with respect to a suitable orthonormal basis, there exists an increasing sequence $(P_n)_{n=1}^{\infty }$![]() of finite rank projections converging to the identity $I$
of finite rank projections converging to the identity $I$![]() strongly as $n\to \infty$
strongly as $n\to \infty$![]() such that
such that
Based on the proof of Aronszajn and Smith's theorem [Reference Aronszajn and Smith3], Halmos [Reference Halmos26] introduced the concept of quasitriangular operators which, somehow, states that $T$![]() has a sequence of ‘approximately invariant’ finite-dimensional subspaces. Compact operators, operators with finite spectrum, decomposable operators in the sense of Colojoară and Foiaş [Reference Colojoară and Foiaş10] or compact perturbations of normal operators are examples of quasitriangular operators. Remarkably, results due to Douglas and Pearcy [Reference Douglas and Pearcy12] and Apostol, Foias and Voiculescu [Reference Apostol, Foiaş and Voiculescu2] state that the Invariant Subspace Problem is reduced to be proved for quasitriangular operators (see Herrero's book [Reference Herrero27] for more on the subject).
has a sequence of ‘approximately invariant’ finite-dimensional subspaces. Compact operators, operators with finite spectrum, decomposable operators in the sense of Colojoară and Foiaş [Reference Colojoară and Foiaş10] or compact perturbations of normal operators are examples of quasitriangular operators. Remarkably, results due to Douglas and Pearcy [Reference Douglas and Pearcy12] and Apostol, Foias and Voiculescu [Reference Apostol, Foiaş and Voiculescu2] state that the Invariant Subspace Problem is reduced to be proved for quasitriangular operators (see Herrero's book [Reference Herrero27] for more on the subject).
Among the most simple quasitriangular operators for which the existence of non-trivial closed invariant subspaces is still open are rank-one perturbations of diagonal operators. If $D\in \mathcal {L}(H)$![]() is a diagonal operator, that is, there exists an orthonormal basis $(e_n)_{n\geq 1}$
is a diagonal operator, that is, there exists an orthonormal basis $(e_n)_{n\geq 1}$![]() of $H$
of $H$![]() and a sequence of complex numbers $(\lambda _n)_{n\geq 1} \subset \mathbb {C}$
and a sequence of complex numbers $(\lambda _n)_{n\geq 1} \subset \mathbb {C}$![]() such that $De_n = \lambda _n e_n$
such that $De_n = \lambda _n e_n$![]() , a rank-one perturbations of $D$
, a rank-one perturbations of $D$![]() can be written as
can be written as
where $u$![]() and $v$
and $v$![]() are non-zero vectors in $H$
are non-zero vectors in $H$![]() and $u\otimes v(x) = \langle {x,\,v}\rangle \, u$
and $u\otimes v(x) = \langle {x,\,v}\rangle \, u$![]() for every $x \in H$
for every $x \in H$![]() . While expression (1.1) is not unique as far as rank-one perturbations of diagonal operators concern, considering the expansions of $u$
. While expression (1.1) is not unique as far as rank-one perturbations of diagonal operators concern, considering the expansions of $u$![]() , $v$
, $v$![]() with respect to the (ordered) orthonormal basis $(e_n)_{n\geq 1}$
with respect to the (ordered) orthonormal basis $(e_n)_{n\geq 1}$![]()
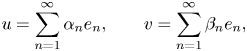
Ionascu showed that whenever both $u$![]() and $v$
and $v$![]() have non-zero components $\alpha _n$
have non-zero components $\alpha _n$![]() and $\beta _n$
and $\beta _n$![]() for every $n\geq 1$
for every $n\geq 1$![]() uniqueness follows (see [Reference Ionascu28, proposition 1.1]). Moreover, he studied rank-one perturbations of diagonal operators from the standpoint of invariant subspaces identifying normal operators as well as contractions within this class. Note that, in particular, rank-one perturbations of normal operators whose eigenvectors span $H$
uniqueness follows (see [Reference Ionascu28, proposition 1.1]). Moreover, he studied rank-one perturbations of diagonal operators from the standpoint of invariant subspaces identifying normal operators as well as contractions within this class. Note that, in particular, rank-one perturbations of normal operators whose eigenvectors span $H$![]() belongs to such a class, since they are unitarily equivalent to those expressed by (1.1).
belongs to such a class, since they are unitarily equivalent to those expressed by (1.1).
Later on, Foias, Jung, Ko and Pearcy showed that there is a large class of such operators each of which has a nontrivial hyperinvariant subspace [Reference Foias, Jung, Ko and Pearcy18]; indeed they are decomposable operators [Reference Foias, Jung, Ko and Pearcy20] (see also the papers by Fang and Xia [Reference Fang and Xia17] and Klaja [Reference Klaja29] for an extension of the results in [Reference Foias, Jung, Ko and Pearcy18] to finite rank and compact perturbations).
In a more general setting, rank-one perturbations of normal operators have been extensively studied for decades (see the recent papers [Reference Baranov4–Reference Baranov and Yakubovich7] and the references therein). Recently, in [Reference Putinar and Yakubovich31], the authors have provided conditions for a possible dissection of the spectrum of $T$![]() along a curve implying a decomposition of $T$
along a curve implying a decomposition of $T$![]() as a direct sum of two operators with localized spectrum and providing sufficient conditions to ensure the existence of invariant subspaces for $T$
as a direct sum of two operators with localized spectrum and providing sufficient conditions to ensure the existence of invariant subspaces for $T$![]() .
.
The aim of this work in this context is studying the existence of reducing subspaces for operators $T$![]() which are rank-one perturbations of diagonal operators and, in general, of normal operators. Recently, there have been an exhaustive study on reducing subspaces for multiplication operators whenever they act on spaces of analytic functions like the Bergman space (see the works by Douglas and coauthors [Reference Douglas, Sun and Zheng13, Reference Douglas, Putinar and Wang14] or those by Guo and Huang [Reference Guo and Huang22–Reference Guo and Huang24], for instance).
which are rank-one perturbations of diagonal operators and, in general, of normal operators. Recently, there have been an exhaustive study on reducing subspaces for multiplication operators whenever they act on spaces of analytic functions like the Bergman space (see the works by Douglas and coauthors [Reference Douglas, Sun and Zheng13, Reference Douglas, Putinar and Wang14] or those by Guo and Huang [Reference Guo and Huang22–Reference Guo and Huang24], for instance).
Our starting point will be a theorem of Ionascu where normal operators are characterized within the class of rank-one perturbations of normal operators. Clearly, the existence of reducing subspaces is trivial for normal operators, since the spectral measure provides plenty of projections commuting with the operator. Nevertheless, as we will show, the spectral picture will play a significant role in order to prove the existence of reducing subspaces for rank-one perturbations of diagonal operators whenever they are not normal. In this regard, the most extreme case is provided when the spectrum of the operator $T=D + u\otimes v$![]() (uniquely determined by such expression) is contained in a line, since in such a case $T$
(uniquely determined by such expression) is contained in a line, since in such a case $T$![]() has a reducing subspace if and only if $T$
has a reducing subspace if and only if $T$![]() is normal (see theorem 2.1, § 2). As a consequence, we will exhibit operators within this class being decomposable (even strongly decomposable) with no reducing subspaces.
is normal (see theorem 2.1, § 2). As a consequence, we will exhibit operators within this class being decomposable (even strongly decomposable) with no reducing subspaces.
When the spectrum of $T=D + u\otimes v$![]() is contained in a circle, which turns out to be the other possible case according to Ionascu's result to ensure that $T$
is contained in a circle, which turns out to be the other possible case according to Ionascu's result to ensure that $T$![]() is a normal operator (see [Reference Ionascu28, corollary 3.2]), the situation differs drastically from the previous case aforementioned. More precisely, it is possible to exhibit non-normal operators with spectrum contained in a circle either having or lacking non-trivial reducing subspaces (see theorem 3.1, § 3).
is a normal operator (see [Reference Ionascu28, corollary 3.2]), the situation differs drastically from the previous case aforementioned. More precisely, it is possible to exhibit non-normal operators with spectrum contained in a circle either having or lacking non-trivial reducing subspaces (see theorem 3.1, § 3).
Indeed, theorem 3.1 is extended in a more general setting in § 4 allowing us to exhibit rank-one perturbations of diagonal operators with arbitrary spectrum lacking non-trivial reducing subspaces. The main result in this context, theorem 4.3, characterizes the reducing subspaces $M$![]() of $T$
of $T$![]() such that the restriction of $T$
such that the restriction of $T$![]() to $M$
to $M$![]() , denoted by $T\mid _M$
, denoted by $T\mid _M$![]() , is normal. In particular, as a consequence of theorem 4.7 it is possible to exhibit rank-one perturbation of completely normal diagonal operators lacking reducing subspaces. Recall that a normal operator is completely normal if all its invariant subspaces are reducing.
, is normal. In particular, as a consequence of theorem 4.7 it is possible to exhibit rank-one perturbation of completely normal diagonal operators lacking reducing subspaces. Recall that a normal operator is completely normal if all its invariant subspaces are reducing.
Besides, we discuss these results in the context of a classical theorem due to Behncke [Reference Behncke8] which provides a decomposition of the underlying Hilbert space in an orthogonal sum of reducing subspaces for essentially normal operators (see also [Reference Guo and Huang25, chapter 8]). We conclude § 4 addressing some of the previous results in the more general context of rank-one perturbations of normal operators.
Finally, in § 5, we present some examples of rank-one perturbations of diagonal operators with multiplicity strictly larger than one in order to illustrate how the picture of the reducing subspaces changes whenever the assumption on the uniform multiplicity one is not assumed. Such assumption plays a key role in the proofs of the results aforementioned.
For the sake of completeness, we close this first section with some preliminaries regarding results about existence of invariant subspaces of rank-one perturbations of diagonal operators as well as of normal operators, which will be of interest throughout the paper.
1.1 Preliminaries
Let $D$![]() be a diagonal operator in $\mathcal {L}(H)$
be a diagonal operator in $\mathcal {L}(H)$![]() and denote by $\Lambda (D)=(\lambda _n)_{n\geq 1}\subset \mathbb {C}$
and denote by $\Lambda (D)=(\lambda _n)_{n\geq 1}\subset \mathbb {C}$![]() its set of eigenvalues with respect to an orthonormal basis $(e_n)_{n\geq 1}$
its set of eigenvalues with respect to an orthonormal basis $(e_n)_{n\geq 1}$![]() of $H$
of $H$![]() . It is well-known that the spectrum of $D$
. It is well-known that the spectrum of $D$![]() is given by the closure of $\Lambda (D)$
is given by the closure of $\Lambda (D)$![]() , that is, $\sigma (D) = \overline {\Lambda (D)}.$
, that is, $\sigma (D) = \overline {\Lambda (D)}.$![]()
Let $u,$![]() and $v$
and $v$![]() be non-zero vectors in $H$
be non-zero vectors in $H$![]() and consider their expansions with respect to the (ordered) orthonormal basis $(e_n)_{n\geq 1}$
and consider their expansions with respect to the (ordered) orthonormal basis $(e_n)_{n\geq 1}$![]()
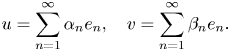
Let $T\in \mathcal {L}(H)$![]() the rank-one perturbation of $D$
the rank-one perturbation of $D$![]() given by expression (1.1), namely
given by expression (1.1), namely
where $u\otimes v(x) = \langle {x,\,v}\rangle \, u$![]() for every $x \in H$
for every $x \in H$![]() . As mentioned previously, Ionascu proved in [Reference Ionascu28, proposition 1.1] that if $\alpha _n \beta _n\neq 0$
. As mentioned previously, Ionascu proved in [Reference Ionascu28, proposition 1.1] that if $\alpha _n \beta _n\neq 0$![]() for every $n$
for every $n$![]() , then (1.1) is unique in the sense that if $T= D + u\otimes v= D' + u'\otimes v'$
, then (1.1) is unique in the sense that if $T= D + u\otimes v= D' + u'\otimes v'$![]() with $D$
with $D$![]() , $D'$
, $D'$![]() diagonal operators and $u,\, v,\, u',\, v'$
diagonal operators and $u,\, v,\, u',\, v'$![]() non-zero vectors in $H$
non-zero vectors in $H$![]() , then $D=D'$
, then $D=D'$![]() and $u\otimes v=u'\otimes v'$
and $u\otimes v=u'\otimes v'$![]() .
.
Moreover, he also proved that if there exists $n_0 \in \mathbb {N}$![]() such that $\alpha _{n_0} \beta _{n_0} = 0$
such that $\alpha _{n_0} \beta _{n_0} = 0$![]() , then either $\lambda _{n_0}$
, then either $\lambda _{n_0}$![]() is an eigenvalue of $T$
is an eigenvalue of $T$![]() or $\overline {\lambda _{n_0}}$
or $\overline {\lambda _{n_0}}$![]() is an eigenvalue of $T^{\ast }$
is an eigenvalue of $T^{\ast }$![]() ; in both cases associated with the same eigenvector $e_{n_0}$
; in both cases associated with the same eigenvector $e_{n_0}$![]() (see [Reference Ionascu28, proposition 2.1]). As a straightforward consequence $T$
(see [Reference Ionascu28, proposition 2.1]). As a straightforward consequence $T$![]() has a reducing subspace whenever there exists $n_0 \in \mathbb {N}$
has a reducing subspace whenever there exists $n_0 \in \mathbb {N}$![]() such that $\alpha _{n_0}=\beta _{n_0}=0$
such that $\alpha _{n_0}=\beta _{n_0}=0$![]() . As we will show in theorem 2.1, this case will exhaust all the possibilities when the spectrum of the given operator $T= D + u\otimes v$
. As we will show in theorem 2.1, this case will exhaust all the possibilities when the spectrum of the given operator $T= D + u\otimes v$![]() is contained in a line.
is contained in a line.
Indeed, there are only two possible spectral pictures for a rank-one perturbation of a diagonal operator $T= D + u\otimes v$![]() with uniqueness expression ($\alpha _n \beta _n\neq 0$
with uniqueness expression ($\alpha _n \beta _n\neq 0$![]() for every $n$
for every $n$![]() ) in order to be a normal operator as stated in proposition 3.1 and corollary 3.2 in [Reference Ionascu28]:
) in order to be a normal operator as stated in proposition 3.1 and corollary 3.2 in [Reference Ionascu28]:
Theorem 1.1 (Ionascu, 2001)
Let $T = N+u\otimes v$![]() be in $\mathcal {L}(H)$
be in $\mathcal {L}(H)$![]() where $N$
where $N$![]() is a normal operator and $u,\, v$
is a normal operator and $u,\, v$![]() are nonzero vectors in $H$
are nonzero vectors in $H$![]() . Then $T$
. Then $T$![]() is a normal operator if and only if either
is a normal operator if and only if either
(i) $u$
 and $v$
and $v$ are linearly dependent and $u$
are linearly dependent and $u$ is an eigenvector for ${\rm Im}\; (\alpha N^{\ast })$
is an eigenvector for ${\rm Im}\; (\alpha N^{\ast })$ where $\alpha = {\langle u,\, v\rangle }/{\|v\|^{2}},$
where $\alpha = {\langle u,\, v\rangle }/{\|v\|^{2}},$ or
or(ii) $u,\, v$
 are linearly independent vectors and there exist $\alpha,\, \beta \in \mathbb {C}$
are linearly independent vectors and there exist $\alpha,\, \beta \in \mathbb {C}$ such that
\[ (N^{{\ast}}-\overline{\alpha} I)u=\|u\|^{2} \beta v \; \mbox{ and } \; (N-\alpha I)v=\|v\|^{2} \overline{\beta} u, \]where ${\rm Re}\; (\beta )=- 1/2$
such that
\[ (N^{{\ast}}-\overline{\alpha} I)u=\|u\|^{2} \beta v \; \mbox{ and } \; (N-\alpha I)v=\|v\|^{2} \overline{\beta} u, \]where ${\rm Re}\; (\beta )=- 1/2$
 .
.
In particular, with the introduced notation, if $D$![]() is a diagonal operator and $\alpha _n \beta _n\neq 0$
is a diagonal operator and $\alpha _n \beta _n\neq 0$![]() for every $n,$
for every $n,$![]() then $T = D+u\otimes v \in \mathcal {L}(H)$
then $T = D+u\otimes v \in \mathcal {L}(H)$![]() is normal if and only if
is normal if and only if
(i′) there exist $\alpha \in \mathbb {C}$
 and $t \in \mathbb {R}$
and $t \in \mathbb {R}$ such that $\Lambda (D)$
such that $\Lambda (D)$ lies on the line $\{z \in \mathbb {C}: {\rm Im}\; (\alpha \overline {z}) = t\}$
lies on the line $\{z \in \mathbb {C}: {\rm Im}\; (\alpha \overline {z}) = t\}$ and $u = \alpha v,$
and $u = \alpha v,$ or
or(ii′) there exist $\alpha \in \mathbb {C}$
 and $t \in \mathbb {R}$
and $t \in \mathbb {R}$ such that $\Lambda (D)$
such that $\Lambda (D)$ lies on the circle $\{z \in \mathbb {C}: |z-\alpha | = t\}$
lies on the circle $\{z \in \mathbb {C}: |z-\alpha | = t\}$ and
\[ \frac{tu}{\| u \|} = {\rm e}^{i\theta}(D-\alpha I) \left( \frac{v}{\|v\|}\right), \]where $\theta \in [0,\,\pi )$
and
\[ \frac{tu}{\| u \|} = {\rm e}^{i\theta}(D-\alpha I) \left( \frac{v}{\|v\|}\right), \]where $\theta \in [0,\,\pi )$
 is determined by the equation $\textrm {Re}\; ({t{\rm e}^{i\theta }}/{(\|u\| \|v\|})) = - {1}/{2} .$
is determined by the equation $\textrm {Re}\; ({t{\rm e}^{i\theta }}/{(\|u\| \|v\|})) = - {1}/{2} .$
As we will show, this dichotomy will allow us to establish the existence of reducing subspaces for rank-one perturbation of diagonal operators as far as their spectrum is contained in a line.
In order to finish this preliminary section, we turn our attention to the multiplicity of the eigenvalues of the diagonal operator. In [Reference Ionascu28, proposition 2.2], it was shown that if $\lambda$![]() is an eigenvalue of $D$
is an eigenvalue of $D$![]() of multiplicity strictly larger than one, then $\lambda$
of multiplicity strictly larger than one, then $\lambda$![]() is an eigenvalue of the rank-one perturbation operator $T = D+u\otimes v$
is an eigenvalue of the rank-one perturbation operator $T = D+u\otimes v$![]() . Indeed, a closer look at the proof shows the following in our context:
. Indeed, a closer look at the proof shows the following in our context:
Proposition 1.2 Assume $\lambda$![]() is an eigenvalue of $D$
is an eigenvalue of $D$![]() of multiplicity strictly larger than one and let $\lambda = \lambda _{n_0} = \lambda _{n_1}$
of multiplicity strictly larger than one and let $\lambda = \lambda _{n_0} = \lambda _{n_1}$![]() for $n_0,\,n_1 \in \mathbb {N}$
for $n_0,\,n_1 \in \mathbb {N}$![]() . Suppose, in addition, that $\alpha _{n_0} = \beta _{n_0}$
. Suppose, in addition, that $\alpha _{n_0} = \beta _{n_0}$![]() and $\alpha _{n_1} = \beta _{n_1}$
and $\alpha _{n_1} = \beta _{n_1}$![]() . Then $T$
. Then $T$![]() has a non-trivial reducing subspace.
has a non-trivial reducing subspace.
Hence, according to proposition 1.2, it turns out to be easy to construct examples of operators having non-trivial reducing subspaces if we do not assume uniform multiplicity one for the diagonal operator. In the last section, § 5, we will address examples in this context showing, in particular, that the assumption of uniform multiplicity one is essential in our approach.
2. Reducing subspaces for rank-one perturbations of diagonal operators: when the spectrum is contained in a line
In this section we will show, in particular, that if $T$![]() is a uniquely determined rank-one perturbation of a diagonal operator with spectrum contained in a line, $T$
is a uniquely determined rank-one perturbation of a diagonal operator with spectrum contained in a line, $T$![]() has a reducing subspace if and only if it is a normal operator. The precise statement is the following:
has a reducing subspace if and only if it is a normal operator. The precise statement is the following:
Theorem 2.1 Let $T = D + u\otimes v \in \mathcal {L}(H)$![]() where $D$
where $D$![]() is a diagonal operator with respect to an orthonormal basis $(e_n)_{n\geq 1}$
is a diagonal operator with respect to an orthonormal basis $(e_n)_{n\geq 1}$![]() and $u =\sum _n \alpha _n e_n,$
and $u =\sum _n \alpha _n e_n,$![]() $v=\sum _n \beta _n e_n$
$v=\sum _n \beta _n e_n$![]() are nonzero vectors in $H$
are nonzero vectors in $H$![]() . Assume $D$
. Assume $D$![]() has uniform multiplicity one and its spectrum $\sigma (D)$
has uniform multiplicity one and its spectrum $\sigma (D)$![]() is contained in a line. Then, $T$
is contained in a line. Then, $T$![]() has a non-trivial reducing subspace if and only if $T$
has a non-trivial reducing subspace if and only if $T$![]() is normal or there exists $n\in \mathbb {N}$
is normal or there exists $n\in \mathbb {N}$![]() such that $\alpha _n=\beta _n= 0.$
such that $\alpha _n=\beta _n= 0.$![]()
Note that since every normal operator $N$![]() whose eigenvectors span $H$
whose eigenvectors span $H$![]() with uniform multiplicity one is unitarily equivalent to a diagonal operator (also with uniform multiplicity one). Theorem 2.1 could be rephrased for rank-one perturbation of such normal operators showing, in particular, the existence of a large class of rank-one perturbation of normal operators lacking non-trivial reducing subspaces. Indeed, by means of Ionascu's theorem, it is enough to consider vectors $u$
with uniform multiplicity one is unitarily equivalent to a diagonal operator (also with uniform multiplicity one). Theorem 2.1 could be rephrased for rank-one perturbation of such normal operators showing, in particular, the existence of a large class of rank-one perturbation of normal operators lacking non-trivial reducing subspaces. Indeed, by means of Ionascu's theorem, it is enough to consider vectors $u$![]() and $v$
and $v$![]() linearly dependent where $u$
linearly dependent where $u$![]() is an eigenvector for $\textrm {Im}\; (\alpha N^{\ast })$
is an eigenvector for $\textrm {Im}\; (\alpha N^{\ast })$![]() with $\alpha = {\langle u,\, v\rangle }/{\|v\|^{2}}$
with $\alpha = {\langle u,\, v\rangle }/{\|v\|^{2}}$![]() .
.
In order to prove theorem 2.1 some previous lemmas will be necessary. Recall that a closed subspace $M \subseteq H$![]() is reducing for an operator $T\in \mathcal {L}(H)$
is reducing for an operator $T\in \mathcal {L}(H)$![]() if and only if the orthogonal projection $P_M : H \rightarrow M$
if and only if the orthogonal projection $P_M : H \rightarrow M$![]() onto $M$
onto $M$![]() commutes with $T$
commutes with $T$![]() , that is, $T P_M = P_M T$
, that is, $T P_M = P_M T$![]() . The notation $\{T\}'$
. The notation $\{T\}'$![]() will stand for the commutant of $T$
will stand for the commutant of $T$![]() .
.
Lemma 2.2 Let $T = D + u\otimes v \in \mathcal {L}(H)$![]() where $D$
where $D$![]() is a diagonal operator and $u,\, v$
is a diagonal operator and $u,\, v$![]() are nonzero vectors in $H$
are nonzero vectors in $H$![]() . Let $M \subseteq H$
. Let $M \subseteq H$![]() be a non-trivial reducing subspace for $T$
be a non-trivial reducing subspace for $T$![]() . If $P_M$
. If $P_M$![]() is the orthogonal projection onto $M$
is the orthogonal projection onto $M$![]() and $Q_M = I - P_M,$
and $Q_M = I - P_M,$![]() then
then
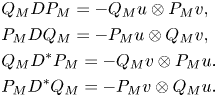
Proof. We show the first equality, since the other ones follow analogously.
Since $M$![]() is reducing for $T$
is reducing for $T$![]() , $Q_MTP_M = 0$
, $Q_MTP_M = 0$![]() and therefore,
and therefore,
In addition, for every $x \in H$![]()
which finally leads to the desired expression.
Next lemma refers, roughly speaking, to the location of the vectors $u$![]() and $v$
and $v$![]() with respect to reducing subspaces of $T=D + u\otimes v$
with respect to reducing subspaces of $T=D + u\otimes v$![]() .
.
Lemma 2.3 Let $T = D + u\otimes v \in \mathcal {L}(H)$![]() where $D$
where $D$![]() is a diagonal operator with respect to an orthonormal basis $(e_n)_{n\geq 1}$
is a diagonal operator with respect to an orthonormal basis $(e_n)_{n\geq 1}$![]() and $u =\sum _n \alpha _n e_n,$
and $u =\sum _n \alpha _n e_n,$![]() $v=\sum _n \beta _n e_n$
$v=\sum _n \beta _n e_n$![]() nonzero vectors in $H$
nonzero vectors in $H$![]() . Assume $D$
. Assume $D$![]() has uniform multiplicity one and $\alpha _n \beta _n\neq 0$
has uniform multiplicity one and $\alpha _n \beta _n\neq 0$![]() for every $n\in \mathbb {N}$
for every $n\in \mathbb {N}$![]() . Let $P_M: H \rightarrow M$
. Let $P_M: H \rightarrow M$![]() be a non-trivial orthogonal projection commuting with $T$
be a non-trivial orthogonal projection commuting with $T$![]() . Then, $u,\,v,\, e_n \notin \ker P_M \cup \ker (I-P_M)$
. Then, $u,\,v,\, e_n \notin \ker P_M \cup \ker (I-P_M)$![]() for all $n \in \mathbb {N}$
for all $n \in \mathbb {N}$![]() .
.
In order to prove lemma 2.3, recall that given a linear space $\mathcal {A}$![]() of $\mathcal {L}(H)$
of $\mathcal {L}(H)$![]() , a vector $x$
, a vector $x$![]() is separating for $\mathcal {A}$
is separating for $\mathcal {A}$![]() if $Ax=0$
if $Ax=0$![]() and $A \in \mathcal {A},$
and $A \in \mathcal {A},$![]() then $A = 0.$
then $A = 0.$![]()
Proof. First, observe that $Q_M= I - P_M$![]() and $P_M$
and $P_M$![]() both commute with $T$
both commute with $T$![]() and $T^{*}$
and $T^{*}$![]() . Now, since $u$
. Now, since $u$![]() is a separating vector for ${\{{T}\}'}$
is a separating vector for ${\{{T}\}'}$![]() and $v$
and $v$![]() for ${\{{T^{*}}\}'}$
for ${\{{T^{*}}\}'}$![]() (see [Reference Foias, Jung, Ko and Pearcy19, theorem 1.4]) it follows that the vectors $P_M u,\, P_M v,\, Q_M u,\, Q_M v$
(see [Reference Foias, Jung, Ko and Pearcy19, theorem 1.4]) it follows that the vectors $P_M u,\, P_M v,\, Q_M u,\, Q_M v$![]() are non-zero. In particular, one deduces that $u,\,v \notin M \cup M^{\perp }$
are non-zero. In particular, one deduces that $u,\,v \notin M \cup M^{\perp }$![]() .
.
On the other hand, since $P_M T = T P_M$![]() then
then
Let $n \in \mathbb {N}$![]() and assume, for the moment, that $e_n \in M$
and assume, for the moment, that $e_n \in M$![]() . Then,
. Then,
Note that $\langle {e_n,\,v}\rangle \neq 0$![]() since $\alpha _n\beta _n \neq 0$
since $\alpha _n\beta _n \neq 0$![]() , so $u = P_Mu$
, so $u = P_Mu$![]() and therefore $u \in M$
and therefore $u \in M$![]() , which is a contradiction. Hence $e_n\not \in M$
, which is a contradiction. Hence $e_n\not \in M$![]() .
.
The case $e_n \in M^{\perp }$![]() is analogous.
is analogous.
As lemma 2.3, the following result deals with the location of $u$![]() and $v$
and $v$![]() but when the assumption $\alpha _n \beta _n \neq 0$
but when the assumption $\alpha _n \beta _n \neq 0$![]() for every $n \in \mathbb {N}$
for every $n \in \mathbb {N}$![]() is replaced by one regarding the spectrum of the diagonal operator $D$
is replaced by one regarding the spectrum of the diagonal operator $D$![]() .
.
Lemma 2.4 Let $T = D + u\otimes v \in \mathcal {L}(H)$![]() where $D$
where $D$![]() is a diagonal operator with respect to an orthonormal basis $(e_n)_{n\geq 1}$
is a diagonal operator with respect to an orthonormal basis $(e_n)_{n\geq 1}$![]() and $u =\sum _n \alpha _n e_n,$
and $u =\sum _n \alpha _n e_n,$![]() $v=\sum _n \beta _n e_n$
$v=\sum _n \beta _n e_n$![]() nonzero vectors in $H$
nonzero vectors in $H$![]() . Assume $D$
. Assume $D$![]() has uniform multiplicity one, its spectrum $\sigma (D)$
has uniform multiplicity one, its spectrum $\sigma (D)$![]() lies in a Jordan curve and $\alpha _n$
lies in a Jordan curve and $\alpha _n$![]() and $\beta _n$
and $\beta _n$![]() are not simultaneously zero. If $P_M: H \rightarrow M$
are not simultaneously zero. If $P_M: H \rightarrow M$![]() is a non-trivial orthogonal projection commuting with $T,$
is a non-trivial orthogonal projection commuting with $T,$![]() then $u,\, v,\, e_n \notin \ker P_M \cup \ker (I-P_M)$
then $u,\, v,\, e_n \notin \ker P_M \cup \ker (I-P_M)$![]() for all $n \in \mathbb {N}$
for all $n \in \mathbb {N}$![]() .
.
Proof. Let us argue by contradiction assuming $P_M v = 0$![]() . Then, by lemma 2.2, we have
. Then, by lemma 2.2, we have
where $Q_M=I-P_M$![]() . Then $0 = (I-P_M)DP_M = DP_M-P_M D P_M$
. Then $0 = (I-P_M)DP_M = DP_M-P_M D P_M$![]() or, equivalently, $DP_M = P_M DP_M$
or, equivalently, $DP_M = P_M DP_M$![]() . Hence the closed subspace $M := P_M(H)$
. Hence the closed subspace $M := P_M(H)$![]() is a non-trivial closed invariant subspace for $D$
is a non-trivial closed invariant subspace for $D$![]() (see [Reference Radjavi and Rosenthal32, theorem 0.1], for instance).
(see [Reference Radjavi and Rosenthal32, theorem 0.1], for instance).
Moreover, $D$![]() is a completely normal operator (see [Reference Wermer39, theorem 3] or [Reference Radjavi and Rosenthal32, chapter 1]). Therefore, every invariant subspace of $D$
is a completely normal operator (see [Reference Wermer39, theorem 3] or [Reference Radjavi and Rosenthal32, chapter 1]). Therefore, every invariant subspace of $D$![]() is reducing and it is spanned by a subset of eigenvectors. Accordingly, $DP_M = P_M D$
is reducing and it is spanned by a subset of eigenvectors. Accordingly, $DP_M = P_M D$![]() and $M = \overline {\textrm {span}\; \{e_n : n \in \Lambda \}},$
and $M = \overline {\textrm {span}\; \{e_n : n \in \Lambda \}},$![]() where $\Lambda$
where $\Lambda$![]() is a proper subset of the natural numbers $\mathbb {N}$
is a proper subset of the natural numbers $\mathbb {N}$![]() . Observe that, in particular, $DP_M = P_M D$
. Observe that, in particular, $DP_M = P_M D$![]() implies that $P_M u = 0$
implies that $P_M u = 0$![]() .
.
On the other hand, since $P_M$![]() is the orthogonal projection onto $M=\overline {\textrm {span}\; \{e_n : n \in \Lambda \}}$
is the orthogonal projection onto $M=\overline {\textrm {span}\; \{e_n : n \in \Lambda \}}$![]() , trivially $P_M$
, trivially $P_M$![]() is a diagonal operator with respect to $(e_n)_{n\geq 1}$
is a diagonal operator with respect to $(e_n)_{n\geq 1}$![]() (since $P_M e_n = e_n$
(since $P_M e_n = e_n$![]() for every $n \in \Lambda$
for every $n \in \Lambda$![]() and $P_M e_n = 0$
and $P_M e_n = 0$![]() for every $n \notin \Lambda$
for every $n \notin \Lambda$![]() ). Having into account that $P_M u = P_M v = 0$
). Having into account that $P_M u = P_M v = 0$![]() , we deduce
, we deduce
Hence, for every $n \in \Lambda$![]() we have $\alpha _n = \beta _n = 0$
we have $\alpha _n = \beta _n = 0$![]() , which is a contradiction unless $\Lambda = \emptyset$
, which is a contradiction unless $\Lambda = \emptyset$![]() . But, in this latter case, it would follow that $P_M = 0$
. But, in this latter case, it would follow that $P_M = 0$![]() which is also absurd since $P_M$
which is also absurd since $P_M$![]() is a non-trivial projection. Therefore, $P_M v \neq 0$
is a non-trivial projection. Therefore, $P_M v \neq 0$![]() as the statement asserts.
as the statement asserts.
The proof of the statement $u\notin \ker P_M \cup \ker (I-P_M)$![]() is analogous, just considering $T^{\ast }$
is analogous, just considering $T^{\ast }$![]() .
.
Finally, in order to show that $e_n \notin \ker P_M \cup \ker (I-P_M)$![]() for all $n \in \mathbb {N}$
for all $n \in \mathbb {N}$![]() , we may argue as in lemma 2.3 considering (2.1) if $e_n$
, we may argue as in lemma 2.3 considering (2.1) if $e_n$![]() would be in $M$
would be in $M$![]() (note that, by assumption, $\alpha _n$
(note that, by assumption, $\alpha _n$![]() and $\beta _n$
and $\beta _n$![]() are not simultaneously zero).
are not simultaneously zero).
With the previous results at hands, we are in position to prove theorem 2.1. The proof will be accomplished by studying firstly the case that the diagonal operator $D$![]() is self-adjoint and therefore, its spectrum is contained in the real numbers.
is self-adjoint and therefore, its spectrum is contained in the real numbers.
Proof of theorem 2.1. Proof of theorem 2.1
Assume that $T = D + u\otimes v \in \mathcal {L}(H)$![]() where $D$
where $D$![]() is a diagonal operator with respect to an orthonormal basis $(e_n)_{n\geq 1}$
is a diagonal operator with respect to an orthonormal basis $(e_n)_{n\geq 1}$![]() and $u =\sum _n \alpha _n e_n$
and $u =\sum _n \alpha _n e_n$![]() , $v=\sum _n \beta _n e_n$
, $v=\sum _n \beta _n e_n$![]() two nonzero vectors in $H$
two nonzero vectors in $H$![]() .
.
Clearly, if $T$![]() is a normal operator, it has non-trivial reducing subspaces. In addition, if there exists $n_0 \in \mathbb {N}$
is a normal operator, it has non-trivial reducing subspaces. In addition, if there exists $n_0 \in \mathbb {N}$![]() such that $\alpha _{n_0} = \beta _{n_0} = 0$
such that $\alpha _{n_0} = \beta _{n_0} = 0$![]() , then the subspace generated by the basis vector $e_{n_0}$
, then the subspace generated by the basis vector $e_{n_0}$![]() is reducing for $T$
is reducing for $T$![]() as pointed out in the preliminary section. In both cases, $T$
as pointed out in the preliminary section. In both cases, $T$![]() has a non-trivial reducing subspace. For the converse, assume that $T$
has a non-trivial reducing subspace. For the converse, assume that $T$![]() has a non-trivial reducing subspace and let us show that $T$
has a non-trivial reducing subspace and let us show that $T$![]() is normal or there exists $n_0 \in \mathbb {N}$
is normal or there exists $n_0 \in \mathbb {N}$![]() such that $\alpha _{n_0} = \beta _{n_0} = 0$
such that $\alpha _{n_0} = \beta _{n_0} = 0$![]() .
.
Case 1: $D$![]() is a self-adjoint operator.
is a self-adjoint operator.
Assume that $T=D + u\otimes v$![]() has a non-trivial reducing subspace $M\subset H$
has a non-trivial reducing subspace $M\subset H$![]() and that $\alpha _n$
and that $\alpha _n$![]() and $\beta _n$
and $\beta _n$![]() are not simultaneously zero. Let $P_M$
are not simultaneously zero. Let $P_M$![]() be the non-trivial orthogonal projection onto $M$
be the non-trivial orthogonal projection onto $M$![]() and $Q_M = I - P_M$
and $Q_M = I - P_M$![]() . By lemma 2.2, both relations
. By lemma 2.2, both relations
and
hold. Moreover, lemma 2.4 ensures that the vectors $P_M u,\, Q_M u,\, P_M v$![]() and $Q_M v$
and $Q_M v$![]() are non-zero.
are non-zero.
A little computation shows that
and since $\left \lvert \left \lvert {P_M u}\right \rvert \right \rvert > 0$![]() , we deduce
, we deduce
In a similar way, we have
Now, let us write $\alpha = {\langle {P_M v,\,P_M u}\rangle }/{\left \lvert \left \lvert {P_M u}\right \rvert \right \rvert ^{2}}$![]() , so $P_M v = \alpha P_M u$
, so $P_M v = \alpha P_M u$![]() and $Q_M v = \overline {\alpha } Q_M u$
and $Q_M v = \overline {\alpha } Q_M u$![]() . Hence,
. Hence,
Notice that it is enough to show that $\alpha \, \in \mathbb {R}$![]() , so $v = \alpha \, u$
, so $v = \alpha \, u$![]() and therefore $T$
and therefore $T$![]() would be a self-adjoint operator, since it would be the sum of two self-adjoint operators.
would be a self-adjoint operator, since it would be the sum of two self-adjoint operators.
Observe that
Moreover,
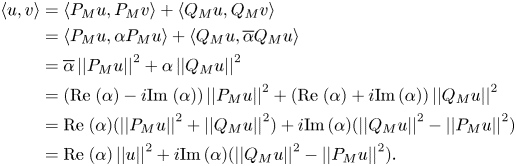
Note that $\alpha u - v \in M^{\perp },$![]() since $P_M(\alpha u - v) = 0.$
since $P_M(\alpha u - v) = 0.$![]() Thus, $Q_M (\alpha u - v) = \alpha u -v$
Thus, $Q_M (\alpha u - v) = \alpha u -v$![]() .
.
Similarly, $\overline {\alpha }u-v \in M$![]() . Furthermore, $(\alpha P_M + \overline {\alpha } Q_M)u = v$
. Furthermore, $(\alpha P_M + \overline {\alpha } Q_M)u = v$![]() . Since $P_M$
. Since $P_M$![]() and $Q_M$
and $Q_M$![]() commute with $T$
commute with $T$![]() , it follows that
, it follows that
Now,
and
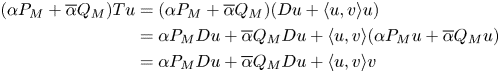
Thus,
So,
Upon applying lemma 2.2 it follows that
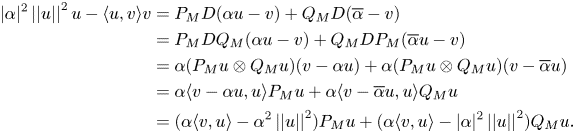
Moreover, $v = \alpha P_M u + \overline {\alpha }Q_M u$![]() , so
, so
Consequently,
and
From the second equality we have
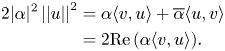
Let us write $\alpha = a+bi$![]() , with $a,\, b \in \mathbb {R}$
, with $a,\, b \in \mathbb {R}$![]() real numbers. The aim is to show that $b=0$
real numbers. The aim is to show that $b=0$![]() .
.
Recall that
Then,
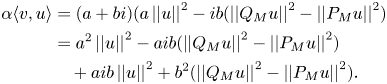
So, $\textrm {Re}\; (a\langle {v,\,u}\rangle ) = a^{2}\left \lvert \left \lvert {u}\right \rvert \right \rvert ^{2} + b^{2} (\left \lvert \left \lvert {Q_M u}\right \rvert \right \rvert ^{2} - \left \lvert \left \lvert {P_M u}\right \rvert \right \rvert ^{2}).$![]() From equation (2.2) we have
From equation (2.2) we have
and therefore,
If $b\neq 0$![]() , this identity yields that $\left \lvert \left \lvert {P_M u}\right \rvert \right \rvert = 0$
, this identity yields that $\left \lvert \left \lvert {P_M u}\right \rvert \right \rvert = 0$![]() , what contradicts lemma 2.4. Accordingly, $b=0$
, what contradicts lemma 2.4. Accordingly, $b=0$![]() and then $\alpha$
and then $\alpha$![]() is a real number as we wish to prove in order to show that $T$
is a real number as we wish to prove in order to show that $T$![]() is a normal operator.
is a normal operator.
Finally, if $T$![]() has a reducing subspace and it is not a normal operator, we deduce that there exists $n \in \mathbb {N}$
has a reducing subspace and it is not a normal operator, we deduce that there exists $n \in \mathbb {N}$![]() such that $\alpha _n = \beta _n = 0$
such that $\alpha _n = \beta _n = 0$![]() , so the proof in case 1 is complete.
, so the proof in case 1 is complete.
Case 2: $D$![]() is not a self-adjoint operator.
is not a self-adjoint operator.
Assume first that the set of eigenvalues $\Lambda (D)=(\lambda _n)_{n\geq 1}$![]() is contained in a line $\Gamma$
is contained in a line $\Gamma$![]() in the complex plane parallel to the real axis. Let $h\in \mathbb {R}$
in the complex plane parallel to the real axis. Let $h\in \mathbb {R}$![]() such that $\Gamma =\{x+ih: x\in \mathbb {R}\}$
such that $\Gamma =\{x+ih: x\in \mathbb {R}\}$![]() .
.
Observe that the linear bounded operator $D - hiI$![]() is a diagonal, self-adjoint operator of uniform multiplicity one. Now, observe that $T$
is a diagonal, self-adjoint operator of uniform multiplicity one. Now, observe that $T$![]() has the same reducing subspaces that $T - hiI$
has the same reducing subspaces that $T - hiI$![]() has. Then, by case 1, it follows that $T-hi I$
has. Then, by case 1, it follows that $T-hi I$![]() has a non-trivial reducing subspace if and only if either $T-hi I$
has a non-trivial reducing subspace if and only if either $T-hi I$![]() is a normal operator or there exists $n\in \mathbb {N}$
is a normal operator or there exists $n\in \mathbb {N}$![]() such that $\alpha _n=\beta _n= 0.$
such that $\alpha _n=\beta _n= 0.$![]() Accordingly, the same conclusion holds for $T$
Accordingly, the same conclusion holds for $T$![]() .
.
Finally, if $\Lambda (D)$![]() is contained in a line $\Gamma$
is contained in a line $\Gamma$![]() that intersects the real axis, let $\theta \in [0,\,\pi )$
that intersects the real axis, let $\theta \in [0,\,\pi )$![]() denote the angle formed by $\Gamma$
denote the angle formed by $\Gamma$![]() and the real axis measured in the positive direction. Then, $\widetilde {D}= {\rm e}^{-i\theta }D$
and the real axis measured in the positive direction. Then, $\widetilde {D}= {\rm e}^{-i\theta }D$![]() satisfies that its set of eigenvalues $\Lambda (\widetilde {D})$
satisfies that its set of eigenvalues $\Lambda (\widetilde {D})$![]() is contained in a line parallel to the real axis. The final statement follows upon applying case 1 to the operator ${\rm e}^{-i\theta }T$
is contained in a line parallel to the real axis. The final statement follows upon applying case 1 to the operator ${\rm e}^{-i\theta }T$![]() . This concludes the proof of theorem 2.1.
. This concludes the proof of theorem 2.1.
Remark 2.5 We point out that the assumption on $D$![]() having uniform multiplicity one in theorem 2.1 is necessary and cannot be dropped off. Indeed, it is not difficult to provide examples of non-normal operators $T=D+ u\otimes v$
having uniform multiplicity one in theorem 2.1 is necessary and cannot be dropped off. Indeed, it is not difficult to provide examples of non-normal operators $T=D+ u\otimes v$![]() having non-trivial reducing subspaces such that the spectrum $\sigma (D)$
having non-trivial reducing subspaces such that the spectrum $\sigma (D)$![]() is contained in a line and $u$
is contained in a line and $u$![]() and $v$
and $v$![]() are non-zero vectors with non-zero components. For instance, if $\ell ^{2}$
are non-zero vectors with non-zero components. For instance, if $\ell ^{2}$![]() denote the classical Hilbert space consisting of complex sequences whose modulus are squared summable and $\{e_n\}_{n\geq 1}$
denote the classical Hilbert space consisting of complex sequences whose modulus are squared summable and $\{e_n\}_{n\geq 1}$![]() the canonical basis in $\ell ^{2}$
the canonical basis in $\ell ^{2}$![]() , let us consider $D$
, let us consider $D$![]() be the diagonal operator defined by
be the diagonal operator defined by
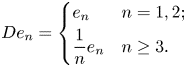
Clearly, $D$![]() is a self-adjoint (even a compact) operator in $\ell ^{2}$
is a self-adjoint (even a compact) operator in $\ell ^{2}$![]() . Now, if $u= \sum _{n\geq 1} ({1}/{n}) e_n$
. Now, if $u= \sum _{n\geq 1} ({1}/{n}) e_n$![]() and $v=e_1+({1}/{2}) e_2+ \sum _{n\geq 3} ({1}/{n^{2}}) e_n$
and $v=e_1+({1}/{2}) e_2+ \sum _{n\geq 3} ({1}/{n^{2}}) e_n$![]() , for instance, the operator $T= D+ u\otimes v$
, for instance, the operator $T= D+ u\otimes v$![]() has non-trivial reducing subspace (indeed the one generated by $e_1$
has non-trivial reducing subspace (indeed the one generated by $e_1$![]() , see proposition 1.2), the spectrum $\sigma (D)$
, see proposition 1.2), the spectrum $\sigma (D)$![]() is $\{1/n\}_{n\geq 1}\cup \{0\}\subset [0,\,1]$
is $\{1/n\}_{n\geq 1}\cup \{0\}\subset [0,\,1]$![]() and clearly $u$
and clearly $u$![]() and $v$
and $v$![]() are non-zero vectors with non-zero components. Nevertheless, $T$
are non-zero vectors with non-zero components. Nevertheless, $T$![]() is not a normal operator since $u$
is not a normal operator since $u$![]() and $v$
and $v$![]() are not proportional vectors, which is required by condition (i$'$
are not proportional vectors, which is required by condition (i$'$![]() ) in Ionascu's theorem (see the preliminary section).
) in Ionascu's theorem (see the preliminary section).
To close this section, we observe that if $D$![]() is a diagonal operator with a set of eigenvalues $\Lambda (D)=(\lambda _n)_{n\geq 1}$
is a diagonal operator with a set of eigenvalues $\Lambda (D)=(\lambda _n)_{n\geq 1}$![]() contained in a line or a circle then $T= D+ u\otimes v$
contained in a line or a circle then $T= D+ u\otimes v$![]() is a decomposable operator by a result due to Radjabalipour and Radjavi (see [Reference Radjabalipour and Radjavi33, corollary 2]). Recall that an operator $T \in \mathcal {L}(H)$
is a decomposable operator by a result due to Radjabalipour and Radjavi (see [Reference Radjabalipour and Radjavi33, corollary 2]). Recall that an operator $T \in \mathcal {L}(H)$![]() is decomposable if for every open cover $U,\,V \subset \mathbb {C}$
is decomposable if for every open cover $U,\,V \subset \mathbb {C}$![]() of $\sigma (T)$
of $\sigma (T)$![]() there exist invariant subspaces $M,\,N \subset H$
there exist invariant subspaces $M,\,N \subset H$![]() for $T$
for $T$![]() such that $M+N = H$
such that $M+N = H$![]() and $\sigma (T_{|_M})\subset \overline {U}$
and $\sigma (T_{|_M})\subset \overline {U}$![]() and $\sigma (T_{|_N})\subset \overline {V}$
and $\sigma (T_{|_N})\subset \overline {V}$![]() .
.
Hence, as a consequence of theorem 2.1, it is possible to exhibit one-rank perturbations of diagonal operators $D$![]() which are decomposable but lack non-trivial reducing subspaces. Indeed, a bit more can be achieved in this context.
which are decomposable but lack non-trivial reducing subspaces. Indeed, a bit more can be achieved in this context.
Recall that a closed subspace $M\subset H$![]() is called a spectral maximal subspace of an operator $T\in \mathcal {L}(H)$
is called a spectral maximal subspace of an operator $T\in \mathcal {L}(H)$![]() if
if
(a) $M$
 is an invariant subspace of $T$
is an invariant subspace of $T$ , and
, and(b) $N \subset M$
 for all closed invariant subspaces $N$
for all closed invariant subspaces $N$ of $T$
of $T$ such that the spectrum of the restriction $T_{|_N}$
such that the spectrum of the restriction $T_{|_N}$ is contained in the spectrum of the restriction $T_{|_M}$
is contained in the spectrum of the restriction $T_{|_M}$ , that is, $\sigma (T_{|_N})\subseteq \sigma (T_{|_M})$
, that is, $\sigma (T_{|_N})\subseteq \sigma (T_{|_M})$ .
.
In addition, $T\in \mathcal {L}(H)$![]() is called strongly decomposable if its restriction to an arbitrary spectral maximal subspace is again decomposable. Indeed, the authors in [Reference Radjabalipour and Radjavi33,corollary 2] state that if $T^{\ast } - T$
is called strongly decomposable if its restriction to an arbitrary spectral maximal subspace is again decomposable. Indeed, the authors in [Reference Radjabalipour and Radjavi33,corollary 2] state that if $T^{\ast } - T$![]() belongs to the Schatten class $S_p(H)$
belongs to the Schatten class $S_p(H)$![]() for $1\leq p < \infty$
for $1\leq p < \infty$![]() , then $T$
, then $T$![]() is strongly decomposable.
is strongly decomposable.
Corollary 2.6 There exist rank-one perturbations of self-adjoint diagonal operators $T=D+u\otimes v \in \mathcal {L}(H)$![]() that are strongly decomposable operators and have no non-trivial reducing subspaces.
that are strongly decomposable operators and have no non-trivial reducing subspaces.
Proof. Let $D$![]() be a self-adjoint diagonal operator of uniform multiplicity one. Let us consider $u$
be a self-adjoint diagonal operator of uniform multiplicity one. Let us consider $u$![]() and $v$
and $v$![]() two non-zero vectors in $H$
two non-zero vectors in $H$![]() with non-zero components and being not real-proportional. Then the operator $T= D+ u\otimes v$
with non-zero components and being not real-proportional. Then the operator $T= D+ u\otimes v$![]() is strongly decomposable since $T^{\ast } - T$
is strongly decomposable since $T^{\ast } - T$![]() is a rank two operator (and hence belongs to the Schatten class $S_p(H)$
is a rank two operator (and hence belongs to the Schatten class $S_p(H)$![]() for every $1\leq p < \infty$
for every $1\leq p < \infty$![]() ). Nevertheless, $T$
). Nevertheless, $T$![]() is not normal and by theorem 2.1, it has no non-trivial reducing subspaces.
is not normal and by theorem 2.1, it has no non-trivial reducing subspaces.
3. Reducing subspaces for rank-one perturbations of diagonal operators: when the spectrum is contained in a circle
In this section, we will focus on rank-one perturbations of a diagonal operator with spectrum contained in a circle. Note that this is the other possible case according to Ionascu's result to ensure that such operators are normal (condition (ii$'$![]() ) in the preliminary section).
) in the preliminary section).
As we will show, the spectral picture does not determine the existence of non-trivial reducing subspaces for non-normal operators within this class. In other words, it is possible to exhibit non-normal operators within this class with spectrum contained in a circle either having or lacking non-trivial reducing subspaces. Our main result in this section reads as follows:
Theorem 3.1 Let $D\in \mathcal {L}(H)$![]() be a diagonal operator with respect to an orthonormal basis $(e_n)_{n\geq 1}$
be a diagonal operator with respect to an orthonormal basis $(e_n)_{n\geq 1}$![]() with uniform multiplicity one. Assume its spectrum $\sigma (D)$
with uniform multiplicity one. Assume its spectrum $\sigma (D)$![]() is contained in a circle with center $\alpha,$
is contained in a circle with center $\alpha,$![]() and let $u \in H$
and let $u \in H$![]() such that $\langle {u,\,e_n}\rangle \neq 0$
such that $\langle {u,\,e_n}\rangle \neq 0$![]() for every $n \in \mathbb {N}$
for every $n \in \mathbb {N}$![]() . Then
. Then
(a) The operator $T_1 = D+u\otimes u \in \mathcal {L}(H)$
 has no non-trivial reducing subspaces.
has no non-trivial reducing subspaces.(b) If $\langle {u,\,Du}\rangle \neq \overline {\alpha }\, \|u\|^{2},$
 there exists $v \in H$
there exists $v \in H$ with $\langle {v,\,e_n}\rangle \neq 0$
with $\langle {v,\,e_n}\rangle \neq 0$ for every $n \in \mathbb {N}$
for every $n \in \mathbb {N}$ and the operator $T_2 = D+u\otimes v \in \mathcal {L}(H)$
and the operator $T_2 = D+u\otimes v \in \mathcal {L}(H)$ is not normal but has non-trivial reducing subspaces.
is not normal but has non-trivial reducing subspaces.
Proof. First, we consider the case that the diagonal operator $D$![]() is a unitary operator and therefore, its spectrum is contained in the unit circle $\mathbb {T}$
is a unitary operator and therefore, its spectrum is contained in the unit circle $\mathbb {T}$![]() .
.
Case 1: $D$![]() is a unitary operator.
is a unitary operator.
Assume, on the contrary, that $M$![]() is a non-trivial reducing subspace for $T=D+u\otimes u$
is a non-trivial reducing subspace for $T=D+u\otimes u$![]() and denote, as usual, $P_M$
and denote, as usual, $P_M$![]() the orthogonal projection onto $M$
the orthogonal projection onto $M$![]() . We may assume, without loss of generality, that $M$
. We may assume, without loss of generality, that $M$![]() is infinite dimensional (otherwise we would argue with $M^{\perp }$
is infinite dimensional (otherwise we would argue with $M^{\perp }$![]() since it would be an infinite-dimensional reducing subspace).
since it would be an infinite-dimensional reducing subspace).
Let $x$![]() be a non-zero vector in $M$
be a non-zero vector in $M$![]() . Clearly, $Tx = Dx+\langle {x,\,u}\rangle u \in M$
. Clearly, $Tx = Dx+\langle {x,\,u}\rangle u \in M$![]() , and since $M$
, and since $M$![]() is reducing, $T^{\ast } x = D^{\ast } x + \langle {x,\,u}\rangle u$
is reducing, $T^{\ast } x = D^{\ast } x + \langle {x,\,u}\rangle u$![]() is also in $M$
is also in $M$![]() . Accordingly, $(D-D^{\ast })x \in M$
. Accordingly, $(D-D^{\ast })x \in M$![]() for every $x \in M$
for every $x \in M$![]() , or equivalently, $M$
, or equivalently, $M$![]() is an infinite-dimensional non-trivial closed invariant subspace for $D-D^{\ast }$
is an infinite-dimensional non-trivial closed invariant subspace for $D-D^{\ast }$![]() .
.
Note that $D-D^{\ast }$![]() is a non-trivial diagonal operator with the spectrum contained in the imaginary axis of the complex plane. Indeed, if $\Lambda (D)=(\lambda _n)_{n\geq 1}$
is a non-trivial diagonal operator with the spectrum contained in the imaginary axis of the complex plane. Indeed, if $\Lambda (D)=(\lambda _n)_{n\geq 1}$![]() denotes the set of eigenvalues of $D$
denotes the set of eigenvalues of $D$![]() , then $\Lambda (D-D^{\ast })=(2 i\textrm{Im}\, (\lambda _n))_{n\geq 1}$
, then $\Lambda (D-D^{\ast })=(2 i\textrm{Im}\, (\lambda _n))_{n\geq 1}$![]() . In particular, by [Reference Radjavi and Rosenthal32, theorems 1.23 and 1.25] $D-D^{\ast }$
. In particular, by [Reference Radjavi and Rosenthal32, theorems 1.23 and 1.25] $D-D^{\ast }$![]() is a completely normal operator and therefore, $M$
is a completely normal operator and therefore, $M$![]() is spanned by eigenvectors of $D-D^{\ast }$
is spanned by eigenvectors of $D-D^{\ast }$![]() .
.
On the other hand, since $D$![]() has uniform multiplicity one then the eigenvalues of $D-D^{\ast }$
has uniform multiplicity one then the eigenvalues of $D-D^{\ast }$![]() has multiplicity at most two. Actually, if $2 i\textrm{Im}\, (\lambda _n)$
has multiplicity at most two. Actually, if $2 i\textrm{Im}\, (\lambda _n)$![]() has multiplicity two, then there exists $m \in \mathbb {N}$
has multiplicity two, then there exists $m \in \mathbb {N}$![]() such that $\textrm {Im}\; (\lambda _n) = \textrm {Im}\; (\lambda _m)$
such that $\textrm {Im}\; (\lambda _n) = \textrm {Im}\; (\lambda _m)$![]() . For each pair of indexes of this form, let us denote by $n$
. For each pair of indexes of this form, let us denote by $n$![]() the smaller index and by $n'$
the smaller index and by $n'$![]() the greater one. That is, let us denote by $\Omega$
the greater one. That is, let us denote by $\Omega$![]() the set of pairs of indexes
the set of pairs of indexes
Doing so, we may consider a disjoint partition of the natural numbers
where $N_1\subset \mathbb {N}$![]() consists of the indexes of the eigenvalues with multiplicity two that are the smaller index of its corresponding pair, $N_2$
consists of the indexes of the eigenvalues with multiplicity two that are the smaller index of its corresponding pair, $N_2$![]() consists of the indexes of the eigenvalues with multiplicity two that are the larger index of its corresponding pair and $N_3$
consists of the indexes of the eigenvalues with multiplicity two that are the larger index of its corresponding pair and $N_3$![]() the indexes of the eigenvalues with multiplicity one. In other words, the set $\Omega =N_1\times N_2$
the indexes of the eigenvalues with multiplicity one. In other words, the set $\Omega =N_1\times N_2$![]() .
.
Then, the eigenvectors of $D-D^{*}$![]() are
are
With the characterization of the eigenvectors of $D-D^{*}$![]() , our goal now will be identify those eigenvectors spanning $M$
, our goal now will be identify those eigenvectors spanning $M$![]() , that is, determine the proper subset $\Lambda$
, that is, determine the proper subset $\Lambda$![]() of $\mathbb {N}$
of $\mathbb {N}$![]() such that
such that
By lemma 2.4 for every $n \in \mathbb {N}$![]() we have $e_n \notin M\cup M^{\perp }$
we have $e_n \notin M\cup M^{\perp }$![]() , so $e_n \notin M$
, so $e_n \notin M$![]() for every $n \in N_3.$
for every $n \in N_3.$![]() Assume for the moment that $N_3\cap \Lambda$
Assume for the moment that $N_3\cap \Lambda$![]() is not empty and let $n_0\in N_3\cap \Lambda$
is not empty and let $n_0\in N_3\cap \Lambda$![]() . Denote by
. Denote by
the orthogonal decomposition of $e_{n_0}$![]() with respect to $H=M\oplus M^{\perp }$
with respect to $H=M\oplus M^{\perp }$![]() . Note that, in particular, $e_{n_0}^{M}$
. Note that, in particular, $e_{n_0}^{M}$![]() is non-zero because otherwise $e_{n_0}\in M^{\perp }$
is non-zero because otherwise $e_{n_0}\in M^{\perp }$![]() .
.
Having in mind that $(D-D^{*}) P_M = P_M (D-D^{*})$![]() because $M$
because $M$![]() is reducing for $D-D^{*}$
is reducing for $D-D^{*}$![]() , we deduce upon applying it to $e_{n_0}$
, we deduce upon applying it to $e_{n_0}$![]() that
that
That is, $2 i\textrm{Im}\, (\lambda _{n_0})$![]() is an eigenvalue of $D-D^{*}$
is an eigenvalue of $D-D^{*}$![]() with eigenspace $\textrm {span}\;\{e_{n_0},\, e_{n_0}^{M}\}$
with eigenspace $\textrm {span}\;\{e_{n_0},\, e_{n_0}^{M}\}$![]() . Hence, $2 i\textrm{Im}\, (\lambda _{n_0})$
. Hence, $2 i\textrm{Im}\, (\lambda _{n_0})$![]() is of multiplicity 2, but this contradicts the fact that $n_0\in N_3$
is of multiplicity 2, but this contradicts the fact that $n_0\in N_3$![]() . Therefore, $N_3\cap \Lambda$
. Therefore, $N_3\cap \Lambda$![]() is empty. Accordingly, we deduce that $\Lambda$
is empty. Accordingly, we deduce that $\Lambda$![]() must be a non-void subset $\Lambda$
must be a non-void subset $\Lambda$![]() of $N_1$
of $N_1$![]() (being possible $\Lambda =N_1$
(being possible $\Lambda =N_1$![]() ), and
), and
Moreover, we observe that for every eigenvector $\lambda e_n + \tau e_{n'} \in M$![]() , the coefficients $\lambda$
, the coefficients $\lambda$![]() and $\tau$
and $\tau$![]() are non-zero (otherwise we would have $e_n$
are non-zero (otherwise we would have $e_n$![]() or $e_{n'} \in M$
or $e_{n'} \in M$![]() ). Accordingly, every eigenvector $\lambda e_n + \tau e_{n'} \in M$
). Accordingly, every eigenvector $\lambda e_n + \tau e_{n'} \in M$![]() is a multiple of $e_n + ({\tau }/{\lambda })e_{n'}$
is a multiple of $e_n + ({\tau }/{\lambda })e_{n'}$![]() . Since $e_{n'}\notin M$
. Since $e_{n'}\notin M$![]() , we deduce that there exists coefficients $\tau _n \in \mathbb {C}$
, we deduce that there exists coefficients $\tau _n \in \mathbb {C}$![]() such that
such that
On the other hand, since $M$![]() is a non-trivial closed invariant subspace under $T$
is a non-trivial closed invariant subspace under $T$![]() , we have that $T(e_n + \tau _n e_{n'}) \in M$
, we have that $T(e_n + \tau _n e_{n'}) \in M$![]() for every $n\in \Lambda \subseteq N_1$
for every $n\in \Lambda \subseteq N_1$![]() with $(n,\,n')\in \Omega$
with $(n,\,n')\in \Omega$![]() . If we consider $u =\sum _n \alpha _n e_n$
. If we consider $u =\sum _n \alpha _n e_n$![]() where $\alpha _n=\langle {u,\,e_n}\rangle \neq 0$
where $\alpha _n=\langle {u,\,e_n}\rangle \neq 0$![]() for every $n \in \mathbb {N}$
for every $n \in \mathbb {N}$![]() by hypotheses, then
by hypotheses, then
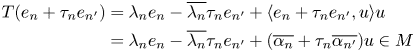
for every $n\in \Lambda \subseteq N_1$![]() with $(n,\,n')\in \Omega$
with $(n,\,n')\in \Omega$![]() .
.
Now, let us prove that $\textrm {Re}\; (\lambda _{n_0})=0$![]() for at least one positive integer $n_0 \in N_1$
for at least one positive integer $n_0 \in N_1$![]() .
.
First, by means of the orthogonality relations of the basis elements $\{e_n\}_{n\in \mathbb {N}}$![]() , it follows that for every vector $x \in M$
, it follows that for every vector $x \in M$![]()
Let $n_0$![]() be any positive integer in $\Lambda$
be any positive integer in $\Lambda$![]() (recall that $\Lambda$
(recall that $\Lambda$![]() is not empty). If
is not empty). If
then by (3.3) the vector
is in $M$![]() which, by means of (3.4) particularized in the index $n_0$
which, by means of (3.4) particularized in the index $n_0$![]() , satisfies
, satisfies
That is,
Having in mind that $\tau _n\neq 0$![]() for every $n\in \mathbb {N}$
for every $n\in \mathbb {N}$![]() , we deduce that $\lambda _{n_0}=- \overline {\lambda _{n_0}}$
, we deduce that $\lambda _{n_0}=- \overline {\lambda _{n_0}}$![]() as far as (3.5) holds, or equivalently $\textrm {Re}\; (\lambda _{n_0}) = 0$
as far as (3.5) holds, or equivalently $\textrm {Re}\; (\lambda _{n_0}) = 0$![]() whenever (3.5) is satisfied.
whenever (3.5) is satisfied.
Assume, now, that (3.5) is not satisfied, that is
Let us consider $m_0\in \Lambda$![]() with $m_0\neq n_0$
with $m_0\neq n_0$![]() . Observe that this is possible since, in particular, $M$
. Observe that this is possible since, in particular, $M$![]() is given by (3.2) and the dimension of $M$
is given by (3.2) and the dimension of $M$![]() is infinite.
is infinite.
Now, by (3.3), the vector
is in $M$![]() . We argue as before upon considering (3.4) at $\textbf {b}$
. We argue as before upon considering (3.4) at $\textbf {b}$![]() and $e_{m_0}$
and $e_{m_0}$![]() , that is, $\tau _{m_0} \langle {\textbf {b},\,e_{m_0}}\rangle = \langle {\textbf {b},\,e_{m_0'}}\rangle$
, that is, $\tau _{m_0} \langle {\textbf {b},\,e_{m_0}}\rangle = \langle {\textbf {b},\,e_{m_0'}}\rangle$![]() . Then
. Then
Since $\overline {\alpha _{n_0}} + \tau _{n_0} \overline {\alpha _{n_0'}} \neq 0$![]() (i.e. our assumption (3.6)), we deduce that
(i.e. our assumption (3.6)), we deduce that
Therefore, having in mind that $e_{m_0} + \tau _{m_0} e_{m_0'}\in M$![]() , we deduce that
, we deduce that
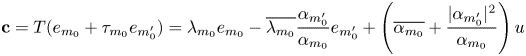
is also in $M$![]() . Once again applying (3.4), we have $\tau _{m_0} \langle {\textbf {c},\,e_{m_0}}\rangle = \langle {\textbf {c},\,e_{m_0'}}\rangle$
. Once again applying (3.4), we have $\tau _{m_0} \langle {\textbf {c},\,e_{m_0}}\rangle = \langle {\textbf {c},\,e_{m_0'}}\rangle$![]() and therefore
and therefore
Multiplying by ${\alpha _{m_0}}/{\alpha _{m_0'}}$![]() we obtain
we obtain
from where, clearly, $\textrm {Re}\; (\lambda _{m_0}) = 0$![]() .
.
Consequently, independently if (3.5) is or not satisfied, there exists at least a positive integer $n_0\in N_1$![]() such that $\textrm {Re}\; (\lambda _{n_0})=0$
such that $\textrm {Re}\; (\lambda _{n_0})=0$![]() , as we wished to show.
, as we wished to show.
In order to finish the proof of case 1, let us show that the existence of such $n_0 \in N_1$![]() yields the desired contradiction. Since $D$
yields the desired contradiction. Since $D$![]() is unitary, its spectrum is contained in the unit circle and therefore, such $\lambda _{n_0}$
is unitary, its spectrum is contained in the unit circle and therefore, such $\lambda _{n_0}$![]() is either $i$
is either $i$![]() or $-i$
or $-i$![]() . Assume $\lambda _{n_0}=i$
. Assume $\lambda _{n_0}=i$![]() (the other case is analogous). If $n_0\in N_1$
(the other case is analogous). If $n_0\in N_1$![]() , by definition, there exist $n_0'\in \mathbb {N}$
, by definition, there exist $n_0'\in \mathbb {N}$![]() with $n_0< n_0'$
with $n_0< n_0'$![]() and $\lambda _{n_0'}$
and $\lambda _{n_0'}$![]() an eigenvalue of $D$
an eigenvalue of $D$![]() , $\lambda _{n_0'} \in \Lambda (D)$
, $\lambda _{n_0'} \in \Lambda (D)$![]() , such that $\textrm {Im}\; (\lambda _{n_0})=\textrm {Im}\; (\lambda _{n_0'})$
, such that $\textrm {Im}\; (\lambda _{n_0})=\textrm {Im}\; (\lambda _{n_0'})$![]() . Hence, $\textrm {Im}\; (\lambda _{n_0'})=1$
. Hence, $\textrm {Im}\; (\lambda _{n_0'})=1$![]() , and therefore $\lambda _{n_0'}$
, and therefore $\lambda _{n_0'}$![]() must be also $i$
must be also $i$![]() . Accordingly, $i$
. Accordingly, $i$![]() is an eigenvalue of $D$
is an eigenvalue of $D$![]() of multiplicity 2, which contradicts the hypotheses that the uniform multiplicity of $D$
of multiplicity 2, which contradicts the hypotheses that the uniform multiplicity of $D$![]() is one.
is one.
Case 2: $D$![]() is not a unitary operator.
is not a unitary operator.
Now, assume $D$![]() is a diagonal operator such that $\sigma (D)$
is a diagonal operator such that $\sigma (D)$![]() is contained in a circle with center $\alpha$
is contained in a circle with center $\alpha$![]() and radius $r>0$
and radius $r>0$![]() . As in case 1, we argue by contradiction assuming $T = D+u \otimes u$
. As in case 1, we argue by contradiction assuming $T = D+u \otimes u$![]() has a non-trivial reducing subspace $M$
has a non-trivial reducing subspace $M$![]() . Since $M$
. Since $M$![]() is reducing for $T$
is reducing for $T$![]() , it is also reducing for $({1}/{r})(T - \alpha I) = ({1}/{r})(D- \alpha I) + ({1}/{r}) u\otimes u,$
, it is also reducing for $({1}/{r})(T - \alpha I) = ({1}/{r})(D- \alpha I) + ({1}/{r}) u\otimes u,$![]() which is the contradiction.
which is the contradiction.
This concludes the proof that statement (a) of theorem 3.1 holds.
Now, we will show statement (b) of theorem 3.1. As before, the key argument will be to prove the result when $D$![]() is a unitary diagonal operator.
is a unitary diagonal operator.
Hence, suppose $D$![]() is a unitary and $u \in H$
is a unitary and $u \in H$![]() such that $\langle {u,\,e_n}\rangle \neq 0$
such that $\langle {u,\,e_n}\rangle \neq 0$![]() for every $n \in \mathbb {N}$
for every $n \in \mathbb {N}$![]() and $\langle {u,\,Du}\rangle \neq 0.$
and $\langle {u,\,Du}\rangle \neq 0.$![]() In order to show that there exists $v \in H$
In order to show that there exists $v \in H$![]() such that $T = D+u\otimes v\in \mathcal {L}(H)$
such that $T = D+u\otimes v\in \mathcal {L}(H)$![]() is not normal but has non-trivial reducing subspaces, we take
is not normal but has non-trivial reducing subspaces, we take
The goal will be showing that the subspace $M:=\textrm {span}\;\{D^{*}u\}$![]() reduces the operator $T = D + u\otimes v$
reduces the operator $T = D + u\otimes v$![]() .
.
First, note that
since $|\lambda _n| = 1$![]() . Then, $\langle {v,\,e_n}\rangle \neq 0$
. Then, $\langle {v,\,e_n}\rangle \neq 0$![]() for every $n \in \mathbb {N}$
for every $n \in \mathbb {N}$![]() .
.
Now, observe that
So, we have
Moreover,
So, $D^{*}u$![]() is a non-zero vector which turns out to be an eigenvector associated with the eigenvalue $0$
is a non-zero vector which turns out to be an eigenvector associated with the eigenvalue $0$![]() for $T$
for $T$![]() and $T^{*}$
and $T^{*}$![]() .
.
Finally, let us show that $T$![]() is not a normal operator. Assume, on the contrary, that $T$
is not a normal operator. Assume, on the contrary, that $T$![]() is normal. Having into account condition (ii$'$
is normal. Having into account condition (ii$'$![]() ) in Ionascu theorem 1.1, we deduce the existence of $\gamma \in \mathbb {C}$
) in Ionascu theorem 1.1, we deduce the existence of $\gamma \in \mathbb {C}$![]() such that $Dv = \gamma u$
such that $Dv = \gamma u$![]() . Then, since $Dv = - ({1}/{\langle {u,\,Du}\rangle })D^{*}u$
. Then, since $Dv = - ({1}/{\langle {u,\,Du}\rangle })D^{*}u$![]() , we have
, we have
That is, $u$![]() is an eigenvector for $D^{*}$
is an eigenvector for $D^{*}$![]() associated with the eigenvalue $-\gamma \langle {u,\,Du}\rangle$
associated with the eigenvalue $-\gamma \langle {u,\,Du}\rangle$![]() . Observe that $\gamma \neq 0$
. Observe that $\gamma \neq 0$![]() since $Dv \neq 0$
since $Dv \neq 0$![]() and $\langle {u,\,Du}\rangle \neq 0$
and $\langle {u,\,Du}\rangle \neq 0$![]() by hypothesis. Therefore, there exists $n_0 \in \mathbb {N}$
by hypothesis. Therefore, there exists $n_0 \in \mathbb {N}$![]() such that $u\in \textrm {span}\;\{e_{n_0}\}$
such that $u\in \textrm {span}\;\{e_{n_0}\}$![]() , and this contradicts the fact that $\langle {u,\,e_n}\rangle \neq 0$
, and this contradicts the fact that $\langle {u,\,e_n}\rangle \neq 0$![]() for every $n\in \mathbb {N}$
for every $n\in \mathbb {N}$![]() . Hence $T$
. Hence $T$![]() is not a normal operator.
is not a normal operator.
Now, let us prove the general case. Assume $D$![]() is not unitary but $\sigma (D)$
is not unitary but $\sigma (D)$![]() is contained in a circle with center $\alpha$
is contained in a circle with center $\alpha$![]() and radius $r>0$
and radius $r>0$![]() . Then the operator $\widetilde {D}= ({1}/{r})(D - \alpha I)$
. Then the operator $\widetilde {D}= ({1}/{r})(D - \alpha I)$![]() is a diagonal unitary operator satisfying $\langle {u,\,\widetilde {D} u}\rangle \neq 0$
is a diagonal unitary operator satisfying $\langle {u,\,\widetilde {D} u}\rangle \neq 0$![]() (since $\langle {u,\, \widetilde {D} u}\rangle = 0$
(since $\langle {u,\, \widetilde {D} u}\rangle = 0$![]() , would imply $\langle {u,\, (D-\alpha I) u}\rangle = 0,$
, would imply $\langle {u,\, (D-\alpha I) u}\rangle = 0,$![]() and therefore $\langle {u,\,Du}\rangle = \overline {\alpha }\left \lvert \left \lvert {u}\right \rvert \right \rvert ^{2},$
and therefore $\langle {u,\,Du}\rangle = \overline {\alpha }\left \lvert \left \lvert {u}\right \rvert \right \rvert ^{2},$![]() which contradicts our hypotheses). Hence, from the unitary case, we ensure the existence of $\widetilde {v} \in H$
which contradicts our hypotheses). Hence, from the unitary case, we ensure the existence of $\widetilde {v} \in H$![]() such that
such that
is not normal but has a non-trivial reducing subspace $M$![]() . Thus,
. Thus,
is a non-normal operator with $M$![]() as a reducing subspace. Accordingly, $v= r \widetilde {v}$
as a reducing subspace. Accordingly, $v= r \widetilde {v}$![]() completes the argument and the proof of theorem 3.1.
completes the argument and the proof of theorem 3.1.
As a consequence, the following corollary holds.
Corollary 3.2 Let $D\in \mathcal {L}(H)$![]() be a diagonal operator with respect to an orthonormal basis $(e_n)_{n\geq 1}$
be a diagonal operator with respect to an orthonormal basis $(e_n)_{n\geq 1}$![]() with uniform multiplicity one. Assume its spectrum $\sigma (D)$
with uniform multiplicity one. Assume its spectrum $\sigma (D)$![]() is contained in a circle with center $\alpha$
is contained in a circle with center $\alpha$![]() , and let $u$
, and let $u$![]() and $v$
and $v$![]() vectors in $H$
vectors in $H$![]() such that both $\langle {u,\,e_n}\rangle$
such that both $\langle {u,\,e_n}\rangle$![]() and $\langle {v,\,e_n}\rangle$
and $\langle {v,\,e_n}\rangle$![]() are not zero for every $n \in \mathbb {N}$
are not zero for every $n \in \mathbb {N}$![]() . If $T = D+u\otimes v \in \mathcal {L}(H)$
. If $T = D+u\otimes v \in \mathcal {L}(H)$![]() has non-trivial reducing subspaces, then $u$
has non-trivial reducing subspaces, then $u$![]() and $v$
and $v$![]() are linearly independent vectors.
are linearly independent vectors.
4. Reducing subspaces for rank-one perturbations of diagonal operators: general case
In this section, we consider the existence of reducing subspaces for rank-one perturbations of diagonal operators $D$![]() with uniform multiplicity one but not imposing restrictions to the spectrum of $D$
with uniform multiplicity one but not imposing restrictions to the spectrum of $D$![]() as in the previous two sections. In particular, we focus on the existence of reducing subspaces $M$
as in the previous two sections. In particular, we focus on the existence of reducing subspaces $M$![]() such that $T\mid _{ M}$
such that $T\mid _{ M}$![]() is normal as well as the existence of reducing subspaces for self-adjoint perturbations. We start by setting a result in the spirit of lemmas 2.3 and 2.4.
is normal as well as the existence of reducing subspaces for self-adjoint perturbations. We start by setting a result in the spirit of lemmas 2.3 and 2.4.
Proposition 4.1 Let $T = D + u\otimes v \in \mathcal {L}(H)$![]() where $D$
where $D$![]() is a diagonal operator with respect to an orthonormal basis $(e_n)_{n\geq 1}$
is a diagonal operator with respect to an orthonormal basis $(e_n)_{n\geq 1}$![]() and $u =\sum _n \alpha _n e_n,$
and $u =\sum _n \alpha _n e_n,$![]() $v=\sum _n \beta _n e_n$
$v=\sum _n \beta _n e_n$![]() nonzero vectors in $H$
nonzero vectors in $H$![]() . Assume $D$
. Assume $D$![]() has uniform multiplicity one and for each $n\in \mathbb {N}$
has uniform multiplicity one and for each $n\in \mathbb {N}$![]() the coordinates $\alpha _n$
the coordinates $\alpha _n$![]() and $\beta _n$
and $\beta _n$![]() are not simultaneously zero. Let $M$
are not simultaneously zero. Let $M$![]() be a reducing subspace for $T$
be a reducing subspace for $T$![]() . If $u,\,v \in M$
. If $u,\,v \in M$![]() or $u,\,v \in M^{\perp }$
or $u,\,v \in M^{\perp }$![]() then $M$
then $M$![]() is trivial.
is trivial.
The key of the proof of proposition 4.1 relies on an argument of a theorem of Wermer [Reference Wermer39], which we isolate and include for the sake of completeness (see also [Reference Radjavi and Rosenthal32, theorem 1.25]). Recall that a normal operator $T\in \mathcal {L}(H)$![]() is diagonalizable if the set of eigenvectors of $T$
is diagonalizable if the set of eigenvectors of $T$![]() spans $H$
spans $H$![]() .
.
Theorem 4.2 (Wermer, 1952)
Let $T\in \mathcal {L}(H)$![]() be a diagonalizable normal operator. Then, every non-zero reducing subspace of $T$
be a diagonalizable normal operator. Then, every non-zero reducing subspace of $T$![]() is spanned by eigenvectors of $T$
is spanned by eigenvectors of $T$![]() .
.
Proof. First, we claim that every non-zero reducing subspace of $T$![]() contains at least one eigenvector. In order to show the claim, let $M$
contains at least one eigenvector. In order to show the claim, let $M$![]() be a non-zero reducing subspace. Since the eigenvectors of $T$
be a non-zero reducing subspace. Since the eigenvectors of $T$![]() span $H$
span $H$![]() , there exists an eigenvector $x$
, there exists an eigenvector $x$![]() not orthogonal to $M$
not orthogonal to $M$![]() . Let $Tx=\lambda x$
. Let $Tx=\lambda x$![]() and write $x=x_1+x_2$
and write $x=x_1+x_2$![]() with respect to the orthogonal decomposition $H=M\oplus M^{\perp }$
with respect to the orthogonal decomposition $H=M\oplus M^{\perp }$![]() . Hence, from
. Hence, from
it follows
and since $M$![]() is reducing, $Tx_1-\lambda x_1 \in M$
is reducing, $Tx_1-\lambda x_1 \in M$![]() and $x_2-T x_2 \in M^{\perp }$
and $x_2-T x_2 \in M^{\perp }$![]() . Thus, $Tx_1=\lambda x_1$
. Thus, $Tx_1=\lambda x_1$![]() and $M$
and $M$![]() contains at least one eigenvector of $T$
contains at least one eigenvector of $T$![]() as claimed.
as claimed.
Now, let us prove the statement of the theorem. Take $M$![]() a non-zero reducing subspace for $T$
a non-zero reducing subspace for $T$![]() and denote by $N$
and denote by $N$![]() the closed subspace of $M$
the closed subspace of $M$![]() generated by all the eigenvectors of $T$
generated by all the eigenvectors of $T$![]() in $M$
in $M$![]() . Note that $N$
. Note that $N$![]() is a non-zero reducing subspace because $T$
is a non-zero reducing subspace because $T$![]() is normal. We claim that $N=M$
is normal. We claim that $N=M$![]() .
.
Indeed, arguing by contradiction, suppose that $N\neq M$![]() . Then $N' = M\cap N^{\perp }$
. Then $N' = M\cap N^{\perp }$![]() is a non-zero invariant subspace for $T$
is a non-zero invariant subspace for $T$![]() which is reducing (since it is the intersection of two reducing subspaces). Accordingly, $N'$
which is reducing (since it is the intersection of two reducing subspaces). Accordingly, $N'$![]() contains at least one eigenvector $z\neq 0$
contains at least one eigenvector $z\neq 0$![]() of $T$
of $T$![]() . Thus $z\in N^{\perp }$
. Thus $z\in N^{\perp }$![]() . But, since $z\in M$
. But, since $z\in M$![]() and is an eigenvector of $T$
and is an eigenvector of $T$![]() , $z\in N$
, $z\in N$![]() by definition. But this implies that $z=0$
by definition. But this implies that $z=0$![]() , which is a contradiction. Accordingly, $N=M$
, which is a contradiction. Accordingly, $N=M$![]() which yields the statement.
which yields the statement.
We are now in position to prove proposition 4.1.
Proof of proposition 4.1. Proof of proposition 4.1
Let $P_M: H \rightarrow M$![]() be the orthogonal projection onto $M$
be the orthogonal projection onto $M$![]() , which clearly commutes with $T$
, which clearly commutes with $T$![]() since $M$
since $M$![]() is reducing. The goal is to show that either $P_M$
is reducing. The goal is to show that either $P_M$![]() is the identity or the zero operator. Assume $P_M$
is the identity or the zero operator. Assume $P_M$![]() is not the zero operator, $Q_M = I-P_M$
is not the zero operator, $Q_M = I-P_M$![]() and suppose first that $u,\,v \in M$
and suppose first that $u,\,v \in M$![]() . Hence, $Q_M u = Q_M v = 0$
. Hence, $Q_M u = Q_M v = 0$![]() .
.
By lemma 2.2 we have $Q_M D P_M = Q_M D^{*} P_M = 0$![]() . Then, $DP_M = P_M D P_M$
. Then, $DP_M = P_M D P_M$![]() and $D^{*}P_M = P_M D^{*} P_M$
and $D^{*}P_M = P_M D^{*} P_M$![]() , so it follows that $M$
, so it follows that $M$![]() is an invariant subspace for $D$
is an invariant subspace for $D$![]() and $D^{*}$
and $D^{*}$![]() , that is, $M$
, that is, $M$![]() is a reducing subspace for $D$
is a reducing subspace for $D$![]() . Thus, according to Wermer's theorem, $M$
. Thus, according to Wermer's theorem, $M$![]() is spanned by a set of eigenvectors of $D$
is spanned by a set of eigenvectors of $D$![]() and, therefore, there exists $\Lambda \subset \mathbb {N}$
and, therefore, there exists $\Lambda \subset \mathbb {N}$![]() such that
such that
Note that, if $n \in \Lambda$![]() we have $Q_M e_n = 0$
we have $Q_M e_n = 0$![]() and if $n \in \mathbb {N}\setminus \Lambda$
and if $n \in \mathbb {N}\setminus \Lambda$![]() then $Q_M e_n = e_n.$
then $Q_M e_n = e_n.$![]()
Now, since $u =\sum _n \alpha _n e_n$![]() and $v=\sum _n \beta _n e_n$
and $v=\sum _n \beta _n e_n$![]() and both $Q_M u = Q_M v = 0$
and both $Q_M u = Q_M v = 0$![]() , we deduce
, we deduce
Hence, $\alpha _n = \beta _n = 0$![]() for every $n \in \mathbb {N}\setminus \Lambda$
for every $n \in \mathbb {N}\setminus \Lambda$![]() which contradicts the hypothesis that $\alpha _n$
which contradicts the hypothesis that $\alpha _n$![]() and $\beta _n$
and $\beta _n$![]() are not simultaneously zero unless $\Lambda = \mathbb {N}$
are not simultaneously zero unless $\Lambda = \mathbb {N}$![]() and, $P_M$
and, $P_M$![]() the identity operator as we wished to prove.
the identity operator as we wished to prove.
The case $u,\,v \in M^{\perp }$![]() is analogous.
is analogous.
With proposition 4.1 at hands, it is possible to characterize the reducing subspaces $M$![]() of $T$
of $T$![]() such that $T\mid _M$
such that $T\mid _M$![]() is normal.
is normal.
Theorem 4.3 Let $T = D+u\otimes v\in \mathcal {L}(H)$![]() where $D$
where $D$![]() is a diagonal operator with respect to an orthonormal basis $(e_n)_{n\geq 1}$
is a diagonal operator with respect to an orthonormal basis $(e_n)_{n\geq 1}$![]() and $u =\sum _n \alpha _n e_n,$
and $u =\sum _n \alpha _n e_n,$![]() $v=\sum _n \beta _n e_n$
$v=\sum _n \beta _n e_n$![]() nonzero vectors in $H$
nonzero vectors in $H$![]() . Assume $D$
. Assume $D$![]() has uniform multiplicity one and for each $n\in \mathbb {N}$
has uniform multiplicity one and for each $n\in \mathbb {N}$![]() the coordinates $\alpha _n$
the coordinates $\alpha _n$![]() and $\beta _n$
and $\beta _n$![]() are not simultaneously zero. Then $T$
are not simultaneously zero. Then $T$![]() has a non-trivial reducing subspace such that $T\mid _M$
has a non-trivial reducing subspace such that $T\mid _M$![]() is normal if and only if one of the following conditions holds:
is normal if and only if one of the following conditions holds:
(a) $T$
 is normal.
is normal.(b) There exists $\alpha,\, \beta \in \mathbb {C}$
 and $x \in H$
and $x \in H$ such that
\[ (D-\alpha I)x = \frac{\langle{(D-\overline{\beta}I)x,x}\rangle}{\langle{u,x}\rangle}u, \mbox{ } (D^{*}-\beta I)x={-}\langle{x,u}\rangle\, v, \]and $M = \textrm {span}\;\{x\}.$
such that
\[ (D-\alpha I)x = \frac{\langle{(D-\overline{\beta}I)x,x}\rangle}{\langle{u,x}\rangle}u, \mbox{ } (D^{*}-\beta I)x={-}\langle{x,u}\rangle\, v, \]and $M = \textrm {span}\;\{x\}.$

Before proceeding with the proof, let us point out that it is possible to exhibit normal operators such that their restrictions to invariant subspaces are not normal (see [Reference Wermer39], for instance). On the other hand, there exist normal operators such that their restrictions to every invariant subspace is normal. This property is equivalent to be a completely normal operator. For instance, every diagonal operator whose spectrum is contained in a Jordan curve is completely normal. As a consequence, every Hermitian operator is completely normal.
The proof of theorem 4.3 depends on the linear independence of $\{u,\, v,\, D^{*}u,\, Dv\}$![]() , which we examine in the next lemma.
, which we examine in the next lemma.
Lemma 4.4 Let $T = D+u\otimes v \in \mathcal {L}(H)$![]() where $D$
where $D$![]() is a diagonal operator with respect to an orthonormal basis $(e_n)_{n\geq 1}$
is a diagonal operator with respect to an orthonormal basis $(e_n)_{n\geq 1}$![]() and $u =\sum _n \alpha _n e_n,$
and $u =\sum _n \alpha _n e_n,$![]() $v=\sum _n \beta _n e_n$
$v=\sum _n \beta _n e_n$![]() nonzero vectors in $H$
nonzero vectors in $H$![]() . Assume $D$
. Assume $D$![]() has uniform multiplicity one and for each $n\in \mathbb {N}$
has uniform multiplicity one and for each $n\in \mathbb {N}$![]() the coordinates $\alpha _n$
the coordinates $\alpha _n$![]() and $\beta _n$
and $\beta _n$![]() are not simultaneously zero. Let $M$
are not simultaneously zero. Let $M$![]() be a reducing subspace for $T$
be a reducing subspace for $T$![]() such that $T\mid _M$
such that $T\mid _M$![]() is normal. Then:
is normal. Then:
(i) If $\{u,\,v,\, D^{*}u,\,Dv\}$
 are linearly independent, then $M = \{0\}.$
are linearly independent, then $M = \{0\}.$
(ii) If $u$
 is an eigenvector for $D^{*}$
is an eigenvector for $D^{*}$ or $v$
or $v$ is for $D,$
is for $D,$ then $M = \{0\}.$
then $M = \{0\}.$
(iii) If $M\neq \{0\}$
 and $u = \alpha v$
and $u = \alpha v$ for some $\alpha \in \mathbb {C},$
for some $\alpha \in \mathbb {C},$ then the spectrum of $D$
then the spectrum of $D$ is contained in a line and $T$
is contained in a line and $T$ is normal.
is normal.(iv) If $M\neq \{0\}$
 and $(D-\alpha I)v = \lambda u$
and $(D-\alpha I)v = \lambda u$ for some $\alpha,\,\lambda \in \mathbb {C}$
for some $\alpha,\,\lambda \in \mathbb {C}$ then the spectrum of $D$
then the spectrum of $D$ is contained in a circle centred in $\alpha$
is contained in a circle centred in $\alpha$ and $T$
and $T$ is normal. The same conclusion follows if it is assumed $M\neq \{0\}$
is normal. The same conclusion follows if it is assumed $M\neq \{0\}$ and $(D^{*}-\beta I)u = \lambda v$
and $(D^{*}-\beta I)u = \lambda v$ for some $\beta,\,\lambda \in \mathbb {C}$
for some $\beta,\,\lambda \in \mathbb {C}$ .
.(v) If $Dv = \alpha u + \beta v + \mu D^{*}u$
 for some scalars $\alpha,\, \beta$
for some scalars $\alpha,\, \beta$ , and $\mu \in \mathbb {C}$
, and $\mu \in \mathbb {C}$ and $T$
and $T$ is not normal, then $\dim M \leq 1.$
is not normal, then $\dim M \leq 1.$
Note that the statements (i)–(v) in lemma 4.4 cover all the possible situations regarding the linear dependence of $\{u,\,v,\,D^{*}u,\,Dv\}.$![]() Clearly, the linear independence case is covered by (i). So, suppose $\{u,\,v,\,D^{*}u,\,Dv\}$
Clearly, the linear independence case is covered by (i). So, suppose $\{u,\,v,\,D^{*}u,\,Dv\}$![]() is a set of linearly dependent vectors. In such a case, (ii) covers the cases where $u$
is a set of linearly dependent vectors. In such a case, (ii) covers the cases where $u$![]() and $D^{*}u$
and $D^{*}u$![]() or $v$
or $v$![]() and $Dv$
and $Dv$![]() are proportional. Statement (iii) deals with the situation in which $u$
are proportional. Statement (iii) deals with the situation in which $u$![]() and $v$
and $v$![]() are proportional, while (iv) considers the cases when $\{u,\,v,\, Dv\}$
are proportional, while (iv) considers the cases when $\{u,\,v,\, Dv\}$![]() or $\{u,\,v,\,D^{*}u \}$
or $\{u,\,v,\,D^{*}u \}$![]() are sets of linearly dependent vectors. Finally, statement (v) deals with the general linear dependence case assuming, in addition, that $T$
are sets of linearly dependent vectors. Finally, statement (v) deals with the general linear dependence case assuming, in addition, that $T$![]() is not normal. Note that this assumption can be made since, otherwise, $T$
is not normal. Note that this assumption can be made since, otherwise, $T$![]() would be normal and Ionascu's theorem would lead us to either statement (iii) or (iv) aforementioned.
would be normal and Ionascu's theorem would lead us to either statement (iii) or (iv) aforementioned.
In what follows, given $T$![]() and $S$
and $S$![]() bounded linear operators in $H$
bounded linear operators in $H$![]() , the commutator of $T$
, the commutator of $T$![]() and $S$
and $S$![]() is the operator in $\mathcal {L}(H)$
is the operator in $\mathcal {L}(H)$![]() defined by
defined by
Clearly, $[T,\,S]=0$![]() if and only if $T$
if and only if $T$![]() and $S$
and $S$![]() commutes.
commutes.
In the proof of lemma 4.4, the following straightforward result will be repeatedly invoked.
Lemma 4.5 Let $A = \sum _{k=1}^{n} x_k\otimes y_k \in \mathcal {L}(H),$![]() where $x_k,\, y_k \in H$
where $x_k,\, y_k \in H$![]() for each $1\leq k \leq n$
for each $1\leq k \leq n$![]() . Suppose that $x_1,\,\ldots,\, x_n$
. Suppose that $x_1,\,\ldots,\, x_n$![]() are linearly independent vectors. If $Ax = 0$
are linearly independent vectors. If $Ax = 0$![]() for $x\in H$
for $x\in H$![]() then $\langle {x,\,y_k}\rangle = 0$
then $\langle {x,\,y_k}\rangle = 0$![]() for every $1\leq k \leq n$
for every $1\leq k \leq n$![]() .
.
Proof of lemma 4.4. Proof of lemma 4.4
Let us begin by proving statement (i). Since $\{u,\,v,\, D^{*}u,\,Dv\}$![]() are linearly independent, Ionascu theorem implies that $T$
are linearly independent, Ionascu theorem implies that $T$![]() is not normal (observe that statement (i) in Ionascu theorem asks $u$
is not normal (observe that statement (i) in Ionascu theorem asks $u$![]() and $v$
and $v$![]() be linearly dependent vectors while (ii) asks $Dv$
be linearly dependent vectors while (ii) asks $Dv$![]() and $u$
and $u$![]() be linearly dependent). Since $T\mid _M$
be linearly dependent). Since $T\mid _M$![]() is normal, we deduce that $M\subsetneq H.$
is normal, we deduce that $M\subsetneq H.$![]()
On the other hand, a straightforward computation shows
By hypotheses, $T\mid _M$![]() is normal so $[T,\,T^{*}]x = 0$
is normal so $[T,\,T^{*}]x = 0$![]() for every $x \in M$
for every $x \in M$![]() . Since $u,\,v,\,D^{*}u,\, Dv$
. Since $u,\,v,\,D^{*}u,\, Dv$![]() are linearly independent, lemma 4.5 yields that
are linearly independent, lemma 4.5 yields that
for every $x \in M$![]() . Hence, $u,\,v \in M^{\perp }$
. Hence, $u,\,v \in M^{\perp }$![]() and therefore, by proposition 4.1, $M$
and therefore, by proposition 4.1, $M$![]() is trivial. Now, $T$
is trivial. Now, $T$![]() is not normal and accordingly $M = \{0\}.$
is not normal and accordingly $M = \{0\}.$![]()
To prove (ii), assume $u$![]() is an eigenvector for $D^{*}$
is an eigenvector for $D^{*}$![]() (a similar reasoning applies if $v$
(a similar reasoning applies if $v$![]() is an eigenvector for $D$
is an eigenvector for $D$![]() ). Since $D$
). Since $D$![]() has uniform multiplicity one, there exists $n_0 \in \mathbb {N}$
has uniform multiplicity one, there exists $n_0 \in \mathbb {N}$![]() such that $u\in \textrm {span}\;\{e_{n_0}\}$
such that $u\in \textrm {span}\;\{e_{n_0}\}$![]() . Without loss of generality, we may assume $u=e_{n_0}$
. Without loss of generality, we may assume $u=e_{n_0}$![]() . Then equation (4.1) becomes
. Then equation (4.1) becomes
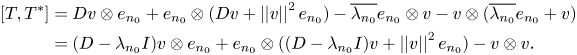
Now, $v=\sum _k \beta _k e_k$![]() and $\beta _k \neq 0$
and $\beta _k \neq 0$![]() for every $k \neq n_0$
for every $k \neq n_0$![]() and each eigenvalue $\lambda _k$
and each eigenvalue $\lambda _k$![]() of $D$
of $D$![]() is of multiplicity one. Hence, $e_{n_0}$
is of multiplicity one. Hence, $e_{n_0}$![]() is linearly independent of $(D-\lambda _{n_0} I)v$
is linearly independent of $(D-\lambda _{n_0} I)v$![]() and $v$
and $v$![]() . Moreover, assume there exists $\beta \in \mathbb {C}\setminus \{0\}$
. Moreover, assume there exists $\beta \in \mathbb {C}\setminus \{0\}$![]() such that
such that
Then $(\lambda _k - \lambda _{n_0}) = \beta$![]() for every $k \neq n_0$
for every $k \neq n_0$![]() which is a contradiction. Accordingly, $(D-\lambda _{n_0} I)v,\, e_{n_0}$
which is a contradiction. Accordingly, $(D-\lambda _{n_0} I)v,\, e_{n_0}$![]() and $v$
and $v$![]() are linearly independent vectors, again lemma 4.5 yields that $v,\, e_{n_0} \in M^{\perp }$
are linearly independent vectors, again lemma 4.5 yields that $v,\, e_{n_0} \in M^{\perp }$![]() and $M\neq H$
and $M\neq H$![]() . Thus, proposition 4.1 yields that $M = \{0\}$
. Thus, proposition 4.1 yields that $M = \{0\}$![]() , as stated in (ii).
, as stated in (ii).
Let us prove now statement (iii). Assume $u = \alpha v$![]() for some $\alpha \in \mathbb {C}\setminus \{0\}$
for some $\alpha \in \mathbb {C}\setminus \{0\}$![]() (observe that $\alpha \neq 0$
(observe that $\alpha \neq 0$![]() since $u$
since $u$![]() is a nonzero vector).
is a nonzero vector).
Assume $M$![]() is a non-zero reducing subspace. We may assume $M\neq H$
is a non-zero reducing subspace. We may assume $M\neq H$![]() since on the contrary, the result is just a consequence of Ionascu theorem condition (i$'$
since on the contrary, the result is just a consequence of Ionascu theorem condition (i$'$![]() ). We are required to show that $\Lambda (D)$
). We are required to show that $\Lambda (D)$![]() is contained in a line and that $T$
is contained in a line and that $T$![]() is a normal operator.
is a normal operator.
First, observe that if $v \in M^{\perp }$![]() then $u \in M^{\perp }$
then $u \in M^{\perp }$![]() and $M = \{0\}$
and $M = \{0\}$![]() by proposition 4.1. Assume, therefore, that $v \notin M^{\perp }.$
by proposition 4.1. Assume, therefore, that $v \notin M^{\perp }.$![]()
Equation (4.1) turns out to be in this case
Now, we claim that the fact that $v \notin M^{\perp }$![]() implies $(\overline {\alpha }D-\alpha D^{*})v = \beta v$
implies $(\overline {\alpha }D-\alpha D^{*})v = \beta v$![]() for some $\beta \in \mathbb {C}$
for some $\beta \in \mathbb {C}$![]() . Indeed, if $x\in M$
. Indeed, if $x\in M$![]() such that $\langle {x,\,v}\rangle \neq 0$
such that $\langle {x,\,v}\rangle \neq 0$![]() , (4.2) yields
, (4.2) yields
from where the claims follows having $\beta =-\langle {x,\,(\overline {\alpha }D-\alpha D^{*})v}\rangle /\langle {x,\,v}\rangle$![]() .
.
So, equation (4.2) becomes
But, once again, since $T\mid _M$![]() is normal and $v \notin M^{\perp }$
is normal and $v \notin M^{\perp }$![]() , it follows that $\textrm {Re}\; (\beta ) = 0$
, it follows that $\textrm {Re}\; (\beta ) = 0$![]() . Hence, $\beta = i t$
. Hence, $\beta = i t$![]() with $t \in \mathbb {R}.$
with $t \in \mathbb {R}.$![]()
Finally, observe that $(\overline {\alpha }D-\alpha D^{*})v = \beta v= i t v$![]() implies
implies
so $\Lambda (D)$![]() lies in the line $\{z \in \mathbb {C}: \textrm {Im}\; ( \alpha \overline {z}) = t \}$
lies in the line $\{z \in \mathbb {C}: \textrm {Im}\; ( \alpha \overline {z}) = t \}$![]() and by Ionascu theorem condition (i$'$
and by Ionascu theorem condition (i$'$![]() ) it follows that $T$
) it follows that $T$![]() is normal.
is normal.
This proves statement (iii).
In order to show condition (iv), assume $Dv -\alpha v = \lambda u$![]() for some $\alpha,\, \lambda \in \mathbb {C}$
for some $\alpha,\, \lambda \in \mathbb {C}$![]() . If $\lambda = 0$
. If $\lambda = 0$![]() , case (ii) yields that $M=\{0\}$
, case (ii) yields that $M=\{0\}$![]() , which is a contradiction. So, we may assume $\lambda \neq 0$
, which is a contradiction. So, we may assume $\lambda \neq 0$![]() . Clearly, without loss of generality, we can also assume $\alpha = 0$
. Clearly, without loss of generality, we can also assume $\alpha = 0$![]() since $D-\alpha I$
since $D-\alpha I$![]() is a diagonal operator of uniform multiplicity one. Thus, $Dv=\lambda u$
is a diagonal operator of uniform multiplicity one. Thus, $Dv=\lambda u$![]() for $\lambda \neq 0$
for $\lambda \neq 0$![]() .
.
In addition, observe that if $u$![]() and $v$
and $v$![]() are linearly dependent then $Dv$
are linearly dependent then $Dv$![]() and $v$
and $v$![]() are linearly dependent, and $M=\{0\}$
are linearly dependent, and $M=\{0\}$![]() by (ii), which is a contradiction. So we may also suppose that $u$
by (ii), which is a contradiction. So we may also suppose that $u$![]() and $v$
and $v$![]() are linearly independent vectors.
are linearly independent vectors.
So, assume $M$![]() is a non-zero reducing subspace, $Dv=\lambda u$
is a non-zero reducing subspace, $Dv=\lambda u$![]() for $\lambda \neq 0$
for $\lambda \neq 0$![]() and $\{u,\,v\}$
and $\{u,\,v\}$![]() are linearly independent. As in the proof of condition (iii), we may assume $M\neq H$
are linearly independent. As in the proof of condition (iii), we may assume $M\neq H$![]() and the goal is to show that $\Lambda (D)$
and the goal is to show that $\Lambda (D)$![]() is contained in a circle and that $T$
is contained in a circle and that $T$![]() is normal.
is normal.
Now, equation (4.1) becomes
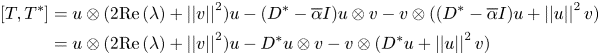
First, let us assume that $v \in M^{\perp }$![]() . Upon applying (4.3) to any vector $x\in M$
. Upon applying (4.3) to any vector $x\in M$![]() , we deduce
, we deduce
which along with the linear independence of $\{u,\, v\}$![]() yields that $(2\textrm{Re}\, (\lambda ) + \left \lvert \left \lvert {v}\right \rvert \right \rvert ^{2}) = 0$
yields that $(2\textrm{Re}\, (\lambda ) + \left \lvert \left \lvert {v}\right \rvert \right \rvert ^{2}) = 0$![]() and $D^{*}u \in M^{\perp }.$
and $D^{*}u \in M^{\perp }.$![]() In addition, since $M$
In addition, since $M$![]() is reducing for $T$
is reducing for $T$![]() if follows that
if follows that
Having in mind that $\textrm {Re}\; (\lambda ) = - \left \lvert \left \lvert {v}\right \rvert \right \rvert ^{2}/2$![]() , we deduce that $Tv \neq 0$
, we deduce that $Tv \neq 0$![]() . Thus, $u \in M^{\perp }$
. Thus, $u \in M^{\perp }$![]() . At this point, we may argue either using proposition 4.1 which would yield that $M = \{0\}$
. At this point, we may argue either using proposition 4.1 which would yield that $M = \{0\}$![]() since $v\in M^{\perp }$
since $v\in M^{\perp }$![]() or as follows. First, $M$
or as follows. First, $M$![]() is a reducing subspace for $D$
is a reducing subspace for $D$![]() since $M$
since $M$![]() is reducing for $T$
is reducing for $T$![]() and $u,\,v \in M^{\perp }$
and $u,\,v \in M^{\perp }$![]() . Then, by means of Wermer theorem, there exists $n_0\in \mathbb {N}$
. Then, by means of Wermer theorem, there exists $n_0\in \mathbb {N}$![]() such that $e_{n_0} \in M$
such that $e_{n_0} \in M$![]() . In particular, this implies that $\langle {u,\,e_{n_0}}\rangle = \langle {v,\,e_{n_0}}\rangle = 0$
. In particular, this implies that $\langle {u,\,e_{n_0}}\rangle = \langle {v,\,e_{n_0}}\rangle = 0$![]() , or equivalent, $\alpha _{n_0} = \beta _{n_0} = 0$
, or equivalent, $\alpha _{n_0} = \beta _{n_0} = 0$![]() , what contradicts the hypotheses of the lemma. This latter argument will be of use in a remark after finishing the proof of lemma 4.4.
, what contradicts the hypotheses of the lemma. This latter argument will be of use in a remark after finishing the proof of lemma 4.4.
Now, let us assume $v\notin M^{\perp }.$![]() Once again, upon applying (4.3) to any vector $x\in M$
Once again, upon applying (4.3) to any vector $x\in M$![]() with $\langle x,\, v\rangle \neq 0$
with $\langle x,\, v\rangle \neq 0$![]() , it follows that
, it follows that
where $\mu,\, \beta \in \mathbb {C}$![]() . It can be assumed that $\beta \neq 0$
. It can be assumed that $\beta \neq 0$![]() . We claim that $\alpha _n \neq 0$
. We claim that $\alpha _n \neq 0$![]() for every $n \in \mathbb {N}$
for every $n \in \mathbb {N}$![]() . Indeed, from $D^{*}u = \mu u+\beta v$
. Indeed, from $D^{*}u = \mu u+\beta v$![]() , it follows that for every $n\in \mathbb {N}$
, it follows that for every $n\in \mathbb {N}$![]()
So, if $\alpha _{n_0} = 0$![]() for some $n_0 \in \mathbb {N}$
for some $n_0 \in \mathbb {N}$![]() , it would imply that $\beta _{n_0} = 0$
, it would imply that $\beta _{n_0} = 0$![]() which contradicts the hypotheses.
which contradicts the hypotheses.
We will show that $\mu =0$![]() in (4.4) since otherwise we are led to a contradiction.
in (4.4) since otherwise we are led to a contradiction.
Assume, on the contrary, that $\mu \neq 0$![]() in (4.4). Applying $D$
in (4.4). Applying $D$![]() to (4.4) we obtain
to (4.4) we obtain
Then, the eigenvalues $\lambda _n$![]() of $D$
of $D$![]() satisfy
satisfy
for every $n \in \mathbb {N}$![]() , since $\alpha _n\neq 0$
, since $\alpha _n\neq 0$![]() for every $n\in \mathbb {N}.$
for every $n\in \mathbb {N}.$![]() Dividing out by $-\beta \lambda$
Dividing out by $-\beta \lambda$![]() (which is different from 0), we deduce that there exist complex numbers $a,\,b \in \mathbb {C}\setminus \{0\}$
(which is different from 0), we deduce that there exist complex numbers $a,\,b \in \mathbb {C}\setminus \{0\}$![]() such that every $\lambda _n$
such that every $\lambda _n$![]() with $n\neq n_0$
with $n\neq n_0$![]() lies in
lies in
The equation $a|z|^{2} +bz = -1$![]() , $z \in \mathbb {C}$
, $z \in \mathbb {C}$![]() is equivalent to the system
is equivalent to the system
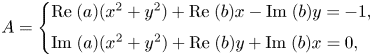
where $x = \textrm {Re}\; (z),\, y = \textrm {Im}\; (z) \in \mathbb {R}$![]() . Observe that $A$
. Observe that $A$![]() is therefore the intersection of two different conics, and hence $A$
is therefore the intersection of two different conics, and hence $A$![]() is a finite set of points, what contradicts the uniform multiplicity one of $D$
is a finite set of points, what contradicts the uniform multiplicity one of $D$![]() .
.
Hence, $\mu = 0$![]() as claimed and (4.4) becomes
as claimed and (4.4) becomes
Note that $u$![]() is linearly independent of $D^{*}u$
is linearly independent of $D^{*}u$![]() because $\{u,\, v\}$
because $\{u,\, v\}$![]() are linearly independent. Having in mind this and applying (4.3) to any vector $x\in M$
are linearly independent. Having in mind this and applying (4.3) to any vector $x\in M$![]() once more time we deduce that
once more time we deduce that
That is, $\textrm {Re}\; (\lambda ) = - {\left \lvert \left \lvert {v}\right \rvert \right \rvert ^{2}}/{2}.$![]() Then, equation (4.3) turns out to be
Then, equation (4.3) turns out to be
On the other hand, having in mind that $Dv = \lambda u$![]() , we deduce
, we deduce
Now, the fact that $\alpha _n \neq 0$![]() for every $n \in \mathbb {N}$
for every $n \in \mathbb {N}$![]() along with the previous equality implies that
along with the previous equality implies that
Note that $\beta \lambda$![]() is a positive number. Accordingly, the spectrum of $D$
is a positive number. Accordingly, the spectrum of $D$![]() is contained in a circle of center $0$
is contained in a circle of center $0$![]() and radius $r=\sqrt {\beta \lambda }>0$
and radius $r=\sqrt {\beta \lambda }>0$![]() , which is half of the statement we wished to prove. Let us see also that $T$
, which is half of the statement we wished to prove. Let us see also that $T$![]() is normal.
is normal.
Now, an easy computation involving coordinates in the expression $Dv = \lambda u$![]() leads to
leads to
and therefore
Since $Dv = \lambda u= |\lambda |{\rm e}^{i\theta }u$![]() for $\theta \in [0,\,2\pi )$
for $\theta \in [0,\,2\pi )$![]() , it follows
, it follows
and by (4.5)
Moreover, from $\textrm {Re}\; (\lambda ) = -\left \lvert \left \lvert {v}\right \rvert \right \rvert ^{2}/2$![]() one deduces $\textrm {Re}\; ( {r{\rm e}^{-i\theta }}/({\left \lvert \left \lvert {u}\right \rvert \right \rvert \left \lvert \left \lvert {v}\right \rvert \right \rvert }) ) = - ({1}/{2}),\,$
one deduces $\textrm {Re}\; ( {r{\rm e}^{-i\theta }}/({\left \lvert \left \lvert {u}\right \rvert \right \rvert \left \lvert \left \lvert {v}\right \rvert \right \rvert }) ) = - ({1}/{2}),\,$![]() which implies that $T$
which implies that $T$![]() is normal by Ionascu theorem condition (ii$'$
is normal by Ionascu theorem condition (ii$'$![]() ). This completes the proof of the statement (iv).
). This completes the proof of the statement (iv).
Finally, let us prove the statement (v). Assume $Dv = \alpha u + \beta v + \mu D^{*}u$![]() for some $\alpha,\, \beta,\,\mu \in \mathbb {C}$
for some $\alpha,\, \beta,\,\mu \in \mathbb {C}$![]() , and $T$
, and $T$![]() is not normal. Since we can express
is not normal. Since we can express
where $\textbf {a}=\alpha + 2\mu \overline {\beta }$![]() , we can assume with no loss of generality that $\beta = 0$
, we can assume with no loss of generality that $\beta = 0$![]() .
.
Observe that, in this case, equation (4.1) becomes
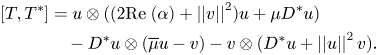
Moreover, we can assume that $D^{*}u,\, u$![]() and $v$
and $v$![]() are linearly independent and $\mu \neq 0$
are linearly independent and $\mu \neq 0$![]() , otherwise cases (iii) and (iv) would yield that $T$
, otherwise cases (iii) and (iv) would yield that $T$![]() is normal, a contradiction.
is normal, a contradiction.
By hypotheses, $[T,\,T^{*}]x = 0$![]() for every $x \in M$
for every $x \in M$![]() , so lemma 4.5 yields that $(2 \textrm {Re}\; (\alpha )+\left \lvert \left \lvert {v}\right \rvert \right \rvert ^{2})u +\mu D^{*}u$
, so lemma 4.5 yields that $(2 \textrm {Re}\; (\alpha )+\left \lvert \left \lvert {v}\right \rvert \right \rvert ^{2})u +\mu D^{*}u$![]() , $\overline {\mu }u-v$
, $\overline {\mu }u-v$![]() and $D^{*}u+\left \lvert \left \lvert {u}\right \rvert \right \rvert ^{2}v$
and $D^{*}u+\left \lvert \left \lvert {u}\right \rvert \right \rvert ^{2}v$![]() belongs to $M^{\perp }.$
belongs to $M^{\perp }.$![]()
We will argue by contradiction. Assume, on the contrary, that the reducing subspace $M$![]() has dimension strictly larger than 1. Then there exists $x \in M\setminus \{0\}$
has dimension strictly larger than 1. Then there exists $x \in M\setminus \{0\}$![]() such that $\langle {x,\,u}\rangle = 0$
such that $\langle {x,\,u}\rangle = 0$![]() . Since $\langle {x,\,\overline {\mu }u - v }\rangle =0,$
. Since $\langle {x,\,\overline {\mu }u - v }\rangle =0,$![]() we have $\langle {x,\,v}\rangle = 0.$
we have $\langle {x,\,v}\rangle = 0.$![]() Moreover, since $x$
Moreover, since $x$![]() is also orthogonal to $D^{*}u+\left \lvert \left \lvert {u}\right \rvert \right \rvert ^{2}v$
is also orthogonal to $D^{*}u+\left \lvert \left \lvert {u}\right \rvert \right \rvert ^{2}v$![]() , we have $\langle {x,\,D^{*}u}\rangle = 0.$
, we have $\langle {x,\,D^{*}u}\rangle = 0.$![]() The fact that $M$
The fact that $M$![]() is invariant under $T$
is invariant under $T$![]() implies, in particular,
implies, in particular,
So, for every $x \in M \cap (\textrm {span}\;\{u\})^{\perp }$![]() , $Dx \in M$
, $Dx \in M$![]() and $\langle {Dx,\,u}\rangle = \langle {x,\,D^{*}u}\rangle = 0$
and $\langle {Dx,\,u}\rangle = \langle {x,\,D^{*}u}\rangle = 0$![]() . Hence, the closed subspace $M\cap (\textrm {span}\;\{u\})^{\perp }$
. Hence, the closed subspace $M\cap (\textrm {span}\;\{u\})^{\perp }$![]() is invariant under $D$
is invariant under $D$![]() .
.
On the other hand, $M$![]() is also invariant under $T^{*}$
is also invariant under $T^{*}$![]() because it is reducing and, therefore,
because it is reducing and, therefore,
Moreover, since $Dv = \alpha u + \mu D^{*}u$![]() we deduce $\langle {D^{*}x,\,v}\rangle = \langle {x,\,Dv}\rangle = 0$
we deduce $\langle {D^{*}x,\,v}\rangle = \langle {x,\,Dv}\rangle = 0$![]() . In addition, from $D^{*}x \in M$
. In addition, from $D^{*}x \in M$![]() , it follows
, it follows
and therefore, $\langle {D^{*}x,\,u}\rangle = 0.$![]() Accordingly, $M\cap (\textrm {span}\;\{u\})^{\perp }$
Accordingly, $M\cap (\textrm {span}\;\{u\})^{\perp }$![]() is a reducing subspace for $D^{*}$
is a reducing subspace for $D^{*}$![]() .
.
Now, since every reducing subspace of $D$![]() contains an eigenvector because of Wermer theorem, it follows that there exists $n_0 \in \mathbb {N}$
contains an eigenvector because of Wermer theorem, it follows that there exists $n_0 \in \mathbb {N}$![]() such that $e_{n_0} \in M\cap (\textrm {span}\;\{u\})^{\perp }$
such that $e_{n_0} \in M\cap (\textrm {span}\;\{u\})^{\perp }$![]() .
.
Now, recalling that $\overline {\mu } u - v \in M^{\perp }$![]() , we deduce $\langle {e_{n_0},\,v}\rangle = 0$
, we deduce $\langle {e_{n_0},\,v}\rangle = 0$![]() . Thereby, $e_{n_0}$
. Thereby, $e_{n_0}$![]() is orthogonal to $u$
is orthogonal to $u$![]() and $v$
and $v$![]() , that is, $\alpha _{n_0} = \beta _{n_0} = 0$
, that is, $\alpha _{n_0} = \beta _{n_0} = 0$![]() , which contradicts the hypotheses of the lemma. Hence, the dimension of $M$
, which contradicts the hypotheses of the lemma. Hence, the dimension of $M$![]() is equal or less than one, as we wished to prove. This concludes the proof of the statement (v) and hence that of lemma 4.4.
is equal or less than one, as we wished to prove. This concludes the proof of the statement (v) and hence that of lemma 4.4.
Remark 4.6 A closer look at the proof of statement (iv), specifically at the argument regarding the intersection of the two different conics, allows us to remark that the hypothesis of the uniform multiplicity one for $D$![]() might be relaxed. Indeed, observe that as far as $u$
might be relaxed. Indeed, observe that as far as $u$![]() and $v$
and $v$![]() are linearly independent, a contradiction would follow if we would just assume that the spectrum of $D$
are linearly independent, a contradiction would follow if we would just assume that the spectrum of $D$![]() contains five or more different eigenvalues, since an intersection of two different conics in the plane consists, at most, of four different points. Moreover, the assumption regarding the multiplicity of $D$
contains five or more different eigenvalues, since an intersection of two different conics in the plane consists, at most, of four different points. Moreover, the assumption regarding the multiplicity of $D$![]() is only used in this argument in the proof of (iv), so our approach allows restating statement (iv) just assuming that $D$
is only used in this argument in the proof of (iv), so our approach allows restating statement (iv) just assuming that $D$![]() has five or more different eigenvalues.
has five or more different eigenvalues.
Now, we can prove theorem 4.3.
Proof of theorem 4.3. Proof of theorem 4.3
If $T$![]() is normal, the spectral theorem for normal operators provides plenty of reducing subspaces for $T$
is normal, the spectral theorem for normal operators provides plenty of reducing subspaces for $T$![]() . In addition, if condition (b) is satisfied, a simple computation shows that $M$
. In addition, if condition (b) is satisfied, a simple computation shows that $M$![]() is reducing for $T$
is reducing for $T$![]() , and since $M$
, and since $M$![]() has dimension $1$
has dimension $1$![]() , $T\mid _M$
, $T\mid _M$![]() is normal.
is normal.
Assume now there exists a non-trivial reducing subspace $M$![]() for $T$
for $T$![]() such that $T\mid _M$
such that $T\mid _M$![]() is normal. By lemma 4.4 we deduce that either $T$
is normal. By lemma 4.4 we deduce that either $T$![]() is normal or $\dim M = 1$
is normal or $\dim M = 1$![]() . Assume $T$
. Assume $T$![]() is not normal. Hence, $\dim M = 1$
is not normal. Hence, $\dim M = 1$![]() and therefore, there exists a non-zero vector $x \in M$
and therefore, there exists a non-zero vector $x \in M$![]() and $\alpha,\,\beta \in \mathbb {C}$
and $\alpha,\,\beta \in \mathbb {C}$![]() such that $Tx = \alpha x$
such that $Tx = \alpha x$![]() and $T^{*}x = \beta x.$
and $T^{*}x = \beta x.$![]() From $Tx = \alpha x$
From $Tx = \alpha x$![]() we have $(D-\alpha I)x + \langle {x,\,v}\rangle u = 0,$
we have $(D-\alpha I)x + \langle {x,\,v}\rangle u = 0,$![]() so
so
From $(T^{*}-\beta I)x = 0$![]() we have $(D^{*}-\beta I)x + \langle {x,\,u}\rangle v = 0.$
we have $(D^{*}-\beta I)x + \langle {x,\,u}\rangle v = 0.$![]() Having into account that $u \notin M^{\perp }$
Having into account that $u \notin M^{\perp }$![]() , we have $\langle {x,\,u}\rangle \neq 0$
, we have $\langle {x,\,u}\rangle \neq 0$![]() , and therefore
, and therefore
Hence,
which yields the result.
Next result generalizes condition (a) in theorem 3.1 whenever rank-one perturbations of diagonal operators with arbitrary spectrum are considered.
Theorem 4.7 Let $D\in \mathcal {L}(H)$![]() be a diagonal operator with respect to an orthonormal basis $(e_n)_{n\geq 1}$
be a diagonal operator with respect to an orthonormal basis $(e_n)_{n\geq 1}$![]() of uniform multiplicity one. Let $u$
of uniform multiplicity one. Let $u$![]() be a nonzero vector in $H$
be a nonzero vector in $H$![]() such that $\langle {u,\,e_n}\rangle \neq 0$
such that $\langle {u,\,e_n}\rangle \neq 0$![]() for every $n \in \mathbb {N}$
for every $n \in \mathbb {N}$![]() and $T = D + u \otimes u$
and $T = D + u \otimes u$![]() . Then, $T$
. Then, $T$![]() has a non-trivial reducing subspace if and only if $T$
has a non-trivial reducing subspace if and only if $T$![]() is normal.
is normal.
Clearly, as a consequence of theorem 4.7, it is possible to exhibit rank-one perturbations of completely normal diagonal operators lacking reducing subspaces.
Proof. It suffices to prove that if $T$![]() has a non-trivial reducing subspace, then $T$
has a non-trivial reducing subspace, then $T$![]() is normal since the converse is straightforward. In addition, we may assume that $D$
is normal since the converse is straightforward. In addition, we may assume that $D$![]() is not self-adjoint, since otherwise $T$
is not self-adjoint, since otherwise $T$![]() would be self-adjoint and the result holds trivially.
would be self-adjoint and the result holds trivially.
Thus, let $M$![]() be a non-trivial reducing subspace and suppose that $D$
be a non-trivial reducing subspace and suppose that $D$![]() is not self-adjoint.
is not self-adjoint.
First, let us assume $T\mid _M$![]() is normal. By theorem 4.3 we have that either $T$
is normal. By theorem 4.3 we have that either $T$![]() is normal or $\dim M = 1$
is normal or $\dim M = 1$![]() . Let us suppose that $\dim M = 1$
. Let us suppose that $\dim M = 1$![]() since otherwise we would be done.
since otherwise we would be done.
Then there exist $\alpha,\, \beta \in \mathbb {C}$![]() such that $Dx + \langle {x,\,u}\rangle u = \alpha x$
such that $Dx + \langle {x,\,u}\rangle u = \alpha x$![]() and $D^{*}x + \langle {x,\,u}\rangle u = \beta x$
and $D^{*}x + \langle {x,\,u}\rangle u = \beta x$![]() . Hence
. Hence
for every $n \in \mathbb {N}$![]() . Now,
. Now,
from where $\textrm {Im}\; (\lambda _n)$![]() is constant for every $n\in \mathbb {N}$
is constant for every $n\in \mathbb {N}$![]() . Thus, the spectrum of $D$
. Thus, the spectrum of $D$![]() is contained in a parallel line to the real axis and by Ionascu's theorem (i$'$
is contained in a parallel line to the real axis and by Ionascu's theorem (i$'$![]() ), it follows $T$
), it follows $T$![]() is normal.
is normal.
If $T\mid _{M^{\perp }}$![]() is normal, we can argue equivalently to show that $T$
is normal, we can argue equivalently to show that $T$![]() is normal.
is normal.
Now, assume that neither $T\mid _M$![]() nor $T\mid _{M^{\perp }}$
nor $T\mid _{M^{\perp }}$![]() are normal operators. If $u$
are normal operators. If $u$![]() and $(D-D^{*})u$
and $(D-D^{*})u$![]() are linearly dependent, then $u$
are linearly dependent, then $u$![]() is an eigenvector for $(D-D^{*})$
is an eigenvector for $(D-D^{*})$![]() , associated with an eigenvalue $\lambda \in \mathbb {C}$
, associated with an eigenvalue $\lambda \in \mathbb {C}$![]() . Since $\langle {u,\,e_n}\rangle \neq 0$
. Since $\langle {u,\,e_n}\rangle \neq 0$![]() for every $n \in \mathbb {N}$
for every $n \in \mathbb {N}$![]() , $\lambda _n - \overline {\lambda _n} = \lambda$
, $\lambda _n - \overline {\lambda _n} = \lambda$![]() for every $n\in \mathbb {N},$
for every $n\in \mathbb {N},$![]() and hence $D-D^{*} = \lambda I$
and hence $D-D^{*} = \lambda I$![]() and $T$
and $T$![]() is normal. So, we may assume that $u$
is normal. So, we may assume that $u$![]() and $(D-D^{*})u$
and $(D-D^{*})u$![]() are linearly independent.
are linearly independent.
By assumption $T\mid _M$![]() and $T\mid _{M^{\perp }}$
and $T\mid _{M^{\perp }}$![]() are not normal, so there exist $x_0 \in M$
are not normal, so there exist $x_0 \in M$![]() and $y_0 \in M^{\perp }$
and $y_0 \in M^{\perp }$![]() such that
such that
Note that in this case
and $u \notin M\cup M^{\perp }$![]() because of proposition 4.1.
because of proposition 4.1.
If $\langle {x_0,\,(D-D^{*})u}\rangle = \langle {y_0,\,(D-D^{*})u}\rangle = 0$![]() , it follows that $(D-D^{*})u \in M \cap M^{\perp },$
, it follows that $(D-D^{*})u \in M \cap M^{\perp },$![]() so $(D-D^{*})u = 0$
so $(D-D^{*})u = 0$![]() and this occurs if and only if $D = D^{*}$
and this occurs if and only if $D = D^{*}$![]() since $\langle {u,\,e_n}\rangle \neq 0$
since $\langle {u,\,e_n}\rangle \neq 0$![]() for every $n \in \mathbb {N}$
for every $n \in \mathbb {N}$![]() . Hence, we can assume $\langle {x_0,\,(D-D^{*})u}\rangle \neq 0$
. Hence, we can assume $\langle {x_0,\,(D-D^{*})u}\rangle \neq 0$![]() .
.
In addition, $u \notin M$![]() so, by means of (4.6) and (4.7), $\langle {x_0,\,u}\rangle \neq 0$
so, by means of (4.6) and (4.7), $\langle {x_0,\,u}\rangle \neq 0$![]() . By considering $P_M$
. By considering $P_M$![]() the orthogonal projection onto $M$
the orthogonal projection onto $M$![]() and $Q_M = I-P_M$
and $Q_M = I-P_M$![]() , it follows that
, it follows that
Moreover, since $Q_M$![]() commutes with $T$
commutes with $T$![]() and $T^{*}$
and $T^{*}$![]() we have
we have
and
so $Q_M(D-D^{*}) = (D-D^{*})Q_M.$![]() Hence, $P_M$
Hence, $P_M$![]() and $Q_M$
and $Q_M$![]() belongs to the commutant ${\{{D-D^{*}}\}'}$
belongs to the commutant ${\{{D-D^{*}}\}'}$![]() . Moreover,
. Moreover,
so $Q_M u$![]() is an eigenvector for $(D-D^{*})$
is an eigenvector for $(D-D^{*})$![]() .
.
Now, let $y_0 \in M^{\perp }$![]() considered in (4.6), that is, $0\neq [T,\,T^{*}]y_0 \in M^{\perp }$
considered in (4.6), that is, $0\neq [T,\,T^{*}]y_0 \in M^{\perp }$![]() . If $\langle {y_0,\,(D-D^{*})u}\rangle = 0$
. If $\langle {y_0,\,(D-D^{*})u}\rangle = 0$![]() then $(D-D^{*})u \in M^{\perp },$
then $(D-D^{*})u \in M^{\perp },$![]() so
so
and therefore $P_M u$![]() is an eigenvector associated with the eigenvalue $0$
is an eigenvector associated with the eigenvalue $0$![]() . If $\langle {y_0,\,(D-D^{*})u}\rangle \neq 0$
. If $\langle {y_0,\,(D-D^{*})u}\rangle \neq 0$![]() , we can argue similarly to deduce that $P_M u$
, we can argue similarly to deduce that $P_M u$![]() is also a eigenvector for $(D-D^{*})$
is also a eigenvector for $(D-D^{*})$![]() .
.
Now, recall that the eigenvalues of $(D-D^{*})$![]() are $(2i\textrm{Im}\, (\lambda _n))_n$
are $(2i\textrm{Im}\, (\lambda _n))_n$![]() and for each $n \in \mathbb {N}$
and for each $n \in \mathbb {N}$![]() , the space of eigenvectors associated with $2i\textrm{Im}\, (\lambda _n)$
, the space of eigenvectors associated with $2i\textrm{Im}\, (\lambda _n)$![]() is given by
is given by
Note that the eigenspaces $M_n$![]() and $M_m$
and $M_m$![]() are orthogonal if $n\neq m.$
are orthogonal if $n\neq m.$![]() Moreover, since $P_M u + Q_M u = u$
Moreover, since $P_M u + Q_M u = u$![]() and $M_n \neq H$
and $M_n \neq H$![]() for every $n \in \mathbb {N}$
for every $n \in \mathbb {N}$![]() ($D$
($D$![]() is not self-adjoint), it follows that both $P_M u$
is not self-adjoint), it follows that both $P_M u$![]() and $Q_M u$
and $Q_M u$![]() are eigenvectors associated with different eigenvalues.
are eigenvectors associated with different eigenvalues.
Moreover, there exists a partition of the positive integers $\mathbb {N}$![]() , that is, non-empty sets $N_1,\, N_2 \subset \mathbb {N}$
, that is, non-empty sets $N_1,\, N_2 \subset \mathbb {N}$![]() such that $N_1\cup N_2 = \mathbb {N}$
such that $N_1\cup N_2 = \mathbb {N}$![]() and $N_1\cap N_2 = \emptyset$
and $N_1\cap N_2 = \emptyset$![]() , such that
, such that
Now,
since $M$![]() is invariant under $T$
is invariant under $T$![]() . Since $Q_M u \in M^{\perp }$
. Since $Q_M u \in M^{\perp }$![]() , we have $\langle {T P_M u,\,Q_M u}\rangle = 0$
, we have $\langle {T P_M u,\,Q_M u}\rangle = 0$![]() . Now, since $D P_M u = \sum _{n\in N_1} \lambda _n \alpha _n e_n$
. Now, since $D P_M u = \sum _{n\in N_1} \lambda _n \alpha _n e_n$![]() it follows that $\langle {D P_M u,\,Q_M u}\rangle = 0,$
it follows that $\langle {D P_M u,\,Q_M u}\rangle = 0,$![]() so we deduce that $\langle {\left \lvert \left \lvert {P_M u}\right \rvert \right \rvert ^{2}u,\, Q_ M u}\rangle = 0,$
so we deduce that $\langle {\left \lvert \left \lvert {P_M u}\right \rvert \right \rvert ^{2}u,\, Q_ M u}\rangle = 0,$![]() but
but
so $P_M u = 0$![]() or $Q_M u = 0$
or $Q_M u = 0$![]() , what contradicts lemma 2.3.
, what contradicts lemma 2.3.
As a byproduct of the previous results, we state the following corollary.
Corollary 4.8 Let $D$![]() a diagonal operator with respect to an orthonormal basis $(e_n)_{n\geq 1}$
a diagonal operator with respect to an orthonormal basis $(e_n)_{n\geq 1}$![]() of uniform multiplicity one and $u \in H$
of uniform multiplicity one and $u \in H$![]() a non-zero vector such that $\langle {u,\,e_n}\rangle \neq 0$
a non-zero vector such that $\langle {u,\,e_n}\rangle \neq 0$![]() for every $n \in \mathbb {N}.$
for every $n \in \mathbb {N}.$![]() Then
Then
(i) $T = D+u\otimes u$
 has a non-trivial reducing subspace if and only if $T$
has a non-trivial reducing subspace if and only if $T$ is normal. In particular, if the spectrum of $D$
is normal. In particular, if the spectrum of $D$ is not contained in a line parallel to the real axis, $T$
is not contained in a line parallel to the real axis, $T$ has no non-trivial reducing subspaces.
has no non-trivial reducing subspaces.(ii) Moreover, if there exists $\alpha,\, \beta \in \mathbb {C}$
 and $x \in H$
and $x \in H$ such that
\[ (D-\alpha I)x = \frac{\langle{(D-\overline{\beta} I)x,x}\rangle}{\langle{u,x}\rangle}u \]and $\langle {x,\,u}\rangle \neq 0,$
such that
\[ (D-\alpha I)x = \frac{\langle{(D-\overline{\beta} I)x,x}\rangle}{\langle{u,x}\rangle}u \]and $\langle {x,\,u}\rangle \neq 0,$
 then $T = D+u\otimes v$
then $T = D+u\otimes v$ has a non-trivial reducing subspace, where $v = (D^{*}-\beta I)x.$
has a non-trivial reducing subspace, where $v = (D^{*}-\beta I)x.$
4.1 A remark on essentially normal operators: Behncke theorem
In this subsection, we recall Behncke's theorem concerning the algebraic structure of essentially normal operators and remark it in the context of the results proved.
Recall that an operator $T$![]() is called essentially normal if $[T,\,T^{*}]$
is called essentially normal if $[T,\,T^{*}]$![]() is compact. Behncke's theorem [Reference Behncke8] generalizes a previous result of [Reference Suzuki38], where the case of $T- T^{*}$
is compact. Behncke's theorem [Reference Behncke8] generalizes a previous result of [Reference Suzuki38], where the case of $T- T^{*}$![]() being compact is addressed (we refer to [Reference Conway11, p. 159, theorem 5.4] and [Reference Guo and Huang25, chapter 8] for more on the subject).
being compact is addressed (we refer to [Reference Conway11, p. 159, theorem 5.4] and [Reference Guo and Huang25, chapter 8] for more on the subject).
Theorem 4.9 (Behncke)
Let $T\in \mathcal {L}(H)$![]() be an essential normal operator. Then $H$
be an essential normal operator. Then $H$![]() admits an orthogonal decomposition
admits an orthogonal decomposition
where
(1) each $H_n$
 is a reducing subspace for $T;$
is a reducing subspace for $T;$
(2) $T_0=T\mid _{H_0}$
 is a maximal normal operator, that is, there is no closed subspace $K_0\varsupsetneq H_0$
is a maximal normal operator, that is, there is no closed subspace $K_0\varsupsetneq H_0$ such that $K_0$
such that $K_0$ is reducing for $T$
is reducing for $T$ and $T\mid _{K_0}$
and $T\mid _{K_0}$ is normal.
is normal.(3) For $n\geq 1$
 each $T_n= T\mid _{H_n}$
each $T_n= T\mid _{H_n}$ has no non-trivial reducing subspaces and it is essentially normal.
has no non-trivial reducing subspaces and it is essentially normal.
Moreover, the decomposition is unique in the sense that if $T_i$![]() and $H_i$
and $H_i$![]() with $i\geq 0$
with $i\geq 0$![]() are replaced with $\widetilde {T_i}$
are replaced with $\widetilde {T_i}$![]() and $\widetilde {H_i}$
and $\widetilde {H_i}$![]() satisfying (1)–(3), and both $T_0$
satisfying (1)–(3), and both $T_0$![]() and $\widetilde {T_0}$
and $\widetilde {T_0}$![]() are maximal normal operators, then after reordering $\widetilde {H_i}$
are maximal normal operators, then after reordering $\widetilde {H_i}$![]() for $i\geq 1,$
for $i\geq 1,$![]() there is a unitary operator $U$
there is a unitary operator $U$![]() commuting with $T$
commuting with $T$![]() such that
such that
Observe that, if $T = D+u\otimes v \in \mathcal {L}(H)$![]() is a non-normal rank-one perturbation of a diagonal operator where $D$
is a non-normal rank-one perturbation of a diagonal operator where $D$![]() , as usual, is a diagonal operator with respect to an orthonormal basis $(e_n)_{n\geq 1}$
, as usual, is a diagonal operator with respect to an orthonormal basis $(e_n)_{n\geq 1}$![]() with uniform multiplicity one and $u =\sum _n \alpha _n e_n$
with uniform multiplicity one and $u =\sum _n \alpha _n e_n$![]() , $v=\sum _n \beta _n e_n$
, $v=\sum _n \beta _n e_n$![]() are nonzero vectors in $H$
are nonzero vectors in $H$![]() with non-simultaneously zero coordinates for each $n\in \mathbb {N}$
with non-simultaneously zero coordinates for each $n\in \mathbb {N}$![]() , we deduce on one hand as a byproduct of lemma 4.4 and Behncke theorem that
, we deduce on one hand as a byproduct of lemma 4.4 and Behncke theorem that
(a) If $\{u,\,v,\, D^{*}u,\,Dv\}$
 are linearly independent, or $u$
are linearly independent, or $u$ is an eigenvector for $D^{*}$
is an eigenvector for $D^{*}$ or $v$
or $v$ is an eigenvector for $D$
is an eigenvector for $D$ , the Hilbert space $H$
, the Hilbert space $H$ admits an orthogonal decomposition
\[ H=H_1 \oplus H_2 \oplus \cdots \]where for every $n\geq 1$
admits an orthogonal decomposition
\[ H=H_1 \oplus H_2 \oplus \cdots \]where for every $n\geq 1$
 , $H_n$
, $H_n$ is a reducing subspace for $T$
is a reducing subspace for $T$ and $T_n= T\mid _{H_n}$
and $T_n= T\mid _{H_n}$ is a non-normal essentially normal operator with no non-trivial reducing subspaces.
is a non-normal essentially normal operator with no non-trivial reducing subspaces.(b) The same conclusion as in (a) follows if $u = \alpha v$
 , or $(D-\alpha I)v = \lambda u$
, or $(D-\alpha I)v = \lambda u$ or $(D^{*}-\beta I)u = \lambda v$
or $(D^{*}-\beta I)u = \lambda v$ for some scalars $\alpha,\, \lambda,\, \beta \in \mathbb {C}$
for some scalars $\alpha,\, \lambda,\, \beta \in \mathbb {C}$ since $T$
since $T$ is not normal.
is not normal.(c) If $Dv = \alpha u + \beta v + \mu D^{*}u$
 for some $\alpha,\, \beta,\, \mu \in \mathbb {C}$
for some $\alpha,\, \beta,\, \mu \in \mathbb {C}$ , then the Hilbert space $H$
, then the Hilbert space $H$ admits an orthogonal decomposition
\[ H=H_0\oplus H_1 \oplus H_2 \oplus \cdots \]where for every $n\geq 0$
admits an orthogonal decomposition
\[ H=H_0\oplus H_1 \oplus H_2 \oplus \cdots \]where for every $n\geq 0$
 , $H_n$
, $H_n$ is a reducing subspace for $T$
is a reducing subspace for $T$ , $H_0$
, $H_0$ is at most a one-dimensional Hilbert space and for each $n\geq 1$
is at most a one-dimensional Hilbert space and for each $n\geq 1$ , the operators $T_n= T\mid _{H_n}$
, the operators $T_n= T\mid _{H_n}$ are non-normal essentially normal operator with no non-trivial reducing subspaces.
are non-normal essentially normal operator with no non-trivial reducing subspaces.
In addition, by means of corollary 4.3 and Behncke theorem, the following consequence holds:
Corollary 4.10 Let $T = D+u\otimes v\in \mathcal {L}(H)$![]() be a non-normal rank-one perturbation of a diagonal operator $D$
be a non-normal rank-one perturbation of a diagonal operator $D$![]() with respect to an orthonormal basis $(e_n)_{n\geq 1},$
with respect to an orthonormal basis $(e_n)_{n\geq 1},$![]() where $u =\sum _n \alpha _n e_n,$
where $u =\sum _n \alpha _n e_n,$![]() $v=\sum _n \beta _n e_n$
$v=\sum _n \beta _n e_n$![]() are nonzero vectors in $H$
are nonzero vectors in $H$![]() with non-zero simultaneously coordinates $\alpha _n$
with non-zero simultaneously coordinates $\alpha _n$![]() and $\beta _n$
and $\beta _n$![]() for each $n\in \mathbb {N}$
for each $n\in \mathbb {N}$![]() . Then $H$
. Then $H$![]() admits an orthogonal decomposition
admits an orthogonal decomposition
satisfying Behncke's theorem conditions (1)–(3) with $H_0$![]() non-trivial if and only if $H_0$
non-trivial if and only if $H_0$![]() is one-dimensional. Moreover, if $H_0= \textrm {span}\;\{x\}$
is one-dimensional. Moreover, if $H_0= \textrm {span}\;\{x\}$![]() for $x\in H\setminus \{0\},$
for $x\in H\setminus \{0\},$![]() there exists $\alpha,\, \beta \in \mathbb {C}$
there exists $\alpha,\, \beta \in \mathbb {C}$![]() such that
such that
On the other hand, in the context of Behncke theorem, one may exhibit easy examples of rank-one perturbation of diagonal operators of multiplicity one such that the orthogonal decomposition of $H$![]() in (4.8) is trivial, namely, $H_0 = \{0\}$
in (4.8) is trivial, namely, $H_0 = \{0\}$![]() , $H_1 = H$
, $H_1 = H$![]() and $H_n=\{0\}$
and $H_n=\{0\}$![]() for every $n\geq 2$
for every $n\geq 2$![]() . Actually, theorem 2.1 or theorem 4.7 in this context provide many of such examples. We state them as corollaries:
. Actually, theorem 2.1 or theorem 4.7 in this context provide many of such examples. We state them as corollaries:
Corollary 4.11 Let $T = D + u\otimes v \in \mathcal {L}(H)$![]() where $D$
where $D$![]() is a diagonal operator with respect to an orthonormal basis $(e_n)_{n\geq 1}$
is a diagonal operator with respect to an orthonormal basis $(e_n)_{n\geq 1}$![]() and $u,$
and $u,$![]() $v$
$v$![]() are nonzero vectors in $H$
are nonzero vectors in $H$![]() satisfying $\langle {u,\,e_n}\rangle \neq 0$
satisfying $\langle {u,\,e_n}\rangle \neq 0$![]() and $\langle {v,\,e_n}\rangle \neq 0$
and $\langle {v,\,e_n}\rangle \neq 0$![]() . Assume $D$
. Assume $D$![]() has uniform multiplicity one and its spectrum $\sigma (D)$
has uniform multiplicity one and its spectrum $\sigma (D)$![]() is contained in a line. Then, the orthogonal decomposition of $H$
is contained in a line. Then, the orthogonal decomposition of $H$![]() in (4.8) satisfying Behncke's theorem conditions (1)–(3) is trivial if and only if $T$
in (4.8) satisfying Behncke's theorem conditions (1)–(3) is trivial if and only if $T$![]() is not normal.
is not normal.
Corollary 4.12 Let $D\in \mathcal {L}(H)$![]() be a diagonal operator with respect to an orthonormal basis $(e_n)_{n\geq 1}$
be a diagonal operator with respect to an orthonormal basis $(e_n)_{n\geq 1}$![]() of uniform multiplicity one. Let $u$
of uniform multiplicity one. Let $u$![]() be a nonzero vector in $H$
be a nonzero vector in $H$![]() such that $\langle {u,\,e_n}\rangle \neq 0$
such that $\langle {u,\,e_n}\rangle \neq 0$![]() for every $n \in \mathbb {N}$
for every $n \in \mathbb {N}$![]() and $T = D + u \otimes u$
and $T = D + u \otimes u$![]() . Then, the orthogonal decomposition of $H$
. Then, the orthogonal decomposition of $H$![]() in (4.8) satisfying Behncke's theorem conditions (1)–(3) is trivial if and only if $T$
in (4.8) satisfying Behncke's theorem conditions (1)–(3) is trivial if and only if $T$![]() is not normal.
is not normal.
4.2 Rank-one perturbations of normal operators
Some of the previous results can be addressed in the context of rank-one perturbations of normal operators of multiplicity one and some consequences can be derived. The first result deals with the class of unitary operators.
Theorem 4.13 Suppose $U \in \mathcal {L}(H)$![]() is a unitary operator and $u \in H$
is a unitary operator and $u \in H$![]() is a vector such that $\langle {u,\, Uu}\rangle \neq 0$
is a vector such that $\langle {u,\, Uu}\rangle \neq 0$![]() and $\{u,\, U^{*} u,\, (U^{*})^{2}u\}$
and $\{u,\, U^{*} u,\, (U^{*})^{2}u\}$![]() are linearly independent. Then there exists $v \in H$
are linearly independent. Then there exists $v \in H$![]() such that $T = U + u\otimes v$
such that $T = U + u\otimes v$![]() has a one-dimensional reducing subspace and $T$
has a one-dimensional reducing subspace and $T$![]() is not a normal operator.
is not a normal operator.
Proof. Let us consider $v = ({-1}/{\langle {u,\, U u}\rangle })(U^{*})^{2}u$![]() . Note that $v$
. Note that $v$![]() is well defined and
is well defined and
Then,
Moreover,
Then, $M:=\textrm {span}\;\{U^{*}u\}$![]() reduces $T$
reduces $T$![]() . It remains to show that $T$
. It remains to show that $T$![]() is not normal.
is not normal.
Assume, on the contrary, that $T$![]() is a normal operator. By [Reference Ionascu28, proposition 3.1] we have two possibilities:
is a normal operator. By [Reference Ionascu28, proposition 3.1] we have two possibilities:
(i) $u$
 and $v$
and $v$ are linearly dependent, which is absurd because $v = ({-1}/{\langle {u,\, Uu}\rangle })(U^{*})^{2}u$
are linearly dependent, which is absurd because $v = ({-1}/{\langle {u,\, Uu}\rangle })(U^{*})^{2}u$ and $u$
and $u$ and $(U^{*})^{2}u$
and $(U^{*})^{2}u$ are linearly independent by hypotheses.
are linearly independent by hypotheses.(ii) $u$
 and $v$
and $v$ are linearly independent and there exists $\alpha,\, \beta \in \mathbb {C}$
are linearly independent and there exists $\alpha,\, \beta \in \mathbb {C}$ such that
\[ (U^{*}-\alpha I)u = \left\lvert\left\lvert{u}\right\rvert\right\rvert^{2}\beta v. \]That is,
such that
\[ (U^{*}-\alpha I)u = \left\lvert\left\lvert{u}\right\rvert\right\rvert^{2}\beta v. \]That is, \[ U^{*}u - \alpha u = \frac{-\left\lvert\left\lvert{u}\right\rvert\right\rvert^{2}\beta }{\langle{u, Uu}\rangle}(U^{*})^{2}u. \]Now $u,\, U^{*}u$
\[ U^{*}u - \alpha u = \frac{-\left\lvert\left\lvert{u}\right\rvert\right\rvert^{2}\beta }{\langle{u, Uu}\rangle}(U^{*})^{2}u. \]Now $u,\, U^{*}u$
 and $(U^{*})^{2}u$
and $(U^{*})^{2}u$ are linearly independent, so $U^{*}u = 0$
are linearly independent, so $U^{*}u = 0$ and therefore $\langle {u,\,Uu}\rangle = \langle {U^{*}u,\,u}\rangle = 0$
and therefore $\langle {u,\,Uu}\rangle = \langle {U^{*}u,\,u}\rangle = 0$ , which yields a contradiction.
, which yields a contradiction.
Hence, $T$![]() is not a normal operator and the proof is finished.
is not a normal operator and the proof is finished.
In the same circle of ideas, the following result holds.
Proposition 4.14 Let $N\in \mathcal {L}(H)$![]() be a normal operator and $u \in H$
be a normal operator and $u \in H$![]() a non-zero vector. Assume that there exist $\alpha,\, \beta \in \mathbb {C}$
a non-zero vector. Assume that there exist $\alpha,\, \beta \in \mathbb {C}$![]() and $x \in H$
and $x \in H$![]() such that $\langle {x,\,u}\rangle \neq 0$
such that $\langle {x,\,u}\rangle \neq 0$![]() and $(N-\alpha I)x = ({\langle {(N-\overline {\beta }I)x,\,x}\rangle }/{\langle {u,\,x}\rangle })u$
and $(N-\alpha I)x = ({\langle {(N-\overline {\beta }I)x,\,x}\rangle }/{\langle {u,\,x}\rangle })u$![]() . Then, the operator $T:= N+u\otimes v$
. Then, the operator $T:= N+u\otimes v$![]() has a non-trivial reducing subspace, where $v = - ({1}/{\langle {x,\,u}\rangle }) (N^{*}-\beta I)x.$
has a non-trivial reducing subspace, where $v = - ({1}/{\langle {x,\,u}\rangle }) (N^{*}-\beta I)x.$![]()
The proof is a just a computation showing that $T$![]() reduces $M:=\textrm {span}\;\{x\}.$
reduces $M:=\textrm {span}\;\{x\}.$![]()
5. Rank-one perturbations of diagonal operators with multiplicity strictly larger than one: examples
In this final section we present some examples of rank-one perturbations of diagonal operators with multiplicity strictly larger than one in order to illustrate how the picture of the reducing subspaces changes if we drop off the uniform multiplicity one assumption.
Example 5.1 There exists $T = D+u\otimes v$![]() a rank-one perturbation of a diagonal operator $D$
a rank-one perturbation of a diagonal operator $D$![]() with multiplicity strictly larger than one and spectrum contained in a line such that $\langle {u,\,e_n}\rangle \neq 0$
with multiplicity strictly larger than one and spectrum contained in a line such that $\langle {u,\,e_n}\rangle \neq 0$![]() and $\langle {v,\,e_n}\rangle \neq 0$
and $\langle {v,\,e_n}\rangle \neq 0$![]() , $T$
, $T$![]() has a non-trivial reducing subspace and it is not a normal operator. It is enough to consider the operator described in remark 2.5.
has a non-trivial reducing subspace and it is not a normal operator. It is enough to consider the operator described in remark 2.5.
As we mentioned in § 2, this example shows that the assumption of uniform multiplicity one cannot be dropped off the hypothesis of theorem 2.1, so the result is sharp in that sense.
Next example is somehow an extreme case regarding rank-one perturbations of diagonal operators with multiplicity strictly larger than one with reducing subspaces such that lemmas 2.3 and 2.4 and proposition 4.1 do not hold.
Example 5.2 Let $u,\,v \in H$![]() and consider $T:= I + u\otimes v,$
and consider $T:= I + u\otimes v,$![]() where $I$
where $I$![]() denote the identity operator. Observe that $I$
denote the identity operator. Observe that $I$![]() is a self-adjoint and unitary diagonal operator, but every closed subspace $M$
is a self-adjoint and unitary diagonal operator, but every closed subspace $M$![]() such that $u,\,v \in M$
such that $u,\,v \in M$![]() is reducing for $T$
is reducing for $T$![]() . Clearly, the behaviour of this operator differs completely from those satisfying theorems 2.1 and 4.3 since the aforementioned lemmas and proposition play an essential role in their corresponding proofs.
. Clearly, the behaviour of this operator differs completely from those satisfying theorems 2.1 and 4.3 since the aforementioned lemmas and proposition play an essential role in their corresponding proofs.
Finally, we use proposition 1.2 to show that the assumption of uniform multiplicity cannot be dropped off theorem 4.7.
Example 5.3 Let $(\lambda _n)_n$![]() be any sequence in the complex plane such that $\lambda _1 = \lambda _2$
be any sequence in the complex plane such that $\lambda _1 = \lambda _2$![]() and let $D$
and let $D$![]() be the diagonal operator such that $De_n = \lambda _ne_n$
be the diagonal operator such that $De_n = \lambda _ne_n$![]() for every $n \in \mathbb {N}$
for every $n \in \mathbb {N}$![]() . Consider $u \in H$
. Consider $u \in H$![]() such that $\langle {u,\,e_n}\rangle \neq 0$
such that $\langle {u,\,e_n}\rangle \neq 0$![]() for every $n \in \mathbb {N}$
for every $n \in \mathbb {N}$![]() . Then, the operator $T := D+u\otimes u$
. Then, the operator $T := D+u\otimes u$![]() has a non-trivial reducing subspace.
has a non-trivial reducing subspace.
Acknowledgements
The authors would like to thank the anonymous referee for reading the manuscript carefully and providing suggestions and remarks which improved considerably its readability.
Financial support
Both authors are partially supported by Plan Nacional I+D grant no. PID2019-105979GB-I00, Spain, the Spanish Ministry of Science and Innovation, through the ‘Severo Ochoa Programme for Centres of Excellence in R&D’ (SEV-2015-0554) and from the Spanish National Research Council, through the ‘Ayuda extraordinaria a Centros de Excelencia Severo Ochoa’ (20205CEX001). The second author also acknowledges support of the Grant SEV-2015-0554-18-3 funded by: MCIN/AEI/10.13039/501100011033.