On the log-concavity of the sequence 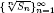 for some combinatorial sequences
for some combinatorial sequences 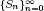
Published online by Cambridge University Press: 22 June 2018
Abstract
Recently, Sun posed a series of conjectures on the log-concavity of the sequence 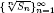 , where
, where 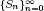 is a familiar combinatorial sequence of positive integers. Luca and Stănică, Hou et al. and Chen et al. proved some of Sun's conjectures. In this paper, we present a criterion on the log-concavity of the sequence
is a familiar combinatorial sequence of positive integers. Luca and Stănică, Hou et al. and Chen et al. proved some of Sun's conjectures. In this paper, we present a criterion on the log-concavity of the sequence 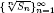 . The criterion is based on the existence of a function f(n) that satisfies some inequalities involving terms related to the sequence
. The criterion is based on the existence of a function f(n) that satisfies some inequalities involving terms related to the sequence 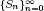 . Furthermore, we present a heuristic approach to compute f(n). As applications, we prove that, for the Zagier numbers
. Furthermore, we present a heuristic approach to compute f(n). As applications, we prove that, for the Zagier numbers 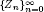 , the sequences
, the sequences 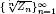 are strictly log-concave, which confirms a conjecture of Sun. We also prove the log-concavity of the sequence
are strictly log-concave, which confirms a conjecture of Sun. We also prove the log-concavity of the sequence 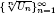 of Cohen–Rhin numbers.
of Cohen–Rhin numbers.
MSC classification
Information
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 148 , Issue 4 , August 2018 , pp. 881 - 892
- Copyright
- Copyright © Royal Society of Edinburgh 2018
- 1
- Cited by

