Hostname: page-component-7dd5485656-tbj44 Total loading time: 0 Render date: 2025-10-31T00:14:27.521Z Has data issue: false hasContentIssue false
  • English
  • Français

Exponential decay for the KdV equation on ℝ with new localized dampings

Part of: Difference equations Equations of mathematical physics and other areas of application Difference and functional equations Partial differential equations

Published online by Cambridge University Press:  05 April 2022

Ming Wang Open the ORCID record for Ming Wang [Opens in a new window]  and
Deqin Zhou
Ming Wang
Affiliation:
Center for Mathematical Sciences, China University of Geosciences, Wuhan 430074, P.R. China (mwang@cug.edu.cn)
Deqin Zhou
Affiliation:
College of Mathematics and Statistics, Chongqing University, Chongqing 401331, P.R. China (deqinzhou1952@126.com)
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we prove several results on the exponential decay in $L^{2}$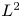 norm of the KdV equation on the real line with localized dampings. First, for the linear KdV equation, the exponential decay holds if and only if the averages of the damping coefficient on all intervals of a fixed length have a positive lower bound. Moreover, under the same damping condition, the exponential decay holds for the (nonlinear) KdV equation with small initial data. Finally, with the aid of certain properties of propagation of regularity in Bourgain spaces for solutions of the associated linear system and the unique continuation property, the exponential decay for the KdV equation with large data holds if the damping coefficient has a positive lower bound on $E$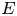, where $E$ 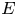is equidistributed over the real line and the complement $E^{c}$ 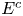has a finite Lebesgue measure.

Keywords

KdV equationexponential decaylocalized damping

MSC classification

Primary: 35Q53: KdV-like equations (Korteweg-de Vries) 35B40: Asymptotic behavior of solutions
Secondary: 39A12: Discrete version of topics in analysis

Information

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 153 , Issue 4 , August 2023 , pp. 1073 - 1098
Check for updates
Copyright
Copyright © The Author(s), 2022. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Berger, M. and Martin, S.. Embedding theorems and quasi-linear elliptic boundary value problems for unbounded domains. Trans. Am. Math. Soc. 172 (1972), 261–278.CrossRefGoogle Scholar
Burq, N. and Joly, R.. Exponential decay for the damped wave equation in unbounded domains. Commun. Contemp. Math. 18 (2016), 1650012.CrossRefGoogle Scholar
Capistrano-Filho, R. A.. Weak damping for the Korteweg–de Vries equation. Electron. J. Qual. Theory Differ. Equ. 43 (2021), 25.Google Scholar
Cavalcanti, M. M., Cavalcanti, V. N. D., Faminskii, A. and Natali, F.. Decay of solutions to damped Korteweg–de Vries type equation. Appl. Math. Optim. 65 (2012), 221–251.CrossRefGoogle Scholar
Cavalcanti, M. M., Cavalcanti, V. N. D., Komornik, V. and Rodrigues, J. H.. Global well-posedness and exponential decay rates for a KdV–Burgers equation with indefinite damping. Ann. Inst. H. Poincaré Anal. Non Linéaire 31 (2014), 1079–1100.CrossRefGoogle Scholar
Duan, Y. L., Wang, L. J. and Zhang, C.. Observability inequalities for the heat equation with bounded potentials on the whole space. SIAM J. Control Optim. 58 (2020), 1939–1960.Google Scholar
Gallego, F. A. and Pazoto, A. F.. On the well-posedness and asymptotic behaviour of the generalized Korteweg–de Vries–Burgers equation. Proc. Roy. Soc. Edinburgh Sect. A 149 (2019), 219–260.Google Scholar
Green, W.. On the energy decay rate of the fractional wave equation on $\mathbb {R}$ with relatively dense damping. Proc. Am. Math. Soc. 148 (2020), 4745–4753.CrossRefGoogle Scholar
Komornik, V. and Pignotti, C.. Well-posedness and exponential decay estimates for a Korteweg–de Vries–Burgers equation with time-delay. Nonlinear Anal. 191 (2020), 111646.CrossRefGoogle Scholar
Le Rousseau, J. and Moyano, I.. Null controllability of the Kolmogorov equation in the whole phase space. J. Differ. Equ. 260 (2016), 3193–3233.Google Scholar
Huang, F. L.. Characteristic conditions for exponential stability of linear dynamical systems in Hilbert spaces. Ann. Differ. Equ. 1 (1985), 43–56.Google Scholar
Kenig, C. E., Ponce, G. and Vega, L.. Oscillatory integrals and regularity of dispersive equations. Indiana Univ. Math. J. 40 (1991), 33–69.Google Scholar
Kenig, C. E., Ponce, G. and Vega, L.. The Cauchy problem for the Korteweg–de Vries equation in Sobolev spaces of negative indices. Duke Math. J. 71 (1993), 1–21.CrossRefGoogle Scholar
Laurent, C., Rosier, L. and Zhang, B.-Y.. Control and stabilization of the Korteweg–de Vries equation on a periodic domain. Commun. Partial Differ. Equ. 35 (2010), 707–744.CrossRefGoogle Scholar
Linares, F. and Pazoto, A. F.. On the exponential decay of the critical generalized Korteweg–de Vries equation with localized damping. Proc. Am. Math. Soc. 135 (2007), 1515–1522.CrossRefGoogle Scholar
Linares, F. and Pazoto, A. F.. Asymptotic behavior of the Korteweg–de Vries equation posed in a quarter plane. J. Differ. Equ. 246 (2009), 1342–1353.CrossRefGoogle Scholar
Menzala, G. P., Vasconcellos, C. F. and Zuazua, E.. Stabilization of the Korteweg–de Vries equation with localized damping. Q. Appl. Math. 60 (2002), 111–129.CrossRefGoogle Scholar
Panthee, M. and Vielma Leal, F.. On the controllability and stabilization of the linearized Benjamin equation on a periodic domain. Nonlinear Anal. Real World Appl. 51 (2020), 102978.CrossRefGoogle Scholar
Panthee, M. and Vielma Leal, F.. On the controllability and stabilization of the Benjamin equation on a periodic domain. Ann. Inst. H. Poincaré Anal. Non Linéaire 38 (2021), 1605–1652.CrossRefGoogle Scholar
Pazy, A.. Semigroups of linear operators and applications to partial differential equations, 44, pp. 13–15 (Springer-Verlag, 1983).Google Scholar
Pazoto, A. F.. Unique continuation and decay for the Korteweg–de Vries equation with localized damping. ESAIM Control Optim. Calc. Var. 11 (2005), 473–486.CrossRefGoogle Scholar
Pazoto, A. F. and Rosier, L.. Uniform stabilization in weighted Sobolev spaces for the KdV equation posed on the half-line. Discrete Contin. Dyn. Syst. B 14 (2010), 1511–1535.Google Scholar
Rosier, L.. Exact boundary controllability for the Korteweg–de Vries equation on a bounded domain. ESAIM Control Optim. Calc. Var. 2 (1997), 33–55.CrossRefGoogle Scholar
Rosier, L. and Zhang, B. Y.. Control and stabilization of the Korteweg–de Vries equation: recent progresses. J. Syst. Sci. Complex. 22 (2009), 647–682.CrossRefGoogle Scholar
Saut, J.-C. and Scheurer, B.. Unique continuation for some evolution equations. J. Differ. Equ. 66 (1987), 118–139.CrossRefGoogle Scholar
Stein, E. M.. Harmonic analysis: real-variable methods, orthogonality, and oscillatory (Princeton University Press, Princeton, New Jersey, 1993).Google Scholar
Taylor, M. E., Partial differential equations II, Qualitative studies of linear equations. 2nd ed., Applied Mathematical Sciences, Vol. 116 (Springer-Verlag, New York, 2011).Google Scholar
Tao, T., Nonlinear dispersive equations: local and global analysis, volume 106 of CBMS Regional Conference Series in Mathematics. Published for the Conference Board of the Mathematical Sciences, Washington, DC, 2006.CrossRefGoogle Scholar
Wang, G., Wang, M., Zhang, C. and Zhang, Y.. Observable set, observability, interpolation inequality and spectral inequality for the heat equation in $\mathbb {R}^{n}$. J. Math. Pure Appl. 126 (2019), 144–194.Google Scholar
Wang, M. and Huang, J.. The global attractor for the weakly damped KdV equation on $\mathbb {R}$ has a finite fractal dimension. Math. Methods Appl. Sci. 43 (2020), 4567–4584.Google Scholar
Wang, M. and Zhou, D.. Exponential decay for the linear KdV with a rough localized damping. Appl. Math. Lett. 120 (2021), 107264.CrossRefGoogle Scholar
Wu, Y.. The Cauchy problem of the Schrödinger–Korteweg–de Vries system. Differ. Int. Equ. 23 (2010), 569–600.Google Scholar
Zhang, B. Y.. Unique continuation for the Korteweg–de Vries equation. SIAM J. Math. Anal. 32 (1992), 55–71.CrossRefGoogle Scholar