Hostname: page-component-7dd5485656-2pp2p Total loading time: 0 Render date: 2025-10-31T13:16:02.291Z Has data issue: false hasContentIssue false
  • English
  • Français

Asymptotically self-similar behaviour of global solutions for semilinear heat equations with algebraically decaying initial data

Part of: Representations of solutions Parabolic equations and systems Partial differential equations

Published online by Cambridge University Press:  26 January 2019

Yūki Naito
Yūki Naito*
Affiliation:
Department of Mathematics, Ehime University, 2-5 Bunkyo, Matsuyama790-8577, Japan (ynaito@ehime-u.ac.jp)
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider the Cauchy problem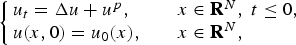

$$\left\{ {\matrix{ {u_t = \Delta u + u^p,\quad } \hfill & {x\in {\bf R}^N,\;t \leq 0,} \hfill \cr {u(x,0) = u_0(x),\quad } \hfill & {x\in {\bf R}^N,} \hfill \cr } } \right.$$
where N > 2, p > 1, and u0 is a bounded continuous non-negative function in RN. We study the case where u0(x) decays at the rate |x|−2/(p−1) as |x| → ∞, and investigate the convergence property of the global solutions to the forward self-similar solutions. We first give the precise description of the relationship between the spatial decay of initial data and the large time behaviour of solutions, and then we show the existence of solutions with a time decay rate slower than the one of self-similar solutions. We also show the existence of solutions that behave in a complicated manner.

Keywords

semilinear heat equationself-similar solutionasymptotic behaviourJoseph-Lundgren critical exponent

MSC classification

Primary: 35K58: Semilinear parabolic equations
Secondary: 35B40: Asymptotic behavior of solutions 35C06: Self-similar solutions

Information

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 150 , Issue 2 , April 2020 , pp. 789 - 811
Copyright
Copyright © Royal Society of Edinburgh 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

1Busca, J., Jendoubi, M. A. and Poláčik, P.. Convergence to equilibrium for semilinear parabolic problems in RN. Comm. Partial Differ. Equ. 27 (2002), 1793–1814.CrossRefGoogle Scholar
2Cazenave, T. and Haraux, A.. An introduction to semilinear evolution equations (New York: Oxford University Press, 1998).Google Scholar
3Cazenave, T. and Weissler, F. B.. Asymptotically self-similar global solutions of the nonlinear Schr”odinger and heat equations. Math. Z. 228 (1998), 83–120.CrossRefGoogle Scholar
4Cazenave, T., Dickstein, F. and Weissler, F.. Universal solutions of a nonlinear heat equation on R N. Ann. Sc. Norm. Super. Pisa Cl. Sci. (5) 2 (2003), 77–117.Google Scholar
5Cazenave, T., Dickstein, F. and Weissler, F.. Multi-scale multi-profile global solutions of parabolic equations in RN. Discrete Contin. Dyn. Syst. Ser. S 5 (2012), 449–472.Google Scholar
6Cortázar, C., del Pino, M. and Elgueta, M.. The problem of uniqueness of the limit in a semilinear heat equation. Comm. Partial Differ. Equ. 24 (1999), 2147–2172.CrossRefGoogle Scholar
7Feireisl, E. and Petzeltová, H.. Convergence to a ground state as a threshold phenomenon in nonlinear parabolic equations. Differ. Integral. Equ. 10 (1997), 181–196.Google Scholar
8Fila, M., Winkler, M. and Yanagida, E.. Grow-up rate of solutions for a supercritical semilinear diffusion equation. J. Differ. Equ. 205 (2004), 365–389.CrossRefGoogle Scholar
9Fila, M., Winkler, M. and Yanagida, E.. Convergence rate for a parabolic equation with supercritical nonlinearity. J. Dynam. Differ. Equ. 17 (2005), 249–269.CrossRefGoogle Scholar
10Fila, M., King, J. R., Winkler, M. and Yanagida, E.. Optimal lower bound of the grow-up rate for a supercritical parabolic equation. J. Differ. Equ. 228 (2006), 339–356.10.1016/j.jde.2006.01.019CrossRefGoogle Scholar
11Fila, M., Winkler, M. and Yanagida, E.. Convergence to self-similar solutions for a semilinear parabolic equation. Discrete Contin. Dyn. Syst. 21 (2008), 703–716.CrossRefGoogle Scholar
12Fujita, H.. On the blowing up of solutions of the Cauchy problem for u t = Δu + u 1 + α. J. Fac. Sci. Univ. Tokyo Sect. I 13 (1966), 109–124.Google Scholar
13Galaktionov, V. A. and Vazquez, J. L.. Continuation of blowup solutions of nonlinear heat equations in several space dimensions. Comm. Pure Appl. Math. 50 (1997), 1–67.3.0.CO;2-H>CrossRefGoogle Scholar
14Gui, C., Ni, W.-M. and Wang, X.. On the stability and instability of positive steady states of a semilinear heat equation in R n. Comm. Pure Appl. Math. 45 (1992), 1153–1181.CrossRefGoogle Scholar
15Gui, C., Ni, W.-M. and Wang, X.. Further study on a nonlinear heat equation. J. Differ. Equ. 169 (2001), 588–613.CrossRefGoogle Scholar
16Haraux, A. and Weissler, F. B.. Non-uniqueness for a semilinear initial value problem. Indiana Univ. Math. J. 31 (1982), 167–189.CrossRefGoogle Scholar
17Hoshino, M. and Yanagida, E.. Sharp estimates of the convergence rate for a semilinear parabolic equation with supercritical nonlinearity. Nonlinear Anal. TMA 69 (2008), 3136–3152.CrossRefGoogle Scholar
18Joseph, D. D. and Lundgren, T. S.. Quasilinear Dirichlet problems driven by positive sources. Arch. Rational Mech. Anal. 49 (1972/73), 241–269.CrossRefGoogle Scholar
19Kavian, O.. Remarks on the large time behavior of a nonlinear diffusion equation. Ann. Inst. H. Poincaré Anal. Non Linéaire 4 (1987), 423–452.CrossRefGoogle Scholar
20Kawanago, T.. Asymptotic behavior of solutions of a semilinear heat equation with subcritical nonlinearity. Ann. Inst. H. Poincaré Anal. Non Linéaire 13 (1996), 1–15.CrossRefGoogle Scholar
21Lee, T.-Y. and Ni, W.-M.. Global existence, large time behavior and life span of solutions of a semilinear parabolic Cauchy problem. Trans. Amer. Math. Soc. 333 (1992), 365–378.CrossRefGoogle Scholar
22Naito, Y.. Non-uniqueness of solutions to the Cauchy problem for semilinear heat equations with singular initial data. Math. Ann. 329 (2004), 161–196.CrossRefGoogle Scholar
23Naito, Y.. An ODE approach to the multiplicity of self-similar solutions for semi-linear heat equations. Proc. Roy. Soc. Edinburgh Sect. A 136 (2006), 807–835.CrossRefGoogle Scholar
24Naito, Y.. Self-similar solutions for a semilinear heat equation with critical Sobolev exponent. Indiana Univ. Math. J. 57 (2008), 1283–1315.CrossRefGoogle Scholar
25Naito, Y.. The role of forward self-similar solutions in the Cauchy problem for semilinear heat equations. J. Differ. Equ. 253 (2012), 3029–3060.CrossRefGoogle Scholar
26Naito, Y.. Convergence rate in the weighted norm for a semilinear heat equation with supercritical nonlinearity. Kodai Math. J. 37 (2014), 646–667.CrossRefGoogle Scholar
27Naito, Y.. Global attractivity and convergence rate in the weighted norm for a supercritical semilinear heat equation. Differ. Integral. Equ. 28 (2015), 777–800.Google Scholar
28Peletier, L. A., Terman, D. and Weissler, F. B.. On the equation $\Delta u + {\textstyle{1 \over 2}}x\cdot \nabla u + f(u) = 0$. Arch. Rational Mech. Anal. 94 (1986), 83–99.CrossRefGoogle Scholar
29Poláčik, P. and Yanagida, E.. On bounded and unbounded global solutions of a supercritical semilinear heat equation. Math. Ann. 327 (2003), 745–771.Google Scholar
30Poláčik, P. and Yanagida, E.. Nonstabilizing solutions and grow-up set for a supercritical semilinear diffusion equation. Differ. Integral. Equ. 17 (2004), 535–548.Google Scholar
31Quittner, P. and Souplet, P.. Superlinear parabolic problems (Basel: Birkhauser Verlag, 2007).Google Scholar
32Snoussi, S., Tayachi, S. and Weissler, F.B.. Asymptotically self-similar global solutions of a general semilinear heat equation. Math. Ann. 321 (2001), 131–155.CrossRefGoogle Scholar
33Souplet, P. and Weissler, F. B.. Regular self-similar solutions of the nonlinear heat equation with initial data above the singular steady state. Ann. Inst. H. Poincare Anal. Non Lineaire 20 (2003), 213–235.10.1016/S0294-1449(02)00003-3CrossRefGoogle Scholar
34Stinner, C.. Very slow convergence rates in a semilinear parabolic equation. NoDEA Nonlinear Differ. Equ. Appl. 17 (2010), 213–227.CrossRefGoogle Scholar
35Stinner, C.. The convergence rate for a semilinear parabolic equation with a critical exponent. Appl. Math. Lett. 24 (2011), 454–459.CrossRefGoogle Scholar
36Wang, X.. On the Cauchy problem for reaction-diffusion equations. Trans. Amer. Math. Soc. 337 (1993), 549–590.CrossRefGoogle Scholar
37Yanagida, E.. Dynamics of global solutions of a semilinear parabolic equation. In Recent progress on reaction-diffusion systems and viscosity solutions (eds. Yihong Du, Hitoshi Ishii and Wei-Yueh), pp. 300–331 (Hackensack, NJ: World Sci. Publ., 2009).CrossRefGoogle Scholar