The normalized scores ![]() $s^{*}_1, s^{*}_2,\ldots, s^{*}_n$ are exchangeable random variables for the fixed
$s^{*}_1, s^{*}_2,\ldots, s^{*}_n$ are exchangeable random variables for the fixed ![]() $n$, i.e., n-exchangeable or finite exchangeable. Their distribution depends on
$n$, i.e., n-exchangeable or finite exchangeable. Their distribution depends on ![]() $n$, and their correlation is a function of
$n$, and their correlation is a function of ![]() $n$. Therefore, if they are a segment of the infinite sequence
$n$. Therefore, if they are a segment of the infinite sequence ![]() $s^{*}_1, s^{*}_2,\dots$, then they are not exchangeable, i.e., not infinite exchangeable and also not stationary. Accordingly, Berman's theorem [Reference Berman2] (Theorem 2.1 in the article) and Theorems 4.5.2. and 5.3.4. from [Reference Leadbetter, Lindgren and Rootzén5], which hold for stationary sequences, cannot be used in the proofs of Results 2.1. and 2.2. However, from Theorem 1 presented and proved below, for
$s^{*}_1, s^{*}_2,\dots$, then they are not exchangeable, i.e., not infinite exchangeable and also not stationary. Accordingly, Berman's theorem [Reference Berman2] (Theorem 2.1 in the article) and Theorems 4.5.2. and 5.3.4. from [Reference Leadbetter, Lindgren and Rootzén5], which hold for stationary sequences, cannot be used in the proofs of Results 2.1. and 2.2. However, from Theorem 1 presented and proved below, for ![]() $P(X_{ij}=1/2)=p\in [1/3, 1)$ or
$P(X_{ij}=1/2)=p\in [1/3, 1)$ or ![]() $p=0$, Results 2.1. and 2.2. follows, and therefore, so do the follow-up Corollaries 2.1. and 2.2.
$p=0$, Results 2.1. and 2.2. follows, and therefore, so do the follow-up Corollaries 2.1. and 2.2.
Let ![]() ${I_{j}^{(n)}=I(s_{j}^{*}\gt x_n(t))}$, where we choose
${I_{j}^{(n)}=I(s_{j}^{*}\gt x_n(t))}$, where we choose ![]() $x_n(t)=a_n t+b_n$, in which
$x_n(t)=a_n t+b_n$, in which ![]() $a_n$ and
$a_n$ and ![]() $b_n$ are as defined in equation (1) in the article:
$b_n$ are as defined in equation (1) in the article:
Set ![]() ${S_n= I_{1}^{(n)}+ I_{2}^{(n)}+\cdots + I_{n}^{(n)}}$.
${S_n= I_{1}^{(n)}+ I_{2}^{(n)}+\cdots + I_{n}^{(n)}}$.
We prove the following result.
Theorem 1. For ![]() $p=0$ or
$p=0$ or ![]() ${p \in [{1}/{3}, 1)}$ and a fixed value of
${p \in [{1}/{3}, 1)}$ and a fixed value of ![]() $k$,
$k$, ![]() $\lim _{n\rightarrow \infty }P(S_n=k)=e^{-\lambda (t)}({\lambda (t)^k}/{k!})$,
$\lim _{n\rightarrow \infty }P(S_n=k)=e^{-\lambda (t)}({\lambda (t)^k}/{k!})$, ![]() $\lambda (t)= e^{-t}$.
$\lambda (t)= e^{-t}$.
For ![]() $p=0$ or
$p=0$ or ![]() ${p \in [{1}/{3}, 1)}$, Results 2.1. and 2.2. follow from Theorem 1, since
${p \in [{1}/{3}, 1)}$, Results 2.1. and 2.2. follow from Theorem 1, since ![]() ${P(s^{*}_{(n-j)}\leq x_n)=P(S_n\leq j)}$, and therefore
${P(s^{*}_{(n-j)}\leq x_n)=P(S_n\leq j)}$, and therefore
 \[ {\lim_{n\rightarrow \infty} P(s^{*}_{(n-j)}\leq x_n)= \lim_{n\rightarrow \infty}P(S_n\leq j)}=e^{{-}e^{{-}t}}\sum_{k=0}^j \frac{e^{{-}tk}}{k!}. \]
\[ {\lim_{n\rightarrow \infty} P(s^{*}_{(n-j)}\leq x_n)= \lim_{n\rightarrow \infty}P(S_n\leq j)}=e^{{-}e^{{-}t}}\sum_{k=0}^j \frac{e^{{-}tk}}{k!}. \]Remark 1. It remains an open problem if Theorem 1 holds also for ![]() ${p \in (0, {1}/{3})}$.
${p \in (0, {1}/{3})}$.
Proof. (Theorem 1) The result follows from Assertions presented below. Set
 \[ \pi_{i}^{(n)}=P(I_{i}^{(n)}=1),\quad W_{n}=\sum_{i=1}^{n}I_{i}^{(n)},\quad \lambda_n=E(W_n)=\sum_{i=1}^{n}\pi_{i}^{(n)}. \]
\[ \pi_{i}^{(n)}=P(I_{i}^{(n)}=1),\quad W_{n}=\sum_{i=1}^{n}I_{i}^{(n)},\quad \lambda_n=E(W_n)=\sum_{i=1}^{n}\pi_{i}^{(n)}. \]Assertion 1.
 \begin{equation} d_{{\rm TV}}({L}(W_n), {\rm Poi}(\lambda_n))\leq \frac{1-e^{\lambda_n}}{\lambda_n}(\lambda_n-{\rm Var}(W_n)) =\frac{1-e^{\lambda_n}}{\lambda_n}\left(\sum_{i=1}^{n}(\pi_{i}^{(n)})^2- \sum_{i\neq j}{\rm Cov} (I_{i}^{(n)}, I_{j}^{(n)})\right), \end{equation}
\begin{equation} d_{{\rm TV}}({L}(W_n), {\rm Poi}(\lambda_n))\leq \frac{1-e^{\lambda_n}}{\lambda_n}(\lambda_n-{\rm Var}(W_n)) =\frac{1-e^{\lambda_n}}{\lambda_n}\left(\sum_{i=1}^{n}(\pi_{i}^{(n)})^2- \sum_{i\neq j}{\rm Cov} (I_{i}^{(n)}, I_{j}^{(n)})\right), \end{equation}
where ![]() ${d_{{\rm TV}}({L}(W_n), {\rm Poi}(\lambda _n))}$ is the total variation distance between distributions of
${d_{{\rm TV}}({L}(W_n), {\rm Poi}(\lambda _n))}$ is the total variation distance between distributions of ![]() $W_n$ and Poisson distribution with mean
$W_n$ and Poisson distribution with mean ![]() $\lambda _n$.
$\lambda _n$.
Assertion 2.
where ![]() ${c_n\sim k_n}$ means
${c_n\sim k_n}$ means ![]() ${\lim _{n\rightarrow \infty } c_n/k_n=1}$.
${\lim _{n\rightarrow \infty } c_n/k_n=1}$.
Assertion 3.
Assertion 4.
In our case, since ![]() $s_1^{*},\ldots,s_{n}^{*}$ are identically distributed,
$s_1^{*},\ldots,s_{n}^{*}$ are identically distributed, ![]() ${\sum _{i=1}^{n}(\pi _{i}^{(n)})^2=n}$
${\sum _{i=1}^{n}(\pi _{i}^{(n)})^2=n}$ ![]() ${P(s^{*}_{1}\gt x_n)P(s^{*}_{1}\gt x_n),}$ and
${P(s^{*}_{1}\gt x_n)P(s^{*}_{1}\gt x_n),}$ and ![]() $\sum _{i\neq j}{\rm Cov}(I_{i}^{(n)}, I_{j}^{(n)})=n(n-1)[P(s_{1}^{*}\gt x_n(t),$
$\sum _{i\neq j}{\rm Cov}(I_{i}^{(n)}, I_{j}^{(n)})=n(n-1)[P(s_{1}^{*}\gt x_n(t),$ ![]() $s_{2}^{*}\gt x_n(t))-P(s_{1}^{*}\gt x_n(t))P(s_{2}^{*}\gt x_n(t))]$. Hence, from (A2) and (A3) it follows that
$s_{2}^{*}\gt x_n(t))-P(s_{1}^{*}\gt x_n(t))P(s_{2}^{*}\gt x_n(t))]$. Hence, from (A2) and (A3) it follows that
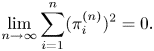 \begin{equation} {\lim_{n\rightarrow \infty}\sum_{i=1}^{n}(\pi_{i}^{(n)})^2=0}. \end{equation}
\begin{equation} {\lim_{n\rightarrow \infty}\sum_{i=1}^{n}(\pi_{i}^{(n)})^2=0}. \end{equation}and from (A3) and (A4) it follows that
Then, from (F1) and (F2) it follows that ![]() ${\lim _{n\rightarrow \infty } d_{{\rm TV}}({L}(W_n), {\rm Poi}(\lambda _n))=0}$, and this completes the proof of Theorem 1.
${\lim _{n\rightarrow \infty } d_{{\rm TV}}({L}(W_n), {\rm Poi}(\lambda _n))=0}$, and this completes the proof of Theorem 1.
Proof. (Assertion 1). If ![]() $p=P(X_{ij})=0$ then
$p=P(X_{ij})=0$ then ![]() $X_{ij}$ has Bernoulli distribution which is log-concave; or if
$X_{ij}$ has Bernoulli distribution which is log-concave; or if ![]() $p\geq 1/3$ then
$p\geq 1/3$ then ![]() $2X_{ij}$ has log-concave distribution (i.e., for integers
$2X_{ij}$ has log-concave distribution (i.e., for integers ![]() $u\geq 1$,
$u\geq 1$, ![]() $(p(u))^2\geq p(u-1)p(u+1)$). Proposition 1 and Corollary 2 [Reference Ross6] hold in our model with
$(p(u))^2\geq p(u-1)p(u+1)$). Proposition 1 and Corollary 2 [Reference Ross6] hold in our model with ![]() $p=0$ or
$p=0$ or ![]() $p\in [1/3, 1)$, and therefore
$p\in [1/3, 1)$, and therefore ![]() ${\sum _{i=1, i\neq j}^{n}I_{i}^{(n)}|I_{j}^{(n)}=1}$ is stochastically smaller than
${\sum _{i=1, i\neq j}^{n}I_{i}^{(n)}|I_{j}^{(n)}=1}$ is stochastically smaller than ![]() ${\sum _{i=1, i\neq j}^{n}I_{i}^{(n)}}$. Therefore, from the Corollary 2.C.2 [Reference Barbour, Holst and Janson1] we obtain (A1).
${\sum _{i=1, i\neq j}^{n}I_{i}^{(n)}}$. Therefore, from the Corollary 2.C.2 [Reference Barbour, Holst and Janson1] we obtain (A1).
Proof. (Assertion 2). Follows from [Reference Feller4, pp. 552–553, Thms. 2 or 3].
Proof. (Assertion 3). Follows from Assertion 2 combined with [Reference Cramér3] result on p. 374 of his book.
Proof. (Assertion 4). Recall that ![]() ${s_1=X_{12}+X_{13}+\cdots +X_{1n}}$ and
${s_1=X_{12}+X_{13}+\cdots +X_{1n}}$ and ![]() ${ s_2=X_{21}+X_{23}+\cdots +X_{2n}}$. Hence, condition on the event
${ s_2=X_{21}+X_{23}+\cdots +X_{2n}}$. Hence, condition on the event ![]() ${X_{12}=k, k\in \{0, 1/2, 1\}}$,
${X_{12}=k, k\in \{0, 1/2, 1\}}$, ![]() $s_1$ and
$s_1$ and ![]() $s_2$ are independent. Let
$s_2$ are independent. Let ![]() ${s_{1{'}}=X_{13}+\cdots +X_{1n}, s_{2{'}}=X_{23}+\cdots +X_{2n}}$ and denote by
${s_{1{'}}=X_{13}+\cdots +X_{1n}, s_{2{'}}=X_{23}+\cdots +X_{2n}}$ and denote by ![]() ${s_{1{'}}^{*}, s_{2{'}}^{*}}$ the corresponding normalized scores (zero expectation and unit variance). We have,
${s_{1{'}}^{*}, s_{2{'}}^{*}}$ the corresponding normalized scores (zero expectation and unit variance). We have,
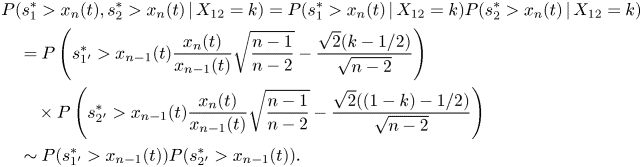 \begin{align} &P(s_{1}^{*}\gt x_n(t), s_{2}^{*}\gt x_n(t)\,|\,X_{12}=k )=P(s_{1}^{*}\gt x_n(t)\,|\,X_{12}=k ) P(s_{2}^{*}\gt x_n(t)\,|\,X_{12}=k )\nonumber\\ &\quad =P\left(s_{1{'}}^{*}\gt x_{n-1}(t)\frac{x_{n}(t)}{x_{n-1}(t)}\sqrt{\frac{n-1}{n-2}}-\frac{\sqrt{2}(k-1/2)}{\sqrt{n-2}}\right)\nonumber\\ &\qquad \times P\left(s_{2{'}}^{*}\gt x_{n-1}(t)\frac{x_{n}(t)}{x_{n-1}(t)}\sqrt{\frac{n-1}{n-2}}-\frac{\sqrt{2}((1-k)-1/2)}{\sqrt{n-2}} \right) \nonumber\\ &\quad \sim P(s_{1{'}}^{*}\gt x_{n-1}(t)) P(s_{2{'}}^{*}\gt x_{n-1}(t)). \end{align}
\begin{align} &P(s_{1}^{*}\gt x_n(t), s_{2}^{*}\gt x_n(t)\,|\,X_{12}=k )=P(s_{1}^{*}\gt x_n(t)\,|\,X_{12}=k ) P(s_{2}^{*}\gt x_n(t)\,|\,X_{12}=k )\nonumber\\ &\quad =P\left(s_{1{'}}^{*}\gt x_{n-1}(t)\frac{x_{n}(t)}{x_{n-1}(t)}\sqrt{\frac{n-1}{n-2}}-\frac{\sqrt{2}(k-1/2)}{\sqrt{n-2}}\right)\nonumber\\ &\qquad \times P\left(s_{2{'}}^{*}\gt x_{n-1}(t)\frac{x_{n}(t)}{x_{n-1}(t)}\sqrt{\frac{n-1}{n-2}}-\frac{\sqrt{2}((1-k)-1/2)}{\sqrt{n-2}} \right) \nonumber\\ &\quad \sim P(s_{1{'}}^{*}\gt x_{n-1}(t)) P(s_{2{'}}^{*}\gt x_{n-1}(t)). \end{align}Combining (F3) with the formula of total probability we obtain
and combining it with Assertion 3 we obtain (A4).
Acknowledgement
I am grateful to Pavel Chigansky for pointing out my mistake.

