1 Introduction
The rotation number was introduced by Poincaré to study the dynamics of circle homeomorphisms
![]() $f:S^{1}\rightarrow S^{1}$
. Given a lift
$f:S^{1}\rightarrow S^{1}$
. Given a lift
![]() $\tilde{f}:\unicode[STIX]{x211D}\rightarrow \unicode[STIX]{x211D}$
of
$\tilde{f}:\unicode[STIX]{x211D}\rightarrow \unicode[STIX]{x211D}$
of
![]() $f$
, the rotation number of
$f$
, the rotation number of
![]() $\tilde{f}$
is defined as
$\tilde{f}$
is defined as
![]() $\unicode[STIX]{x1D70C}(\tilde{f})=\lim _{n\rightarrow \infty }(\tilde{f}^{n}(x)-x)/n\in \unicode[STIX]{x211D}$
, for any
$\unicode[STIX]{x1D70C}(\tilde{f})=\lim _{n\rightarrow \infty }(\tilde{f}^{n}(x)-x)/n\in \unicode[STIX]{x211D}$
, for any
![]() $x\in \unicode[STIX]{x211D}$
. The limit is independent of
$x\in \unicode[STIX]{x211D}$
. The limit is independent of
![]() $x$
and only depends on the lift
$x$
and only depends on the lift
![]() $\tilde{f}$
up to an integer constant. The rotation number
$\tilde{f}$
up to an integer constant. The rotation number
![]() $\unicode[STIX]{x1D70C}(f)=\unicode[STIX]{x1D70C}(\tilde{f})~\text{mod}~\unicode[STIX]{x2124}\in \unicode[STIX]{x211D}/\unicode[STIX]{x2124}$
measures the speed at which points rotate under the iteration of
$\unicode[STIX]{x1D70C}(f)=\unicode[STIX]{x1D70C}(\tilde{f})~\text{mod}~\unicode[STIX]{x2124}\in \unicode[STIX]{x211D}/\unicode[STIX]{x2124}$
measures the speed at which points rotate under the iteration of
![]() $f$
and essentially classifies the dynamics.
$f$
and essentially classifies the dynamics.
The definition of rotation number does not extend smoothly to homeomorphisms of the annulus
![]() $f:S^{1}\times [-1,1]=\unicode[STIX]{x1D538}\rightarrow \unicode[STIX]{x1D538}$
. Consider the universal cover of
$f:S^{1}\times [-1,1]=\unicode[STIX]{x1D538}\rightarrow \unicode[STIX]{x1D538}$
. Consider the universal cover of
![]() $\unicode[STIX]{x1D538}$
identified to
$\unicode[STIX]{x1D538}$
identified to
![]() $\unicode[STIX]{x211D}\times [-1,1]$
and let
$\unicode[STIX]{x211D}\times [-1,1]$
and let
![]() $\tilde{f}:\unicode[STIX]{x211D}\times [-1,1]\rightarrow \unicode[STIX]{x211D}\times [-1,1]$
be a lift of
$\tilde{f}:\unicode[STIX]{x211D}\times [-1,1]\rightarrow \unicode[STIX]{x211D}\times [-1,1]$
be a lift of
![]() $f$
. Denote
$f$
. Denote
![]() $(x)_{1}$
the first coordinate of a point
$(x)_{1}$
the first coordinate of a point
![]() $x\in \unicode[STIX]{x211D}\times [-1,1]$
. Then
$x\in \unicode[STIX]{x211D}\times [-1,1]$
. Then
![]() $\lim _{n\rightarrow \infty }((\tilde{f}^{n}(x))_{1}-(x)_{1})/n$
now depends on
$\lim _{n\rightarrow \infty }((\tilde{f}^{n}(x))_{1}-(x)_{1})/n$
now depends on
![]() $x$
and, even worse, may not exist. Instead of looking at orbits it is useful to consider
$x$
and, even worse, may not exist. Instead of looking at orbits it is useful to consider
![]() $f$
-invariant probabilities
$f$
-invariant probabilities
![]() $\unicode[STIX]{x1D707}$
in
$\unicode[STIX]{x1D707}$
in
![]() $\unicode[STIX]{x1D538}$
and define
$\unicode[STIX]{x1D538}$
and define
where
![]() $s:S^{1}\times [-1,1]\rightarrow \unicode[STIX]{x211D}\times [-1,1]$
is a section of the universal cover
$s:S^{1}\times [-1,1]\rightarrow \unicode[STIX]{x211D}\times [-1,1]$
is a section of the universal cover
![]() $\unicode[STIX]{x1D70B}:\unicode[STIX]{x211D}\times [-1,1]\rightarrow S^{1}\times [-1,1]$
, i.e.
$\unicode[STIX]{x1D70B}:\unicode[STIX]{x211D}\times [-1,1]\rightarrow S^{1}\times [-1,1]$
, i.e.
![]() $s\unicode[STIX]{x1D70B}=\text{id}$
. More generally, denote
$s\unicode[STIX]{x1D70B}=\text{id}$
. More generally, denote
for any
![]() $f$
-invariant set
$f$
-invariant set
![]() $X\subset \unicode[STIX]{x1D538}$
. Since the space of invariant Borel probabilities endowed with the weak topology is compact and convex it follows that
$X\subset \unicode[STIX]{x1D538}$
. Since the space of invariant Borel probabilities endowed with the weak topology is compact and convex it follows that
![]() $\unicode[STIX]{x1D70C}_{\text{mes}}(\tilde{f},X)$
is a compact interval.
$\unicode[STIX]{x1D70C}_{\text{mes}}(\tilde{f},X)$
is a compact interval.
A continuum
![]() $X\subset \text{int}(\unicode[STIX]{x1D538})$
is essential if the two boundary components
$X\subset \text{int}(\unicode[STIX]{x1D538})$
is essential if the two boundary components
![]() $S^{1}\times \{-1\}$
and
$S^{1}\times \{-1\}$
and
![]() $S^{1}\times \{1\}$
of
$S^{1}\times \{1\}$
of
![]() $\unicode[STIX]{x1D538}$
belong to different connected components, denoted, respectively,
$\unicode[STIX]{x1D538}$
belong to different connected components, denoted, respectively,
![]() $U_{-}$
and
$U_{-}$
and
![]() $U_{+}$
, of
$U_{+}$
, of
![]() $\unicode[STIX]{x1D538}\setminus X$
. It is called an (essential) annular continuum if, additionally,
$\unicode[STIX]{x1D538}\setminus X$
. It is called an (essential) annular continuum if, additionally,
![]() $\unicode[STIX]{x1D538}\setminus X=U_{-}\cup U_{+}$
. The previous notions of rotation can be applied to study the dynamics of invariant annular continua. In contrast with the one-dimensional case, the coexistence of different rotation numbers is typical. An example is the Birkhoff attractor
$\unicode[STIX]{x1D538}\setminus X=U_{-}\cup U_{+}$
. The previous notions of rotation can be applied to study the dynamics of invariant annular continua. In contrast with the one-dimensional case, the coexistence of different rotation numbers is typical. An example is the Birkhoff attractor
![]() $\unicode[STIX]{x1D6EC}$
[Reference Le CalvezL88], which is the global attractor of a dissipative diffeomorphism of the open annulus. Even though
$\unicode[STIX]{x1D6EC}$
[Reference Le CalvezL88], which is the global attractor of a dissipative diffeomorphism of the open annulus. Even though
![]() $\unicode[STIX]{x1D6EC}$
has empty interior, it contains infinitely many periodic orbits with different rotation numbers.
$\unicode[STIX]{x1D6EC}$
has empty interior, it contains infinitely many periodic orbits with different rotation numbers.
There is yet another way of measuring the rotation of an invariant annular continuum. After identifying
![]() $S^{1}\times \{1\}$
to a point,
$S^{1}\times \{1\}$
to a point,
![]() $U_{+}$
is transformed into an invariant open topological disk. Carathéodory’s prime end theory (see [Reference Mather, Rassias and RassiasM82]) permits to compactify this new domain with a boundary circle, the set of prime ends of
$U_{+}$
is transformed into an invariant open topological disk. Carathéodory’s prime end theory (see [Reference Mather, Rassias and RassiasM82]) permits to compactify this new domain with a boundary circle, the set of prime ends of
![]() $U_{+}$
, producing a closed topological disk
$U_{+}$
, producing a closed topological disk
![]() $\hat{U} _{+}$
. The construction being topological allows the homeomorphism
$\hat{U} _{+}$
. The construction being topological allows the homeomorphism
![]() $f$
to be extended to a homeomorphism
$f$
to be extended to a homeomorphism
![]() $\hat{f}:\hat{U} _{+}\rightarrow \hat{U} _{+}$
. Furthermore, a lift
$\hat{f}:\hat{U} _{+}\rightarrow \hat{U} _{+}$
. Furthermore, a lift
![]() $\tilde{f}$
of
$\tilde{f}$
of
![]() $f$
uniquely determines a lift
$f$
uniquely determines a lift
![]() $\hat{F}:\unicode[STIX]{x211D}\rightarrow \unicode[STIX]{x211D}$
of the restriction of
$\hat{F}:\unicode[STIX]{x211D}\rightarrow \unicode[STIX]{x211D}$
of the restriction of
![]() $\hat{f}$
to the circle of prime ends of
$\hat{f}$
to the circle of prime ends of
![]() $U_{+}$
, boundary of
$U_{+}$
, boundary of
![]() $\hat{U} _{+}$
, and vice versa. The upper prime end rotation number of the lift
$\hat{U} _{+}$
, and vice versa. The upper prime end rotation number of the lift
![]() $\tilde{f}$
in
$\tilde{f}$
in
![]() $X$
is defined as the rotation number of
$X$
is defined as the rotation number of
![]() $\hat{F}$
and denoted
$\hat{F}$
and denoted
![]() $\unicode[STIX]{x1D70C}_{+}(\tilde{f},X)$
. The lower prime end rotation number
$\unicode[STIX]{x1D70C}_{+}(\tilde{f},X)$
. The lower prime end rotation number
![]() $\unicode[STIX]{x1D70C}_{-}(\tilde{f},X)$
is defined analogously. One can think of these rotation numbers as measures of the rotation of the boundary of
$\unicode[STIX]{x1D70C}_{-}(\tilde{f},X)$
is defined analogously. One can think of these rotation numbers as measures of the rotation of the boundary of
![]() $X$
as seen from the exterior.
$X$
as seen from the exterior.
An alternative intuitive approach to the prime end rotation numbers in terms of accessible points is discussed in [Reference Barge and GilletteBG91]. A point
![]() $p$
is called accessible from a domain
$p$
is called accessible from a domain
![]() $U$
,
$U$
,
![]() $p\notin U$
, provided there is an arc
$p\notin U$
, provided there is an arc
![]() $\unicode[STIX]{x1D6FE}:[0,1]\rightarrow U\cup \{p\}$
such that
$\unicode[STIX]{x1D6FE}:[0,1]\rightarrow U\cup \{p\}$
such that
![]() $\unicode[STIX]{x1D6FE}([0,1))\subset U$
and
$\unicode[STIX]{x1D6FE}([0,1))\subset U$
and
![]() $\unicode[STIX]{x1D6FE}(1)=p$
. Denote
$\unicode[STIX]{x1D6FE}(1)=p$
. Denote
![]() $\tilde{U} _{+},\tilde{X}$
the lifts of
$\tilde{U} _{+},\tilde{X}$
the lifts of
![]() $U_{+},X$
to the universal cover
$U_{+},X$
to the universal cover
![]() $\unicode[STIX]{x211D}\times [-1,1]$
of
$\unicode[STIX]{x211D}\times [-1,1]$
of
![]() $\unicode[STIX]{x1D538}$
. Let
$\unicode[STIX]{x1D538}$
. Let
![]() $x\neq x^{\prime }\in \tilde{X}$
be accessible from
$x\neq x^{\prime }\in \tilde{X}$
be accessible from
![]() $U_{+}$
and
$U_{+}$
and
![]() $\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FE}^{\prime }:[0,1]\rightarrow \unicode[STIX]{x211D}\times [-1,1]$
be two disjoint arcs such that
$\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FE}^{\prime }:[0,1]\rightarrow \unicode[STIX]{x211D}\times [-1,1]$
be two disjoint arcs such that
![]() $\unicode[STIX]{x1D6FE}(0),\unicode[STIX]{x1D6FE}^{\prime }(0)\in \unicode[STIX]{x211D}\times \{1\}$
,
$\unicode[STIX]{x1D6FE}(0),\unicode[STIX]{x1D6FE}^{\prime }(0)\in \unicode[STIX]{x211D}\times \{1\}$
,
![]() $\unicode[STIX]{x1D6FE}([0,1)),\unicode[STIX]{x1D6FE}^{\prime }([0,1))\subset \tilde{U} _{+}$
and
$\unicode[STIX]{x1D6FE}([0,1)),\unicode[STIX]{x1D6FE}^{\prime }([0,1))\subset \tilde{U} _{+}$
and
![]() $\unicode[STIX]{x1D6FE}(1)=x$
and
$\unicode[STIX]{x1D6FE}(1)=x$
and
![]() $\unicode[STIX]{x1D6FE}^{\prime }(1)=x^{\prime }$
. Denote
$\unicode[STIX]{x1D6FE}^{\prime }(1)=x^{\prime }$
. Denote
![]() $\unicode[STIX]{x1D6FE}(0)=(r,0),\unicode[STIX]{x1D6FE}^{\prime }(0)=(r^{\prime },0)$
and define
$\unicode[STIX]{x1D6FE}(0)=(r,0),\unicode[STIX]{x1D6FE}^{\prime }(0)=(r^{\prime },0)$
and define
![]() $x\prec x^{\prime }$
if and only if
$x\prec x^{\prime }$
if and only if
![]() $r<r^{\prime }$
. Then,
$r<r^{\prime }$
. Then,
![]() $\prec$
defines a linear order in the set of points of
$\prec$
defines a linear order in the set of points of
![]() $X$
accessible from
$X$
accessible from
![]() $U_{+}$
. For any
$U_{+}$
. For any
![]() $x,y$
in that set and
$x,y$
in that set and
![]() $n\in \unicode[STIX]{x2124}$
there is a unique
$n\in \unicode[STIX]{x2124}$
there is a unique
![]() $k=k(x,y)$
such that
$k=k(x,y)$
such that
![]() $T^{k}(y)\preccurlyeq x\prec T^{k+1}(y)$
, where
$T^{k}(y)\preccurlyeq x\prec T^{k+1}(y)$
, where
![]() $T$
denotes the deck transformation of the universal cover. One can prove that
$T$
denotes the deck transformation of the universal cover. One can prove that
![]() $\lim _{n\rightarrow \infty }(k(\tilde{f}^{n}(x),y))/n$
is independent of
$\lim _{n\rightarrow \infty }(k(\tilde{f}^{n}(x),y))/n$
is independent of
![]() $x$
and
$x$
and
![]() $y$
and is equal to
$y$
and is equal to
![]() $\unicode[STIX]{x1D70C}_{+}(\tilde{f},X)$
.
$\unicode[STIX]{x1D70C}_{+}(\tilde{f},X)$
.
The goal of this article is to give an elementary proof of the following theorem due to Matsumoto [Reference MatsumotoM12].
Theorem 1. Let
![]() $f:\unicode[STIX]{x1D538}\rightarrow \unicode[STIX]{x1D538}$
be a homeomorphism isotopic to the identity and
$f:\unicode[STIX]{x1D538}\rightarrow \unicode[STIX]{x1D538}$
be a homeomorphism isotopic to the identity and
![]() $X\subset \text{int}(\unicode[STIX]{x1D538})$
an invariant annular continuum. For any lift
$X\subset \text{int}(\unicode[STIX]{x1D538})$
an invariant annular continuum. For any lift
![]() $\tilde{f}$
of
$\tilde{f}$
of
![]() $f$
$f$
Recall that a classical result due to Epstein shows that
![]() $f:\unicode[STIX]{x1D538}\rightarrow \unicode[STIX]{x1D538}$
is isotopic to the identity if and only if preserves orientation and each of the boundary circles.
$f:\unicode[STIX]{x1D538}\rightarrow \unicode[STIX]{x1D538}$
is isotopic to the identity if and only if preserves orientation and each of the boundary circles.
Matsumoto’s proof of Theorem 1 uses Le Calvez’s deep theorem on the existence of a foliation by Brouwer lines for any orientation preserving homeomorphism of
![]() $\unicode[STIX]{x211D}^{2}$
in its equivariant form [Reference Le CalvezL05] for the torus
$\unicode[STIX]{x211D}^{2}$
in its equivariant form [Reference Le CalvezL05] for the torus
![]() $\unicode[STIX]{x1D54B}^{2}$
. The proof then goes on concluding the result in each of several cases, depending on the topological type of the aforementioned foliation. In this paper an alternative proof of Theorem 1 is presented. The arguments involve only basic facts from planar topology and prime end theory making our approach elementary in nature.
$\unicode[STIX]{x1D54B}^{2}$
. The proof then goes on concluding the result in each of several cases, depending on the topological type of the aforementioned foliation. In this paper an alternative proof of Theorem 1 is presented. The arguments involve only basic facts from planar topology and prime end theory making our approach elementary in nature.
Theorem 1 allows to estimate the size of the rotation set of
![]() $X$
,
$X$
,
![]() $\unicode[STIX]{x1D70C}_{\text{mes}}(\tilde{f},X)$
, without precise information of the dynamics within
$\unicode[STIX]{x1D70C}_{\text{mes}}(\tilde{f},X)$
, without precise information of the dynamics within
![]() $X$
. It can be subsequently applied to conclude the existence of periodic orbits in
$X$
. It can be subsequently applied to conclude the existence of periodic orbits in
![]() $X$
of any rotation number
$X$
of any rotation number
![]() $p/q\in [\unicode[STIX]{x1D70C}_{\pm }(\tilde{f},X),\unicode[STIX]{x1D70C}_{\mp }(\tilde{f},X)]\subset \unicode[STIX]{x1D70C}_{\text{mes}}(\tilde{f},X)$
provided some extra hypothesis is satisfied: either
$p/q\in [\unicode[STIX]{x1D70C}_{\pm }(\tilde{f},X),\unicode[STIX]{x1D70C}_{\mp }(\tilde{f},X)]\subset \unicode[STIX]{x1D70C}_{\text{mes}}(\tilde{f},X)$
provided some extra hypothesis is satisfied: either
![]() $f_{|X}$
is chain-recurrent (polishing an argument due to Franks [Reference FranksF88], see [Reference KoropeckiK15, Reference MatsumotoM12]) or
$f_{|X}$
is chain-recurrent (polishing an argument due to Franks [Reference FranksF88], see [Reference KoropeckiK15, Reference MatsumotoM12]) or
![]() $f$
is area-preserving [Reference Franks and Le CalvezFL03] or
$f$
is area-preserving [Reference Franks and Le CalvezFL03] or
![]() $X$
is a cofrontier [Reference Barge and GilletteBG91] or, more generally, a circloid [Reference KoropeckiK15].
$X$
is a cofrontier [Reference Barge and GilletteBG91] or, more generally, a circloid [Reference KoropeckiK15].
In order to ease the notation, for any integer
![]() $k$
the action
$k$
the action
![]() $T^{k}(S)$
of the deck transformation
$T^{k}(S)$
of the deck transformation
![]() $T$
on a set
$T$
on a set
![]() $S\subset \unicode[STIX]{x211D}\times [-1,1]$
will be denoted by
$S\subset \unicode[STIX]{x211D}\times [-1,1]$
will be denoted by
![]() $S+k$
. Additionally, the projection
$S+k$
. Additionally, the projection
![]() $p(S)$
of
$p(S)$
of
![]() $S$
under the first coordinate map
$S$
under the first coordinate map
![]() $p:\unicode[STIX]{x211D}\times [-1,1]\rightarrow \unicode[STIX]{x211D}$
will be denoted by
$p:\unicode[STIX]{x211D}\times [-1,1]\rightarrow \unicode[STIX]{x211D}$
will be denoted by
![]() $(S)_{1}$
.
$(S)_{1}$
.
2 Proof of Theorem 1
Next lemma follows directly from the definitions.
Lemma 2. For any integer
![]() $k$
,
$k$
,
The proof of Theorem 1 presented here only deals with the upper prime rotation number and shows that
![]() $\unicode[STIX]{x1D70C}_{+}(\tilde{f})\geqslant \inf \unicode[STIX]{x1D70C}(\tilde{f},X)$
, the other cases being completely analogous.
$\unicode[STIX]{x1D70C}_{+}(\tilde{f})\geqslant \inf \unicode[STIX]{x1D70C}(\tilde{f},X)$
, the other cases being completely analogous.
Argue by contradiction: suppose there are integers
![]() $p,q$
such that
$p,q$
such that
![]() $\unicode[STIX]{x1D70C}_{+}(\tilde{f})<p/q<\inf \unicode[STIX]{x1D70C}(\tilde{f},X)$
. As a consequence of Lemma 2,
$\unicode[STIX]{x1D70C}_{+}(\tilde{f})<p/q<\inf \unicode[STIX]{x1D70C}(\tilde{f},X)$
. As a consequence of Lemma 2,
![]() $\unicode[STIX]{x1D70C}_{+}(T^{-p}\tilde{f}^{q})<0<\inf \unicode[STIX]{x1D70C}(T^{-p}\tilde{f}^{q},X)$
. Thus, after renaming, it is possible to assume
$\unicode[STIX]{x1D70C}_{+}(T^{-p}\tilde{f}^{q})<0<\inf \unicode[STIX]{x1D70C}(T^{-p}\tilde{f}^{q},X)$
. Thus, after renaming, it is possible to assume
Some notation to describe the shape of
![]() $\tilde{U} _{+}$
is now introduced. Let
$\tilde{U} _{+}$
is now introduced. Let
![]() $\unicode[STIX]{x1D702}=\max \{y\in \unicode[STIX]{x211D}:(0,y)\in \tilde{X}\}$
and
$\unicode[STIX]{x1D702}=\max \{y\in \unicode[STIX]{x211D}:(0,y)\in \tilde{X}\}$
and
![]() $\unicode[STIX]{x1D6FD}:[0,1]\rightarrow \unicode[STIX]{x211D}\times [-1,1]$
be a vertical arc with endpoints
$\unicode[STIX]{x1D6FD}:[0,1]\rightarrow \unicode[STIX]{x211D}\times [-1,1]$
be a vertical arc with endpoints
![]() $\unicode[STIX]{x1D6FD}(0)=(0,1)\in \unicode[STIX]{x211D}\times \{1\}$
and
$\unicode[STIX]{x1D6FD}(0)=(0,1)\in \unicode[STIX]{x211D}\times \{1\}$
and
![]() $\unicode[STIX]{x1D6FD}(1)=(0,\unicode[STIX]{x1D702})\in \tilde{X}$
. Denote
$\unicode[STIX]{x1D6FD}(1)=(0,\unicode[STIX]{x1D702})\in \tilde{X}$
. Denote
![]() $x_{0}=\unicode[STIX]{x1D6FD}(1)$
and use
$x_{0}=\unicode[STIX]{x1D6FD}(1)$
and use
![]() $\unicode[STIX]{x1D6FD}$
also to denote the image of the arc
$\unicode[STIX]{x1D6FD}$
also to denote the image of the arc
![]() $\unicode[STIX]{x1D6FD}$
. This abuse of notation is present throughout the text. The arcs
$\unicode[STIX]{x1D6FD}$
. This abuse of notation is present throughout the text. The arcs
![]() $\unicode[STIX]{x1D6FD}^{\prime }=\unicode[STIX]{x1D6FD}\setminus \{x_{0}\}$
and
$\unicode[STIX]{x1D6FD}^{\prime }=\unicode[STIX]{x1D6FD}\setminus \{x_{0}\}$
and
![]() $\unicode[STIX]{x1D6FD}^{\prime }+1$
bound a region in
$\unicode[STIX]{x1D6FD}^{\prime }+1$
bound a region in
![]() $\tilde{U} _{+}$
which contains the segment
$\tilde{U} _{+}$
which contains the segment
![]() $(0,1)\times \{1\}$
. The closure of this region, as a subset of
$(0,1)\times \{1\}$
. The closure of this region, as a subset of
![]() $\tilde{U} _{+}$
, will be denoted by
$\tilde{U} _{+}$
, will be denoted by
![]() $V$
and thought of as a fundamental region. Clearly,
$V$
and thought of as a fundamental region. Clearly,
and
![]() $(V-1)\cap V=\unicode[STIX]{x1D6FD}^{\prime }$
. Define
$(V-1)\cap V=\unicode[STIX]{x1D6FD}^{\prime }$
. Define
Note that
![]() $x_{0}\in \tilde{X}$
is accessible both from
$x_{0}\in \tilde{X}$
is accessible both from
![]() $\tilde{U} _{+}$
and from
$\tilde{U} _{+}$
and from
![]() $V$
. The following lemma is based on the interpretation of the prime end rotation number in terms of accessible points and their induced order
$V$
. The following lemma is based on the interpretation of the prime end rotation number in terms of accessible points and their induced order
![]() $\prec$
as was discussed in the introduction.
$\prec$
as was discussed in the introduction.
Lemma 3.
-
(1) For every point
 $x$
accessible from
$x$
accessible from
 $\tilde{U} _{+}$
there exists
$\tilde{U} _{+}$
there exists
 $k\in \unicode[STIX]{x2124}$
such that
$k\in \unicode[STIX]{x2124}$
such that
 $x$
is accessible from
$x$
is accessible from
 $V+k$
.
$V+k$
. -
(2) If
 $x$
is accessible from
$x$
is accessible from
 $V+k$
then
$V+k$
then
 $\tilde{f}^{n}(x)$
is accessible from
$\tilde{f}^{n}(x)$
is accessible from
 $(V+k)^{+}$
, if
$(V+k)^{+}$
, if
 $n\leqslant 0$
, or from
$n\leqslant 0$
, or from
 $(V+k)^{-}$
, if
$(V+k)^{-}$
, if
 $n\geqslant 0$
.
$n\geqslant 0$
. -
(3) Suppose
 $x\in \tilde{X}$
is accessible from
$x\in \tilde{X}$
is accessible from
 $V+k_{1}$
and
$V+k_{1}$
and
 $\tilde{f}^{-1}(x)$
is accessible from
$\tilde{f}^{-1}(x)$
is accessible from
 $V+k_{2}$
. Then, for any point
$V+k_{2}$
. Then, for any point
 $z\in \tilde{X}$
accessible from
$z\in \tilde{X}$
accessible from
 $\tilde{U} _{+}$
there exists an integer
$\tilde{U} _{+}$
there exists an integer
 $n$
so that
$n$
so that
 $\tilde{f}^{n}(z)$
is accessible from
$\tilde{f}^{n}(z)$
is accessible from
 $V+j$
, for some
$V+j$
, for some
 $k_{1}\leqslant j\leqslant k_{2}$
.
$k_{1}\leqslant j\leqslant k_{2}$
.
A crosscut of
![]() $\tilde{U} _{+}$
is an arc
$\tilde{U} _{+}$
is an arc
![]() $c$
whose endpoints lie in
$c$
whose endpoints lie in
![]() $\tilde{X}$
and whose interior is contained in
$\tilde{X}$
and whose interior is contained in
![]() $\tilde{U} _{+}$
. By definition, the endpoints of
$\tilde{U} _{+}$
. By definition, the endpoints of
![]() $c$
are accessible from
$c$
are accessible from
![]() $\tilde{U} _{+}$
. Recall a standard fact from prime end theory:
$\tilde{U} _{+}$
. Recall a standard fact from prime end theory:
![]() $c$
separates
$c$
separates
![]() $\tilde{U} _{+}$
in exactly two connected components.
$\tilde{U} _{+}$
in exactly two connected components.
Definition 4. An arc
![]() $\unicode[STIX]{x1D6FE}:[0,1]\rightarrow V$
is said to be a hair of
$\unicode[STIX]{x1D6FE}:[0,1]\rightarrow V$
is said to be a hair of
![]() $V$
if
$V$
if
![]() $\unicode[STIX]{x1D6FE}(0)\in \unicode[STIX]{x211D}\times \{1\}$
. More generally, an arc
$\unicode[STIX]{x1D6FE}(0)\in \unicode[STIX]{x211D}\times \{1\}$
. More generally, an arc
![]() $\unicode[STIX]{x1D6FE}:[0,1]\rightarrow \tilde{U} _{+}$
is a hair if
$\unicode[STIX]{x1D6FE}:[0,1]\rightarrow \tilde{U} _{+}$
is a hair if
![]() $\unicode[STIX]{x1D6FE}-k$
is a hair of
$\unicode[STIX]{x1D6FE}-k$
is a hair of
![]() $V$
for some
$V$
for some
![]() $k\in \unicode[STIX]{x2124}$
. In that case
$k\in \unicode[STIX]{x2124}$
. In that case
![]() $\unicode[STIX]{x1D6FE}$
is called a hair of
$\unicode[STIX]{x1D6FE}$
is called a hair of
![]() $V+k$
(see Figure 1).
$V+k$
(see Figure 1).

Figure 1.
![]() $c$
is a crosscut of
$c$
is a crosscut of
![]() $\tilde{U} _{+}$
and
$\tilde{U} _{+}$
and
![]() $\unicode[STIX]{x1D6FE}$
is a hair of
$\unicode[STIX]{x1D6FE}$
is a hair of
![]() $V+1$
.
$V+1$
.
Lemma 5. There exist
![]() $m\geqslant 1$
satisfying
$m\geqslant 1$
satisfying
![]() $(\tilde{f}^{m}(x))_{1}\geqslant (x)_{1}+1$
for every
$(\tilde{f}^{m}(x))_{1}\geqslant (x)_{1}+1$
for every
![]() $x\in \tilde{X}$
. Furthermore, there exists
$x\in \tilde{X}$
. Furthermore, there exists
![]() $M>1$
such that if
$M>1$
such that if
![]() $x$
is a point in
$x$
is a point in
![]() $V$
for which every hair
$V$
for which every hair
![]() $\unicode[STIX]{x1D6FE}$
of
$\unicode[STIX]{x1D6FE}$
of
![]() $V$
ending at
$V$
ending at
![]() $x$
satisfies
$x$
satisfies
![]() $\text{diam}((\unicode[STIX]{x1D6FE})_{1})>M$
then
$\text{diam}((\unicode[STIX]{x1D6FE})_{1})>M$
then
![]() $(\tilde{f}^{m}(x))_{1}\geqslant (x)_{1}+1/2$
.
$(\tilde{f}^{m}(x))_{1}\geqslant (x)_{1}+1/2$
.
Proof. For the first part, suppose on the contrary that there are integers
![]() $\{n_{i}\}_{i\geqslant 1}\rightarrow +\infty$
and points
$\{n_{i}\}_{i\geqslant 1}\rightarrow +\infty$
and points
![]() $\{x_{i}\}_{i\geqslant 1}$
in
$\{x_{i}\}_{i\geqslant 1}$
in
![]() $\tilde{X}$
such that
$\tilde{X}$
such that
![]() $(\tilde{f}^{n_{i}}(x_{i}))_{1}<(x_{i})_{1}+1$
. The probability measures defined on
$(\tilde{f}^{n_{i}}(x_{i}))_{1}<(x_{i})_{1}+1$
. The probability measures defined on
![]() $X$
by
$X$
by
satisfy
![]() $\unicode[STIX]{x1D70C}(\tilde{f},\unicode[STIX]{x1D707}_{i})=(\tilde{f}^{n_{i}}(x_{i}))_{1}/n_{i}-(x_{i})_{1}/n_{i}<1/n_{i}$
. The space of Borel probability measures on
$\unicode[STIX]{x1D70C}(\tilde{f},\unicode[STIX]{x1D707}_{i})=(\tilde{f}^{n_{i}}(x_{i}))_{1}/n_{i}-(x_{i})_{1}/n_{i}<1/n_{i}$
. The space of Borel probability measures on
![]() $X$
endowed with the weak topology being compact and metric, there is a subsequence
$X$
endowed with the weak topology being compact and metric, there is a subsequence
![]() $\{\unicode[STIX]{x1D707}_{i_{j}}\}_{j\geqslant 1}$
,
$\{\unicode[STIX]{x1D707}_{i_{j}}\}_{j\geqslant 1}$
,
![]() $i_{j}\rightarrow +\infty$
, of
$i_{j}\rightarrow +\infty$
, of
![]() $\{\unicode[STIX]{x1D707}_{i}\}$
whose limit is a Borel probability measure
$\{\unicode[STIX]{x1D707}_{i}\}$
whose limit is a Borel probability measure
![]() $\unicode[STIX]{x1D707}$
. By continuity of the pushforward operator
$\unicode[STIX]{x1D707}$
. By continuity of the pushforward operator
![]() $\unicode[STIX]{x1D707}$
is
$\unicode[STIX]{x1D707}$
is
![]() $f$
-invariant, and by the weak convergence
$f$
-invariant, and by the weak convergence
![]() $\unicode[STIX]{x1D707}_{i_{j}}\rightarrow \unicode[STIX]{x1D707}$
$\unicode[STIX]{x1D707}_{i_{j}}\rightarrow \unicode[STIX]{x1D707}$
which contradicts (1).
For the second, let
![]() ${\tilde{Y}}=\{z\in \unicode[STIX]{x211D}\times [-1,1]:(\tilde{f}^{m}(z))_{1}\geqslant (z)_{1}+1/2\}$
be a neighborhood of
${\tilde{Y}}=\{z\in \unicode[STIX]{x211D}\times [-1,1]:(\tilde{f}^{m}(z))_{1}\geqslant (z)_{1}+1/2\}$
be a neighborhood of
![]() $\tilde{X}$
. Clearly, the projection
$\tilde{X}$
. Clearly, the projection
![]() $Y=\unicode[STIX]{x1D70B}({\tilde{Y}})$
of
$Y=\unicode[STIX]{x1D70B}({\tilde{Y}})$
of
![]() ${\tilde{Y}}$
onto
${\tilde{Y}}$
onto
![]() $\unicode[STIX]{x1D538}$
is a compact neighborhood of
$\unicode[STIX]{x1D538}$
is a compact neighborhood of
![]() $X$
and
$X$
and
![]() $\text{dist}(X,\unicode[STIX]{x2202}Y)=\unicode[STIX]{x1D6FF}>0$
. If the statement does not hold one can find points
$\text{dist}(X,\unicode[STIX]{x2202}Y)=\unicode[STIX]{x1D6FF}>0$
. If the statement does not hold one can find points
![]() $z_{n}\in V\setminus {\tilde{Y}}$
such that any hair
$z_{n}\in V\setminus {\tilde{Y}}$
such that any hair
![]() $\unicode[STIX]{x1D6FE}$
of
$\unicode[STIX]{x1D6FE}$
of
![]() $V$
ending at
$V$
ending at
![]() $z_{n}$
satisfies
$z_{n}$
satisfies
![]() $\text{diam}((\unicode[STIX]{x1D6FE})_{1})>n$
, for every
$\text{diam}((\unicode[STIX]{x1D6FE})_{1})>n$
, for every
![]() $n\geqslant 1$
. It is possible to choose an infinite subsequence
$n\geqslant 1$
. It is possible to choose an infinite subsequence
![]() $\{z_{n_{j}}\}_{j}$
of
$\{z_{n_{j}}\}_{j}$
of
![]() $\{z_{n}\}_{n}$
so that the balls centered at
$\{z_{n}\}_{n}$
so that the balls centered at
![]() $z_{n_{j}}$
of radius
$z_{n_{j}}$
of radius
![]() $\unicode[STIX]{x1D6FF}$
are pairwise disjoint and contained in
$\unicode[STIX]{x1D6FF}$
are pairwise disjoint and contained in
![]() $V$
. This is impossible because
$V$
. This is impossible because
![]() $V$
has finite area.◻
$V$
has finite area.◻
For simplicity, for the rest of the proof replace
![]() $f$
by
$f$
by
![]() $f^{m}$
, where
$f^{m}$
, where
![]() $m$
is as in the previous lemma. Then,
$m$
is as in the previous lemma. Then,
![]() $(\tilde{f}(x))_{1}\geqslant (x)_{1}+1$
for any
$(\tilde{f}(x))_{1}\geqslant (x)_{1}+1$
for any
![]() $x\in \tilde{X}$
and (1) still holds.
$x\in \tilde{X}$
and (1) still holds.
The following object gives a way to roughly describe the shape of
![]() $V$
. Construct hairs
$V$
. Construct hairs
![]() $\unicode[STIX]{x1D6FE}_{n}$
,
$\unicode[STIX]{x1D6FE}_{n}$
,
![]() $n\geqslant 1$
, in
$n\geqslant 1$
, in
![]() $V$
such that
$V$
such that
![]() $l_{n+1}<l_{n}$
,
$l_{n+1}<l_{n}$
,
![]() $r_{n+1}>r_{n}$
, where
$r_{n+1}>r_{n}$
, where
![]() $l_{n}=\min (\unicode[STIX]{x1D6FE}_{n})_{1}$
and
$l_{n}=\min (\unicode[STIX]{x1D6FE}_{n})_{1}$
and
![]() $r_{n}=\max (\unicode[STIX]{x1D6FE}_{n})_{1}$
.
$r_{n}=\max (\unicode[STIX]{x1D6FE}_{n})_{1}$
.
There are three mutually exclusive cases depending on
![]() $V$
:
$V$
:
-
(i) It is not possible to have
 $\lim _{n}l_{n}=-\infty$
.
$\lim _{n}l_{n}=-\infty$
. -
(ii) There is an infinite sequence of hairs
 $\{\unicode[STIX]{x1D6FE}_{n}\}_{n}$
such that
$\{\unicode[STIX]{x1D6FE}_{n}\}_{n}$
such that
 $\lim _{n}l_{n}=-\infty$
and
$\lim _{n}l_{n}=-\infty$
and
 $\{r_{n}\}_{n}$
is bounded.
$\{r_{n}\}_{n}$
is bounded. -
(iii) For any infinite sequence of hairs
 $\{\unicode[STIX]{x1D6FE}_{n}\}_{n}$
such that
$\{\unicode[STIX]{x1D6FE}_{n}\}_{n}$
such that
 $\lim _{n}l_{n}=-\infty$
, always
$\lim _{n}l_{n}=-\infty$
, always
 $\lim _{n}r_{n}=+\infty$
.
$\lim _{n}r_{n}=+\infty$
.
They correspond to: (i)
![]() $(V)_{1}$
is bounded from below, (ii)
$(V)_{1}$
is bounded from below, (ii)
![]() $(V)_{1}$
unbounded from below but bounded from above and (iii)
$(V)_{1}$
unbounded from below but bounded from above and (iii)
![]() $(V)_{1}$
is unbounded both from below and above.
$(V)_{1}$
is unbounded both from below and above.
The proof of Theorem 1 deals separately with these three cases. Lemmas 3 and 5 are extensively used to derive a contradiction with Inequality (1) in each of them.
Case (i):
![]() $(V)_{1}$
is bounded from below.
$(V)_{1}$
is bounded from below.
In this case there exists
![]() $L\in \unicode[STIX]{x211D}$
such that every point
$L\in \unicode[STIX]{x211D}$
such that every point
![]() $x\in \tilde{X}$
accessible from
$x\in \tilde{X}$
accessible from
![]() $V$
satisfies
$V$
satisfies
![]() $L<(x)_{1}$
. Consider
$L<(x)_{1}$
. Consider
![]() $k$
so that
$k$
so that
![]() $\tilde{f}(x_{0})$
is accessible from
$\tilde{f}(x_{0})$
is accessible from
![]() $V+k$
. Lemma 3 ensures
$V+k$
. Lemma 3 ensures
![]() $k\leqslant 0$
. It follows that for any point
$k\leqslant 0$
. It follows that for any point
![]() $z\in \tilde{X}$
accessible from
$z\in \tilde{X}$
accessible from
![]() $V^{-}$
there exists
$V^{-}$
there exists
![]() $n\geqslant 0$
such that
$n\geqslant 0$
such that
![]() $\tilde{f}^{-n}(z)$
is accessible from
$\tilde{f}^{-n}(z)$
is accessible from
![]() $V+j$
, for some
$V+j$
, for some
![]() $k\leqslant j\leqslant 0$
. The lower bound on
$k\leqslant j\leqslant 0$
. The lower bound on
![]() $(V)_{1}$
implies
$(V)_{1}$
implies
![]() $L+k<(\tilde{f}^{-n}(z))_{1}$
so, by Lemma 5,
$L+k<(\tilde{f}^{-n}(z))_{1}$
so, by Lemma 5,
![]() $L+k<(z)_{1}$
, which is absurd.◻
$L+k<(z)_{1}$
, which is absurd.◻
Case (ii):
![]() $(V)_{1}$
is unbounded from below but bounded from above.
$(V)_{1}$
is unbounded from below but bounded from above.
The union of
![]() $\unicode[STIX]{x1D6FE}_{n}$
,
$\unicode[STIX]{x1D6FE}_{n}$
,
![]() $n\geqslant 1$
, is contained in
$n\geqslant 1$
, is contained in
![]() $V$
and divides
$V$
and divides
![]() $\tilde{U} _{+}$
in many connected components. Denote
$\tilde{U} _{+}$
in many connected components. Denote
![]() $B$
the component which contains
$B$
the component which contains
![]() $(V-1)^{-}$
. Clearly,
$(V-1)^{-}$
. Clearly,
![]() $B$
is unbounded from the left but satisfies
$B$
is unbounded from the left but satisfies
![]() $\sup (B)_{1}\leqslant M$
, where
$\sup (B)_{1}\leqslant M$
, where
![]() $M$
is an upper bound for
$M$
is an upper bound for
![]() $\{r_{n}\}_{n}$
.
$\{r_{n}\}_{n}$
.
Let
![]() $x\in \tilde{X}$
be accessible from
$x\in \tilde{X}$
be accessible from
![]() $V-1\subset B$
. For every
$V-1\subset B$
. For every
![]() $n\geqslant 1$
, by Lemma 3 the point
$n\geqslant 1$
, by Lemma 3 the point
![]() $\tilde{f}^{n}(x)$
is accessible from
$\tilde{f}^{n}(x)$
is accessible from
![]() $(V-1)^{-}$
and thus from
$(V-1)^{-}$
and thus from
![]() $B$
as well. However, for large
$B$
as well. However, for large
![]() $n\geqslant 0$
, Lemma 5 implies
$n\geqslant 0$
, Lemma 5 implies
![]() $(\tilde{f}^{n}(x))_{1}>M$
and, in particular,
$(\tilde{f}^{n}(x))_{1}>M$
and, in particular,
![]() $\tilde{f}^{n}(x)$
cannot belong to the adherence of
$\tilde{f}^{n}(x)$
cannot belong to the adherence of
![]() $B$
.◻
$B$
.◻
Case (iii):
![]() $(V)_{1}$
is unbounded both from below and above.
$(V)_{1}$
is unbounded both from below and above.
This case is more involved and some preliminary results are needed. First, the shape of the region
![]() $V$
is shown to be snake–like. This idea is made precise in the following proposition.
$V$
is shown to be snake–like. This idea is made precise in the following proposition.
Proposition 6. There exist sequences
![]() $\{L_{n}\}_{n},\{R_{n}\}_{n}$
of real numbers such that
$\{L_{n}\}_{n},\{R_{n}\}_{n}$
of real numbers such that
-
(1)
 $R_{1}>1,L_{1}<0$
.
$R_{1}>1,L_{1}<0$
. -
(2)
 $\{L_{n}\}_{n}$
is decreasing and tends to
$\{L_{n}\}_{n}$
is decreasing and tends to
 $-\infty$
.
$-\infty$
. -
(3)
 $\{R_{n}\}_{n}$
is increasing and tends to
$\{R_{n}\}_{n}$
is increasing and tends to
 $+\infty$
.
$+\infty$
.
such that
-
(i) If
 $\unicode[STIX]{x1D6FE}$
is a hair of
$\unicode[STIX]{x1D6FE}$
is a hair of
 $V$
and
$V$
and
 $(\unicode[STIX]{x1D6FE}(1))_{1}<L_{n}$
then
$(\unicode[STIX]{x1D6FE}(1))_{1}<L_{n}$
then
 $R_{n}\in (\unicode[STIX]{x1D6FE})_{1}$
.
$R_{n}\in (\unicode[STIX]{x1D6FE})_{1}$
. -
(ii) If
 $\unicode[STIX]{x1D6FE}$
is a hair of
$\unicode[STIX]{x1D6FE}$
is a hair of
 $V$
and
$V$
and
 $(\unicode[STIX]{x1D6FE}(1))_{1}>R_{n}$
then
$(\unicode[STIX]{x1D6FE}(1))_{1}>R_{n}$
then
 $L_{n-1}\in (\unicode[STIX]{x1D6FE})_{1}$
.
$L_{n-1}\in (\unicode[STIX]{x1D6FE})_{1}$
.
Proof. Let
![]() $\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FE}$
be hairs of
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FE}$
be hairs of
![]() $V$
. Notice the following simple fact:
$V$
. Notice the following simple fact:
![]() $\unicode[STIX]{x1D6FE}$
does not intersect any translated
$\unicode[STIX]{x1D6FE}$
does not intersect any translated
![]() $\unicode[STIX]{x1D6FC}+k$
unless
$\unicode[STIX]{x1D6FC}+k$
unless
![]() $k=0$
. As a consequence:
$k=0$
. As a consequence:
- (
 $\star$
)
$\star$
) -
If
 $(\unicode[STIX]{x1D6FE}(1))_{1}>\max (\unicode[STIX]{x1D6FC})_{1}+1$
then
$(\unicode[STIX]{x1D6FE}(1))_{1}>\max (\unicode[STIX]{x1D6FC})_{1}+1$
then
 $\min (\unicode[STIX]{x1D6FE})_{1}<\min (\unicode[STIX]{x1D6FC})_{1}+1$
.
$\min (\unicode[STIX]{x1D6FE})_{1}<\min (\unicode[STIX]{x1D6FC})_{1}+1$
. - (
 $\star \star$
)
$\star \star$
) -
If
 $(\unicode[STIX]{x1D6FE}(1))_{1}<\min (\unicode[STIX]{x1D6FC})_{1}-1$
then
$(\unicode[STIX]{x1D6FE}(1))_{1}<\min (\unicode[STIX]{x1D6FC})_{1}-1$
then
 $\max (\unicode[STIX]{x1D6FE})_{1}>\max (\unicode[STIX]{x1D6FC})_{1}-1$
.
$\max (\unicode[STIX]{x1D6FE})_{1}>\max (\unicode[STIX]{x1D6FC})_{1}-1$
.
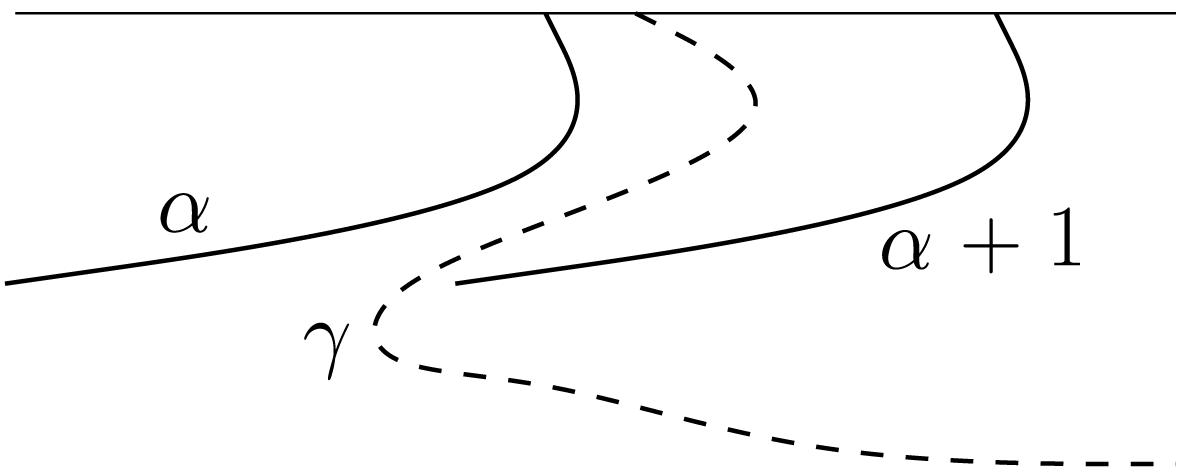
Figure 2. Figure for statement (
![]() $\star$
).
$\star$
).
The proof goes on following a mechanical routine using the sequence of hairs
![]() $\{\unicode[STIX]{x1D6FE}_{n}\}_{n}$
and the associated scalar sequences
$\{\unicode[STIX]{x1D6FE}_{n}\}_{n}$
and the associated scalar sequences
![]() $\{l_{n}\}_{n},\{r_{n}\}_{n}$
. First, choose
$\{l_{n}\}_{n},\{r_{n}\}_{n}$
. First, choose
![]() $m_{1}$
so that
$m_{1}$
so that
![]() $r_{m_{1}}>2$
and
$r_{m_{1}}>2$
and
![]() $l_{m_{1}}<1$
. Take
$l_{m_{1}}<1$
. Take
![]() $R_{1}=r_{m_{1}}-1$
and
$R_{1}=r_{m_{1}}-1$
and
![]() $L_{1}=l_{m_{1}}-1$
and note that by (
$L_{1}=l_{m_{1}}-1$
and note that by (
![]() $\star \star$
) with
$\star \star$
) with
![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FE}_{m_{1}}$
the statement (i) holds for
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FE}_{m_{1}}$
the statement (i) holds for
![]() $n=1$
. Then, take
$n=1$
. Then, take
![]() $m_{2}^{\prime }$
so that
$m_{2}^{\prime }$
so that
![]() $l_{m_{2}^{\prime }}<L_{1}-1$
and set
$l_{m_{2}^{\prime }}<L_{1}-1$
and set
![]() $R_{2}=\max (\unicode[STIX]{x1D6FE}_{m_{2}^{\prime }})_{1}+1$
. Clearly (
$R_{2}=\max (\unicode[STIX]{x1D6FE}_{m_{2}^{\prime }})_{1}+1$
. Clearly (
![]() $\star$
) forces (i) to hold for
$\star$
) forces (i) to hold for
![]() $n=2$
. Let
$n=2$
. Let
![]() $m_{2}$
such that
$m_{2}$
such that
![]() $r_{m_{2}}>R_{2}+1$
and define
$r_{m_{2}}>R_{2}+1$
and define
![]() $L_{2}=\min (\unicode[STIX]{x1D6FE}_{m_{2}})_{1}-1$
. Using again (
$L_{2}=\min (\unicode[STIX]{x1D6FE}_{m_{2}})_{1}-1$
. Using again (
![]() $\star \star$
) it follows that (i) holds for
$\star \star$
) it follows that (i) holds for
![]() $n=2$
. This procedure can be continued indefinitely and yields the sequences
$n=2$
. This procedure can be continued indefinitely and yields the sequences
![]() $\{L_{n}\}_{n}$
and
$\{L_{n}\}_{n}$
and
![]() $\{R_{n}\}_{n}$
.◻
$\{R_{n}\}_{n}$
.◻
The next two lemmas are obtained as corollaries of the previous proposition.
Lemma 7. For every
![]() $L<0$
there exists
$L<0$
there exists
![]() $R>1$
such that if
$R>1$
such that if
![]() $\unicode[STIX]{x1D6FE}$
is a hair contained in
$\unicode[STIX]{x1D6FE}$
is a hair contained in
![]() $V^{-}$
and
$V^{-}$
and
![]() $(\unicode[STIX]{x1D6FE}(1))_{1}\geqslant R$
then
$(\unicode[STIX]{x1D6FE}(1))_{1}\geqslant R$
then
![]() $L\in (\unicode[STIX]{x1D6FE})_{1}$
.
$L\in (\unicode[STIX]{x1D6FE})_{1}$
.
Proof. Fix
![]() $n$
so that
$n$
so that
![]() $L_{n-1}\leqslant L$
and define
$L_{n-1}\leqslant L$
and define
![]() $R=R_{n}$
. Then
$R=R_{n}$
. Then
![]() $\unicode[STIX]{x1D6FE}$
is a hair in
$\unicode[STIX]{x1D6FE}$
is a hair in
![]() $V^{-}$
whose endpoint is not on the left of
$V^{-}$
whose endpoint is not on the left of
![]() $R_{n}$
, that is,
$R_{n}$
, that is,
![]() $(\unicode[STIX]{x1D6FE}(1))_{1}\geqslant R=R_{n}$
. By Proposition 6,
$(\unicode[STIX]{x1D6FE}(1))_{1}\geqslant R=R_{n}$
. By Proposition 6,
![]() $L_{n-1}\in (\unicode[STIX]{x1D6FE})_{1}$
and, consequently,
$L_{n-1}\in (\unicode[STIX]{x1D6FE})_{1}$
and, consequently,
![]() $L\in (\unicode[STIX]{x1D6FE})_{1}$
.◻
$L\in (\unicode[STIX]{x1D6FE})_{1}$
.◻
Lemma 8. For every
![]() $R>1$
there exists
$R>1$
there exists
![]() $L^{\prime }<0$
such that if
$L^{\prime }<0$
such that if
![]() $\unicode[STIX]{x1D6FE}$
is a hair contained in
$\unicode[STIX]{x1D6FE}$
is a hair contained in
![]() $V^{+}$
and
$V^{+}$
and
![]() $(\unicode[STIX]{x1D6FE}(1))_{1}\leqslant L^{\prime }$
then
$(\unicode[STIX]{x1D6FE}(1))_{1}\leqslant L^{\prime }$
then
![]() $R\in (\unicode[STIX]{x1D6FE})_{1}$
.
$R\in (\unicode[STIX]{x1D6FE})_{1}$
.
In the setting of Lemma 8, there is a crosscut
![]() $c$
in
$c$
in
![]() $\tilde{U} _{+}$
which separates
$\tilde{U} _{+}$
which separates
![]() $\unicode[STIX]{x1D6FE}(1)$
from
$\unicode[STIX]{x1D6FE}(1)$
from
![]() $\unicode[STIX]{x211D}\times \{1\}$
and such that
$\unicode[STIX]{x211D}\times \{1\}$
and such that
![]() $(c)_{1}=\{R\}$
.
$(c)_{1}=\{R\}$
.
Let finish the proof of case (iii). Apply Lemma 7 to
![]() $L=-M$
(where
$L=-M$
(where
![]() $M$
comes from Lemma 5) to obtain
$M$
comes from Lemma 5) to obtain
![]() $R>1$
. Consider the family
$R>1$
. Consider the family
By definition,
![]() ${\mathcal{A}}$
is invariant by integer translations. It is not empty because
${\mathcal{A}}$
is invariant by integer translations. It is not empty because
![]() $(V)_{1}$
is not bounded from above. In addition,
$(V)_{1}$
is not bounded from above. In addition,
![]() ${\mathcal{A}}$
is
${\mathcal{A}}$
is
![]() $\tilde{f}$
-invariant. Indeed, if
$\tilde{f}$
-invariant. Indeed, if
![]() $c\in {\mathcal{A}}$
then by Lemma 5 it is automatically contained in the region
$c\in {\mathcal{A}}$
then by Lemma 5 it is automatically contained in the region
![]() $\{x\in \unicode[STIX]{x211D}\times [-1,1]:(\tilde{f}(x))_{1}>(x)_{1}\}$
. Consequently,
$\{x\in \unicode[STIX]{x211D}\times [-1,1]:(\tilde{f}(x))_{1}>(x)_{1}\}$
. Consequently,
![]() $\min (\tilde{f}(c))_{1}>\min (c)_{1}\geqslant R+k$
. Since
$\min (\tilde{f}(c))_{1}>\min (c)_{1}\geqslant R+k$
. Since
![]() $c\subset (V+k)^{-}$
, it then follows from Lemma 3 that
$c\subset (V+k)^{-}$
, it then follows from Lemma 3 that
![]() $\tilde{f}(c)$
is contained in
$\tilde{f}(c)$
is contained in
![]() $(V+k)^{-}$
. Thus,
$(V+k)^{-}$
. Thus,
![]() $\tilde{f}(c)\in {\mathcal{A}}$
.
$\tilde{f}(c)\in {\mathcal{A}}$
.
Apply now Lemma 8 to
![]() $R$
to obtain
$R$
to obtain
![]() $L^{\prime }$
. Denote
$L^{\prime }$
. Denote
![]() $x_{n}=\tilde{f}^{n}(x_{0})$
the orbit of
$x_{n}=\tilde{f}^{n}(x_{0})$
the orbit of
![]() $x_{0}$
. Since
$x_{0}$
. Since
![]() $(x_{n})_{1}\rightarrow -\infty$
as
$(x_{n})_{1}\rightarrow -\infty$
as
![]() $n$
tends to
$n$
tends to
![]() $-\infty$
, there is
$-\infty$
, there is
![]() $m>0$
such that
$m>0$
such that
![]() $(x_{-m})_{1}\leqslant L^{\prime }$
. By Lemma 3, the points
$(x_{-m})_{1}\leqslant L^{\prime }$
. By Lemma 3, the points
![]() $x_{n}$
are accessible from
$x_{n}$
are accessible from
![]() $V^{+}$
for
$V^{+}$
for
![]() $n\leqslant 0$
, so
$n\leqslant 0$
, so
![]() $x_{-m}+k$
is accessible from
$x_{-m}+k$
is accessible from
![]() $V$
for some
$V$
for some
![]() $k\leqslant 0$
. Since
$k\leqslant 0$
. Since
![]() $(x_{-m}+k)_{1}\leqslant L^{\prime }+k\leqslant L^{\prime }$
, remark after Lemma 8 provides a crosscut
$(x_{-m}+k)_{1}\leqslant L^{\prime }+k\leqslant L^{\prime }$
, remark after Lemma 8 provides a crosscut
![]() $c$
of
$c$
of
![]() $\tilde{U} _{+}$
in
$\tilde{U} _{+}$
in
![]() $V$
which separates
$V$
which separates
![]() $x_{-m}+k$
from
$x_{-m}+k$
from
![]() $\unicode[STIX]{x211D}\times \{1\}$
and
$\unicode[STIX]{x211D}\times \{1\}$
and
![]() $\min (c)_{1}=R$
. Thus,
$\min (c)_{1}=R$
. Thus,
![]() $c\in {\mathcal{A}}$
and
$c\in {\mathcal{A}}$
and
![]() $c_{-m}=c-k\in {\mathcal{A}}$
.
$c_{-m}=c-k\in {\mathcal{A}}$
.
The crosscut
![]() $c_{-m}\in {\mathcal{A}}$
separates
$c_{-m}\in {\mathcal{A}}$
separates
![]() $x_{-m}$
from
$x_{-m}$
from
![]() $\unicode[STIX]{x211D}\times \{1\}$
in
$\unicode[STIX]{x211D}\times \{1\}$
in
![]() $\tilde{U} _{+}$
. Thus,
$\tilde{U} _{+}$
. Thus,
![]() $\tilde{f}^{m}(c_{-m})\in {\mathcal{A}}$
separates
$\tilde{f}^{m}(c_{-m})\in {\mathcal{A}}$
separates
![]() $\tilde{f}^{m}(x_{-m})=x_{0}$
from
$\tilde{f}^{m}(x_{-m})=x_{0}$
from
![]() $\unicode[STIX]{x211D}\times \{1\}$
. However, the arc
$\unicode[STIX]{x211D}\times \{1\}$
. However, the arc
![]() $\unicode[STIX]{x1D6FD}$
joins
$\unicode[STIX]{x1D6FD}$
joins
![]() $x_{0}$
and
$x_{0}$
and
![]() $\unicode[STIX]{x211D}\times \{1\}$
and does not meet any element of
$\unicode[STIX]{x211D}\times \{1\}$
and does not meet any element of
![]() ${\mathcal{A}}$
because
${\mathcal{A}}$
because
![]() $(\unicode[STIX]{x1D6FD})_{1}=\{0\}$
is disjoint to
$(\unicode[STIX]{x1D6FD})_{1}=\{0\}$
is disjoint to
![]() $[R,+\infty )$
.◻
$[R,+\infty )$
.◻
Acknowledgments
The author gratefully acknowledges Prof. Shigenori Matsumoto for pointing out an error in a draft version of this work and warmly thanks Prof. Andrés Koropecki for useful conversations which brought Matsumoto’s work to attention. As an aside, special compliments go to Spanish administration for its diligence.



