Hostname: page-component-7dd5485656-jtdwj Total loading time: 0 Render date: 2025-10-30T15:24:50.381Z Has data issue: false hasContentIssue false
  • English
  • Français

Rings which are residually ℤ

Published online by Cambridge University Press:  26 February 2010

I. M. Chiswell
I. M. Chiswell
Affiliation:
School of Mathematical Sciences, Queen Mary and Westfield College, University of London, Mile End Road, London E1 4NS.
Get access

Extract

Let 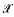be a class of structures for a first-order language and let n be a positive integer. A structure A for the language is said to be n-residually 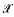if, given elements a1, … an and b1, … bn of A with ai≠bi for 1 ≤i≤n, there exist B ∈ 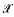and an epimorphism φ:A → B such that φ(ai≠φ(bi for 1 ≤i ≤ n. We abbreviate 1 -residually 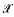to residually 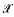, and A is said to be fully residually 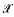if it is n-residually for all n ≤ 1. We shall only be using two cases. One is where the language is the first-order language of groups, {·−1,1}, and A and all members of 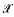are groups. In this case we may take all the bi in the definition to be equal to 1. However, we are mainly interested in the first-order language of rings, {+,−·,0,1}. Again if A and all members of 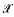are rings, we may take all bi to be zero in the definition.

Information

Type
Research Article
Information
Mathematika , Volume 46 , Issue 1 , June 1999 , pp. 175 - 183
Copyright
Copyright © University College London 1999

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

1.Chang, C. C. and Keisler, H. J.. Model Theory (North-Holland, 1973).Google Scholar
2.Chiswell, I. M.. Introduction to Λ-trees. In Semigroups, formal languages and groups (ed. Fountain, J. pp. 255–293 (Kluwer, 1995).CrossRefGoogle Scholar
3.Humphreys, J. E.. Linear algebraic groups. (Springer, 1981).Google Scholar
4.Remeslennikov, V. N.. Ǝ-free group, Siberian math. J., 30 (1989) 193–197.Google Scholar
5.Steinberg., R.. Conjugacy classes in algebraic groups, Lecture Notes in Mathematics, 366. (Springer 1974).Google Scholar
6.van den Dries, L.. Some model theory and number theory for models of weak systems of arithmetic. In Model theory of algebra and arithmetic, (ed. Pacholski, L. and others), Lecture Notes in Mathematics, 834 (Springer 1980).Google Scholar