Hostname: page-component-7dd5485656-j7khd Total loading time: 0 Render date: 2025-10-30T08:28:41.325Z Has data issue: false hasContentIssue false
  • English
  • Français

On extensions generated by roots of lifting polynomials

Part of: General field theory

Published online by Cambridge University Press:  26 February 2010

Saurabh Bhatia  and
Sudesh K. Khanduja
Saurabh Bhatia
Affiliation:
Department of Mathematics, Panjab University, Chandigarh-160014, India. E-mail:math_r@pu.ac.in
Sudesh K. Khanduja
Affiliation:
Department of Mathematics, Panjab University, Chandirgarh-160014. India. E-mail:skhand@pu.ac.in
Get access

Abstract

Let v be a Henselian valuation of any rank of a field K and 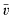its unique prolongation to a fixed algebraic closure 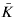of K having value group 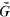. For any subfield L of 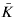, let R(L) denote the residue field of the valuation obtained by restricting 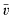to L. Using the canonical homomorphism from the valuation ring of v onto its residue field R(K), one can lift any monic irreducible polynomial with coefficients in R(K) to yield a monic irreducible polynomial with coefficients in K. In an attempt to generalize this concept, Popescu and Zaharescu introduced the notion of lifting with respect to a (K, v)-minimal pair (α, δ) belonging to 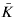× 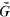. As in the case of usual lifting, a given monic irreducible polynomial Q(y) belonging to R(K(α))[y] gives rise to several monic irreducible polynomials over K which are obtained by lifting with respect to a fixed (K, v)-minimal pair (α, δ). If F, F1 are two such lifted polynomials with coefficients in K having roots θ, θ1, respectively, then it is proved in the present paper that 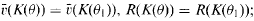in case (K, v) is a tame field, it is shown that K(θ) and K(θ1) are indeed K-isomorphic.

MSC classification

Secondary: 12E05: Polynomials (irreducibility, etc.)

Information

Type
Research Article
Information
Mathematika , Volume 49 , Issue 1-2 , June 2002 , pp. 107 - 118
Copyright
Copyright © University College London 2002

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

1.Alexandru, V., Popescu, N. and Zaharescu, A.. A theorem of characterization of residual transcendental extensions of a valuation. J. Math. Kyoto Univ., 28 (1988). 579–592.Google Scholar
2.Beauville, A., Colliot-Thélène, J. L., Sansue, J.-J. and SirSwinnerton-Dyer, Peter. Varietes stablement rationnelles non rationnelles. Annals Math., 121 (1986). 283–315.CrossRefGoogle Scholar
3.Endler, O.. Valuation Theory (Springer-Verlag, 1972).Google Scholar
4.Khanduja, S. K.. On valuations of K(x). Proc. Edinburgh Math. Soc., 35 (1992) 419–426.Google Scholar
5.Khanduja, S. K. and Saha, J.. On a generalization of Eisenstein's irreducibility criterion. Mathematika, 44 (1997), 37–41.Google Scholar
6.Khanduja, S. K. and Saha, J.. A generalized fundamental principle. Mathemalika. 46 (1999). 83–92.Google Scholar
7.Nagata, M.. A theorem on valuation rings and its applications. Nagova Math. J., 29 (1967). 85–91.Google Scholar
8.Ohm, J.. The Ruled Residue Theorem for simple transcendental extensions of valued fields. Proc Amer. Math. Soc., 89 (1983), 16–18.Google Scholar
9.Popescu, L. and Popescu, N.. Sur la definition des prolongements residucls transcendents d'une valuation sur un corps K à K(x). Bull. Math. Sci. Math. R. S. Roumanie. 33 (81). (1989). 257–264.Google Scholar
10.Popescu, N. and Zaharescu, A.. On the structure of the irreducible polynomials over local fields. J. Number Theory, 52 (1995), 98–118.Google Scholar
11.Popescu, N. and Zaharescu, A.. On the roots of a class of lifting polynomials. Scminarberichte aus clem Fachbereich Mathematik, Band 63 (1998). Teil 4, 587–600.Google Scholar
12.Ostrowski, A.. Untersuchungen zur arithmetischen Theorie der Kéerper, Teil I. II. III. Math. Zeit., 39 (1934), 269–404.Google Scholar