We solve a randomized version of the following open question: is there a strictly convex, bounded curve 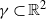$\gamma \subset { \mathbb{R} }^{2} $ such that the number of rational points on 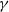$\gamma $, with denominator $n$, approaches infinity with $n$? Although this natural problem appears to be out of reach using current methods, we consider a probabilistic analogue using a spatial Poisson process that simulates the refined rational lattice 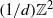$(1/ d){ \mathbb{Z} }^{2} $, which we call 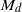${M}_{d} $, for each natural number 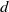$d$. The main result here is that with probability 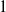$1$ there exists a strictly convex, bounded curve 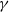$\gamma $ such that 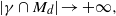$\vert \gamma \cap {M}_{d} \vert \rightarrow + \infty , $ as 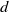$d$ tends to infinity. The methods include the notion of a generalized affine length of a convex curve as defined by F. V. Petrov [Estimates for the number of rational points on convex curves and surfaces. Zap. Nauchn. Sem. S.-Peterburg. Otdel. Mat. Inst. Steklov. (POMI) 344 (2007), 174–189; Engl. transl. J. Math. Sci. 147(6) (2007), 7218–7226].