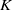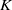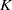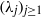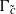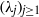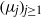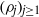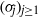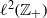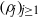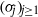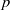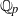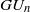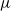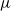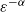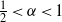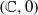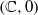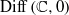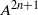Contents
Research Article
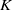 $K$ -theory of one-dimensional rings via pro-excision
$K$ -theory of one-dimensional rings via pro-excision
- Part of:
-
- Published online by Cambridge University Press:
- 23 July 2013, pp. 225-272
-
- Article
- Export citation
Inverse spectral problems for compact Hankel operators
- Part of:
-
- Published online by Cambridge University Press:
- 18 April 2013, pp. 273-301
-
- Article
- Export citation
Topological flatness of local models for ramified unitary groups. II. The even dimensional case
- Part of:
-
- Published online by Cambridge University Press:
- 10 July 2013, pp. 303-393
-
- Article
- Export citation
Global well-posedness for 3D Navier–Stokes equations with ill-prepared initial data
-
- Published online by Cambridge University Press:
- 19 July 2013, pp. 395-411
-
- Article
- Export citation
Cyclic stabilizers and infinitely many hyperbolic orbits for pseudogroups on
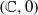 $( \mathbb{C} , 0)$
$( \mathbb{C} , 0)$
- Part of:
-
- Published online by Cambridge University Press:
- 06 August 2013, pp. 413-446
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
JMJ volume 13 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 25 February 2014, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (IBC, OBC) and matter
JMJ volume 13 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 25 February 2014, pp. b1-b4
-
- Article
-
- You have access
- Export citation