Hostname: page-component-7dd5485656-jtdwj Total loading time: 0 Render date: 2025-10-31T16:38:11.909Z Has data issue: false hasContentIssue false
  • English
  • Français

THE RENORMALIZED VOLUME AND UNIFORMIZATION OF CONFORMAL STRUCTURES

Part of: Classical differential geometry Spaces and manifolds of mappings

Published online by Cambridge University Press:  30 June 2016

Colin Guillarmou ,
Sergiu Moroianu  and
Jean-Marc Schlenker
Colin Guillarmou
Affiliation:
DMA, U.M.R. 8553 CNRS, École Normale Superieure, 45 rue d’Ulm, 75230 Paris Cedex 05, France (cguillar@dma.ens.fr)
Sergiu Moroianu
Affiliation:
Institutul de Matematică al Academiei Române, P.O. Box 1-764, RO-014700 Bucharest, Romania (moroianu@alum.mit.edu)
Jean-Marc Schlenker
Affiliation:
University of Luxembourg, Campus Kirchberg, Mathematics Research Unit, BLG, 6, rue Richard Coudenhove-Kalergi, L-1359 Luxembourg, Luxembourg (jean-marc.schlenker@uni.lu)
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the renormalized volume of asymptotically hyperbolic Einstein (AHE in short) manifolds 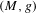$(M,g)$ when the conformal boundary 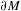$\unicode[STIX]{x2202}M$ has dimension $n$ even. Its definition depends on the choice of metric 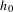$h_{0}$ on 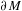$\unicode[STIX]{x2202}M$ in the conformal class at infinity determined by $g$, we denote it by 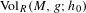$\text{Vol}_{R}(M,g;h_{0})$. We show that 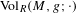$\text{Vol}_{R}(M,g;\cdot )$ is a functional admitting a ‘Polyakov type’ formula in the conformal class 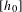$[h_{0}]$ and we describe the critical points as solutions of some non-linear equation 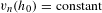$v_{n}(h_{0})=\text{constant}$, satisfied in particular by Einstein metrics. When 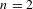$n=2$, choosing extremizers in the conformal class amounts to uniformizing the surface, while if 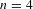$n=4$ this amounts to solving the 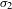$\unicode[STIX]{x1D70E}_{2}$-Yamabe problem. Next, we consider the variation of 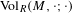$\text{Vol}_{R}(M,\cdot ;\cdot )$ along a curve of AHE metrics 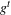$g^{t}$ with boundary metric 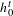$h_{0}^{t}$ and we use this to show that, provided conformal classes can be (locally) parametrized by metrics 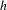$h$ solving 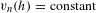$v_{n}(h)=\text{constant}$ and 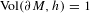$\text{Vol}(\unicode[STIX]{x2202}M,h)=1$, the set of ends of AHE manifolds (up to diffeomorphisms isotopic to the identity) can be viewed as a Lagrangian submanifold in the cotangent space to the space 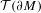${\mathcal{T}}(\unicode[STIX]{x2202}M)$ of conformal structures on 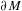$\unicode[STIX]{x2202}M$. We obtain, as a consequence, a higher-dimensional version of McMullen’s quasi-Fuchsian reciprocity. We finally show that conformal classes admitting negatively curved Einstein metrics are local minima for the renormalized volume for a warped product type filling.

Keywords

differential geometryglobal analysisanalysis on manifoldsrenormalized volumePoincaré–Einstein metricsconformal structures

MSC classification

Primary: 53A30: Conformal differential geometry 58D17: Manifolds of metrics (esp. Riemannian)

Information

Type
Research Article
Information
Journal of the Institute of Mathematics of Jussieu , Volume 17 , Issue 4 , September 2018 , pp. 853 - 912
Copyright
© Cambridge University Press 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

C. G. was partially supported by the A.N.R. project ACG ANR-10-BLAN-0105. S. M. was partially supported by the CNCS project PN-II-RU-TE-2011-3-0053; he thanks the Fondation des Sciences Mathématiques de Paris and the École Normale Supérieure for additional support. J.-M. S. was partially supported by the A.N.R. through projects ETTT, ANR-09-BLAN-0116-01, and ACG, ANR-10-BLAN-0105.

References

Ahlfors, L. and Bers, L., Riemann’s mapping theorem for variable metrics, Ann. of Math. (2) 72 (1960), 385–404.Google Scholar
Albin, P., Renormalizing curvature integrals on Poincaré–Einstein manifolds, Adv. Math. 221(1) (2009), 140–169.Google Scholar
Anderson, M. T., L 2 curvature and renormalization of AHE metrics on 4-manifolds, Math. Res. Lett. 8 (2001), 171–188.Google Scholar
Bär, C., Gauduchon, P. and Moroianu, A., Generalized cylinders in semi-Riemannian and spin geometry, Math. Z. 249(3) (2005), 545–580.Google Scholar
Bers, L., Simultaneous uniformization, Bull. Amer. Math. Soc. 66 (1960), 94–97.Google Scholar
Besse, A., Einstein Manifolds, Ergebnisse der Mathematik und ihrer Grenzgebiete (3), Volume 10 (Springer, Berlin, 1987).Google Scholar
Biquard, O., Métriques d’Einstein asymptotiquement symétriques, Astérisque 265 (2000).Google Scholar
Biquard, O., Autodual Einstein versus Kähler–Einstein, Geom. Funct. Anal. 15(3) (2005), 598–633.Google Scholar
Biquard, O., Continuation unique à partir de l’infini conforme pour les métriques d’Einstein, Math. Res. Lett. 15(6) (2008), 1091–1099.Google Scholar
Bochner, S., Vector fields and Ricci curvature, Bull. Amer. Math. Soc. 52 (1946), 776–797.Google Scholar
Caffarelli, L., Nirenberg, L. and Spruck, J., The Dirichlet problem for nonlinear second-order elliptic equations. III. Functions of the eigenvalues of the Hessian, Acta Math. 155(3–4) (1985), 261–301.Google Scholar
Chang, S.-Y. A. and Fang, H., A class of variational functionals in conformal geometry, Int. Math. Res. Not. IMRN (7) (2008), Art. ID rnn008.Google Scholar
Chang, S.-Y. A., Fang, H. and Graham, C. R., A note on renormalized volume functionals, Differential Geom. Appl. 33(Suppl) (2014), 246–258.Google Scholar
Chang, S.-Y. A., Gursky, M. J. and Yang, P. C., An equation of Monge–Ampre type in conformal geometry, and four-manifolds of positive Ricci curvature, Ann. of Math. (2) 155(3) (2002), 709–787.Google Scholar
Chang, S.-Y. A., Gursky, M. J. and Yang, P. C., An a priori estimate for a fully nonlinear equation on four-manifolds, J. Anal. Math. 87 (2002), 151–186. Dedicated to the memory of Thomas H. Wolff.Google Scholar
Chang, S.-Y. A., Qing, J. and Yang, P., On the topology of conformally compact Einstein 4-manifolds, in Noncompact Problems at the Intersection of Geometry, Analysis, and Topology, Contemporary Mathematics, Volume 350, pp. 49–61 (American Mathematical Society, Providence, RI, 2004).Google Scholar
Chang, S.-Y. A., Qing, J. and Yang, P. C., On the renormalized volumes for conformally compact Einstein manifolds, in Proceeding Conf. in Geometric Analysis, Moscow 2005.Google Scholar
Chrusciel, P., Delay, E., Lee, J. M. and Skinner, D. N., Boundary regularity of conformally compact Einstein metrics, J. Differential Geom. 69(1) (2005), 111–136.Google Scholar
de Haro, S., Skenderis, K. and Solodukhin, S. N., Holographic reconstruction of space time and renormalization in the AdS/CFT correspondence, Comm. Math. Phys. 217 (2001), 595–622.Google Scholar
Delay, E., TT-eigentensors for the Lichnerowicz Laplacian on some asymptotically hyperbolic manifolds with warped products metrics, Manuscripta Math. 123(2) (2007), 147–165.Google Scholar
Ebin, D. G., The manifold of Riemannian metrics, in Global Analysis (Proc. Sympos. Pure Math., Vol. XV, Berkeley, Calif., 1968), pp. 11–40 (American Mathematical Society, Providence, RI, 1970).Google Scholar
Djadli, Z., Guillarmou, C. and Herzlich, M., Opérateurs géométriques, invariants conformes et variétés asymptotiquement hyperboliques, Panoramas et Synthèses, Volume 26 (Société Mathématique de France, Paris, 2008).Google Scholar
Fefferman, C. and Graham, C. R., The Ambient Metric, Annals of Mathematics Studies, Volume 178 (Princeton University Press, Princeton, NJ, 2012), x+113 pp.Google Scholar
Fischer, A. E. and Moncrief, V., The structure of quantum conformal superspace, in Global Structure and Evolution in General Relativity (Karlovassi, 1994), Lecture Notes in Physics, Volume 460, pp. 111–173 (Springer, Berlin, 1996).Google Scholar
Frankel, T., On theorems of Hurwitz and Bochner, J. Math. Mech. 15 (1966), 373–377.Google Scholar
Graham, C. R., Volume and area renormalizations for conformally compact Einstein metrics, Rend. Circ. Mat. Palermo Ser. II 63(Suppl) (2000), 31–42.Google Scholar
Graham, C. R., Dirichlet-to-Neumann map for Poincaré–Einstein metrics, Announc. Oberwolfach Rep. 2(3) (2005), 2200–2203.Google Scholar
Graham, C. R., Extended obstruction tensors and renormalized volume coefficients, Adv. Math. 220(6) (2009), 1956–1985.Google Scholar
Graham, C. R. and Hirachi, K., The ambient obstruction tensor and Q-curvature, in AdS/CFT Correspondence: Einstein Metrics and their Conformal Boundaries, IRMA Lectures in Mathematics and Theoretical Physics, Volume 8, pp. 59–71 (European Mathematical Society, Zürich, 2005).Google Scholar
Graham, C. R. and Juhl, A., Holographic formula for Q-curvature, Adv. Math. 216(2) (2007), 841–853.Google Scholar
Graham, C. R. and Lee, J., Einstein metrics with prescribed conformal infinity on the ball, Adv. Math. 87 (1991), 186–225.Google Scholar
Graham, C. R. and Zworski, M., Scattering matrix in conformal geometry, Invent. Math. 152(1) (2003), 89–118.Google Scholar
Guillarmou, C., Meromorphic properties of the resolvent on asymptotically hyperbolic manifolds, Duke Math. J. 129(1) (2005), 1–37.Google Scholar
Guillarmou, C. and Moroianu, S., Chern-Simons line bundle on Teichmüller space, Geom. Topol. 18(1) (2014), 327–377.Google Scholar
Guan, P., Viaclovsky, J. and Wang, G., Some properties of the Schouten tensor and applications to conformal geometry, Trans. Amer. Math. Soc. 355 (2003), 925–933.Google Scholar
Guillopé, L. and Zworski, M., Upper bounds on the number of resonances for non-compact Riemann surfaces, J. Funct. Anal. 129(2) (1995), 363–389.Google Scholar
Gursky, M. and Viaclovsky, J., Fully nonlinear equations on Riemannian manifolds with negative curvature, Indiana Univ. Math. J. 52(2) (2003), 399–419.Google Scholar
Gursky, M. and Viaclovsky, J., Volume comparison and the k-Yamabe problem, Adv. Math. 187(2) (2004), 447–487.Google Scholar
Hamilton, R. S., The inverse function theorem of Nash and Moser, Bull. Amer. Math. Soc. 7(1) (1982), 65–222.Google Scholar
Henningson, M. and Skenderis, K., The holographic Weyl anomaly, J. High Energy Phys. (7) (1998), Paper 23, 12 pp. (electronic).Google Scholar
Juhl, A., Families of Conformally Covariant Differential Operators, Q-Curvature and Holography, Progress in Mathematics, Volume 275 (Birkhäuser, 2009).Google Scholar
Krasnov, K., Holography and Riemann surfaces, Adv. Theor. Math. Phys. 4(4) (2000), 929–979.Google Scholar
Krasnov, K. and Schlenker, J.-M., On the renormalized volume of hyperbolic 3-manifolds, Comm. Math. Phys. 279(3) (2008), 637–668.Google Scholar
Lee, J. M., Fredholm operators and Einstein metrics on conformally compact manifolds, Mem. Amer. Math. Soc. 183(864) (2006).Google Scholar
Marden, A., The geometry of finitely generated kleinian groups, Ann. of Math. (2) 99 (1974), 383–462.Google Scholar
Marden, A., Deformation of Kleinian groups, in Handbook of Teichmüller Theory, Volume I,(ed. Papadopoulos, A.), IRMA Lectures in Mathematics and Theoretical Physics, Volume 11 (European Mathematical Society, 2007). chapter 9.Google Scholar
Matsumoto, Y., A GJMS construction for 2-tensors and the second variation of the total Q-curvature, Pacific J. Math. 262(2) (2013), 437–455.Google Scholar
Mazzeo, R., Elliptic theory of differential edge operators. I, Comm. Partial Differential Equations 16(10) (1991), 1615–1664.Google Scholar
Melrose, R. B., Calculus of conormal distributions on manifolds with corners, Int. Math. Res. Not. 3 (1992), 51–61.Google Scholar
Melrose, R. B., Manifolds with Corners, Available at http://math.mit.edu/∼rbm/book.html (in preparation).Google Scholar
Mcmullen, C. T., The moduli space of Riemann surfaces is Kähler hyperbolic, Ann. of Math. (2) 151(1) (2000), 327–357.Google Scholar
Obata, M., Certain conditions for a Riemannian manifold to be isometric with a sphere, J. Math. Soc. Japan 14 (1962), 333–340.Google Scholar
Obata, M., The conjectures on conformal transformations of Riemannian manifolds, J. Differential Geometry 6 (1971/72), 247–258.Google Scholar
Osgood, B., Phillips, R. and Sarnak, P., Extremals for determinants of Laplacians, J. Funct. Anal. 80 (1988), 148–211.Google Scholar
Patterson, S. J. and Perry, P., The divisor of Selberg’s zeta function for Kleinian groups (appendix A by Charles Epstein), Duke Math. J. 106 (2001), 321–391.Google Scholar
Payne, K. R., Smooth tame Fréchet algebras and Lie groups of pseudodifferential operators, Comm. Pure Appl. Math. 44(3) (1991), 309–337.Google Scholar
Reilly, R. C., On the Hessian of a function and the curvatures of its graph, Michigan Math. J. 20 (1973), 373–383.Google Scholar
Rivin, I. and Schlenker, J.-M., The Schläfli formula in Einstein manifolds with boundary, Electron. Res. Announc. Amer. Math. Soc. 5 (1999), 18–23.Google Scholar
Schlenker, J.-M., The renormalized volume and the volume of the convex core of quasifuchsian manifolds, Math. Res. Lett. 20(4) (2013), 773–786.Google Scholar
Sheng, W., Trudinger, N. S. and Wang, X.-J., The Yamabe problem for higher order curvature, J. Differential Geom. 77 (2007), 515–553.Google Scholar
Skenderis, K. and Solodukin, S. N., Quantum effective action from the AdS/CFT correspondence, Phys. Lett. B 472 (2000), 316–322.Google Scholar
Takhtajan, L. A. and Teo, L.-P., Liouville action and Weil-Petersson metric on deformation spaces, global Kleinian reciprocity and holography, Comm. Math. Phys. 239(1–2) (2003), 183–240.Google Scholar
Taylor, M. E., Partial differential equations III, in Nonlinear Equations, 2nd ed., Applied Mathematical Sciences, Volume 117 (Springer, New York, 2011), xxii+715 pp.Google Scholar
Viaclosvky, J., Estimates and existence results for some fully nonlinear elliptic equations on Riemannian manifolds, Comm. Anal. Geom. 10(4) (2002), 815–846.Google Scholar
Wang, F., Dirichlet-to-Neumann map for Poincaré–Einstein metrics in even dimension, arXiv:0905.2457.Google Scholar
Yano, K., On Harmonic and Killing Vector Fields, Ann. of Math. (2) 55(1) (1952), 38–45.Google Scholar
Zograf, P. G., Liouville action on moduli spaces and uniformization of degenerate Riemann surfaces, Algebra i Analiz 1(4) (1989), 136–160; (in Russian), Engl. transl.: Leningrad Math. J. 1(4) (1990), 941–965.Google Scholar