No CrossRef data available.
Article contents
NONREALIZABILITY OF CERTAIN REPRESENTATIONS IN FUSION SYSTEMS
Published online by Cambridge University Press: 11 April 2023
Abstract
For a finite abelian p-group A and a subgroup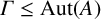 
$\Gamma \le \operatorname {\mathrm {Aut}}(A)$, we say that the pair 
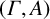$(\Gamma ,A)$ is fusion realizable if there is a saturated fusion system 
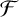${\mathcal {F}}$ over a finite p-group 
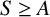$S\ge A$ such that 
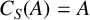$C_S(A)=A$, 
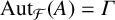$\operatorname {\mathrm {Aut}}_{{\mathcal {F}}}(A)=\Gamma $ as subgroups of 
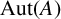$\operatorname {\mathrm {Aut}}(A)$, and 
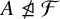. In this paper, we develop tools to show that certain representations are not fusion realizable in this sense. For example, we show, for 
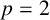$p=2$ or 
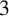$3$ and 
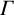$\Gamma $ one of the Mathieu groups, that the only 
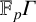${\mathbb {F}}_p\Gamma $-modules that are fusion realizable (up to extensions by trivial modules) are the Todd modules and in some cases their duals.
Information
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.
Footnotes
Communicated by Michael Giudici
B. Oliver is partially supported by UMR 7539 of the CNRS. Part of this work was carried out at the Isaac Newton Institute for Mathematical Sciences during the GRA2 programme, supported by EPSRC Grant No. EP/K032208/1.
References
Aschbacher, M., Kessar, R. and Oliver, B., Fusion Systems in Algebra and Topology (Cambridge University Press, Cambridge, 2011).CrossRefGoogle Scholar
Alperin, J., ‘Sylow 2-subgroups of 2-rank three’, in: Finite Groups’ 72: Proceedings of the Gainesville Conference on Finite Groups, North-Holland Mathematics Studies, 7 (eds. Gagen, T., Hale, M. P. Jr and Shult, E. E.) (North-Holland, Amsterdam, 1973), 3–5.CrossRefGoogle Scholar
Conway, J., Curtis, R., Norton, S., Parker, R. and Wilson, R., ATLAS of Finite Groups (Clarendon Press, New York–Evanston–London, 1985).Google Scholar
Broto, C., Levi, R. and Oliver, B., ‘The homotopy theory of fusion systems’, J. Amer. Math. Soc. 16 (2003), 779–856.CrossRefGoogle Scholar
Craven, D., Oliver, B. and Semeraro, J., ‘Reduced fusion systems over
$p$
-groups with abelian subgroup of index
$p$
: II’, Adv. Math. 322 (2017), 201–268.CrossRefGoogle Scholar
$p$
-groups with abelian subgroup of index
$p$
: II’, Adv. Math. 322 (2017), 201–268.CrossRefGoogle ScholarCraven, D., The Theory of Fusion Systems (Cambridge University Press, Cambridge, 2011).CrossRefGoogle Scholar
Goldschmidt, D., ‘2-Fusion in finite groups’, Ann. of Math. (2) 99 (1974), 70–117.CrossRefGoogle Scholar
Gorenstein, D. and Lyons, R., The Local Structure of Finite Groups of Characteristic 2 Type, Memoirs of the American Mathematical Society, 276 (American Mathematical Society, Providence, RI, 1983).CrossRefGoogle Scholar
Jansen, C., Lux, K., Parker, R. and Wilson, R., An Atlas of Brauer Characters (Oxford University Press, Oxford, 1995).Google Scholar
Kızmaz, Y., ‘A generalization of Alperin’s fusion theorem and its applications’, Preprint, 2022, arXiv:2204.11303.Google Scholar
Meierfrankenfeld, U. and Stellmacher, B., ‘The general
$\mathrm{FF}$
-module theorem’, J. Algebra 351 (2012), 1–63.CrossRefGoogle Scholar
$\mathrm{FF}$
-module theorem’, J. Algebra 351 (2012), 1–63.CrossRefGoogle ScholarOliver, B., ‘Simple fusion systems over
$p$
-groups with abelian subgroup of index
$p$
: I’, J. Algebra 398 (2014), 527–541.CrossRefGoogle Scholar
$p$
-groups with abelian subgroup of index
$p$
: I’, J. Algebra 398 (2014), 527–541.CrossRefGoogle ScholarOliver, B., ‘Fusion systems realizing certain Todd modules’, J. Group Theory, to appear, arXiv:2204.07750.Google Scholar
O’Nan, M., ‘Some evidence for the existence of a new simple group’, Proc. Lond. Math. Soc. (3) 32 (1976), 421–479.CrossRefGoogle Scholar
Pogorelov, B., ‘Primitive permutation groups of low degree I’, Algebra Logic 19 (1980), 230–254.CrossRefGoogle Scholar
Weibel, C., An Introduction to Homological Algebra (Cambridge University Press, Cambridge, 1994).CrossRefGoogle Scholar