Hostname: page-component-7dd5485656-dk7s8 Total loading time: 0 Render date: 2025-10-31T13:16:01.177Z Has data issue: false hasContentIssue false
  • English
  • Français

ASYMPTOTIC BEHAVIOUR OF THE LEAST ENERGY SOLUTIONS TO FRACTIONAL NEUMANN PROBLEMS

Part of: Elliptic equations and systems Miscellaneous topics - Partial differential equations Representations of solutions Partial differential equations

Published online by Cambridge University Press:  13 September 2024

SOMNATH GANDAL  and
JAGMOHAN TYAGI
SOMNATH GANDAL
Affiliation:
Indian Institute of Technology Gandhinagar Palaj, Gnadhinagar, Gujarat 382055, India e-mail: gandal_somnath@iitgn.ac.in
JAGMOHAN TYAGI*
Affiliation:
Indian Institute of Technology Gandhinagar Palaj, Gandhinagar, Gujarat 382055, India e-mail: jtyagi1@gmail.com
*
e-mail: jtyagi@iitgn.ac.in
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the asymptotic behaviour of the least energy solutions to the following class of nonlocal Neumann problems: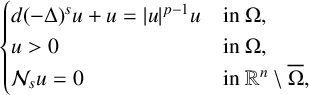

$$ \begin{align*} \begin{cases} { d(-\Delta)^{s}u+ u= \vert u\vert^{p-1}u } & \text{in } \Omega, \\ {u>0} & \text{in } \Omega, \\ { \mathcal{N}_{s}u=0 } & \text{in } \mathbb{R}^{n}\setminus \overline{\Omega}, \end{cases} \end{align*} $$

where 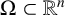$\Omega \subset \mathbb {R}^{n}$ is a bounded domain of class 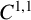$C^{1,1}$, 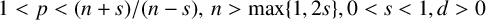$1<p<({n+s})/({n-s}),\,n>\max \{1, 2s \}, 0<s<1, d>0$ and 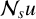$\mathcal {N}_{s}u$ is the nonlocal Neumann derivative. We show that for small 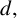$d,$ the least energy solutions 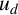$u_d$ of the above problem achieve an 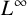$L^{\infty }$-bound independent of 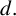$d.$ Using this together with suitable 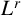$L^{r}$-estimates on 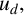$u_d,$ we show that the least energy solution 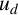$u_d$ achieves a maximum on the boundary of $\Omega $ for d sufficiently small.

Keywords

semilinear Neumann problemfractional Laplacianpositive solutionsasymptotic behaviour

MSC classification

Primary: 35J60: Nonlinear elliptic equations 35B09: Positive solutions 35B40: Asymptotic behavior of solutions
Secondary: 35J61: Semilinear elliptic equations 35R11: Fractional partial differential equations 35D30: Weak solutions

Information

Type
Research Article
Information
Journal of the Australian Mathematical Society , Volume 118 , Issue 2 , April 2025 , pp. 178 - 209
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

Communicated by Florica C. Cîrstea

References

Adimurthi, and Mancini, G., ‘The Neumann problem for elliptic equations with critical non-linearity. A tribute in honour of G, Prodi’, Ann. Sc. Norm. Super. Pisa Cl. Sci. (5) 1 (1991), 09–25.Google Scholar
Adimurthi, , Pacella, F. and Yadava, S. L., ‘Interaction between the geometry of the boundary and positive solutions of a semilinear Neumann problem with critical nonlinearity’, J. Funct. Anal. 113 (1993), 318–350.CrossRefGoogle Scholar
Arumugam, G. and Tyagi, J., ‘Keller–Segel chemotaxis models: a review’, Acta Appl. Math. 171 (2021), Paper no. 6, 82 pages.CrossRefGoogle Scholar
Barrios, B., Montoro, L., Peral, I. and Soria, F., ‘Neumann conditions for the higher order $s$ -fractional Laplacian ${\left(-\varDelta \right)}^s$ with $s>1$ ’, Nonlinear Anal. 193 (2020), Paper no. 111368, 34 pages.CrossRef1$+’,+Nonlinear+Anal.+193+(2020),+Paper+no.+111368,+34+pages.>Google Scholar
Bartumeus, F., Peters, F., Pueyo, S., Marrasé, C. and Catalan, J., ‘Helical Lévy walks: adjusting searching statistics to resource availability in microzooplankton’, Proc. Natl. Acad. Sci. USA 100 (2003), 1581–1633.CrossRefGoogle ScholarPubMed
Biagi, S., Dipierro, S., Valdinoci, E. and Vecchi, E., ‘Mixed local and nonlocal elliptic operators: regularity and maximum principles’, Comm. Partial Differential Equations 47(3) (2022), 585–629.Google Scholar
Chen, G., ‘Singularly perturbed Neumann problem for fractional Schrödinger equations’, Sci. China Math. 61(4) (2018), 695–708.CrossRefGoogle Scholar
Chen, J. and Gao, Z., ‘Ground state solutions for fractional Schrödinger equation with variable potential and Berestycki–Lions type nonlinearity’, Bound. Value Probl. 2019 (2019), Paper no. 148, 24 pages.CrossRefGoogle Scholar
Choi, W., Kim, S. and Lee, K.-A., ‘Asymptotic behavior of solutions for nonlinear elliptic problems with the fractional Laplacian’, J. Funct. Anal. 266(11) (2014), 6531–6598.CrossRefGoogle Scholar
Cinti, E. and Colasuonno, F., ‘A nonlocal supercritical Neumann problem’, J. Differential Equations 268 (2020), 2246–2279.CrossRefGoogle Scholar
Cinti, E. and Colasuonno, F., ‘Existence and non-existence results for a semilinear fractional Neumann problem’, NoDEA Nonlinear Differential Equations Appl. 30(6) (2023), Paper no. 79, 20 pages.CrossRefGoogle Scholar
Di Nezza, E., Palatucci, G. and Valdinoci, E., ‘Hitchhiker’s guide to the fractional Sobolev spaces’, Bull. Sci. Math. 136(5) (2012), 521–573.CrossRefGoogle Scholar
Dipierro, S., Palatucci, G. and Valdinoci, E., ‘Existence and symmetry results for a Schrödinger type problem involving the fractional Laplacian’, Matematiche (Catania) 68(1) (2013), 201–216.Google Scholar
Dipierro, S., Ros-Oton, X. and Valdinoci, E., ‘Nonlocal problems with Neumann boundary conditions’, Rev. Mat. Iberoam. 33(2) (2017), 377–416.CrossRefGoogle Scholar
Dipierro, S., Soave, N. and Valdinoci, E., ‘On fractional elliptic equations in Lipschitz sets and epigraphs: regularity, monotonicity and rigidity results’, Math. Ann. 369(3–4) (2017), 1283–1326.CrossRefGoogle Scholar
Dipierro, S. and Valdinoci, E., ‘Description of an ecological niche for a mixed local/nonlocal dispersal: an evolution equation and a new Neumann condition arising from the superposition of Brownian and Lévy processes’, Phys. A 575 (2021), Paper no. 126052, 20 pages.CrossRefGoogle Scholar
Du, X., Jin, T., Xiong, J. and Yang, H., ‘Blow up limits of the fractional Laplacian and their applications to the fractional Nirenberg problem’, Proc. Amer. Math. Soc. 151(11) (2023), 4693–4701.CrossRefGoogle Scholar
Escudero, C., ‘The fractional Keller–Segel model’, Nonlinearity 19 (2006), 2909–2918.Google Scholar
Fall, M. M., ‘Regularity results for nonlocal equations and applications’, Calc. Var. Partial Differential Equations 59 (2020), 181.Google Scholar
Felmer, P. and Quaas, A., ‘Positive solutions of the nonlinear Schrödinger equation with the fractional Laplacian’, Proc. Roy. Soc. Edinburgh Sect. A 142(6) (2012), 1237–1262.Google Scholar
Felmer, P. and Wang, Y., ‘Radial symmetry of positive solutions to equations involving the fractional Laplacian’, Commun. Contemp. Math. 16(1) (2014), Paper no. 1350023, 24 pages.CrossRefGoogle Scholar
Gandal, S. and Tyagi, J., ‘The Neumann problem for a class of semilinear fractional equations with critical exponent’, Bull. Sci. Math. 188 (2023), Paper no. 103322, 35 pages.CrossRefGoogle Scholar
He, X., Rădulescu, V. D. and Zou, W., ‘Normalized ground states for the critical fractional Choquard equation with a local perturbation’, J. Geom. Anal. 32(10) (2022), Paper no. 252, 51 pages.CrossRefGoogle Scholar
Horstmann, D., ‘From 1970 until present: the Keller–Segel model in chemotaxis and its consequences I’, Jahresber. Dtsch. Math.-Ver. 105 (2003), 103–165.Google Scholar
Horstmann, D., ‘From 1970 until present: the Keller–Segel model in chemotaxis and its consequences II’, Jahresber. Dtsch. Math.-Ver. 106 (2004), 51–69.Google Scholar
Huang, H. and Liu, J., ‘Well-posedness for the Keller–Segel equation with fractional Laplacian and the theory of propagation of chaos’, Kinet. Relat. Models 9 (2016), 715–748.Google Scholar
Kabeya, Y. and Ni, W.-M., ‘Stationary Keller–Segel model with the linear sensitivity’, RIMS K $\check{o}$ ky $\check{u}$ roku Bessatsu 1025 (1998), 44–65.Google Scholar
Keller, E. F. and Segel, L. A., ‘Initiation of slime mold aggregation viewed as an instability’, J. Theoret. Biol. 26 (1970), 399–415.CrossRefGoogle Scholar
Levandowsky, M., White, B. S. and Schuste, F. L., ‘Random movements of soil amebas’, Acta Protozool 36 (1997), 237–248.Google Scholar
Lin, C. S. and Ni, W.-M., ‘On the diffusion coefficient of a semilinear Neumann problem’, in: Calculus of Variations and Partial Differential Equations, Lecture Notes in Mathematics, 1340 (eds. Hildebrandt, S., Kinderlehrer, D. and Miranda, M.) (Springer, New York–Berlin, 1986).Google Scholar
Lin, C. S., Ni, W.-M. and Takagi, I., ‘Large amplitude stationary solutions to a chemotaxis system’, J. Differential Equations 72 (1988), 1–27.Google Scholar
Molica Bisci, G., Rădulescu, V. D. and Servadei, R., Variational Methods for Nonlocal Fractional Problems, Encyclopedia of Mathematics and its Applications, 162 (Cambridge University Press, Cambridge, 2016).Google Scholar
Mugnai, D., Perera, K. and Proietti Lippi, E., ‘A priori estimates for the fractional $p$ -Laplacian with nonlocal Neumann boundary conditions and applications’, Commun. Pure Appl. Anal. 21(1) (2022), 275–292.Google Scholar
Ni, W.-M. and Takagi, I., ‘On the existence and shape of solutions to a semilinear Neumann problem’, in: Proceedings of the Conference on Nonlinear Diffusion Equations and their Equilibrium States, 3, Gregynog (eds. Lloyd, N. G., Ni, W. M., Peletier, L. A. and Serrin, J.) (Birkhäuser, Boston, MA, 1989), 425–436.Google Scholar
Ni, W.-M. and Takagi, I., ‘On the shape of least energy solutions to a semilinear Neumann problem’, Comm. Pure Appl. Math. 44 (1991), 819–851.CrossRefGoogle Scholar
Ros-Oton, X. and Serra, J., ‘The Dirichlet problem for the fractional Laplacian: regularity up to the boundary’, J. Math. Pures Appl. (9) 101 (2012), 275–302.CrossRefGoogle Scholar
Secchi, S., ‘On fractional Schrödinger equations in ${\mathbb{R}}^n$ without the Ambrosetti–Rabinowitz condition’, Topol. Methods Nonlinear Anal. 47(1) (2016), 19–41.Google Scholar
Servadei, R. and Valdinoci, E., ‘Mountain pass solutions for non-local elliptic operators’, J. Math. Anal. Appl. 389(2) (2012), 887–898.CrossRefGoogle Scholar
Servadei, R. and Valdinoci, E., ‘The Brezis–Nirenberg result for the fractional Laplacian’, Trans. Amer. Math. Soc. 367(1) (2015), 67–102.CrossRefGoogle Scholar