Hostname: page-component-7dd5485656-bt4hw Total loading time: 0 Render date: 2025-10-29T11:14:42.582Z Has data issue: false hasContentIssue false
  • English
  • Français

A LOPEZ-ESCOBAR THEOREM FOR CONTINUOUS DOMAINS

Part of: Computability and recursion theory Model theory

Published online by Cambridge University Press:  15 March 2024

NIKOLAY BAZHENOV Open the ORCID record for NIKOLAY BAZHENOV [Opens in a new window] ,
EKATERINA FOKINA Open the ORCID record for EKATERINA FOKINA [Opens in a new window] ,
DINO ROSSEGGER Open the ORCID record for DINO ROSSEGGER [Opens in a new window] ,
ALEXANDRA SOSKOVA Open the ORCID record for ALEXANDRA SOSKOVA [Opens in a new window]  and
STEFAN VATEV Open the ORCID record for STEFAN VATEV [Opens in a new window]
NIKOLAY BAZHENOV
Affiliation:
SOBOLEV INSTITUTE OF MATHEMATICS NOVOSIBIRSK AND NOVOSIBIRSK STATE UNIVERSITY NOVOSIBIRSK, RUSSIA E-mail: bazhenov@math.nsc.ru
EKATERINA FOKINA
Affiliation:
INSTITUTE OF DISCRETE MATHEMATICS AND GEOMETRY TECHNISCHE UNIVERSITÄT WIEN VIENNA, AUSTRIA E-mail: ekaterina.fokina@tuwien.ac.at
DINO ROSSEGGER
Affiliation:
INSTITUTE OF DISCRETE MATHEMATICS AND GEOMETRY TECHNISCHE UNIVERSITÄT WIEN VIENNA, AUSTRIA E-mail: dino.rossegger@tuwien.ac.at
ALEXANDRA SOSKOVA
Affiliation:
FACULTY OF MATHEMATICS AND INFORMATICS SOFIA UNIVERSITY SOFIA, BULGARIA E-mail: asoskova@fmi.uni-sofia.bg
STEFAN VATEV*
Affiliation:
FACULTY OF MATHEMATICS AND INFORMATICS SOFIA UNIVERSITY SOFIA, BULGARIA
*
E-mail: stefanv@fmi.uni-sofia.bg
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove an effective version of the Lopez-Escobar theorem for continuous domains. Let 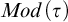$Mod(\tau )$ be the set of countable structures with universe 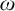$\omega $ in vocabulary 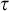$\tau $ topologized by the Scott topology. We show that an invariant set 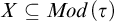$X\subseteq Mod(\tau )$ is 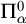$\Pi ^0_\alpha $ in the Borel hierarchy of this topology if and only if it is definable by a 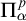$\Pi ^p_\alpha $-formula, a positive 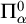$\Pi ^0_\alpha $ formula in the infinitary logic 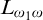$L_{\omega _1\omega }$. As a corollary of this result we obtain a new pullback theorem for positive computable embeddings: Let 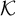$\mathcal {K}$ be positively computably embeddable in 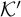$\mathcal {K}'$ by 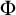$\Phi $, then for every 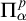$\Pi ^p_\alpha $ formula 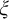$\xi $ in the vocabulary of 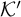$\mathcal {K}'$ there is a 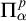$\Pi ^p_\alpha $ formula 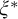$\xi ^{*}$ in the vocabulary of 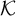$\mathcal {K}$ such that for all 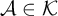$\mathcal {A}\in \mathcal {K}$, 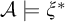$\mathcal {A}\models \xi ^{*}$ if and only if 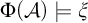$\Phi (\mathcal {A})\models \xi $. We use this to obtain new results on the possibility of positive computable embeddings into the class of linear orderings.

Keywords

enumeration operatorsBorel hierarchycomputable infinitary formulas

MSC classification

Primary: 03C57: Effective and recursion-theoretic model theory 03D45: Theory of numerations, effectively presented structures 03C70: Logic on admissible sets

Information

Type
Article
Information
The Journal of Symbolic Logic , Volume 90 , Issue 2 , June 2025 , pp. 854 - 871
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Ash, C. and Knight, J., Computable Structures and the Hyperarithmetical Hierarchy , Studies in Logic and the Foundations of Mathematics, vol. 144, Elsevier, Amsterdam, 2000.Google Scholar
Ash, C., Knight, J., Manasse, M., and Slaman, T., Generic copies of countable structures . Annals of Pure and Applied Logic , vol. 42 (1989), no. 3, pp. 195–205.CrossRefGoogle Scholar
Bazhenov, N. A., Ganchev, H., and Vatev, S., Computable embeddings for pairs of linear orders . Algebra and Logic , vol. 60 (2021), no. 3, pp. 163–187.CrossRefGoogle Scholar
Vanden Boom, M., The effective Borel hierarchy . Fundamenta Mathematicae , vol. 3 (2007), no. 195, pp. 269–289CrossRefGoogle Scholar
Boone, W. W., The word problem . Annals of Mathematics (2) , vol. 70 (1959), pp. 207–265.CrossRefGoogle Scholar
de Brecht, M., Quasi-polish spaces . Annals of Pure and Applied Logic , vol. 164 (2013), no. 3, pp. 356–381.***CrossRefGoogle Scholar
Calvert, W., Cummins, D., Knight, J. F., and Miller, S., Comparing classes of finite structures . Algebra and Logic , vol. 43 (2004), no. 6, pp. 374–392.CrossRefGoogle Scholar
Cenzer, D., Harizanov, V., and Remmel, J. B., $\varSigma 01$ and $\varPi 01$ equivalence structures . Annals of Pure and Applied Logic , vol. 162 (2011), no. 7, pp. 490–503.CrossRefGoogle Scholar
Cenzer, D., Harizanov, V., and Remmel, J. B., Computability-theoretic properties of injection structures . Algebra and Logic , vol. 53 (2014), no. 1, pp. 39–69.CrossRefGoogle Scholar
Chisholm, J., Effective model theory vs. recursive model theory, Journal of Symbolic Logic, vol. 55 (1990), no. 3, pp. 1168–1191.Google Scholar
Chisholm, J., Knight, J. F., and Miller, S., Computable embeddings and strongly minimal theories, Journal of Symbolic Logic, vol. 72 (2007), no. 3, pp. 1031–1040.Google Scholar
Csima, B. F., MacLean, L., and Rossegger, D., Relations enumerable from positive information, preprint, 2022, arXiv:2206.01135.Google Scholar
Csima, B. F., Rossegger, D., and Yu, D., Positive enumerable functors , Conference on Computability in Europe , Lecture Notes in Computer Science (LNCS, vol. 12813), Springer, Cham, 2021, pp. 385–394.Google Scholar
Dimitrov, R. D. and Harizanov, V., The lattice of computably enumerable vector spaces , Computability and Complexity , Lecture Notes in Computer Science, vol. 10010, Springer, Cham, 2017, pp. 366–393.CrossRefGoogle Scholar
Friedberg, R. M. and Rogers, H. Jr., Reducibility and completeness for sets of integers . Mathematical Logic Quarterly , vol. 5 (1959), pp. 117–125.CrossRefGoogle Scholar
Ganchev, H., Kalimullin, I. S., and Vatev, S., Computable embedding of classes of algebraic structures with congruence relation . Uchenye Zapiski Kazanskogo Universiteta-Seriya Fiziko-Matematicheskie Nauki , vol. 160 (2018), no. 4, pp. 731–737.Google Scholar
Gavruskin, A., Jain, S., Khoussainov, B., and Stephan, F., Graphs realised by r.e. equivalence relations . Annals of Pure and Applied Logic , vol. 165 (2014), nos. 7–8, pp. 1263–1290.CrossRefGoogle Scholar
Godziszewski, M. T. and Hamkins, J. D., Computable quotient presentations of models of arithmetic and set theory , Logic, Language, Information, and Computation—24th International Workshop, WoLLIC 2017, London, UK, July 18–21, 2017, Proceedings (Kennedy, J. and de Queiroz, R. J. G. B., editors), Lecture Notes in Computer Science, vol. 10388, Springer, Berlin–Heidelberg, 2017, pp. 140–152.Google Scholar
Kalimullin, I., Algorithmic reducibilities of algebraic structures . Journal of Logic & Computation , vol. 22 (2012), no. 4, pp. 831–843.CrossRefGoogle Scholar
Kalimullin, I. S., Computable embeddings of classes of structures under enumeration and Turing operators . Lobachevskii Journal of Mathematics , vol. 39 (2018), no. 1, pp. 84–88.CrossRefGoogle Scholar
Khoussainov, B., A journey to computably enumerable structures (tutorial lectures) , Sailing Routes in the World of Computation , Lecture Notes in Computer Science, vol. 10936, Springer, Cham, 2018, pp. 1–19.CrossRefGoogle Scholar
Knight, J. F., Degrees coded in jumps of orderings, Journal of Symbolic Logic, vol. 51 (1986), no. 4, pp. 1034–1042.Google Scholar
Knight, J. F., Miller, S., and Vanden Boom, M., Turing computable embeddings, Journal of Symbolic Logic, vol. 72 (2007), no. 3, pp. 901–918.Google Scholar
Lopez-Escobar, E. G. K., An interpolation theorem for denumerably long formulas . Fundamenta Mathematicae , vol. 57 (1965), pp. 253–272.CrossRefGoogle Scholar
Mal’cev, A. I., Constructive algebras. I . Uspekhi Matematicheskikh Nauk , vol. 16 (1961), no. 3(99), pp. 3–60.Google Scholar
Markov, A., On the impossibility of certain algorithms in the theory of associative systems . Comptes rendus (Doklady) de l’Académie des Sciences de léURSS (N. S.) , vol. 55 (1947), pp. 583–586.Google Scholar
Montalbán, A., Computable structure theory: Beyond the arithmetic, draft, 2022.CrossRefGoogle Scholar
Novikov, P. S.. Ob algoritmičeskoj nerazrešimosti problemy toždestva slov v teorii grupp , Trudy Mat. Inst. Steklov., vol. 44, Izdat. Akad. Nauk SSSR, Moscow, 1955, p. 143.Google Scholar
Richter, L. J., Degrees of structures, Journal of Symbolic Logic, vol. 46 (1981), pp. 723–731.Google Scholar
Scott, D., Logic with denumerably long formulas and finite strings of quantifiers , The Theory of Models , Elsevier, North-Holland, Amsterdam, 1963, pp. 329–341.Google Scholar
Selivanov, V., Positive structures , Computability and Models , University Series in Mathematics, Kluwer/Plenum, New York, 2003, pp. 321–350.CrossRefGoogle Scholar
Selivanov, V. L., Hierarchies in $\varphi$ -spaces and applications . Mathematical Logic Quarterly , vol. 51 (2005), no. 1, pp. 45–61.CrossRefGoogle Scholar
Selivanov, V. L., Towards a descriptive set theory for domain-like structures . Theoretical Computer Science , vol. 365 (2006), no. 3, pp. 258–282.CrossRefGoogle Scholar
Soskov, I. N., Degree spectra and co-spectra of structures . Annuaire de L’Universite de Sofia , vol. 96 (2004), pp. 45–68.Google Scholar
Soskov, I. N. and Baleva, V., Ash’s theorem for abstract structures , Logic Colloquium ‘02 (Chatzidakis, Z., Koepke, P., and Pohlers, W., editors), Lecture Notes in Logic, vol. 27, Cambridge University Press, Cambridge, 2006, pp. 327–341.Google Scholar
Soskova, A. and Soskova, M., Enumeration reducibility and computable structure theory , Computability and Complexity , Springer, Cham, 2017, pp. 271–301.CrossRefGoogle Scholar
Vaught, R., Invariant sets in topology and logic . Fundamenta Mathematicae , vol. 82 (1974), pp. 269–294.CrossRefGoogle Scholar