In this article we introduce and study hyperclass-forcing (where the conditions of the forcing notion are themselves classes) in the context of an extension of Morse-Kelley class theory, called MK**. We define this forcing by using a symmetry between MK** models and models of ZFC− plus there exists a strongly inaccessible cardinal (called SetMK**). We develop a coding between β-models 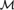${\cal M}$ of MK** and transitive models M + of SetMK** which will allow us to go from 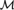${\cal M}$ to M + and vice versa. So instead of forcing with a hyperclass in MK** we can force over the corresponding SetMK** model with a class of conditions. For class-forcing to work in the context of ZFC− we show that the SetMK** model M + can be forced to look like L K* [X], where κ* is the height of M + , κ strongly inaccessible in M + and 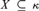$X \subseteq \kappa$ . Over such a model we can apply definable class forcing and we arrive at an extension of M + from which we can go back to the corresponding β-model of MK**, which will in turn be an extension of the original 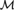${\cal M}$ . Our main result combines hyperclass forcing with coding methods of [3] and [4] to show that every β-model of MK** can be extended to a minimal such model of MK** with the same ordinals. A simpler version of the proof also provides a new and analogous minimality result for models of second-order arithmetic.