No CrossRef data available.
Article contents
STRUCTURE OF SUMMABLE TALL IDEALS UNDER KATĚTOV ORDER
Part of:
Set theory
Published online by Cambridge University Press: 20 April 2023
Abstract
We show that Katětov and Rudin–Blass orders on summable tall ideals coincide. We prove that Katětov order on summable tall ideals is Galois–Tukey equivalent to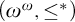 
$(\omega ^\omega ,\le ^*)$. It follows that Katětov order on summable tall ideals is upwards directed which answers a question of Minami and Sakai. In addition, we prove that 
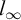${l_\infty }$ is Borel bireducible to an equivalence relation induced by Katětov order on summable tall ideals.
MSC classification
Information
- Type
- Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of The Association for Symbolic Logic
References
Blass, A., Combinatorial cardinal characteristics of the continumm, Handbook of Set Theory (Foreman, M. and Kanamori, A., editors), Springer, Berlin, 2010, pp. 395–489.CrossRefGoogle Scholar
Farah, I., Analytic ideals and their quotients, Ph.D. thesis, University of Toronto, 1997.Google Scholar
Hrušák, M., Combinatorics of filters and ideals, Set Theory and Its Applications (L. Babinkostova, A. E. Caicedo, S. Geschke, and M. Scheepers, editors), Contemporary Mathematics, vol. 533, American Mathematical Society, Providence, RI, 2011, pp. 29–69.CrossRefGoogle Scholar
Mazur, K.,
${F}_{\sigma }$
-ideals and
${\omega}_1{\omega}_1^{\ast }$
-gaps in the Boolean algebras
$\mathbf{\mathcal{P}}\left(\omega \right) / \mathbf{\mathcal{I}}$
$.$
Fundamenta Mathematicae, vol. 138 (1991), no. 2, pp. 103–111.CrossRefGoogle Scholar
${F}_{\sigma }$
-ideals and
${\omega}_1{\omega}_1^{\ast }$
-gaps in the Boolean algebras
$\mathbf{\mathcal{P}}\left(\omega \right) / \mathbf{\mathcal{I}}$
$.$
Fundamenta Mathematicae, vol. 138 (1991), no. 2, pp. 103–111.CrossRefGoogle ScholarMinami, H. and Sakai, H., Katětov and Katětov-Blass orders on
${F}_{\sigma }$
-ideals. Archive for Mathematical Logic, vol. 55 (2016), pp. 883–898.CrossRefGoogle Scholar
${F}_{\sigma }$
-ideals. Archive for Mathematical Logic, vol. 55 (2016), pp. 883–898.CrossRefGoogle ScholarRosendal, C., Cofinal families of Borel equivalence relations and quasiorders, this Journal, vol. 70 (2005), no. 4, pp. 1325–1340.Google Scholar
Vojtáš, P., Generalized Galois-Tukey connections between explicit relations on classical objects of real analysis, Set Theory of the Reals (Judah, H., editor), Israel Mathematical Conference Proceedings, vol. 6, American Mathematical Society, Providence, RI, 1993, pp. 619–643.Google Scholar