Hostname: page-component-7dd5485656-k8lnt Total loading time: 0 Render date: 2025-10-29T22:34:29.302Z Has data issue: false hasContentIssue false
  • English
  • Français

Flat sets

Published online by Cambridge University Press:  12 March 2014

Arthur D. Grainger
Arthur D. Grainger*
Affiliation:
Department of Mathematics, Morgan State University, Baltimore, Maryland 21239
Get access Rights & Permissions [Opens in a new window]

Abstract

Let X be a set, and let 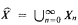be the superstructure of X, where X0 = X and 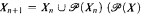is the power set of X) for n ∈ ω. The set X is called a flat set if and only if 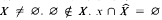for each x ∈ X, and x ∩ ŷ = ø for x, y ∈ X such that x ≠ y. where 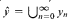is the superstructure of y. In this article, it is shown that there exists a bijection of any nonempty set onto a flat set. Also, if 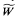is an ultrapower of 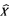(generated by any infinite set I and any nonprincipal ultrafilter on I), it is shown that 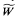is a nonstandard model of X: i.e., the Transfer Principle holds for 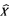and 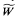, if X is a flat set. Indeed, it is obvious that 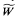is not a nonstandard model of X when X is an infinite ordinal number. The construction of flat sets only requires the ZF axioms of set theory. Therefore, the assumption that X is a set of individuals (i.e., x ≠ ϕ and a ∈ x does not hold for x ∈ X and for any element a) is not needed for 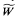to be a nonstandard model of X.

Information

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 59 , Issue 3 , September 1994 , pp. 1012 - 1021
Copyright
Copyright © Association for Symbolic Logic 1994

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

REFERENCES

[1]Davis, M., Applied nonstandard analysis, John Wiley & Sons, New York, 1977.Google Scholar
[2]Hrbacek, K. and Jech, T., Introduction to set theory, Marcel Dekker, New York, 1984.Google Scholar
[3]Hurd, A. E. and Loeb, P. A., An introduction to nonstandard real analysis, Academic Press, New York, 1985.Google Scholar
[4]Jech, T., Set theory, Academic Press, New York. 1978.Google Scholar
[5]Lindstrom, T., An invitation to nonstandard analysis, Nonstandard analysis and its applications (Cutland, N., editor), Cambridge University Press, New York, 1988.Google Scholar
[6]Luxemburg, W. A. J., A general theory of monads, Applications of model theory to algebra, analysis, and probability (Luxemburg, W. A. J., editor), Holt, Rinehart. and Winston, New York, 1969, pp. 109–122.Google Scholar
[7]Robinson, A., Nonstandard analysis, North-Holland, Amsterdam, 1966.Google Scholar
[8]Robinson, A. and Zakon, E., A set-theoretical characterization of enlargements, Applications of model theory to algebra, analysis, and probability (Luxemburg, W. A. J., editor), Holt, Rinehart and Winston, New York, 1969. pp. 109–122.Google Scholar
[9]Roitman, J., Introduction to modern set theory, John Wiley & Sons, New York, 1990.Google Scholar
[10]Stroyan, K. D. and Luxemburg, W. A. J., Introduction to the theory of infinitesimals, Academic Press, New York, 1976.Google Scholar