1. Background
The Greenland and Antarctic ice sheets have distinct regions of fast ice flow, called ice streams, separated by slow-flowing ice ridges. Ice streams were also present in paleo ice sheets during the last glacial period (Hubbard and others, Reference Hubbard2009; Stokes and others, Reference Stokes, Corner, Winsborrow, Husum and Andreassen2014; Clark and Spagnolo, Reference Clark and Spagnolo2016; Greenwood and others, Reference Greenwood, Clason, Nyberg, Jakobsson and Holmlund2017). Ice streams are the primary ice drainage networks for ice sheets and are currently responsible for the majority of discharge from the West Antarctic Ice Sheet (Oppenheimer, Reference Oppenheimer1998; Bamber and others, Reference Bamber, Vaughan and Joughin2000; Smith and others, Reference Smith2020). Many drainage catchments, like the Siple Coast of West Antarctica, are organized into a parallel array of ice streams that display complex spatial patterns that are not primarily controlled by bed topography (Shabtaie and Bentley, Reference Shabtaie and Bentley1987, Reference Shabtaie and Bentley1988; Retzlaff and others, Reference Retzlaff, Lord and Bentley1993). Instead, the flow of these ice streams may be governed primarily by thermal conditions along the bed and within shear margins. Radar observations typically indicate wet beds for active ice streams and frozen beds beneath ice ridges and inactive ice streams (with the exception of Kamb Ice Stream) (Bentley and others, Reference Bentley, Lord and Liu1998). In addition, the morphological indicators of Siple Coast ice flow from observed morphology indicate an unsteady evolution of the ice stream system, suggesting thermal and hydrologic controls (Catania and others, Reference Catania, Hulbe, Conway, Scambos and Raymond2012).
Understanding the thermomechanics of fast ice stream flow is key to projecting the centennial-scale response of ice sheets to climate forcing. Ice streams experience geometric changes, through thinning or thickening, lateral boundary migration, flow reorganization, or other complex spatial changes (Bindschadler and Vornberger, Reference Bindschadler and Vornberger1998; Fahnestock and others, Reference Fahnestock, Joughin, Scambos, Kwok, Krabill and Gogineni2001). They also experience kinematic changes, such as stagnation or reactivation. Stagnation is evidenced by relict fast-flow morphologies in currently slow-moving ice streams, like Kamb Ice Stream in West Antarctica (Rose, Reference Rose1979; Catania and others, Reference Catania, Scambos, Conway and Raymond2006), and more recent observations of slowdown in fast-flowing ice streams, like Whillans Ice Stream (Joughin and Tulaczyk, Reference Joughin and Tulaczyk2002; Beem and others, Reference Beem, Tulaczyk, King, Bougamont, Fricker and Christoffersen2014). The opposite may also occur: slow, stagnant ice streams can accelerate (Engelhardt and Kamb, Reference Engelhardt and Kamb1997; Bougamont and others, Reference Bougamont, Christoffersen, Price, Fricker, Tulaczyk and Carter2015). New ice streams could possibly form in seemingly inactive catchments, like those in the colder regions of East Antarctica (Dawson and others, Reference Dawson, Schroeder, Chu, Mantelli and Seroussi2022, Reference Dawson, Schroeder, Chu, Mantelli and Seroussi2024).
An improved understanding of these processes can also help in reconstructing past ice sheet changes. Heinrich events were periods of intense discharge from the ice streams of the Laurentide ice sheet (and possibly others), which occurred approximately every 6-8 thousand years during glacial periods, as evidenced by Ice Rafted Debris (IRD) within marine sediments (Heinrich, Reference Heinrich1988; Bond and others, Reference Bond1993; Hemming, Reference Hemming2004). These events potentially offer paleohistorical precedent for changes observed in contemporary ice sheets. There is a longstanding debate over the relative influence of internal ice sheet dynamical processes (MacAyeal, Reference MacAyeal1993a; Alley and MacAyeal, Reference Alley and MacAyeal1994; Tulaczyk and others, Reference Tulaczyk, Kamb and Engelhardt2000b; Sayag and Tziperman, Reference Sayag and Tziperman2009, Reference Sayag and Tziperman2011; Bougamont and others, Reference Bougamont, Price, Christoffersen and Payne2011; Robel and others, Reference Robel, Degiuli, Schoof and Tziperman2013, Reference Robel, Schoof and Tziperman2014) versus oceanic and other external climate forcings (Ganopolski and Rahmstorf, Reference Ganopolski and Rahmstorf2001; Hulbe and others, Reference Hulbe, MacAyeal, Denton, Kleman and Lowell2004; Shaffer and others, Reference Shaffer, Olsen and Bjerrum2004; Marcott and others, Reference Marcott2011; Alvarez-Solas and others, Reference Alvarez-Solas, Robinson, Montoya and Ritz2013; Bassis and others, Reference Bassis, Petersen and Cathles2017; Mann and others, Reference Mann, Robel and Meyer2021; Edwards and others, Reference Edwards, Blackburn, Piccione, Tulaczyk, Miller and Sikes2022) in driving Heinrich events. A comprehensive theory of ice sheet change could leverage the data preserved in the geological record to enhance our understanding of modern changes in the Antarctic and Greenland ice sheets. However, the details of thermally controlled ice flow remain active areas of research.
Feedback mediated by basal sliding is a possible mechanism for ice stream formation and evolution. Hydraulic feedback can occur when basal temperatures are at the pressure melting point: faster sliding leads to frictional heat dissipation, meltwater generation, and thus even faster sliding (Fowler and Schiavi, Reference Fowler and Schiavi1998; Sayag and Tziperman, Reference Sayag and Tziperman2008; Bougamont and others, Reference Bougamont, Price, Christoffersen and Payne2011; Kyrke-Smith and others, Reference Kyrke-Smith, Katz and Fowler2014). Thermo-frictional feedbacks also occur, in the absence of a developed drainage network, at temperatures below the bulk melting point if subtemperate sliding is taken into account: small amounts of slip mediated by regelation and premelting dissipate heat along the bed, which in turn raises basal temperature, thus leading to even faster sliding. These instabilities could complicate the assumptions embedded in large-scale, process-based ice sheet models that are used to make ice loss and sea level rise projections (Seroussi and others, Reference Seroussi2020, Reference Seroussi2023). Approaches that invert for basal friction from surface observations can reproduce the present-day flow field, including modern ice stream features (MacAyeal, Reference MacAyeal1993b; Ranganathan and others, Reference Ranganathan, Minchew, Meyer and Gudmundsson2021), by means of a spatially variable friction coefficient. However, if frictional parameterizations are held static over long model runs, they may overconstrain the model toward present-day behavior, without enabling unsteady processes that could reorganize the flow field. Coupling ice sheet models to subglacial hydrology models is a promising approach (Bougamont and others, Reference Bougamont, Christoffersen, Hubbard, Fitzpatrick, Doyle and Carter2014; Kyrke-Smith and others, Reference Kyrke-Smith, Katz and Fowler2014; Bueler and van Pelt, Reference Bueler and van Pelt2015; Sommers and others, Reference Sommers2024). However, increases in model complexity come with a trade-off in terms of additional degrees of freedom and computational expense, increasing the potential for overparameterization.
Ultimately, ice sheet models will require both a more expansive observational record and a more complete physical representation of subglacial processes to generate credible long-term climate predictions (Aschwanden and others, Reference Aschwanden, Bartholomaus, Brinkerhoff and Truffer2021). In this study, we aim to understand how the inclusion of subtemperate sliding may qualitatively change ice stream dynamics and surge cycling. We examine the temporal dynamics of thermo-frictional feedbacks at the bed, with a simple, spatially lumped, coupled ice sheet-hydrology model. Our results indicate that the inclusion of subtemperate sliding alters ice sheet dynamics over the time scales of Heinrich events, most evident in large reductions in event period, even with very modest amounts of subtemperate sliding. Furthermore, results suggest that subtemperate sliding should be an important process on timescales characterizing centennial-scale variability of West Antarctic ice streams.
2. Mathematical formulation of subtemperate sliding
Ice sheet models apply sliding laws to capture the dynamics of ice-bed interfaces or match observations through empirical functions with tunable parameters. Sliding laws relate the subglacial slip velocity, ub, to the resistive shear stress at the ice-bed interface, τb, and the effective pressure, N. Approaches that seek to capture thermal effects incorporate the bed temperature, Tb, to specify some relationship for friction at the bed arising from the bed’s thermal state, 
$u_b= f(\tau_b, N, T_b)$. This often takes the form of a ‘hard-switch’ (e.g.
Hutter and Olunloyo, Reference Hutter and Olunloyo1981; Barcilon and MacAyeal, Reference Barcilon and MacAyeal1993; Payne and Baldwin, Reference Payne and Baldwin2000; Payne and others, Reference Payne2000; Moore and others, Reference Moore, Iverson and Cohen2009),
\begin{equation}
u_b = \begin{cases}
f(\tau_b, N), \ \ &\text{if}\ \ T_b=T_m\\
0, \ \ \ \ \ \ \ &\text{if} \ \ T_b \lt T_m
\end{cases},
\end{equation} where sliding can only occur when the temperature of the bed is at the pressure-melting point of ice, 
$T_b=T_m$ (i.e. temperate). When the temperature of the bed is below the pressure-melting point, 
$T_b \lt T_m$ (i.e. subtemperate), a no-slip boundary condition is applied (Robel and others, Reference Robel, Degiuli, Schoof and Tziperman2013). As an alternative to the no-slip condition, some models apply a hard switch from slow to fast sliding when the bed reaches the melting point (Brinkerhoff and Johnson, Reference Brinkerhoff and Johnson2015). The hard-switch approach may be acceptable in mechanical models of ice flow so long as horizontal length scales comparable with the ice thickness are resolved (i.e. Stokes mechanics are employed), but coupling to a thermal model inevitably leads to mathematical inconsistencies and numerical difficulties (Mantelli and others, Reference Mantelli, Haseloff and Schoof2019a). If ice flows from a non-sliding, sub-freezing region to a sliding, temperate one, ice flux must be conserved at the spatial onset of sliding, requiring a decrease in along-flow pressure gradient and surface slope. The subsequent reduction in vertical shear reduces the rate of heat dissipation, which should lead to refreezing. This leads to the paradoxical result that the thermal onset of sliding must cause a drawdown of cold ice, shutting down sliding at any potential onset location (Fowler and Larson, Reference Fowler and Larson1980; Fowler, Reference Fowler, Straughan, Greve, Ehrentraut and Wang2001). Mantelli and others (Reference Mantelli, Haseloff and Schoof2019a) expanded on this concept with a boundary layer analysis of the flow near the frozen-temperate transition to demonstrate that there is no mechanism for heat dissipation at realistic Pèclet numbers that can balance the downward advection of cold ice without refreezing. Therefore, an abrupt onset of sliding is entirely impossible under conditions likely to exist for terrestrial ice sheets.
Instead, Mantelli and Schoof (Reference Mantelli and Schoof2019b) conclude that, for a laterally/radially uniform ice sheet, the onset of sliding must occur over horizontal length scales asymptotically larger than the ice thickness, so that the speed-up is never localized over shorter distances where advection dominates. In their analysis, they adopt a subtemperate sliding law in a similar form proposed by Fowler (Reference Fowler1986)
\begin{equation}
u_b = f(\tau_b,N) g(T_b)
\end{equation} where 
$g(T_b)$ is some continuous function of the bed temperature, such that sliding may occur at temperatures in a narrow range below the melting point. Subtemperate sliding may be physically justified by either regelation and premelting for hard beds (Shreve, Reference Shreve1984; McCarthy and others, Reference McCarthy, Savage and Nettles2017; Rempel and Meyer, Reference Rempel and Meyer2019) or till deformation for soft beds (Meyer and others, Reference Meyer, Downey and Rempel2018, Reference Meyer, Schoof and Rempel2023, Reference Meyer, Bellamy and Rempel2024; Zoet and Iverson, Reference Zoet and Iverson2020; Hansen and others, Reference Hansen, Warburton, Zoet, Meyer, Rempel and Stubblefield2024). Subtemperate sliding has been observed in the field (Shreve, Reference Shreve1984; Echelmeyer and Zhongxiang, Reference Echelmeyer and Zhongxiang1987; Cuffey and others, Reference Cuffey, Conway, Hallet, Gades and Raymond1999) and implemented in some larger-scale ice sheet models (Greve and others, Reference Greve, Takahama and Calov2006; Hank and others, Reference Hank, Tarasov and Mantelli2023), but its implications are not entirely understood.
In this study, we adapt the ice stream model from Robel and others (Reference Robel, Degiuli, Schoof and Tziperman2013) (hereafter, R13), a simple box model (full model description in supplemental materials section S1, default parameters in Table 1), to include subtemperate sliding. The R13 model has been used in various forms to investigate ice stream variability under the influence of stochastic climate forcings (Mantelli and others, Reference Mantelli, Bertagni and Ridolfi2016), frozen fringe and sediment freeze-on (Meyer and others, Reference Meyer, Robel and Rempel2019), and synchronization of Heinrich and Dansgaard-Oeschger (DO) events through ice ocean interactions (Mann and others, Reference Mann, Robel and Meyer2021). The R13 model simulates the dynamics and temporal variability of ice stream flow by coupling ice stream hydrology to ice stream dynamics in a spatially lumped system of two ordinary differential equations: A prognostic equation describes the evolution of a spatially averaged ice thickness, h,
\begin{equation}
\frac{d h}{d t} = a_c - \frac{u_b h}{L}
\end{equation}Table 1. Parameters used in the default, subtemperate sliding model
as a balance of accumulation, ac, and ice flux, 
$u_b h /L$, where L is the ice stream trunk length. Heat and hydrology is expressed in a conservation equation for a volumetric (spatially lumped) enthalpy, E,
\begin{align}
\frac{dE}{dt} &= \frac{\rho_iL_f}{h_b}\left(m -Q_d\right)
\end{align}where ρi is the density of ice, Lf is the latent heat of fusion, hb is the thickness of the temperate basal ice layer, m is the melt rate (expresses a heat balance in the subtemperate case)
\begin{equation}
m = \frac{1}{\rho_i L_f}\left[G + \frac{k_i (T_s-T_b)}{h} + \tau_b u_b\right],
\end{equation}and Qd is the rate of volumetric water discharge through all subglacial conduits. In R13, drainage is active once the till water content reaches saturation, balancing meltwater production m. Basal temperature, Tb and meltwater, w can be calculated diagnostically from volumetric energy density, as
\begin{equation}
E = C_i T_b + \frac{\rho_i L_f}{h_b} w,
\end{equation}where Ci is the volumetric heat capacity of ice. A detailed description of the R13 model, including drainage and frozen fringe propagation, is available in the supplementary materials section S1. This formulation of R13 is similar to other enthalpy-gradient models (Aschwanden and others, Reference Aschwanden, Bueler, Khroulev and Blatter2012; Hewitt and Schoof, Reference Hewitt and Schoof2017).
R13 assumes a plastic Coulomb-type friction law, such that no slip occurs when driving stress, τd, does not exceed a yield stress, τy, determined by the subglacial hydrology model. When the bed thaws, water saturates the till leading to a reduction of the yield stress and a rapid onset of fast flow. During these surges, the centerline sliding velocity is calculated with an approximation derived by Raymond (Reference Raymond1996). Here, we modify the sliding law from R13 by replacing their equation (5) in Robel and others (Reference Robel, Degiuli, Schoof and Tziperman2013) so as to enable subtemperate sliding when 
$T_b \lt T_m$ and 
$\tau_d \lt \tau_y$.
\begin{equation}
u_b = C\tau_b^m e^{\frac{T_b-T_m}{T_0}} + \frac{A_g W^{n+1}}{4^n (n+1) h^n}\text{max}(\tau_d-\tau_y, 0)^n.
\end{equation} Basal resistive stress, 
$\tau_b = \min{[\tau_d, \tau_y]}$ balances driving stress, τd, in the stagnant phase and yield stress, τy, in the active phase allowing a continuous transition to surging behavior when 
$\tau_d \gt \tau_y$. The first term corresponds to Weertman (power law) sliding, where C and m are the traditional friction coefficient and exponent. The exponential coefficient,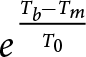 
$e^{\frac{T_b-T_m}{T_0}}$, allows significant subtemperate sliding in a temperature range, T 0, below the melting temperature, Tm, that we call the premelting temperature range (supplemental materials figure S1). The second term corresponds to Coulomb plastic bed yielding, as in the original sliding law used in R13 (their equation 5), where Ag is the Glen’s law rate factor (fluidity parameter), n is the rheological exponent (taken here to be n = 3, corresponding to shear-thinning flow), W is the width of an ice stream, and h is the ice stream thickness. R13 embeds an assumption of negligible vertical shear, which our model also adopts, under the premise that it should be insignificant to the dynamical evolution of this system. Vertical shear in transitions from slow-flowing to fast-flowing ice streams could be incorporated, as in Warburton and others (Reference Warburton, Hewitt, Meyer and Neufeld2023); but we contend, as in R13, that the sliding velocity primarily determines the temporal evolution of the system.
3. Results
The sliding law originally implemented in the R13 model (their eq. 5) produces two distinct flow regimes with either steady streaming or oscillating ice flow velocities. In the steady-streaming regime, warm surface temperatures, Ts, or high geothermal heat fluxes, G, allow the system to come to a steady state with constant sliding velocity, ub. In the oscillatory regime, relatively low geothermal heat or surface temperatures lead to periodic oscillations between stagnant (
$u_b=0$) and active (
$u_b \gt 0$, generally much higher than in the steady-streaming regime) ice stream phases, similar to MacAyeal (Reference MacAyeal1993a).
In Fig. 1a–c, we show simulation results in the oscillatory regime without subtemperate sliding. When the ice sheet is thin, cold atmospheric temperatures conduct heat through the ice and away from the bed, maintaining a frozen till and gradual thickening of the ice stream, as a result of snowfall. Eventually, when the ice stream is thick enough to insulate the base and weaken the vertical temperature gradient, basal ice can warm to its pressure-melting point. When this meltwater eventually saturates the till to a critical void ratio, the till layer fails and the ice stream reactivates, thinning the ice stream, until the cycle begins again. Without subtemperate sliding, the ice stops sliding between surges, so there is no frictional heat dissipation. This means that the thermal evolution of the bed is only governed by the time required to 1) thicken the ice stream, insulating the bed to the pressure melting point, and 2) generate sufficient meltwater to weaken the till layer.
Figure 1. (a–c) depicts simulation results without subtemperate sliding (ξ = 0). (d–f) depicts results with modest subtemperate sliding (ξ = 0.01). Panels display temporal evolution of: ice thickness, h, subglacial slip velocity, ub, plotted on a logarithmic scale, subglacial water content (blue), w, and bed temperature (red), Tb. For velocity panels, a cutoff is imposed at 10−1 m yr−1, for the purpose of representing 0 velocity in the no-slip case. Parameters: Surface Temperature, 
$T_s = -30$ ∘C, Geothermal heat, G = 0.03 W m−2, Premelting Temperature range, 
$T_0 = 1$ ∘C. All variables plotted are as a function of time.
With subtemperate sliding added (Fig. 1d–f), the sliding law (Eq. 7) is now coupled with the basal thermal state of the ice stream, such that increasing the bed temperature continuously increases the sliding velocity. This results in a two-way feedback during both stagnant and active periods. We non-dimensionalize the sliding law, such that 
$\xi = C[\tau_d]^m/[u_b]$ represents a nondimensional friction coefficient for the subtemperate component of the sliding law and 
$[ \ \cdot \ ]$ brackets denote relevant scales. We choose values for this parameter such that the maximum subtemperate sliding velocity is 
$O(10^1)$ m yr−1, compared to the 
$O(10^3)$ m yr−1 velocities that occur in a fast-flowing ice stream.
Despite an increase in net ice flux during stagnant periods, surges become more frequent and subtemperate sliding causes a ∼33% decrease in the oscillatory period compared to the same parameter regime in the R13 model (Fig. 1). The evolution of sliding velocity, bed temperature, and till water content (Fig. 1d–f) illustrates the cause of this earlier surging behavior: During the stagnant period, subtemperate sliding generates frictional heat, which is initially insignificant to the thermal balance, but it does slightly increase the subglacial slip velocity. Later in the stagnant phase, as velocity increases, frictional heat dissipation from subtemperate sliding becomes significant to the thermal balance, accelerating the warming of the bed. Eventually, frictional heating dominates the thermal balance of the bed. Once the melting temperature is reached, subtemperate sliding continues as the temperature remains constant 
$T_b=T_m$, and this continued basal slip dissipates significant amounts of heat and subglacial water, hastening the onset of rapid till deformation. For a relatively brief period after the surge, continued Weertman sliding and heat dissipation maintain a temperate bed. This post-surge phase of sliding is the only phase that contributes to an increase for the period between surges.
Next, we investigate the effect of the premelting temperature range, T 0. This value determines the temperature below the melting point at which subtemperate sliding is significant. The range of subtemperate sliding is related to the physics of premelting (Dash and others, Reference Dash, Rempel and Wettlaufer2006), but this connection has not yet been made nor has the influence on the ice sheet scale been articulated (see supplemental materials section S3). In Fig. 2; we compare 4 different values of T 0. For all experiments, temperature increases linearly in time, as ice thickens during the early stagnant period. However, once bed temperatures approach the T 0 range, thermal feedbacks initiate. Subtemperate sliding can accelerate the onset of a surge centuries or millennia earlier than without subtemperate sliding, depending on our choice of parameters. We can interpret the nonlinear increase in basal temperature in Figs. 1f and 2 as the effect of thermofrictional feedback.
Figure 2. Temporal evolution of a) ice velocity, ub, and b) bed temperature, Tb, given different values of the premelting temperature range, T 0, (color coded).
3.1. Importance of subtemperate sliding across parameter space
Fig. 1 shows that subtemperate sliding can substantially reduce the period between surges for a single parameter set. Here, we set out to determine: (1) whether these results hold with different parameters, and (2) whether subtemperate sliding can change the range of parameters under which oscillatory behavior occurs. To answer these questions, we nondimensionalize to the minimum number of unconstrained parameters (supplement materials section S2) and run the model under a wider range of climatic and basal conditions to determine the oscillation period (the time between surges). The oscillation period is a useful metric for determining the change to the basic model behavior that occurs with subtemperate sliding, because it defines the temporal sensitivity to the parameter regime for oscillatory systems. As we show in Fig. 3; we perform parameter sweeps through the surface temperature, Ts, and the subtemperate sliding parameter, ξ. Increasing the surface temperature, Ts, decreases the event period, until the regime changes from an oscillatory regime to a steady streaming one. The white space above 
$T_s\approx-10$ ∘C represents steady streaming in parameter space, which necessarily has no event period, because the system reaches a steady state with constant velocity. Subtemperate sliding decreases event periods across broad swaths of parameter space, even with very small amounts of subtemperate sliding. This also remains true, for a wide range of premelting temperature ranges, T 0 (see supplemental materials section S3) and geothermal heat fluxes, G (see supplemental materials section S4). These sweeps can be rescaled to demonstrate this effect for other unconstrained parameters (e.g. accumulation rate ac).
Figure 3. Parameter sweep of R13 with subtemperate sliding for parameters: surface temperature, Ts, on the y-axis, and subtemperate sliding parameter, 
$\xi = C[\tau_d]^m/[u_b]$, on the x-axis. The white space represents the steady streaming region of parameter space, which has no event period. The top dotted line represents the stability boundary between oscillations and steady streaming (calculated in supplemental materials section S2). The bottom dotted line represents the oscillation mode boundary, identified heuristically. a) Represents the event period (time between surges). b) Represents the percentage decrease in event period, relative to the case without subtemperate sliding (ξ = 0).
Following the terminology in R13, we distinguish between weak vs. strong oscillations. Weak oscillations occur when the ice-bed interface remains temperate throughout the cycle, and hydrologic processes alone determine the oscillation period. Strong oscillations occur when the bed is below the melting point during longer stagnant periods. In Fig. 3; we identify the boundary between weak and strong oscillations heuristically from the results of numerical simulations. We call this the oscillation mode boundary, and it is particularly evident in Fig. 3b (denoted by the lower dotted line), corresponding to a change in how the system responds to subtemperate sliding.
The reduction in event period is particularly notable for ice streams with colder surface temperatures, characterized by strong oscillations. Small amounts of subtemperate sliding (ξ ≈ 0.01; Fig. 1) can lead to significant reductions in event period of around ∼20-30%. Faster subtemperate sliding speeds, at the higher end of plausibility (ξ ≈ 0.05), result in ∼40% reductions in event period. For colder surface temperatures, the bed is subtemperate for almost all of the stagnant phase, allowing more time for thermal feedbacks to accelerate warming of basal ice, leading to a departure from results without subtemperate sliding (ξ = 0). This means that the oscillatory period is almost entirely dictated by the time required to warm the bed to the melting point.
Weak oscillations are primarily governed by changes in till water content caused by changes in the thermal heat budget. Despite this, sliding during the stagnant phase still significantly impacts the event period. Small amounts of sliding over stagnant temperate beds allow the dissipation of frictional heat, generating more meltwater and hastening the process of till saturation and failure. This leads to reductions in event period ranging up to 30%.
Despite its impact on the event period, subtemperate sliding has little influence on the primary stability boundary between oscillations and steady streaming, plotted in Fig. 3 as the top dotted line. Close to this boundary, activations occur before heat dissipation becomes a dominant part of the basal heat budget, although they still impact the thermal evolution of the system. We repeat the stability analysis from the supplemental materials of R13 (our supplemental materials section S2) and show that, in agreement with these numerical results, subtemperate sliding is asymptotically small in its influence on the steady streaming boundary.
However, subtemperate sliding does influence the location of the oscillation mode boundary between strong vs. weak oscillations. Frictional heat dissipation during a subtemperate phase accelerates the onset of the temperate phase before the surge and prolongs the temperate phase after the surge, allowing weak oscillations under colder conditions. In Fig. 3b; the percentage decrease in event period reaches a local minimum along this boundary. Strong oscillations close to the oscillation mode boundary spend less time in the subtemperate phase, where very significant decreases can occur. Weak oscillations close to the boundary have higher baseline event periods, which results in a smaller relative decrease.
4. Discussion
Theory and observations demonstrate that glaciers can slide when the bed is subtemperate (Shreve, Reference Shreve1984; Echelmeyer and Zhongxiang, Reference Echelmeyer and Zhongxiang1987; Cuffey and others, Reference Cuffey, Conway, Hallet, Gades and Raymond1999; Mantelli and others, Reference Mantelli, Haseloff and Schoof2019a). Thermally activated hard-switch sliding laws introduce physical inconsistencies into models, which must be corrected with a temperature-dependent subtemperate sliding law to investigate the onset of fast sliding (Mantelli and others, Reference Mantelli, Haseloff and Schoof2019a). When this friction law is introduced into ice flow models, it enables a feedback which can give rise to both temporal (Mantelli and Schoof, Reference Mantelli and Schoof2019b) and spatial (Schoof and Mantelli, Reference Schoof and Mantelli2021) instabilities. These temporal instabilities are challenging to model in spatially resolved models because they involve all scales from the ice thickness to the ice sheet scale. Here we focus on the temporal instabilities arising from subtemperate sliding, but in a spatially lumped, rather than spatially resolved, ice stream model. This allows for a straightforward examination of the temporal evolution, in isolation from other processes.
Our results demonstrate that frictional heat during stagnant phases of ice stream flow can initiate a feedback loop, warming basal ice and accelerating the onset of fast sliding (Fig. 4). This feedback proceeds as follows: (1) subtemperate sliding occurs during a period of stagnant ice stream flow with a subtemperate bed, (2) subtemperate sliding generates small amounts of frictional heat, and then (3) frictional heat increases the temperature of the bed, which accelerates sliding. The cycle then repeats. Slip at the ice-bed interface is still active during the temperate phase, before and after the surge. Prior to the surge, heat dissipation accelerates meltwater production, which reduces the total event period. After the surge, heat dissipation can maintain a temperate bed for a relatively brief period while meltwater freezes onto the bed, which contributes a modest increase to the total event period. Across all of our parameter sweeps (both here and in supplemental materials), subtemperate sliding leads to a reduction in inter-surge period, changing the relevant parameter space for Heinrich events and other forms of ice stream variability. These results demonstrate that thermo-frictional feedback can qualitatively change the dynamics of every phase of the surge cycle. In ice stream systems, this feedback is hypothesized to play a major role in ice stream formation, reactivation of stagnant ice streams, and complex flow reorganization in regions like the Siple Coast. This has important implications for ice sheet models and sea level rise projections on centennial timescales. Thermal feedbacks at the bed are observed across a wide range of parameters in this study, demonstrating that this effect is not just a small contributor to ice discharge, but capable of dominating the temporal evolution of ice streams in both past and current ice sheets.
Figure 4. Schematics are purely illustrative, depicting surge cycling with subtemperate sliding, where arrows represent velocity. [center panel] velocity result from Figure 1e. a) Subtemperate sliding occurs between a thin ice sheet and a frozen bed. Small amounts of heat are dissipated as the ice thickens leading to a warmer bed and thus more subtemperate sliding. b) Eventually, the ice bed interface reaches the melting temperature, and the additional sliding accelerates meltwater generation. c) Eventually, water saturated till fails leading to a surge that quickly thins the ice sheet. d) For a brief period after the surge, frictional feedbacks prolong the temperate phase, as continued sliding leads to sufficient heat dissipation sufficient to keep the bed at the melting temperature as subglacial water freezes.
Kamb Ice Stream (KIS) has been identified as a possible source of increasing ice loss from the Siple Coast region of West Antarctica. The modeling experiments in Bougamont and others (Reference Bougamont, Christoffersen, Price, Fricker, Tulaczyk and Carter2015) demonstrated a potential for KIS reactivation in the next century, using a traditional hard-switch sliding law. In this scenario, reactivation begins at the upstream tributaries of KIS in ∼50 yrs, and the trunk of KIS briefly reactivates at ∼ 100 yrs, before cold basal conditions slow the process down until ∼250 yrs. This leads to complex flow reorganization, causing mass balance projections for the Siple Coast region to become more negative, from +30 Gt yr−1 to -3 Gt yr−1 and adding ∼5 mm to sea level rise projections in the next century. Including the effects of subtemperate sliding in these experiments could accelerate this timeline or lead to entirely different reorganization scenarios, and Figs. 2–3 indicate that the timing of a KIS reactivation is subject to the parameters chosen.
Using a spatially lumped model limits our ability to extend these results to the full spatio-temporal system. Spatial transition zones between a subtemperate and temperate bed take on the character of a free boundary problem, and subtemperate sliding impacts the migration of ice stream shear margins and onset boundaries (Haseloff and others, Reference Haseloff, Schoof and Gagliardini2018; Schoof and Mantelli, Reference Schoof and Mantelli2021). For example, subtemperate sliding could lead to easier surge propagation in space, which could draw in ice from a larger spatial area, increasing the total thinning of the ice sheet. This could prolong the inter-surge period (Hank and others, Reference Hank, Tarasov and Mantelli2023) through processes that cannot be represented in a spatially lumped model. However, it remains difficult to determine causality and disentangle effects from numerical error in many-dimensional, potentially unstable, nonlinear systems. The spatially lumped model is useful for identifying the basic dynamical modes of ice stream variability, and understanding processes which could have important implications for spatially resolved models (Robel and others, Reference Robel, Schoof and Tziperman2014). In addition, the presumption that oscillatory dynamics in subglacial till properties may explain systems like Kamb Ice Stream has not yet been proven. Our results show that subtemperate sliding does not meaningfully impact the stability boundary between oscillations and steady-streaming, so the lower, millenial-scale, limits on periodicity are mostly unchanged from R13. This limits our ability to draw firm conclusions about the dynamical causes of centennial-scale ice stream and ice sheet change.
This study offers multiple future avenues of investigation for the long-term behavior of Antarctic ice streams. Small changes in ice stream velocity or basal thermal conditions could correspond to modal shifts in dynamics. A better understanding of these processes can inform our analysis of critical transitions of the Antarctic ice sheet’s dynamical behavior by correctly identifying pertinent early indicators of more abrupt changes. For Heinrich events, these results provide a compelling mechanism for more abrupt and rapid discharge. Within glacial systems, subtemperate sliding may provide a heat source that can express itself in sudden changes to the dynamical behavior of an ice sheet on centennial timescales.
Supplementary material
The supplementary material for this article can be found at https://doi.org/10.1017/jog.2025.10098.
Acknowledgements
We thank three anonymous reviewers for their very thoughtful efforts, which helped improve the manuscript. We acknowledge support from the National Science Foundation (2012958), the Army Research Office (78811EG), and the National Science Foundation Graduate Research Fellowship Program (2023313629). EM was supported by the European Union (ERC-2022-STG, grant no. 101076793) and by funding from the Helmholtz Association. Views and opinions expressed are, however, those of the author(s) only and do not necessarily reflect those of the European Union or the European Research Council Executive Agency. Neither the European Union nor the granting authority can be held responsible for them.
Open access
