Hostname: page-component-7f64f4797f-n5rmq Total loading time: 0 Render date: 2025-11-04T06:55:06.231Z Has data issue: false hasContentIssue false
  • English
  • Français

On intersection probabilities of four lines inside a planar convex domain

Part of: Geometric probability and stochastic geometry Global differential geometry General convexity

Published online by Cambridge University Press:  07 December 2022

Davit Martirosyan  and
Victor Ohanyan
Davit Martirosyan*
Affiliation:
Yerevan State University
Victor Ohanyan*
Affiliation:
Yerevan State University
*
*Postal address: Faculty of Mathematics and Mechanics, 1 Alek Manukyan St, Yerevan 0025, Armenia.
*Postal address: Faculty of Mathematics and Mechanics, 1 Alek Manukyan St, Yerevan 0025, Armenia.
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 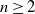$n\geq 2$ random lines intersect a planar convex domain D. Consider the probabilities 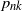$p_{nk}$, 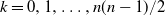$k=0,1, \ldots, {n(n-1)}/{2}$ that the lines produce exactly k intersection points inside D. The objective is finding 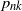$p_{nk}$ through geometric invariants of D. Using Ambartzumian’s combinatorial algorithm, the known results are instantly reestablished for 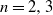$n=2, 3$. When 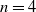$n=4$, these probabilities are expressed by new invariants of D. When D is a disc of radius r, the simplest forms of all invariants are found. The exact values of 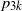$p_{3k}$ and 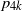$p_{4k}$ are established.

Keywords

Stochastic geometryconvex domain invariantscombinatorial algorithmcounting intersection pointsrandom chord length moments

MSC classification

Primary: 60D05: Geometric probability and stochastic geometry 53C65: Integral geometry
Secondary: 52A22: Random convex sets and integral geometry 52A10: Convex sets in $2$ dimensions (including convex curves)

Information

Type
Original Article
Information
Journal of Applied Probability , Volume 60 , Issue 2 , June 2023 , pp. 504 - 527
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Aharonyan, N. and Khalatyan, V. (2020). Distribution of the distance between two random points in a body from $\textbf{R}^n$ . J. Contemp. Math. Anal. 55, 329–334.CrossRefGoogle Scholar
Aharonyan, N. G. and Ohanyan, V. K. (2018). Calculation of geometric probabilities using covariogram of convex bodies. J. Contemp. Math. Anal. 53, 113–120.CrossRefGoogle Scholar
Ambartzumian, R. V. (1990). Factorization Calculus and Geometric Probability. Cambridge University Press.CrossRefGoogle Scholar
Ambartzumian, R. V. (1992). Remarks on measure generation in the space of lines in $\mathbb{R}^3$ . J. Contemp. Math. Anal. 27, 1–21.Google Scholar
Gardner, R. (2006). Geometric Tomography, 2nd edn. Cambridge University Press.CrossRefGoogle Scholar
Harutyunyan, H. S. and Ohanyan, V. K. (2009). Chord length distribution function for regular polygons. Adv. Appl. Prob. 41, 358–366.CrossRefGoogle Scholar
Ohanyan, V. K. and Martirosyan, D. M. (2020). Orientation-dependent chord length distribution function for right prisms with rectangular or right trapezoidal bases. J. Contemp. Math. Anal. 55, 344–355.CrossRefGoogle Scholar
Santaló, L. A. (2004). Integral Geometry and Geometric Probability. Cambridge University Press.CrossRefGoogle Scholar
Schneider, R. and Weil, W. (2008). Stochastic and Integral Geometry. Springer, Berlin.CrossRefGoogle Scholar
Sulanke, R. (1965). Schnittpunkte zufalliger Geraden. Arch. Math. 16, 320–324.CrossRefGoogle Scholar