Hostname: page-component-7f64f4797f-vhqbp Total loading time: 0 Render date: 2025-11-03T06:15:48.799Z Has data issue: false hasContentIssue false
  • English
  • Français

The limiting spectral distribution of large random permutation matrices

Part of: Probability theory on algebraic and topological structures Multivariate analysis

Published online by Cambridge University Press:  12 April 2024

Jianghao Li Open the ORCID record for Jianghao Li [Opens in a new window] ,
Huanchao Zhou ,
Zhidong Bai  and
Jiang Hu
Jianghao Li*
Affiliation:
KLASMOE and Northeast Normal University
Huanchao Zhou*
Affiliation:
KLASMOE and Northeast Normal University
Zhidong Bai*
Affiliation:
KLASMOE and Northeast Normal University
Jiang Hu*
Affiliation:
KLASMOE and Northeast Normal University
*
*Postal address: School of Mathematics and Statistics, Northeast Normal University, Changchun, China.
*Postal address: School of Mathematics and Statistics, Northeast Normal University, Changchun, China.
*Postal address: School of Mathematics and Statistics, Northeast Normal University, Changchun, China.
*Postal address: School of Mathematics and Statistics, Northeast Normal University, Changchun, China.
Get access Rights & Permissions [Opens in a new window]

Abstract

We explore the limiting spectral distribution of large-dimensional random permutation matrices, assuming the underlying population distribution possesses a general dependence structure. Let 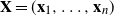$\textbf X = (\textbf x_1,\ldots,\textbf x_n)$ 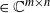$\in \mathbb{C} ^{m \times n}$ be an 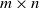$m \times n$ data matrix after self-normalization (n samples and m features), where 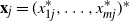$\textbf x_j = (x_{1j}^{*},\ldots, x_{mj}^{*} )^{*}$. Specifically, we generate a permutation matrix 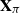$\textbf X_\pi$ by permuting the entries of 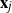$\textbf x_j$ 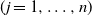$(j=1,\ldots,n)$ and demonstrate that the empirical spectral distribution of 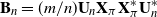$\textbf {B}_n = ({m}/{n})\textbf{U} _{n} \textbf{X} _\pi \textbf{X} _\pi^{*} \textbf{U} _{n}^{*}$ weakly converges to the generalized Marčenko–Pastur distribution with probability 1, where 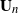$\textbf{U} _n$ is a sequence of 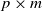$p \times m$ non-random complex matrices. The conditions we require are 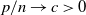$p/n \to c >0$ and 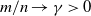$m/n \to \gamma > 0$.

Keywords

Random permutation matricesStieltjes transformlimiting spectral distribution

MSC classification

Primary: 60B20: Random matrices (probabilistic aspects; for algebraic aspects see )
Secondary: 62H10: Distribution of statistics 60B12: Limit theorems for vector-valued random variables (infinite-dimensional case)

Information

Type
Original Article
Information
Journal of Applied Probability , Volume 61 , Issue 4 , December 2024 , pp. 1301 - 1318
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Anderson, T. W. (2003). An Introduction to Multivariate Statistical Analysis, 3rd edn. John Wiley, Hoboken, NJ.Google Scholar
Bai, Z. D. (1999). Methodologies in spectral analysis of large-dimensional random matrices, a review. Statist. Sinica 9, 611–677.Google Scholar
Bai, Z. D. and Silverstein, J. (2010). Spectral Analysis of Large-Dimensional Random Matrices, 2nd edn. Springer, New York.CrossRefGoogle Scholar
Bai, Z. D. and Yin, Y. Q. (1988). Convergence to the semicircle law. Ann. Prob. 16, 863–875.CrossRefGoogle Scholar
Bai, Z. D. and Zhou, W. (2008). Large sample covariance matrices without independence structures in columns. Statist. Sinica 18, 425–442.Google Scholar
Brockwell, P. and Davis, R. (1991). Time Series: Theory and Methods, 2nd edn. Springer, New York.CrossRefGoogle Scholar
Buja, A. and Eyuboglu, N. (1992). Remarks on parallel analysis. Multivariate Behav. Res. 27, 509–540.CrossRefGoogle Scholar
Chen, C., Davis, R. and Brockwell, P. (1996). Order determination for multivariate autoregressive processes using resampling methods. J. Multivariate Anal. 57, 175–190.CrossRefGoogle Scholar
Chen, C., Davis, R., Brockwell, P. and Bai, Z. D. (1993). Order determination for autoregressive processes using resampling methods. Statist. Sinica 3, 481–500.Google Scholar
Couillet, R. and Debbah, M. (2011). Random Matrix Methods for Wireless Communications. Cambridge University Press.CrossRefGoogle Scholar
Dobriban, E. (2020). Permutation methods for factor analysis and PCA. Ann. Statist. 48, 2824–2847.CrossRefGoogle Scholar
Fisher, R. (1935). The Design of Experiments. Hafner, New York.Google Scholar
Geronimo, J. and Hill, T. (2003). Necessary and sufficient condition that the limit of Stieltjes transforms is a Stieltjes transform. J. Approx. Theory 121, 54–60.CrossRefGoogle Scholar
Hong, D., Sheng, Y. and Dobriban, E. (2020). Selecting the number of components in pca via random signflips. Preprint, arXiv:2012.02985.Google Scholar
Hu, J., Wang, S., Zhang, Y. and Zhou, W. (2023). Sampling without replacement from a high-dimensional finite population. Bernoulli 29, 3198–3220.CrossRefGoogle Scholar
Jeong, M., Dytso, A. and Cardone, M. (2021). Retrieving data permutations from noisy observations: High and low noise asymptotics. In Proc. 2021 IEEE Int. Symp. Information Theory (ISIT), pp. 1100–1105.CrossRefGoogle Scholar
Jolliffe, I. T. (2002). Principal Component Analysis, 2nd ed,. Springer, New York.Google Scholar
Jonsson, D. (1982). Some limit theorems for the eigenvalues of a sample covariance matrix. J. Multivariate Anal. 12, 1–38.CrossRefGoogle Scholar
Liang, G., Wilkes, D. and Cadzow, J. (1993). ARMA model order estimation based on the eigenvalues of the covariance matrix. IEEE Trans. Sig. Proc. 41, 3003–3009.CrossRefGoogle Scholar
Ma, R., Cai, T. T. and Li, H. (2021). Optimal permutation recovery in permuted monotone matrix model. J. Amer. Statist. Assoc. 116, 1358–1372.CrossRefGoogle ScholarPubMed
Marčenko, V. and Pastur, L. (1967). Distribution of eigenvalues for some sets of random matrices. Matematicheskii Sbornik 114, 507–536.CrossRefGoogle Scholar
Silverstein, J. (1995). Strong convergence of the empirical distribution of eigenvalues of large-dimensional random matrices. J. Multivariate Anal. 55, 331–339.CrossRefGoogle Scholar
Silverstein, J. (2009). The Stieltjes transform and its role in eigenvalue behavior of large dimensional random matrices. In Random Matrix Theory and its Applications (Lect. Notes Ser. Inst. Math. Sci. Natl. Univ. Singapore 18). World Scientific, Hackensack, NJ, pp. 1–25.CrossRefGoogle Scholar
Silverstein, J. and Bai, Z. D. (1995). On the empirical distribution of eigenvalues of a class of large-dimensional random matrices. J. Multivariate Anal. 54, 175–192.CrossRefGoogle Scholar
Silverstein, J. and Choi, S. (1995). Analysis of the limiting spectral distribution of large-dimensional random matrices. J. Multivariate Anal. 54, 295–309.CrossRefGoogle Scholar
Wachter, K. (1978). The strong limits of random matrix spectra for sample matrices of independent elements. Ann. Prob. 6, 1–18.CrossRefGoogle Scholar
Wax, M. and Kailath, T. (1985). Detection of signals by information theoretic criteria. IEEE Trans. Acoust. Speech Sig. Proc. 33, 387–392.CrossRefGoogle Scholar
Yao, J., Zheng, S. and Bai, Z. (2015). Large Sample Covariance Matrices and High-Dimensional Data Analysis (Camb. Ser. Statist. Probabilistic Math. 39). Cambridge University Press.Google Scholar
Yin, Y. Q. (1986). Limiting spectral distribution for a class of random matrices. J. Multivariate Anal. 20, 50–68.CrossRefGoogle Scholar