No CrossRef data available.
Article contents
Multiplicative forms and nonassociative algebras
Published online by Cambridge University Press: 18 May 2009
Extract
In [1], we introduced the notion of multiplicative forms on associative algebras 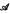 of finite rank over integral domains D, and obtained a complete classification when D ⊆, the complex field. We propose here to remove the hypothesis of associativity, using a refinement of the technique of Schafer [2]. In [l], it was noted that multiplicative forms extend uniquely under the adjunction of an identity when
of finite rank over integral domains D, and obtained a complete classification when D ⊆, the complex field. We propose here to remove the hypothesis of associativity, using a refinement of the technique of Schafer [2]. In [l], it was noted that multiplicative forms extend uniquely under the adjunction of an identity when 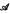 is associative but not unitary; this appears difficult to verify in the general case, so that some mild restriction on
is associative but not unitary; this appears difficult to verify in the general case, so that some mild restriction on 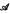 is required. We shall assume that
is required. We shall assume that 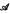 is biregular, that is that
is biregular, that is that 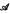 contains elements eL, eR such that the linear maps x
contains elements eL, eR such that the linear maps x 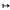 eL x and x
eL x and x 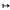 xeR, are bijective on
xeR, are bijective on 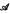 We can then (§1) reduce the biregular case to the unitary case, which is handled in §2.
We can then (§1) reduce the biregular case to the unitary case, which is handled in §2.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Glasgow Mathematical Journal Trust 1974

