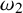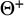1 Introduction
Kunen [Reference Kunen9] famously showed that the existence of a nontrivial elementary embedding
![]() $j:V_{\lambda +2} \to V_{\lambda +2}$
is inconsistent with
$j:V_{\lambda +2} \to V_{\lambda +2}$
is inconsistent with
![]() $\mathsf {ZFC}$
. The intractability of the question whether
$\mathsf {ZFC}$
. The intractability of the question whether
![]() $\mathsf {ZF}$
refutes the existence of such an embedding led Woodin to define, in his set theory seminar in the 1990s, a large cardinal notion to test whether
$\mathsf {ZF}$
refutes the existence of such an embedding led Woodin to define, in his set theory seminar in the 1990s, a large cardinal notion to test whether
![]() $\mathsf {ZF}$
can prove even one nontrivial inconsistency. A cardinal
$\mathsf {ZF}$
can prove even one nontrivial inconsistency. A cardinal
![]() $\kappa $
is a Berkeley cardinal if for every transitive set M with
$\kappa $
is a Berkeley cardinal if for every transitive set M with
![]() $\kappa \in M$
, and for any ordinal
$\kappa \in M$
, and for any ordinal
![]() $\eta <\kappa $
, there is a nontrivial elementary embedding
$\eta <\kappa $
, there is a nontrivial elementary embedding
![]() $j:M\to M$
with
$j:M\to M$
with
![]() $\eta <\mathrm {crit }(j)<\kappa $
. In addition to revealing tension between axioms of infinity and the Axiom of Choice, if Berkeley cardinals are consistent with
$\eta <\mathrm {crit }(j)<\kappa $
. In addition to revealing tension between axioms of infinity and the Axiom of Choice, if Berkeley cardinals are consistent with
![]() $\mathsf {ZF}$
, then the Ultimate L Conjecture is false [Reference Bagaria, Koellner and Woodin1, §8.1].
$\mathsf {ZF}$
, then the Ultimate L Conjecture is false [Reference Bagaria, Koellner and Woodin1, §8.1].
We answer the determinacy version of this consistency question. Solovay showed that assuming
![]() $\mathsf {AD}$
, every subset of
$\mathsf {AD}$
, every subset of
![]() $\omega _1$
is constructible from a real, and hence, there is a nontrivial elementary embedding from any
$\omega _1$
is constructible from a real, and hence, there is a nontrivial elementary embedding from any
![]() $\mathsf {ZFC}$
model of height
$\mathsf {ZFC}$
model of height
![]() $\omega _1$
to itself with critical point less than
$\omega _1$
to itself with critical point less than
![]() $\omega _1$
. Thus,
$\omega _1$
. Thus,
![]() $\omega _1$
is ‘
$\omega _1$
is ‘
![]() $\mathsf {ZFC}$
-Berkeley’ for structures of height
$\mathsf {ZFC}$
-Berkeley’ for structures of height
![]() $\omega _1$
. We generalize this to transitive sets of any size less than
$\omega _1$
. We generalize this to transitive sets of any size less than
![]() $\Theta $
which are coded by sets of ordinals. Moreover, we can ensure that for every club in
$\Theta $
which are coded by sets of ordinals. Moreover, we can ensure that for every club in
![]() $\omega _1$
and every such set, there is an embedding with critical point in that club – that is, adapting some terminology of [Reference Bagaria, Koellner and Woodin1],
$\omega _1$
and every such set, there is an embedding with critical point in that club – that is, adapting some terminology of [Reference Bagaria, Koellner and Woodin1],
Theorem 1.1. Assume
![]() $\textsf {AD}^{+}$
. Then
$\textsf {AD}^{+}$
. Then
![]() $\omega _1$
is club
$\omega _1$
is club
![]() $\Theta $
-Berkeley.
$\Theta $
-Berkeley.
A cardinal
![]() $\kappa $
is a
$\kappa $
is a
![]() $\textsf {HOD}$
-Berkeley cardinal if for all transitive sets
$\textsf {HOD}$
-Berkeley cardinal if for all transitive sets
![]() $M\in \textsf {HOD}$
with
$M\in \textsf {HOD}$
with
![]() $\kappa \in M$
, and for every ordinal
$\kappa \in M$
, and for every ordinal
![]() $\eta <\kappa $
, there is a nontrivial elementary embedding
$\eta <\kappa $
, there is a nontrivial elementary embedding
![]() $j:M\to M$
with
$j:M\to M$
with
![]() $\eta <\mathrm {crit }(j)<\kappa $
[Reference Bagaria, Koellner and Woodin1]. In
$\eta <\mathrm {crit }(j)<\kappa $
[Reference Bagaria, Koellner and Woodin1]. In
![]() $\textsf {ZFC}$
, the existence of a
$\textsf {ZFC}$
, the existence of a
![]() $\textsf {HOD}$
-Berkeley cardinal implies the failure of the
$\textsf {HOD}$
-Berkeley cardinal implies the failure of the
![]() $\textsf {HOD}$
Conjecture (and hence the Ultimate L conjecture) [Reference Bagaria, Koellner and Woodin1, Theorem 8.5]. It is an immediate corollary of Theorem 1.1 that in a
$\textsf {HOD}$
Conjecture (and hence the Ultimate L conjecture) [Reference Bagaria, Koellner and Woodin1, Theorem 8.5]. It is an immediate corollary of Theorem 1.1 that in a
![]() $\textsf {ZFC}$
forcing extension,
$\textsf {ZFC}$
forcing extension,
![]() $\omega _1$
is a
$\omega _1$
is a
![]() $\textsf {HOD}$
-Berkeley cardinal for structures which are ordinal definable from a real and belong to
$\textsf {HOD}$
-Berkeley cardinal for structures which are ordinal definable from a real and belong to
![]() $H_{\omega _3}$
; see Corollary 8.2.
$H_{\omega _3}$
; see Corollary 8.2.
Recall that a set of reals A is
![]() $\kappa $
-Suslin if A is the projection of a tree on
$\kappa $
-Suslin if A is the projection of a tree on
![]() $\omega \times \kappa $
, and
$\omega \times \kappa $
, and
![]() $\kappa $
is a Suslin cardinal if there is a
$\kappa $
is a Suslin cardinal if there is a
![]() $\kappa $
-Suslin set of reals which is not
$\kappa $
-Suslin set of reals which is not
![]() $\gamma $
-Suslin for any
$\gamma $
-Suslin for any
![]() $\gamma <\kappa $
. We show that every regular Suslin cardinal
$\gamma <\kappa $
. We show that every regular Suslin cardinal
![]() $\kappa $
is
$\kappa $
is
![]() $\omega $
-club
$\omega $
-club
![]() $\Theta $
-Berkeley (i.e., for all
$\Theta $
-Berkeley (i.e., for all
![]() $\omega $
-clubs
$\omega $
-clubs
![]() $C\subseteq \kappa $
and all transitive sets M with
$C\subseteq \kappa $
and all transitive sets M with
![]() $\kappa \in M$
and of size less than
$\kappa \in M$
and of size less than
![]() $\Theta $
, there is a nontrivial elementary embedding
$\Theta $
, there is a nontrivial elementary embedding
![]() $j:M\to M$
with
$j:M\to M$
with
![]() $\mathrm {crit }(j)\in C$
).
$\mathrm {crit }(j)\in C$
).
Theorem 1.2. Assume
![]() $\textsf {AD}^+$
. Then every regular Suslin cardinal is
$\textsf {AD}^+$
. Then every regular Suslin cardinal is
![]() $\omega $
-club
$\omega $
-club
![]() $\Theta $
-Berkeley. Thus, every limit Suslin cardinal is a
$\Theta $
-Berkeley. Thus, every limit Suslin cardinal is a
![]() $\Theta $
-Berkeley cardinal.Footnote
1
$\Theta $
-Berkeley cardinal.Footnote
1
Of course,
![]() $\omega _1$
is a regular Suslin cardinal. What seems to distinguish the arguments for Theorems 1.1 and 1.2 is whether the club or
$\omega _1$
is a regular Suslin cardinal. What seems to distinguish the arguments for Theorems 1.1 and 1.2 is whether the club or
![]() $\omega $
-club filter on the cardinal in question is an ultrafilter. For example, we expect that if
$\omega $
-club filter on the cardinal in question is an ultrafilter. For example, we expect that if
![]() $\kappa $
is the largest Suslin cardinal (e.g.,
$\kappa $
is the largest Suslin cardinal (e.g., ![]() in
in
![]() $L(\mathbb {R})$
), then
$L(\mathbb {R})$
), then
![]() $\kappa $
is club
$\kappa $
is club
![]() $\Theta $
-Berkeley.
$\Theta $
-Berkeley.
Theorem 1.2 establishes the existence of limit
![]() $\omega $
-club
$\omega $
-club
![]() $\Theta $
-Berkeley cardinals,
$\Theta $
-Berkeley cardinals,
![]() $\omega $
-club
$\omega $
-club
![]() $\Theta $
-Berkeley cardinals which are limits of
$\Theta $
-Berkeley cardinals which are limits of
![]() $\Theta $
-Berkeley cardinals.
$\Theta $
-Berkeley cardinals.
Corollary 1.3. Assume
![]() $\mathsf {AD}^+$
. Then every regular limit Suslin cardinal is a limit
$\mathsf {AD}^+$
. Then every regular limit Suslin cardinal is a limit
![]() $\omega $
-club
$\omega $
-club
![]() $\Theta $
-Berkeley cardinal.
$\Theta $
-Berkeley cardinal.
Recall that for every n, the projective ordinal ![]() is the supremum of the lengths of
is the supremum of the lengths of ![]() prewellorderings of the reals. The projective ordinals are analogues of
prewellorderings of the reals. The projective ordinals are analogues of
![]() $\mathsf {ZFC}$
cardinals in the setting of
$\mathsf {ZFC}$
cardinals in the setting of
![]() $\mathsf {AD}$
. We show that the even projective ordinals are
$\mathsf {AD}$
. We show that the even projective ordinals are
![]() $\Theta $
-Berkeley.
$\Theta $
-Berkeley.
Theorem 1.4. Assume
![]() $\mathsf {AD}^+$
. Then for all n,
$\mathsf {AD}^+$
. Then for all n, ![]() is
is
![]() $\Theta $
-Berkeley.
$\Theta $
-Berkeley.
In particular,
![]() $\omega _2$
is
$\omega _2$
is
![]() $\Theta $
-Berkeley.
$\Theta $
-Berkeley.
A few words are in order about how these
![]() $\mathsf {AD}^+$
theorems bear on the questions whether
$\mathsf {AD}^+$
theorems bear on the questions whether
![]() $\mathsf {ZF}$
+ ‘there is a Berkeley cardinal’ or
$\mathsf {ZF}$
+ ‘there is a Berkeley cardinal’ or
![]() $\mathsf {ZFC}$
+ ‘there is a
$\mathsf {ZFC}$
+ ‘there is a
![]() $\mathsf {HOD}$
-Berkeley cardinal’ are consistent. Consider the latter question. Historically, large cardinals witnessed by elementary embeddings have been isolated first and subsequently shown to hold, in their measure formulations and assuming
$\mathsf {HOD}$
-Berkeley cardinal’ are consistent. Consider the latter question. Historically, large cardinals witnessed by elementary embeddings have been isolated first and subsequently shown to hold, in their measure formulations and assuming
![]() $\mathsf {AD}$
, at small cardinals. Thus,
$\mathsf {AD}$
, at small cardinals. Thus,
![]() $\omega _1$
is measurable, strongly compact, supercompact and huge, and
$\omega _1$
is measurable, strongly compact, supercompact and huge, and
![]() $\omega _2$
is measurable and has a significant degree of supercompactness. Presumably, this could have happened in reverse. Then we would need to see whether
$\omega _2$
is measurable and has a significant degree of supercompactness. Presumably, this could have happened in reverse. Then we would need to see whether
![]() $\mathsf {ZF}$
large cardinal notions like Berkeley cardinals can ‘survive’ the Axiom of Choice. Full Berkeley cardinals cannot. Perhaps
$\mathsf {ZF}$
large cardinal notions like Berkeley cardinals can ‘survive’ the Axiom of Choice. Full Berkeley cardinals cannot. Perhaps
![]() $\mathsf {HOD}$
-Berkeley cardinals do. This paper opens the door for that eventuality.
$\mathsf {HOD}$
-Berkeley cardinals do. This paper opens the door for that eventuality.
2 Preliminaries
2.1 Inner model theory
The proofs of Theorem 3.1 and Theorem 7.1 require inner model theory. We will use the full normalization technique, and [Reference Steel31, Theorem 1.4] in particular will play a crucial role. We will also use the HOD analysis, references for which include [Reference Steel and Woodin33], [Reference Steel, Foreman and Kanamori30, Chapter 8], [Reference Sargsyan13] and [Reference Steel32]. We will only need the HOD analysis in models of the form
![]() $L^\Psi ({\mathbb {R}})$
, where
$L^\Psi ({\mathbb {R}})$
, where
![]() $\Psi $
is an iteration strategy, and the HOD analysis that we will need is the one that, for a given
$\Psi $
is an iteration strategy, and the HOD analysis that we will need is the one that, for a given
![]() $x\in {\mathbb {R}}$
, represents
$x\in {\mathbb {R}}$
, represents
![]() ${\textsf {HOD}}_{\Psi , x}|\Theta ^{L^\Psi ({\mathbb {R}})}$
as a
${\textsf {HOD}}_{\Psi , x}|\Theta ^{L^\Psi ({\mathbb {R}})}$
as a
![]() $\Psi $
-premouse over x. In this regard, the HOD analysis we need is essentially the HOD analysis of
$\Psi $
-premouse over x. In this regard, the HOD analysis we need is essentially the HOD analysis of
![]() $L({\mathbb {R}})$
.
$L({\mathbb {R}})$
.
The following notation will be used throughout. Suppose
![]() ${\mathcal {M}}$
is some fine structural premouse (e.g., a hybrid premouse, hod premouse or just a pure premouse). We say that a cardinal
${\mathcal {M}}$
is some fine structural premouse (e.g., a hybrid premouse, hod premouse or just a pure premouse). We say that a cardinal
![]() $\kappa $
is a cutpoint of
$\kappa $
is a cutpoint of
![]() ${\mathcal {M}}$
if there is no extender
${\mathcal {M}}$
if there is no extender
![]() $E\in \vec {E}^{\mathcal {M}}$
such that
$E\in \vec {E}^{\mathcal {M}}$
such that
![]() $\mathrm {crit }(E)<\kappa \leq \mathrm {lh}(E)$
. By a theorem of Schlutzenberg (see [Reference Schlutzenberg18]), one can remove the condition that
$\mathrm {crit }(E)<\kappa \leq \mathrm {lh}(E)$
. By a theorem of Schlutzenberg (see [Reference Schlutzenberg18]), one can remove the condition that
![]() $E\in \vec {E}^{\mathcal {M}}$
.
$E\in \vec {E}^{\mathcal {M}}$
.
When we write ‘
![]() $\kappa $
is a measurable cardinal of
$\kappa $
is a measurable cardinal of
![]() ${\mathcal {M}}$
’ or similar expressions, we mean that
${\mathcal {M}}$
’ or similar expressions, we mean that
![]() $\kappa $
is a measurable cardinal in
$\kappa $
is a measurable cardinal in
![]() ${\mathcal {M}}$
as witnessed by the extender sequence of
${\mathcal {M}}$
as witnessed by the extender sequence of
![]() ${\mathcal {M}}$
. The aforementioned result of Schlutzenberg makes this convention unnecessary, but it is easier to communicate results with it.
${\mathcal {M}}$
. The aforementioned result of Schlutzenberg makes this convention unnecessary, but it is easier to communicate results with it.
Given a premouse (or any model with an extender sequence)
![]() ${\mathcal {M}}$
and an
${\mathcal {M}}$
and an
![]() ${\mathcal {M}}$
-cardinal
${\mathcal {M}}$
-cardinal
![]() $\nu $
, we let
$\nu $
, we let
![]() $o^{\mathcal {M}}(\nu )=\sup (\{\mathrm {lh}(E): E\in \vec {E}^{\mathcal {M}} \wedge \mathrm {crit }(E)=\nu \})$
. That is,
$o^{\mathcal {M}}(\nu )=\sup (\{\mathrm {lh}(E): E\in \vec {E}^{\mathcal {M}} \wedge \mathrm {crit }(E)=\nu \})$
. That is,
![]() $o^{\mathcal {M}}(\nu )$
is the Mitchell order of
$o^{\mathcal {M}}(\nu )$
is the Mitchell order of
![]() $\nu $
.
$\nu $
.
Following [Reference Steel, Foreman and Kanamori30, Definition 2.2], for a premouse
![]() ${\mathcal {M}}$
and
${\mathcal {M}}$
and
![]() $E\in \vec {E}^{\mathcal {M}}$
with
$E\in \vec {E}^{\mathcal {M}}$
with
![]() $\kappa =\mathrm {crit }(E)$
, we let
$\kappa =\mathrm {crit }(E)$
, we let
![]() $\nu (E)=\sup ((\kappa ^+)^{\mathcal {M}}\cup \{\xi +1: \xi $
is a generator of
$\nu (E)=\sup ((\kappa ^+)^{\mathcal {M}}\cup \{\xi +1: \xi $
is a generator of
![]() $E\})$
. We also let
$E\})$
. We also let
![]() $\pi _E^{\mathcal {M}}$
be the ultrapower embedding given by E. We will often omit
$\pi _E^{\mathcal {M}}$
be the ultrapower embedding given by E. We will often omit
![]() ${\mathcal {M}}$
.
${\mathcal {M}}$
.
If
![]() ${\mathcal {M}}$
is a non-tame premouse such that
${\mathcal {M}}$
is a non-tame premouse such that
![]() ${\mathcal {M}}\vDash $
‘there are no Woodin cardinals’, then
${\mathcal {M}}\vDash $
‘there are no Woodin cardinals’, then
![]() ${\mathcal {M}}$
has at most one
${\mathcal {M}}$
has at most one
![]() $\omega _1+1$
-iteration strategy, and under
$\omega _1+1$
-iteration strategy, and under
![]() $\textsf {AD}$
, because
$\textsf {AD}$
, because
![]() $\omega _1$
is a measurable cardinal,
$\omega _1$
is a measurable cardinal,
![]() ${\mathcal {M}}$
has at most one
${\mathcal {M}}$
has at most one
![]() $\omega _1$
-iteration strategy. For more details, see [Reference Steel, Foreman and Kanamori30].
$\omega _1$
-iteration strategy. For more details, see [Reference Steel, Foreman and Kanamori30].
Suppose
![]() ${\mathcal {M}}$
is a premouse and
${\mathcal {M}}$
is a premouse and
![]() $\Sigma $
is an iteration strategy for
$\Sigma $
is an iteration strategy for
![]() ${\mathcal {M}}$
. If
${\mathcal {M}}$
. If
![]() ${\mathcal {N}}$
is a normal
${\mathcal {N}}$
is a normal
![]() $\Sigma $
-iterate of
$\Sigma $
-iterate of
![]() ${\mathcal {M}}$
, then we let
${\mathcal {M}}$
, then we let
![]() ${\mathcal {T}}^\Sigma _{{\mathcal {M}}, {\mathcal {N}}}$
be the normal
${\mathcal {T}}^\Sigma _{{\mathcal {M}}, {\mathcal {N}}}$
be the normal
![]() ${\mathcal {M}}$
-to-
${\mathcal {M}}$
-to-
![]() ${\mathcal {N}}$
tree that is according to
${\mathcal {N}}$
tree that is according to
![]() $\Sigma $
, and if the main branch of
$\Sigma $
, and if the main branch of
![]() ${\mathcal {T}}^\Sigma _{{\mathcal {M}}, {\mathcal {N}}}$
does not drop, then we let
${\mathcal {T}}^\Sigma _{{\mathcal {M}}, {\mathcal {N}}}$
does not drop, then we let
![]() $\pi ^\Sigma _{{\mathcal {M}}, {\mathcal {N}}}:{\mathcal {M}}\rightarrow {\mathcal {N}}$
be the iteration embedding given by
$\pi ^\Sigma _{{\mathcal {M}}, {\mathcal {N}}}:{\mathcal {M}}\rightarrow {\mathcal {N}}$
be the iteration embedding given by
![]() ${\mathcal {T}}^\Sigma _{{\mathcal {M}}, {\mathcal {N}}}$
. If
${\mathcal {T}}^\Sigma _{{\mathcal {M}}, {\mathcal {N}}}$
. If
![]() ${\mathcal {N}}$
is a
${\mathcal {N}}$
is a
![]() $\Sigma $
-iterate of
$\Sigma $
-iterate of
![]() ${\mathcal {M}}$
, then
${\mathcal {M}}$
, then
![]() $\Sigma _{\mathcal {N}}$
is the iteration strategy for
$\Sigma _{\mathcal {N}}$
is the iteration strategy for
![]() ${\mathcal {N}}$
given by
${\mathcal {N}}$
given by
![]() $\Sigma _{\mathcal {N}}({\mathcal {U}})=\Sigma (({\mathcal {T}}^\Sigma _{{\mathcal {M}}, {\mathcal {N}}})^{\frown } {\mathcal {U}})$
.
$\Sigma _{\mathcal {N}}({\mathcal {U}})=\Sigma (({\mathcal {T}}^\Sigma _{{\mathcal {M}}, {\mathcal {N}}})^{\frown } {\mathcal {U}})$
.
In the above situation, we say
![]() ${\mathcal {N}}$
is a complete
${\mathcal {N}}$
is a complete
![]() $\Sigma $
-iterate of
$\Sigma $
-iterate of
![]() ${\mathcal {M}}$
if
${\mathcal {M}}$
if
![]() $\pi _{{\mathcal {M}}, {\mathcal {N}}}$
is defined. When discussing direct limit constructions, we will use
$\pi _{{\mathcal {M}}, {\mathcal {N}}}$
is defined. When discussing direct limit constructions, we will use
![]() ${\mathcal {M}}_\infty ({\mathcal {M}}, \Sigma )$
for the direct limit of all complete
${\mathcal {M}}_\infty ({\mathcal {M}}, \Sigma )$
for the direct limit of all complete
![]() $\Sigma $
-iterates of
$\Sigma $
-iterates of
![]() ${\mathcal {M}}$
and
${\mathcal {M}}$
and
![]() $\pi _{{\mathcal {M}}, \infty }^\Sigma :{\mathcal {M}}\rightarrow {\mathcal {M}}_\infty ({\mathcal {M}}, \Sigma )$
will be the direct limit embedding. If
$\pi _{{\mathcal {M}}, \infty }^\Sigma :{\mathcal {M}}\rightarrow {\mathcal {M}}_\infty ({\mathcal {M}}, \Sigma )$
will be the direct limit embedding. If
![]() ${\mathcal {N}}$
is a complete
${\mathcal {N}}$
is a complete
![]() $\Sigma $
-iterate of
$\Sigma $
-iterate of
![]() ${\mathcal {M}}$
, then
${\mathcal {M}}$
, then
![]() $\pi ^\Sigma _{{\mathcal {N}}, \infty }:{\mathcal {N}}\rightarrow {\mathcal {M}}_\infty ({\mathcal {M}}, \Sigma )$
is the iteration embedding.
$\pi ^\Sigma _{{\mathcal {N}}, \infty }:{\mathcal {N}}\rightarrow {\mathcal {M}}_\infty ({\mathcal {M}}, \Sigma )$
is the iteration embedding.
We will often omit
![]() $\Sigma $
from the superscripts in the notation introduced above.
$\Sigma $
from the superscripts in the notation introduced above.
2.2 Woodin’s Derived Model Theorem
Assume
![]() ${\textsf {ZFC-Powerset}}+\text {`}\lambda $
is a limit of Woodin cardinals”
${\textsf {ZFC-Powerset}}+\text {`}\lambda $
is a limit of Woodin cardinals”
![]() $+\text {"}\lambda ^+$
exists’, and suppose
$+\text {"}\lambda ^+$
exists’, and suppose
![]() $g\subseteq Coll(\omega , <\lambda )$
is a generic. For
$g\subseteq Coll(\omega , <\lambda )$
is a generic. For
![]() $\alpha <\lambda $
, let
$\alpha <\lambda $
, let
![]() $g_\alpha =g\cap Coll(\omega , \alpha )$
. Set
$g_\alpha =g\cap Coll(\omega , \alpha )$
. Set
![]() ${\mathbb {R}}^{*}=\cup _{\alpha <\lambda }{\mathbb {R}}^{V[g_\alpha ]}$
and, working in
${\mathbb {R}}^{*}=\cup _{\alpha <\lambda }{\mathbb {R}}^{V[g_\alpha ]}$
and, working in
![]() $V({\mathbb {R}}^{*})$
, let
$V({\mathbb {R}}^{*})$
, let
![]() $\Gamma ^{*}$
be the set of those
$\Gamma ^{*}$
be the set of those
![]() $A\subseteq {\mathbb {R}}^{*}$
such that for some
$A\subseteq {\mathbb {R}}^{*}$
such that for some
![]() $\alpha <\lambda $
and for some
$\alpha <\lambda $
and for some
![]() $(T, S)\in V[g_\alpha ]$
,
$(T, S)\in V[g_\alpha ]$
,
![]() $V[g_\alpha ]\vDash \text {"}(T, S)$
are
$V[g_\alpha ]\vDash \text {"}(T, S)$
are
![]() $<\lambda $
-absolutely complementing” and
$<\lambda $
-absolutely complementing” and
![]() $A=\cup _{\beta \in [\alpha , \lambda )}(p[T])^{V[g_\beta ]}$
.
$A=\cup _{\beta \in [\alpha , \lambda )}(p[T])^{V[g_\beta ]}$
.
Theorem 2.1 (Woodin’s
 ${\textsf {Derived\ Model\ Theorem}}$
, [Reference Steel26, Reference Steel, Cooper, Geuvers, Pillay and Väänänen29]).
${\textsf {Derived\ Model\ Theorem}}$
, [Reference Steel26, Reference Steel, Cooper, Geuvers, Pillay and Väänänen29]).
Assume
![]() ${\textsf {ZFC-Powerset}}+\text {`}\lambda $
is a limit of Woodin cardinals’ + ‘
${\textsf {ZFC-Powerset}}+\text {`}\lambda $
is a limit of Woodin cardinals’ + ‘
![]() $\lambda ^+$
exists’. Suppose
$\lambda ^+$
exists’. Suppose
![]() $g\subseteq Coll(\omega , <\lambda )$
is a generic. Then
$g\subseteq Coll(\omega , <\lambda )$
is a generic. Then
![]() $L(\Gamma ^{*}, {\mathbb {R}}^{*})\vDash {\textsf {AD}^+}$
.
$L(\Gamma ^{*}, {\mathbb {R}}^{*})\vDash {\textsf {AD}^+}$
.
The model
![]() $L(\Gamma ^{*}, {\mathbb {R}}^{*})$
is the derived model of V at
$L(\Gamma ^{*}, {\mathbb {R}}^{*})$
is the derived model of V at
![]() $\lambda $
induced by g. We denote it by
$\lambda $
induced by g. We denote it by
![]() $D(V, \lambda , g)$
. While
$D(V, \lambda , g)$
. While
![]() $D(V, \lambda , g)$
is not in V, its theory is, and in V, we can refer to
$D(V, \lambda , g)$
is not in V, its theory is, and in V, we can refer to
![]() $D(V, \lambda , g)$
via the forcing language.
$D(V, \lambda , g)$
via the forcing language.
Notation 2.2. Suppose
![]() $\lambda $
is as above,
$\lambda $
is as above,
![]() $X\in V_\lambda $
, A is a
$X\in V_\lambda $
, A is a
![]() $<\lambda $
-uB set and
$<\lambda $
-uB set and
![]() $\phi $
is a formula. We write
$\phi $
is a formula. We write
![]() $V\vDash \phi ^{D(\lambda )}[X, A]$
if whenever
$V\vDash \phi ^{D(\lambda )}[X, A]$
if whenever
![]() $g\subseteq Coll(\omega , <\lambda )$
is generic,
$g\subseteq Coll(\omega , <\lambda )$
is generic,
![]() $D(V, \lambda , g)\vDash \phi [X, A_g]$
, where
$D(V, \lambda , g)\vDash \phi [X, A_g]$
, where
![]() $A_g$
is the interpretation of A in
$A_g$
is the interpretation of A in
![]() $V[g]$
.
$V[g]$
.
Suppose
![]() $({\mathcal {P} }, \Sigma )$
is a mouse pair of some kind and
$({\mathcal {P} }, \Sigma )$
is a mouse pair of some kind and
![]() ${\mathcal {P} }$
has infinitely many Woodin cardinals. Let
${\mathcal {P} }$
has infinitely many Woodin cardinals. Let
![]() $\lambda $
be a limit of Woodin cardinals of
$\lambda $
be a limit of Woodin cardinals of
![]() ${\mathcal {P} }$
. Then M is a derived model of
${\mathcal {P} }$
. Then M is a derived model of
![]() $({\mathcal {P} }, \Sigma )$
at
$({\mathcal {P} }, \Sigma )$
at
![]() $\lambda $
if there is some genericity iterationFootnote
2
of
$\lambda $
if there is some genericity iterationFootnote
2
of
![]() ${\mathcal {P} }$
via
${\mathcal {P} }$
via
![]() $\Sigma $
with last model
$\Sigma $
with last model
![]() ${\mathcal {P} }_\omega $
such that if
${\mathcal {P} }_\omega $
such that if
![]() $\pi :{\mathcal {P} }\rightarrow {\mathcal {P} }_\omega $
is the iteration embedding, then
$\pi :{\mathcal {P} }\rightarrow {\mathcal {P} }_\omega $
is the iteration embedding, then
![]() $\pi (\lambda )=\omega _1$
and M is the derived model of
$\pi (\lambda )=\omega _1$
and M is the derived model of
![]() ${\mathcal {P} }_\omega $
at
${\mathcal {P} }_\omega $
at
![]() $\omega _1^V$
as computed by some
$\omega _1^V$
as computed by some
![]() $g\subseteq Coll(\omega , <\omega _1^V)$
which is
$g\subseteq Coll(\omega , <\omega _1^V)$
which is
![]() ${\mathcal {P} }_\omega $
-generic and
${\mathcal {P} }_\omega $
-generic and
![]() $({\mathbb {R}}^{*})^{{\mathcal {P} }_\omega [g]}={\mathbb {R}}$
.
$({\mathbb {R}}^{*})^{{\mathcal {P} }_\omega [g]}={\mathbb {R}}$
.
3
 $\omega _1$
is club
$\omega _1$
is club
 $\Theta $
-Berkeley
$\Theta $
-Berkeley
Before the proof of the main theorem, we present a proof of a special but representative case. This proof has the advantage of being more accessible while featuring most of the main ideas.
The main ideas. We present the main idea behind the proofs of Theorem 3.1 and Theorem 7.1 assuming that
![]() ${\mathcal {M}}_\omega ^\#$
exists. Let
${\mathcal {M}}_\omega ^\#$
exists. Let
![]() ${\mathcal {M}}={\mathcal {M}}_\omega ^\#$
and let
${\mathcal {M}}={\mathcal {M}}_\omega ^\#$
and let
![]() $\delta $
be the least Woodin cardinal of
$\delta $
be the least Woodin cardinal of
![]() ${\mathcal {M}}$
. Let
${\mathcal {M}}$
. Let
![]() ${\mathcal {P} }={\mathcal {M}}|(\delta ^+)^{\mathcal {M}}$
, and let
${\mathcal {P} }={\mathcal {M}}|(\delta ^+)^{\mathcal {M}}$
, and let
![]() $\Sigma $
be the
$\Sigma $
be the
![]() $\omega _1+1$
-iteration strategy of
$\omega _1+1$
-iteration strategy of
![]() ${\mathcal {P} }$
. It is a theorem of Woodin that if
${\mathcal {P} }$
. It is a theorem of Woodin that if
![]() ${\mathcal {N}}$
is the direct limit of all countable iterates of
${\mathcal {N}}$
is the direct limit of all countable iterates of
![]() ${\mathcal {P} }$
via
${\mathcal {P} }$
via
![]() $\Sigma $
, then
$\Sigma $
, then
![]() $\pi _{{\mathcal {P} }, {\mathcal {N}}}(\delta )=\Theta ^{L({\mathbb {R}})}$
and the universe of
$\pi _{{\mathcal {P} }, {\mathcal {N}}}(\delta )=\Theta ^{L({\mathbb {R}})}$
and the universe of
![]() ${\mathcal {N}}|\Theta ^{L({\mathbb {R}})}$
is just
${\mathcal {N}}|\Theta ^{L({\mathbb {R}})}$
is just
![]() $({\textsf {HOD}}|\Theta )^{L({\mathbb {R}})}$
. Our goal now is to generate a nontrivial embedding
$({\textsf {HOD}}|\Theta )^{L({\mathbb {R}})}$
. Our goal now is to generate a nontrivial embedding
Theorem 9.14 shows that such an embedding cannot exist in
![]() $L({\mathbb {R}})$
, but we can hope to find such an embedding j with the additional property that if
$L({\mathbb {R}})$
, but we can hope to find such an embedding j with the additional property that if
![]() $\gamma <\Theta ^{L({\mathbb {R}})}$
, then
$\gamma <\Theta ^{L({\mathbb {R}})}$
, then
![]() $j\restriction ({\textsf {HOD}}|\gamma )^{L({\mathbb {R}})}\in L({\mathbb {R}})$
. We obtain such an embedding as follows. Let E be the total Mitchell order 0 extender on the extender sequence of
$j\restriction ({\textsf {HOD}}|\gamma )^{L({\mathbb {R}})}\in L({\mathbb {R}})$
. We obtain such an embedding as follows. Let E be the total Mitchell order 0 extender on the extender sequence of
![]() ${\mathcal {P} }$
with the property that
${\mathcal {P} }$
with the property that
![]() $\mathrm {crit }(E)$
is the least measurable cardinal of
$\mathrm {crit }(E)$
is the least measurable cardinal of
![]() ${\mathcal {P} }$
. Set
${\mathcal {P} }$
. Set
![]() $\tau =\mathrm { crit }(E)$
,
$\tau =\mathrm { crit }(E)$
,
![]() ${\mathcal {P} }_0={\mathcal {P} }|(\tau ^{++})^{\mathcal {P} }$
,
${\mathcal {P} }_0={\mathcal {P} }|(\tau ^{++})^{\mathcal {P} }$
,
![]() ${\mathcal { Q}}_0=\pi _E({\mathcal {P} }_0)$
and
${\mathcal { Q}}_0=\pi _E({\mathcal {P} }_0)$
and
![]() ${\mathcal { Q}}=Ult({\mathcal {P} }, E)$
. Let
${\mathcal { Q}}=Ult({\mathcal {P} }, E)$
. Let
![]() $\Lambda $
be the fragment of
$\Lambda $
be the fragment of
![]() $\Sigma $
that acts on iteration trees that are above
$\Sigma $
that acts on iteration trees that are above
![]() ${\textsf {Ord}}\cap {\mathcal {P} }_0$
, and similarly, let
${\textsf {Ord}}\cap {\mathcal {P} }_0$
, and similarly, let
![]() $\Phi $
be the fragment of
$\Phi $
be the fragment of
![]() $\Sigma _{\mathcal { Q}}$
that acts on iterations that are above
$\Sigma _{\mathcal { Q}}$
that acts on iterations that are above
![]() ${\textsf {Ord}}\cap {\mathcal { Q}}_0$
. Let
${\textsf {Ord}}\cap {\mathcal { Q}}_0$
. Let
![]() ${\mathcal R}$
be the direct limit of all countable
${\mathcal R}$
be the direct limit of all countable
![]() $\Lambda $
-iterates of
$\Lambda $
-iterates of
![]() ${\mathcal {P} }$
and
${\mathcal {P} }$
and
![]() ${\mathcal {S}}$
be the direct limit of all countable
${\mathcal {S}}$
be the direct limit of all countable
![]() $\Phi $
-iterates of
$\Phi $
-iterates of
![]() ${\mathcal { Q}}$
. Then
${\mathcal { Q}}$
. Then
![]() $\pi _E$
generates an embedding
$\pi _E$
generates an embedding
![]() $j^+:{\mathcal R}\rightarrow {\mathcal {S}}$
such that
$j^+:{\mathcal R}\rightarrow {\mathcal {S}}$
such that
![]() $j\restriction {\mathcal {P} }_0=\pi _E\restriction {\mathcal {P} }_0$
. Moreover, setting
$j\restriction {\mathcal {P} }_0=\pi _E\restriction {\mathcal {P} }_0$
. Moreover, setting
![]() $j=j^+\restriction ({\textsf {HOD}}|\gamma )^{L({\mathbb {R}})}$
, j is as desired.
$j=j^+\restriction ({\textsf {HOD}}|\gamma )^{L({\mathbb {R}})}$
, j is as desired.
Theorem 3.1. Assume
![]() ${\textsf {AD}} + V=L({\mathbb {R}})$
. Then
${\textsf {AD}} + V=L({\mathbb {R}})$
. Then
![]() $\omega _1$
is a club
$\omega _1$
is a club
![]() $\Theta $
-Berkeley cardinal.
$\Theta $
-Berkeley cardinal.
Proof. Toward a contradiction, assume not. Fix a transitive
![]() $N'$
such that
$N'$
such that
-
(1.1)
 $\left |N'\right |<\Theta $
,
$\left |N'\right |<\Theta $
, -
(1.2)
 $\omega _1\subseteq N'$
and
$\omega _1\subseteq N'$
and -
(1.3) the set of
 $\alpha <\omega _1$
such that there is no elementary embedding
$\alpha <\omega _1$
such that there is no elementary embedding
 $j: N'\rightarrow N'$
with the property that
$j: N'\rightarrow N'$
with the property that
 $\mathrm {crit }(j)=\alpha $
is stationary in
$\mathrm {crit }(j)=\alpha $
is stationary in
 $\omega _1$
.
$\omega _1$
.
Let
![]() $\phi (u)$
be the formula expressing (1.1)–(1.3). Thus,
$\phi (u)$
be the formula expressing (1.1)–(1.3). Thus,
![]() $\phi [N']$
holds.
$\phi [N']$
holds.
Fix a real
![]() $x_0$
such that
$x_0$
such that
![]() $N'$
is ordinal definable from
$N'$
is ordinal definable from
![]() $x_0$
. By minimizing the ordinal parameter, we can find N such that N is the
$x_0$
. By minimizing the ordinal parameter, we can find N such that N is the
![]() ${\textsf {OD}}_{x_0}$
-leastFootnote
3
M such that
${\textsf {OD}}_{x_0}$
-leastFootnote
3
M such that
![]() $\phi [M]$
holds.
$\phi [M]$
holds.
We observe that ![]() .Footnote
4
Indeed, because
.Footnote
4
Indeed, because ![]() , we have some
, we have some ![]() such that
such that
![]() $L_\alpha ({\mathbb {R}})\vDash {\textsf {ZF-Powerset}}$
and such that for some
$L_\alpha ({\mathbb {R}})\vDash {\textsf {ZF-Powerset}}$
and such that for some
![]() $K\in L_\alpha ({\mathbb {R}})$
,
$K\in L_\alpha ({\mathbb {R}})$
,
![]() $L_\alpha ({\mathbb {R}})\vDash \text {`}K$
is
$L_\alpha ({\mathbb {R}})\vDash \text {`}K$
is
![]() ${\textsf {OD}}_{x_0}$
and
${\textsf {OD}}_{x_0}$
and
![]() $\phi [K]$
’. Since any function
$\phi [K]$
’. Since any function
![]() $k: K\rightarrow K$
is essentially a set of ordinals, Moschovakis’ Coding LemmaFootnote
5
implies that
$k: K\rightarrow K$
is essentially a set of ordinals, Moschovakis’ Coding LemmaFootnote
5
implies that
![]() $L({\mathbb {R}})\vDash \text {`}K$
is
$L({\mathbb {R}})\vDash \text {`}K$
is
![]() ${\textsf {OD}}_{x_0}$
and
${\textsf {OD}}_{x_0}$
and
![]() $\phi [K]$
’. Since N was the
$\phi [K]$
’. Since N was the
![]() ${\textsf {OD}}_{x_0}$
-least, it follows that
${\textsf {OD}}_{x_0}$
-least, it follows that
![]() $N\in L_\alpha ({\mathbb {R}})$
.
$N\in L_\alpha ({\mathbb {R}})$
.
Now let ![]() be such that
be such that
-
(2.1)
 $L_\alpha ({\mathbb {R}})\vDash {\textsf {ZF-Replacement}}+\text {`}N$
is the
$L_\alpha ({\mathbb {R}})\vDash {\textsf {ZF-Replacement}}+\text {`}N$
is the
 ${\textsf {OD}}_{x_0}$
-least K such that
${\textsf {OD}}_{x_0}$
-least K such that  ’.
’. -
(2.2)
 $L_\alpha ({\mathbb {R}})$
is the derived model of some pair
$L_\alpha ({\mathbb {R}})$
is the derived model of some pair
 $({\mathcal {P} }, \Sigma )$
Footnote
6
such that
$({\mathcal {P} }, \Sigma )$
Footnote
6
such that
 ${\mathcal {P} }$
is an
${\mathcal {P} }$
is an
 $x_0$
-mouse and
$x_0$
-mouse and  $$ \begin{align*} ({\textsf{HOD}}_{x_0}|\Theta)^{L_\alpha({\mathbb{R}})}={\mathcal{M}}_\infty({\mathcal{P} }, \Sigma)|\Theta^{L_\alpha({\mathbb{R}})}. \end{align*} $$
$$ \begin{align*} ({\textsf{HOD}}_{x_0}|\Theta)^{L_\alpha({\mathbb{R}})}={\mathcal{M}}_\infty({\mathcal{P} }, \Sigma)|\Theta^{L_\alpha({\mathbb{R}})}. \end{align*} $$
-
(2.3) LettingFootnote 7
 $(\delta ^i_{\mathcal {P} }: i\leq \omega )$
be the Woodin cardinals of
$(\delta ^i_{\mathcal {P} }: i\leq \omega )$
be the Woodin cardinals of
 ${\mathcal {P} }$
and their limit, for some
${\mathcal {P} }$
and their limit, for some
 ${\mathcal {P} }$
-successor cutpoint cardinal
${\mathcal {P} }$
-successor cutpoint cardinal
 $\nu <\delta ^0_{\mathcal {P} }$
,
$\nu <\delta ^0_{\mathcal {P} }$
,
 ${\textsf {Ord}}\cap N<\pi _{{\mathcal {P} }, \infty }^\Sigma (\nu )$
.
${\textsf {Ord}}\cap N<\pi _{{\mathcal {P} }, \infty }^\Sigma (\nu )$
. -
(2.4) For every
 ${\mathcal {P} }$
-successor cutpoint cardinal
${\mathcal {P} }$
-successor cutpoint cardinal
 $\nu <\delta ^0_{\mathcal {P} }$
,
$\nu <\delta ^0_{\mathcal {P} }$
,
 $\Sigma _{{\mathcal {P} }|\nu }\in L_\alpha ({\mathbb {R}})$
.Footnote
8
$\Sigma _{{\mathcal {P} }|\nu }\in L_\alpha ({\mathbb {R}})$
.Footnote
8
-
(2.5)
 $\Sigma $
has full normalization.
$\Sigma $
has full normalization.
To obtain
![]() $({\mathcal {P} }, \Sigma )$
as above, we first let
$({\mathcal {P} }, \Sigma )$
as above, we first let
![]() $\alpha $
be the least satisfying clause (2.1) and then use [Reference Sargsyan and Steel17, Lemma 2.5] to build
$\alpha $
be the least satisfying clause (2.1) and then use [Reference Sargsyan and Steel17, Lemma 2.5] to build
![]() $({\mathcal {P} }, \Sigma )$
. (2.5) follows from the results of [Reference Steel32] and [Reference Steel31, Theorem 1.4]. Now let
$({\mathcal {P} }, \Sigma )$
. (2.5) follows from the results of [Reference Steel32] and [Reference Steel31, Theorem 1.4]. Now let
![]() ${\mathcal {M}}={\mathcal {M}}_\infty ({\mathcal {P} }, \Sigma )$
. Let
${\mathcal {M}}={\mathcal {M}}_\infty ({\mathcal {P} }, \Sigma )$
. Let
![]() $\tau $
be the least measurable cardinal of
$\tau $
be the least measurable cardinal of
![]() ${\mathcal {P} }$
and let
${\mathcal {P} }$
and let
![]() $E\in \vec {E}^{\mathcal {P} }$
be such that
$E\in \vec {E}^{\mathcal {P} }$
be such that
-
(3.1)
 $\mathrm {crit }(E)=\tau $
and E is total, and
$\mathrm {crit }(E)=\tau $
and E is total, and -
(3.2)
 $\mathrm {lh}(E)$
is the least among all extenders of
$\mathrm {lh}(E)$
is the least among all extenders of
 $\vec {E}^{\mathcal {P} }$
that satisfy (3.1).
$\vec {E}^{\mathcal {P} }$
that satisfy (3.1).
Set
![]() ${\mathcal { Q}}=Ult({\mathcal {P} }, E)$
. We let
${\mathcal { Q}}=Ult({\mathcal {P} }, E)$
. We let
![]() ${\mathcal {P} }_0={\mathcal {P} }|(\tau ^{++})^{\mathcal {P} }$
and
${\mathcal {P} }_0={\mathcal {P} }|(\tau ^{++})^{\mathcal {P} }$
and
![]() ${\mathcal { Q}}_0=\pi _E({\mathcal {P} }_0)$
. Notice that we can view
${\mathcal { Q}}_0=\pi _E({\mathcal {P} }_0)$
. Notice that we can view
![]() ${\mathcal {P} }$
as a premouse over
${\mathcal {P} }$
as a premouse over
![]() ${\mathcal {P} }_0$
and
${\mathcal {P} }_0$
and
![]() ${\mathcal { Q}}$
as a premouse over
${\mathcal { Q}}$
as a premouse over
![]() ${\mathcal { Q}}_0$
. We then let
${\mathcal { Q}}_0$
. We then let
![]() $\Lambda $
be the fragment of
$\Lambda $
be the fragment of
![]() $\Sigma $
that acts on iteration trees on
$\Sigma $
that acts on iteration trees on
![]() ${\mathcal {P} }$
which are above
${\mathcal {P} }$
which are above
![]() $(\tau ^{++})^{\mathcal {P} }$
, and let
$(\tau ^{++})^{\mathcal {P} }$
, and let
![]() $\Phi $
be the fragment of
$\Phi $
be the fragment of
![]() $\Sigma _{\mathcal { Q}}$
that acts on iteration trees on
$\Sigma _{\mathcal { Q}}$
that acts on iteration trees on
![]() ${\mathcal { Q}}$
which are above
${\mathcal { Q}}$
which are above
![]() $\pi _E((\tau ^{++})^{\mathcal {P} })$
. We then have that
$\pi _E((\tau ^{++})^{\mathcal {P} })$
. We then have that
-
(4.1)
 ${\mathcal {M}}_\infty ({\mathcal {P} }, \Lambda )|\Theta ^{L_\alpha ({\mathbb {R}})}=({\textsf {HOD}}_{{\mathcal {P} }_0}|\Theta )^{L_\alpha ({\mathbb {R}})}$
and
${\mathcal {M}}_\infty ({\mathcal {P} }, \Lambda )|\Theta ^{L_\alpha ({\mathbb {R}})}=({\textsf {HOD}}_{{\mathcal {P} }_0}|\Theta )^{L_\alpha ({\mathbb {R}})}$
and
 ${\mathcal {M}}_\infty ({\mathcal { Q}}, \Phi )|\Theta ^{L_\alpha ({\mathbb {R}})}=({\textsf {HOD}}_{{\mathcal { Q}}_0}|\Theta )^{L_\alpha ({\mathbb {R}})}$
.
${\mathcal {M}}_\infty ({\mathcal { Q}}, \Phi )|\Theta ^{L_\alpha ({\mathbb {R}})}=({\textsf {HOD}}_{{\mathcal { Q}}_0}|\Theta )^{L_\alpha ({\mathbb {R}})}$
.
We now define an elementary embedding
![]() $j_{{\mathcal {P} }, \Sigma }=_{def}j:{\mathcal {M}}_\infty ({\mathcal {P} }, \Lambda )\rightarrow {\mathcal {M}}_\infty ({\mathcal { Q}}, \Phi )$
such that
$j_{{\mathcal {P} }, \Sigma }=_{def}j:{\mathcal {M}}_\infty ({\mathcal {P} }, \Lambda )\rightarrow {\mathcal {M}}_\infty ({\mathcal { Q}}, \Phi )$
such that
![]() $j\restriction {\mathcal {P} }_0=\pi _E\restriction {\mathcal {P} }_0$
.
$j\restriction {\mathcal {P} }_0=\pi _E\restriction {\mathcal {P} }_0$
.
Given
![]() $x\in {\mathcal {M}}_\infty ({\mathcal {P} }, \Lambda )$
, fix some normal
$x\in {\mathcal {M}}_\infty ({\mathcal {P} }, \Lambda )$
, fix some normal
![]() $\Lambda $
-iterate
$\Lambda $
-iterate
![]() ${\mathcal R}$
of
${\mathcal R}$
of
![]() ${\mathcal {P} }$
such that for some
${\mathcal {P} }$
such that for some
![]() $y\in {\mathcal R}$
,
$y\in {\mathcal R}$
,
![]() $\pi ^{\Lambda _{\mathcal R}}_{{\mathcal R}, \infty }(y)=x$
. Let
$\pi ^{\Lambda _{\mathcal R}}_{{\mathcal R}, \infty }(y)=x$
. Let
![]() ${\mathcal {T}}={\mathcal {T}}_{{\mathcal {P} }, {\mathcal R}}$
. Let
${\mathcal {T}}={\mathcal {T}}_{{\mathcal {P} }, {\mathcal R}}$
. Let
![]() ${\mathcal {U}}$
be the full normalization of
${\mathcal {U}}$
be the full normalization of
![]() ${\mathcal {T}}^{\frown } \{E\}$
.Footnote
9
Clearly,
${\mathcal {T}}^{\frown } \{E\}$
.Footnote
9
Clearly,
![]() ${\mathcal {U}}$
starts with E and continues with the minimal
${\mathcal {U}}$
starts with E and continues with the minimal
![]() $\pi _E$
-copy of
$\pi _E$
-copy of
![]() ${\mathcal {T}}$
.Footnote
10
Thus,
${\mathcal {T}}$
.Footnote
10
Thus,
![]() ${\mathcal {U}}$
can be written as
${\mathcal {U}}$
can be written as
![]() $\{E\}^{\frown } {\mathcal {W} }$
, where
$\{E\}^{\frown } {\mathcal {W} }$
, where
![]() ${\mathcal {W} }$
is a normal iteration tree on
${\mathcal {W} }$
is a normal iteration tree on
![]() ${\mathcal { Q}}$
according to
${\mathcal { Q}}$
according to
![]() $\Phi $
. If
$\Phi $
. If
![]() ${\mathcal {S}}$
is the last model of
${\mathcal {S}}$
is the last model of
![]() ${\mathcal {W} }$
, then
${\mathcal {W} }$
, then
![]() ${\mathcal {S}}=Ult({\mathcal R}, E)$
. We set
${\mathcal {S}}=Ult({\mathcal R}, E)$
. We set
![]() $j(x)=\pi _{{\mathcal {S}}, \infty }^{\Phi _{\mathcal {S}}}(\pi _E^{\mathcal R}(y))$
.
$j(x)=\pi _{{\mathcal {S}}, \infty }^{\Phi _{\mathcal {S}}}(\pi _E^{\mathcal R}(y))$
.
Claim 3.2.
![]() $j(x)$
is independent of the choice of
$j(x)$
is independent of the choice of
![]() ${\mathcal R}$
.Footnote
11
${\mathcal R}$
.Footnote
11
Proof. Pick another normal
![]() $\Lambda $
-iterate
$\Lambda $
-iterate
![]() ${\mathcal R}'$
of
${\mathcal R}'$
of
![]() ${\mathcal {P} }$
such that for some
${\mathcal {P} }$
such that for some
![]() $y'\in {\mathcal R}'$
,
$y'\in {\mathcal R}'$
,
![]() $\pi _{{\mathcal R}', \infty }^{\Lambda _{{\mathcal R}'}}(y')=x$
. It then follows from full normalization that we can compare
$\pi _{{\mathcal R}', \infty }^{\Lambda _{{\mathcal R}'}}(y')=x$
. It then follows from full normalization that we can compare
![]() $({\mathcal R}, \Lambda _{{\mathcal R}})$
and
$({\mathcal R}, \Lambda _{{\mathcal R}})$
and
![]() $({\mathcal R}', \Lambda _{{\mathcal R}'})$
via the least-extender-disagreement process and get some common iterate
$({\mathcal R}', \Lambda _{{\mathcal R}'})$
via the least-extender-disagreement process and get some common iterate
![]() $({\mathcal R}", \Lambda _{{\mathcal R}"})$
.Footnote
12
It then follows that
$({\mathcal R}", \Lambda _{{\mathcal R}"})$
.Footnote
12
It then follows that
![]() $\pi _{{\mathcal R}, {\mathcal R}"}(y)=\pi _{{\mathcal R}', {\mathcal R}"}(y')$
. Set then
$\pi _{{\mathcal R}, {\mathcal R}"}(y)=\pi _{{\mathcal R}', {\mathcal R}"}(y')$
. Set then
![]() $y"= \pi _{{\mathcal R}, {\mathcal R}"}(y)$
.
$y"= \pi _{{\mathcal R}, {\mathcal R}"}(y)$
.
Next, let
![]() ${\mathcal {T}}={\mathcal {T}}_{{\mathcal {P} }, {\mathcal R}}$
,
${\mathcal {T}}={\mathcal {T}}_{{\mathcal {P} }, {\mathcal R}}$
,
![]() ${\mathcal {T}}'={\mathcal {T}}_{{\mathcal {P} }, {\mathcal R}'}$
,
${\mathcal {T}}'={\mathcal {T}}_{{\mathcal {P} }, {\mathcal R}'}$
,
![]() ${\mathcal {U}}={\mathcal {T}}_{{\mathcal R}, {\mathcal R}"}$
and
${\mathcal {U}}={\mathcal {T}}_{{\mathcal R}, {\mathcal R}"}$
and
![]() ${\mathcal {U}}'={\mathcal {T}}_{{\mathcal R}', {\mathcal R}"}$
. Let
${\mathcal {U}}'={\mathcal {T}}_{{\mathcal R}', {\mathcal R}"}$
. Let
![]() ${\mathcal R}_E=Ult({\mathcal R}, E)$
,
${\mathcal R}_E=Ult({\mathcal R}, E)$
,
![]() ${\mathcal R}^{\prime }_E=Ult({\mathcal R}', E)$
and
${\mathcal R}^{\prime }_E=Ult({\mathcal R}', E)$
and
![]() ${\mathcal R}^{\prime \prime }_E=Ult({\mathcal R}", E)$
. Notice that
${\mathcal R}^{\prime \prime }_E=Ult({\mathcal R}", E)$
. Notice that
-
(5.1)
 ${\mathcal R}_E$
is the last model of the full normalization of
${\mathcal R}_E$
is the last model of the full normalization of
 ${\mathcal {T}}^{\frown } \{E\}$
,
${\mathcal {T}}^{\frown } \{E\}$
, -
(5.2)
 ${\mathcal R}^{\prime }_E$
is the last model of the full normalization of
${\mathcal R}^{\prime }_E$
is the last model of the full normalization of
 ${\mathcal {T}}^{\prime \frown } \{E\}$
,
${\mathcal {T}}^{\prime \frown } \{E\}$
, -
(5.3)
 ${\mathcal R}^{\prime \prime }_E$
is the last model of the full normalization of
${\mathcal R}^{\prime \prime }_E$
is the last model of the full normalization of
 ${\mathcal {U}}^{\frown } \{E\}$
and the full normalization of
${\mathcal {U}}^{\frown } \{E\}$
and the full normalization of
 ${\mathcal {U}}^{\prime \frown } \{E\}$
,
${\mathcal {U}}^{\prime \frown } \{E\}$
, -
(5.4)
 ${\mathcal R}_E$
is a
${\mathcal R}_E$
is a
 $\Phi $
-iterate of
$\Phi $
-iterate of
 ${\mathcal { Q}}$
via some normal tree
${\mathcal { Q}}$
via some normal tree
 ${\mathcal {X}}$
such that the full normalization of
${\mathcal {X}}$
such that the full normalization of
 ${\mathcal {T}}^{\frown } \{E\}$
is
${\mathcal {T}}^{\frown } \{E\}$
is
 $\{E\}^{\frown } {\mathcal {X}}$
,
$\{E\}^{\frown } {\mathcal {X}}$
, -
(5.5)
 ${\mathcal R}^{\prime }_E$
is a
${\mathcal R}^{\prime }_E$
is a
 $\Phi $
-iterate of
$\Phi $
-iterate of
 ${\mathcal { Q}}$
via some normal tree
${\mathcal { Q}}$
via some normal tree
 ${\mathcal {X}}'$
such that the full normalization of
${\mathcal {X}}'$
such that the full normalization of
 ${\mathcal {T}}^{\prime \frown } \{E\}$
is
${\mathcal {T}}^{\prime \frown } \{E\}$
is
 $\{E\}^{\frown } {\mathcal {X}}'$
,
$\{E\}^{\frown } {\mathcal {X}}'$
, -
(5.6) letting
 ${\mathcal {Y}}$
and
${\mathcal {Y}}$
and
 ${\mathcal {Y}}'$
be the iteration trees according to
${\mathcal {Y}}'$
be the iteration trees according to
 $\Phi _{{\mathcal R}_E}$
and
$\Phi _{{\mathcal R}_E}$
and
 $\Phi _{{\mathcal R}_E'}$
, respectively, such that
$\Phi _{{\mathcal R}_E'}$
, respectively, such that
 $\{E\}^{\frown } {\mathcal {Y}}$
is the full normalization of
$\{E\}^{\frown } {\mathcal {Y}}$
is the full normalization of
 ${\mathcal {U}}^{\frown }\{E\}$
and
${\mathcal {U}}^{\frown }\{E\}$
and
 $\{E\}^{\frown } {\mathcal {Y}}'$
is the full normalization of
$\{E\}^{\frown } {\mathcal {Y}}'$
is the full normalization of
 ${\mathcal {U}}^{\prime \frown }\{E\}$
, then
${\mathcal {U}}^{\prime \frown }\{E\}$
, then
 ${\mathcal R}^{\prime \prime }_E$
is the last model of both
${\mathcal R}^{\prime \prime }_E$
is the last model of both
 ${\mathcal {Y}}$
and
${\mathcal {Y}}$
and
 ${\mathcal {Y}}'$
, and hence,
${\mathcal {Y}}'$
, and hence,
 ${\mathcal R}^{\prime \prime }_E$
is a
${\mathcal R}^{\prime \prime }_E$
is a
 $\Phi $
-iterate of
$\Phi $
-iterate of
 ${\mathcal { Q}}$
via both
${\mathcal { Q}}$
via both
 ${\mathcal {X}}^{\frown } {\mathcal {Y}}$
and
${\mathcal {X}}^{\frown } {\mathcal {Y}}$
and
 ${\mathcal {X}}^{\prime \frown } {\mathcal {Y}}'$
.
${\mathcal {X}}^{\prime \frown } {\mathcal {Y}}'$
.
We want to see that
It follows from (5.1)–(5.6) that (here, we drop script
![]() $\Phi $
to make the formulas readable; all iteration embeddings appearing below are defined using
$\Phi $
to make the formulas readable; all iteration embeddings appearing below are defined using
![]() $\Phi $
)
$\Phi $
)
-
(6.1)
 $\pi _{{\mathcal R}_E, \infty }(\pi _E^{\mathcal R}(y))=\pi _{{\mathcal R}^{\prime \prime }_E, \infty }(\pi _{{\mathcal R}_E,{\mathcal R}_E^{\prime \prime }} (\pi _E^{\mathcal R}(y)))$
,
$\pi _{{\mathcal R}_E, \infty }(\pi _E^{\mathcal R}(y))=\pi _{{\mathcal R}^{\prime \prime }_E, \infty }(\pi _{{\mathcal R}_E,{\mathcal R}_E^{\prime \prime }} (\pi _E^{\mathcal R}(y)))$
, -
(6.2)
 $\pi _{{\mathcal R}^{\prime }_E, \infty }(\pi _E^{{\mathcal R}'}(y))=\pi _{{\mathcal R}^{\prime \prime }_E, \infty }(\pi _{{\mathcal R}^{\prime }_E,{\mathcal R}_E^{\prime \prime }} (\pi _E^{{\mathcal R}'}(y')))$
,
$\pi _{{\mathcal R}^{\prime }_E, \infty }(\pi _E^{{\mathcal R}'}(y))=\pi _{{\mathcal R}^{\prime \prime }_E, \infty }(\pi _{{\mathcal R}^{\prime }_E,{\mathcal R}_E^{\prime \prime }} (\pi _E^{{\mathcal R}'}(y')))$
, -
(6.3)
 $\pi _{{\mathcal R}_E,{\mathcal R}_E^{\prime \prime }} (\pi _E^{\mathcal R}(y))=\pi _E^{{\mathcal R}"}(\pi _{{\mathcal R}, {\mathcal R}"}(y))$
,
$\pi _{{\mathcal R}_E,{\mathcal R}_E^{\prime \prime }} (\pi _E^{\mathcal R}(y))=\pi _E^{{\mathcal R}"}(\pi _{{\mathcal R}, {\mathcal R}"}(y))$
, -
(6.4)
 $\pi _{{\mathcal R}^{\prime }_E,{\mathcal R}_E^{\prime \prime }} (\pi _E^{{\mathcal R}'}(y'))=\pi _E^{{\mathcal R}"}(\pi _{{\mathcal R}', {\mathcal R}"}(y'))$
,
$\pi _{{\mathcal R}^{\prime }_E,{\mathcal R}_E^{\prime \prime }} (\pi _E^{{\mathcal R}'}(y'))=\pi _E^{{\mathcal R}"}(\pi _{{\mathcal R}', {\mathcal R}"}(y'))$
, -
(6.5)
 $\pi _{{\mathcal R}, {\mathcal R}"}(y)=\pi _{{\mathcal R}', {\mathcal R}"}(y')$
Footnote
13
.
$\pi _{{\mathcal R}, {\mathcal R}"}(y)=\pi _{{\mathcal R}', {\mathcal R}"}(y')$
Footnote
13
.
(*) now easily follows from (6.1)–(6.5). Indeed,
 $$ \begin{align*} \pi_{{\mathcal R}_E, \infty}(\pi_E^{\mathcal R}(y))&=\pi_{{\mathcal R}^{\prime\prime}_E, \infty}(\pi_{{\mathcal R}_E,{\mathcal R}_E^{\prime\prime}} (\pi_E^{\mathcal R}(y)))\\ &=\pi_{{\mathcal R}^{\prime\prime}_E, \infty}(\pi_E^{{\mathcal R}"}(\pi_{{\mathcal R}, {\mathcal R}"}(y)))\\ &=\pi_{{\mathcal R}^{\prime\prime}_E, \infty}(\pi_E^{{\mathcal R}"}(\pi_{{\mathcal R}', {\mathcal R}"}(y')))\\ &=\pi_{{\mathcal R}^{\prime}_E, \infty}(\pi_E^{{\mathcal R}'}(y')).\\[-34pt] \end{align*} $$
$$ \begin{align*} \pi_{{\mathcal R}_E, \infty}(\pi_E^{\mathcal R}(y))&=\pi_{{\mathcal R}^{\prime\prime}_E, \infty}(\pi_{{\mathcal R}_E,{\mathcal R}_E^{\prime\prime}} (\pi_E^{\mathcal R}(y)))\\ &=\pi_{{\mathcal R}^{\prime\prime}_E, \infty}(\pi_E^{{\mathcal R}"}(\pi_{{\mathcal R}, {\mathcal R}"}(y)))\\ &=\pi_{{\mathcal R}^{\prime\prime}_E, \infty}(\pi_E^{{\mathcal R}"}(\pi_{{\mathcal R}', {\mathcal R}"}(y')))\\ &=\pi_{{\mathcal R}^{\prime}_E, \infty}(\pi_E^{{\mathcal R}'}(y')).\\[-34pt] \end{align*} $$
The next claim essentially finishes the proof of Theorem 3.1.
Claim 3.3.
![]() $j(N)=N$
.
$j(N)=N$
.
Proof. Working in
![]() ${\mathcal {P} }$
, let
${\mathcal {P} }$
, let
![]() $N_{\mathcal {P} }$
be the set of
$N_{\mathcal {P} }$
be the set of
![]() $x\in {\mathcal {P} }|\delta ^0_{{\mathcal {P} }}$
such that
$x\in {\mathcal {P} }|\delta ^0_{{\mathcal {P} }}$
such that
![]() $\pi _{{\mathcal {P} }, \infty }^\Lambda (x)\in N$
.
$\pi _{{\mathcal {P} }, \infty }^\Lambda (x)\in N$
.
![]() $N_{\mathcal {P} }$
is definable in
$N_{\mathcal {P} }$
is definable in
![]() ${\mathcal {P} }$
by the following formula. Let
${\mathcal {P} }$
by the following formula. Let
![]() $(\delta ^i_{\mathcal {P} }: i\leq \omega )$
be the Woodin cardinals of
$(\delta ^i_{\mathcal {P} }: i\leq \omega )$
be the Woodin cardinals of
![]() ${\mathcal {P} }$
and their limit. Let
${\mathcal {P} }$
and their limit. Let
![]() $\sigma [u, v, y, c]$
be a formula in the language containing
$\sigma [u, v, y, c]$
be a formula in the language containing
![]() $\{\in , c\}$
, where c is a constant for
$\{\in , c\}$
, where c is a constant for
![]() $x_0$
, expressing the following:
$x_0$
, expressing the following:
-
(7.1) v is a premouse and u is an
 $\omega _1$
-iteration strategy for v,
$\omega _1$
-iteration strategy for v, -
(7.2)
 $y\in v$
,
$y\in v$
, -
(7.3) if w is the
 ${\textsf {OD}}_c$
-least
${\textsf {OD}}_c$
-least
 $w'$
such that
$w'$
such that
 $\phi [w']$
, then
$\phi [w']$
, then
 $\pi _{v, \infty }^u(x)\in w$
.
$\pi _{v, \infty }^u(x)\in w$
.
We then have that
-
(a)
 $x\in N_{\mathcal {P} }$
if and only if
$x\in N_{\mathcal {P} }$
if and only if -
(a.1) there is a
 ${\mathcal {P} }$
-successor cutpoint cardinal
${\mathcal {P} }$
-successor cutpoint cardinal
 $\beta <\delta ^0_{\mathcal {P} }$
such that
$\beta <\delta ^0_{\mathcal {P} }$
such that
 $x\in N_{\mathcal {P} }|\beta $
, and
$x\in N_{\mathcal {P} }|\beta $
, and -
(a.2) whenever
 $\beta>(\tau ^{++})^{\mathcal {P} }$
is a successor cutpoint cardinal of
$\beta>(\tau ^{++})^{\mathcal {P} }$
is a successor cutpoint cardinal of
 ${\mathcal {P} }$
such that
${\mathcal {P} }$
such that
 $x\in {\mathcal {P} }|\beta $
,
$x\in {\mathcal {P} }|\beta $
,  $$ \begin{align*} {\mathcal{P} }\vDash (\exists \Psi \sigma[\Psi, {\mathcal{P} }|\beta, x, x_0])^{D(\delta^\omega_{\mathcal{P} })}. \end{align*} $$
$$ \begin{align*} {\mathcal{P} }\vDash (\exists \Psi \sigma[\Psi, {\mathcal{P} }|\beta, x, x_0])^{D(\delta^\omega_{\mathcal{P} })}. \end{align*} $$
It is important to note that the strategy
![]() $\Psi $
is just
$\Psi $
is just
![]() $\Lambda _{{\mathcal {P} }|\beta }$
, as
$\Lambda _{{\mathcal {P} }|\beta }$
, as
![]() ${\mathcal {P} }|\beta $
has a unique iteration strategy. Moreover, since
${\mathcal {P} }|\beta $
has a unique iteration strategy. Moreover, since
![]() $\beta $
is a successor cutpoint cardinal of
$\beta $
is a successor cutpoint cardinal of
![]() ${\mathcal {P} }$
,
${\mathcal {P} }$
,
![]() $\pi _{{\mathcal {P} }, \infty }^\Lambda (x)=\pi ^\Psi _{{\mathcal {P} }|\beta , \infty }(x)$
.Footnote
14
$\pi _{{\mathcal {P} }, \infty }^\Lambda (x)=\pi ^\Psi _{{\mathcal {P} }|\beta , \infty }(x)$
.Footnote
14
Now let
![]() $\psi (u, v, w)$
be the formula on the right side of the above equivalence. Then
$\psi (u, v, w)$
be the formula on the right side of the above equivalence. Then
![]() $x\in N_{\mathcal {P} }$
if and only if
$x\in N_{\mathcal {P} }$
if and only if
![]() ${\mathcal {P} }\vDash \psi [x]$
.
${\mathcal {P} }\vDash \psi [x]$
.
Notice that
![]() $\pi _E(N_{\mathcal {P} })=N_{\mathcal { Q}}$
, where
$\pi _E(N_{\mathcal {P} })=N_{\mathcal { Q}}$
, where
![]() $N_{\mathcal { Q}}$
is such that
$N_{\mathcal { Q}}$
is such that
![]() $x\in N_{\mathcal { Q}}$
if and only if
$x\in N_{\mathcal { Q}}$
if and only if
![]() ${\mathcal { Q}}\vDash \psi [x]$
. To finish the proof of the claim, we need to show that
${\mathcal { Q}}\vDash \psi [x]$
. To finish the proof of the claim, we need to show that
We only establish the first equality, as the second is very similar.Footnote 15
Suppose
![]() $x\in \pi _{{\mathcal {P} },\infty }^\Lambda (N_{\mathcal {P} })$
. We want to see that
$x\in \pi _{{\mathcal {P} },\infty }^\Lambda (N_{\mathcal {P} })$
. We want to see that
![]() $x\in N$
. Let
$x\in N$
. Let
![]() ${\mathcal {S}}$
be a
${\mathcal {S}}$
be a
![]() $\Lambda $
-iterate of
$\Lambda $
-iterate of
![]() ${\mathcal {P} }$
such that
${\mathcal {P} }$
such that
![]() $x=\pi _{{\mathcal {S}}, \infty }^{\Lambda _{\mathcal {S}}}(y)$
for some
$x=\pi _{{\mathcal {S}}, \infty }^{\Lambda _{\mathcal {S}}}(y)$
for some
![]() $y\in {\mathcal {S}}$
. We then have that
$y\in {\mathcal {S}}$
. We then have that
![]() ${\mathcal {S}}\vDash \psi [y]$
. Since we can realize
${\mathcal {S}}\vDash \psi [y]$
. Since we can realize
![]() $L_\alpha ({\mathbb {R}})$
as the derived model of
$L_\alpha ({\mathbb {R}})$
as the derived model of
![]() ${\mathcal {S}}$
, we have that
${\mathcal {S}}$
, we have that
![]() $\pi _{{\mathcal {S}}, \infty }^{\Lambda _{\mathcal {S}}}(y)\in N$
.
$\pi _{{\mathcal {S}}, \infty }^{\Lambda _{\mathcal {S}}}(y)\in N$
.
Conversely, suppose
![]() $x\in N$
. Let
$x\in N$
. Let
![]() $(y, {\mathcal {S}})$
be such that
$(y, {\mathcal {S}})$
be such that
![]() ${\mathcal {S}}$
is a
${\mathcal {S}}$
is a
![]() $\Lambda $
-iterate of
$\Lambda $
-iterate of
![]() ${\mathcal {P} }$
,
${\mathcal {P} }$
,
![]() $y\in {\mathcal {S}}$
, and
$y\in {\mathcal {S}}$
, and
![]() $\pi _{{\mathcal {S}}, \infty }^{\Lambda _{\mathcal {S}}}(y)=x$
. Then
$\pi _{{\mathcal {S}}, \infty }^{\Lambda _{\mathcal {S}}}(y)=x$
. Then
![]() ${\mathcal {S}}\vDash \psi [y]$
, which implies that
${\mathcal {S}}\vDash \psi [y]$
, which implies that
![]() $y\in \pi _{{\mathcal {P} }, {\mathcal {S}}}(N_{\mathcal {P} })$
. Therefore,
$y\in \pi _{{\mathcal {P} }, {\mathcal {S}}}(N_{\mathcal {P} })$
. Therefore,
![]() $x=\pi _{{\mathcal {S}}, \infty }^{\Lambda _{\mathcal {S}}}(y)\in \pi _{{\mathcal {P} }, \infty }^\Lambda (N_{\mathcal {P} })$
.
$x=\pi _{{\mathcal {S}}, \infty }^{\Lambda _{\mathcal {S}}}(y)\in \pi _{{\mathcal {P} }, \infty }^\Lambda (N_{\mathcal {P} })$
.
To finish the proof of Theorem 3.1, we need to produce a club
![]() $C\subseteq \omega _1$
such that for each
$C\subseteq \omega _1$
such that for each
![]() $\alpha \in C$
, there is an embedding
$\alpha \in C$
, there is an embedding
![]() $k: N\rightarrow N$
with
$k: N\rightarrow N$
with
![]() $\mathrm {crit }(k)=\alpha $
. Above, we have produced an elementary embedding
$\mathrm {crit }(k)=\alpha $
. Above, we have produced an elementary embedding
![]() $j_{{\mathcal {P} }, \Sigma }:N\rightarrow N$
such that
$j_{{\mathcal {P} }, \Sigma }:N\rightarrow N$
such that
![]() $\mathrm { crit }(j_{{\mathcal {P} }, \Sigma })=\tau $
, for
$\mathrm { crit }(j_{{\mathcal {P} }, \Sigma })=\tau $
, for
![]() $\tau $
the least measurable cardinal of
$\tau $
the least measurable cardinal of
![]() ${\mathcal {P} }$
. Let
${\mathcal {P} }$
. Let
![]() $({\mathcal {P} }_\alpha : \alpha <\omega _1)$
be the sequence of linear iterates of
$({\mathcal {P} }_\alpha : \alpha <\omega _1)$
be the sequence of linear iterates of
![]() ${\mathcal {P} }$
by E and its images, and let
${\mathcal {P} }$
by E and its images, and let
![]() $\tau _\alpha $
be the least measurable cardinal of
$\tau _\alpha $
be the least measurable cardinal of
![]() ${\mathcal {P} }_\alpha $
. Then
${\mathcal {P} }_\alpha $
. Then
![]() $\mathrm {crit }(j_{{\mathcal {P} }_\alpha , \Sigma _{{\mathcal {P} }_\alpha }})=\tau _\alpha $
, and since
$\mathrm {crit }(j_{{\mathcal {P} }_\alpha , \Sigma _{{\mathcal {P} }_\alpha }})=\tau _\alpha $
, and since
![]() $C=\{\tau _\alpha : \alpha <\omega _1\}$
is a club, we get a contradiction to the fact that
$C=\{\tau _\alpha : \alpha <\omega _1\}$
is a club, we get a contradiction to the fact that
![]() $\phi [N]$
is true.
$\phi [N]$
is true.
4 Good and very-good pointclasses, a review of [Reference Sargsyan14]
We review concepts from coarse descriptive inner model theory used in the proof of Theorem 7.1. Many of the concepts have appeared in [Reference Sargsyan14] and elsewhere, and many of them are due to Woodin. A reader familiar with them can skip this section and return to it as needed.
4.1 Very good pointclasses
Let
![]() ${\mathbb {R}}$
be the Baire space. Following [Reference Steel24, Chapter 3]), we say that
${\mathbb {R}}$
be the Baire space. Following [Reference Steel24, Chapter 3]), we say that
![]() $\Gamma $
is a good pointclass if
$\Gamma $
is a good pointclass if
-
1.
 $\Gamma $
is closed under recursive substitution and number quantification,
$\Gamma $
is closed under recursive substitution and number quantification, -
2.
 $\Gamma $
is
$\Gamma $
is
 $\omega $
-parametrized,Footnote
16
$\omega $
-parametrized,Footnote
16
-
3.
 $\Gamma $
has the scale property, and
$\Gamma $
has the scale property, and -
4.
 $\Gamma $
is closed under
$\Gamma $
is closed under
 $\exists ^{\mathbb {R}}$
.
$\exists ^{\mathbb {R}}$
.
Each good pointclass has its associated
![]() $C_\Gamma $
operator. For
$C_\Gamma $
operator. For
![]() $x\in {\mathbb {R}}$
,
$x\in {\mathbb {R}}$
,
TheFootnote
17
![]() $C_\Gamma $
operator can be extended to sets in
$C_\Gamma $
operator can be extended to sets in
![]() ${\textsf {HC}}$
via the category quantifier.Footnote
18
${\textsf {HC}}$
via the category quantifier.Footnote
18
Let
![]() $C_\Gamma ^{\alpha }$
denote the
$C_\Gamma ^{\alpha }$
denote the
![]() $\alpha $
th iterate of
$\alpha $
th iterate of
![]() $C_\Gamma $
so that, for example,
$C_\Gamma $
so that, for example,
![]() $C^2_\Gamma (a)=C_\Gamma (C_\Gamma (a))$
. We only need this notion for
$C^2_\Gamma (a)=C_\Gamma (C_\Gamma (a))$
. We only need this notion for
![]() $\alpha \leq \omega $
. Set
$\alpha \leq \omega $
. Set
![]() $C^\omega _\Gamma (a)=\cup _{n<\omega }C^n_{\Gamma }(a)$
.
$C^\omega _\Gamma (a)=\cup _{n<\omega }C^n_{\Gamma }(a)$
.
Suppose T is the tree of a
![]() $\Gamma $
-scale. For each
$\Gamma $
-scale. For each
![]() $\alpha <\omega _1$
, we let
$\alpha <\omega _1$
, we let
![]() $\kappa _\alpha $
be the
$\kappa _\alpha $
be the
![]() $\alpha $
th-infinite cardinal of
$\alpha $
th-infinite cardinal of
![]() $L[T,a]$
. We can then simply set
$L[T,a]$
. We can then simply set
![]() $C^{\alpha }_\Gamma (a)=H_{\kappa _\alpha }^{L[T, a]}$
. Then, using this definition, we have
$C^{\alpha }_\Gamma (a)=H_{\kappa _\alpha }^{L[T, a]}$
. Then, using this definition, we have
![]() $C_\Gamma (a)=C^1_\Gamma (a)$
.
$C_\Gamma (a)=C^1_\Gamma (a)$
.
Given a transitive
![]() $P\vDash {\textsf {ZFC-Replacement}}$
, we say P is a
$P\vDash {\textsf {ZFC-Replacement}}$
, we say P is a
![]() $\Gamma $
-Woodin if for some
$\Gamma $
-Woodin if for some
![]() $\delta $
,
$\delta $
,
-
1.
 $P\vDash \text {`}\delta $
is the only Woodin cardinal’,
$P\vDash \text {`}\delta $
is the only Woodin cardinal’, -
2.
 $P=C^\omega _\Gamma (P)$
,
$P=C^\omega _\Gamma (P)$
, -
3. for every P-cardinal
 $\eta <\delta $
,
$\eta <\delta $
,
 $C_\Gamma (V^P_\eta )\vDash \text {`}\eta $
is not a Woodin cardinal’.
$C_\Gamma (V^P_\eta )\vDash \text {`}\eta $
is not a Woodin cardinal’.
We let
![]() $\delta ^P$
be the Woodin cardinal of P.
$\delta ^P$
be the Woodin cardinal of P.
A sequence
![]() $(A_n: n<\omega )\subseteq {\mathbb {R}}^{\omega }$
is a self-justifying-system (sjs) if for each
$(A_n: n<\omega )\subseteq {\mathbb {R}}^{\omega }$
is a self-justifying-system (sjs) if for each
![]() $n\in \omega $
,
$n\in \omega $
,
-
1. there is a sequence
 $(A_{m_k}: k\in \omega )$
that codes a scale on
$(A_{m_k}: k\in \omega )$
that codes a scale on
 $A_n$
, and
$A_n$
, and -
2. there is
 $m<\omega $
such that
$m<\omega $
such that
 $A_n^c=A_m$
.
$A_n^c=A_m$
.
Let
![]() $T_0$
be the theory
$T_0$
be the theory
-
1.
 $\textsf {AD}^{+}+{\textsf {ZF}}-{\textsf {Powerset\ Axiom}}$
,
$\textsf {AD}^{+}+{\textsf {ZF}}-{\textsf {Powerset\ Axiom}}$
, -
2. ‘
 $\Theta $
exists’,Footnote
19
and
$\Theta $
exists’,Footnote
19
and -
3.
 $V=L_{\Theta ^{+}}(C, {\mathbb {R}})$
for some
$V=L_{\Theta ^{+}}(C, {\mathbb {R}})$
for some
 $C\subseteq {\mathbb {R}}$
.
$C\subseteq {\mathbb {R}}$
.
Definition 4.1. Suppose
![]() $\Gamma $
is a good pointclass. Then
$\Gamma $
is a good pointclass. Then
![]() $\Gamma $
is a very good pointclass (vg-pointclass) if there is a sjs
$\Gamma $
is a very good pointclass (vg-pointclass) if there is a sjs
![]() $\vec {A}=(A_n: n\in \omega )$
,
$\vec {A}=(A_n: n\in \omega )$
,
![]() $\gamma <\Theta ^{L(\vec {A}, {\mathbb {R}})}$
, a
$\gamma <\Theta ^{L(\vec {A}, {\mathbb {R}})}$
, a
![]() $\Sigma _1$
-formula
$\Sigma _1$
-formula
![]() $\phi $
, and a real x such that
$\phi $
, and a real x such that
![]() $L_{\gamma }(\vec {A}, {\mathbb {R}})$
is the least initial segment of
$L_{\gamma }(\vec {A}, {\mathbb {R}})$
is the least initial segment of
![]() $L(\vec {A}, {\mathbb {R}})$
that satisfies
$L(\vec {A}, {\mathbb {R}})$
that satisfies
![]() $T_0+\phi (x)$
and
$T_0+\phi (x)$
and
![]() $\Gamma =(\Sigma ^2_1(\vec {A}))^{L_{\gamma }(\vec {A}, {\mathbb {R}}))}$
. We say
$\Gamma =(\Sigma ^2_1(\vec {A}))^{L_{\gamma }(\vec {A}, {\mathbb {R}}))}$
. We say
![]() $M_\Gamma =_{def}L_{\gamma }(\vec {A}, {\mathbb {R}})$
is the parent of
$M_\Gamma =_{def}L_{\gamma }(\vec {A}, {\mathbb {R}})$
is the parent of
![]() $\Gamma $
.
$\Gamma $
.
If
![]() $\Gamma $
is a vg-pointclass and
$\Gamma $
is a vg-pointclass and
![]() $M_\Gamma =L_{\gamma }(\vec {A}, {\mathbb {R}})$
is its parent, then for any countable transitive a,
$M_\Gamma =L_{\gamma }(\vec {A}, {\mathbb {R}})$
is its parent, then for any countable transitive a,
![]() $C_\Gamma (a)={\textsf {OD}}^{M_\Gamma }(\vec {A}, a)$
.
$C_\Gamma (a)={\textsf {OD}}^{M_\Gamma }(\vec {A}, a)$
.
4.2
 $\Gamma $
-excellent pairs
$\Gamma $
-excellent pairs
Suppose
![]() $\Gamma $
is a vg-pointclass. We say that
$\Gamma $
is a vg-pointclass. We say that
![]() $\vec {B}\subseteq {\mathbb {R}}^{\omega }$
is a weakly
$\vec {B}\subseteq {\mathbb {R}}^{\omega }$
is a weakly
![]() $\Gamma $
-condensing sequence if
$\Gamma $
-condensing sequence if
-
1.
 $B_0$
codes a sjs such that
$B_0$
codes a sjs such that
 $M_\Gamma =L_{\gamma }(B_0, {\mathbb {R}})$
and
$M_\Gamma =L_{\gamma }(B_0, {\mathbb {R}})$
and
 $\Gamma =(\Sigma ^2_1(B_0))^{L_{\gamma }(B_0, {\mathbb {R}})}$
,
$\Gamma =(\Sigma ^2_1(B_0))^{L_{\gamma }(B_0, {\mathbb {R}})}$
, -
2.
 $B_1=\{ (x, y)\in {\mathbb {R}}^2: y\in C_\Gamma (x)\}$
,
$B_1=\{ (x, y)\in {\mathbb {R}}^2: y\in C_\Gamma (x)\}$
, -
3.
 $B_2=B_1^c$
,
$B_2=B_1^c$
, -
4.
 $B_3$
is any
$B_3$
is any
 ${\textsf {OD}}^{M_\Gamma }(B_0)$
set,Footnote
20
${\textsf {OD}}^{M_\Gamma }(B_0)$
set,Footnote
20
-
5.
 $(B_{2i+1}: i\in [2, \omega ))\subseteq \Gamma $
is a scale on
$(B_{2i+1}: i\in [2, \omega ))\subseteq \Gamma $
is a scale on
 $B_1$
,
$B_1$
, -
6.
 $(B_{2i}: i\in [2, \omega ))\subseteq M_\Gamma $
is a scale on
$(B_{2i}: i\in [2, \omega ))\subseteq M_\Gamma $
is a scale on
 $B_2$
, and
$B_2$
, and -
7. for every
 $i\in [2, \omega )$
,
$i\in [2, \omega )$
,
 $M_\Gamma \vDash \text {`}B_{2i}$
is ordinal definable from
$M_\Gamma \vDash \text {`}B_{2i}$
is ordinal definable from
 $B_0$
’.
$B_0$
’.
Suppose
![]() $\Gamma $
is a vg-pointclass and
$\Gamma $
is a vg-pointclass and
![]() $M_\Gamma =L_{\gamma }(\vec {A}, {\mathbb {R}})$
is its parent. Suppose
$M_\Gamma =L_{\gamma }(\vec {A}, {\mathbb {R}})$
is its parent. Suppose
![]() $B\in M_\Gamma \cap {\wp }({\mathbb {R}})$
is
$B\in M_\Gamma \cap {\wp }({\mathbb {R}})$
is
![]() ${\textsf {OD}}^{M_\Gamma }(\vec {A})$
and a is a transitive hereditarily countable set. Let
${\textsf {OD}}^{M_\Gamma }(\vec {A})$
and a is a transitive hereditarily countable set. Let
![]() $\tau ^a_B$
be the term relation consisting of pairs
$\tau ^a_B$
be the term relation consisting of pairs
![]() $(p, \sigma )$
such that
$(p, \sigma )$
such that
-
1.
 $p\in Coll(\omega , a)$
,
$p\in Coll(\omega , a)$
, -
2.
 $\sigma \in C_\Gamma (a)$
is a standard
$\sigma \in C_\Gamma (a)$
is a standard
 $Coll(\omega , a)$
-name for a real, and
$Coll(\omega , a)$
-name for a real, and -
3. for co-meager many
 $g\subseteq Coll(\omega , a)$
such that
$g\subseteq Coll(\omega , a)$
such that
 $p\in g$
,
$p\in g$
,
 $\sigma (g)\in B$
.Footnote
21
$\sigma (g)\in B$
.Footnote
21
Then because
![]() $\tau ^a_B$
is
$\tau ^a_B$
is
![]() ${\textsf {OD}}^{M_\Gamma }(\vec {A}, a)$
, we have that
${\textsf {OD}}^{M_\Gamma }(\vec {A}, a)$
, we have that
![]() $\tau ^a_B\in C_\Gamma (C_\Gamma (a))$
. Given
$\tau ^a_B\in C_\Gamma (C_\Gamma (a))$
. Given
![]() $k\in \omega $
, we let
$k\in \omega $
, we let
Thus, for every
![]() $k\in \omega $
,
$k\in \omega $
,
![]() $\tau ^a_{B, k}\in C^{k+2}_\Gamma (a)$
.
$\tau ^a_{B, k}\in C^{k+2}_\Gamma (a)$
.
A weakly
![]() $\Gamma $
-condensing sequence
$\Gamma $
-condensing sequence
![]() $\vec {B}$
is a
$\vec {B}$
is a
![]() $\Gamma $
-condensing sequence if for any transitive sets
$\Gamma $
-condensing sequence if for any transitive sets
![]() $a, b, M\in HC$
such that
$a, b, M\in HC$
such that
-
1.
 $a\in M$
and
$a\in M$
and -
2. there is an embedding
 $\pi : M\rightarrow _{\Sigma _1} C^\omega _\Gamma (b)$
such that
$\pi : M\rightarrow _{\Sigma _1} C^\omega _\Gamma (b)$
such that
 $\pi (a)=b$
and for every
$\pi (a)=b$
and for every
 $i, k\in \omega $
,
$i, k\in \omega $
,
 $\tau ^b_{B_i, k}\in rng(\pi )$
,
$\tau ^b_{B_i, k}\in rng(\pi )$
,
![]() $M=C^\omega (a)$
and for any
$M=C^\omega (a)$
and for any
![]() $i, k\in \omega $
,
$i, k\in \omega $
,
![]() $\pi ^{-1}(\tau ^b_{B_i, k})=\tau ^a_{B_i, k}$
. If P is a
$\pi ^{-1}(\tau ^b_{B_i, k})=\tau ^a_{B_i, k}$
. If P is a
![]() $\Gamma $
-Woodin and
$\Gamma $
-Woodin and
![]() $B\in {\textsf {OD}}^{M_\Gamma }(\vec {A})$
, then for
$B\in {\textsf {OD}}^{M_\Gamma }(\vec {A})$
, then for
![]() $k\in \omega $
, we let
$k\in \omega $
, we let
![]() $\tau ^P_{B, k}=\tau ^{V_{\delta ^P}^P}_{B, k}$
.
$\tau ^P_{B, k}=\tau ^{V_{\delta ^P}^P}_{B, k}$
.
Definition 4.2 [Reference Sargsyan14, Definition 1.6].
Suppose
![]() $\Gamma $
is a vg-pointclass and
$\Gamma $
is a vg-pointclass and
![]() $M_\Gamma =L_{\gamma }(\vec {A}, {\mathbb {R}})$
is its parent. Suppose P is a
$M_\Gamma =L_{\gamma }(\vec {A}, {\mathbb {R}})$
is its parent. Suppose P is a
![]() $\Gamma $
-Woodin and
$\Gamma $
-Woodin and
![]() $\Sigma $
is an
$\Sigma $
is an
![]() $\omega _1$
-iteration strategy for P. Suppose
$\omega _1$
-iteration strategy for P. Suppose
![]() $B\in M_\Gamma \cap {\wp }({\mathbb {R}})$
is
$B\in M_\Gamma \cap {\wp }({\mathbb {R}})$
is
![]() ${\textsf {OD}}^{M_\Gamma }(\vec {A})$
.
${\textsf {OD}}^{M_\Gamma }(\vec {A})$
.
-
1.
 $\Sigma $
is a
$\Sigma $
is a
 $\Gamma $
-fullness preserving strategy for P if whenever
$\Gamma $
-fullness preserving strategy for P if whenever
 $i:P\rightarrow Q$
is an iteration of P via
$i:P\rightarrow Q$
is an iteration of P via
 $\Sigma $
, Q is a
$\Sigma $
, Q is a
 $\Gamma $
-Woodin.
$\Gamma $
-Woodin. -
2. Given that
 $\Sigma $
is
$\Sigma $
is
 $\Gamma $
-fullness preserving,
$\Gamma $
-fullness preserving,
 $\Sigma $
respects B if whenever
$\Sigma $
respects B if whenever
 $i:P\rightarrow Q$
is an iteration of P via
$i:P\rightarrow Q$
is an iteration of P via
 $\Sigma $
, for every k,
$\Sigma $
, for every k,
 $i(\tau ^P_{B, k})=\tau ^Q_{B, k}$
.
$i(\tau ^P_{B, k})=\tau ^Q_{B, k}$
.
The following theorem, which probably is originally due to Woodin, is unpublished. For its proof, see the discussion after [Reference Sargsyan14, Theorem 1.7].
Theorem 4.3. Assume
![]() $\textsf {AD}^{+}$
. Suppose
$\textsf {AD}^{+}$
. Suppose
![]() $\Gamma $
is a vg-pointclass, and let
$\Gamma $
is a vg-pointclass, and let
![]() $M_\Gamma =L_{\gamma }(\vec {A}, {\mathbb {R}})$
Footnote
22
be its parent. Let
$M_\Gamma =L_{\gamma }(\vec {A}, {\mathbb {R}})$
Footnote
22
be its parent. Let
![]() $A\in {\textsf {OD}}(\vec {A})^{M_\Gamma }$
. Then there is a pair
$A\in {\textsf {OD}}(\vec {A})^{M_\Gamma }$
. Then there is a pair
![]() $(R, \Psi )$
and a
$(R, \Psi )$
and a
![]() $\Gamma $
-condensing sequence
$\Gamma $
-condensing sequence
![]() $\vec {B}$
such that
$\vec {B}$
such that
-
1. R is a
 $\Gamma $
-Woodin,
$\Gamma $
-Woodin, -
2.
 $\Psi $
is a
$\Psi $
is a
 $\Gamma $
-fullness preserving
$\Gamma $
-fullness preserving
 $\omega _1$
-iteration strategy for P,
$\omega _1$
-iteration strategy for P, -
3. for each i,
 $\Psi $
respects
$\Psi $
respects
 $B_i$
,
$B_i$
, -
4. for every
 $\Psi $
-iterate Q of R, for every
$\Psi $
-iterate Q of R, for every
 $i\in \omega $
, and for every Q-generic
$i\in \omega $
, and for every Q-generic
 $g\subseteq Coll(\omega , \delta ^Q)$
,
$g\subseteq Coll(\omega , \delta ^Q)$
,
 $\tau ^Q_i(g)=Q[g]\cap B_i$
,
$\tau ^Q_i(g)=Q[g]\cap B_i$
, -
5. for any iteration tree
 ${\mathcal {T}}\in \mathrm {dom}(\Psi )$
,
${\mathcal {T}}\in \mathrm {dom}(\Psi )$
,
 $\Sigma ({\mathcal {T}})=b$
if and only if either
$\Sigma ({\mathcal {T}})=b$
if and only if either-
(a)
 $C_\Gamma ({\mathcal {M}}({\mathcal {T}}))\vDash \text {`}\delta ({\mathcal {T}})$
is not a Woodin cardinal’ and b is the unique well-founded cofinal branch c of
$C_\Gamma ({\mathcal {M}}({\mathcal {T}}))\vDash \text {`}\delta ({\mathcal {T}})$
is not a Woodin cardinal’ and b is the unique well-founded cofinal branch c of
 ${\mathcal {T}}$
such that
${\mathcal {T}}$
such that
 $C_\Gamma ({\mathcal {M}}({\mathcal {T}}))\in {\mathcal {M}}^{\mathcal {T}}_c$
, or
$C_\Gamma ({\mathcal {M}}({\mathcal {T}}))\in {\mathcal {M}}^{\mathcal {T}}_c$
, or -
(b)
 $C_\Gamma ({\mathcal {M}}({\mathcal {T}}))\vDash \text {`}\delta ({\mathcal {T}})$
is a Woodin cardinal’ and b is the unique well-founded cofinal branch c of
$C_\Gamma ({\mathcal {M}}({\mathcal {T}}))\vDash \text {`}\delta ({\mathcal {T}})$
is a Woodin cardinal’ and b is the unique well-founded cofinal branch c of
 ${\mathcal {T}}$
such that letting
${\mathcal {T}}$
such that letting
 $Q=C^\omega _\Gamma ({\mathcal {M}}({\mathcal {T}}))$
,
$Q=C^\omega _\Gamma ({\mathcal {M}}({\mathcal {T}}))$
,
 ${\mathcal {M}}^{\mathcal {T}}_c=Q$
, and for every
${\mathcal {M}}^{\mathcal {T}}_c=Q$
, and for every
 $i\in \omega $
,
$i\in \omega $
,
 $\pi ^{\mathcal {T}}_c(\tau ^R_{B_i})=\tau ^Q_{B_i}$
, and
$\pi ^{\mathcal {T}}_c(\tau ^R_{B_i})=\tau ^Q_{B_i}$
, and
-
-
6.
 $\Psi $
respects A.
$\Psi $
respects A.
Moreover, for any set
![]() $a\in {\textsf {HC}}$
, there is
$a\in {\textsf {HC}}$
, there is
![]() $(R, \Psi )$
as above such that
$(R, \Psi )$
as above such that
![]() $a\in R$
.
$a\in R$
.
Definition 4.4. Suppose
![]() $\Gamma $
is a vg-pointclass. Then
$\Gamma $
is a vg-pointclass. Then
![]() $(R, \Psi )$
is a
$(R, \Psi )$
is a
![]() $\Gamma $
-excellent pair if for some
$\Gamma $
-excellent pair if for some
![]() $\Gamma $
-condensing sequence
$\Gamma $
-condensing sequence
![]() $\vec {B}$
,
$\vec {B}$
,
![]() $(R, \Psi )$
has properties 1–5 described in Theorem 4.3 as witnessed by
$(R, \Psi )$
has properties 1–5 described in Theorem 4.3 as witnessed by
![]() $\vec {B}$
.
$\vec {B}$
.
4.3 Reflection points
Suppose
![]() $(P, \Psi )$
is a
$(P, \Psi )$
is a
![]() $\Gamma $
-excellent pair. For
$\Gamma $
-excellent pair. For
![]() $n\leq \omega $
, we let
$n\leq \omega $
, we let
![]() ${\mathcal {M}}_n^{\Psi , \#}$
be the minimal active
${\mathcal {M}}_n^{\Psi , \#}$
be the minimal active
![]() $\Psi $
-mouse that has exactly n Woodin cardinals. Under
$\Psi $
-mouse that has exactly n Woodin cardinals. Under
![]() ${\textsf {AD}}$
,
${\textsf {AD}}$
,
![]() ${\mathcal {M}}_n^{\Psi , \#}$
, as a
${\mathcal {M}}_n^{\Psi , \#}$
, as a
![]() $\Psi $
-mouse, has a unique
$\Psi $
-mouse, has a unique
![]() $\omega _1$
-iteration strategy. Letting
$\omega _1$
-iteration strategy. Letting
![]() $\Psi ^+_n$
be this iteration strategy, we have that
$\Psi ^+_n$
be this iteration strategy, we have that
![]() ${\textsf {Code}}(\Psi )$
is projective in
${\textsf {Code}}(\Psi )$
is projective in
![]() ${\textsf {Code}}(\Psi ^+_n)$
.Footnote
23
${\textsf {Code}}(\Psi ^+_n)$
.Footnote
23
Suppose
![]() $(P, \Psi )$
is a
$(P, \Psi )$
is a
![]() $\Gamma $
-excellent pair. Then
$\Gamma $
-excellent pair. Then
![]() $L^\Psi ({\mathbb {R}})$
is the minimal
$L^\Psi ({\mathbb {R}})$
is the minimal
![]() $\Psi $
-mouse containing all the ordinals and reals. It can be defined as in [Reference Sargsyan and Steel17] and in [Reference Sargsyan13, Chapter 3.7]. Because
$\Psi $
-mouse containing all the ordinals and reals. It can be defined as in [Reference Sargsyan and Steel17] and in [Reference Sargsyan13, Chapter 3.7]. Because
![]() ${\mathbb {R}}$
is not well-ordered, the above references build
${\mathbb {R}}$
is not well-ordered, the above references build
![]() $L^\Psi ({\mathbb {R}})$
relative to
$L^\Psi ({\mathbb {R}})$
relative to
![]() $\Psi ^+_2$
, though in the case of excellent pairs, the same construction would work relative to
$\Psi ^+_2$
, though in the case of excellent pairs, the same construction would work relative to
![]() $\Psi $
.Footnote
24
$\Psi $
.Footnote
24
Suppose
![]() $(P, \Psi )$
is a
$(P, \Psi )$
is a
![]() $\Gamma $
-excellent pair. Then
$\Gamma $
-excellent pair. Then ![]() is the least ordinal
is the least ordinal
![]() $\alpha $
such that
$\alpha $
such that
![]() $L_\alpha ^\Psi ({\mathbb {R}})\prec ^{{\mathbb {R}}}_{1} L^\Psi ({\mathbb {R}})$
. Here,
$L_\alpha ^\Psi ({\mathbb {R}})\prec ^{{\mathbb {R}}}_{1} L^\Psi ({\mathbb {R}})$
. Here,
![]() $\prec _{n}^X$
stands for elementarity with respect to
$\prec _{n}^X$
stands for elementarity with respect to
![]() $\Sigma _n$
-formulas with parameters from X. When discussing
$\Sigma _n$
-formulas with parameters from X. When discussing
![]() $L^\Psi ({\mathbb {R}})$
, we will omit the superscript
$L^\Psi ({\mathbb {R}})$
, we will omit the superscript
![]() ${\mathbb {R}}$
, as it is part of the language of
${\mathbb {R}}$
, as it is part of the language of
![]() $L^\Psi ({\mathbb {R}})$
(see [Reference Koellner and Woodin8, Chapter 2.4]).
$L^\Psi ({\mathbb {R}})$
(see [Reference Koellner and Woodin8, Chapter 2.4]).
![]() $\Sigma _1$
-reflection for
$\Sigma _1$
-reflection for
![]() $L^\Psi ({\mathbb {R}})$
. Suppose
$L^\Psi ({\mathbb {R}})$
. Suppose
![]() $(P, \Psi )$
is a
$(P, \Psi )$
is a
![]() $\Gamma $
-excellent pair,
$\Gamma $
-excellent pair,
![]() $\phi $
is a formula, and x is a real. Then
$\phi $
is a formula, and x is a real. Then ![]() is a
is a
![]() $(T_0, \phi , x)$
-reflection point if
$(T_0, \phi , x)$
-reflection point if
-
1.
 $L^\Psi _\beta ({\mathbb {R}})\vDash T_0$
,
$L^\Psi _\beta ({\mathbb {R}})\vDash T_0$
, -
2.
 $L^\Psi _\beta ({\mathbb {R}})\vDash \phi [x]$
, and
$L^\Psi _\beta ({\mathbb {R}})\vDash \phi [x]$
, and -
3.
 ${\wp }({\mathbb {R}})\cap (L^\Psi _{\beta +2}({\mathbb {R}})-L^\Psi _{\beta +1}({\mathbb {R}}))\not =\emptyset $
.
${\wp }({\mathbb {R}})\cap (L^\Psi _{\beta +2}({\mathbb {R}})-L^\Psi _{\beta +1}({\mathbb {R}}))\not =\emptyset $
.
For each
![]() $(\phi , x)$
such that
$(\phi , x)$
such that
![]() $L({\mathbb {R}})\vDash \phi [x]$
, the set of
$L({\mathbb {R}})\vDash \phi [x]$
, the set of
![]() $(T_0, \phi , x)$
-reflection points is unbounded below
$(T_0, \phi , x)$
-reflection points is unbounded below ![]() (see [Reference Koellner and Woodin8, Chapter 2.4], [Reference Steel22] and [Reference Schlutzenberg and Trang20]).
(see [Reference Koellner and Woodin8, Chapter 2.4], [Reference Steel22] and [Reference Schlutzenberg and Trang20]).
Suppose
![]() $(P, \Psi )$
is a
$(P, \Psi )$
is a
![]() $\Gamma $
-excellent pair. Modifying the terminology of [Reference Steel22], we say
$\Gamma $
-excellent pair. Modifying the terminology of [Reference Steel22], we say
![]() $\beta $
ends a
$\beta $
ends a
![]() $(T_0, \Psi )$
-gap if clause (1) and (3) above hold. If
$(T_0, \Psi )$
-gap if clause (1) and (3) above hold. If
![]() $\beta $
ends a
$\beta $
ends a
![]() $(T_0, \Psi )$
-gap, then we set
$(T_0, \Psi )$
-gap, then we set
![]() $\Theta ^\beta =\Theta ^{M_\beta }$
,
$\Theta ^\beta =\Theta ^{M_\beta }$
,
![]() $M_\beta =L_\beta ^\Psi ({\mathbb {R}})$
, and
$M_\beta =L_\beta ^\Psi ({\mathbb {R}})$
, and
![]() ${\mathcal { H}}_{Y, x}^{\beta }=(\mathrm {{HOD}}(Y, x))^{M_\beta }$
.
${\mathcal { H}}_{Y, x}^{\beta }=(\mathrm {{HOD}}(Y, x))^{M_\beta }$
.
It is shown in [Reference Larson10] that for each
![]() $\beta $
that is a
$\beta $
that is a
![]() $(T_0, \phi , x)$
-reflection point, for any set
$(T_0, \phi , x)$
-reflection point, for any set
![]() $Y\in M_\beta $
, and for any real x,
$Y\in M_\beta $
, and for any real x,
![]() ${\mathcal { H}}_{\Psi , Y, x}^{\beta }={\mathcal { H}}_{\Psi , Y}^\beta [x]$
.Footnote
25
${\mathcal { H}}_{\Psi , Y, x}^{\beta }={\mathcal { H}}_{\Psi , Y}^\beta [x]$
.Footnote
25
4.4 Coarse tuples
The following definition is essential for the arguments to come.
Definition 4.5. Suppose
![]() $\nu <\Theta $
. Then
$\nu <\Theta $
. Then
![]() $(R, \Psi , H, \alpha )$
is a coarse tuple if the following conditions hold:
$(R, \Psi , H, \alpha )$
is a coarse tuple if the following conditions hold:
-
1. For some very-good pointclass
 $\Gamma $
,
$\Gamma $
,
 $(R, \Psi )$
is a
$(R, \Psi )$
is a
 $\Gamma $
-excellent pair.
$\Gamma $
-excellent pair. -
2.
 $H: {\mathbb {R}}\rightarrow V$
is a partial function such that
$H: {\mathbb {R}}\rightarrow V$
is a partial function such that
 $\mathrm {dom}(H)\subseteq \{x\in {\mathbb {R}}: R\in L_1[x]\}$
.
$\mathrm {dom}(H)\subseteq \{x\in {\mathbb {R}}: R\in L_1[x]\}$
. -
3. For every
 $x\in \mathrm {dom}(H)$
, setting
$x\in \mathrm {dom}(H)$
, setting
 $H(x)=({\mathcal {P} }_x, \Sigma _x)$
,
$H(x)=({\mathcal {P} }_x, \Sigma _x)$
,
 $({\mathcal {P} }_x, \Sigma _x)$
is a
$({\mathcal {P} }_x, \Sigma _x)$
is a
 $\Psi $
-mouse pair over x.
$\Psi $
-mouse pair over x. -
4. For every x,
 ${\mathcal {P} }_x\vDash {\textsf {ZFC}}$
and has exactly
${\mathcal {P} }_x\vDash {\textsf {ZFC}}$
and has exactly
 $\omega $
-Woodin cardinals.
$\omega $
-Woodin cardinals. -
5.
 ${\mathcal {P} }$
is
${\mathcal {P} }$
is
 $\omega $
-small with respect to
$\omega $
-small with respect to
 $\Psi $
.Footnote
26
$\Psi $
.Footnote
26
-
6.
 $\alpha $
is a
$\alpha $
is a
 $(T_0, \Psi , \phi )$
-reflection point and for each
$(T_0, \Psi , \phi )$
-reflection point and for each
 $x\in \mathrm {dom}(H)$
, the derived model of
$x\in \mathrm {dom}(H)$
, the derived model of
 $({\mathcal {P} }_x, \Sigma _x)$
is
$({\mathcal {P} }_x, \Sigma _x)$
is
 $L_\alpha ^\Psi ({\mathbb {R}})$
.Footnote
27
$L_\alpha ^\Psi ({\mathbb {R}})$
.Footnote
27
-
7.
 ${\mathcal {M}}_\infty ({\mathcal {P} }_x, \Sigma _x)|\Theta ^{\alpha }={\mathcal { H}}_x^{\alpha }|\Theta ^{\alpha }$
Footnote
28
and
${\mathcal {M}}_\infty ({\mathcal {P} }_x, \Sigma _x)|\Theta ^{\alpha }={\mathcal { H}}_x^{\alpha }|\Theta ^{\alpha }$
Footnote
28
and
 $\Theta ^{\alpha }=\pi _{{\mathcal {P} }_x, \infty }^{\Sigma _x}(\delta )$
, where
$\Theta ^{\alpha }=\pi _{{\mathcal {P} }_x, \infty }^{\Sigma _x}(\delta )$
, where
 $\delta $
is the least Woodin cardinal of
$\delta $
is the least Woodin cardinal of
 ${\mathcal {P} }_x$
.
${\mathcal {P} }_x$
. -
8. For any
 $x\in \mathrm {dom}(H)$
and any
$x\in \mathrm {dom}(H)$
and any
 ${\mathcal {P} }$
-successor cutpoint cardinal
${\mathcal {P} }$
-successor cutpoint cardinal
 $\beta <\delta $
, where
$\beta <\delta $
, where
 $\delta $
is the least Woodin cardinal of
$\delta $
is the least Woodin cardinal of
 ${\mathcal {P} }_x$
,
${\mathcal {P} }_x$
,
 $(\Sigma _x)_{{\mathcal {P} }_x|\beta }\in L_\alpha ^\Psi ({\mathbb {R}})$
.
$(\Sigma _x)_{{\mathcal {P} }_x|\beta }\in L_\alpha ^\Psi ({\mathbb {R}})$
.
We say that
![]() $(R, \Psi , H, \alpha )$
absorbs
$(R, \Psi , H, \alpha )$
absorbs
![]() $\nu $
if
$\nu $
if
![]() $(R, \Psi , H, \alpha )$
is a coarse tuple such that
$(R, \Psi , H, \alpha )$
is a coarse tuple such that ![]() .Footnote
29
.Footnote
29
Remark 4.6. Assuming
![]() $V=L({\mathbb {R}})$
, we could just work with ordinary pure mouse pairs. In this case,
$V=L({\mathbb {R}})$
, we could just work with ordinary pure mouse pairs. In this case,
![]() $H(x)$
is simply the least initial segment of
$H(x)$
is simply the least initial segment of
![]() ${\mathcal {M}}^\#_\omega (x)$
that has the desired properties.
${\mathcal {M}}^\#_\omega (x)$
that has the desired properties.
Theorem 4.7. Assume
![]() $\textsf {AD}^{+}$
and suppose
$\textsf {AD}^{+}$
and suppose
![]() $(R, \Psi )$
is a
$(R, \Psi )$
is a
![]() $\Gamma $
-excellent pair for some
$\Gamma $
-excellent pair for some
![]() $\Gamma $
. Suppose
$\Gamma $
. Suppose
![]() $\nu $
is less than the largest Suslin cardinal of
$\nu $
is less than the largest Suslin cardinal of
![]() $L^\Psi ({\mathbb {R}})$
. Then there is a coarse tuple
$L^\Psi ({\mathbb {R}})$
. Then there is a coarse tuple
![]() $(R, \Psi , H, \alpha )$
absorbing
$(R, \Psi , H, \alpha )$
absorbing
![]() $\nu $
.
$\nu $
.
Theorem 4.7 can be demonstrated by combining Theorem 4.3, the hod analysis of
![]() $L({\mathbb {R}})$
relativized to
$L({\mathbb {R}})$
relativized to
![]() $L^\Psi ({\mathbb {R}})$
,Footnote
30
and the results of [Reference Sargsyan and Steel17].Footnote
31
$L^\Psi ({\mathbb {R}})$
,Footnote
30
and the results of [Reference Sargsyan and Steel17].Footnote
31
Remark 4.8. Suppose
![]() $(R, \Psi , H, \alpha )$
witnesses Theorem 4.7. Let
$(R, \Psi , H, \alpha )$
witnesses Theorem 4.7. Let
![]() $x\in \mathrm {dom}(H)$
, and let
$x\in \mathrm {dom}(H)$
, and let
![]() $\delta $
be the least Woodin cardinal of
$\delta $
be the least Woodin cardinal of
![]() ${\mathcal {P} }_x$
. Set
${\mathcal {P} }_x$
. Set
![]() ${\mathcal {P} }={\mathcal {P} }_x|(\delta ^{+\omega })^{{\mathcal {P} }_x}$
and
${\mathcal {P} }={\mathcal {P} }_x|(\delta ^{+\omega })^{{\mathcal {P} }_x}$
and
![]() $\Sigma =\Sigma _{{\mathcal {P} }_x}$
. Then it can be shown that some complete
$\Sigma =\Sigma _{{\mathcal {P} }_x}$
. Then it can be shown that some complete
![]() $\Sigma $
-iterate of
$\Sigma $
-iterate of
![]() ${\mathcal { Q}}$
of
${\mathcal { Q}}$
of
![]() ${\mathcal {P} }_x$
is such that
${\mathcal {P} }_x$
is such that
![]() $({\mathcal { Q}}, \Sigma )$
is
$({\mathcal { Q}}, \Sigma )$
is
![]() $\Gamma $
-excellent, where letting
$\Gamma $
-excellent, where letting
![]() $\alpha $
witness clause (6) of Definition 4.5,
$\alpha $
witness clause (6) of Definition 4.5,
![]() $\Gamma =(\Sigma ^2_1({\textsf {Code}}(\Psi ), x))^{L_\alpha ^\Psi ({\mathbb {R}})}$
. This is because, by the results of [Reference Steel22] and [Reference Schlutzenberg and Trang20], there is a weakly
$\Gamma =(\Sigma ^2_1({\textsf {Code}}(\Psi ), x))^{L_\alpha ^\Psi ({\mathbb {R}})}$
. This is because, by the results of [Reference Steel22] and [Reference Schlutzenberg and Trang20], there is a weakly
![]() $\Gamma $
-condensing sequence
$\Gamma $
-condensing sequence
![]() $\vec {A}=(A_i: i<\omega )$
such that for each i,
$\vec {A}=(A_i: i<\omega )$
such that for each i,
![]() $A_i\in {\textsf {OD}}_{\Psi , x}^{L_\alpha ^\Psi ({\mathbb {R}})}$
.
$A_i\in {\textsf {OD}}_{\Psi , x}^{L_\alpha ^\Psi ({\mathbb {R}})}$
.
![]() ${\mathcal { Q}}$
is then a
${\mathcal { Q}}$
is then a
![]() $\Sigma $
-iterate of
$\Sigma $
-iterate of
![]() ${\mathcal {P} }$
such that
${\mathcal {P} }$
such that
![]() $\Sigma _{\mathcal { Q}}$
respects each
$\Sigma _{\mathcal { Q}}$
respects each
![]() $A_i$
. We can find such a
$A_i$
. We can find such a
![]() ${\mathcal { Q}}$
using standard arguments from the hod analysis. See [Reference Steel and Woodin33], [Reference Steel, Foreman and Kanamori30, Chapter 8] and [Reference Sargsyan13].
${\mathcal { Q}}$
using standard arguments from the hod analysis. See [Reference Steel and Woodin33], [Reference Steel, Foreman and Kanamori30, Chapter 8] and [Reference Sargsyan13].
5 Cutpoint Suslin cardinals on a cone
In order to prove that every regular Suslin cardinal is
![]() $\omega $
-club
$\omega $
-club
![]() $\Theta $
-Berkeley, we need to represent Suslin cardinals as cutpoint cardinals in various
$\Theta $
-Berkeley, we need to represent Suslin cardinals as cutpoint cardinals in various
![]() ${\textsf {HOD}}$
-like models. This topic has been studied in [Reference Steel31] and [Reference Jackson, Sargsyan and Steel4]. The present method is motivated by a precursor of [Reference Jackson, Sargsyan and Steel4, Theorem 0.3].
${\textsf {HOD}}$
-like models. This topic has been studied in [Reference Steel31] and [Reference Jackson, Sargsyan and Steel4]. The present method is motivated by a precursor of [Reference Jackson, Sargsyan and Steel4, Theorem 0.3].
Theorem 5.1. Assume
![]() $\textsf {AD}^{+}$
and that
$\textsf {AD}^{+}$
and that
![]() $\delta $
is a regular Suslin cardinal such that there is a triple
$\delta $
is a regular Suslin cardinal such that there is a triple
![]() $(R, \Psi , H, \alpha )$
absorbing
$(R, \Psi , H, \alpha )$
absorbing
![]() $\delta $
. Then letting
$\delta $
. Then letting
![]() $H(x)=({\mathcal {P} }_x, \Sigma _x)$
, for a Turing cone of x,
$H(x)=({\mathcal {P} }_x, \Sigma _x)$
, for a Turing cone of x,
![]() $\delta $
is a limit of cutpoint cardinals in
$\delta $
is a limit of cutpoint cardinals in
![]() ${\mathcal {M}}_\infty ({\mathcal {P} }_x, \Sigma _x)$
, and hence,
${\mathcal {M}}_\infty ({\mathcal {P} }_x, \Sigma _x)$
, and hence,
![]() $\delta $
is also a cutpoint cardinal.
$\delta $
is also a cutpoint cardinal.
Proof. For each
![]() $x\in \mathrm {dom}(H)$
, set
$x\in \mathrm {dom}(H)$
, set
![]() ${\mathcal {M}}_x={\mathcal {M}}_\infty ({\mathcal {P} }_x, \Sigma _x)$
. We assume toward a contradiction that
${\mathcal {M}}_x={\mathcal {M}}_\infty ({\mathcal {P} }_x, \Sigma _x)$
. We assume toward a contradiction that
-
(*) for a Turing cone of x, there is
 $\kappa <\delta $
such that
$\kappa <\delta $
such that
 $o^{{\mathcal {M}}_x}(\kappa )\geq \delta $
.
$o^{{\mathcal {M}}_x}(\kappa )\geq \delta $
.
Because
![]() $\delta $
is a regular cardinal, we have that for every
$\delta $
is a regular cardinal, we have that for every
![]() $x\in {\mathbb {R}}$
,
$x\in {\mathbb {R}}$
,
![]() ${\mathcal {M}}_x\vDash \text {`}\delta $
is a measurable cardinal’. To see this, assume not. Let
${\mathcal {M}}_x\vDash \text {`}\delta $
is a measurable cardinal’. To see this, assume not. Let
![]() ${\mathcal { Q}}$
be a
${\mathcal { Q}}$
be a
![]() $\Sigma _x$
-iterate of
$\Sigma _x$
-iterate of
![]() ${\mathcal {P} }_x$
such that
${\mathcal {P} }_x$
such that
![]() $\delta \in \mathrm {rge}(\pi _{{\mathcal { Q}}, \infty })$
, and set
$\delta \in \mathrm {rge}(\pi _{{\mathcal { Q}}, \infty })$
, and set
![]() $\delta _{\mathcal { Q}}=\pi _{{\mathcal { Q}}, \infty }^{-1}(\delta )$
. We then have that
$\delta _{\mathcal { Q}}=\pi _{{\mathcal { Q}}, \infty }^{-1}(\delta )$
. We then have that
![]() ${\mathcal { Q}}\vDash \text {`}\delta _{\mathcal { Q}}$
is a regular non-measurable cardinal’. But then
${\mathcal { Q}}\vDash \text {`}\delta _{\mathcal { Q}}$
is a regular non-measurable cardinal’. But then
![]() $\pi _{{\mathcal { Q}}, \infty }[\delta _{\mathcal { Q}}]$
is cofinal in
$\pi _{{\mathcal { Q}}, \infty }[\delta _{\mathcal { Q}}]$
is cofinal in
![]() $\delta $
, implying that
$\delta $
, implying that
![]() $\mathrm {cf}(\delta )=\omega $
. It then follows from (*) that
$\mathrm {cf}(\delta )=\omega $
. It then follows from (*) that
-
(**) for a Turing cone of x, there is
 $\kappa <\delta $
such that
$\kappa <\delta $
such that
 $o^{{\mathcal {M}}_x}(\kappa )\geq (\delta ^+)^{{\mathcal {M}}_x}$
.
$o^{{\mathcal {M}}_x}(\kappa )\geq (\delta ^+)^{{\mathcal {M}}_x}$
.
Because
![]() $\delta $
is a Suslin cardinal, we have a tree T on
$\delta $
is a Suslin cardinal, we have a tree T on
![]() $\omega \times \delta $
such that
$\omega \times \delta $
such that
![]() $p[T]$
is not
$p[T]$
is not
![]() $\alpha $
-Suslin for any
$\alpha $
-Suslin for any
![]() $\alpha <\delta $
. Because
$\alpha <\delta $
. Because
![]() $(R, \Psi , H, \alpha )$
absorbs
$(R, \Psi , H, \alpha )$
absorbs
![]() $\delta $
, we have that for a Turing cone of x,
$\delta $
, we have that for a Turing cone of x,
![]() $T\in {\mathcal {M}}_x$
. Thus, we have an
$T\in {\mathcal {M}}_x$
. Thus, we have an
![]() $x\in \mathrm {dom}(H)$
such that
$x\in \mathrm {dom}(H)$
such that
-
(***) there is
 $\kappa <\delta $
such that
$\kappa <\delta $
such that
 $o^{{\mathcal {M}}_x}(\kappa )\geq (\delta ^+)^{{\mathcal {M}}_x}$
and
$o^{{\mathcal {M}}_x}(\kappa )\geq (\delta ^+)^{{\mathcal {M}}_x}$
and
 $T\in {\mathcal {M}}_x$
.
$T\in {\mathcal {M}}_x$
.
Let
![]() $(\kappa , \iota )$
be the lexicographically least pair
$(\kappa , \iota )$
be the lexicographically least pair
![]() $(\nu , \zeta )$
such that
$(\nu , \zeta )$
such that
![]() $\nu $
witnesses (***) and, letting
$\nu $
witnesses (***) and, letting
![]() $F=\vec {E}^{{\mathcal {M}}_x}(\zeta )$
,
$F=\vec {E}^{{\mathcal {M}}_x}(\zeta )$
,
![]() $\mathrm {crit }(F)=\nu $
and
$\mathrm {crit }(F)=\nu $
and
![]() $T\in Ult({\mathcal {M}}_x, F)$
. Thus,
$T\in Ult({\mathcal {M}}_x, F)$
. Thus,
![]() $\kappa $
is a limit of cutpoints of
$\kappa $
is a limit of cutpoints of
![]() ${\mathcal {M}}_x$
. Let
${\mathcal {M}}_x$
. Let
![]() ${\mathcal { Q}}$
be a
${\mathcal { Q}}$
be a
![]() $\Sigma _x$
-iterate of
$\Sigma _x$
-iterate of
![]() ${\mathcal {P} }_x$
such that
${\mathcal {P} }_x$
such that
![]() $(\kappa , \delta , T, E)\in \mathrm {rge}(\pi _{{\mathcal { Q}}, \infty })$
where
$(\kappa , \delta , T, E)\in \mathrm {rge}(\pi _{{\mathcal { Q}}, \infty })$
where
![]() $E=\vec {E}^{{\mathcal {M}}_x}(\iota )$
. Set
$E=\vec {E}^{{\mathcal {M}}_x}(\iota )$
. Set
![]() $\Lambda =(\Sigma _x)_{\mathcal { Q}}$
. Given a complete
$\Lambda =(\Sigma _x)_{\mathcal { Q}}$
. Given a complete
![]() $\Lambda $
-iterate
$\Lambda $
-iterate
![]() ${\mathcal R}$
of
${\mathcal R}$
of
![]() ${\mathcal { Q}}$
, let
${\mathcal { Q}}$
, let
![]() $s_{\mathcal R}=_{def}(\kappa _{\mathcal R}, \delta _{\mathcal R}, T_{\mathcal R}, E_{\mathcal R})\in {\mathcal R}$
be such that
$s_{\mathcal R}=_{def}(\kappa _{\mathcal R}, \delta _{\mathcal R}, T_{\mathcal R}, E_{\mathcal R})\in {\mathcal R}$
be such that
If
![]() ${\mathcal R}$
is a complete
${\mathcal R}$
is a complete
![]() $\Lambda $
-iterate of
$\Lambda $
-iterate of
![]() ${\mathcal { Q}}$
, let
${\mathcal { Q}}$
, let
![]() ${\mathcal R}_E=Ult({\mathcal R}, E_{\mathcal R})$
. Let
${\mathcal R}_E=Ult({\mathcal R}, E_{\mathcal R})$
. Let
![]() $(f_{\mathcal { Q}}, s_{\mathcal { Q}})\in {\mathcal { Q}}$
be such that
$(f_{\mathcal { Q}}, s_{\mathcal { Q}})\in {\mathcal { Q}}$
be such that
![]() $s_{\mathcal { Q}}\in \nu (E_{\mathcal { Q}})^{<\omega }$
,
$s_{\mathcal { Q}}\in \nu (E_{\mathcal { Q}})^{<\omega }$
,
![]() $f_{\mathcal { Q}}:[\kappa _{\mathcal { Q}}]^{\left |s_{\mathcal { Q}}\right |}\rightarrow {\mathcal { Q}}|\kappa _{\mathcal { Q}}$
, and
$f_{\mathcal { Q}}:[\kappa _{\mathcal { Q}}]^{\left |s_{\mathcal { Q}}\right |}\rightarrow {\mathcal { Q}}|\kappa _{\mathcal { Q}}$
, and
![]() $\pi _{E_{\mathcal { Q}}}(f_{\mathcal { Q}})(s_{\mathcal { Q}})=T_{\mathcal { Q}}$
. Thus, if
$\pi _{E_{\mathcal { Q}}}(f_{\mathcal { Q}})(s_{\mathcal { Q}})=T_{\mathcal { Q}}$
. Thus, if
![]() ${\mathcal R}$
is a complete
${\mathcal R}$
is a complete
![]() $\Lambda $
-iterate of
$\Lambda $
-iterate of
![]() ${\mathcal { Q}}$
, then
${\mathcal { Q}}$
, then
![]() $\pi _{E_{\mathcal R}}(f_{\mathcal R})(s_{\mathcal R})=T_{\mathcal R}$
.
$\pi _{E_{\mathcal R}}(f_{\mathcal R})(s_{\mathcal R})=T_{\mathcal R}$
.
Say
![]() $(\lambda , s)\in \kappa \times \kappa ^{<\omega }$
is good if there is a complete
$(\lambda , s)\in \kappa \times \kappa ^{<\omega }$
is good if there is a complete
![]() $\Lambda $
-iterate
$\Lambda $
-iterate
![]() ${\mathcal R}$
of
${\mathcal R}$
of
![]() ${\mathcal { Q}}$
such that
${\mathcal { Q}}$
such that
![]() $(\lambda , s)=\pi _{{\mathcal R}_E, \infty }(\delta _{\mathcal R}, s_{\mathcal R})$
. Suppose
$(\lambda , s)=\pi _{{\mathcal R}_E, \infty }(\delta _{\mathcal R}, s_{\mathcal R})$
. Suppose
![]() $(\lambda , s)$
is good and
$(\lambda , s)$
is good and
![]() ${\mathcal R}$
witnesses it. Then let
${\mathcal R}$
witnesses it. Then let
Lemma 5.2. Suppose
![]() $(\lambda , s)$
is good as witnessed by
$(\lambda , s)$
is good as witnessed by
![]() ${\mathcal R}$
and
${\mathcal R}$
and
![]() ${\mathcal R}'$
. Then
${\mathcal R}'$
. Then
![]() $T_{{\mathcal R}, \lambda , s}=T_{{\mathcal R}', \lambda , s}$
.
$T_{{\mathcal R}, \lambda , s}=T_{{\mathcal R}', \lambda , s}$
.
Proof. Let
![]() ${\mathcal {T}}={\mathcal {T}}_{{\mathcal { Q}}, {\mathcal R}}$
and
${\mathcal {T}}={\mathcal {T}}_{{\mathcal { Q}}, {\mathcal R}}$
and
![]() ${\mathcal {T}}'={\mathcal {T}}_{{\mathcal { Q}}, {\mathcal R}'}$
. Let
${\mathcal {T}}'={\mathcal {T}}_{{\mathcal { Q}}, {\mathcal R}'}$
. Let
![]() $\zeta $
be the
$\zeta $
be the
![]() ${\mathcal R}_E$
-successor of
${\mathcal R}_E$
-successor of
![]() $o^{{\mathcal R}_E}(\kappa _{\mathcal R})$
and
$o^{{\mathcal R}_E}(\kappa _{\mathcal R})$
and
![]() $\zeta '$
be the
$\zeta '$
be the
![]() ${\mathcal R}'$
-successor of
${\mathcal R}'$
-successor of
![]() $o^{{\mathcal R}^{\prime }_E}(\kappa _{{\mathcal R}'})$
. Let
$o^{{\mathcal R}^{\prime }_E}(\kappa _{{\mathcal R}'})$
. Let
![]() $({\mathcal R}", \Phi )$
be a common iterate of
$({\mathcal R}", \Phi )$
be a common iterate of
![]() $({\mathcal R}_E|\zeta , \Lambda _{{\mathcal R}_E})$
and
$({\mathcal R}_E|\zeta , \Lambda _{{\mathcal R}_E})$
and
![]() $({\mathcal R}^{\prime }_E|\zeta ', \Lambda _{{\mathcal R}^{\prime }_E})$
.Footnote
32
$({\mathcal R}^{\prime }_E|\zeta ', \Lambda _{{\mathcal R}^{\prime }_E})$
.Footnote
32
It is enough to show that
![]() $\pi _{{\mathcal R}_E|\zeta , {\mathcal R}"}(T_{\mathcal R})=\pi _{{\mathcal R}^{\prime }_E|\zeta ', {\mathcal R}"}(T_{{\mathcal R}'})$
.
$\pi _{{\mathcal R}_E|\zeta , {\mathcal R}"}(T_{\mathcal R})=\pi _{{\mathcal R}^{\prime }_E|\zeta ', {\mathcal R}"}(T_{{\mathcal R}'})$
.
Let now
![]() ${\mathcal {Y}}$
be the result of copying
${\mathcal {Y}}$
be the result of copying
![]() ${\mathcal {T}}_{{\mathcal R}_E|\zeta , {\mathcal R}"}$
onto
${\mathcal {T}}_{{\mathcal R}_E|\zeta , {\mathcal R}"}$
onto
![]() ${\mathcal R}_E$
via
${\mathcal R}_E$
via
![]() $id$
,
$id$
,
![]() ${\mathcal {Y}}'$
be the result of copying
${\mathcal {Y}}'$
be the result of copying
![]() ${\mathcal {T}}_{{\mathcal R}^{\prime }_E|\zeta ', {\mathcal R}"}$
onto
${\mathcal {T}}_{{\mathcal R}^{\prime }_E|\zeta ', {\mathcal R}"}$
onto
![]() ${\mathcal R}_E'$
via
${\mathcal R}_E'$
via
![]() $id$
,
$id$
,
![]() ${\mathcal {X}}={\mathcal {T}}^{\frown } \{E_{\mathcal R}\}^{\frown } {\mathcal {Y}}$
, and
${\mathcal {X}}={\mathcal {T}}^{\frown } \{E_{\mathcal R}\}^{\frown } {\mathcal {Y}}$
, and
![]() ${\mathcal {X}}'={\mathcal {T}}^{\prime \frown }\{E_{{\mathcal R}'}\}^{\frown } {\mathcal {Y}}'$
. Notice that we have
${\mathcal {X}}'={\mathcal {T}}^{\prime \frown }\{E_{{\mathcal R}'}\}^{\frown } {\mathcal {Y}}'$
. Notice that we have
-
(1.1)
 $\pi ^{\mathcal {Y}}\restriction {\mathcal R}_E|\zeta =\pi ^{{\mathcal {T}}_{{\mathcal R}_E|\zeta , {\mathcal R}"}}$
and
$\pi ^{\mathcal {Y}}\restriction {\mathcal R}_E|\zeta =\pi ^{{\mathcal {T}}_{{\mathcal R}_E|\zeta , {\mathcal R}"}}$
and
 $\pi ^{{\mathcal {Y}}'}\restriction {\mathcal R}^{\prime }_E|\zeta '=\pi ^{{\mathcal {T}}_{{\mathcal R}^{\prime }_E|\zeta ', {\mathcal R}"}}$
,
$\pi ^{{\mathcal {Y}}'}\restriction {\mathcal R}^{\prime }_E|\zeta '=\pi ^{{\mathcal {T}}_{{\mathcal R}^{\prime }_E|\zeta ', {\mathcal R}"}}$
, -
(1.2)
 $\pi _{{\mathcal R}_E|\zeta , {\mathcal R}"}(\kappa _{\mathcal R}, \delta _{\mathcal R}, s_{\mathcal R})=\pi _{{\mathcal R}^{\prime }_E|\zeta , {\mathcal R}"}(\kappa _{{\mathcal R}'}, \delta _{{\mathcal R}'}, s_{{\mathcal R}'})=_{def}(\kappa _0, \delta _0, s_0)$
,
$\pi _{{\mathcal R}_E|\zeta , {\mathcal R}"}(\kappa _{\mathcal R}, \delta _{\mathcal R}, s_{\mathcal R})=\pi _{{\mathcal R}^{\prime }_E|\zeta , {\mathcal R}"}(\kappa _{{\mathcal R}'}, \delta _{{\mathcal R}'}, s_{{\mathcal R}'})=_{def}(\kappa _0, \delta _0, s_0)$
, -
(1.3)
 $\pi _{{\mathcal R}_E|\zeta , {\mathcal R}"}(T_{\mathcal R})=\pi ^{\mathcal {X}}(f_{\mathcal { Q}})(\pi _{{\mathcal R}_E|\zeta , {\mathcal R}"}(s_{\mathcal R}))=\pi ^{\mathcal {X}}(f_{\mathcal { Q}})(s_0)$
,
$\pi _{{\mathcal R}_E|\zeta , {\mathcal R}"}(T_{\mathcal R})=\pi ^{\mathcal {X}}(f_{\mathcal { Q}})(\pi _{{\mathcal R}_E|\zeta , {\mathcal R}"}(s_{\mathcal R}))=\pi ^{\mathcal {X}}(f_{\mathcal { Q}})(s_0)$
, -
(1.4)
 $\pi _{{\mathcal R}^{\prime }_E|\zeta ', {\mathcal R}"}(T_{{\mathcal R}'})=\pi ^{{\mathcal {X}}'}(f_{\mathcal { Q}})(\pi _{{\mathcal R}^{\prime }_E|\zeta ', {\mathcal R}"}(s_{{\mathcal R}'}))=\pi ^{{\mathcal {X}}'}(f_{\mathcal { Q}})(s_0)$
.
$\pi _{{\mathcal R}^{\prime }_E|\zeta ', {\mathcal R}"}(T_{{\mathcal R}'})=\pi ^{{\mathcal {X}}'}(f_{\mathcal { Q}})(\pi _{{\mathcal R}^{\prime }_E|\zeta ', {\mathcal R}"}(s_{{\mathcal R}'}))=\pi ^{{\mathcal {X}}'}(f_{\mathcal { Q}})(s_0)$
.
Let
![]() ${\mathcal {U}}$
be the full normalization of
${\mathcal {U}}$
be the full normalization of
![]() ${\mathcal {X}}$
and
${\mathcal {X}}$
and
![]() ${\mathcal {U}}'$
be the full normalization of
${\mathcal {U}}'$
be the full normalization of
![]() ${\mathcal {X}}'$
. Notice that if
${\mathcal {X}}'$
. Notice that if
![]() ${\mathcal {S}}$
is the last model of
${\mathcal {S}}$
is the last model of
![]() ${\mathcal {U}}$
, and
${\mathcal {U}}$
, and
![]() ${\mathcal {S}}'$
is the last model of
${\mathcal {S}}'$
is the last model of
![]() ${\mathcal {U}}'$
, then
${\mathcal {U}}'$
, then
-
(2.1)
 ${\mathcal R}"\trianglelefteq {\mathcal {S}}$
and
${\mathcal R}"\trianglelefteq {\mathcal {S}}$
and
 ${\mathcal R}"\trianglelefteq {\mathcal {S}}'$
,
${\mathcal R}"\trianglelefteq {\mathcal {S}}'$
, -
(2.2)
 $(\Lambda _{{\mathcal {S}}})_{{\mathcal R}"}=(\Lambda _{{\mathcal {S}}'})_{{\mathcal R}"}$
,Footnote
33
and
$(\Lambda _{{\mathcal {S}}})_{{\mathcal R}"}=(\Lambda _{{\mathcal {S}}'})_{{\mathcal R}"}$
,Footnote
33
and -
(2.3) the least-extender-disagreement comparison of
 $({\mathcal {S}}, \Lambda _{\mathcal {S}})$
and
$({\mathcal {S}}, \Lambda _{\mathcal {S}})$
and
 $({\mathcal {S}}', \Lambda _{{\mathcal {S}}'})$
is above
$({\mathcal {S}}', \Lambda _{{\mathcal {S}}'})$
is above
 ${\textsf {Ord}}\cap {\mathcal R}"$
.
${\textsf {Ord}}\cap {\mathcal R}"$
.
Let then
![]() $({\mathcal {W} }, \Lambda _{\mathcal {W} })$
be the common iterate of
$({\mathcal {W} }, \Lambda _{\mathcal {W} })$
be the common iterate of
![]() $({\mathcal {S}}, \Lambda _{\mathcal {S}})$
and
$({\mathcal {S}}, \Lambda _{\mathcal {S}})$
and
![]() $({\mathcal {S}}', \Lambda _{{\mathcal {S}}'})$
obtained via the least-extender-disagreement comparison process. We then have that
$({\mathcal {S}}', \Lambda _{{\mathcal {S}}'})$
obtained via the least-extender-disagreement comparison process. We then have that
-
(3.1)
 $\pi _{{\mathcal R}_E|\zeta , {\mathcal R}"}(T_{\mathcal R})=\pi _{{\mathcal { Q}}, {\mathcal {W} }}(f_{\mathcal { Q}})(s_0)$
,
$\pi _{{\mathcal R}_E|\zeta , {\mathcal R}"}(T_{\mathcal R})=\pi _{{\mathcal { Q}}, {\mathcal {W} }}(f_{\mathcal { Q}})(s_0)$
, -
(3.2)
 $\pi _{{\mathcal R}^{\prime }_E|\zeta ', {\mathcal R}"}(T_{{\mathcal R}'})=\pi _{{\mathcal { Q}}, {\mathcal {W} }}(f_{\mathcal { Q}})(s_0)$
.
$\pi _{{\mathcal R}^{\prime }_E|\zeta ', {\mathcal R}"}(T_{{\mathcal R}'})=\pi _{{\mathcal { Q}}, {\mathcal {W} }}(f_{\mathcal { Q}})(s_0)$
.
It then follows from (3.1)–(3.2) that
![]() $\pi _{{\mathcal R}_E, {\mathcal R}"}(T_{\mathcal R})=\pi _{{\mathcal R}', {\mathcal R}"}(T_{{\mathcal R}'})$
.
$\pi _{{\mathcal R}_E, {\mathcal R}"}(T_{\mathcal R})=\pi _{{\mathcal R}', {\mathcal R}"}(T_{{\mathcal R}'})$
.
Thus,
![]() $T_{{\mathcal R}, \lambda , s}$
is independent of
$T_{{\mathcal R}, \lambda , s}$
is independent of
![]() ${\mathcal R}$
, and so we let
${\mathcal R}$
, and so we let
![]() $T_{\lambda , s}=T_{{\mathcal R}, \lambda , s}$
.
$T_{\lambda , s}=T_{{\mathcal R}, \lambda , s}$
.
Lemma 5.3. For each good
![]() $(\lambda , s)$
,
$(\lambda , s)$
,
![]() $p[T_{\lambda , s}]\subseteq p[T]$
.
$p[T_{\lambda , s}]\subseteq p[T]$
.
Proof. Suppose
![]() $(y, h)\in p[T_{\lambda , s}]$
. Let
$(y, h)\in p[T_{\lambda , s}]$
. Let
![]() ${\mathcal R}$
witness that
${\mathcal R}$
witness that
![]() $(\lambda , s)$
is good. Let
$(\lambda , s)$
is good. Let
![]() ${\mathcal {S}}$
be a complete
${\mathcal {S}}$
be a complete
![]() $\Lambda _{{\mathcal R}_E}$
-iterate of
$\Lambda _{{\mathcal R}_E}$
-iterate of
![]() ${\mathcal R}_E$
such that
${\mathcal R}_E$
such that
![]() $h\subseteq \mathrm {rge}(\pi _{{\mathcal {S}}, \infty })$
. We can further assume that
$h\subseteq \mathrm {rge}(\pi _{{\mathcal {S}}, \infty })$
. We can further assume that
![]() ${\mathcal {T}}=_{def}{\mathcal {T}}_{{\mathcal R}_E, {\mathcal {S}}}$
is based on
${\mathcal {T}}=_{def}{\mathcal {T}}_{{\mathcal R}_E, {\mathcal {S}}}$
is based on
![]() ${\mathcal R}|\zeta $
, where
${\mathcal R}|\zeta $
, where
![]() $\zeta $
is the
$\zeta $
is the
![]() ${\mathcal R}_E$
-successor of
${\mathcal R}_E$
-successor of
![]() $o^{{\mathcal R}_E}(\kappa _{\mathcal R})$
. Let
$o^{{\mathcal R}_E}(\kappa _{\mathcal R})$
. Let
![]() $(\alpha _n: n\in \omega )$
be such that
$(\alpha _n: n\in \omega )$
be such that
![]() $h(n)=\pi _{{\mathcal {S}}, \infty }(\alpha _n)$
. Let
$h(n)=\pi _{{\mathcal {S}}, \infty }(\alpha _n)$
. Let
![]() $U=\pi _{{\mathcal R}_E, {\mathcal {S}}}(T_{\mathcal R})$
. Thus, if
$U=\pi _{{\mathcal R}_E, {\mathcal {S}}}(T_{\mathcal R})$
. Thus, if
![]() $h'(n)=\alpha _n$
, then
$h'(n)=\alpha _n$
, then
![]() $(y, h')\in [U]$
.
$(y, h')\in [U]$
.
Notice that
![]() $\{E_{\mathcal R}\}^{\frown } {\mathcal {T}}$
is not a normal tree, and its full normalization
$\{E_{\mathcal R}\}^{\frown } {\mathcal {T}}$
is not a normal tree, and its full normalization
![]() ${\mathcal {U}}$
starts with
${\mathcal {U}}$
starts with
![]() ${\mathcal {T}}$
. Notice also that for each
${\mathcal {T}}$
. Notice also that for each
![]() $\alpha +1<\mathrm {lh}({\mathcal {T}})$
, if
$\alpha +1<\mathrm {lh}({\mathcal {T}})$
, if
![]() $E^{\mathcal {T}}_\alpha $
used on the main branch of
$E^{\mathcal {T}}_\alpha $
used on the main branch of
![]() ${\mathcal {T}}$
at
${\mathcal {T}}$
at
![]() $\beta <\mathrm {lh}({\mathcal {T}})$
, then
$\beta <\mathrm {lh}({\mathcal {T}})$
, then
![]() $\mathrm {crit }(E_\alpha ^{\mathcal {T}})<\pi _{0, \beta }^{\mathcal {T}}(\delta _{\mathcal R})$
. This is because
$\mathrm {crit }(E_\alpha ^{\mathcal {T}})<\pi _{0, \beta }^{\mathcal {T}}(\delta _{\mathcal R})$
. This is because
![]() ${\mathcal R}_E\vDash \left |o^{{\mathcal R}_E}(\kappa _{\mathcal R})\right |=\delta _{\mathcal R}$
, as otherwise there would be another extender
${\mathcal R}_E\vDash \left |o^{{\mathcal R}_E}(\kappa _{\mathcal R})\right |=\delta _{\mathcal R}$
, as otherwise there would be another extender
![]() $F\in \vec {E}^{{\mathcal R}_E}\cap \vec {E}^{\mathcal R}$
such that
$F\in \vec {E}^{{\mathcal R}_E}\cap \vec {E}^{\mathcal R}$
such that
![]() $\mathrm {crit }(F)=\kappa _{\mathcal R}$
and
$\mathrm {crit }(F)=\kappa _{\mathcal R}$
and
![]() $T_{\mathcal R}\in Ult({\mathcal R}, F)$
, contradicting the minimality of
$T_{\mathcal R}\in Ult({\mathcal R}, F)$
, contradicting the minimality of
![]() $E_{\mathcal R}$
. Let
$E_{\mathcal R}$
. Let
![]() $\alpha $
be such that
$\alpha $
be such that
![]() ${\mathcal {T}}={\mathcal {U}}\restriction \alpha +1$
. Our discussion shows that
${\mathcal {T}}={\mathcal {U}}\restriction \alpha +1$
. Our discussion shows that
![]() $\pi ^{\mathcal {U}}_{0, \alpha }$
is defined.
$\pi ^{\mathcal {U}}_{0, \alpha }$
is defined.
Set
![]() ${\mathcal {S}}'={\mathcal {M}}_\alpha ^{\mathcal {U}}$
and
${\mathcal {S}}'={\mathcal {M}}_\alpha ^{\mathcal {U}}$
and
![]() $h^{*}(n)=\pi ^{\Lambda _{{\mathcal {S}}'}}_{{\mathcal {S}}', \infty }(\alpha _n)$
. We now have that
$h^{*}(n)=\pi ^{\Lambda _{{\mathcal {S}}'}}_{{\mathcal {S}}', \infty }(\alpha _n)$
. We now have that
![]() $(y, h')\in [T_{{\mathcal {S}}'}]$
. This is simply because
$(y, h')\in [T_{{\mathcal {S}}'}]$
. This is simply because
![]() $T_{{\mathcal {S}}'}=U$
. It then follows that
$T_{{\mathcal {S}}'}=U$
. It then follows that
![]() $(y, h^{*})\in [T]$
, and hence,
$(y, h^{*})\in [T]$
, and hence,
![]() $y\in p[T]$
.
$y\in p[T]$
.
Lemma 5.4. For each
![]() $y\in p[T]$
, there is a good
$y\in p[T]$
, there is a good
![]() $(\lambda , s)$
such that
$(\lambda , s)$
such that
![]() $y\in p[T_{\lambda , s}]$
.
$y\in p[T_{\lambda , s}]$
.
Proof. Fix
![]() $y\in p[T]$
, and let
$y\in p[T]$
, and let
![]() $h\in \kappa ^\omega $
be such that
$h\in \kappa ^\omega $
be such that
![]() $(y, h)\in [T]$
. We can find a complete
$(y, h)\in [T]$
. We can find a complete
![]() $\Lambda $
-iterate
$\Lambda $
-iterate
![]() ${\mathcal R}$
of
${\mathcal R}$
of
![]() ${\mathcal { Q}}$
such that for each n,
${\mathcal { Q}}$
such that for each n,
![]() $h(n)\in \mathrm { rge}(\pi _{{\mathcal R}, \infty })$
. Set
$h(n)\in \mathrm { rge}(\pi _{{\mathcal R}, \infty })$
. Set
![]() $h'(n)=\pi ^{-1}_{{\mathcal R}, \infty }(h(n))$
. Let
$h'(n)=\pi ^{-1}_{{\mathcal R}, \infty }(h(n))$
. Let
![]() $(\lambda , s)=\pi _{{\mathcal R}_E, \infty }(\delta _{\mathcal R}, s_{\mathcal R})$
. As
$(\lambda , s)=\pi _{{\mathcal R}_E, \infty }(\delta _{\mathcal R}, s_{\mathcal R})$
. As
![]() $(y, h')\in [T_{\mathcal R}]$
, we easily get that
$(y, h')\in [T_{\mathcal R}]$
, we easily get that
![]() $(y, \pi _{{\mathcal R}_E, \infty }[h'])\in [T_{\lambda , s}]$
. Hence,
$(y, \pi _{{\mathcal R}_E, \infty }[h'])\in [T_{\lambda , s}]$
. Hence,
![]() $y\in p[T_{\lambda , s}]$
.
$y\in p[T_{\lambda , s}]$
.
We thus have that
![]() $p[T]=\bigcup \{ p[T_{\lambda , s}]: (\lambda , s)\in \kappa \times \kappa ^{<\omega }$
and
$p[T]=\bigcup \{ p[T_{\lambda , s}]: (\lambda , s)\in \kappa \times \kappa ^{<\omega }$
and
![]() $(\lambda , s)$
is good
$(\lambda , s)$
is good
![]() $\}$
. Consider now the tree U give by:
$\}$
. Consider now the tree U give by:
![]() $(u, h)\in U$
if and only if
$(u, h)\in U$
if and only if
-
1. if
 $0\in \mathrm {dom}(h)$
, then
$0\in \mathrm {dom}(h)$
, then
 $h(0)=(\lambda _0, s_0)$
is good, and
$h(0)=(\lambda _0, s_0)$
is good, and -
2. if
 $\mathrm {dom}(u)=\mathrm {dom}(h)=_{def}m>1$
, then
$\mathrm {dom}(u)=\mathrm {dom}(h)=_{def}m>1$
, then  $$ \begin{align*} (\langle u(0),..., u(m-2)\rangle, \langle h(1), h(2),..., h(m-1) \rangle)\in T_{\lambda_0, s_0}. \end{align*} $$
$$ \begin{align*} (\langle u(0),..., u(m-2)\rangle, \langle h(1), h(2),..., h(m-1) \rangle)\in T_{\lambda_0, s_0}. \end{align*} $$
Then if
![]() $(x, h)\in [U]$
, then
$(x, h)\in [U]$
, then
![]() $(x, h')\in [T]$
, where
$(x, h')\in [T]$
, where
![]() $h'(n)=h(n+1)$
. Also, if
$h'(n)=h(n+1)$
. Also, if
![]() $(x, h)\in [T]$
, then for some good
$(x, h)\in [T]$
, then for some good
![]() $(\lambda , s)$
and
$(\lambda , s)$
and
![]() $g\in \lambda ^\omega $
,
$g\in \lambda ^\omega $
,
![]() $(x, g)\in [T_{\lambda , s}]$
. Consequently,
$(x, g)\in [T_{\lambda , s}]$
. Consequently,
![]() $(x, g')\in [U]$
, where
$(x, g')\in [U]$
, where
![]() $g'(0)=(\lambda , s)$
and for
$g'(0)=(\lambda , s)$
and for
![]() $n\geq 1$
,
$n\geq 1$
,
![]() $g'(n)=h(n-1)$
. We thus have that
$g'(n)=h(n-1)$
. We thus have that
![]() $p[T]=p[U]$
, and as U can be represented as a tree on
$p[T]=p[U]$
, and as U can be represented as a tree on
![]() $\omega \times \kappa $
and
$\omega \times \kappa $
and
![]() $\kappa <\delta $
, we get a contradiction to our assumption that
$\kappa <\delta $
, we get a contradiction to our assumption that
![]() $p[T]$
is not
$p[T]$
is not
![]() $\alpha $
-Suslin for any
$\alpha $
-Suslin for any
![]() $\alpha <\delta $
.
$\alpha <\delta $
.
6 On X-hod analysis
Definition 6.1. Suppose
![]() ${\mathcal {P} }$
is a premouse, an lbr premouse, or just some kind of hybrid premouse. Suppose
${\mathcal {P} }$
is a premouse, an lbr premouse, or just some kind of hybrid premouse. Suppose
![]() $F\in \vec {E}^{\mathcal {P} }$
. Then F is completely total if F is a total extender of
$F\in \vec {E}^{\mathcal {P} }$
. Then F is completely total if F is a total extender of
![]() ${\mathcal {P} }$
and
${\mathcal {P} }$
and
![]() $\nu (F)$
is a regular cardinal of F.
$\nu (F)$
is a regular cardinal of F.
Definition 6.2. Suppose
![]() ${\mathcal {P} }$
is a premouse, an lbr premouse or just some kind of hybrid premouse. Suppose
${\mathcal {P} }$
is a premouse, an lbr premouse or just some kind of hybrid premouse. Suppose
![]() $\xi <\gamma <{\textsf {Ord}}\cap {\mathcal {P} }$
, and
$\xi <\gamma <{\textsf {Ord}}\cap {\mathcal {P} }$
, and
![]() ${\mathcal {T}}$
is an iteration tree on
${\mathcal {T}}$
is an iteration tree on
![]() ${\mathcal {P} }$
. Then
${\mathcal {P} }$
. Then
![]() ${\mathcal {T}}$
omits
${\mathcal {T}}$
omits
![]() $(\xi , \gamma )$
if whenever
$(\xi , \gamma )$
if whenever
![]() $\alpha <\mathrm {lh}({\mathcal {T}})$
is such that
$\alpha <\mathrm {lh}({\mathcal {T}})$
is such that
![]() $\pi ^{{\mathcal {T}}}_{0, \alpha }$
is defined, then
$\pi ^{{\mathcal {T}}}_{0, \alpha }$
is defined, then
-
1.
 $\mathrm {lh}(E_\alpha ^{{\mathcal {T}}})\not \in (\pi _{0, \alpha }^{\mathcal {T}}(\xi ), \pi _{0, \alpha }^{\mathcal {T}}(\gamma ))$
, and
$\mathrm {lh}(E_\alpha ^{{\mathcal {T}}})\not \in (\pi _{0, \alpha }^{\mathcal {T}}(\xi ), \pi _{0, \alpha }^{\mathcal {T}}(\gamma ))$
, and -
2.
 $\mathrm {crit }(E_\alpha ^{{\mathcal {T}}_{{\mathcal {P} }, {\mathcal { Q}}}})\not \in (\pi _{0, \alpha }^{\mathcal {T}}(\xi ), \pi _{0, \alpha }^{\mathcal {T}}(\gamma ))$
.
$\mathrm {crit }(E_\alpha ^{{\mathcal {T}}_{{\mathcal {P} }, {\mathcal { Q}}}})\not \in (\pi _{0, \alpha }^{\mathcal {T}}(\xi ), \pi _{0, \alpha }^{\mathcal {T}}(\gamma ))$
.
Suppose
![]() $F\in \vec {E}^{\mathcal {P} }$
is a completely total extender and
$F\in \vec {E}^{\mathcal {P} }$
is a completely total extender and
![]() ${\mathcal {T}}$
is an iteration tree on
${\mathcal {T}}$
is an iteration tree on
![]() ${\mathcal {P} }$
. Then
${\mathcal {P} }$
. Then
![]() ${\mathcal {T}}$
omits F if
${\mathcal {T}}$
omits F if
![]() ${\mathcal {T}}$
omits the interval
${\mathcal {T}}$
omits the interval
![]() $(\nu (F), \mathrm {lh}(F)+1)$
.
$(\nu (F), \mathrm {lh}(F)+1)$
.
If
![]() $({\mathcal {M}}, \Lambda )$
is a mouse pair and
$({\mathcal {M}}, \Lambda )$
is a mouse pair and
![]() $F\in \vec {E}^{\mathcal {M}}$
is a completely total extender, we let
$F\in \vec {E}^{\mathcal {M}}$
is a completely total extender, we let
![]() $\mathcal {F}({\mathcal {M}}, \Lambda , F)$
Footnote
34
be the set of complete
$\mathcal {F}({\mathcal {M}}, \Lambda , F)$
Footnote
34
be the set of complete
![]() $\Lambda $
-iterates
$\Lambda $
-iterates
![]() ${\mathcal {N}}$
of
${\mathcal {N}}$
of
![]() ${\mathcal {M}}$
such that
${\mathcal {M}}$
such that
![]() ${\mathcal {T}}_{{\mathcal {N}}, {\mathcal {M}}}$
omits F.
${\mathcal {T}}_{{\mathcal {N}}, {\mathcal {M}}}$
omits F.
Definition 6.3. Suppose
![]() $(P, \Psi , H, \alpha )$
is a coarse tuple and
$(P, \Psi , H, \alpha )$
is a coarse tuple and
![]() $x\in \mathrm {dom}(H)$
. Set
$x\in \mathrm {dom}(H)$
. Set
![]() $H(x)=({\mathcal {P} }, \Sigma )$
, and suppose
$H(x)=({\mathcal {P} }, \Sigma )$
, and suppose
![]() $F\in \vec {E}^{\mathcal {P} }$
is a completely total extender such that
$F\in \vec {E}^{\mathcal {P} }$
is a completely total extender such that
![]() $\mathrm {crit }(F)$
is a cutpoint cardinal of
$\mathrm {crit }(F)$
is a cutpoint cardinal of
![]() ${\mathcal {P} }$
. Let
${\mathcal {P} }$
. Let
![]() $F^+$
, if it exists, be the extender on the extender sequence of
$F^+$
, if it exists, be the extender on the extender sequence of
![]() ${\mathcal {P} }$
such that
${\mathcal {P} }$
such that
![]() $\mathrm {crit }(F^+)=\mathrm {crit }(F)$
,
$\mathrm {crit }(F^+)=\mathrm {crit }(F)$
,
![]() $\mathrm {lh}(F^+)>\mathrm { lh}(F)$
, and
$\mathrm {lh}(F^+)>\mathrm { lh}(F)$
, and
![]() $\mathrm {lh}(F)$
is a cutpoint of
$\mathrm {lh}(F)$
is a cutpoint of
![]() $Ult({\mathcal {P} }, F^+)$
. Let
$Ult({\mathcal {P} }, F^+)$
. Let
![]() ${\mathcal {P} }(F)=Ult({\mathcal {P} }, F^+)$
, if
${\mathcal {P} }(F)=Ult({\mathcal {P} }, F^+)$
, if
![]() $F^+$
is defined, and otherwise
$F^+$
is defined, and otherwise
![]() ${\mathcal {P} }(F)={\mathcal {P} }$
.
${\mathcal {P} }(F)={\mathcal {P} }$
.
Given
![]() ${\mathcal { Q}}, {\mathcal R}\in \mathcal {F}({\mathcal {P} }(F), \Sigma , F)$
, we set
${\mathcal { Q}}, {\mathcal R}\in \mathcal {F}({\mathcal {P} }(F), \Sigma , F)$
, we set
![]() ${\mathcal { Q}}\leq _{{\mathcal {P} }, \Sigma , F} {\mathcal R}$
if
${\mathcal { Q}}\leq _{{\mathcal {P} }, \Sigma , F} {\mathcal R}$
if
![]() ${\mathcal R}\in \mathcal {F}({\mathcal { Q}}, \Sigma _{\mathcal { Q}}, \pi _{{\mathcal {P} }(F), {\mathcal { Q}}}(F))$
.
${\mathcal R}\in \mathcal {F}({\mathcal { Q}}, \Sigma _{\mathcal { Q}}, \pi _{{\mathcal {P} }(F), {\mathcal { Q}}}(F))$
.
Theorem 6.4. Continuing with the set up of Definition 6.3,
![]() $\leq _{{\mathcal {P} }, \Sigma , F}$
is directed.
$\leq _{{\mathcal {P} }, \Sigma , F}$
is directed.
Proof. We will use the following straightforward lemma.
Lemma 6.5. Suppose
![]() $({\mathcal {P} }, \Sigma )$
is a mouse pair, and suppose
$({\mathcal {P} }, \Sigma )$
is a mouse pair, and suppose
![]() ${\mathcal {T}}$
and
${\mathcal {T}}$
and
![]() ${\mathcal {U}}$
are two distinct iteration trees on
${\mathcal {U}}$
are two distinct iteration trees on
![]() ${\mathcal {P} }$
according to
${\mathcal {P} }$
according to
![]() $\Sigma $
with last models
$\Sigma $
with last models
![]() ${\mathcal { Q}}$
and
${\mathcal { Q}}$
and
![]() ${\mathcal R}$
, respectively. Suppose further that
${\mathcal R}$
, respectively. Suppose further that
![]() $\gamma $
is the least such that
$\gamma $
is the least such that
![]() ${\mathcal { Q}}|\gamma ={\mathcal R}|\gamma $
and
${\mathcal { Q}}|\gamma ={\mathcal R}|\gamma $
and
![]() ${\mathcal { Q}}||\gamma \not ={\mathcal R}||\gamma $
, and
${\mathcal { Q}}||\gamma \not ={\mathcal R}||\gamma $
, and
![]() $\xi $
is such that
$\xi $
is such that
![]() ${\mathcal {T}}\restriction \xi ={\mathcal {U}}\restriction \xi $
, but
${\mathcal {T}}\restriction \xi ={\mathcal {U}}\restriction \xi $
, but
![]() ${\mathcal {T}}\restriction \xi +1\not ={\mathcal {U}}\restriction \xi +1$
. Assume
${\mathcal {T}}\restriction \xi +1\not ={\mathcal {U}}\restriction \xi +1$
. Assume
![]() $\mathrm { lh}(E_\xi ^{\mathcal {T}})<\mathrm {lh}(E_\xi ^{\mathcal {U}})$
. Then
$\mathrm { lh}(E_\xi ^{\mathcal {T}})<\mathrm {lh}(E_\xi ^{\mathcal {U}})$
. Then
![]() $\gamma \in \mathrm {dom}(\vec {E}^{\mathcal { Q}})\cup \mathrm {dom}(\vec {E}^{\mathcal R})$
,
$\gamma \in \mathrm {dom}(\vec {E}^{\mathcal { Q}})\cup \mathrm {dom}(\vec {E}^{\mathcal R})$
,
![]() $\gamma \not \in \vec {E}^{\mathcal { Q}}$
and
$\gamma \not \in \vec {E}^{\mathcal { Q}}$
and
![]() $\vec {E}^{\mathcal R}(\gamma )=E_\xi ^{\mathcal {T}}$
.
$\vec {E}^{\mathcal R}(\gamma )=E_\xi ^{\mathcal {T}}$
.
Fix
![]() ${\mathcal { Q}}, {\mathcal R}\in \mathcal {F}({\mathcal {P} }, \Sigma , F)$
, and let
${\mathcal { Q}}, {\mathcal R}\in \mathcal {F}({\mathcal {P} }, \Sigma , F)$
, and let
![]() ${\mathcal {T}}={\mathcal {T}}^\Sigma _{{\mathcal {P} }, {\mathcal { Q}}}$
and
${\mathcal {T}}={\mathcal {T}}^\Sigma _{{\mathcal {P} }, {\mathcal { Q}}}$
and
![]() ${\mathcal {U}}={\mathcal {T}}^\Sigma _{{\mathcal {P} }, {\mathcal R}}$
. It follows from full normalization that the least-extender-disagreement comparison between
${\mathcal {U}}={\mathcal {T}}^\Sigma _{{\mathcal {P} }, {\mathcal R}}$
. It follows from full normalization that the least-extender-disagreement comparison between
![]() $({\mathcal { Q}}, \Sigma _{\mathcal { Q}})$
and
$({\mathcal { Q}}, \Sigma _{\mathcal { Q}})$
and
![]() $({\mathcal R}, \Sigma _{\mathcal R})$
produces a common iterate
$({\mathcal R}, \Sigma _{\mathcal R})$
produces a common iterate
![]() $({\mathcal {S}}, \Sigma _{\mathcal {S}})$
. We want to see that
$({\mathcal {S}}, \Sigma _{\mathcal {S}})$
. We want to see that
![]() ${\mathcal {S}}\in \mathcal {F}({\mathcal {P} }, \Sigma , F)$
, which amounts to showing that
${\mathcal {S}}\in \mathcal {F}({\mathcal {P} }, \Sigma , F)$
, which amounts to showing that
![]() ${\mathcal {Z}}=_{def}{\mathcal {T}}^\Sigma _{{\mathcal {P} }, {\mathcal {S}}}$
omits F.Footnote
35
Set
${\mathcal {Z}}=_{def}{\mathcal {T}}^\Sigma _{{\mathcal {P} }, {\mathcal {S}}}$
omits F.Footnote
35
Set
![]() ${\mathcal {X}}={\mathcal {T}}_{{\mathcal { Q}}, {\mathcal {S}}}$
and
${\mathcal {X}}={\mathcal {T}}_{{\mathcal { Q}}, {\mathcal {S}}}$
and
![]() ${\mathcal {Y}}={\mathcal {T}}_{{\mathcal R}, {\mathcal {S}}}$
. Then
${\mathcal {Y}}={\mathcal {T}}_{{\mathcal R}, {\mathcal {S}}}$
. Then
![]() ${\mathcal {Z}}$
is the full normalization of
${\mathcal {Z}}$
is the full normalization of
![]() ${\mathcal {T}}^{\frown } {\mathcal {X}}$
.
${\mathcal {T}}^{\frown } {\mathcal {X}}$
.
We now assume that
![]() ${\mathcal {X}}$
and
${\mathcal {X}}$
and
![]() ${\mathcal {Y}}$
were built by allowing padding, so that
${\mathcal {Y}}$
were built by allowing padding, so that
![]() $\mathrm { lh}({\mathcal {X}})=\mathrm {lh}({\mathcal {Y}})$
, and our strategy is to analyze the full normalization process that produces
$\mathrm { lh}({\mathcal {X}})=\mathrm {lh}({\mathcal {Y}})$
, and our strategy is to analyze the full normalization process that produces
![]() ${\mathcal {Z}}$
out of
${\mathcal {Z}}$
out of
![]() $({\mathcal {T}}, {\mathcal {X}})$
and
$({\mathcal {T}}, {\mathcal {X}})$
and
![]() $({\mathcal {T}}, {\mathcal {Y}})$
. We review some facts about the normalization process, and we do this for
$({\mathcal {T}}, {\mathcal {Y}})$
. We review some facts about the normalization process, and we do this for
![]() $({\mathcal {T}}, {\mathcal {X}})$
.
$({\mathcal {T}}, {\mathcal {X}})$
.
Recall that the full normalization process for
![]() ${\mathcal {T}}^{\frown } {\mathcal {X}}$
produces iteration trees
${\mathcal {T}}^{\frown } {\mathcal {X}}$
produces iteration trees
![]() $({\mathcal {Z}}_\alpha : \alpha <\mathrm {lh}({\mathcal {X}}))$
on
$({\mathcal {Z}}_\alpha : \alpha <\mathrm {lh}({\mathcal {X}}))$
on
![]() ${\mathcal {P} }$
, and
${\mathcal {P} }$
, and
![]() ${\mathcal {Z}}$
is simply
${\mathcal {Z}}$
is simply
![]() ${\mathcal {Z}}_{\mathrm {lh}({\mathcal {X}})-1}$
(e.g., see [Reference Schlutzenberg19] or [Reference Siskind and Steel21]). The sequence satisfies the following conditions.
${\mathcal {Z}}_{\mathrm {lh}({\mathcal {X}})-1}$
(e.g., see [Reference Schlutzenberg19] or [Reference Siskind and Steel21]). The sequence satisfies the following conditions.
-
(1.1) The last model of each
 ${\mathcal {Z}}_\alpha $
is
${\mathcal {Z}}_\alpha $
is
 ${\mathcal {M}}_\alpha ^{\mathcal {X}}$
.
${\mathcal {M}}_\alpha ^{\mathcal {X}}$
. -
(1.2) For
 $\alpha +1<\mathrm {lh}({\mathcal {X}})$
,
$\alpha +1<\mathrm {lh}({\mathcal {X}})$
,
 ${\mathcal {Z}}_{\alpha +1}$
is obtained by letting
${\mathcal {Z}}_{\alpha +1}$
is obtained by letting
 $\beta $
be the
$\beta $
be the
 ${\mathcal {X}}$
-predecessor of
${\mathcal {X}}$
-predecessor of
 $\alpha +1$
, and minimally inflating
$\alpha +1$
, and minimally inflating
 ${\mathcal {Z}}_\beta $
by
${\mathcal {Z}}_\beta $
by
 $E_\alpha ^{\mathcal {X}}$
. More precisely, letting
$E_\alpha ^{\mathcal {X}}$
. More precisely, letting
 $\gamma _0$
be the least
$\gamma _0$
be the least
 $\gamma $
such that
$\gamma $
such that
 $E_\alpha ^{\mathcal {X}}\in \vec {E}^{{\mathcal {M}}_{\gamma }^{{\mathcal {Z}}_\alpha }}$
and
$E_\alpha ^{\mathcal {X}}\in \vec {E}^{{\mathcal {M}}_{\gamma }^{{\mathcal {Z}}_\alpha }}$
and
 $\gamma _1$
be the least
$\gamma _1$
be the least
 $\gamma $
such that
$\gamma $
such that
 $\mathrm {lh}(E_{\gamma }^{{\mathcal {Z}}_\beta })>\mathrm {crit }(E_\alpha ^{\mathcal {X}})$
,
$\mathrm {lh}(E_{\gamma }^{{\mathcal {Z}}_\beta })>\mathrm {crit }(E_\alpha ^{\mathcal {X}})$
,
 ${\mathcal {Z}}_{\alpha +1}\restriction \gamma _0+1={\mathcal {Z}}_\alpha \restriction \gamma _0+1$
, and for
${\mathcal {Z}}_{\alpha +1}\restriction \gamma _0+1={\mathcal {Z}}_\alpha \restriction \gamma _0+1$
, and for
 $\iota>0$
such that
$\iota>0$
such that
 $\gamma _0+\iota <\mathrm {lh}({\mathcal {Z}}_{\alpha +1})$
,
$\gamma _0+\iota <\mathrm {lh}({\mathcal {Z}}_{\alpha +1})$
,
 ${\mathcal {M}}_{\gamma _0+\iota }^{{\mathcal {Z}}_{\alpha +1}}=Ult({\mathcal {M}}_{\gamma _1+\iota -1}^{{\mathcal {Z}}_\beta }, E_\alpha ^{\mathcal {X}})$
. Also, for
${\mathcal {M}}_{\gamma _0+\iota }^{{\mathcal {Z}}_{\alpha +1}}=Ult({\mathcal {M}}_{\gamma _1+\iota -1}^{{\mathcal {Z}}_\beta }, E_\alpha ^{\mathcal {X}})$
. Also, for
 $\iota <\gamma _0$
,
$\iota <\gamma _0$
,
 $E_\iota ^{{\mathcal {Z}}_{\alpha +1}}=E_\iota ^{{\mathcal {Z}}_\alpha }$
,
$E_\iota ^{{\mathcal {Z}}_{\alpha +1}}=E_\iota ^{{\mathcal {Z}}_\alpha }$
,
 $E_{\gamma _0}^{{\mathcal {Z}}_\alpha }=E_\alpha ^{\mathcal {X}}$
and for
$E_{\gamma _0}^{{\mathcal {Z}}_\alpha }=E_\alpha ^{\mathcal {X}}$
and for
 $\iota>0$
such that
$\iota>0$
such that
 $\gamma _0+\iota <\mathrm {lh}({\mathcal {Z}}_{\alpha +1})$
,
$\gamma _0+\iota <\mathrm {lh}({\mathcal {Z}}_{\alpha +1})$
,
 $E_{\gamma _0+\iota }^{{\mathcal {Z}}_{\alpha +1}}$
is the last extender of
$E_{\gamma _0+\iota }^{{\mathcal {Z}}_{\alpha +1}}$
is the last extender of
 $Ult({\mathcal {M}}_\iota ^{{\mathcal {Z}}_\beta }||\mathrm {lh}(E_\iota ^{{\mathcal {Z}}_\beta }), E_\alpha ^{\mathcal {X}})$
.
$Ult({\mathcal {M}}_\iota ^{{\mathcal {Z}}_\beta }||\mathrm {lh}(E_\iota ^{{\mathcal {Z}}_\beta }), E_\alpha ^{\mathcal {X}})$
. -
(1.3) Clause (1.2) above describes a natural embedding
 $\pi _{\beta , \alpha +1}: {\mathcal {Z}}_\beta \rightarrow {\mathcal {Z}}_{\alpha +1}$
, a tree embedding. If now
$\pi _{\beta , \alpha +1}: {\mathcal {Z}}_\beta \rightarrow {\mathcal {Z}}_{\alpha +1}$
, a tree embedding. If now
 $\alpha <\mathrm {lh}({\mathcal {X}})$
is a limit ordinal, then
$\alpha <\mathrm {lh}({\mathcal {X}})$
is a limit ordinal, then
 ${\mathcal {Z}}_\alpha $
is obtained as the direct limit of the system
${\mathcal {Z}}_\alpha $
is obtained as the direct limit of the system
 $({\mathcal {Z}}_\beta , \pi _{\beta , \beta '}: \beta <\beta ', \beta \in [0, \alpha )_{\mathcal {X}}, \beta '\in [0, \alpha )_{\mathcal {X}})$
.
$({\mathcal {Z}}_\beta , \pi _{\beta , \beta '}: \beta <\beta ', \beta \in [0, \alpha )_{\mathcal {X}}, \beta '\in [0, \alpha )_{\mathcal {X}})$
.
Now set
![]() $p=({\mathcal {T}}, {\mathcal {X}})$
and
$p=({\mathcal {T}}, {\mathcal {X}})$
and
![]() $q=({\mathcal {U}}, {\mathcal {Y}})$
, and let
$q=({\mathcal {U}}, {\mathcal {Y}})$
, and let
![]() $({\mathcal {Z}}_\alpha ^p, {\mathcal {Z}}_\alpha ^q: \alpha <\mathrm {lh}({\mathcal {X}}))$
be the two sequences produced by the respective normalization processes. To show that
$({\mathcal {Z}}_\alpha ^p, {\mathcal {Z}}_\alpha ^q: \alpha <\mathrm {lh}({\mathcal {X}}))$
be the two sequences produced by the respective normalization processes. To show that
![]() ${\mathcal {Z}}$
omits F, we inductively show that for
${\mathcal {Z}}$
omits F, we inductively show that for
![]() $\alpha <\mathrm {lh}({\mathcal {X}})$
,
$\alpha <\mathrm {lh}({\mathcal {X}})$
,
![]() ${\mathcal {Z}}_\alpha ^p$
and
${\mathcal {Z}}_\alpha ^p$
and
![]() ${\mathcal {Z}}_\alpha ^q$
omit F, and a close examination shows that the limit case is trivial.
${\mathcal {Z}}_\alpha ^q$
omit F, and a close examination shows that the limit case is trivial.
We now examine the successor stage of the induction. Suppose
![]() $\alpha +1<\mathrm {lh}({\mathcal {X}})$
is such that
$\alpha +1<\mathrm {lh}({\mathcal {X}})$
is such that
![]() ${\mathcal {Z}}_\alpha ^p$
and
${\mathcal {Z}}_\alpha ^p$
and
![]() ${\mathcal {Z}}_\alpha ^q$
omit F. We want to see that
${\mathcal {Z}}_\alpha ^q$
omit F. We want to see that
![]() ${\mathcal {Z}}_{\alpha +1}^p$
and
${\mathcal {Z}}_{\alpha +1}^p$
and
![]() ${\mathcal {Z}}_{\alpha +1}^q$
also omit F. Let
${\mathcal {Z}}_{\alpha +1}^q$
also omit F. Let
![]() $\gamma $
be such that
$\gamma $
be such that
![]() ${\mathcal {Z}}_\alpha ^p\restriction \gamma ={\mathcal {Z}}_\alpha ^q\restriction \gamma $
,
${\mathcal {Z}}_\alpha ^p\restriction \gamma ={\mathcal {Z}}_\alpha ^q\restriction \gamma $
,
![]() $\gamma +1\leq \max (\mathrm {lh}({\mathcal {Z}}_\alpha ^p), \mathrm {lh}({\mathcal {Z}}_\alpha ^q))$
and
$\gamma +1\leq \max (\mathrm {lh}({\mathcal {Z}}_\alpha ^p), \mathrm {lh}({\mathcal {Z}}_\alpha ^q))$
and
![]() $E_{\gamma }^{{\mathcal {Z}}_\alpha ^p}\not = E_{\gamma }^{{\mathcal {Z}}_\alpha ^q}$
. Assume without loss of generality that
$E_{\gamma }^{{\mathcal {Z}}_\alpha ^p}\not = E_{\gamma }^{{\mathcal {Z}}_\alpha ^q}$
. Assume without loss of generality that
![]() $\mathrm {lh}(E_{\gamma }^{{\mathcal {Z}}_\alpha ^q})<\mathrm { lh}(E_{\gamma }^{{\mathcal {Z}}_\alpha ^p})$
. In this case, setting
$\mathrm {lh}(E_{\gamma }^{{\mathcal {Z}}_\alpha ^q})<\mathrm { lh}(E_{\gamma }^{{\mathcal {Z}}_\alpha ^p})$
. In this case, setting
![]() $G=E_{\gamma }^{{\mathcal {Z}}_\alpha ^q}$
, we have that
$G=E_{\gamma }^{{\mathcal {Z}}_\alpha ^q}$
, we have that
![]() ${\mathcal {Z}}_{\alpha +1}^q={\mathcal {Z}}_{\alpha }^q$
and
${\mathcal {Z}}_{\alpha +1}^q={\mathcal {Z}}_{\alpha }^q$
and
![]() ${\mathcal {Z}}_{\alpha +1}^p$
is the full normalization of
${\mathcal {Z}}_{\alpha +1}^p$
is the full normalization of
![]() $({\mathcal {Z}}_{\alpha }^p)^{\frown }\{G\}$
.
$({\mathcal {Z}}_{\alpha }^p)^{\frown }\{G\}$
.
Notice that since
![]() $G=E_{\gamma }^{{\mathcal {Z}}_\alpha ^q}$
and
$G=E_{\gamma }^{{\mathcal {Z}}_\alpha ^q}$
and
![]() ${\mathcal {Z}}_\alpha ^q$
omits F, G cannot witness that
${\mathcal {Z}}_\alpha ^q$
omits F, G cannot witness that
![]() ${\mathcal {Z}}_{\alpha +1}^p$
does not omit F. Also, because
${\mathcal {Z}}_{\alpha +1}^p$
does not omit F. Also, because
![]() ${\mathcal {Z}}_{\alpha +1}^p\restriction \gamma +1={\mathcal {Z}}_{\alpha }^p\restriction \gamma +1$
, we have that
${\mathcal {Z}}_{\alpha +1}^p\restriction \gamma +1={\mathcal {Z}}_{\alpha }^p\restriction \gamma +1$
, we have that
![]() ${\mathcal {Z}}_{\alpha +1}^p\restriction \gamma +2$
omits F.
${\mathcal {Z}}_{\alpha +1}^p\restriction \gamma +2$
omits F.
Fix some
![]() $\iota>0$
, and let
$\iota>0$
, and let
![]() $\xi \leq \gamma $
be the predecessor of
$\xi \leq \gamma $
be the predecessor of
![]() $\gamma +1$
in
$\gamma +1$
in
![]() ${\mathcal {Z}}_{\alpha +1}^p$
. Then
${\mathcal {Z}}_{\alpha +1}^p$
. Then
![]() ${\mathcal {M}}_{\gamma +\iota }^{{\mathcal {Z}}_{\alpha +1}^p}=Ult({\mathcal {M}}_{\xi +\iota -1}^{{\mathcal {Z}}_\alpha ^p}, G)$
, and
${\mathcal {M}}_{\gamma +\iota }^{{\mathcal {Z}}_{\alpha +1}^p}=Ult({\mathcal {M}}_{\xi +\iota -1}^{{\mathcal {Z}}_\alpha ^p}, G)$
, and
![]() $E_{\gamma +\iota }^{{\mathcal {Z}}_{\alpha +1}^p}$
is the last extender of
$E_{\gamma +\iota }^{{\mathcal {Z}}_{\alpha +1}^p}$
is the last extender of
![]() $Ult({\mathcal {M}}_{\xi +\iota -1}||\mathrm {lh}(E_{\xi +\iota -1}^{{\mathcal {Z}}_\alpha ^p}), G)$
. Because
$Ult({\mathcal {M}}_{\xi +\iota -1}||\mathrm {lh}(E_{\xi +\iota -1}^{{\mathcal {Z}}_\alpha ^p}), G)$
. Because
![]() ${\mathcal {Z}}_\alpha ^p$
omits F, it is now straightforward to verify that
${\mathcal {Z}}_\alpha ^p$
omits F, it is now straightforward to verify that
![]() ${\mathcal {Z}}_{\alpha +1}^p\restriction \gamma +\iota +1$
omits F.
${\mathcal {Z}}_{\alpha +1}^p\restriction \gamma +\iota +1$
omits F.
The preceding proof can be modified to show the following corollary.
Corollary 6.6. Suppose
![]() $({\mathcal {P} }, \Sigma )$
is a mouse pair and
$({\mathcal {P} }, \Sigma )$
is a mouse pair and
![]() $\eta <{\textsf {Ord}}\cap {\mathcal {P} }$
. Suppose
$\eta <{\textsf {Ord}}\cap {\mathcal {P} }$
. Suppose
![]() ${\mathcal { Q}}$
and
${\mathcal { Q}}$
and
![]() ${\mathcal R}$
are two
${\mathcal R}$
are two
![]() $\Sigma $
-iterates of
$\Sigma $
-iterates of
![]() ${\mathcal {P} }$
such that both
${\mathcal {P} }$
such that both
![]() ${\mathcal {T}}_{{\mathcal {P} }, {\mathcal { Q}}}$
and
${\mathcal {T}}_{{\mathcal {P} }, {\mathcal { Q}}}$
and
![]() ${\mathcal {T}}_{{\mathcal {P} }, {\mathcal R}}$
are strictly above
${\mathcal {T}}_{{\mathcal {P} }, {\mathcal R}}$
are strictly above
![]() $\eta $
. Then the least-extender-comparison of
$\eta $
. Then the least-extender-comparison of
![]() $({\mathcal { Q}}, \Sigma _{\mathcal { Q}})$
and
$({\mathcal { Q}}, \Sigma _{\mathcal { Q}})$
and
![]() $({\mathcal R}, \Sigma _{\mathcal R})$
produces iteration trees that are strictly above
$({\mathcal R}, \Sigma _{\mathcal R})$
produces iteration trees that are strictly above
![]() $\eta $
.
$\eta $
.
Suppose
![]() $(P, \Psi , H, \alpha )$
is a coarse tuple and
$(P, \Psi , H, \alpha )$
is a coarse tuple and
![]() $x\in \mathrm {dom}(H)$
. Set
$x\in \mathrm {dom}(H)$
. Set
![]() $({\mathcal {P} }, \Sigma )=({\mathcal {P} }_x, \Sigma _x)$
. Let
$({\mathcal {P} }, \Sigma )=({\mathcal {P} }_x, \Sigma _x)$
. Let
![]() $(\delta ^{i}_{\mathcal {P} }: i\leq \omega )$
be the sequence of Woodin cardinals of
$(\delta ^{i}_{\mathcal {P} }: i\leq \omega )$
be the sequence of Woodin cardinals of
![]() ${\mathcal {P} }$
and their limit. If
${\mathcal {P} }$
and their limit. If
![]() ${\mathcal { Q}}$
is a complete
${\mathcal { Q}}$
is a complete
![]() $\Sigma $
-iterate of
$\Sigma $
-iterate of
![]() ${\mathcal {P} }$
, then we write
${\mathcal {P} }$
, then we write
![]() $\delta ^i_{\mathcal { Q}}=\pi _{{\mathcal {P} }, {\mathcal { Q}}}(\delta ^i)$
.
$\delta ^i_{\mathcal { Q}}=\pi _{{\mathcal {P} }, {\mathcal { Q}}}(\delta ^i)$
.
Suppose
![]() $\mu <\delta ^0_{\mathcal {P} }$
is a measurable cutpoint of
$\mu <\delta ^0_{\mathcal {P} }$
is a measurable cutpoint of
![]() ${\mathcal {P} }$
such that
${\mathcal {P} }$
such that
![]() $\mu $
is below the least
$\mu $
is below the least
![]() $<\delta _0$
-strong cardinal of
$<\delta _0$
-strong cardinal of
![]() ${\mathcal {P} }$
and
${\mathcal {P} }$
and
![]() $F\in \vec {E}^{\mathcal {P} }$
is a completely total extender with
$F\in \vec {E}^{\mathcal {P} }$
is a completely total extender with
![]() $\mathrm {crit }(F)=\mu $
. Set
$\mathrm {crit }(F)=\mu $
. Set
![]() ${\mathcal {P} }_F=Ult({\mathcal {P} }, F)$
, and let
${\mathcal {P} }_F=Ult({\mathcal {P} }, F)$
, and let
![]() $\kappa _{{\mathcal {P} }, \Sigma , F}=\pi _{{\mathcal {P} }_F, \infty }(\mu )$
and
$\kappa _{{\mathcal {P} }, \Sigma , F}=\pi _{{\mathcal {P} }_F, \infty }(\mu )$
and
![]() $\tau _{{\mathcal {P} }, \Sigma , F}=o^{{\mathcal {M}}_\infty ({\mathcal {P} }, \Sigma )}(\kappa _{{\mathcal {P} }, \Sigma , F})$
. Let
$\tau _{{\mathcal {P} }, \Sigma , F}=o^{{\mathcal {M}}_\infty ({\mathcal {P} }, \Sigma )}(\kappa _{{\mathcal {P} }, \Sigma , F})$
. Let
![]() ${\mathcal {T}}_{{\mathcal {P} }, \Sigma , F}=_{def}{\mathcal {T}}$
be the least initial segment of
${\mathcal {T}}_{{\mathcal {P} }, \Sigma , F}=_{def}{\mathcal {T}}$
be the least initial segment of
![]() ${\mathcal {T}}_{{\mathcal {P} }, {\mathcal {M}}_\infty ({\mathcal {P} }, \Sigma )}$
such that if
${\mathcal {T}}_{{\mathcal {P} }, {\mathcal {M}}_\infty ({\mathcal {P} }, \Sigma )}$
such that if
![]() ${\mathcal R}$
is the last model of
${\mathcal R}$
is the last model of
![]() ${\mathcal {T}}$
, then
${\mathcal {T}}$
, then
![]() ${\mathcal R}|\tau _{{\mathcal {P} }, \Sigma , F}={\mathcal {M}}_\infty ({\mathcal {P} }, \Sigma )|\tau _{{\mathcal {P} }, \Sigma , F}$
. We then set
${\mathcal R}|\tau _{{\mathcal {P} }, \Sigma , F}={\mathcal {M}}_\infty ({\mathcal {P} }, \Sigma )|\tau _{{\mathcal {P} }, \Sigma , F}$
. We then set
![]() $E_{{\mathcal {P} }, \Sigma , F}=_{def}E=\pi ^{\mathcal {T}}(F)$
,Footnote
36
$E_{{\mathcal {P} }, \Sigma , F}=_{def}E=\pi ^{\mathcal {T}}(F)$
,Footnote
36
![]() $X_{{\mathcal {P} }, \Sigma , F}={\mathcal R}||\mathrm {lh}(E)=_{def} X$
, and
$X_{{\mathcal {P} }, \Sigma , F}={\mathcal R}||\mathrm {lh}(E)=_{def} X$
, and
![]() ${\mathcal { H}}({\mathcal {P} }, \Sigma , F)=({\textsf {HOD}}_{\Psi ,X}|\Theta )^W$
.
${\mathcal { H}}({\mathcal {P} }, \Sigma , F)=({\textsf {HOD}}_{\Psi ,X}|\Theta )^W$
.
Theorem 6.7. In the above setup, setting
![]() $W=L_\alpha ^\Psi ({\mathbb {R}})$
,
$W=L_\alpha ^\Psi ({\mathbb {R}})$
,
Proof. TheFootnote
37
argument is somewhat standard, so we will only give an outline. The key fact to keep in mind is that if
![]() ${\mathcal {T}}$
is an iteration tree on
${\mathcal {T}}$
is an iteration tree on
![]() ${\mathcal {P} }(F)$
which omits F, then
${\mathcal {P} }(F)$
which omits F, then
![]() ${\mathcal {T}}$
can be split into two components
${\mathcal {T}}$
can be split into two components
![]() ${\mathcal {T}}_l^{\frown } {\mathcal {T}}_r$
such that
${\mathcal {T}}_l^{\frown } {\mathcal {T}}_r$
such that
![]() ${\mathcal {T}}_l$
is based on
${\mathcal {T}}_l$
is based on
![]() ${\mathcal {P} }|\nu (F)$
, and if
${\mathcal {P} }|\nu (F)$
, and if
![]() ${\mathcal {T}}_l\not ={\mathcal {T}}$
, then
${\mathcal {T}}_l\not ={\mathcal {T}}$
, then
![]() $\pi ^{{\mathcal {T}}_l}$
is defined and
$\pi ^{{\mathcal {T}}_l}$
is defined and
![]() ${\mathcal {T}}_r$
is strictly above
${\mathcal {T}}_r$
is strictly above
![]() $\mathrm {lh}(\pi ^{{\mathcal {T}}_l}(F))$
. Below and elsewhere,
$\mathrm {lh}(\pi ^{{\mathcal {T}}_l}(F))$
. Below and elsewhere,
![]() $F_{\mathcal { Q}}=\pi ^{{\mathcal {T}}_{{\mathcal {P} }(F), {\mathcal { Q}}}}(F)$
.
$F_{\mathcal { Q}}=\pi ^{{\mathcal {T}}_{{\mathcal {P} }(F), {\mathcal { Q}}}}(F)$
.
Claim 6.8. Suppose
![]() $j:{\mathcal {P} }(F)\rightarrow {\mathcal { Q}}$
is an
$j:{\mathcal {P} }(F)\rightarrow {\mathcal { Q}}$
is an
![]() ${\mathbb {R}}$
-genericity iteration according to
${\mathbb {R}}$
-genericity iteration according to
![]() $\Sigma $
in which all iteration trees used omit F. Then
$\Sigma $
in which all iteration trees used omit F. Then
-
1.
 $X_{{\mathcal {P} }, \Sigma , F}\in {\mathcal { Q}}$
,
$X_{{\mathcal {P} }, \Sigma , F}\in {\mathcal { Q}}$
, -
2.
 $X_{{\mathcal {P} }, \Sigma , F}$
is a
$X_{{\mathcal {P} }, \Sigma , F}$
is a
 $\Sigma _{{\mathcal { Q}}||\mathrm {lh}(F_{\mathcal { Q}})}$
-iterate of
$\Sigma _{{\mathcal { Q}}||\mathrm {lh}(F_{\mathcal { Q}})}$
-iterate of
 ${\mathcal { Q}}||\mathrm {lh}(F_{\mathcal { Q}})$
, and
${\mathcal { Q}}||\mathrm {lh}(F_{\mathcal { Q}})$
, and -
3.
 ${\mathcal {T}}_{{\mathcal { Q}}||\mathrm {lh}(F_{\mathcal { Q}}), X_{{\mathcal {P} }, \Sigma , F}}\in {\mathcal { Q}}$
.
${\mathcal {T}}_{{\mathcal { Q}}||\mathrm {lh}(F_{\mathcal { Q}}), X_{{\mathcal {P} }, \Sigma , F}}\in {\mathcal { Q}}$
.
We merely sketch Claim 6.8, as it follows from standard facts from the HOD analysis (see [Reference Steel and Woodin33]). The key point is that if
![]() $\eta $
is the least Woodin cardinal of
$\eta $
is the least Woodin cardinal of
![]() ${\mathcal { Q}}$
,
${\mathcal { Q}}$
,
![]() ${\mathcal {U}}$
is
${\mathcal {U}}$
is
![]() ${\mathcal {P} }(F)$
-to-
${\mathcal {P} }(F)$
-to-
![]() ${\mathcal { Q}}$
iteration tree according to
${\mathcal { Q}}$
iteration tree according to
![]() $\Sigma $
, and
$\Sigma $
, and
![]() $\alpha <\mathrm { lh}({\mathcal {U}})$
is the least such that the generators of
$\alpha <\mathrm { lh}({\mathcal {U}})$
is the least such that the generators of
![]() ${\mathcal {U}}\restriction \alpha +1$
are contained in
${\mathcal {U}}\restriction \alpha +1$
are contained in
![]() $\eta $
, then letting
$\eta $
, then letting
![]() ${\mathcal {S}}={\mathcal {M}}_\alpha ^{\mathcal {U}}$
, we have
${\mathcal {S}}={\mathcal {M}}_\alpha ^{\mathcal {U}}$
, we have
![]() ${\mathcal {S}}\in \mathcal {F}({\mathcal {P} }(F), \Sigma , F)$
. Then if
${\mathcal {S}}\in \mathcal {F}({\mathcal {P} }(F), \Sigma , F)$
. Then if
![]() $i: {\mathcal {P} }\rightarrow {\mathcal {S}}$
and
$i: {\mathcal {P} }\rightarrow {\mathcal {S}}$
and
![]() $k:{\mathcal {S}}\rightarrow {\mathcal { Q}}$
are the iteration embeddings,Footnote
38
then
$k:{\mathcal {S}}\rightarrow {\mathcal { Q}}$
are the iteration embeddings,Footnote
38
then
![]() $j=k\circ i$
and
$j=k\circ i$
and
![]() ${\mathcal {M}}_\infty ({\mathcal {P} }(F), \Sigma , F)={\mathcal {M}}_\infty ({\mathcal {S}}, \Sigma _{\mathcal {S}}, i(F))$
. In addition,
${\mathcal {M}}_\infty ({\mathcal {P} }(F), \Sigma , F)={\mathcal {M}}_\infty ({\mathcal {S}}, \Sigma _{\mathcal {S}}, i(F))$
. In addition,
![]() $X_{{\mathcal {P} }, \Sigma , F}\triangleleft {\mathcal {M}}_\infty ({\mathcal {S}}|\eta , \Sigma _{{\mathcal {S}}|\eta }, i(F))$
. Now let
$X_{{\mathcal {P} }, \Sigma , F}\triangleleft {\mathcal {M}}_\infty ({\mathcal {S}}|\eta , \Sigma _{{\mathcal {S}}|\eta }, i(F))$
. Now let
![]() $\zeta $
be the least inaccessible cardinal of
$\zeta $
be the least inaccessible cardinal of
![]() ${\mathcal {S}}$
such that
${\mathcal {S}}$
such that
![]() $i(F)\in {\mathcal {S}}|\zeta $
. It follows that
$i(F)\in {\mathcal {S}}|\zeta $
. It follows that
![]() $X_{{\mathcal {P} }, \Sigma , F}\triangleleft {\mathcal {M}}_\infty ({\mathcal {S}}|\eta , \Sigma _{{\mathcal {S}}|\eta }, i(F))$
, and we have that
$X_{{\mathcal {P} }, \Sigma , F}\triangleleft {\mathcal {M}}_\infty ({\mathcal {S}}|\eta , \Sigma _{{\mathcal {S}}|\eta }, i(F))$
, and we have that
![]() ${\mathcal { Q}}|\zeta ={\mathcal {S}}|\zeta $
. The last missing piece is that
${\mathcal { Q}}|\zeta ={\mathcal {S}}|\zeta $
. The last missing piece is that
![]() $\Sigma _{{\mathcal { Q}}|\zeta }$
is captured by
$\Sigma _{{\mathcal { Q}}|\zeta }$
is captured by
![]() ${\mathcal { Q}}$
, and
${\mathcal { Q}}$
, and
![]() ${\mathcal { Q}}$
can compute
${\mathcal { Q}}$
can compute
![]() ${\mathcal {M}}_\infty ({\mathcal {S}}|\eta , \Sigma _{{\mathcal {S}}|\eta }, i(F))$
.Footnote
39
${\mathcal {M}}_\infty ({\mathcal {S}}|\eta , \Sigma _{{\mathcal {S}}|\eta }, i(F))$
.Footnote
39
We can then develop the concept of suitable premouse, A-iterable suitable premouse, and other concepts used in the HOD analysis for iterations that omit F. For example, we define
![]() ${\mathcal {S}}$
to be suitable if, in addition to the usual properties of suitability (see [Reference Steel and Woodin33]), for some
${\mathcal {S}}$
to be suitable if, in addition to the usual properties of suitability (see [Reference Steel and Woodin33]), for some
![]() $G\in \vec {{\mathcal {S}}}$
,
$G\in \vec {{\mathcal {S}}}$
,
![]() $X_{{\mathcal {P} }, \Sigma , F}$
is a complete iterate of
$X_{{\mathcal {P} }, \Sigma , F}$
is a complete iterate of
![]() ${\mathcal {S}}||\mathrm {lh}(G)$
. A-iterability is defined for those
${\mathcal {S}}||\mathrm {lh}(G)$
. A-iterability is defined for those
![]() $A\subseteq {\mathbb {R}}$
which are ordinal definable from
$A\subseteq {\mathbb {R}}$
which are ordinal definable from
![]() $X_{{\mathcal {P} }, \Sigma , F}$
, and given a suitable
$X_{{\mathcal {P} }, \Sigma , F}$
, and given a suitable
![]() ${\mathcal {S}}$
we define the concept of A-iterability only for those iterations of
${\mathcal {S}}$
we define the concept of A-iterability only for those iterations of
![]() ${\mathcal {S}}$
that omit G, where G is as above. Claim 6.8 can now be used to show that for every
${\mathcal {S}}$
that omit G, where G is as above. Claim 6.8 can now be used to show that for every
![]() $A\subseteq {\mathbb {R}}$
that is ordinal definable from
$A\subseteq {\mathbb {R}}$
that is ordinal definable from
![]() $X_{{\mathcal {P} }, \Sigma , F}$
, there is a strongly A-iterable pair. The rest is just like in the ordinary HOD analysis, and we leave it to the reader.
$X_{{\mathcal {P} }, \Sigma , F}$
, there is a strongly A-iterable pair. The rest is just like in the ordinary HOD analysis, and we leave it to the reader.
For
![]() $({\mathcal {P} }, \Sigma , F)$
as above, let
$({\mathcal {P} }, \Sigma , F)$
as above, let
![]() $\Sigma ^F$
be the fragment of
$\Sigma ^F$
be the fragment of
![]() $\Sigma _{{\mathcal {P} }(F)}$
that acts on stacks that omit F, and let
$\Sigma _{{\mathcal {P} }(F)}$
that acts on stacks that omit F, and let
![]() $\pi _{{\mathcal {P} }(F), \infty }^{\Sigma ^F}:{\mathcal {P} }(F)\rightarrow {\mathcal {M}}_\infty ({\mathcal {P} }, \Sigma , F)$
be the direct limit embedding.
$\pi _{{\mathcal {P} }(F), \infty }^{\Sigma ^F}:{\mathcal {P} }(F)\rightarrow {\mathcal {M}}_\infty ({\mathcal {P} }, \Sigma , F)$
be the direct limit embedding.
7 Regular Suslin cardinals are
 $\omega $
-club
$\omega $
-club
 $\Theta $
-Berkeley
$\Theta $
-Berkeley
Theorem 7.1. Assume
![]() $\textsf {AD}^{+}$
. Then every regular Suslin cardinal is
$\textsf {AD}^{+}$
. Then every regular Suslin cardinal is
![]() $\omega $
-club
$\omega $
-club
![]() $\Theta $
-Berkeley.
$\Theta $
-Berkeley.
Proof. Fix a regular Suslin cardinal
![]() $\delta $
, and toward a contradiction, assume that
$\delta $
, and toward a contradiction, assume that
![]() $\delta $
is not an
$\delta $
is not an
![]() $\omega $
-club
$\omega $
-club
![]() $\Theta $
-Berkeley cardinal. Fix a transitive
$\Theta $
-Berkeley cardinal. Fix a transitive
![]() $N'$
such that
$N'$
such that
-
(1.1)
 $\left |N'\right |<\Theta $
,
$\left |N'\right |<\Theta $
, -
(1.2)
 $\delta \subseteq N'$
, and
$\delta \subseteq N'$
, and -
(1.3) the set of
 $\alpha <\delta $
such that there is no elementary embedding
$\alpha <\delta $
such that there is no elementary embedding
 $j: N'\rightarrow N'$
with the property that
$j: N'\rightarrow N'$
with the property that
 $\mathrm {crit }(j)=\alpha $
is
$\mathrm {crit }(j)=\alpha $
is
 $\omega $
-stationary in
$\omega $
-stationary in
 $\delta $
.Footnote
40
$\delta $
.Footnote
40
Let
![]() $\phi (u, v)$
be the formula expressing (1.1)–(1.3). Thus,
$\phi (u, v)$
be the formula expressing (1.1)–(1.3). Thus,
![]() $\phi [\delta , N']$
holds. Since
$\phi [\delta , N']$
holds. Since
![]() $L({\wp }({\mathbb {R}}))\vDash \phi [\delta , N']$
, we can assume that
$L({\wp }({\mathbb {R}}))\vDash \phi [\delta , N']$
, we can assume that
![]() $V=L({\wp }({\mathbb {R}}))$
. Without loss of generality, assume that
$V=L({\wp }({\mathbb {R}}))$
. Without loss of generality, assume that
![]() $\delta $
is the least regular Suslin cardinal
$\delta $
is the least regular Suslin cardinal
![]() $\kappa $
such that
$\kappa $
such that
![]() $\phi [\kappa , M]$
holds for some M. It then immediately follows that
$\phi [\kappa , M]$
holds for some M. It then immediately follows that
![]() $\delta $
cannot be the largest Suslin cardinal, as if
$\delta $
cannot be the largest Suslin cardinal, as if
![]() $\delta $
were the largest Suslin cardinal, then for some
$\delta $
were the largest Suslin cardinal, then for some
![]() $\alpha <\delta $
and some
$\alpha <\delta $
and some
![]() $\beta <\delta $
, letting
$\beta <\delta $
, letting
![]() $\Delta =\{A\subseteq {\mathbb {R}}: w(A)<\beta \},$
Footnote
41
$\Delta =\{A\subseteq {\mathbb {R}}: w(A)<\beta \},$
Footnote
41
![]() $L_\alpha (\Delta )\vDash {\textsf {ZF-Replacement}}+\exists \kappa \exists M\phi [\kappa , M]$
.Footnote
42
A similar reflection argument shows that we can assume without losing generality that
$L_\alpha (\Delta )\vDash {\textsf {ZF-Replacement}}+\exists \kappa \exists M\phi [\kappa , M]$
.Footnote
42
A similar reflection argument shows that we can assume without losing generality that
![]() $\left |N'\right |$
is less than some Suslin cardinal
$\left |N'\right |$
is less than some Suslin cardinal
![]() $\delta '$
such that
$\delta '$
such that
![]() $\delta <\delta '$
and
$\delta <\delta '$
and
![]() $\delta '$
is not the largest Suslin cardinal. Fix now such a
$\delta '$
is not the largest Suslin cardinal. Fix now such a
![]() $\delta '$
so that
$\delta '$
so that
![]() $\left |N'\right |<\delta '$
.
$\left |N'\right |<\delta '$
.
Let
![]() $(R, \Psi , H, \alpha )$
be as in Theorem 4.7 absorbing
$(R, \Psi , H, \alpha )$
be as in Theorem 4.7 absorbing
![]() $\delta '$
. Notice that our discussion above implies that
$\delta '$
. Notice that our discussion above implies that
![]() $W\vDash \phi [\delta , N']$
, for
$W\vDash \phi [\delta , N']$
, for
![]() $W=L_\alpha ^\Psi ({\mathbb {R}})$
. We can then find
$W=L_\alpha ^\Psi ({\mathbb {R}})$
. We can then find
![]() $x_0$
such that
$x_0$
such that
![]() $N'$
is
$N'$
is
![]() ${\textsf {OD}}^W_{\Psi , x_0}$
, and then by minimizing, we can let N be the
${\textsf {OD}}^W_{\Psi , x_0}$
, and then by minimizing, we can let N be the
![]() ${\textsf {OD}}^W_{\Psi , x_0}$
-least M such that
${\textsf {OD}}^W_{\Psi , x_0}$
-least M such that
![]() $W\vDash \phi [\delta , M]$
. We now fix
$W\vDash \phi [\delta , M]$
. We now fix
![]() $x_1\in \mathrm {dom}(H)$
such that
$x_1\in \mathrm {dom}(H)$
such that
-
(2.1)
 $x_1$
is Turing above
$x_1$
is Turing above
 $x_0$
and
$x_0$
and
 $N\in {\mathcal {M}}_\infty ({\mathcal {P} }_{x_1}, \Sigma _{x_1})$
, where
$N\in {\mathcal {M}}_\infty ({\mathcal {P} }_{x_1}, \Sigma _{x_1})$
, where
 $({\mathcal {P} }_{x_1}, \Sigma _{x_1})=H(x_1)$
, and
$({\mathcal {P} }_{x_1}, \Sigma _{x_1})=H(x_1)$
, and -
(2.2)
 $\delta $
is a limit of cutpoints of
$\delta $
is a limit of cutpoints of
 ${\mathcal {M}}_\infty ({\mathcal {P} }, \Sigma )$
, where
${\mathcal {M}}_\infty ({\mathcal {P} }, \Sigma )$
, where
 $({\mathcal {P} }, \Sigma )=({\mathcal {P} }_{x_1}, \Sigma _{x_1})$
.
$({\mathcal {P} }, \Sigma )=({\mathcal {P} }_{x_1}, \Sigma _{x_1})$
.
Without loss of generality, we assume that
![]() $\delta \in \mathrm {rge}(\pi ^\Sigma _{{\mathcal {P} }, \infty })$
, and for
$\delta \in \mathrm {rge}(\pi ^\Sigma _{{\mathcal {P} }, \infty })$
, and for
![]() ${\mathcal { Q}}$
a complete
${\mathcal { Q}}$
a complete
![]() $\Sigma $
-iterate of
$\Sigma $
-iterate of
![]() ${\mathcal {P} }$
, we let
${\mathcal {P} }$
, we let
![]() $\delta _{\mathcal { Q}}=\pi _{{\mathcal { Q}}, \infty }^{-1}(\delta )$
.
$\delta _{\mathcal { Q}}=\pi _{{\mathcal { Q}}, \infty }^{-1}(\delta )$
.
Fix now any completely total extender
![]() $F\in \vec {E}^{\mathcal {P} }$
such that
$F\in \vec {E}^{\mathcal {P} }$
such that
![]() $\mathrm {crit }(F)=\delta _{\mathcal {P} }$
, and set
$\mathrm {crit }(F)=\delta _{\mathcal {P} }$
, and set
![]() $X_{\mathcal {P} }=X_{{\mathcal {P} }, \Sigma , F}$
. Let
$X_{\mathcal {P} }=X_{{\mathcal {P} }, \Sigma , F}$
. Let
![]() ${\mathcal { Q}}=Ult({\mathcal {P} }(F), F)$
,
${\mathcal { Q}}=Ult({\mathcal {P} }(F), F)$
,
![]() $F_{\mathcal { Q}}=\pi _F(F)$
and
$F_{\mathcal { Q}}=\pi _F(F)$
and
![]() $X_{\mathcal { Q}}=X_{{\mathcal { Q}}, \Sigma _{\mathcal { Q}}, F_{\mathcal { Q}}}$
. We set
$X_{\mathcal { Q}}=X_{{\mathcal { Q}}, \Sigma _{\mathcal { Q}}, F_{\mathcal { Q}}}$
. We set
![]() $\Lambda =\Sigma ^F$
and
$\Lambda =\Sigma ^F$
and
![]() $\Phi =\Sigma ^{F_{\mathcal { Q}}}_{\mathcal { Q}}$
. As in the proof of Theorem 3.1, we define
$\Phi =\Sigma ^{F_{\mathcal { Q}}}_{\mathcal { Q}}$
. As in the proof of Theorem 3.1, we define
![]() $j: {\mathcal {M}}_\infty ({\mathcal {P} }, \Sigma , F)\rightarrow {\mathcal {M}}_\infty ({\mathcal { Q}}, \Sigma _{\mathcal { Q}}, F_{\mathcal { Q}})$
. It follows from Theorem 6.7 and the proof of Claim 3.3 that
$j: {\mathcal {M}}_\infty ({\mathcal {P} }, \Sigma , F)\rightarrow {\mathcal {M}}_\infty ({\mathcal { Q}}, \Sigma _{\mathcal { Q}}, F_{\mathcal { Q}})$
. It follows from Theorem 6.7 and the proof of Claim 3.3 that
![]() $N\in {\mathcal {M}}_\infty ({\mathcal {P} }, \Sigma , F)\cap {\mathcal {M}}_\infty ({\mathcal { Q}}, \Sigma _{\mathcal { Q}}, F_{\mathcal { Q}})$
and
$N\in {\mathcal {M}}_\infty ({\mathcal {P} }, \Sigma , F)\cap {\mathcal {M}}_\infty ({\mathcal { Q}}, \Sigma _{\mathcal { Q}}, F_{\mathcal { Q}})$
and
![]() $j(N)=N$
, and therefore, defining j is all that we will do.
$j(N)=N$
, and therefore, defining j is all that we will do.
Fix
![]() $u\in {\mathcal {M}}_\infty ({\mathcal {P} }, \Sigma , F)$
, and let
$u\in {\mathcal {M}}_\infty ({\mathcal {P} }, \Sigma , F)$
, and let
![]() ${\mathcal {S}}$
be a complete
${\mathcal {S}}$
be a complete
![]() $\Lambda $
-iterate of
$\Lambda $
-iterate of
![]() ${\mathcal {P} }(F)$
such that
${\mathcal {P} }(F)$
such that
![]() $u=\pi _{{\mathcal {S}}, \infty }^{\Lambda }(u_{\mathcal {S}})$
for some
$u=\pi _{{\mathcal {S}}, \infty }^{\Lambda }(u_{\mathcal {S}})$
for some
![]() $u_{\mathcal {S}}\in {\mathcal {S}}$
. Let
$u_{\mathcal {S}}\in {\mathcal {S}}$
. Let
![]() $F_{\mathcal {S}}=\pi _{{\mathcal {P} }(F), {\mathcal {S}}}(F)$
Footnote
43
and
$F_{\mathcal {S}}=\pi _{{\mathcal {P} }(F), {\mathcal {S}}}(F)$
Footnote
43
and
![]() ${\mathcal {S}}_F=Ult({\mathcal {S}}, F_{\mathcal {S}})$
. We then letFootnote
44
${\mathcal {S}}_F=Ult({\mathcal {S}}, F_{\mathcal {S}})$
. We then letFootnote
44
The definition of
![]() $j(u)$
makes sense, as full normalization implies that
$j(u)$
makes sense, as full normalization implies that
![]() ${\mathcal {S}}_F$
is a complete
${\mathcal {S}}_F$
is a complete
![]() $\Phi $
-iterate of
$\Phi $
-iterate of
![]() ${\mathcal { Q}}$
. To prove this and other claims in this section, we set
${\mathcal { Q}}$
. To prove this and other claims in this section, we set
![]() ${\mathcal {P} }={\mathcal {P} }(F)$
to simplify the notation.
${\mathcal {P} }={\mathcal {P} }(F)$
to simplify the notation.
Claim 7.2. The definition of j is meaningful; more precisely,
![]() ${\mathcal {S}}_F$
is a compete
${\mathcal {S}}_F$
is a compete
![]() $\Phi $
-iterate of
$\Phi $
-iterate of
![]() ${\mathcal { Q}}$
.
${\mathcal { Q}}$
.
Proof. Notice that
![]() ${\mathcal {T}}_{{\mathcal {P} }, {\mathcal {S}}}$
can be split into
${\mathcal {T}}_{{\mathcal {P} }, {\mathcal {S}}}$
can be split into
![]() $({\mathcal {T}}^l_{{\mathcal {P} }, {\mathcal {S}}})^{\frown } {\mathcal {T}}^r_{{\mathcal {P} }, {\mathcal {S}}}$
, where
$({\mathcal {T}}^l_{{\mathcal {P} }, {\mathcal {S}}})^{\frown } {\mathcal {T}}^r_{{\mathcal {P} }, {\mathcal {S}}}$
, where
![]() ${\mathcal {T}}^l_{{\mathcal {P} }, {\mathcal {S}}}$
is the longest portion of
${\mathcal {T}}^l_{{\mathcal {P} }, {\mathcal {S}}}$
is the longest portion of
![]() ${\mathcal {T}}_{{\mathcal {P} }, {\mathcal {S}}}$
that is based on
${\mathcal {T}}_{{\mathcal {P} }, {\mathcal {S}}}$
that is based on
![]() ${\mathcal {P} }|\nu (F)$
and
${\mathcal {P} }|\nu (F)$
and
![]() ${\mathcal {T}}^r_{{\mathcal {P} }, {\mathcal {S}}}$
is the rest of
${\mathcal {T}}^r_{{\mathcal {P} }, {\mathcal {S}}}$
is the rest of
![]() ${\mathcal {T}}_{{\mathcal {P} }, {\mathcal {S}}}$
. If
${\mathcal {T}}_{{\mathcal {P} }, {\mathcal {S}}}$
. If
![]() ${\mathcal {T}}^r_{{\mathcal {P} }, {\mathcal {S}}}$
is defined, then it is above
${\mathcal {T}}^r_{{\mathcal {P} }, {\mathcal {S}}}$
is defined, then it is above
![]() $\mathrm {lh}(\pi ^{{\mathcal {T}}^l_{{\mathcal {P} }, {\mathcal {S}}}}(F))$
. It then follows that the full normalization of
$\mathrm {lh}(\pi ^{{\mathcal {T}}^l_{{\mathcal {P} }, {\mathcal {S}}}}(F))$
. It then follows that the full normalization of
![]() $({\mathcal {T}}_{{\mathcal {P} }, {\mathcal {S}}})^{\frown } \{F_{\mathcal {S}}\}$
Footnote
45
is
$({\mathcal {T}}_{{\mathcal {P} }, {\mathcal {S}}})^{\frown } \{F_{\mathcal {S}}\}$
Footnote
45
is
![]() $({\mathcal {T}}^l_{{\mathcal {P} }, {\mathcal {S}}})^{\frown }\{ F_{\mathcal {S}}\}^{\frown } {\mathcal {U}}$
,Footnote
46
where
$({\mathcal {T}}^l_{{\mathcal {P} }, {\mathcal {S}}})^{\frown }\{ F_{\mathcal {S}}\}^{\frown } {\mathcal {U}}$
,Footnote
46
where
![]() ${\mathcal {U}}$
is above
${\mathcal {U}}$
is above
![]() $\mathrm { lh}(F_{\mathcal {S}})$
. Notice next that the full normalization of
$\mathrm { lh}(F_{\mathcal {S}})$
. Notice next that the full normalization of
![]() $\{F\}^{\frown } {\mathcal {T}}^l_{{\mathcal {P} }, {\mathcal {S}}}$
is
$\{F\}^{\frown } {\mathcal {T}}^l_{{\mathcal {P} }, {\mathcal {S}}}$
is
![]() $({\mathcal {T}}^l_{{\mathcal {P} }, {\mathcal {S}}})^{\frown }\{ F_{\mathcal {S}}\}$
. Thus,
$({\mathcal {T}}^l_{{\mathcal {P} }, {\mathcal {S}}})^{\frown }\{ F_{\mathcal {S}}\}$
. Thus,
![]() ${\mathcal {S}}_F$
is a
${\mathcal {S}}_F$
is a
![]() $\Phi $
-iterate of
$\Phi $
-iterate of
![]() ${\mathcal { Q}}$
and
${\mathcal { Q}}$
and
![]() ${\mathcal {T}}_{{\mathcal { Q}}, {\mathcal {S}}_F}=({\mathcal {T}}^l_{{\mathcal {P} }, {\mathcal {S}}})^{\frown } {\mathcal {U}}$
.
${\mathcal {T}}_{{\mathcal { Q}}, {\mathcal {S}}_F}=({\mathcal {T}}^l_{{\mathcal {P} }, {\mathcal {S}}})^{\frown } {\mathcal {U}}$
.
Claim 7.3.
![]() $j(u)$
is independent of the choice of
$j(u)$
is independent of the choice of
![]() ${\mathcal {S}}$
.
${\mathcal {S}}$
.
Proof. To see this, pick another normal
![]() $\Lambda $
-iterate
$\Lambda $
-iterate
![]() ${\mathcal {S}}'$
of
${\mathcal {S}}'$
of
![]() ${\mathcal {P} }$
such that
${\mathcal {P} }$
such that
![]() $\pi _{{\mathcal {S}}', \infty }^{\Lambda _{{\mathcal {S}}'}}(u_{{\mathcal {S}}'})=u$
. It then follows from Lemma 6.4 that we can compare
$\pi _{{\mathcal {S}}', \infty }^{\Lambda _{{\mathcal {S}}'}}(u_{{\mathcal {S}}'})=u$
. It then follows from Lemma 6.4 that we can compare
![]() $({\mathcal {S}}, \Lambda _{\mathcal {S}})$
and
$({\mathcal {S}}, \Lambda _{\mathcal {S}})$
and
![]() $({\mathcal {S}}', \Lambda _{{\mathcal {S}}'})$
via the least-extender-disagreement process and get some common iterate
$({\mathcal {S}}', \Lambda _{{\mathcal {S}}'})$
via the least-extender-disagreement process and get some common iterate
![]() $({\mathcal {S}}", \Lambda _{{\mathcal {S}}"})$
. It then follows that
$({\mathcal {S}}", \Lambda _{{\mathcal {S}}"})$
. It then follows that
![]() $\pi _{{\mathcal {S}}, {\mathcal {S}}"}(u_S)=\pi _{{\mathcal {S}}', {\mathcal {S}}"}(u_{{\mathcal {S}}'})=u_{{\mathcal {S}}"}$
.
$\pi _{{\mathcal {S}}, {\mathcal {S}}"}(u_S)=\pi _{{\mathcal {S}}', {\mathcal {S}}"}(u_{{\mathcal {S}}'})=u_{{\mathcal {S}}"}$
.
Consider now
![]() ${\mathcal {S}}_F, {\mathcal {S}}^{\prime }_F$
, and
${\mathcal {S}}_F, {\mathcal {S}}^{\prime }_F$
, and
![]() ${\mathcal {S}}^{\prime \prime }_F$
. We want to see that
${\mathcal {S}}^{\prime \prime }_F$
. We want to see that
To show (*), we observe that
-
(3.1)
 ${\mathcal {S}}^{\prime \prime }_F$
is a complete
${\mathcal {S}}^{\prime \prime }_F$
is a complete
 $\Phi _{{\mathcal {S}}_F}$
-iterate of
$\Phi _{{\mathcal {S}}_F}$
-iterate of
 ${\mathcal {S}}_F$
,
${\mathcal {S}}_F$
, -
(3.2)
 ${\mathcal {S}}^{\prime \prime }_F$
is a complete
${\mathcal {S}}^{\prime \prime }_F$
is a complete
 $\Phi _{{\mathcal {S}}^{\prime }_F}$
-iterate of
$\Phi _{{\mathcal {S}}^{\prime }_F}$
-iterate of
 ${\mathcal {S}}^{\prime }_F$
,
${\mathcal {S}}^{\prime }_F$
, -
(3.3)
 $\pi _{{\mathcal {S}}_F, {\mathcal {S}}^{\prime \prime }_F}(\pi _{F_{\mathcal {S}}}(u_{\mathcal {S}}))=\pi _{{\mathcal {S}}^{\prime }_F, {\mathcal {S}}^{\prime \prime }_F}(\pi _{F_{{\mathcal {S}}'}}(u_{{\mathcal {S}}'}))$
$\pi _{{\mathcal {S}}_F, {\mathcal {S}}^{\prime \prime }_F}(\pi _{F_{\mathcal {S}}}(u_{\mathcal {S}}))=\pi _{{\mathcal {S}}^{\prime }_F, {\mathcal {S}}^{\prime \prime }_F}(\pi _{F_{{\mathcal {S}}'}}(u_{{\mathcal {S}}'}))$
Notice that (3.3) implies (*). (3.3) is an immediate consequence of (3.1) and (3.2), and (3.2) has the same proof as (3.1), and (3.1) follows from the proof of Claim 7.2.
Claim 7.4.
![]() $\mathrm {crit }(j)=\mathrm {crit }(E_{{\mathcal {P} }, \Sigma , F})$
$\mathrm {crit }(j)=\mathrm {crit }(E_{{\mathcal {P} }, \Sigma , F})$
Proof. Suppose
![]() $\alpha <\mathrm {crit }(E_{{\mathcal {P} }, \Sigma , F})$
. Let
$\alpha <\mathrm {crit }(E_{{\mathcal {P} }, \Sigma , F})$
. Let
![]() ${\mathcal {S}}$
be a
${\mathcal {S}}$
be a
![]() $\Phi $
-iterate of
$\Phi $
-iterate of
![]() ${\mathcal {P} }$
such that
${\mathcal {P} }$
such that
![]() ${\mathcal {T}}_{{\mathcal {P} }, {\mathcal {S}}}$
is based on
${\mathcal {T}}_{{\mathcal {P} }, {\mathcal {S}}}$
is based on
![]() ${\mathcal {P} }|\nu (F)$
and
${\mathcal {P} }|\nu (F)$
and
![]() $\alpha \in \mathrm {rge}(\pi ^\Sigma _{{\mathcal {P} }, {\mathcal {S}}})$
. We then have that if
$\alpha \in \mathrm {rge}(\pi ^\Sigma _{{\mathcal {P} }, {\mathcal {S}}})$
. We then have that if
![]() $\alpha _{\mathcal {S}}=(\pi ^{\Sigma }_{{\mathcal {P} }, {\mathcal {S}}})^{-1}(\alpha )$
, then
$\alpha _{\mathcal {S}}=(\pi ^{\Sigma }_{{\mathcal {P} }, {\mathcal {S}}})^{-1}(\alpha )$
, then
![]() $\pi ^\Lambda _{{\mathcal {S}}, \infty }(\alpha _{\mathcal {S}})=\alpha $
. Notice next that
$\pi ^\Lambda _{{\mathcal {S}}, \infty }(\alpha _{\mathcal {S}})=\alpha $
. Notice next that
![]() $j(x)=\pi ^\Phi _{{\mathcal {S}}_F, \infty }(\pi _{F_{\mathcal {S}}}(\alpha _{\mathcal {S}}))$
, and since
$j(x)=\pi ^\Phi _{{\mathcal {S}}_F, \infty }(\pi _{F_{\mathcal {S}}}(\alpha _{\mathcal {S}}))$
, and since
![]() $\pi _{F_{\mathcal {S}}}(\alpha _{\mathcal {S}})=\alpha _{\mathcal {S}}$
,Footnote
47
setting
$\pi _{F_{\mathcal {S}}}(\alpha _{\mathcal {S}})=\alpha _{\mathcal {S}}$
,Footnote
47
setting
![]() ${\mathcal {W} }={\mathcal {S}}_F|\nu (\pi _{{\mathcal {P} }, {\mathcal {S}}}(F))$
,
${\mathcal {W} }={\mathcal {S}}_F|\nu (\pi _{{\mathcal {P} }, {\mathcal {S}}}(F))$
,
![]() $\pi ^{\Phi }_{{\mathcal {S}}_F, \infty }(\alpha _{\mathcal {S}})=\pi ^{\Sigma _{{\mathcal {W} }}}_{{\mathcal {W} }, \infty }(\alpha _{\mathcal {S}})$
. Since
$\pi ^{\Phi }_{{\mathcal {S}}_F, \infty }(\alpha _{\mathcal {S}})=\pi ^{\Sigma _{{\mathcal {W} }}}_{{\mathcal {W} }, \infty }(\alpha _{\mathcal {S}})$
. Since
![]() ${\mathcal {W} }={\mathcal {S}}|\nu (\pi _{{\mathcal {P} }, {\mathcal {S}}}(F))$
, we have that
${\mathcal {W} }={\mathcal {S}}|\nu (\pi _{{\mathcal {P} }, {\mathcal {S}}}(F))$
, we have that
![]() $\pi ^{\Phi }_{{\mathcal {S}}_F, \infty }(\alpha _{\mathcal {S}})=\alpha $
, implying that
$\pi ^{\Phi }_{{\mathcal {S}}_F, \infty }(\alpha _{\mathcal {S}})=\alpha $
, implying that
![]() $j(\alpha )=\alpha $
.
$j(\alpha )=\alpha $
.
To finish the proof of Theorem 7.1, we need to produce an
![]() $\omega $
-club
$\omega $
-club
![]() $C\subseteq \omega _1$
such that for each
$C\subseteq \omega _1$
such that for each
![]() $\alpha \in C$
, there is an embedding
$\alpha \in C$
, there is an embedding
![]() $k: N\rightarrow N$
with
$k: N\rightarrow N$
with
![]() $\mathrm {crit }(k)=\alpha $
. Above, we have produced an elementary embedding
$\mathrm {crit }(k)=\alpha $
. Above, we have produced an elementary embedding
![]() $j_{{\mathcal {P} }, \Sigma , F}:N\rightarrow N$
such that
$j_{{\mathcal {P} }, \Sigma , F}:N\rightarrow N$
such that
![]() $\mathrm {crit }(j_{{\mathcal {P} }, \Sigma , F})=\mathrm {crit }(E_{{\mathcal {P} }, \Sigma , F})$
. We then apply this fact to the Mitchell order 0 extender F such that
$\mathrm {crit }(j_{{\mathcal {P} }, \Sigma , F})=\mathrm {crit }(E_{{\mathcal {P} }, \Sigma , F})$
. We then apply this fact to the Mitchell order 0 extender F such that
![]() $\mathrm {crit }(F)=\delta _{\mathcal {P} }$
. Let C consist of ordinals
$\mathrm {crit }(F)=\delta _{\mathcal {P} }$
. Let C consist of ordinals
![]() $\kappa $
such that for some complete
$\kappa $
such that for some complete
![]() $\Sigma $
-iterate
$\Sigma $
-iterate
![]() ${\mathcal { Q}}$
of
${\mathcal { Q}}$
of
![]() ${\mathcal {P} }$
,
${\mathcal {P} }$
,
![]() $\kappa =\mathrm {crit }(E_{{\mathcal { Q}}, \Sigma _{\mathcal { Q}}, F_{\mathcal { Q}}})$
. Then C is an
$\kappa =\mathrm {crit }(E_{{\mathcal { Q}}, \Sigma _{\mathcal { Q}}, F_{\mathcal { Q}}})$
. Then C is an
![]() $\omega $
-clubFootnote
48
and is such that for each
$\omega $
-clubFootnote
48
and is such that for each
![]() $\kappa \in C$
, there is
$\kappa \in C$
, there is
![]() $j: N\rightarrow N$
such that
$j: N\rightarrow N$
such that
![]() $\mathrm {crit }(j)=\kappa $
. This finishes the proof of Theorem 7.1.
$\mathrm {crit }(j)=\kappa $
. This finishes the proof of Theorem 7.1.
Remark 7.5. The proof of Theorem 7.1 demonstrates that
![]() $\omega _2$
is
$\omega _2$
is
![]() $\Theta $
-Berkeley. Indeed, fix some
$\Theta $
-Berkeley. Indeed, fix some
![]() $\eta <\omega _2$
, and pick
$\eta <\omega _2$
, and pick
![]() $x\in \mathrm {dom}(H)$
such that if
$x\in \mathrm {dom}(H)$
such that if
![]() $\tau _x$
is the second measurable cardinal of
$\tau _x$
is the second measurable cardinal of
![]() ${\mathcal {P} }_x$
, then
${\mathcal {P} }_x$
, then
![]() $\pi _{{\mathcal {P} }_x, \infty }(\tau _x)>\eta $
. Let
$\pi _{{\mathcal {P} }_x, \infty }(\tau _x)>\eta $
. Let
![]() $F\in \vec {E}^{{\mathcal {P} }_x}$
be the Mitchell order 0 extender with
$F\in \vec {E}^{{\mathcal {P} }_x}$
be the Mitchell order 0 extender with
![]() $\mathrm { crit }(F)=\tau _x$
. We now repeat the proof of Theorem 7.1 and get that
$\mathrm { crit }(F)=\tau _x$
. We now repeat the proof of Theorem 7.1 and get that
![]() $\pi _{{\mathcal {P} }_x, \infty }(\tau _x)$
is a limit of ordinals
$\pi _{{\mathcal {P} }_x, \infty }(\tau _x)$
is a limit of ordinals
![]() $\alpha $
such that there is a
$\alpha $
such that there is a
![]() $j: N\rightarrow N$
with
$j: N\rightarrow N$
with
![]() $\mathrm { crit }(j)=\alpha $
. Since ordinals of the form
$\mathrm { crit }(j)=\alpha $
. Since ordinals of the form
![]() $\pi _{{\mathcal {P} }_x, \infty }(\tau _x)$
are cofinal in
$\pi _{{\mathcal {P} }_x, \infty }(\tau _x)$
are cofinal in
![]() $\omega _2$
, we get that
$\omega _2$
, we get that
![]() $\omega _2$
is a
$\omega _2$
is a
![]() $\Theta $
-Berkeley cardinal.
$\Theta $
-Berkeley cardinal.
The same argument can be used to show that for any n, ![]() is
is
![]() $\Theta $
-Berkeley. This is because for each n and for each
$\Theta $
-Berkeley. This is because for each n and for each
![]() $x\in \mathrm {dom}(H)$
,
$x\in \mathrm {dom}(H)$
,
![]() ${\mathcal {M}}_\infty ({\mathcal {P} }_x, \Sigma _x)$
has a cutpoint cardinal that belongs to the interval
${\mathcal {M}}_\infty ({\mathcal {P} }_x, \Sigma _x)$
has a cutpoint cardinal that belongs to the interval ![]() ,Footnote
49
and
,Footnote
49
and ![]() is a limit of measurable cardinals of
is a limit of measurable cardinals of
![]() ${\mathcal {M}}_\infty ({\mathcal {P} }_x, \Sigma _x)$
. If now
${\mathcal {M}}_\infty ({\mathcal {P} }_x, \Sigma _x)$
. If now ![]() is the least cutpoint measurable of
is the least cutpoint measurable of
![]() ${\mathcal {M}}_\infty ({\mathcal {P} }_x, \Sigma _x)$
, then the proof of Theorem 7.1 shows that for unboundedly many
${\mathcal {M}}_\infty ({\mathcal {P} }_x, \Sigma _x)$
, then the proof of Theorem 7.1 shows that for unboundedly many
![]() $\alpha <\kappa _x$
, there is
$\alpha <\kappa _x$
, there is
![]() $j: N\rightarrow N$
such that
$j: N\rightarrow N$
such that
![]() $\mathrm {crit }(j)=\alpha $
. Since
$\mathrm {crit }(j)=\alpha $
. Since ![]() is a limit of ordinals of the form
is a limit of ordinals of the form
![]() $\kappa _x$
, we have that
$\kappa _x$
, we have that ![]() is
is
![]() $\Theta $
-Berkeley.
$\Theta $
-Berkeley.
8 Toward
 $\textsf {HOD}$
-Berkeley cardinals
$\textsf {HOD}$
-Berkeley cardinals
Remark 7.5 leaves open how ubiquitous
![]() $\Theta $
-Berkeley cardinals are.
$\Theta $
-Berkeley cardinals are.
Question 8.1. Assume
![]() $\textsf {AD}^{+}$
. Is there an uncountable cardinal
$\textsf {AD}^{+}$
. Is there an uncountable cardinal
![]() $\kappa <\Theta $
that is not
$\kappa <\Theta $
that is not
![]() $\Theta $
-Berkeley? Is every regular cardinal club
$\Theta $
-Berkeley? Is every regular cardinal club
![]() $\Theta $
-Berkeley?
$\Theta $
-Berkeley?
A regular cardinal
![]() $\kappa $
is a club
$\kappa $
is a club
![]() $({\textsf {OD}}, \lambda )$
-Berkeley if for every
$({\textsf {OD}}, \lambda )$
-Berkeley if for every
![]() $x\in H_\kappa $
and every transitive structure M of size
$x\in H_\kappa $
and every transitive structure M of size
![]() $<\lambda $
such that M is ordinal definable from x, there is a club
$<\lambda $
such that M is ordinal definable from x, there is a club
![]() $C\subseteq \kappa $
such that for each
$C\subseteq \kappa $
such that for each
![]() $\alpha \in C$
, there is an elementary embedding
$\alpha \in C$
, there is an elementary embedding
![]() $j: M\rightarrow M$
with
$j: M\rightarrow M$
with
![]() $\mathrm {crit }(j)=\alpha $
. The following is an easy corollary to Theorem 7.1. It follows from the fact that
$\mathrm {crit }(j)=\alpha $
. The following is an easy corollary to Theorem 7.1. It follows from the fact that
![]() $\mathbb {P}_{{\textsf {max}}}*Add(1, \omega _3)$
is a countably closed homogeneous poset.
$\mathbb {P}_{{\textsf {max}}}*Add(1, \omega _3)$
is a countably closed homogeneous poset.
Corollary 8.2. Assume
![]() ${\textsf {AD}}_{{\mathbb {R}}}+V=L({\wp }({\mathbb {R}}))+\text {`}\Theta $
is a regular cardinal’. Let
${\textsf {AD}}_{{\mathbb {R}}}+V=L({\wp }({\mathbb {R}}))+\text {`}\Theta $
is a regular cardinal’. Let
![]() $G\subseteq \mathbb {P}_{{\textsf {max}}}*Add(1, \omega _3)$
be V-generic. Then in
$G\subseteq \mathbb {P}_{{\textsf {max}}}*Add(1, \omega _3)$
be V-generic. Then in
![]() $V[G]$
,
$V[G]$
,
![]() $\omega _1$
is club
$\omega _1$
is club
![]() $({\textsf {OD}}, \omega _3)$
-Berkeley.
$({\textsf {OD}}, \omega _3)$
-Berkeley.
Obtaining a model of
![]() $\mathsf {ZFC} + $
‘there is a
$\mathsf {ZFC} + $
‘there is a
![]() $\mathsf {HOD}$
-Berkeley cardinal’ by forcing seems like a hard problem. In this direction, Gabriel Goldberg has shown the following proposition. We include his argument with permission.Footnote
50
$\mathsf {HOD}$
-Berkeley cardinal’ by forcing seems like a hard problem. In this direction, Gabriel Goldberg has shown the following proposition. We include his argument with permission.Footnote
50
Proposition 8.3 (Goldberg).
Suppose there is a
![]() ${\textsf {HOD}}$
-Berkeley cardinal. Then
${\textsf {HOD}}$
-Berkeley cardinal. Then
![]() $A^{\#}$
exists for all sets A.
$A^{\#}$
exists for all sets A.
Proof. Since every set of ordinals is set generic over HOD, it is enough to show that every set of ordinals that belongs to HOD has a sharp. Let A be a set of ordinals in
![]() $\textsf {HOD}$
with
$\textsf {HOD}$
with
![]() $\sup A =\lambda $
, and let
$\sup A =\lambda $
, and let
![]() $\gamma $
be a
$\gamma $
be a
![]() $\Sigma _2$
-correct ordinal
$\Sigma _2$
-correct ordinal
![]() $>\lambda $
of uncountable cofinality. Let
$>\lambda $
of uncountable cofinality. Let
![]() $j:V_{\gamma }^{\textsf {HOD}}\to V_{\gamma }^{\textsf {HOD}}$
be an elementary embedding. (Notice j is not definable over V; if it were, it would belong to a
$j:V_{\gamma }^{\textsf {HOD}}\to V_{\gamma }^{\textsf {HOD}}$
be an elementary embedding. (Notice j is not definable over V; if it were, it would belong to a
![]() ${<}\gamma $
-generic extension of
${<}\gamma $
-generic extension of
![]() $\textsf {HOD}$
, contrary to Woodin’s proof [Reference Kanamori7, p. 320] of the Kunen Inconsistency.) Letting E be the extender of length
$\textsf {HOD}$
, contrary to Woodin’s proof [Reference Kanamori7, p. 320] of the Kunen Inconsistency.) Letting E be the extender of length
![]() $\lambda +1$
derived from j, we have that j factors into embeddings
$\lambda +1$
derived from j, we have that j factors into embeddings
![]() $j_E: V_{\gamma }^{\textsf {HOD}}\to M$
and
$j_E: V_{\gamma }^{\textsf {HOD}}\to M$
and
![]() $k:M\to V_{\gamma }^{\textsf {HOD}}$
. Since j is not definable and hence is not the extender ultrapower, k must be nontrivial with
$k:M\to V_{\gamma }^{\textsf {HOD}}$
. Since j is not definable and hence is not the extender ultrapower, k must be nontrivial with
![]() $\mathrm {crit }(k)>\lambda $
. Then
$\mathrm {crit }(k)>\lambda $
. Then
![]() $k:L_{\gamma }[A]\to L_{\gamma }[A]$
is a nontrivial elementary embedding with
$k:L_{\gamma }[A]\to L_{\gamma }[A]$
is a nontrivial elementary embedding with
![]() $\mathrm {crit }(k)>\lambda $
.
$\mathrm {crit }(k)>\lambda $
.
With a stronger hypothesis, we can get
![]() ${\mathcal {M}}_1^\#$
.
${\mathcal {M}}_1^\#$
.
Proposition 8.4. Suppose there is a
![]() ${\textsf {HOD}}$
-Berkeley cardinal and a measurable cardinal above it. Then
${\textsf {HOD}}$
-Berkeley cardinal and a measurable cardinal above it. Then
![]() ${\mathcal {M}}_1^\#$
exists and is
${\mathcal {M}}_1^\#$
exists and is
![]() ${\textsf {Ord}}$
-iterable.
${\textsf {Ord}}$
-iterable.
Proof. Let
![]() $\iota $
be a measurable cardinal above the least
$\iota $
be a measurable cardinal above the least
![]() ${\textsf {HOD}}$
-Berkeley cardinal. We first show that the core model
${\textsf {HOD}}$
-Berkeley cardinal. We first show that the core model
![]() $K=_{def}K^{V_\iota }$
does not exist. Toward a contradiction, assume that it does. Since
$K=_{def}K^{V_\iota }$
does not exist. Toward a contradiction, assume that it does. Since
![]() $K\in \textsf {HOD}$
, we have a nontrivial embedding
$K\in \textsf {HOD}$
, we have a nontrivial embedding
![]() $j: K\rightarrow K$
. But then [Reference Steel23, Theorem 8.8] gives a contradiction. It now follows from the same aforementioned theorem that in fact
$j: K\rightarrow K$
. But then [Reference Steel23, Theorem 8.8] gives a contradiction. It now follows from the same aforementioned theorem that in fact
![]() $(K^c)^{V_\iota }\vDash $
‘there is a Woodin cardinal’, and since V is closed under sharps by Proposition 8.3, we get that
$(K^c)^{V_\iota }\vDash $
‘there is a Woodin cardinal’, and since V is closed under sharps by Proposition 8.3, we get that
![]() ${\mathcal {M}}_1^\#\trianglelefteq (K^c)^{V_\iota }$
. Because V is closed under sharps, it follows that
${\mathcal {M}}_1^\#\trianglelefteq (K^c)^{V_\iota }$
. Because V is closed under sharps, it follows that
![]() ${\mathcal {M}}_1^\#$
is
${\mathcal {M}}_1^\#$
is
![]() ${\textsf {Ord}}$
-iterable (see [Reference Steel and Woodin33]).
${\textsf {Ord}}$
-iterable (see [Reference Steel and Woodin33]).
Combining the arguments for Proposition 8.3 and Proposition 8.4, we get some definable determinacy.
Theorem 8.5. Suppose there is a
![]() ${\textsf {HOD}}$
-Berkeley cardinal and a class of measurable cardinals. Then Projective Determinacy holds.
${\textsf {HOD}}$
-Berkeley cardinal and a class of measurable cardinals. Then Projective Determinacy holds.
Proof. The proof is via the core model induction as in [Reference Steel25]. We show that
![]() ${\mathcal {M}}_2^\#$
exists and leave the rest to the reader. To show that
${\mathcal {M}}_2^\#$
exists and leave the rest to the reader. To show that
![]() ${\mathcal {M}}_2^\#$
exists, it is enough to show that V is closed under the
${\mathcal {M}}_2^\#$
exists, it is enough to show that V is closed under the
![]() ${\mathcal {M}}_1^\#$
-operator and
${\mathcal {M}}_1^\#$
-operator and
![]() $K^c\vDash $
‘There is a Woodin cardinal’. The second statement is very much like the proof of Proposition 8.4, and so we only show that V is closed under the
$K^c\vDash $
‘There is a Woodin cardinal’. The second statement is very much like the proof of Proposition 8.4, and so we only show that V is closed under the
![]() ${\mathcal {M}}_1^\#$
-operator.
${\mathcal {M}}_1^\#$
-operator.
As in the proof of Proposition 8.3, it is enough to show that for every set of ordinals
![]() $A\in {\textsf {HOD}}$
,
$A\in {\textsf {HOD}}$
,
![]() ${\mathcal {M}}_1^\#(A)$
exists, and to show this, it is enough to show that for every
${\mathcal {M}}_1^\#(A)$
exists, and to show this, it is enough to show that for every
![]() $A\in {\textsf {HOD}}$
,
$A\in {\textsf {HOD}}$
,
![]() $K(A)$
does not exist.
$K(A)$
does not exist.
Fix now
![]() $A\in {\textsf {HOD}}$
,
$A\in {\textsf {HOD}}$
,
![]() $A\subseteq \lambda $
, and let
$A\subseteq \lambda $
, and let
![]() $\iota>\lambda $
be a measurable cardinal above the least
$\iota>\lambda $
be a measurable cardinal above the least
![]() ${\textsf {HOD}}$
-Berkeley cardinal. Assume that
${\textsf {HOD}}$
-Berkeley cardinal. Assume that
![]() $K=K(A)^{V_\iota }$
exists. Notice that
$K=K(A)^{V_\iota }$
exists. Notice that
![]() $K\in {\textsf {HOD}}$
. Let
$K\in {\textsf {HOD}}$
. Let
![]() $\gamma>\iota $
be a
$\gamma>\iota $
be a
![]() $\Sigma _2$
-correct cardinal, and let
$\Sigma _2$
-correct cardinal, and let
![]() $M\in {\textsf {HOD}}$
be such that, letting
$M\in {\textsf {HOD}}$
be such that, letting
![]() $a=\{V_{\gamma }^{\textsf {HOD}}, K\}$
,
$a=\{V_{\gamma }^{\textsf {HOD}}, K\}$
,
![]() $a\in M$
and a is definable in M (see [Reference Bagaria, Koellner and Woodin1, Lemma 3.1]). Let
$a\in M$
and a is definable in M (see [Reference Bagaria, Koellner and Woodin1, Lemma 3.1]). Let
![]() $j': M\rightarrow M$
be nontrivial and elementary.
$j': M\rightarrow M$
be nontrivial and elementary.
Let
![]() $j=j'\restriction V_{\gamma }^{\textsf {HOD}}$
. Notice that
$j=j'\restriction V_{\gamma }^{\textsf {HOD}}$
. Notice that
![]() $j(K)=K$
. Let
$j(K)=K$
. Let
![]() $\kappa =\mathrm {crit }(j)$
, and let F be the
$\kappa =\mathrm {crit }(j)$
, and let F be the
![]() $(\kappa , \lambda )$
-extender derived from j. As in the proof of Proposition 8.3, if
$(\kappa , \lambda )$
-extender derived from j. As in the proof of Proposition 8.3, if
![]() $k': Ult(V_{\gamma }^{\textsf {HOD}}, F)\rightarrow V_{\gamma }^{\textsf {HOD}}$
is the canonical factor map, then
$k': Ult(V_{\gamma }^{\textsf {HOD}}, F)\rightarrow V_{\gamma }^{\textsf {HOD}}$
is the canonical factor map, then
![]() $\mathrm {crit }(k')>\lambda $
. Let then
$\mathrm {crit }(k')>\lambda $
. Let then
![]() ${\mathcal {M}}=\pi _F(K)$
, and set
${\mathcal {M}}=\pi _F(K)$
, and set
![]() $\pi _F=i$
and
$\pi _F=i$
and
![]() $k'\restriction {\mathcal {M}}=k$
. We thus have that
$k'\restriction {\mathcal {M}}=k$
. We thus have that
![]() $i:K\rightarrow {\mathcal {M}}$
and
$i:K\rightarrow {\mathcal {M}}$
and
![]() $k:{\mathcal {M}}\rightarrow K$
. Moreover,
$k:{\mathcal {M}}\rightarrow K$
. Moreover,
![]() $\mathrm {crit }(k)>\lambda $
.
$\mathrm {crit }(k)>\lambda $
.
Because
![]() $i:K\rightarrow {\mathcal {M}}$
, it follows that
$i:K\rightarrow {\mathcal {M}}$
, it follows that
![]() ${\mathcal {M}}$
is universal among A-mice of ordinal height
${\mathcal {M}}$
is universal among A-mice of ordinal height
![]() $\iota $
, and therefore, there is
$\iota $
, and therefore, there is
![]() $\sigma : K\rightarrow {\mathcal {M}}$
such that
$\sigma : K\rightarrow {\mathcal {M}}$
such that
![]() $\mathrm {crit }(\sigma )>\lambda $
(see [Reference Steel23]). It follows that
$\mathrm {crit }(\sigma )>\lambda $
(see [Reference Steel23]). It follows that
![]() $k\circ \sigma :K\rightarrow K$
, and so we can get a contradiction as in Proposition 8.4.
$k\circ \sigma :K\rightarrow K$
, and so we can get a contradiction as in Proposition 8.4.
These theorems show that obtaining
![]() ${\textsf {HOD}}$
-Berkeley cardinals requires significant large cardinals. We believe that the proof of Theorem 8.5 can be extended to show that
${\textsf {HOD}}$
-Berkeley cardinals requires significant large cardinals. We believe that the proof of Theorem 8.5 can be extended to show that
![]() $L({\mathbb {R}})\vDash {\textsf {AD}}$
and the hypothesis that there is a class of measurable cardinals is unnecessary (see [Reference Jensen and Steel6]). But establishing these beliefs is beyond the scope of this paper, and we conclude this discussion with the following conjecture.
$L({\mathbb {R}})\vDash {\textsf {AD}}$
and the hypothesis that there is a class of measurable cardinals is unnecessary (see [Reference Jensen and Steel6]). But establishing these beliefs is beyond the scope of this paper, and we conclude this discussion with the following conjecture.
Conjecture 8.6. Suppose there is a
![]() ${\textsf {HOD}}$
-Berkeley cardinal. Then the minimal model of
${\textsf {HOD}}$
-Berkeley cardinal. Then the minimal model of
![]() ${\textsf {AD}}_{{\mathbb {R}}}+\text {`}\Theta $
is a regular cardinal’ exists.
${\textsf {AD}}_{{\mathbb {R}}}+\text {`}\Theta $
is a regular cardinal’ exists.
9 Theorem 3.1 is optimal
In this section, we use the main idea of Proposition 8.3, ideas from [Reference Jensen, Schimmerling, Schindler and Steel5], and the HOD analysis of
![]() $L({\mathbb {R}})$
(see [Reference Steel and Woodin33]) to show that Theorem 3.1 cannot be improved, assuming that
$L({\mathbb {R}})$
(see [Reference Steel and Woodin33]) to show that Theorem 3.1 cannot be improved, assuming that
![]() $V=L({\mathbb {R}})$
.
$V=L({\mathbb {R}})$
.
9.1 Hod-like pairs
Our strategy for proving Theorem 9.14 is the following. Assume
![]() $V=L({\wp }({\mathbb {R}}))+{\textsf {AD}}$
, and suppose there is an embedding
$V=L({\wp }({\mathbb {R}}))+{\textsf {AD}}$
, and suppose there is an embedding
![]() $j:{\textsf {HOD}}|\Theta \rightarrow {\textsf {HOD}}|\Theta $
. We want to show that j can be extended to
$j:{\textsf {HOD}}|\Theta \rightarrow {\textsf {HOD}}|\Theta $
. We want to show that j can be extended to
![]() $j^+:{\textsf {HOD}}\rightarrow {\textsf {HOD}}$
. Via the reasoning of Proposition 8.3, this leads to a contradiction.
$j^+:{\textsf {HOD}}\rightarrow {\textsf {HOD}}$
. Via the reasoning of Proposition 8.3, this leads to a contradiction.
To implement our strategy, we need to use more of the HOD analysis than the previous sections required. The HOD analysis that we need is developed in [Reference Steel and Woodin33, Chapter 6], in particular [Reference Steel and Woodin33, Theorem 6.1]. Recall from [Reference Steel and Woodin33, Theorem 6.1] that assuming
![]() $V=L({\mathbb {R}})$
,
$V=L({\mathbb {R}})$
,
![]() ${\textsf {HOD}}=L[{\mathcal {M}}_\infty ^+, \Lambda ]$
. While [Reference Steel and Woodin33, Theorem 6.1] is proved assuming
${\textsf {HOD}}=L[{\mathcal {M}}_\infty ^+, \Lambda ]$
. While [Reference Steel and Woodin33, Theorem 6.1] is proved assuming
![]() ${\mathcal {M}}_\omega ^\#$
exists, the proof can also be done by first reflecting and then picking a coarse tuple as we have done in the arguments presented in the previous sections (see Definition 4.5). The proof simply needs a pair
${\mathcal {M}}_\omega ^\#$
exists, the proof can also be done by first reflecting and then picking a coarse tuple as we have done in the arguments presented in the previous sections (see Definition 4.5). The proof simply needs a pair
![]() $({\mathcal {P} }, \Sigma )$
whose derived model is
$({\mathcal {P} }, \Sigma )$
whose derived model is
![]() $L({\mathbb {R}})$
, or
$L({\mathbb {R}})$
, or
![]() $L_\alpha ({\mathbb {R}})$
, as we will do below.
$L_\alpha ({\mathbb {R}})$
, as we will do below.
The exact meaning of
![]() ${\mathcal {M}}_\infty ^+$
and
${\mathcal {M}}_\infty ^+$
and
![]() $\Lambda $
are very important for us, and we will set up some notation to discuss these object.
$\Lambda $
are very important for us, and we will set up some notation to discuss these object.
Notation 9.1. Suppose
![]() ${\mathcal {P} }$
is a premouse. Then
${\mathcal {P} }$
is a premouse. Then
![]() $(\delta ^{\alpha }_{\mathcal {P} }: \alpha \leq \iota )$
denotes the increasing enumeration of the Woodin cardinals of
$(\delta ^{\alpha }_{\mathcal {P} }: \alpha \leq \iota )$
denotes the increasing enumeration of the Woodin cardinals of
![]() ${\mathcal {P} }$
and their limits, and
${\mathcal {P} }$
and their limits, and
![]() $\eta ^{\alpha }_{\mathcal {P} }$
denotes the
$\eta ^{\alpha }_{\mathcal {P} }$
denotes the
![]() ${\mathcal {P} }$
-successor of
${\mathcal {P} }$
-successor of
![]() $\delta ^{\alpha }_{\mathcal {P} }$
, if it exists.
$\delta ^{\alpha }_{\mathcal {P} }$
, if it exists.
Definition 9.2. Suppose
![]() ${\mathcal {P} }$
is a premouse with exactly
${\mathcal {P} }$
is a premouse with exactly
![]() $\omega $
many Woodin cardinals. Let
$\omega $
many Woodin cardinals. Let
![]() ${\mathcal { H}}_{\mathcal {P} }$
be the premouse representation of
${\mathcal { H}}_{\mathcal {P} }$
be the premouse representation of
![]() $({\textsf {HOD}}|\Theta )^{D({\mathcal {P} }, \delta ^\omega _{\mathcal {P} })}$
.Footnote
51
$({\textsf {HOD}}|\Theta )^{D({\mathcal {P} }, \delta ^\omega _{\mathcal {P} })}$
.Footnote
51
We say
![]() ${\mathcal {P} }$
is hod-like if
${\mathcal {P} }$
is hod-like if
-
1.
 ${\mathcal {P} }\vDash {\textsf {ZFC-Replacement}}$
, and
${\mathcal {P} }\vDash {\textsf {ZFC-Replacement}}$
, and -
2. there is a tree
 ${\mathcal {T}}\in {\mathcal {P} }$
of limit length such that
${\mathcal {T}}\in {\mathcal {P} }$
of limit length such that
 ${\textsf {cop}}({\mathcal {T}})={\mathcal { H}}_{\mathcal {P} }$
and
${\textsf {cop}}({\mathcal {T}})={\mathcal { H}}_{\mathcal {P} }$
and
 ${\mathcal {T}}$
is based on
${\mathcal {T}}$
is based on
 ${\mathcal {P} }|\delta ^0_{\mathcal {P} }$
.Footnote
52
${\mathcal {P} }|\delta ^0_{\mathcal {P} }$
.Footnote
52
If
![]() ${\mathcal {P} }$
is hod-like, then we let
${\mathcal {P} }$
is hod-like, then we let
![]() ${\mathcal {T}}_{\mathcal {P} }$
be the normal tree
${\mathcal {T}}_{\mathcal {P} }$
be the normal tree
![]() ${\mathcal {T}}$
such that
${\mathcal {T}}$
such that
![]() ${\textsf {cop}}({\mathcal {T}})={\mathcal { H}}_{\mathcal {P} }$
.
${\textsf {cop}}({\mathcal {T}})={\mathcal { H}}_{\mathcal {P} }$
.
Suppose
![]() ${\mathcal {P} }$
is a hod-like and b is a branch of
${\mathcal {P} }$
is a hod-like and b is a branch of
![]() ${\mathcal {T}}_{\mathcal {P} }$
. We say b is friendly to
${\mathcal {T}}_{\mathcal {P} }$
. We say b is friendly to
![]() ${\mathcal {P} }$
if
${\mathcal {P} }$
if
![]() $\pi ^{\mathcal {T}}_b(\delta ^0_{\mathcal {P} })=\Theta ^{D({\mathcal {P} }, \delta ^\omega _{\mathcal {P} })}$
.
$\pi ^{\mathcal {T}}_b(\delta ^0_{\mathcal {P} })=\Theta ^{D({\mathcal {P} }, \delta ^\omega _{\mathcal {P} })}$
.
Suppose
![]() ${\mathcal {P} }$
is hod-like and b is friendly to
${\mathcal {P} }$
is hod-like and b is friendly to
![]() ${\mathcal {P} }$
. We then let
${\mathcal {P} }$
. We then let
![]() $\xi _{\mathcal {P} }=\mathrm {lh}({\mathcal {T}}_{\mathcal {P} })$
,
$\xi _{\mathcal {P} }=\mathrm {lh}({\mathcal {T}}_{\mathcal {P} })$
,
![]() $b({\mathcal {P} })=\{\eta ^\omega _{\mathcal {P} }+i: i\in b\}$
and
$b({\mathcal {P} })=\{\eta ^\omega _{\mathcal {P} }+i: i\in b\}$
and
We then say
![]() ${\mathcal {V}}'({\mathcal {P} }, b)$
is the pre-Varsovian model
Footnote
53
induced by
${\mathcal {V}}'({\mathcal {P} }, b)$
is the pre-Varsovian model
Footnote
53
induced by
![]() $({\mathcal {P} }, b)$
. We say
$({\mathcal {P} }, b)$
. We say
![]() $({\mathcal {P} }, b)$
is hod-like if the core of
$({\mathcal {P} }, b)$
is hod-like if the core of
![]() ${\mathcal {V}}'({\mathcal {P} }, b)$
is definedFootnote
54
and both its
${\mathcal {V}}'({\mathcal {P} }, b)$
is definedFootnote
54
and both its
![]() $\Sigma _1$
-projectum and projectum are
$\Sigma _1$
-projectum and projectum are
![]() $\delta ^0_{\mathcal {P} }$
. If
$\delta ^0_{\mathcal {P} }$
. If
![]() $({\mathcal {P} }, b)$
is hod-like, then we let
$({\mathcal {P} }, b)$
is hod-like, then we let
![]() ${\mathcal {V}}({\mathcal {P} }, b)$
be the core of
${\mathcal {V}}({\mathcal {P} }, b)$
be the core of
![]() ${\mathcal {V}}'({\mathcal {P} }, b)$
.
${\mathcal {V}}'({\mathcal {P} }, b)$
.
We treat
![]() ${\mathcal {V}}({\mathcal {P} }, b)$
as a hybrid premouse, see [Reference Schlutzenberg and Trang20]. Next, we introduce hod-like pairs.
${\mathcal {V}}({\mathcal {P} }, b)$
as a hybrid premouse, see [Reference Schlutzenberg and Trang20]. Next, we introduce hod-like pairs.
Definition 9.3. We say
![]() $({\mathcal {P} }, \Sigma )$
resembles a hod-like pair if it is a pure mouse pair such that the following conditions hold:
$({\mathcal {P} }, \Sigma )$
resembles a hod-like pair if it is a pure mouse pair such that the following conditions hold:
-
1.
 $\Sigma $
is an
$\Sigma $
is an
 $\omega _1+1$
-iteration strategy.
$\omega _1+1$
-iteration strategy. -
2.
 ${\mathcal {P} }$
is hod-like.
${\mathcal {P} }$
is hod-like. -
3. If
 $b=\Sigma ({\mathcal {T}}_{\mathcal {P} })$
, then
$b=\Sigma ({\mathcal {T}}_{\mathcal {P} })$
, then
 $({\mathcal {P} }, b)$
is hod-like.
$({\mathcal {P} }, b)$
is hod-like.
To turn pairs that resemble hod-like pairs into true hod-like pairs, we need to impose some conditions which fall naturally out of the HOD analysis.
Definition 9.4. A pair
![]() $({\mathcal {P} }, \Sigma )$
is a hod-like pair if it resembles a hod-like pair and the following conditions hold:
$({\mathcal {P} }, \Sigma )$
is a hod-like pair if it resembles a hod-like pair and the following conditions hold:
-
1. Self-capturing: For every cutpoint successor cardinal
 $\nu $
of
$\nu $
of
 ${\mathcal {P} }$
and ordinal
${\mathcal {P} }$
and ordinal
 $\gamma <\nu $
, if
$\gamma <\nu $
, if
 ${\mathcal {P} }$
has no Woodin cardinals in the interval
${\mathcal {P} }$
has no Woodin cardinals in the interval
 $(\gamma , \nu )$
, then the fragment of
$(\gamma , \nu )$
, then the fragment of
 $\Sigma $
that acts on iterations that are based on
$\Sigma $
that acts on iterations that are based on
 ${\mathcal {P} }|\nu $
and are above
${\mathcal {P} }|\nu $
and are above
 $\gamma $
is in the derived model of
$\gamma $
is in the derived model of
 $({\mathcal {P} }, \Sigma )$
.
$({\mathcal {P} }, \Sigma )$
. -
2. Self-similar: For every
 $i\in [1, \omega )$
, if
$i\in [1, \omega )$
, if
 ${\mathcal {W} }$
is the output of the fully backgrounded construction of
${\mathcal {W} }$
is the output of the fully backgrounded construction of
 ${\mathcal {P} }|\delta ^i_{\mathcal {P} }$
in which all extenders used have critical points
${\mathcal {P} }|\delta ^i_{\mathcal {P} }$
in which all extenders used have critical points
 $>\delta ^{i-1}_{\mathcal {P} }$
, then
$>\delta ^{i-1}_{\mathcal {P} }$
, then
 ${\mathcal {W} }$
is a
${\mathcal {W} }$
is a
 $\Sigma _{{\mathcal {P} }|\delta ^0_{\mathcal {P} }}$
-iterate of
$\Sigma _{{\mathcal {P} }|\delta ^0_{\mathcal {P} }}$
-iterate of
 ${\mathcal {P} }|\delta ^0$
.
${\mathcal {P} }|\delta ^0$
.
Suppose now that
![]() ${\mathcal {P} }$
is hod-like with exactly
${\mathcal {P} }$
is hod-like with exactly
![]() $\omega $
many Woodin cardinals. Then
$\omega $
many Woodin cardinals. Then
![]() ${\mathcal {P} }$
is self-similar if for every
${\mathcal {P} }$
is self-similar if for every
![]() $i\in \omega $
and
$i\in \omega $
and
![]() $\gamma \in [\delta ^i_{\mathcal {P} }, \delta ^{i+1}_{\mathcal {P} })$
, letting
$\gamma \in [\delta ^i_{\mathcal {P} }, \delta ^{i+1}_{\mathcal {P} })$
, letting
![]() ${\mathcal {W} }^i$
be the output of the fully backgrounded construction of
${\mathcal {W} }^i$
be the output of the fully backgrounded construction of
![]() ${\mathcal {P} }|\delta ^{i+1}_{\mathcal {P} }$
, there is a normal iteration tree
${\mathcal {P} }|\delta ^{i+1}_{\mathcal {P} }$
, there is a normal iteration tree
![]() ${\mathcal {T}}^i\in {\mathcal {P} }$
on
${\mathcal {T}}^i\in {\mathcal {P} }$
on
![]() ${\mathcal {P} }$
such that
${\mathcal {P} }$
such that
![]() ${\mathcal {T}}^i$
is based on
${\mathcal {T}}^i$
is based on
![]() ${\mathcal {P} }|\delta ^0_{\mathcal {P} }$
and
${\mathcal {P} }|\delta ^0_{\mathcal {P} }$
and
![]() ${\textsf {cop}}({\mathcal {T}}^i)={\mathcal {W} }^i$
.
${\textsf {cop}}({\mathcal {T}}^i)={\mathcal {W} }^i$
.
Lastly, we introduce abstract Varsovian models and self-determining Varsovian models.
Definition 9.5. We say
![]() ${\mathcal {V}}$
is a Varsovian model if for some hod-like
${\mathcal {V}}$
is a Varsovian model if for some hod-like
![]() $({\mathcal {P} }, b)$
with
$({\mathcal {P} }, b)$
with
![]() ${\mathcal {P} }$
self-similar,
${\mathcal {P} }$
self-similar,
![]() ${\mathcal {V}}={\mathcal {V}}'({\mathcal {P} }, b)$
. If
${\mathcal {V}}={\mathcal {V}}'({\mathcal {P} }, b)$
. If
![]() ${\mathcal {V}}$
is a Varsovian model witnessed by
${\mathcal {V}}$
is a Varsovian model witnessed by
![]() $({\mathcal {P} }, b)$
, then we let
$({\mathcal {P} }, b)$
, then we let
![]() ${\mathcal {X}}^{\mathcal {V}}={\mathcal {P} }$
,
${\mathcal {X}}^{\mathcal {V}}={\mathcal {P} }$
,
![]() ${\mathcal {U}}^{\mathcal {V}}={\mathcal {T}}_{\mathcal {P} }$
,
${\mathcal {U}}^{\mathcal {V}}={\mathcal {T}}_{\mathcal {P} }$
,
![]() ${\mathcal { H}}^{\mathcal {V}}={\mathcal { H}}_{\mathcal {P} }$
,
${\mathcal { H}}^{\mathcal {V}}={\mathcal { H}}_{\mathcal {P} }$
,
![]() $b^{\mathcal {V}}=b$
, and for
$b^{\mathcal {V}}=b$
, and for
![]() $i\in \omega $
,
$i\in \omega $
,
![]() $({\mathcal {W} }_i^{\mathcal {V}}, {\mathcal {T}}_i^{\mathcal {V}})=({\mathcal {W} }_i, {\mathcal {T}}_i)$
where
$({\mathcal {W} }_i^{\mathcal {V}}, {\mathcal {T}}_i^{\mathcal {V}})=({\mathcal {W} }_i, {\mathcal {T}}_i)$
where
![]() $({\mathcal {W} }_i, {\mathcal {T}}_i)$
is as in Definition 9.4.
$({\mathcal {W} }_i, {\mathcal {T}}_i)$
is as in Definition 9.4.
Definition 9.6. Suppose
![]() ${\mathcal {V}}={\mathcal {V}}'({\mathcal {P} }, b)$
is a Varsovian model. Then
${\mathcal {V}}={\mathcal {V}}'({\mathcal {P} }, b)$
is a Varsovian model. Then
![]() ${\mathcal {V}}$
is self-determining if for each
${\mathcal {V}}$
is self-determining if for each
![]() $i\in \omega $
, letting
$i\in \omega $
, letting
![]() $({\mathcal {W} }_i, {\mathcal {T}}_i)=({\mathcal {W} }_i^{\mathcal {V}}, {\mathcal {T}}_i^{\mathcal {V}})$
, there is
$({\mathcal {W} }_i, {\mathcal {T}}_i)=({\mathcal {W} }_i^{\mathcal {V}}, {\mathcal {T}}_i^{\mathcal {V}})$
, there is
![]() ${\mathcal {U}}_i\in {\mathcal {P} }$
on
${\mathcal {U}}_i\in {\mathcal {P} }$
on
![]() ${\mathcal {P} }$
such that
${\mathcal {P} }$
such that
![]() ${\textsf {cop}}({\mathcal {U}}_i)={\mathcal { H}}^{\mathcal {V}}$
and there is a unique pair of branches
${\textsf {cop}}({\mathcal {U}}_i)={\mathcal { H}}^{\mathcal {V}}$
and there is a unique pair of branches
![]() $(c_i, d_i)$
such that
$(c_i, d_i)$
such that
![]() $\pi ^{{\mathcal {U}}^{\mathcal {V}}}_{b^{\mathcal {V}}}=\pi ^{{\mathcal {U}}_i}_{d_i}\circ \pi ^{{\mathcal {T}}_i}_{c_i}$
.
$\pi ^{{\mathcal {U}}^{\mathcal {V}}}_{b^{\mathcal {V}}}=\pi ^{{\mathcal {U}}_i}_{d_i}\circ \pi ^{{\mathcal {T}}_i}_{c_i}$
.
In the above situation, we let
![]() $({\mathcal {U}}_i, c_i, d_i)=({\mathcal {U}}_i^{\mathcal {V}}, c_i^{\mathcal {V}}, d_i^{\mathcal {V}})$
.
$({\mathcal {U}}_i, c_i, d_i)=({\mathcal {U}}_i^{\mathcal {V}}, c_i^{\mathcal {V}}, d_i^{\mathcal {V}})$
.
Definition 9.7. We say that
![]() $({\mathcal {V}}, \Lambda )$
is a Varsovian pair if
$({\mathcal {V}}, \Lambda )$
is a Varsovian pair if
![]() ${\mathcal {V}}={\mathcal {V}}'({\mathcal {P} }, b)$
is a self-determining Varsovian model and
${\mathcal {V}}={\mathcal {V}}'({\mathcal {P} }, b)$
is a self-determining Varsovian model and
![]() $\Lambda $
is an iteration strategy for
$\Lambda $
is an iteration strategy for
![]() ${\mathcal {V}}$
such that, whenever
${\mathcal {V}}$
such that, whenever
![]() ${\mathcal {V}}'$
is a complete
${\mathcal {V}}'$
is a complete
![]() $\Lambda $
-iterate of
$\Lambda $
-iterate of
![]() ${\mathcal {V}}$
,
${\mathcal {V}}$
,
![]() ${\mathcal {V}}'$
is self-determining, all the iteration trees
${\mathcal {V}}'$
is self-determining, all the iteration trees
![]() ${\mathcal {U}}^{{\mathcal {V}}'}, {\mathcal {U}}_i^{{\mathcal {V}}'}, {\mathcal {T}}_i^{{\mathcal {V}}'}$
and the associated branches
${\mathcal {U}}^{{\mathcal {V}}'}, {\mathcal {U}}_i^{{\mathcal {V}}'}, {\mathcal {T}}_i^{{\mathcal {V}}'}$
and the associated branches
![]() $b^{{\mathcal {V}}'}, c_i^{{\mathcal {V}}'}, d^{{\mathcal {V}}'}_i$
are according to
$b^{{\mathcal {V}}'}, c_i^{{\mathcal {V}}'}, d^{{\mathcal {V}}'}_i$
are according to
![]() $\Lambda _{{\mathcal {V}}'|\delta ^0_{{\mathcal {V}}'}}$
.
$\Lambda _{{\mathcal {V}}'|\delta ^0_{{\mathcal {V}}'}}$
.
Definition 9.8. Suppose
![]() ${\mathcal {V}}={\mathcal {V}}'({\mathcal {P} }, b)$
is a Varsovian model and
${\mathcal {V}}={\mathcal {V}}'({\mathcal {P} }, b)$
is a Varsovian model and
![]() $\Gamma $
is an iteration strategy for
$\Gamma $
is an iteration strategy for
![]() ${\mathcal {P} }|\delta ^0_{\mathcal {P} }$
. Then
${\mathcal {P} }|\delta ^0_{\mathcal {P} }$
. Then
![]() $({\mathcal {V}}, \Lambda )$
is a
$({\mathcal {V}}, \Lambda )$
is a
![]() $\Gamma $
-Varsovian pair if
$\Gamma $
-Varsovian pair if
![]() ${\mathcal {V}}$
has a
${\mathcal {V}}$
has a
![]() $\left |{\mathcal {V}}\right |{}^++1$
-iteration strategy
$\left |{\mathcal {V}}\right |{}^++1$
-iteration strategy
![]() $\Lambda $
such that
$\Lambda $
such that
![]() $\Lambda _{{\mathcal {V}}|\delta ^0_{\mathcal {V}}}=\Gamma $
.
$\Lambda _{{\mathcal {V}}|\delta ^0_{\mathcal {V}}}=\Gamma $
.
We say
![]() ${\mathcal {V}}$
is
${\mathcal {V}}$
is
![]() $\Gamma $
-Varsovian model if there is a unique
$\Gamma $
-Varsovian model if there is a unique
![]() $\Lambda $
such that
$\Lambda $
such that
![]() $({\mathcal {V}}, \Lambda )$
is a
$({\mathcal {V}}, \Lambda )$
is a
![]() $\Gamma $
-Varsovian pair.
$\Gamma $
-Varsovian pair.
The following useful lemma is easy to verify, and we leave it to the reader.
Lemma 9.9. Suppose
![]() $({\mathcal {V}}, \Lambda )$
is a Varsovian pair and
$({\mathcal {V}}, \Lambda )$
is a Varsovian pair and
![]() $i\in \omega $
. Let
$i\in \omega $
. Let
![]() ${\mathcal {T}}$
be an iteration tree on
${\mathcal {T}}$
be an iteration tree on
![]() ${\mathcal {V}}$
according to
${\mathcal {V}}$
according to
![]() $\Lambda $
such that
$\Lambda $
such that
![]() ${\mathcal {T}}$
has a limit length,
${\mathcal {T}}$
has a limit length,
![]() ${\mathcal {T}}$
is based on
${\mathcal {T}}$
is based on
![]() $(\delta ^i_{\mathcal {V}}, \delta ^{i+1}_{\mathcal {V}})$
,Footnote
55
and letting
$(\delta ^i_{\mathcal {V}}, \delta ^{i+1}_{\mathcal {V}})$
,Footnote
55
and letting
![]() $a=\Lambda ({\mathcal {T}})$
, a is non-dropping. Then for every
$a=\Lambda ({\mathcal {T}})$
, a is non-dropping. Then for every
![]() $\alpha <\delta ^0_{\mathcal {V}}$
and
$\alpha <\delta ^0_{\mathcal {V}}$
and
![]() $k\in \omega $
,
$k\in \omega $
,
Hence, if
![]() $\pi ^{\mathcal {T}}_a(\delta ^{i+1}_{\mathcal {V}})=\delta ({\mathcal {T}})$
, then a is the unique branch e of
$\pi ^{\mathcal {T}}_a(\delta ^{i+1}_{\mathcal {V}})=\delta ({\mathcal {T}})$
, then a is the unique branch e of
![]() ${\mathcal {T}}$
such that
${\mathcal {T}}$
such that
![]() $\pi ^{{\mathcal {T}}^{{\mathcal {V}}'}_i}_{c^{{\mathcal {V}}'}_i}[\delta ^0_{\mathcal {V}}]\subseteq \mathrm { rge}(\pi ^{\mathcal {T}}_e)$
.
$\pi ^{{\mathcal {T}}^{{\mathcal {V}}'}_i}_{c^{{\mathcal {V}}'}_i}[\delta ^0_{\mathcal {V}}]\subseteq \mathrm { rge}(\pi ^{\mathcal {T}}_e)$
.
The last clause of Lemma 9.9 is important because it shows that
![]() $\Lambda _{{\mathcal {V}}|\delta ^0_{\mathcal {V}}}$
determines
$\Lambda _{{\mathcal {V}}|\delta ^0_{\mathcal {V}}}$
determines
![]() $\Lambda $
. Indeed,
$\Lambda $
. Indeed,
![]() $\pi ^{{\mathcal {T}}^{{\mathcal {V}}'}_i}_{c^{{\mathcal {V}}'}_i}$
depends only on
$\pi ^{{\mathcal {T}}^{{\mathcal {V}}'}_i}_{c^{{\mathcal {V}}'}_i}$
depends only on
![]() $\Lambda _{{\mathcal {V}}|\delta ^0_{\mathcal {V}}}$
and
$\Lambda _{{\mathcal {V}}|\delta ^0_{\mathcal {V}}}$
and
![]() ${\textsf {cop}}({\mathcal {T}})$
. We thus have that if
${\textsf {cop}}({\mathcal {T}})$
. We thus have that if
![]() $({\mathcal {V}}, \Lambda )$
is a Varsovian pair, then
$({\mathcal {V}}, \Lambda )$
is a Varsovian pair, then
![]() ${\mathcal {V}}$
is
${\mathcal {V}}$
is
![]() $\Lambda _{{\mathcal {V}}|\delta ^0_{\mathcal {V}}}$
-Varsovian.
$\Lambda _{{\mathcal {V}}|\delta ^0_{\mathcal {V}}}$
-Varsovian.
We finish this section by introducing the universes that are the companions of hod-like pairs.
Definition 9.10. We say that M and
![]() $({\mathcal {P} }, \Sigma )$
are companions if the following conditions hold.
$({\mathcal {P} }, \Sigma )$
are companions if the following conditions hold.
-
1. Letting
 $\alpha ={\textsf {Ord}}\cap M$
,
$\alpha ={\textsf {Ord}}\cap M$
,
 $M=L_\alpha ({\mathbb {R}})$
, and for some sentence
$M=L_\alpha ({\mathbb {R}})$
, and for some sentence
 $\phi $
,
$\phi $
,
 $\alpha $
is the least
$\alpha $
is the least
 $\beta $
such that
$\beta $
such that
 $L_\beta ({\mathbb {R}})\vDash \text {`}{\textsf {ZF-Replacement}}+\phi $
.’
$L_\beta ({\mathbb {R}})\vDash \text {`}{\textsf {ZF-Replacement}}+\phi $
.’ -
2. M is the derived model of
 $({\mathcal {P} }, \Sigma )$
.
$({\mathcal {P} }, \Sigma )$
. -
3. There is a sjs
 $(B_i: i<\omega )\subseteq {\wp }({\mathbb {R}})\cap L_\alpha ({\mathbb {R}})$
such that for each
$(B_i: i<\omega )\subseteq {\wp }({\mathbb {R}})\cap L_\alpha ({\mathbb {R}})$
such that for each
 $i<\omega $
,
$i<\omega $
,
 $B_i$
is ordinal definable in M, and
$B_i$
is ordinal definable in M, and
 $\Sigma $
is the unique
$\Sigma $
is the unique
 $\omega _1+1$
-iteration strategy
$\omega _1+1$
-iteration strategy
 $\Lambda $
such that for every
$\Lambda $
such that for every
 $i\in \omega $
,
$i\in \omega $
,
 $\Lambda $
respects
$\Lambda $
respects
 $B_i$
.
$B_i$
.
We say M has a companion if there is a pair
![]() $({\mathcal {P} }, \Sigma )$
such that M and
$({\mathcal {P} }, \Sigma )$
such that M and
![]() $({\mathcal {P} }, \Sigma )$
are companions.
$({\mathcal {P} }, \Sigma )$
are companions.
The next theorem, the main result on companions, can be proved using the methods of [Reference Sargsyan and Steel17].
Theorem 9.11. Assume
![]() $V=L({\mathbb {R}})+{\textsf {AD}}$
. Suppose
$V=L({\mathbb {R}})+{\textsf {AD}}$
. Suppose
![]() $\alpha $
is such that for some sentence
$\alpha $
is such that for some sentence
![]() $\phi $
,
$\phi $
,
![]() $\alpha $
is the least
$\alpha $
is the least
![]() $\beta $
such that
$\beta $
such that
![]() $L_\beta ({\mathbb {R}})\vDash `{\textsf {ZF-Replacement}}+\phi $
.’ Then
$L_\beta ({\mathbb {R}})\vDash `{\textsf {ZF-Replacement}}+\phi $
.’ Then
![]() $L_\alpha ({\mathbb {R}})$
has a companion.
$L_\alpha ({\mathbb {R}})$
has a companion.
Remark 9.12. In Theorem 9.11, the desired
![]() $({\mathcal {P} }, \Sigma )$
is built using hod pair constructions as in [Reference Sargsyan and Steel17]. Clause 3 of Definition 9.10 can be achieved by fixing a sjs system for
$({\mathcal {P} }, \Sigma )$
is built using hod pair constructions as in [Reference Sargsyan and Steel17]. Clause 3 of Definition 9.10 can be achieved by fixing a sjs system for
![]() $L_\alpha ({\mathbb {R}})$
, which can be done by the results of [Reference Steel28], [Reference Jackson3], [Reference Sargsyan13], [Reference Wilson35] and [Reference Wilson36]. Clause 2 of Definition 9.4 is more or less automatic and has been treated extensively in the literature (e.g., [Reference Sargsyan15]).
$L_\alpha ({\mathbb {R}})$
, which can be done by the results of [Reference Steel28], [Reference Jackson3], [Reference Sargsyan13], [Reference Wilson35] and [Reference Wilson36]. Clause 2 of Definition 9.4 is more or less automatic and has been treated extensively in the literature (e.g., [Reference Sargsyan15]).
9.2 On HOD analysis
We exposit the HOD analysis of
![]() $L_\alpha ({\mathbb {R}})$
. Fix some ordinal
$L_\alpha ({\mathbb {R}})$
. Fix some ordinal
![]() $\alpha $
such that
$\alpha $
such that
![]() $L_\alpha ({\mathbb {R}})\vDash {\textsf {ZF-Replacement}}$
. We allow
$L_\alpha ({\mathbb {R}})\vDash {\textsf {ZF-Replacement}}$
. We allow
![]() $\alpha ={\textsf {Ord}}$
.
$\alpha ={\textsf {Ord}}$
.
Recall from [Reference Steel and Woodin33, Theorem 6.1] that assuming
![]() $V=L({\mathbb {R}})$
,
$V=L({\mathbb {R}})$
,
![]() ${\textsf {HOD}}=L[{\mathcal {M}}_\infty ^+, \Lambda ]$
. Hence,
${\textsf {HOD}}=L[{\mathcal {M}}_\infty ^+, \Lambda ]$
. Hence,
![]() ${\textsf {HOD}}^{L_\alpha ({\mathbb {R}})}=L[{\mathcal {M}}_\infty ^{ +, \alpha }, \Lambda ^{\alpha }]$
, where
${\textsf {HOD}}^{L_\alpha ({\mathbb {R}})}=L[{\mathcal {M}}_\infty ^{ +, \alpha }, \Lambda ^{\alpha }]$
, where
![]() ${\mathcal {M}}_\infty ^{+, \alpha }$
is a hod-like premouse with exactly
${\mathcal {M}}_\infty ^{+, \alpha }$
is a hod-like premouse with exactly
![]() $\omega $
-Woodin cardinals,
$\omega $
-Woodin cardinals,
![]() ${\textsf {ORD}}\cap {\mathcal {M}}_\infty ^{+, \alpha }=\alpha $
and
${\textsf {ORD}}\cap {\mathcal {M}}_\infty ^{+, \alpha }=\alpha $
and
![]() ${\mathcal {M}}^{+, \alpha }_\infty $
is definable in
${\mathcal {M}}^{+, \alpha }_\infty $
is definable in
![]() $L_\alpha ({\mathbb {R}})$
via a direct limit construction (see [Reference Steel and Woodin33]). We set
$L_\alpha ({\mathbb {R}})$
via a direct limit construction (see [Reference Steel and Woodin33]). We set
![]() ${\mathcal {M}}^{\alpha }={\mathcal {M}}_{\infty }^{+, \alpha }$
.
${\mathcal {M}}^{\alpha }={\mathcal {M}}_{\infty }^{+, \alpha }$
.
![]() $\Lambda ^{\alpha }$
is a partial iteration strategy for
$\Lambda ^{\alpha }$
is a partial iteration strategy for
![]() ${\mathcal {M}}^{\alpha }$
that acts on iteration trees which are in
${\mathcal {M}}^{\alpha }$
that acts on iteration trees which are in
![]() ${\mathcal {M}}^{\alpha }|\delta ^\omega _{{\mathcal {M}}^{\alpha }}$
and are based on
${\mathcal {M}}^{\alpha }|\delta ^\omega _{{\mathcal {M}}^{\alpha }}$
and are based on
![]() ${\mathcal {M}}^{\alpha }|\delta ^0_{{\mathcal {M}}^{\alpha }}$
.
${\mathcal {M}}^{\alpha }|\delta ^0_{{\mathcal {M}}^{\alpha }}$
.
![]() $\Lambda ^{\alpha }$
induces a branch
$\Lambda ^{\alpha }$
induces a branch
![]() $b^{\alpha }$
for
$b^{\alpha }$
for
![]() ${\mathcal {T}}^{\alpha }=_{def}{\mathcal {T}}_{{\mathcal {M}}^{\alpha }}$
that is friendly to
${\mathcal {T}}^{\alpha }=_{def}{\mathcal {T}}_{{\mathcal {M}}^{\alpha }}$
that is friendly to
![]() ${\mathcal {M}}^{\alpha }$
. In fact,
${\mathcal {M}}^{\alpha }$
. In fact,
![]() $\Lambda ^{\alpha }$
and
$\Lambda ^{\alpha }$
and
![]() $b^{\alpha }$
are definable from each other (see [Reference Steel and Woodin33]). We set
$b^{\alpha }$
are definable from each other (see [Reference Steel and Woodin33]). We set
![]() ${\mathcal {V}}^{\prime }_\alpha ={\mathcal {V}}'({\mathcal {M}}^{\alpha }, b^{\alpha })$
and
${\mathcal {V}}^{\prime }_\alpha ={\mathcal {V}}'({\mathcal {M}}^{\alpha }, b^{\alpha })$
and
![]() ${\mathcal {V}}_\alpha ={\mathcal {V}}({\mathcal {M}}^{\alpha }, b^{\alpha })$
.Footnote
56
We then have that
${\mathcal {V}}_\alpha ={\mathcal {V}}({\mathcal {M}}^{\alpha }, b^{\alpha })$
.Footnote
56
We then have that
![]() ${\textsf {HOD}}^{L_\alpha ({\mathbb {R}})}=L_\alpha [{\mathcal {V}}_\alpha ]$
.Footnote
57
In fact, more is true. Below and elsewhere, when studying objects like
${\textsf {HOD}}^{L_\alpha ({\mathbb {R}})}=L_\alpha [{\mathcal {V}}_\alpha ]$
.Footnote
57
In fact, more is true. Below and elsewhere, when studying objects like
![]() ${\mathcal {V}}=_{def}{\mathcal {V}}({\mathcal {P} }, b)$
, we will let
${\mathcal {V}}=_{def}{\mathcal {V}}({\mathcal {P} }, b)$
, we will let
![]() ${\mathcal {X}}^{\mathcal {V}}={\mathcal {P} }$
,
${\mathcal {X}}^{\mathcal {V}}={\mathcal {P} }$
,
![]() ${\mathcal {T}}^{\mathcal {V}}={\mathcal {T}}_{\mathcal {P} }$
and
${\mathcal {T}}^{\mathcal {V}}={\mathcal {T}}_{\mathcal {P} }$
and
![]() $b^{\mathcal {V}}=b$
.
$b^{\mathcal {V}}=b$
.
Proposition 9.13. Suppose
![]() $L_\alpha ({\mathbb {R}})$
and
$L_\alpha ({\mathbb {R}})$
and
![]() $({\mathcal {P} }, \Sigma )$
are companions. There is a Varsovian pair
$({\mathcal {P} }, \Sigma )$
are companions. There is a Varsovian pair
![]() $({\mathcal R}, \Psi )$
such that
$({\mathcal R}, \Psi )$
such that
![]() ${\mathcal {V}}_\alpha $
is the direct limit of all complete
${\mathcal {V}}_\alpha $
is the direct limit of all complete
![]() $\Psi $
-iterates
$\Psi $
-iterates
![]() ${\mathcal { Q}}$
of
${\mathcal { Q}}$
of
![]() ${\mathcal R}$
such that
${\mathcal R}$
such that
![]() ${\mathcal {T}}_{{\mathcal R}, {\mathcal { Q}}}$
is based on
${\mathcal {T}}_{{\mathcal R}, {\mathcal { Q}}}$
is based on
![]() ${\mathcal R}|\delta ^0_{\mathcal R}$
.
${\mathcal R}|\delta ^0_{\mathcal R}$
.
Proof. First, find some coarse tuple
![]() $(R_0, \Psi _0, H, \alpha ')$
that absorbs
$(R_0, \Psi _0, H, \alpha ')$
that absorbs
![]() $\alpha $
, as in Theorem 4.7.Footnote
58
Next, let
$\alpha $
, as in Theorem 4.7.Footnote
58
Next, let
![]() $x\in \mathrm {dom}(H)$
be such that, letting
$x\in \mathrm {dom}(H)$
be such that, letting
![]() $({\mathcal { Q}}, \Lambda )=H(x)$
,
$({\mathcal { Q}}, \Lambda )=H(x)$
,
![]() $\Sigma $
is Suslin, co-Suslin captured by
$\Sigma $
is Suslin, co-Suslin captured by
![]() $({\mathcal { Q}}, \Lambda )$
.
$({\mathcal { Q}}, \Lambda )$
.
Following [Reference Sargsyan13] and [Reference Steel32], we can find a complete
![]() $\Sigma $
-iterate
$\Sigma $
-iterate
![]() ${\mathcal {W} }$
that is built using the fully backgrounded construction of
${\mathcal {W} }$
that is built using the fully backgrounded construction of
![]() ${\mathcal { Q}}$
. Let
${\mathcal { Q}}$
. Let
![]() $\Phi =\Sigma _{{\mathcal {W} }}$
. It follows from the results of [Reference Sargsyan13] and [Reference Steel32] that
$\Phi =\Sigma _{{\mathcal {W} }}$
. It follows from the results of [Reference Sargsyan13] and [Reference Steel32] that
![]() $\Phi $
is the strategy of
$\Phi $
is the strategy of
![]() ${\mathcal {W} }$
induced by
${\mathcal {W} }$
induced by
![]() $\Lambda $
. It follows from [Reference Sargsyan13] and [Reference Steel32] that
$\Lambda $
. It follows from [Reference Sargsyan13] and [Reference Steel32] that
![]() ${\mathcal {W} }$
is hod-like, and if
${\mathcal {W} }$
is hod-like, and if
![]() $b=\Phi ({\mathcal {T}}_{\mathcal {W} })$
, then
$b=\Phi ({\mathcal {T}}_{\mathcal {W} })$
, then
![]() $({\mathcal {W} }, b)$
is hod-like. Set
$({\mathcal {W} }, b)$
is hod-like. Set
![]() ${\mathcal R}'={\mathcal {V}}'({\mathcal {W} }, b)$
, and let
${\mathcal R}'={\mathcal {V}}'({\mathcal {W} }, b)$
, and let
![]() $\Psi '$
be the strategy of
$\Psi '$
be the strategy of
![]() ${\mathcal R}'$
.
${\mathcal R}'$
.
It follows that whenever
![]() ${\mathcal R}"$
is a complete
${\mathcal R}"$
is a complete
![]() $\Psi '$
-iterate of
$\Psi '$
-iterate of
![]() ${\mathcal R}'$
,
${\mathcal R}'$
,
![]() $b^{{\mathcal R}"}$
is according to
$b^{{\mathcal R}"}$
is according to
![]() $\Psi ^{\prime }_{{\mathcal {X}}^{{\mathcal R}"}}=\Sigma _{{\mathcal {X}}^{{\mathcal R}"}}$
. Because
$\Psi ^{\prime }_{{\mathcal {X}}^{{\mathcal R}"}}=\Sigma _{{\mathcal {X}}^{{\mathcal R}"}}$
. Because
![]() ${\mathcal {M}}^{\alpha }={\mathcal {M}}_\infty ({\mathcal {P} }, \Sigma )$
, we have that
${\mathcal {M}}^{\alpha }={\mathcal {M}}_\infty ({\mathcal {P} }, \Sigma )$
, we have that
![]() ${\mathcal {V}}^{\prime }_\alpha ={\mathcal {M}}_\infty ({\mathcal R}', \Psi ')$
. Hence, the core of
${\mathcal {V}}^{\prime }_\alpha ={\mathcal {M}}_\infty ({\mathcal R}', \Psi ')$
. Hence, the core of
![]() ${\mathcal {V}}^{\prime }_\alpha $
is defined, and letting
${\mathcal {V}}^{\prime }_\alpha $
is defined, and letting
![]() ${\mathcal R}={\mathcal {V}}({\mathcal {W} }, b)$
and
${\mathcal R}={\mathcal {V}}({\mathcal {W} }, b)$
and
![]() $\Psi $
be the strategy of
$\Psi $
be the strategy of
![]() ${\mathcal R}$
induced by
${\mathcal R}$
induced by
![]() $\Psi '$
,
$\Psi '$
,
![]() ${\mathcal {V}}_\alpha $
is the direct limit of all complete
${\mathcal {V}}_\alpha $
is the direct limit of all complete
![]() $\Psi $
-iterates
$\Psi $
-iterates
![]() ${\mathcal { Q}}$
of
${\mathcal { Q}}$
of
![]() ${\mathcal R}$
such that
${\mathcal R}$
such that
![]() ${\mathcal {T}}_{{\mathcal R}, {\mathcal { Q}}}$
is based on
${\mathcal {T}}_{{\mathcal R}, {\mathcal { Q}}}$
is based on
![]() ${\mathcal R}|\delta ^0_{\mathcal R}$
.Footnote
59
${\mathcal R}|\delta ^0_{\mathcal R}$
.Footnote
59
9.3 Theorem 3.1 cannot be improved
Theorem 9.14. Assume
![]() $V=L({\mathbb {R}})+{\textsf {AD}}$
. Let
$V=L({\mathbb {R}})+{\textsf {AD}}$
. Let
![]() ${\mathcal { H}}$
be the premouse representation of
${\mathcal { H}}$
be the premouse representation of
![]() $V_\Theta ^{\textsf {HOD}}$
, and suppose
$V_\Theta ^{\textsf {HOD}}$
, and suppose
![]() $j: {\mathcal { H}}\rightarrow {\mathcal { H}}$
is elementary. Then
$j: {\mathcal { H}}\rightarrow {\mathcal { H}}$
is elementary. Then
![]() $j=id$
.
$j=id$
.
Proof. It is a well-known theorem of Woodin that in
![]() $L({\mathbb {R}})$
,
$L({\mathbb {R}})$
,
![]() ${\mathcal { H}}=L[A]$
, where
${\mathcal { H}}=L[A]$
, where
![]() $A\subseteq \Theta $
is the set of ordinals coding the Vopenka algebra in some natural way (see [Reference Larson10], [Reference Trang34], or [Reference Steel and Woodin33]). We now want to show that j can be extended to
$A\subseteq \Theta $
is the set of ordinals coding the Vopenka algebra in some natural way (see [Reference Larson10], [Reference Trang34], or [Reference Steel and Woodin33]). We now want to show that j can be extended to
![]() $j^+: L[A]\rightarrow L[A]$
. Because
$j^+: L[A]\rightarrow L[A]$
. Because
![]() $j^+$
cannot be added to HOD by a set forcing, we can then use the proof of Proposition 8.3 to show that in fact
$j^+$
cannot be added to HOD by a set forcing, we can then use the proof of Proposition 8.3 to show that in fact
![]() $A^\#$
exists. We then have an embedding
$A^\#$
exists. We then have an embedding
![]() $k: {\textsf {HOD}}\rightarrow {\textsf {HOD}}$
with
$k: {\textsf {HOD}}\rightarrow {\textsf {HOD}}$
with
![]() $\mathrm {crit }(k)>\Theta $
, which then induces
$\mathrm {crit }(k)>\Theta $
, which then induces
![]() $k^+: L({\mathbb {R}})\rightarrow L({\mathbb {R}})$
. This is because
$k^+: L({\mathbb {R}})\rightarrow L({\mathbb {R}})$
. This is because
![]() $L({\mathbb {R}})$
is a symmetric extension of
$L({\mathbb {R}})$
is a symmetric extension of
![]() ${\textsf {HOD}}$
by a poset of size
${\textsf {HOD}}$
by a poset of size
![]() $\Theta $
(see [Reference Larson10]). Below
$\Theta $
(see [Reference Larson10]). Below
![]() $\Theta ^{\gamma }=\Theta ^{L_{\gamma }({\mathbb {R}})}$
.
$\Theta ^{\gamma }=\Theta ^{L_{\gamma }({\mathbb {R}})}$
.
Lemma 9.15. Let E be the extender derived from j.Footnote
60
Then
![]() $Ult(L[{\mathcal {V}}_{{\textsf {Ord}}}], E)$
is well-founded and is equal to
$Ult(L[{\mathcal {V}}_{{\textsf {Ord}}}], E)$
is well-founded and is equal to
![]() $L[{\mathcal {V}}_{{\textsf {Ord}}}]$
.
$L[{\mathcal {V}}_{{\textsf {Ord}}}]$
.
Proof. Let
![]() $\phi $
be the sentence we are trying to prove. Toward a contradiction, assume
$\phi $
be the sentence we are trying to prove. Toward a contradiction, assume
![]() $\phi $
is false. Let
$\phi $
is false. Let
![]() $\alpha $
be the least
$\alpha $
be the least
![]() $\gamma $
such that
$\gamma $
such that
![]() $L_{\gamma }({\mathbb {R}})\vDash \text {`}{\textsf {ZF-Replacement}}+\neg \phi $
’ and
$L_{\gamma }({\mathbb {R}})\vDash \text {`}{\textsf {ZF-Replacement}}+\neg \phi $
’ and
![]() $\gamma $
is a limit of ordinals
$\gamma $
is a limit of ordinals
![]() $\beta $
such that
$\beta $
such that
![]() $L_\beta ({\mathbb {R}})\vDash \text {`}{\textsf {ZF-Replacement}}+\neg \phi $
’. Let
$L_\beta ({\mathbb {R}})\vDash \text {`}{\textsf {ZF-Replacement}}+\neg \phi $
’. Let
![]() $({\mathcal R}, \Psi )$
be as in Proposition 9.13 applied to
$({\mathcal R}, \Psi )$
be as in Proposition 9.13 applied to
![]() $\alpha $
.
$\alpha $
.
We now reflect inside
![]() $L_\alpha ({\mathbb {R}})$
and find
$L_\alpha ({\mathbb {R}})$
and find
-
(1.1)
 $\beta \in (\Theta ^{\alpha }, \alpha )$
such that
$\beta \in (\Theta ^{\alpha }, \alpha )$
such that
 $L_\beta ({\mathbb {R}})\vDash \text {`}{\textsf {ZF-Replacement}}+\neg \phi $
’, and
$L_\beta ({\mathbb {R}})\vDash \text {`}{\textsf {ZF-Replacement}}+\neg \phi $
’, and -
(1.2)
 $\gamma <\Theta ^{\alpha }$
and
$\gamma <\Theta ^{\alpha }$
and
 $\sigma : L_{\gamma }({\mathbb {R}})\rightarrow L_\beta ({\mathbb {R}})$
such that
$\sigma : L_{\gamma }({\mathbb {R}})\rightarrow L_\beta ({\mathbb {R}})$
such that
 $j\in \mathrm {rge}(\sigma )$
and
$j\in \mathrm {rge}(\sigma )$
and
 $\Theta ^{\gamma }$
is a regular cardinal.Footnote
61
$\Theta ^{\gamma }$
is a regular cardinal.Footnote
61
We thus have that, letting
![]() $F=\sigma ^{-1}(E)$
,
$F=\sigma ^{-1}(E)$
,
-
(2.1)
 $L_{\gamma }({\mathbb {R}})\vDash \text {`}Ult(L[{\mathcal {V}}_{\gamma }], F)$
is ill-founded or
$L_{\gamma }({\mathbb {R}})\vDash \text {`}Ult(L[{\mathcal {V}}_{\gamma }], F)$
is ill-founded or
 $L[{\mathcal {V}}_{\gamma }]\not = Ult(L[{\mathcal {V}}_{\gamma }], F)$
’.
$L[{\mathcal {V}}_{\gamma }]\not = Ult(L[{\mathcal {V}}_{\gamma }], F)$
’.
We now establish a sequence of claims leading to the proof of Lemma 9.15.
Because
![]() $\sigma \restriction {\mathcal {V}}^{\prime }_{\gamma }:{\mathcal {V}}^{\prime }_{\gamma }\rightarrow {\mathcal {V}}^{\prime }_\beta $
, we have that
$\sigma \restriction {\mathcal {V}}^{\prime }_{\gamma }:{\mathcal {V}}^{\prime }_{\gamma }\rightarrow {\mathcal {V}}^{\prime }_\beta $
, we have that
![]() ${\mathcal {V}}^{\prime }_{\gamma }$
is iterable via the
${\mathcal {V}}^{\prime }_{\gamma }$
is iterable via the
![]() $\sigma $
-pullback of
$\sigma $
-pullback of
![]() $\Psi _{{\mathcal {V}}^{\prime }_\alpha }$
. Let
$\Psi _{{\mathcal {V}}^{\prime }_\alpha }$
. Let
![]() $\Phi $
be the
$\Phi $
be the
![]() $\sigma $
-pullback of
$\sigma $
-pullback of
![]() $\Psi _{{\mathcal {V}}^{\prime }_\alpha }$
and
$\Psi _{{\mathcal {V}}^{\prime }_\alpha }$
and
![]() $\Phi '$
be the fragment of
$\Phi '$
be the fragment of
![]() $\Phi $
that acts on iteration trees that are above
$\Phi $
that acts on iteration trees that are above
![]() $\Theta ^{\gamma }$
. Notice that
$\Theta ^{\gamma }$
. Notice that
-
(3.1)
 $\Phi _{{\mathcal {V}}^{\prime }_{\gamma }|\Theta ^{\gamma }}= \Psi _{{\mathcal {M}}^{\alpha }|\Theta ^{\gamma }}$
.
$\Phi _{{\mathcal {V}}^{\prime }_{\gamma }|\Theta ^{\gamma }}= \Psi _{{\mathcal {M}}^{\alpha }|\Theta ^{\gamma }}$
.
Claim 9.16.
![]() ${\mathcal {V}}^{\prime }_{\gamma }\in {\mathcal {M}}^{\alpha }$
,
${\mathcal {V}}^{\prime }_{\gamma }\in {\mathcal {M}}^{\alpha }$
,
![]() $\Phi '\restriction {\mathcal {M}}^{\alpha }|\Theta ^{\alpha } \in {\mathcal {M}}^{\alpha }$
, and
$\Phi '\restriction {\mathcal {M}}^{\alpha }|\Theta ^{\alpha } \in {\mathcal {M}}^{\alpha }$
, and
![]() $\Phi '\restriction {\mathcal {M}}^{\alpha }|\Theta ^{\alpha }$
has a
$\Phi '\restriction {\mathcal {M}}^{\alpha }|\Theta ^{\alpha }$
has a
![]() $\Theta ^{\alpha }+1$
-extension in
$\Theta ^{\alpha }+1$
-extension in
![]() ${\mathcal {M}}^{\alpha }$
.
${\mathcal {M}}^{\alpha }$
.
Proof. Because
![]() ${\mathcal {V}}^{\prime }_{\gamma }\in {\textsf {HOD}}^{L_{\gamma }({\mathbb {R}})}$
, we have that
${\mathcal {V}}^{\prime }_{\gamma }\in {\textsf {HOD}}^{L_{\gamma }({\mathbb {R}})}$
, we have that
![]() ${\mathcal {V}}^{\prime }_{\gamma }\in {\mathcal {M}}^{\alpha }$
. We show that
${\mathcal {V}}^{\prime }_{\gamma }\in {\mathcal {M}}^{\alpha }$
. We show that
![]() $\Phi '\restriction {\mathcal {M}}^{\alpha }|\Theta ^{\alpha } \in {\mathcal {M}}^{\alpha }$
. The proof will also show the third clause.
$\Phi '\restriction {\mathcal {M}}^{\alpha }|\Theta ^{\alpha } \in {\mathcal {M}}^{\alpha }$
. The proof will also show the third clause.
Suppose
![]() ${\mathcal {T}}$
is a normal tree on
${\mathcal {T}}$
is a normal tree on
![]() ${\mathcal {V}}^{\prime }_{\gamma }$
that is above
${\mathcal {V}}^{\prime }_{\gamma }$
that is above
![]() $\Theta ^{\gamma }$
. Then
$\Theta ^{\gamma }$
. Then
![]() ${\mathcal {T}}$
naturally splits into a stack of
${\mathcal {T}}$
naturally splits into a stack of
![]() $\omega $
-many normal iteration trees such that the ith normal iteration tree in the stack is based on the ith window (where by window we mean a maximal interval
$\omega $
-many normal iteration trees such that the ith normal iteration tree in the stack is based on the ith window (where by window we mean a maximal interval
![]() $(\xi , \xi ')$
that contains no Woodin cardinals). In light of this observation, it is enough to show that for each
$(\xi , \xi ')$
that contains no Woodin cardinals). In light of this observation, it is enough to show that for each
![]() $i<\omega $
, if
$i<\omega $
, if
![]() ${\mathcal {T}}\in {\mathcal {M}}^{\alpha }|\Theta ^{\alpha }$
is a normal iteration tree according to
${\mathcal {T}}\in {\mathcal {M}}^{\alpha }|\Theta ^{\alpha }$
is a normal iteration tree according to
![]() $\Phi '$
with last model
$\Phi '$
with last model
![]() ${\mathcal {S}}$
such that
${\mathcal {S}}$
such that
![]() ${\mathcal {T}}$
is based on
${\mathcal {T}}$
is based on
![]() ${\mathcal {V}}^{\prime }_{\gamma }|\delta ^i_{{\mathcal {V}}^{\prime }_{\gamma }}$
and the main branch of
${\mathcal {V}}^{\prime }_{\gamma }|\delta ^i_{{\mathcal {V}}^{\prime }_{\gamma }}$
and the main branch of
![]() ${\mathcal {T}}$
does not drop, then the fragment of
${\mathcal {T}}$
does not drop, then the fragment of
![]() $\Phi ^{\prime }_{{\mathcal {S}}}\restriction {\mathcal {M}}^{\alpha }|\Theta ^{\alpha }$
that acts on stacks that are above
$\Phi ^{\prime }_{{\mathcal {S}}}\restriction {\mathcal {M}}^{\alpha }|\Theta ^{\alpha }$
that acts on stacks that are above
![]() $\delta ^i_{\mathcal {S}}$
and below
$\delta ^i_{\mathcal {S}}$
and below
![]() $\delta ^{i+1}_{\mathcal {S}}$
is in
$\delta ^{i+1}_{\mathcal {S}}$
is in
![]() ${\mathcal {M}}^{\alpha }$
.
${\mathcal {M}}^{\alpha }$
.
We prove this assuming
![]() ${\mathcal {T}}=\emptyset $
to simplify the notation, the general proof being only notationally more complex. Thus, set
${\mathcal {T}}=\emptyset $
to simplify the notation, the general proof being only notationally more complex. Thus, set
![]() ${\mathcal {S}}={\mathcal {V}}^{\prime }_{\gamma }$
, and notice that
${\mathcal {S}}={\mathcal {V}}^{\prime }_{\gamma }$
, and notice that
![]() $\Phi \restriction {\mathcal {M}}^{\alpha }|\delta ^\omega _{{\mathcal {M}}^{\alpha }}\in {\mathcal {M}}^{\alpha }$
. We thus prove the above claim for
$\Phi \restriction {\mathcal {M}}^{\alpha }|\delta ^\omega _{{\mathcal {M}}^{\alpha }}\in {\mathcal {M}}^{\alpha }$
. We thus prove the above claim for
![]() $i=1$
. More precisely, we show that if
$i=1$
. More precisely, we show that if
![]() $\Lambda $
is the fragment of
$\Lambda $
is the fragment of
![]() $\Phi '\restriction {\mathcal {M}}^{\alpha }|\Theta ^{\alpha }$
that acts on normal iteration trees that are based on the interval
$\Phi '\restriction {\mathcal {M}}^{\alpha }|\Theta ^{\alpha }$
that acts on normal iteration trees that are based on the interval
![]() $(\delta ^0_{\mathcal {S}}, \delta ^1_{{\mathcal {S}}})$
, then
$(\delta ^0_{\mathcal {S}}, \delta ^1_{{\mathcal {S}}})$
, then
![]() $\Lambda \in {\mathcal {M}}^{\alpha }$
.
$\Lambda \in {\mathcal {M}}^{\alpha }$
.
Suppose then
![]() ${\mathcal {U}}\in {\mathcal {M}}^{\alpha }|\Theta ^{\alpha }$
is a normal iteration tree on
${\mathcal {U}}\in {\mathcal {M}}^{\alpha }|\Theta ^{\alpha }$
is a normal iteration tree on
![]() ${\mathcal {S}}$
based on the interval
${\mathcal {S}}$
based on the interval
![]() $(\delta ^0_{\mathcal {S}}, \delta ^1_{{\mathcal {S}}})$
such that
$(\delta ^0_{\mathcal {S}}, \delta ^1_{{\mathcal {S}}})$
such that
![]() ${\mathcal {U}}$
has a limit length and is according to
${\mathcal {U}}$
has a limit length and is according to
![]() $\Lambda $
. It is enough to show that if
$\Lambda $
. It is enough to show that if
![]() $c=\Lambda ({\mathcal {U}})$
, then c is uniformly definable over
$c=\Lambda ({\mathcal {U}})$
, then c is uniformly definable over
![]() ${\mathcal {M}}^{\alpha }$
from
${\mathcal {M}}^{\alpha }$
from
![]() ${\mathcal {U}}$
and
${\mathcal {U}}$
and
![]() $\Theta ^{\gamma }$
.
$\Theta ^{\gamma }$
.
We have two cases. Suppose first that either c has a drop or
![]() $\pi ^{\mathcal {U}}_c(\delta ^1_{\mathcal {S}})>\delta ({\mathcal {U}})$
. Either way,
$\pi ^{\mathcal {U}}_c(\delta ^1_{\mathcal {S}})>\delta ({\mathcal {U}})$
. Either way,
![]() ${\mathcal { Q}}(c, {\mathcal {U}})$
is defined, and whenever
${\mathcal { Q}}(c, {\mathcal {U}})$
is defined, and whenever
![]() $\tau : {\mathcal {W} }\rightarrow {\mathcal { Q}}(c, {\mathcal {U}})$
is such that
$\tau : {\mathcal {W} }\rightarrow {\mathcal { Q}}(c, {\mathcal {U}})$
is such that
![]() $\tau \in L_\alpha ({\mathbb {R}})$
and
$\tau \in L_\alpha ({\mathbb {R}})$
and
![]() ${\mathcal {W} }$
is countable,
${\mathcal {W} }$
is countable,
![]() ${\mathcal {W} }$
has a
${\mathcal {W} }$
has a
![]() $\omega _1+1$
-iteration strategy in
$\omega _1+1$
-iteration strategy in
![]() $L_\alpha ({\mathbb {R}})$
. It now follows that
$L_\alpha ({\mathbb {R}})$
. It now follows that
![]() ${\mathcal { Q}}(c, {\mathcal {U}})\in {\mathcal {M}}^{\alpha }$
and is uniformly definable from
${\mathcal { Q}}(c, {\mathcal {U}})\in {\mathcal {M}}^{\alpha }$
and is uniformly definable from
![]() ${\mathcal {U}}$
and
${\mathcal {U}}$
and
![]() $\Theta ^{\gamma }$
.Footnote
62
$\Theta ^{\gamma }$
.Footnote
62
Suppose c does not have a drop and
![]() $\pi ^{\mathcal {U}}_c(\delta ^1_{\mathcal {S}})=\delta ({\mathcal {U}})$
. Let
$\pi ^{\mathcal {U}}_c(\delta ^1_{\mathcal {S}})=\delta ({\mathcal {U}})$
. Let
![]() ${\mathcal {S}}'={\mathcal {M}}^{\mathcal {U}}_c$
. Let
${\mathcal {S}}'={\mathcal {M}}^{\mathcal {U}}_c$
. Let
![]() ${\mathcal {Y}}\in {\mathcal {S}}$
be the normal tree on
${\mathcal {Y}}\in {\mathcal {S}}$
be the normal tree on
![]() ${\mathcal {S}}|\delta ^0_{\mathcal {S}}(={\mathcal {V}}^{\prime }_{\gamma }|\Theta ^{\gamma })$
such that
${\mathcal {S}}|\delta ^0_{\mathcal {S}}(={\mathcal {V}}^{\prime }_{\gamma }|\Theta ^{\gamma })$
such that
![]() ${\textsf {cop}}({\mathcal {Y}})$
is the output of the fully backgrounded construction of
${\textsf {cop}}({\mathcal {Y}})$
is the output of the fully backgrounded construction of
![]() ${\mathcal {S}}|\delta ^1_{\mathcal {S}}$
using extenders whose critical points are above
${\mathcal {S}}|\delta ^1_{\mathcal {S}}$
using extenders whose critical points are above
![]() $\delta ^0_{\mathcal {S}}$
. Notice that
$\delta ^0_{\mathcal {S}}$
. Notice that
![]() ${\mathcal {Y}}'=_{def}\pi ^{\mathcal {U}}_c({\mathcal {Y}})$
only depends on
${\mathcal {Y}}'=_{def}\pi ^{\mathcal {U}}_c({\mathcal {Y}})$
only depends on
![]() ${\textsf {cop}}({\mathcal {U}})$
, and also if
${\textsf {cop}}({\mathcal {U}})$
, and also if
![]() $\Phi ({\mathcal {Y}})=d$
and
$\Phi ({\mathcal {Y}})=d$
and
![]() $\Phi ({\mathcal {Y}}')=d'$
, then
$\Phi ({\mathcal {Y}}')=d'$
, then
![]() $\pi ^{{\mathcal {Y}}'}_{d'}=\pi ^{\mathcal {U}}_c\restriction \delta ^1_{\mathcal {S}} \circ \pi ^{\mathcal {Y}}_d$
.Footnote
63
Since
$\pi ^{{\mathcal {Y}}'}_{d'}=\pi ^{\mathcal {U}}_c\restriction \delta ^1_{\mathcal {S}} \circ \pi ^{\mathcal {Y}}_d$
.Footnote
63
Since
![]() $\Phi \restriction {\mathcal {M}}^{\alpha }|\Theta ^{\alpha }\in {\mathcal {M}}^{\alpha }$
, we have that
$\Phi \restriction {\mathcal {M}}^{\alpha }|\Theta ^{\alpha }\in {\mathcal {M}}^{\alpha }$
, we have that
![]() $({\mathcal {Y}}', d')\in {\mathcal {M}}^{\alpha }$
is uniformly definable from
$({\mathcal {Y}}', d')\in {\mathcal {M}}^{\alpha }$
is uniformly definable from
![]() ${\mathcal {U}}$
. We now have that c is the unique branch of
${\mathcal {U}}$
. We now have that c is the unique branch of
![]() ${\mathcal {U}}$
such that
${\mathcal {U}}$
such that
![]() $\mathrm {rge}(\pi ^{{\mathcal {Y}}'}_{d'})\subseteq \mathrm { rge}(\pi ^{\mathcal {U}}_c)$
. Hence,
$\mathrm {rge}(\pi ^{{\mathcal {Y}}'}_{d'})\subseteq \mathrm { rge}(\pi ^{\mathcal {U}}_c)$
. Hence,
![]() $c\in {\mathcal {M}}^{\alpha }$
and is uniformly definable in
$c\in {\mathcal {M}}^{\alpha }$
and is uniformly definable in
![]() ${\mathcal {M}}^{\alpha }$
from
${\mathcal {M}}^{\alpha }$
from
![]() ${\mathcal {U}}$
and
${\mathcal {U}}$
and
![]() $\Theta ^{\gamma }$
.
$\Theta ^{\gamma }$
.
The next claim follows immediately from Claim 9.16. Because
![]() ${\mathcal {V}}^{\prime }_{\gamma }\in {\mathcal {M}}^{\alpha }$
, and because
${\mathcal {V}}^{\prime }_{\gamma }\in {\mathcal {M}}^{\alpha }$
, and because
![]() $Ult({\mathcal {M}}^{\alpha }, F)$
is well-founded (as F is derived from j),
$Ult({\mathcal {M}}^{\alpha }, F)$
is well-founded (as F is derived from j),
![]() $Ult(L_{\gamma }[{\mathcal {V}}^{\prime }_{\gamma }], F)$
is well-founded. We thus need to show that
$Ult(L_{\gamma }[{\mathcal {V}}^{\prime }_{\gamma }], F)$
is well-founded. We thus need to show that
![]() $Ult(L_{\gamma }[{\mathcal {V}}^{\prime }_{\gamma }], F)=L_{\gamma }[{\mathcal {V}}^{\prime }_{\gamma }]$
. Notice that
$Ult(L_{\gamma }[{\mathcal {V}}^{\prime }_{\gamma }], F)=L_{\gamma }[{\mathcal {V}}^{\prime }_{\gamma }]$
. Notice that
![]() $L_{\gamma }[{\mathcal {V}}_{\gamma }]=L_{\gamma }[{\mathcal {V}}^{\prime }_{\gamma }]={\textsf {HOD}}^{L_{\gamma }({\mathbb {R}})}$
, so it is enough to show that
$L_{\gamma }[{\mathcal {V}}_{\gamma }]=L_{\gamma }[{\mathcal {V}}^{\prime }_{\gamma }]={\textsf {HOD}}^{L_{\gamma }({\mathbb {R}})}$
, so it is enough to show that
![]() $Ult(L_{\gamma }[{\mathcal {V}}_{\gamma }], F)=L_{\gamma }[{\mathcal {V}}_{\gamma }]$
.
$Ult(L_{\gamma }[{\mathcal {V}}_{\gamma }], F)=L_{\gamma }[{\mathcal {V}}_{\gamma }]$
.
For
![]() $\xi <\Theta ^{\alpha }$
, let
$\xi <\Theta ^{\alpha }$
, let
![]() ${\mathcal { K}}_\xi \trianglelefteq {\mathcal {M}}^{\alpha }$
be the longest initial segment
${\mathcal { K}}_\xi \trianglelefteq {\mathcal {M}}^{\alpha }$
be the longest initial segment
![]() ${\mathcal {X}}$
of
${\mathcal {X}}$
of
![]() ${\mathcal {M}}^{\alpha }$
such that
${\mathcal {M}}^{\alpha }$
such that
![]() ${\mathcal {X}}\vDash \text {`}\xi $
is a Woodin cardinal’. Let
${\mathcal {X}}\vDash \text {`}\xi $
is a Woodin cardinal’. Let
![]() $\Lambda _\xi \in {\mathcal {M}}^{\alpha }$
be the unique
$\Lambda _\xi \in {\mathcal {M}}^{\alpha }$
be the unique
![]() $(\xi ^+)^{{\mathcal {M}}^{\alpha }}+1$
-strategy of
$(\xi ^+)^{{\mathcal {M}}^{\alpha }}+1$
-strategy of
![]() ${\mathcal { K}}_\xi $
.
${\mathcal { K}}_\xi $
.
Claim 9.17. In
![]() ${\mathcal {M}}^{\alpha }|\Theta ^{\alpha }$
,
${\mathcal {M}}^{\alpha }|\Theta ^{\alpha }$
,
![]() ${\mathcal {V}}_{\gamma }$
is the unique
${\mathcal {V}}_{\gamma }$
is the unique
![]() $\Theta ^{\gamma }$
-sound
$\Theta ^{\gamma }$
-sound
![]() $\Lambda _{\Theta ^{\gamma }}$
-Varsovian model.Footnote
64
$\Lambda _{\Theta ^{\gamma }}$
-Varsovian model.Footnote
64
Claim 9.18.
![]() $\pi _F^{L_{\gamma }[{\mathcal {V}}_{\gamma }]}({\mathcal {V}}_{\gamma })={\mathcal {V}}_{\gamma }$
.
$\pi _F^{L_{\gamma }[{\mathcal {V}}_{\gamma }]}({\mathcal {V}}_{\gamma })={\mathcal {V}}_{\gamma }$
.
Proof. Just like with
![]() ${\mathcal {V}}^{\prime }_{\gamma }$
, we have that
${\mathcal {V}}^{\prime }_{\gamma }$
, we have that
![]() ${\mathcal {V}}_{\gamma }\in {\mathcal {M}}^{\alpha }$
. Let
${\mathcal {V}}_{\gamma }\in {\mathcal {M}}^{\alpha }$
. Let
![]() $k: Ult({\mathcal {M}}^{\alpha }|\Theta ^{\alpha }, F)\rightarrow {\mathcal {M}}^{\alpha }|\Theta ^{\alpha }$
be such that
$k: Ult({\mathcal {M}}^{\alpha }|\Theta ^{\alpha }, F)\rightarrow {\mathcal {M}}^{\alpha }|\Theta ^{\alpha }$
be such that
![]() $j=k\circ \pi _F^{{\mathcal {M}}^{\alpha }|\Theta ^{\alpha }}$
. Notice that
$j=k\circ \pi _F^{{\mathcal {M}}^{\alpha }|\Theta ^{\alpha }}$
. Notice that
![]() $\mathrm {crit }(k)\geq \Theta ^{\gamma }$
, and that we have
$\mathrm {crit }(k)\geq \Theta ^{\gamma }$
, and that we have
![]() $\tau : \pi _F^{L_{\gamma }[{\mathcal {V}}_{\gamma }]}({\mathcal {V}}_{\gamma })\rightarrow \pi _F^{{\mathcal {M}}^{\alpha }|\Theta ^{\alpha }}({\mathcal {V}}_{\gamma })$
with
$\tau : \pi _F^{L_{\gamma }[{\mathcal {V}}_{\gamma }]}({\mathcal {V}}_{\gamma })\rightarrow \pi _F^{{\mathcal {M}}^{\alpha }|\Theta ^{\alpha }}({\mathcal {V}}_{\gamma })$
with
![]() $\mathrm {crit }(\tau )\geq \Theta ^{\gamma }$
such that
$\mathrm {crit }(\tau )\geq \Theta ^{\gamma }$
such that
![]() $\pi _F^{{\mathcal {M}}^{\alpha }|\Theta ^{\alpha }}\restriction {\mathcal {V}}_{\gamma }=\tau \circ \pi _F^{L_{\gamma }[{\mathcal {V}}_{\gamma }]}\restriction {\mathcal {V}}_{\gamma }$
. We thus have that
$\pi _F^{{\mathcal {M}}^{\alpha }|\Theta ^{\alpha }}\restriction {\mathcal {V}}_{\gamma }=\tau \circ \pi _F^{L_{\gamma }[{\mathcal {V}}_{\gamma }]}\restriction {\mathcal {V}}_{\gamma }$
. We thus have that
It is enough to show that
![]() $\pi _F^{L_{\gamma }[{\mathcal {V}}_{\gamma }]}({\mathcal {V}}_{\gamma })\in {\mathcal {M}}^{\alpha }$
and
$\pi _F^{L_{\gamma }[{\mathcal {V}}_{\gamma }]}({\mathcal {V}}_{\gamma })\in {\mathcal {M}}^{\alpha }$
and
![]() ${\mathcal {M}}^{\alpha }\vDash \text {"}\pi _F^{L_{\gamma }[{\mathcal {V}}_{\gamma }]}({\mathcal {V}}_{\gamma })$
is the
${\mathcal {M}}^{\alpha }\vDash \text {"}\pi _F^{L_{\gamma }[{\mathcal {V}}_{\gamma }]}({\mathcal {V}}_{\gamma })$
is the
![]() $\Lambda _{\Theta ^{\gamma }}$
-Varsovian model over
$\Lambda _{\Theta ^{\gamma }}$
-Varsovian model over
![]() ${\mathcal {M}}^{\alpha }|\Theta ^{\gamma }$
”. Notice that
${\mathcal {M}}^{\alpha }|\Theta ^{\gamma }$
”. Notice that
-
(4.1)
 ${\mathcal {M}}^{\alpha }|\Theta ^{\alpha }\vDash \text {`}j({\mathcal {V}}_{\gamma })$
is the unique
${\mathcal {M}}^{\alpha }|\Theta ^{\alpha }\vDash \text {`}j({\mathcal {V}}_{\gamma })$
is the unique
 $j(\Theta ^{\gamma })$
-sound
$j(\Theta ^{\gamma })$
-sound
 $\Lambda _{j(\Theta ^{\gamma })}$
-Varsovian model’.
$\Lambda _{j(\Theta ^{\gamma })}$
-Varsovian model’. -
(4.2)
 $\Lambda _{\Theta ^{\gamma }}$
is the
$\Lambda _{\Theta ^{\gamma }}$
is the
 $k\circ \tau $
-pullback of
$k\circ \tau $
-pullback of
 $\Lambda _{j(\Theta ^{\gamma })}$
.
$\Lambda _{j(\Theta ^{\gamma })}$
.
It then follows from (4.1) and (4.2), and from the fact that
![]() $\pi _F^{L_{\gamma }[{\mathcal {V}}_{\gamma }]}(\Theta ^{\gamma })=\Theta ^{\gamma }$
, that
$\pi _F^{L_{\gamma }[{\mathcal {V}}_{\gamma }]}(\Theta ^{\gamma })=\Theta ^{\gamma }$
, that
![]() $\pi _F^{L_{\gamma }[{\mathcal {V}}_{\gamma }]}({\mathcal {V}}_{\gamma })$
is the unique
$\pi _F^{L_{\gamma }[{\mathcal {V}}_{\gamma }]}({\mathcal {V}}_{\gamma })$
is the unique
![]() $\Theta ^{\gamma }$
-sound
$\Theta ^{\gamma }$
-sound
![]() $\Lambda _{\Theta ^{\gamma }}$
-Varsovian model. Hence, it follows from Claim 9.17 that
$\Lambda _{\Theta ^{\gamma }}$
-Varsovian model. Hence, it follows from Claim 9.17 that
![]() $\pi _F^{L_{\gamma }[{\mathcal {V}}_{\gamma }]}({\mathcal {V}}_{\gamma })={\mathcal {V}}_{\gamma }$
.
$\pi _F^{L_{\gamma }[{\mathcal {V}}_{\gamma }]}({\mathcal {V}}_{\gamma })={\mathcal {V}}_{\gamma }$
.
This finishes the proof of Lemma 9.15.
Since
![]() $L[{\mathcal {V}}_{{\textsf {Ord}}}]={\textsf {HOD}}^{L({\mathbb {R}})}$
, Lemma 9.15 implies Theorem 9.14.
$L[{\mathcal {V}}_{{\textsf {Ord}}}]={\textsf {HOD}}^{L({\mathbb {R}})}$
, Lemma 9.15 implies Theorem 9.14.
The proof of Theorem 9.14, [Reference Sargsyan13] and [Reference Trang34] can be used to show the following.
Theorem 9.19. Suppose V is the minimal model of
![]() ${\textsf {AD}}_{{\mathbb {R}}}+ \text{`}\Theta $
is a regular cardinal’,
${\textsf {AD}}_{{\mathbb {R}}}+ \text{`}\Theta $
is a regular cardinal’,
![]() ${\mathcal { H}}$
is the hod premouse representation of
${\mathcal { H}}$
is the hod premouse representation of
![]() $V_\Theta ^{\textsf {HOD}}$
and
$V_\Theta ^{\textsf {HOD}}$
and
![]() $j:{\mathcal { H}}\rightarrow {\mathcal { H}}$
is an elementary embedding. Then
$j:{\mathcal { H}}\rightarrow {\mathcal { H}}$
is an elementary embedding. Then
![]() $j=id$
.
$j=id$
.
Acknowledgements
The authors thank Gabriel Goldberg for fruitful discussion about choiceless cardinal phenomena under
![]() $\mathsf {AD}$
and for raising the question Theorem 9.14 addresses. We are also grateful to the referee for very helpful comments.
$\mathsf {AD}$
and for raising the question Theorem 9.14 addresses. We are also grateful to the referee for very helpful comments.
Competing interest
The authors have no competing interests to declare.
Financial support
This research was supported by the National Science Centre, Poland under the WeaveUNISONO call in the Weave Programme, registration number UMO-2021/03/Y/ST1/00281.









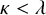
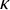

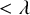


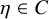


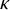
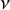
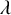




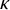

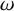



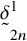 ’s are
’s are