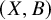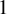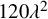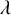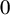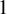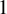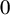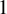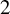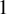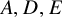1 Introduction
Fano varieties and Calabi–Yau varieties are two of the three building blocks of algebraic varieties. In the former case, the canonical divisor is antiample, while in the latter case it is numerically trivial. In this article, we study the coregularity of Fano and Calabi–Yau varieties. This invariant measures the dimension of the dual complexes corresponding to log Calabi–Yau structures on the variety. We show that if the coregularity is at most two, we can control the index of a Calabi–Yau variety and the complements of a Fano variety. In [Reference Moraga35], the third named author relates various problems about Fano varieties with the concept of coregularity.
1.1 Log Calabi–Yau pairs
A log Calabi–Yau pair
![]() $(X,B)$
is a projective log canonical pair for which
$(X,B)$
is a projective log canonical pair for which
![]() $K_X+B\equiv 0$
. By the abundance conjecture, which is known in this special case [Reference Gongyo21], it is also known that
$K_X+B\equiv 0$
. By the abundance conjecture, which is known in this special case [Reference Gongyo21], it is also known that
![]() $K_X+B\sim _{\mathbb {Q}} 0$
. The index of
$K_X+B\sim _{\mathbb {Q}} 0$
. The index of
![]() $(X,B)$
is the smallest positive integer I for which
$(X,B)$
is the smallest positive integer I for which
![]() $I(K_X+B)\sim 0$
. It is conjectured that the index I of
$I(K_X+B)\sim 0$
. It is conjectured that the index I of
![]() $(X,B)$
admits an upper bound depending on the dimension of X and the set of coefficients of B. This is known as the index conjecture. For instance, if
$(X,B)$
admits an upper bound depending on the dimension of X and the set of coefficients of B. This is known as the index conjecture. For instance, if
![]() $(X,B)$
is two-dimensional and the coefficients of B are standard (i.e., of the form
$(X,B)$
is two-dimensional and the coefficients of B are standard (i.e., of the form
![]() $1-\frac {1}{m}$
for some
$1-\frac {1}{m}$
for some
![]() $m\in \mathbb {Z}_{>0}$
), then
$m\in \mathbb {Z}_{>0}$
), then
![]() $I(K_X+B)\sim 0$
for some
$I(K_X+B)\sim 0$
for some
![]() $I\leq 66$
(see, e.g., [Reference Ishii26, Theorem 4.11]). The bound
$I\leq 66$
(see, e.g., [Reference Ishii26, Theorem 4.11]). The bound
![]() $66$
is optimal, and it can be obtained by considering nonsymplectic finite actions on K3 surfaces [Reference Machida and Oguiso34]. In [Reference Esser, Totaro and Wang9], the authors exhibit a sequence of klt Calabi–Yau varieties
$66$
is optimal, and it can be obtained by considering nonsymplectic finite actions on K3 surfaces [Reference Machida and Oguiso34]. In [Reference Esser, Totaro and Wang9], the authors exhibit a sequence of klt Calabi–Yau varieties
![]() $X_d$
with index
$X_d$
with index
![]() $i_d$
that grows doubly exponentially with the dimension d. The coregularity of a log Calabi–Yau pair
$i_d$
that grows doubly exponentially with the dimension d. The coregularity of a log Calabi–Yau pair
![]() $(X,B)$
is defined to be
$(X,B)$
is defined to be
![]() $\dim X - \dim \mathcal {D}(X,B)-1$
. Here,
$\dim X - \dim \mathcal {D}(X,B)-1$
. Here,
![]() $\mathcal {D}(X,B)$
is the dual complex of
$\mathcal {D}(X,B)$
is the dual complex of
![]() $(X,B)$
. This is a pseudo-manifold that encodes the combinatorial data of log canonical centers of a dlt modification of
$(X,B)$
. This is a pseudo-manifold that encodes the combinatorial data of log canonical centers of a dlt modification of
![]() $(X,B)$
. The dimension
$(X,B)$
. The dimension
![]() $\dim \mathcal {D}(X,B)$
is independent of the chosen dlt modification, so it is an intrinsic invariant of
$\dim \mathcal {D}(X,B)$
is independent of the chosen dlt modification, so it is an intrinsic invariant of
![]() $(X,B)$
. In the following subsection, we present theorems regarding the index of log Calabi–Yau pairs of coregularity
$(X,B)$
. In the following subsection, we present theorems regarding the index of log Calabi–Yau pairs of coregularity
![]() $0$
and
$0$
and
![]() $1$
.
$1$
.
1.2 Index and coregularity of log Calabi–Yau pairs
First, we study log Calabi–Yau pairs of coregularity 0 and 1. We use the language of generalized pairs as in [Reference Birkar3, Reference Filipazzi11]. This gives a larger scope for the theorems and also facilitates inductive arguments. In the case of generalized log Calabi–Yau pairs of coregularity
![]() $0$
, the following theorem is proved in [Reference Filipazzi, Mauri and Moraga13].
$0$
, the following theorem is proved in [Reference Filipazzi, Mauri and Moraga13].
Theorem 1. Let
![]() $(X,B,\mathbf {M})$
be a projective generalized log Calabi–Yau pairFootnote
1
of coregularity
$(X,B,\mathbf {M})$
be a projective generalized log Calabi–Yau pairFootnote
1
of coregularity
![]() $0$
, and let be
$0$
, and let be
![]() $\lambda $
a positive integer. Assume that
$\lambda $
a positive integer. Assume that
![]() $\lambda (K_X+B+{\mathbf {M}_{X}})$
is Weil. Then, we have that
$\lambda (K_X+B+{\mathbf {M}_{X}})$
is Weil. Then, we have that
![]() $2\lambda (K_X+B+{\mathbf {M}_{X}})\sim 0$
.
$2\lambda (K_X+B+{\mathbf {M}_{X}})\sim 0$
.
Note that in order to have a linear equivalence
![]() $D\sim 0$
, the divisor D must be Weil. Hence, multiplying
$D\sim 0$
, the divisor D must be Weil. Hence, multiplying
![]() $K_X+B+{\mathbf {M}_{X}}$
by
$K_X+B+{\mathbf {M}_{X}}$
by
![]() $\lambda $
is indeed needed to compute its index. In [Reference Filipazzi, Mauri and Moraga13, Example 7.4], the authors give an example for which
$\lambda $
is indeed needed to compute its index. In [Reference Filipazzi, Mauri and Moraga13, Example 7.4], the authors give an example for which
![]() $(X,B)$
is log Calabi–Yau of coregularity
$(X,B)$
is log Calabi–Yau of coregularity
![]() $0$
, B is a Weil divisor,
$0$
, B is a Weil divisor,
![]() $2(K_X+B)\sim 0$
, and
$2(K_X+B)\sim 0$
, and
![]() $K_X+B$
is not linearly equivalent to 0. Hence, the factor
$K_X+B$
is not linearly equivalent to 0. Hence, the factor
![]() $2\lambda $
in the previous theorem is optimal. Indeed, the factor
$2\lambda $
in the previous theorem is optimal. Indeed, the factor
![]() $2$
is often related to the orientability of the pseudo-manifold
$2$
is often related to the orientability of the pseudo-manifold
![]() $\mathcal {D}(X,B)$
(see [Reference Filipazzi, Mauri and Moraga13, § 5]). In [Reference Filipazzi, Mauri and Moraga13], the authors use topological methods and birational geometry to prove the previous theorem. In this article, we recover this statement using birational geometry and the theory of complements.
$\mathcal {D}(X,B)$
(see [Reference Filipazzi, Mauri and Moraga13, § 5]). In [Reference Filipazzi, Mauri and Moraga13], the authors use topological methods and birational geometry to prove the previous theorem. In this article, we recover this statement using birational geometry and the theory of complements.
Our next theorem deals with the index of log Calabi–Yau pairs of coregularity
![]() $1$
. This is a generalization of the previous statement to the case of coregularity
$1$
. This is a generalization of the previous statement to the case of coregularity
![]() $1$
.
$1$
.
Theorem 2. Let
![]() $(X,B,\mathbf {M})$
be a projective generalized log Calabi–Yau pair of coregularity
$(X,B,\mathbf {M})$
be a projective generalized log Calabi–Yau pair of coregularity
![]() $1$
and
$1$
and
![]() $\lambda $
be a positive integer. Assume the two following conditions hold:
$\lambda $
be a positive integer. Assume the two following conditions hold:
-
• the generalized pair
 $(X,B,\mathbf {M})$
has Weil index
$(X,B,\mathbf {M})$
has Weil index
 $\lambda $
; and
$\lambda $
; and -
• the variety X is rationally connected or
 $\mathbf {M}=0$
.
$\mathbf {M}=0$
.
Then, we have that
![]() $I(K_X+B+{\mathbf {M}_{X}})\sim 0$
for
$I(K_X+B+{\mathbf {M}_{X}})\sim 0$
for
![]() $I=m\lambda $
with
$I=m\lambda $
with
![]() $m\leq 120\lambda $
.
$m\leq 120\lambda $
.
We emphasize that the previous theorem does not hold if X is not rationally connected and
![]() $\mathbf {M}$
is nontrivial. For instance, we can let X be an elliptic curve and
$\mathbf {M}$
is nontrivial. For instance, we can let X be an elliptic curve and
![]() $\mathbf {M}$
be an I-torsion point in
$\mathbf {M}$
be an I-torsion point in
![]() $\mathrm {Pic}^0(X)$
. Then, we have that
$\mathrm {Pic}^0(X)$
. Then, we have that
![]() $I(K_X+{\mathbf {M}_{X}})\sim I{\mathbf {M}_{X}} \sim 0$
is minimal and
$I(K_X+{\mathbf {M}_{X}})\sim I{\mathbf {M}_{X}} \sim 0$
is minimal and
![]() $(X,\mathbf {M})$
is a generalized log Calabi–Yau pair of coregularity
$(X,\mathbf {M})$
is a generalized log Calabi–Yau pair of coregularity
![]() $1$
. Note that this is not an issue if X is rationally connected. In this case, the torsion of components of the b-nef divisor is controlled by their Weil index. Theorem 1 and Theorem 2 are still valid if the coefficients of B belong to a set of rational numbers satisfying the descending chain condition (DCC) condition. This follows from the global ascending chain condition for generalized log Calabi–Yau pairs with bounded coregularity (see [Reference Figueroa, Moraga and Peng10, Theorem 2]). Finally, in the case of coregularity
$1$
. Note that this is not an issue if X is rationally connected. In this case, the torsion of components of the b-nef divisor is controlled by their Weil index. Theorem 1 and Theorem 2 are still valid if the coefficients of B belong to a set of rational numbers satisfying the descending chain condition (DCC) condition. This follows from the global ascending chain condition for generalized log Calabi–Yau pairs with bounded coregularity (see [Reference Figueroa, Moraga and Peng10, Theorem 2]). Finally, in the case of coregularity
![]() $1$
, we obtain the following statement.
$1$
, we obtain the following statement.
Theorem 3. Let
![]() $(X,B,\mathbf {M})$
be a projective generalized log Calabi–Yau pair of coregularity
$(X,B,\mathbf {M})$
be a projective generalized log Calabi–Yau pair of coregularity
![]() $1$
. Assume that the following conditions hold:
$1$
. Assume that the following conditions hold:
-
• the coefficients of B are standard;
-
• the divisor
 $2\mathbf {M}$
is b-Cartier; and
$2\mathbf {M}$
is b-Cartier; and -
• the variety X is rationally connected or
 $\mathbf {M}=0$
.
$\mathbf {M}=0$
.
Then, we have that
![]() $I(K_X+B+{\mathbf {M}_{X}})\sim 0$
for some
$I(K_X+B+{\mathbf {M}_{X}})\sim 0$
for some
![]() $I\in \{1,2,3,4,6\}$
.
$I\in \{1,2,3,4,6\}$
.
1.3 Fano varieties
Given a klt Fano variety X, the anticanonical divisor
![]() $-K_X$
is ample. Hence, the linear system
$-K_X$
is ample. Hence, the linear system
![]() $|-mK_X|$
is basepoint free for m sufficiently large and divisible. In particular, we can find an effective divisor
$|-mK_X|$
is basepoint free for m sufficiently large and divisible. In particular, we can find an effective divisor
![]() $B \in |-mK_X|$
such that the pair
$B \in |-mK_X|$
such that the pair
![]() $(X,B/m)$
is klt (Kawamata log terminal) and log Calabi–Yau. This means that every Fano variety admits a log Calabi–Yau structure. In [Reference Birkar3], Birkar showed that an n-dimensional Fano variety X admits an
$(X,B/m)$
is klt (Kawamata log terminal) and log Calabi–Yau. This means that every Fano variety admits a log Calabi–Yau structure. In [Reference Birkar3], Birkar showed that an n-dimensional Fano variety X admits an
![]() $N(n)$
-complement, that is, a boundary B for which
$N(n)$
-complement, that is, a boundary B for which
![]() $(X,B)$
is log canonical and
$(X,B)$
is log canonical and
![]() $N(n)(K_X+B)\sim 0$
. This can be thought of as an effective log Calabi–Yau structure on X. In [Reference Filipazzi, Moraga and Xu15], Filipazzi, Moraga and Xu proved that a 3-fold that admits a
$N(n)(K_X+B)\sim 0$
. This can be thought of as an effective log Calabi–Yau structure on X. In [Reference Filipazzi, Moraga and Xu15], Filipazzi, Moraga and Xu proved that a 3-fold that admits a
![]() $\mathbb {Q}$
-complementFootnote
2
also admits a
$\mathbb {Q}$
-complementFootnote
2
also admits a
![]() $N_3$
-complement.
$N_3$
-complement.
Let X be an n-dimensional Fano variety. We can define the absolute coregularity to be:
By definition, the absolute coregularity of X is at most n. It is expected that a Fano variety of absolute coregularity c admits an
![]() $N(c)$
-complement (see, e.g., [Reference Moraga35, Conjecture 4.1]). Indeed, following the philosophy of Kawamata’s X-method, one expects to lift complements from minimal log canonical centers. In the case of a Fano variety of absolute coregularity c, we can produce minimal log canonical centers having dimension c [on a suitable dlt (divisorially log terminal) modification]. In the following subsection, we present some theorems regarding complements of Fano type varieties of absolute coregularity
$N(c)$
-complement (see, e.g., [Reference Moraga35, Conjecture 4.1]). Indeed, following the philosophy of Kawamata’s X-method, one expects to lift complements from minimal log canonical centers. In the case of a Fano variety of absolute coregularity c, we can produce minimal log canonical centers having dimension c [on a suitable dlt (divisorially log terminal) modification]. In the following subsection, we present some theorems regarding complements of Fano type varieties of absolute coregularity
![]() $0$
and
$0$
and
![]() $1$
.
$1$
.
1.4 Complements and coregularity of Fano type varieties
Our main theorem in this direction states that a Fano type variety of absolute coregularity 0 admits a
![]() $1$
-complement or a
$1$
-complement or a
![]() $2$
-complement.
$2$
-complement.
Theorem 4. Let
![]() $(X,B,\mathbf {M})$
be a projective generalized Fano type pair of absolute coregularity
$(X,B,\mathbf {M})$
be a projective generalized Fano type pair of absolute coregularity
![]() $0$
. Assume that the following conditions hold:
$0$
. Assume that the following conditions hold:
-
• the coefficients of B are standard;
-
• the b-nef divisor
 $2\mathbf {M}$
is b-Cartier.
$2\mathbf {M}$
is b-Cartier.
Then, there exists a boundary
![]() $B^+ \geq B$
satisfying the following conditions:
$B^+ \geq B$
satisfying the following conditions:
-
• the generalized pair
 $(X,B^+,\mathbf {M})$
is generalized log canonical;
$(X,B^+,\mathbf {M})$
is generalized log canonical; -
• we have that
 $2(K_X+B^{+}+{\mathbf {M}_{X}})\sim 0$
; and
$2(K_X+B^{+}+{\mathbf {M}_{X}})\sim 0$
; and -
• the equality
 $\mathrm {coreg}(X,B^+,\mathbf {M})=0$
holds.
$\mathrm {coreg}(X,B^+,\mathbf {M})=0$
holds.
In the case that
![]() $B=\mathbf {M}=0$
, the previous theorem says that, for a Fano variety X of absolute coregularity
$B=\mathbf {M}=0$
, the previous theorem says that, for a Fano variety X of absolute coregularity
![]() $0$
, the linear system
$0$
, the linear system
![]() $|-2K_X|$
contains an element with nice singularities. In particular, the linear system
$|-2K_X|$
contains an element with nice singularities. In particular, the linear system
![]() $|-2K_X|$
is nonempty. In [Reference Totaro42, § 8], Totaro investigates Fano varieties with large bottom weight, which is the smallest positive integer m for which
$|-2K_X|$
is nonempty. In [Reference Totaro42, § 8], Totaro investigates Fano varieties with large bottom weight, which is the smallest positive integer m for which
![]() $H^0(X,-mK_X)\neq 0$
. In particular, [Reference Totaro42, Theorem 8.1] implies the existence of a Fano
$H^0(X,-mK_X)\neq 0$
. In particular, [Reference Totaro42, Theorem 8.1] implies the existence of a Fano
![]() $4$
-fold that does not admit an m-complement for
$4$
-fold that does not admit an m-complement for
![]() $m\leq 1799233$
. This shows that the constant
$m\leq 1799233$
. This shows that the constant
![]() $N(4)$
obtained by Birkar in [Reference Birkar3] is at least
$N(4)$
obtained by Birkar in [Reference Birkar3] is at least
![]() $1799233$
. More generally, [Reference Totaro42, Theorem 8.1] shows that
$1799233$
. More generally, [Reference Totaro42, Theorem 8.1] shows that
![]() $N(d)$
grows at least doubly exponentially with d. In contrast to this, our statement shows that a Fano variety of absolute coregularity
$N(d)$
grows at least doubly exponentially with d. In contrast to this, our statement shows that a Fano variety of absolute coregularity
![]() $0$
either admits a
$0$
either admits a
![]() $1$
-complement or a
$1$
-complement or a
![]() $2$
-complement. In [Reference Moraga35, Example 3.15], the third author gives an example of a Fano surface of absolute coregularity
$2$
-complement. In [Reference Moraga35, Example 3.15], the third author gives an example of a Fano surface of absolute coregularity
![]() $0$
for which there is no
$0$
for which there is no
![]() $1$
-complement. Thus, the previous theorem is sharp. In the case of absolute coregularity
$1$
-complement. Thus, the previous theorem is sharp. In the case of absolute coregularity
![]() $1$
, we obtain a similar result.
$1$
, we obtain a similar result.
Theorem 5. Let
![]() $(X,B,\mathbf {M})$
be a projective generalized Fano type pair of absolute coregularity
$(X,B,\mathbf {M})$
be a projective generalized Fano type pair of absolute coregularity
![]() $1$
. Assume that the following conditions hold:
$1$
. Assume that the following conditions hold:
-
• the coefficients of B are standard;
-
• the b-nef divisor
 $2\mathbf {M}$
is b-Cartier.
$2\mathbf {M}$
is b-Cartier.
Then, there exists a boundary
![]() $B^+\geq B$
satisfying the following conditions:
$B^+\geq B$
satisfying the following conditions:
-
• the generalized pair
 $(X,B^+,\mathbf {M})$
is generalized log canonical;
$(X,B^+,\mathbf {M})$
is generalized log canonical; -
• we have that
 $N(K_X+B^{+}+\mathbf {M})\sim 0$
, where
$N(K_X+B^{+}+\mathbf {M})\sim 0$
, where
 $N\in \{1,2,3,4,6\}$
; and
$N\in \{1,2,3,4,6\}$
; and -
• the equality
 $\mathrm {coreg}(X,B^+,\mathbf {M})=1$
holds.
$\mathrm {coreg}(X,B^+,\mathbf {M})=1$
holds.
In Table 1, we summarize the unconditional theorems regarding complements of Fano varieties. The entry
![]() $(d,c)$
in the table corresponds to the minimum integer
$(d,c)$
in the table corresponds to the minimum integer
![]() $N_{d,c}$
for which every d-dimensional Fano variety of coregularity c admits at most a
$N_{d,c}$
for which every d-dimensional Fano variety of coregularity c admits at most a
![]() $N_{d,c}$
-complement. In the blank spots, there set of such Fano varieties is empty. Due to the work of Liu [Reference Liu33], we know that
$N_{d,c}$
-complement. In the blank spots, there set of such Fano varieties is empty. Due to the work of Liu [Reference Liu33], we know that
![]() $N_2\leq {10^{10}}^{11}$
. However, it is expected that we can take
$N_2\leq {10^{10}}^{11}$
. However, it is expected that we can take
![]() $N_2=66$
. By the work of Totaro [Reference Totaro42], we know that
$N_2=66$
. By the work of Totaro [Reference Totaro42], we know that
![]() $N_d$
grows at least doubly exponentially with d.
$N_d$
grows at least doubly exponentially with d.
Table 1 Dimension, coregularity and complements

1.5 Calabi–Yau pairs of higher coregularity
In the case of higher coregularity, we need to deal with klt Calabi–Yau varieties of higher dimensions. We show that controlling the index of log Calabi–Yau pairs of coregularity c can be reduced to a problem about c-dimensional klt Calabi–Yau pairs. In order to state our next theorem, we need to introduce two conjectures about Calabi–Yau pairs. The first one is the boundedness of the index for klt Calabi–Yau pairs.
Conjecture 1. Let d be a positive integer, and let
![]() $\Lambda $
be a set of rational numbers satisfying the descending chain condition. There exists a constant
$\Lambda $
be a set of rational numbers satisfying the descending chain condition. There exists a constant ![]() , satisfying the following property. For every projective d-dimensional klt log Calabi–Yau pair
, satisfying the following property. For every projective d-dimensional klt log Calabi–Yau pair
![]() $(X,B)$
such that B has coefficients in
$(X,B)$
such that B has coefficients in
![]() $\Lambda $
, we have that
$\Lambda $
, we have that
The previous conjecture is stated in [Reference Birkar5, Conjecture 2.33]. The second conjecture is known as the boundedness of B-representations. It predicts that the birational automorphism group of a log Calabi–Yau pair acts on the sections of
![]() $I(K_X+B)\sim 0$
with bounded order (see, e.g., [Reference Fujino18, Conjecture 3.2]).
$I(K_X+B)\sim 0$
with bounded order (see, e.g., [Reference Fujino18, Conjecture 3.2]).
Conjecture 2. Let d and I be two positive integers. There is a constant ![]() satisfying the following property. For every projective d-dimensional klt log Calabi–Yau pair
satisfying the following property. For every projective d-dimensional klt log Calabi–Yau pair
![]() $(X,B)$
with
$(X,B)$
with
![]() $I(K_X+B)\sim 0$
, the image of
$I(K_X+B)\sim 0$
, the image of
![]() $\mathrm {Bir}(X,B)$
in
$\mathrm {Bir}(X,B)$
in
![]() $GL(H^0(I(K_X+B)))\simeq \mathbb {K}^*$
is finite and has order at most b.
$GL(H^0(I(K_X+B)))\simeq \mathbb {K}^*$
is finite and has order at most b.
Now, we can state our main theorem about the index of log Calabi–Yau pairs. It shows that the boundedness of the index of generalized log Calabi–Yau pairs of coregularity c can be reduced to the previous two conjectures in dimension c.
Theorem 6. Let c and p be positive integers and
![]() $\Lambda \subset \mathbb {Q}$
be a set satisfying the descending chain condition. Assume that Conjecture 1 and Conjecture 2 hold in dimension c. There is a constant
$\Lambda \subset \mathbb {Q}$
be a set satisfying the descending chain condition. Assume that Conjecture 1 and Conjecture 2 hold in dimension c. There is a constant ![]() satisfying the following property. Let
satisfying the following property. Let
![]() $(X,B,\mathbf {M})$
be a projective generalized log Calabi–Yau pair of coregularity c for which:
$(X,B,\mathbf {M})$
be a projective generalized log Calabi–Yau pair of coregularity c for which:
-
• either X is rationally connected or
 $\mathbf {M}=0$
;
$\mathbf {M}=0$
; -
• the coefficients of B are contained in
 $\Lambda $
; and
$\Lambda $
; and -
• the b-nef divisor
 $p\mathbf {M}$
is b-Cartier.
$p\mathbf {M}$
is b-Cartier.
Then, we have that
![]() $I(K_X+B+{\mathbf {M}_{X}})\sim 0$
.
$I(K_X+B+{\mathbf {M}_{X}})\sim 0$
.
1.6 Fano varieties of higher coregularity.
In the case of Fano varieties of higher absolute coregularity, we get the boundedness of complements of Fano type varieties with bounded absolute coregularity subject to the previous conjectures.
Theorem 7. Let c and p be positive integers and
![]() $\Lambda \subset \mathbb {Q}$
be a closed set satisfying the descending chain condition. Assume that Conjecture 1 and Conjecture 2 hold in dimension c. There is a constant
$\Lambda \subset \mathbb {Q}$
be a closed set satisfying the descending chain condition. Assume that Conjecture 1 and Conjecture 2 hold in dimension c. There is a constant ![]() satisfying the following. Let
satisfying the following. Let
![]() $(X,B,\mathbf {M})$
be a projective generalized Fano type pair of absolute coregularity c for which:
$(X,B,\mathbf {M})$
be a projective generalized Fano type pair of absolute coregularity c for which:
-
• the divisor B has coefficients in
 $\Lambda $
;
$\Lambda $
; -
• the b-nef divisor
 $p\mathbf {M}$
is Cartier where it descends.
$p\mathbf {M}$
is Cartier where it descends.
Then, there exists a boundary
![]() $B^+\geq B$
satisfying the following conditions:
$B^+\geq B$
satisfying the following conditions:
-
• the generalized pair
 $(X,B^+,\mathbf {M})$
is generalized log canonical;
$(X,B^+,\mathbf {M})$
is generalized log canonical; -
• we have that
 $N(K_X+B^{+}+{\mathbf {M}_{X}})\sim 0$
; and
$N(K_X+B^{+}+{\mathbf {M}_{X}})\sim 0$
; and -
• the equality
 $\mathrm {coreg}(X,B^+,\mathbf {M})=c$
holds.
$\mathrm {coreg}(X,B^+,\mathbf {M})=c$
holds.
We stress that Conjecture 1 is known up to dimension
![]() $3$
. On the other hand, Conjecture 2 is known up to dimension
$3$
. On the other hand, Conjecture 2 is known up to dimension
![]() $2$
. In particular, both Theorem 6 and Theorem 7 hold unconditionally in the case of coregularity 2.
$2$
. In particular, both Theorem 6 and Theorem 7 hold unconditionally in the case of coregularity 2.
1.7 Coregularity and the canonical bundle formula
The canonical bundle formula plays a fundamental role in the theory of complements. In many cases, we need to lift complements from the base of a log Calabi–Yau fibration. We will prove the following statement that relates the canonical bundle formula with the coregularity.
Theorem 8. Let c and p be nonnegative integers and
![]() $\Lambda \subset \mathbb {Q}$
be a set satisfying the descending chain condition. Assume that Conjecture 1 and Conjecture 2 hold in dimension at most
$\Lambda \subset \mathbb {Q}$
be a set satisfying the descending chain condition. Assume that Conjecture 1 and Conjecture 2 hold in dimension at most
![]() $c-1$
. There exists a set
$c-1$
. There exists a set ![]() satisfying the descending chain condition and a positive integer
satisfying the descending chain condition and a positive integer ![]() , satisfying the following property. Let
, satisfying the following property. Let
![]() $\pi \colon X\rightarrow Z$
be a Fano type morphism between projective varieties. Let
$\pi \colon X\rightarrow Z$
be a Fano type morphism between projective varieties. Let
![]() $(X,B,\mathbf {M})$
be a projective generalized pair of coregularity c for which:
$(X,B,\mathbf {M})$
be a projective generalized pair of coregularity c for which:
-
• the generalized pair
 $(X,B,\mathbf {M})$
is log Calabi–Yau over Z;
$(X,B,\mathbf {M})$
is log Calabi–Yau over Z; -
• the coefficients of B belong to
 $\Lambda $
;
$\Lambda $
; -
• the b-nef divisor
 $p\mathbf {M}$
is Cartier where it descends;
$p\mathbf {M}$
is Cartier where it descends; -
• the b-nef divisor
 $\mathbf {M}$
is
$\mathbf {M}$
is
 $\mathbb {Q}$
-trivial on the general fiber of
$\mathbb {Q}$
-trivial on the general fiber of
 $X\rightarrow Z$
;
$X\rightarrow Z$
; -
• every generalized log canonical center of
 $(X,B,\mathbf {M})$
is a log canonical center of
$(X,B,\mathbf {M})$
is a log canonical center of
 $(X,B)$
; and
$(X,B)$
; and -
• every log canonical center of
 $(X,B)$
dominates Z.
$(X,B)$
dominates Z.
Then, we can write
where the following conditions hold:
-
•
 $B_Z$
is the discriminant part of the adjunction for
$B_Z$
is the discriminant part of the adjunction for
 $(X,B,\mathbf {M})$
over Z;
$(X,B,\mathbf {M})$
over Z; -
• the coefficients of
 $B_Z$
belong to
$B_Z$
belong to
 $\Omega $
; and
$\Omega $
; and -
• the b-nef divisor
 $q\mathbf {N}$
is b-Cartier.
$q\mathbf {N}$
is b-Cartier.
1.8 Kawamata log terminal singularities
Finally, we show some applications of the previous theorems of this article to the study of klt singularities. We obtain the following result about klt singularities of absolute coregularity
![]() $0$
.
$0$
.
Theorem 9. Let
![]() $(X;x)$
be a klt singularity of absolute coregularity
$(X;x)$
be a klt singularity of absolute coregularity
![]() $0$
. Then, there exists a boundary
$0$
. Then, there exists a boundary
![]() $\Gamma $
through x satisfying the following conditions:
$\Gamma $
through x satisfying the following conditions:
-
• we have that
 $2(K_X+\Gamma )\sim 0$
on a neighborhood of x;
$2(K_X+\Gamma )\sim 0$
on a neighborhood of x; -
• the coregularity of
 $(X,\Gamma )$
at x is equal to
$(X,\Gamma )$
at x is equal to
 $0$
.
$0$
.
In particular, the pair
![]() $(X,\Gamma ;x)$
is strictly log canonical at x.
$(X,\Gamma ;x)$
is strictly log canonical at x.
Analogously, we obtain a similar result in the context of klt singularities of absolute coregularity
![]() $1$
.
$1$
.
Theorem 10. Let
![]() $(X;x)$
be a klt singularity of absolute coregularity
$(X;x)$
be a klt singularity of absolute coregularity
![]() $1$
. Then, there exists a boundary
$1$
. Then, there exists a boundary
![]() $\Gamma $
through x satisfying the following conditions:
$\Gamma $
through x satisfying the following conditions:
-
• we have that
 $N(K_X+\Gamma )\sim 0$
for some
$N(K_X+\Gamma )\sim 0$
for some
 $N\in \{1,2,3,4,6\}$
;
$N\in \{1,2,3,4,6\}$
; -
• the coregularity of
 $(X,\Gamma )$
at x is equal to
$(X,\Gamma )$
at x is equal to
 $1$
.
$1$
.
In particular, the pair
![]() $(X,\Gamma ;x)$
is strictly log canonical at x.
$(X,\Gamma ;x)$
is strictly log canonical at x.
The two previous theorems generalize the
![]() $A,D,E$
-type classification of klt surface singularities to higher-dimensional klt singularities. The A-type klt surface singularities are the toric surface singularities. In the Gorenstein case, these are the
$A,D,E$
-type classification of klt surface singularities to higher-dimensional klt singularities. The A-type klt surface singularities are the toric surface singularities. In the Gorenstein case, these are the
![]() $A_n$
-singularities. The A-type singularities are the klt surface singularities of absolute coregularity
$A_n$
-singularities. The A-type singularities are the klt surface singularities of absolute coregularity
![]() $0$
that admit a
$0$
that admit a
![]() $1$
-complement. The D-type klt surface singularities are quotients of toric singularities via an involution. In the Gorenstein case, these are
$1$
-complement. The D-type klt surface singularities are quotients of toric singularities via an involution. In the Gorenstein case, these are
![]() $D_n$
-singularities. The D-type singularities are the surface singularities of absolute coregularity
$D_n$
-singularities. The D-type singularities are the surface singularities of absolute coregularity
![]() $0$
that admit a
$0$
that admit a
![]() $2$
-complement but no
$2$
-complement but no
![]() $1$
-complement. The E-type klt surface singularities are the exceptional surface singularities. In the Gorenstein case, these are exactly the
$1$
-complement. The E-type klt surface singularities are the exceptional surface singularities. In the Gorenstein case, these are exactly the
![]() $E_6$
,
$E_6$
,
![]() $E_7$
and
$E_7$
and
![]() $E_8$
singularities. These are the klt surface singularities that have absolute coregularity
$E_8$
singularities. These are the klt surface singularities that have absolute coregularity
![]() $1$
. They admit a
$1$
. They admit a
![]() $3$
-,
$3$
-,
![]() $4$
- or
$4$
- or
![]() $6$
-complement but not a
$6$
-complement but not a
![]() $1$
-complement or
$1$
-complement or
![]() $2$
-complement. The aforementioned results about complements and coregularity of two-dimensional klt singularities are proved in [Reference Moraga35, Section 3.2].
$2$
-complement. The aforementioned results about complements and coregularity of two-dimensional klt singularities are proved in [Reference Moraga35, Section 3.2].
1.9 On the techniques of the article
The theory of complements was introduced by Shokurov in the early 2000s (see, e.g., [Reference Shokurov40]), although these objects already appeared in the work of Keel and McKernan on quasi-projective surfaces [Reference Kollár, Mori, Clemens and Corti30]. In this work, complements were called tigers. Since then, it has been understood that vanishing theorems, the canonical bundle formula and the minimal model program are indispensable tools to produce complements on a variety (see, e.g., [Reference Prokhorov and Shokurov38, Reference Petersen and Süss37, Reference Kollár, Mori, Clemens and Corti30]). Using the aforementioned techniques, the language of generalized pairs and the boundedness of exceptional Fano varieties, Birkar proved the boundedness of complements for Fano varieties [Reference Birkar3]. Since then, the theory of complements has been expanded to Fano pairs with more general coefficients [Reference Filipazzi and Moraga14, Reference Han, Liu and Shokurov24, Reference Shokurov41], to log canonical Fano varieties [Reference Xu44] and to log Calabi–Yau
![]() $3$
-folds [Reference Filipazzi, Moraga and Xu15]. In this article, we study the theory of complements through the lens of the coregularity. The techniques are similar to the ones in the aforementioned papers. However, in order to obtain novel results, we need to re-prove several parts of this theory keeping track of this new invariant. The fact that our results are independent of dimension imposes an extra difficulty. At the same time, we will need to use some recent results regarding the coregularity and its connections to singularities [Reference Figueroa, Moraga and Peng10] and Calabi–Yau pairs [Reference Filipazzi, Mauri and Moraga13].
$3$
-folds [Reference Filipazzi, Moraga and Xu15]. In this article, we study the theory of complements through the lens of the coregularity. The techniques are similar to the ones in the aforementioned papers. However, in order to obtain novel results, we need to re-prove several parts of this theory keeping track of this new invariant. The fact that our results are independent of dimension imposes an extra difficulty. At the same time, we will need to use some recent results regarding the coregularity and its connections to singularities [Reference Figueroa, Moraga and Peng10] and Calabi–Yau pairs [Reference Filipazzi, Mauri and Moraga13].
Strategy of the proof
In this section, we give a sketch of the proof of the main theorems of this article, namely Theorem 6, Theorem 7 and Theorem 8. The other theorems will be obtained using the same strategy and an analysis of the coefficients throughout the proof. We write Theorem
![]() $X(c)$
for Theorem X in coregularity at most c. Theorem 6
$X(c)$
for Theorem X in coregularity at most c. Theorem 6
![]() $(0)$
follows from [Reference Filipazzi, Mauri and Moraga13, Theorem 1], while Theorem 8
$(0)$
follows from [Reference Filipazzi, Mauri and Moraga13, Theorem 1], while Theorem 8
![]() $(0)$
is trivial. We will prove the following four statements:
$(0)$
is trivial. We will prove the following four statements:
We write Theorem
![]() $X(d,c)$
for Theorem X in dimension at most d and coregularity at most c. For instance, Theorem 7
$X(d,c)$
for Theorem X in dimension at most d and coregularity at most c. For instance, Theorem 7
![]() $(d,c)$
is known by [Reference Birkar3, Theorem 1.7]. Thus, we may write
$(d,c)$
is known by [Reference Birkar3, Theorem 1.7]. Thus, we may write
![]() $N(\Lambda ,d,c,p)$
for the positive integer provided by Theorem 7
$N(\Lambda ,d,c,p)$
for the positive integer provided by Theorem 7
![]() $(d,c)$
. We may suppress
$(d,c)$
. We may suppress
![]() $\Lambda $
and p from the notation whenever they are clear from the context. Our aim is to show that, once we fix c, there is an upper bound
$\Lambda $
and p from the notation whenever they are clear from the context. Our aim is to show that, once we fix c, there is an upper bound
![]() $N(c)$
for all
$N(c)$
for all
![]() $N(d,c)$
. Similarly, Theorem 8
$N(d,c)$
. Similarly, Theorem 8
![]() $(d,c)$
is known due to [Reference Birkar3, Proposition 6.3]. We write
$(d,c)$
is known due to [Reference Birkar3, Proposition 6.3]. We write
![]() $q(d,c)$
for the constant provided by Theorem 8
$q(d,c)$
for the constant provided by Theorem 8
![]() $(d,c)$
, and we show that
$(d,c)$
, and we show that
![]() $q(d,c)$
is bounded above by a constant only depending on c. Theorem 6
$q(d,c)$
is bounded above by a constant only depending on c. Theorem 6
![]() $(d,c)$
is not known even if we fix the dimension. In this case, the aim is twofold: to prove the existence of an upper bound
$(d,c)$
is not known even if we fix the dimension. In this case, the aim is twofold: to prove the existence of an upper bound
![]() $I(d,c)$
for fixed dimension d and to show that all the
$I(d,c)$
for fixed dimension d and to show that all the
![]() $I(d,c)$
are bounded above in terms of c. The proof of implication (i) is similar to that of (iv). In the following three subsections, we sketch the proofs of (ii), (iii) and (iv).
$I(d,c)$
are bounded above in terms of c. The proof of implication (i) is similar to that of (iv). In the following three subsections, we sketch the proofs of (ii), (iii) and (iv).
A canonical bundle formula
Let
![]() $(X,B,\mathbf {M})\rightarrow Z$
be as in the setting of Theorem 8
$(X,B,\mathbf {M})\rightarrow Z$
be as in the setting of Theorem 8
![]() $(d,c)$
.
$(d,c)$
.
First, we show that for every
![]() $z\in Z$
closed, we may find a relative
$z\in Z$
closed, we may find a relative
![]() $N(c-1)$
-complement for
$N(c-1)$
-complement for
![]() $(X,B,\mathbf {M})$
over z. We pick an effective Cartier divisor E on Z through z. We let t be the largest positive number for which
$(X,B,\mathbf {M})$
over z. We pick an effective Cartier divisor E on Z through z. We let t be the largest positive number for which
![]() $(X,B+t\pi ^*E,\mathbf {M})$
has generalized log canonical singularities around z. By the connectedness theorem, the coregularity of
$(X,B+t\pi ^*E,\mathbf {M})$
has generalized log canonical singularities around z. By the connectedness theorem, the coregularity of
![]() $(X,B+t\pi ^*E,\mathbf {M})$
is at most
$(X,B+t\pi ^*E,\mathbf {M})$
is at most
![]() $c-1$
. Indeed, since all the generalized log canonical centers of
$c-1$
. Indeed, since all the generalized log canonical centers of
![]() $(X,B,\mathbf {M})$
are horizontal over Z, introducing a vertical generalized log canonical center will strictly decrease the coregularity. Taking a dlt modification of
$(X,B,\mathbf {M})$
are horizontal over Z, introducing a vertical generalized log canonical center will strictly decrease the coregularity. Taking a dlt modification of
![]() $(X,B+t\pi ^*E,\mathbf {M})$
, we can produce a new generalized pair
$(X,B+t\pi ^*E,\mathbf {M})$
, we can produce a new generalized pair
![]() $(X',B',\mathbf {M})$
such that z is contained in the image of a component S of
$(X',B',\mathbf {M})$
such that z is contained in the image of a component S of
![]() $\lfloor B'\rfloor $
. By perturbing the coefficients, we may assume that the coefficients of
$\lfloor B'\rfloor $
. By perturbing the coefficients, we may assume that the coefficients of
![]() $B'$
belong to
$B'$
belong to
![]() $\Lambda $
. We replace
$\Lambda $
. We replace
![]() $(X,B,\mathbf {M})$
by
$(X,B,\mathbf {M})$
by
![]() $(X',B',\mathbf {M})$
and assume there is a vertical divisorial log canonical center S. Notice that this replacement changes the crepant birational class of the original generalized pair
$(X',B',\mathbf {M})$
and assume there is a vertical divisorial log canonical center S. Notice that this replacement changes the crepant birational class of the original generalized pair
![]() $(X,B,\mathbf {M})$
in order to create a new log canonical center. Running a suitable Minimal Model Program (MMP) over Z, we reduce to the case in which
$(X,B,\mathbf {M})$
in order to create a new log canonical center. Running a suitable Minimal Model Program (MMP) over Z, we reduce to the case in which
![]() $S\rightarrow \pi (S)\ni z$
is a Fano type morphism. The generalized pair
$S\rightarrow \pi (S)\ni z$
is a Fano type morphism. The generalized pair
![]() $(S,B_S,{\mathbf {M}_{S}})$
obtained by adjunction of
$(S,B_S,{\mathbf {M}_{S}})$
obtained by adjunction of
![]() $(X,B,\mathbf {M})$
to S has dimension at most
$(X,B,\mathbf {M})$
to S has dimension at most
![]() $d-1$
and coregularity at most
$d-1$
and coregularity at most
![]() $c-1$
. If
$c-1$
. If
![]() $q(S)=z$
, then we may apply Theorem 7
$q(S)=z$
, then we may apply Theorem 7
![]() $(d-1,c-1)$
to conclude that
$(d-1,c-1)$
to conclude that
![]() $(S,B_S,{\mathbf {M}_{S}})$
admits an
$(S,B_S,{\mathbf {M}_{S}})$
admits an
![]() $N(d-1,c-1)$
-complement. Since we are assuming Theorem 7
$N(d-1,c-1)$
-complement. Since we are assuming Theorem 7
![]() $(c-1)$
, this is also an
$(c-1)$
, this is also an
![]() $N(c-1)$
-complement. If
$N(c-1)$
-complement. If
![]() $\dim \pi (S)\geq 1$
, then we construct an
$\dim \pi (S)\geq 1$
, then we construct an
![]() $N(c-1)$
-complement by induction on the dimension. In any case, we obtain an
$N(c-1)$
-complement by induction on the dimension. In any case, we obtain an
![]() $N(c-1)$
-complement for
$N(c-1)$
-complement for
![]() $(S,B_S,{\mathbf {M}_{S}})$
around z. Using Kawamata–Viehweg vanishing, we lift such complement to an
$(S,B_S,{\mathbf {M}_{S}})$
around z. Using Kawamata–Viehweg vanishing, we lift such complement to an
![]() $N(c-1)$
-complement for
$N(c-1)$
-complement for
![]() $(X,B,\mathbf {M})$
around the fiber of
$(X,B,\mathbf {M})$
around the fiber of
![]() $z\in Z$
. The details of this proof can be found in § 5, where we discuss relative complements. In § 5.1, we explain how to lift complements from divisors.
$z\in Z$
. The details of this proof can be found in § 5, where we discuss relative complements. In § 5.1, we explain how to lift complements from divisors.
Now, we can assume the existence of bounded relative
![]() $N(c-1)$
-complements for
$N(c-1)$
-complements for
![]() $(X,B,\mathbf {M})\rightarrow Z$
. The existence of bounded relative complements allows us to find q in the statement of Theorem 8
$(X,B,\mathbf {M})\rightarrow Z$
. The existence of bounded relative complements allows us to find q in the statement of Theorem 8
![]() $(d,c)$
. Indeed, we can take
$(d,c)$
. Indeed, we can take
![]() $q(d,c)=N(c-1)$
. The main difficulty is to control the coefficients of
$q(d,c)=N(c-1)$
. The main difficulty is to control the coefficients of
![]() ${\mathbf {N}_{Z}}$
in the model where it descends. In order to do so, we will cut the base with hypersurfaces to reduce to the case in which the base is a curve. Once the base is a curve C, we will study the coefficients of a relative complement over a closed point
${\mathbf {N}_{Z}}$
in the model where it descends. In order to do so, we will cut the base with hypersurfaces to reduce to the case in which the base is a curve. Once the base is a curve C, we will study the coefficients of a relative complement over a closed point
![]() $c\in C$
. Analyzing the coefficients of this relative complement will show that
$c\in C$
. Analyzing the coefficients of this relative complement will show that
![]() $q{\mathbf {N}_{Z}}$
is integral. A similar argument on a suitable resolution
$q{\mathbf {N}_{Z}}$
is integral. A similar argument on a suitable resolution
![]() $Z'\rightarrow Z$
proves that
$Z'\rightarrow Z$
proves that
![]() $q{\mathbf {N}_{Z'}}$
is integral, where
$q{\mathbf {N}_{Z'}}$
is integral, where
![]() $Z'$
is a model on which
$Z'$
is a model on which
![]() ${\mathbf {N}_{Z}}$
descends. This finishes the proof of Theorem 8
${\mathbf {N}_{Z}}$
descends. This finishes the proof of Theorem 8
![]() $(c)$
using Theorem 7
$(c)$
using Theorem 7
![]() $(c-1)$
. The details of this proof are given in § 6.
$(c-1)$
. The details of this proof are given in § 6.
Index of log Calabi–Yau pairs
Let
![]() $(X,B,\mathbf {M})$
be a generalized log Calabi–Yau pair as in Theorem 6
$(X,B,\mathbf {M})$
be a generalized log Calabi–Yau pair as in Theorem 6
![]() $(d,c)$
. By [Reference Figueroa, Moraga and Peng10, Theorem 2], we may assume that the set
$(d,c)$
. By [Reference Figueroa, Moraga and Peng10, Theorem 2], we may assume that the set
![]() $\Lambda $
in the statement of the theorem is finite. By [Reference Filipazzi and Svaldi16, Theorem 4.2], we can replace
$\Lambda $
in the statement of the theorem is finite. By [Reference Filipazzi and Svaldi16, Theorem 4.2], we can replace
![]() $(X,B,\mathbf {M})$
by a Kollár–Xu model (see § 2.7). We have a Fano type contraction
$(X,B,\mathbf {M})$
by a Kollár–Xu model (see § 2.7). We have a Fano type contraction
![]() $q\colon X\rightarrow Z$
such that all the generalized log canonical centers of
$q\colon X\rightarrow Z$
such that all the generalized log canonical centers of
![]() $(X,B,\mathbf {M})$
dominate the base Z. Both the index and Weil index of
$(X,B,\mathbf {M})$
dominate the base Z. Both the index and Weil index of
![]() $K_X+B+{\mathbf {M}_{X}}$
are preserved by the Kollár–Xu model. We will proceed with the proof in three different cases, depending on the dimension of the base of the Kollár–Xu model and the coefficient sets of B and
$K_X+B+{\mathbf {M}_{X}}$
are preserved by the Kollár–Xu model. We will proceed with the proof in three different cases, depending on the dimension of the base of the Kollár–Xu model and the coefficient sets of B and
![]() $\mathbf {M}$
. We argue by induction on the dimension d of X. The base of the induction is the klt case which follows by Conjecture 1 (see, e.g., Lemma 2.30).
$\mathbf {M}$
. We argue by induction on the dimension d of X. The base of the induction is the klt case which follows by Conjecture 1 (see, e.g., Lemma 2.30).
Case 1: the moduli part
![]() $\mathbf {M}=0$
.
$\mathbf {M}=0$
.
In this case, we know that
![]() $K_X+B\sim _{\mathbb {Q}} 0$
. We do not assume that X is rationally connected. We choose a component S of
$K_X+B\sim _{\mathbb {Q}} 0$
. We do not assume that X is rationally connected. We choose a component S of
![]() $\lfloor B\rfloor $
and run a
$\lfloor B\rfloor $
and run a
![]() $(K_X+B-\epsilon S)$
-MMP. This minimal model program terminates with a Mori fiber space on which S is ample over the base. Observe that the variety S may not be normal. However, the pair obtained by adjunction
$(K_X+B-\epsilon S)$
-MMP. This minimal model program terminates with a Mori fiber space on which S is ample over the base. Observe that the variety S may not be normal. However, the pair obtained by adjunction
![]() $(S,B_S)$
is semilog canonical. In § 4, we show that the statement of Theorem 6
$(S,B_S)$
is semilog canonical. In § 4, we show that the statement of Theorem 6
![]() $(d-1,c)$
holds for semilog canonical pairs provided it holds for log canonical pairs. To do so, we use Conjecture 1 and Conjecture 2 in dimension c. Here, it is crucial that we work with pairs instead of generalized pairs. Indeed, Conjecture 2 is not known for generalized pairs, even in dimension
$(d-1,c)$
holds for semilog canonical pairs provided it holds for log canonical pairs. To do so, we use Conjecture 1 and Conjecture 2 in dimension c. Here, it is crucial that we work with pairs instead of generalized pairs. Indeed, Conjecture 2 is not known for generalized pairs, even in dimension
![]() $2$
. Hence, we conclude that
$2$
. Hence, we conclude that
![]() $I(\Lambda ,d-1,c,0)(K_S+B_S)\sim 0$
.
$I(\Lambda ,d-1,c,0)(K_S+B_S)\sim 0$
.
Thus, in this case, we conclude that the index of
![]() $(X,B)$
is at most
$(X,B)$
is at most
![]() $I(\Lambda ,d-1,c,0)$
.
$I(\Lambda ,d-1,c,0)$
.
Case 2: the base Z of the Kollár–Xu model is positive-dimensional, the divisor
![]() $\{B\}+{\mathbf {M}_{X}}$
is trivial on the general fiber of
$\{B\}+{\mathbf {M}_{X}}$
is trivial on the general fiber of
![]() $X\to Z$
and the b-nef divisor
$X\to Z$
and the b-nef divisor
![]() $\mathbf {M}$
is nontrivial.
$\mathbf {M}$
is nontrivial.
In this case, we apply Theorem 8
![]() $(c)$
. We can write
$(c)$
. We can write
The variety Z has dimension at most c. The integer q only depends on
![]() $\Lambda ,c$
and p. The coefficients of
$\Lambda ,c$
and p. The coefficients of
![]() $B_Z$
belong to a DCC set that only depends on
$B_Z$
belong to a DCC set that only depends on
![]() $\Lambda ,c$
and p. The b-nef divisor
$\Lambda ,c$
and p. The b-nef divisor
![]() $q\mathbf {N}$
is b-Cartier. The variety X is rationally connected, as we are assuming that the b-nef divisor
$q\mathbf {N}$
is b-Cartier. The variety X is rationally connected, as we are assuming that the b-nef divisor
![]() $\mathbf {M}$
is nontrivial. Hence, Z is also rationally connected. Let
$\mathbf {M}$
is nontrivial. Hence, Z is also rationally connected. Let
![]() $Z'\rightarrow Z$
be the model where
$Z'\rightarrow Z$
be the model where
![]() ${\mathbf {N}_{Z}}$
descends. In particular,
${\mathbf {N}_{Z}}$
descends. In particular,
![]() $Z'$
is rationally connected. Note that in general,
$Z'$
is rationally connected. Note that in general,
![]() ${\mathbf {N}_{Z'}}$
may have torsion components. However, since
${\mathbf {N}_{Z'}}$
may have torsion components. However, since
![]() $Z'$
is rationally connected, the q-th multiple of such torsion components are linearly equivalent to zero (see [Reference Filipazzi, Mauri and Moraga13, Corollary 3.9]). Using Conjecture 1, we will show that the index of
$Z'$
is rationally connected, the q-th multiple of such torsion components are linearly equivalent to zero (see [Reference Filipazzi, Mauri and Moraga13, Corollary 3.9]). Using Conjecture 1, we will show that the index of
![]() $K_Z+B_Z+{\mathbf {N}_{Z}}$
only depends on
$K_Z+B_Z+{\mathbf {N}_{Z}}$
only depends on
![]() $\Lambda ,c$
and p. Thus, by the linear equivalence (1.1), we conclude that the index of
$\Lambda ,c$
and p. Thus, by the linear equivalence (1.1), we conclude that the index of
![]() $(X,B,\mathbf {M})$
is bounded above by a constant
$(X,B,\mathbf {M})$
is bounded above by a constant
![]() $I_0(\Lambda ,c,p)$
.
$I_0(\Lambda ,c,p)$
.
Case 3: the divisor
![]() $\{B\}+{\mathbf {M}_{X}}$
is nontrivial on the general fiber of
$\{B\}+{\mathbf {M}_{X}}$
is nontrivial on the general fiber of
![]() $X\rightarrow Z$
and the b-nef divisor
$X\rightarrow Z$
and the b-nef divisor
![]() $\mathbf {M}$
is nontrivial.
$\mathbf {M}$
is nontrivial.
We run a
![]() $(K_X+\lfloor B\rfloor )$
-MMP over Z. Since
$(K_X+\lfloor B\rfloor )$
-MMP over Z. Since
![]() $K_X+\lfloor B\rfloor $
is not pseudo-effective over Z, this minimal model program terminates with a Mori fiber space
$K_X+\lfloor B\rfloor $
is not pseudo-effective over Z, this minimal model program terminates with a Mori fiber space
![]() $p\colon X'\rightarrow W$
over Z. We denote by
$p\colon X'\rightarrow W$
over Z. We denote by
![]() $B'$
the push-forward of B on
$B'$
the push-forward of B on
![]() $X'$
. the divisor
$X'$
. the divisor
![]() $K_{X'}+\lfloor B'\rfloor $
is antiample over W. Since
$K_{X'}+\lfloor B'\rfloor $
is antiample over W. Since
![]() $\lfloor B\rfloor $
is big over Z, the divisor
$\lfloor B\rfloor $
is big over Z, the divisor
![]() $\lfloor B'\rfloor $
has a component S that dominates W. By construction, the general fibers of
$\lfloor B'\rfloor $
has a component S that dominates W. By construction, the general fibers of
![]() $S\rightarrow W$
are of Fano type. In this case, X and
$S\rightarrow W$
are of Fano type. In this case, X and
![]() $X'$
are rationally connected, as we are assuming that the b-nef divisor
$X'$
are rationally connected, as we are assuming that the b-nef divisor
![]() $\mathbf {M}$
is nontrivial. Hence, the image W of
$\mathbf {M}$
is nontrivial. Hence, the image W of
![]() $X'$
is rationally connected. Since a general fiber of
$X'$
is rationally connected. Since a general fiber of
![]() $S\rightarrow W$
is of Fano type, they are rationally connected. Thus, S is rationally connected, being the base and general fibers of
$S\rightarrow W$
is of Fano type, they are rationally connected. Thus, S is rationally connected, being the base and general fibers of
![]() $S\rightarrow W$
rationally connected. In particular, if
$S\rightarrow W$
rationally connected. In particular, if
![]() $(S,B_S+{\mathbf {M}_{S}})$
is the generalized pair obtained by adjunction, then we know that
$(S,B_S+{\mathbf {M}_{S}})$
is the generalized pair obtained by adjunction, then we know that
![]() $I(\Lambda ,d-1,c,p)(K_S+B_S+{\mathbf {M}_{S}})\sim 0$
. Here, we argued by induction on the dimension and used Theorem 6
$I(\Lambda ,d-1,c,p)(K_S+B_S+{\mathbf {M}_{S}})\sim 0$
. Here, we argued by induction on the dimension and used Theorem 6
![]() $(d-1,c)$
. Depending on the dimension of W, we either use Kawamata–Viehweg vanishing or Kollár’s torsion-free theorem to conclude that
$(d-1,c)$
. Depending on the dimension of W, we either use Kawamata–Viehweg vanishing or Kollár’s torsion-free theorem to conclude that
![]() $I(\Lambda ,d-1,c,p)(K_{X'}+B'+{\mathbf {M}_{X'}})\sim 0$
. Hence, the index of
$I(\Lambda ,d-1,c,p)(K_{X'}+B'+{\mathbf {M}_{X'}})\sim 0$
. Hence, the index of
![]() $(X,B,\mathbf {M})$
is at most
$(X,B,\mathbf {M})$
is at most
![]() $I(\Lambda ,d-1,c,p)$
. These lifting arguments are explained in § 5.1.
$I(\Lambda ,d-1,c,p)$
. These lifting arguments are explained in § 5.1.
In summary, a generalized log Calabi–Yau pair
![]() $(X,B,\mathbf {M})$
as in Theorem 6
$(X,B,\mathbf {M})$
as in Theorem 6
![]() $(d,c)$
has index at most
$(d,c)$
has index at most
Thus, we have that
Hence, there is an upper bound for
![]() $I(\Lambda ,d,c,p)$
which only depends on
$I(\Lambda ,d,c,p)$
which only depends on
![]() $\Lambda ,c$
and p. This finishes the sketch of the proof of Theorem 6
$\Lambda ,c$
and p. This finishes the sketch of the proof of Theorem 6
![]() $(c)$
using Theorem 8
$(c)$
using Theorem 8
![]() $(c)$
.
$(c)$
.
Complements on Fano varieties
Let
![]() $(X,B,\mathbf {M})$
be a Fano type pair as in Theorem 7
$(X,B,\mathbf {M})$
be a Fano type pair as in Theorem 7
![]() $(d,c)$
. In § 3, we reduce to the case in which
$(d,c)$
. In § 3, we reduce to the case in which
![]() $\Lambda $
finite. This is crucial for lifting complements from divisors (see § 5.1). By the assumption on the absolute coregularity of
$\Lambda $
finite. This is crucial for lifting complements from divisors (see § 5.1). By the assumption on the absolute coregularity of
![]() $(X,B,\mathbf {M})$
, we may find a generalized log Calabi–Yau structure
$(X,B,\mathbf {M})$
, we may find a generalized log Calabi–Yau structure
![]() $(X,B+\Gamma ,\mathbf {M})$
of coregularity c. By dimensional reasons and the assumption on the absolute coregularity of
$(X,B+\Gamma ,\mathbf {M})$
of coregularity c. By dimensional reasons and the assumption on the absolute coregularity of
![]() $(X,B,\mathbf {M})$
,
$(X,B,\mathbf {M})$
,
![]() $(X,B+\Gamma ,\mathbf {M})$
may be generalized klt only if
$(X,B+\Gamma ,\mathbf {M})$
may be generalized klt only if
![]() $d = c$
and
$d = c$
and
![]() $(X,B,\mathbf {M})$
is exceptional; this case is settled by [Reference Birkar3, Theorem 1.7] in dimension c. Therefore, in the rest of this sketch, we may assume that
$(X,B,\mathbf {M})$
is exceptional; this case is settled by [Reference Birkar3, Theorem 1.7] in dimension c. Therefore, in the rest of this sketch, we may assume that
![]() $(X,B+\Gamma ,\mathbf {M})$
is not generalized klt. Let
$(X,B+\Gamma ,\mathbf {M})$
is not generalized klt. Let
![]() $(Y,B_Y+\Gamma _Y+E,\mathbf {M})$
be a dlt modification of
$(Y,B_Y+\Gamma _Y+E,\mathbf {M})$
be a dlt modification of
![]() $(X,B+\Gamma ,\mathbf {M})$
. Here,
$(X,B+\Gamma ,\mathbf {M})$
. Here,
![]() $B_Y$
(resp.
$B_Y$
(resp.
![]() $\Gamma _Y$
) is the strict transform of the fractional part of B (resp.
$\Gamma _Y$
) is the strict transform of the fractional part of B (resp.
![]() $\Gamma $
), while we set
$\Gamma $
), while we set
![]() $E=\lfloor B_Y+\Gamma _Y+E \rfloor $
. Since
$E=\lfloor B_Y+\Gamma _Y+E \rfloor $
. Since
![]() $(X,B+\Gamma ,\mathbf {M})$
is not generalized klt, we have
$(X,B+\Gamma ,\mathbf {M})$
is not generalized klt, we have
![]() $E \neq 0$
. Since X is of Fano type, it easily follows that so is Y. In particular, Y is a Mori dream space. We run a
$E \neq 0$
. Since X is of Fano type, it easily follows that so is Y. In particular, Y is a Mori dream space. We run a
![]() $-(K_Y+B_Y+E+{\mathbf {M}_{Y}})$
-MMP. Note that
$-(K_Y+B_Y+E+{\mathbf {M}_{Y}})$
-MMP. Note that
![]() $-(K_Y+B_Y+E+{\mathbf {M}_{Y}})$
is a pseudo-effective divisor. Hence, this minimal model program must terminate with a good minimal model Z. We let
$-(K_Y+B_Y+E+{\mathbf {M}_{Y}})$
is a pseudo-effective divisor. Hence, this minimal model program must terminate with a good minimal model Z. We let
![]() $B_Z$
and
$B_Z$
and
![]() $E_Z$
be the push-forwards to Z of
$E_Z$
be the push-forwards to Z of
![]() $B_Y$
and E, respectively. In order to produce a complement for
$B_Y$
and E, respectively. In order to produce a complement for
![]() $(X,B)$
, it suffices to produce a complement for
$(X,B)$
, it suffices to produce a complement for
![]() $(Z,B_Z+E_Z,{\mathbf {M}_{Z}})$
. Replacing
$(Z,B_Z+E_Z,{\mathbf {M}_{Z}})$
. Replacing
![]() $(X,B,\mathbf {M})$
by
$(X,B,\mathbf {M})$
by
![]() $(Z,B_Z+E_Z,{\mathbf {M}_{Z}})$
, we may assume that
$(Z,B_Z+E_Z,{\mathbf {M}_{Z}})$
, we may assume that
![]() $-(K_X+B+{\mathbf {M}_{X}})$
is semiample and
$-(K_X+B+{\mathbf {M}_{X}})$
is semiample and
![]() $\mathrm {coreg}(X,B,\mathbf {M})=c$
. Notice that this reduction does not alter the coefficients set for the boundary part of
$\mathrm {coreg}(X,B,\mathbf {M})=c$
. Notice that this reduction does not alter the coefficients set for the boundary part of
![]() $(X,B,\mathbf {M})$
, since the only divisors that may have been introduced in the boundary have coefficient 1. Furthermore, by the choice of the MMP run, it follows that E cannot be contracted. In particular, after this reduction, we may assume that
$(X,B,\mathbf {M})$
, since the only divisors that may have been introduced in the boundary have coefficient 1. Furthermore, by the choice of the MMP run, it follows that E cannot be contracted. In particular, after this reduction, we may assume that
![]() $\lfloor B \rfloor \neq 0$
. We will proceed in three different cases depending on the dimension of the ample model W of the divisor
$\lfloor B \rfloor \neq 0$
. We will proceed in three different cases depending on the dimension of the ample model W of the divisor
![]() $-(K_X+B+{\mathbf {M}_{X}})$
.
$-(K_X+B+{\mathbf {M}_{X}})$
.
Case 1: the dimension of W is
![]() $0$
.
$0$
.
In this case, we have that
![]() $K_X+B+{\mathbf {M}_{X}}\sim _{\mathbb {Q}} 0$
. Hence, producing a complement for
$K_X+B+{\mathbf {M}_{X}}\sim _{\mathbb {Q}} 0$
. Hence, producing a complement for
![]() $(X,B,\mathbf {M})$
is the same as controlling the index of the generalized pair. Thus, the statement follows from Theorem 6
$(X,B,\mathbf {M})$
is the same as controlling the index of the generalized pair. Thus, the statement follows from Theorem 6
![]() $(c)$
.
$(c)$
.
Case 2: the dimension of W is d.
In this case, we have that
![]() $-(K_X+B+{\mathbf {M}_{X}})$
is semiample and big. Furthermore, the round-down
$-(K_X+B+{\mathbf {M}_{X}})$
is semiample and big. Furthermore, the round-down
![]() $\lfloor B\rfloor $
is nontrivial. We pass to a suitable birational model of
$\lfloor B\rfloor $
is nontrivial. We pass to a suitable birational model of
![]() $(X,B,\mathbf {M})$
where a component S of
$(X,B,\mathbf {M})$
where a component S of
![]() $\lfloor B\rfloor $
is of Fano type. Performing adjunction to S, we obtain a log Fano pair of dimension
$\lfloor B\rfloor $
is of Fano type. Performing adjunction to S, we obtain a log Fano pair of dimension
![]() $d-1$
and coregularity c. Using Theorem 7
$d-1$
and coregularity c. Using Theorem 7
![]() $(d-1,c)$
, we produce an
$(d-1,c)$
, we produce an
![]() $N(\Lambda ,d-1,c,p)$
-complement on S that can be lifted to an
$N(\Lambda ,d-1,c,p)$
-complement on S that can be lifted to an
![]() $N(\Lambda ,d-1,c,p)$
-complement of
$N(\Lambda ,d-1,c,p)$
-complement of
![]() $(X,B)$
.
$(X,B)$
.
Case 3: The dimension of W is positive and strictly less than d.
The fibration
![]() $\pi \colon (X,B,\mathbf {M})\rightarrow W$
is a log Calabi–Yau fibration for
$\pi \colon (X,B,\mathbf {M})\rightarrow W$
is a log Calabi–Yau fibration for
![]() $(X,B,\mathbf {M})$
. If
$(X,B,\mathbf {M})$
. If
![]() $\{B\}+\mathbf {M}$
is big over W, then by perturbing the coefficients of B we reduce to Case 2. Otherwise, we may replace W with the ample model of
$\{B\}+\mathbf {M}$
is big over W, then by perturbing the coefficients of B we reduce to Case 2. Otherwise, we may replace W with the ample model of
![]() $\{B\}+\mathbf {M}$
over W. Doing so, we may assume
$\{B\}+\mathbf {M}$
over W. Doing so, we may assume
![]() $\{B\}+\mathbf {M}$
is trivial on the general fiber of
$\{B\}+\mathbf {M}$
is trivial on the general fiber of
![]() $X\rightarrow W$
. If all the generalized log canonical centers of
$X\rightarrow W$
. If all the generalized log canonical centers of
![]() $(X,B)$
dominate W, then we are in the situation of Theorem 8
$(X,B)$
dominate W, then we are in the situation of Theorem 8
![]() $(c)$
. The generalized pair
$(c)$
. The generalized pair
![]() $(W,B_W,{\mathbf {N}_{W}})$
induced on the base is of Fano type and exceptional. By [Reference Birkar3, Theorem 1.7] in dimension c or less, we can find an
$(W,B_W,{\mathbf {N}_{W}})$
induced on the base is of Fano type and exceptional. By [Reference Birkar3, Theorem 1.7] in dimension c or less, we can find an
![]() $N(\Omega ,c)$
-complement for
$N(\Omega ,c)$
-complement for
![]() $(W,B_W,{\mathbf {N}_{W}})$
. Here,
$(W,B_W,{\mathbf {N}_{W}})$
. Here,
![]() $\Omega $
only depends on
$\Omega $
only depends on
![]() $\Lambda ,c$
and p. Then, we can pull the complement back via
$\Lambda ,c$
and p. Then, we can pull the complement back via
![]() $\pi $
to obtain an
$\pi $
to obtain an
![]() $N(\Omega ,c)$
-complement for
$N(\Omega ,c)$
-complement for
![]() $(X,B,\mathbf {M})$
. Finally, we may assume that
$(X,B,\mathbf {M})$
. Finally, we may assume that
![]() $\{B\}+\mathbf {M}$
is trivial on the general fiber of
$\{B\}+\mathbf {M}$
is trivial on the general fiber of
![]() $X\rightarrow W$
and there is some component
$X\rightarrow W$
and there is some component
![]() $S\subset \lfloor B\rfloor $
that is vertical over W. In this case,
$S\subset \lfloor B\rfloor $
that is vertical over W. In this case,
![]() $B_{\mathrm {hor}}$
is big over W. Here,
$B_{\mathrm {hor}}$
is big over W. Here,
![]() $B_{\mathrm {hor}}$
stands for the sum of the components of B which are horizontal over W. Again, we can perturb the coefficients of B to reduce to Case 2.
$B_{\mathrm {hor}}$
stands for the sum of the components of B which are horizontal over W. Again, we can perturb the coefficients of B to reduce to Case 2.
In summary, a generalized pair
![]() $(X,B,\mathbf {M})$
as in Theorem 7
$(X,B,\mathbf {M})$
as in Theorem 7
![]() $(d,c)$
admits an N-complement, where
$(d,c)$
admits an N-complement, where
![]() $N\leq \max \{N(\Omega ,c),N(\Lambda ,d-1,c,p)\}$
. Thus, we have
$N\leq \max \{N(\Omega ,c),N(\Lambda ,d-1,c,p)\}$
. Thus, we have
Hence, there is an upper bound for
![]() $N(\Lambda ,d,c,p)$
which only depends on
$N(\Lambda ,d,c,p)$
which only depends on
![]() $\Lambda ,c$
and p. This finishes the proof of Theorem 7
$\Lambda ,c$
and p. This finishes the proof of Theorem 7
![]() $(c)$
using Theorem 6
$(c)$
using Theorem 6
![]() $(c)$
and Theorem 8
$(c)$
and Theorem 8
![]() $(c)$
.
$(c)$
.
2 Preliminaries
We work over an algebraically closed field
![]() $\mathbb {K}$
of characteristic zero. Our varieties are connected and quasi-projective unless otherwise stated. In this section, we introduce some preliminaries regarding singularities, Fano varieties, Calabi–Yau pairs and coregularity.
$\mathbb {K}$
of characteristic zero. Our varieties are connected and quasi-projective unless otherwise stated. In this section, we introduce some preliminaries regarding singularities, Fano varieties, Calabi–Yau pairs and coregularity.
2.1 Divisors, b-divisors and generalized pairs
In this subsection, we recall some basics about b-divisors and generalized pairs.
Definition 2.1. Let X be a normal variety. A b-divisor
![]() $\mathbf {M}$
on X is a function which associates any birational map
$\mathbf {M}$
on X is a function which associates any birational map
![]() $X'\dashrightarrow X$
with an
$X'\dashrightarrow X$
with an
![]() $\mathbb {R}$
-divisor
$\mathbb {R}$
-divisor
![]() ${\mathbf {M}_{X'}}$
on
${\mathbf {M}_{X'}}$
on
![]() $X'$
. The set of divisors
$X'$
. The set of divisors
![]() $\{{\mathbf {M}_{X'}} \colon X'\dashrightarrow X\}$
satisfies the following compatibility condition: If
$\{{\mathbf {M}_{X'}} \colon X'\dashrightarrow X\}$
satisfies the following compatibility condition: If
![]() $g \colon X_1\to X_2$
is a birational morphism over X, then
$g \colon X_1\to X_2$
is a birational morphism over X, then
![]() $g_*{\mathbf {M}_{X_1}} = {\mathbf {M}_{X_2}}$
. We say that a b-divisor
$g_*{\mathbf {M}_{X_1}} = {\mathbf {M}_{X_2}}$
. We say that a b-divisor
![]() $\mathbf {M}$
on X descends on some birational model
$\mathbf {M}$
on X descends on some birational model
![]() $X'$
of X if
$X'$
of X if
![]() ${\mathbf {M}_{X'}}$
is
${\mathbf {M}_{X'}}$
is
![]() $\mathbb {R}$
-Cartier and
$\mathbb {R}$
-Cartier and
![]() $\mathbf {M}$
is equivalent to
$\mathbf {M}$
is equivalent to
![]() $( X'\to X, {\mathbf {M}_{X'}})$
. In other words, for any birational map
$( X'\to X, {\mathbf {M}_{X'}})$
. In other words, for any birational map
![]() $h \colon Y\to X'$
over X, we have
$h \colon Y\to X'$
over X, we have
![]() $h^*{\mathbf {M}_{X'}} = {\mathbf {M}_{Y}}$
. In the previous case, we say that
$h^*{\mathbf {M}_{X'}} = {\mathbf {M}_{Y}}$
. In the previous case, we say that
![]() $\mathbf {M}$
is a b-
$\mathbf {M}$
is a b-
![]() $\mathbb {R}$
-Cartier divisor.
$\mathbb {R}$
-Cartier divisor.
Let
![]() $X\to Z$
be a projective morphism. The b-divisor
$X\to Z$
be a projective morphism. The b-divisor
![]() $\mathbf {M}$
is said to be b-Cartier (resp. b-nef, b-nef/ Z) if
$\mathbf {M}$
is said to be b-Cartier (resp. b-nef, b-nef/ Z) if
![]() ${\mathbf {M}_{X'}}$
is Cartier (resp. nef, relatively nef over Z) on some birational model
${\mathbf {M}_{X'}}$
is Cartier (resp. nef, relatively nef over Z) on some birational model
![]() $X'$
over X where
$X'$
over X where
![]() $\mathbf {M}$
descends.
$\mathbf {M}$
descends.
The b-Cartier closure of an
![]() $\mathbb {R}$
-Cartier divisor M is a b-divisor
$\mathbb {R}$
-Cartier divisor M is a b-divisor
![]() $\mathbf {M}$
whose trace on every birational model
$\mathbf {M}$
whose trace on every birational model
![]() $f:Y\rightarrow X$
is
$f:Y\rightarrow X$
is
![]() $f^*M$
.
$f^*M$
.
Definition 2.2. Let X be a normal variety and
![]() $\pi \colon X\to Z$
be a projective morphism. A generalized pair on X over Z is a triple
$\pi \colon X\to Z$
be a projective morphism. A generalized pair on X over Z is a triple
![]() $(X,B,\mathbf {M})$
where
$(X,B,\mathbf {M})$
where
-
• B is an effective
 $\mathbb {R}$
-divisor on X;
$\mathbb {R}$
-divisor on X; -
•
 $\mathbf {M}$
is a b-nef/Z b-
$\mathbf {M}$
is a b-nef/Z b-
 $\mathbb {R}$
-Cartier on X; and
$\mathbb {R}$
-Cartier on X; and -
•
 $K_X+B+{\mathbf {M}_{X}}$
is
$K_X+B+{\mathbf {M}_{X}}$
is
 $\mathbb {R}$
-Cartier.
$\mathbb {R}$
-Cartier.
When Z is a point, we simply call
![]() $(X,B,\mathbf {M})$
a generalized pair.
$(X,B,\mathbf {M})$
a generalized pair.
2.2 Singularities of generalized pairs
In this subsection, we define the notions of singularities for generalized pairs.
Definition 2.3. Let X be a normal variety and
![]() $(X,B,\mathbf {M})$
be a generalized pair on X. Let D be a divisor over X. Pick a log resolution
$(X,B,\mathbf {M})$
be a generalized pair on X. Let D be a divisor over X. Pick a log resolution
![]() $f \colon X'\to X$
of
$f \colon X'\to X$
of
![]() $(X,B)$
such that D is a divisor on
$(X,B)$
such that D is a divisor on
![]() $X'$
and
$X'$
and
![]() $\mathbf {M}$
descends on
$\mathbf {M}$
descends on
![]() $X'$
. We can write
$X'$
. We can write
for some uniquely determined
![]() $B'$
. Define the generalized log discrepancy
$B'$
. Define the generalized log discrepancy
![]() $a_D(X,B,\mathbf {M})$
to be
$a_D(X,B,\mathbf {M})$
to be
![]() $1-\operatorname {\mathrm {coeff}}_D (B')$
.
$1-\operatorname {\mathrm {coeff}}_D (B')$
.
We say that
![]() $(X,B,\mathbf {M})$
is generalized log canonical (resp. generalized klt) if
$(X,B,\mathbf {M})$
is generalized log canonical (resp. generalized klt) if
![]() $a_D(X,B,\mathbf {M})$
is nonnegative (resp. positive) for any divisor D over X. A generalized non-klt place (resp. generalized log canonical place) of
$a_D(X,B,\mathbf {M})$
is nonnegative (resp. positive) for any divisor D over X. A generalized non-klt place (resp. generalized log canonical place) of
![]() $(X,B,\mathbf {M})$
is a prime divisor D over X with
$(X,B,\mathbf {M})$
is a prime divisor D over X with
![]() $a_D(X,B,\mathbf {M})\leq 0$
(resp.
$a_D(X,B,\mathbf {M})\leq 0$
(resp.
![]() $a_D(X,B,\mathbf {M})=0$
). A generalized non-klt center of
$a_D(X,B,\mathbf {M})=0$
). A generalized non-klt center of
![]() $(X,B,\mathbf {M})$
is the image of a generalized non-klt place. We denote the set of generalized non-klt centers of
$(X,B,\mathbf {M})$
is the image of a generalized non-klt place. We denote the set of generalized non-klt centers of
![]() $(X,B,\mathbf {M})$
by
$(X,B,\mathbf {M})$
by
![]() $\mathrm {Nklt}(X,B,\mathbf {M})$
. A generalized log canonical center of
$\mathrm {Nklt}(X,B,\mathbf {M})$
. A generalized log canonical center of
![]() $(X,B,\mathbf {M})$
is the image Z of a generalized non-klt place such that every generalized non-klt place whose image on X contains Z is a generalized log canonical place.
$(X,B,\mathbf {M})$
is the image Z of a generalized non-klt place such that every generalized non-klt place whose image on X contains Z is a generalized log canonical place.
We say that
![]() $(X,B,\mathbf {M})$
is generalized dlt if it is generalized log canonical and satisfies the following condition: for any generalized log canonical center V of
$(X,B,\mathbf {M})$
is generalized dlt if it is generalized log canonical and satisfies the following condition: for any generalized log canonical center V of
![]() $(X,B,\mathbf {M})$
, the pair
$(X,B,\mathbf {M})$
, the pair
![]() $(X,B)$
is log smooth around the generic point of V and
$(X,B)$
is log smooth around the generic point of V and
![]() $\mathbf {M}$
descends on X in a neighborhood of the generic point of V. We say that
$\mathbf {M}$
descends on X in a neighborhood of the generic point of V. We say that
![]() $(X,B,\mathbf {M})$
is generalized plt if it is generalized dlt and every connected component of
$(X,B,\mathbf {M})$
is generalized plt if it is generalized dlt and every connected component of
![]() $\lfloor B\rfloor $
is irreducible.
$\lfloor B\rfloor $
is irreducible.
Let
![]() $(X,B,\mathbf {M})$
be a generalized log canonical pair over a base Z. Let
$(X,B,\mathbf {M})$
be a generalized log canonical pair over a base Z. Let
![]() $f \colon Y\to X$
be a birational morphism and write
$f \colon Y\to X$
be a birational morphism and write
We say that
![]() $(Y,B_Y,\mathbf {M})$
is a
$(Y,B_Y,\mathbf {M})$
is a
![]() $\mathbb {Q}$
-factorial generalized dlt modification of
$\mathbb {Q}$
-factorial generalized dlt modification of
![]() $(X,B,\mathbf {M})$
if the variety Y is
$(X,B,\mathbf {M})$
if the variety Y is
![]() $\mathbb {Q}$
-factorial,
$\mathbb {Q}$
-factorial,
![]() $(Y,B_Y,\mathbf {M})$
is generalized dlt and every f-exceptional divisor appears in
$(Y,B_Y,\mathbf {M})$
is generalized dlt and every f-exceptional divisor appears in
![]() $B_Y$
with coefficient 1.
$B_Y$
with coefficient 1.
Lemma 2.4 [Reference Filipazzi and Svaldi16, Theorem 2.9].
Every generalized log canonical pair over a base Z has a
![]() $\mathbb {Q}$
-factorial generalized dlt modification.
$\mathbb {Q}$
-factorial generalized dlt modification.
The following lemma states that the singularities of the pair
![]() $(X,B)$
are milder than the singularities of
$(X,B)$
are milder than the singularities of
![]() $(X,B,\mathbf {M})$
.
$(X,B,\mathbf {M})$
.
Lemma 2.5 [Reference Birkar and Zhang7, Remark 4.2.(3)].
Let
![]() $(X,B,\mathbf {M})$
be a generalized log canonical pair over Z. Suppose
$(X,B,\mathbf {M})$
be a generalized log canonical pair over Z. Suppose
![]() $K_X+B$
is
$K_X+B$
is
![]() $\mathbb {R}$
-Cartier. Then for any divisor D over X, the log discrepancies satisfy
$\mathbb {R}$
-Cartier. Then for any divisor D over X, the log discrepancies satisfy
In particular, the pair
![]() $(X,B)$
is log canonical.
$(X,B)$
is log canonical.
2.3 Crepant birational maps
In this subsection, we recall the notion of crepant birational map and group of crepant birational automorphisms.
Definition 2.6. Let
![]() $(X_1,B_1,\mathbf {M})$
and
$(X_1,B_1,\mathbf {M})$
and
![]() $(X_2,B_2,\mathbf {M})$
be generalized pairs over Z. We say that they are crepant if there exists a common resolution
$(X_2,B_2,\mathbf {M})$
be generalized pairs over Z. We say that they are crepant if there exists a common resolution
![]() $\alpha _1 \colon X' \rightarrow X_1$
and
$\alpha _1 \colon X' \rightarrow X_1$
and
![]() $\alpha _2 \colon X' \rightarrow X_2$
, where each
$\alpha _2 \colon X' \rightarrow X_2$
, where each
![]() $\alpha _i$
is proper, such that
$\alpha _i$
is proper, such that
holds, where we have
![]() ${K_{X'}} + B^{\prime }_i + {\mathbf {M}_{X'}}= \alpha _i^*({K_{X_i}} + B_i + {\mathbf {M}_{X_i}})$
for
${K_{X'}} + B^{\prime }_i + {\mathbf {M}_{X'}}= \alpha _i^*({K_{X_i}} + B_i + {\mathbf {M}_{X_i}})$
for
![]() $i=1,2$
.
$i=1,2$
.
In the case of pairs, we recall the notion of B-birational map, originally due to Fujino [Reference Fujino17, Definition 1.5]. Observe that, for our purposes in later sections, it is important to deal with possibly reducible varieties.
Definition 2.7. Let
![]() $(X,\Delta ) = \sqcup (X_i,\Delta _i)$
and
$(X,\Delta ) = \sqcup (X_i,\Delta _i)$
and
![]() $(X',\Delta ') = \sqcup (X^{\prime }_i,\Delta ^{\prime }_i)$
be possibly reducible normal pairs. We say that
$(X',\Delta ') = \sqcup (X^{\prime }_i,\Delta ^{\prime }_i)$
be possibly reducible normal pairs. We say that
![]() $f \colon X \dashrightarrow X'$
is a B-birational map if
$f \colon X \dashrightarrow X'$
is a B-birational map if
![]() $(X,\Delta )$
and
$(X,\Delta )$
and
![]() $(X',\Delta ')$
are crepant. That is, X and
$(X',\Delta ')$
are crepant. That is, X and
![]() $X'$
have the same number of irreducible components, and there exists a permutation
$X'$
have the same number of irreducible components, and there exists a permutation
![]() $\sigma $
of the index set of the irreducible component such that, for every i, the restriction
$\sigma $
of the index set of the irreducible component such that, for every i, the restriction
![]() $f_i \colon X_i \dashrightarrow X^{\prime }_{\sigma (i)}$
is birational and
$f_i \colon X_i \dashrightarrow X^{\prime }_{\sigma (i)}$
is birational and
![]() $(X_i,\Delta _i)$
is crepant to
$(X_i,\Delta _i)$
is crepant to
![]() $(X^{\prime }_{\sigma (i)},\Delta ^{\prime }_{\sigma (i)})$
.
$(X^{\prime }_{\sigma (i)},\Delta ^{\prime }_{\sigma (i)})$
.
Definition 2.8. Given a pair
![]() $(X,\Delta )=\sqcup (X_i,\Delta _i)$
as in Definition 2.7, we define
$(X,\Delta )=\sqcup (X_i,\Delta _i)$
as in Definition 2.7, we define
The set
![]() $\mathrm {Bir}(X,\Delta )$
forms a group under composition.
$\mathrm {Bir}(X,\Delta )$
forms a group under composition.
We observe that Definition 2.7 and Definition 2.8 naturally extend to the case of generalized pairs.
2.4 Complements
In this subsection, we introduce the notion of relative complements.
Definition 2.9. A contraction is a projective morphism of quasi-projective varieties
![]() $f \colon X \rightarrow Z$
such that
$f \colon X \rightarrow Z$
such that
![]() $f_* {\mathcal {O}_{X}}={\mathcal {O}_{Z}}$
. Notice that, if X is normal, then so is Z. A fibration is a contraction
$f_* {\mathcal {O}_{X}}={\mathcal {O}_{Z}}$
. Notice that, if X is normal, then so is Z. A fibration is a contraction
![]() $X \rightarrow Z$
such that
$X \rightarrow Z$
such that
![]() $\dim Z < \dim X$
.
$\dim Z < \dim X$
.
Definition 2.10. Let
![]() $(X,B)$
be a pair and
$(X,B)$
be a pair and
![]() $X\to Z$
a contraction. We say that a pair
$X\to Z$
a contraction. We say that a pair
![]() $(X,B)$
is log Fano (resp. weak log Fano or log Calabi–Yau) over Z if it is log canonical and
$(X,B)$
is log Fano (resp. weak log Fano or log Calabi–Yau) over Z if it is log canonical and
![]() $-(K_X+B)$
is ample over Z (resp.
$-(K_X+B)$
is ample over Z (resp.
![]() $-(K_X+B)$
is nef and big over Z or
$-(K_X+B)$
is nef and big over Z or
![]() $K_X+B$
is
$K_X+B$
is
![]() $\mathbb {R}$
-trivial over Z).
$\mathbb {R}$
-trivial over Z).
We say that
![]() $(X,B)$
is of Fano type (resp. log Calabi–Yau type) over Z if
$(X,B)$
is of Fano type (resp. log Calabi–Yau type) over Z if
![]() $(X,B+\Delta )$
is klt and weak log Fano (resp. log Calabi–Yau) for some choice of
$(X,B+\Delta )$
is klt and weak log Fano (resp. log Calabi–Yau) for some choice of
![]() $\Delta \geq 0$
.
$\Delta \geq 0$
.
If
![]() $(X,0)$
is of Fano type (resp. log Calabi–Yau type) over Z, we say that
$(X,0)$
is of Fano type (resp. log Calabi–Yau type) over Z, we say that
![]() $X\to Z$
is a Fano type morphism (resp. log Calabi–Yau type morphism). If
$X\to Z$
is a Fano type morphism (resp. log Calabi–Yau type morphism). If
![]() $(X,B)$
is log Fano (resp. log Calabi–Yau, Fano type, Calabi–Yau type) over a point, we simply say that
$(X,B)$
is log Fano (resp. log Calabi–Yau, Fano type, Calabi–Yau type) over a point, we simply say that
![]() $(X,B)$
is log Fano (resp. log Calabi–Yau, Fano type, Calabi–Yau type).
$(X,B)$
is log Fano (resp. log Calabi–Yau, Fano type, Calabi–Yau type).
Definition 2.11. Let
![]() $X\to Z$
be a contraction and
$X\to Z$
be a contraction and
![]() $(X,B,\mathbf {M})$
be a generalized pair over Z. Let N be a positive integer. An N-complement of
$(X,B,\mathbf {M})$
be a generalized pair over Z. Let N be a positive integer. An N-complement of
![]() $K_X+B+{\mathbf {M}_{X}}$
over a point
$K_X+B+{\mathbf {M}_{X}}$
over a point
![]() $z\in Z$
is a divisor
$z\in Z$
is a divisor
![]() $K_X+B^++{\mathbf {M}_{X}}$
such that over some neighborhood of z, we have:
$K_X+B^++{\mathbf {M}_{X}}$
such that over some neighborhood of z, we have:
-
•
 $(X,B^+,\mathbf {M})$
is generalized log canonical;
$(X,B^+,\mathbf {M})$
is generalized log canonical; -
•
 $N(K_X+B^++{\mathbf {M}_{X}})\sim _Z 0$
;
$N(K_X+B^++{\mathbf {M}_{X}})\sim _Z 0$
; -
•
 $N\mathbf {M}$
is b-Cartier; and
$N\mathbf {M}$
is b-Cartier; and -
•
 $B^+\geq B$
.
$B^+\geq B$
.
If the above conditions hold for
![]() $K_X+B^++{\mathbf {M}_{X}}$
over every
$K_X+B^++{\mathbf {M}_{X}}$
over every
![]() $z\in Z$
, we say that
$z\in Z$
, we say that
![]() $K_X+B^++{\mathbf {M}_{X}}$
is an N-complement of
$K_X+B^++{\mathbf {M}_{X}}$
is an N-complement of
![]() $K_X+B+{\mathbf {M}_{X}}$
over Z. We say that
$K_X+B+{\mathbf {M}_{X}}$
over Z. We say that
![]() $K_X+B^+ + {\mathbf {M}_{X}}$
is a
$K_X+B^+ + {\mathbf {M}_{X}}$
is a
![]() $\mathbb {Q}$
-complement of
$\mathbb {Q}$
-complement of
![]() $K_X+B+{\mathbf {M}_{X}}$
over
$K_X+B+{\mathbf {M}_{X}}$
over
![]() $z\in Z$
(resp.
$z\in Z$
(resp.
![]() $\mathbb {Q}$
-complement of
$\mathbb {Q}$
-complement of
![]() $K_X+B+{\mathbf {M}_{X}}$
over Z) it is a q-complement for some
$K_X+B+{\mathbf {M}_{X}}$
over Z) it is a q-complement for some
![]() $q\in \mathbb {Z}_{>0}$
.
$q\in \mathbb {Z}_{>0}$
.
The following lemma states that complements can be pulled back via
![]() $K_X$
-positive birational contractions (see [Reference Birkar3, 6.1.(3)]).
$K_X$
-positive birational contractions (see [Reference Birkar3, 6.1.(3)]).
Lemma 2.12. Let
![]() $(X,B,\mathbf {M})$
be a generalized log canonical pair over a base Z. Suppose
$(X,B,\mathbf {M})$
be a generalized log canonical pair over a base Z. Suppose
![]() $f \colon X\dashrightarrow X'$
is a
$f \colon X\dashrightarrow X'$
is a
![]() $(K_X+B+{\mathbf {M}_{X}})$
-nonnegative birational contraction over Z. Let
$(K_X+B+{\mathbf {M}_{X}})$
-nonnegative birational contraction over Z. Let
![]() $B'=f_*B$
and N be a positive integer. If
$B'=f_*B$
and N be a positive integer. If
![]() $K_{X'}+B'+{\mathbf {M}_{X'}}$
has an N-complement over
$K_{X'}+B'+{\mathbf {M}_{X'}}$
has an N-complement over
![]() $z\in Z$
, then
$z\in Z$
, then
![]() $K_X+B+{\mathbf {M}_{X}}$
also has an N-complement over
$K_X+B+{\mathbf {M}_{X}}$
also has an N-complement over
![]() $z\in Z$
.
$z\in Z$
.
The following lemma says that extracting divisors with small log discrepancy from a Fano type variety preserves the Fano type property (see [Reference Birkar3, 6.13.(7)]).
Lemma 2.13. Let
![]() $X\rightarrow Z$
be a contraction. Let X be a Fano type variety over Z and
$X\rightarrow Z$
be a contraction. Let X be a Fano type variety over Z and
![]() $(X,B)$
a log Calabi–Yau pair over Z. Let
$(X,B)$
a log Calabi–Yau pair over Z. Let
![]() $f\colon Y\rightarrow X$
be a birational morphism. Suppose that every f-exceptional divisor E satisfies
$f\colon Y\rightarrow X$
be a birational morphism. Suppose that every f-exceptional divisor E satisfies
![]() $a_E(X,B)<1$
. Then Y is of Fano type over Z.
$a_E(X,B)<1$
. Then Y is of Fano type over Z.
Furthermore, let
![]() $K_Y+B_Y$
be the log pull-back of
$K_Y+B_Y$
be the log pull-back of
![]() $K_X+B$
. If
$K_X+B$
. If
![]() $K_Y+B_Y$
has an N-complement over
$K_Y+B_Y$
has an N-complement over
![]() $z\in Z$
, then
$z\in Z$
, then
![]() $(X,B)$
also has an N-complement over
$(X,B)$
also has an N-complement over
![]() $z\in Z$
.
$z\in Z$
.
2.5 Coefficients under adjunction
In this subsection, we study the coefficients of a pair under adjunction.
Definition 2.14. Let
![]() $\mathcal {R}$
be a set of rational numbers. We define
$\mathcal {R}$
be a set of rational numbers. We define
![]() $I_{\mathcal {R}}$
to be the minimal integer I such that for any
$I_{\mathcal {R}}$
to be the minimal integer I such that for any
![]() $r\in R$
and
$r\in R$
and
![]() $n \in \mathbb {N}$
, we have that
$n \in \mathbb {N}$
, we have that
If there does not exist such an integer, we define
![]() $I_{\mathcal {R}}$
to be
$I_{\mathcal {R}}$
to be
![]() $0$
.
$0$
.
Note that when the set
![]() $\mathcal {R}$
is finite
$\mathcal {R}$
is finite
![]() $I_{\mathcal {R}}$
exists as the least common multiple of the denominators will satisfy the previous inequality. When
$I_{\mathcal {R}}$
exists as the least common multiple of the denominators will satisfy the previous inequality. When
![]() $\mathcal {R}$
is the set of standard coefficients
$\mathcal {R}$
is the set of standard coefficients
![]() $I_{\mathcal {R}}$
=1. If
$I_{\mathcal {R}}$
=1. If
![]() $\mathcal {R}$
is finite, then
$\mathcal {R}$
is finite, then
![]() $I_{\mathcal {R}}$
is bounded above by the least common multiple of the rational numbers in
$I_{\mathcal {R}}$
is bounded above by the least common multiple of the rational numbers in
![]() $\mathcal {R}$
that are not standard.
$\mathcal {R}$
that are not standard.
Definition 2.15. Let
![]() $\Lambda $
be a set of real numbers in
$\Lambda $
be a set of real numbers in
![]() $[0,1]$
. Define the derived set of
$[0,1]$
. Define the derived set of
![]() $\Lambda $
as
$\Lambda $
as

We also define
![]() $D_{\lambda _0}(\Lambda )\subset D(\Lambda )$
to be the subset in which, in the definition of a, at least one
$D_{\lambda _0}(\Lambda )\subset D(\Lambda )$
to be the subset in which, in the definition of a, at least one
![]() $\lambda _i$
is equal to
$\lambda _i$
is equal to
![]() $\lambda _0$
. The set
$\lambda _0$
. The set
![]() $\Lambda $
is said to be derived if
$\Lambda $
is said to be derived if
![]() $\Lambda =D(\Lambda )$
. If
$\Lambda =D(\Lambda )$
. If
![]() $\lambda $
is a positive integer, then we set
$\lambda $
is a positive integer, then we set ![]() .
.
For instance, the set of standard coefficients ![]() is derived. The following lemmata describe some properties of derived sets.
is derived. The following lemmata describe some properties of derived sets.
Lemma 2.16 [Reference Hacon and Xu22, Proposition 3.4.1].
Let
![]() $\Lambda $
be a set of real numbers in
$\Lambda $
be a set of real numbers in
![]() $[0,1]$
. Then
$[0,1]$
. Then
![]() $D(\Lambda ) = D(D(\Lambda ))$
, that is,
$D(\Lambda ) = D(D(\Lambda ))$
, that is,
![]() $D(\Lambda )$
is a derived set.
$D(\Lambda )$
is a derived set.
The following lemma allows us to control the coefficients of the generalized pairs obtained by divisorial adjunction. The lemma is a special case of [Reference Birkar3, Lemma 3.3]; we refer to the proof of [Reference Filipazzi, Mauri and Moraga13, Lemma 3.8] for the details of this adaptation.
Lemma 2.17 [Reference Birkar3, Lemma 3.3].
Let
![]() $(X,B,\mathbf {M})$
be a generalized log canonical pair over Z and
$(X,B,\mathbf {M})$
be a generalized log canonical pair over Z and
![]() $\Lambda $
be a set of rational numbers in
$\Lambda $
be a set of rational numbers in
![]() $[0,1]$
. Suppose the coefficients of B and
$[0,1]$
. Suppose the coefficients of B and
![]() ${\mathbf {M}_{X'}}$
belong to
${\mathbf {M}_{X'}}$
belong to
![]() $\Lambda $
for some model
$\Lambda $
for some model
![]() $X'$
where
$X'$
where
![]() $\mathbf {M}$
descends. Let S be the normalization of a component of
$\mathbf {M}$
descends. Let S be the normalization of a component of
![]() $\lfloor B\rfloor $
. Write
$\lfloor B\rfloor $
. Write
for the generalized adjunction on S, where
![]() $B_S$
is the boundary part and
$B_S$
is the boundary part and
![]() $\mathbf {N}$
the moduli part. Then the coefficients of
$\mathbf {N}$
the moduli part. Then the coefficients of
![]() $B_S$
and
$B_S$
and
![]() ${\mathbf {N}_{S'}}$
belong to the derived set
${\mathbf {N}_{S'}}$
belong to the derived set
![]() $D(\Lambda )$
for some model
$D(\Lambda )$
for some model
![]() $S'$
where
$S'$
where
![]() $\mathbf {N}$
descends.
$\mathbf {N}$
descends.
The following lemma is used in the proof of Theorem 6.1 to control the coefficients of the discriminant part of a log Calabi–Yau fibration over a curve.
Lemma 2.18. Let q be a positive integer. Let
![]() $\Lambda $
be a set of nonnegative rational numbers. Suppose
$\Lambda $
be a set of nonnegative rational numbers. Suppose
![]() $\Lambda $
satisfies the DCC and has rational accumulation points. Then the set
$\Lambda $
satisfies the DCC and has rational accumulation points. Then the set

satisfies the ascending chain condition and has rational accumulation points.
Proof. We first show that
![]() $\Sigma _q$
satisfies the ascending chain condition. Suppose in
$\Sigma _q$
satisfies the ascending chain condition. Suppose in
![]() $\Sigma _q$
we can find an increasing sequence
$\Sigma _q$
we can find an increasing sequence
 $$\begin{align*}\frac{b_1^+-b_1}{m_1} < \frac{b_2^+-b_2}{m_2} < \cdots < \frac{b_k^+-b_k}{m_k} < \cdots \end{align*}$$
$$\begin{align*}\frac{b_1^+-b_1}{m_1} < \frac{b_2^+-b_2}{m_2} < \cdots < \frac{b_k^+-b_k}{m_k} < \cdots \end{align*}$$
Since
![]() $b_k^+ \in \{i/q \colon 0\leq i\leq q\}$
has only finitely many choices, we may assume, by passing to a subsequence, that all
$b_k^+ \in \{i/q \colon 0\leq i\leq q\}$
has only finitely many choices, we may assume, by passing to a subsequence, that all
![]() $b_k^+$
are the same and equal to the number
$b_k^+$
are the same and equal to the number
![]() $b^+$
. Furthermore, note that
$b^+$
. Furthermore, note that
 $$\begin{align*}m_k < \frac{m_1(b_k^+-b_k)}{b_1^+-b_1} \leq \frac{m_1}{b^+-b_1}. \end{align*}$$
$$\begin{align*}m_k < \frac{m_1(b_k^+-b_k)}{b_1^+-b_1} \leq \frac{m_1}{b^+-b_1}. \end{align*}$$
The second inequality holds as
![]() $1\geq b_k^+ \geq b_k^+-b_k$
. Hence, the sequence
$1\geq b_k^+ \geq b_k^+-b_k$
. Hence, the sequence
![]() $m_k$
is bounded above. Thus, by passing to a subsequence we may assume that
$m_k$
is bounded above. Thus, by passing to a subsequence we may assume that
![]() $m_k = m$
for all k. Now, we obtain a decreasing sequence
$m_k = m$
for all k. Now, we obtain a decreasing sequence
which violates the descending chain condition of
![]() $\Lambda $
. Thus,
$\Lambda $
. Thus,
![]() $\Sigma _q$
satisfies the ascending chain condition.
$\Sigma _q$
satisfies the ascending chain condition.
Let
![]() $a\neq 0$
be an accumulation point of
$a\neq 0$
be an accumulation point of
![]() $\Sigma _q$
. Since
$\Sigma _q$
. Since
![]() $\Sigma _q$
satisfies the ascending chain condition, we may find a sequence
$\Sigma _q$
satisfies the ascending chain condition, we may find a sequence
 $$\begin{align*}\frac{b_1^+-b_1}{m_1} \geq \frac{b_2^+-b_2}{m_2} \geq \cdots \geq \frac{b_k^+-b_k}{m_k} \geq \cdots \end{align*}$$
$$\begin{align*}\frac{b_1^+-b_1}{m_1} \geq \frac{b_2^+-b_2}{m_2} \geq \cdots \geq \frac{b_k^+-b_k}{m_k} \geq \cdots \end{align*}$$
whose limit is a. We may assume that
![]() $b_k^+ = b^+$
for all k. Then
$b_k^+ = b^+$
for all k. Then
The second inequality holds as
![]() $1\geq b_k^+ \geq b_k^+-b_k$
. Hence, the sequence
$1\geq b_k^+ \geq b_k^+-b_k$
. Hence, the sequence
![]() $m_k$
is bounded above. By passing to a subsequence, we may assume that
$m_k$
is bounded above. By passing to a subsequence, we may assume that
![]() $m_k = m$
for all k. Since
$m_k = m$
for all k. Since
![]() $\Lambda $
has rational accumulation points,
$\Lambda $
has rational accumulation points,
as desired.
2.6 Coregularity of pairs
In this subsection, we define the coregularity of a generalized pair and prove some of its properties.
Definition 2.19. Let
![]() $(X,B,\mathbf {M})$
be a generalized log canonical pair. Let
$(X,B,\mathbf {M})$
be a generalized log canonical pair. Let
![]() $f \colon Y \to X$
be a generalized dlt modification, and write
$f \colon Y \to X$
be a generalized dlt modification, and write
Let
be a simple normal crossing divisor on Y.
The dual complex
![]() $\mathcal {D}(Y,B_Y +{\mathbf {M}_{Y}})$
is a simplicial complex constructed as follows:
$\mathcal {D}(Y,B_Y +{\mathbf {M}_{Y}})$
is a simplicial complex constructed as follows:
-
• For every
 $1\leq i\leq r$
, there is a vertex
$1\leq i\leq r$
, there is a vertex
 $v_i$
in
$v_i$
in
 $\mathcal {D}(Y,B_Y+{\mathbf {M}_{Y}})$
corresponding to the divisor
$\mathcal {D}(Y,B_Y+{\mathbf {M}_{Y}})$
corresponding to the divisor
 $E_i$
. For every subset
$E_i$
. For every subset
 $I\subseteq \{1,2,\ldots ,r\}$
and every irreducible component Z of
$I\subseteq \{1,2,\ldots ,r\}$
and every irreducible component Z of
 $\bigcap _{i\in I} E_i$
, there is a simplex
$\bigcap _{i\in I} E_i$
, there is a simplex
 $v_Z$
of dimension
$v_Z$
of dimension
 $\# I - 1$
corresponding to Z;
$\# I - 1$
corresponding to Z; -
• For every
 $I\subseteq \{1,2,\ldots ,r\}$
and
$I\subseteq \{1,2,\ldots ,r\}$
and
 $j\in I$
, there is a gluing map constructed as follows. Let
$j\in I$
, there is a gluing map constructed as follows. Let
 $Z\subseteq \bigcap _{i\in I} E_i$
be any irreducible component. Let W be the unique component of
$Z\subseteq \bigcap _{i\in I} E_i$
be any irreducible component. Let W be the unique component of
 $\bigcap _{i\in I\setminus \{j\}}E_i$
containing Z. Them, the gluing map is the inclusion of
$\bigcap _{i\in I\setminus \{j\}}E_i$
containing Z. Them, the gluing map is the inclusion of
 $v_W$
into
$v_W$
into
 $v_Z$
as the face of
$v_Z$
as the face of
 $v_Z$
that does not contain the vertex
$v_Z$
that does not contain the vertex
 $v_i$
.
$v_i$
.
Define the dimension of
![]() $\mathcal {D}(Y,B_Y+{\mathbf {M}_{Y}})$
to be the smallest dimension of the maximal simplex, with respect to the inclusion, of
$\mathcal {D}(Y,B_Y+{\mathbf {M}_{Y}})$
to be the smallest dimension of the maximal simplex, with respect to the inclusion, of
![]() $\mathcal {D}(Y,B_Y+{\mathbf {M}_{Y}})$
. When
$\mathcal {D}(Y,B_Y+{\mathbf {M}_{Y}})$
. When
![]() $\mathcal {D}(Y,B_Y+{\mathbf {M}_{Y}}) = \varnothing $
, set its dimension to be
$\mathcal {D}(Y,B_Y+{\mathbf {M}_{Y}}) = \varnothing $
, set its dimension to be
![]() $-1$
.
$-1$
.
The dual complex
![]() $\mathcal {D}(Y,B_Y,{\mathbf {M}_{Y}})$
depends on the dlt modification Y. However, its PL-homeomorphism type is independent of the dlt modification (see, e.g., [Reference Filipazzi and Svaldi16, Theorem 1.6]).
$\mathcal {D}(Y,B_Y,{\mathbf {M}_{Y}})$
depends on the dlt modification Y. However, its PL-homeomorphism type is independent of the dlt modification (see, e.g., [Reference Filipazzi and Svaldi16, Theorem 1.6]).
Define the dual complex
![]() $\mathcal {D}(X,B,\mathbf {M})$
associated to the generalized pair
$\mathcal {D}(X,B,\mathbf {M})$
associated to the generalized pair
![]() $(X,B,\mathbf {M})$
as the homeomorphism type of the complex
$(X,B,\mathbf {M})$
as the homeomorphism type of the complex
![]() $\mathcal {D}(Y,B_Y+{\mathbf {M}_{Y}})$
. Thus, for any dlt modification we have
$\mathcal {D}(Y,B_Y+{\mathbf {M}_{Y}})$
. Thus, for any dlt modification we have
When
![]() $\mathbf {M} = 0$
, we write
$\mathbf {M} = 0$
, we write
![]() $\mathcal {D}(X,B)$
instead of
$\mathcal {D}(X,B)$
instead of
![]() $\mathcal {D}(X,B,0)$
for simplicity.
$\mathcal {D}(X,B,0)$
for simplicity.
Definition 2.20. Let
![]() $(X,B,\mathbf {M})$
be a generalized log canonical pair over Z. We define its coregularity to be
$(X,B,\mathbf {M})$
be a generalized log canonical pair over Z. We define its coregularity to be
Definition 2.21. Let
![]() $(X,B,\mathbf {M})$
be a generalized log canonical pair over Z. We define the absolute coregularity over Z of
$(X,B,\mathbf {M})$
be a generalized log canonical pair over Z. We define the absolute coregularity over Z of
![]() $(X,B,\mathbf {M})$
, denoted by
$(X,B,\mathbf {M})$
, denoted by
![]() $\hat {\mathrm {coreg}}(X/Z,B,\mathbf {M})$
, as follows:
$\hat {\mathrm {coreg}}(X/Z,B,\mathbf {M})$
, as follows:
-
• if
 $(X,B^+,\mathbf {M})$
is not a generalized log Calabi–Yau pair over Z for every divisor
$(X,B^+,\mathbf {M})$
is not a generalized log Calabi–Yau pair over Z for every divisor
 $B^+\geq B$
, we set
$B^+\geq B$
, we set
 $\hat {\mathrm {coreg}}(X/Z,B,\mathbf {M})$
to be
$\hat {\mathrm {coreg}}(X/Z,B,\mathbf {M})$
to be
 $\infty $
;
$\infty $
; -
• otherwise, we set
 $\hat {\mathrm {coreg}}(X/Z,B,\mathbf {M})$
to be the smallest value of
$\hat {\mathrm {coreg}}(X/Z,B,\mathbf {M})$
to be the smallest value of
 $\mathrm {coreg}(X,B^+,\mathbf {M})$
, over all divisors
$\mathrm {coreg}(X,B^+,\mathbf {M})$
, over all divisors
 $B^+\geq B$
for which
$B^+\geq B$
for which
 $(X,B^+,\mathbf {M})$
is generalized log Calabi–Yau over Z.
$(X,B^+,\mathbf {M})$
is generalized log Calabi–Yau over Z.
Let
![]() $z\in Z$
be a point. We define the absolute coregularity of
$z\in Z$
be a point. We define the absolute coregularity of
![]() $(X,B,\mathbf {M})$
over
$(X,B,\mathbf {M})$
over
![]() $z\in Z$
, denoted by
$z\in Z$
, denoted by
![]() $\hat {\mathrm {coreg}}_z(X,B,\mathbf {M})$
to be the minimum of
$\hat {\mathrm {coreg}}_z(X,B,\mathbf {M})$
to be the minimum of
![]() $\hat {\mathrm {coreg}}(\pi ^{-1}(U)/U,B,\mathbf {M})$
where U runs over all neighborhoods of
$\hat {\mathrm {coreg}}(\pi ^{-1}(U)/U,B,\mathbf {M})$
where U runs over all neighborhoods of
![]() $z\in Z$
.
$z\in Z$
.
By definition, we have that
If
![]() $X\rightarrow Z$
is the structure morphism of X and
$X\rightarrow Z$
is the structure morphism of X and
![]() $\mathrm {coreg}(X,B,\mathbf {M})=\dim X$
, then we say that
$\mathrm {coreg}(X,B,\mathbf {M})=\dim X$
, then we say that
![]() $(X,B,\mathbf {M})$
is an exceptional generalized pair.
$(X,B,\mathbf {M})$
is an exceptional generalized pair.
By the negativity lemma, the coregularity is preserved under certain MMP.
Lemma 2.22. Let
![]() $(X,B,\mathbf {M})$
be a generalized log canonical pair over Z. Let
$(X,B,\mathbf {M})$
be a generalized log canonical pair over Z. Let
![]() $z\in Z$
be a point. Suppose
$z\in Z$
be a point. Suppose
![]() $f \colon X\dashrightarrow Y$
is a
$f \colon X\dashrightarrow Y$
is a
![]() $(K_X+B+{\mathbf {M}_{X}})$
-nonnegative birational contraction over Z. Write
$(K_X+B+{\mathbf {M}_{X}})$
-nonnegative birational contraction over Z. Write
![]() $B_Y = f_*B$
. Then
$B_Y = f_*B$
. Then
Proof. Up to shrinking Z around z, we can find a generalized log Calabi–Yau pair
![]() $(X,B+\Gamma ,\mathbf {M})$
over Z that computes the absolute coregularity of
$(X,B+\Gamma ,\mathbf {M})$
over Z that computes the absolute coregularity of
![]() $(X,B,\mathbf {M})$
over z. Let
$(X,B,\mathbf {M})$
over z. Let
![]() $\Gamma _Y=f_*\Gamma $
. Since
$\Gamma _Y=f_*\Gamma $
. Since
![]() $(X,B+\Gamma ,\mathbf {M})$
is generalized log Calabi–Yau over Z, we conclude that
$(X,B+\Gamma ,\mathbf {M})$
is generalized log Calabi–Yau over Z, we conclude that
![]() $(Y,B_Y+\Gamma _Y,\mathbf {M})$
is generalized log canonical. As
$(Y,B_Y+\Gamma _Y,\mathbf {M})$
is generalized log canonical. As
![]() $(X,B+\Gamma ,\mathbf {M})$
and
$(X,B+\Gamma ,\mathbf {M})$
and
![]() $(Y,B_Y+\Gamma _Y,\mathbf {M})$
are crepant equivalent, we conclude that they have the same coregularity. Hence, we deduce that
$(Y,B_Y+\Gamma _Y,\mathbf {M})$
are crepant equivalent, we conclude that they have the same coregularity. Hence, we deduce that
On the other hand, up to shrinking Z around z, we can find an effective divisor
![]() $D_Y$
on Y that computes the absolute coregularity of
$D_Y$
on Y that computes the absolute coregularity of
![]() $(Y,B_Y,\mathbf {M})$
over z. Let
$(Y,B_Y,\mathbf {M})$
over z. Let
![]() $p\colon W \rightarrow X$
and
$p\colon W \rightarrow X$
and
![]() $q\colon W\rightarrow Y$
be a common resolution. Write
$q\colon W\rightarrow Y$
be a common resolution. Write
By the negativity lemma, we know that D is an effective divisor. Hence,
![]() $(X,B+D,\mathbf {M})$
is a generalized log Calabi–Yau pair over Z. As above, we conclude that the absolute coregularity of
$(X,B+D,\mathbf {M})$
is a generalized log Calabi–Yau pair over Z. As above, we conclude that the absolute coregularity of
![]() $(X,B,\mathbf {M})$
over
$(X,B,\mathbf {M})$
over
![]() $z\in Z$
is at most the absolute coregularity of
$z\in Z$
is at most the absolute coregularity of
![]() $(Y,B_Y,\mathbf {M})$
over
$(Y,B_Y,\mathbf {M})$
over
![]() $z\in Z$
. This finishes the proof.
$z\in Z$
. This finishes the proof.
The following lemma states the coregularity behaves well under adjunction for generalized log Calabi–Yau pairs.
Lemma 2.23. Let
![]() $(X,B,\mathbf {M})$
be a generalized log Calabi–Yau pair over Z. Let
$(X,B,\mathbf {M})$
be a generalized log Calabi–Yau pair over Z. Let
![]() $z\in Z$
be a point. Let S be the normalization of a component of
$z\in Z$
be a point. Let S be the normalization of a component of
![]() $\lfloor B\rfloor $
whose image on Z contains z. Let
$\lfloor B\rfloor $
whose image on Z contains z. Let
![]() $B_S$
and
$B_S$
and
![]() $\mathbf {N}$
be the boundary and moduli parts defined by generalized adjunction, so that
$\mathbf {N}$
be the boundary and moduli parts defined by generalized adjunction, so that
![]() $(K_X+B+{\mathbf {M}_{X}})|_S\sim K_S+B_S+{\mathbf {N}_{S}}.$
Then, we have that
$(K_X+B+{\mathbf {M}_{X}})|_S\sim K_S+B_S+{\mathbf {N}_{S}}.$
Then, we have that
holds after possibly shrinking around
![]() $z\in Z$
.
$z\in Z$
.
Proof. By passing to a generalized dlt modification, we may assume that both generalized pairs
![]() $(X,B,\mathbf {M})$
and
$(X,B,\mathbf {M})$
and
![]() $(S,B_S,\mathbf {N})$
are generalized dlt. Since any minimal generalized log canonical center of
$(S,B_S,\mathbf {N})$
are generalized dlt. Since any minimal generalized log canonical center of
![]() $(S,B_S,\mathbf {N})$
is a minimal generalized log canonical center of
$(S,B_S,\mathbf {N})$
is a minimal generalized log canonical center of
![]() $(X,B,\mathbf {M})$
, we have that
$(X,B,\mathbf {M})$
, we have that
![]() $\mathrm {coreg}(S,B_S,\mathbf {N})\geq \mathrm {coreg}(X,B,\mathbf {M})$
. On the other hand, let W be a minimal generalized log canonical center of
$\mathrm {coreg}(S,B_S,\mathbf {N})\geq \mathrm {coreg}(X,B,\mathbf {M})$
. On the other hand, let W be a minimal generalized log canonical center of
![]() $(X,B,\mathbf {M})$
whose image on Z contains z. By [Reference Filipazzi and Svaldi16, Theorem 1.4],
$(X,B,\mathbf {M})$
whose image on Z contains z. By [Reference Filipazzi and Svaldi16, Theorem 1.4],
![]() $(S,B_S,\mathbf {N})$
admits a generalized log canonical center
$(S,B_S,\mathbf {N})$
admits a generalized log canonical center
![]() $W_S$
that is
$W_S$
that is
![]() $\mathbb {P}^1$
-linked to W, thus
$\mathbb {P}^1$
-linked to W, thus
![]() $\dim W_S =\dim W$
. This implies that
$\dim W_S =\dim W$
. This implies that
![]() $\mathrm {coreg}(X,B,\mathbf {M})\geq \mathrm {coreg}(S,B_S,\mathbf {N})$
.
$\mathrm {coreg}(X,B,\mathbf {M})\geq \mathrm {coreg}(S,B_S,\mathbf {N})$
.
See [Reference Birkar3, § 3] for the construction of generalized adjunction. By altering the pairs, we can get the same result for pairs with nef anticanonical class.
Lemma 2.24. Let
![]() $(X,B,\mathbf {M})$
be a generalized log canonical pair over Z. Assume that
$(X,B,\mathbf {M})$
be a generalized log canonical pair over Z. Assume that
![]() $-(K_X+B+{\mathbf {M}_{X}})$
nef over Z. Let S be the normalization of a component of
$-(K_X+B+{\mathbf {M}_{X}})$
nef over Z. Let S be the normalization of a component of
![]() $\lfloor B\rfloor $
. Let
$\lfloor B\rfloor $
. Let
![]() $B_S$
and
$B_S$
and
![]() $\mathbf {N}$
be the boundary and moduli parts defined by generalized adjunction so that
$\mathbf {N}$
be the boundary and moduli parts defined by generalized adjunction so that
![]() $(K_X+B+{\mathbf {M}_{X}})|_S\sim K_S+B_S+{\mathbf {N}_{S}}$
. Then, we have that
$(K_X+B+{\mathbf {M}_{X}})|_S\sim K_S+B_S+{\mathbf {N}_{S}}$
. Then, we have that
Proof. Define ![]() and let
and let
![]() $\mathbf {P}$
denote its b-Cartier closure. Then,
$\mathbf {P}$
denote its b-Cartier closure. Then,
![]() $\mathbf {P}$
is a b-nef
$\mathbf {P}$
is a b-nef
![]() $\mathbb {Q}$
-Cartier divisor. We can apply Lemma 2.23 to the generalized log Calabi–Yau pair
$\mathbb {Q}$
-Cartier divisor. We can apply Lemma 2.23 to the generalized log Calabi–Yau pair
![]() $(X,B,\mathbf {M}+ \mathbf {P})$
. Therefore,
$(X,B,\mathbf {M}+ \mathbf {P})$
. Therefore,
![]() $\mathrm {coreg} (S,B_S, \mathbf {N}+ \mathbf {P}|_{S} )=\mathrm {coreg} (X,B, \mathbf {M} + \mathbf {P})$
. Since
$\mathrm {coreg} (S,B_S, \mathbf {N}+ \mathbf {P}|_{S} )=\mathrm {coreg} (X,B, \mathbf {M} + \mathbf {P})$
. Since
![]() $\mathbf {P}$
descends on S, we conclude that
$\mathbf {P}$
descends on S, we conclude that
![]() $\mathrm {coreg}(S,B_S,\mathbf {N}+\mathbf {P}|_{S})=\mathrm {coreg}(S,B_S,\mathbf {N})$
. Hence,
$\mathrm {coreg}(S,B_S,\mathbf {N}+\mathbf {P}|_{S})=\mathrm {coreg}(S,B_S,\mathbf {N})$
. Hence,
![]() $\mathrm {coreg}(S,B_S, \mathbf {N})=\mathrm {coreg}(X,B, \mathbf {M})$
.
$\mathrm {coreg}(S,B_S, \mathbf {N})=\mathrm {coreg}(X,B, \mathbf {M})$
.
The following lemma will be used to cut down the dimension of the base Z in a fibration
![]() $X\to Z$
.
$X\to Z$
.
Lemma 2.25. Let
![]() $(X,B)$
be a log canonical pair over Z and
$(X,B)$
be a log canonical pair over Z and
![]() $\pi \colon X\to Z$
be a fibration with
$\pi \colon X\to Z$
be a fibration with
![]() $\dim Z\geq 2$
. Suppose
$\dim Z\geq 2$
. Suppose
-
• the pair
 $(X,B)$
is log Calabi–Yau over Z;
$(X,B)$
is log Calabi–Yau over Z; -
•
 $\phi $
is of Fano type over an open set U of Z;
$\phi $
is of Fano type over an open set U of Z; -
• every log canonical center of
 $(X,B)$
dominates Z; and
$(X,B)$
dominates Z; and -
• the coregularity of
 $(X,B)$
is at most c.
$(X,B)$
is at most c.
Let H be a general hyperplane section of Z and G be the pull-back of H to X. Write
Then we have
-
• the pair
 $(G,B_G)$
is log canonical;
$(G,B_G)$
is log canonical; -
• the pair
 $(G,B_G)$
is log Calabi–Yau over H;
$(G,B_G)$
is log Calabi–Yau over H; -
• the induced map
 $G\to H$
is of Fano type over
$G\to H$
is of Fano type over
 $U\cap H$
;
$U\cap H$
; -
• every log canonical center of
 $(G,B_G)$
dominates H; and
$(G,B_G)$
dominates H; and -
• the coregularity of
 $(G,B_G)$
is at most c.
$(G,B_G)$
is at most c.
Furthermore, let
![]() $B_Z$
and
$B_Z$
and
![]() $B_H$
denote the discriminant parts of the adjunction for
$B_H$
denote the discriminant parts of the adjunction for
![]() $(X,B)$
over Z and
$(X,B)$
over Z and
![]() $(G,B_G)$
over H, respectively. Let D be a prime divisor on Z and C a component of
$(G,B_G)$
over H, respectively. Let D be a prime divisor on Z and C a component of
![]() $D\cap H$
. Then
$D\cap H$
. Then
Proof. We follow the proof of [Reference Birkar2, Lemma 3.2].
Since G is the pull-back of a general hyperplane section on Z,
![]() $(X,B+G)$
is log canonical. Thus, by adjunction,
$(X,B+G)$
is log canonical. Thus, by adjunction,
![]() $(G,B_G)$
is log canonical and log Calabi–Yau over H. Moreover, every log canonical center of
$(G,B_G)$
is log canonical and log Calabi–Yau over H. Moreover, every log canonical center of
![]() $(G,B_G)$
is a component of the intersection of a log canonical center of
$(G,B_G)$
is a component of the intersection of a log canonical center of
![]() $(X,B+G)$
and G, and hence must dominate H. By 2.23, we have an equality
$(X,B+G)$
and G, and hence must dominate H. By 2.23, we have an equality
Denote the map
![]() $G\to H$
by
$G\to H$
by
![]() $\psi $
. Let t be the log canonical threshold of
$\psi $
. Let t be the log canonical threshold of
![]() $\pi ^*D$
with respect to
$\pi ^*D$
with respect to
![]() $(X,B)$
over the generic point of D. Then there is a non-klt center W of
$(X,B)$
over the generic point of D. Then there is a non-klt center W of
![]() $(X,B+t\pi ^*D)$
which dominates D and the pair
$(X,B+t\pi ^*D)$
which dominates D and the pair
![]() $(X,B+t\pi ^*D)$
is lc over the generic point of D. Since G is a general pull-back,
$(X,B+t\pi ^*D)$
is lc over the generic point of D. Since G is a general pull-back,
![]() $(X,B+G+t\pi ^*D)$
is also lc over the generic point of D. By inversion of adjunction [Reference Kawakita27], there exists a component of
$(X,B+G+t\pi ^*D)$
is also lc over the generic point of D. By inversion of adjunction [Reference Kawakita27], there exists a component of
![]() $G\cap W$
which is a non-klt center of
$G\cap W$
which is a non-klt center of
![]() $(G,B_G+t\pi ^*C)$
and
$(G,B_G+t\pi ^*C)$
and
![]() $(G,B_G+t\pi ^*C)$
is lc near the generic point of C. Thus, t is the log canonical threshold of
$(G,B_G+t\pi ^*C)$
is lc near the generic point of C. Thus, t is the log canonical threshold of
![]() $\psi ^*C$
with respect to
$\psi ^*C$
with respect to
![]() $(G,B_G)$
. In particular, we have
$(G,B_G)$
. In particular, we have
Definition 2.26. We say that a log canonical threshold
![]() $t=\mathrm {lct}((X,B);\Gamma )$
has coregularity c if
$t=\mathrm {lct}((X,B);\Gamma )$
has coregularity c if
![]() $\mathrm {coreg}(X,B+t\Gamma )=c$
and the support of
$\mathrm {coreg}(X,B+t\Gamma )=c$
and the support of
![]() $\Gamma $
contains the image on X of a c-dimensional log canonical center on a dlt modification.
$\Gamma $
contains the image on X of a c-dimensional log canonical center on a dlt modification.
2.7 Kollár–Xu models for log Calabi–Yau pairs
In this subsection, we introduce the concept of Kollár–Xu models. Using a theorem due to Filipazzi and Svaldi, we conclude that every generalized log Calabi–Yau pair admits a Kollár–Xu model.
Definition 2.27. Let
![]() $(X,B,\mathbf {M})$
be a projective generalized log Calabi–Yau pair. We say that
$(X,B,\mathbf {M})$
be a projective generalized log Calabi–Yau pair. We say that
![]() $(X,B,\mathbf {M})$
is a Kollár–Xu generalized pair if there exists a projective contraction
$(X,B,\mathbf {M})$
is a Kollár–Xu generalized pair if there exists a projective contraction
![]() $\pi \colon X \rightarrow Z$
for which the following conditions are satisfied:
$\pi \colon X \rightarrow Z$
for which the following conditions are satisfied:
-
(1) the generalized pair
 $(X,B,\mathbf {M})$
is generalized dlt;
$(X,B,\mathbf {M})$
is generalized dlt; -
(2) every generalized log canonical center of
 $(X,B,\mathbf {M})$
dominates Z; and
$(X,B,\mathbf {M})$
dominates Z; and -
(3) the divisor
 $\lfloor B\rfloor $
fully supports a
$\lfloor B\rfloor $
fully supports a
 $\pi $
-big and
$\pi $
-big and
 $\pi $
-semiample divisor.
$\pi $
-semiample divisor.
In particular, the morphism
![]() $\pi \colon Y\rightarrow Z$
is of Fano type.
$\pi \colon Y\rightarrow Z$
is of Fano type.
Let
![]() $(X,B,\mathbf {M})$
be a generalized log Calabi–Yau pair. Let
$(X,B,\mathbf {M})$
be a generalized log Calabi–Yau pair. Let
![]() $\pi \colon Y\dashrightarrow X$
be a birational map. Assume that
$\pi \colon Y\dashrightarrow X$
be a birational map. Assume that
![]() $\pi $
only extracts log canonical places of
$\pi $
only extracts log canonical places of
![]() $(X,B,\mathbf {M})$
and is an isomorphism over
$(X,B,\mathbf {M})$
and is an isomorphism over
![]() $X\setminus \operatorname {\mathrm {Supp}} \lfloor B\rfloor $
. If
$X\setminus \operatorname {\mathrm {Supp}} \lfloor B\rfloor $
. If
![]() $(Y,B_Y,\mathbf {M})$
is a Kollár–Xu generalized pair, then we say that
$(Y,B_Y,\mathbf {M})$
is a Kollár–Xu generalized pair, then we say that
![]() $Y\dashrightarrow X$
is a Kollár–Xu model for
$Y\dashrightarrow X$
is a Kollár–Xu model for
![]() $(X,B,\mathbf {M})$
. We may also say that
$(X,B,\mathbf {M})$
. We may also say that
![]() $(Y,B_Y,\mathbf {M})$
, together with
$(Y,B_Y,\mathbf {M})$
, together with
![]() $\pi $
, defines a Kollár–Xu model for
$\pi $
, defines a Kollár–Xu model for
![]() $(X,B,\mathbf {M})$
.
$(X,B,\mathbf {M})$
.
The following theorem is a generalization of [Reference Kollár and Xu31, Theorem 49] to the context of generalized pairs. We refer the reader to [Reference Filipazzi and Svaldi16, Theorem 4.2]. It gives a first approximation for the existence of Kollár–Xu models in the following theorem.
Theorem 2.28. Let
![]() $(X,B,\mathbf {M})$
be a projective
$(X,B,\mathbf {M})$
be a projective
![]() $\mathbb {Q}$
-factorial generalized dlt log Calabi–Yau pair. Then, there exists a crepant birational map
$\mathbb {Q}$
-factorial generalized dlt log Calabi–Yau pair. Then, there exists a crepant birational map
![]() $\phi \colon X \dashrightarrow \overline {X}$
, a generalized pair
$\phi \colon X \dashrightarrow \overline {X}$
, a generalized pair
![]() $(\overline {X}, \overline {B}, \mathbf M)$
and a morphism
$(\overline {X}, \overline {B}, \mathbf M)$
and a morphism
![]() $\pi \colon \overline {X} \rightarrow Z$
such that:
$\pi \colon \overline {X} \rightarrow Z$
such that:
-
(1)
 $\lfloor \overline {B} \rfloor $
fully supports a
$\lfloor \overline {B} \rfloor $
fully supports a
 $\pi $
-ample divisor;
$\pi $
-ample divisor; -
(2) every generalized log canonical center of
 $(\overline {X},\overline {B},\mathbf {M})$
dominates Z;
$(\overline {X},\overline {B},\mathbf {M})$
dominates Z; -
(3)
 $\overline {E} \subset \operatorname {\mathrm {Supp}}\lfloor \overline {B}\rfloor $
for every
$\overline {E} \subset \operatorname {\mathrm {Supp}}\lfloor \overline {B}\rfloor $
for every
 $\phi ^{-1}$
-exceptional divisor
$\phi ^{-1}$
-exceptional divisor
 $\overline {E} \subset \overline {X}$
; and
$\overline {E} \subset \overline {X}$
; and -
(4)
 $\phi ^{-1}$
is an isomorphism over
$\phi ^{-1}$
is an isomorphism over
 $\overline {X} \setminus \operatorname {\mathrm {Supp}} \lfloor \overline {B}\rfloor $
.
$\overline {X} \setminus \operatorname {\mathrm {Supp}} \lfloor \overline {B}\rfloor $
.
We observe that the model
![]() $\overline {X}$
in Theorem 2.28 is not necessarily
$\overline {X}$
in Theorem 2.28 is not necessarily
![]() $\mathbb {Q}$
-factorial. However, using
$\mathbb {Q}$
-factorial. However, using
![]() $\mathbb {Q}$
-factorial dlt modifications, we construct a Kollár–Xu model.
$\mathbb {Q}$
-factorial dlt modifications, we construct a Kollár–Xu model.
Theorem 2.29. Let
![]() $(X,B,\mathbf {M})$
be a projective generalized log Calabi–Yau pair. Then, it admits a Kollár–Xu model
$(X,B,\mathbf {M})$
be a projective generalized log Calabi–Yau pair. Then, it admits a Kollár–Xu model
![]() $Y\dashrightarrow X$
. Furthermore, if
$Y\dashrightarrow X$
. Furthermore, if
![]() $(X,B,\mathbf {M})$
has coregularity c, then so does
$(X,B,\mathbf {M})$
has coregularity c, then so does
![]() $(Y,B_Y,\mathbf {M})$
.
$(Y,B_Y,\mathbf {M})$
.
In the context of Theorem 2.29, if
![]() $c=0$
, then
$c=0$
, then
![]() $Z=\operatorname {Spec} (\mathbb {K})$
and Y is a variety of Fano type.
$Z=\operatorname {Spec} (\mathbb {K})$
and Y is a variety of Fano type.
Proof. Let
![]() $(X,B,\mathbf {M})$
be a generalized pair as in the statement. Then, we first consider a
$(X,B,\mathbf {M})$
be a generalized pair as in the statement. Then, we first consider a
![]() $\mathbb {Q}$
-factorial generalized dlt modification and then apply Theorem 2.28 to such modification. Call
$\mathbb {Q}$
-factorial generalized dlt modification and then apply Theorem 2.28 to such modification. Call
![]() $(\overline {X},\overline {B},\mathbf {M})$
the resulting model and
$(\overline {X},\overline {B},\mathbf {M})$
the resulting model and
![]() $\pi \colon \overline {X} \rightarrow Z$
the morphism claimed in Theorem 2.28. Since
$\pi \colon \overline {X} \rightarrow Z$
the morphism claimed in Theorem 2.28. Since
![]() $(X,B,\mathbf {M})$
has coregularity c, then so does
$(X,B,\mathbf {M})$
has coregularity c, then so does
![]() $(\overline {X},\overline {B},\mathbf {M})$
. In particular,
$(\overline {X},\overline {B},\mathbf {M})$
. In particular,
![]() $(\overline {X},\overline {B},\mathbf {M})$
has a c-dimensional generalized log canonical center. Then, by (2) in Theorem 2.28, it follows that Z has dimension at most c. By (1) in Theorem 2.28,
$(\overline {X},\overline {B},\mathbf {M})$
has a c-dimensional generalized log canonical center. Then, by (2) in Theorem 2.28, it follows that Z has dimension at most c. By (1) in Theorem 2.28,
![]() $\overline {B}$
fully supports a
$\overline {B}$
fully supports a
![]() $\pi $
-ample divisor, which we will denote by
$\pi $
-ample divisor, which we will denote by
![]() $\overline {H}$
. Now, let
$\overline {H}$
. Now, let
![]() $(Y,B_Y,\mathbf {M})$
be a
$(Y,B_Y,\mathbf {M})$
be a
![]() $\mathbb {Q}$
-factorial generalized dlt modification of
$\mathbb {Q}$
-factorial generalized dlt modification of
![]() $(\overline {X},\overline {B},\mathbf {M})$
, with morphism
$(\overline {X},\overline {B},\mathbf {M})$
, with morphism
![]() $p \colon Y \rightarrow \overline {X}$
. We denote by
$p \colon Y \rightarrow \overline {X}$
. We denote by
![]() $\pi _Y$
the induced morphism
$\pi _Y$
the induced morphism
![]() $\pi _Y \colon Y \rightarrow Z$
. Note that every generalized log canonical center of
$\pi _Y \colon Y \rightarrow Z$
. Note that every generalized log canonical center of
![]() $(Y,B_Y,\mathbf {M})$
dominates Z. Then, (2) in Definition 2.27 holds. By [Reference Filipazzi and Svaldi16, Remark 4.3], we have
$(Y,B_Y,\mathbf {M})$
dominates Z. Then, (2) in Definition 2.27 holds. By [Reference Filipazzi and Svaldi16, Remark 4.3], we have
![]() $\mathrm {Nklt}(\overline {X},\overline {B},\mathbf {M})=\operatorname {\mathrm {Supp}}\lfloor \overline {B}\rfloor $
. Since p only extracts generalized log canonical places, it then follows that every p-exceptional divisor has positive coefficients in
$\mathrm {Nklt}(\overline {X},\overline {B},\mathbf {M})=\operatorname {\mathrm {Supp}}\lfloor \overline {B}\rfloor $
. Since p only extracts generalized log canonical places, it then follows that every p-exceptional divisor has positive coefficients in ![]() and that
and that
![]() $\operatorname {\mathrm {Supp}} H_Y= \operatorname {\mathrm {Supp}} \lfloor B_Y \rfloor $
. Then, it follows that
$\operatorname {\mathrm {Supp}} H_Y= \operatorname {\mathrm {Supp}} \lfloor B_Y \rfloor $
. Then, it follows that
![]() $\lfloor B_Y \rfloor $
fully supports a
$\lfloor B_Y \rfloor $
fully supports a
![]() $\pi _Y$
-big and
$\pi _Y$
-big and
![]() $\pi _Y$
-semiample divisor. Thus, (3) in Definition 2.27 holds. The statements (1) and (3) in Definition 2.27 hold by construction. We conclude that
$\pi _Y$
-semiample divisor. Thus, (3) in Definition 2.27 holds. The statements (1) and (3) in Definition 2.27 hold by construction. We conclude that
![]() $(Y,B_Y,\mathbf {M})$
, together with
$(Y,B_Y,\mathbf {M})$
, together with
![]() $\pi _Y$
, are a Kollár–Xu model of
$\pi _Y$
, are a Kollár–Xu model of
![]() $(X,B,\mathbf {M})$
. Lastly,
$(X,B,\mathbf {M})$
. Lastly,
![]() $(Y,B_Y,\mathbf {M})$
has coregularity c, since it is crepant to a generalized pair of coregularity c.
$(Y,B_Y,\mathbf {M})$
has coregularity c, since it is crepant to a generalized pair of coregularity c.
2.8 Index of generalized klt pairs
In this subsection, we reduce the index conjecture for generalized klt pairs to the standard index conjecture.
Lemma 2.30. Let d and p be two positive integers. Let
![]() $\Lambda $
be a set of rational numbers satisfying the descending chain condition. Assume Conjecture 1
$\Lambda $
be a set of rational numbers satisfying the descending chain condition. Assume Conjecture 1
![]() $(d)$
holds. Then, there exists a positive integer
$(d)$
holds. Then, there exists a positive integer ![]() , satisfying the following. Let
, satisfying the following. Let
![]() $(X,B,\mathbf {M})$
be a generalized klt Calabi–Yau pair for which:
$(X,B,\mathbf {M})$
be a generalized klt Calabi–Yau pair for which:
-
• the variety X has dimension d;
-
• the coefficients of B belong to
 $\Lambda $
;
$\Lambda $
; -
• the divisor
 $p\mathbf {M}$
is Cartier where it descends.
$p\mathbf {M}$
is Cartier where it descends.
Then, we have that
![]() $I(K_X+B+{\mathbf {M}_{X}})\sim 0$
.
$I(K_X+B+{\mathbf {M}_{X}})\sim 0$
.
Proof. By the global ascending chain condition (ACC) [Reference Birkar and Zhang7, Theorem 1.6], we may assume that
![]() $\Lambda $
is a finite set of rational numbers. The statement is clear in dimension
$\Lambda $
is a finite set of rational numbers. The statement is clear in dimension
![]() $1$
. We proceed by induction on the dimension. If
$1$
. We proceed by induction on the dimension. If
![]() $\mathbf {M}=0$
, then the statement follows from the conjecture. Since
$\mathbf {M}=0$
, then the statement follows from the conjecture. Since
![]() $(X,B,\mathbf {M})$
is generalized klt, it admits a small
$(X,B,\mathbf {M})$
is generalized klt, it admits a small
![]() $\mathbb {Q}$
-factorialization. Therefore, we may assume that X is
$\mathbb {Q}$
-factorialization. Therefore, we may assume that X is
![]() $\mathbb {Q}$
-factorial. By the ACC for generalized log canonical thresholds, we may assume
$\mathbb {Q}$
-factorial. By the ACC for generalized log canonical thresholds, we may assume
![]() $(X,B,\mathbf {M})$
is
$(X,B,\mathbf {M})$
is
![]() $\epsilon $
-log canonical for some
$\epsilon $
-log canonical for some
![]() $\epsilon $
that only depends on d, p and
$\epsilon $
that only depends on d, p and
![]() $\Lambda $
. Then, it follows that X is itself
$\Lambda $
. Then, it follows that X is itself
![]() $\epsilon $
-log canonical. We run a
$\epsilon $
-log canonical. We run a
![]() $K_X$
-MMP which terminates with a Mori fiber space
$K_X$
-MMP which terminates with a Mori fiber space
![]() $X\dashrightarrow X'\rightarrow Z$
. If Z is zero-dimensional, then
$X\dashrightarrow X'\rightarrow Z$
. If Z is zero-dimensional, then
![]() $X'$
belongs to a bounded family by [Reference Birkar4]. By [Reference Filipazzi and Moraga14, Theorem 1.2]
$X'$
belongs to a bounded family by [Reference Birkar4]. By [Reference Filipazzi and Moraga14, Theorem 1.2]
![]() $(K_{X'}+B'+{\mathbf {M}_{X'}})$
admits an I-complement for some I that only depends on
$(K_{X'}+B'+{\mathbf {M}_{X'}})$
admits an I-complement for some I that only depends on
![]() $\Lambda ,d$
and p. Since
$\Lambda ,d$
and p. Since
![]() $K_{X'}+B'+{\mathbf {M}_{X'}}\sim _{\mathbb {Q}} 0$
, we conclude that
$K_{X'}+B'+{\mathbf {M}_{X'}}\sim _{\mathbb {Q}} 0$
, we conclude that
![]() $I(K_{X'}+B'+{\mathbf {M}_{X'}})\sim 0$
, so the statement follows for X as well. Now, assume that Z is positive-dimensional. We write
$I(K_{X'}+B'+{\mathbf {M}_{X'}})\sim 0$
, so the statement follows for X as well. Now, assume that Z is positive-dimensional. We write
![]() $\pi '\colon X'\rightarrow Z$
for the corresponding contraction. By [Reference Filipazzi and Moraga14, Lemma 5.4], we can write
$\pi '\colon X'\rightarrow Z$
for the corresponding contraction. By [Reference Filipazzi and Moraga14, Lemma 5.4], we can write
where the coefficients of
![]() $B_Z$
belong to
$B_Z$
belong to
![]() $\Omega $
which satisfies the DCC and only depends on
$\Omega $
which satisfies the DCC and only depends on
![]() $\Lambda ,d$
and p. Furthermore, q only depends on
$\Lambda ,d$
and p. Furthermore, q only depends on
![]() $\Lambda ,d$
and p and
$\Lambda ,d$
and p and
![]() $q\mathbf {N}$
is Cartier where it descends. The generalized pair
$q\mathbf {N}$
is Cartier where it descends. The generalized pair
![]() $(Z,B_Z, \mathbf {N})$
is generalized log canonical since it comes from the generalized canonical bundle formula [Reference Filipazzi11, Theorem 1.4]. By induction on the dimension, we know that
$(Z,B_Z, \mathbf {N})$
is generalized log canonical since it comes from the generalized canonical bundle formula [Reference Filipazzi11, Theorem 1.4]. By induction on the dimension, we know that
![]() $I_0(K_Z+B_Z+{\mathbf {N}_{Z}})\sim 0$
for some
$I_0(K_Z+B_Z+{\mathbf {N}_{Z}})\sim 0$
for some
![]() $I_0$
that only depends on
$I_0$
that only depends on
![]() $\Lambda ,d$
and p. Thus, we conclude that
$\Lambda ,d$
and p. Thus, we conclude that
![]() $I(K_X+B+{\mathbf {M}_{X}})\sim 0$
, where
$I(K_X+B+{\mathbf {M}_{X}})\sim 0$
, where
![]() $I=\mathrm {lcm}(q,I_0)$
.
$I=\mathrm {lcm}(q,I_0)$
.
2.9 Lifting sections using fibrations
In this subsection, we give some lemmata regarding the lifting of sections using fibrations.
Theorem 2.31. Let
![]() $\lambda ,d$
and c be nonnegative integers. Assume that Theorem 6
$\lambda ,d$
and c be nonnegative integers. Assume that Theorem 6
![]() $(d-1,c)$
holds, and let
$(d-1,c)$
holds, and let ![]() be the integer provided by this theorem. Let
be the integer provided by this theorem. Let
![]() $(X,B,\mathbf {M})$
be a d-dimensional rationally connected generalized log Calabi–Yau pair. Assume that the following conditions hold:
$(X,B,\mathbf {M})$
be a d-dimensional rationally connected generalized log Calabi–Yau pair. Assume that the following conditions hold:
-
• X is
 $\mathbb {Q}$
-factorial and
$\mathbb {Q}$
-factorial and
 $(X,B,\mathbf {M})$
is generalized dlt;
$(X,B,\mathbf {M})$
is generalized dlt; -
• there is a fibration
 $X\rightarrow W$
, which is a
$X\rightarrow W$
, which is a
 $(K_X + \lfloor B \rfloor )$
-Mori fiber space;
$(K_X + \lfloor B \rfloor )$
-Mori fiber space; -
• a component
 $S\subset \operatorname {\mathrm {Supp}}\lfloor B\rfloor $
is rationally connected and ample over W;
$S\subset \operatorname {\mathrm {Supp}}\lfloor B\rfloor $
is rationally connected and ample over W; -
• the coefficients of B belong to
 $D_\lambda $
;
$D_\lambda $
; -
• we have that
 $\lambda \mathbf {M}$
is b-Cartier; and
$\lambda \mathbf {M}$
is b-Cartier; and -
• the generalized pair
 $(X,B,\mathbf {M})$
has coregularity c.
$(X,B,\mathbf {M})$
has coregularity c.
Then, we have that
![]() $I(K_X+B+{\mathbf {M}_{X}})\sim 0$
.
$I(K_X+B+{\mathbf {M}_{X}})\sim 0$
.
Proof. Let
![]() $(X,B,\mathbf {M})$
, S,
$(X,B,\mathbf {M})$
, S,
![]() $f \colon X \rightarrow W$
and
$f \colon X \rightarrow W$
and ![]() be as in the statement. First, we show that we can apply the inductive hypothesis to S.
be as in the statement. First, we show that we can apply the inductive hypothesis to S.
Since
![]() $(X,\lfloor B \rfloor )$
is dlt, S is normal. Furthermore, we have
$(X,\lfloor B \rfloor )$
is dlt, S is normal. Furthermore, we have
![]() $\mathrm {Nklt}(X,S)=S$
. Since
$\mathrm {Nklt}(X,S)=S$
. Since
![]() $-({K_{X}} + S)$
is f-ample, by the connectedness principle [Reference Filipazzi and Svaldi16], it follows that
$-({K_{X}} + S)$
is f-ample, by the connectedness principle [Reference Filipazzi and Svaldi16], it follows that
![]() $S \rightarrow W$
has connected fibers. Now, let
$S \rightarrow W$
has connected fibers. Now, let
![]() $(S,B_S,\mathbf {N})$
be the generalized pair induced on S by generalized divisorial adjunction. By Lemma 2.23,
$(S,B_S,\mathbf {N})$
be the generalized pair induced on S by generalized divisorial adjunction. By Lemma 2.23,
![]() $(S,B_S,\mathbf {N})$
has coregularity c. Furthermore, by Lemma 2.17 and Lemma 2.16, it satisfies the assumptions of Theorem 6
$(S,B_S,\mathbf {N})$
has coregularity c. Furthermore, by Lemma 2.17 and Lemma 2.16, it satisfies the assumptions of Theorem 6
![]() $(d-1,c)$
with constant I. Thus, we have
$(d-1,c)$
with constant I. Thus, we have
By [Reference Figueroa, Moraga and Peng10, Theorem 3.1], the coefficients of
![]() $B_S$
belong to a finite set only depending on
$B_S$
belong to a finite set only depending on
![]() $\lambda $
and c. In particular, they are divisible by I, as so are the coefficients of
$\lambda $
and c. In particular, they are divisible by I, as so are the coefficients of
![]() ${\mathbf {N}_{S}}$
. Then, these coefficients control the coefficients of
${\mathbf {N}_{S}}$
. Then, these coefficients control the coefficients of
![]() $\mathrm {Diff}_S(0)$
, as we explain in what follows. By [Reference Kollár29, 3.35], along the codimension 2 points of X contained in S, X has cyclic singularities.
$\mathrm {Diff}_S(0)$
, as we explain in what follows. By [Reference Kollár29, 3.35], along the codimension 2 points of X contained in S, X has cyclic singularities.
Then, given a prime divisor P in S, an étale local neighbourhood of a general point
![]() $p \in P$
is isomorphic to
$p \in P$
is isomorphic to
where
![]() $Z \simeq (\mathbb {A}^2=(x,y))/(\mathbb {Z}/m\mathbb {Z})$
,
$Z \simeq (\mathbb {A}^2=(x,y))/(\mathbb {Z}/m\mathbb {Z})$
,
![]() $S=(x=0)$
and
$S=(x=0)$
and
![]() $S'=(y=0)$
. Since the class group of Z is generated by
$S'=(y=0)$
. Since the class group of Z is generated by
![]() $S'$
, there exists an integer
$S'$
, there exists an integer
![]() $\mu $
such that
$\mu $
such that
By adjunction,
![]() $S'|_S \sim _{\mathbb {Q}} \frac {1}{m}\{0\}$
. We also have that
$S'|_S \sim _{\mathbb {Q}} \frac {1}{m}\{0\}$
. We also have that
![]() $I(K_X+B+{\mathbf {M}_{X}})|_S\sim 0$
, as the denominators of the coefficients of
$I(K_X+B+{\mathbf {M}_{X}})|_S\sim 0$
, as the denominators of the coefficients of
![]() $B_S$
and
$B_S$
and
![]() ${\mathbf {N}_{S}}$
divide I and hence it is a Cartier divisor on a smooth germ.
${\mathbf {N}_{S}}$
divide I and hence it is a Cartier divisor on a smooth germ.
Then, we can write
We conclude that m divides
![]() $\mu $
. In particular, we have that
$\mu $
. In particular, we have that
![]() $\mu S$
is a Cartier divisor, as the Cartier index of any Weil divisor of X through
$\mu S$
is a Cartier divisor, as the Cartier index of any Weil divisor of X through
![]() $\{0\}$
divides m. By the linear equivalence (2.2), we conclude that the divisor
$\{0\}$
divides m. By the linear equivalence (2.2), we conclude that the divisor
![]() $I(K_X+B+M)$
is Cartier at the generic point of P. Note that this argument is independent of P, so we conclude that
$I(K_X+B+M)$
is Cartier at the generic point of P. Note that this argument is independent of P, so we conclude that
![]() $I(K_X+B+M)$
is Cartier at the generic point of every divisor on S. Thus,
$I(K_X+B+M)$
is Cartier at the generic point of every divisor on S. Thus,
![]() $I(K_X+B+M)$
is Cartier along a set U that contains the generic point of every divisor of S.
$I(K_X+B+M)$
is Cartier along a set U that contains the generic point of every divisor of S.
Then, by [Reference Birkar3, 2.41 and Lemma 2.42], we have the following short exact sequence
Since
![]() $I(K_{X}+B + {\mathbf {M}_{X}})-S\sim _{\mathbb {Q},f} -S$
, the divisor
$I(K_{X}+B + {\mathbf {M}_{X}})-S\sim _{\mathbb {Q},f} -S$
, the divisor
![]() $-S$
is f-ample and
$-S$
is f-ample and
![]() $\dim W < \dim X$
, we have
$\dim W < \dim X$
, we have
Similarly, we write
Note that X is klt and
![]() $B-S+{\mathbf {M}_{X}} = B^{<1}+{\mathbf {M}_{X}} + (B^{=1} - S)$
is f-ample since f is a Mori fiber space and the divisor
$B-S+{\mathbf {M}_{X}} = B^{<1}+{\mathbf {M}_{X}} + (B^{=1} - S)$
is f-ample since f is a Mori fiber space and the divisor
![]() $B^{<1}+{\mathbf {M}_{X}}$
is f-ample. Thus, by the relative version of Kawamata–Viehweg vanishing, we have
$B^{<1}+{\mathbf {M}_{X}}$
is f-ample. Thus, by the relative version of Kawamata–Viehweg vanishing, we have
Therefore, by pushing forward (2.3) via f, we obtain
Now, taking global sections, we have
By Lemma [Reference Filipazzi, Mauri and Moraga13, Lemma 3.1], (2.4) implies that
![]() $I(K_{X}+B+ {\mathbf {M}_{X}}) \sim 0$
.
$I(K_{X}+B+ {\mathbf {M}_{X}}) \sim 0$
.
Theorem 2.32. Let
![]() $\lambda ,d$
and c be nonnegative integers. Assume that Theorem 6
$\lambda ,d$
and c be nonnegative integers. Assume that Theorem 6
![]() $(d-1,c)$
holds, and let
$(d-1,c)$
holds, and let ![]() be the integer provided by this theorem. Assume that I is divisible by
be the integer provided by this theorem. Assume that I is divisible by
![]() $2\lambda $
. Let
$2\lambda $
. Let
![]() $(X,B)$
be a d-dimensional log Calabi–Yau pair. Assume that the following conditions hold:
$(X,B)$
be a d-dimensional log Calabi–Yau pair. Assume that the following conditions hold:
-
• X is
 $\mathbb {Q}$
-factorial and klt;
$\mathbb {Q}$
-factorial and klt; -
• there is a fibration
 $X\rightarrow W$
;
$X\rightarrow W$
; -
• S is a prime component of
 $\lfloor B \rfloor $
that is ample over W;
$\lfloor B \rfloor $
that is ample over W; -
•
 $(X,B-S)$
is dlt;
$(X,B-S)$
is dlt; -
• the morphism
 $S \rightarrow W$
does not have connected fibers;
$S \rightarrow W$
does not have connected fibers; -
• the coefficients of B belong to
 $D_\lambda $
; and
$D_\lambda $
; and -
• the pair
 $(X,B)$
has coregularity c.
$(X,B)$
has coregularity c.
Then, we have that
![]() $I(K_X+B)\sim 0$
.
$I(K_X+B)\sim 0$
.
Proof. Let
![]() $(X,B)$
, S,
$(X,B)$
, S,
![]() $f \colon X \rightarrow W$
and
$f \colon X \rightarrow W$
and ![]() be as in the statement. We will proceed in several steps.
be as in the statement. We will proceed in several steps.
Step 1: In this step, we observe that
![]() $\dim X - \dim W=1$
, f is generically a
$\dim X - \dim W=1$
, f is generically a
![]() ${\mathbb {P}^{1}}$
-fibration and
${\mathbb {P}^{1}}$
-fibration and
![]() $B_{\mathrm {hor}}=S$
.
$B_{\mathrm {hor}}=S$
.
Since
![]() $(X,B)$
is log canonical and X is
$(X,B)$
is log canonical and X is
![]() $\mathbb {Q}$
-factorial, then
$\mathbb {Q}$
-factorial, then
![]() $(X,S)$
is log canonical. By considering a general fiber of f, the restriction of S induces a disconnected ample divisor. Therefore, by [Reference Hartshorne25, Exercise III.11.3], it follows that the general fiber of f is a curve. By the log Calabi–Yau condition and the fact that
$(X,S)$
is log canonical. By considering a general fiber of f, the restriction of S induces a disconnected ample divisor. Therefore, by [Reference Hartshorne25, Exercise III.11.3], it follows that the general fiber of f is a curve. By the log Calabi–Yau condition and the fact that
![]() $0 \neq B_{\mathrm {hor}} \geq S$
, it follows that f is generically a
$0 \neq B_{\mathrm {hor}} \geq S$
, it follows that f is generically a
![]() ${\mathbb {P}^{1}}$
-fibration. Since
${\mathbb {P}^{1}}$
-fibration. Since
![]() $S \rightarrow W$
does not have connected fibers and
$S \rightarrow W$
does not have connected fibers and
![]() $\deg K_{{\mathbb {P}^{1}}}=-2$
, it follows that S is the only component of
$\deg K_{{\mathbb {P}^{1}}}=-2$
, it follows that S is the only component of
![]() $\operatorname {\mathrm {Supp}} B$
that dominates W, that is, we have
$\operatorname {\mathrm {Supp}} B$
that dominates W, that is, we have
![]() $B_{\mathrm {hor}} =S$
. In particular, we may find a nonempty open subset
$B_{\mathrm {hor}} =S$
. In particular, we may find a nonempty open subset
![]() $U \subseteq W$
such that
$U \subseteq W$
such that
![]() $K_X+S \sim _{\mathbb {Q}} 0 /U$
.
$K_X+S \sim _{\mathbb {Q}} 0 /U$
.
Step 2: In this step, we show that
![]() $\dim W> 0$
.
$\dim W> 0$
.
By Step 1,
![]() $X \rightarrow W$
is generically a
$X \rightarrow W$
is generically a
![]() ${\mathbb {P}^{1}}$
-fibration, and S determines two distinct points on the geometric generic fiber of f. Thus, if
${\mathbb {P}^{1}}$
-fibration, and S determines two distinct points on the geometric generic fiber of f. Thus, if
![]() $\dim W =0$
, it would follow that
$\dim W =0$
, it would follow that
![]() $(X,B) \simeq ({\mathbb {P}^{1}},\{ 0 \} + \{\infty \})$
, with S identified with
$(X,B) \simeq ({\mathbb {P}^{1}},\{ 0 \} + \{\infty \})$
, with S identified with
![]() $\{ 0 \} + \{\infty \}$
. Since we assumed that S is a prime divisor, this leads to the sought contradiction.
$\{ 0 \} + \{\infty \}$
. Since we assumed that S is a prime divisor, this leads to the sought contradiction.
Step 3: In this step, we show that we may replace X birationally so that
![]() $(X,S)$
is plt,
$(X,S)$
is plt,
![]() $K_X +S \sim _{\mathbb {Q}} 0/W$
and f is a Mori fiber space.
$K_X +S \sim _{\mathbb {Q}} 0/W$
and f is a Mori fiber space.
Since
![]() $(X,B)$
is log canonical and X is
$(X,B)$
is log canonical and X is
![]() $\mathbb {Q}$
-factorial, then
$\mathbb {Q}$
-factorial, then
![]() $(X,S)$
is log canonical. Let
$(X,S)$
is log canonical. Let
![]() $X'$
be a
$X'$
be a
![]() $\mathbb {Q}$
-factorial dlt modification of
$\mathbb {Q}$
-factorial dlt modification of
![]() $(X,S)$
, and let
$(X,S)$
, and let
![]() $S'$
denote the strict transform of S. In particular,
$S'$
denote the strict transform of S. In particular,
![]() $(X',S')$
is plt. By [Reference Hacon and Xu23, Theorem 1.1],
$(X',S')$
is plt. By [Reference Hacon and Xu23, Theorem 1.1],
![]() $(X',S')$
has a relatively good minimal model over W, which we denote by
$(X',S')$
has a relatively good minimal model over W, which we denote by
![]() $(\tilde X, \tilde S)$
. Since
$(\tilde X, \tilde S)$
. Since
![]() $S'$
dominates W and
$S'$
dominates W and
![]() $\dim X - \dim W =1$
,
$\dim X - \dim W =1$
,
![]() $S'$
is relatively big over W. Therefore,
$S'$
is relatively big over W. Therefore,
![]() $S'$
cannot be contracted on
$S'$
cannot be contracted on
![]() $\tilde X$
, and therefore
$\tilde X$
, and therefore
![]() $\tilde S$
is a divisor. Since
$\tilde S$
is a divisor. Since
![]() $(X',S')$
is plt, then so is
$(X',S')$
is plt, then so is
![]() $(\tilde X,\tilde S)$
. We denote by
$(\tilde X,\tilde S)$
. We denote by
![]() $\tilde W$
the relatively ample model, which is birational to W. Now, we run a
$\tilde W$
the relatively ample model, which is birational to W. Now, we run a
![]() ${K_{\tilde X}}$
-MMP with scaling over
${K_{\tilde X}}$
-MMP with scaling over
![]() $\tilde W$
, which terminates with a Mori fiber space
$\tilde W$
, which terminates with a Mori fiber space
![]() $\hat f \colon \hat X \rightarrow \hat W$
over
$\hat f \colon \hat X \rightarrow \hat W$
over
![]() $\tilde W$
. Since
$\tilde W$
. Since
![]() $\dim X -\dim W =1$
, it follows that
$\dim X -\dim W =1$
, it follows that
![]() $\hat W \rightarrow \tilde W$
is birational. As before, since
$\hat W \rightarrow \tilde W$
is birational. As before, since
![]() $\tilde S$
dominates
$\tilde S$
dominates
![]() $\tilde W$
and is relatively big over
$\tilde W$
and is relatively big over
![]() $\tilde W$
as
$\tilde W$
as
![]() $\dim X - \dim W =1$
, it follows that
$\dim X - \dim W =1$
, it follows that
![]() $\tilde S$
cannot be contracted on
$\tilde S$
cannot be contracted on
![]() $\hat X$
. Let
$\hat X$
. Let
![]() $\hat S$
be its strict transform on
$\hat S$
be its strict transform on
![]() $\hat X$
. Lastly, as
$\hat X$
. Lastly, as
![]() ${K_{\tilde X}} + \tilde S \sim _{\mathbb {Q}} 0 /\tilde W$
and
${K_{\tilde X}} + \tilde S \sim _{\mathbb {Q}} 0 /\tilde W$
and
![]() $\tilde S$
is the only log canonical place of
$\tilde S$
is the only log canonical place of
![]() $(\tilde X,\tilde S)$
,
$(\tilde X,\tilde S)$
,
![]() $\hat S$
is the only log canonical place of
$\hat S$
is the only log canonical place of
![]() $(\hat X,\hat S)$
. But then, since
$(\hat X,\hat S)$
. But then, since
![]() $\hat S$
is a divisor on
$\hat S$
is a divisor on
![]() $\hat X$
, it follows that
$\hat X$
, it follows that
![]() $(\hat X,\hat S)$
is plt. In particular,
$(\hat X,\hat S)$
is plt. In particular,
![]() $\hat S$
is normal. Thus, by [Reference Filipazzi, Mauri and Moraga13, Corollary 3.3], up to replacing X, S and Z with
$\hat S$
is normal. Thus, by [Reference Filipazzi, Mauri and Moraga13, Corollary 3.3], up to replacing X, S and Z with
![]() $\hat X$
,
$\hat X$
,
![]() $\hat S$
and
$\hat S$
and
![]() $\hat Z$
, respectively, in the following of the proof, we may further assume that
$\hat Z$
, respectively, in the following of the proof, we may further assume that
![]() $(X,S)$
is plt,
$(X,S)$
is plt,
![]() $K_X +S \sim _{\mathbb {Q}} 0/W$
and f is a Mori fiber space.
$K_X +S \sim _{\mathbb {Q}} 0/W$
and f is a Mori fiber space.
Step 4: In this step, we introduce a suitable pair structure on the base W.
Let
![]() $(S,B_S)$
denote the pair induced by adjunction from
$(S,B_S)$
denote the pair induced by adjunction from
![]() $(X,B)$
to S. By Lemma 2.23,
$(X,B)$
to S. By Lemma 2.23,
![]() $(S,B_S)$
has coregularity c. Then, by Lemma 2.17, the inductive hypothesis applies to
$(S,B_S)$
has coregularity c. Then, by Lemma 2.17, the inductive hypothesis applies to
![]() $(S,B_{S})$
for the same value of I. We also let
$(S,B_{S})$
for the same value of I. We also let
![]() $(S,\mathrm {Diff}_S(0))$
be the pair structure induced from
$(S,\mathrm {Diff}_S(0))$
be the pair structure induced from
![]() $(X,S)$
to S. By Step 1,
$(X,S)$
to S. By Step 1,
![]() $f_S \colon S \rightarrow W$
is generically 2:1 and hence Galois. By [Reference Kollár29, Proposition 4.37.(3)],
$f_S \colon S \rightarrow W$
is generically 2:1 and hence Galois. By [Reference Kollár29, Proposition 4.37.(3)],
![]() $(S,\mathrm {Diff}_S(0))$
is invariant under the rational Galois involution. Then, since
$(S,\mathrm {Diff}_S(0))$
is invariant under the rational Galois involution. Then, since
![]() ${K_{X}} + S \sim _{\mathbb {Q}} 0 /W$
and f is a Mori fiber space, it follows that
${K_{X}} + S \sim _{\mathbb {Q}} 0 /W$
and f is a Mori fiber space, it follows that
![]() $B-S$
is the pull-back of a
$B-S$
is the pull-back of a
![]() $\mathbb {Q}$
-divisor on W. Then, it follows that also
$\mathbb {Q}$
-divisor on W. Then, it follows that also
![]() $(S,B_S)$
is Galois invariant. Then, by considering the Stein factorization of
$(S,B_S)$
is Galois invariant. Then, by considering the Stein factorization of
![]() $S \rightarrow W$
and descending the pair structure thanks to the fact that
$S \rightarrow W$
and descending the pair structure thanks to the fact that
![]() ${K_{S}} +B_S \sim _{\mathbb {Q}} 0$
, it follows that we can induce a pair structure
${K_{S}} +B_S \sim _{\mathbb {Q}} 0$
, it follows that we can induce a pair structure
![]() $(W,B_W)$
such that
$(W,B_W)$
such that
![]() $f_S^*({K_{W}} + B_W)={K_{S}} + B_S$
. Since
$f_S^*({K_{W}} + B_W)={K_{S}} + B_S$
. Since
![]() $(S,B_S)$
has coregularity c, by [Reference Filipazzi, Mauri and Moraga13, Proposition 3.11], then so does
$(S,B_S)$
has coregularity c, by [Reference Filipazzi, Mauri and Moraga13, Proposition 3.11], then so does
![]() $(W,B_W)$
. Furthermore, since
$(W,B_W)$
. Furthermore, since
![]() $(S,B_S)$
has coefficients in
$(S,B_S)$
has coefficients in
![]() $D_\lambda $
, then so does
$D_\lambda $
, then so does
![]() $(W,B_W)$
. Indeed, at the codimension 1 points of W where
$(W,B_W)$
. Indeed, at the codimension 1 points of W where
![]() $S \rightarrow W$
is étale, we will have the same coefficients on
$S \rightarrow W$
is étale, we will have the same coefficients on
![]() $B_W$
and
$B_W$
and
![]() $B_S$
for the corresponding divisors. Then, we can consider a prime divisor
$B_S$
for the corresponding divisors. Then, we can consider a prime divisor
![]() $Q \subset W$
such that
$Q \subset W$
such that
![]() $S \rightarrow W$
ramifies of order 2 at the generic point of Q. Then, over the generic point of Q, by the Riemann–Hurwitz formula, we have
$S \rightarrow W$
ramifies of order 2 at the generic point of Q. Then, over the generic point of Q, by the Riemann–Hurwitz formula, we have
 $$\begin{align*}{K_{S}}+ cP=f_S^*\left(K_W+\frac{1}{2}Q+\frac{c}{2}Q \right), \end{align*}$$
$$\begin{align*}{K_{S}}+ cP=f_S^*\left(K_W+\frac{1}{2}Q+\frac{c}{2}Q \right), \end{align*}$$
where P is the unique prime divisor in S dominating Q, in other words
![]() $\operatorname {\mathrm {coeff}}_P(B_S)= c \in D_\lambda $
and
$\operatorname {\mathrm {coeff}}_P(B_S)= c \in D_\lambda $
and
![]() $\operatorname {\mathrm {coeff}}_Q(B_W)=\frac {1+c}{2}$
. By the definition of
$\operatorname {\mathrm {coeff}}_Q(B_W)=\frac {1+c}{2}$
. By the definition of
![]() $D_\lambda $
, we must have
$D_\lambda $
, we must have
![]() $c=\frac {m-1+a\lambda ^{-1}}{m}$
for some
$c=\frac {m-1+a\lambda ^{-1}}{m}$
for some
![]() $m \in \mathbb {Z}_{>0}$
and
$m \in \mathbb {Z}_{>0}$
and
![]() $a \in \mathbb {Z}_{\geq 0}$
, and it follows that
$a \in \mathbb {Z}_{\geq 0}$
, and it follows that
Thus, by the inductive hypothesis, we have
Step 5: In this step, we introduce a suitable generalized pair structure on W, and we compare it with
![]() $(W,B_W)$
.
$(W,B_W)$
.
By the canonical bundle formula, the lc-trivial fibration
![]() $f \colon (X,B) \rightarrow W$
induces a generalized pair structure
$f \colon (X,B) \rightarrow W$
induces a generalized pair structure
![]() $(W,\Delta _W,\mathbf {N})$
on W. By [Reference Prokhorov and Shokurov38, § 7.5, (7.5.5)] and the fact that the generic fiber of
$(W,\Delta _W,\mathbf {N})$
on W. By [Reference Prokhorov and Shokurov38, § 7.5, (7.5.5)] and the fact that the generic fiber of
![]() $f \colon (X,B) \rightarrow W$
is a conic with two points, we have
$f \colon (X,B) \rightarrow W$
is a conic with two points, we have
Furthermore, the representatives of the b-divisor
![]() $\mathbf {N}$
are determined up to
$\mathbf {N}$
are determined up to
![]() $\mathbb {Z}$
-linear equivalence.
$\mathbb {Z}$
-linear equivalence.
By [Reference Fujino and Gongyo20, proof of Theorem 1.1], in an lc-trivial fibration
![]() $(Y,\Gamma ) \rightarrow C$
, the total space of the fibration and a minimal (with respect to inclusion) log canonical center
$(Y,\Gamma ) \rightarrow C$
, the total space of the fibration and a minimal (with respect to inclusion) log canonical center
![]() $\Xi $
dominating the base C induce the same generalized pair on the base space. More precisely, they induce the same boundary divisor as
$\Xi $
dominating the base C induce the same generalized pair on the base space. More precisely, they induce the same boundary divisor as
![]() $\mathbb {Q}$
-Weil divisor and the same moduli divisor as
$\mathbb {Q}$
-Weil divisor and the same moduli divisor as
![]() $\mathbb {Q}$
-b-divisor class. Yet, this comparison is possible after the base change induced by the Stein factorization of
$\mathbb {Q}$
-b-divisor class. Yet, this comparison is possible after the base change induced by the Stein factorization of
![]() $\Xi \rightarrow C$
, as
$\Xi \rightarrow C$
, as
![]() $\Xi \rightarrow C$
may not have connected fibers. We observe that the identification between the boundary divisors can also be obtained by inversion of adjunction together with the connectedness principle.
$\Xi \rightarrow C$
may not have connected fibers. We observe that the identification between the boundary divisors can also be obtained by inversion of adjunction together with the connectedness principle.
In our situation, this implies that
![]() $(X,B)$
and
$(X,B)$
and
![]() $(S,B_S)$
induce the same generalized pair on W, up to pull-back to the Stein factorization on
$(S,B_S)$
induce the same generalized pair on W, up to pull-back to the Stein factorization on
![]() $S \rightarrow W$
. In this case, S is generically a 2:1 cover of W. Thus, it follows that
$S \rightarrow W$
. In this case, S is generically a 2:1 cover of W. Thus, it follows that
![]() $(W,\Delta _W,\mathbf {N})$
and
$(W,\Delta _W,\mathbf {N})$
and
![]() $(W,B_W)$
agree once pulled back to S. By construction, we have
$(W,B_W)$
agree once pulled back to S. By construction, we have
![]() $f_S^{\prime *}({K_{W}} + B_W)={K_{S}} + B_S$
, and the moduli b-divisor is trivial. In turn, this implies that
$f_S^{\prime *}({K_{W}} + B_W)={K_{S}} + B_S$
, and the moduli b-divisor is trivial. In turn, this implies that
![]() $\Delta _W=B_W$
and
$\Delta _W=B_W$
and
![]() $f_S^* {\mathbf {N}_{W}} \sim 0$
. As for the moduli b-divisor, we only claim
$f_S^* {\mathbf {N}_{W}} \sim 0$
. As for the moduli b-divisor, we only claim
![]() $\mathbb {Z}$
-linear equivalence, as a representative of the b-divisorial class can be replaced in the
$\mathbb {Z}$
-linear equivalence, as a representative of the b-divisorial class can be replaced in the
![]() $\mathbb {Z}$
-linear equivalence class.
$\mathbb {Z}$
-linear equivalence class.
Let
![]() $S'$
denote the Stein factorization of
$S'$
denote the Stein factorization of
![]() $S \to W$
, with induced morphism
$S \to W$
, with induced morphism
![]() $f_{S'} \colon S' \rightarrow W$
. Then,
$f_{S'} \colon S' \rightarrow W$
. Then,
![]() $f_{S'}$
is a finite Galois morphism of degree 2,
$f_{S'}$
is a finite Galois morphism of degree 2,
![]() $f_{S'}^* {\mathbf {N}_{W}} \sim 0$
. By construction,
$f_{S'}^* {\mathbf {N}_{W}} \sim 0$
. By construction,
![]() $f_{S'}^* {\mathbf {N}_{W}}$
is Galois invariant since it is the
$f_{S'}^* {\mathbf {N}_{W}}$
is Galois invariant since it is the
![]() $\mathbb {Q}$
-Cartier pull-back of a
$\mathbb {Q}$
-Cartier pull-back of a
![]() $\mathbb {Q}$
-divisor on W via the finite morphism
$\mathbb {Q}$
-divisor on W via the finite morphism
![]() $f_{S'}$
. We observe that this implies that
$f_{S'}$
. We observe that this implies that
![]() $2 {\mathbf {N}_{W}}$
is a
$2 {\mathbf {N}_{W}}$
is a
![]() $\mathbb {Z}$
-divisor and that
$\mathbb {Z}$
-divisor and that
![]() $2f_{S'}^* {\mathbf {N}_{W}}$
is the integral pull-back of the integral divisor
$2f_{S'}^* {\mathbf {N}_{W}}$
is the integral pull-back of the integral divisor
![]() $2 {\mathbf {N}_{W}}$
.
$2 {\mathbf {N}_{W}}$
.
Now, let s be a trivializing section of
![]() $f_{S'}^* {\mathbf {N}_{W}}$
, and let
$f_{S'}^* {\mathbf {N}_{W}}$
, and let
![]() $\tau $
be the nontrivial element in the Galois group of
$\tau $
be the nontrivial element in the Galois group of
![]() $S' \rightarrow W$
. By the invariance of
$S' \rightarrow W$
. By the invariance of
![]() $f_{S'}^* {\mathbf {N}_{W}}$
, we have that
$f_{S'}^* {\mathbf {N}_{W}}$
, we have that
![]() $f_{S'}^* {\mathbf {N}_{W}} + \tau ^*f_{S'}^* {\mathbf {N}_{W}}=2f_{S'}^* {\mathbf {N}_{W}}$
. But then,
$f_{S'}^* {\mathbf {N}_{W}} + \tau ^*f_{S'}^* {\mathbf {N}_{W}}=2f_{S'}^* {\mathbf {N}_{W}}$
. But then,
![]() $s \otimes \tau ^*s$
is a Galois invariant trivializing section of
$s \otimes \tau ^*s$
is a Galois invariant trivializing section of
![]() $2f_{S'}^* {\mathbf {N}_{W}}$
. Then, this section descends to W, thus implying that
$2f_{S'}^* {\mathbf {N}_{W}}$
. Then, this section descends to W, thus implying that
Step 6: In this step, we conclude the proof.
Combining the previous steps and using the fact that
![]() $2|I$
, we have
$2|I$
, we have
 $$ \begin{align*} I({K_{X}} + B) &\sim If^*({K_{W}} + B_W + {\mathbf{N}_{W}})\\ &\sim If^*({K_{W}}+B_W) + If^* {\mathbf{N}_{W}}\\ &\sim f^*(I({K_{W}} + B_W)) + f^* I{\mathbf{N}_{W}}\\ &\sim f^*0 + f^*0 \sim 0, \end{align*} $$
$$ \begin{align*} I({K_{X}} + B) &\sim If^*({K_{W}} + B_W + {\mathbf{N}_{W}})\\ &\sim If^*({K_{W}}+B_W) + If^* {\mathbf{N}_{W}}\\ &\sim f^*(I({K_{W}} + B_W)) + f^* I{\mathbf{N}_{W}}\\ &\sim f^*0 + f^*0 \sim 0, \end{align*} $$
where the first linear equivalence follows from Equation (2.6), the second one follows from the fact that
![]() $K_W+B_W$
is
$K_W+B_W$
is
![]() $\mathbb {Q}$
-Cartier, the third one follows from the definition of pull-back of
$\mathbb {Q}$
-Cartier, the third one follows from the definition of pull-back of
![]() $\mathbb {Q}$
-divisors, while the last line follows from Equations (2.5) and (2.7). This concludes the proof.
$\mathbb {Q}$
-divisors, while the last line follows from Equations (2.5) and (2.7). This concludes the proof.
3 Finite coefficients
In this section, we explain how to reduce the problem of boundedness of complements from pairs with DCC coefficients to pairs with finite coefficients. First, we prove two lemmata that will be used in the proof of the main proposition of this section.
Lemma 3.1. Let
![]() $\phi \colon X\rightarrow Z$
be a contraction from a projective
$\phi \colon X\rightarrow Z$
be a contraction from a projective
![]() $\mathbb {Q}$
-factorial variety X. Let
$\mathbb {Q}$
-factorial variety X. Let
![]() $(X,B,\mathbf {M})$
be a generalized dlt pair over Z. Assume
$(X,B,\mathbf {M})$
be a generalized dlt pair over Z. Assume
![]() $(X,B,\mathbf {M})$
is generalized log Calabi–Yau over Z. Assume there is a component
$(X,B,\mathbf {M})$
is generalized log Calabi–Yau over Z. Assume there is a component
![]() $S\subseteq \lfloor B\rfloor $
that is vertical over Z. Then, there exists a birational contraction
$S\subseteq \lfloor B\rfloor $
that is vertical over Z. Then, there exists a birational contraction
![]() $X\dashrightarrow X'$
over Z
$X\dashrightarrow X'$
over Z

satisfying the following conditions:
-
(i) the generalized pair
 $(X',B',\mathbf {M})$
is generalized log canonical;
$(X',B',\mathbf {M})$
is generalized log canonical; -
(ii) the strict transform
 $S'$
of S in
$S'$
of S in
 $X'$
is a divisorial generalized log canonical center of
$X'$
is a divisorial generalized log canonical center of
 $(X',B',\mathbf {M})$
;
$(X',B',\mathbf {M})$
; -
(iii) we have that
 ${\phi '}^{-1}(\phi (S))=S'$
holds set-theoretically; and
${\phi '}^{-1}(\phi (S))=S'$
holds set-theoretically; and -
(iv) the generalized pair obtained by adjunction of
 $(X',B',\mathbf {M})$
to
$(X',B',\mathbf {M})$
to
 $S'$
is generalized semilog canonical.
$S'$
is generalized semilog canonical.
Proof. By [Reference Moraga and Svaldi36, Lemma 3.5], we may run an MMP for
![]() $(X,B-S,\mathbf {M})$
over Z with scaling of an ample divisor A. By the negativity lemma, the divisor S is not contracted by this MMP. Furthermore, this MMP is
$(X,B-S,\mathbf {M})$
over Z with scaling of an ample divisor A. By the negativity lemma, the divisor S is not contracted by this MMP. Furthermore, this MMP is
![]() $(K_X+B+{\mathbf {M}_{X}})$
-trivial. Hence, conditions (i) and (ii) hold for any model in this minimal model program.
$(K_X+B+{\mathbf {M}_{X}})$
-trivial. Hence, conditions (i) and (ii) hold for any model in this minimal model program.
We argue that after finitely many steps condition (iii) holds. Let
![]() $X_i\dashrightarrow X_{i+1}$
be the i-th step of this MMP and
$X_i\dashrightarrow X_{i+1}$
be the i-th step of this MMP and
![]() $\phi _i\colon X_i\rightarrow Z$
be the induced projective morphism. We let
$\phi _i\colon X_i\rightarrow Z$
be the induced projective morphism. We let
![]() $\lambda _i$
the positive real number for which the birational map
$\lambda _i$
the positive real number for which the birational map
![]() $X_i\dashrightarrow X_{i+1}$
is
$X_i\dashrightarrow X_{i+1}$
is
![]() $(K_{X_i}+B_i-S_i+{\mathbf {M}_{X_i}}+\lambda _i A_i)$
-trivial. Let
$(K_{X_i}+B_i-S_i+{\mathbf {M}_{X_i}}+\lambda _i A_i)$
-trivial. Let
![]() $\lambda _\infty =\lim _i \lambda _i$
. If
$\lambda _\infty =\lim _i \lambda _i$
. If
![]() $\lambda _\infty>0$
, then the previous MMP is also an MMP for
$\lambda _\infty>0$
, then the previous MMP is also an MMP for
![]() $(X,B-S+\lambda _\infty A,\mathbf {M})$
. By [Reference Moraga and Svaldi36, Lemma 3.7], this is also an MMP for a klt pair with big boundary over Z which must terminate by [Reference Birkar, Cascini and Hacon6]. Let
$(X,B-S+\lambda _\infty A,\mathbf {M})$
. By [Reference Moraga and Svaldi36, Lemma 3.7], this is also an MMP for a klt pair with big boundary over Z which must terminate by [Reference Birkar, Cascini and Hacon6]. Let
![]() $X'$
be the model where this MMP terminates. In
$X'$
be the model where this MMP terminates. In
![]() $X'$
, we have that
$X'$
, we have that
![]() $-S'$
is nef over Z. So
$-S'$
is nef over Z. So
![]() $S'$
must be the set-theoretic preimage of
$S'$
must be the set-theoretic preimage of
![]() $\phi '(S')$
.
$\phi '(S')$
.
From now on, we assume that
![]() $\lambda _\infty =0$
. Let
$\lambda _\infty =0$
. Let
![]() $W_1,\dots ,W_k$
be the irreducible components of
$W_1,\dots ,W_k$
be the irreducible components of
![]() $\phi ^{-1}(\phi (S))$
different than S. Note that every step of the MMP is S-positive. Thus, if the strict transform of any component
$\phi ^{-1}(\phi (S))$
different than S. Note that every step of the MMP is S-positive. Thus, if the strict transform of any component
![]() $W_j$
is contained in the exceptional locus of
$W_j$
is contained in the exceptional locus of
![]() $X_i\dashrightarrow X_{i+1}$
, then the number of components of
$X_i\dashrightarrow X_{i+1}$
, then the number of components of
![]() $\phi _i^{-1}(\phi (S))$
drops. Henceforth, it suffices to show that each such component is eventually contained in the exceptional locus of a step of the MMP. Assume
$\phi _i^{-1}(\phi (S))$
drops. Henceforth, it suffices to show that each such component is eventually contained in the exceptional locus of a step of the MMP. Assume
![]() $\phi (W_1)\subseteq \phi (S)$
is maximal among the sets
$\phi (W_1)\subseteq \phi (S)$
is maximal among the sets
![]() $\phi (W_j)$
’s with respect to the inclusion. Let
$\phi (W_j)$
’s with respect to the inclusion. Let
![]() $z\in \phi (W_1)$
be a general point. Up to reordering the
$z\in \phi (W_1)$
be a general point. Up to reordering the
![]() $W_j$
’s, since
$W_j$
’s, since
![]() $X \rightarrow Z$
has connected fibers, we may assume that
$X \rightarrow Z$
has connected fibers, we may assume that
![]() $\phi ^{-1}(z)\cap W_1\cap S$
is nonempty. Hence, for a general point
$\phi ^{-1}(z)\cap W_1\cap S$
is nonempty. Hence, for a general point
![]() $w \in \phi ^{-1}(z)\cap W_1$
, we can find a curve C such that
$w \in \phi ^{-1}(z)\cap W_1$
, we can find a curve C such that
![]() $w \in C$
,
$w \in C$
,
![]() $C \nsubseteq S$
, and C intersects S nontrivially. In particular, we have that
$C \nsubseteq S$
, and C intersects S nontrivially. In particular, we have that
![]() $C\subseteq \mathrm {Bs}_{-}(K_X+B-S+{\mathbf {M}_{X}}/Z)$
. In particular, since we have
$C\subseteq \mathrm {Bs}_{-}(K_X+B-S+{\mathbf {M}_{X}}/Z)$
. In particular, since we have
![]() $w \in C$
, it follows that
$w \in C$
, it follows that
![]() $w \in \mathrm {Bs}_{-}(K_X+B-S+{\mathbf {M}_{X}}/Z)$
. Since w is a general point in
$w \in \mathrm {Bs}_{-}(K_X+B-S+{\mathbf {M}_{X}}/Z)$
. Since w is a general point in
![]() $\phi ^{-1}(z)\cap W_1$
, we also get that
$\phi ^{-1}(z)\cap W_1$
, we also get that
![]() $\phi ^{-1}(z)\cap W_1 \subseteq \mathrm {Bs}_{-}(K_X+B-S+{\mathbf {M}_{X}}/Z)$
. Since z is general, we conclude that
$\phi ^{-1}(z)\cap W_1 \subseteq \mathrm {Bs}_{-}(K_X+B-S+{\mathbf {M}_{X}}/Z)$
. Since z is general, we conclude that
![]() $W_1 \subset \mathrm {Bs}_{-}(K_X+B-S+{\mathbf {M}_{X}}/Z)$
. For
$W_1 \subset \mathrm {Bs}_{-}(K_X+B-S+{\mathbf {M}_{X}}/Z)$
. For
![]() $\lambda _1>0$
small enough, we have that
$\lambda _1>0$
small enough, we have that
Since
![]() $\lambda _\infty =0$
, we conclude that for some i the birational map
$\lambda _\infty =0$
, we conclude that for some i the birational map
![]() $X\dashrightarrow X_i$
is a minimal model for
$X\dashrightarrow X_i$
is a minimal model for
![]() $(X,B-S+\lambda _1A,\mathbf {M}/Z)$
. In particular,
$(X,B-S+\lambda _1A,\mathbf {M}/Z)$
. In particular,
![]() $W_1$
must be contained in the exceptional locus of
$W_1$
must be contained in the exceptional locus of
![]() $X\dashrightarrow X_i$
. Hence, after finitely many steps of this MMP, condition (iii) is satisfied.
$X\dashrightarrow X_i$
. Hence, after finitely many steps of this MMP, condition (iii) is satisfied.
Let
![]() $X'$
be a model where condition (iii) holds. By construction, the generalized pair
$X'$
be a model where condition (iii) holds. By construction, the generalized pair
![]() $(X',B',\mathbf {M})$
is obtained by a partial run
$(X',B',\mathbf {M})$
is obtained by a partial run
![]() $X\dashrightarrow X'$
of the MMP for
$X\dashrightarrow X'$
of the MMP for
![]() $(X,B-S,\mathbf {M})$
. In particular,
$(X,B-S,\mathbf {M})$
. In particular,
![]() $(X',B'-S',\mathbf {M})$
is generalized dlt and
$(X',B'-S',\mathbf {M})$
is generalized dlt and
![]() $\mathbb {Q}$
-factorial. Hence,
$\mathbb {Q}$
-factorial. Hence,
![]() $(X',B'-\epsilon \lfloor B'\rfloor )$
is klt, where
$(X',B'-\epsilon \lfloor B'\rfloor )$
is klt, where
![]() $0 < \epsilon \ll 1$
. By [Reference Fujino and Gongyo19, Example 2.6], the pair obtained by adjunction of
$0 < \epsilon \ll 1$
. By [Reference Fujino and Gongyo19, Example 2.6], the pair obtained by adjunction of
![]() $(X',B'-\epsilon \lfloor B'\rfloor +\epsilon S')$
to
$(X',B'-\epsilon \lfloor B'\rfloor +\epsilon S')$
to
![]() $S'$
is semilog canonical. In turn, by letting
$S'$
is semilog canonical. In turn, by letting
![]() $\epsilon \to 0$
, it follows that the pair obtained by adjunction of
$\epsilon \to 0$
, it follows that the pair obtained by adjunction of
![]() $(X',B')$
to
$(X',B')$
to
![]() $S'$
is semilog canonical. Hence, the generalized pair obtained by adjunction of
$S'$
is semilog canonical. Hence, the generalized pair obtained by adjunction of
![]() $(X',B',\mathbf {M})$
to
$(X',B',\mathbf {M})$
to
![]() $S'$
is generalized semilog canonical.
$S'$
is generalized semilog canonical.
Lemma 3.2. Let c and p be nonnegative integers and
![]() $\Lambda \subset \mathbb {Q}_{>0}$
be a closed set satisfying the DCC. There exists a finite subset
$\Lambda \subset \mathbb {Q}_{>0}$
be a closed set satisfying the DCC. There exists a finite subset ![]() satisfying the following. Let
satisfying the following. Let
![]() $(X,B,\mathbf {M})$
be a generalized log canonical pair over Z and
$(X,B,\mathbf {M})$
be a generalized log canonical pair over Z and
![]() $X\rightarrow Z$
be a fibration for which the following conditions hold:
$X\rightarrow Z$
be a fibration for which the following conditions hold:
-
• the generalized pair
 $(X,B,\mathbf {M})$
is log Calabi–Yau over Z;
$(X,B,\mathbf {M})$
is log Calabi–Yau over Z; -
• the generalized pair
 $(X,B,\mathbf {M})$
has coregularity c;
$(X,B,\mathbf {M})$
has coregularity c; -
•
 $p\mathbf {M}$
is b-Cartier; and
$p\mathbf {M}$
is b-Cartier; and -
• the coefficients of B belong to
 $\Lambda $
.
$\Lambda $
.
Then, the coefficients of
![]() $B_{\mathrm {hor}}$
belong to
$B_{\mathrm {hor}}$
belong to
![]() $\mathcal {R}$
.
$\mathcal {R}$
.
Proof. Let
![]() $(X_i,B_i,{\mathbf {M}_{i}})$
be a sequence of generalized pairs as in the statement and
$(X_i,B_i,{\mathbf {M}_{i}})$
be a sequence of generalized pairs as in the statement and
![]() $\phi _i\colon X_i\rightarrow Z_i$
be the corresponding contractions. Assume there exist prime divisors
$\phi _i\colon X_i\rightarrow Z_i$
be the corresponding contractions. Assume there exist prime divisors
![]() $P_i\subset X_i$
for which
$P_i\subset X_i$
for which ![]() is strictly increasing and
is strictly increasing and
![]() $P_i$
dominates
$P_i$
dominates
![]() $Z_i$
. Assume that some generalized log canonical center of
$Z_i$
. Assume that some generalized log canonical center of
![]() $(X_i,B_i,{\mathbf {M}_{i}})$
is vertical over
$(X_i,B_i,{\mathbf {M}_{i}})$
is vertical over
![]() $Z_i$
. We may replace
$Z_i$
. We may replace
![]() $(X_i,B_i,{\mathbf {M}_{i}})$
with a generalized dlt modification and assume there is a component
$(X_i,B_i,{\mathbf {M}_{i}})$
with a generalized dlt modification and assume there is a component
![]() $S_i\subseteq \lfloor B_i\rfloor $
that is vertical over
$S_i\subseteq \lfloor B_i\rfloor $
that is vertical over
![]() $Z_i$
. Furthermore, up to choosing a different vertical component possibly dominating a different subset of
$Z_i$
. Furthermore, up to choosing a different vertical component possibly dominating a different subset of
![]() $Z_i$
, we may assume that there is a generalized log canonical center of
$Z_i$
, we may assume that there is a generalized log canonical center of
![]() $(X_i,B_i,{\mathbf {M}_{i}})$
dimension c contained in
$(X_i,B_i,{\mathbf {M}_{i}})$
dimension c contained in
![]() $S_i$
. By Lemma 3.1, up to losing the dlt property for
$S_i$
. By Lemma 3.1, up to losing the dlt property for
![]() $(X_i,B_i,{\mathbf {M}_{i}})$
, we may assume that
$(X_i,B_i,{\mathbf {M}_{i}})$
, we may assume that
![]() $S_i$
is the set-theoretic preimage of
$S_i$
is the set-theoretic preimage of
![]() $\phi $
. Let
$\phi $
. Let
![]() $W_i$
be the normalization of
$W_i$
be the normalization of
![]() $S_i$
, and let
$S_i$
, and let
![]() $W_i\rightarrow Z_{W_i}$
be the fibration obtained by the Stein factorization of
$W_i\rightarrow Z_{W_i}$
be the fibration obtained by the Stein factorization of
![]() $W_i\rightarrow \phi _i(S_i)$
. Let
$W_i\rightarrow \phi _i(S_i)$
. Let
![]() $(W_i,B_i,{\mathbf {N}_{i}})$
be the generalized pair obtained by generalized adjunction of
$(W_i,B_i,{\mathbf {N}_{i}})$
be the generalized pair obtained by generalized adjunction of
![]() $(X_i,B_i,{\mathbf {M}_{i}})$
to
$(X_i,B_i,{\mathbf {M}_{i}})$
to
![]() $W_i$
. Note that
$W_i$
. Note that
![]() $P_i\cap S_i$
dominates
$P_i\cap S_i$
dominates
![]() $\phi (S_i)$
. Hence, there is a component of
$\phi (S_i)$
. Hence, there is a component of
![]() $B_{W_i}$
with coefficient in
$B_{W_i}$
with coefficient in
![]() $D_{d_i}(\Lambda )$
which is horizontal over
$D_{d_i}(\Lambda )$
which is horizontal over
![]() $Z_{W_i}$
(see Lemma 2.17). Observe that the following conditions hold:
$Z_{W_i}$
(see Lemma 2.17). Observe that the following conditions hold:
-
• the generalized pair
 $(W_i,B_i,{\mathbf {N}_{i}})$
is log Calabi–Yau over
$(W_i,B_i,{\mathbf {N}_{i}})$
is log Calabi–Yau over
 $Z_{W_i}$
;
$Z_{W_i}$
; -
• the generalized pair
 $(W_i,B_i,{\mathbf {N}_{i}})$
has coregularity c;
$(W_i,B_i,{\mathbf {N}_{i}})$
has coregularity c; -
•
 $p{\mathbf {N}_{i}}$
is b-Cartier;
$p{\mathbf {N}_{i}}$
is b-Cartier; -
• the coefficients of
 $B_{W_i}$
belong to
$B_{W_i}$
belong to
 $D(\Lambda )$
; and
$D(\Lambda )$
; and -
• there is a component
 $Q_i$
of
$Q_i$
of
 $B_{W_i}$
horizontal over
$B_{W_i}$
horizontal over
 $Z_i$
whose coefficient belong to
$Z_i$
whose coefficient belong to
 $D_{d_i}(\Lambda )$
.
$D_{d_i}(\Lambda )$
.
We replace
![]() $(X_i,B_i,{\mathbf {M}_{i}})$
with
$(X_i,B_i,{\mathbf {M}_{i}})$
with
![]() $(W_i,B_{W_i},{\mathbf {N}_{i}})$
and
$(W_i,B_{W_i},{\mathbf {N}_{i}})$
and
![]() $P_i$
with
$P_i$
with
![]() $Q_i$
. After finitely many replacements, we may assume that for every i the generalized log canonical centers of
$Q_i$
. After finitely many replacements, we may assume that for every i the generalized log canonical centers of
![]() $(X_i,B_i,{\mathbf {M}_{i}})$
are horizontal over
$(X_i,B_i,{\mathbf {M}_{i}})$
are horizontal over
![]() $Z_i$
. [Reference Figueroa, Moraga and Peng10, Theorem 2] applied to the general fiber of
$Z_i$
. [Reference Figueroa, Moraga and Peng10, Theorem 2] applied to the general fiber of
![]() $X_i\rightarrow Z_i$
implies that the coefficients of
$X_i\rightarrow Z_i$
implies that the coefficients of
![]() $B_{\mathrm {hor}}$
belong to an ACC set. Thus, we conclude that the coefficients of
$B_{\mathrm {hor}}$
belong to an ACC set. Thus, we conclude that the coefficients of
![]() $B_{\mathrm {hor}}$
belong to a finite set
$B_{\mathrm {hor}}$
belong to a finite set
![]() $\mathcal {R}$
which only depends on c, p and
$\mathcal {R}$
which only depends on c, p and
![]() $\Lambda $
.
$\Lambda $
.
The proof of the following corollary is verbatim from the previous proof by replacing [Reference Figueroa, Moraga and Peng10, Theorem 2] with [Reference Filipazzi, Mauri and Moraga13, Corollary 3].
Corollary 3.3. Let
![]() $(X,B,\mathbf {M})$
be a generalized log canonical pair over Z and
$(X,B,\mathbf {M})$
be a generalized log canonical pair over Z and
![]() $X\rightarrow Z$
be a fibration for which the following conditions hold:
$X\rightarrow Z$
be a fibration for which the following conditions hold:
-
• the generalized pair
 $(X,B,\mathbf {M})$
is log Calabi–Yau over Z;
$(X,B,\mathbf {M})$
is log Calabi–Yau over Z; -
• the generalized pair
 $(X,B,\mathbf {M})$
has coregularity
$(X,B,\mathbf {M})$
has coregularity
 $0$
;
$0$
; -
•
 $2\mathbf {M}$
is b-Cartier; and
$2\mathbf {M}$
is b-Cartier; and -
• the coefficients of B belong to
 $\mathcal {S}$
.
$\mathcal {S}$
.
Then, the coefficients of
![]() $B_{\mathrm {hor}}$
belong to
$B_{\mathrm {hor}}$
belong to
![]() $\{1,\frac {1}{2}\}$
.
$\{1,\frac {1}{2}\}$
.
Notation 3.4. Let
![]() $\Lambda \subset \mathbb {Q}_{>0}$
be a closed set of rational numbers satisfying the DCC. Given a natural number
$\Lambda \subset \mathbb {Q}_{>0}$
be a closed set of rational numbers satisfying the DCC. Given a natural number
![]() $m\in \mathbb {Z}_{>0}$
, we consider the partition
$m\in \mathbb {Z}_{>0}$
, we consider the partition

of the interval
![]() $[0,1]$
. Denote by
$[0,1]$
. Denote by
![]() $I(b,m)$
the interval of
$I(b,m)$
the interval of
![]() $\mathcal {P}_m$
containing
$\mathcal {P}_m$
containing
![]() $b\in \Lambda $
. Define the number
$b\in \Lambda $
. Define the number
For every positive integer m and every
![]() $b \in \Lambda $
, we have that
$b \in \Lambda $
, we have that
![]() $b\leq b_m$
as
$b\leq b_m$
as
![]() $b\in \Lambda \cap I(b,m)$
. If
$b\in \Lambda \cap I(b,m)$
. If
![]() $b\in \Lambda $
is fixed and m divisible enough, we have that
$b\in \Lambda $
is fixed and m divisible enough, we have that
![]() $b=b_m$
. The set
$b=b_m$
. The set ![]() is finite, and we have that the set
is finite, and we have that the set
satisfies the DCC. Given a boundary divisor
![]() $B\geq 0$
on a quasi-projective variety X, we can write
$B\geq 0$
on a quasi-projective variety X, we can write
![]() $B=\sum _j b^{(j)}B^{(j)}$
in a unique way such that the
$B=\sum _j b^{(j)}B^{(j)}$
in a unique way such that the
![]() $B^{(j)}$
’s are pairwise different prime divisors on X. If the coefficients of B belong to
$B^{(j)}$
’s are pairwise different prime divisors on X. If the coefficients of B belong to
![]() $\Lambda $
, we define
$\Lambda $
, we define
It follows that
![]() $B\leq B_m$
.
$B\leq B_m$
.
Theorem 3.5. Let c and p be nonnegative integers and
![]() $\Lambda \subset \mathbb {Q}_{>0}$
be a set satisfying the DCC with rational accumulation points. There exists a finite subset
$\Lambda \subset \mathbb {Q}_{>0}$
be a set satisfying the DCC with rational accumulation points. There exists a finite subset ![]() satisfying the following. Let
satisfying the following. Let
![]() $(X,B,\mathbf {M})$
be a generalized log canonical pair over Z,
$(X,B,\mathbf {M})$
be a generalized log canonical pair over Z,
![]() $X\rightarrow Z$
be a contraction and
$X\rightarrow Z$
be a contraction and
![]() $z\in Z$
be a point. Assume the following conditions are satisfied:
$z\in Z$
be a point. Assume the following conditions are satisfied:
-
• the variety X is of Fano type over Z;
-
• the divisor B has coefficients in
 $\Lambda $
;
$\Lambda $
; -
•
 $p\mathbf {M}$
is b-Cartier;
$p\mathbf {M}$
is b-Cartier; -
• the generalized pair
 $(X,B,\mathbf {M})$
has coregularity c around z; and
$(X,B,\mathbf {M})$
has coregularity c around z; and -
• the divisor
 $-(K_X+B+{\mathbf {M}_{X}})$
is nef over Z.
$-(K_X+B+{\mathbf {M}_{X}})$
is nef over Z.
There exists a birational transformation
![]() $X\dashrightarrow X'$
over Z and a generalized pair
$X\dashrightarrow X'$
over Z and a generalized pair
![]() $(X',\Gamma ',\mathbf {M})$
satisfying the following:
$(X',\Gamma ',\mathbf {M})$
satisfying the following:
-
• the coefficients of
 $\Gamma '$
belong to
$\Gamma '$
belong to
 $\mathcal {R}$
;
$\mathcal {R}$
; -
• the pair
 $(X',\Gamma ',\mathbf {M})$
has coregularity c over z;
$(X',\Gamma ',\mathbf {M})$
has coregularity c over z; -
• the divisor
 $-(K_{X'}+\Gamma '+{\mathbf {M}_{X'}})$
is nef over a neighborhood of
$-(K_{X'}+\Gamma '+{\mathbf {M}_{X'}})$
is nef over a neighborhood of
 $z\in Z$
; and
$z\in Z$
; and -
• if
 $(X',\Gamma ',\mathbf {M})$
is N-complemented over
$(X',\Gamma ',\mathbf {M})$
is N-complemented over
 $z\in Z$
, then
$z\in Z$
, then
 $(X,B,\mathbf {M})$
is N-complemented over
$(X,B,\mathbf {M})$
is N-complemented over
 $z\in Z$
.
$z\in Z$
.
Proof. Let
![]() $(X,B,\mathbf {M})$
be a generalized pair as in the conditions of the theorem. By passing to a
$(X,B,\mathbf {M})$
be a generalized pair as in the conditions of the theorem. By passing to a
![]() $\mathbb {Q}$
-factorial generalized dlt modification, we may assume the considered generalized pairs are gdlt and
$\mathbb {Q}$
-factorial generalized dlt modification, we may assume the considered generalized pairs are gdlt and
![]() $\mathbb {Q}$
-factorial. We denote by
$\mathbb {Q}$
-factorial. We denote by
![]() $m(X,B,\mathbf {M})$
the minimal m for which
$m(X,B,\mathbf {M})$
the minimal m for which
![]() $\mathcal {R}=\mathcal {C}_{m}$
satisfies the statement of the theorem for
$\mathcal {R}=\mathcal {C}_{m}$
satisfies the statement of the theorem for
![]() $(X,B,\mathbf {M})$
. Since
$(X,B,\mathbf {M})$
. Since
![]() $B_m=B$
for m large enough, then
$B_m=B$
for m large enough, then
![]() $m(X,b,\mathbf {M})$
is finite. It suffices to show that
$m(X,b,\mathbf {M})$
is finite. It suffices to show that
![]() $m(X,B,\mathbf {M})$
is bounded above by a constant that only depends on c, p and
$m(X,B,\mathbf {M})$
is bounded above by a constant that only depends on c, p and
![]() $\Lambda $
. Assume that this is not the case. Then, we may find a sequence of generalized pairs
$\Lambda $
. Assume that this is not the case. Then, we may find a sequence of generalized pairs
![]() $(X_i,B_i, {\mathbf {M}_{i}})$
, contractions
$(X_i,B_i, {\mathbf {M}_{i}})$
, contractions
![]() $X_i\rightarrow Z_i$
and closed points
$X_i\rightarrow Z_i$
and closed points
![]() $z_i\in Z_i$
, satisfying the conditions of the theorem, for which
$z_i\in Z_i$
, satisfying the conditions of the theorem, for which ![]() is strictly increasing. In particular, we have that
is strictly increasing. In particular, we have that
![]() $B_{i,m_i}-B_i$
is a nontrivial effective divisor. Let
$B_{i,m_i}-B_i$
is a nontrivial effective divisor. Let
![]() $P_i$
be a prime component of
$P_i$
be a prime component of
![]() $B_{i,m_i}-B_i$
that intersects the fiber over z. We study how the singularities of
$B_{i,m_i}-B_i$
that intersects the fiber over z. We study how the singularities of
![]() $(X_i,B_i,{\mathbf {M}_{i}})$
over
$(X_i,B_i,{\mathbf {M}_{i}})$
over
![]() $z_i\in Z_i$
and the nefness of
$z_i\in Z_i$
and the nefness of
![]() $-(K_{X_i}+B_i+{\mathbf {M}_{i}})$
over
$-(K_{X_i}+B_i+{\mathbf {M}_{i}})$
over
![]() $Z_i$
change as we increase the coefficient at
$Z_i$
change as we increase the coefficient at
![]() $P_i$
.
$P_i$
.
Step 1: For the generalized pair
![]() $(X_i,B_i,{\mathbf {M}_{i}})$
, we will produce a positive real number
$(X_i,B_i,{\mathbf {M}_{i}})$
, we will produce a positive real number
![]() $t_i$
which either computes a log canonical threshold or a pseudo-effective threshold.
$t_i$
which either computes a log canonical threshold or a pseudo-effective threshold.
For each generalized pair
![]() $(X_i,B_i,{\mathbf {M}_{i}})$
, we will define a real number
$(X_i,B_i,{\mathbf {M}_{i}})$
, we will define a real number
![]() $t_i$
as follows. We consider the generalized pairs
$t_i$
as follows. We consider the generalized pairs
Let
![]() $t_{i,0}$
be the largest real number for which the generalized pair (3.1) is generalized log canonical over
$t_{i,0}$
be the largest real number for which the generalized pair (3.1) is generalized log canonical over
![]() $z_i\in Z_i$
and
$z_i\in Z_i$
and
is nef over a neighborhood of
![]() $z_i\in Z_i$
. Assume that
$z_i\in Z_i$
. Assume that
![]() $t_{i,0}<1$
. Then, for
$t_{i,0}<1$
. Then, for
![]() $t>t_{i,0}$
close enough to
$t>t_{i,0}$
close enough to
![]() $t_{i,0}$
one of the following conditions hold:
$t_{i,0}$
one of the following conditions hold:
-
(i) the generalized pair
 $(X_i,B_{i,t},{\mathbf {M}_{i}})$
is not generalized log canonical over
$(X_i,B_{i,t},{\mathbf {M}_{i}})$
is not generalized log canonical over
 $z_i\in Z_i$
; or
$z_i\in Z_i$
; or -
(ii) the divisor
 $-(K_{X_i}+B_{i,t}+{\mathbf {M}_{i,X_i}})$
is not pseudo-effective over a neighborhood of
$-(K_{X_i}+B_{i,t}+{\mathbf {M}_{i,X_i}})$
is not pseudo-effective over a neighborhood of
 $z_i\in Z_i$
and
$z_i\in Z_i$
and
 $(X_i,B_{i,t},{\mathbf {M}_{i}})$
is generalized log canonical over a neighborhood of
$(X_i,B_{i,t},{\mathbf {M}_{i}})$
is generalized log canonical over a neighborhood of
 $z_i \in Z_i$
; or
$z_i \in Z_i$
; or -
(iii) the divisor
 $-(K_{X_i}+B_{i,t}+{\mathbf {M}_{i,X_i}})$
is pseudo-effective, but it is not nef over every neighborhood of
$-(K_{X_i}+B_{i,t}+{\mathbf {M}_{i,X_i}})$
is pseudo-effective, but it is not nef over every neighborhood of
 $z_i\in Z_i$
and
$z_i\in Z_i$
and
 $(X_i,B_{i,t},{\mathbf {M}_{i}})$
is generalized log canonical over a neighborhood of
$(X_i,B_{i,t},{\mathbf {M}_{i}})$
is generalized log canonical over a neighborhood of
 $z_i \in Z_i$
.
$z_i \in Z_i$
.
Assume that case (i) holds. Then, we set
We show that
![]() $t_i$
computes a generalized log canonical threshold of coregularity at most c. Indeed, we have that
$t_i$
computes a generalized log canonical threshold of coregularity at most c. Indeed, we have that
so
![]() $t_i$
is a generalized log canonical threshold over
$t_i$
is a generalized log canonical threshold over
![]() $z_i\in Z_i$
. By construction, the support of
$z_i\in Z_i$
. By construction, the support of
![]() $P_i$
contains a generalized log canonical center of the generalized pair
$P_i$
contains a generalized log canonical center of the generalized pair
![]() $(X_i,B_i+t_iP_i,{\mathbf {M}_{i}})$
. Set
$(X_i,B_i+t_iP_i,{\mathbf {M}_{i}})$
. Set ![]() as a nef b-divisor over
as a nef b-divisor over
![]() $Z_i$
, that is, we set
$Z_i$
, that is, we set
![]() ${\mathbf {N}_{i}}$
to be the b-Cartier closure of
${\mathbf {N}_{i}}$
to be the b-Cartier closure of
![]() $-(K_{X_i}+B_i+t_iP_i+{\mathbf {M}_{i,X_i}})$
. Then, we have that
$-(K_{X_i}+B_i+t_iP_i+{\mathbf {M}_{i,X_i}})$
. Then, we have that
is a generalized log Calabi–Yau pair over
![]() $Z_i$
. Furthermore, the generalized log canonical centers of Equation (3.2) are the same as the generalized log canonical centers of
$Z_i$
. Furthermore, the generalized log canonical centers of Equation (3.2) are the same as the generalized log canonical centers of
![]() $(X_i,B_i+t_iP_i,{\mathbf {M}_{i}})$
. By [Reference Filipazzi and Svaldi16, Theorem 1.4], up to replacing
$(X_i,B_i+t_iP_i,{\mathbf {M}_{i}})$
. By [Reference Filipazzi and Svaldi16, Theorem 1.4], up to replacing
![]() $(X_i,B_i+t_iP_i,{\mathbf {M}_{i}})$
with a generalized dlt modification, the support of
$(X_i,B_i+t_iP_i,{\mathbf {M}_{i}})$
with a generalized dlt modification, the support of
![]() $P_i$
contains a generalized log canonical center of
$P_i$
contains a generalized log canonical center of
![]() $(X_i,B_i+t_iP_i,{\mathbf {M}_{i}})$
of dimension at most c. Hence,
$(X_i,B_i+t_iP_i,{\mathbf {M}_{i}})$
of dimension at most c. Hence,
![]() $t_i$
is a generalized log canonical threshold of coregularity at most c.
$t_i$
is a generalized log canonical threshold of coregularity at most c.
Assume that case (ii) holds. Then, we set
In this case, we can find a Mori fiber space structure
![]() $X^{\prime }_i\rightarrow W_i$
over
$X^{\prime }_i\rightarrow W_i$
over
![]() $Z_i$
such that the following conditions are satisfied:
$Z_i$
such that the following conditions are satisfied:
-
• the generalized pair
 $(X^{\prime }_i,B^{\prime }_i-\mathrm {coeff}_{P^{\prime }_i}(B^{\prime }_i)P^{\prime }_i+t_iP^{\prime }_i,{\mathbf {M}_{i}})$
is generalized log Calabi–Yau over
$(X^{\prime }_i,B^{\prime }_i-\mathrm {coeff}_{P^{\prime }_i}(B^{\prime }_i)P^{\prime }_i+t_iP^{\prime }_i,{\mathbf {M}_{i}})$
is generalized log Calabi–Yau over
 $W_i$
;
$W_i$
; -
• the prime divisor
 $P^{\prime }_i$
is ample over
$P^{\prime }_i$
is ample over
 $W_i$
.
$W_i$
.
Note that
![]() $(X^{\prime }_i,B^{\prime }_i-\mathrm {coeff}_{P^{\prime }_i}(B^{\prime }_i)P^{\prime }_i+t_iB^{\prime }_i,{\mathbf {M}_{i}})$
has coregularity at most c. We have that
$(X^{\prime }_i,B^{\prime }_i-\mathrm {coeff}_{P^{\prime }_i}(B^{\prime }_i)P^{\prime }_i+t_iB^{\prime }_i,{\mathbf {M}_{i}})$
has coregularity at most c. We have that
![]() $t_i$
is the coefficient of a component of
$t_i$
is the coefficient of a component of
![]() $B^{\prime }_i-\mathrm {coeff}_{P^{\prime }_i}(B^{\prime }_i)+t_iP^{\prime }_i$
which is horizontal over
$B^{\prime }_i-\mathrm {coeff}_{P^{\prime }_i}(B^{\prime }_i)+t_iP^{\prime }_i$
which is horizontal over
![]() $W_i$
.
$W_i$
.
From now on, we assume that (i) and (ii) do not happen. Assume that (iii) holds. Then, there exists a birational contraction
![]() $X_i\dashrightarrow X^{\prime }_i$
which is
$X_i\dashrightarrow X^{\prime }_i$
which is
![]() $(K_{X_i}+B_{i,t_{i,0}}+{\mathbf {M}_{i,X_i}})$
-trivial. Indeed, this contraction is defined by the partial
$(K_{X_i}+B_{i,t_{i,0}}+{\mathbf {M}_{i,X_i}})$
-trivial. Indeed, this contraction is defined by the partial
![]() $-(K_{X_i}+B_{i,t'}+{\mathbf {M}_{i,X_i}})$
-MMP with scaling of
$-(K_{X_i}+B_{i,t'}+{\mathbf {M}_{i,X_i}})$
-MMP with scaling of
![]() $P_i$
, for
$P_i$
, for
![]() $t'$
close enough to
$t'$
close enough to
![]() $t_{i,0}$
as in (iii). By construction, the first scaling factor is
$t_{i,0}$
as in (iii). By construction, the first scaling factor is
![]() $t'-t_{i,0}$
, and since
$t'-t_{i,0}$
, and since
![]() $-(K_{X_i}+B_{i,t'}+{\mathbf {M}_{i,X_i}})$
is pseudo-effective over
$-(K_{X_i}+B_{i,t'}+{\mathbf {M}_{i,X_i}})$
is pseudo-effective over
![]() $Z_i$
and
$Z_i$
and
![]() $X_i \rightarrow Z_i$
is of Fano type, this MMP terminates with a good minimal model. In particular, at the last step of this MMP, the scaling factor is 0. Then,
$X_i \rightarrow Z_i$
is of Fano type, this MMP terminates with a good minimal model. In particular, at the last step of this MMP, the scaling factor is 0. Then,
![]() $X_i'$
is the outcome of the last step where the scaling factor is
$X_i'$
is the outcome of the last step where the scaling factor is
![]() $t'-t_{i,0}$
. In particular, we have that
$t'-t_{i,0}$
. In particular, we have that
![]() $-(K_{X^{\prime }_i}+B^{\prime }_{i,t}+{\mathbf {M}_{i, X_i'}})$
is nef over
$-(K_{X^{\prime }_i}+B^{\prime }_{i,t}+{\mathbf {M}_{i, X_i'}})$
is nef over
![]() $Z_i$
for
$Z_i$
for
![]() $t>t_{i,0}$
close enough to
$t>t_{i,0}$
close enough to
![]() $t_{i,0}$
. Note that an N-complement of
$t_{i,0}$
. Note that an N-complement of
![]() $(X_i',B^{\prime }_{i,t_{i,0}},{\mathbf {M}_{X_i'}})$
induces an N-complement of
$(X_i',B^{\prime }_{i,t_{i,0}},{\mathbf {M}_{X_i'}})$
induces an N-complement of
![]() $(X_i,B_{i,t_{i,0}},{\mathbf {M}_{i}})$
by pulling back, and so an N-complement of
$(X_i,B_{i,t_{i,0}},{\mathbf {M}_{i}})$
by pulling back, and so an N-complement of
![]() $(X_i,B_i,{\mathbf {M}_{i}})$
. Henceforth, we may replace
$(X_i,B_i,{\mathbf {M}_{i}})$
. Henceforth, we may replace
![]() $X_i$
with
$X_i$
with
![]() $X^{\prime }_i$
and keep increasing t. Since
$X^{\prime }_i$
and keep increasing t. Since
![]() $X_i$
is of Fano type over
$X_i$
is of Fano type over
![]() $Z_i$
, there are only finitely many birational contractions
$Z_i$
, there are only finitely many birational contractions
![]() $X_i\dashrightarrow X^{\prime }_i$
. Therefore, we can replace
$X_i\dashrightarrow X^{\prime }_i$
. Therefore, we can replace
![]() $X_i$
with
$X_i$
with
![]() $X_i'$
only finitely many times. Thus, after finitely many birational contractions, we either have that
$X_i'$
only finitely many times. Thus, after finitely many birational contractions, we either have that
![]() $t_{i,0}=1$
, that
$t_{i,0}=1$
, that
![]() $t_i<1$
is a log canonical threshold or that
$t_i<1$
is a log canonical threshold or that
![]() $t_i<1$
is a pseudo-effective threshold.
$t_i<1$
is a pseudo-effective threshold.
We assume that
![]() $t_{i,0}=1$
. Then there exists a birational contraction
$t_{i,0}=1$
. Then there exists a birational contraction
![]() $X_i \dashrightarrow X^{\prime }_i$
and a generalized log canonical pair
$X_i \dashrightarrow X^{\prime }_i$
and a generalized log canonical pair
for which the divisor
is nef over
![]() $Z_i$
. Note that the coefficients of the boundary of the generalized pair (3.3) belong to
$Z_i$
. Note that the coefficients of the boundary of the generalized pair (3.3) belong to
![]() $\Lambda $
and the variety
$\Lambda $
and the variety
![]() $X^{\prime }_i$
is of Fano type over
$X^{\prime }_i$
is of Fano type over
![]() $Z_i$
. The b-nef divisor
$Z_i$
. The b-nef divisor
![]() $p{\mathbf {M}_{X^{\prime }_i}}$
is b-Cartier. By construction, if the generalized pair (3.3) admits an N-complement, then so does
$p{\mathbf {M}_{X^{\prime }_i}}$
is b-Cartier. By construction, if the generalized pair (3.3) admits an N-complement, then so does
![]() $(X_i,B_i,{\mathbf {M}_{i}})$
. We can replace
$(X_i,B_i,{\mathbf {M}_{i}})$
. We can replace
![]() $(X_i,B_i,{\mathbf {M}_{i}})$
with the generalized pair (3.3). By doing so, we decrease the number of components of
$(X_i,B_i,{\mathbf {M}_{i}})$
with the generalized pair (3.3). By doing so, we decrease the number of components of
![]() $B_{i,m_i}-B_i$
. By the choice of
$B_{i,m_i}-B_i$
. By the choice of
![]() $m_i$
, the divisor
$m_i$
, the divisor
![]() $B_{i,m_i}-B_i$
cannot be zero after this replacement. Thus, we may pick a new component and start increasing its coefficient (to this end, notice that
$B_{i,m_i}-B_i$
cannot be zero after this replacement. Thus, we may pick a new component and start increasing its coefficient (to this end, notice that
![]() $X_i'$
is
$X_i'$
is
![]() $\mathbb {Q}$
-factorial by construction). Note that this process must terminate either with
$\mathbb {Q}$
-factorial by construction). Note that this process must terminate either with
![]() $t_i<1$
a log canonical threshold or
$t_i<1$
a log canonical threshold or
![]() $t_i<1$
a pseudo-effective threshold. Otherwise, we contradict the definition of
$t_i<1$
a pseudo-effective threshold. Otherwise, we contradict the definition of
![]() $m_i$
.
$m_i$
.
Step 2: We show that a subsequence of the
![]() $t_i$
’s is strictly increasing.
$t_i$
’s is strictly increasing.
Up to passing to a subsequence, we may assume that
![]() $t_i$
is either strictly increasing, strictly decreasing or it stabilizes. The condition
$t_i$
is either strictly increasing, strictly decreasing or it stabilizes. The condition
![]() $t_i\in [\mathrm {coeff}_P(B_i),\mathrm {coeff}_P(B_{i,m_i}))$
implies that
$t_i\in [\mathrm {coeff}_P(B_i),\mathrm {coeff}_P(B_{i,m_i}))$
implies that
![]() $t_i$
must be strictly increasing.
$t_i$
must be strictly increasing.
Step 3: We finish the proof of the statement.
If case (i) happens infinitely many times, then we get a contradiction to the ACC for generalized log canonical thresholds with bounded coregularity [Reference Figueroa, Moraga and Peng10, Theorem 1]. If case (ii) happens infinitely many times, then we get a contradiction to Lemma 3.2. In any case, we get a contradiction. Hence, the sequence
![]() $m_i$
has an upper bound.
$m_i$
has an upper bound.
4 Semilog canonical pairs
In this section, we discuss the index of semilog canonical pairs. We show that to control the index of a semilog canonical log Calabi–Yau pair of coregularity c it suffices to control the index of dlt log Calabi–Yau pairs of coregularity c. To prove the main statement of this section, we will need to use the language of admissible and preadmissible sections. The preliminary results for this section are taken from [Reference Fujino and Gongyo19, Reference Fujino17, Reference Xu44].
The following definition is due to Fujino [Reference Fujino17, Definition 4.1].
Definition 4.1. Let
![]() $(X,B)$
be a possibly disconnected projective semi-dlt pair of dimension n, and assume that
$(X,B)$
be a possibly disconnected projective semi-dlt pair of dimension n, and assume that
![]() $N(K_X+B)$
is Cartier. Let
$N(K_X+B)$
is Cartier. Let
![]() $(X',B')$
be its normalization and
$(X',B')$
be its normalization and
![]() $D^n\subset X'$
be the normalization of
$D^n\subset X'$
be the normalization of
![]() $\lfloor B' \rfloor $
. As usual, we denote by
$\lfloor B' \rfloor $
. As usual, we denote by
![]() $(D^n,B_{D^n})$
the dlt pair obtained by adjunction of
$(D^n,B_{D^n})$
the dlt pair obtained by adjunction of
![]() $(X',B')$
to
$(X',B')$
to
![]() $D^n$
. We define the concept of preadmissible and admissible sections in
$D^n$
. We define the concept of preadmissible and admissible sections in
![]() $H^0(X,{\mathcal {O}_{X}} (I(K_X+B)))$
by induction on the dimension using the two following rules:
$H^0(X,{\mathcal {O}_{X}} (I(K_X+B)))$
by induction on the dimension using the two following rules:
-
1. we say that a section
is preadmissible if $$\begin{align*}s\in H^0(X,\mathcal{O}_X(I(K_X+B))) \end{align*}$$
$$\begin{align*}s\in H^0(X,\mathcal{O}_X(I(K_X+B))) \end{align*}$$
 $s|_{D^n} \in H^0(D^n,\mathcal {O}_{D^n}(I(K_{D^n}+B_{D^n})))$
is admissible. This set is denoted by
$s|_{D^n} \in H^0(D^n,\mathcal {O}_{D^n}(I(K_{D^n}+B_{D^n})))$
is admissible. This set is denoted by
 $PA(X,I(K_X+B))$
; and
$PA(X,I(K_X+B))$
; and
-
2. we say that
is admissible if s is preadmissible and $$\begin{align*}s\in H^0(X,\mathcal{O}_X(I(K_X+B)) \end{align*}$$
$$\begin{align*}s\in H^0(X,\mathcal{O}_X(I(K_X+B)) \end{align*}$$
 $g^*(s|_{X^{\prime }_i}) = s|_{X^{\prime }_j}$
holds for every crepant birational map
$g^*(s|_{X^{\prime }_i}) = s|_{X^{\prime }_j}$
holds for every crepant birational map
 $g\colon (X^{\prime }_i,B_{X^{\prime }_i})\dashrightarrow (X^{\prime }_j,B_{X^{\prime }_j})$
, where
$g\colon (X^{\prime }_i,B_{X^{\prime }_i})\dashrightarrow (X^{\prime }_j,B_{X^{\prime }_j})$
, where
 $X'=\sqcup X^{\prime }_i$
are the irreducible components of
$X'=\sqcup X^{\prime }_i$
are the irreducible components of
 $X'$
. The set of admissible sections is denoted by
$X'$
. The set of admissible sections is denoted by
 $A(X,I(K_X+B))$
.
$A(X,I(K_X+B))$
.
The following lemma is due to Gongyo [Reference Gongyo21, Remark 5.2].
Lemma 4.2. Let
![]() $(X,B)$
be a projective semi-dlt pair for which
$(X,B)$
be a projective semi-dlt pair for which
![]() $I(K_X+B)\sim 0$
. Let
$I(K_X+B)\sim 0$
. Let
![]() $\pi \colon (X',B')\rightarrow (X,B)$
be its normalization. Then, a section
$\pi \colon (X',B')\rightarrow (X,B)$
be its normalization. Then, a section
![]() $s\in H^0(X,{\mathcal {O}_{X}}(I(K_X+B)))$
is preadmissible (resp. admissible) if and only if
$s\in H^0(X,{\mathcal {O}_{X}}(I(K_X+B)))$
is preadmissible (resp. admissible) if and only if
![]() $\pi ^*s \in H^0(X',{\mathcal {O}_{X}}(I(K_{X'}+B')))$
is preadmissible (resp. admissible).
$\pi ^*s \in H^0(X',{\mathcal {O}_{X}}(I(K_{X'}+B')))$
is preadmissible (resp. admissible).
The following lemma allows us to descend linear equivalence from normal varieties to semilog canonical varieties (see, e.g., [Reference Fujino17, Lemma 4.2]).
Lemma 4.3. Let
![]() $(X,B)$
be a projective semilog canonical pair for which
$(X,B)$
be a projective semilog canonical pair for which
![]() $I(K_X+B)$
is an integral divisor. Let
$I(K_X+B)$
is an integral divisor. Let
![]() $(X',B')\rightarrow (X,B)$
be its normalization and
$(X',B')\rightarrow (X,B)$
be its normalization and
![]() $(Y,B_Y)$
a
$(Y,B_Y)$
a
![]() $\mathbb {Q}$
-factorial dlt modification of
$\mathbb {Q}$
-factorial dlt modification of
![]() $(X',B')$
. Assume that
$(X',B')$
. Assume that
![]() $I(K_Y+B_Y)$
is Cartier. Then, a section
$I(K_Y+B_Y)$
is Cartier. Then, a section
![]() $s\in PA(I(K_Y+B_Y))$
descends to
$s\in PA(I(K_Y+B_Y))$
descends to
![]() $H^0(X,{\mathcal {O}_{X}} (I(K_X+B)))$
. In particular, if we have that
$H^0(X,{\mathcal {O}_{X}} (I(K_X+B)))$
. In particular, if we have that
![]() $I(K_Y+B_Y)\sim 0$
, and there exists a nowhere vanishing section
$I(K_Y+B_Y)\sim 0$
, and there exists a nowhere vanishing section
![]() $0\neq s\in PA(I(K_Y+B_Y))$
, then we have that
$0\neq s\in PA(I(K_Y+B_Y))$
, then we have that
![]() $I(K_X+B)\sim 0$
.
$I(K_X+B)\sim 0$
.
Proof. The first part of the statement is [Reference Fujino17, Lemma 4.2]. Now,
![]() $s \in PA(I(K_Y+B_Y))$
is nowhere vanishing, it descends to a nowhere vanishing section of
$s \in PA(I(K_Y+B_Y))$
is nowhere vanishing, it descends to a nowhere vanishing section of
![]() ${\mathcal {O}_{X}}(I(K_X+B))$
, thus showing that
${\mathcal {O}_{X}}(I(K_X+B))$
, thus showing that
![]() ${I(K_X+B)\sim 0}$
.
${I(K_X+B)\sim 0}$
.
In the context of connected dlt pairs, the set of admissible sections is the same as the set of preadmissible sections (see, e.g., [Reference Fujino17, Proposition 4.7]).
Lemma 4.4. Let
![]() $(X,B)$
be a connected projective dlt pair with
$(X,B)$
be a connected projective dlt pair with
![]() $\lfloor B \rfloor \neq 0$
. Assume that
$\lfloor B \rfloor \neq 0$
. Assume that
![]() $I(K_X+B)\sim 0$
and I is even. Then, we have that
$I(K_X+B)\sim 0$
and I is even. Then, we have that
On the other hand, in the dlt setting, we can lift admissible sections from the boundary to preadmissible sections on the whole pair (see, e.g., [Reference Xu44, Lemma 3.2.14]).
Lemma 4.5. Assume that
![]() $(X,B)$
is a possibly disconnected projective dlt pair. Assume that
$(X,B)$
is a possibly disconnected projective dlt pair. Assume that
![]() $I(K_X+B)\sim 0$
and I is even. Assume that
$I(K_X+B)\sim 0$
and I is even. Assume that
Then, there exists
for which
![]() $t|_{\lfloor B\rfloor }=s$
.
$t|_{\lfloor B\rfloor }=s$
.
The following lemma states that the boundedness of indices for klt Calabi–Yau pairs together with the boundedness of B-representations imply the existence of admissible sections (see, e.g., [Reference Xu44, Proposition 3.2.7]).
Lemma 4.6. Let c be a nonnegative integer and
![]() $\Lambda $
be a set of rational numbers satisfying the descending chain condition. Assume Conjecture 1 and Conjecture 2 in dimension c. There is a constant
$\Lambda $
be a set of rational numbers satisfying the descending chain condition. Assume Conjecture 1 and Conjecture 2 in dimension c. There is a constant
![]() $I(\Lambda ,c)$
, only depending on
$I(\Lambda ,c)$
, only depending on
![]() $\Lambda $
and c, satisfying the following. Let
$\Lambda $
and c, satisfying the following. Let
![]() $(X,B)$
be a projective klt log Calabi–Yau pair with coefficients in
$(X,B)$
be a projective klt log Calabi–Yau pair with coefficients in
![]() $\Lambda $
and dimension c. Then, there is a section
$\Lambda $
and dimension c. Then, there is a section
Note that for a klt log Calabi–Yau pair an admissible section is nothing else than a section which is invariant under the pull-back via crepant birational transformations.
Finally, we prove the following lemma that allows us to produce admissible sections on possibly disconnected dlt pairs, once we know the existence of admissible sections on connected dlt pairs. The proof is similar to that of [Reference Xu44, Proposition 3.2.8].
Lemma 4.7. Let d be a positive integer. Let
![]() $(X,B)$
be a possibly disconnected projective dlt log Calabi–Yau pair. Assume that for every component
$(X,B)$
be a possibly disconnected projective dlt log Calabi–Yau pair. Assume that for every component
![]() $(X_i,B_i)$
of
$(X_i,B_i)$
of
![]() $(X,B)$
, we have a nontrivial section on
$(X,B)$
, we have a nontrivial section on
![]() $A(X_i,I(K_{X_i}+B_i))$
. Then, we have that
$A(X_i,I(K_{X_i}+B_i))$
. Then, we have that
![]() $A(X,I(K_X+B))$
admits a nowhere vanishing section.
$A(X,I(K_X+B))$
admits a nowhere vanishing section.
Proof. Let
![]() $(X,B)$
be a possibly disconnected projective dlt log Calabi–Yau pair. We write
$(X,B)$
be a possibly disconnected projective dlt log Calabi–Yau pair. We write
![]() $(X_i,B_i)$
for its components for
$(X_i,B_i)$
for its components for
![]() $i\in \{1,\dots ,k\}$
. By assumption, for each i, we have
$i\in \{1,\dots ,k\}$
. By assumption, for each i, we have
For
![]() $\lambda _i\in \mathbb {C}$
, we define
$\lambda _i\in \mathbb {C}$
, we define
Let
![]() $G=\mathrm {Bir}(X,B)$
. We claim that the image of G in
$G=\mathrm {Bir}(X,B)$
. We claim that the image of G in
![]() $GL(H^0(X,{\mathcal {O}_{X}} (I(K_X+B))))$
is finite. We denote by
$GL(H^0(X,{\mathcal {O}_{X}} (I(K_X+B))))$
is finite. We denote by
the usual map induced by pulling back sections. Thus, we want to show that
![]() $\rho _I(G)$
is finite. By [Reference Fujino and Gongyo19], the finiteness of
$\rho _I(G)$
is finite. By [Reference Fujino and Gongyo19], the finiteness of
![]() $\rho _I(G)$
is known if X is connected. Thus, we need to reduce the disconnected case to the connected one. Note that for every
$\rho _I(G)$
is known if X is connected. Thus, we need to reduce the disconnected case to the connected one. Note that for every
![]() $g\in G$
, we have that
$g\in G$
, we have that
![]() $\rho _I(g)^{k!}$
has finite order by [Reference Fujino and Gongyo19, Theorem 3.15] and the fact that the order of any permutation in
$\rho _I(g)^{k!}$
has finite order by [Reference Fujino and Gongyo19, Theorem 3.15] and the fact that the order of any permutation in
![]() $S_k$
divides
$S_k$
divides
![]() $k!$
. Hence, we conclude that
$k!$
. Hence, we conclude that
![]() $\rho _I(G)$
is a finitely generated subgroup of finite exponent of a general linear group, where the bound is determined by
$\rho _I(G)$
is a finitely generated subgroup of finite exponent of a general linear group, where the bound is determined by
![]() $k!$
and the least common multiple of the orders of the pluricanonical representations of each irreducible component. Indeed, notice that
$k!$
and the least common multiple of the orders of the pluricanonical representations of each irreducible component. Indeed, notice that
![]() $\rho _I(G)$
is finitely generated, as it is the extension of two finite groups: the image via
$\rho _I(G)$
is finitely generated, as it is the extension of two finite groups: the image via
![]() $\rho _I$
of the subgroup fixing the irreducible components of X, which is isomorphic to the product of the pluricanonical representations of each irreducible component (hence, a finite group by [Reference Fujino and Gongyo19]), and a subgroup of
$\rho _I$
of the subgroup fixing the irreducible components of X, which is isomorphic to the product of the pluricanonical representations of each irreducible component (hence, a finite group by [Reference Fujino and Gongyo19]), and a subgroup of
![]() $S_k$
. By a theorem due to Burnside, known as the bounded Burnside problem for linear groups [Reference Ceccherini-Silberstein and D’Adderio8, Theorem 6.13], we conclude that
$S_k$
. By a theorem due to Burnside, known as the bounded Burnside problem for linear groups [Reference Ceccherini-Silberstein and D’Adderio8, Theorem 6.13], we conclude that
![]() $\rho _I(G)$
is finite.
$\rho _I(G)$
is finite.
Consider the section
By construction, we have that
![]() $t\in A(X,I(K_X+B))$
. Indeed, t is invariant under the action of any birational transformation of
$t\in A(X,I(K_X+B))$
. Indeed, t is invariant under the action of any birational transformation of
![]() $(X,B)$
. Thus, the restriction of t to every log canonical center is also invariant. It suffices to show that t is nontrivial on each component of X. By considering orbits of the action, we may assume that
$(X,B)$
. Thus, the restriction of t to every log canonical center is also invariant. It suffices to show that t is nontrivial on each component of X. By considering orbits of the action, we may assume that
![]() $\mathrm {Bir}(X,B)$
acts transitively on the components of X. Consider the basis
$\mathrm {Bir}(X,B)$
acts transitively on the components of X. Consider the basis
![]() $((0,\dots ,s_i,\dots ,0))_{1 \leq i \leq k}$
of
$((0,\dots ,s_i,\dots ,0))_{1 \leq i \leq k}$
of
![]() $H^0(X,{\mathcal {O}_{X}} (I(K_X+B)))$
. Since the sections
$H^0(X,{\mathcal {O}_{X}} (I(K_X+B)))$
. Since the sections
![]() $s_i$
are admissible, in this basis, the action of
$s_i$
are admissible, in this basis, the action of
![]() $\rho _I(g)$
is represented by a matrix whose diagonal entries are either 0 (if
$\rho _I(g)$
is represented by a matrix whose diagonal entries are either 0 (if
![]() $g(X_i)\neq X_i$
) or 1 (if
$g(X_i)\neq X_i$
) or 1 (if
![]() $g(X_i)=X_i$
). Hence, by observing that the matrix associated to the identity element of G is the identity matrix, it follows that the action of
$g(X_i)=X_i$
). Hence, by observing that the matrix associated to the identity element of G is the identity matrix, it follows that the action of
![]() $\sum _{\sigma \in G}\sigma $
in this basis is given by a nontrivial matrix whose diagonal entries are all integers greater than or equal to 1. By the transitivity of the action and the fact that the action of
$\sum _{\sigma \in G}\sigma $
in this basis is given by a nontrivial matrix whose diagonal entries are all integers greater than or equal to 1. By the transitivity of the action and the fact that the action of
![]() $\sum _{\sigma \in G}\sigma $
is given by a matrix whose diagonal are positive integers, we deduce that we can find
$\sum _{\sigma \in G}\sigma $
is given by a matrix whose diagonal are positive integers, we deduce that we can find
![]() $\lambda _i\in \mathbb {C}$
for which t is nonzero on all components.
$\lambda _i\in \mathbb {C}$
for which t is nonzero on all components.
Now, we are ready to prove the main theorem of this section.
Theorem 4.8. Let c be a nonnegative integer and
![]() $\Lambda $
be a set of rational numbers satisfying the descending chain condition. Assume Conjecture 1 and Conjecture 2 in dimension c. There is a constant
$\Lambda $
be a set of rational numbers satisfying the descending chain condition. Assume Conjecture 1 and Conjecture 2 in dimension c. There is a constant
![]() $I(\Lambda ,c)$
, only depending on
$I(\Lambda ,c)$
, only depending on
![]() $\Lambda $
and c, satisfying the following. Let
$\Lambda $
and c, satisfying the following. Let
![]() $(X,B)$
be a projective dlt pair with coefficients in
$(X,B)$
be a projective dlt pair with coefficients in
![]() $\Lambda $
and coregularity c. Assume that
$\Lambda $
and coregularity c. Assume that
![]() $I(\Lambda ,c)(K_X+B)\sim 0$
. Then, there is a nowhere vanishing admissible section
$I(\Lambda ,c)(K_X+B)\sim 0$
. Then, there is a nowhere vanishing admissible section
Proof. Let
![]() $I(\Lambda ,c)$
be the positive integer given by Lemma 4.6. Without loss of generality, we may assume that
$I(\Lambda ,c)$
be the positive integer given by Lemma 4.6. Without loss of generality, we may assume that
![]() $I(\Lambda ,c)$
is even.
$I(\Lambda ,c)$
is even.
By induction on i, we prove that every i-dimensional log canonical center V of
![]() $(X,B)$
satisfies that
$(X,B)$
satisfies that
where
![]() $(V,B_V)$
is the pair obtained by dlt adjunction of
$(V,B_V)$
is the pair obtained by dlt adjunction of
![]() $(X,B)$
to V. If
$(X,B)$
to V. If
![]() $i=c$
, then the pair is klt and the statement follows from Lemma 4.6.
$i=c$
, then the pair is klt and the statement follows from Lemma 4.6.
Now, assume that the statement holds for every irreducible i-dimensional dlt center of
![]() $(X,B)$
. Let W be a log canonical center of
$(X,B)$
. Let W be a log canonical center of
![]() $(X,B)$
of dimension
$(X,B)$
of dimension
![]() $i+1$
. The pair
$i+1$
. The pair
![]() $(W,B_W)$
obtained from adjunction is dlt of dimension
$(W,B_W)$
obtained from adjunction is dlt of dimension
![]() $i+1$
and it holds that
$i+1$
and it holds that
![]() $I(\Lambda ,c)(K_W+B_W)\sim 0$
. Let
$I(\Lambda ,c)(K_W+B_W)\sim 0$
. Let
![]() $W_0$
be the union of all the log canonical centers of
$W_0$
be the union of all the log canonical centers of
![]() $(W,B_W)$
. Let
$(W,B_W)$
. Let
![]() $(W_0,B_{W_0})$
be the pair obtained by performing adjunction of
$(W_0,B_{W_0})$
be the pair obtained by performing adjunction of
![]() $(W,B_W)$
to
$(W,B_W)$
to
![]() $(W_0,B_{W_0})$
. Hence,
$(W_0,B_{W_0})$
. Hence,
![]() $(W_0,B_{W_0})$
is an i-dimensional semi-dlt pair with
$(W_0,B_{W_0})$
is an i-dimensional semi-dlt pair with
![]() $I(\Lambda ,c)(K_{W_0}+B_{W_0})\sim 0$
. Observe that
$I(\Lambda ,c)(K_{W_0}+B_{W_0})\sim 0$
. Observe that
![]() $W_0$
may have multiple irreducible components. Let
$W_0$
may have multiple irreducible components. Let
![]() $n_U\colon U\rightarrow W_0$
be the normalization of
$n_U\colon U\rightarrow W_0$
be the normalization of
![]() $W_0$
. Let
$W_0$
. Let
![]() $(U,B_{U})$
be the pair obtained by log pull-back of
$(U,B_{U})$
be the pair obtained by log pull-back of
![]() $(W_0,B_{W_0})$
to U. Then, we have that
$(W_0,B_{W_0})$
to U. Then, we have that
![]() $(U,B_{U})$
is a possibly disconnected projective dlt pair of dimension i and coregularity c. By [Reference Filipazzi and Svaldi16, Theorem 1.4], we know that every component has coregularity c. Furthermore, we have that
$(U,B_{U})$
is a possibly disconnected projective dlt pair of dimension i and coregularity c. By [Reference Filipazzi and Svaldi16, Theorem 1.4], we know that every component has coregularity c. Furthermore, we have that
![]() $I(\Lambda ,c)(K_{U}+B_{U})\sim 0$
. By Equation (4.1) in dimension i, we have that each irreducible component
$I(\Lambda ,c)(K_{U}+B_{U})\sim 0$
. By Equation (4.1) in dimension i, we have that each irreducible component
![]() $U_j$
of U satisfies that
$U_j$
of U satisfies that
By Lemma 4.7, we conclude that there exists a nowhere vanishing section
By Lemma 4.3, we conclude that this section descends to
![]() $s_{W_0} \in H^0(W_{0},{\mathcal {O}_{W_0}}(I(\Lambda ,c)(K_{W_0}+B_{W_0})))$
. Note that we have
$s_{W_0} \in H^0(W_{0},{\mathcal {O}_{W_0}}(I(\Lambda ,c)(K_{W_0}+B_{W_0})))$
. Note that we have
![]() $n_U^* s_{W_0}=s_U$
. By Lemma 4.2, we conclude that
$n_U^* s_{W_0}=s_U$
. By Lemma 4.2, we conclude that
![]() $s_{W_0} \in A(W_0,I(\Lambda ,c)(K_{W_0}+B_{W_0}))$
. By Lemma 4.5, we conclude that there exists
$s_{W_0} \in A(W_0,I(\Lambda ,c)(K_{W_0}+B_{W_0}))$
. By Lemma 4.5, we conclude that there exists
Finally, since W is connected, we conclude by Lemma 4.4, that there is a section
This finishes the inductive step.
We conclude, that for every
![]() $i \in \{c,\dots ,\dim X\}$
, every i-dimensional log canonical center of
$i \in \{c,\dots ,\dim X\}$
, every i-dimensional log canonical center of
![]() $(X,B)$
admits an admissible section. In particular, we get a nowhere vanishing section
$(X,B)$
admits an admissible section. In particular, we get a nowhere vanishing section
![]() $0\neq s_X \in A(X,I(\Lambda ,c)(K_X+B))$
as claimed.
$0\neq s_X \in A(X,I(\Lambda ,c)(K_X+B))$
as claimed.
The previous theorem allows controlling the index of semilog canonical pairs once we can control the index of their normalization.
Theorem 4.9. Let c be a nonnegative integer and
![]() $\Lambda $
be a set of rational numbers satisfying the descending chain condition. Assume Conjecture 1 and Conjecture 2 in dimension c. There is a constant
$\Lambda $
be a set of rational numbers satisfying the descending chain condition. Assume Conjecture 1 and Conjecture 2 in dimension c. There is a constant
![]() $I(\Lambda ,c)$
, only depending on
$I(\Lambda ,c)$
, only depending on
![]() $\Lambda $
and c, satisfying the following. Let
$\Lambda $
and c, satisfying the following. Let
![]() $(X,B)$
be a projective semilog canonical pair with coefficients in
$(X,B)$
be a projective semilog canonical pair with coefficients in
![]() $\Lambda $
and coregularity c. Let
$\Lambda $
and coregularity c. Let
![]() $(Y,B_Y)$
be a
$(Y,B_Y)$
be a
![]() $\mathbb {Q}$
-factorial dlt modification of a normalization of
$\mathbb {Q}$
-factorial dlt modification of a normalization of
![]() $(X,B)$
. Assume that
$(X,B)$
. Assume that
![]() $I(\Lambda ,c)(K_Y+B_Y)\sim 0$
. Then, we have that
$I(\Lambda ,c)(K_Y+B_Y)\sim 0$
. Then, we have that
![]() $I(\Lambda ,c)(K_X+B)\sim 0$
.
$I(\Lambda ,c)(K_X+B)\sim 0$
.
Proof. We can consider
![]() $I(\Lambda ,c)$
as in Theorem 4.8. By Theorem 4.8 and Lemma 4.7, we know that there exists a nowhere vanishing preadmissible section
$I(\Lambda ,c)$
as in Theorem 4.8. By Theorem 4.8 and Lemma 4.7, we know that there exists a nowhere vanishing preadmissible section
By Lemma 4.3, we conclude that the linear equivalence
![]() $I(\Lambda ,c)(K_X+B)\sim 0$
holds.
$I(\Lambda ,c)(K_X+B)\sim 0$
holds.
In the case of dimension 0, Conjecture 1 and Conjecture 2 are trivial. Indeed, the only variety of interest is
![]() $\mathrm {Spec}(\mathbb K)$
, no boundary is allowed for dimensional reasons, and
$\mathrm {Spec}(\mathbb K)$
, no boundary is allowed for dimensional reasons, and
![]() $\mathrm {Bir}(\mathrm {Spec}(\mathbb K))$
is trivial. Thus, we get the following statement.
$\mathrm {Bir}(\mathrm {Spec}(\mathbb K))$
is trivial. Thus, we get the following statement.
Theorem 4.10. Let
![]() $(X,B)$
be a projective semilog canonical Calabi–Yau pair of coregularity 0 and
$(X,B)$
be a projective semilog canonical Calabi–Yau pair of coregularity 0 and
![]() $\lambda $
be its Weil index. Let
$\lambda $
be its Weil index. Let
![]() $(Y,B_Y)$
be a
$(Y,B_Y)$
be a
![]() $\mathbb {Q}$
-factorial dlt modification of a normalization of
$\mathbb {Q}$
-factorial dlt modification of a normalization of
![]() $(X,B)$
. If
$(X,B)$
. If
![]() $2\lambda (K_Y+B_Y)\sim 0$
, then
$2\lambda (K_Y+B_Y)\sim 0$
, then
![]() $2\lambda (K_X+B)\sim 0$
.
$2\lambda (K_X+B)\sim 0$
.
Finally, Conjecture 1 and Conjecture 2 are known in the case of klt pairs of dimension 1 or 2 (see, e.g., [Reference Xu44]). We get the following statement.
Theorem 4.11. Let
![]() $\Lambda $
be a set of rational numbers satisfying the descending chain condition. There exists a constant
$\Lambda $
be a set of rational numbers satisfying the descending chain condition. There exists a constant
![]() $I(\Lambda )$
, only depending on
$I(\Lambda )$
, only depending on
![]() $\Lambda $
, satisfying the following. Let
$\Lambda $
, satisfying the following. Let
![]() $(X,B)$
be a projective semilog canonical Calabi–Yau pair of coregularity 1 (resp. 2) such that B has coefficients in
$(X,B)$
be a projective semilog canonical Calabi–Yau pair of coregularity 1 (resp. 2) such that B has coefficients in
![]() $\Lambda $
. Let
$\Lambda $
. Let
![]() $(Y,B_Y)$
be a
$(Y,B_Y)$
be a
![]() $\mathbb {Q}$
-factorial dlt modification of a normalization of
$\mathbb {Q}$
-factorial dlt modification of a normalization of
![]() $(X,B)$
. If
$(X,B)$
. If
![]() $I(\Lambda )(K_Y+B_Y)\sim 0$
, then
$I(\Lambda )(K_Y+B_Y)\sim 0$
, then
![]() $I(\Lambda )(K_X+B)\sim 0$
.
$I(\Lambda )(K_X+B)\sim 0$
.
Let us note that Conjecture 1 is known for klt
![]() $3$
-folds (see, e.g., [Reference Xu44]). However, Conjecture 2 is still unknown in the case of klt Calabi–Yau
$3$
-folds (see, e.g., [Reference Xu44]). However, Conjecture 2 is still unknown in the case of klt Calabi–Yau
![]() $3$
-folds.
$3$
-folds.
4.1 Lifting complements from nonnormal divisors in fibrations
In this subsection, we prove a statement about lifting complements from nonnormal divisors in fibrations.
Theorem 4.12. Let
![]() $\lambda $
, d and c be nonnegative integers. Assume that Conjecture 1
$\lambda $
, d and c be nonnegative integers. Assume that Conjecture 1
![]() $(c)$
and Conjecture 2
$(c)$
and Conjecture 2
![]() $(c)$
hold. Let
$(c)$
hold. Let ![]() be the integer provided by Theorem 6
be the integer provided by Theorem 6
![]() $(d-1,c)$
. Up to replacing I with a bounded multiple, further assume that I is divisible by the integer provided by Theorem 4.9
$(d-1,c)$
. Up to replacing I with a bounded multiple, further assume that I is divisible by the integer provided by Theorem 4.9
![]() $(D_\lambda ,c)$
. Let
$(D_\lambda ,c)$
. Let
![]() $(X,B)$
be a projective d-dimensional log Calabi–Yau pair. Assume that the following conditions hold:
$(X,B)$
be a projective d-dimensional log Calabi–Yau pair. Assume that the following conditions hold:
-
• X is
 $\mathbb {Q}$
-factorial and klt;
$\mathbb {Q}$
-factorial and klt; -
• there is a fibration
 $X\rightarrow W$
, which is a
$X\rightarrow W$
, which is a
 $(K_X + B - S)$
-Mori fiber space;
$(K_X + B - S)$
-Mori fiber space; -
• a component
 $S\subset \lfloor B\rfloor $
which is ample over the base and
$S\subset \lfloor B\rfloor $
which is ample over the base and
 $(X,B-S)$
is dlt;
$(X,B-S)$
is dlt; -
• the morphism
 $S \rightarrow W$
has connected fibers;
$S \rightarrow W$
has connected fibers; -
• the coefficients of B belong to
 $D_\lambda $
; and
$D_\lambda $
; and -
• the pair
 $(X,B)$
has coregularity c.
$(X,B)$
has coregularity c.
Then, we have that
![]() $I(K_X+B)\sim 0$
.
$I(K_X+B)\sim 0$
.
Proof. The proof is formally identical to the proof of Theorem 2.31, with the only difference that we need to appeal to the results in § 4 since S may not be normal. For completeness, we include a full proof of the statement.
Let
![]() $(X,B)$
, S,
$(X,B)$
, S,
![]() $f \colon X \rightarrow W$
and
$f \colon X \rightarrow W$
and ![]() be as in the statement. First, we show that we can apply the inductive hypothesis to S.
be as in the statement. First, we show that we can apply the inductive hypothesis to S.
By [Reference Fujino and Gongyo19, Example 2.6], the pair obtained by adjunction of
![]() $(X,B-\epsilon \lfloor B\rfloor +\epsilon S)$
to S is semilog canonical. In particular, S is
$(X,B-\epsilon \lfloor B\rfloor +\epsilon S)$
to S is semilog canonical. In particular, S is
![]() $S_2$
. In turn, by letting
$S_2$
. In turn, by letting
![]() $\epsilon \to 0$
, it follows that the pair obtained by adjunction of
$\epsilon \to 0$
, it follows that the pair obtained by adjunction of
![]() $(X,B)$
to S is semilog canonical. In particular, let
$(X,B)$
to S is semilog canonical. In particular, let
![]() $(S,B_S)$
denote the pair obtained by adjunction from
$(S,B_S)$
denote the pair obtained by adjunction from
![]() $(X,B)$
, and let
$(X,B)$
, and let
![]() $(S^\nu , {B}_{S^{\nu }})$
denote its normalization. By [Reference Figueroa, Moraga and Peng10, Lemma 2.28],
$(S^\nu , {B}_{S^{\nu }})$
denote its normalization. By [Reference Figueroa, Moraga and Peng10, Lemma 2.28],
![]() $(S^\nu ,{B}_{S^{\nu }})$
has coregularity c. Then, by Lemma 2.17,
$(S^\nu ,{B}_{S^{\nu }})$
has coregularity c. Then, by Lemma 2.17,
![]() $(S^\nu ,B _{S^{\nu }})$
satisfies the assumptions of Theorem 6
$(S^\nu ,B _{S^{\nu }})$
satisfies the assumptions of Theorem 6
![]() $(d-1,c)$
with constant I. Then, by Theorem 4.9, we have
$(d-1,c)$
with constant I. Then, by Theorem 4.9, we have
By [Reference Kollár29, Proposition 4.32], S is seminormal. Then, by [Reference Filipazzi and Inchiostro12, Lemma 2.3] and the fact that
![]() $S \rightarrow W$
has connected fibers, we have
$S \rightarrow W$
has connected fibers, we have
![]() $f_* {\mathcal {O}_{S}} = {\mathcal {O}_{W}}$
. Lastly, we observe that, if
$f_* {\mathcal {O}_{S}} = {\mathcal {O}_{W}}$
. Lastly, we observe that, if
![]() $\dim X - \dim W =1$
, since
$\dim X - \dim W =1$
, since
![]() $S \rightarrow W$
has connected fibers, it follows that
$S \rightarrow W$
has connected fibers, it follows that
![]() $(B-S)_{\mathrm {hor}} \neq 0$
.
$(B-S)_{\mathrm {hor}} \neq 0$
.
Now, consider the short exact sequence
The exactness of Equation (4.3) follows verbatim as the exactness of Equation (2.3). Since
![]() $I(K_{X}+B)-S\sim _{\mathbb {Q},f} -S$
, the divisor
$I(K_{X}+B)-S\sim _{\mathbb {Q},f} -S$
, the divisor
![]() $-S$
is f-ample and
$-S$
is f-ample and
![]() $\dim W < \dim X$
, we have
$\dim W < \dim X$
, we have
Similarly, we write
First, assume that
![]() $B_{\mathrm {hor}} \neq S$
. Note that X is klt and
$B_{\mathrm {hor}} \neq S$
. Note that X is klt and
![]() $B-S$
is f-ample since f is a Mori fiber space and the assumption that
$B-S$
is f-ample since f is a Mori fiber space and the assumption that
![]() $B_{\mathrm {hor}} \neq S$
. Thus, by the relative version of Kawamata–Viehweg vanishing, we have
$B_{\mathrm {hor}} \neq S$
. Thus, by the relative version of Kawamata–Viehweg vanishing, we have
Now, assume that
![]() $B_{\mathrm {hor}}=S$
. By the equality
$B_{\mathrm {hor}}=S$
. By the equality
![]() $B_{\mathrm {hor}}=S$
and the fact that f is a Mori fiber space, we have
$B_{\mathrm {hor}}=S$
and the fact that f is a Mori fiber space, we have
Thus, we obtain
Since X is a klt variety, by [Reference Kawamata, Matsuda and Matsuki28, Theorem 1-2-7], we have that
![]() $R^1f_* {\mathcal {O}_{X}}(I(K_X+B)-S)$
is torsion free. To conclude that it vanishes, it suffices to show that it has rank 0. As observed at the end of the previous paragraph, we have that
$R^1f_* {\mathcal {O}_{X}}(I(K_X+B)-S)$
is torsion free. To conclude that it vanishes, it suffices to show that it has rank 0. As observed at the end of the previous paragraph, we have that
![]() $\dim X \geq \dim Z +2$
under the additional assumption
$\dim X \geq \dim Z +2$
under the additional assumption
![]() $B_{\mathrm {hor}}=S$
. Then, by applying Kawamata–Viehweg vanishing to a general fiber [Reference Kollár, Mori, Clemens and Corti30, Theorem 2.70], we conclude that the rank of
$B_{\mathrm {hor}}=S$
. Then, by applying Kawamata–Viehweg vanishing to a general fiber [Reference Kollár, Mori, Clemens and Corti30, Theorem 2.70], we conclude that the rank of
![]() $R^1f_*{\mathcal {O}_{X}}(I(K_{X}+B)-S)$
is 0, thus implying that
$R^1f_*{\mathcal {O}_{X}}(I(K_{X}+B)-S)$
is 0, thus implying that
![]() $R^1f_*{\mathcal {O}_{X}}(I(K_{X}+B)-S)=0$
.
$R^1f_*{\mathcal {O}_{X}}(I(K_{X}+B)-S)=0$
.
Therefore, by pushing forward Equation (4.3) via f, we obtain
Now, taking global sections, we have
By [Reference Filipazzi, Mauri and Moraga13, Lemma 3.1], (4.4) implies that
![]() $I(K_{X}+B) \sim 0$
.
$I(K_{X}+B) \sim 0$
.
5 Relative complements
In this section, we prove an inductive statement regarding the existence of complements for Fano type morphisms with bounded coregularity.
5.1 Lifting sections from a divisor
In this subsection, we introduce some tools to lift complements from a divisor of a log Fano pair. Let X be a Fano type variety and
![]() $(X,B,\mathbf {M})$
be a generalized log canonical pair for which
$(X,B,\mathbf {M})$
be a generalized log canonical pair for which
![]() $-(K_X+B+{\mathbf {M}_{X}})$
is nef. The main theorem of this subsection implies that we can lift complements for
$-(K_X+B+{\mathbf {M}_{X}})$
is nef. The main theorem of this subsection implies that we can lift complements for
![]() $(X,B,\mathbf {M})$
from a component S of
$(X,B,\mathbf {M})$
from a component S of
![]() $\lfloor B\rfloor $
under some suitable conditions explained in the following theorem.
$\lfloor B\rfloor $
under some suitable conditions explained in the following theorem.
Theorem 5.1. Let d, c and p be nonnegative integers and
![]() $\mathcal {R} \subset \mathbb {Q}_{>0}$
be a finite set. Let
$\mathcal {R} \subset \mathbb {Q}_{>0}$
be a finite set. Let ![]() be the integer provided by Theorem 7
be the integer provided by Theorem 7
![]() $(d-1,c)$
. Assume that N is divisible by p and by
$(d-1,c)$
. Assume that N is divisible by p and by
![]() $I_{\mathcal {R}}$
. Let
$I_{\mathcal {R}}$
. Let
![]() $\pi \colon X \rightarrow Z$
be a Fano type morphism, where X is a d-dimensional variety. Let
$\pi \colon X \rightarrow Z$
be a Fano type morphism, where X is a d-dimensional variety. Let
![]() $(X,B,\mathbf {M})$
be a generalized log canonical pair over Z and
$(X,B,\mathbf {M})$
be a generalized log canonical pair over Z and
![]() $z \in Z$
a point satisfying the following conditions:
$z \in Z$
a point satisfying the following conditions:
-
• the generalized pair
 $(X,B, \mathbf {M})$
has coregularity at most c over z;
$(X,B, \mathbf {M})$
has coregularity at most c over z; -
• the divisor B has coefficients in
 $\mathcal {R}$
;
$\mathcal {R}$
; -
•
 $p\mathbf {M}$
is b-Cartier; and
$p\mathbf {M}$
is b-Cartier; and -
• the divisor
 $-(K_X+B+{\mathbf {M}_{X}})$
is nef over Z.
$-(K_X+B+{\mathbf {M}_{X}})$
is nef over Z.
Assume that there exists
![]() $B_1\leq B$
and
$B_1\leq B$
and
![]() $\alpha \in (0,1]$
for which:
$\alpha \in (0,1]$
for which:
-
• the generalized pair
 $(X,B_1,\alpha \mathbf {M})$
is generalized log canonical but it is not generalized klt over z;
$(X,B_1,\alpha \mathbf {M})$
is generalized log canonical but it is not generalized klt over z; -
• the divisor
 $-(K_X+B_1+\alpha {\mathbf {M}_{X}})$
is big and nef over Z.
$-(K_X+B_1+\alpha {\mathbf {M}_{X}})$
is big and nef over Z.
Then,
![]() $(X,B,\mathbf {M})$
admits an N-complement over z.
$(X,B,\mathbf {M})$
admits an N-complement over z.
In order to prove the main theorem of this section, we take inspiration from [Reference Birkar3, § 6.6]. In particular, we will first prove a weaker statement.
Proposition 5.2. Let d, c and p be nonnegative integers and
![]() $\mathcal {R} \subset \mathbb {Q}_{>0}$
be a finite set. Let
$\mathcal {R} \subset \mathbb {Q}_{>0}$
be a finite set. Let ![]() be the integer provided by Theorem 7
be the integer provided by Theorem 7
![]() $(d-1,c)$
. Assume that N is divisible by p and by
$(d-1,c)$
. Assume that N is divisible by p and by
![]() $I_{\mathcal {R}}$
. Let
$I_{\mathcal {R}}$
. Let
![]() $\pi \colon X \rightarrow Z$
be a Fano type morphism, where X is a d-dimensional variety. Let
$\pi \colon X \rightarrow Z$
be a Fano type morphism, where X is a d-dimensional variety. Let
![]() $(X,B,\mathbf {M})$
be a
$(X,B,\mathbf {M})$
be a
![]() $\mathbb {Q}$
-factorial generalized log canonical pair over Z and
$\mathbb {Q}$
-factorial generalized log canonical pair over Z and
![]() $z \in Z$
a point satisfying the following conditions:
$z \in Z$
a point satisfying the following conditions:
-
• the generalized pair
 $(X,B, \mathbf {M})$
has coregularity at most c over z;
$(X,B, \mathbf {M})$
has coregularity at most c over z; -
• the divisor B has coefficients in
 $\mathcal {R}$
;
$\mathcal {R}$
; -
•
 $p\mathbf {M}$
is b-Cartier; and
$p\mathbf {M}$
is b-Cartier; and -
• the divisor
 $-(K_X+B+{\mathbf {M}_{X}})$
is nef over Z.
$-(K_X+B+{\mathbf {M}_{X}})$
is nef over Z.
Assume there exists a boundary
![]() $\Gamma $
on X and
$\Gamma $
on X and
![]() $\alpha \in (0,1)$
for which:
$\alpha \in (0,1)$
for which:
-
• the generalized pair
 $(X,\Gamma ,\alpha \mathbf {M})$
is generalized plt over z;
$(X,\Gamma ,\alpha \mathbf {M})$
is generalized plt over z; -
• we have that
 $S=\lfloor \Gamma \rfloor \subset \lfloor B \rfloor $
intersects the fiber over z; and
$S=\lfloor \Gamma \rfloor \subset \lfloor B \rfloor $
intersects the fiber over z; and -
• the divisor
 $-(K_X+\Gamma +\alpha {\mathbf {M}_{X}})$
is ample over Z.
$-(K_X+\Gamma +\alpha {\mathbf {M}_{X}})$
is ample over Z.
Then,
![]() $(X,B,\mathbf {M})$
admits an N-complement over z.
$(X,B,\mathbf {M})$
admits an N-complement over z.
Proof. We will proceed by induction on the dimension, keeping the coregularity constant. Over several steps, we will lift a complement from a divisor. Since the statement is local over
![]() $z \in Z$
, in the course of the proof we are free to shrink Z around z. In particular, all linear equivalences that are relative to Z can be assumed to hold globally. We add the fractions with denominator p to the set
$z \in Z$
, in the course of the proof we are free to shrink Z around z. In particular, all linear equivalences that are relative to Z can be assumed to hold globally. We add the fractions with denominator p to the set
![]() $\mathcal {R}$
. This does not change the value of N, hence proving the statement for this new finite set is the same as proving it for the original
$\mathcal {R}$
. This does not change the value of N, hence proving the statement for this new finite set is the same as proving it for the original
![]() $\mathcal {R}$
.
$\mathcal {R}$
.
Step 1. In this step, we reduce to the case where
![]() $(X,B,\mathbf {M})$
is
$(X,B,\mathbf {M})$
is
![]() $\mathbb {Q}$
-factorial generalized dlt.
$\mathbb {Q}$
-factorial generalized dlt.
Let
![]() $(X',B', \mathbf {M})$
be a
$(X',B', \mathbf {M})$
be a
![]() $\mathbb {Q}$
-factorial dlt modification of
$\mathbb {Q}$
-factorial dlt modification of
![]() $(X,B,\mathbf {M})$
. Pick E exceptional such that
$(X,B,\mathbf {M})$
. Pick E exceptional such that
![]() $-E$
is ample over X. Notice that the existence of E is guaranteed by the hypothesis that X is
$-E$
is ample over X. Notice that the existence of E is guaranteed by the hypothesis that X is
![]() $\mathbb Q$
-factorial. Also, let
$\mathbb Q$
-factorial. Also, let
![]() $(X',\Gamma ',\alpha \mathbf {M})$
be the trace of
$(X',\Gamma ',\alpha \mathbf {M})$
be the trace of
![]() $(X,\Gamma ,\mathbf {M})$
on
$(X,\Gamma ,\mathbf {M})$
on
![]() $X'$
. We observe that
$X'$
. We observe that
![]() $\Gamma '$
may no longer be effective.
$\Gamma '$
may no longer be effective.
Since
![]() $(X,\Gamma ,\alpha \mathbf {M})$
is generalized plt with
$(X,\Gamma ,\alpha \mathbf {M})$
is generalized plt with
![]() $\lfloor \Gamma \rfloor \subset \lfloor B \rfloor $
and
$\lfloor \Gamma \rfloor \subset \lfloor B \rfloor $
and
![]() $X' \rightarrow X$
only extracts divisor that appear with coeffcient 1 in
$X' \rightarrow X$
only extracts divisor that appear with coeffcient 1 in
![]() $B'$
, for
$B'$
, for
![]() $0 < \lambda \ll 1$
, the datum of
$0 < \lambda \ll 1$
, the datum of
![]() $(X',(1-\lambda )B'+\lambda \Gamma ',(1-\lambda + \lambda \alpha )\mathbf {M})$
is actually a generalized pair (i.e., its boundary is effective) and it is generalized plt with
$(X',(1-\lambda )B'+\lambda \Gamma ',(1-\lambda + \lambda \alpha )\mathbf {M})$
is actually a generalized pair (i.e., its boundary is effective) and it is generalized plt with
![]() $1-\lambda + \lambda \alpha \in (0,1)$
. Furthermore,
$1-\lambda + \lambda \alpha \in (0,1)$
. Furthermore,
is the pull-back of a divisor on X that is relatively ample over Z. Thus, for
![]() $\varepsilon>0$
small enough, we have that
$\varepsilon>0$
small enough, we have that
is ample over Z. Hence, up to replacing
![]() $(X,B,\mathbf {M})$
with
$(X,B,\mathbf {M})$
with
![]() $(X',B',\mathbf {M})$
and
$(X',B',\mathbf {M})$
and
![]() $(X,\Gamma ,\alpha \mathbf {M})$
with
$(X,\Gamma ,\alpha \mathbf {M})$
with
![]() $(X',(1-\lambda )B'+\lambda \Gamma ' + \varepsilon E,(1-\lambda + \lambda \alpha )\mathbf {M})$
we can assume that X is
$(X',(1-\lambda )B'+\lambda \Gamma ' + \varepsilon E,(1-\lambda + \lambda \alpha )\mathbf {M})$
we can assume that X is
![]() $\mathbb {Q}$
-factorial and
$\mathbb {Q}$
-factorial and
![]() $(X,B, \mathbf {M})$
is generalized dlt.
$(X,B, \mathbf {M})$
is generalized dlt.
Step 2. In this step, we prove that
![]() $S \rightarrow \pi (S)$
is a contraction.
$S \rightarrow \pi (S)$
is a contraction.
As
![]() $\alpha {\mathbf {M}_{X}}$
is the push-forward of a divisor that is nef over Z, its diminished base locus does not contain any divisor. Let
$\alpha {\mathbf {M}_{X}}$
is the push-forward of a divisor that is nef over Z, its diminished base locus does not contain any divisor. Let
![]() $\pi : X' \rightarrow X$
be a model where
$\pi : X' \rightarrow X$
be a model where
![]() $\mathbf {M}$
descends. Let
$\mathbf {M}$
descends. Let
![]() $K_{X'}+\Gamma '+\alpha {\mathbf {M}_{X'}}$
be the crepant pullback of
$K_{X'}+\Gamma '+\alpha {\mathbf {M}_{X'}}$
be the crepant pullback of
![]() $K_X +\Gamma + \alpha {\mathbf {M}_{X}}$
(this
$K_X +\Gamma + \alpha {\mathbf {M}_{X}}$
(this
![]() $\Gamma '$
is different from the one defined in step 1). For any
$\Gamma '$
is different from the one defined in step 1). For any
![]() $0<\delta < 1 $
, we can write
$0<\delta < 1 $
, we can write
As
![]() $\alpha {\mathbf {M}_{X'}}$
is nef and
$\alpha {\mathbf {M}_{X'}}$
is nef and
![]() $-(K_{X'}+\Gamma ' +\alpha {\mathbf {M}_{X'}})$
is big and nef over Z, by [Reference Lazarsfeld32, Example 2.2.19] there exists an effective divisor
$-(K_{X'}+\Gamma ' +\alpha {\mathbf {M}_{X'}})$
is big and nef over Z, by [Reference Lazarsfeld32, Example 2.2.19] there exists an effective divisor
![]() $E'$
such that
$E'$
such that
![]() $\alpha {\mathbf {M}_{X'}}-\delta (K_{X'}+\Gamma ' +\alpha {\mathbf {M}_{X'}}) \sim _{\mathbb {Q}} A_{k}'+\frac {1}{k}E'$
, for all positive integers k, where each
$\alpha {\mathbf {M}_{X'}}-\delta (K_{X'}+\Gamma ' +\alpha {\mathbf {M}_{X'}}) \sim _{\mathbb {Q}} A_{k}'+\frac {1}{k}E'$
, for all positive integers k, where each
![]() $A_k'$
is ample over Z.
$A_k'$
is ample over Z.
So, we can write
![]() $(1-\delta )(K_{X'}+\Gamma ' +\alpha {\mathbf {M}_{X'}})\sim _{\mathbb {Q}} K_{X'}+\Gamma '+A_k'+\frac {1}{k}E' $
. If we choose k large enough and
$(1-\delta )(K_{X'}+\Gamma ' +\alpha {\mathbf {M}_{X'}})\sim _{\mathbb {Q}} K_{X'}+\Gamma '+A_k'+\frac {1}{k}E' $
. If we choose k large enough and
![]() $A_k'$
generically, then the subpair
$A_k'$
generically, then the subpair
![]() $(X',\Gamma '+A_k'+\frac {1}{k}E')$
is sub-plt. With those choices fixed, we define
$(X',\Gamma '+A_k'+\frac {1}{k}E')$
is sub-plt. With those choices fixed, we define
![]() $A=\pi _\ast A_k'$
,
$A=\pi _\ast A_k'$
,
![]() $E=\frac {1}{k}\pi _\ast E'$
. Therefore,
$E=\frac {1}{k}\pi _\ast E'$
. Therefore,
with
![]() $(X,A+E+\Gamma )$
being plt. Call
$(X,A+E+\Gamma )$
being plt. Call ![]() . For
. For
![]() $\delta $
small enough, we have that
$\delta $
small enough, we have that
![]() $-(K_X+G)$
is ample over Z and
$-(K_X+G)$
is ample over Z and
![]() $\lfloor G \rfloor = S$
. From the exact sequence
$\lfloor G \rfloor = S$
. From the exact sequence
we get the exact sequence
Since
![]() $-S= K_X+G -S -(K_X +G) $
, with
$-S= K_X+G -S -(K_X +G) $
, with
![]() $(X,G-S)$
being klt and
$(X,G-S)$
being klt and
![]() $-(K_X+G)$
being ample over Z, we have that
$-(K_X+G)$
being ample over Z, we have that
![]() $R^1 \pi _* \mathcal {O}_X(-S)=0$
by the relative Kawamata–Viehweg vanishing theorem. Therefore,
$R^1 \pi _* \mathcal {O}_X(-S)=0$
by the relative Kawamata–Viehweg vanishing theorem. Therefore,
![]() $\pi _* \mathcal {O}_X \rightarrow \pi _*\mathcal {O}_S$
is surjective.
$\pi _* \mathcal {O}_X \rightarrow \pi _*\mathcal {O}_S$
is surjective.
Let
![]() $g \circ \pi ' \colon S \rightarrow Z' \rightarrow Z$
be the Stein factorization of
$g \circ \pi ' \colon S \rightarrow Z' \rightarrow Z$
be the Stein factorization of
![]() $\pi \colon S \rightarrow Z$
. Then
$\pi \colon S \rightarrow Z$
. Then
![]() $\mathcal {O}_Z=\pi _* (\mathcal {O}_X)\rightarrow \pi _* \mathcal {O}_S=g_*\mathcal {O}_{Z'}$
is surjective. As
$\mathcal {O}_Z=\pi _* (\mathcal {O}_X)\rightarrow \pi _* \mathcal {O}_S=g_*\mathcal {O}_{Z'}$
is surjective. As
![]() $\mathcal {O}_Z \rightarrow g_*\mathcal {O}_{Z'}$
factors as
$\mathcal {O}_Z \rightarrow g_*\mathcal {O}_{Z'}$
factors as
![]() $\mathcal {O}_Z \rightarrow \mathcal {O}_{\pi (S)}\rightarrow g_*\mathcal {O}_{Z'}$
, the morphism
$\mathcal {O}_Z \rightarrow \mathcal {O}_{\pi (S)}\rightarrow g_*\mathcal {O}_{Z'}$
, the morphism
![]() $\mathcal {O}_{\pi (S)} \rightarrow g_*(\mathcal {O}_{Z'})$
is surjective. Then, it is an isomorphism, as the map
$\mathcal {O}_{\pi (S)} \rightarrow g_*(\mathcal {O}_{Z'})$
is surjective. Then, it is an isomorphism, as the map
![]() $Z' \rightarrow Z$
is finite. Hence,
$Z' \rightarrow Z$
is finite. Hence,
![]() $Z' \rightarrow \pi (S)$
is an isomorphism and
$Z' \rightarrow \pi (S)$
is an isomorphism and
![]() $S \rightarrow \pi (S)$
is a contraction. Restricting
$S \rightarrow \pi (S)$
is a contraction. Restricting
![]() $K_X+G$
to S shows that S is of Fano type over
$K_X+G$
to S shows that S is of Fano type over
![]() $\pi (S)$
.
$\pi (S)$
.
Step 3. In this step, we use adjunction and consider a complement on S.
Consider a log resolution
![]() $f \colon X' \rightarrow X$
of
$f \colon X' \rightarrow X$
of
![]() $(X,B, \mathbf {M})$
such that
$(X,B, \mathbf {M})$
such that
![]() $\mathbf {M}$
descends on
$\mathbf {M}$
descends on
![]() $X'$
, and write
$X'$
, and write ![]() . Let
. Let
![]() $S'$
be the strict transform of S and
$S'$
be the strict transform of S and
![]() $g \colon S' \rightarrow S$
be the induced morphism. Let
$g \colon S' \rightarrow S$
be the induced morphism. Let
![]() $(S, B_S, \mathbf {N})$
be the generalized pair obtained by adjunction of
$(S, B_S, \mathbf {N})$
be the generalized pair obtained by adjunction of
![]() $(X,B,\mathbf {M})$
to S. By Lemma 2.17, the coefficients of
$(X,B,\mathbf {M})$
to S. By Lemma 2.17, the coefficients of
![]() $B_S$
are in
$B_S$
are in
![]() $D(\mathcal {R})$
and the b-divisor
$D(\mathcal {R})$
and the b-divisor
![]() $p\mathbf {N}$
is b-Cartier. By Lemma 2.24, the coregularity of
$p\mathbf {N}$
is b-Cartier. By Lemma 2.24, the coregularity of
![]() $(S,B_S,\mathbf {N})$
is at most c. By Theorem 7
$(S,B_S,\mathbf {N})$
is at most c. By Theorem 7
![]() $(d-1,c)$
if
$(d-1,c)$
if
![]() $\dim \pi (S) =0$
or by the inductive hypothesis if
$\dim \pi (S) =0$
or by the inductive hypothesis if
![]() $\dim \pi (S)>0$
, the divisor
$\dim \pi (S)>0$
, the divisor
![]() $K_S+B_S+{\mathbf {M}_{S}}$
has an N complement
$K_S+B_S+{\mathbf {M}_{S}}$
has an N complement
![]() $B_{S}^{+}$
over z with coregularity at most c. In the following steps, we will lift
$B_{S}^{+}$
over z with coregularity at most c. In the following steps, we will lift
![]() $B_{S}^{+}$
to an N-complement
$B_{S}^{+}$
to an N-complement
![]() $B_X^{+}$
of
$B_X^{+}$
of
![]() $K_X+B+{\mathbf {M}_{X}}$
over z with coregularity at most c.
$K_X+B+{\mathbf {M}_{X}}$
over z with coregularity at most c.
Step 4. In this step, we introduce some divisors and prove some properties of these divisors.
Define ![]() and
and ![]() . We write
. We write ![]() . Now, we define a divisor
. Now, we define a divisor
![]() $P_{X'}$
in the following way. For any prime divisor
$P_{X'}$
in the following way. For any prime divisor
![]() $D_{X'} \neq S'$
, we set
$D_{X'} \neq S'$
, we set
![]() $\operatorname {\mathrm {coeff}}_{D_{X'}}(P_{X'})=-\operatorname {\mathrm {coeff}}_{D_{X'}}\lfloor \Gamma _{X'}+N\Omega _{X'}-\lfloor (N+1)\Omega _{X'} \rfloor \rfloor $
and
$\operatorname {\mathrm {coeff}}_{D_{X'}}(P_{X'})=-\operatorname {\mathrm {coeff}}_{D_{X'}}\lfloor \Gamma _{X'}+N\Omega _{X'}-\lfloor (N+1)\Omega _{X'} \rfloor \rfloor $
and
![]() $\operatorname {\mathrm {coeff}}_{S'}(P_{X'})=0$
. Hence,
$\operatorname {\mathrm {coeff}}_{S'}(P_{X'})=0$
. Hence,
![]() $P_{X'}$
is an integral divisor such that
$P_{X'}$
is an integral divisor such that ![]() is a boundary,
is a boundary,
![]() $(X',J_{X'}, \alpha {\mathbf {M}_{X'}})$
is generalized plt and
$(X',J_{X'}, \alpha {\mathbf {M}_{X'}})$
is generalized plt and
![]() $\lfloor J_{X'} \rfloor =S'$
. For
$\lfloor J_{X'} \rfloor =S'$
. For
![]() $D_{X'}\neq S'$
not exceptional over X, as
$D_{X'}\neq S'$
not exceptional over X, as
![]() $NB$
is integral, we have that
$NB$
is integral, we have that
![]() $\operatorname {\mathrm {coeff}}_{D_{X'}}(N\Omega _{X'})$
is an integer. Thus,
$\operatorname {\mathrm {coeff}}_{D_{X'}}(N\Omega _{X'})$
is an integer. Thus,
![]() $\operatorname {\mathrm {coeff}}_{D_{X'}}\lfloor (N+1)\Omega _{X'}\rfloor = \operatorname {\mathrm {coeff}}_{D_{X'}} (N\Omega _{X'})$
. So,
$\operatorname {\mathrm {coeff}}_{D_{X'}}\lfloor (N+1)\Omega _{X'}\rfloor = \operatorname {\mathrm {coeff}}_{D_{X'}} (N\Omega _{X'})$
. So,
![]() $\operatorname {\mathrm {coeff}}_{D_{X'}}(P_{X'})=-\operatorname {\mathrm {coeff}}_{D_{X'}}(\Gamma _{X'})=0.$
We conclude that
$\operatorname {\mathrm {coeff}}_{D_{X'}}(P_{X'})=-\operatorname {\mathrm {coeff}}_{D_{X'}}(\Gamma _{X'})=0.$
We conclude that
![]() $P_{X'}$
is exceptional over X.
$P_{X'}$
is exceptional over X.
Step 5. In this step, we lift sections from
![]() $S'$
to
$S'$
to
![]() $X'$
using Kawamata–Viehweg vanishing.
$X'$
using Kawamata–Viehweg vanishing.
Observe that:
 $$ \begin{align*} T_{X'}+ P_{X'} &= N \Omega_{X'} - \lfloor (N+1)\Omega_{X'} \rfloor -N (K_{X'}+B_{X'}+{\mathbf{M}_{X'}}) +P_{X'}\\ &= K_{X'} +\Gamma_{X'}-(K_{X'} +\Gamma_{X'}) +N \Omega_{X'} - \lfloor (N+1)\Omega_{X'} \rfloor -N (K_{X'}+B_{X'}+ {\mathbf{M}_{X'}}) +P_{X'}\\ &= K_{X'} +J_{X'} -(K_{X'}+\Gamma_{X'})-N(K_{X'}+B_{X'}+ {\mathbf{M}_{X'}}). \end{align*} $$
$$ \begin{align*} T_{X'}+ P_{X'} &= N \Omega_{X'} - \lfloor (N+1)\Omega_{X'} \rfloor -N (K_{X'}+B_{X'}+{\mathbf{M}_{X'}}) +P_{X'}\\ &= K_{X'} +\Gamma_{X'}-(K_{X'} +\Gamma_{X'}) +N \Omega_{X'} - \lfloor (N+1)\Omega_{X'} \rfloor -N (K_{X'}+B_{X'}+ {\mathbf{M}_{X'}}) +P_{X'}\\ &= K_{X'} +J_{X'} -(K_{X'}+\Gamma_{X'})-N(K_{X'}+B_{X'}+ {\mathbf{M}_{X'}}). \end{align*} $$
Then, we have that
![]() $-(K_{X'}+\Gamma _{X'}+\alpha {\mathbf {M}_{X'}})-N(K_{X'}+B_{X'}+{\mathbf {M}_{X'}})+\alpha {\mathbf {M}_{X'}}$
is big and nef over Z and
$-(K_{X'}+\Gamma _{X'}+\alpha {\mathbf {M}_{X'}})-N(K_{X'}+B_{X'}+{\mathbf {M}_{X'}})+\alpha {\mathbf {M}_{X'}}$
is big and nef over Z and
![]() $(X',J_{X'}-S')$
is klt. Therefore, up to shrinking Z around z, the relative Kawamata–Viehweg vanishing theorem implies that
$(X',J_{X'}-S')$
is klt. Therefore, up to shrinking Z around z, the relative Kawamata–Viehweg vanishing theorem implies that
![]() $h^1(X',{\mathcal {O}_{X'}}(T_{X'}+P_{X'}-S'))=0$
. So, we obtain
$h^1(X',{\mathcal {O}_{X'}}(T_{X'}+P_{X'}-S'))=0$
. So, we obtain
This means that we can lift sections of
![]() $(T_{X'}+P_{X'})\mid _{S'}$
from
$(T_{X'}+P_{X'})\mid _{S'}$
from
![]() $S'$
to
$S'$
to
![]() $X'$
.
$X'$
.
Step 6. In this step, we introduce a divisor
![]() $G_{S'}$
which is linearly equivalent to
$G_{S'}$
which is linearly equivalent to
![]() $(T_{X'}+P_{X'})|_{S'}$
.
$(T_{X'}+P_{X'})|_{S'}$
.
We have
![]() $-N(K_S +B_S+{\mathbf {N}_{S}}) = -N(K_S+B^+_S+B_S-B^+_S +{\mathbf {N}_{S}})\sim -N(B_S-B^+_S)=N(B^+_S-B_S) \geq 0$
. Define
$-N(K_S +B_S+{\mathbf {N}_{S}}) = -N(K_S+B^+_S+B_S-B^+_S +{\mathbf {N}_{S}})\sim -N(B_S-B^+_S)=N(B^+_S-B_S) \geq 0$
. Define ![]() . Then, we have that
. Then, we have that
![]() $-N(K_{S'}+B_{S'}+{\mathbf {N}_{S'}})\sim Ng^*( B^+_S-B_S) \geq 0$
. Then, it follows that
$-N(K_{S'}+B_{S'}+{\mathbf {N}_{S'}})\sim Ng^*( B^+_S-B_S) \geq 0$
. Then, it follows that
![]() $-N(K_{X'}+B_{X'}+{\mathbf {M}_{X'}})\mid _{S'}= -N(K_{S'} +B_{S'}+{\mathbf {N}_{S'}})\sim N g^*(B^+_S-B_S)$
. We define
$-N(K_{X'}+B_{X'}+{\mathbf {M}_{X'}})\mid _{S'}= -N(K_{S'} +B_{S'}+{\mathbf {N}_{S'}})\sim N g^*(B^+_S-B_S)$
. We define ![]() . By definition, we have
. By definition, we have
![]() $G_{S'} \sim (T_{X'}+P_{X'})\mid _{S'}$
.
$G_{S'} \sim (T_{X'}+P_{X'})\mid _{S'}$
.
Step 7. In this step, we prove that
![]() $G_{S'}$
is effective and that it lifts to an effective divisor
$G_{S'}$
is effective and that it lifts to an effective divisor
![]() $G_{X'}$
on
$G_{X'}$
on
![]() $X'$
.
$X'$
.
Assume
![]() $G_{S'}$
is not effective, then there exists some prime divisor
$G_{S'}$
is not effective, then there exists some prime divisor
![]() $C_{S'}$
with
$C_{S'}$
with
![]() $\operatorname {\mathrm {coeff}}_{C_{S'}}(G_{S'})<0$
. As
$\operatorname {\mathrm {coeff}}_{C_{S'}}(G_{S'})<0$
. As
![]() $N g^*(B^+_S-B_S)$
and
$N g^*(B^+_S-B_S)$
and
![]() $P_{X'}$
are effective, we must have that
$P_{X'}$
are effective, we must have that
![]() $\operatorname {\mathrm {coeff}} _{C_{S'}}(N \Omega _{X'}\mid _{S'} - \lfloor (N+1)\Omega _{X'}\mid _{S'} \rfloor )$
is negative. Since
$\operatorname {\mathrm {coeff}} _{C_{S'}}(N \Omega _{X'}\mid _{S'} - \lfloor (N+1)\Omega _{X'}\mid _{S'} \rfloor )$
is negative. Since
![]() $X'$
is a log resolution, we have that the restriction to
$X'$
is a log resolution, we have that the restriction to
![]() $S'$
commutes with taking the integral (resp. fractional) part of a divisor whose support is involved in the log resolution. In particular, observe that
$S'$
commutes with taking the integral (resp. fractional) part of a divisor whose support is involved in the log resolution. In particular, observe that
As
![]() $G_{S'}$
is integral by the previous inequality its coefficients cannot be negative. Therefore, by Step 4, we can lift
$G_{S'}$
is integral by the previous inequality its coefficients cannot be negative. Therefore, by Step 4, we can lift
![]() $G_{S'}$
to an effective divisor
$G_{S'}$
to an effective divisor
![]() $G_{X'} \sim T_{X'}+P_{X'}$
with support not containing
$G_{X'} \sim T_{X'}+P_{X'}$
with support not containing
![]() $S'$
and such that
$S'$
and such that
![]() $G_{X'}\mid _{S'} =G_{S'}$
.
$G_{X'}\mid _{S'} =G_{S'}$
.
Step 8. In this step, we introduce a divisor
![]() $B^+\geq B$
for which
$B^+\geq B$
for which
![]() $NB^+ \sim -N(K_X+{\mathbf {M}_{X}})$
.
$NB^+ \sim -N(K_X+{\mathbf {M}_{X}})$
.
Since
![]() $NB$
is integral,
$NB$
is integral,
![]() $\lfloor (N+1)\Omega \rfloor = N\Omega $
, where
$\lfloor (N+1)\Omega \rfloor = N\Omega $
, where
![]() $\Omega $
is the push-forward of
$\Omega $
is the push-forward of
![]() $\Omega _{X'}$
. Similarly, we call T, P and G the push-forwards of
$\Omega _{X'}$
. Similarly, we call T, P and G the push-forwards of
![]() $T_{X'}$
,
$T_{X'}$
,
![]() $P_{X'}$
and
$P_{X'}$
and
![]() $G_{X'}$
, respectively. We have that
$G_{X'}$
, respectively. We have that
![]() $P=0$
as
$P=0$
as
![]() $P_{X'}$
is exceptional and therefore
$P_{X'}$
is exceptional and therefore
![]() $T=T+P \sim G$
. Hence, we have that
$T=T+P \sim G$
. Hence, we have that
![]() $-N(K_X+B+{\mathbf {M}_{X}})=T=T+P\sim G \geq 0$
. Therefore,
$-N(K_X+B+{\mathbf {M}_{X}})=T=T+P\sim G \geq 0$
. Therefore,
![]() $N(K_X+B^+ + {\mathbf {M}_{X}})\sim 0$
, where we define
$N(K_X+B^+ + {\mathbf {M}_{X}})\sim 0$
, where we define ![]() .
.
Step 9. In this step, we prove that
![]() $(X,B^+, \mathbf {M})$
is generalized log canonical over some neighbourhood of z, thus proving that
$(X,B^+, \mathbf {M})$
is generalized log canonical over some neighbourhood of z, thus proving that
![]() $B^+$
is an N-complement for
$B^+$
is an N-complement for
![]() $(X,B,\mathbf {M})$
over z.
$(X,B,\mathbf {M})$
over z.
We first prove that
![]() $\frac {1}{N}G \mid _S =B^+_S-B_S$
. Note that we have the following chain of
$\frac {1}{N}G \mid _S =B^+_S-B_S$
. Note that we have the following chain of
![]() $\mathbb {Q}$
-linear equivalences:
$\mathbb {Q}$
-linear equivalences:
Since
![]() $N\Omega $
is integral, we have that
$N\Omega $
is integral, we have that
![]() $\lfloor (N+1)\Omega \rfloor =N\Omega $
. Therefore, as
$\lfloor (N+1)\Omega \rfloor =N\Omega $
. Therefore, as
![]() $P_{X'}$
is f-exceptional,
$P_{X'}$
is f-exceptional,
![]() $f_{*}(R_{X'})=G$
and
$f_{*}(R_{X'})=G$
and
![]() $R_{X'}$
is the pull-back of G. Observe that
$R_{X'}$
is the pull-back of G. Observe that
Therefore,
![]() $g^*(B^+_S-B_S)=\frac {1}{N} R_{X'}\mid _{S'}=g^*(\frac {1}{N}G\mid _{S})$
, implying that
$g^*(B^+_S-B_S)=\frac {1}{N} R_{X'}\mid _{S'}=g^*(\frac {1}{N}G\mid _{S})$
, implying that
![]() $B^+_S-B_S=\frac {1}{N}G\mid _{S}.$
$B^+_S-B_S=\frac {1}{N}G\mid _{S}.$
We now have that
![]() $K_S +B_S^++{\mathbf {N}_{S}}= K_S+B_S+B_S^+-B_S+{\mathbf {N}_{S}}=(K_X+B+\frac {1}{N}R+{\mathbf {M}_{X}})\mid _S=(K_X+B^++{\mathbf {M}_{X}})\mid _S$
. By inversion of adjunction,
$K_S +B_S^++{\mathbf {N}_{S}}= K_S+B_S+B_S^+-B_S+{\mathbf {N}_{S}}=(K_X+B+\frac {1}{N}R+{\mathbf {M}_{X}})\mid _S=(K_X+B^++{\mathbf {M}_{X}})\mid _S$
. By inversion of adjunction,
![]() $(X,B^+, \mathbf {M})$
is generalized log canonical near S. Moreover, it has coregularity c by [Reference Figueroa, Moraga and Peng10, Lemma 2.30].
$(X,B^+, \mathbf {M})$
is generalized log canonical near S. Moreover, it has coregularity c by [Reference Figueroa, Moraga and Peng10, Lemma 2.30].
If
![]() $(X,B^+, \mathbf {M})$
is not generalized log canonical near the fiber over z, then
$(X,B^+, \mathbf {M})$
is not generalized log canonical near the fiber over z, then
![]() $(X,aB^++(1-a)\Gamma ),\mathbf {M} )$
is also not generalized log canonical near the fiber over z for
$(X,aB^++(1-a)\Gamma ),\mathbf {M} )$
is also not generalized log canonical near the fiber over z for
![]() $a<1$
close enough to 1. The generalized pair
$a<1$
close enough to 1. The generalized pair
![]() $(X,B^+,\mathbf {M})$
is generalized log canonical near S, therefore a component of the generalized non-klt locus of
$(X,B^+,\mathbf {M})$
is generalized log canonical near S, therefore a component of the generalized non-klt locus of
![]() $(X,aB^++(1-a)\Gamma ),\mathbf {M} )$
is not near S. But S is also a component of the generalized log canonical locus. Hence, the generalized non-klt locus of
$(X,aB^++(1-a)\Gamma ),\mathbf {M} )$
is not near S. But S is also a component of the generalized log canonical locus. Hence, the generalized non-klt locus of
![]() $(X,aB^++(1-a)\Gamma ),\mathbf {M} )$
is disconnected near the fiber over z. This is a contradiction as
$(X,aB^++(1-a)\Gamma ),\mathbf {M} )$
is disconnected near the fiber over z. This is a contradiction as
![]() $-(K_X+aB^++(1-a)\Gamma +\mathbf {M})=-a(K_X+B^++\mathbf {M})-(1-a)(K_X+\Gamma +\mathbf {M})$
, is big and nef over Z, so the connectedness principle can be applied (see, e.g., [Reference Birkar3, Lemma 2.14]). Therefore,
$-(K_X+aB^++(1-a)\Gamma +\mathbf {M})=-a(K_X+B^++\mathbf {M})-(1-a)(K_X+\Gamma +\mathbf {M})$
, is big and nef over Z, so the connectedness principle can be applied (see, e.g., [Reference Birkar3, Lemma 2.14]). Therefore,
![]() $(X,B^+, \mathbf {M})$
is generalized log canonical near the fiber over z.
$(X,B^+, \mathbf {M})$
is generalized log canonical near the fiber over z.
Proof of Theorem 5.1.
We will proceed in several steps to reduce to Proposition 5.2. Without loss of generality, we may replace X with a small
![]() $\mathbb {Q}$
-factorial modification.
$\mathbb {Q}$
-factorial modification.
Step 1. In this step, we define a boundary divisor
![]() $B_2 \leq B_1$
and reduce to the case where
$B_2 \leq B_1$
and reduce to the case where
![]() $-(K_X+B_2+\alpha b {\mathbf {M}_{X}})$
is big and nef for some
$-(K_X+B_2+\alpha b {\mathbf {M}_{X}})$
is big and nef for some
![]() $b \in (0,1)$
.
$b \in (0,1)$
.
For any
![]() $0 < a < 1$
, we have that
$0 < a < 1$
, we have that
is antibig and anti-nef, hence we can replace
![]() $B_1$
by
$B_1$
by
![]() $aB+(1-a)B_1$
and
$aB+(1-a)B_1$
and
![]() $\alpha $
by
$\alpha $
by
![]() $a+(1-a)\alpha $
to obtain
$a+(1-a)\alpha $
to obtain
![]() $B_1$
with coefficients as close as needed to the coefficients of B.
$B_1$
with coefficients as close as needed to the coefficients of B.
Let ![]() for some
for some
![]() $b <1$
. Since X is of Fano type over Z,
$b <1$
. Since X is of Fano type over Z,
![]() $-(K_X+B_1+\alpha {\mathbf {M}_{X}} )$
defines a contraction
$-(K_X+B_1+\alpha {\mathbf {M}_{X}} )$
defines a contraction
![]() $X \rightarrow V$
over Z. We run an MMP on
$X \rightarrow V$
over Z. We run an MMP on
![]() $-(K_X+B_2+\alpha b {\mathbf {M}_{X}})$
over V. In the resulting model
$-(K_X+B_2+\alpha b {\mathbf {M}_{X}})$
over V. In the resulting model
![]() $-(K_{X'}+B_2'+\alpha b {\mathbf {M}_{X'}})$
is big and nef over V. By the definition of V,
$-(K_{X'}+B_2'+\alpha b {\mathbf {M}_{X'}})$
is big and nef over V. By the definition of V,
![]() $-(K_{X'}+B_2'+\alpha b {\mathbf {M}_{X'}})(1-t)-(K_{X'}+B_1'+\alpha {\mathbf {M}_{X'}})t$
is nef over Z for t close enough to 1, which is equivalent to saying that
$-(K_{X'}+B_2'+\alpha b {\mathbf {M}_{X'}})(1-t)-(K_{X'}+B_1'+\alpha {\mathbf {M}_{X'}})t$
is nef over Z for t close enough to 1, which is equivalent to saying that
![]() $-(K_{X'}+B_2'+ \alpha b {\mathbf {M}_{X'}})$
is nef over Z for b close enough to 1.
$-(K_{X'}+B_2'+ \alpha b {\mathbf {M}_{X'}})$
is nef over Z for b close enough to 1.
By taking a close enough to 1, we have that
![]() $K_X+B+{\mathbf {M}_{X}}$
is nonnegative over V, hence the MMP we ran is
$K_X+B+{\mathbf {M}_{X}}$
is nonnegative over V, hence the MMP we ran is
![]() $(K_X+B+{\mathbf {M}_{X}})$
-nonnegative. So, by Lemma 2.22 the coregularity of
$(K_X+B+{\mathbf {M}_{X}})$
-nonnegative. So, by Lemma 2.22 the coregularity of
![]() $(X,B, {\mathbf {M}_{X}})$
remains unchanged.
$(X,B, {\mathbf {M}_{X}})$
remains unchanged.
Then, we can replace
![]() $(X,B,\mathbf {M})$
with
$(X,B,\mathbf {M})$
with
![]() $(X',B', \mathbf {M})$
,
$(X',B', \mathbf {M})$
,
![]() $B_1$
with
$B_1$
with
![]() $B_1'$
and
$B_1'$
and
![]() $B_2$
with
$B_2$
with
![]() $B_2'$
to have also that
$B_2'$
to have also that
![]() $-(K_{X'}+B_2'+\alpha b {\mathbf {M}_{X'}})$
is big and nef over Z. As
$-(K_{X'}+B_2'+\alpha b {\mathbf {M}_{X'}})$
is big and nef over Z. As
![]() $-(K_X+B_1+\alpha {\mathbf {M}_{X}})$
is big and nef over Z, we have that there is A ample and E effective, such that
$-(K_X+B_1+\alpha {\mathbf {M}_{X}})$
is big and nef over Z, we have that there is A ample and E effective, such that
![]() $-(K_X+B_1+\alpha {\mathbf {M}_{X}}) \sim _{\mathbb {Q},Z} A+E$
.
$-(K_X+B_1+\alpha {\mathbf {M}_{X}}) \sim _{\mathbb {Q},Z} A+E$
.
Step 2. In this step, we separate into cases depending on whether the generalized log canonical centers of
![]() $(X,B_1,\alpha \mathbf {M})$
are contained in the support of E.
$(X,B_1,\alpha \mathbf {M})$
are contained in the support of E.
We can take a generalized dlt modification of
![]() $(X,B_1, \alpha {\mathbf {M}_{X}})$
, so we can assume that
$(X,B_1, \alpha {\mathbf {M}_{X}})$
, so we can assume that
![]() $(X,B_1, \alpha {\mathbf {M}_{X}})$
is generalized dlt. If
$(X,B_1, \alpha {\mathbf {M}_{X}})$
is generalized dlt. If
![]() $\operatorname {\mathrm {Supp}}{E}$
contains no generalized log canonical center of
$\operatorname {\mathrm {Supp}}{E}$
contains no generalized log canonical center of
![]() $(X,B_1,\alpha \mathbf {M})$
, then
$(X,B_1,\alpha \mathbf {M})$
, then
![]() $(X,B_1+\varepsilon E,\alpha \mathbf {M})$
is generalized dlt for
$(X,B_1+\varepsilon E,\alpha \mathbf {M})$
is generalized dlt for
![]() $\varepsilon>0$
small enough.
$\varepsilon>0$
small enough.
We have that
![]() $-(K_X+B_1+\varepsilon E+\alpha {\mathbf {M}_{X}}) \sim _{\mathbb {Q}.Z}(1-\varepsilon )( \frac {\varepsilon }{1-\varepsilon }A+-(K_X+B_1+\alpha {\mathbf {M}_{X}}))$
is ample over Z. Hence, by altering the coefficients of
$-(K_X+B_1+\varepsilon E+\alpha {\mathbf {M}_{X}}) \sim _{\mathbb {Q}.Z}(1-\varepsilon )( \frac {\varepsilon }{1-\varepsilon }A+-(K_X+B_1+\alpha {\mathbf {M}_{X}}))$
is ample over Z. Hence, by altering the coefficients of
![]() $B_1+\varepsilon E$
, we can produce a divisor
$B_1+\varepsilon E$
, we can produce a divisor
![]() $\Gamma $
that lets us conclude by Proposition 5.2.
$\Gamma $
that lets us conclude by Proposition 5.2.
If
![]() $\operatorname {\mathrm {Supp}}{E}$
does contain some generalized log canonical center of
$\operatorname {\mathrm {Supp}}{E}$
does contain some generalized log canonical center of
![]() $(X,B_1,\alpha \mathbf {M})$
, then for
$(X,B_1,\alpha \mathbf {M})$
, then for
![]() $0<r<1$
we define
$0<r<1$
we define ![]() and
and ![]() . Then, we define
. Then, we define
![]() $t_r$
to be the generalized log canonical threshold of
$t_r$
to be the generalized log canonical threshold of
![]() $E+B_1-B_r$
with respect to
$E+B_1-B_r$
with respect to
![]() $(X,B_r,\alpha _r \mathbf {M})$
over z. Since X is of Fano type, it is klt. Furthermore, since
$(X,B_r,\alpha _r \mathbf {M})$
over z. Since X is of Fano type, it is klt. Furthermore, since
![]() $(X,B,\mathbf {M})$
is generalized log canonical and
$(X,B,\mathbf {M})$
is generalized log canonical and
![]() $0 <b,r < 1$
, it follows that
$0 <b,r < 1$
, it follows that
![]() $(X,B_r,\alpha _r \mathbf {M})$
is generalized klt. In particular, we have
$(X,B_r,\alpha _r \mathbf {M})$
is generalized klt. In particular, we have
![]() $t_r>0$
. We have
$t_r>0$
. We have
 $$ \begin{align*} -(K_X+B_r+t_r(E+B_1-B_r)+ \alpha_r {\mathbf{M}_{X}})&=-(K_X+B_1+\alpha{\mathbf{M}_{X}})+B_1-B_r-t(E+B_1-B_r)+ (\alpha-\alpha_r) {\mathbf{M}_{X}}\\ &\sim_{\mathbb{R},Z} A+E +(1-t_r)(B_1-B_r)-tE+(\alpha-\alpha_r) {\mathbf{M}_{X}}\\ &=t_rA+(1-t_r)(A+E+(B_1-B_r))+ (\alpha-\alpha_r) {\mathbf{M}_{X}}\\ &\sim_{\mathbb{R},Z} t_rA -(1-t_r)(K_X+B_r+\alpha {\mathbf{M}_{X}})+ (\alpha-\alpha_r){\mathbf{M}_{X}}\\ &\sim_{\mathbb{R},Z} t_rA -(1-t_r)(K_X+B_r+\alpha_r {\mathbf{M}_{X}})+ t_r(\alpha-\alpha_r){\mathbf{M}_{X}}\\ &=t_r(A+(\alpha-\alpha_r) {\mathbf{M}_{X}})-(1-t_r)(K_X+B_r+\alpha_r {\mathbf{M}_{X}}). \end{align*} $$
$$ \begin{align*} -(K_X+B_r+t_r(E+B_1-B_r)+ \alpha_r {\mathbf{M}_{X}})&=-(K_X+B_1+\alpha{\mathbf{M}_{X}})+B_1-B_r-t(E+B_1-B_r)+ (\alpha-\alpha_r) {\mathbf{M}_{X}}\\ &\sim_{\mathbb{R},Z} A+E +(1-t_r)(B_1-B_r)-tE+(\alpha-\alpha_r) {\mathbf{M}_{X}}\\ &=t_rA+(1-t_r)(A+E+(B_1-B_r))+ (\alpha-\alpha_r) {\mathbf{M}_{X}}\\ &\sim_{\mathbb{R},Z} t_rA -(1-t_r)(K_X+B_r+\alpha {\mathbf{M}_{X}})+ (\alpha-\alpha_r){\mathbf{M}_{X}}\\ &\sim_{\mathbb{R},Z} t_rA -(1-t_r)(K_X+B_r+\alpha_r {\mathbf{M}_{X}})+ t_r(\alpha-\alpha_r){\mathbf{M}_{X}}\\ &=t_r(A+(\alpha-\alpha_r) {\mathbf{M}_{X}})-(1-t_r)(K_X+B_r+\alpha_r {\mathbf{M}_{X}}). \end{align*} $$
If we pick r close enough to 1, then
![]() $\alpha -\alpha _r$
tends to
$\alpha -\alpha _r$
tends to
![]() $0$
, hence
$0$
, hence
![]() $A-(\alpha -\alpha _r) {\mathbf {M}_{X}}$
is ample over Z for r close enough to 1. Fixing such an r, it follows that
$A-(\alpha -\alpha _r) {\mathbf {M}_{X}}$
is ample over Z for r close enough to 1. Fixing such an r, it follows that
![]() $-(K_X+B_r+t_r(E+B_1-B_r)+ \alpha _r {\mathbf {M}_{X}})$
is ample over Z.
$-(K_X+B_r+t_r(E+B_1-B_r)+ \alpha _r {\mathbf {M}_{X}})$
is ample over Z.
Step 3. In this step, we separate into cases according to the round-down of the divisor ![]() .
.
If we have
![]() $\lfloor \Theta \rfloor =0$
, then we let
$\lfloor \Theta \rfloor =0$
, then we let
![]() $(X',\Theta ',\alpha _r \mathbf {M})$
be a dlt modification of
$(X',\Theta ',\alpha _r \mathbf {M})$
be a dlt modification of
![]() $(X,\Theta ,\alpha _r \mathbf {M})$
. We can assume that every component of
$(X,\Theta ,\alpha _r \mathbf {M})$
. We can assume that every component of
![]() $\lfloor \Theta ' \rfloor $
intersects the fiber over z, after shrinking Z. Furthermore, since
$\lfloor \Theta ' \rfloor $
intersects the fiber over z, after shrinking Z. Furthermore, since
![]() $(X,B_r,\alpha _r \mathbf {M})$
is generalized klt,
$(X,B_r,\alpha _r \mathbf {M})$
is generalized klt,
![]() $\lfloor \Theta ' \rfloor $
is the exceptional divisor of
$\lfloor \Theta ' \rfloor $
is the exceptional divisor of
![]() $X' \rightarrow X$
. An MMP on
$X' \rightarrow X$
. An MMP on
![]() $K_{X'}+\lfloor \Theta ' \rfloor +\alpha b {\mathbf {M}_{X'}}$
over X ends with X, as
$K_{X'}+\lfloor \Theta ' \rfloor +\alpha b {\mathbf {M}_{X'}}$
over X ends with X, as
![]() $\lfloor \Theta ' \rfloor $
is the exceptional divisor of
$\lfloor \Theta ' \rfloor $
is the exceptional divisor of
![]() $X' \rightarrow X$
and X is klt and
$X' \rightarrow X$
and X is klt and
![]() $\mathbb {Q}$
-factorial. The last step of this MMP would be a divisorial contraction
$\mathbb {Q}$
-factorial. The last step of this MMP would be a divisorial contraction
![]() $X"\rightarrow X$
contracting one prime divisor
$X"\rightarrow X$
contracting one prime divisor
![]() $S"$
with
$S"$
with
![]() $(X",S", \alpha _r{\mathbf {M}_{X"}})$
generalized plt and
$(X",S", \alpha _r{\mathbf {M}_{X"}})$
generalized plt and
![]() $-(K_{X"}+S"+ \alpha _r{\mathbf {M}_{X"}})$
ample over X. Furthermore
$-(K_{X"}+S"+ \alpha _r{\mathbf {M}_{X"}})$
ample over X. Furthermore
![]() $S"$
is a component of both
$S"$
is a component of both
![]() $\Theta "$
and
$\Theta "$
and
![]() $B_1"$
, where
$B_1"$
, where
![]() $K_{X"}+\Theta "$
and
$K_{X"}+\Theta "$
and
![]() $K_{X"}+B_1"$
are the pull-backs of
$K_{X"}+B_1"$
are the pull-backs of
![]() $K_X+\Theta $
and
$K_X+\Theta $
and
![]() $K_X+B_1$
, respectively.
$K_X+B_1$
, respectively.
As
![]() $-(K_X+\Theta +\alpha _r {\mathbf {M}_{X}})$
is ample over Z and
$-(K_X+\Theta +\alpha _r {\mathbf {M}_{X}})$
is ample over Z and
![]() $-(K_{X"}+S"+\alpha _r {\mathbf {M}_{X"}})$
is ample over X, a linear combination of
$-(K_{X"}+S"+\alpha _r {\mathbf {M}_{X"}})$
is ample over X, a linear combination of
![]() $S"$
and
$S"$
and
![]() $\Theta "$
yields
$\Theta "$
yields
![]() $\Gamma "$
such that
$\Gamma "$
such that
![]() $-(K_{X"}+\Gamma "+\alpha _r {\mathbf {M}_{X"}})$
is ample over Z and
$-(K_{X"}+\Gamma "+\alpha _r {\mathbf {M}_{X"}})$
is ample over Z and
![]() $(X",\Gamma ",\alpha _r {\mathbf {M}_{X"}})$
is plt with
$(X",\Gamma ",\alpha _r {\mathbf {M}_{X"}})$
is plt with
![]() $\lfloor \Gamma " \rfloor =S"$
. We can apply Proposition 5.2 here. As an N-complement on
$\lfloor \Gamma " \rfloor =S"$
. We can apply Proposition 5.2 here. As an N-complement on
![]() $X"$
would induce an N-complement on X, we have reduced to the case where
$X"$
would induce an N-complement on X, we have reduced to the case where
![]() $\lfloor \Theta \rfloor \neq 0$
.
$\lfloor \Theta \rfloor \neq 0$
.
It only remains to deal with the case where
![]() $\lfloor \Theta \rfloor \neq 0$
. In this case, there is a component S of
$\lfloor \Theta \rfloor \neq 0$
. In this case, there is a component S of
![]() $\lfloor \Theta \rfloor \leq \lfloor B_1 \rfloor \leq \lfloor B \rfloor $
. On a dlt modification of
$\lfloor \Theta \rfloor \leq \lfloor B_1 \rfloor \leq \lfloor B \rfloor $
. On a dlt modification of
![]() $(X,S, \alpha _r {\mathbf {M}_{X}})$
, we can perturb the coefficients of
$(X,S, \alpha _r {\mathbf {M}_{X}})$
, we can perturb the coefficients of
![]() $\Theta '$
to get that
$\Theta '$
to get that
![]() $\lfloor \Theta " \rfloor $
is irreducible and
$\lfloor \Theta " \rfloor $
is irreducible and
![]() $-(K_{X'} +\Gamma + \alpha _r {\mathbf {M}_{X}})$
is ample. Therefore, we can obtain the N-complement by Proposition 5.2, as desired. As an N-complement on
$-(K_{X'} +\Gamma + \alpha _r {\mathbf {M}_{X}})$
is ample. Therefore, we can obtain the N-complement by Proposition 5.2, as desired. As an N-complement on
![]() $X"$
induces an N-complement on X, we are done.
$X"$
induces an N-complement on X, we are done.
5.2 Relative complements
In this subsection, we study the existence of complements in the relative setting. The main theorem of this subsection states that we can lift complements from lower coregularity pairs when all the generalized log canonical centers are horizontal over the base.
Theorem 5.3. Let d, c and p be nonnegative integers and
![]() $\Lambda \subset \mathbb {Q}$
be a closed set satisfying the DCC. Assume Theorem 7
$\Lambda \subset \mathbb {Q}$
be a closed set satisfying the DCC. Assume Theorem 7
![]() $(c-1)$
holds. There exists a constant
$(c-1)$
holds. There exists a constant ![]() satisfying the following.
satisfying the following.
Let
![]() $\pi \colon X \rightarrow Z$
be a Fano type morphism, where X is a d-dimensional variety, and
$\pi \colon X \rightarrow Z$
be a Fano type morphism, where X is a d-dimensional variety, and
![]() $\dim Z>0$
. Let
$\dim Z>0$
. Let
![]() $(X,B, \mathbf {M})$
be a generalized log canonical pair over Z and
$(X,B, \mathbf {M})$
be a generalized log canonical pair over Z and
![]() $z \in Z$
a point satisfying the following conditions:
$z \in Z$
a point satisfying the following conditions:
-
• the generalized pair
 $(X,B, \mathbf {M})$
has coregularity at most c over z;
$(X,B, \mathbf {M})$
has coregularity at most c over z; -
• the coefficients of B belong to
 $\Lambda $
;
$\Lambda $
; -
• every generalized log canonical center of
 $(X,B,\mathbf {M})$
dominates Z;
$(X,B,\mathbf {M})$
dominates Z; -
•
 $p \mathbf {M}$
is b-Cartier; and
$p \mathbf {M}$
is b-Cartier; and -
• the divisor
 $-(K_X+B+{\mathbf {M}_{X}})$
is nef over Z.
$-(K_X+B+{\mathbf {M}_{X}})$
is nef over Z.
Then, there exists an N-complement for
![]() $(X,B,\mathbf {M})$
over z.
$(X,B,\mathbf {M})$
over z.
Proof. We will proceed in several steps to be able to lift complements using Theorem 5.1.
Step 1. In this step, we reduce to the case in which the boundary coefficients belong to a finite set,
![]() $(X,B, \mathbf {M})$
has coregularity
$(X,B, \mathbf {M})$
has coregularity
![]() $c-1$
over, and
$c-1$
over, and
![]() $\lfloor B \rfloor $
has a vertical component intersecting the fiber over
$\lfloor B \rfloor $
has a vertical component intersecting the fiber over
![]() $z.$
$z.$
By Theorem 3.5, there exists a finite set
![]() $\mathcal {R}$
and a relative pair
$\mathcal {R}$
and a relative pair
![]() $(X',B',\mathbf {M})$
with
$(X',B',\mathbf {M})$
with
![]() $\operatorname {\mathrm {coeff}}(B')\subset \mathcal {R}$
such that if
$\operatorname {\mathrm {coeff}}(B')\subset \mathcal {R}$
such that if
![]() $(X',B',\mathbf {M})$
is N-complemented, then so is
$(X',B',\mathbf {M})$
is N-complemented, then so is
![]() $(X,B,\mathbf {M})$
. So, we can replace our generalized pair
$(X,B,\mathbf {M})$
. So, we can replace our generalized pair
![]() $(X,B,\mathbf {M})$
with
$(X,B,\mathbf {M})$
with
![]() $(X',B',\mathbf {M})$
. Hence, we may assume the coefficients of B belong to the finite set
$(X',B',\mathbf {M})$
. Hence, we may assume the coefficients of B belong to the finite set
![]() $\mathcal {R}$
. Up to taking a
$\mathcal {R}$
. Up to taking a
![]() $\mathbb {Q}$
-factorial dlt modification, we may further assume that X is
$\mathbb {Q}$
-factorial dlt modification, we may further assume that X is
![]() $\mathbb {Q}$
-factorial.
$\mathbb {Q}$
-factorial.
We pick an effective Cartier divisor N on Z passing through z. We let t be the generalized log canonical threshold of
![]() $q^*N$
with respect to
$q^*N$
with respect to
![]() $(X,B, \mathbf {M})$
over z. By the connectedness principle [Reference Filipazzi and Svaldi16, Theorem 1.7] and the assumption that all the generalized log canonical centers of
$(X,B, \mathbf {M})$
over z. By the connectedness principle [Reference Filipazzi and Svaldi16, Theorem 1.7] and the assumption that all the generalized log canonical centers of
![]() $(X,B,\mathbf {M})$
dominate Z, we know that the coregularity of
$(X,B,\mathbf {M})$
dominate Z, we know that the coregularity of
![]() $(X,B+tq^*N,\mathbf {M})$
is at most
$(X,B+tq^*N,\mathbf {M})$
is at most
![]() $c-1$
.
$c-1$
.
Let
![]() $(X',T', \mathbf {M})$
be a generalized dlt modification of
$(X',T', \mathbf {M})$
be a generalized dlt modification of
![]() $(X,B+tq^*N,\mathbf {M})$
over z. Let
$(X,B+tq^*N,\mathbf {M})$
over z. Let
![]() $B'$
be the strict transform of B on
$B'$
be the strict transform of B on
![]() $X'$
. Let
$X'$
. Let
![]() $\Omega '$
be a boundary such that
$\Omega '$
be a boundary such that
![]() $B' \leq \Omega ' \leq T'$
,
$B' \leq \Omega ' \leq T'$
,
![]() $\operatorname {\mathrm {coeff}}(\Omega ')\subset \mathcal {R} $
and some component S of
$\operatorname {\mathrm {coeff}}(\Omega ')\subset \mathcal {R} $
and some component S of
![]() $\lfloor \Omega ' \rfloor $
is vertical over Z intersecting the fiber
$\lfloor \Omega ' \rfloor $
is vertical over Z intersecting the fiber
![]() $\pi ^{-1}(z)$
. Let
$\pi ^{-1}(z)$
. Let
![]() $\Omega = \pi _\ast \Omega '$
.
$\Omega = \pi _\ast \Omega '$
.
We run an MMP over Z on
![]() $-(K_{X'}+\Omega '+{\mathbf {M}_{X'}})$
. As
$-(K_{X'}+\Omega '+{\mathbf {M}_{X'}})$
. As
![]() $-(K_{X'}+\Omega '+{\mathbf {M}_{X'}})=-(K_{X'}+T'+{\mathbf {M}_{X'}})+(T'-\Omega '),$
with
$-(K_{X'}+\Omega '+{\mathbf {M}_{X'}})=-(K_{X'}+T'+{\mathbf {M}_{X'}})+(T'-\Omega '),$
with
![]() $-(K_{X'}+T'+\mathbf {M}'.)$
nef over Z and
$-(K_{X'}+T'+\mathbf {M}'.)$
nef over Z and
![]() $(T'-\Omega ')$
effective, the MMP ends with a minimal model, which we denote by
$(T'-\Omega ')$
effective, the MMP ends with a minimal model, which we denote by
![]() $X"$
.
$X"$
.
If
![]() $(X",\Omega ", {\mathbf {M}_{X"}})$
has an N-complement over z, then
$(X",\Omega ", {\mathbf {M}_{X"}})$
has an N-complement over z, then
![]() $(X',\Omega ', {\mathbf {M}_{X'}})$
has an N-complement over z by Lemma 2.12. As
$(X',\Omega ', {\mathbf {M}_{X'}})$
has an N-complement over z by Lemma 2.12. As
![]() $B \leq \Omega $
, we have that also
$B \leq \Omega $
, we have that also
![]() $(X,B, {\mathbf {M}_{X}})$
has an N-complement by Lemma 2.13. So, we can replace
$(X,B, {\mathbf {M}_{X}})$
has an N-complement by Lemma 2.13. So, we can replace
![]() $(X,B, {\mathbf {M}_{X}})$
with
$(X,B, {\mathbf {M}_{X}})$
with
![]() $(X",\Omega ", {\mathbf {M}_{X"}})$
, to obtain
$(X",\Omega ", {\mathbf {M}_{X"}})$
, to obtain
![]() $\lfloor B \rfloor $
having a component intersecting the fiber over z, with
$\lfloor B \rfloor $
having a component intersecting the fiber over z, with
![]() $-(K_X+B+{\mathbf {M}_{X}})$
nef over Z. Notice that, after this reduction, the coregularity has decreased, and it is no longer the case that all generalized log canonical centers dominate Z.
$-(K_X+B+{\mathbf {M}_{X}})$
nef over Z. Notice that, after this reduction, the coregularity has decreased, and it is no longer the case that all generalized log canonical centers dominate Z.
Step 2. In this step, we define a divisor
![]() $B_1$
which satisfies the hypothesis of Theorem 5.1.
$B_1$
which satisfies the hypothesis of Theorem 5.1.
For any prime divisor D that vertical is over Z, we set ![]() . For any prime divisor D horizontal over Z, we set
. For any prime divisor D horizontal over Z, we set ![]() for
for
![]() $a<1$
, close enough to 1.
$a<1$
, close enough to 1.
As X is of Fano type over Z, we have that
![]() $-K_X$
is big over Z. Therefore,
$-K_X$
is big over Z. Therefore,
![]() $-(K_X+aB+a {\mathbf {M}_{X}})=-a(K_X+B+{\mathbf {M}_{X}})-(1-a)K_X$
and
$-(K_X+aB+a {\mathbf {M}_{X}})=-a(K_X+B+{\mathbf {M}_{X}})-(1-a)K_X$
and
![]() $-(K_X+ B_1+a{\mathbf {M}_{X}})$
are big over Z. The generalized pair
$-(K_X+ B_1+a{\mathbf {M}_{X}})$
are big over Z. The generalized pair
![]() $(X,B_1, a\mathbf {M})$
is generalized log canonical as
$(X,B_1, a\mathbf {M})$
is generalized log canonical as
![]() $B_1 \leq B$
and
$B_1 \leq B$
and
![]() $\lfloor B_1 \rfloor $
contains the same vertical component as
$\lfloor B_1 \rfloor $
contains the same vertical component as
![]() $\lfloor B \rfloor $
intersecting the fiber of z.
$\lfloor B \rfloor $
intersecting the fiber of z.
Step 3. In this step, we reduce to the case in which
![]() $-(K_X+B_1+{\mathbf {M}_{X}})$
is big and nef over Z.
$-(K_X+B_1+{\mathbf {M}_{X}})$
is big and nef over Z.
Since
![]() $\pi $
is a Fano type morphism and
$\pi $
is a Fano type morphism and
![]() $-(K_X+B+{\mathbf {M}_{X}})$
is nef over Z,
$-(K_X+B+{\mathbf {M}_{X}})$
is nef over Z,
![]() $-(K_X+B+{\mathbf {M}_{X}})$
is semiample over Z. Let
$-(K_X+B+{\mathbf {M}_{X}})$
is semiample over Z. Let
![]() $X \rightarrow V$
over Z be the contraction defined by
$X \rightarrow V$
over Z be the contraction defined by
![]() $-(K_X+B+{\mathbf {M}_{X}})$
. We run an MMP on
$-(K_X+B+{\mathbf {M}_{X}})$
. We run an MMP on
![]() $-(K_X+B_1+a{\mathbf {M}_{X}})$
over V. In the resulting model
$-(K_X+B_1+a{\mathbf {M}_{X}})$
over V. In the resulting model
![]() $-(K_X'+B_1'+a{\mathbf {M}_{X'}})$
is big and nef over V. By the definition of V,
$-(K_X'+B_1'+a{\mathbf {M}_{X'}})$
is big and nef over V. By the definition of V,
![]() $-(K_{X'}+B_1'+a{\mathbf {M}_{X'}})(1-t)-(K_{X'}+B'+{\mathbf {M}_{X'}})t$
is nef over Z for t close enough to 1, which is equivalent to picking a close enough to 1. We have that
$-(K_{X'}+B_1'+a{\mathbf {M}_{X'}})(1-t)-(K_{X'}+B'+{\mathbf {M}_{X'}})t$
is nef over Z for t close enough to 1, which is equivalent to picking a close enough to 1. We have that
![]() $K_X+B+{\mathbf {M}_{X}}$
is trivial over V, hence the MMP is
$K_X+B+{\mathbf {M}_{X}}$
is trivial over V, hence the MMP is
![]() $(K_X+B+{\mathbf {M}_{X}})$
-nonnegative. Applying Lemma 2.22, the coregularity of
$(K_X+B+{\mathbf {M}_{X}})$
-nonnegative. Applying Lemma 2.22, the coregularity of
![]() $(X,B,\mathbf {M})$
remains unchanged after this MMP. Thus, we can replace
$(X,B,\mathbf {M})$
remains unchanged after this MMP. Thus, we can replace
![]() $(X,B,\mathbf {M})$
, with
$(X,B,\mathbf {M})$
, with
![]() $(X',B', \mathbf {M})$
and
$(X',B', \mathbf {M})$
and
![]() $B_1$
with
$B_1$
with
![]() $B_1'$
with a close enough to 1.
$B_1'$
with a close enough to 1.
Step 4. In this step, we conclude by applying Theorem 5.1.
Let
![]() $N(\mathcal {R},c-1,p)$
be the positive integer provided by Theorem 7
$N(\mathcal {R},c-1,p)$
be the positive integer provided by Theorem 7
![]() $(c-1)$
. Taking N to be the least common multiple of
$(c-1)$
. Taking N to be the least common multiple of
![]() $N(\mathcal {R},c-1,p)$
,
$N(\mathcal {R},c-1,p)$
,
![]() $I_{\mathcal {R}}$
and p. Hence, N depends only on
$I_{\mathcal {R}}$
and p. Hence, N depends only on
![]() $\Lambda $
,
$\Lambda $
,
![]() $c-1$
and p. Indeed,
$c-1$
and p. Indeed,
![]() $\mathcal {R}$
only depends on
$\mathcal {R}$
only depends on
![]() $\Lambda ,c$
and p. By Theorem 5.1 the generalized pair
$\Lambda ,c$
and p. By Theorem 5.1 the generalized pair
![]() $(X,B, \mathbf {M})$
admits an N-complement, where N only depends on
$(X,B, \mathbf {M})$
admits an N-complement, where N only depends on
![]() $\Lambda $
, c and p.
$\Lambda $
, c and p.
6 Canonical bundle formula
In this section, we prove a special version of the canonical bundle formula. We obtain an effective canonical bundle formula that is independent of the dimension of the domain. It only depends on the coregularity of the fibers.
Theorem 6.1. Let d, c be nonnegative integers and
![]() $\Lambda \subset \mathbb {Q}$
be a closed set satisfying the descending chain condition. Assume Theorem 7
$\Lambda \subset \mathbb {Q}$
be a closed set satisfying the descending chain condition. Assume Theorem 7
![]() $(c-1)$
holds. There exists a set
$(c-1)$
holds. There exists a set ![]() satisfying the descending chain condition and a positive integer
satisfying the descending chain condition and a positive integer ![]() satisfying the following. Let
satisfying the following. Let
![]() $\pi \colon X\rightarrow Z$
be a fibration from a d-dimensional projective variety X to a projective base Z with
$\pi \colon X\rightarrow Z$
be a fibration from a d-dimensional projective variety X to a projective base Z with
![]() $\dim Z> 0$
. Let
$\dim Z> 0$
. Let
![]() $(X,B)$
be a log canonical pair satisfying the following conditions:
$(X,B)$
be a log canonical pair satisfying the following conditions:
-
• the fibration
 $\pi $
is of Fano type over a nonempty open set U of Z;
$\pi $
is of Fano type over a nonempty open set U of Z; -
• every log canonical center of
 $(X,B)$
is horizontal over Z;
$(X,B)$
is horizontal over Z; -
• the pair
 $(X,B)$
is log Calabi–Yau over Z;
$(X,B)$
is log Calabi–Yau over Z; -
• the coefficients of B are in
 $\Lambda $
; and
$\Lambda $
; and -
• the coregularity of
 $(X,B)$
is at most c.
$(X,B)$
is at most c.
Then, we can write
where
![]() $(Z,B_Z,\mathbf {N})$
is a generalized log canonical pair such that
$(Z,B_Z,\mathbf {N})$
is a generalized log canonical pair such that
-
•
 $B_Z$
is the discriminant part of the adjunction for
$B_Z$
is the discriminant part of the adjunction for
 $(X,B)$
over Z;
$(X,B)$
over Z; -
• the coefficients of
 $B_Z$
belong to
$B_Z$
belong to
 $\Omega $
; and
$\Omega $
; and -
• the divisor
 $q\mathbf {N}$
is b-nef and b-Cartier.
$q\mathbf {N}$
is b-nef and b-Cartier.
Proof. The proof is given in several steps. In Step 1, we make a choice of q and
![]() $\mathbf {N}$
. In Steps 2–4, we find
$\mathbf {N}$
. In Steps 2–4, we find
![]() $\Omega $
and show that the coefficients of
$\Omega $
and show that the coefficients of
![]() $B_Z$
belong to
$B_Z$
belong to
![]() $\Omega $
. We also prove that
$\Omega $
. We also prove that
![]() $q{\mathbf {N}_{Z}}$
is integral. In Step 5, we show that
$q{\mathbf {N}_{Z}}$
is integral. In Step 5, we show that
![]() $q\mathbf {N}$
is b-Cartier. We observe that, by the assumptions on the log canonical centers of
$q\mathbf {N}$
is b-Cartier. We observe that, by the assumptions on the log canonical centers of
![]() $(X,B)$
and on the coregularity of
$(X,B)$
and on the coregularity of
![]() $(X,B)$
, it follows that
$(X,B)$
, it follows that
![]() $\dim Z \leq c$
.
$\dim Z \leq c$
.
Step 1. In this step, we find q and make a choice of
![]() $\mathbf {N}$
.
$\mathbf {N}$
.
Let q be the integer N in the statement of Theorem 5.3
![]() $(d,c-1)$
. Here, we assumed Theorem 7
$(d,c-1)$
. Here, we assumed Theorem 7
![]() $(c-1)$
. Fix a general closed point
$(c-1)$
. Fix a general closed point
![]() $z\in U$
. Let H be a general hyperplane section of U passing through z. Then
$z\in U$
. Let H be a general hyperplane section of U passing through z. Then
![]() $(X,B+\pi ^*H)$
is log Calabi–Yau and satisfies
$(X,B+\pi ^*H)$
is log Calabi–Yau and satisfies
This implies that the absolute coregularity of
![]() $(X,B)$
over z is at most
$(X,B)$
over z is at most
![]() $c-1$
. By Theorem 5.3
$c-1$
. By Theorem 5.3
![]() $(d,c-1)$
, there is a q-complement
$(d,c-1)$
, there is a q-complement
![]() $K_X+B^+$
of
$K_X+B^+$
of
![]() $K_X+B$
over z with
$K_X+B$
over z with
![]() $B^+\geq B$
. Note that q only depends on
$B^+\geq B$
. Note that q only depends on
![]() $\Lambda $
and c. Since
$\Lambda $
and c. Since
![]() $K_X+B$
is
$K_X+B$
is
![]() $\mathbb {Q}$
-trivial over Z,
$\mathbb {Q}$
-trivial over Z,
![]() $B^+-B\sim _{\mathbb {Q}}0$
over z and hence
$B^+-B\sim _{\mathbb {Q}}0$
over z and hence
![]() $B^+=B$
near the generic fiber of
$B^+=B$
near the generic fiber of
![]() $\pi $
. Therefore,
$\pi $
. Therefore,
![]() $q(K_X+B)\sim 0$
over the generic point of Z. Thus, we can find a rational function s on X such that
$q(K_X+B)\sim 0$
over the generic point of Z. Thus, we can find a rational function s on X such that ![]() is zero over the generic point of Z. Note that
is zero over the generic point of Z. Note that
![]() $L\sim _{\mathbb {Q}} 0$
over Z, so we can write
$L\sim _{\mathbb {Q}} 0$
over Z, so we can write
![]() $L = \pi ^* L_Z$
for some
$L = \pi ^* L_Z$
for some
![]() $\mathbb {Q}$
-Cartier
$\mathbb {Q}$
-Cartier
![]() $\mathbb {Q}$
-divisor
$\mathbb {Q}$
-divisor
![]() $L_Z$
on Z. Define
$L_Z$
on Z. Define
where
![]() $B_Z$
is the discriminant part of adjunction for
$B_Z$
is the discriminant part of adjunction for
![]() $(X,B)$
over Z. Similarly, for any birational morphism
$(X,B)$
over Z. Similarly, for any birational morphism
![]() $g \colon Z'\to Z$
, we can define
$g \colon Z'\to Z$
, we can define
![]() ${\mathbf {N}}_{Z'}$
as follows. Let
${\mathbf {N}}_{Z'}$
as follows. Let
![]() $f \colon X'\to X$
be a higher birational model of X such that the rational map
$f \colon X'\to X$
be a higher birational model of X such that the rational map
![]() $X'\dashrightarrow Z'$
is a morphism. Write
$X'\dashrightarrow Z'$
is a morphism. Write
![]() $K_{X'} + B_{X'} $
for the pull-back of
$K_{X'} + B_{X'} $
for the pull-back of
![]() $K_X+B$
and
$K_X+B$
and
![]() $B_{Z'}$
be the discriminant part of adjunction for
$B_{Z'}$
be the discriminant part of adjunction for
![]() $(X', B_{X'})$
over
$(X', B_{X'})$
over
![]() $Z'$
. We define
$Z'$
. We define
The data of
![]() ${\mathbf {N}_{Z'}}$
, for all birational models
${\mathbf {N}_{Z'}}$
, for all birational models
![]() $Z'\to Z$
, determine a b-divisor
$Z'\to Z$
, determine a b-divisor
![]() $\mathbf {N}$
on Z.
$\mathbf {N}$
on Z.
Step 2. In this step, we reduce to the case when the base Z is a curve.
Assume
![]() $\dim Z \geq 2$
. Let H be a general hyperplane section of Z and G be the pull-back of H to X. By adjunction, we can write
$\dim Z \geq 2$
. Let H be a general hyperplane section of Z and G be the pull-back of H to X. By adjunction, we can write
for some divisor
![]() $B_G$
on G. By Lemma 2.17, there exists a set
$B_G$
on G. By Lemma 2.17, there exists a set
![]() $\Lambda '$
satisfying the DCC, having rational accumulation points and depending only on
$\Lambda '$
satisfying the DCC, having rational accumulation points and depending only on
![]() $\Lambda $
such that the coefficients of
$\Lambda $
such that the coefficients of
![]() $B_G$
belong to
$B_G$
belong to
![]() $\Lambda '$
. We may replace
$\Lambda '$
. We may replace
![]() $\Lambda $
with
$\Lambda $
with
![]() $\Lambda '$
to assume that the coefficients of
$\Lambda '$
to assume that the coefficients of
![]() $B_G$
belong to
$B_G$
belong to
![]() $\Lambda $
. Since
$\Lambda $
. Since
![]() $\dim Z \leq c$
, this replacement can only happen at most
$\dim Z \leq c$
, this replacement can only happen at most
![]() $c-1$
times and is hence allowed. By Lemma 2.25, the pair
$c-1$
times and is hence allowed. By Lemma 2.25, the pair
![]() $(G,B_G)$
over H satisfies the same conditions as
$(G,B_G)$
over H satisfies the same conditions as
![]() $(X,B)$
over Z in the statement of this theorem. Furthermore, let
$(X,B)$
over Z in the statement of this theorem. Furthermore, let
![]() $B_H$
denote the discriminant part of the adjunction for
$B_H$
denote the discriminant part of the adjunction for
![]() $(G,B_G)$
over H. Let D be any prime divisor on Z and C a component of
$(G,B_G)$
over H. Let D be any prime divisor on Z and C a component of
![]() $D\cap H$
. Then
$D\cap H$
. Then
Pick a general
![]() $H'\sim H$
, and let
$H'\sim H$
, and let
![]() $K_H = (K_Z+H')|_H$
, which is properly defined as a Weil divisor. Define
$K_H = (K_Z+H')|_H$
, which is properly defined as a Weil divisor. Define
Similarly to the way we defined the b-divisor
![]() $\mathbf {N}$
on Z, we can define
$\mathbf {N}$
on Z, we can define
![]() $\mathbf {N}'$
as a b-divisor on H. Then, we have
$\mathbf {N}'$
as a b-divisor on H. Then, we have
Thus,
![]() ${\mathbf {N}_{H}}'$
is the moduli part of
${\mathbf {N}_{H}}'$
is the moduli part of
![]() $(G,B_G)$
over H. Moreover, we have
$(G,B_G)$
over H. Moreover, we have
![]() $B_H+{{\mathbf {N}_{H}}'} = (B_Z+{\mathbf {N}_{Z}})|_H$
. This implies that
$B_H+{{\mathbf {N}_{H}}'} = (B_Z+{\mathbf {N}_{Z}})|_H$
. This implies that
![]() $ \operatorname {\mathrm {coeff}}_C(B_H+{{\mathbf {N}_{H}}'} ) = \operatorname {\mathrm {coeff}}_D(B_Z + {\mathbf {N}_{Z}}) $
and hence
$ \operatorname {\mathrm {coeff}}_C(B_H+{{\mathbf {N}_{H}}'} ) = \operatorname {\mathrm {coeff}}_D(B_Z + {\mathbf {N}_{Z}}) $
and hence
![]() $ \operatorname {\mathrm {coeff}}_C({{\mathbf {N}_{H}}'} ) = \operatorname {\mathrm {coeff}}_D({\mathbf {N}_{Z}}). $
In particular,
$ \operatorname {\mathrm {coeff}}_C({{\mathbf {N}_{H}}'} ) = \operatorname {\mathrm {coeff}}_D({\mathbf {N}_{Z}}). $
In particular,
![]() $q{\mathbf {N}_{H}}'$
is integral if and only if
$q{\mathbf {N}_{H}}'$
is integral if and only if
![]() $q{\mathbf {N}_{H}}$
is integral.
$q{\mathbf {N}_{H}}$
is integral.
As a result, to prove that
![]() $\operatorname {\mathrm {coeff}}(B_Z)$
belongs to a fixed set
$\operatorname {\mathrm {coeff}}(B_Z)$
belongs to a fixed set
![]() $\Omega $
and that
$\Omega $
and that
![]() $q{\mathbf {N}_{Z}}$
is integral, we may replace
$q{\mathbf {N}_{Z}}$
is integral, we may replace
![]() $(X,B) \to Z$
with
$(X,B) \to Z$
with
![]() $(G,B_G)\to H$
. By repeating this process until the base of the fibration is a curve, we may assume that
$(G,B_G)\to H$
. By repeating this process until the base of the fibration is a curve, we may assume that
![]() $\dim Z = 1$
.
$\dim Z = 1$
.
Step 3. In this step, we show the existence of
![]() $\Omega $
.
$\Omega $
.
By Step 2, we can assume
![]() $\dim Z = 1$
. By [Reference Birkar3, Lemma 2.11], the variety X is of Fano type over Z. Pick any closed point
$\dim Z = 1$
. By [Reference Birkar3, Lemma 2.11], the variety X is of Fano type over Z. Pick any closed point
![]() $z\in Z$
. Let t be the log canonical threshold of
$z\in Z$
. Let t be the log canonical threshold of
![]() $\pi ^*z$
with respect to
$\pi ^*z$
with respect to
![]() $(X,B)$
around z. Set
$(X,B)$
around z. Set
![]() $\Gamma = B+t\pi ^*z$
, and let
$\Gamma = B+t\pi ^*z$
, and let
![]() $(X',\Gamma ')$
be a
$(X',\Gamma ')$
be a
![]() $\mathbb {Q}$
-factorial dlt modification of
$\mathbb {Q}$
-factorial dlt modification of
![]() $(X,\Gamma )$
. Then
$(X,\Gamma )$
. Then
![]() $K_{X'}+\Gamma ' \sim _{\mathbb {Q}} 0$
over Z and
$K_{X'}+\Gamma ' \sim _{\mathbb {Q}} 0$
over Z and
![]() $\Gamma '$
has a component with coefficient 1 mapping to z. Pick a boundary
$\Gamma '$
has a component with coefficient 1 mapping to z. Pick a boundary
![]() $B'$
on
$B'$
on
![]() $X'$
satisfying the following conditions:
$X'$
satisfying the following conditions:
-
• we have
 $\tilde {B}\leq B'\leq \Gamma '$
, where
$\tilde {B}\leq B'\leq \Gamma '$
, where
 $\tilde {B}$
is the strict transform of B on
$\tilde {B}$
is the strict transform of B on
 $X'$
;
$X'$
; -
• the coefficients of
 $B'$
are in
$B'$
are in
 $\Lambda $
; and
$\Lambda $
; and -
• the divisors
 $B'$
and
$B'$
and
 $\Gamma '$
have the same round-down, that is,
$\Gamma '$
have the same round-down, that is,
 $\lfloor B'\rfloor = \lfloor \Gamma '\rfloor $
.
$\lfloor B'\rfloor = \lfloor \Gamma '\rfloor $
.
By construction,
![]() $\operatorname {Supp}(\Gamma '-B')$
is contained in the strict transform of
$\operatorname {Supp}(\Gamma '-B')$
is contained in the strict transform of
![]() $\operatorname {Supp}(\pi ^*z)$
. If
$\operatorname {Supp}(\pi ^*z)$
. If
![]() $t<1$
,
$t<1$
,
![]() $\lfloor B'\rfloor $
has a component T mapping to z which is exceptional over X. Note that
$\lfloor B'\rfloor $
has a component T mapping to z which is exceptional over X. Note that
![]() $X'$
is of Fano type over Z. We run a
$X'$
is of Fano type over Z. We run a
![]() $-(K_{X'}+B')$
-MMP with scaling over Z. Since
$-(K_{X'}+B')$
-MMP with scaling over Z. Since
![]() $-(K_{X'}+B')\sim _{\mathbb {Q}} \Gamma '-B'$
is pseudo-effective, this MMP terminates with a model
$-(K_{X'}+B')\sim _{\mathbb {Q}} \Gamma '-B'$
is pseudo-effective, this MMP terminates with a model
![]() $(X",B")$
such that
$(X",B")$
such that
![]() $-(K_{X"}+B")$
is semiample over Z by [Reference Birkar1, Theorem 1.1]. The divisor T is not contracted by this MMP because
$-(K_{X"}+B")$
is semiample over Z by [Reference Birkar1, Theorem 1.1]. The divisor T is not contracted by this MMP because
![]() $T\not \subseteq \operatorname {Supp}(\Gamma '-B')$
. Furthermore, by Lemma 2.22, we have
$T\not \subseteq \operatorname {Supp}(\Gamma '-B')$
. Furthermore, by Lemma 2.22, we have
As a result, up to losing the dlt condition, we may replace
![]() $(X',B')$
by
$(X',B')$
by
![]() $(X",B")$
to assume that the following properties hold:
$(X",B")$
to assume that the following properties hold:
-
•
 $X'$
is Fano type over Z;
$X'$
is Fano type over Z; -
•
 $(X',B')$
is a log canonical pair over Z;
$(X',B')$
is a log canonical pair over Z; -
• the coefficients of
 $B'$
are in
$B'$
are in
 $\Lambda $
;
$\Lambda $
; -
•
 $\mathrm {coreg}(X',B')\leq c$
;
$\mathrm {coreg}(X',B')\leq c$
; -
•
 $-(K_{X'}+B')$
is semiample over Z; and
$-(K_{X'}+B')$
is semiample over Z; and -
•
 $\lfloor B'\rfloor $
has a component mapping to z.
$\lfloor B'\rfloor $
has a component mapping to z.
If
![]() $t = 1$
, we may simply take
$t = 1$
, we may simply take
![]() $B' = \Gamma '$
so the above conditions hold as well for
$B' = \Gamma '$
so the above conditions hold as well for
![]() $(X',B')$
.
$(X',B')$
.
By Theorem 5.1 and our choice of q, the pair
![]() $(X',B')$
has a q-complement
$(X',B')$
has a q-complement
![]() $(X',B^+)$
over z with
$(X',B^+)$
over z with
![]() $B^{\prime }+\geq B'$
. Pushing forward
$B^{\prime }+\geq B'$
. Pushing forward
![]() $B^{\prime }+$
to X gives a q-complement
$B^{\prime }+$
to X gives a q-complement
![]() $(X,B^+)$
of
$(X,B^+)$
of
![]() $(X,B)$
over z with
$(X,B)$
over z with
![]() $B^+\geq B$
. Furthermore,
$B^+\geq B$
. Furthermore,
![]() $K_X+B^+$
has a non-klt center mapping to z, since its pull-back
$K_X+B^+$
has a non-klt center mapping to z, since its pull-back
![]() $K_{X'}+B^{\prime }+$
does. Note that
$K_{X'}+B^{\prime }+$
does. Note that
![]() $B^+-B\sim _{\mathbb {Q}} 0$
over z, so
$B^+-B\sim _{\mathbb {Q}} 0$
over z, so
![]() $B^+-B$
must be a multiple of
$B^+-B$
must be a multiple of
![]() $\pi ^*z$
over z. This implies that
$\pi ^*z$
over z. This implies that
![]() $B^+ = B+t\pi ^*z$
over z since
$B^+ = B+t\pi ^*z$
over z since
![]() $K_X+B^+$
has a non-klt center mapping to z.
$K_X+B^+$
has a non-klt center mapping to z.
Pick a component S of
![]() $\pi ^*z$
. Let b,
$\pi ^*z$
. Let b,
![]() $b^+$
and m be the coefficients of S in B,
$b^+$
and m be the coefficients of S in B,
![]() $B^+$
and
$B^+$
and
![]() $\pi ^*z$
, respectively. Then
$\pi ^*z$
, respectively. Then
![]() $b^+ = b+tm$
and
$b^+ = b+tm$
and
![]() $t = \frac {b^+-b}{m}$
. By construction,
$t = \frac {b^+-b}{m}$
. By construction,
![]() $qb^+$
and m are integers,
$qb^+$
and m are integers,
![]() $b^+\leq 1$
and
$b^+\leq 1$
and
![]() $b\in \Lambda $
. By Lemma 2.18, t belongs to a fixed set
$b\in \Lambda $
. By Lemma 2.18, t belongs to a fixed set
![]() $\Sigma $
(depending only on
$\Sigma $
(depending only on
![]() $I,\Lambda $
) which satisfies ACC and has rational accumulation points. Since the coefficient of z in
$I,\Lambda $
) which satisfies ACC and has rational accumulation points. Since the coefficient of z in
![]() $B_Z$
is
$B_Z$
is
![]() $1-t$
, it belongs to a set
$1-t$
, it belongs to a set
![]() $\Omega $
depending only on I and
$\Omega $
depending only on I and
![]() $\Lambda $
such that
$\Lambda $
such that
![]() $\Omega $
satisfies DCC and has rational accumulation points.
$\Omega $
satisfies DCC and has rational accumulation points.
Step 4. In this step, we show that
![]() $q{\mathbf {N}_{Z}}$
is integral.
$q{\mathbf {N}_{Z}}$
is integral.
By Step 2, we can assume that Z is a curve. By Step 1, the equivalence
![]() $q(K_X+B)\sim 0$
holds over some nonempty open subset
$q(K_X+B)\sim 0$
holds over some nonempty open subset
![]() $V\subseteq Z$
such that
$V\subseteq Z$
such that
![]() $\operatorname {\mathrm {Supp}} B_Z \subseteq Z\setminus V$
. Let
$\operatorname {\mathrm {Supp}} B_Z \subseteq Z\setminus V$
. Let
where
![]() $t_z$
is the log canonical threshold of
$t_z$
is the log canonical threshold of
![]() $\pi ^*z$
with respect to
$\pi ^*z$
with respect to
![]() $(X,B)$
over z. Note that
$(X,B)$
over z. Note that
![]() $K_X+\Theta \sim _{\mathbb {Q}} 0$
over Z. Let
$K_X+\Theta \sim _{\mathbb {Q}} 0$
over Z. Let
![]() $\Theta _Z$
be the discriminant part of adjunction for
$\Theta _Z$
be the discriminant part of adjunction for
![]() $(X,\Theta )$
over Z. Then
$(X,\Theta )$
over Z. Then
is an integral divisor. Moreover, by Step 3, the pair
![]() $(X,\Theta )$
is a q-complement of
$(X,\Theta )$
is a q-complement of
![]() $(X,B)$
over each
$(X,B)$
over each
![]() $z\in Z\setminus V$
. Over V, we have
$z\in Z\setminus V$
. Over V, we have
![]() $q(K_X+\Theta ) \sim q(K_X+B)\sim 0$
. Thus,
$q(K_X+\Theta ) \sim q(K_X+B)\sim 0$
. Thus,
![]() $q(K_X+\Theta ) \sim 0$
over Z by [Reference Birkar3, Lemma 2.4]. Furthermore, from the equalities
$q(K_X+\Theta ) \sim 0$
over Z by [Reference Birkar3, Lemma 2.4]. Furthermore, from the equalities
we obtain that
![]() $q(K_Z+\Theta _Z+{\mathbf {N}_{Z}})$
is an integral divisor and hence
$q(K_Z+\Theta _Z+{\mathbf {N}_{Z}})$
is an integral divisor and hence
![]() $q{\mathbf {N}_{Z}}$
is integral.
$q{\mathbf {N}_{Z}}$
is integral.
Step 5. In this step, we show that
![]() $q{\mathbf {N}_{Z'}}$
is nef Cartier on some resolution
$q{\mathbf {N}_{Z'}}$
is nef Cartier on some resolution
![]() $Z'\to Z$
.
$Z'\to Z$
.
The nefness follows from [Reference Birkar3, Theorem 3.6], so we just need to show that
![]() $q{\mathbf {N}_{Z'}}$
is integral. Denote the birational morphism
$q{\mathbf {N}_{Z'}}$
is integral. Denote the birational morphism
![]() $Z'\to Z$
by g. As in Step 1, let
$Z'\to Z$
by g. As in Step 1, let
![]() $f \colon X'\to (X,B)$
be a log resolution such that the rational map
$f \colon X'\to (X,B)$
be a log resolution such that the rational map
![]() $\pi ' \colon X'\dashrightarrow Z'$
is a morphism. Let
$\pi ' \colon X'\dashrightarrow Z'$
is a morphism. Let
![]() $U_0\subseteq U$
be a nonempty open set such that
$U_0\subseteq U$
be a nonempty open set such that ![]() is an isomorphism. Let
is an isomorphism. Let
![]() $\Delta '$
be the sum of the birational transform of B and reduced exceptional divisors of f but with all components mapping outside of
$\Delta '$
be the sum of the birational transform of B and reduced exceptional divisors of f but with all components mapping outside of
![]() $U_0$
removed. Then, the generic point of every log canonical center of
$U_0$
removed. Then, the generic point of every log canonical center of
![]() $(X',\Delta ')$
lies inside
$(X',\Delta ')$
lies inside
![]() $U_0$
.
$U_0$
.
Let T be the normalization of the main component of
![]() $Z'\times _Z X$
. Run an MMP on
$Z'\times _Z X$
. Run an MMP on
![]() $K_{X'}+\Delta '$
over T with scaling of some ample divisor. This MMP terminates with a
$K_{X'}+\Delta '$
over T with scaling of some ample divisor. This MMP terminates with a
![]() $\mathbb {Q}$
-factorial dlt pair
$\mathbb {Q}$
-factorial dlt pair
![]() $(X",\Delta ")$
such that
$(X",\Delta ")$
such that
![]() $K_{X"}+\Delta "$
is nef over T. Let
$K_{X"}+\Delta "$
is nef over T. Let
![]() $X_0 = \pi ^{-1}(U_0)$
. Over
$X_0 = \pi ^{-1}(U_0)$
. Over
![]() $U_0\cong U_0'$
, we have
$U_0\cong U_0'$
, we have
![]() $Z'\times _Z X\cong X_0$
, and hence
$Z'\times _Z X\cong X_0$
, and hence
![]() $K_{X"}+\Delta "$
is nef over
$K_{X"}+\Delta "$
is nef over
![]() $X_0\subseteq X$
. By the negativity lemma, over
$X_0\subseteq X$
. By the negativity lemma, over
![]() $U_0'$
, the divisor
$U_0'$
, the divisor
![]() $K_{X"}+\Delta "$
is equal to the log pull-back of
$K_{X"}+\Delta "$
is equal to the log pull-back of
![]() $K_X+B$
. This shows that
$K_X+B$
. This shows that
![]() $(X",\Delta ")$
is a dlt modification of
$(X",\Delta ")$
is a dlt modification of
![]() $(X,B)$
over
$(X,B)$
over
![]() $U_0$
. In particular,
$U_0$
. In particular,
![]() $X"$
is Fano type over
$X"$
is Fano type over
![]() $U_0'$
. Furthermore, every log canonical center of
$U_0'$
. Furthermore, every log canonical center of
![]() $(X",\Delta ")$
dominates
$(X",\Delta ")$
dominates
![]() $U_0'$
. Indeed,
$U_0'$
. Indeed,
![]() $(X,B)$
satisfies the same property and the generic point of every log canonical center of
$(X,B)$
satisfies the same property and the generic point of every log canonical center of
![]() $(X",\Delta ")$
lies inside
$(X",\Delta ")$
lies inside
![]() $U_0'$
. Thus, we have
$U_0'$
. Thus, we have
By [Reference Birkar1, Theorem 1.4], we can run an MMP on
![]() $K_{X"}+\Delta '$
over
$K_{X"}+\Delta '$
over
![]() $Z'$
which terminates with a good minimal model over
$Z'$
which terminates with a good minimal model over
![]() $Z'$
. Since this MMP is trivial over
$Z'$
. Since this MMP is trivial over
![]() $U_0'$
, the dual complex and hence the coregularity of
$U_0'$
, the dual complex and hence the coregularity of
![]() $(X",\Delta ")$
does not change under this MMP. Abusing the notation, we again denote the good minimal model by
$(X",\Delta ")$
does not change under this MMP. Abusing the notation, we again denote the good minimal model by
![]() $X"$
. Let
$X"$
. Let
![]() $\pi " \colon X"\to Z"$
over
$\pi " \colon X"\to Z"$
over
![]() $Z'$
be the morphism induced by the relatively semiample divisor
$Z'$
be the morphism induced by the relatively semiample divisor
![]() $K_{X"}+\Delta "$
. Since
$K_{X"}+\Delta "$
. Since
![]() $K_{X"}+\Delta "\sim _{\mathbb {Q}} 0$
over
$K_{X"}+\Delta "\sim _{\mathbb {Q}} 0$
over
![]() $U_0'$
,
$U_0'$
,
![]() $Z"\to Z'$
is birational and
$Z"\to Z'$
is birational and
![]() $U_0"$
, the preimage of
$U_0"$
, the preimage of
![]() $U_0'$
in
$U_0'$
in
![]() $Z"$
, is isomorphic to
$Z"$
, is isomorphic to
![]() $U_0'$
. Thus, every log canonical center of
$U_0'$
. Thus, every log canonical center of
![]() $(X",\Delta ")$
also dominates
$(X",\Delta ")$
also dominates
![]() $Z"$
.
$Z"$
.
Let W be a common resolution of X and
![]() $X"$
, and set
$X"$
, and set
![]() $\alpha \colon W\to X$
and
$\alpha \colon W\to X$
and
![]() $\beta \colon W\to X"$
. By construction, over the preimage of
$\beta \colon W\to X"$
. By construction, over the preimage of
![]() $U_0$
in W, we have
$U_0$
in W, we have
![]() $\alpha ^*(K_X+B) = \beta ^*(K_{X"}+\Delta ")$
. Write
$\alpha ^*(K_X+B) = \beta ^*(K_{X"}+\Delta ")$
. Write
![]() $K_{X"}+B" = \beta _*\alpha ^*(K_X+B)$
and
$K_{X"}+B" = \beta _*\alpha ^*(K_X+B)$
and
![]() $L" = \beta _*\alpha ^*L$
, where
$L" = \beta _*\alpha ^*L$
, where
![]() $qL = q(K_X+B) + \text {Div}(s)$
as in Step 1. Let
$qL = q(K_X+B) + \text {Div}(s)$
as in Step 1. Let
![]() $P" = \Delta "-B"$
, which is
$P" = \Delta "-B"$
, which is
![]() $\mathbb {Q}$
-trivial over
$\mathbb {Q}$
-trivial over
![]() $Z"$
and supported outside of
$Z"$
and supported outside of
![]() $U_0"$
. Hence,
$U_0"$
. Hence,
![]() $P" = \pi ^{\prime }{\prime }*P_{Z"}$
for some
$P" = \pi ^{\prime }{\prime }*P_{Z"}$
for some
![]() $\mathbb {Q}$
-divisor
$\mathbb {Q}$
-divisor
![]() $P_{Z"}$
on
$P_{Z"}$
on
![]() $Z"$
. Let
$Z"$
. Let
![]() $\Delta _{Z"}$
be the discriminant part of adjunction for
$\Delta _{Z"}$
be the discriminant part of adjunction for
![]() $(X",\Delta ")$
on
$(X",\Delta ")$
on
![]() $Z"$
. Let
$Z"$
. Let
![]() $B_{Z"} = \Delta _{Z"} - P_{Z"}$
, then
$B_{Z"} = \Delta _{Z"} - P_{Z"}$
, then
![]() $B_{Z"}$
is the discriminant part of adjunction for
$B_{Z"}$
is the discriminant part of adjunction for
![]() $(X",B")$
on
$(X",B")$
on
![]() $Z"$
. By the definition of
$Z"$
. By the definition of
![]() $\mathbf {N}$
in Step 1, we have
$\mathbf {N}$
in Step 1, we have
Here,
![]() $L_{Z"}$
is the pull-back of
$L_{Z"}$
is the pull-back of
![]() $L_Z$
in Step 1. This shows that
$L_Z$
in Step 1. This shows that
![]() ${\mathbf {N}_{Z"}}$
is the moduli part of
${\mathbf {N}_{Z"}}$
is the moduli part of
![]() $(X",\Delta ")$
over
$(X",\Delta ")$
over
![]() $Z"$
. Since the coefficients of
$Z"$
. Since the coefficients of
![]() $\Delta "$
are in
$\Delta "$
are in
![]() $\Lambda $
and the coregularity of
$\Lambda $
and the coregularity of
![]() $(X",\Delta ")$
is at most c, we may apply Steps 2–4 to show that
$(X",\Delta ")$
is at most c, we may apply Steps 2–4 to show that
![]() $q {\mathbf {N}_{Z"}}$
is an integral divisor. Thus,
$q {\mathbf {N}_{Z"}}$
is an integral divisor. Thus,
![]() $q{\mathbf {N}_{Z'}}$
is also an integral divisor and hence Cartier as
$q{\mathbf {N}_{Z'}}$
is also an integral divisor and hence Cartier as
![]() $Z'$
is smooth.
$Z'$
is smooth.
We show that Theorem 6.1 also holds for generalized pairs
![]() $(X,B,\mathbf {M})$
in the special case that
$(X,B,\mathbf {M})$
in the special case that
![]() ${\mathbf {M}_{X}}\sim _{\mathbb {Q}} 0$
over the base Z.
${\mathbf {M}_{X}}\sim _{\mathbb {Q}} 0$
over the base Z.
Theorem 6.2. Let d, c and p be nonnegative integers and
![]() $\Lambda \subset \mathbb {Q}$
be a closed set satisfying the descending chain condition. Assume Theorem 7
$\Lambda \subset \mathbb {Q}$
be a closed set satisfying the descending chain condition. Assume Theorem 7
![]() $(c-1)$
holds. There exists a set
$(c-1)$
holds. There exists a set ![]() satisfying the descending chain condition and a positive integer
satisfying the descending chain condition and a positive integer ![]() , both
, both
![]() $\Omega $
and q only depending on
$\Omega $
and q only depending on
![]() $\Lambda $
and c, and satisfying the following. Let
$\Lambda $
and c, and satisfying the following. Let
![]() $\pi \colon X\rightarrow Z$
be fibration from a d-dimensional projective variety X to a projective base Z with
$\pi \colon X\rightarrow Z$
be fibration from a d-dimensional projective variety X to a projective base Z with
![]() $\dim Z> 0$
. Let
$\dim Z> 0$
. Let
![]() $(X,B,\mathbf {M})$
be a generalized pair for which
$(X,B,\mathbf {M})$
be a generalized pair for which
-
• the generalized pair
 $(X,B,\mathbf {M})$
is generalized log canonical;
$(X,B,\mathbf {M})$
is generalized log canonical; -
• the fibration
 $\pi $
is of Fano type over a nonempty open set U of Z;
$\pi $
is of Fano type over a nonempty open set U of Z; -
• every generalized log canonical center of
 $(X,B,\mathbf {M})$
is horizontal over Z;
$(X,B,\mathbf {M})$
is horizontal over Z; -
• the divisors
 $K_X+B+{\mathbf {M}_{X}}$
and
$K_X+B+{\mathbf {M}_{X}}$
and
 ${\mathbf {M}_{X}}$
are
${\mathbf {M}_{X}}$
are
 $\mathbb {Q}$
-trivial over Z;
$\mathbb {Q}$
-trivial over Z; -
• the coefficients of B are in
 $\Lambda $
,
$\Lambda $
, -
•
 $p\mathbf {M}$
is b-Cartier; and
$p\mathbf {M}$
is b-Cartier; and -
• the coregularity of
 $(X,B)$
is at most c.
$(X,B)$
is at most c.
Then, we can write
where
![]() $(Z,B_Z,\mathbf {N})$
is a generalized log canonical pair such that
$(Z,B_Z,\mathbf {N})$
is a generalized log canonical pair such that
-
•
 $B_Z$
is the discriminant part of the adjunction for
$B_Z$
is the discriminant part of the adjunction for
 $(X,B,\mathbf {M})$
over Z;
$(X,B,\mathbf {M})$
over Z; -
• the coefficients of
 $B_Z$
belong to
$B_Z$
belong to
 $\Omega $
; and
$\Omega $
; and -
• the divisor
 $q\mathbf {N}$
is b-nef and b-Cartier.
$q\mathbf {N}$
is b-nef and b-Cartier.
Proof. We proceed in several steps. In the first step, we apply the canonical bundle formula for pairs. In the rest of the proof, we show that
![]() $\mathbf {M}$
is the pull-back of a b-nef divisor on the base and control the Cartier index of this b-nef divisor where it descends.
$\mathbf {M}$
is the pull-back of a b-nef divisor on the base and control the Cartier index of this b-nef divisor where it descends.
Step 1. We show that the pair
![]() $(X,B)$
satisfies the conditions in the statement of Theorem 6.1.
$(X,B)$
satisfies the conditions in the statement of Theorem 6.1.
By Lemma 2.5,
![]() $(X,B)$
is log canonical. Furthermore, every log canonical center of
$(X,B)$
is log canonical. Furthermore, every log canonical center of
![]() $(X,B)$
is also a log canonical center of
$(X,B)$
is also a log canonical center of
![]() $(X,B,\mathbf {M})$
, and hence it dominates U.
$(X,B,\mathbf {M})$
, and hence it dominates U.
Thus, by Theorem 6.1, there exists
![]() $\Omega $
and I, depending only on
$\Omega $
and I, depending only on
![]() $\Lambda $
and c such that
$\Lambda $
and c such that
where
![]() $B_Z$
and
$B_Z$
and
![]() $\mathbf {P}$
are the discriminant and moduli part of adjunction for the fibration
$\mathbf {P}$
are the discriminant and moduli part of adjunction for the fibration
![]() $(X,B) \to Z$
. Since
$(X,B) \to Z$
. Since
![]() $(X,B)$
is log canonical,
$(X,B)$
is log canonical,
![]() $(Z,B_Z,\mathbf {P})$
is generalized log canonical. Furthermore, the coefficients of
$(Z,B_Z,\mathbf {P})$
is generalized log canonical. Furthermore, the coefficients of
![]() $B_Z$
belong to
$B_Z$
belong to
![]() $\Omega $
and
$\Omega $
and
![]() $q\mathbf {P}$
is nef Cartier on any high resolution of Z. By replacing q with
$q\mathbf {P}$
is nef Cartier on any high resolution of Z. By replacing q with
![]() $pq$
, we can assume that q is a multiple of p.
$pq$
, we can assume that q is a multiple of p.
Step 2. In this step, we express
![]() $\mathbf {M}$
as a pull-back of some b-divisor from Z.
$\mathbf {M}$
as a pull-back of some b-divisor from Z.
Let
![]() $g \colon Z'\to Z$
be a log resolution of
$g \colon Z'\to Z$
be a log resolution of
![]() $(Z,B_Z+\mathbf {P})$
such that
$(Z,B_Z+\mathbf {P})$
such that
![]() $\mathbf {P}$
descends on
$\mathbf {P}$
descends on
![]() $Z'$
and
$Z'$
and
![]() ${\mathbf {P}_{Z'}}$
is nef. Let
${\mathbf {P}_{Z'}}$
is nef. Let
![]() $f \colon X'\to X$
be a resolution such that the rational map
$f \colon X'\to X$
be a resolution such that the rational map
![]() $\pi ' \colon X'\dashrightarrow Z'$
is a morphism and
$\pi ' \colon X'\dashrightarrow Z'$
is a morphism and
![]() ${\mathbf {M}_{X'}}$
is nef. By the negativity lemma, we can write
${\mathbf {M}_{X'}}$
is nef. By the negativity lemma, we can write
for some effective f-exceptional
![]() $\mathbb {Q}$
-divisor
$\mathbb {Q}$
-divisor
![]() $E_{X'}$
. Since
$E_{X'}$
. Since
![]() ${\mathbf {M}_{X}} \sim _{\mathbb {Q}} 0$
over Z,
${\mathbf {M}_{X}} \sim _{\mathbb {Q}} 0$
over Z,
![]() $E_{X'}$
is vertical over Z, so there is a nonempty subset of U over which
$E_{X'}$
is vertical over Z, so there is a nonempty subset of U over which
![]() $E_{X'}=0$
and
$E_{X'}=0$
and
![]() ${\mathbf {M}_{X'}}\sim _{\mathbb {Q}} 0$
. Since
${\mathbf {M}_{X'}}\sim _{\mathbb {Q}} 0$
. Since
![]() $\pi $
is of Fano type over U, the general fibers of
$\pi $
is of Fano type over U, the general fibers of
![]() $\pi $
are of Fano type and hence rationally connected. Thus, the general fibers of
$\pi $
are of Fano type and hence rationally connected. Thus, the general fibers of
![]() $\pi '$
are also rationally connected. By [Reference Birkar3, Lemma 2.44], after replacing
$\pi '$
are also rationally connected. By [Reference Birkar3, Lemma 2.44], after replacing
![]() $X'$
and
$X'$
and
![]() $Z'$
with possibly higher birational models, we can write
$Z'$
with possibly higher birational models, we can write
for some
![]() $\mathbb {Q}$
-divisor
$\mathbb {Q}$
-divisor
![]() $T_{Z'}$
on
$T_{Z'}$
on
![]() $Z'$
such that
$Z'$
such that
![]() $pT_{Z'}$
is nef Cartier. Let
$pT_{Z'}$
is nef Cartier. Let
![]() $\mathbf {T}$
be the b-divisor on Z with the data
$\mathbf {T}$
be the b-divisor on Z with the data
![]() $g \colon Z'\to Z$
and
$g \colon Z'\to Z$
and
![]() $T_{Z'}$
(i.e.,
$T_{Z'}$
(i.e.,
![]() $\mathbf {T}$
descends on
$\mathbf {T}$
descends on
![]() $Z'$
as
$Z'$
as
![]() $T_{Z'}$
).
$T_{Z'}$
).
Step 3. In this step, we show that
![]() $q{\mathbf {M}_{X}} \sim q\pi ^* {\mathbf {T}_{Z}}$
.
$q{\mathbf {M}_{X}} \sim q\pi ^* {\mathbf {T}_{Z}}$
.
As in Step 2, write
Then
![]() $E_{X'}$
is vertical and
$E_{X'}$
is vertical and
![]() $\mathbb {Q}$
-linearly trivial over
$\mathbb {Q}$
-linearly trivial over
![]() $Z'$
(since
$Z'$
(since
![]() ${\mathbf {M}_{X'}} \sim _{\mathbb {Q}} 0$
over
${\mathbf {M}_{X'}} \sim _{\mathbb {Q}} 0$
over
![]() $Z'$
), so we can write
$Z'$
), so we can write
![]() ${E_{X'} = \pi ^{\prime }* E_{Z'}}$
for some effective
${E_{X'} = \pi ^{\prime }* E_{Z'}}$
for some effective
![]() $\mathbb {Q}$
-divisor
$\mathbb {Q}$
-divisor
![]() $E_{Z'}$
. If
$E_{Z'}$
. If
![]() $E_{Z'}$
has a component
$E_{Z'}$
has a component
![]() $D_{Z'}$
which maps onto a divisor D in Z, then
$D_{Z'}$
which maps onto a divisor D in Z, then
![]() $E_{X'} = \pi ^{\prime }*E_{Z'}$
has a component mapping onto D, contradicting the fact that
$E_{X'} = \pi ^{\prime }*E_{Z'}$
has a component mapping onto D, contradicting the fact that
![]() $E_{X'}$
is f-exceptional. Thus,
$E_{X'}$
is f-exceptional. Thus,
![]() $E_{Z'}$
is g-exceptional. Note that
$E_{Z'}$
is g-exceptional. Note that
![]() $\pi ^{\prime }*({\mathbf {T}_{Z'}} + E_{Z'}) = {\mathbf {M}_{X'}}+E_{X'} \sim _{\mathbb {Q}} 0$
over Z, so
$\pi ^{\prime }*({\mathbf {T}_{Z'}} + E_{Z'}) = {\mathbf {M}_{X'}}+E_{X'} \sim _{\mathbb {Q}} 0$
over Z, so
![]() ${\mathbf {T}_{Z'}} +E_{Z'} \sim _{\mathbb {Q}}0$
over Z. This implies that
${\mathbf {T}_{Z'}} +E_{Z'} \sim _{\mathbb {Q}}0$
over Z. This implies that
![]() $g^*{\mathbf {T}_{Z}} = {\mathbf {T}_{Z'}} + E_{Z'}$
. Now, we have
$g^*{\mathbf {T}_{Z}} = {\mathbf {T}_{Z'}} + E_{Z'}$
. Now, we have
and hence
![]() $q{\mathbf {M}_{X}}\sim q\pi ^*{\mathbf {T}_{Z}}$
. In particular,
$q{\mathbf {M}_{X}}\sim q\pi ^*{\mathbf {T}_{Z}}$
. In particular,
![]() $q\mathbf {T}$
is a b-Cartier divisor. From now on, we consider
$q\mathbf {T}$
is a b-Cartier divisor. From now on, we consider
![]() $(Z, B_Z,\mathbf {P} + \mathbf {T})$
as a generalized pair, with moduli part
$(Z, B_Z,\mathbf {P} + \mathbf {T})$
as a generalized pair, with moduli part
![]() $\mathbf {P}+\mathbf {T}$
.
$\mathbf {P}+\mathbf {T}$
.
Step 4. In this step, we show that the generalized pair
![]() $(Z,B_Z,\mathbf {P}+\mathbf {T})$
is generalized log canonical.
$(Z,B_Z,\mathbf {P}+\mathbf {T})$
is generalized log canonical.
Write
![]() $K_{X'}+B_{X'} = f^*(K_X+B)$
. Let
$K_{X'}+B_{X'} = f^*(K_X+B)$
. Let
![]() $B_{Z'}$
be the discriminant part of the adjunction for
$B_{Z'}$
be the discriminant part of the adjunction for
![]() $(X',B_{X'})$
over
$(X',B_{X'})$
over
![]() $Z'$
. We can assume that
$Z'$
. We can assume that
![]() $(Z', \operatorname {\mathrm {Supp}} B_{Z'}+\operatorname {\mathrm {Supp}} E_{Z'}+\operatorname {\mathrm {Supp}} {\mathbf {P}_{Z'}}+\operatorname {\mathrm {Supp}}{\mathbf {T}_{Z'}})$
is log smooth. By construction, we have
$(Z', \operatorname {\mathrm {Supp}} B_{Z'}+\operatorname {\mathrm {Supp}} E_{Z'}+\operatorname {\mathrm {Supp}} {\mathbf {P}_{Z'}}+\operatorname {\mathrm {Supp}}{\mathbf {T}_{Z'}})$
is log smooth. By construction, we have
Thus, it suffices to show that every coefficient of
![]() $B_{Z'} + E_{Z'}$
is at most one. Let D be a prime divisor on
$B_{Z'} + E_{Z'}$
is at most one. Let D be a prime divisor on
![]() $Z'$
. Let
$Z'$
. Let
![]() $t_D$
be the log canonical threshold of
$t_D$
be the log canonical threshold of
![]() $(X',B_{X'})$
with respect to
$(X',B_{X'})$
with respect to
![]() $\pi ^{\prime }*D$
over the generic point of D. Since
$\pi ^{\prime }*D$
over the generic point of D. Since
![]() $(X,B,\mathbf {M})$
is generalized log canonical,
$(X,B,\mathbf {M})$
is generalized log canonical,
![]() $(X',B_{X'}+E_{X'})$
is sublog canonical. Furthermore,
$(X',B_{X'}+E_{X'})$
is sublog canonical. Furthermore,
![]() $E_{X'} = \pi ^{\prime }*E_{Z'}$
, so the coefficient of D in
$E_{X'} = \pi ^{\prime }*E_{Z'}$
, so the coefficient of D in
![]() $E_{Z'}$
is at most
$E_{Z'}$
is at most
![]() $t_D$
(otherwise
$t_D$
(otherwise
![]() $E_{X'}\geq (t_D+\epsilon )\pi ^{\prime }*D$
for some
$E_{X'}\geq (t_D+\epsilon )\pi ^{\prime }*D$
for some
![]() $\epsilon> 0$
and this violates the sublog canonical condition). By definition,
$\epsilon> 0$
and this violates the sublog canonical condition). By definition,
![]() $\operatorname {\mathrm {coeff}}_D(B_{Z'}) = 1-t_D$
. Thus,
$\operatorname {\mathrm {coeff}}_D(B_{Z'}) = 1-t_D$
. Thus,
![]() $\operatorname {\mathrm {coeff}}_D(B_{Z'}+E_{Z'}) \leq 1-t_D + t_D = 1$
, as desired.
$\operatorname {\mathrm {coeff}}_D(B_{Z'}+E_{Z'}) \leq 1-t_D + t_D = 1$
, as desired.
Step 5. In this step, we conclude that the generalized pair
![]() $(Z, B_Z, \mathbf {P}+\mathbf {T})$
satisfies the desired properties.
$(Z, B_Z, \mathbf {P}+\mathbf {T})$
satisfies the desired properties.
By Step 1, the coefficients of
![]() $B_Z$
belong to
$B_Z$
belong to
![]() $\Omega $
and
$\Omega $
and
![]() $q\mathbf {P}$
is b-nef and b-Cartier. By Steps 2 and 3,
$q\mathbf {P}$
is b-nef and b-Cartier. By Steps 2 and 3,
![]() $q\mathbf {T}$
is b-Cartier. By Step 4,
$q\mathbf {T}$
is b-Cartier. By Step 4,
![]() $(Z,B_Z, \mathbf {P}+\mathbf {T})$
is generalized log canonical. Finally, by Steps 1 and 3, we have
$(Z,B_Z, \mathbf {P}+\mathbf {T})$
is generalized log canonical. Finally, by Steps 1 and 3, we have
Proof. Theorem 7
![]() $(c-1)$
implies that Theorem 6.2
$(c-1)$
implies that Theorem 6.2
![]() $(c)$
holds.
$(c)$
holds.
Let
![]() $(X,B,\mathbf {M})$
be a generalized pair in the statement of Theorem 8
$(X,B,\mathbf {M})$
be a generalized pair in the statement of Theorem 8
![]() $(c)$
. We may replace
$(c)$
. We may replace
![]() $(X,B,\mathbf {M})$
by a
$(X,B,\mathbf {M})$
by a
![]() $\mathbb {Q}$
-factorial generalized dlt modification and assume that
$\mathbb {Q}$
-factorial generalized dlt modification and assume that
![]() $(X,B,\mathbf {M})$
is
$(X,B,\mathbf {M})$
is
![]() $\mathbb {Q}$
-factorial generalized dlt. Since X is of Fano type over Z, we can run an MMP on
$\mathbb {Q}$
-factorial generalized dlt. Since X is of Fano type over Z, we can run an MMP on
![]() ${\mathbf {M}_{X}}$
over Z to get a model
${\mathbf {M}_{X}}$
over Z to get a model
![]() $(X',B',\mathbf {M})$
such that
$(X',B',\mathbf {M})$
such that
![]() ${\mathbf {M}_{X'}}$
is semiample over Z. After replacing
${\mathbf {M}_{X'}}$
is semiample over Z. After replacing
![]() $(X,B,\mathbf {M})$
with
$(X,B,\mathbf {M})$
with
![]() $(X',B',\mathbf {M})$
, up to losing the generalized dlt property for
$(X',B',\mathbf {M})$
, up to losing the generalized dlt property for
![]() $(X,B,\mathbf {M})$
, we may assume that
$(X,B,\mathbf {M})$
, we may assume that
![]() ${\mathbf {M}_{X}}$
is semiample over Z. Let
${\mathbf {M}_{X}}$
is semiample over Z. Let
![]() $X\to Z'$
be the morphism induced by
$X\to Z'$
be the morphism induced by
![]() $\mathbf {M}$
. Since
$\mathbf {M}$
. Since
![]() $\mathbf {M}$
is trivial on a general fiber of
$\mathbf {M}$
is trivial on a general fiber of
![]() $\pi $
, the morphism
$\pi $
, the morphism
![]() $Z'\to Z$
is birational. After replacing Z with
$Z'\to Z$
is birational. After replacing Z with
![]() $Z'$
, we may assume that
$Z'$
, we may assume that
![]() $\mathbf {M}\sim _{\mathbb {Q}}0$
over Z. Now, the result follows from Theorem 6.2
$\mathbf {M}\sim _{\mathbb {Q}}0$
over Z. Now, the result follows from Theorem 6.2
![]() $(c)$
.
$(c)$
.
7 Proof of the theorems
In this section, we prove the main theorems of this article. In this section, we use the notation from Section: ‘Strategy of the Proof’, we write Theorem
![]() $X(d,c)$
for Theorem X in dimension d and coregularity at most c. The following is the boundedness of complements for Fano type pairs of coregularity
$X(d,c)$
for Theorem X in dimension d and coregularity at most c. The following is the boundedness of complements for Fano type pairs of coregularity
![]() $0$
. Note that the following theorem is an unconditional version of Theorem 7
$0$
. Note that the following theorem is an unconditional version of Theorem 7
![]() $(0)$
.
$(0)$
.
Theorem 7.1. Let p be a positive integer. Let
![]() $\Lambda \subset \mathbb {Q}$
be a closed set satisfying the descending chain condition. There exists a constant
$\Lambda \subset \mathbb {Q}$
be a closed set satisfying the descending chain condition. There exists a constant ![]() satisfying the following. Let X be a Fano type variety and
satisfying the following. Let X be a Fano type variety and
![]() $(X,B,\mathbf {M})$
be a generalized pair of absolute coregularity
$(X,B,\mathbf {M})$
be a generalized pair of absolute coregularity
![]() $0$
. Assume that the following conditions hold:
$0$
. Assume that the following conditions hold:
-
• the coefficients of B belong to
 $\Lambda $
;
$\Lambda $
; -
•
 $p\mathbf {M}$
is b-Cartier.
$p\mathbf {M}$
is b-Cartier.
Then, there exists a boundary
![]() $B^+\geq B$
such that
$B^+\geq B$
such that
-
• the generalized pair
 $(X,B^+,\mathbf {M})$
is generalized log canonical;
$(X,B^+,\mathbf {M})$
is generalized log canonical; -
• we have that
 $N(K_X+B^+ +\mathbf {M})\sim 0$
; and
$N(K_X+B^+ +\mathbf {M})\sim 0$
; and -
• the equality
 $\mathrm {coreg}(X,B^+,\mathbf {M})=0$
holds.
$\mathrm {coreg}(X,B^+,\mathbf {M})=0$
holds.
Proof. First, we replace
![]() $\Lambda $
with its derived closure (see Lemma 2.16). We let
$\Lambda $
with its derived closure (see Lemma 2.16). We let ![]() be the finite subset provided by Theorem 3.5. This finite subset only depends on
be the finite subset provided by Theorem 3.5. This finite subset only depends on
![]() $\Lambda $
and p.
$\Lambda $
and p.
By [Reference Filipazzi and Moraga14, Theorem 1.2], there is a constant
![]() $N(\Lambda ,d,0,p)$
such that every generalized pair
$N(\Lambda ,d,0,p)$
such that every generalized pair
![]() $(X,B,\mathbf {M})$
as in the statement and of dimension at most d admits an
$(X,B,\mathbf {M})$
as in the statement and of dimension at most d admits an
![]() $N(\Lambda ,d,0,p)$
-complement. We will proceed by induction on d. We may assume that
$N(\Lambda ,d,0,p)$
-complement. We will proceed by induction on d. We may assume that
![]() $N(\Lambda ,d,0,p)$
is divisible by
$N(\Lambda ,d,0,p)$
is divisible by
![]() $I(\Lambda )$
and p for every d. Throughout the proof, we assume that
$I(\Lambda )$
and p for every d. Throughout the proof, we assume that
![]() $N(\Lambda ,d,0,p)$
is minimal with such properties.
$N(\Lambda ,d,0,p)$
is minimal with such properties.
By Theorem 3.5, we may assume that the coefficients of B belong to
![]() $\mathcal {R}$
. Let
$\mathcal {R}$
. Let
![]() $B+\Gamma $
be a
$B+\Gamma $
be a
![]() $\mathbb {Q}$
-complement of
$\mathbb {Q}$
-complement of
![]() $(X,B,\mathbf {M})$
of coregularity
$(X,B,\mathbf {M})$
of coregularity
![]() $0$
. Let
$0$
. Let
![]() $(Y,B_Y+\Gamma _Y,\mathbf {M})$
be a generalized dlt modification of
$(Y,B_Y+\Gamma _Y,\mathbf {M})$
be a generalized dlt modification of
![]() $(X,B+\Gamma ,\mathbf {M})$
. Here,
$(X,B+\Gamma ,\mathbf {M})$
. Here,
![]() $\Gamma _Y$
is the strict transform of the fractional part of
$\Gamma _Y$
is the strict transform of the fractional part of
![]() $\Gamma $
and
$\Gamma $
and
![]() $B_Y$
is the reduced exceptional plus the strict transform of
$B_Y$
is the reduced exceptional plus the strict transform of
![]() $B+\lfloor \Gamma \rfloor $
. By Lemma 2.13, Y is a Fano type variety. Thus, we may run a
$B+\lfloor \Gamma \rfloor $
. By Lemma 2.13, Y is a Fano type variety. Thus, we may run a
![]() $-(K_Y+B_Y+{\mathbf {M}_{Y}})$
-MMP which terminates with a good minimal model Z since
$-(K_Y+B_Y+{\mathbf {M}_{Y}})$
-MMP which terminates with a good minimal model Z since
![]() $-(K_Y+B_Y+{\mathbf {M}_{Y}})\sim _{\mathbb {Q}}\Gamma _Y$
is effective. Let
$-(K_Y+B_Y+{\mathbf {M}_{Y}})\sim _{\mathbb {Q}}\Gamma _Y$
is effective. Let
![]() $B_Z$
be the strict transform of
$B_Z$
be the strict transform of
![]() $B_Y$
on Z and
$B_Y$
on Z and
![]() ${\mathbf {M}_{Z}}$
be the trace of
${\mathbf {M}_{Z}}$
be the trace of
![]() $\mathbf {M}$
on Z. Note that
$\mathbf {M}$
on Z. Note that
![]() $(Z,B_Z,\mathbf {M})$
is a generalized pair of coregularity
$(Z,B_Z,\mathbf {M})$
is a generalized pair of coregularity
![]() $0$
and
$0$
and
![]() $-(K_Z+B_Z+{\mathbf {M}_{Z}})$
is a semiample divisor. In order to produce an N-complement for
$-(K_Z+B_Z+{\mathbf {M}_{Z}})$
is a semiample divisor. In order to produce an N-complement for
![]() $(X,B,\mathbf {M})$
, it suffices to produce an N-complement for
$(X,B,\mathbf {M})$
, it suffices to produce an N-complement for
![]() $(Z,B_Z,\mathbf {M})$
(see Lemma 2.12 and Lemma 2.13). Hence, we may replace
$(Z,B_Z,\mathbf {M})$
(see Lemma 2.12 and Lemma 2.13). Hence, we may replace
![]() $(X,B,\mathbf {M})$
with
$(X,B,\mathbf {M})$
with
![]() $(Z,B_Z,\mathbf {M})$
and assume that
$(Z,B_Z,\mathbf {M})$
and assume that
![]() $-(K_X+B+{\mathbf {M}_{X}})$
is semiample and that
$-(K_X+B+{\mathbf {M}_{X}})$
is semiample and that
![]() $(X,B,\mathbf {M})$
has coregularity 0. By [Reference Filipazzi and Moraga14, Theorem 1.2], then this reduction shows that Theorem 7
$(X,B,\mathbf {M})$
has coregularity 0. By [Reference Filipazzi and Moraga14, Theorem 1.2], then this reduction shows that Theorem 7
![]() $(d,0)$
holds for any d; this will be used to then appeal to Theorem 5.1.
$(d,0)$
holds for any d; this will be used to then appeal to Theorem 5.1.
If
![]() $K_X+B+{\mathbf {M}_{X}} \sim _{\mathbb {Q}} 0$
, then the statement follows from [Reference Filipazzi, Mauri and Moraga13, Theorem 1]. Hence, we may assume that the ample model W of
$K_X+B+{\mathbf {M}_{X}} \sim _{\mathbb {Q}} 0$
, then the statement follows from [Reference Filipazzi, Mauri and Moraga13, Theorem 1]. Hence, we may assume that the ample model W of
![]() $-(K_X+B+{\mathbf {M}_{X}})$
is positive-dimensional. Since
$-(K_X+B+{\mathbf {M}_{X}})$
is positive-dimensional. Since
![]() $(X,B,\mathbf {M})$
has coregularity
$(X,B,\mathbf {M})$
has coregularity
![]() $0$
and
$0$
and
![]() $\dim W>0$
, then some generalized log canonical center of
$\dim W>0$
, then some generalized log canonical center of
![]() $(X,B,\mathbf {M})$
is vertical over W. We may replace
$(X,B,\mathbf {M})$
is vertical over W. We may replace
![]() $(X,B,\mathbf {M})$
with a generalized dlt modification and assume that some
$(X,B,\mathbf {M})$
with a generalized dlt modification and assume that some
![]() $S\subset \operatorname {\mathrm {Supp}} \lfloor B\rfloor $
is vertical over W. Write
$S\subset \operatorname {\mathrm {Supp}} \lfloor B\rfloor $
is vertical over W. Write
![]() $\Xi =B-S$
. Let
$\Xi =B-S$
. Let
![]() $X'$
be the ample model of
$X'$
be the ample model of
![]() $\Xi +{\mathbf {M}_{X}}$
over W. Notice that, since X is of Fano type and S is vertical over W,
$\Xi +{\mathbf {M}_{X}}$
over W. Notice that, since X is of Fano type and S is vertical over W,
![]() $X \dashrightarrow X'$
is a birational contraction. Let
$X \dashrightarrow X'$
is a birational contraction. Let
![]() $\Xi ', B'$
be the push-forward of
$\Xi ', B'$
be the push-forward of
![]() $\Xi , B$
on
$\Xi , B$
on
![]() $X'$
. Note that S is not contained in
$X'$
. Note that S is not contained in
![]() $\mathrm {Bs}(\Xi +{\mathbf {M}_{X}}/W)$
. Hence, S is a generalized log canonical place of
$\mathrm {Bs}(\Xi +{\mathbf {M}_{X}}/W)$
. Hence, S is a generalized log canonical place of
![]() $(X',B'-\epsilon \Xi ',(1-\epsilon )\mathbf {M})$
for every
$(X',B'-\epsilon \Xi ',(1-\epsilon )\mathbf {M})$
for every
![]() $\epsilon>0$
small enough. Let
$\epsilon>0$
small enough. Let
![]() $(Y,B_Y,\mathbf {M})$
be a
$(Y,B_Y,\mathbf {M})$
be a
![]() $\mathbb {Q}$
-factorial generalized dlt modification of
$\mathbb {Q}$
-factorial generalized dlt modification of
![]() $(X',B',\mathbf {M})$
. Let
$(X',B',\mathbf {M})$
. Let
![]() $\pi \colon Y\rightarrow X'$
be the associated projective morphism. We write
$\pi \colon Y\rightarrow X'$
be the associated projective morphism. We write
![]() $\Xi _Y+{\mathbf {M}_{Y}}=\pi ^*(\Xi +{\mathbf {M}_{X}})$
.
$\Xi _Y+{\mathbf {M}_{Y}}=\pi ^*(\Xi +{\mathbf {M}_{X}})$
.
By construction, the following conditions hold:
-
• the generalized pair
 $(Y,B_Y,\mathbf {M})$
is generalized dlt and
$(Y,B_Y,\mathbf {M})$
is generalized dlt and
 $-(K_Y+B_Y+{\mathbf {M}_{Y}})$
is nef;
$-(K_Y+B_Y+{\mathbf {M}_{Y}})$
is nef; -
• the generalized pair
 $(Y,B_Y-\epsilon \Xi _Y,(1-\epsilon )\mathbf {M})$
is generalized dlt, it is not generalized klt, and the divisor
$(Y,B_Y-\epsilon \Xi _Y,(1-\epsilon )\mathbf {M})$
is generalized dlt, it is not generalized klt, and the divisor
 $-(K_Y+B_Y-\epsilon \Xi _Y+(1-\epsilon ) {\mathbf {M}_{Y}})$
is big and nef.
$-(K_Y+B_Y-\epsilon \Xi _Y+(1-\epsilon ) {\mathbf {M}_{Y}})$
is big and nef.
By Lemma 2.12 and Lemma 2.13, an N-complement of
![]() $(Y,B_Y,\mathbf {M})$
induces an N-complement of
$(Y,B_Y,\mathbf {M})$
induces an N-complement of
![]() $(X,B,\mathbf {M})$
. By Theorem 5.1, we conclude that
$(X,B,\mathbf {M})$
. By Theorem 5.1, we conclude that
![]() $(Y,B_Y,\mathbf {M})$
admits an
$(Y,B_Y,\mathbf {M})$
admits an
![]() $N(D(\mathcal {R}),d-1,0,p)$
-complement. Notice that we can rely on Theorem 5.1 in lower dimension, since we are proceeding by induction on d, and the conjectures to which Theorem 5.1 is conditional are known in coregularity 0 (by the remarks under the statement of Theorem 7). Hence,
$N(D(\mathcal {R}),d-1,0,p)$
-complement. Notice that we can rely on Theorem 5.1 in lower dimension, since we are proceeding by induction on d, and the conjectures to which Theorem 5.1 is conditional are known in coregularity 0 (by the remarks under the statement of Theorem 7). Hence,
![]() $(X,B,\mathbf {M})$
admits a
$(X,B,\mathbf {M})$
admits a
![]() $N(D(\mathcal {R}),d-1,0,p)$
-complement. Note that
$N(D(\mathcal {R}),d-1,0,p)$
-complement. Note that
![]() $D(\mathcal {R})\subset \Lambda $
. So this is also a
$D(\mathcal {R})\subset \Lambda $
. So this is also a
![]() $N(\Lambda ,d-1,0,p)$
-complement. Thus, by the minimality of
$N(\Lambda ,d-1,0,p)$
-complement. Thus, by the minimality of
![]() $N(\Lambda ,d,0,p)$
, we have that
$N(\Lambda ,d,0,p)$
, we have that
This implies that
![]() $N(\Lambda ,d,0,p)$
is bounded above by
$N(\Lambda ,d,0,p)$
is bounded above by
![]() $N(\Lambda ,1,0,p)$
. This finishes the proof.
$N(\Lambda ,1,0,p)$
. This finishes the proof.
Proof of Theorem 4.
We follow the notation of the proof of Theorem 7.1. By [Reference Filipazzi, Mauri and Moraga13, Corollary 3], a log Calabi–Yau pair with standard coefficients and coregularity
![]() $0$
has coefficients in
$0$
has coefficients in
![]() $\left \{\frac {1}{2},1\right \}$
. In particular, a generalized log canonical threshold with standard coefficients and coregularity
$\left \{\frac {1}{2},1\right \}$
. In particular, a generalized log canonical threshold with standard coefficients and coregularity
![]() $0$
belongs to
$0$
belongs to
![]() $\left \{\frac {1}{2},1\right \}$
(see Definition 2.26 and [Reference Figueroa, Moraga and Peng10, Theorem 4.3]). On the other hand, by Corollary 3.3, a generalized pseudo-effective threshold with standard coefficients and coregularity 0 is either
$\left \{\frac {1}{2},1\right \}$
(see Definition 2.26 and [Reference Figueroa, Moraga and Peng10, Theorem 4.3]). On the other hand, by Corollary 3.3, a generalized pseudo-effective threshold with standard coefficients and coregularity 0 is either
![]() $\frac {1}{2}$
or
$\frac {1}{2}$
or
![]() $1$
. In the proof of Theorem 3.5, the set
$1$
. In the proof of Theorem 3.5, the set
![]() $\mathcal {R}(\mathcal {S},0,2)$
only consists of log canonical thresholds of coregularity 0 and pseudo-effective thresholds of coregularity 0. Hence, by the proof of Theorem 3.5, we may assume that the coefficients of B belong to
$\mathcal {R}(\mathcal {S},0,2)$
only consists of log canonical thresholds of coregularity 0 and pseudo-effective thresholds of coregularity 0. Hence, by the proof of Theorem 3.5, we may assume that the coefficients of B belong to
![]() $\{\frac {1}{2},1\}$
, that is, we have that
$\{\frac {1}{2},1\}$
, that is, we have that

Note that
![]() $I_{\mathcal {S}}=1$
(see Definition 2.14) and
$I_{\mathcal {S}}=1$
(see Definition 2.14) and
![]() $p=2$
in this case. By the proof of Theorem 7.1, we conclude that
$p=2$
in this case. By the proof of Theorem 7.1, we conclude that
for every
![]() $d\geq 2$
. Then, the proof follows as
$d\geq 2$
. Then, the proof follows as
![]() $N(\mathcal {S},1,0,2)=2$
.
$N(\mathcal {S},1,0,2)=2$
.
Proof. By Lemma 2.16, we may assume that
![]() $\Lambda $
is derived. By [Reference Filipazzi, Mauri and Moraga13, Theorem 2], we may assume that the coefficients of B belong to a finite subset
$\Lambda $
is derived. By [Reference Filipazzi, Mauri and Moraga13, Theorem 2], we may assume that the coefficients of B belong to a finite subset
![]() $\Lambda _0\subset \Lambda $
. Let
$\Lambda _0\subset \Lambda $
. Let
![]() $\lambda _0$
be the smallest positive integer such that
$\lambda _0$
be the smallest positive integer such that
![]() $\lambda _0\Lambda _0 \subset \mathbb {Z}$
and p divides
$\lambda _0\Lambda _0 \subset \mathbb {Z}$
and p divides
![]() $\lambda _0$
. Let
$\lambda _0$
. Let
![]() $I(\Lambda _0,c,d,p)$
be the smallest positive integer that is divisible by the index of all the generalized pairs as in the statement of dimension at most d. A priori,
$I(\Lambda _0,c,d,p)$
be the smallest positive integer that is divisible by the index of all the generalized pairs as in the statement of dimension at most d. A priori,
![]() $I(\Lambda _0,c,d,p)$
may not exist. However, due to Conjecture 1 and Lemma 2.30, we know that
$I(\Lambda _0,c,d,p)$
may not exist. However, due to Conjecture 1 and Lemma 2.30, we know that
![]() $I(\Lambda _0,c,c,p)$
is finite. We proceed by induction on the dimension d. Assume that
$I(\Lambda _0,c,c,p)$
is finite. We proceed by induction on the dimension d. Assume that
![]() $I(\Lambda _0,d-1,c,p)$
is finite. We may assume that
$I(\Lambda _0,d-1,c,p)$
is finite. We may assume that
![]() $I(\Lambda _0,d-1,c,p)$
is divisible by
$I(\Lambda _0,d-1,c,p)$
is divisible by
![]() $\lambda _0$
. Let
$\lambda _0$
. Let
![]() $(X,B,\mathbf {M})$
be a d-dimensional generalized pair as in the statement. We write
$(X,B,\mathbf {M})$
be a d-dimensional generalized pair as in the statement. We write
![]() $I(X,B,\mathbf {M})$
for the index of this generalized log Calabi–Yau pair.
$I(X,B,\mathbf {M})$
for the index of this generalized log Calabi–Yau pair.
By Theorem 2.29, we may replace
![]() $(X,B,\mathbf {M})$
with a Kollár–Xu model and assume the following conditions hold:
$(X,B,\mathbf {M})$
with a Kollár–Xu model and assume the following conditions hold:
-
• the generalized pair
 $(X,B,\mathbf {M})$
is generalized dlt;
$(X,B,\mathbf {M})$
is generalized dlt; -
• there is a contraction
 $\pi \colon X\rightarrow Z$
for which
$\pi \colon X\rightarrow Z$
for which
 $\lfloor B\rfloor $
fully supports a
$\lfloor B\rfloor $
fully supports a
 $\pi $
-semiample and
$\pi $
-semiample and
 $\pi $
-big divisor; and
$\pi $
-big divisor; and -
• every generalized log canonical center of
 $(X,B,\mathbf {M})$
dominates Z.
$(X,B,\mathbf {M})$
dominates Z.
In particular, we know that Z has dimension at most c.
We will proceed in two different cases, depending on the coefficients of
![]() $B+{\mathbf {M}_{X}}$
and the rational connectedness of X.
$B+{\mathbf {M}_{X}}$
and the rational connectedness of X.
Case 1: We assume that
![]() $\mathbf {M}$
is numerically nontrivial and X is rationally connected.
$\mathbf {M}$
is numerically nontrivial and X is rationally connected.
We will proceed in two different sub-cases, depending on the coefficients of
![]() $\{B\}+{\mathbf {M}_{X}}$
.
$\{B\}+{\mathbf {M}_{X}}$
.
Case 1.1: We assume that
![]() $\{B\}+{\mathbf {M}_{X}}$
is
$\{B\}+{\mathbf {M}_{X}}$
is
![]() $\mathbb {Q}$
-trivial on the general fiber of
$\mathbb {Q}$
-trivial on the general fiber of
![]() $\pi $
.
$\pi $
.
We observe that, given the running assumption that
![]() $\mathbf {M}$
is numerically nontrivial, in this subcase we have
$\mathbf {M}$
is numerically nontrivial, in this subcase we have
![]() $\dim Z> 0$
. By Theorem 8
$\dim Z> 0$
. By Theorem 8
![]() $(c)$
, we can write
$(c)$
, we can write
where
![]() $(Z,B_Z,\mathbf {N})$
is a generalized klt log Calabi–Yau pair and the positive integer q only depends on
$(Z,B_Z,\mathbf {N})$
is a generalized klt log Calabi–Yau pair and the positive integer q only depends on
![]() $\Lambda _0$
, c and p. The coefficients of
$\Lambda _0$
, c and p. The coefficients of
![]() $B_Z$
belong to a set
$B_Z$
belong to a set
![]() $\Omega $
, which satisfies the DCC, and only depends on
$\Omega $
, which satisfies the DCC, and only depends on
![]() $\Lambda _0$
, c and p. Finally, the divisor
$\Lambda _0$
, c and p. Finally, the divisor
![]() $q\mathbf {N}$
is b-Cartier. We conclude that
$q\mathbf {N}$
is b-Cartier. We conclude that
Note that the value on the r.h.s. only depends on
![]() $\Lambda _0,c$
and p.
$\Lambda _0,c$
and p.
Case 1.2: We assume that
![]() $\{B\}+{\mathbf {M}_{X}}$
is nontrivial on the general fiber of
$\{B\}+{\mathbf {M}_{X}}$
is nontrivial on the general fiber of
![]() $\pi $
.
$\pi $
.
We run a
![]() $(K_X+\lfloor B\rfloor )$
-MMP over Z. Since
$(K_X+\lfloor B\rfloor )$
-MMP over Z. Since
![]() $K_X+\lfloor B\rfloor $
is not pseudo-effective over Z, this minimal model program terminates with a Mori fiber space
$K_X+\lfloor B\rfloor $
is not pseudo-effective over Z, this minimal model program terminates with a Mori fiber space
![]() $\pi '\colon X' \rightarrow W$
over Z. We denote the push-forward of B to
$\pi '\colon X' \rightarrow W$
over Z. We denote the push-forward of B to
![]() $X'$
by
$X'$
by
![]() $B'$
. We may replace
$B'$
. We may replace
![]() $(X,B,\mathbf {M})$
with
$(X,B,\mathbf {M})$
with
![]() $(X',B',\mathbf {M})$
and assume that
$(X',B',\mathbf {M})$
and assume that
![]() $K_X+\lfloor B\rfloor $
is antiample over W. In this reduction, we may give up the generalized dlt property for
$K_X+\lfloor B\rfloor $
is antiample over W. In this reduction, we may give up the generalized dlt property for
![]() $(X,B,\mathbf {M})$
, while
$(X,B,\mathbf {M})$
, while
![]() $(X,\lfloor B \rfloor ,\mathbf {M})$
remains generalized dlt. By the reduction to the Kollár–Xu model, the divisor
$(X,\lfloor B \rfloor ,\mathbf {M})$
remains generalized dlt. By the reduction to the Kollár–Xu model, the divisor
![]() $\lfloor B\rfloor $
contains a prime component S which dominates W. By construction, the general fiber of
$\lfloor B\rfloor $
contains a prime component S which dominates W. By construction, the general fiber of
![]() $S\rightarrow W$
is rationally connected. Since W is rationally connected, we conclude that S is rationally connected. Since
$S\rightarrow W$
is rationally connected. Since W is rationally connected, we conclude that S is rationally connected. Since
![]() $(X,\lfloor B \rfloor ,\mathbf {M})$
is generalized dlt, S is normal. Let
$(X,\lfloor B \rfloor ,\mathbf {M})$
is generalized dlt, S is normal. Let
![]() $(S,B_S,\mathbf {N})$
be the generalized pair obtained by adjunction. Then, by Lemma 2.17 and [Reference Figueroa, Moraga and Peng10, Theorem 2], we know that the coefficients of
$(S,B_S,\mathbf {N})$
be the generalized pair obtained by adjunction. Then, by Lemma 2.17 and [Reference Figueroa, Moraga and Peng10, Theorem 2], we know that the coefficients of
![]() $B_S$
belong to
$B_S$
belong to
![]() $\Lambda _0$
and
$\Lambda _0$
and
![]() $p\mathbf {N}$
is b-Cartier. We conclude that
$p\mathbf {N}$
is b-Cartier. We conclude that
By Theorem 2.31, we conclude that
Putting Case 1.1 and Case 1.2 together, we conclude that if
![]() $\mathbf {M}$
is numerically nontrivial and X is rationally connected, then we have that
$\mathbf {M}$
is numerically nontrivial and X is rationally connected, then we have that
Case 2: We assume that either
![]() $\mathbf {M}$
is the trivial b-divisor or
$\mathbf {M}$
is the trivial b-divisor or
![]() $\mathbf {M}$
is numerically trivial and X is rationally connected.
$\mathbf {M}$
is numerically trivial and X is rationally connected.
In the latter case, by [Reference Filipazzi, Mauri and Moraga13, Lemma 3.9] we know that
![]() $p{\mathbf {M}_{X'}}\sim 0$
where
$p{\mathbf {M}_{X'}}\sim 0$
where
![]() $X'\rightarrow X$
is a resolution on which
$X'\rightarrow X$
is a resolution on which
![]() $\mathbf {M}$
descends. Replacing
$\mathbf {M}$
descends. Replacing
![]() $\mathbf {M}$
with
$\mathbf {M}$
with
![]() $p\mathbf {M}$
, we may assume that the first case holds.
$p\mathbf {M}$
, we may assume that the first case holds.
Let
![]() $(X,B)$
be a log Calabi–Yau pair as in the statement. We assume that the coefficients of B belong to
$(X,B)$
be a log Calabi–Yau pair as in the statement. We assume that the coefficients of B belong to
![]() $\Lambda _0$
. We may assume that
$\Lambda _0$
. We may assume that
![]() $d>c$
. We replace
$d>c$
. We replace
![]() $(X,B)$
with a
$(X,B)$
with a
![]() $\mathbb {Q}$
-factorial dlt modification. Let
$\mathbb {Q}$
-factorial dlt modification. Let
![]() $S\subset \lfloor B\rfloor $
be a prime component. We run a
$S\subset \lfloor B\rfloor $
be a prime component. We run a
![]() $(K_X+B-S)$
-MMP. This terminates with a Mori fiber space
$(K_X+B-S)$
-MMP. This terminates with a Mori fiber space
![]() $\pi '\colon X'\rightarrow W$
. We denote by
$\pi '\colon X'\rightarrow W$
. We denote by
![]() $B'$
the push-forward of B to
$B'$
the push-forward of B to
![]() $X'$
. We replace
$X'$
. We replace
![]() $(X,B)$
with
$(X,B)$
with
![]() $(X',B')$
. Note that S is ample over the base W and
$(X',B')$
. Note that S is ample over the base W and
![]() $(X,B-S)$
is dlt. Let
$(X,B-S)$
is dlt. Let
![]() $(S,B_S)$
be the pair obtained by adjunction. Then,
$(S,B_S)$
be the pair obtained by adjunction. Then,
![]() $(S,B_S)$
is a semilog canonical log Calabi–Yau pair by [Reference Fujino and Gongyo19, Example 2.6]. Furthermore, by Lemma 2.17 and [Reference Figueroa, Moraga and Peng10, Theorem 2], the coefficients of
$(S,B_S)$
is a semilog canonical log Calabi–Yau pair by [Reference Fujino and Gongyo19, Example 2.6]. Furthermore, by Lemma 2.17 and [Reference Figueroa, Moraga and Peng10, Theorem 2], the coefficients of
![]() $B_S$
belong to
$B_S$
belong to
![]() $\Lambda _0$
. By Theorem 4.9, up to replacing
$\Lambda _0$
. By Theorem 4.9, up to replacing
![]() $I(\Lambda _0,d-1,c)$
with
$I(\Lambda _0,d-1,c)$
with
![]() $\mathrm {lcm}(I(\Lambda _0,d-1,c),I_a(\Lambda _0,c))$
, we may assume that
$\mathrm {lcm}(I(\Lambda _0,d-1,c),I_a(\Lambda _0,c))$
, we may assume that
Here,
![]() $I_a(\Lambda _0,c)$
is the constant from Theorem 4.9. By construction, we have that
$I_a(\Lambda _0,c)$
is the constant from Theorem 4.9. By construction, we have that
![]() $(X,B-S)$
is dlt, X is
$(X,B-S)$
is dlt, X is
![]() $\mathbb {Q}$
-factorial and klt, and
$\mathbb {Q}$
-factorial and klt, and
![]() $S\subset \lfloor B\rfloor $
is ample over W. If the fibers of
$S\subset \lfloor B\rfloor $
is ample over W. If the fibers of
![]() $S\rightarrow W$
are connected, then we can apply Theorem 4.12, to conclude that
$S\rightarrow W$
are connected, then we can apply Theorem 4.12, to conclude that
Otherwise, we can apply Theorem 2.32, to conclude that
Putting Case 1 and Case 2 together, we conclude that every generalized pair
![]() $(X,B,\mathbf {M})$
of dimension d as in the statement satisfies that
$(X,B,\mathbf {M})$
of dimension d as in the statement satisfies that
Hence, we have that
Proceeding inductively, we conclude that
The r.h.s. does not depend on d. This finishes the proof of the proposition.
Lemma 7.3. Let
![]() $\lambda $
be a positive integer. Let
$\lambda $
be a positive integer. Let
![]() $(\mathbb {P}^1,B_{\mathbb {P}^1},{\mathbf {M}_{\mathbb {P}^1}})$
be a generalized log Calabi–Yau pair. Assume that the coefficients of
$(\mathbb {P}^1,B_{\mathbb {P}^1},{\mathbf {M}_{\mathbb {P}^1}})$
be a generalized log Calabi–Yau pair. Assume that the coefficients of
![]() $B_{\mathbb {P}^1}$
belong to
$B_{\mathbb {P}^1}$
belong to
![]() $D_\lambda $
and
$D_\lambda $
and
![]() $2\lambda {\mathbf {M}_{\mathbb {P}^1}}$
is Weil. Then,
$2\lambda {\mathbf {M}_{\mathbb {P}^1}}$
is Weil. Then,
![]() $I(K_{\mathbb {P}}^1+B_{\mathbb {P}^1}+{\mathbf {M}_{\mathbb {P}^1}})\sim 0$
for some
$I(K_{\mathbb {P}}^1+B_{\mathbb {P}^1}+{\mathbf {M}_{\mathbb {P}^1}})\sim 0$
for some
![]() $I=m\lambda $
, where
$I=m\lambda $
, where
![]() $m \leq 120\lambda $
is an even positive integer. Furthermore, if
$m \leq 120\lambda $
is an even positive integer. Furthermore, if
![]() ${\mathbf {M}_{\mathbb {P}^1}}=0$
, then
${\mathbf {M}_{\mathbb {P}^1}}=0$
, then
![]() $H^0(\mathbb {P}^1,\mathcal {O}_{\mathbb {P}^1}(I(K_{\mathbb {P}}^1+B_{\mathbb {P}^1})))$
admits an admissible section.
$H^0(\mathbb {P}^1,\mathcal {O}_{\mathbb {P}^1}(I(K_{\mathbb {P}}^1+B_{\mathbb {P}^1})))$
admits an admissible section.
Proof. We prove the second statement. Let
![]() $G=\mathrm {Aut}(\mathbb {P}^1,B_{\mathbb {P}^1})$
. The group G is a finite extension of a torus. First, we assume that G is finite, which turns to imply that
$G=\mathrm {Aut}(\mathbb {P}^1,B_{\mathbb {P}^1})$
. The group G is a finite extension of a torus. First, we assume that G is finite, which turns to imply that
![]() $B_{\mathbb {P}^1}$
is supported in at least three points. Let
$B_{\mathbb {P}^1}$
is supported in at least three points. Let
![]() $(\mathbb {P}^1,B_{\mathbb {P}^1})\rightarrow (\mathbb {P}^1,B^{\prime }_{\mathbb {P}^1})$
be the quotient by G given by the Hurwitz formula. By pulling back to
$(\mathbb {P}^1,B_{\mathbb {P}^1})\rightarrow (\mathbb {P}^1,B^{\prime }_{\mathbb {P}^1})$
be the quotient by G given by the Hurwitz formula. By pulling back to
![]() $\mathbb {P}^1$
, it suffices to show that
$\mathbb {P}^1$
, it suffices to show that
for some
![]() $I=m\lambda $
, where
$I=m\lambda $
, where
![]() $m\leq 120\lambda $
. We write
$m\leq 120\lambda $
. We write
 $$\begin{align*}B^{\prime}_{\mathbb{P}^1}=\sum_{i=1}^k\left( 1-\frac{1}{m_i}+\frac{\sum_{j=1}^{l_k}\frac{p_{j,k}}{\lambda}}{m_i} \right)\{p_i\}, \end{align*}$$
$$\begin{align*}B^{\prime}_{\mathbb{P}^1}=\sum_{i=1}^k\left( 1-\frac{1}{m_i}+\frac{\sum_{j=1}^{l_k}\frac{p_{j,k}}{\lambda}}{m_i} \right)\{p_i\}, \end{align*}$$
where the
![]() $p_{j,k}$
’s are positive integers. We may assume that
$p_{j,k}$
’s are positive integers. We may assume that
![]() $m_1\geq \dots \geq m_k$
. If
$m_1\geq \dots \geq m_k$
. If
![]() $m_1\leq 5$
, then for
$m_1\leq 5$
, then for
![]() $I=120\lambda $
, we have that
$I=120\lambda $
, we have that
![]() $IB^{\prime }_{\mathbb {P}^1}$
is Weil. If
$IB^{\prime }_{\mathbb {P}^1}$
is Weil. If
![]() $m_1>5$
, then
$m_1>5$
, then
![]() $m_3=\dots =m_k=1$
. If
$m_3=\dots =m_k=1$
. If
![]() $m_2>2\lambda $
, then
$m_2>2\lambda $
, then
![]() $m_1>2\lambda $
and
$m_1>2\lambda $
and
 $$\begin{align*}\mathrm{coeff}_{p_1}(B^{\prime}_{\mathbb{P}^1}) + \mathrm{coeff}_{p_2}(B^{\prime}_{\mathbb{P}^1}) + \mathrm{coeff}_{p_3}(B^{\prime}_{\mathbb{P}^1})> \left(1-\frac{1}{2\lambda}\right) + \left(1-\frac{1}{2\lambda}\right) +\frac{1}{\lambda} = 2. \end{align*}$$
$$\begin{align*}\mathrm{coeff}_{p_1}(B^{\prime}_{\mathbb{P}^1}) + \mathrm{coeff}_{p_2}(B^{\prime}_{\mathbb{P}^1}) + \mathrm{coeff}_{p_3}(B^{\prime}_{\mathbb{P}^1})> \left(1-\frac{1}{2\lambda}\right) + \left(1-\frac{1}{2\lambda}\right) +\frac{1}{\lambda} = 2. \end{align*}$$
This leads to a contradiction. Hence, we may assume that
![]() $m_2\leq 2\lambda $
. In this case, we have that
$m_2\leq 2\lambda $
. In this case, we have that
![]() $m_2\lambda B^{\prime }_{\mathbb {P}^1}$
is Weil. Thus, it suffices to take
$m_2\lambda B^{\prime }_{\mathbb {P}^1}$
is Weil. Thus, it suffices to take
![]() $I=m_2\lambda $
with
$I=m_2\lambda $
with
![]() $m_2\leq 2\lambda $
.
$m_2\leq 2\lambda $
.
Now, we assume that G is a finite extension of a torus. This implies that
![]() $B_{\mathbb {P}^1}$
is supported in two points, so we may assume that
$B_{\mathbb {P}^1}$
is supported in two points, so we may assume that
![]() $B_{\mathbb {P}^1}=\{0\}+\{\infty \}$
and that
$B_{\mathbb {P}^1}=\{0\}+\{\infty \}$
and that
![]() $G\simeq \mathbb {G}_m\rtimes \mathbb {Z}_2$
. Note that
$G\simeq \mathbb {G}_m\rtimes \mathbb {Z}_2$
. Note that
![]() $\mathbb {G}_m$
acts trivially on B-representations as it is connected. Hence, in this case,
$\mathbb {G}_m$
acts trivially on B-representations as it is connected. Hence, in this case,
![]() $2(K_{\mathbb {P}^1}+B_{\mathbb {P}^1})$
admits an admissible section.
$2(K_{\mathbb {P}^1}+B_{\mathbb {P}^1})$
admits an admissible section.
In the first statement, we need to control the index of the generalized pair. The same argument we used in the previous paragraph to control the index of
![]() $(\mathbb {P}^1,B^{\prime }_{\mathbb {P}^1})$
applies to
$(\mathbb {P}^1,B^{\prime }_{\mathbb {P}^1})$
applies to
![]() $(\mathbb {P}^1,B_{\mathbb {P}^1},{\mathbf {M}_{\mathbb {P}^1}})$
. The only difference is that due to the presence of
$(\mathbb {P}^1,B_{\mathbb {P}^1},{\mathbf {M}_{\mathbb {P}^1}})$
. The only difference is that due to the presence of
![]() $\mathbf {M}$
, it could be that
$\mathbf {M}$
, it could be that
![]() $B_{{\mathbb {P}^{1}}}$
is supported at only one point or it could even be empty. In this case,
$B_{{\mathbb {P}^{1}}}$
is supported at only one point or it could even be empty. In this case,
![]() $2\lambda (K_{{\mathbb {P}^{1}}}+ B_{{\mathbb {P}^{1}}} + {\mathbf {M}_{\mathbb {P}^1}})$
is integral, and the claims follow.
$2\lambda (K_{{\mathbb {P}^{1}}}+ B_{{\mathbb {P}^{1}}} + {\mathbf {M}_{\mathbb {P}^1}})$
is integral, and the claims follow.
Proof of Theorem 2.
Let
![]() $(X,B,\mathbf {M})$
be a d-dimensional generalized log Calabi–Yau pair as in the statement. We follow the proof of Proposition 7.2. In Case 1.1, we can write
$(X,B,\mathbf {M})$
be a d-dimensional generalized log Calabi–Yau pair as in the statement. We follow the proof of Proposition 7.2. In Case 1.1, we can write
where
![]() $(\mathbb {P}^1,B_{\mathbb {P}^1},{\mathbf {M}_{\mathbb {P}^1}})$
is a generalized log Calabi–Yau pair for which the coefficients of
$(\mathbb {P}^1,B_{\mathbb {P}^1},{\mathbf {M}_{\mathbb {P}^1}})$
is a generalized log Calabi–Yau pair for which the coefficients of
![]() $B_{\mathbb {P}^1}$
belong to a DCC set
$B_{\mathbb {P}^1}$
belong to a DCC set
![]() $\Omega $
and
$\Omega $
and
![]() $2\lambda {\mathbf {M}_{\mathbb {P}^1}}$
is Weil. Here, we can take
$2\lambda {\mathbf {M}_{\mathbb {P}^1}}$
is Weil. Here, we can take
![]() $q(\lambda )=2\lambda $
. Indeed, the constant
$q(\lambda )=2\lambda $
. Indeed, the constant
![]() $q(\lambda )$
in the canonical bundle formula depends on the existence of bounded complements with standard coefficients and relative absolute coregularity
$q(\lambda )$
in the canonical bundle formula depends on the existence of bounded complements with standard coefficients and relative absolute coregularity
![]() $0$
. By Theorem 5.3 and Theorem 4 such relative complement can be chosen to be a
$0$
. By Theorem 5.3 and Theorem 4 such relative complement can be chosen to be a
![]() $2\lambda $
-complement. On the other hand, we can take
$2\lambda $
-complement. On the other hand, we can take
![]() $\Omega =D_\lambda $
. Indeed, in this case,
$\Omega =D_\lambda $
. Indeed, in this case,
![]() $(X,B,\mathbf {M})$
admits a log canonical center which has a finite dominant map to
$(X,B,\mathbf {M})$
admits a log canonical center which has a finite dominant map to
![]() ${\mathbb {P}^1}$
. Thus, the coefficients of
${\mathbb {P}^1}$
. Thus, the coefficients of
![]() $B_{\mathbb {P}^1}$
can be computed by the adjunction formula and Riemann–Hurwitz. By Lemma 7.3, we conclude that
$B_{\mathbb {P}^1}$
can be computed by the adjunction formula and Riemann–Hurwitz. By Lemma 7.3, we conclude that
![]() $I(K_{\mathbb {P}^1}+B_{\mathbb {P}^1}+{\mathbf {M}_{\mathbb {P}^1}})\sim 0$
for some integer
$I(K_{\mathbb {P}^1}+B_{\mathbb {P}^1}+{\mathbf {M}_{\mathbb {P}^1}})\sim 0$
for some integer
![]() $I=m\lambda $
where
$I=m\lambda $
where
![]() $m\leq 120\lambda $
. We conclude that
$m\leq 120\lambda $
. We conclude that
![]() $I(K_X+B+{\mathbf {M}_{X}})\sim 0$
for the same choice of I.
$I(K_X+B+{\mathbf {M}_{X}})\sim 0$
for the same choice of I.
In Case 1.2 and Case 2, the index of
![]() $(X,B,\mathbf {M})$
divides the index of a possibly nonnormal log Calabi–Yau pair of coregularity 1 and dimension
$(X,B,\mathbf {M})$
divides the index of a possibly nonnormal log Calabi–Yau pair of coregularity 1 and dimension
![]() $d-1$
. Inductively, we reduce to the one-dimensional case which follows by Theorem 4.9 and Lemma 7.3.
$d-1$
. Inductively, we reduce to the one-dimensional case which follows by Theorem 4.9 and Lemma 7.3.
Proof of Theorem 3.
In a similar fashion as the proof of Theorem 2, this follows from the proof of Proposition 7.2 and the classification of log Calabi–Yau pair structures on
![]() $\mathbb {P}^1$
with standard coefficients.
$\mathbb {P}^1$
with standard coefficients.
Proposition 7.4. Assume that Theorem 6
![]() $(c)$
holds and Theorem 8
$(c)$
holds and Theorem 8
![]() $(c)$
holds. Then, Theorem 7
$(c)$
holds. Then, Theorem 7
![]() $(c)$
holds.
$(c)$
holds.
Proof. By Lemma 2.16, we may assume that
![]() $\Lambda $
is derived. Let
$\Lambda $
is derived. Let
![]() $N(\Lambda ,d,c,p)$
be the smallest positive integer for which every generalized pair
$N(\Lambda ,d,c,p)$
be the smallest positive integer for which every generalized pair
![]() $(X,B,\mathbf {M})$
of dimension d as in the statement admits an N-complement. By Theorem 3.5, there exists a finite subset
$(X,B,\mathbf {M})$
of dimension d as in the statement admits an N-complement. By Theorem 3.5, there exists a finite subset
![]() $\mathcal {R}\subset \Lambda $
for which
$\mathcal {R}\subset \Lambda $
for which
for every d. We proceed by induction on d. We may assume that every complement throughout the proof is divisible by p and
![]() $I_{\mathcal {R}}$
. We write
$I_{\mathcal {R}}$
. We write
![]() $N(X,B,\mathbf {M})$
for the smallest positive integer for which
$N(X,B,\mathbf {M})$
for the smallest positive integer for which
![]() $(X,B,\mathbf {M})$
admits an N-complement of coregularity c. Let
$(X,B,\mathbf {M})$
admits an N-complement of coregularity c. Let
![]() $B+\Gamma $
be a
$B+\Gamma $
be a
![]() $\mathbb {Q}$
-complement of
$\mathbb {Q}$
-complement of
![]() $(X,B,\mathbf {M})$
that computes the absolute coregularity. Let
$(X,B,\mathbf {M})$
that computes the absolute coregularity. Let
![]() $(Y,B_Y+\Gamma _Y+E,\mathbf {M})$
be a generalized
$(Y,B_Y+\Gamma _Y+E,\mathbf {M})$
be a generalized
![]() $\mathbb {Q}$
-factorial dlt modification of
$\mathbb {Q}$
-factorial dlt modification of
![]() $(X,B+\Gamma _Y,\mathbf {M})$
, where
$(X,B+\Gamma _Y,\mathbf {M})$
, where
![]() $B_Y$
(resp.
$B_Y$
(resp.
![]() $\Gamma _Y$
) is the strict transform of the fractional part of B (resp.
$\Gamma _Y$
) is the strict transform of the fractional part of B (resp.
![]() $\Gamma $
). Then, the generalized pair
$\Gamma $
). Then, the generalized pair
![]() $(Y,B_Y+E,\mathbf {M})$
has coregularity c. We run a
$(Y,B_Y+E,\mathbf {M})$
has coregularity c. We run a
![]() $-(K_Y+B_Y+E)$
-MMP with scaling, which terminates with a good minimal model Z. By Lemma 2.22, the generalized pair
$-(K_Y+B_Y+E)$
-MMP with scaling, which terminates with a good minimal model Z. By Lemma 2.22, the generalized pair
![]() $(Z,B_Z+E_Z)$
has coregularity c. By Lemma 2.13 and Lemma 2.12, we have that
$(Z,B_Z+E_Z)$
has coregularity c. By Lemma 2.13 and Lemma 2.12, we have that
![]() $N(X,B,\mathbf {M})\leq N(Z,B_Z+E_Z,\mathbf {M})$
. In order to give an upper bound for
$N(X,B,\mathbf {M})\leq N(Z,B_Z+E_Z,\mathbf {M})$
. In order to give an upper bound for
![]() $N(X,B,\mathbf {M})$
, we may replace
$N(X,B,\mathbf {M})$
, we may replace
![]() $(X,B,\mathbf {M})$
with
$(X,B,\mathbf {M})$
with
![]() $(Z,B_Z+E_Z,\mathbf {M})$
. Thus, we may assume that
$(Z,B_Z+E_Z,\mathbf {M})$
. Thus, we may assume that
![]() $\mathrm {coreg}(X,B,\mathbf {M})=c$
and
$\mathrm {coreg}(X,B,\mathbf {M})=c$
and
![]() $-(K_X+B+{\mathbf {M}_{X}})$
is semiample. Let W be the ample model of
$-(K_X+B+{\mathbf {M}_{X}})$
is semiample. Let W be the ample model of
![]() $-(K_X+B+{\mathbf {M}_{X}})$
. We proceed in three different cases, depending on the dimension of W.
$-(K_X+B+{\mathbf {M}_{X}})$
. We proceed in three different cases, depending on the dimension of W.
Case 1: In this case, we can assume that
![]() $\dim W=0$
.
$\dim W=0$
.
Then, we have that
![]() $N(K_X+B+{\mathbf {M}_{X}})\sim 0$
for some N that only depends on
$N(K_X+B+{\mathbf {M}_{X}})\sim 0$
for some N that only depends on
![]() $\Lambda $
, c and p by Theorem 6
$\Lambda $
, c and p by Theorem 6
![]() $(c)$
.
$(c)$
.
Case 2: In this case, we assume that
![]() $\dim W=\dim X$
.
$\dim W=\dim X$
.
In this case, we have that
![]() $-(K_X+B+{\mathbf {M}_{X}})$
is a nef and big divisor. We may assume that
$-(K_X+B+{\mathbf {M}_{X}})$
is a nef and big divisor. We may assume that
![]() $(X,B,\mathbf {M})$
is
$(X,B,\mathbf {M})$
is
![]() $\mathbb {Q}$
-factorial and generalized dlt. By Theorem 5.1, we conclude that
$\mathbb {Q}$
-factorial and generalized dlt. By Theorem 5.1, we conclude that
![]() $N(X',B',\mathbf {M})\leq N(\Lambda ,d-1,c,p)=N(\mathcal {R},d-1,c,p)$
. In this case, we conclude that
$N(X',B',\mathbf {M})\leq N(\Lambda ,d-1,c,p)=N(\mathcal {R},d-1,c,p)$
. In this case, we conclude that
Case 3: In this case, we assume that
![]() $0<\dim W < \dim X$
.
$0<\dim W < \dim X$
.
We run a
![]() $(\{B\}+{\mathbf {M}_{X}})$
-MMP over W which terminates with a good minimal model
$(\{B\}+{\mathbf {M}_{X}})$
-MMP over W which terminates with a good minimal model
![]() $X\dashrightarrow X'\rightarrow W$
over W. By Lemma 2.22, the coregularity of
$X\dashrightarrow X'\rightarrow W$
over W. By Lemma 2.22, the coregularity of
![]() $(X,B,\mathbf {M})$
is unaffected by this MMP. Let
$(X,B,\mathbf {M})$
is unaffected by this MMP. Let
![]() $W'\rightarrow W$
be the ample model of
$W'\rightarrow W$
be the ample model of
![]() $\{B\}+{\mathbf {M}_{X}}$
over the base. First, assume that
$\{B\}+{\mathbf {M}_{X}}$
over the base. First, assume that
![]() $\dim W'=\dim X$
. In this case,
$\dim W'=\dim X$
. In this case,
![]() $\{B'\}+{\mathbf {M}_{X'}}$
is big over W. Hence, for
$\{B'\}+{\mathbf {M}_{X'}}$
is big over W. Hence, for
![]() $\epsilon>0$
small enough, we have that the generalized pair
$\epsilon>0$
small enough, we have that the generalized pair
![]() $(X',B'-\epsilon \{B'\},(1-\epsilon )\mathbf {M})$
is generalized log canonical but not generalized klt and the divisor
$(X',B'-\epsilon \{B'\},(1-\epsilon )\mathbf {M})$
is generalized log canonical but not generalized klt and the divisor
is big and nef. Note that
![]() $N(X,B,\mathbf {M})=N(X',B',\mathbf {M})$
. By Theorem 5.1, we conclude that
$N(X,B,\mathbf {M})=N(X',B',\mathbf {M})$
. By Theorem 5.1, we conclude that
From now on, we assume that
![]() $0<\dim W' < \dim X$
. We separate in two cases, depending on the log canonical centers of
$0<\dim W' < \dim X$
. We separate in two cases, depending on the log canonical centers of
![]() $(X',B',\mathbf {M})$
.
$(X',B',\mathbf {M})$
.
Case 3.1: In this case, we assume that there is a generalized log canonical center of
![]() $(X',B',\mathbf {M})$
that is vertical over
$(X',B',\mathbf {M})$
that is vertical over
![]() $W'$
.
$W'$
.
We may assume that
![]() $(X',B',\mathbf {M})$
is generalized dlt. Let
$(X',B',\mathbf {M})$
is generalized dlt. Let
![]() $S'\subset \lfloor B'\rfloor $
be a prime component that is vertical over
$S'\subset \lfloor B'\rfloor $
be a prime component that is vertical over
![]() $W'$
. In this case,
$W'$
. In this case,
![]() $B^{\prime }_{\mathrm {hor}}$
is big over the base. We run a
$B^{\prime }_{\mathrm {hor}}$
is big over the base. We run a
![]() $B^{\prime }_{\mathrm {hor}}$
-MMP over
$B^{\prime }_{\mathrm {hor}}$
-MMP over
![]() $W'$
which terminates with a good minimal model
$W'$
which terminates with a good minimal model
![]() $X^{\prime }_0$
, and we consider its ample model
$X^{\prime }_0$
, and we consider its ample model
![]() $X"$
over
$X"$
over
![]() $W'$
. We have the following commutative diagram:
$W'$
. We have the following commutative diagram:

Note that all the previous models are crepant. Hence, we have that
By construction, the following conditions are satisfied:
-
• the variety W is an ample model for
 $-(K_X+B+{\mathbf {M}_{X}})$
;
$-(K_X+B+{\mathbf {M}_{X}})$
; -
• the variety
 $W'$
is an ample model for
$W'$
is an ample model for
 $\{B'\}+M_{X'}$
over W;
$\{B'\}+M_{X'}$
over W; -
• the variety
 $X^{\prime }_0$
is a good minimal model for
$X^{\prime }_0$
is a good minimal model for
 $B^{\prime }_{0,\mathrm {hor}}$
over
$B^{\prime }_{0,\mathrm {hor}}$
over
 $W'$
; and
$W'$
; and -
• the variety
 $X"$
is an ample model for
$X"$
is an ample model for
 $B^{\prime \prime }_{\mathrm {hor}}$
over
$B^{\prime \prime }_{\mathrm {hor}}$
over
 $W'$
.
$W'$
.
We conclude that the divisor
is ample for
![]() $\epsilon \gg \delta>0$
small enough. We claim that the generalized pair
$\epsilon \gg \delta>0$
small enough. We claim that the generalized pair
is generalized log canonical but not generalized klt. Note that
![]() $(X^{\prime }_0, B^{\prime }_0-\epsilon \{B^{\prime }_0\}-\delta B^{\prime }_{0,\mathrm {hor}},(1-\epsilon )\mathbf {M})$
is generalized log canonical and not generalized klt as
$(X^{\prime }_0, B^{\prime }_0-\epsilon \{B^{\prime }_0\}-\delta B^{\prime }_{0,\mathrm {hor}},(1-\epsilon )\mathbf {M})$
is generalized log canonical and not generalized klt as
![]() $S^{\prime }_0$
is a component of
$S^{\prime }_0$
is a component of
![]() $\lfloor B^{\prime }_0-\epsilon \{B^{\prime }_0\}-\delta B^{\prime }_{0,\mathrm {hor}}\rfloor $
. The morphism
$\lfloor B^{\prime }_0-\epsilon \{B^{\prime }_0\}-\delta B^{\prime }_{0,\mathrm {hor}}\rfloor $
. The morphism
![]() $\psi $
is
$\psi $
is
![]() $(K_{X_0'}+B_0'-\epsilon \{B_0'\}-\delta B^{\prime }_{0,\mathrm {hor}}+(1-\epsilon )\mathbf {M}_{X^{\prime }_0})$
-trivial, so the claim follows. By Theorem 5.1 and the sequence of equalities (7.1), we conclude that
$(K_{X_0'}+B_0'-\epsilon \{B_0'\}-\delta B^{\prime }_{0,\mathrm {hor}}+(1-\epsilon )\mathbf {M}_{X^{\prime }_0})$
-trivial, so the claim follows. By Theorem 5.1 and the sequence of equalities (7.1), we conclude that
Thus, in this case, we have that
![]() $N(X,B,\mathbf {M})\leq N(\mathcal {R},d-1,c)$
.
$N(X,B,\mathbf {M})\leq N(\mathcal {R},d-1,c)$
.
Case 3.2: In this case, we assume that all the generalized log canonical centers of
![]() $(X',B',\mathbf {M})$
are horizontal over
$(X',B',\mathbf {M})$
are horizontal over
![]() $W'$
.
$W'$
.
Let
![]() $\pi '\colon X'\rightarrow W'$
be the projective contraction. We may apply Theorem 8
$\pi '\colon X'\rightarrow W'$
be the projective contraction. We may apply Theorem 8
![]() $(c)$
to obtain a linear equivalence:
$(c)$
to obtain a linear equivalence:
where the following conditions are satisfied:
-
• the generalized pair
 $(W',B_{W'},\mathbf {N})$
is of Fano type, has dimension
$(W',B_{W'},\mathbf {N})$
is of Fano type, has dimension
 $d_{W'}\leq c$
and is exceptional (i.e., its absolute coregularity is equal to its dimension
$d_{W'}\leq c$
and is exceptional (i.e., its absolute coregularity is equal to its dimension
 $d_{W'}$
);
$d_{W'}$
); -
• the positive integer q only depends on
 $\Lambda $
, c and p;
$\Lambda $
, c and p; -
• the coefficients of
 $B_{W'}$
belong to a DCC set
$B_{W'}$
belong to a DCC set
 $\Omega $
which only depends on
$\Omega $
which only depends on
 $\Lambda $
, c and p; and
$\Lambda $
, c and p; and -
• the b-nef divisor
 $q\mathbf {N}$
is b-Cartier.
$q\mathbf {N}$
is b-Cartier.
Indeed, if
![]() $(W',B_{W'},\mathbf {N})$
is not exceptional, by pulling back a non-klt complement of it, we obtain a complement for
$(W',B_{W'},\mathbf {N})$
is not exceptional, by pulling back a non-klt complement of it, we obtain a complement for
![]() $(X',B',\mathbf {M})$
of coregularity strictly less than c. This leads to a contradiction. By [Reference Filipazzi and Moraga14, Theorem 1.2], any generalized pair
$(X',B',\mathbf {M})$
of coregularity strictly less than c. This leads to a contradiction. By [Reference Filipazzi and Moraga14, Theorem 1.2], any generalized pair
![]() $(W',B_{W'},\mathbf {N})$
as above admits an
$(W',B_{W'},\mathbf {N})$
as above admits an
![]() $N(\Omega ,d_{W'},d_{W'},q)$
-complement. By pulling back, we obtain an N-complement for
$N(\Omega ,d_{W'},d_{W'},q)$
-complement. By pulling back, we obtain an N-complement for
![]() $(X',B',\mathbf {M})$
for some
$(X',B',\mathbf {M})$
for some
Putting Case
![]() $1$
through Case
$1$
through Case
![]() $3$
together, we conclude that
$3$
together, we conclude that
for every d-dimensional generalized pair
![]() $(X,B,\mathbf {M})$
as in the statement. Proceeding inductively, we conclude that every generalized pair
$(X,B,\mathbf {M})$
as in the statement. Proceeding inductively, we conclude that every generalized pair
![]() $(X,B,\mathbf {M})$
as in the statement of the theorem satisfies that
$(X,B,\mathbf {M})$
as in the statement of the theorem satisfies that
Observe that the number on the r.h.s. only depends on
![]() $\Lambda ,c$
and p. This finishes the proof of the implication.
$\Lambda ,c$
and p. This finishes the proof of the implication.
Lemma 7.5. Let
![]() $(\mathbb {P}^1,B_{\mathbb {P}^1},{\mathbf {M}_{\mathbb {P}^1}})$
be a generalized log Calabi–Yau pair for which
$(\mathbb {P}^1,B_{\mathbb {P}^1},{\mathbf {M}_{\mathbb {P}^1}})$
be a generalized log Calabi–Yau pair for which
![]() $\mathrm {coeff}(B_{\mathbb {P}^1})\in D_t(\mathbb {Z}_{>0})$
and
$\mathrm {coeff}(B_{\mathbb {P}^1})\in D_t(\mathbb {Z}_{>0})$
and
![]() $2{\mathbf {M}_{\mathbb {P}^1}}$
is Cartier. If
$2{\mathbf {M}_{\mathbb {P}^1}}$
is Cartier. If
![]() $t>\frac {5}{6}$
, then
$t>\frac {5}{6}$
, then
![]() $t=1$
.
$t=1$
.
Proof. Each coefficient of
![]() $B_{\mathbb {P}^1}$
is either standard or of the form
$B_{\mathbb {P}^1}$
is either standard or of the form
The only sets of standard coefficients whose sum is less than
![]() $\frac {7}{6}$
are
$\frac {7}{6}$
are
![]() $\{1\}$
and
$\{1\}$
and
![]() $\{\frac {1}{2},\frac {1}{2}\}$
. Thus,
$\{\frac {1}{2},\frac {1}{2}\}$
. Thus,
![]() $B_{\mathbb {P}^1}$
is supported in at most
$B_{\mathbb {P}^1}$
is supported in at most
![]() $3$
points and
$3$
points and
![]() $t=1$
.
$t=1$
.
Proof of Theorem 5.
Let
![]() $(X,B,\mathbf {M})$
be a d-dimensional generalized pair as in the statement. Following Step 1 of the proof of Theorem 3.5, let t be a log canonical threshold of coregularity
$(X,B,\mathbf {M})$
be a d-dimensional generalized pair as in the statement. Following Step 1 of the proof of Theorem 3.5, let t be a log canonical threshold of coregularity
![]() $1$
(or a pseudo-effective threshold) of a prime divisor with respect to
$1$
(or a pseudo-effective threshold) of a prime divisor with respect to
![]() $(X,B,\mathbf {M})$
. By [Reference Figueroa, Moraga and Peng10, Lemma 3.2] (or proof of Lemma 3.2 in the case where t is a pseudo-effective threshold), we can construct a generalized log Calabi–Yau pair
$(X,B,\mathbf {M})$
. By [Reference Figueroa, Moraga and Peng10, Lemma 3.2] (or proof of Lemma 3.2 in the case where t is a pseudo-effective threshold), we can construct a generalized log Calabi–Yau pair
for which
![]() $\mathrm {coeff}(B_{\mathbb {P}^1})\in D_{t}(\{1\})$
and
$\mathrm {coeff}(B_{\mathbb {P}^1})\in D_{t}(\{1\})$
and
![]() $2{\mathbf {M}_{\mathbb {P}^1}}$
is Cartier. By Lemma 7.5, we conclude that
$2{\mathbf {M}_{\mathbb {P}^1}}$
is Cartier. By Lemma 7.5, we conclude that
![]() $t=1$
provided that
$t=1$
provided that
![]() $t>5/6$
. Hence, by the proof of Theorem 3.5, we may assume that the coefficients of B belong to
$t>5/6$
. Hence, by the proof of Theorem 3.5, we may assume that the coefficients of B belong to

Proceeding as in the proof of Proposition 7.4, we conclude that
Note that we can take
![]() $q=2$
due to Theorem 1. We conclude that
$q=2$
due to Theorem 1. We conclude that
![]() $N\in \{2,4,6\}$
.
$N\in \{2,4,6\}$
.
We prove the three main theorems of the article. The theorems are proved together inductively.
Proof of Theorems 6, 7 and 8.
Note that Theorem 8
![]() $(0)$
is trivial. By [Reference Filipazzi, Mauri and Moraga13, Theorem 1], we conclude that Theorem 6
$(0)$
is trivial. By [Reference Filipazzi, Mauri and Moraga13, Theorem 1], we conclude that Theorem 6
![]() $(0)$
holds. By Theorem 7.1, we know that Theorem 7
$(0)$
holds. By Theorem 7.1, we know that Theorem 7
![]() $(0)$
holds. Assume that Theorem 6
$(0)$
holds. Assume that Theorem 6
![]() $(c-1)$
, Theorem 7
$(c-1)$
, Theorem 7
![]() $(c-1)$
and Theorem 8
$(c-1)$
and Theorem 8
![]() $(c-1)$
hold. By Proposition 6.3, we conclude that Theorem 8
$(c-1)$
hold. By Proposition 6.3, we conclude that Theorem 8
![]() $(c)$
holds. By Proposition 7.2, we conclude that Theorem 6
$(c)$
holds. By Proposition 7.2, we conclude that Theorem 6
![]() $(c)$
holds. By Proposition 7.4, we conclude that Theorem 7
$(c)$
holds. By Proposition 7.4, we conclude that Theorem 7
![]() $(c)$
holds. This finishes the proof of the theorems.
$(c)$
holds. This finishes the proof of the theorems.
Finally, we prove the application to klt singularities.
Proof of Theorem 9.
Let
![]() $(X;x)$
be a klt singularity of absolute coregularity
$(X;x)$
be a klt singularity of absolute coregularity
![]() $0$
. Let
$0$
. Let
![]() $(X,\Gamma _0;x)$
be a strictly log canonical pair of coregularity
$(X,\Gamma _0;x)$
be a strictly log canonical pair of coregularity
![]() $0$
at x. By [Reference Xu43, Lemma 1], there exists a plt blow-up
$0$
at x. By [Reference Xu43, Lemma 1], there exists a plt blow-up
![]() $\pi \colon Y\rightarrow X$
that extracts a unique exceptional divisor E that is a log canonical place of
$\pi \colon Y\rightarrow X$
that extracts a unique exceptional divisor E that is a log canonical place of
![]() $(X,\Gamma _0;x)$
.Footnote
3
In particular, the pair
$(X,\Gamma _0;x)$
.Footnote
3
In particular, the pair
![]() $(E,\mathrm {Diff}_E(0))$
is a Fano pair of absolute coregularity 0 and with standard coefficients (see, e.g., [Reference Shokurov39, Proposition 3.9]). By Theorem 4,
$(E,\mathrm {Diff}_E(0))$
is a Fano pair of absolute coregularity 0 and with standard coefficients (see, e.g., [Reference Shokurov39, Proposition 3.9]). By Theorem 4,
![]() $(E,\mathrm {Diff}_E(0))$
admits a 1- or 2-complement. By Steps 4–9 of the proof of Proposition 5.2, we can lift this complement to a 1- or 2-complement of
$(E,\mathrm {Diff}_E(0))$
admits a 1- or 2-complement. By Steps 4–9 of the proof of Proposition 5.2, we can lift this complement to a 1- or 2-complement of
![]() $(X;x)$
at x.
$(X;x)$
at x.
Acknowledgements
This project was initiated in the Minimal Model Program Learning Seminar. The authors would like to thank Mirko Mauri for many discussions that led to some of the ideas of this article. Lastly, the authors would like to thank the anonymous referee for useful comments and suggestions that helped the authors improve the clarity of this work.
Funding statement
SF was partially supported by ERC starting grant #804334. FF received partial financial support by the NSF under János Kollár’s grant number DMS-1901855.
Competing interest
The authors have no competing interest to declare.