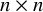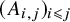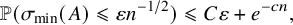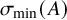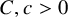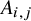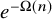1 Introduction
Let A be an
![]() $n\times n$
random symmetric matrix whose entries on and above the diagonal
$n\times n$
random symmetric matrix whose entries on and above the diagonal
![]() $(A_{i,j})_{i\leqslant j}$
are independent and identically distributed (i.i.d.) with mean
$(A_{i,j})_{i\leqslant j}$
are independent and identically distributed (i.i.d.) with mean
![]() $0$
and variance
$0$
and variance
![]() $1$
. This matrix model, sometimes called the Wigner matrix ensemble, was introduced in the 1950s in the seminal work of Wigner [Reference Wigner50], who established the famous “semicircular law” for the eigenvalues of such matrices.
$1$
. This matrix model, sometimes called the Wigner matrix ensemble, was introduced in the 1950s in the seminal work of Wigner [Reference Wigner50], who established the famous “semicircular law” for the eigenvalues of such matrices.
In this paper, we study the extreme behavior of the least singular value of A, which we denote by
![]() $\sigma _{\min }(A)$
. Heuristically, we expect that
$\sigma _{\min }(A)$
. Heuristically, we expect that
![]() $\sigma _{\min }(A) = \Theta (n^{-1/2})$
, and thus it is natural to consider
$\sigma _{\min }(A) = \Theta (n^{-1/2})$
, and thus it is natural to consider
for all
![]() $\varepsilon \geqslant 0$
(see Section 1.2). In this paper, we prove a bound on this quantity which is optimal up to constants, for all random symmetric matrices with i.i.d. subgaussian entries. This confirms the folklore conjecture, explicitly stated by Vershynin in [Reference Vershynin46].
$\varepsilon \geqslant 0$
(see Section 1.2). In this paper, we prove a bound on this quantity which is optimal up to constants, for all random symmetric matrices with i.i.d. subgaussian entries. This confirms the folklore conjecture, explicitly stated by Vershynin in [Reference Vershynin46].
Theorem 1.1. Let
![]() $\zeta $
be a subgaussian random variable with mean
$\zeta $
be a subgaussian random variable with mean
![]() $0$
and variance
$0$
and variance
![]() $1$
, and let A be an
$1$
, and let A be an
![]() $n \times n$
random symmetric matrix whose entries above the diagonal
$n \times n$
random symmetric matrix whose entries above the diagonal
![]() $(A_{i,j})_{i\leqslant j}$
are independent and distributed according to
$(A_{i,j})_{i\leqslant j}$
are independent and distributed according to
![]() $\zeta $
. Then for every
$\zeta $
. Then for every
![]() $\varepsilon \geqslant 0$
,
$\varepsilon \geqslant 0$
,
where
![]() $C,c>0$
depend only on
$C,c>0$
depend only on
![]() $\zeta $
.
$\zeta $
.
This conjecture is sharp up to the value of the constants
![]() $C,c>0$
and resolves the “up-to-constants” analogue of the Spielman–Teng [Reference Spielman and Teng38] conjecture for random symmetric matrices (see Section 1.2). Also note that the special case
$C,c>0$
and resolves the “up-to-constants” analogue of the Spielman–Teng [Reference Spielman and Teng38] conjecture for random symmetric matrices (see Section 1.2). Also note that the special case
![]() $\varepsilon = 0 $
tells us that the singularity probability of any random symmetric A with subgaussian entry distribution is exponentially small, generalizing our previous work [Reference Campos, Jenssen, Michelen and Sahasrabudhe4] on the
$\varepsilon = 0 $
tells us that the singularity probability of any random symmetric A with subgaussian entry distribution is exponentially small, generalizing our previous work [Reference Campos, Jenssen, Michelen and Sahasrabudhe4] on the
![]() $\{-1,1\}$
case.
$\{-1,1\}$
case.
1.1 Repeated eigenvalues
Before we discuss the history of the least singular value problem, we highlight one further contribution of this paper: a proof that a random symmetric matrix has no repeated eigenvalues with probability
![]() $1-e^{-\Omega (n)}$
.
$1-e^{-\Omega (n)}$
.
In the 1980s, Babai [Reference Tao and Vu43] conjectured that the adjacency matrix of the binomial random graph
![]() $G(n,1/2)$
has no repeated eigenvalues with probability
$G(n,1/2)$
has no repeated eigenvalues with probability
![]() $1-o(1)$
(see [Reference Tao and Vu43]). Tao and Vu [Reference Tao and Vu43] proved this conjecture in 2014 and, in subsequent work on the topic with Nguyen [Reference Nguyen, Tao and Vu24], went on to conjecture the probability that a random symmetric matrix with i.i.d. subgaussian entries has no repeated eigenvalues is
$1-o(1)$
(see [Reference Tao and Vu43]). Tao and Vu [Reference Tao and Vu43] proved this conjecture in 2014 and, in subsequent work on the topic with Nguyen [Reference Nguyen, Tao and Vu24], went on to conjecture the probability that a random symmetric matrix with i.i.d. subgaussian entries has no repeated eigenvalues is
![]() $1-e^{-\Omega (n)}$
. In this paper, we prove this conjecture en route to proving Theorem 1.1, our main theorem.
$1-e^{-\Omega (n)}$
. In this paper, we prove this conjecture en route to proving Theorem 1.1, our main theorem.
Theorem 1.2. Let
![]() $\zeta $
be a subgaussian random variable with mean
$\zeta $
be a subgaussian random variable with mean
![]() $0$
and variance
$0$
and variance
![]() $1$
, and let A be an
$1$
, and let A be an
![]() $n \times n$
random symmetric matrix, where
$n \times n$
random symmetric matrix, where
![]() $(A_{i,j})_{i\leqslant j}$
are independent and distributed according to
$(A_{i,j})_{i\leqslant j}$
are independent and distributed according to
![]() $\zeta $
. Then A has no repeated eigenvalues with probability at least
$\zeta $
. Then A has no repeated eigenvalues with probability at least
![]() $1-e^{-cn}$
, where
$1-e^{-cn}$
, where
![]() $c>0$
is a constant depending only on
$c>0$
is a constant depending only on
![]() $\zeta $
.
$\zeta $
.
Theorem 1.2 is easily seen to be sharp whenever
![]() $A_{i,j}$
is discrete: consider the event that three rows of A are identical; this event has probability
$A_{i,j}$
is discrete: consider the event that three rows of A are identical; this event has probability
![]() $e^{-\Theta (n)}$
and results in two
$e^{-\Theta (n)}$
and results in two
![]() $0$
eigenvalues. Also note that the constant in Theorem 1.2 can be made arbitrary small; consider the entry distribution
$0$
eigenvalues. Also note that the constant in Theorem 1.2 can be made arbitrary small; consider the entry distribution
![]() $\zeta $
, which takes value
$\zeta $
, which takes value
![]() $0$
with probability
$0$
with probability
![]() $1-p$
and each of
$1-p$
and each of
![]() $\{-p^{-1/2},p^{-1/2}\}$
with probability
$\{-p^{-1/2},p^{-1/2}\}$
with probability
![]() $p/2$
. Here, the probability of
$p/2$
. Here, the probability of
![]() $0$
being a repeated root is
$0$
being a repeated root is
![]() $\geqslant e^{-(3+o(1))pn}$
.
$\geqslant e^{-(3+o(1))pn}$
.
We in fact prove a more refined version of Theorem 1.2, which gives an upper bound on the probability that two eigenvalues of A fall into an interval of length
![]() $\varepsilon $
. This is the main result of Section 7. For this, we let
$\varepsilon $
. This is the main result of Section 7. For this, we let
![]() $\lambda _1(A)\geqslant \ldots \geqslant \lambda _n(A)$
denote the eigenvalues of the
$\lambda _1(A)\geqslant \ldots \geqslant \lambda _n(A)$
denote the eigenvalues of the
![]() $n\times n$
real symmetric matrix A.
$n\times n$
real symmetric matrix A.
Theorem 1.3. Let
![]() $\zeta $
be a subgaussian random variable with mean
$\zeta $
be a subgaussian random variable with mean
![]() $0$
and variance
$0$
and variance
![]() $1$
, and let A be an
$1$
, and let A be an
![]() $n \times n$
random symmetric matrix, where
$n \times n$
random symmetric matrix, where
![]() $(A_{i,j})_{i\leqslant j}$
are independent and distributed according to
$(A_{i,j})_{i\leqslant j}$
are independent and distributed according to
![]() $\zeta $
. Then for each
$\zeta $
. Then for each
![]() $\ell < cn$
and all
$\ell < cn$
and all
![]() $\varepsilon \geqslant 0$
, we have
$\varepsilon \geqslant 0$
, we have
where
![]() $C,c>0$
are constants, depending only on
$C,c>0$
are constants, depending only on
![]() $\zeta $
.
$\zeta $
.
In the following subsection, we describe the history of the least singular value problem. In Section 1.3, we discuss a technical theme which is developed in this paper, and then, in Section 2, we go on to give a sketch of Theorem 1.1.
1.2 History of the least singular value problem
The behavior of the least singular value was first studied for random matrices
![]() $B_n$
with i.i.d. coefficients, rather than for symmetric random matrices. For this model, the history goes back to von Neumann [Reference Von Neumann48], who suggested that one typically has
$B_n$
with i.i.d. coefficients, rather than for symmetric random matrices. For this model, the history goes back to von Neumann [Reference Von Neumann48], who suggested that one typically has
while studying approximate solutions to linear systems. This was then more rigorously conjectured by Smale [Reference Smale36] and proved by Szarek [Reference Szarek39] and Edelman [Reference Edelman8] in the case that
![]() $B_n = G_n$
is a random matrix with i.i.d. standard gaussian entries. Edelman found an exact expression for the density of the least singular value in this case. By analyzing this expression, one can deduce that
$B_n = G_n$
is a random matrix with i.i.d. standard gaussian entries. Edelman found an exact expression for the density of the least singular value in this case. By analyzing this expression, one can deduce that
for all
![]() $\varepsilon \geqslant 0$
(see, e.g. [Reference Spielman and Teng38]). While this gives a very satisfying understanding of the gaussian case, one encounters serious difficulties when trying to extend this result to other distributions. Indeed, Edelman’s proof relies crucially on an exact description of the joint distribution of eigenvalues that is available in the gaussian setting. In the last 20 or so years, intense study of the least singular value of i.i.d. random matrices has been undertaken with the overall goal of proving an appropriate version of (1.3) for different entry distributions and models of random matrices.
$\varepsilon \geqslant 0$
(see, e.g. [Reference Spielman and Teng38]). While this gives a very satisfying understanding of the gaussian case, one encounters serious difficulties when trying to extend this result to other distributions. Indeed, Edelman’s proof relies crucially on an exact description of the joint distribution of eigenvalues that is available in the gaussian setting. In the last 20 or so years, intense study of the least singular value of i.i.d. random matrices has been undertaken with the overall goal of proving an appropriate version of (1.3) for different entry distributions and models of random matrices.
An important and challenging feature of the more general problem arises in the case of discrete distributions, where the matrix
![]() $B_n$
can become singular with nonzero probability. This singularity event will affect the quantity (1.1) for very small
$B_n$
can become singular with nonzero probability. This singularity event will affect the quantity (1.1) for very small
![]() $\varepsilon $
and thus estimating the probability that
$\varepsilon $
and thus estimating the probability that
![]() $\sigma _{\min }(B_n) = 0$
is a crucial aspect of generalizing (1.3). This is reflected in the famous and influential Spielman–Teng conjecture [Reference Spielman and Teng37] which proposes the bound
$\sigma _{\min }(B_n) = 0$
is a crucial aspect of generalizing (1.3). This is reflected in the famous and influential Spielman–Teng conjecture [Reference Spielman and Teng37] which proposes the bound
where
![]() $B_n$
is a Bernoulli random matrix. Here, this added exponential term “comes from” the singularity probability of
$B_n$
is a Bernoulli random matrix. Here, this added exponential term “comes from” the singularity probability of
![]() $B_n$
. In this direction, a key breakthrough was made by Rudelson [Reference Rudelson30], who proved that if
$B_n$
. In this direction, a key breakthrough was made by Rudelson [Reference Rudelson30], who proved that if
![]() $B_n$
has i.i.d. subgaussian entries, then
$B_n$
has i.i.d. subgaussian entries, then
This result was extended in a series of works [Reference Rudelson and Vershynin32, Reference Tao and Vu40, Reference Tao and Vu44, Reference Vu and Tao49], culminating in the influential work of Rudelson and Vershynin [Reference Rudelson and Vershynin31], who showed the “up-to-constants” version of Spielman-Teng:
where
![]() $B_n$
is a matrix with i.i.d. entries that follow any subgaussian distribution and
$B_n$
is a matrix with i.i.d. entries that follow any subgaussian distribution and
![]() $C,c>0$
depend only on
$C,c>0$
depend only on
![]() $\zeta $
. A key ingredient in the proof of (1.5) is a novel approach to the “inverse Littlewood-Offord problem,” a perspective pioneered by Tao and Vu [Reference Tao and Vu44] (see Section 1.3 for more discussion).
$\zeta $
. A key ingredient in the proof of (1.5) is a novel approach to the “inverse Littlewood-Offord problem,” a perspective pioneered by Tao and Vu [Reference Tao and Vu44] (see Section 1.3 for more discussion).
Another very different approach was taken by Tao and Vu [Reference Tao and Vu41], who showed that the distribution of the least singular value of
![]() $B_n$
is identical to the least singular value of the Gaussian matrix
$B_n$
is identical to the least singular value of the Gaussian matrix
![]() $G_n$
, up to scales of size
$G_n$
, up to scales of size
![]() $n^{-c}$
. In particular, they prove that
$n^{-c}$
. In particular, they prove that
thus resolving the Spielman-Teng conjecture for
![]() $\varepsilon \geqslant n^{-c_0}$
, in a rather strong form. While falling just short of the Spielman-Teng conjecture, the work of Tao and Vu [Reference Tao and Vu41], Rudelson and Vershynin [Reference Rudelson and Vershynin31], and subsequent refinements by Tikhomirov [Reference Tikhomirov45] and Livshyts et al. [Reference Livshyts, Tikhomirov and Vershynin22] (see also [Reference Livshyts21, Reference Rebrova and Tikhomirov29]) leave us with a very strong understanding of the least singular value for i.i.d. matrix models. However, progress on the analogous problem for random symmetric matrices, or Wigner random matrices, has come somewhat more slowly and more recently: In the symmetric case, even proving that
$\varepsilon \geqslant n^{-c_0}$
, in a rather strong form. While falling just short of the Spielman-Teng conjecture, the work of Tao and Vu [Reference Tao and Vu41], Rudelson and Vershynin [Reference Rudelson and Vershynin31], and subsequent refinements by Tikhomirov [Reference Tikhomirov45] and Livshyts et al. [Reference Livshyts, Tikhomirov and Vershynin22] (see also [Reference Livshyts21, Reference Rebrova and Tikhomirov29]) leave us with a very strong understanding of the least singular value for i.i.d. matrix models. However, progress on the analogous problem for random symmetric matrices, or Wigner random matrices, has come somewhat more slowly and more recently: In the symmetric case, even proving that
![]() $A_n$
is nonsingular with probability
$A_n$
is nonsingular with probability
![]() $1-o(1)$
was not resolved until the important 2006 paper of Costello et al. [Reference Costello, Tao and Vu7].
$1-o(1)$
was not resolved until the important 2006 paper of Costello et al. [Reference Costello, Tao and Vu7].
Progress on the symmetric version of Spielman–Teng continued with Nguyen [Reference Nguyen25, Reference Nguyen26] and, independently, Vershynin [Reference Vershynin46]. Nguyen proved that for any
![]() $B>0$
, there exists an
$B>0$
, there exists an
![]() $A>0$
for whichFootnote
1
$A>0$
for whichFootnote
1
Vershynin [Reference Vershynin46] proved that if
![]() $A_n$
is a matrix with subgaussian entries then, for all
$A_n$
is a matrix with subgaussian entries then, for all
![]() $\varepsilon>0$
, we have
$\varepsilon>0$
, we have
for all
![]() $\eta>0$
, where the constants
$\eta>0$
, where the constants
![]() $C_\eta ,c> 0$
may depend on the underlying subgaussian random variable. He went on to conjecture that
$C_\eta ,c> 0$
may depend on the underlying subgaussian random variable. He went on to conjecture that
![]() $\varepsilon $
should replace
$\varepsilon $
should replace
![]() $\varepsilon ^{1/8 - \varepsilon }$
as the correct order of magnitude, and that
$\varepsilon ^{1/8 - \varepsilon }$
as the correct order of magnitude, and that
![]() $e^{-cn}$
should replace
$e^{-cn}$
should replace
![]() $e^{-n^{c}}$
.
$e^{-n^{c}}$
.
After Vershynin, a series of works [Reference Campos, Jenssen, Michelen and Sahasrabudhe3, Reference Campos, Mattos, Morris and Morrison5, Reference Ferber and Jain16, Reference Ferber, Jain, Luh and Samotij17, Reference Jain, Sah and Sawhney19] made progress on singularity probability (i.e., the
![]() $\varepsilon = 0$
case of Vershynin’s conjecture), and we, in [Reference Campos, Jenssen, Michelen and Sahasrabudhe4], ultimately showed that the singularity probability is exponentially small, when
$\varepsilon = 0$
case of Vershynin’s conjecture), and we, in [Reference Campos, Jenssen, Michelen and Sahasrabudhe4], ultimately showed that the singularity probability is exponentially small, when
![]() $A_{i,j}$
is uniform in
$A_{i,j}$
is uniform in
![]() $\{-1,1\}$
:
$\{-1,1\}$
:
which is sharp up to the value of
![]() $c>0$
.
$c>0$
.
However, for general
![]() $\varepsilon $
, the state of the art is due to Jain et al. [Reference Jain, Sah and Sawhney19], who improved on Vershynin’s bound (1.7) by showing
$\varepsilon $
, the state of the art is due to Jain et al. [Reference Jain, Sah and Sawhney19], who improved on Vershynin’s bound (1.7) by showing
under the subgaussian hypothesis on
![]() $A_n$
.
$A_n$
.
For large
![]() $\varepsilon $
, for example,
$\varepsilon $
, for example,
![]() $\varepsilon \geqslant n^{-c}$
, another very different and powerful set of techniques have been developed, which in fact apply more generally to the distribution of other “bulk” eigenvalues and additionally give distributional information on the eigenvalues. The works of Tao and Vu [Reference Tao and Vu40, Reference Tao and Vu42], Erdős, Schlein and Yau [Reference Erdős, Schlein and Yau10, Reference Erdős, Schlein and Yau11, Reference Erdős, Schlein and Yau13], Erdős et al. [Reference Erdős, Ramírez, Schlein, Tao, Vu and Yau9], and specifically, Bourgade et al. [Reference Bourgade, Erdős, Yau and Yin2] tell us that
$\varepsilon \geqslant n^{-c}$
, another very different and powerful set of techniques have been developed, which in fact apply more generally to the distribution of other “bulk” eigenvalues and additionally give distributional information on the eigenvalues. The works of Tao and Vu [Reference Tao and Vu40, Reference Tao and Vu42], Erdős, Schlein and Yau [Reference Erdős, Schlein and Yau10, Reference Erdős, Schlein and Yau11, Reference Erdős, Schlein and Yau13], Erdős et al. [Reference Erdős, Ramírez, Schlein, Tao, Vu and Yau9], and specifically, Bourgade et al. [Reference Bourgade, Erdős, Yau and Yin2] tell us that
thus obtaining the correct dependenceFootnote
2
on
![]() $\varepsilon $
when n is sufficiently large compared to
$\varepsilon $
when n is sufficiently large compared to
![]() $\varepsilon $
. These results are similar in flavor to (1.6) in that they show the distribution of various eigenvalue statistics is closely approximated by the corresponding statistics in the gaussian case. We note, however, that it appears these techniques are limited to these large
$\varepsilon $
. These results are similar in flavor to (1.6) in that they show the distribution of various eigenvalue statistics is closely approximated by the corresponding statistics in the gaussian case. We note, however, that it appears these techniques are limited to these large
![]() $\varepsilon $
and different ideas are required for
$\varepsilon $
and different ideas are required for
![]() $\varepsilon < n^{-C}$
, and certainly for
$\varepsilon < n^{-C}$
, and certainly for
![]() $\varepsilon $
as small as
$\varepsilon $
as small as
![]() $e^{-\Theta (n)}$
.
$e^{-\Theta (n)}$
.
Our main theorem, Theorem 1.1, proves Vershynin’s conjecture and thus proves the optimal dependence on
![]() $\varepsilon $
for all
$\varepsilon $
for all
![]() $\varepsilon> e^{-cn}$
, up to constants.
$\varepsilon> e^{-cn}$
, up to constants.
1.3 Approximate negative correlation
Before we sketch the proof of Theorem 1.1, we highlight a technical theme of this paper: the approximate negative correlation of certain “linear events.” While this is only one of several new ingredients in this paper, we isolate these ideas here, as they seem to be particularly amenable to wider application. We refer the reader to Section 2 for a more complete overview of the new ideas in this paper.
We say that two events
![]() $A,B$
in a probability space are negatively correlated if
$A,B$
in a probability space are negatively correlated if
Here, we state and discuss two approximate negative correlation results: one of which is from our paper [Reference Campos, Jenssen, Michelen and Sahasrabudhe4], but is used in an entirely different context, and one of which is new.
We start by describing the latter result, which says that a “small ball” event is approximately negatively correlated with a large deviation event. This complements our result from [Reference Campos, Jenssen, Michelen and Sahasrabudhe4], which says that two “small ball events,” of different types, are negatively correlated. In particular, we prove something in the spirit of the following inequality, though in a slightly more technical form.
where
![]() $u, v$
are unit vectors and
$u, v$
are unit vectors and
![]() $t,\varepsilon>0$
and
$t,\varepsilon>0$
and
![]() $X = (X_1,\ldots ,X_n)$
with i.i.d. subgaussian random variables with mean
$X = (X_1,\ldots ,X_n)$
with i.i.d. subgaussian random variables with mean
![]() $0$
and variance
$0$
and variance
![]() $1$
.
$1$
.
To state and understand our result, it makes sense to first consider, in isolation, the two events present in (1.9). The easier of the two events is
![]() $\langle X, u \rangle>t$
, which is a large deviation event for which we may apply the essentially sharp and classical inequality (see Chapter 3.4 in [Reference Vershynin47])
$\langle X, u \rangle>t$
, which is a large deviation event for which we may apply the essentially sharp and classical inequality (see Chapter 3.4 in [Reference Vershynin47])
where
![]() $c>0$
is a constant depending only on the distribution of X.
$c>0$
is a constant depending only on the distribution of X.
We now turn to understand the more complicated small-ball event
![]() $|\langle X , v \rangle | \leqslant \varepsilon $
appearing in (1.9). Here, we have a more subtle interaction between v and the distribution of X, and thus we first consider the simplest possible case: when X has i.i.d. standard gaussian entries. Here, one may calculate
$|\langle X , v \rangle | \leqslant \varepsilon $
appearing in (1.9). Here, we have a more subtle interaction between v and the distribution of X, and thus we first consider the simplest possible case: when X has i.i.d. standard gaussian entries. Here, one may calculate
for all
![]() $\varepsilon>0$
, where
$\varepsilon>0$
, where
![]() $C>0$
is an absolute constant. However, as we depart from the case when X is gaussian, a much richer behavior emerges when the vector v admits some “arithmetic structure.” For example, if
$C>0$
is an absolute constant. However, as we depart from the case when X is gaussian, a much richer behavior emerges when the vector v admits some “arithmetic structure.” For example, if
![]() $v = n^{-1/2}(1,\ldots ,1)$
and the
$v = n^{-1/2}(1,\ldots ,1)$
and the
![]() $X_i$
are uniform in
$X_i$
are uniform in
![]() $\{-1,1\}$
, then
$\{-1,1\}$
, then
for any
![]() $0< \varepsilon < n^{-1/2}$
. This, of course, stands in contrast to (1.10) for all
$0< \varepsilon < n^{-1/2}$
. This, of course, stands in contrast to (1.10) for all
![]() $\varepsilon \ll n^{-1/2}$
and suggests that we employ an appropriate measure of the arithmetic structure of v.
$\varepsilon \ll n^{-1/2}$
and suggests that we employ an appropriate measure of the arithmetic structure of v.
For this, we use the notion of the “least common denominator” of a vector, introduced by Rudelson and Vershynin [Reference Rudelson and Vershynin31]. For parameters
![]() $\alpha ,\gamma \in (0,1)$
define the least common denominator (LCD) of
$\alpha ,\gamma \in (0,1)$
define the least common denominator (LCD) of
![]() $v \in \mathbb {R}^n$
to be
$v \in \mathbb {R}^n$
to be
 $$ \begin{align} D_{\alpha,\gamma}(v):=\inf\bigg\{\phi>0:~\|\phi v\|_{\mathbb{T}}\leqslant \min\left\{\gamma\phi\|v\|_2, \sqrt{\alpha n}\right\}\bigg\}, \end{align} $$
$$ \begin{align} D_{\alpha,\gamma}(v):=\inf\bigg\{\phi>0:~\|\phi v\|_{\mathbb{T}}\leqslant \min\left\{\gamma\phi\|v\|_2, \sqrt{\alpha n}\right\}\bigg\}, \end{align} $$
where
![]() $ \| v \|_{\mathbb {T}} : = \mathrm {dist}(v,\mathbb {Z}^n)$
, for all
$ \| v \|_{\mathbb {T}} : = \mathrm {dist}(v,\mathbb {Z}^n)$
, for all
![]() $v \in \mathbb {R}^n$
. What makes this definition useful is the important “inverse Littlewood-Offord theorem” of Rudelson and Vershynin [Reference Rudelson and Vershynin31], which tells us (roughly speaking) that one has (1.10) whenever
$v \in \mathbb {R}^n$
. What makes this definition useful is the important “inverse Littlewood-Offord theorem” of Rudelson and Vershynin [Reference Rudelson and Vershynin31], which tells us (roughly speaking) that one has (1.10) whenever
![]() $D_{\alpha ,\gamma }(v) = \Omega (\varepsilon ^{-1})$
. This notion of least common denominator is inspired by Tao and Vu’s introduction and development of “inverse Littlewood-Offord theory,” which is a collection of results guided by the meta-hypothesis: “If
$D_{\alpha ,\gamma }(v) = \Omega (\varepsilon ^{-1})$
. This notion of least common denominator is inspired by Tao and Vu’s introduction and development of “inverse Littlewood-Offord theory,” which is a collection of results guided by the meta-hypothesis: “If
![]() $\mathbb {P}_X( \langle X,v\rangle = 0 )$
is large then v must have structure.” We refer the reader to the paper of Tao and Vu [Reference Tao and Vu44] and the survey of Nguyen and Vu [Reference Nguyen and Vu28] for more background and history on inverse Littlewood-Offord theory and its role in random matrix theory. We may now state our version of (1.9), which uses
$\mathbb {P}_X( \langle X,v\rangle = 0 )$
is large then v must have structure.” We refer the reader to the paper of Tao and Vu [Reference Tao and Vu44] and the survey of Nguyen and Vu [Reference Nguyen and Vu28] for more background and history on inverse Littlewood-Offord theory and its role in random matrix theory. We may now state our version of (1.9), which uses
![]() $D_{\alpha ,\gamma }(v)^{-1}$
as a proxy for
$D_{\alpha ,\gamma }(v)^{-1}$
as a proxy for
![]() $\mathbb {P}(|\langle X, v \rangle | \leqslant \varepsilon )$
.
$\mathbb {P}(|\langle X, v \rangle | \leqslant \varepsilon )$
.
Theorem 1.4. For
![]() $n \in \mathbb {N}$
,
$n \in \mathbb {N}$
,
![]() $\varepsilon ,t>0$
and
$\varepsilon ,t>0$
and
![]() $\alpha ,\gamma \in (0,1)$
, let
$\alpha ,\gamma \in (0,1)$
, let
![]() $v \in {\mathbb {S}}^{n-1}$
satisfy
$v \in {\mathbb {S}}^{n-1}$
satisfy
![]() $D_{\alpha ,\gamma }(v)> C/\varepsilon $
and let
$D_{\alpha ,\gamma }(v)> C/\varepsilon $
and let
![]() $u \in {\mathbb {S}}^{n-1}$
. Let
$u \in {\mathbb {S}}^{n-1}$
. Let
![]() $\zeta $
be a subgaussian random variable, and let
$\zeta $
be a subgaussian random variable, and let
![]() $X \in \mathbb {R}^n$
be a random vector whose coordinates are i.i.d. copies of
$X \in \mathbb {R}^n$
be a random vector whose coordinates are i.i.d. copies of
![]() $\zeta $
. Then
$\zeta $
. Then
where
![]() $C,c>0$
depend only on
$C,c>0$
depend only on
![]() $\gamma $
and the distribution of
$\gamma $
and the distribution of
![]() $\zeta $
.
$\zeta $
.
In fact, we need a significantly more complicated version of this result (Lemma 5.2), where the small-ball event
![]() $|\langle X,v\rangle | \leqslant \varepsilon $
is replaced with a small-ball event of the form
$|\langle X,v\rangle | \leqslant \varepsilon $
is replaced with a small-ball event of the form
where f is a quadratic polynomial in variables
![]() $X_1,\ldots ,X_n$
. The proof of this result is carried out in Section 5 and is an important aspect of this paper. Theorem 1.4 is stated here to illustrate the general flavor of this result, and is not actually used in this paper. We do provide a proof in Appendix 9 for completeness and to suggest further inquiry into inequalities of the form (1.9).
$X_1,\ldots ,X_n$
. The proof of this result is carried out in Section 5 and is an important aspect of this paper. Theorem 1.4 is stated here to illustrate the general flavor of this result, and is not actually used in this paper. We do provide a proof in Appendix 9 for completeness and to suggest further inquiry into inequalities of the form (1.9).
We now turn to discuss our second approximate negative dependence result, which deals with the intersection of two different small ball events. This was originally proved in our paper [Reference Campos, Jenssen, Michelen and Sahasrabudhe4], but is put to a different use here. This result tells us that the events
are approximately negatively correlated, where
![]() $X = (X_1,\ldots ,X_n)$
is a vector with i.i.d. subgaussian entries and
$X = (X_1,\ldots ,X_n)$
is a vector with i.i.d. subgaussian entries and
![]() $w_1,\ldots ,w_k$
are orthonormal. That is, we prove something in the spirit of
$w_1,\ldots ,w_k$
are orthonormal. That is, we prove something in the spirit of
 $$\begin{align*}\mathbb{P}_X\bigg(\{ |\langle X, v\rangle| \leqslant \varepsilon \} \cap \bigcap_{i=1}^k \{ |\langle X, w_i \rangle| \ll 1 \}\bigg) \lesssim \mathbb{P}_X\big( |\langle X, v \rangle| \leqslant \varepsilon \big)\mathbb{P}_X\bigg( \bigcap_{i=1}^k \{ |\langle X, w_i \rangle| \ll 1 \}\bigg),\end{align*}$$
$$\begin{align*}\mathbb{P}_X\bigg(\{ |\langle X, v\rangle| \leqslant \varepsilon \} \cap \bigcap_{i=1}^k \{ |\langle X, w_i \rangle| \ll 1 \}\bigg) \lesssim \mathbb{P}_X\big( |\langle X, v \rangle| \leqslant \varepsilon \big)\mathbb{P}_X\bigg( \bigcap_{i=1}^k \{ |\langle X, w_i \rangle| \ll 1 \}\bigg),\end{align*}$$
though in a more technical form.
To understand our result, again, it makes sense to consider the two events in (1.12) in isolation. Since we have already discussed the subtle event
![]() $|\langle X, v \rangle | \leqslant \varepsilon $
, we consider the event on the right of (1.12). Returning to the gaussian case, we note that if X has independent standard gaussian entries, then one may compute directly that
$|\langle X, v \rangle | \leqslant \varepsilon $
, we consider the event on the right of (1.12). Returning to the gaussian case, we note that if X has independent standard gaussian entries, then one may compute directly that
by rotational invariance of the gaussian. Here, the generalization to other random variables is not as subtle, and the well-known Hanson-Wright [Reference Hanson and Wright18] inequality tells us that (1.13) holds more generally when X has general i.i.d. subgaussian entries.
Our innovation in this line is our second “approximate negative correlation theorem,” which allows us to control these two events simultaneously. Again, we use
![]() $D_{\alpha ,\gamma }(v)^{-1}$
as a proxy for
$D_{\alpha ,\gamma }(v)^{-1}$
as a proxy for
![]() $\mathbb {P}(|\langle X,v \rangle | \leqslant \varepsilon )$
.
$\mathbb {P}(|\langle X,v \rangle | \leqslant \varepsilon )$
.
Here, for ease of exposition, we state a less general version for
![]() $X = (X_1,\ldots ,X_n) \in \{-1,0,1\}$
with i.i.d. c-lazy coordinates, meaning that
$X = (X_1,\ldots ,X_n) \in \{-1,0,1\}$
with i.i.d. c-lazy coordinates, meaning that
![]() $\mathbb {P}(X_i = 0) \geqslant 1-c$
. Our theorem is stated in full generality in Section 9 (see Theorem 9.2).
$\mathbb {P}(X_i = 0) \geqslant 1-c$
. Our theorem is stated in full generality in Section 9 (see Theorem 9.2).
Theorem 1.5. Let
![]() $\gamma \in (0,1)$
,
$\gamma \in (0,1)$
,
![]() $d \in \mathbb {N}$
,
$d \in \mathbb {N}$
,
![]() $\alpha \in (0,1)$
,
$\alpha \in (0,1)$
,
![]() $0\leqslant k \leqslant c_1 \alpha d$
, and
$0\leqslant k \leqslant c_1 \alpha d$
, and
![]() $\varepsilon \geqslant \exp (-c_1\alpha d)$
. Let
$\varepsilon \geqslant \exp (-c_1\alpha d)$
. Let
![]() $v \in {\mathbb {S}}^{d-1}$
, let
$v \in {\mathbb {S}}^{d-1}$
, let
![]() $w_1,\ldots ,w_k \in {\mathbb {S}}^{d-1}$
be orthogonal, and let W be the matrix with rows
$w_1,\ldots ,w_k \in {\mathbb {S}}^{d-1}$
be orthogonal, and let W be the matrix with rows
![]() $w_1,\ldots ,w_k$
.
$w_1,\ldots ,w_k$
.
If
![]() $X \in \{-1,0,1 \}^d$
is a
$X \in \{-1,0,1 \}^d$
is a
![]() $1/4$
-lazy random vector and
$1/4$
-lazy random vector and
![]() $D_{\alpha ,\gamma }(v)> 16/\varepsilon $
, then
$D_{\alpha ,\gamma }(v)> 16/\varepsilon $
, then
where
![]() $C,c_1,c_2>0$
are constants, depending only on
$C,c_1,c_2>0$
are constants, depending only on
![]() $\gamma $
.
$\gamma $
.
In this paper, we will put Theorem 1.5 to a very different use than to that in [Reference Campos, Jenssen, Michelen and Sahasrabudhe4], where we used it to prove a version of the following statement.
Let
![]() $v \in {\mathbb {S}}^{d-1}$
be a vector on the sphere, and let H be an
$v \in {\mathbb {S}}^{d-1}$
be a vector on the sphere, and let H be an
![]() $n \times d$
random
$n \times d$
random
![]() $\{-1,0,1\}$
-matrix conditioned on the event
$\{-1,0,1\}$
-matrix conditioned on the event
![]() $\|Hv\|_2 \leqslant \varepsilon n^{1/2}$
, for some
$\|Hv\|_2 \leqslant \varepsilon n^{1/2}$
, for some
![]() $\varepsilon> e^{-cn}$
. Here,
$\varepsilon> e^{-cn}$
. Here,
![]() $d = cn$
and
$d = cn$
and
![]() $c>0$
is a sufficiently small constant. Then the probability that the rank of H is
$c>0$
is a sufficiently small constant. Then the probability that the rank of H is
![]() $n-k$
is
$n-k$
is
![]() $\leqslant e^{-ckn}$
.
$\leqslant e^{-ckn}$
.
In this paper, we use (the generalization of) Theorem 1.5 to obtain good bounds on quantities of the form
where B is a fixed matrix with an exceptionally large eigenvalue (possibly as large as
![]() $e^{cn}$
), but is otherwise pseudo-random, meaning (among other things) that the rest of the spectrum does not deviate too much from that of a random matrix. We use Theorem 1.5 to decouple the interaction of X with the largest eigenvector of B, from the interaction of X with the rest of B. We refer the reader to (2.10) in the sketch in Section 2 and to Section 9 for more details.
$e^{cn}$
), but is otherwise pseudo-random, meaning (among other things) that the rest of the spectrum does not deviate too much from that of a random matrix. We use Theorem 1.5 to decouple the interaction of X with the largest eigenvector of B, from the interaction of X with the rest of B. We refer the reader to (2.10) in the sketch in Section 2 and to Section 9 for more details.
The proof of Theorem 9.2 follows closely along the lines of the proof of Theorem 1.5 from [Reference Campos, Jenssen, Michelen and Sahasrabudhe4], requiring only technical modifications and adjustments. So as not to distract from the new ideas of this paper, we have sidelined this proof to the Appendix.
Finally, we note that it may be interesting to investigate these approximate negative correlation results in their own right, and investigate to what extent they can be sharpened.
2 Proof sketch
Here, we sketch the proof of Theorem 1.1. We begin by giving the rough “shape” of the proof, while making a few simplifying assumptions, (2.2) and (2.3). We shall then come to discuss the substantial new ideas of this paper in Section 2.2, where we describe the considerable lengths we must go to in order to remove our simplifying assumptions. Indeed, if one were to only tackle these assumptions using standard tools, one cannot hope for a bound much better than
![]() $\varepsilon ^{1/3}$
in Theorem 1.1 (see Section 2.2.2).
$\varepsilon ^{1/3}$
in Theorem 1.1 (see Section 2.2.2).
2.1 The shape of the proof
Recall that
![]() $A_{n+1}$
is a
$A_{n+1}$
is a
![]() $(n+1)\times (n+1)$
random symmetric matrix with subgaussian entries. Let
$(n+1)\times (n+1)$
random symmetric matrix with subgaussian entries. Let
![]() ${X := X_1,\ldots ,X_{n+1}}$
be the columns of
${X := X_1,\ldots ,X_{n+1}}$
be the columns of
![]() $A_{n+1}$
, let
$A_{n+1}$
, let
and let
![]() $A_n$
be the matrix
$A_n$
be the matrix
![]() $A_{n+1}$
with the first row and column removed. We now use an important observation from Rudelson and Vershynin [Reference Rudelson and Vershynin31] that allows for a geometric perspective on the least singular value problemFootnote
3
$A_{n+1}$
with the first row and column removed. We now use an important observation from Rudelson and Vershynin [Reference Rudelson and Vershynin31] that allows for a geometric perspective on the least singular value problemFootnote
3
Here, our first significant challenge presents itself: X and V are not independent, and thus the event
![]() $\mathrm {dist}(X,V) \leqslant \varepsilon $
is hard to understand directly. However, one can establish a formula for
$\mathrm {dist}(X,V) \leqslant \varepsilon $
is hard to understand directly. However, one can establish a formula for
![]() $\mathrm {dist}(X,V)$
that is a rational function in the vector X with coefficients that depend only on V. This brings us to the useful inequalityFootnote
4
due to Vershynin [Reference Vershynin46],
$\mathrm {dist}(X,V)$
that is a rational function in the vector X with coefficients that depend only on V. This brings us to the useful inequalityFootnote
4
due to Vershynin [Reference Vershynin46],
where we are ignoring the possibility of
![]() $A_n$
being singular for now. We thus arrive at our main technical focus of this paper, bounding the quantity on the right-hand side of (2.1).
$A_n$
being singular for now. We thus arrive at our main technical focus of this paper, bounding the quantity on the right-hand side of (2.1).
We now make our two simplifying assumptions that shall allow us to give the overall shape of our proof without any added complexity. We shall then layer-on further complexities as we discuss how to remove these assumptions.
As a first simplifying assumption, let us assume that the collection of X that dominates the probability at (2.1) satisfies
This is not, at first blush, an unreasonable assumption to make as
![]() $\mathbb {E}_X\, \|A_n^{-1}X\|_2^2 = \|A_n^{-1}\|_{\mathrm {HS}}^2 $
. Indeed, the Hanson-Wright inequality tells us that
$\mathbb {E}_X\, \|A_n^{-1}X\|_2^2 = \|A_n^{-1}\|_{\mathrm {HS}}^2 $
. Indeed, the Hanson-Wright inequality tells us that
![]() $ \|A_n^{-1}X\|_2 $
is concentrated about its mean, for all reasonable
$ \|A_n^{-1}X\|_2 $
is concentrated about its mean, for all reasonable
![]() $A_n^{-1}$
. However, as we will see, this concentration is not strong enough for us here.
$A_n^{-1}$
. However, as we will see, this concentration is not strong enough for us here.
As a second assumption, we assume that the relevant matrices
![]() $A_n$
in the right-hand side of (2.1) satisfy
$A_n$
in the right-hand side of (2.1) satisfy
This turns out to be a very delicate assumption, as we will soon see, but is not entirely unreasonable to make for the moment: for example, we have
![]() $\|A_n^{-1}\|_{\mathrm {HS}} = \Theta _{\delta }(n^{1/2})$
with probability
$\|A_n^{-1}\|_{\mathrm {HS}} = \Theta _{\delta }(n^{1/2})$
with probability
![]() $1-\delta $
. This, for example, follows from Vershynin’s theorem [Reference Vershynin46] along with Corollary 8.4, which is based on the work of [Reference Erdős, Schlein and Yau13].
$1-\delta $
. This, for example, follows from Vershynin’s theorem [Reference Vershynin46] along with Corollary 8.4, which is based on the work of [Reference Erdős, Schlein and Yau13].
With these assumptions, we return to (2.1) and obverse our task has reduced to proving
for all
![]() $\varepsilon> e^{-cn}$
, where we have written
$\varepsilon> e^{-cn}$
, where we have written
![]() $A^{-1} = A_{n}^{-1}$
and think of
$A^{-1} = A_{n}^{-1}$
and think of
![]() $A^{-1}$
as a fixed (pseudo-random) matrix.
$A^{-1}$
as a fixed (pseudo-random) matrix.
We observe, for a general fixed matrix
![]() $A^{-1}$
, there is no hope in proving such an inequality: Indeed, if
$A^{-1}$
, there is no hope in proving such an inequality: Indeed, if
![]() $A^{-1} = n^{-1/2}J$
, where J is the all-ones matrix, then the left-hand side of (2.4) is
$A^{-1} = n^{-1/2}J$
, where J is the all-ones matrix, then the left-hand side of (2.4) is
![]() $\geqslant cn^{-1/2}$
for all
$\geqslant cn^{-1/2}$
for all
![]() $\varepsilon>0$
, falling vastly short of our desired (2.4).
$\varepsilon>0$
, falling vastly short of our desired (2.4).
Thus, we need to introduce a collection of fairly strong “quasi-randomness properties” of A that hold with, probably
![]() $1-e^{-cn}$
. These will ensure that
$1-e^{-cn}$
. These will ensure that
![]() $A^{-1}$
is sufficiently “non-structured” to make our goal (2.4) possible. The most important and difficult of these quasi-randomness conditions is to show that the eigenvectors v of A satisfy
$A^{-1}$
is sufficiently “non-structured” to make our goal (2.4) possible. The most important and difficult of these quasi-randomness conditions is to show that the eigenvectors v of A satisfy
for some appropriate
![]() $\alpha ,\gamma $
, where
$\alpha ,\gamma $
, where
![]() $D_{\alpha ,\gamma }(v)$
is the least common denominator of v defined at (1.11). Roughly, this means that none of the eigenvectors of A “correlate” with a rescaled copy of the integer lattice
$D_{\alpha ,\gamma }(v)$
is the least common denominator of v defined at (1.11). Roughly, this means that none of the eigenvectors of A “correlate” with a rescaled copy of the integer lattice
![]() $t\mathbb {Z}^n$
, for any
$t\mathbb {Z}^n$
, for any
![]() $e^{-cn} \leqslant t \leqslant 1$
.
$e^{-cn} \leqslant t \leqslant 1$
.
To prove that these quasi-randomness properties hold with probability
![]() $1-e^{-cn}$
is a difficult task and depends fundamentally on the ideas in our previous paper [Reference Campos, Jenssen, Michelen and Sahasrabudhe4]. Since we don’t want these ideas to distract from the new ideas in this paper, we have opted to carry out the details in the Appendix. With these quasi-randomness conditions in tow, we can return to (2.4) and apply Esseen’s inequality to bound the left-hand side of (2.4) in terms of the characteristic function
$1-e^{-cn}$
is a difficult task and depends fundamentally on the ideas in our previous paper [Reference Campos, Jenssen, Michelen and Sahasrabudhe4]. Since we don’t want these ideas to distract from the new ideas in this paper, we have opted to carry out the details in the Appendix. With these quasi-randomness conditions in tow, we can return to (2.4) and apply Esseen’s inequality to bound the left-hand side of (2.4) in terms of the characteristic function
![]() ${\varphi }({\theta })$
of the random variable
${\varphi }({\theta })$
of the random variable
![]() $\langle A^{-1}X, X \rangle $
,
$\langle A^{-1}X, X \rangle $
,
 $$\begin{align*}\min_r \mathbb{P}_{X}\big( |\langle A^{-1}X, X \rangle - r| \leqslant \varepsilon n^{1/2} \big) \lesssim \varepsilon \int_{-1/\varepsilon}^{1/\varepsilon} |{\varphi}({\theta})| \, d\theta. \end{align*}$$
$$\begin{align*}\min_r \mathbb{P}_{X}\big( |\langle A^{-1}X, X \rangle - r| \leqslant \varepsilon n^{1/2} \big) \lesssim \varepsilon \int_{-1/\varepsilon}^{1/\varepsilon} |{\varphi}({\theta})| \, d\theta. \end{align*}$$
While this maneuver has been quite successful in work on characteristic functions for (linear) sums of independent random variables, the characteristic function of such quadratic functions has proved to be a more elusive object. For example, even the analogue of the Littlewood-Offord theorem is not fully understood in the quadratic case [Reference Costello6, Reference Meka, Nguyen and Vu23]. Here, we appeal to our quasi-random conditions to avoid some of the traditional difficulties: we use an application of Jensen’s inequality to decouple the quadratic form and bound
![]() ${\varphi }({\theta })$
pointwise in terms of an average over a related collection of characteristic functions of linear sums of independent random variables
${\varphi }({\theta })$
pointwise in terms of an average over a related collection of characteristic functions of linear sums of independent random variables
where Y is a random vector with i.i.d. entries and
![]() ${\varphi }(v; {\theta })$
denotes the characteristic function of the sum
${\varphi }(v; {\theta })$
denotes the characteristic function of the sum
![]() $\sum _{i} v_iX_i$
, where
$\sum _{i} v_iX_i$
, where
![]() $X_i$
are i.i.d. distributed according to the original distribution
$X_i$
are i.i.d. distributed according to the original distribution
![]() $\zeta $
. We can then use our pseudo-random conditions on A to bound
$\zeta $
. We can then use our pseudo-random conditions on A to bound
for all but exponentially few Y, allowing us to show
 $$\begin{align*}\int_{-1/\varepsilon}^{1/\varepsilon} |{\varphi}({\theta})| \, d\theta \leqslant \int_{-1/\varepsilon}^{1/\varepsilon} \left[ \mathbb{E}_{Y} |{\varphi}(A^{-1}Y; {\theta})| \right]^{1/2} \leqslant \int_{-1/\varepsilon}^{1/\varepsilon} \left(\exp\left( -c{\theta}^{2} \right) + e^{-cn}\right)\, d{\theta} = O(1) \end{align*}$$
$$\begin{align*}\int_{-1/\varepsilon}^{1/\varepsilon} |{\varphi}({\theta})| \, d\theta \leqslant \int_{-1/\varepsilon}^{1/\varepsilon} \left[ \mathbb{E}_{Y} |{\varphi}(A^{-1}Y; {\theta})| \right]^{1/2} \leqslant \int_{-1/\varepsilon}^{1/\varepsilon} \left(\exp\left( -c{\theta}^{2} \right) + e^{-cn}\right)\, d{\theta} = O(1) \end{align*}$$
and thus completing the proof, up to our simplifying assumptions.
2.2 Removing the simplifying assumptions
While this is a good story to work with, the challenge starts when we turn to remove our simplifying assumptions (2.2), (2.3). We also note that if one only applies standard methods to remove these assumptions, then one would get stuck at the “base case” outlined below. We start by discussing how to remove the simplifying assumption (2.3), whose resolution governs the overall structure of the paper.
2.2.1 Removing the assumption (2.3)
What is most concerning about making the assumption
![]() $\|A_n^{-1}\|_{\mathrm {HS}} \approx n^{-1/2}$
is that it is, in a sense, circular: If we assume the modest-looking hypothesis
$\|A_n^{-1}\|_{\mathrm {HS}} \approx n^{-1/2}$
is that it is, in a sense, circular: If we assume the modest-looking hypothesis
![]() $\mathbb {E}\, \|A^{-1}\|_{\mathrm {HS}} \lesssim n^{1/2}$
, we would be able to deduce
$\mathbb {E}\, \|A^{-1}\|_{\mathrm {HS}} \lesssim n^{1/2}$
, we would be able to deduce
by Markov. In other words, showing that
![]() $\|A^{-1}\|_{\mathrm {HS}}$
is concentrated about
$\|A^{-1}\|_{\mathrm {HS}}$
is concentrated about
![]() $n^{-1/2}$
(in the above sense) actually implies Theorem 1.1. However, this is not as worrisome as it appears at first. Indeed, if we are trying to prove Theorem 1.1 for
$n^{-1/2}$
(in the above sense) actually implies Theorem 1.1. However, this is not as worrisome as it appears at first. Indeed, if we are trying to prove Theorem 1.1 for
![]() $(n+1) \times (n+1)$
matrices using the above outline, we only need to control the Hilbert-Schmidt norm of the inverse of the minor
$(n+1) \times (n+1)$
matrices using the above outline, we only need to control the Hilbert-Schmidt norm of the inverse of the minor
![]() $A_n^{-1}$
. This suggests an inductive or (as we use) an iterative “bootstrapping argument” to successively improve the bound. Thus, in effect, we look to prove
$A_n^{-1}$
. This suggests an inductive or (as we use) an iterative “bootstrapping argument” to successively improve the bound. Thus, in effect, we look to prove
for successively larger
![]() $\alpha \in (0,1]$
. Note, we have to cut out the event of A being singular from our expectation, as this event has nonzero probability.
$\alpha \in (0,1]$
. Note, we have to cut out the event of A being singular from our expectation, as this event has nonzero probability.
2.2.2 Base case
In the first step of our iteration, we prove a “base case” of
without the assumption (2.3) which is equivalent to
To prove this “base case,” we upgrade (2.1) to
 $$ \begin{align} \mathbb{P}\left(\sigma_{\min}(A_{n+1}) \leqslant \varepsilon n^{-1/2} \right) \lesssim \varepsilon + \sup_{r \in \mathbb{R}}\, \mathbb{P}\left(\frac{|\langle A_n^{-1}X, X\rangle - r|}{ \|A_n^{-1} X \|_2} \leqslant C \varepsilon , \|A_{n}^{-1}\|_{\mathrm{HS}} \leqslant \frac{n^{1/2}}{\varepsilon} \right) \,.\end{align} $$
$$ \begin{align} \mathbb{P}\left(\sigma_{\min}(A_{n+1}) \leqslant \varepsilon n^{-1/2} \right) \lesssim \varepsilon + \sup_{r \in \mathbb{R}}\, \mathbb{P}\left(\frac{|\langle A_n^{-1}X, X\rangle - r|}{ \|A_n^{-1} X \|_2} \leqslant C \varepsilon , \|A_{n}^{-1}\|_{\mathrm{HS}} \leqslant \frac{n^{1/2}}{\varepsilon} \right) \,.\end{align} $$
In other words, we can intersect with the event
at a loss of only
![]() $C\varepsilon $
in probability.
$C\varepsilon $
in probability.
We then push through the proof outlined in Section 2.1 to obtain our initial weak bound of (2.5). For this, we first use the Hanson-Wright inequality to give a weak version of (2.2), and then use (2.7) as a weak version of our assumption (2.3). We note that this base step (2.5) already improves the best known bounds on the least singular value problem for random symmetric matrices.
2.2.3 Bootstrapping
To improve on this bound, we use a “bootstrapping” lemma which, after applying it three times, allows us to improve (2.5) to the near-optimal result
Proving this bootstrapping lemma essentially reduces to the problem of getting good estimates on
where A is a matrix with
![]() $\|A^{-1}\|_{op} = \delta ^{-1}$
and
$\|A^{-1}\|_{op} = \delta ^{-1}$
and
![]() $ \delta \in (\varepsilon , c n^{-1/2})$
but is “otherwise pseudo-random.” Here, we require two additional ingredients.
$ \delta \in (\varepsilon , c n^{-1/2})$
but is “otherwise pseudo-random.” Here, we require two additional ingredients.
To start unpacking (2.9), we use that
![]() $\|A^{-1}\|_{op} = \delta ^{-1}$
to see that if v is a unit eigenvector corresponding to the largest eigenvalue of
$\|A^{-1}\|_{op} = \delta ^{-1}$
to see that if v is a unit eigenvector corresponding to the largest eigenvalue of
![]() $A^{-1}$
, then
$A^{-1}$
, then
While this leads to a decent first bound of
![]() $O(\delta s)$
on the probability (2.9) (after using the quasi-randomness properties of A), however, this is not enough for our purposes, and in fact, we have to use the additional information that X must also have small inner product with many other eigenvectors of A (assuming s is sufficiently small). Working along these lines, we show that (2.9) is bounded above by
$O(\delta s)$
on the probability (2.9) (after using the quasi-randomness properties of A), however, this is not enough for our purposes, and in fact, we have to use the additional information that X must also have small inner product with many other eigenvectors of A (assuming s is sufficiently small). Working along these lines, we show that (2.9) is bounded above by
 $$ \begin{align} \mathbb{P}_X\bigg( |\langle X, v_1 \rangle| \leqslant s \delta \text{ and } |\langle X, v_i\rangle| \leqslant \sigma_i s \text{ for all } i =2,\dots, n-1 \bigg), \end{align} $$
$$ \begin{align} \mathbb{P}_X\bigg( |\langle X, v_1 \rangle| \leqslant s \delta \text{ and } |\langle X, v_i\rangle| \leqslant \sigma_i s \text{ for all } i =2,\dots, n-1 \bigg), \end{align} $$
where
![]() $w_i$
is a unit eigenvector of A corresponding to the singular value
$w_i$
is a unit eigenvector of A corresponding to the singular value
![]() $\sigma _i = \sigma _i(A)$
. Now, appealing to the quasi-random properties of the eigenvectors of
$\sigma _i = \sigma _i(A)$
. Now, appealing to the quasi-random properties of the eigenvectors of
![]() $A^{-1}$
, we may apply our approximate negative correlation theorem (Theorem 1.5) to see that (2.10) is at most
$A^{-1}$
, we may apply our approximate negative correlation theorem (Theorem 1.5) to see that (2.10) is at most
where
![]() $c>0$
is a constant and
$c>0$
is a constant and
![]() $N_{A}(a,b)$
denotes the number of eigenvalues of the matrix A in the interval
$N_{A}(a,b)$
denotes the number of eigenvalues of the matrix A in the interval
![]() $(a,b)$
. The first
$(a,b)$
. The first
![]() $O(\delta s)$
factor comes from the event
$O(\delta s)$
factor comes from the event
![]() $|\langle X, v_1 \rangle | \leqslant s\delta $
, and the second factor comes from approximating
$|\langle X, v_1 \rangle | \leqslant s\delta $
, and the second factor comes from approximating
This bound is now sufficiently strong for our purposes, provided the spectrum of A adheres sufficiently closely to the typical spectrum of
![]() $A_n$
. This now leads us to understand the rest of the spectrum of
$A_n$
. This now leads us to understand the rest of the spectrum of
![]() $A_n$
and, in particular, the next smallest singular values
$A_n$
and, in particular, the next smallest singular values
![]() $\sigma _{n-1},\sigma _{n-2},\ldots $
.
$\sigma _{n-1},\sigma _{n-2},\ldots $
.
Now, this might seem like a step in the wrong direction, as we are now led to understand the behavior of many singular values and not just the smallest. However, this “loss” is outweighed by the fact that we need only to understand these eigenvalues on scales of size
![]() $\Omega ( n^{-1/2} )$
, which is now well understood due to the important work of Erdős et al. [Reference Erdős, Schlein and Yau13].
$\Omega ( n^{-1/2} )$
, which is now well understood due to the important work of Erdős et al. [Reference Erdős, Schlein and Yau13].
These results ultimately allow us to derive sufficiently strong results on quantities of the form (2.9), which, in turn, allow us to prove our “bootstrapping lemma.” We then use this lemma to prove the near-optimal result
2.2.4 Removing the assumption (2.2) and the last jump to Theorem 1.1
We now turn to discuss how to remove our simplifying assumption (2.2), made above, which will allow us to close the gap between (2.13) and Theorem 1.1.
To achieve this, we need to consider how
![]() $\|A^{-1}X\|_2$
varies about
$\|A^{-1}X\|_2$
varies about
![]() $\|A^{-1}\|_{\mathrm {HS}}$
, where we are, again, thinking of
$\|A^{-1}\|_{\mathrm {HS}}$
, where we are, again, thinking of
![]() $A^{-1} = A_{n}^{-1}$
as a sufficiently quasi-random matrix. Now, the Hanson-Wright inequality tells us that, indeed,
$A^{-1} = A_{n}^{-1}$
as a sufficiently quasi-random matrix. Now, the Hanson-Wright inequality tells us that, indeed,
![]() $\|A^{-1}X \|_2$
is concentrated about
$\|A^{-1}X \|_2$
is concentrated about
![]() $\|A^{-1} \|_{\mathrm {HS}}$
, on a scale
$\|A^{-1} \|_{\mathrm {HS}}$
, on a scale
![]() $ \lesssim \|A^{-1}\|_{op}$
. While this is certainly useful for us, it is far from enough to prove Theorem 1.1. For this, we need to rule out any “macroscopic” correlation between the events
$ \lesssim \|A^{-1}\|_{op}$
. While this is certainly useful for us, it is far from enough to prove Theorem 1.1. For this, we need to rule out any “macroscopic” correlation between the events
for all
![]() $K> 0$
. Our first step toward understanding (2.14) is to replace the quadratic large deviation event
$K> 0$
. Our first step toward understanding (2.14) is to replace the quadratic large deviation event
![]() $\|A^{-1}X\|_2> K\|A^{-1}\|_{\mathrm {HS}} $
with a collection of linear large deviation events:
$\|A^{-1}X\|_2> K\|A^{-1}\|_{\mathrm {HS}} $
with a collection of linear large deviation events:
where
![]() $w_n,w_{n-1},\ldots ,w_1$
are the eigenvectors of A corresponding to singular values
$w_n,w_{n-1},\ldots ,w_1$
are the eigenvectors of A corresponding to singular values
![]() $\sigma _n \leqslant \sigma _{n-1} \leqslant \ldots \leqslant \sigma _1$
, respectively, and the
$\sigma _n \leqslant \sigma _{n-1} \leqslant \ldots \leqslant \sigma _1$
, respectively, and the
![]() $\log (i+1)$
factor should be seen as a weight function that assigns more weight to the smaller singular values.
$\log (i+1)$
factor should be seen as a weight function that assigns more weight to the smaller singular values.
Interestingly, we run into a similar obstacle as before: If the “bulk” of the spectrum of
![]() $A^{-1}$
is sufficiently erratic, this replacement step will be too lossy for our purposes. Thus, we are led to prove another result, showing that we may assume that the spectrum of
$A^{-1}$
is sufficiently erratic, this replacement step will be too lossy for our purposes. Thus, we are led to prove another result, showing that we may assume that the spectrum of
![]() $A^{-1}$
adheres sufficiently to the typical spectrum of
$A^{-1}$
adheres sufficiently to the typical spectrum of
![]() $A_n$
. This reduces to proving
$A_n$
. This reduces to proving
 $$\begin{align*}\mathbb{E}_{A_n}\, \left[\frac{ \sum_{i=1}^n \sigma_{n-i-1}^{-2} (\log i )^2}{ \sum_{i=1}^n \sigma_{n-i-1}^{-2} } \right] = O(1) ,\end{align*}$$
$$\begin{align*}\mathbb{E}_{A_n}\, \left[\frac{ \sum_{i=1}^n \sigma_{n-i-1}^{-2} (\log i )^2}{ \sum_{i=1}^n \sigma_{n-i-1}^{-2} } \right] = O(1) ,\end{align*}$$
where the left-hand side is a statistic which measures the degree of distortion of the smallest singular values of
![]() $A_n$
. To prove this, we again lean on the work of Erdős et al. [Reference Erdős, Schlein and Yau13].
$A_n$
. To prove this, we again lean on the work of Erdős et al. [Reference Erdős, Schlein and Yau13].
Thus, we have reduced the task of proving the approximate independence of the events at (2.14) to proving the approximate independence of the collection of events
This is something, it turns out, that we can handle on the Fourier side by using a quadratic analogue of our negative correlation inequality, Theorem 1.4. The idea, here, is to prove an Esseen-type bound of the form
 $$ \begin{align} \mathbb{P}( |\langle A^{-1} X, X \rangle - t| < \delta, \langle X,u \rangle \geqslant s ) \lesssim \delta e^{-s}\int_{-1/\delta}^{1/\delta} \left|\mathbb{E} e^{2\pi i \theta \langle A^{-1} X, X \rangle + \langle X,u \rangle }\right|\,d\theta\,.\end{align} $$
$$ \begin{align} \mathbb{P}( |\langle A^{-1} X, X \rangle - t| < \delta, \langle X,u \rangle \geqslant s ) \lesssim \delta e^{-s}\int_{-1/\delta}^{1/\delta} \left|\mathbb{E} e^{2\pi i \theta \langle A^{-1} X, X \rangle + \langle X,u \rangle }\right|\,d\theta\,.\end{align} $$
Which introduces this extra “exponential tilt” to the characteristic function. From here, one can carry out the plan sketched in Section 2.1 with this more complicated version of Esseen, then integrate over s to upgrade (2.13) to Theorem 1.1.
2.3 Outline of the rest of the paper
In the next short section, we introduce some key definitions, notation, and preliminaries that we use throughout the paper. In Section 4, we establish a collection of crucial quasi-randomness properties that hold for the random symmetric matrix
![]() $A_n$
with probability
$A_n$
with probability
![]() $1-e^{-\Omega (n)}$
. We shall condition on these events for most of the paper. In Section 5, we detail our Fourier decoupling argument and establish an inequality of the form (2.15). This allows us to prove our new approximate negative correlation result Lemma 5.2. In Section 6, we prepare the ground for our iterative argument by establishing (2.6), thereby switching our focus to the study of the quadratic form
$1-e^{-\Omega (n)}$
. We shall condition on these events for most of the paper. In Section 5, we detail our Fourier decoupling argument and establish an inequality of the form (2.15). This allows us to prove our new approximate negative correlation result Lemma 5.2. In Section 6, we prepare the ground for our iterative argument by establishing (2.6), thereby switching our focus to the study of the quadratic form
![]() $\langle A_n^{-1}X, X\rangle $
. In Section 7, we prove Theorem 1.2 and Theorem 1.3, which tell us that the eigenvalues of A cannot “crowd” small intervals. In Section 8, we establish regularity properties for the bulk of the spectrum of
$\langle A_n^{-1}X, X\rangle $
. In Section 7, we prove Theorem 1.2 and Theorem 1.3, which tell us that the eigenvalues of A cannot “crowd” small intervals. In Section 8, we establish regularity properties for the bulk of the spectrum of
![]() $A^{-1}$
. In Section 9, we deploy the approximate negative correlation result (Theorem 1.5) in order to carry out the portion of the proof sketched between (2.9) and (2.12). In Section 10, we establish our base step (2.5) and bootstrap this to prove the near optimal bound (2.13). In the final section, Section 11, we complete the proof of our main Theorem 1.1.
$A^{-1}$
. In Section 9, we deploy the approximate negative correlation result (Theorem 1.5) in order to carry out the portion of the proof sketched between (2.9) and (2.12). In Section 10, we establish our base step (2.5) and bootstrap this to prove the near optimal bound (2.13). In the final section, Section 11, we complete the proof of our main Theorem 1.1.
3 Key definitions and preliminaries
We first need a few notions out of the way, which are related to our paper [Reference Campos, Jenssen, Michelen and Sahasrabudhe4] on the singularity of random symmetric matrices.
3.1 Subgaussian and matrix definitions
Throughout,
![]() $\zeta $
will be a mean
$\zeta $
will be a mean
![]() $0$
, variance
$0$
, variance
![]() $1$
random variable. We define the subgaussian moment of
$1$
random variable. We define the subgaussian moment of
![]() $\zeta $
to be
$\zeta $
to be
A mean
![]() $0$
, variance
$0$
, variance
![]() $1$
random variable is said to be subgaussian if
$1$
random variable is said to be subgaussian if
![]() $ \| \zeta \|_{\psi _2}$
is finite. We define
$ \| \zeta \|_{\psi _2}$
is finite. We define
![]() $\Gamma $
to be the set of subgaussian random variables and, for
$\Gamma $
to be the set of subgaussian random variables and, for
![]() $B>0$
, we define
$B>0$
, we define
![]() $\Gamma _B \subseteq \Gamma $
to be a subset of
$\Gamma _B \subseteq \Gamma $
to be a subset of
![]() $\zeta $
with
$\zeta $
with
![]() $\| \zeta \|_{\psi _2} \leqslant B$
.
$\| \zeta \|_{\psi _2} \leqslant B$
.
For
![]() $\zeta \in \Gamma $
, define
$\zeta \in \Gamma $
, define
![]() $\mathrm {Sym\,}_{n}(\zeta )$
to be the probability space on
$\mathrm {Sym\,}_{n}(\zeta )$
to be the probability space on
![]() $n \times n$
symmetric matrices A for which
$n \times n$
symmetric matrices A for which
![]() $(A_{i,j})_{i \geqslant j}$
are independent and distributed according to
$(A_{i,j})_{i \geqslant j}$
are independent and distributed according to
![]() $\zeta $
. Similarly, we write
$\zeta $
. Similarly, we write
![]() $X \sim \mathrm {Col\,}_n(\zeta )$
if
$X \sim \mathrm {Col\,}_n(\zeta )$
if
![]() $X \in \mathbb {R}^n$
is a random vector whose coordinates are i.i.d. copies of
$X \in \mathbb {R}^n$
is a random vector whose coordinates are i.i.d. copies of
![]() $\zeta $
.
$\zeta $
.
We shall think of the spaces
![]() $\{\mathrm {Sym\,}_n(\zeta )\}_{n}$
as coupled in the natural way: The matrix
$\{\mathrm {Sym\,}_n(\zeta )\}_{n}$
as coupled in the natural way: The matrix
![]() $A_{n+1} \sim \mathrm {Sym\,}_{n+1}(\zeta )$
can be sampled by first sampling
$A_{n+1} \sim \mathrm {Sym\,}_{n+1}(\zeta )$
can be sampled by first sampling
![]() $A_n \sim \mathrm {Sym\,}_n(\zeta )$
, which we think of as the principal minor
$A_n \sim \mathrm {Sym\,}_n(\zeta )$
, which we think of as the principal minor
![]() $(A_{n+1})_{[2,n+1] \times [2,n+1]}$
, and then generating the first row and column of
$(A_{n+1})_{[2,n+1] \times [2,n+1]}$
, and then generating the first row and column of
![]() $A_{n+1}$
by generating a random column
$A_{n+1}$
by generating a random column
![]() $X \sim \mathrm {Col\,}_n(\zeta )$
. In fact, it will make sense to work with a random
$X \sim \mathrm {Col\,}_n(\zeta )$
. In fact, it will make sense to work with a random
![]() $(n+1)\times (n+1)$
matrix, which we call
$(n+1)\times (n+1)$
matrix, which we call
![]() $A_{n+1}$
throughout. This is justified, as much of the work is done with the principal minor
$A_{n+1}$
throughout. This is justified, as much of the work is done with the principal minor
![]() $A_n$
of
$A_n$
of
![]() $A_{n+1}$
, due to the bound (2.1) as well as Lemma 6.1.
$A_{n+1}$
, due to the bound (2.1) as well as Lemma 6.1.
3.2 Compressible vectors
We shall require the now-standard notions of compressible vectors, as defined by Rudelson and Vershynin [Reference Rudelson and Vershynin31].
For parameters
![]() $\rho ,\delta \in (0,1)$
, we define the set of compressible vectors
$\rho ,\delta \in (0,1)$
, we define the set of compressible vectors
![]() $\mathrm {Comp\,}(\delta ,\rho )$
to be the set of vectors in
$\mathrm {Comp\,}(\delta ,\rho )$
to be the set of vectors in
![]() ${\mathbb {S}}^{n-1}$
that are distance at most
${\mathbb {S}}^{n-1}$
that are distance at most
![]() $\rho $
from a vector supported on at most
$\rho $
from a vector supported on at most
![]() $\delta n$
coordinates. We then define the set of incompressible vectors to be all other unit vectors, that is
$\delta n$
coordinates. We then define the set of incompressible vectors to be all other unit vectors, that is
![]() $\mathrm {Incomp\,}(\delta ,\rho ) := {\mathbb {S}}^{n-1} \setminus \mathrm {Comp\,}(\delta ,\rho ).$
The following basic fact about incompressible vectors from [Reference Rudelson and Vershynin31] will be useful throughout:
$\mathrm {Incomp\,}(\delta ,\rho ) := {\mathbb {S}}^{n-1} \setminus \mathrm {Comp\,}(\delta ,\rho ).$
The following basic fact about incompressible vectors from [Reference Rudelson and Vershynin31] will be useful throughout:
Fact 3.1. For each
![]() $\delta ,\rho \in (0,1)$
, there is a constant
$\delta ,\rho \in (0,1)$
, there is a constant
![]() $c_{\rho ,\delta } \in (0,1)$
, so that for all
$c_{\rho ,\delta } \in (0,1)$
, so that for all
![]() $v \in \mathrm {Incomp\,}(\delta ,\rho )$
, we have that
$v \in \mathrm {Incomp\,}(\delta ,\rho )$
, we have that
![]() $|v_j|n^{1/2} \in [ c_{\rho ,\delta }, c_{\rho ,\delta }^{-1}]$
for at least
$|v_j|n^{1/2} \in [ c_{\rho ,\delta }, c_{\rho ,\delta }^{-1}]$
for at least
![]() $c_{\rho ,\delta } n$
values of j.
$c_{\rho ,\delta } n$
values of j.
Fact 3.1 assures us that for each incompressible vector, we can find a large subvector that is “flat.” Using the work of Vershynin [Reference Vershynin46], we will safely be able to ignore compressible vectors. In particular, [Reference Vershynin46, Proposition 4.2] implies the following lemma. We refer the reader to Appendix XII for details.
Lemma 3.2. For
![]() $B>0$
and
$B>0$
and
![]() $\zeta \in \Gamma _B$
, let
$\zeta \in \Gamma _B$
, let
![]() $A \sim \mathrm {Sym\,}_n(\zeta )$
. Then there exist constants
$A \sim \mathrm {Sym\,}_n(\zeta )$
. Then there exist constants
![]() $\rho ,\delta ,c \in (0,1) $
, depending only on B, so that
$\rho ,\delta ,c \in (0,1) $
, depending only on B, so that
and
The first statement says, roughly, that
![]() $A^{-1} u$
is incompressible for each fixed u; the second states that all unit eigenvectors are incompressible.
$A^{-1} u$
is incompressible for each fixed u; the second states that all unit eigenvectors are incompressible.
Remark 3.3 (Choice of constants,
 $\rho ,\delta ,c_{\rho ,\delta }$
).
$\rho ,\delta ,c_{\rho ,\delta }$
).
Throughout, we let
![]() $\rho ,\delta $
denote the constants guaranteed by Lemma 3.2 and
$\rho ,\delta $
denote the constants guaranteed by Lemma 3.2 and
![]() $c_{\rho ,\delta }$
the corresponding constant from Fact 3.1. These constants shall appear throughout the paper and shall always be considered as fixed.
$c_{\rho ,\delta }$
the corresponding constant from Fact 3.1. These constants shall appear throughout the paper and shall always be considered as fixed.
Lemma 3.2 follows easily from [Reference Vershynin46, Proposition 4.2] with a simple net argument.
3.3 Notation
We quickly define some notation. For a random variable X, we use the notation
![]() $\mathbb {E}_X$
for the expectation with respect to X and we use the notation
$\mathbb {E}_X$
for the expectation with respect to X and we use the notation
![]() $\mathbb {P}_X$
analogously. For an event
$\mathbb {P}_X$
analogously. For an event
![]() $\mathcal {E}$
, we write
$\mathcal {E}$
, we write
![]() ${\mathbf {1}}_{\mathcal {E}}$
or
${\mathbf {1}}_{\mathcal {E}}$
or
![]() ${\mathbf {1}} \{ \mathcal {E}\}$
for the indicator function of the event
${\mathbf {1}} \{ \mathcal {E}\}$
for the indicator function of the event
![]() $\mathcal {E}$
. We write
$\mathcal {E}$
. We write
![]() $\mathbb {E}^{\mathcal {E}}$
to be the expectation defined by
$\mathbb {E}^{\mathcal {E}}$
to be the expectation defined by
![]() $\mathbb {E}^{\mathcal {E}}[\, \cdot \, ] = \mathbb {E}[\, \cdot \, {\mathbf {1}}_{\mathcal {E}}]$
. For a vector
$\mathbb {E}^{\mathcal {E}}[\, \cdot \, ] = \mathbb {E}[\, \cdot \, {\mathbf {1}}_{\mathcal {E}}]$
. For a vector
![]() $v \in \mathbb {R}^{n}$
and
$v \in \mathbb {R}^{n}$
and
![]() $J \subset [n]$
, we write
$J \subset [n]$
, we write
![]() $v_J$
for the vector whose ith coordinate is
$v_J$
for the vector whose ith coordinate is
![]() $v_i$
if
$v_i$
if
![]() $i \in J$
and
$i \in J$
and
![]() $0$
otherwise.
$0$
otherwise.
We shall use the notation
![]() $X \lesssim Y$
to indicate that there exists a constant
$X \lesssim Y$
to indicate that there exists a constant
![]() $C>0$
for which
$C>0$
for which
![]() $X \leqslant CY$
. In a slight departure from convention, we will always allow this constant to depend on the subgaussian constant B, if present. We shall also let our constants implicit in big-O notation to depend on B, if this constant is relevant in the context. We hope that we have been clear as to where the subgaussian constant is relevant, and so this convention is to just reduce added clutter.
$X \leqslant CY$
. In a slight departure from convention, we will always allow this constant to depend on the subgaussian constant B, if present. We shall also let our constants implicit in big-O notation to depend on B, if this constant is relevant in the context. We hope that we have been clear as to where the subgaussian constant is relevant, and so this convention is to just reduce added clutter.
4 Quasi-randomness properties
In this technical section, we define a list of “quasi-random” properties of
![]() $A_n$
that hold with probability
$A_n$
that hold with probability
![]() $1-e^{-\Omega (n)}$
. This probability is large enough that we can assume that these properties hold for all the principal minors of
$1-e^{-\Omega (n)}$
. This probability is large enough that we can assume that these properties hold for all the principal minors of
![]() $A_{n+1}$
. Showing that several of these quasi-random properties hold with probability
$A_{n+1}$
. Showing that several of these quasi-random properties hold with probability
![]() $1-e^{-\Omega (n)}$
will prove to be a challenging task, and our proof will depend deeply on ideas from our previous paper [Reference Campos, Jenssen, Michelen and Sahasrabudhe4], on the singularity probability of a random symmetric matrix. So as not to distract from the new ideas in this paper, we do most of this work in the Appendix.
$1-e^{-\Omega (n)}$
will prove to be a challenging task, and our proof will depend deeply on ideas from our previous paper [Reference Campos, Jenssen, Michelen and Sahasrabudhe4], on the singularity probability of a random symmetric matrix. So as not to distract from the new ideas in this paper, we do most of this work in the Appendix.
4.1 Defining the properties
It will be convenient to assume throughout that every minor of
![]() $A_{n+1}$
is invertible, and so we will perturb the matrix slightly so that we may assume this. If we add to
$A_{n+1}$
is invertible, and so we will perturb the matrix slightly so that we may assume this. If we add to
![]() $A_{n+1}$
an independent random symmetric matrix whose upper triangular entries are independent gaussian random variables with mean
$A_{n+1}$
an independent random symmetric matrix whose upper triangular entries are independent gaussian random variables with mean
![]() $0$
and variance
$0$
and variance
![]() $n^{-n}$
, then with probability
$n^{-n}$
, then with probability
![]() $1 - e^{-\Omega (n)}$
, the singular values of
$1 - e^{-\Omega (n)}$
, the singular values of
![]() $A_{n+1}$
move by at most, say,
$A_{n+1}$
move by at most, say,
![]() $n^{-n/3}$
. Further, after adding this random gaussian matrix, every minor of the resulting matrix is invertible with probability
$n^{-n/3}$
. Further, after adding this random gaussian matrix, every minor of the resulting matrix is invertible with probability
![]() $1$
. Thus, we will assume without loss of generality throughout that every minor of
$1$
. Thus, we will assume without loss of generality throughout that every minor of
![]() $A_{n+1}$
is invertible.
$A_{n+1}$
is invertible.
In what follows, we let
![]() $A=A_n \sim \mathrm {Sym\,}_n(\zeta )$
and let
$A=A_n \sim \mathrm {Sym\,}_n(\zeta )$
and let
![]() $X \sim \mathrm {Col\,}_{n}(\zeta )$
be a random vector, independent of A. Our first quasi-random property is standard from the concentration of the operator norm of a random symmetric matrix. We define
$X \sim \mathrm {Col\,}_{n}(\zeta )$
be a random vector, independent of A. Our first quasi-random property is standard from the concentration of the operator norm of a random symmetric matrix. We define
![]() $\mathcal {E}_{1}$
by
$\mathcal {E}_{1}$
by
For the next property, we need a definition. Let
![]() $X,X' \sim \mathrm {Col\,}_n(\zeta )$
, and define the random vector in
$X,X' \sim \mathrm {Col\,}_n(\zeta )$
, and define the random vector in
![]() $\mathbb {R}^n$
as
$\mathbb {R}^n$
as
![]() $\tilde {X} := X_J - X^{\prime }_J$
, where
$\tilde {X} := X_J - X^{\prime }_J$
, where
![]() $J \subseteq [n]$
is a
$J \subseteq [n]$
is a
![]() $\mu $
-random subset, that is, for each
$\mu $
-random subset, that is, for each
![]() $j \in [n]$
, we have
$j \in [n]$
, we have
![]() $j \in J$
independently with probability
$j \in J$
independently with probability
![]() $\mu $
. The reason behind this definition is slightly opaque at present, but will be clear in the context of Lemma 5.2 in Section 5. Until we get there, it is reasonable to think of
$\mu $
. The reason behind this definition is slightly opaque at present, but will be clear in the context of Lemma 5.2 in Section 5. Until we get there, it is reasonable to think of
![]() $\tilde {X}$
as being essentially X; in particular, it is a random vector with i.i.d. subgaussian entries with mean
$\tilde {X}$
as being essentially X; in particular, it is a random vector with i.i.d. subgaussian entries with mean
![]() $0$
and variance
$0$
and variance
![]() $\mu $
. We now define
$\mu $
. We now define
![]() $\mathcal {E}_{2}$
to be the event in A defined by
$\mathcal {E}_{2}$
to be the event in A defined by
We remind the reader that
![]() $\mathrm {Comp\,}(\delta ,\rho )$
is defined in Section 3.2, and
$\mathrm {Comp\,}(\delta ,\rho )$
is defined in Section 3.2, and
![]() $\delta ,\rho \in (0,1)$
are constants, fixed throughout the paper, and chosen according to Lemma 3.2. In the (rare) case that
$\delta ,\rho \in (0,1)$
are constants, fixed throughout the paper, and chosen according to Lemma 3.2. In the (rare) case that
![]() $\widetilde {X} = 0$
, we interpret
$\widetilde {X} = 0$
, we interpret
![]() $\mathbb {P}_{\widetilde {X}}( A^{-1} \widetilde {X} / \|A^{-1} \widetilde {X}\|_2 \in \mathrm {Comp\,}(\delta ,\rho ) ) = 1$
.
$\mathbb {P}_{\widetilde {X}}( A^{-1} \widetilde {X} / \|A^{-1} \widetilde {X}\|_2 \in \mathrm {Comp\,}(\delta ,\rho ) ) = 1$
.
Recalling the least common denominator defined at (1.11), we now define the event
![]() $\mathcal {E}_3$
by
$\mathcal {E}_3$
by
The next condition tells us that the random vector
![]() $A^{-1}\widetilde {X}$
is typically unstructured. We will need a slightly stronger notion of structure than just looking at the LCD, in that, we will need all sufficiently large subvectors to be unstructured. For
$A^{-1}\widetilde {X}$
is typically unstructured. We will need a slightly stronger notion of structure than just looking at the LCD, in that, we will need all sufficiently large subvectors to be unstructured. For
![]() $\mu \in (0,1)$
, define the subvector least common denominator, as
$\mu \in (0,1)$
, define the subvector least common denominator, as
 $$ \begin{align*}\hat{D}_{\alpha,\gamma,\mu}(v) :=\min_{\substack{I\subset [n]\\|I|\geqslant (1-2\mu)n}}D_{\alpha,\gamma}\left(v_I/\|v_I\|_2\right)\,.\end{align*} $$
$$ \begin{align*}\hat{D}_{\alpha,\gamma,\mu}(v) :=\min_{\substack{I\subset [n]\\|I|\geqslant (1-2\mu)n}}D_{\alpha,\gamma}\left(v_I/\|v_I\|_2\right)\,.\end{align*} $$
We note that this is closely related to the notion of “regularized least common denominator” introduced by Vershynin in [Reference Vershynin46].
Now, if we define the random vector
![]() $v = v(\widetilde {X}) := A^{-1} \widetilde {X}$
, then we define
$v = v(\widetilde {X}) := A^{-1} \widetilde {X}$
, then we define
![]() $\mathcal {E}_4$
to be the event that A satisfies
$\mathcal {E}_4$
to be the event that A satisfies
As is the case for
![]() $\mathcal {E}_2$
, under the event that
$\mathcal {E}_2$
, under the event that
![]() $\widetilde {X} = 0$
, we interpret
$\widetilde {X} = 0$
, we interpret
![]() $\mathbb {P}_{\widetilde {X}}( \hat {D}_{\alpha ,\gamma ,\mu }(v ) < e^{c_4 n} ) = 1$
.
$\mathbb {P}_{\widetilde {X}}( \hat {D}_{\alpha ,\gamma ,\mu }(v ) < e^{c_4 n} ) = 1$
.
We now define our main quasi-randomness event
![]() $\mathcal {E}$
to be the intersection of these events:
$\mathcal {E}$
to be the intersection of these events:
The following lemma essentially allows us to assume that
![]() $\mathcal {E}$
holds in what follows.
$\mathcal {E}$
holds in what follows.
Lemma 4.1. For
![]() $B>0$
,
$B>0$
,
![]() $\zeta \in \Gamma _{B}$
, and all sufficiently small
$\zeta \in \Gamma _{B}$
, and all sufficiently small
![]() $\alpha ,\gamma ,\mu \in (0,1)$
, there exist constants
$\alpha ,\gamma ,\mu \in (0,1)$
, there exist constants
![]() $c_2,c_3,c_4 \in (0,1)$
appearing in (4.2), (4.3), and (4.4) so that
$c_2,c_3,c_4 \in (0,1)$
appearing in (4.2), (4.3), and (4.4) so that
Remark 4.2 (Choice of constants,
 $\alpha ,\gamma , \mu $
).
$\alpha ,\gamma , \mu $
).
We take
![]() $\alpha ,\gamma \in (0,1)$
to be sufficiently small so that Lemma 4.1 holds. For
$\alpha ,\gamma \in (0,1)$
to be sufficiently small so that Lemma 4.1 holds. For
![]() $\mu $
, we will choose it to be sufficiently small so that (1) Lemma 4.1 holds; (2) we have
$\mu $
, we will choose it to be sufficiently small so that (1) Lemma 4.1 holds; (2) we have
![]() $\mu \in (0,2^{-15})$
; and so that (3)
$\mu \in (0,2^{-15})$
; and so that (3)
![]() $\mu>0$
is small enough to guarantee that every set
$\mu>0$
is small enough to guarantee that every set
![]() $I \subseteq [n]$
with
$I \subseteq [n]$
with
![]() $|I| \geqslant (1-2\mu )n$
satisfies
$|I| \geqslant (1-2\mu )n$
satisfies
for every
![]() $w \in \mathrm {Incomp\,}(\delta ,\rho )$
. This is possible by Fact 3.1. These constants
$w \in \mathrm {Incomp\,}(\delta ,\rho )$
. This is possible by Fact 3.1. These constants
![]() $\alpha ,\gamma ,\mu $
will appear throughout the paper and will always be thought of as fixed according to this choice.
$\alpha ,\gamma ,\mu $
will appear throughout the paper and will always be thought of as fixed according to this choice.
4.2 Statement of our master quasi-randomness theorem and the deduction of Lemma 4.1
We will deduce Lemma 4.1 from a “master quasi-randomness theorem” together with a handful of now-standard results in the area.
For the purposes of the following sections, we shall informally consider a vector as “structured” if
where
![]() $c_\Sigma \in (0,1)$
is a small constant, to be chosen shortly. Thus, it makes sense to define the set of “structured directions” on the sphere
$c_\Sigma \in (0,1)$
is a small constant, to be chosen shortly. Thus, it makes sense to define the set of “structured directions” on the sphere
We now introduce our essential quasi-randomness measure of a random matrix. For
![]() $\zeta \in \Gamma $
,
$\zeta \in \Gamma $
,
![]() ${A \sim \mathrm {Sym\,}_n(\zeta )}$
, and a given vector
${A \sim \mathrm {Sym\,}_n(\zeta )}$
, and a given vector
![]() $w \in \mathbb {R}^n$
, define
$w \in \mathbb {R}^n$
, define
and set
We now state our “master quasi-randomness theorem,” from which we deduce Lemma 4.1.
Theorem 4.3 (Master quasi-randomness theorem).
For
![]() $B>0$
and
$B>0$
and
![]() $\zeta \in \Gamma _B$
, there exist constants
$\zeta \in \Gamma _B$
, there exist constants
![]() $\alpha ,\gamma ,\mu ,c_{\Sigma },c \in (0,1)$
depending only on B so that
$\alpha ,\gamma ,\mu ,c_{\Sigma },c \in (0,1)$
depending only on B so that
The proof of Theorem 4.3 is quite similar to the main theorem of [Reference Campos, Jenssen, Michelen and Sahasrabudhe4], albeit with a few technical adaptations, and is proved in the Appendix. Note that
![]() $q_n(\alpha ,\gamma ,\mu )$
is monotone decreasing as
$q_n(\alpha ,\gamma ,\mu )$
is monotone decreasing as
![]() $\alpha ,\gamma $
, and
$\alpha ,\gamma $
, and
![]() $\mu $
decrease. As such, Theorem 4.3 implies that its conclusion holds for all sufficiently small
$\mu $
decrease. As such, Theorem 4.3 implies that its conclusion holds for all sufficiently small
![]() $\alpha ,\gamma ,\mu $
as well.
$\alpha ,\gamma ,\mu $
as well.
We now prove that our pseudo-random event
![]() $\mathcal {E} = \mathcal {E}_1 \cap \mathcal {E}_2 \cap \mathcal {E}_3 \cap \mathcal {E}_4$
holds with probability
$\mathcal {E} = \mathcal {E}_1 \cap \mathcal {E}_2 \cap \mathcal {E}_3 \cap \mathcal {E}_4$
holds with probability
![]() $1-e^{-\Omega (n)}$
.
$1-e^{-\Omega (n)}$
.
Proof of Lemma 4.1.
The event
![]() $\mathcal {E}_1$
: From [Reference Feldheim and Sodin15], we may deduceFootnote
5
the following concentration bound
$\mathcal {E}_1$
: From [Reference Feldheim and Sodin15], we may deduceFootnote
5
the following concentration bound
which holdsFootnote
6
for all
![]() $t \geqslant 0$
. Thus, by (4.11), the event
$t \geqslant 0$
. Thus, by (4.11), the event
![]() $\mathcal {E}_1$
at (4.1) fails with probability
$\mathcal {E}_1$
at (4.1) fails with probability
![]() $\lesssim e^{-\Omega (n)}$
.
$\lesssim e^{-\Omega (n)}$
.
The event
![]() $\mathcal {E}_2$
: By Lemma 3.2, there is a
$\mathcal {E}_2$
: By Lemma 3.2, there is a
![]() $c> 0$
so that for each
$c> 0$
so that for each
![]() $u \neq 0$
, we have
$u \neq 0$
, we have
Applying Markov’s inequality shows
and so the event in (4.2) fails with probability at most
![]() $O\left (e^{-\Omega (n)}\right )$
, under the event
$O\left (e^{-\Omega (n)}\right )$
, under the event
![]() $\widetilde {X} \neq 0$
. By Theorem 3.1.1, in [Reference Vershynin47], we have that
$\widetilde {X} \neq 0$
. By Theorem 3.1.1, in [Reference Vershynin47], we have that
Choosing
![]() $c_2$
small enough shows an exponential bound on
$c_2$
small enough shows an exponential bound on
![]() $\mathbb {P}(\mathcal {E}_2^c)$
.
$\mathbb {P}(\mathcal {E}_2^c)$
.
The event
![]() $\mathcal {E}_3$
: If
$\mathcal {E}_3$
: If
![]() $D_{\alpha ,\gamma }(u) \leqslant e^{c_3n}$
, for an u an eigenvector
$D_{\alpha ,\gamma }(u) \leqslant e^{c_3n}$
, for an u an eigenvector
![]() $Au = {\lambda } v$
, we have that
$Au = {\lambda } v$
, we have that
where the first inequality is immediate from the definition. Now, note that if
![]() $\mathcal {E}_1$
holds, then
$\mathcal {E}_1$
holds, then
![]() ${\lambda } \in [-4\sqrt {n},4\sqrt {n}]$
, and so
${\lambda } \in [-4\sqrt {n},4\sqrt {n}]$
, and so
where the first inequality holds if we choose
![]() $c_3\leqslant c_\Sigma $
. We now apply Theorem 4.3 to see
$c_3\leqslant c_\Sigma $
. We now apply Theorem 4.3 to see
![]() $q_n(0) \leqslant q_n \lesssim e^{-\Omega (n)}$
, yielding the desired result.
$q_n(0) \leqslant q_n \lesssim e^{-\Omega (n)}$
, yielding the desired result.
The event
![]() $\mathcal {E}_4$
: Note first that, by (4.12), we may assume
$\mathcal {E}_4$
: Note first that, by (4.12), we may assume
![]() $\widetilde {X} \neq 0$
. For a fixed instance of
$\widetilde {X} \neq 0$
. For a fixed instance of
![]() $\widetilde {X} \not = 0 $
, we have
$\widetilde {X} \not = 0 $
, we have
which is at most
![]() $e^{-\Omega (n)}$
, by Theorem 4.3. Here, the first inequality holds when
$e^{-\Omega (n)}$
, by Theorem 4.3. Here, the first inequality holds when
![]() $c_4 \leqslant c_{\Sigma }$
.
$c_4 \leqslant c_{\Sigma }$
.
We now write
![]() $v = A^{-1}\tilde {X}/\|\tilde {X}\|_2$
and apply Markov’s inequality
$v = A^{-1}\tilde {X}/\|\tilde {X}\|_2$
and apply Markov’s inequality
where the last line follows when
![]() $c_4$
is taken small relative to the implicit constant in the bound on the right-hand side of (4.13).
$c_4$
is taken small relative to the implicit constant in the bound on the right-hand side of (4.13).
Since we have shown that each of
![]() $\mathcal {E}_1,\mathcal {E}_2,\mathcal {E}_3,\mathcal {E}_4$
holds with probability
$\mathcal {E}_1,\mathcal {E}_2,\mathcal {E}_3,\mathcal {E}_4$
holds with probability
![]() $1-e^{-\Omega (n)}$
, the intersection fails with exponentially small probability.
$1-e^{-\Omega (n)}$
, the intersection fails with exponentially small probability.
5 Decoupling quadratic forms
In this section, we will prove our Esseen-type inequality that will allow us to deal with a small ball event and a large deviation event simultaneously.
Lemma 5.1. For
![]() $B>0$
, let
$B>0$
, let
![]() $\zeta \in \Gamma _B$
and
$\zeta \in \Gamma _B$
and
![]() $X \sim \mathrm {Col\,}_n(\zeta )$
. Let M be an
$X \sim \mathrm {Col\,}_n(\zeta )$
. Let M be an
![]() $n \times n $
symmetric matrix,
$n \times n $
symmetric matrix,
![]() $u\in \mathbb {R}^n$
,
$u\in \mathbb {R}^n$
,
![]() $t \in \mathbb {R}$
, and
$t \in \mathbb {R}$
, and
![]() $s, \delta \geqslant 0$
. Then
$s, \delta \geqslant 0$
. Then
 $$ \begin{align} \mathbb{P}( |\langle M X, X \rangle - t| < \delta, \langle X,u \rangle \geqslant s ) \lesssim \delta e^{-s}\int_{-1/\delta}^{1/\delta} \left|\mathbb{E}\, e^{2\pi i \theta \langle M X, X \rangle + \langle X,u \rangle }\right|\,d\theta\,. \end{align} $$
$$ \begin{align} \mathbb{P}( |\langle M X, X \rangle - t| < \delta, \langle X,u \rangle \geqslant s ) \lesssim \delta e^{-s}\int_{-1/\delta}^{1/\delta} \left|\mathbb{E}\, e^{2\pi i \theta \langle M X, X \rangle + \langle X,u \rangle }\right|\,d\theta\,. \end{align} $$
We will then bound the integrand (our so-called “titled” characteristic function) with a decoupling maneuver, somewhat similar to a “van der Corput trick” in classical Fourier analysis. This amounts to a clever application of Cauchy-Schwarz, inspired by Kwan and Sauermann’s work on Costello’s conjecture [Reference Kwan and Sauermann20] (a similar technique appears in [Reference Berkowitz1] and [Reference Nguyen25]). We shall then be able to mix in our quasi-random conditions on our matrix A to ultimately obtain Lemma 5.2, which gives us a rather tractable bound on the left-hand side of (5.1). To state this lemma, let us recall that
![]() $\mathcal {E}$
(defined at (4.5)) is the set of symmetric matrices satisfying the quasi-randomness conditions in the previous section, Section 4. Also recall that the constant
$\mathcal {E}$
(defined at (4.5)) is the set of symmetric matrices satisfying the quasi-randomness conditions in the previous section, Section 4. Also recall that the constant
![]() $\mu \in (0,2^{-15})$
is defined in Section 4 so that Lemma 4.1 holds and is treated as a fixed constant throughout this paper.
$\mu \in (0,2^{-15})$
is defined in Section 4 so that Lemma 4.1 holds and is treated as a fixed constant throughout this paper.
Lemma 5.2. For
![]() $B>0$
, let
$B>0$
, let
![]() $\zeta \in \Gamma _B$
,
$\zeta \in \Gamma _B$
,
![]() $X \sim \mathrm {Col\,}_n(\zeta )$
and let A be a real symmetric
$X \sim \mathrm {Col\,}_n(\zeta )$
and let A be a real symmetric
![]() $n\times n$
matrix with
$n\times n$
matrix with
![]() $A \in \mathcal {E}$
and set
$A \in \mathcal {E}$
and set
![]() $\mu _1 := \sigma _{\max }(A^{-1})$
. Also let
$\mu _1 := \sigma _{\max }(A^{-1})$
. Also let
![]() $s \geqslant 0, \delta> e^{-c n}$
and
$s \geqslant 0, \delta> e^{-c n}$
and
![]() $u \in {\mathbb {S}}^{n-1}$
. Then
$u \in {\mathbb {S}}^{n-1}$
. Then
 $$\begin{align*}\mathbb{P}_X\left(\left|\langle A^{-1} X,X\rangle - t \right| \leqslant \delta \mu_1, \langle X, u \rangle \geqslant s \right) \lesssim \delta e^{-s} \int_{-1/\delta}^{1/\delta} I(\theta) ^{1/2}\,d\theta + e^{-\Omega(n)}\, , \end{align*}$$
$$\begin{align*}\mathbb{P}_X\left(\left|\langle A^{-1} X,X\rangle - t \right| \leqslant \delta \mu_1, \langle X, u \rangle \geqslant s \right) \lesssim \delta e^{-s} \int_{-1/\delta}^{1/\delta} I(\theta) ^{1/2}\,d\theta + e^{-\Omega(n)}\, , \end{align*}$$
where
 $$\begin{align*}I(\theta) := \mathbb{E}_{J,X_J,X_J^{\prime }} \, \exp\bigg( \langle (X + X')_J,u \rangle -c\theta^2 \mu_1^{-2} \|A^{-1}(X - X')_J \|_2^2\bigg)\,, \end{align*}$$
$$\begin{align*}I(\theta) := \mathbb{E}_{J,X_J,X_J^{\prime }} \, \exp\bigg( \langle (X + X')_J,u \rangle -c\theta^2 \mu_1^{-2} \|A^{-1}(X - X')_J \|_2^2\bigg)\,, \end{align*}$$
![]() $X' \sim \mathrm {Col\,}_n(\zeta )$
is independent of X, and
$X' \sim \mathrm {Col\,}_n(\zeta )$
is independent of X, and
![]() $J \subseteq [n]$
is a
$J \subseteq [n]$
is a
![]() $\mu $
-random set. Here,
$\mu $
-random set. Here,
![]() $c> 0$
is a constant depending only on B.
$c> 0$
is a constant depending only on B.
While the definition of
![]() $I({\theta })$
(and therefore the conclusion of the lemma) is a bit mysterious at this point, we assure the reader that this is a step in the right direction.
$I({\theta })$
(and therefore the conclusion of the lemma) is a bit mysterious at this point, we assure the reader that this is a step in the right direction.
All works bounding the singularity probability for random symmetric matrices contain a related decoupling step [Reference Campos, Jenssen, Michelen and Sahasrabudhe3, Reference Campos, Jenssen, Michelen and Sahasrabudhe4, Reference Campos, Mattos, Morris and Morrison5, Reference Ferber and Jain16, Reference Nguyen25, Reference Vershynin46], starting with Costello et al.’s breakthrough [Reference Costello, Tao and Vu7], building off of Costello’s earlier work [Reference Costello6] on anticoncentration of bilinear and quadratic forms. A subtle difference in the decoupling approach from [Reference Kwan and Sauermann20] used here is that the quadratic form is decoupled after bounding a small ball probability in terms of the integral of a characteristic function rather than on the probability itself; the effect of this approach is that we do not lose a power of
![]() $\delta $
, but only lose by a square root “under the integral” on the integrand
$\delta $
, but only lose by a square root “under the integral” on the integrand
![]() $I(\theta )$
.
$I(\theta )$
.
5.1 Proofs
We now dive in and prove our Esseen-type inequality. For this, we shall appeal to the classical Esseen inequality [Reference Esseen14]: If Z is a random variable taking values in
![]() $\mathbb {R}$
with characteristic function
$\mathbb {R}$
with characteristic function
![]() ${\varphi }_Z({\theta }):= \mathbb {E}_Z\, e^{2\pi i \theta Z}$
, then for all
${\varphi }_Z({\theta }):= \mathbb {E}_Z\, e^{2\pi i \theta Z}$
, then for all
![]() $t \in \mathbb {R}$
, we have
$t \in \mathbb {R}$
, we have
 $$\begin{align*}\mathbb{P}_X( |Z - t| \leqslant \delta ) \lesssim \delta \int_{-1/\delta}^{1/\delta}\, |{\varphi}_Z( {\theta} )| \, d{\theta}. \end{align*}$$
$$\begin{align*}\mathbb{P}_X( |Z - t| \leqslant \delta ) \lesssim \delta \int_{-1/\delta}^{1/\delta}\, |{\varphi}_Z( {\theta} )| \, d{\theta}. \end{align*}$$
We shall also use the following basic fact about subgaussian random vectors (see, for example, [Reference Vershynin47, Proposition 2.6.1]): If
![]() $\zeta \in \Gamma _B$
and
$\zeta \in \Gamma _B$
and
![]() $Y \sim \mathrm {Col\,}_n(\zeta )$
, then for every vector
$Y \sim \mathrm {Col\,}_n(\zeta )$
, then for every vector
![]() $u \in \mathbb {R}^n$
, we have
$u \in \mathbb {R}^n$
, we have
Proof of Lemma 5.1.
Since
![]() ${\mathbf {1}}\{ x \geqslant s \} \leqslant e^{x - s}$
, we may bound
${\mathbf {1}}\{ x \geqslant s \} \leqslant e^{x - s}$
, we may bound
Define the random variable
![]() $Y \in \mathbb {R}^n$
by
$Y \in \mathbb {R}^n$
by
for all open
![]() $U \subseteq \mathbb {R}^n$
. Note that the expectation
$U \subseteq \mathbb {R}^n$
. Note that the expectation
![]() $\mathbb {E}_X e^{\langle X, u \rangle }$
is finite by (5.2). We now use this definition to rewrite the expectation on the right-hand side of (5.3),
$\mathbb {E}_X e^{\langle X, u \rangle }$
is finite by (5.2). We now use this definition to rewrite the expectation on the right-hand side of (5.3),
Thus, we may apply Esseen’s lemma to the random variable Y to obtain
 $$ \begin{align*}\mathbb{P}_Y( |\langle MY,Y\rangle - t| \leqslant \delta ) \lesssim \delta \int_{-1/\delta}^{1/\delta} |\mathbb{E}_Y\, e^{2\pi i\theta \langle MY,Y\rangle}| \, d\theta\,.\end{align*} $$
$$ \begin{align*}\mathbb{P}_Y( |\langle MY,Y\rangle - t| \leqslant \delta ) \lesssim \delta \int_{-1/\delta}^{1/\delta} |\mathbb{E}_Y\, e^{2\pi i\theta \langle MY,Y\rangle}| \, d\theta\,.\end{align*} $$
By the definition of Y, we have
completing the lemma.
To control the integral on the right-hand side of Lemma 5.1, we will appeal to the following decoupling lemma, which is adapted from Lemma 3.3 from [Reference Kwan and Sauermann20].
Lemma 5.3 (Decoupling with an exponential tilt).
Let
![]() $\zeta \in \Gamma $
, let
$\zeta \in \Gamma $
, let
![]() $X,X' \sim \mathrm {Col\,}_n(\zeta )$
be independent, and let
$X,X' \sim \mathrm {Col\,}_n(\zeta )$
be independent, and let
![]() $J\cup I = [n]$
be a partition of
$J\cup I = [n]$
be a partition of
![]() $[n]$
. Let M be an
$[n]$
. Let M be an
![]() $n \times n$
symmetric matrix and let
$n \times n$
symmetric matrix and let
![]() $u\in \mathbb {R}^n$
. Then
$u\in \mathbb {R}^n$
. Then
Proof. After partitioning the coordinates of X according to J and writing
![]() $\mathbb {E}_X = \mathbb {E}_{X_I}\mathbb {E}_{X_J}$
, we apply Jensen’s inequality to obtain
$\mathbb {E}_X = \mathbb {E}_{X_I}\mathbb {E}_{X_J}$
, we apply Jensen’s inequality to obtain
We now expand the square
![]() $\left |\mathbb {E}_{X_J}e^{2\pi i \theta \langle MX,X\rangle + \langle X,u \rangle } \right |{}^2$
as
$\left |\mathbb {E}_{X_J}e^{2\pi i \theta \langle MX,X\rangle + \langle X,u \rangle } \right |{}^2$
as
 $$ \begin{align*} &\mathbb{E}_{X_J,X_J^{\prime}} e^{2\pi i \theta \langle M(X_I + X_J),(X_I + X_J)\rangle + \langle (X_I + X_J),u\rangle - 2\pi i \theta \langle M(X_I + X_J^{\prime}),(X_I + X_J^{\prime})\rangle + \langle (X_I + X_J^{\prime}),u\rangle } \\ &= \mathbb{E}_{X_J,X_J^{\prime}} e^{4\pi i \theta \langle M(X_J - X_J^{\prime}),X_I\rangle + \langle X_J + X_J^{\prime}, u \rangle + 2\langle X_I,u\rangle + 2\pi i \langle M X_J, X_J \rangle - 2\pi i \langle M X_J^{\prime},X_J^{\prime}\rangle }, \end{align*} $$
$$ \begin{align*} &\mathbb{E}_{X_J,X_J^{\prime}} e^{2\pi i \theta \langle M(X_I + X_J),(X_I + X_J)\rangle + \langle (X_I + X_J),u\rangle - 2\pi i \theta \langle M(X_I + X_J^{\prime}),(X_I + X_J^{\prime})\rangle + \langle (X_I + X_J^{\prime}),u\rangle } \\ &= \mathbb{E}_{X_J,X_J^{\prime}} e^{4\pi i \theta \langle M(X_J - X_J^{\prime}),X_I\rangle + \langle X_J + X_J^{\prime}, u \rangle + 2\langle X_I,u\rangle + 2\pi i \langle M X_J, X_J \rangle - 2\pi i \langle M X_J^{\prime},X_J^{\prime}\rangle }, \end{align*} $$
where we used the fact that M is symmetric. Thus, swapping expectations yields
 $$ \begin{align*} E &\leqslant \mathbb{E}_{X_J,X_J^{\prime}} \mathbb{E}_{X_I} e^{4\pi i \theta \langle M(X_J - X_J^{\prime}),X_I\rangle + \langle X_J + X_J^{\prime}, u \rangle + 2\langle X_I,u\rangle + 2\pi i \langle M X_J, X_J \rangle - 2\pi i \langle M X_J^{\prime},X_J^{\prime}\rangle } \\ &\leqslant \mathbb{E}_{X_J,X_J^{\prime}} \left|\mathbb{E}_{X_I} e^{4\pi i \theta \langle M(X_J - X_J^{\prime}),X_I\rangle + \langle X_J + X_J^{\prime}, u \rangle + 2\langle X_I,u\rangle + 2\pi i \langle M X_J, X_J \rangle - 2\pi i \langle M X_J^{\prime},X_J^{\prime}\rangle } \right| \\ & = \mathbb{E}_{X_J,X_J^{\prime}}\, e^{\langle X_J + X_J^{\prime},u \rangle } \left|\mathbb{E}_{X_I} e^{4\pi i\theta \langle M(X - X')_J, X_I \rangle + 2\langle X_I,u\rangle } \right|,\, \end{align*} $$
$$ \begin{align*} E &\leqslant \mathbb{E}_{X_J,X_J^{\prime}} \mathbb{E}_{X_I} e^{4\pi i \theta \langle M(X_J - X_J^{\prime}),X_I\rangle + \langle X_J + X_J^{\prime}, u \rangle + 2\langle X_I,u\rangle + 2\pi i \langle M X_J, X_J \rangle - 2\pi i \langle M X_J^{\prime},X_J^{\prime}\rangle } \\ &\leqslant \mathbb{E}_{X_J,X_J^{\prime}} \left|\mathbb{E}_{X_I} e^{4\pi i \theta \langle M(X_J - X_J^{\prime}),X_I\rangle + \langle X_J + X_J^{\prime}, u \rangle + 2\langle X_I,u\rangle + 2\pi i \langle M X_J, X_J \rangle - 2\pi i \langle M X_J^{\prime},X_J^{\prime}\rangle } \right| \\ & = \mathbb{E}_{X_J,X_J^{\prime}}\, e^{\langle X_J + X_J^{\prime},u \rangle } \left|\mathbb{E}_{X_I} e^{4\pi i\theta \langle M(X - X')_J, X_I \rangle + 2\langle X_I,u\rangle } \right|,\, \end{align*} $$
as desired. Here, we could swap expectations, since all expectations are finite, due to the subgaussian assumption on
![]() $\zeta $
.
$\zeta $
.
We need a basic bound that will be useful for bounding our tilted characteristic function. This bound appears in the proof of Theorem 6.3 in Vershynin’s paper [Reference Vershynin46].
Fact 5.4. For
![]() $B>0$
, let
$B>0$
, let
![]() $\zeta \in \Gamma _B$
, let
$\zeta \in \Gamma _B$
, let
![]() $\zeta '$
be an independent copy of
$\zeta '$
be an independent copy of
![]() $\zeta $
, and set
$\zeta $
, and set
![]() $\xi = \zeta - \zeta '$
. Then for all
$\xi = \zeta - \zeta '$
. Then for all
![]() $a \in \mathbb {R}^n$
, we have
$a \in \mathbb {R}^n$
, we have
 $$ \begin{align*}\prod_{j}\mathbb{E}_{\xi}\, |\cos(2\pi \xi a_j)| \leqslant \exp\left(-c \min_{r \in [1,c^{-1}]} \| r a\|_{\mathbb{T}}^2\right)\,,\end{align*} $$
$$ \begin{align*}\prod_{j}\mathbb{E}_{\xi}\, |\cos(2\pi \xi a_j)| \leqslant \exp\left(-c \min_{r \in [1,c^{-1}]} \| r a\|_{\mathbb{T}}^2\right)\,,\end{align*} $$
where
![]() $c>0$
depends only on B.
$c>0$
depends only on B.
A simple symmetrization trick along with Cauchy-Schwarz will allow us to prove a similar bound for the tilted characteristic function.
Lemma 5.5. For
![]() $B>0$
, let
$B>0$
, let
![]() $\zeta \in \Gamma _B$
,
$\zeta \in \Gamma _B$
,
![]() $X \sim \mathrm {Col\,}_n(\zeta )$
and let
$X \sim \mathrm {Col\,}_n(\zeta )$
and let
![]() $u ,v \in \mathbb {R}^n$
. Then
$u ,v \in \mathbb {R}^n$
. Then
 $$ \begin{align} \left|\mathbb{E}_X e^{2\pi i \langle X,v \rangle + \langle X,u \rangle} \right| \leqslant \exp\left(-c\min_{r \in [1,c^{-1}]} \|rv\|_{\mathbb{T}}^2 + c^{-1} \|u \|_2^2\right)\, , \end{align} $$
$$ \begin{align} \left|\mathbb{E}_X e^{2\pi i \langle X,v \rangle + \langle X,u \rangle} \right| \leqslant \exp\left(-c\min_{r \in [1,c^{-1}]} \|rv\|_{\mathbb{T}}^2 + c^{-1} \|u \|_2^2\right)\, , \end{align} $$
where
![]() $c \in (0,1)$
depends only on B.
$c \in (0,1)$
depends only on B.
Proof. Let
![]() $\zeta '$
be an independent copy of
$\zeta '$
be an independent copy of
![]() $\zeta $
, and note that
$\zeta $
, and note that
Let
![]() $\widetilde {X} = (\widetilde {X}_i)_{i=1}^n$
,
$\widetilde {X} = (\widetilde {X}_i)_{i=1}^n$
,
![]() $\widetilde {Y} = (Y_i)_{i=1}^n$
denote vectors with i.i.d. coordinates distributed as
$\widetilde {Y} = (Y_i)_{i=1}^n$
denote vectors with i.i.d. coordinates distributed as
![]() $\xi :=\zeta - \zeta '$
and
$\xi :=\zeta - \zeta '$
and
![]() $\zeta + \zeta '$
, respectively. We have
$\zeta + \zeta '$
, respectively. We have
 $$ \begin{align} \left|\mathbb{E}_X e^{2\pi i \langle X,v \rangle + \langle X,u \rangle} \right|^2 \leqslant \mathbb{E}\, e^{\langle \widetilde{Y},u\rangle} \prod_{j } \cos (2\pi\widetilde{X}_jv_j) \leqslant \left(\mathbb{E}_{\widetilde{Y}} e^{2\langle \widetilde{Y},u\rangle }\right)^{1/2} \left( \prod_{j} \mathbb{E}_{\xi} |\cos(2\pi \xi v_j)| \right)^{1/2}, \end{align} $$
$$ \begin{align} \left|\mathbb{E}_X e^{2\pi i \langle X,v \rangle + \langle X,u \rangle} \right|^2 \leqslant \mathbb{E}\, e^{\langle \widetilde{Y},u\rangle} \prod_{j } \cos (2\pi\widetilde{X}_jv_j) \leqslant \left(\mathbb{E}_{\widetilde{Y}} e^{2\langle \widetilde{Y},u\rangle }\right)^{1/2} \left( \prod_{j} \mathbb{E}_{\xi} |\cos(2\pi \xi v_j)| \right)^{1/2}, \end{align} $$
where we have applied the Cauchy-Schwarz inequality along with the bound
![]() $|\cos (x)|^2 \leqslant |\cos (x)|$
to obtain the last inequality. By (5.2), the first expectation on the right-hand side of (5.6) is at most
$|\cos (x)|^2 \leqslant |\cos (x)|$
to obtain the last inequality. By (5.2), the first expectation on the right-hand side of (5.6) is at most
![]() $\exp (O(\|u\|_2^2))$
. Applying Fact 5.4 completes the lemma.
$\exp (O(\|u\|_2^2))$
. Applying Fact 5.4 completes the lemma.
5.2 Quasi-random properties for triples
 $(J,X_J,X^{\prime }_J)$
$(J,X_J,X^{\prime }_J)$
We now prepare for the proof of Lemma 5.2 by introducing a quasi-randomness notion on triples
![]() $(J,X_J,X^{\prime }_J)$
. Here,
$(J,X_J,X^{\prime }_J)$
. Here,
![]() $J \subseteq [n]$
and
$J \subseteq [n]$
and
![]() $X,X' \in \mathbb {R}^n$
. For this, we fix an
$X,X' \in \mathbb {R}^n$
. For this, we fix an
![]() $n\times n$
real symmetric matrix
$n\times n$
real symmetric matrix
![]() $A \in \mathcal {E}$
and define the event
$A \in \mathcal {E}$
and define the event
![]() $\mathcal {F} = \mathcal {F}(A)$
as the intersection of the events
$\mathcal {F} = \mathcal {F}(A)$
as the intersection of the events
![]() $\mathcal {F}_1,\mathcal {F}_2,\mathcal {F}_3$
, and
$\mathcal {F}_1,\mathcal {F}_2,\mathcal {F}_3$
, and
![]() $\mathcal {F}_4$
, which are defined as follows. Given a triple
$\mathcal {F}_4$
, which are defined as follows. Given a triple
![]() $(J,X_J,X^{\prime }_J)$
, we write
$(J,X_J,X^{\prime }_J)$
, we write
![]() $\tilde {X} := X_J - X_J^{\prime }$
.
$\tilde {X} := X_J - X_J^{\prime }$
.
Define events
![]() $\mathcal {F}_1,\mathcal {F}_2,\mathcal {F}_3(A)$
by
$\mathcal {F}_1,\mathcal {F}_2,\mathcal {F}_3(A)$
by
Finally, we write
![]() $v = v(\tilde {X}) := A^{-1} \widetilde {X}$
and
$v = v(\tilde {X}) := A^{-1} \widetilde {X}$
and
![]() $I := [n] \setminus J$
and then define
$I := [n] \setminus J$
and then define
![]() $\mathcal {F}_4(A)$
by
$\mathcal {F}_4(A)$
by
 $$ \begin{align} \mathcal{F}_4(A) := \left\{D_{\alpha,\gamma}\left(\frac{v_I}{\|v_I\|} \right)> e^{c n} \right\}\,. \end{align} $$
$$ \begin{align} \mathcal{F}_4(A) := \left\{D_{\alpha,\gamma}\left(\frac{v_I}{\|v_I\|} \right)> e^{c n} \right\}\,. \end{align} $$
We now define
![]() $\mathcal {F}(A) := \mathcal {F}_1 \cap \mathcal {F}_2 \cap \mathcal {F}_3(A) \cap \mathcal {F}_4(A)$
and prove the following basic lemma that will allow us to essentially assume that (5.7),(5.8),(5.9),(5.10) hold in all that follows. We recall that the constants
$\mathcal {F}(A) := \mathcal {F}_1 \cap \mathcal {F}_2 \cap \mathcal {F}_3(A) \cap \mathcal {F}_4(A)$
and prove the following basic lemma that will allow us to essentially assume that (5.7),(5.8),(5.9),(5.10) hold in all that follows. We recall that the constants
![]() $\delta ,\rho ,\mu ,\alpha ,\gamma $
were chosen in Lemmas 3.2 and 4.1 as a function of the subgaussian moment B. Thus, the only new parameter in
$\delta ,\rho ,\mu ,\alpha ,\gamma $
were chosen in Lemmas 3.2 and 4.1 as a function of the subgaussian moment B. Thus, the only new parameter in
![]() $\mathcal {F}$
is the constant c in lines (5.8) and (5.10).
$\mathcal {F}$
is the constant c in lines (5.8) and (5.10).
Lemma 5.6. For
![]() $B>0$
, let
$B>0$
, let
![]() $\zeta \in \Gamma _B$
, let
$\zeta \in \Gamma _B$
, let
![]() $X,X' \sim \mathrm {Col\,}_n(\zeta )$
be independent, and let
$X,X' \sim \mathrm {Col\,}_n(\zeta )$
be independent, and let
![]() $J \subseteq [n]$
be a
$J \subseteq [n]$
be a
![]() $\mu $
-random subset. Let A be an
$\mu $
-random subset. Let A be an
![]() $n \times n$
real symmetric matrix with
$n \times n$
real symmetric matrix with
![]() $A \in \mathcal {E}$
. We may choose the constant
$A \in \mathcal {E}$
. We may choose the constant
![]() $c \in (0,1)$
appearing in (5.8) and (5.10) as a function of B and
$c \in (0,1)$
appearing in (5.8) and (5.10) as a function of B and
![]() $\mu $
so that
$\mu $
so that
Proof. For
![]() $\mathcal {F}_1$
, we use Hoeffding’s inequality to see
$\mathcal {F}_1$
, we use Hoeffding’s inequality to see
![]() $\mathbb {P}(\mathcal {F}_1^c) \lesssim e^{-\Omega (n)}$
. To bound
$\mathbb {P}(\mathcal {F}_1^c) \lesssim e^{-\Omega (n)}$
. To bound
![]() $\mathbb {P}(\mathcal {F}_2^c)$
, we note that the entries of
$\mathbb {P}(\mathcal {F}_2^c)$
, we note that the entries of
![]() $\widetilde {X}$
are independent, subgaussian, and have variance
$\widetilde {X}$
are independent, subgaussian, and have variance
![]() $2\mu $
, and so
$2\mu $
, and so
![]() $\widetilde {X}/(\sqrt {2\mu })$
has i.i.d. entries with mean zero, variance
$\widetilde {X}/(\sqrt {2\mu })$
has i.i.d. entries with mean zero, variance
![]() $1$
and subgaussian moment bounded by
$1$
and subgaussian moment bounded by
![]() $B/\sqrt {2\mu }$
. Thus, from Theorem 3.1.1 in [Reference Vershynin47], we have
$B/\sqrt {2\mu }$
. Thus, from Theorem 3.1.1 in [Reference Vershynin47], we have
For
![]() $\mathcal {F}_3(A), \mathcal {F}_4(A)$
, recall that
$\mathcal {F}_3(A), \mathcal {F}_4(A)$
, recall that
![]() $A \in \mathcal {E}$
means that (4.2) and (4.4) hold, thus exponential bounds on
$A \in \mathcal {E}$
means that (4.2) and (4.4) hold, thus exponential bounds on
![]() $\mathbb {P}(\mathcal {F}_3^c)$
and
$\mathbb {P}(\mathcal {F}_3^c)$
and
![]() $\mathbb {P}(\mathcal {F}_4^c)$
follow from Markov’s inequality.
$\mathbb {P}(\mathcal {F}_4^c)$
follow from Markov’s inequality.
5.3 Proof of Lemma 5.2
We now prove Lemma 5.2 by applying the previous three lemmas in sequence.
Proof of Lemma 5.2.
Let
![]() $\delta \geqslant e^{-c_1n}$
, where we will choose
$\delta \geqslant e^{-c_1n}$
, where we will choose
![]() $c_1>0$
to be sufficiently small later in the proof. Apply Lemma 5.1 to write
$c_1>0$
to be sufficiently small later in the proof. Apply Lemma 5.1 to write
 $$ \begin{align} \mathbb{P}_X\left(\left|\langle A^{-1} X,X\rangle - t \right| \leqslant \delta \mu_1, \langle X, u \rangle \geqslant s \right) \lesssim \delta e^{-s} \int_{-1/\delta}^{1/\delta}\left| \mathbb{E}_X \, e^{2\pi i \theta \frac{\langle A^{-1} X,X \rangle}{\mu_1} + \langle X,u\rangle } \right| \,d\theta\, , \end{align} $$
$$ \begin{align} \mathbb{P}_X\left(\left|\langle A^{-1} X,X\rangle - t \right| \leqslant \delta \mu_1, \langle X, u \rangle \geqslant s \right) \lesssim \delta e^{-s} \int_{-1/\delta}^{1/\delta}\left| \mathbb{E}_X \, e^{2\pi i \theta \frac{\langle A^{-1} X,X \rangle}{\mu_1} + \langle X,u\rangle } \right| \,d\theta\, , \end{align} $$
where we recall that
![]() $\mu _1 = \sigma _{\max }(A^{-1})$
. We now look to apply our decoupling lemma, Lemma 5.3. Let J be a
$\mu _1 = \sigma _{\max }(A^{-1})$
. We now look to apply our decoupling lemma, Lemma 5.3. Let J be a
![]() $\mu $
-random subset of
$\mu $
-random subset of
![]() $[n]$
, define
$[n]$
, define
![]() $I:=[n] \setminus J$
, and let
$I:=[n] \setminus J$
, and let
![]() $X'$
be an independent copy of X. By Lemma 5.3, we have
$X'$
be an independent copy of X. By Lemma 5.3, we have
 $$ \begin{align} &\left|\mathbb{E}_X\, e^{2\pi i \theta \frac{\langle A^{-1} X,X \rangle}{\mu_1} + \langle X,u\rangle } \right|^2 \leqslant \mathbb{E}_{J}\mathbb{E}_{X_J, X^{\prime}_J}\, e^{\langle (X + X')_J,u \rangle } \cdot \left| \mathbb{E}_{X_I}\, e^{4\pi i \theta\left\langle\frac{A^{-1}\widetilde{X}}{\mu_1} ,X_I\right\rangle+2\langle X_I,u\rangle}\right| \,, \end{align} $$
$$ \begin{align} &\left|\mathbb{E}_X\, e^{2\pi i \theta \frac{\langle A^{-1} X,X \rangle}{\mu_1} + \langle X,u\rangle } \right|^2 \leqslant \mathbb{E}_{J}\mathbb{E}_{X_J, X^{\prime}_J}\, e^{\langle (X + X')_J,u \rangle } \cdot \left| \mathbb{E}_{X_I}\, e^{4\pi i \theta\left\langle\frac{A^{-1}\widetilde{X}}{\mu_1} ,X_I\right\rangle+2\langle X_I,u\rangle}\right| \,, \end{align} $$
where we recall that
![]() $\widetilde {X}=(X-X')_J$
.
$\widetilde {X}=(X-X')_J$
.
We first consider the contribution to the expectation on the right-hand side of (5.12) from triples
![]() $(J,X_J,X_J^{\prime }) \not \in \mathcal {F}$
. For this, let Y be a random vector, such that
$(J,X_J,X_J^{\prime }) \not \in \mathcal {F}$
. For this, let Y be a random vector, such that
![]() $Y_j=X_j+X^{\prime }_j$
, if
$Y_j=X_j+X^{\prime }_j$
, if
![]() $j\in J$
, and
$j\in J$
, and
![]() $Y_j=2X_j$
, if
$Y_j=2X_j$
, if
![]() $j\in I$
. Applying the triangle inequality, we have
$j\in I$
. Applying the triangle inequality, we have
 $$ \begin{align*} \mathbb{E}_{J, X_J, X_J^{\prime}}^{\mathcal{F}^c}\, e^{\langle (X + X')_J,u \rangle } \cdot \left|\mathbb{E}_{X_I}\, e^{4\pi i \theta\langle \frac{A^{-1} \widetilde{X} }{\mu_1},X_I\rangle+2\langle X_I,u\rangle} \right| &\leqslant \mathbb{E}_{J, X_J, X_J^{\prime}}^{\mathcal{F}^c}\, e^{\langle (X + X')_J,u \rangle }\mathbb{E}_{X_I}\, e^{2\langle X_I,u\rangle} \\ &= \mathbb{E}_{J,X,X'}^{\mathcal{F}^c}e^{\langle Y,u \rangle } .\end{align*} $$
$$ \begin{align*} \mathbb{E}_{J, X_J, X_J^{\prime}}^{\mathcal{F}^c}\, e^{\langle (X + X')_J,u \rangle } \cdot \left|\mathbb{E}_{X_I}\, e^{4\pi i \theta\langle \frac{A^{-1} \widetilde{X} }{\mu_1},X_I\rangle+2\langle X_I,u\rangle} \right| &\leqslant \mathbb{E}_{J, X_J, X_J^{\prime}}^{\mathcal{F}^c}\, e^{\langle (X + X')_J,u \rangle }\mathbb{E}_{X_I}\, e^{2\langle X_I,u\rangle} \\ &= \mathbb{E}_{J,X,X'}^{\mathcal{F}^c}e^{\langle Y,u \rangle } .\end{align*} $$
By Cauchy-Schwarz, (5.2), and Lemma 5.6, we have
We now consider the contribution to the expectation on the right-hand side of (5.12) from triples
![]() $(J,X_J,X_J^{\prime }) \in \mathcal {F}$
. For this, let
$(J,X_J,X_J^{\prime }) \in \mathcal {F}$
. For this, let
![]() $w=w(X):=\frac {A^{-1}\widetilde {X}}{\mu _1}$
and assume
$w=w(X):=\frac {A^{-1}\widetilde {X}}{\mu _1}$
and assume
![]() $(J,X_J,X_J^{\prime }) \in \mathcal {F}$
. By Lemma 5.5, we have
$(J,X_J,X_J^{\prime }) \in \mathcal {F}$
. By Lemma 5.5, we have
 $$ \begin{align} \big|\mathbb{E}_{X_I} e^{ 4\pi i {\theta} \langle X_I, w\rangle +\langle X_I,2u \rangle }\big| \lesssim \exp\left(-c \min_{r \in [1,c^{-1}]} \|2r\theta w_I\|_{\mathbb{T}}^2\right). \end{align} $$
$$ \begin{align} \big|\mathbb{E}_{X_I} e^{ 4\pi i {\theta} \langle X_I, w\rangle +\langle X_I,2u \rangle }\big| \lesssim \exp\left(-c \min_{r \in [1,c^{-1}]} \|2r\theta w_I\|_{\mathbb{T}}^2\right). \end{align} $$
Note that
![]() $\|w_I\|_2\leqslant \|\widetilde {X}\|_2\leqslant c^{-1}\sqrt {n}$
, by the definition of
$\|w_I\|_2\leqslant \|\widetilde {X}\|_2\leqslant c^{-1}\sqrt {n}$
, by the definition of
![]() $\mu _1 = \sigma _{\max }(A^{-1})$
and line (5.8) in the definition of
$\mu _1 = \sigma _{\max }(A^{-1})$
and line (5.8) in the definition of
![]() $\mathcal {F}(A)$
.
$\mathcal {F}(A)$
.
Now, from property (5.10) in that definition and by the hypothesis
![]() $\delta> e^{-c_1 n}$
, we may choose
$\delta> e^{-c_1 n}$
, we may choose
![]() $c_1> 0$
small enough so that
$c_1> 0$
small enough so that
By the definition of the least common denominator, for
![]() $|\theta | \leqslant 1/\delta $
, we have
$|\theta | \leqslant 1/\delta $
, we have
 $$ \begin{align} \min_{r \in [1,c^{-1}]} \| 2r\theta w_I \|_{\mathbb{T}} = \min_{r \in [1,c^{-1}]} \left\|2r\theta\|w_I\|_2\cdot \frac{w_I}{\|w_I\|_2}\right\|_{\mathbb{T}} \geqslant \min\left\lbrace \gamma\theta\|w_I\|_2, \sqrt{\alpha |I|}\right\rbrace. \end{align} $$
$$ \begin{align} \min_{r \in [1,c^{-1}]} \| 2r\theta w_I \|_{\mathbb{T}} = \min_{r \in [1,c^{-1}]} \left\|2r\theta\|w_I\|_2\cdot \frac{w_I}{\|w_I\|_2}\right\|_{\mathbb{T}} \geqslant \min\left\lbrace \gamma\theta\|w_I\|_2, \sqrt{\alpha |I|}\right\rbrace. \end{align} $$
So, for
![]() $|\theta |\leqslant 1/\delta $
, we use (5.15) in (5.14) to bound the right-hand side of (5.12) as
$|\theta |\leqslant 1/\delta $
, we use (5.15) in (5.14) to bound the right-hand side of (5.12) as
We now use that
![]() $(J,X_J,X_J^{\prime }) \in \mathcal {F}$
to see that
$(J,X_J,X_J^{\prime }) \in \mathcal {F}$
to see that
![]() $w \in \mathrm {Incomp\,}(\delta ,\rho )$
and that we chose
$w \in \mathrm {Incomp\,}(\delta ,\rho )$
and that we chose
![]() $\mu $
to be sufficiently small, compared to
$\mu $
to be sufficiently small, compared to
![]() $\rho ,\delta $
, to guarantee that
$\rho ,\delta $
, to guarantee that
for some
![]() $C> 0$
(see (4.7)). Thus, the right-hand side of (5.16) is
$C> 0$
(see (4.7)). Thus, the right-hand side of (5.16) is
Combining this with (5.16), (5.12) obtains the desired bound in the case
![]() $(J,X_J,X^{\prime }_J) \in \mathcal {F}$
. Combining this with (5.13) completes the proof of Lemma 5.2.
$(J,X_J,X^{\prime }_J) \in \mathcal {F}$
. Combining this with (5.13) completes the proof of Lemma 5.2.
6 Preparation for the “base step” of the iteration
As we mentioned at (2.1), Vershynin [Reference Vershynin46] gave a natural way of bounding the least singular value of a random symmetric matrix:
where we recall that
![]() $A_n$
is obtained from
$A_n$
is obtained from
![]() $A_{n+1}$
by deleting its first row and column. The main goal of this section is to prove the following lemma which tells us that we may intersect with the event
$A_{n+1}$
by deleting its first row and column. The main goal of this section is to prove the following lemma which tells us that we may intersect with the event
![]() $\sigma _{\min }(A_{n}) \geqslant \varepsilon n^{-1/2}$
in the probability on the right-hand side, at a loss of
$\sigma _{\min }(A_{n}) \geqslant \varepsilon n^{-1/2}$
in the probability on the right-hand side, at a loss of
![]() $C\varepsilon $
. This will be crucial for the base step in our iteration, since the bound we obtain on
$C\varepsilon $
. This will be crucial for the base step in our iteration, since the bound we obtain on
![]() $\mathbb {P}( \sigma _{\min }(A_{n+1}) \leqslant \varepsilon n^{-1/2} )$
deteriorates as
$\mathbb {P}( \sigma _{\min }(A_{n+1}) \leqslant \varepsilon n^{-1/2} )$
deteriorates as
![]() $\sigma _{\min }(A_n)$
decreases.
$\sigma _{\min }(A_n)$
decreases.
Lemma 6.1. For
![]() $B> 0$
,
$B> 0$
,
![]() $\zeta \in \Gamma _B$
, let
$\zeta \in \Gamma _B$
, let
![]() $A_{n+1} \sim \mathrm {Sym\,}_{n+1}(\zeta ) $
and let
$A_{n+1} \sim \mathrm {Sym\,}_{n+1}(\zeta ) $
and let
![]() $X \sim \mathrm {Col\,}_n(\zeta )$
. Then
$X \sim \mathrm {Col\,}_n(\zeta )$
. Then
 $$ \begin{align*}\mathbb{P}\left(\sigma_{\min}(A_{n+1}) \leqslant \varepsilon n^{-1/2} \right) \lesssim \varepsilon + \sup_{r \in \mathbb{R}}\, \mathbb{P}\left(\frac{|\langle A_n^{-1}X, X\rangle - r|}{ \|A_n^{-1} X \|_2} \leqslant C \varepsilon , \sigma_{\min}(A_{n}) \geqslant \varepsilon n^{-1/2} \right) + e^{-\Omega(n)} \,,\end{align*} $$
$$ \begin{align*}\mathbb{P}\left(\sigma_{\min}(A_{n+1}) \leqslant \varepsilon n^{-1/2} \right) \lesssim \varepsilon + \sup_{r \in \mathbb{R}}\, \mathbb{P}\left(\frac{|\langle A_n^{-1}X, X\rangle - r|}{ \|A_n^{-1} X \|_2} \leqslant C \varepsilon , \sigma_{\min}(A_{n}) \geqslant \varepsilon n^{-1/2} \right) + e^{-\Omega(n)} \,,\end{align*} $$
for all
![]() $\varepsilon>0$
. Here,
$\varepsilon>0$
. Here,
![]() $C> 0$
depends only on B.
$C> 0$
depends only on B.
We deduce Lemma 6.1 from a geometric form of the lemma, which we state here. Let
![]() $X_j$
denote the jth column of
$X_j$
denote the jth column of
![]() $A_{n+1}$
, and let
$A_{n+1}$
, and let
We shall prove the following “geometric” version of Lemma 6.1.
Lemma 6.2. For
![]() $B>0$
,
$B>0$
,
![]() $\zeta \in \Gamma _B$
, let
$\zeta \in \Gamma _B$
, let
![]() $A_{n+1} \sim \mathrm {Sym\,}_{n+1}(\zeta )$
. Then for all
$A_{n+1} \sim \mathrm {Sym\,}_{n+1}(\zeta )$
. Then for all
![]() $\varepsilon>0$
,
$\varepsilon>0$
,
where
![]() $C> 0$
depends only on B.
$C> 0$
depends only on B.
The deduction of Lemma 6.1 from Lemma 6.2 is straightforward given the ideas from [Reference Vershynin46]; so we turn to discuss the proof of Lemma 6.2.
For this, we want to intersect the event
![]() $\sigma _{\min }(A_{n+1}) \leqslant \varepsilon n^{-1/2}$
with the event
$\sigma _{\min }(A_{n+1}) \leqslant \varepsilon n^{-1/2}$
with the event
![]() $\sigma _{\min }(A_n) \geqslant \varepsilon n^{-1/2}$
, where we understand
$\sigma _{\min }(A_n) \geqslant \varepsilon n^{-1/2}$
, where we understand
![]() $A_n$
to be the principal minor
$A_n$
to be the principal minor
![]() $A_{n+1}^{(n+1)}$
of
$A_{n+1}^{(n+1)}$
of
![]() $A_{n+1}$
. To do this, we first consider the related “pathological” event
$A_{n+1}$
. To do this, we first consider the related “pathological” event
and then split our probability of interest into the sum
and work with each term separately. Here,
![]() $c = c_{\rho ,\delta }/2$
, where
$c = c_{\rho ,\delta }/2$
, where
![]() $c_{\rho ,\delta }$
is the constant defined in Section 4.
$c_{\rho ,\delta }$
is the constant defined in Section 4.
We deal with the second term on the right-hand side by showing
by a straightforward argument in a manner similar to Rudelson and Vershynin in [Reference Rudelson and Vershynin31]. We then deal with the first term on the right-hand side of (6.1) by showing that
Putting these two inequalities together then implies Lemma 6.2.
6.1 Proof of the inequality at (6.2)
Here, we prove (6.2) in the following form.
Lemma 6.3. For
![]() $B>0$
,
$B>0$
,
![]() $\zeta \in \Gamma _B$
, let
$\zeta \in \Gamma _B$
, let
![]() $A_{n+1} \sim \mathrm {Sym\,}_{n+1}(\zeta )$
. Then, for all
$A_{n+1} \sim \mathrm {Sym\,}_{n+1}(\zeta )$
. Then, for all
![]() $\varepsilon>0$
, we have
$\varepsilon>0$
, we have
For this, we use a basic but important fact which is at the heart of the geometric approach of Rudelson and Vershynin (see, e.g. [Reference Rudelson and Vershynin31, Lemma 3.5]).
Fact 6.4. Let M be an
![]() $n \times n$
matrix and v be a unit vector satisfying
$n \times n$
matrix and v be a unit vector satisfying
![]() $\| M v \|_2 = \sigma _{\min }(M)$
. Then
$\| M v \|_2 = \sigma _{\min }(M)$
. Then
We are now ready to prove the inequality mentioned at (6.2).
Proof of Lemma 6.3.
We rule out another pathological event: Let v denote a unit eigenvector corresponding to the least singular value of
![]() $A_{n+1}$
, and let
$A_{n+1}$
, and let
![]() $\mathcal {C}$
denote the event that v is
$\mathcal {C}$
denote the event that v is
![]() $(\rho ,\delta )$
-compressible.Footnote
7
By Lemma 3.2,
$(\rho ,\delta )$
-compressible.Footnote
7
By Lemma 3.2,
![]() $\mathbb {P}(\mathcal {C})\leqslant e^{-\Omega (n)}$
. Thus
$\mathbb {P}(\mathcal {C})\leqslant e^{-\Omega (n)}$
. Thus
We now look to bound this event in terms of the distance of the column
![]() $X_j$
to the subspace
$X_j$
to the subspace
![]() $H_j$
, in the style of [Reference Rudelson and Vershynin31]. For this, we define
$H_j$
, in the style of [Reference Rudelson and Vershynin31]. For this, we define
We now claim
To see this, fix a matrix A satisfying the left-hand side of (6.5) and let v be an eigenvector corresponding to the least singular value. Now, since v is not compressible, there are
![]() $\geqslant c_{\rho ,\delta } n$
values of
$\geqslant c_{\rho ,\delta } n$
values of
![]() $j \in [n+1]$
for which
$j \in [n+1]$
for which
![]() $|v_j| \geqslant c_{\rho ,\delta }n^{-1/2}$
. Thus, Fact 6.4 immediately tells us there are
$|v_j| \geqslant c_{\rho ,\delta }n^{-1/2}$
. Thus, Fact 6.4 immediately tells us there are
![]() $\geqslant c_{\rho ,\delta } n$
values of
$\geqslant c_{\rho ,\delta } n$
values of
![]() $j \in [n+1]$
for which
$j \in [n+1]$
for which
![]() $d_{j}(A) \leqslant \varepsilon /c_{\rho ,\delta }$
. Finally, by definition of
$d_{j}(A) \leqslant \varepsilon /c_{\rho ,\delta }$
. Finally, by definition of
![]() $\mathcal {P}^c$
, at most
$\mathcal {P}^c$
, at most
![]() $c_{\rho ,\delta }n/2$
of these values of j satisfy
$c_{\rho ,\delta }n/2$
of these values of j satisfy
![]() $\sigma _{n+1}(A^{(j)}) \leqslant \varepsilon n^{-1/2}$
, and so (6.5) is proved.
$\sigma _{n+1}(A^{(j)}) \leqslant \varepsilon n^{-1/2}$
, and so (6.5) is proved.
We now use (6.5) along with Markov’s inequality to bound
Now, by definition of S and symmetry of the coordinates, we have
 $$ \begin{align*} \mathbb{E} |S| &= \sum_j \mathbb{P}\big( d_j(A_{n+1}) \leqslant \varepsilon/c_{\rho, \delta}, ~\sigma_{\min}(A_{n+1}^{(j)}) \geqslant \varepsilon n^{-1/2} \big) \\ &= n\cdot \mathbb{P}\big(d_1(A_{n+1}) \leqslant \varepsilon/c_{\rho, \delta},~\sigma_{\min}(A_{n+1}^{(1)}) \geqslant \varepsilon n^{-1/2} \big)\,. \end{align*} $$
$$ \begin{align*} \mathbb{E} |S| &= \sum_j \mathbb{P}\big( d_j(A_{n+1}) \leqslant \varepsilon/c_{\rho, \delta}, ~\sigma_{\min}(A_{n+1}^{(j)}) \geqslant \varepsilon n^{-1/2} \big) \\ &= n\cdot \mathbb{P}\big(d_1(A_{n+1}) \leqslant \varepsilon/c_{\rho, \delta},~\sigma_{\min}(A_{n+1}^{(1)}) \geqslant \varepsilon n^{-1/2} \big)\,. \end{align*} $$
Putting this together with (6.6) and (6.5) finishes the proof.
6.2 Proof of the inequality at (6.3)
We now prove the inequality discussed at (6.3) in the following form.
Lemma 6.5. For
![]() $B>0$
,
$B>0$
,
![]() $\zeta \in \Gamma _B$
, let
$\zeta \in \Gamma _B$
, let
![]() $A_{n+1} \sim \mathrm {Sym\,}_{n+1}(\zeta )$
. Then, for all
$A_{n+1} \sim \mathrm {Sym\,}_{n+1}(\zeta )$
. Then, for all
![]() $\varepsilon>0$
, we have
$\varepsilon>0$
, we have
For the proof of this lemma, we will need a few results from the random matrix literature. The first such result is a more sophisticated version of Lemma 3.2, which tells us that the mass of the eigenvectors of A does not “localize” on a set of coordinates of size
![]() $o(n)$
. The theorem we need, due to Rudelson and Vershynin (Theorem 1.5 in [Reference Rudelson and Vershynin35]), tells us that the mass of the eigenvectors of our random matrix does not “localize” on a set of coordinates of size
$o(n)$
. The theorem we need, due to Rudelson and Vershynin (Theorem 1.5 in [Reference Rudelson and Vershynin35]), tells us that the mass of the eigenvectors of our random matrix does not “localize” on a set of coordinates of size
![]() $(1-c)n$
, for any fixed
$(1-c)n$
, for any fixed
![]() $c>0$
. We state this result in a way to match our application.
$c>0$
. We state this result in a way to match our application.
Theorem 6.6. For
![]() $B>0$
,
$B>0$
,
![]() $\zeta \in \Gamma _B$
, let
$\zeta \in \Gamma _B$
, let
![]() $A \sim \mathrm {Sym\,}_{n}(\zeta )$
and let v denote the unit eigenvector of A corresponding to the least singular value of A. Then there exists
$A \sim \mathrm {Sym\,}_{n}(\zeta )$
and let v denote the unit eigenvector of A corresponding to the least singular value of A. Then there exists
![]() $c_2>0$
, such that for all sufficiently small
$c_2>0$
, such that for all sufficiently small
![]() $c_1>0$
, we have
$c_1>0$
, we have
for n sufficiently large.
We also require an elementary, but extremely useful, fact from linear algebra. This fact is a key step in the work of Nguyen et al. on eigenvalue repulsion in random matrices (see [Reference Nguyen, Tao and Vu24, Section 4]); we state it here in a form best suited for our application.
Fact 6.7. Let M be an
![]() $n\times n$
real symmetric matrix, and let
$n\times n$
real symmetric matrix, and let
![]() ${\lambda }$
be an eigenvalue of M with corresponding unit eigenvector u. Let
${\lambda }$
be an eigenvalue of M with corresponding unit eigenvector u. Let
![]() $j\in [n]$
, and let
$j\in [n]$
, and let
![]() ${\lambda }'$
be an eigenvector of the minor
${\lambda }'$
be an eigenvector of the minor
![]() $M^{(j)}$
with corresponding unit eigenvector v. Then
$M^{(j)}$
with corresponding unit eigenvector v. Then
where
![]() $X^{(j)}$
is the jth column of M with the jth entry removed.
$X^{(j)}$
is the jth column of M with the jth entry removed.
Proof. Without loss of generality, take
![]() $j = n$
and express
$j = n$
and express
![]() $u = (w,u_{n})$
, where
$u = (w,u_{n})$
, where
![]() $w \in \mathbb {R}^{n-1}$
. Then we have
$w \in \mathbb {R}^{n-1}$
. Then we have
![]() $(M^{(n)} - \lambda I )w + X^{(n)} u_{n} = 0$
. Multiplying on the left by
$(M^{(n)} - \lambda I )w + X^{(n)} u_{n} = 0$
. Multiplying on the left by
![]() $v^T$
yields
$v^T$
yields
We shall also need the inverse Littlewood-Offord theorem of Rudelson and Vershynin [Reference Rudelson and Vershynin31], which we have stated here in simplified form. Recall that
![]() $D_{\alpha ,\gamma }(v)$
is the least common denominator of the vector v, as defined at (1.11).
$D_{\alpha ,\gamma }(v)$
is the least common denominator of the vector v, as defined at (1.11).
Theorem 6.8. For
![]() $n\in \mathbb {N}$
,
$n\in \mathbb {N}$
,
![]() $B>0$
,
$B>0$
,
![]() $\gamma ,\alpha \in (0,1)$
, and
$\gamma ,\alpha \in (0,1)$
, and
![]() $\varepsilon> 0$
, let
$\varepsilon> 0$
, let
![]() $v\in {\mathbb {S}}^{n-1}$
satisfy
$v\in {\mathbb {S}}^{n-1}$
satisfy
![]() $D_{\alpha ,\gamma }(v)> c\varepsilon ^{-1}$
and let
$D_{\alpha ,\gamma }(v)> c\varepsilon ^{-1}$
and let
![]() $X \sim \mathrm {Col\,}_n(\zeta )$
, where
$X \sim \mathrm {Col\,}_n(\zeta )$
, where
![]() $\zeta \in \Gamma _B$
. Then
$\zeta \in \Gamma _B$
. Then
Here,
![]() $c>0$
depends only on B and
$c>0$
depends only on B and
![]() $\gamma $
.
$\gamma $
.
We are now in a position to prove Lemma 6.5.
Proof of Lemma 6.5.
Let A be an instance of our random matrix, and let v be the unit eigenvector corresponding to the least singular value of A. Let
![]() $w_j = w(A^{(j)})$
denote a unit eigenvector of
$w_j = w(A^{(j)})$
denote a unit eigenvector of
![]() $A^{(j)}$
corresponding to the least singular value of
$A^{(j)}$
corresponding to the least singular value of
![]() $A^{(j)}$
.
$A^{(j)}$
.
We introduce two “quasi-randomness” events
![]() $\mathcal {Q}$
and
$\mathcal {Q}$
and
![]() $\mathcal {A}$
that will hold with probability
$\mathcal {A}$
that will hold with probability
![]() $1-e^{\Omega (n)}$
. Indeed, define
$1-e^{\Omega (n)}$
. Indeed, define
Here,
![]() $\alpha , \gamma , c_3$
are chosen according to Lemma 4.1, which tells us that
$\alpha , \gamma , c_3$
are chosen according to Lemma 4.1, which tells us that
![]() $\mathbb {P}(\mathcal {Q}^c) \leqslant e^{-\Omega (n)}$
. Define
$\mathbb {P}(\mathcal {Q}^c) \leqslant e^{-\Omega (n)}$
. Define
Note that
![]() $\mathcal {P}$
holds exactly when
$\mathcal {P}$
holds exactly when
![]() $|S_1| \geqslant cn $
. Let
$|S_1| \geqslant cn $
. Let
![]() $\mathcal {A}$
be the “non-localization” event that
$\mathcal {A}$
be the “non-localization” event that
![]() $|S_2| \geqslant (1-c/2)n$
. By Theorem 6.6, we have
$|S_2| \geqslant (1-c/2)n$
. By Theorem 6.6, we have
![]() $\mathbb {P}(\mathcal {A}^c)\leqslant e^{-\Omega (n)}$
. Here,
$\mathbb {P}(\mathcal {A}^c)\leqslant e^{-\Omega (n)}$
. Here,
![]() $c/2 = c_{\rho ,\delta }/4$
. Now, if we let
$c/2 = c_{\rho ,\delta }/4$
. Now, if we let
![]() $X^{(j)}$
denote the jth column of A with the jth entry removed, we define
$X^{(j)}$
denote the jth column of A with the jth entry removed, we define
where
![]() $C = 2^7/(c_2c)^6$
. We now claim
$C = 2^7/(c_2c)^6$
. We now claim
To see this, first note that if
![]() $\mathcal {P} \cap \mathcal {A}$
holds, then
$\mathcal {P} \cap \mathcal {A}$
holds, then
![]() $|S_1\cap S_2| \geqslant cn/2$
. Also, for each
$|S_1\cap S_2| \geqslant cn/2$
. Also, for each
![]() $j \in S_1 \cap S_2$
, we may apply Fact 6.7 to see that
$j \in S_1 \cap S_2$
, we may apply Fact 6.7 to see that
![]() $|\langle w_j, X^{(j)}\rangle | \leqslant C \varepsilon $
since j is such that
$|\langle w_j, X^{(j)}\rangle | \leqslant C \varepsilon $
since j is such that
![]() $\sigma _{\min }( A^{(j)}) \leqslant \varepsilon n^{-1/2}$
and
$\sigma _{\min }( A^{(j)}) \leqslant \varepsilon n^{-1/2}$
and
![]() $\sigma _{\min }(A) \leqslant \varepsilon n^{-1/2}$
. This proves (6.8).
$\sigma _{\min }(A) \leqslant \varepsilon n^{-1/2}$
. This proves (6.8).
To finish the proof of Lemma 6.5, we define the random variable
 $$\begin{align*}R = n^{-1} \sum_j {\mathbf{1}}\left( |\langle w_j , X^{(j)} \rangle| \leqslant C\varepsilon \text{ and } \mathcal{Q}_j \right),\end{align*}$$
$$\begin{align*}R = n^{-1} \sum_j {\mathbf{1}}\left( |\langle w_j , X^{(j)} \rangle| \leqslant C\varepsilon \text{ and } \mathcal{Q}_j \right),\end{align*}$$
and observe that
![]() $ \mathbb {P}(\sigma _{\min }(A_{n+1}) \leqslant \varepsilon n^{-1/2} \cap \mathcal {P} ) $
is at most
$ \mathbb {P}(\sigma _{\min }(A_{n+1}) \leqslant \varepsilon n^{-1/2} \cap \mathcal {P} ) $
is at most
We now apply Markov and expand the definition of R to bound
 $$\begin{align*}\mathbb{P}( R \geqslant c/4) \lesssim n^{-1} \sum_{j} \mathbb{E}_{A^{(j)}_{n+1}}\mathbb{P}_{X^{(j)}}\left( |\langle w_j , X^{(j)} \rangle| \leqslant C\varepsilon \cap \mathcal{Q}_j \right) \lesssim \varepsilon + e^{-\Omega(n)},\end{align*}$$
$$\begin{align*}\mathbb{P}( R \geqslant c/4) \lesssim n^{-1} \sum_{j} \mathbb{E}_{A^{(j)}_{n+1}}\mathbb{P}_{X^{(j)}}\left( |\langle w_j , X^{(j)} \rangle| \leqslant C\varepsilon \cap \mathcal{Q}_j \right) \lesssim \varepsilon + e^{-\Omega(n)},\end{align*}$$
where the last inequality follows from the fact that
![]() $X^{(j)}$
is independent of the events
$X^{(j)}$
is independent of the events
![]() $Q_j$
and
$Q_j$
and
![]() $w_j$
, and therefore we may put the property
$w_j$
, and therefore we may put the property
![]() $\mathcal {Q}_j$
to use by applying the inverse Littlewood-Offord theorem of Rudelson and Vershynin, Theorem 6.8.
$\mathcal {Q}_j$
to use by applying the inverse Littlewood-Offord theorem of Rudelson and Vershynin, Theorem 6.8.
6.3 Proofs of Lemmas 6.2 and 6.1
All that remains is to put the pieces together and prove Lemmas 6.2 and 6.1.
Proof of Lemma 6.2.
As we saw at (6.1), we simply express
![]() $\mathbb {P}( \sigma _{\min }(A_{n+1})\leqslant \varepsilon n^{-1/2} )$
as
$\mathbb {P}( \sigma _{\min }(A_{n+1})\leqslant \varepsilon n^{-1/2} )$
as
and then apply Lemma 6.5 to the first term and Lemma 6.3 to the second term.
Proof of Lemma 6.1.
If we set
![]() $a_{1,1}$
to be the first entry of
$a_{1,1}$
to be the first entry of
![]() $A = A_{n+1}$
, then, by [Reference Vershynin46, Proposition 5.1], we have that
$A = A_{n+1}$
, then, by [Reference Vershynin46, Proposition 5.1], we have that
 $$ \begin{align*}d_1(A_{n+1}) = \frac{|\langle A^{-1} X, X \rangle - a_{1,1} |}{\sqrt{1 + \|A^{-1}X\|_2^2 } }\,.\end{align*} $$
$$ \begin{align*}d_1(A_{n+1}) = \frac{|\langle A^{-1} X, X \rangle - a_{1,1} |}{\sqrt{1 + \|A^{-1}X\|_2^2 } }\,.\end{align*} $$
Additionally, by [Reference Vershynin46, Proposition 8.2], we have
![]() $\|A^{-1}X\|_2> 1/15$
with probability at least
$\|A^{-1}X\|_2> 1/15$
with probability at least
![]() $1 - e^{-\Omega (n)}$
. Replacing
$1 - e^{-\Omega (n)}$
. Replacing
![]() $a_{1,1}$
with r and taking a supremum completes the proof of Lemma 6.1.
$a_{1,1}$
with r and taking a supremum completes the proof of Lemma 6.1.
7 Eigenvalue crowding (and the proofs of Theorems 1.2 and 1.3)
The main purpose of this section is to prove the following theorem, which gives an upper bound on the probability that
![]() $k \geqslant 2$
eigenvalues of a random matrix fall in an interval of length
$k \geqslant 2$
eigenvalues of a random matrix fall in an interval of length
![]() $\varepsilon $
. The case
$\varepsilon $
. The case
![]() $\varepsilon = 0$
of this theorem tells us that the probability that a random symmetric matrix has simple spectrum (that is, has no repeated eigenvalue) is
$\varepsilon = 0$
of this theorem tells us that the probability that a random symmetric matrix has simple spectrum (that is, has no repeated eigenvalue) is
![]() $1-e^{-\Omega (n)}$
, which is sharp and confirms a conjecture of Nguyen et al. [Reference Nguyen, Tao and Vu24].
$1-e^{-\Omega (n)}$
, which is sharp and confirms a conjecture of Nguyen et al. [Reference Nguyen, Tao and Vu24].
Given an
![]() $n\times n$
real symmetric matrix M, we let
$n\times n$
real symmetric matrix M, we let
![]() $\lambda _1(M)\geqslant \ldots \geqslant \lambda _n(M)$
denote its eigenvalues.
$\lambda _1(M)\geqslant \ldots \geqslant \lambda _n(M)$
denote its eigenvalues.
Theorem 7.1. For
![]() $B>0$
,
$B>0$
,
![]() $\zeta \in \Gamma _B$
, let
$\zeta \in \Gamma _B$
, let
![]() $A_{n+1} \sim \mathrm {Sym\,}_{n+1}(\zeta ) $
. Then for each
$A_{n+1} \sim \mathrm {Sym\,}_{n+1}(\zeta ) $
. Then for each
![]() $j \leqslant cn$
and all
$j \leqslant cn$
and all
![]() $\varepsilon \geqslant 0$
, we have
$\varepsilon \geqslant 0$
, we have
where
![]() $C,c>0$
are constants depending on B.
$C,c>0$
are constants depending on B.
We suspect that the bound in Lemma 1.3 is actually far from the truth, for
![]() $\varepsilon> e^{-cn}$
and
$\varepsilon> e^{-cn}$
and
![]() $j \geqslant 1 $
. In fact, one expects quadratic dependence on j in the exponent of
$j \geqslant 1 $
. In fact, one expects quadratic dependence on j in the exponent of
![]() $\varepsilon $
. This type of dependence was recently confirmed by Nguyen [Reference Nguyen27] for
$\varepsilon $
. This type of dependence was recently confirmed by Nguyen [Reference Nguyen27] for
![]() $\varepsilon> e^{-n^{c}}$
.
$\varepsilon> e^{-n^{c}}$
.
For the proof of Lemma 1.3, we remind the reader that if
![]() $u \in \mathbb {R}^n \cap \mathrm {Incomp\,}(\rho ,\delta )$
, then at least
$u \in \mathbb {R}^n \cap \mathrm {Incomp\,}(\rho ,\delta )$
, then at least
![]() $c_{\rho ,\delta }n$
coordinates of u have absolute value at least
$c_{\rho ,\delta }n$
coordinates of u have absolute value at least
![]() $c_{\rho ,\delta }n^{-1/2}$
.
$c_{\rho ,\delta }n^{-1/2}$
.
In what follows, for an
![]() $n \times n$
symmetric matrix A, we use the notation
$n \times n$
symmetric matrix A, we use the notation
![]() $A^{(i_1,\ldots , i_r)}$
to refer to the minor of A for which the rows and columns indexed by
$A^{(i_1,\ldots , i_r)}$
to refer to the minor of A for which the rows and columns indexed by
![]() $i_1,\ldots ,i_r$
have been deleted. We also use the notation
$i_1,\ldots ,i_r$
have been deleted. We also use the notation
![]() $A_{S \times T}$
to refer to the
$A_{S \times T}$
to refer to the
![]() $|S| \times |T|$
submatrix of A defined by
$|S| \times |T|$
submatrix of A defined by
![]() $(A_{i,j})_{i \in S, j\in T}$
.
$(A_{i,j})_{i \in S, j\in T}$
.
The following fact contains the key linear algebra required for the proof of Theorem 1.3.
Fact 7.2. For
![]() $1\leqslant k +j < n$
, let A be an
$1\leqslant k +j < n$
, let A be an
![]() $n \times n$
symmetric matrix for which
$n \times n$
symmetric matrix for which
Let
![]() $(i_1,\ldots ,i_j) \in [n]^j$
be such that
$(i_1,\ldots ,i_j) \in [n]^j$
be such that
![]() $i_1,\ldots , i_j$
are distinct. Then there exist unit vectors
$i_1,\ldots , i_j$
are distinct. Then there exist unit vectors
![]() $w^{(1)},\ldots ,w^{(k)}$
for which
$w^{(1)},\ldots ,w^{(k)}$
for which
where
![]() $X_r \in \mathbb {R}^{n-r} $
is the
$X_r \in \mathbb {R}^{n-r} $
is the
![]() $i_r$
th column of A with coordinates indexed by
$i_r$
th column of A with coordinates indexed by
![]() $i_1,\ldots ,i_r$
removed. That is,
$i_1,\ldots ,i_r$
removed. That is,
![]() $X_r := A_{ [n] \setminus \{i_1,\ldots , i_r \} \times \{i_r\} }$
and
$X_r := A_{ [n] \setminus \{i_1,\ldots , i_r \} \times \{i_r\} }$
and
![]() $w^{(r)}$
is a unit eigenvector corresponding to
$w^{(r)}$
is a unit eigenvector corresponding to
![]() ${\lambda }_{k}(A^{(i_1,\ldots , i_r)})$
.
${\lambda }_{k}(A^{(i_1,\ldots , i_r)})$
.
Proof. For
![]() $(i_1,\ldots ,i_j)\in [n]^j$
, define the matrices
$(i_1,\ldots ,i_j)\in [n]^j$
, define the matrices
![]() $M_0,M_1,\ldots ,M_j$
by setting
$M_0,M_1,\ldots ,M_j$
by setting
![]() $M_r = A^{(i_1,\ldots ,i_r)}$
for
$M_r = A^{(i_1,\ldots ,i_r)}$
for
![]() $r = 1,\ldots , j$
and then
$r = 1,\ldots , j$
and then
![]() $M_0 := A$
. Now if
$M_0 := A$
. Now if
then Cauchy’s interlacing theorem implies
for all
![]() $r = 1,\ldots ,j$
. So let
$r = 1,\ldots ,j$
. So let
![]() $w^{(r)}$
denote a unit eigenvector of
$w^{(r)}$
denote a unit eigenvector of
![]() $M_r$
corresponding to eigenvalue
$M_r$
corresponding to eigenvalue
![]() $\lambda _k(M_r)$
. Thus, by Fact 6.7, we see that
$\lambda _k(M_r)$
. Thus, by Fact 6.7, we see that
for
![]() $r=1, \ldots , j$
, where
$r=1, \ldots , j$
, where
![]() $X_r \in \mathbb {R}^{n-r}$
is the
$X_r \in \mathbb {R}^{n-r}$
is the
![]() $i_r$
th column of
$i_r$
th column of
![]() $M_{r-1}$
, with the diagonal entry removed. In other words,
$M_{r-1}$
, with the diagonal entry removed. In other words,
![]() $X_r \in \mathbb {R}^{n-r} $
is the
$X_r \in \mathbb {R}^{n-r} $
is the
![]() $i_r$
th column of A with coordinates indexed by
$i_r$
th column of A with coordinates indexed by
![]() $i_1,\ldots ,i_r$
removed. This completes the proof of Fact 7.2.
$i_1,\ldots ,i_r$
removed. This completes the proof of Fact 7.2.
Proof of Theorem 1.3.
Note, we may assume that
![]() $\varepsilon> e^{-cn}$
; the general case follows by taking c sufficiently small. Now, define
$\varepsilon> e^{-cn}$
; the general case follows by taking c sufficiently small. Now, define
![]() $\mathcal {A}$
to be the event that all unit eigenvectors v of all
$\mathcal {A}$
to be the event that all unit eigenvectors v of all
![]() $\binom {n}{j}$
of the minors
$\binom {n}{j}$
of the minors
![]() $A^{(i_1,\ldots ,i_j)}_n$
lie in
$A^{(i_1,\ldots ,i_j)}_n$
lie in
![]() $\mathrm {Incomp\,}(\rho ,\delta )$
and satisfy
$\mathrm {Incomp\,}(\rho ,\delta )$
and satisfy
![]() $D_{\alpha , \gamma }(v)>e^{c_3 n}$
, where
$D_{\alpha , \gamma }(v)>e^{c_3 n}$
, where
![]() $\alpha , \gamma , c_3$
are chosen according to Lemma 4.1. Note that by Lemmas 4.1 and 3.2, we have
$\alpha , \gamma , c_3$
are chosen according to Lemma 4.1. Note that by Lemmas 4.1 and 3.2, we have
 $$\begin{align*}\mathbb{P}(\mathcal{A}^c) \leqslant \binom{n}{j+1} e^{-\Omega(n)} \leqslant n\left(\frac{en}{j} \right)^{j} e^{-\Omega(n)} \lesssim e^{-cn},\end{align*}$$
$$\begin{align*}\mathbb{P}(\mathcal{A}^c) \leqslant \binom{n}{j+1} e^{-\Omega(n)} \leqslant n\left(\frac{en}{j} \right)^{j} e^{-\Omega(n)} \lesssim e^{-cn},\end{align*}$$
by taking c small enough, so that
![]() $j\log (en/j) < cn$
is smaller than the
$j\log (en/j) < cn$
is smaller than the
![]() $\Omega (n)$
term.
$\Omega (n)$
term.
With Fact 7.2 in mind, we define the event,
![]() $ \mathcal {E}_{i_1,\ldots ,i_j}$
, for each
$ \mathcal {E}_{i_1,\ldots ,i_j}$
, for each
![]() $(i_1,\ldots ,i_j) \in [n]^j$
,
$(i_1,\ldots ,i_j) \in [n]^j$
,
![]() $i_r$
distinct, to be the event that
$i_r$
distinct, to be the event that
where
![]() $X_r \in \mathbb {R}^{n-r} $
is the
$X_r \in \mathbb {R}^{n-r} $
is the
![]() $i_r$
th column of A with coordinates indexed by
$i_r$
th column of A with coordinates indexed by
![]() $i_1,\ldots ,i_r$
removed and
$i_1,\ldots ,i_r$
removed and
![]() $w^{(r)}$
is a unit eigenvector corresponding to
$w^{(r)}$
is a unit eigenvector corresponding to
![]() ${\lambda }_{k}(A^{(i_1,\ldots , i_r)})$
.
${\lambda }_{k}(A^{(i_1,\ldots , i_r)})$
.
If
![]() $\mathcal {A}$
holds, then each
$\mathcal {A}$
holds, then each
![]() $w^{(r)}$
has at least
$w^{(r)}$
has at least
![]() $c_{\rho ,\delta }n$
coordinates with absolute value at least
$c_{\rho ,\delta }n$
coordinates with absolute value at least
![]() $c_{\rho ,\delta }n^{-1/2}$
. Thus, if additionally we have
$c_{\rho ,\delta }n^{-1/2}$
. Thus, if additionally we have
Fact 7.2 tells us that
![]() $\mathcal {E}_{i_1,\ldots ,i_j}$
occurs for at least
$\mathcal {E}_{i_1,\ldots ,i_j}$
occurs for at least
![]() $(c_{\rho ,\delta }n /2)^j$
tuples
$(c_{\rho ,\delta }n /2)^j$
tuples
![]() $(i_1,\ldots ,i_j)$
.
$(i_1,\ldots ,i_j)$
.
Define N to be the number of indices
![]() $(i_1,\ldots ,i_j)$
for which
$(i_1,\ldots ,i_j)$
for which
![]() $\mathcal {E}_{i_1,\ldots ,i_j}$
occurs, and note
$\mathcal {E}_{i_1,\ldots ,i_j}$
occurs, and note
 $$ \begin{align} &\qquad\qquad\qquad\quad\qquad\qquad\qquad\leqslant \left(\frac{2}{c_{\rho,\delta}}\right)^j\mathbb{P}(\mathcal{E}_{1,\ldots,j} \cap \mathcal{A} ) + O(e^{-cn}) , \end{align} $$
$$ \begin{align} &\qquad\qquad\qquad\quad\qquad\qquad\qquad\leqslant \left(\frac{2}{c_{\rho,\delta}}\right)^j\mathbb{P}(\mathcal{E}_{1,\ldots,j} \cap \mathcal{A} ) + O(e^{-cn}) , \end{align} $$
where, for the second inequality, we applied Markov’s inequality and used the symmetry of the events
![]() $\mathcal {E}_{i_1,\ldots ,i_j}$
.
$\mathcal {E}_{i_1,\ldots ,i_j}$
.
Thus, we need only show that there exists
![]() $C>0$
, such that
$C>0$
, such that
![]() $\mathbb {P}(\mathcal {E}_{1,\ldots ,j} \cap \mathcal {A} ) \leqslant (C\varepsilon )^j$
. To use independence, we replace each of
$\mathbb {P}(\mathcal {E}_{1,\ldots ,j} \cap \mathcal {A} ) \leqslant (C\varepsilon )^j$
. To use independence, we replace each of
![]() $w^{(r)}$
with the worst case vector, under
$w^{(r)}$
with the worst case vector, under
![]() $\mathcal {A}$
$\mathcal {A}$
 $$ \begin{align} &\kern1pt\quad\ \,\leqslant \max_{w_1,\ldots,w_j : D_{\alpha, \gamma}(w_i)> e^{c_3n}} \prod_{r=1}^j \mathbb{P}_{X_r}\big(\, |\langle w_r, X_r \rangle | \leqslant \varepsilon/c_{\rho,\delta}\, \big), \leqslant (C\varepsilon)^j, \end{align} $$
$$ \begin{align} &\kern1pt\quad\ \,\leqslant \max_{w_1,\ldots,w_j : D_{\alpha, \gamma}(w_i)> e^{c_3n}} \prod_{r=1}^j \mathbb{P}_{X_r}\big(\, |\langle w_r, X_r \rangle | \leqslant \varepsilon/c_{\rho,\delta}\, \big), \leqslant (C\varepsilon)^j, \end{align} $$
where the first inequality follows from the independence of the vectors
![]() $\{X_r \}_{r\leqslant j}$
and the last inequality follows from the fact that
$\{X_r \}_{r\leqslant j}$
and the last inequality follows from the fact that
![]() $D_{\alpha ,\gamma }(w_r)> e^{c_3 n}\gtrsim 1/\varepsilon $
(by choosing
$D_{\alpha ,\gamma }(w_r)> e^{c_3 n}\gtrsim 1/\varepsilon $
(by choosing
![]() $c>0$
small enough relative to
$c>0$
small enough relative to
![]() $c_3$
), and the Littlewood-Offord theorem of Rudelson and Vershynin, Lemma 6.8. Putting (7.2) and (7.4) together completes the proof of Theorem 1.3.
$c_3$
), and the Littlewood-Offord theorem of Rudelson and Vershynin, Lemma 6.8. Putting (7.2) and (7.4) together completes the proof of Theorem 1.3.
Of course, the proof of Theorem 1.2 follows immediately.
8 Properties of the spectrum
In this section, we describe and deduce Lemma 8.1 and Corollary 8.2, which are the tools we will use to control the “bulk” of the eigenvalues of
![]() $A^{-1}$
. Here, we understand “bulk” relative to the spectral measure of
$A^{-1}$
. Here, we understand “bulk” relative to the spectral measure of
![]() $A^{-1}$
: our interest in an eigenvalue
$A^{-1}$
: our interest in an eigenvalue
![]() ${\lambda }$
of
${\lambda }$
of
![]() $A^{-1}$
is proportional to its contribution to
$A^{-1}$
is proportional to its contribution to
![]() $\|A^{-1}\|_{\mathrm {HS}}$
. Thus, the behavior of smallest singular values of A are of the highest importance for us.
$\|A^{-1}\|_{\mathrm {HS}}$
. Thus, the behavior of smallest singular values of A are of the highest importance for us.
For this, we let
![]() $\sigma _n \leqslant \sigma _{n-1} \leqslant \cdots \leqslant \sigma _1$
be the singular values of A and let
$\sigma _n \leqslant \sigma _{n-1} \leqslant \cdots \leqslant \sigma _1$
be the singular values of A and let
![]() $\mu _1 \geqslant \ldots \geqslant \mu _n$
be the singular values of
$\mu _1 \geqslant \ldots \geqslant \mu _n$
be the singular values of
![]() $A^{-1}$
. Of course, we have
$A^{-1}$
. Of course, we have
![]() $\mu _k=1/\sigma _{n-k+1}$
for
$\mu _k=1/\sigma _{n-k+1}$
for
![]() $1\leqslant k \leqslant n$
.
$1\leqslant k \leqslant n$
.
In short, these two lemmas, when taken together, tell us that
for all
![]() $n \geqslant k \gg 1$
in some appropriate sense.
$n \geqslant k \gg 1$
in some appropriate sense.
Lemma 8.1. For
![]() $p> 1$
,
$p> 1$
,
![]() $B>0$
and
$B>0$
and
![]() $\zeta \in \Gamma _B$
, let
$\zeta \in \Gamma _B$
, let
![]() $A \sim \mathrm {Sym\,}_n(\zeta )$
. There is a constant
$A \sim \mathrm {Sym\,}_n(\zeta )$
. There is a constant
![]() $C_p$
depending on
$C_p$
depending on
![]() $B,p$
so that
$B,p$
so that
 $$ \begin{align*}\mathbb{E}\, \left( \frac{\sqrt{n}}{\mu_k k}\right)^p \leqslant C_p\,,\end{align*} $$
$$ \begin{align*}\mathbb{E}\, \left( \frac{\sqrt{n}}{\mu_k k}\right)^p \leqslant C_p\,,\end{align*} $$
for all k.
We shall deduce Lemma 8.1 from the “local semicircular law” of Erdős et al. [Reference Erdős, Schlein and Yau13], which gives us good control of the bulk of the spectrum at “scales” of size
![]() $\gg n^{-1/2}$
.
$\gg n^{-1/2}$
.
We also record a useful corollary of this lemma. For this, we define the function
![]() $\| \cdot \|_{\ast } $
for an
$\| \cdot \|_{\ast } $
for an
![]() $n \times n$
symmetric matrix M to be
$n \times n$
symmetric matrix M to be
 $$ \begin{align} \|M\|_\ast^2 = \sum_{k = 1}^n \sigma_k(M)^2 (\log(1 + k))^2. \end{align} $$
$$ \begin{align} \|M\|_\ast^2 = \sum_{k = 1}^n \sigma_k(M)^2 (\log(1 + k))^2. \end{align} $$
The point of this definition is to give some measure to how the spectrum of
![]() $A^{-1}$
is “distorted” from what it “should be,” according to the heuristic at (8.1). Indeed, if we have
$A^{-1}$
is “distorted” from what it “should be,” according to the heuristic at (8.1). Indeed, if we have
![]() $\sigma _{n - k+1} = \Theta ( k/\sqrt {n})$
for all k, say, then we have that
$\sigma _{n - k+1} = \Theta ( k/\sqrt {n})$
for all k, say, then we have that
Conversely, any deviation from this captures some macroscopic misbehavior on the part of the spectrum. In particular, the “weight function”
![]() $k \mapsto (\log (1+k))^2$
is designed to bias the smallest singular values, and thus we are primarily looking at this range for any poor behavior.
$k \mapsto (\log (1+k))^2$
is designed to bias the smallest singular values, and thus we are primarily looking at this range for any poor behavior.
Corollary 8.2. For
![]() $p> 1$
,
$p> 1$
,
![]() $B>0$
, and
$B>0$
, and
![]() $\zeta \in \Gamma _B$
, let
$\zeta \in \Gamma _B$
, let
![]() $A \sim \mathrm {Sym\,}_n(\zeta )$
. Then there exists constants
$A \sim \mathrm {Sym\,}_n(\zeta )$
. Then there exists constants
![]() $C_p, c_p>0$
depending on
$C_p, c_p>0$
depending on
![]() $B,p$
, such that
$B,p$
, such that
 $$ \begin{align*}\mathbb{E} \left[\left(\frac{\|A^{-1}\|_\ast}{\mu_1} \right)^p \right] \leqslant C_p\,.\end{align*} $$
$$ \begin{align*}\mathbb{E} \left[\left(\frac{\|A^{-1}\|_\ast}{\mu_1} \right)^p \right] \leqslant C_p\,.\end{align*} $$
In the remainder of this section, we describe the results of Erdős et al. [Reference Erdős, Schlein and Yau13] and deduce Lemma 8.1. We then deduce Corollary 8.2.
8.1 The local semicircular law and Lemma 8.1
For
![]() $ a < b $
, we define
$ a < b $
, we define
![]() $N_A(a,b)$
to be the number of eigenvalues of A in the interval
$N_A(a,b)$
to be the number of eigenvalues of A in the interval
![]() $(a,b)$
. One of the most fundamental results in the theory of random symmetric matrices is the semicircular law, which says that
$(a,b)$
. One of the most fundamental results in the theory of random symmetric matrices is the semicircular law, which says that
 $$\begin{align*}\lim_{n \rightarrow \infty} \frac{N_A(a\sqrt{n},b\sqrt{n})}{n} = \frac{1}{2\pi}\int_{a}^b(4 - x^2)^{1/2}_+\,dx, \end{align*}$$
$$\begin{align*}\lim_{n \rightarrow \infty} \frac{N_A(a\sqrt{n},b\sqrt{n})}{n} = \frac{1}{2\pi}\int_{a}^b(4 - x^2)^{1/2}_+\,dx, \end{align*}$$
almost surely, where
![]() $A \sim \mathrm {Sym\,}_n(\zeta )$
.
$A \sim \mathrm {Sym\,}_n(\zeta )$
.
We use a powerful “local” version of the semicircle law developed by Erdős et al. in a series of important papers [Reference Erdős, Schlein and Yau10, Reference Erdős, Schlein and Yau11, Reference Erdős, Schlein and Yau13]. Their results show that the spectrum of a random symmetric matrix actually adheres surprisingly closely to the semicircular law. In this paper, we need control on the number of eigenvalues in intervals of the form
![]() $[-t,t]$
, where
$[-t,t]$
, where
![]() $1/n^{1/2} \ll t \ll n^{1/2}$
. The semicircular law predicts that
$1/n^{1/2} \ll t \ll n^{1/2}$
. The semicircular law predicts that
 $$\begin{align*}N_A(-t,t) \approx \frac{n}{2\pi} \int_{-t n^{-1/2}}^{tn^{-1/2}}(4 - x^2)^{1/2}_+\,dx = \frac{2t n^{1/2}}{\pi}(1+o(1)). \end{align*}$$
$$\begin{align*}N_A(-t,t) \approx \frac{n}{2\pi} \int_{-t n^{-1/2}}^{tn^{-1/2}}(4 - x^2)^{1/2}_+\,dx = \frac{2t n^{1/2}}{\pi}(1+o(1)). \end{align*}$$
Theorem 1.11 of [Reference Erdős12] makes this prediction rigorous.Footnote 8
Theorem 8.3. Let
![]() $B>0$
,
$B>0$
,
![]() $\zeta \in \Gamma _B$
, and let
$\zeta \in \Gamma _B$
, and let
![]() $A \sim \mathrm {Sym\,}_n(\zeta )$
. Then, for
$A \sim \mathrm {Sym\,}_n(\zeta )$
. Then, for
![]() $t \in [C n^{-1/2}, n^{1/2}]$
,
$t \in [C n^{-1/2}, n^{1/2}]$
,
 $$ \begin{align} \mathbb{P}\left(\, \left| \frac{N_A(-t,t)}{n^{1/2}t} - 2\pi^{-1} \right|> \pi \right) \lesssim \exp\left(-c_1(t^2n)^{1/4} \right)\, , \end{align} $$
$$ \begin{align} \mathbb{P}\left(\, \left| \frac{N_A(-t,t)}{n^{1/2}t} - 2\pi^{-1} \right|> \pi \right) \lesssim \exp\left(-c_1(t^2n)^{1/4} \right)\, , \end{align} $$
where
![]() $C,c_1>0$
are absolute constants.
$C,c_1>0$
are absolute constants.
Lemma 8.1 follows quickly from Theorem 8.3. In fact, we shall only use two corollaries.
Corollary 8.4. Let
![]() $B>0$
,
$B>0$
,
![]() $\zeta \in \Gamma _B$
, and let
$\zeta \in \Gamma _B$
, and let
![]() $A \sim \mathrm {Sym\,}_n(\zeta )$
. Then for all
$A \sim \mathrm {Sym\,}_n(\zeta )$
. Then for all
![]() $s \geqslant C$
and
$s \geqslant C$
and
![]() $k \in \mathbb {N}$
satisfying
$k \in \mathbb {N}$
satisfying
![]() $sk \leqslant n$
, we have
$sk \leqslant n$
, we have
 $$ \begin{align*}\mathbb{P}\left( \frac{\sqrt{n}}{\mu_k k} \geqslant s\right) \lesssim \exp\big(-c(sk)^{1/2}\big)\,,\end{align*} $$
$$ \begin{align*}\mathbb{P}\left( \frac{\sqrt{n}}{\mu_k k} \geqslant s\right) \lesssim \exp\big(-c(sk)^{1/2}\big)\,,\end{align*} $$
where
![]() $C,c>0$
are absolute constants.
$C,c>0$
are absolute constants.
Proof. Let C be the maximum of the constant C from Lemma 8.3 and
![]() $\pi $
. If
$\pi $
. If
![]() $\frac {\sqrt {n}}{\mu _k k} \geqslant s$
, then
$\frac {\sqrt {n}}{\mu _k k} \geqslant s$
, then
![]() $N_A(-sk n^{-1/2},skn^{-1/2}) \leqslant k$
. We now apply Lemma 8.3 with
$N_A(-sk n^{-1/2},skn^{-1/2}) \leqslant k$
. We now apply Lemma 8.3 with
![]() $t = sk n^{-1/2} \geqslant sn^{-1/2} \geqslant Cn^{-1/2}$
to see that this event occurs with probability
$t = sk n^{-1/2} \geqslant sn^{-1/2} \geqslant Cn^{-1/2}$
to see that this event occurs with probability
![]() $\lesssim \exp (-c\sqrt {sk})$
.
$\lesssim \exp (-c\sqrt {sk})$
.
An identical argument provides a similar bound in the other direction.
Corollary 8.5. Let
![]() $B>0$
,
$B>0$
,
![]() $\zeta \in \Gamma _B$
, and let
$\zeta \in \Gamma _B$
, and let
![]() $A \sim \mathrm {Sym\,}_n(\zeta )$
. Then for all
$A \sim \mathrm {Sym\,}_n(\zeta )$
. Then for all
![]() $k \in \mathbb {N}$
, we have
$k \in \mathbb {N}$
, we have
 $$ \begin{align*}\mathbb{P}\left( \mu_k \geqslant \frac{C \sqrt{n}}{k}\right) \lesssim \exp\big(-c k^{1/2}\big)\,, \end{align*} $$
$$ \begin{align*}\mathbb{P}\left( \mu_k \geqslant \frac{C \sqrt{n}}{k}\right) \lesssim \exp\big(-c k^{1/2}\big)\,, \end{align*} $$
where
![]() $C,c>0$
are absolute constants.
$C,c>0$
are absolute constants.
Proof of Lemma 8.1.
Let
![]() $ C $
be the constant from Corollary 8.4. From the standard tail estimates on
$ C $
be the constant from Corollary 8.4. From the standard tail estimates on
![]() $\|A\|_{op}$
, like (4.11) for example, we immediately see that for all
$\|A\|_{op}$
, like (4.11) for example, we immediately see that for all
![]() $k \geqslant n/C$
, we have
$k \geqslant n/C$
, we have
 $$\begin{align*}\mathbb{E}\, \left(\frac{\sqrt{n}}{\mu_kk} \right)^p \leqslant \mathbb{E}_A\left( \frac{\sigma_{1}(A)\sqrt{n}}{k} \right)^p = O_p((n/k)^p) = O_p(1).\end{align*}$$
$$\begin{align*}\mathbb{E}\, \left(\frac{\sqrt{n}}{\mu_kk} \right)^p \leqslant \mathbb{E}_A\left( \frac{\sigma_{1}(A)\sqrt{n}}{k} \right)^p = O_p((n/k)^p) = O_p(1).\end{align*}$$
Thus, we can restrict our attention to the case when
![]() $k \leqslant n/C$
. Define the events
$k \leqslant n/C$
. Define the events
 $$ \begin{align*}E_1 = \left\{\frac{\sqrt{n}}{\mu_kk} \leqslant C\right\}, \quad E_2 = \left\{\frac{\sqrt{n}}{\mu_kk} \in [C, n/k ] \right\}, \quad E_3 = \left\{\frac{\sqrt{n}}{\mu_kk} \geqslant \frac{n}{k} \right\}.\end{align*} $$
$$ \begin{align*}E_1 = \left\{\frac{\sqrt{n}}{\mu_kk} \leqslant C\right\}, \quad E_2 = \left\{\frac{\sqrt{n}}{\mu_kk} \in [C, n/k ] \right\}, \quad E_3 = \left\{\frac{\sqrt{n}}{\mu_kk} \geqslant \frac{n}{k} \right\}.\end{align*} $$
We may bound
 $$ \begin{align} \mathbb{E}\, \left(\frac{\sqrt{n}}{\mu_kk} \right)^p \leqslant C^p+ \mathbb{E}\, \left(\frac{\sqrt{n}}{\mu_kk}\right)^p {\mathbf{1}}_{E_2} +\mathbb{E} \left(\frac{\sqrt{n}}{\mu_kk}\right)^p {\mathbf{1}}_{E_3} \,. \end{align} $$
$$ \begin{align} \mathbb{E}\, \left(\frac{\sqrt{n}}{\mu_kk} \right)^p \leqslant C^p+ \mathbb{E}\, \left(\frac{\sqrt{n}}{\mu_kk}\right)^p {\mathbf{1}}_{E_2} +\mathbb{E} \left(\frac{\sqrt{n}}{\mu_kk}\right)^p {\mathbf{1}}_{E_3} \,. \end{align} $$
To deal with the second term in (8.4), we use Corollary 8.4 to see that
 $$\begin{align*}\mathbb{E}\, \left(\frac{\sqrt{n}}{\mu_kk}\right)^p {\mathbf{1}}_{E_2} \lesssim \int_{C}^{n/k} ps^{p-1}e^{-c\sqrt{sk}} ds = O_p(1).\end{align*}$$
$$\begin{align*}\mathbb{E}\, \left(\frac{\sqrt{n}}{\mu_kk}\right)^p {\mathbf{1}}_{E_2} \lesssim \int_{C}^{n/k} ps^{p-1}e^{-c\sqrt{sk}} ds = O_p(1).\end{align*}$$
To deal with the third term in (8.4), we note that since
![]() $n/k \geqslant C$
, we may apply Corollary 8.4, with
$n/k \geqslant C$
, we may apply Corollary 8.4, with
![]() $s=n/k$
, to conclude that
$s=n/k$
, to conclude that
![]() $\mathbb {P}(E_3) \lesssim e^{-c\sqrt {n}}$
. Thus, by Cauchy-Schwarz, we have
$\mathbb {P}(E_3) \lesssim e^{-c\sqrt {n}}$
. Thus, by Cauchy-Schwarz, we have
 $$\begin{align*}\mathbb{E} \left(\frac{\sqrt{n}}{\mu_kk}\right)^p {\mathbf{1}}_{E_3} \leqslant \left(\mathbb{E} \left(\frac{\sigma_{1}\sqrt{n}}{k}\right)^{2p}\right)^{1/2} \mathbb{P}(E_3)^{1/2} \leqslant O_p(1) \cdot n^{p} e^{-c\sqrt{n}} = O_p(1), \end{align*}$$
$$\begin{align*}\mathbb{E} \left(\frac{\sqrt{n}}{\mu_kk}\right)^p {\mathbf{1}}_{E_3} \leqslant \left(\mathbb{E} \left(\frac{\sigma_{1}\sqrt{n}}{k}\right)^{2p}\right)^{1/2} \mathbb{P}(E_3)^{1/2} \leqslant O_p(1) \cdot n^{p} e^{-c\sqrt{n}} = O_p(1), \end{align*}$$
where we have used the upper tail estimate in
![]() $\sigma _1$
from (4.11) to see
$\sigma _1$
from (4.11) to see
![]() $\mathbb {E}\, \sigma _1^{2p} = O_p(n^{p})$
.
$\mathbb {E}\, \sigma _1^{2p} = O_p(n^{p})$
.
8.2 Deduction of Corollary 8.2
We now conclude this section by deducing Corollary 8.2 from Lemma 8.1 and Corollary 8.5.
Proof of Corollary 8.2.
Recall
 $$\begin{align*}\|A^{-1}\|_{\ast}^2 = \sum_{k = 1}^n \mu_k^2 (\log(1 + k))^2.\end{align*}$$
$$\begin{align*}\|A^{-1}\|_{\ast}^2 = \sum_{k = 1}^n \mu_k^2 (\log(1 + k))^2.\end{align*}$$
By Hölder’s inequality, we may assume without loss of generality that
![]() $p \geqslant 2$
. Applying the triangle inequality for the
$p \geqslant 2$
. Applying the triangle inequality for the
![]() $L^{p/2}$
norm gives
$L^{p/2}$
norm gives
 $$\begin{align*}\left[ \mathbb{E} \left( \sum_{k = 1}^n \frac{\mu_k^2 (\log (1 + k))^2}{\mu_1^2} \right)^{p/2}\right]^{2/p} \leqslant \sum_{k = 1}^n (\log(1 + k))^2 \mathbb{E} \left[\frac{\mu_k^{p}}{\mu_1^{p}}\right]^{2/p }\,. \end{align*}$$
$$\begin{align*}\left[ \mathbb{E} \left( \sum_{k = 1}^n \frac{\mu_k^2 (\log (1 + k))^2}{\mu_1^2} \right)^{p/2}\right]^{2/p} \leqslant \sum_{k = 1}^n (\log(1 + k))^2 \mathbb{E} \left[\frac{\mu_k^{p}}{\mu_1^{p}}\right]^{2/p }\,. \end{align*}$$
Taking C to be the constant from Corollary 8.5 bound
 $$ \begin{align*} \mathbb{E} \left[\frac{\mu_k^{p}}{\mu_1^{p}}\right]&\leqslant C^pk^{-p} \mathbb{E}\left[\left(\frac{\sqrt{n}}{\mu_1}\right)^p \right] + \mathbb{P}\left(\mu_k \geqslant C \frac{\sqrt{n}}{k} \right) \lesssim C^p k^{-p} ,\end{align*} $$
$$ \begin{align*} \mathbb{E} \left[\frac{\mu_k^{p}}{\mu_1^{p}}\right]&\leqslant C^pk^{-p} \mathbb{E}\left[\left(\frac{\sqrt{n}}{\mu_1}\right)^p \right] + \mathbb{P}\left(\mu_k \geqslant C \frac{\sqrt{n}}{k} \right) \lesssim C^p k^{-p} ,\end{align*} $$
where we used Lemma 8.1 and Corollary 8.5 for the second inequality. Combining the previous two equations completes the proof.
9 Controlling small balls and large deviations
The goal of this section is to prove the following lemma, which will be a main ingredient in our iteration in Section 10. We shall then use it again in the final step and proof of Theorem 1.1, in Section 11.
Lemma 9.1. For
![]() $B>0$
and
$B>0$
and
![]() $\zeta \in \Gamma _B$
, let
$\zeta \in \Gamma _B$
, let
![]() $A = A_n \sim \mathrm {Sym\,}_{n}(\zeta )$
and let
$A = A_n \sim \mathrm {Sym\,}_{n}(\zeta )$
and let
![]() $X \sim \mathrm {Col\,}_n(\zeta )$
. Let
$X \sim \mathrm {Col\,}_n(\zeta )$
. Let
![]() $u\in \mathbb {R}^{n-1}$
be a random vector with
$u\in \mathbb {R}^{n-1}$
be a random vector with
![]() $\|u\|_2 \leqslant 1$
that depends only on A. Then, for
$\|u\|_2 \leqslant 1$
that depends only on A. Then, for
![]() $\delta , \varepsilon> e^{-cn}$
and
$\delta , \varepsilon> e^{-cn}$
and
![]() $s\geqslant 0$
, we have
$s\geqslant 0$
, we have
 $$ \begin{align} &\mathbb{E}_A \sup_r\mathbb{P}_X\left(\frac{|\langle A^{-1}X,X\rangle -r|}{\|A^{-1}\|_{\ast}} \leqslant \delta,~\langle X, u\rangle\geqslant s,~ \frac{\mu_1}{\sqrt{n}} \leqslant \varepsilon^{-1} \right) \nonumber \\ &\qquad \lesssim \delta e^{-s} \left[ \mathbb{E}_{A} \left(\frac{\mu_1}{\sqrt{n}}\right)^{7/9} {\mathbf{1}}\left\{\frac{\mu_1}{\sqrt{n}} \leqslant \varepsilon^{-1} \right\} \right]^{6/7} + e^{-cn}\,, \end{align} $$
$$ \begin{align} &\mathbb{E}_A \sup_r\mathbb{P}_X\left(\frac{|\langle A^{-1}X,X\rangle -r|}{\|A^{-1}\|_{\ast}} \leqslant \delta,~\langle X, u\rangle\geqslant s,~ \frac{\mu_1}{\sqrt{n}} \leqslant \varepsilon^{-1} \right) \nonumber \\ &\qquad \lesssim \delta e^{-s} \left[ \mathbb{E}_{A} \left(\frac{\mu_1}{\sqrt{n}}\right)^{7/9} {\mathbf{1}}\left\{\frac{\mu_1}{\sqrt{n}} \leqslant \varepsilon^{-1} \right\} \right]^{6/7} + e^{-cn}\,, \end{align} $$
where
![]() $c>0$
depends only on
$c>0$
depends only on
![]() $B>0$
.
$B>0$
.
Note that with this lemma, we have eliminated all “fine-grained” information about the spectrum of
![]() $A^{-1}$
and all that remains is
$A^{-1}$
and all that remains is
![]() $\mu _1$
, which is the reciprocal of the least singular value of the matrix A. We also note that we will only need the full power of Lemma 9.1 in Section 11; until then, we will apply it with
$\mu _1$
, which is the reciprocal of the least singular value of the matrix A. We also note that we will only need the full power of Lemma 9.1 in Section 11; until then, we will apply it with
![]() $s=0, u=0$
.
$s=0, u=0$
.
We now turn our attention to proving Lemma 9.1. We start with an application of Theorem 1.5, our negative correlation theorem, which we restate here in its full-fledged form.
Theorem 9.2. For
![]() $n \in \mathbb {N}$
,
$n \in \mathbb {N}$
,
![]() $\alpha ,\gamma \in (0,1), B> 0$
, and
$\alpha ,\gamma \in (0,1), B> 0$
, and
![]() $\mu \in (0,2^{-15})$
, there are constants
$\mu \in (0,2^{-15})$
, there are constants
![]() $c,R> 0$
depending only on
$c,R> 0$
depending only on
![]() $\alpha ,\gamma ,\mu ,B$
so that the following holds. Let
$\alpha ,\gamma ,\mu ,B$
so that the following holds. Let
![]() $0\leqslant k \leqslant c \alpha n$
and
$0\leqslant k \leqslant c \alpha n$
and
![]() $\varepsilon \geqslant \exp (-c\alpha n)$
, let
$\varepsilon \geqslant \exp (-c\alpha n)$
, let
![]() $v \in {\mathbb {S}}^{n-1}$
, and let
$v \in {\mathbb {S}}^{n-1}$
, and let
![]() $w_1,\ldots ,w_k \in {\mathbb {S}}^{n-1}$
be orthogonal. For
$w_1,\ldots ,w_k \in {\mathbb {S}}^{n-1}$
be orthogonal. For
![]() $\zeta \in \Gamma _B$
, let
$\zeta \in \Gamma _B$
, let
![]() $\zeta '$
be an independent copy of
$\zeta '$
be an independent copy of
![]() $\zeta $
and
$\zeta $
and
![]() $Z_\mu $
a Bernoulli variable with parameter
$Z_\mu $
a Bernoulli variable with parameter
![]() $\mu $
; let
$\mu $
; let
![]() $\widetilde {X} \in \mathbb {R}^n$
be a random vector whose coordinates are i.i.d. copies of the random variable
$\widetilde {X} \in \mathbb {R}^n$
be a random vector whose coordinates are i.i.d. copies of the random variable
![]() $(\zeta - \zeta ')Z_\mu $
.
$(\zeta - \zeta ')Z_\mu $
.
If
![]() $D_{\alpha ,\gamma }(v)> 1/\varepsilon $
, then
$D_{\alpha ,\gamma }(v)> 1/\varepsilon $
, then
 $$ \begin{align} \mathbb{P}_X\left( |\langle \widetilde{X}, v \rangle| \leqslant \varepsilon\, \text{ and }\, \sum_{j = 1}^k \langle w_j, \widetilde{X}\rangle^2 \leqslant c k \right) \leqslant R \varepsilon \cdot e^{-c k}\,. \end{align} $$
$$ \begin{align} \mathbb{P}_X\left( |\langle \widetilde{X}, v \rangle| \leqslant \varepsilon\, \text{ and }\, \sum_{j = 1}^k \langle w_j, \widetilde{X}\rangle^2 \leqslant c k \right) \leqslant R \varepsilon \cdot e^{-c k}\,. \end{align} $$
The proof of Theorem 9.2 is provided in the Appendix. We now prove Lemma 9.3.
Lemma 9.3. Let A be an
![]() $n \times n$
real symmetric matrix with
$n \times n$
real symmetric matrix with
![]() $A \in \mathcal {E}$
, and set
$A \in \mathcal {E}$
, and set
![]() $ \mu _i := \sigma _{i}(A^{-1})$
, for all
$ \mu _i := \sigma _{i}(A^{-1})$
, for all
![]() $i \in [n]$
. For
$i \in [n]$
. For
![]() $B>0$
,
$B>0$
,
![]() $\zeta \in \Gamma _B$
, let
$\zeta \in \Gamma _B$
, let
![]() $X,X' \sim \mathrm {Col\,}_n(\zeta )$
be independent, let
$X,X' \sim \mathrm {Col\,}_n(\zeta )$
be independent, let
![]() $J \subseteq [n]$
be a
$J \subseteq [n]$
be a
![]() $\mu $
-random subset with
$\mu $
-random subset with
![]() $\mu \in (0, 2^{-15})$
, and set
$\mu \in (0, 2^{-15})$
, and set
![]() $\widetilde {X} := (X - X')_J$
. If
$\widetilde {X} := (X - X')_J$
. If
![]() $k \in [1,c n]$
is such that
$k \in [1,c n]$
is such that
![]() $s \in (e^{-c n} , \mu _k/\mu _1)$
, then
$s \in (e^{-c n} , \mu _k/\mu _1)$
, then
where
![]() $c> 0$
depends only on B.
$c> 0$
depends only on B.
Proof. For each
![]() $j\in [n]$
, we let
$j\in [n]$
, we let
![]() $v_j$
denote a unit eigenvector of
$v_j$
denote a unit eigenvector of
![]() $A^{-1}$
corresponding to
$A^{-1}$
corresponding to
![]() $\mu _j$
. Using the resulting singular value decomposition of
$\mu _j$
. Using the resulting singular value decomposition of
![]() $A^{-1}$
, we may express
$A^{-1}$
, we may express
 $$\begin{align*}\|A^{-1} \widetilde{X}\|^2_2 = \langle A^{-1} \widetilde{X} , A^{-1}\widetilde{X} \rangle = \sum_{j=1}^n \mu_j^2 \langle \widetilde{X}, v_j \rangle^2, \end{align*}$$
$$\begin{align*}\|A^{-1} \widetilde{X}\|^2_2 = \langle A^{-1} \widetilde{X} , A^{-1}\widetilde{X} \rangle = \sum_{j=1}^n \mu_j^2 \langle \widetilde{X}, v_j \rangle^2, \end{align*}$$
and thus
 $$ \begin{align} \mathbb{P}_{\widetilde{X}}\left( \|A^{-1} \widetilde{X}\|_2 \mu_1^{-1} \leqslant s \right) \leqslant \mathbb{P}_{\widetilde{X}}\left( |\langle v_1 , \widetilde{X} \rangle| \leqslant s \text{ and } \sum_{j = 2}^k \frac{\mu_j^2}{\mu_1^2}\langle v_j, \widetilde{X} \rangle^2 \leqslant s^2 \right). \end{align} $$
$$ \begin{align} \mathbb{P}_{\widetilde{X}}\left( \|A^{-1} \widetilde{X}\|_2 \mu_1^{-1} \leqslant s \right) \leqslant \mathbb{P}_{\widetilde{X}}\left( |\langle v_1 , \widetilde{X} \rangle| \leqslant s \text{ and } \sum_{j = 2}^k \frac{\mu_j^2}{\mu_1^2}\langle v_j, \widetilde{X} \rangle^2 \leqslant s^2 \right). \end{align} $$
We now use that
![]() $s \leqslant 1$
and
$s \leqslant 1$
and
![]() $\mu _k/\mu _1 \leqslant 1$
in (9.4) to obtain
$\mu _k/\mu _1 \leqslant 1$
in (9.4) to obtain
 $$ \begin{align} \mathbb{P}_{\widetilde{X}}\left( \|A^{-1} \widetilde{X}\|_2 \mu_1^{-1} \leqslant s \right) \leqslant \mathbb{P}_{\widetilde{X}}\left( |\langle v_1 , \widetilde{X} \rangle| \leqslant s \text{ and } \sum_{j = 2}^k \langle v_j, \widetilde{X} \rangle^2 \leqslant 1 \right) \,. \end{align} $$
$$ \begin{align} \mathbb{P}_{\widetilde{X}}\left( \|A^{-1} \widetilde{X}\|_2 \mu_1^{-1} \leqslant s \right) \leqslant \mathbb{P}_{\widetilde{X}}\left( |\langle v_1 , \widetilde{X} \rangle| \leqslant s \text{ and } \sum_{j = 2}^k \langle v_j, \widetilde{X} \rangle^2 \leqslant 1 \right) \,. \end{align} $$
We now carefully observe that we are in a position to apply Theorem 1.5 to the right-hand side of (9.5). The coordinates of
![]() $\widetilde {X}$
are of the form
$\widetilde {X}$
are of the form
![]() $(\zeta -\zeta ')Z_{\mu }$
, where
$(\zeta -\zeta ')Z_{\mu }$
, where
![]() $Z_{\mu }$
is a Bernoulli random variable taking
$Z_{\mu }$
is a Bernoulli random variable taking
![]() $1$
with probability
$1$
with probability
![]() $\mu \in (0,2^{-15})$
and
$\mu \in (0,2^{-15})$
and
![]() $0$
otherwise. Also, the
$0$
otherwise. Also, the
![]() $ v_2,\ldots ,v_k$
are orthogonal and, importantly, we use that
$ v_2,\ldots ,v_k$
are orthogonal and, importantly, we use that
![]() $A \in \mathcal {E}$
to learn thatFootnote
9
$A \in \mathcal {E}$
to learn thatFootnote
9
![]() $D_{\alpha ,\gamma }(v_1)>1/s$
by property (4.3), provided we choose the constant
$D_{\alpha ,\gamma }(v_1)>1/s$
by property (4.3), provided we choose the constant
![]() $c>0$
(in the statement of Lemma 9.3) to be sufficiently small, depending on
$c>0$
(in the statement of Lemma 9.3) to be sufficiently small, depending on
![]() $\mu ,B$
. Thus, we may apply Theorem 1.5 and complete the proof of the Lemma 9.3.
$\mu ,B$
. Thus, we may apply Theorem 1.5 and complete the proof of the Lemma 9.3.
With this lemma in hand, we establish the following corollary of Lemma 5.2.
Lemma 9.4. For
![]() $B>0$
and
$B>0$
and
![]() $\zeta \in \Gamma _B$
, let
$\zeta \in \Gamma _B$
, let
![]() $X \sim \mathrm {Col\,}_n(\zeta )$
and let A be an
$X \sim \mathrm {Col\,}_n(\zeta )$
and let A be an
![]() $n\times n$
real symmetric matrix with
$n\times n$
real symmetric matrix with
![]() $A \in \mathcal {E}$
. If
$A \in \mathcal {E}$
. If
![]() $s>0$
,
$s>0$
,
![]() $\delta \in (e^{-c n},1)$
and
$\delta \in (e^{-c n},1)$
and
![]() $u \in {\mathbb {S}}^{n-1}$
, then
$u \in {\mathbb {S}}^{n-1}$
, then
 $$ \begin{align} \sup_r\mathbb{P}_{X}\big( \left|\langle A^{-1} X, X \rangle -r \right| \leqslant \delta \mu_1 ,\langle X, u \rangle \geqslant s \big) \lesssim \delta e^{-s} \sum_{k = 2}^{cn} e^{-ck}\left(\frac{\mu_1}{\mu_k} \right)^{2/3} + e^{-cn}\, , \end{align} $$
$$ \begin{align} \sup_r\mathbb{P}_{X}\big( \left|\langle A^{-1} X, X \rangle -r \right| \leqslant \delta \mu_1 ,\langle X, u \rangle \geqslant s \big) \lesssim \delta e^{-s} \sum_{k = 2}^{cn} e^{-ck}\left(\frac{\mu_1}{\mu_k} \right)^{2/3} + e^{-cn}\, , \end{align} $$
where
![]() $c>0$
is a constant depending only on B.
$c>0$
is a constant depending only on B.
Proof. We apply Lemma 5.2 to the left-hand side of (9.6) to get
 $$ \begin{align} \sup_r\mathbb{P}_{X}\big( \left|\langle A^{-1} X, X \rangle - r \right| \leqslant \delta \mu_1 ,\langle X, u \rangle \geqslant s \big) \lesssim \delta e^{-s} \int_{-1/\delta}^{1/\delta} I({\theta})^{1/2} \,d{\theta} + e^{-\Omega(n)} \, , \end{align} $$
$$ \begin{align} \sup_r\mathbb{P}_{X}\big( \left|\langle A^{-1} X, X \rangle - r \right| \leqslant \delta \mu_1 ,\langle X, u \rangle \geqslant s \big) \lesssim \delta e^{-s} \int_{-1/\delta}^{1/\delta} I({\theta})^{1/2} \,d{\theta} + e^{-\Omega(n)} \, , \end{align} $$
where
and
![]() $c' = c'(B)>0 $
is a constant depending only on B and
$c' = c'(B)>0 $
is a constant depending only on B and
![]() $J \subseteq [n]$
is a
$J \subseteq [n]$
is a
![]() $\mu $
-random subset. Set
$\mu $
-random subset. Set
and apply Hölder’s inequality
Thus, we apply (5.2) to see that the second term on the right-hand side of (9.8) is
![]() $O(1)$
. Thus, for each
$O(1)$
. Thus, for each
![]() ${\theta }> 0$
, we have
${\theta }> 0$
, we have
As a result, we have
 $$ \begin{align*}\int_{-1/\delta}^{1/\delta} I({\theta})^{1/2} \,d\theta \lesssim 1 + \int_{1}^{1/\delta} \mathbb{P}_{\widetilde{X}}(\|v\|_2 \leqslant \mu_1 \theta^{-9/10} )^{4/9}\,d\theta\, \lesssim 1 + \int_{\delta}^{1} s^{-19/9} \mathbb{P}_{\widetilde{X}}(\|v\|_2 \leqslant \mu_1 s )^{4/9}\, ds .\end{align*} $$
$$ \begin{align*}\int_{-1/\delta}^{1/\delta} I({\theta})^{1/2} \,d\theta \lesssim 1 + \int_{1}^{1/\delta} \mathbb{P}_{\widetilde{X}}(\|v\|_2 \leqslant \mu_1 \theta^{-9/10} )^{4/9}\,d\theta\, \lesssim 1 + \int_{\delta}^{1} s^{-19/9} \mathbb{P}_{\widetilde{X}}(\|v\|_2 \leqslant \mu_1 s )^{4/9}\, ds .\end{align*} $$
To bound this integral, we partition
![]() $ [\delta ,1] = [\delta , \mu _{c n}/\mu _1 ] \cup \bigcup _{k=2}^{c n} [\mu _{k}/\mu _1,\mu _{k-1}/\mu _1]$
and apply Lemma 9.3 to bound the integrand depending on which interval s lies in. Note, this lemma is applicable since
$ [\delta ,1] = [\delta , \mu _{c n}/\mu _1 ] \cup \bigcup _{k=2}^{c n} [\mu _{k}/\mu _1,\mu _{k-1}/\mu _1]$
and apply Lemma 9.3 to bound the integrand depending on which interval s lies in. Note, this lemma is applicable since
![]() $A \in \mathcal {E}$
. We obtain
$A \in \mathcal {E}$
. We obtain
 $$\begin{align*}\int_{\mu_k/\mu_1}^{\mu_{k-1}/\mu_1} s^{-19/9} \mathbb{P}_{\widetilde{X}}(\|v\|_2 \leqslant \mu_1 s )^{4/9} \leqslant e^{-ck} \int_{\mu_k/\mu_1}^{\mu_{k-1}/\mu_1} s^{-15/9} \, ds \leqslant e^{-ck}(\mu_1/\mu_k)^{2/3}, \end{align*}$$
$$\begin{align*}\int_{\mu_k/\mu_1}^{\mu_{k-1}/\mu_1} s^{-19/9} \mathbb{P}_{\widetilde{X}}(\|v\|_2 \leqslant \mu_1 s )^{4/9} \leqslant e^{-ck} \int_{\mu_k/\mu_1}^{\mu_{k-1}/\mu_1} s^{-15/9} \, ds \leqslant e^{-ck}(\mu_1/\mu_k)^{2/3}, \end{align*}$$
while
 $$\begin{align*}\int_{\delta}^{\mu_{c n}/\mu_1} s^{-19/9} \mathbb{P}_{\widetilde{X}}(\|v\|_2 \leqslant \mu_1 s )^{4/9} \leqslant e^{-c n} \delta^{-3/2} \leqslant e^{-\Omega(n)}. \end{align*}$$
$$\begin{align*}\int_{\delta}^{\mu_{c n}/\mu_1} s^{-19/9} \mathbb{P}_{\widetilde{X}}(\|v\|_2 \leqslant \mu_1 s )^{4/9} \leqslant e^{-c n} \delta^{-3/2} \leqslant e^{-\Omega(n)}. \end{align*}$$
Summing over all k and plugging the result into (9.7) completes the lemma.
We may now prove Lemma 9.1 by using the previous Lemma 9.4 along with the properties of the spectrum of A established in Section 8.
Proof of Lemma 9.1.
Let
![]() $\mathcal {E}$
be our quasi-random event as defined in Section 4, and let
$\mathcal {E}$
be our quasi-random event as defined in Section 4, and let
 $$\begin{align*}\mathcal{E}_0=\mathcal{E}\cap \left\lbrace\frac{\mu_1}{\sqrt{n}} \leqslant \varepsilon^{-1}\right\rbrace.\end{align*}$$
$$\begin{align*}\mathcal{E}_0=\mathcal{E}\cap \left\lbrace\frac{\mu_1}{\sqrt{n}} \leqslant \varepsilon^{-1}\right\rbrace.\end{align*}$$
For fixed
![]() $A \in \mathcal {E}_0$
and
$A \in \mathcal {E}_0$
and
![]() $u = u(A) \in \mathbb {R}^{n}$
with
$u = u(A) \in \mathbb {R}^{n}$
with
![]() $\|u\|_2\leqslant 1$
, we may apply Lemma 9.4 with
$\|u\|_2\leqslant 1$
, we may apply Lemma 9.4 with
![]() $\delta ' =\delta \frac {\|A^{-1}\|_{\ast }}{\mu _1}$
to see that
$\delta ' =\delta \frac {\|A^{-1}\|_{\ast }}{\mu _1}$
to see that
 $$\begin{align*}\sup_{r \in \mathbb{R}} \mathbb{P}_{X}\big( \left|\langle A^{-1} X, X \rangle -r \right| \leqslant \delta \|A\|_{\ast} ,\langle X, u \rangle \geqslant s \big) \lesssim \delta e^{-s} \left(\frac{\|A^{-1}\|_{*}}{\mu_1}\right) \sum_{k = 2}^{cn} e^{-ck}\left(\frac{\mu_1}{\mu_k} \right)^{2/3} + e^{-cn}\, .\end{align*}$$
$$\begin{align*}\sup_{r \in \mathbb{R}} \mathbb{P}_{X}\big( \left|\langle A^{-1} X, X \rangle -r \right| \leqslant \delta \|A\|_{\ast} ,\langle X, u \rangle \geqslant s \big) \lesssim \delta e^{-s} \left(\frac{\|A^{-1}\|_{*}}{\mu_1}\right) \sum_{k = 2}^{cn} e^{-ck}\left(\frac{\mu_1}{\mu_k} \right)^{2/3} + e^{-cn}\, .\end{align*}$$
By Lemma 4.1,
![]() $\mathbb {P}_A(\mathcal {E}^c)\lesssim \exp (-\Omega (n))$
. Therefore, it is enough to show that
$\mathbb {P}_A(\mathcal {E}^c)\lesssim \exp (-\Omega (n))$
. Therefore, it is enough to show that
 $$ \begin{align} \mathbb{E}_A^{\mathcal{E}_0} \left(\frac{\|A^{-1}\|_{*}}{\mu_1}\right) \left(\frac{\mu_1}{\mu_k} \right)^{2/3} \lesssim k\cdot \mathbb{E}_{A}^{\mathcal{E}_0} \left[ \left(\frac{\mu_1}{\sqrt{n}}\right)^{7/9}\right]^{6/7},\end{align} $$
$$ \begin{align} \mathbb{E}_A^{\mathcal{E}_0} \left(\frac{\|A^{-1}\|_{*}}{\mu_1}\right) \left(\frac{\mu_1}{\mu_k} \right)^{2/3} \lesssim k\cdot \mathbb{E}_{A}^{\mathcal{E}_0} \left[ \left(\frac{\mu_1}{\sqrt{n}}\right)^{7/9}\right]^{6/7},\end{align} $$
for each
![]() $k \in [2,c n]$
. For this, apply Hölder’s inequality to the left-hand side of (9.9) to get
$k \in [2,c n]$
. For this, apply Hölder’s inequality to the left-hand side of (9.9) to get
 $$\begin{align*}\mathbb{E}_A^{\mathcal{E}_0} \left(\frac{\|A^{-1}\|_{*}}{\mu_1}\right)\left(\frac{\mu_1}{\mu_k} \right)^{2/3}\leqslant \mathbb{E}_A^{\mathcal{E}_0} \left[\left(\frac{\|A^{-1}\|_{*}}{\mu_1}\right)^{14}\right]^{1/14}\mathbb{E}_A^{\mathcal{E}_0} \left[\left(\frac{\sqrt{n}}{\mu_k}\right)^{28/3}\right]^{1/14}\mathbb{E}_A^{\mathcal{E}_0} \left[\left(\frac{\mu_1}{\sqrt{n}} \right)^{7/9}\right]^{6/7}.\end{align*}$$
$$\begin{align*}\mathbb{E}_A^{\mathcal{E}_0} \left(\frac{\|A^{-1}\|_{*}}{\mu_1}\right)\left(\frac{\mu_1}{\mu_k} \right)^{2/3}\leqslant \mathbb{E}_A^{\mathcal{E}_0} \left[\left(\frac{\|A^{-1}\|_{*}}{\mu_1}\right)^{14}\right]^{1/14}\mathbb{E}_A^{\mathcal{E}_0} \left[\left(\frac{\sqrt{n}}{\mu_k}\right)^{28/3}\right]^{1/14}\mathbb{E}_A^{\mathcal{E}_0} \left[\left(\frac{\mu_1}{\sqrt{n}} \right)^{7/9}\right]^{6/7}.\end{align*}$$
We now apply Corollary 8.2 to see the first term is
![]() $O(1)$
and Lemma 8.1 to see that the second term is
$O(1)$
and Lemma 8.1 to see that the second term is
![]() $O(k)$
. This establishes (9.9) and thus Lemma 9.1.
$O(k)$
. This establishes (9.9) and thus Lemma 9.1.
10 Intermediate bounds: Bootstrapping the lower tail
In this short section, we will use the tools developed so far to prove an “up-to-logarithms” version of Theorem 1.1. In the next section, Section 11, we will bootstrap this result (once again) to prove Theorem 1.1.
Lemma 10.1. For
![]() $B>0 $
, let
$B>0 $
, let
![]() $\zeta \in \Gamma _B$
, and let
$\zeta \in \Gamma _B$
, and let
![]() $A_n \sim \mathrm {Sym\,}_{n}(\zeta )$
. Then for all
$A_n \sim \mathrm {Sym\,}_{n}(\zeta )$
. Then for all
![]() $\varepsilon>0$
$\varepsilon>0$
To prove Lemma 10.1, we first prove the following “base step” (Lemma 10.3), which we then improve upon in three increments, ultimately arriving at Lemma 10.1.
The “base step” is an easy consequence of Lemmas 6.2 and 9.1 and actually already improves upon the best known bounds on the least-singular value problem for random symmetric matrices. For this, we will need the well-known theorem due to Hanson and Wright [Reference Hanson and Wright18, Reference Wright51]. See [Reference Vershynin47, Theorem 6.2.1]) for a modern exposition.
Theorem 10.2 (Hanson-Wright).
For
![]() $B>0$
, let
$B>0$
, let
![]() $\zeta \in \Gamma _B$
, let
$\zeta \in \Gamma _B$
, let
![]() $X \sim \mathrm {Col\,}_n(\zeta )$
, and let M be an
$X \sim \mathrm {Col\,}_n(\zeta )$
, and let M be an
![]() $m\times n$
matrix. Then for any
$m\times n$
matrix. Then for any
![]() $t\geqslant 0$
, we have
$t\geqslant 0$
, we have
 $$\begin{align*}\mathbb{P}_X\big( \left| \|MX\|_2 - \|M\|_{\mathrm{HS}} \right|>t \big) \leqslant 2 \exp\left(- \frac{ct^2}{B^4\|M\|^2} \right)\, , \end{align*}$$
$$\begin{align*}\mathbb{P}_X\big( \left| \|MX\|_2 - \|M\|_{\mathrm{HS}} \right|>t \big) \leqslant 2 \exp\left(- \frac{ct^2}{B^4\|M\|^2} \right)\, , \end{align*}$$
where
![]() $c>0$
is absolute constant.
$c>0$
is absolute constant.
We now prove the base step of our iteration.
Lemma 10.3 (Base step).
For
![]() $B>0$
, let
$B>0$
, let
![]() $\zeta \in \Gamma _B$
and let
$\zeta \in \Gamma _B$
and let
![]() $A_{n+1} \sim \mathrm {Sym\,}_{n+1}(\zeta )$
. Then
$A_{n+1} \sim \mathrm {Sym\,}_{n+1}(\zeta )$
. Then
for all
![]() $\varepsilon>0$
.
$\varepsilon>0$
.
Proof. As usual, we let
![]() $A := A_{n}$
. By Lemma 6.1, it will be sufficient to show that for
$A := A_{n}$
. By Lemma 6.1, it will be sufficient to show that for
![]() $r\in \mathbb {R}$
,
$r\in \mathbb {R}$
,
 $$ \begin{align} \mathbb{P}_{A,X}\left(\, \frac{|\langle A^{-1} X, X \rangle - r|}{\|A^{-1}X\|_2} \leqslant C\varepsilon,\, \sigma_n(A)\geqslant \varepsilon n^{-1/2} \right) \lesssim \varepsilon^{1/4} + e^{-\Omega(n)}\,. \end{align} $$
$$ \begin{align} \mathbb{P}_{A,X}\left(\, \frac{|\langle A^{-1} X, X \rangle - r|}{\|A^{-1}X\|_2} \leqslant C\varepsilon,\, \sigma_n(A)\geqslant \varepsilon n^{-1/2} \right) \lesssim \varepsilon^{1/4} + e^{-\Omega(n)}\,. \end{align} $$
By the Hanson-Wright inequality (Theorem 10.2), there exists
![]() $C'>0$
so that
$C'>0$
so that
and so the left-hand side of (10.1) is bounded above by
 $$\begin{align*}\varepsilon + \mathbb{P}_{A,X}\left(\, \frac{|\langle A^{-1} X, X \rangle - r|}{\|A^{-1}\|_{\mathrm{HS}}} \leqslant \delta,\, \sigma_n(A)\geqslant \varepsilon n^{-1/2} \right) \, , \end{align*}$$
$$\begin{align*}\varepsilon + \mathbb{P}_{A,X}\left(\, \frac{|\langle A^{-1} X, X \rangle - r|}{\|A^{-1}\|_{\mathrm{HS}}} \leqslant \delta,\, \sigma_n(A)\geqslant \varepsilon n^{-1/2} \right) \, , \end{align*}$$
where
![]() $\delta :=C" \varepsilon \cdot ( \log \varepsilon ^{-1} )^{1/2}$
. Now, by Lemma 9.1 with the choice of
$\delta :=C" \varepsilon \cdot ( \log \varepsilon ^{-1} )^{1/2}$
. Now, by Lemma 9.1 with the choice of
![]() $u=0, s=0$
, we have
$u=0, s=0$
, we have
 $$ \begin{align} \mathbb{P}_{A,X}\left(\, \frac{|\langle A^{-1} X, X \rangle - r|}{\|A^{-1}\|_{\mathrm{HS}}} \leqslant \delta,\, \sigma_n(A)\geqslant \varepsilon n^{-1/2} \right) \lesssim \delta \varepsilon^{-2/3} + e^{-\Omega(n)} \lesssim \varepsilon^{1/4} + e^{-\Omega(n)}\, , \end{align} $$
$$ \begin{align} \mathbb{P}_{A,X}\left(\, \frac{|\langle A^{-1} X, X \rangle - r|}{\|A^{-1}\|_{\mathrm{HS}}} \leqslant \delta,\, \sigma_n(A)\geqslant \varepsilon n^{-1/2} \right) \lesssim \delta \varepsilon^{-2/3} + e^{-\Omega(n)} \lesssim \varepsilon^{1/4} + e^{-\Omega(n)}\, , \end{align} $$
where we have used that
![]() $\|A^{-1}\|_{\ast }\geqslant \|A^{-1}\|_{\mathrm {HS}}$
. We also note that Lemma 9.1 actually gives an upper bound on
$\|A^{-1}\|_{\ast }\geqslant \|A^{-1}\|_{\mathrm {HS}}$
. We also note that Lemma 9.1 actually gives an upper bound on
![]() $\mathbb {E}_A \sup _r \mathbb {P}_X( \mathcal {A})$
, where
$\mathbb {E}_A \sup _r \mathbb {P}_X( \mathcal {A})$
, where
![]() $\mathcal {A}$
is the event on the left-hand side of (10.7). Since
$\mathcal {A}$
is the event on the left-hand side of (10.7). Since
![]() $\sup _r \mathbb {P}_{A,X}(\mathcal {A}) \leqslant \mathbb {E}_A \sup _r \mathbb {P}_X( \mathcal {A}) $
, the bound (10.3), and thus Lemma 10.3, follows.
$\sup _r \mathbb {P}_{A,X}(\mathcal {A}) \leqslant \mathbb {E}_A \sup _r \mathbb {P}_X( \mathcal {A}) $
, the bound (10.3), and thus Lemma 10.3, follows.
The next lemma is our “bootstrapping step”: Given bounds of the form
this lemma will produce better bounds for the same problem with
![]() $A_{n+1}$
in place of
$A_{n+1}$
in place of
![]() $A_n$
.
$A_n$
.
Lemma 10.4 (Bootstrapping step).
For
![]() $B>0$
, let
$B>0$
, let
![]() $\zeta \in \Gamma _B$
, let
$\zeta \in \Gamma _B$
, let
![]() $A_{n+1} \sim \mathrm {Sym\,}_{n+1}(\zeta )$
, and let
$A_{n+1} \sim \mathrm {Sym\,}_{n+1}(\zeta )$
, and let
![]() ${\kappa } \in (0,1) \setminus \{7/10\}$
. If for all
${\kappa } \in (0,1) \setminus \{7/10\}$
. If for all
![]() $\varepsilon>0$
, and all n, we have
$\varepsilon>0$
, and all n, we have
then for all
![]() $\varepsilon>0$
and all n, we have
$\varepsilon>0$
and all n, we have
Proof. Let
![]() $c>0$
denote the implicit constant in the exponent on the right-hand side of (10.4). Note that if
$c>0$
denote the implicit constant in the exponent on the right-hand side of (10.4). Note that if
![]() $0< \varepsilon <e^{-cn}$
, by the assumption of the lemma, then we have
$0< \varepsilon <e^{-cn}$
, by the assumption of the lemma, then we have
for all n, in which case, we are done. So we may assume
![]() $\varepsilon> e^{-cn}$
.
$\varepsilon> e^{-cn}$
.
As in the proof of the “base step,” Lemma 10.3, we look to apply Lemmas 6.2 and 9.1 in sequence. For this, we write
![]() $A = A_n$
and bound (9.1) as in the conclusion of Lemma 9.1
$A = A_n$
and bound (9.1) as in the conclusion of Lemma 9.1
 $$ \begin{align} \mathbb{E}_{A}\, \left(\frac{\mu_1}{\sqrt{n}}\right)^{7/9} {\mathbf{1}}\left\{\frac{\mu_1}{\sqrt{n}} \leqslant \varepsilon^{-1} \right\} \leqslant \int_{0}^{\varepsilon^{-7/9}}\mathbb{P}\left(\sigma_{\min}(A)\leqslant x^{-9/7} n^{-1/2} \right)\, dx ,\end{align} $$
$$ \begin{align} \mathbb{E}_{A}\, \left(\frac{\mu_1}{\sqrt{n}}\right)^{7/9} {\mathbf{1}}\left\{\frac{\mu_1}{\sqrt{n}} \leqslant \varepsilon^{-1} \right\} \leqslant \int_{0}^{\varepsilon^{-7/9}}\mathbb{P}\left(\sigma_{\min}(A)\leqslant x^{-9/7} n^{-1/2} \right)\, dx ,\end{align} $$
where we used that
![]() $\sigma _{\min }(A)=1/\mu _1(A)$
. Now use assumption (10.4) to see the right-hand side of (10.5) is
$\sigma _{\min }(A)=1/\mu _1(A)$
. Now use assumption (10.4) to see the right-hand side of (10.5) is
 $$ \begin{align} \lesssim 1 + \int_{1}^{\varepsilon^{-7/9}} (x^{-9\kappa/7}+ e^{-cn})\,dx \lesssim \max\left\{1, \varepsilon^{\kappa-7/9}\right\}\,. \end{align} $$
$$ \begin{align} \lesssim 1 + \int_{1}^{\varepsilon^{-7/9}} (x^{-9\kappa/7}+ e^{-cn})\,dx \lesssim \max\left\{1, \varepsilon^{\kappa-7/9}\right\}\,. \end{align} $$
Now, we apply Lemma 9.1 with
![]() $\delta = C\varepsilon \cdot (\log \varepsilon ^{-1} )^{1/2}$
,
$\delta = C\varepsilon \cdot (\log \varepsilon ^{-1} )^{1/2}$
,
![]() $s=0$
, and
$s=0$
, and
![]() $u=0$
to see that
$u=0$
to see that
 $$ \begin{align} \mathbb{P}_{A,X}\left(\frac{|\langle A^{-1}X,X\rangle - r |}{\|A^{-1}\|_{\mathrm{HS}}} \leqslant \delta,\, \frac{\mu_1}{\sqrt{n}} \leqslant \varepsilon^{-1} \right) &\lesssim \max\left\{\varepsilon, \varepsilon^{6\kappa/7+1/3}\right\} \cdot (\log \varepsilon^{-1} )^{1/2} + e^{-\Omega(n)}\, , \end{align} $$
$$ \begin{align} \mathbb{P}_{A,X}\left(\frac{|\langle A^{-1}X,X\rangle - r |}{\|A^{-1}\|_{\mathrm{HS}}} \leqslant \delta,\, \frac{\mu_1}{\sqrt{n}} \leqslant \varepsilon^{-1} \right) &\lesssim \max\left\{\varepsilon, \varepsilon^{6\kappa/7+1/3}\right\} \cdot (\log \varepsilon^{-1} )^{1/2} + e^{-\Omega(n)}\, , \end{align} $$
for all r. Here, we used that
![]() $\|A^{-1}\|_{\mathrm {HS}} \leqslant \|A^{-1}\|_{\ast }$
.
$\|A^{-1}\|_{\mathrm {HS}} \leqslant \|A^{-1}\|_{\ast }$
.
Now, by Hanson-Wright (Theorem 10.2), there exists
![]() $C'>0$
, such that
$C'>0$
, such that
Thus, we choose
![]() $C"$
to be large enough, so that
$C"$
to be large enough, so that
 $$ \begin{align*}\mathbb{P}_{A,X}\left(\, \frac{|\langle A^{-1}X,X\rangle -r |}{\|A^{-1} X\|_2} \leqslant C"\varepsilon , \sigma_{n}(A) \geqslant \varepsilon n^{-1/2}\, \right) \lesssim \max\left\{\varepsilon, \varepsilon^{6\kappa/7+1/3}\right\} \cdot (\log \varepsilon^{-1} )^{1/2} + e^{-\Omega(n)} \, ,\end{align*} $$
$$ \begin{align*}\mathbb{P}_{A,X}\left(\, \frac{|\langle A^{-1}X,X\rangle -r |}{\|A^{-1} X\|_2} \leqslant C"\varepsilon , \sigma_{n}(A) \geqslant \varepsilon n^{-1/2}\, \right) \lesssim \max\left\{\varepsilon, \varepsilon^{6\kappa/7+1/3}\right\} \cdot (\log \varepsilon^{-1} )^{1/2} + e^{-\Omega(n)} \, ,\end{align*} $$
Lemma 10.1 now follows by iterating Lemma 10.4 three times.
Proof of Lemma 10.1.
By Lemmas 10.3 and 10.4, we have
for some small
![]() $\eta>0$
. Applying Lemma 10.4 twice more gives an exponent of
$\eta>0$
. Applying Lemma 10.4 twice more gives an exponent of
![]() $\frac {127}{147}-\frac {6}{7}\eta $
and then
$\frac {127}{147}-\frac {6}{7}\eta $
and then
![]() $1$
, for
$1$
, for
![]() $\eta $
small, thus completing the proof.
$\eta $
small, thus completing the proof.
11 Proof of Theorem 1.1
We are now ready to prove our main result, Theorem 1.1. We use Lemma 6.1 (as in the proof of Lemma 10.1) and the inequality at (4.5) to see that it is enough to prove
 $$ \begin{align} \mathbb{P}^{\mathcal{E}}\left(\, \frac{|\langle A^{-1}X,X\rangle-r|}{\|A^{-1}X\|_2}\leqslant C\varepsilon, \text{ and } \sigma_n(A) \geqslant \varepsilon n^{-1/2} \right) \lesssim \varepsilon + e^{-\Omega(n)} \,, \end{align} $$
$$ \begin{align} \mathbb{P}^{\mathcal{E}}\left(\, \frac{|\langle A^{-1}X,X\rangle-r|}{\|A^{-1}X\|_2}\leqslant C\varepsilon, \text{ and } \sigma_n(A) \geqslant \varepsilon n^{-1/2} \right) \lesssim \varepsilon + e^{-\Omega(n)} \,, \end{align} $$
where C is as in Lemma 6.1 and the implied constants do not depend on r. Recall that
![]() $\mathcal {E}$
is the quasi-random event defined in Section 4.
$\mathcal {E}$
is the quasi-random event defined in Section 4.
To prepare ourselves for what follows, we put
![]() $\mathcal {E}_0 := \mathcal {E} \cap \{\sigma _{\min }(A) \geqslant \varepsilon n^{-1/2} \}$
and
$\mathcal {E}_0 := \mathcal {E} \cap \{\sigma _{\min }(A) \geqslant \varepsilon n^{-1/2} \}$
and
 $$\begin{align*}Q(A, X):=\frac{|\langle A^{-1}X,X\rangle-r|}{\|A^{-1}X\|_2}\, \, \text{ and } \, Q_{\ast}(A, X):=\frac{|\langle A^{-1}X,X\rangle-r|}{\|A^{-1}\|_{\ast}} ,\end{align*}$$
$$\begin{align*}Q(A, X):=\frac{|\langle A^{-1}X,X\rangle-r|}{\|A^{-1}X\|_2}\, \, \text{ and } \, Q_{\ast}(A, X):=\frac{|\langle A^{-1}X,X\rangle-r|}{\|A^{-1}\|_{\ast}} ,\end{align*}$$
where
 $$\begin{align*}\|A^{-1}\|_{*}^2 =\sum_{k=1}^n \mu_k^{2}(\log (1 + k) )^2 \, ,\end{align*}$$
$$\begin{align*}\|A^{-1}\|_{*}^2 =\sum_{k=1}^n \mu_k^{2}(\log (1 + k) )^2 \, ,\end{align*}$$
as defined in Section 8. We now split the left-hand side of (11.1) as
 $$ \begin{align} \mathbb{P}^{\mathcal{E}_0}\left( Q(A, X)\leqslant C\varepsilon \right) &\leqslant \mathbb{P}^{\mathcal{E}_0}\left(Q_{\ast}(A, X)\leqslant 2C\varepsilon \right) + \mathbb{P}^{\mathcal{E}_0}\left(Q(A, X)\leqslant C\varepsilon, \frac{\|A^{-1}X\|_2}{\|A^{-1}\|_{\ast}}\geqslant 2 \right)\,. \end{align} $$
$$ \begin{align} \mathbb{P}^{\mathcal{E}_0}\left( Q(A, X)\leqslant C\varepsilon \right) &\leqslant \mathbb{P}^{\mathcal{E}_0}\left(Q_{\ast}(A, X)\leqslant 2C\varepsilon \right) + \mathbb{P}^{\mathcal{E}_0}\left(Q(A, X)\leqslant C\varepsilon, \frac{\|A^{-1}X\|_2}{\|A^{-1}\|_{\ast}}\geqslant 2 \right)\,. \end{align} $$
We can take care of the first term easily by combining Lemmas 9.1 and 10.1.
Lemma 11.1. For
![]() $\varepsilon>0$
,
$\varepsilon>0$
,
Proof. Apply Lemma 9.1, with
![]() $\delta =2C\varepsilon $
,
$\delta =2C\varepsilon $
,
![]() $u=0$
, and
$u=0$
, and
![]() $s=0$
to obtain
$s=0$
to obtain
 $$ \begin{align*}\mathbb{P}^{\mathcal{E}_0}(Q_{\ast}(A, X)\leqslant 2 C \varepsilon ) \lesssim \varepsilon \left( \mathbb{E}_{A} \left(\frac{\mu_1}{\sqrt{n}} \right)^{7/9} {\mathbf{1}}\left\lbrace\frac{\mu_1}{\sqrt{n}}\leqslant \varepsilon^{-1} \right\rbrace \right)^{6/7} + e^{-\Omega(n)}\,.\end{align*} $$
$$ \begin{align*}\mathbb{P}^{\mathcal{E}_0}(Q_{\ast}(A, X)\leqslant 2 C \varepsilon ) \lesssim \varepsilon \left( \mathbb{E}_{A} \left(\frac{\mu_1}{\sqrt{n}} \right)^{7/9} {\mathbf{1}}\left\lbrace\frac{\mu_1}{\sqrt{n}}\leqslant \varepsilon^{-1} \right\rbrace \right)^{6/7} + e^{-\Omega(n)}\,.\end{align*} $$
By Lemma 10.1 and the calculation at (10.6), the expectation on the right is bounded by a constant.
We now focus on the latter term on the right-hand side of (11.2). By considering the dyadic partition
![]() $ 2^j \leqslant \|A^{-1}X\|_2 / \|A^{-1}\|_{*} \leqslant 2^{j+1}$
, we see the second term on the right hand side (RHS) of (11.2) is
$ 2^j \leqslant \|A^{-1}X\|_2 / \|A^{-1}\|_{*} \leqslant 2^{j+1}$
, we see the second term on the right hand side (RHS) of (11.2) is
 $$ \begin{align} \lesssim \sum_{j=1}^{\log n}\mathbb{P}^{\mathcal{E}_0}\left(Q_{\ast}(A, X) \leqslant 2^{j+1}C \varepsilon\,, \frac{\|A^{-1}X\|_2}{ \|A^{-1}\|_{*}}\geqslant 2^{j}\right)\ + e^{-\Omega(n)}\,. \end{align} $$
$$ \begin{align} \lesssim \sum_{j=1}^{\log n}\mathbb{P}^{\mathcal{E}_0}\left(Q_{\ast}(A, X) \leqslant 2^{j+1}C \varepsilon\,, \frac{\|A^{-1}X\|_2}{ \|A^{-1}\|_{*}}\geqslant 2^{j}\right)\ + e^{-\Omega(n)}\,. \end{align} $$
Here, we have dealt with the terms for which
![]() $j \geqslant \log n$
by using the fact that
$j \geqslant \log n$
by using the fact that
which follows from Hanson-Wright and the inequality
![]() $\|A^{-1}\|_{\ast }\geqslant \|A^{-1}\|_{\mathrm {HS}}$
.
$\|A^{-1}\|_{\ast }\geqslant \|A^{-1}\|_{\mathrm {HS}}$
.
We now show that the event
![]() $\|A^{-1}X\|_2 \geqslant t \|A^{-1}\|_\ast $
implies that X must correlate with one of the eigenvectors of A.
$\|A^{-1}X\|_2 \geqslant t \|A^{-1}\|_\ast $
implies that X must correlate with one of the eigenvectors of A.
Lemma 11.2. For
![]() $t>0$
, we have
$t>0$
, we have
 $$ \begin{align*} \mathbb{P}_{X}\left(Q_{\ast}(A,X)\leqslant 2Ct \varepsilon, \frac{ \|A^{-1}X\|_2}{ \|A^{-1}\|_{*}}\geqslant t\right) \leqslant 2\sum_{k=1}^n\mathbb{P}_X\left(Q_{\ast}(A,X)\leqslant 2Ct \varepsilon , \langle X,v_k\rangle\geqslant t \log (1 + k)\right) ,\end{align*} $$
$$ \begin{align*} \mathbb{P}_{X}\left(Q_{\ast}(A,X)\leqslant 2Ct \varepsilon, \frac{ \|A^{-1}X\|_2}{ \|A^{-1}\|_{*}}\geqslant t\right) \leqslant 2\sum_{k=1}^n\mathbb{P}_X\left(Q_{\ast}(A,X)\leqslant 2Ct \varepsilon , \langle X,v_k\rangle\geqslant t \log (1 + k)\right) ,\end{align*} $$
where
![]() $\{v_k\}$
is an orthonormal basis of eigenvectors of A.
$\{v_k\}$
is an orthonormal basis of eigenvectors of A.
Proof. Assume that
![]() $\|A^{-1}X\|_2 \geqslant t \|A^{-1}\|_{*}$
, and use the singular value decomposition associated with
$\|A^{-1}X\|_2 \geqslant t \|A^{-1}\|_{*}$
, and use the singular value decomposition associated with
![]() $\{v_k\}_k$
to write
$\{v_k\}_k$
to write
Thus
To finish the proof of Lemma 11.2, we union bound and treat the case of
![]() $-X$
the same as X (by possibly changing the sign of
$-X$
the same as X (by possibly changing the sign of
![]() $v_k$
) at the cost of a factor of
$v_k$
) at the cost of a factor of
![]() $2$
.
$2$
.
Proof of Theorem 1.1.
Recall that it suffices to establish (11.1). Combining (11.2) with Lemma 11.2 and Lemma 11.1 tells us that
 $$ \begin{align} \mathbb{P}^{\mathcal{E}_0}\left(Q(A,X) \leqslant C\varepsilon \right) \lesssim \varepsilon + 2\sum_{j=1}^{\log n}\sum_{k = 1}^n \mathbb{P}^{\mathcal{E}_0}\left(Q_{\ast}(A,X)\leqslant 2^{j+1}C \varepsilon , \langle X,v_k\rangle\geqslant 2^j \log(1 + k)\right) + e^{-\Omega(n)} \,. \end{align} $$
$$ \begin{align} \mathbb{P}^{\mathcal{E}_0}\left(Q(A,X) \leqslant C\varepsilon \right) \lesssim \varepsilon + 2\sum_{j=1}^{\log n}\sum_{k = 1}^n \mathbb{P}^{\mathcal{E}_0}\left(Q_{\ast}(A,X)\leqslant 2^{j+1}C \varepsilon , \langle X,v_k\rangle\geqslant 2^j \log(1 + k)\right) + e^{-\Omega(n)} \,. \end{align} $$
We now apply Lemma 9.1 for all
![]() $t>0$
, with
$t>0$
, with
![]() $\delta = 2Ct\varepsilon $
,
$\delta = 2Ct\varepsilon $
,
![]() $s=t \log (k+1)$
and
$s=t \log (k+1)$
and
![]() $u=v_k$
to see that,
$u=v_k$
to see that,
where
 $$\begin{align*}I := \mathbb{E}_{A} \left(\frac{\mu_1(A)}{\sqrt{n}}\right)^{7/9} {\mathbf{1}}\left\{\frac{\mu_1(A)}{\sqrt{n}} \leqslant \varepsilon^{-1} \right\}. \end{align*}$$
$$\begin{align*}I := \mathbb{E}_{A} \left(\frac{\mu_1(A)}{\sqrt{n}}\right)^{7/9} {\mathbf{1}}\left\{\frac{\mu_1(A)}{\sqrt{n}} \leqslant \varepsilon^{-1} \right\}. \end{align*}$$
 $$\begin{align*}\mathbb{P}^{\mathcal{E}_0}(Q(A,X) \leqslant C\varepsilon ) \lesssim \varepsilon I^{6/7} \sum_{j=1}^{\log n}\sum_{k = 1}^{n} 2^j(k+1)^{-2^j} + e^{-\Omega(n)} \lesssim \varepsilon \cdot I^{6/7} + e^{-\Omega(n)}, \end{align*}$$
$$\begin{align*}\mathbb{P}^{\mathcal{E}_0}(Q(A,X) \leqslant C\varepsilon ) \lesssim \varepsilon I^{6/7} \sum_{j=1}^{\log n}\sum_{k = 1}^{n} 2^j(k+1)^{-2^j} + e^{-\Omega(n)} \lesssim \varepsilon \cdot I^{6/7} + e^{-\Omega(n)}, \end{align*}$$
since
![]() $\sum _{j=1}^{\infty }\sum _{k = 1}^{\infty } 2^j(k+1)^{-2^j} = O(1)$
. Now we write
$\sum _{j=1}^{\infty }\sum _{k = 1}^{\infty } 2^j(k+1)^{-2^j} = O(1)$
. Now we write
 $$\begin{align*}I = \mathbb{E}_{A}\, \left(\frac{\mu_1(A)}{\sqrt{n}}\right)^{7/9} {\mathbf{1}}\left\{\frac{\mu_1(A)}{\sqrt{n}} \leqslant \varepsilon^{-1} \right\} \leqslant \int_{0}^{\varepsilon^{-7/9}}\mathbb{P}\left(\sigma_{\min}(A)\leqslant x^{-9/7} n^{-1/2} \right)\, dx\end{align*}$$
$$\begin{align*}I = \mathbb{E}_{A}\, \left(\frac{\mu_1(A)}{\sqrt{n}}\right)^{7/9} {\mathbf{1}}\left\{\frac{\mu_1(A)}{\sqrt{n}} \leqslant \varepsilon^{-1} \right\} \leqslant \int_{0}^{\varepsilon^{-7/9}}\mathbb{P}\left(\sigma_{\min}(A)\leqslant x^{-9/7} n^{-1/2} \right)\, dx\end{align*}$$
and apply Lemma 10.1 to see
 $$\begin{align*}\int_{0}^{\varepsilon^{-7/9}}\mathbb{P}\left(\sigma_{\min}(A)\leqslant x^{-9/7} n^{-1/2} \right)\, dx \lesssim \int_{1}^{\infty} s^{-9/7} \, ds + 1 \lesssim 1. \end{align*}$$
$$\begin{align*}\int_{0}^{\varepsilon^{-7/9}}\mathbb{P}\left(\sigma_{\min}(A)\leqslant x^{-9/7} n^{-1/2} \right)\, dx \lesssim \int_{1}^{\infty} s^{-9/7} \, ds + 1 \lesssim 1. \end{align*}$$
I Introduction to the appendices
In these appendices, we lay out the proof of Theorem 4.3, the “master quasi-randomness theorem,” which we left unproved in the main body of the paper, and the proof of Theorem 9.2. The proofs of these results are technical adaptations of the authors’ previous work on the singularity of random symmetric matrices [Reference Campos, Jenssen, Michelen and Sahasrabudhe4]. The last three appendices also tie up some other loose ends in the main body of the text.
In particular, the proof of Theorem 4.3 is similar to the proof of the main theorem in [Reference Campos, Jenssen, Michelen and Sahasrabudhe4], with only a few tweaks and additions required to make the adaptation go through. In several places, we need only update the constants and will be satisfied in pointing the interested reader to [Reference Campos, Jenssen, Michelen and Sahasrabudhe4] for more detail. Elsewhere, more significant adaptations are required, and we outline these changes in full detail. As such, parts of these appendices will bore the restless expert, but we hope it will provide a useful source for those who are taking up the subject or want to avoid writing out the (sometimes extensive) details for oneself.
I.1 Definitions
We collect a few definitions from the main body of the text that are most relevant for us here. Throughout,
![]() $\zeta $
will be a random variable with mean
$\zeta $
will be a random variable with mean
![]() $0$
and variance
$0$
and variance
![]() $1$
. Such a random variable is said to be subgaussian if the subgaussian moment
$1$
. Such a random variable is said to be subgaussian if the subgaussian moment
is finite. For
![]() $B>0$
, we let
$B>0$
, we let
![]() $\Gamma _B$
denote the set of mean
$\Gamma _B$
denote the set of mean
![]() $0$
variance
$0$
variance
![]() $1$
random variables with subgaussian moment
$1$
random variables with subgaussian moment
![]() $\leqslant B$
, and we let
$\leqslant B$
, and we let
![]() $\Gamma = \bigcup _{B>0} \Gamma _B$
.
$\Gamma = \bigcup _{B>0} \Gamma _B$
.
For
![]() $\zeta \in \Gamma $
, let
$\zeta \in \Gamma $
, let
![]() $\mathrm {Sym\,}_{n}(\zeta )$
denote the probability space of
$\mathrm {Sym\,}_{n}(\zeta )$
denote the probability space of
![]() $n \times n$
symmetric matrices with
$n \times n$
symmetric matrices with
![]() $(A_{i,j})_{i\leqslant j} $
i.i.d. distributed according to
$(A_{i,j})_{i\leqslant j} $
i.i.d. distributed according to
![]() $\zeta $
. Let
$\zeta $
. Let
![]() $\mathrm {Col\,}_n(\zeta )$
be the probability space on vectors of length n with independent coordinates distributed according to
$\mathrm {Col\,}_n(\zeta )$
be the probability space on vectors of length n with independent coordinates distributed according to
![]() $\zeta $
.
$\zeta $
.
For
![]() $v\in {\mathbb {S}}^{n-1}$
and
$v\in {\mathbb {S}}^{n-1}$
and
![]() $\mu ,\alpha ,\gamma \in (0,1)$
, define the least common denominator (LCD) of the vector v via
$\mu ,\alpha ,\gamma \in (0,1)$
, define the least common denominator (LCD) of the vector v via
where
![]() $\|w\|_{\mathbb {T}} := \mathrm {dist}(w,\mathbb {Z}^n)$
. We also define
$\|w\|_{\mathbb {T}} := \mathrm {dist}(w,\mathbb {Z}^n)$
. We also define
 $$ \begin{align} \hat{D}_{\alpha,\gamma,\mu}(v) := \min_{\substack{I\subset [n]\\|I|\geqslant (1-2\mu)n}}D_{\alpha,\gamma}\left(v_I\right)\,. \end{align} $$
$$ \begin{align} \hat{D}_{\alpha,\gamma,\mu}(v) := \min_{\substack{I\subset [n]\\|I|\geqslant (1-2\mu)n}}D_{\alpha,\gamma}\left(v_I\right)\,. \end{align} $$
Remark I.1. We note that in the main body of the paper, we work with a slightly different notion of
![]() $\hat {D}$
, where we define
$\hat {D}$
, where we define
![]() $\hat {D}_{\alpha ,\gamma ,\mu }(v) = \min _I D_{\alpha ,\gamma } (v_I/\|v_I\|_2)$
. This makes no difference for us, as Lemma II.6 below eliminates those v for which
$\hat {D}_{\alpha ,\gamma ,\mu }(v) = \min _I D_{\alpha ,\gamma } (v_I/\|v_I\|_2)$
. This makes no difference for us, as Lemma II.6 below eliminates those v for which
![]() $\|v_I\|_2$
is less than a constant. Thus, we work with the slightly simpler definition (I.2) throughout.
$\|v_I\|_2$
is less than a constant. Thus, we work with the slightly simpler definition (I.2) throughout.
We define the set of “structured direction on the sphere”
Now, for
![]() $\zeta \in \Gamma $
,
$\zeta \in \Gamma $
,
![]() $A \sim \mathrm {Sym\,}_n(\zeta )$
and a given vector
$A \sim \mathrm {Sym\,}_n(\zeta )$
and a given vector
![]() $w \in \mathbb {R}^n$
, we define the quantity (as in Section 4)
$w \in \mathbb {R}^n$
, we define the quantity (as in Section 4)
We then recall (see (4.10))
I.2 Main theorems of the appendix
Let us now restate the two main objectives of this appendix. Our first goal is to prove the following.
Theorem I.2 (Master quasi-randomness theorem).
For
![]() $B>0$
and
$B>0$
and
![]() $\zeta \in \Gamma _B$
, there exist constants
$\zeta \in \Gamma _B$
, there exist constants
![]() $\alpha ,\gamma ,\mu ,c_{\Sigma },c \in (0,1)$
depending only on B so that
$\alpha ,\gamma ,\mu ,c_{\Sigma },c \in (0,1)$
depending only on B so that
The second main goal of this appendix is to prove Theorem 9.2, which we will prove on our way to proving Theorem I.2.
Theorem I.3. For
![]() $B>0$
, let
$B>0$
, let
![]() $\zeta \in \Gamma _B$
. For
$\zeta \in \Gamma _B$
. For
![]() $d \in \mathbb {N}$
,
$d \in \mathbb {N}$
,
![]() $\alpha ,\gamma \in (0,1)$
, and
$\alpha ,\gamma \in (0,1)$
, and
![]() $\nu \in (0,2^{-15})$
, there are constants
$\nu \in (0,2^{-15})$
, there are constants
![]() $c_0,R> 0$
depending only on
$c_0,R> 0$
depending only on
![]() $\alpha ,\gamma ,\nu ,B$
so that the following holds. Let
$\alpha ,\gamma ,\nu ,B$
so that the following holds. Let
![]() $0\leqslant k \leqslant c_0 \alpha d$
and
$0\leqslant k \leqslant c_0 \alpha d$
and
![]() $t \geqslant \exp (-c_0\alpha d)$
; let
$t \geqslant \exp (-c_0\alpha d)$
; let
![]() $v \in {\mathbb {S}}^{d-1}$
, and let
$v \in {\mathbb {S}}^{d-1}$
, and let
![]() $w_1,\ldots ,w_k \in {\mathbb {S}}^{d-1}$
be orthogonal.
$w_1,\ldots ,w_k \in {\mathbb {S}}^{d-1}$
be orthogonal.
Let
![]() $\zeta '$
be an independent copy of
$\zeta '$
be an independent copy of
![]() $\zeta $
, let
$\zeta $
, let
![]() $Z_\nu $
be a Bernoulli random variable with parameter
$Z_\nu $
be a Bernoulli random variable with parameter
![]() $\nu $
, and let
$\nu $
, and let
![]() $\tau \in \mathbb {R}^d$
be a random vector whose coordinates are i.i.d. copies of the random variable with distribution
$\tau \in \mathbb {R}^d$
be a random vector whose coordinates are i.i.d. copies of the random variable with distribution
![]() $(\zeta - \zeta ')Z_\nu $
.
$(\zeta - \zeta ')Z_\nu $
.
If
![]() $D_{\alpha ,\gamma }(v)> 1/t$
, then
$D_{\alpha ,\gamma }(v)> 1/t$
, then
 $$ \begin{align*} \mathbb{P}\left( |\langle \tau, v \rangle| \leqslant t\, \text{ and }\, \sum_{j = 1}^k \langle w_j, \tau\rangle^2 \leqslant c_0 k \right) \leqslant R t \cdot e^{-c_0 k}\,. \end{align*} $$
$$ \begin{align*} \mathbb{P}\left( |\langle \tau, v \rangle| \leqslant t\, \text{ and }\, \sum_{j = 1}^k \langle w_j, \tau\rangle^2 \leqslant c_0 k \right) \leqslant R t \cdot e^{-c_0 k}\,. \end{align*} $$
The proofs of Theorems I.2 and I.3 follow the same path as [Reference Campos, Jenssen, Michelen and Sahasrabudhe4], where the authors proved analogous statements for the case where the entries of A are uniform in
![]() $\{-1,1\}$
. We refer the reader to the following Section I.3 for a discussion of how this appendix is structured relative to [Reference Campos, Jenssen, Michelen and Sahasrabudhe4].
$\{-1,1\}$
. We refer the reader to the following Section I.3 for a discussion of how this appendix is structured relative to [Reference Campos, Jenssen, Michelen and Sahasrabudhe4].
I.3 A Reader’s guide for the appendices
Here, we describe the correspondence between sections in this appendix and sections in [Reference Campos, Jenssen, Michelen and Sahasrabudhe4] and point out the key changes that come up.
In Section II, we set up many of the basic notions that we will need for the proof of Theorem I.2. The main novelty here is in the definitions of several auxiliary random variables, related to
![]() $\zeta $
, that will be used to study
$\zeta $
, that will be used to study
![]() $\zeta $
in the course of the paper.
$\zeta $
in the course of the paper.
In Section III, we turn to prove Theorem I.2, while assuming several key results that we either import from [Reference Campos, Jenssen, Michelen and Sahasrabudhe4] or prove in later sections. This section is the analogue of Section 9 in [Reference Campos, Jenssen, Michelen and Sahasrabudhe4], and the main difference between these sections arises from the different definitions of
![]() $q_n$
in these two papers (see (4.10)). Here,
$q_n$
in these two papers (see (4.10)). Here,
![]() $q_n$
is defined in terms of the least common denominator
$q_n$
is defined in terms of the least common denominator
![]() $D_{\alpha ,\gamma }$
, rather than the threshold
$D_{\alpha ,\gamma }$
, rather than the threshold
![]() $\mathcal {T}_L$
(see (II.7)). In the course of the proof, we also need to break things up according to
$\mathcal {T}_L$
(see (II.7)). In the course of the proof, we also need to break things up according to
![]() $\mathcal {T}_L$
, and define nets as we did in [Reference Campos, Jenssen, Michelen and Sahasrabudhe4], but another net argument is required to exclude vectors with
$\mathcal {T}_L$
, and define nets as we did in [Reference Campos, Jenssen, Michelen and Sahasrabudhe4], but another net argument is required to exclude vectors with
![]() $\mathcal {T}_L$
small but
$\mathcal {T}_L$
small but
![]() $D_{\alpha ,\gamma }$
large.
$D_{\alpha ,\gamma }$
large.
In Section IV, we define many of the key Fourier-related notions that we will need to prove the remaining results, including Theorem I.3. The main differences between the two papers in these sections comes from the different definition of the sublevel sets
![]() $S_W$
(see (IV.1)). This new definition requires us to reprove a few of our basic lemmas from [Reference Campos, Jenssen, Michelen and Sahasrabudhe4], however, the proofs go through easily.
$S_W$
(see (IV.1)). This new definition requires us to reprove a few of our basic lemmas from [Reference Campos, Jenssen, Michelen and Sahasrabudhe4], however, the proofs go through easily.
In Section IV.2, we state our main inverse Littlewood-Offord Theorem for conditioned random walks and deduce Theorem I.3 from it. Lemma IV.3 in this section is also one of the main ingredients that goes into Theorem III.2. This section corresponds to Section 3 of [Reference Campos, Jenssen, Michelen and Sahasrabudhe4].
Section V deals with Fourier replacement and is the analogue of Appendix B in [Reference Campos, Jenssen, Michelen and Sahasrabudhe4]. Here, the only difference between the sections is that here we lack an explicit form for the Fourier transform. However, this difficulty is easily overcome.
In Section VI, we prove Lemma IV.3. This corresponds to Sections 4 and 5 of [Reference Campos, Jenssen, Michelen and Sahasrabudhe4], from which several key geometric facts are imported wholesale, making our task significantly lighter here. The difference in the definitions from Section IV are salient here, but the majority of the proof is the same as in [Reference Campos, Jenssen, Michelen and Sahasrabudhe4, Section 5], up to the constants involved.
The next three sections, Sections VII, VIII, and IX, correspond to Sections 6, 7, and 8 respectively of [Reference Campos, Jenssen, Michelen and Sahasrabudhe4]. Here, the adaptation to this paper requires little more than updating constants. These three sections amount to converting Lemma IV.3 into the main net bound Theorem III.2.
Finally, in Section X, we deduce the Hanson-Wright inequality, Lemma VI.7, from Talagrand’s inequality; this corresponds to Appendix E of [Reference Campos, Jenssen, Michelen and Sahasrabudhe4] where the difference, again, is only up to constants.
II Preparations
II.1 Symmetrizing and truncating the random variable
We will work with symmetrized, truncated, and lazy versions of the variable
![]() $\zeta $
. This is primarily because these altered versions will have better behaved Fourier properties. Here, we introduce these random variables and also note some properties of their characteristic functions. These properties are not so important until Section IV, but we have them here to help motivate some of the definitions.
$\zeta $
. This is primarily because these altered versions will have better behaved Fourier properties. Here, we introduce these random variables and also note some properties of their characteristic functions. These properties are not so important until Section IV, but we have them here to help motivate some of the definitions.
Let
![]() $\zeta '$
be an independent copy of
$\zeta '$
be an independent copy of
![]() $\zeta $
and define
$\zeta $
and define
We will want to truncate
![]() $\tilde {\zeta }$
to a bounded window, as this will be useful for our construction of a nondegenerate and not-too-large LCD in Section VI. In this direction, define
$\tilde {\zeta }$
to a bounded window, as this will be useful for our construction of a nondegenerate and not-too-large LCD in Section VI. In this direction, define
![]() $I_B = (1,16B^2)$
and
$I_B = (1,16B^2)$
and
![]() $p := \mathbb {P}(|\tilde {\zeta }| \in I_B)$
. Our first step is to uniformly bound p in terms of B.
$p := \mathbb {P}(|\tilde {\zeta }| \in I_B)$
. Our first step is to uniformly bound p in terms of B.
Lemma II.1.
![]() $p \geqslant \frac {1}{2^{7} B^4}$
.
$p \geqslant \frac {1}{2^{7} B^4}$
.
Proof. By the Paley-Zygmund inequality
 $$\begin{align*}\mathbb{P}(|\tilde{\zeta}|> 1) = \mathbb{P}(|\tilde{\zeta}|^2 > \mathbb{E} |\tilde{\zeta}|^2 / 2) \geqslant \frac{(1 - \frac{1}{2})^{2}(\mathbb{E} \tilde{\zeta}^2)^{2} }{(\mathbb{E} \tilde{\zeta}^4 )} \geqslant \frac{1}{2^6 B^4} ,\end{align*}$$
$$\begin{align*}\mathbb{P}(|\tilde{\zeta}|> 1) = \mathbb{P}(|\tilde{\zeta}|^2 > \mathbb{E} |\tilde{\zeta}|^2 / 2) \geqslant \frac{(1 - \frac{1}{2})^{2}(\mathbb{E} \tilde{\zeta}^2)^{2} }{(\mathbb{E} \tilde{\zeta}^4 )} \geqslant \frac{1}{2^6 B^4} ,\end{align*}$$
where we have used
![]() $\mathbb {E} \tilde {\zeta }^4= 2 \mathbb {E} \zeta ^4+6 \leqslant 2^5B^4 +6$
and
$\mathbb {E} \tilde {\zeta }^4= 2 \mathbb {E} \zeta ^4+6 \leqslant 2^5B^4 +6$
and
![]() $B\geqslant 1$
. By Chebyshev’s inequality, we have
$B\geqslant 1$
. By Chebyshev’s inequality, we have
Combining the bounds completes the proof.
For a parameter
![]() $\nu \in (0,1)$
, define
$\nu \in (0,1)$
, define
![]() $\xi _\nu $
by
$\xi _\nu $
by
where
![]() $Z_\nu $
is an independent Bernoulli variable with mean
$Z_\nu $
is an independent Bernoulli variable with mean
![]() $\nu $
. For
$\nu $
. For
![]() $\nu \in (0,1)$
and
$\nu \in (0,1)$
and
![]() $d \in \mathbb {N}$
, we write
$d \in \mathbb {N}$
, we write
![]() $X \sim \Xi _\nu (d; \zeta )$
to indicate that X is a random vector in
$X \sim \Xi _\nu (d; \zeta )$
to indicate that X is a random vector in
![]() $\mathbb {R}^d$
whose entries are i.i.d. copies of the variable
$\mathbb {R}^d$
whose entries are i.i.d. copies of the variable
![]() $\xi _\nu $
; similarly, we write
$\xi _\nu $
; similarly, we write
![]() $X\sim \Phi _\nu (d; \zeta )$
to denote a random vector whose entries are i.i.d. copies of the random variable
$X\sim \Phi _\nu (d; \zeta )$
to denote a random vector whose entries are i.i.d. copies of the random variable
![]() $\tilde {\zeta } Z_\nu $
.
$\tilde {\zeta } Z_\nu $
.
We compute the characteristic function of
![]() $\xi _\nu $
to be
$\xi _\nu $
to be
Define the variable
![]() $\bar {\zeta }$
as
$\bar {\zeta }$
as
![]() $\tilde {\zeta }$
conditioned on
$\tilde {\zeta }$
conditioned on
![]() $|\tilde {\zeta }| \in I_B$
, where we note that this conditioning makes sense since Lemma II.1 shows
$|\tilde {\zeta }| \in I_B$
, where we note that this conditioning makes sense since Lemma II.1 shows
![]() $p> 0$
. In other words, for every Borel set S,
$p> 0$
. In other words, for every Borel set S,
Therefore we can write the characteristic function of
![]() $\xi _{\nu }$
as
$\xi _{\nu }$
as
For
![]() $x\in \mathbb {R}$
, define
$x\in \mathbb {R}$
, define
![]() $\|x \|_{\mathbb {T}} := \mathrm {dist}(x,\mathbb {Z})$
, and note the elementary inequalities
$\|x \|_{\mathbb {T}} := \mathrm {dist}(x,\mathbb {Z})$
, and note the elementary inequalities
for
![]() $a\in \mathbb {R}$
. These imply that
$a\in \mathbb {R}$
. These imply that
Also note that since
![]() $\phi _{\tilde {\zeta } Z_\nu }(t)=1-\nu +\nu \mathbb {E}_{\tilde {\zeta }}[\cos (2\pi t\tilde {\zeta })]$
, we have
$\phi _{\tilde {\zeta } Z_\nu }(t)=1-\nu +\nu \mathbb {E}_{\tilde {\zeta }}[\cos (2\pi t\tilde {\zeta })]$
, we have
II.2 Properties of subgaussian random variables and matrices
We will use a basic fact about exponential moments of one-dimensional projections of subgaussian random variables (see, e.g. [Reference Vershynin47, Proposition 2.6.1]).
Fact II.2. For
![]() $B>0$
, let
$B>0$
, let
![]() $Y = (Y_1,\ldots ,Y_d)$
be a random vector with
$Y = (Y_1,\ldots ,Y_d)$
be a random vector with
![]() $Y_1,\ldots ,Y_d \in \Gamma _{B}$
. Then for all
$Y_1,\ldots ,Y_d \in \Gamma _{B}$
. Then for all
![]() $u \in {\mathbb {S}}^{d-1}$
, we have
$u \in {\mathbb {S}}^{d-1}$
, we have
![]() $\mathbb {E}\, e^{\langle Y, u \rangle } = O_B(1)$
.
$\mathbb {E}\, e^{\langle Y, u \rangle } = O_B(1)$
.
We will also use a large deviation bound for the operator norm of A (see (4.11)).
Fact II.3. For
![]() $B>0$
, let
$B>0$
, let
![]() $\zeta \in \Gamma $
and
$\zeta \in \Gamma $
and
![]() $A \sim \mathrm {Sym\,}_n(\zeta )$
. Then
$A \sim \mathrm {Sym\,}_n(\zeta )$
. Then
We also define the event
![]() $\mathcal {K} = \{\|A\|_{op} \geqslant 4\sqrt {n}\}$
, and define the measure
$\mathcal {K} = \{\|A\|_{op} \geqslant 4\sqrt {n}\}$
, and define the measure
![]() $\mathbb {P}^{\mathcal {K}}$
by
$\mathbb {P}^{\mathcal {K}}$
by
for every event
![]() $\mathcal {E}$
.
$\mathcal {E}$
.
II.3 Compressibility and eliminating nonflat vectors
As in [Reference Campos, Jenssen, Michelen and Sahasrabudhe4], we may limit our attention to vectors that are “flat” on a constant proportion of their coordinates. This reduction is a consequence of the now-classical work of Rudelson and Vershynin on compressible and incompressible vectors [Reference Rudelson and Vershynin31].
Following [Reference Rudelson and Vershynin31], we say that a vector in
![]() ${\mathbb {S}}^{n-1}$
is
${\mathbb {S}}^{n-1}$
is
![]() $(\delta ,\rho )$
-compressible if it has distance at most
$(\delta ,\rho )$
-compressible if it has distance at most
![]() $\rho $
from a vector with support of size at most
$\rho $
from a vector with support of size at most
![]() $\delta n$
. For
$\delta n$
. For
![]() $\delta ,\rho \in (0,1)$
, let
$\delta ,\rho \in (0,1)$
, let
![]() $\mathrm {Comp\,}(\delta ,\rho )$
denote the set of all such compressible vectors in
$\mathrm {Comp\,}(\delta ,\rho )$
denote the set of all such compressible vectors in
![]() ${\mathbb {S}}^{n-1}$
. Proposition 4.2 from Vershynin’s paper [Reference Vershynin46] takes care of all compressible vectors.
${\mathbb {S}}^{n-1}$
. Proposition 4.2 from Vershynin’s paper [Reference Vershynin46] takes care of all compressible vectors.
Lemma II.4. For
![]() $B>0$
, let
$B>0$
, let
![]() $\zeta \in \Gamma _B$
, let
$\zeta \in \Gamma _B$
, let
![]() $A_n \sim \mathrm {Sym\,}_{n}(\zeta )$
, and let
$A_n \sim \mathrm {Sym\,}_{n}(\zeta )$
, and let
![]() $K \geqslant 1$
. Then there exist
$K \geqslant 1$
. Then there exist
![]() $\rho ,\delta ,c>0$
depending only on
$\rho ,\delta ,c>0$
depending only on
![]() $K, B$
, so that for every
$K, B$
, so that for every
![]() ${\lambda } \in \mathbb {R}$
and
${\lambda } \in \mathbb {R}$
and
![]() $w\in \mathbb {R}^n$
, we have
$w\in \mathbb {R}^n$
, we have
For the remainder of the paper, we let
![]() $\delta ,\rho $
be the constants given in Lemma II.4. Define
$\delta ,\rho $
be the constants given in Lemma II.4. Define
to be the set of
![]() $(\delta ,\rho )$
-incompressible vectors. The key property of incompressible vectors is that they are “flat” for a constant proportion of coordinates. This is made quantitative in the following lemma of Rudelson and Vershynin [Reference Rudelson and Vershynin31].
$(\delta ,\rho )$
-incompressible vectors. The key property of incompressible vectors is that they are “flat” for a constant proportion of coordinates. This is made quantitative in the following lemma of Rudelson and Vershynin [Reference Rudelson and Vershynin31].
Lemma II.5. Let
![]() $v\in \mathrm {Incomp\,}(\delta ,\rho )$
. Then
$v\in \mathrm {Incomp\,}(\delta ,\rho )$
. Then
for at least
![]() $\rho ^2\delta n/2$
values of
$\rho ^2\delta n/2$
values of
![]() $i\in [n]$
.
$i\in [n]$
.
We now fix a few more constants to be held fixed throughout the paper. Let
![]() ${\kappa }_0 = \rho /3$
and
${\kappa }_0 = \rho /3$
and
![]() ${\kappa }_1 = \delta ^{-1/2}+\rho /6$
, where
${\kappa }_1 = \delta ^{-1/2}+\rho /6$
, where
![]() $\delta ,\rho $
are as in Lemma II.4. For
$\delta ,\rho $
are as in Lemma II.4. For
![]() $D\subseteq [n]$
, define the set of directions in
$D\subseteq [n]$
, define the set of directions in
![]() ${\mathbb {S}}^{n-1}$
that are “flat on D”:
${\mathbb {S}}^{n-1}$
that are “flat on D”:
and let
Applying Lemmas II.4 and II.5 in tandem will allow us to eliminate vectors outside of
![]() $\mathcal {I}$
.
$\mathcal {I}$
.
Lemma II.6. Let
![]() $\delta ,\rho , c>0$
be the constants defined in Lemma II.4, and let
$\delta ,\rho , c>0$
be the constants defined in Lemma II.4, and let
![]() $d < \rho ^2 \delta n/2$
. Then
$d < \rho ^2 \delta n/2$
. Then
Proof. Lemma II.5, along with the definitions of
![]() ${\kappa }_0,{\kappa }_1$
, and
${\kappa }_0,{\kappa }_1$
, and
![]() $\mathcal {I}$
, implies that
$\mathcal {I}$
, implies that
Now, fix a
![]() $w \in \mathbb {R}^{n}$
and take a
$w \in \mathbb {R}^{n}$
and take a
![]() $c\sqrt {n}/8$
-net
$c\sqrt {n}/8$
-net
![]() $\mathcal {N}$
for
$\mathcal {N}$
for
![]() $[-4\sqrt {n},4\sqrt {n}]^2$
of size
$[-4\sqrt {n},4\sqrt {n}]^2$
of size
![]() $O(c^{-2})$
to see that
$O(c^{-2})$
to see that
![]() $\|Av-sv-tw\|_2 \leqslant c \sqrt {n}/2$
implies that there exists
$\|Av-sv-tw\|_2 \leqslant c \sqrt {n}/2$
implies that there exists
![]() $(s',t')\in \mathcal {N}$
for which
$(s',t')\in \mathcal {N}$
for which
Thus, the left-hand side of (II.5) is
where the final inequality follows by first intersecting each term in the sum with the event
![]() $\mathcal {E} := \{ \|A - s'I\|_{op} \leqslant 16n^{1/2} \}$
(noting that
$\mathcal {E} := \{ \|A - s'I\|_{op} \leqslant 16n^{1/2} \}$
(noting that
![]() $\mathbb {P}(\mathcal {E}^c) \leqslant 2e^{-\Omega (n)}$
, by Fact II.3) and applying Lemma II.4 to each term in the sum with
$\mathbb {P}(\mathcal {E}^c) \leqslant 2e^{-\Omega (n)}$
, by Fact II.3) and applying Lemma II.4 to each term in the sum with
![]() $\lambda = -s'$
and
$\lambda = -s'$
and
![]() $K = 16$
.
$K = 16$
.
II.4 Zeroed out matrices
To study our original matrix A, it will be useful to work with random symmetric matrices that have large blocks that are “zeroed out” and entries that are distributed like
![]() $\tilde {\zeta } Z_\nu $
elsewhere (see [Reference Campos, Jenssen, Michelen and Sahasrabudhe4] for more discussion on this). For this, we set
$\tilde {\zeta } Z_\nu $
elsewhere (see [Reference Campos, Jenssen, Michelen and Sahasrabudhe4] for more discussion on this). For this, we set
![]() $d :=c_0^2 n$
(where
$d :=c_0^2 n$
(where
![]() $c_0>0$
is a small constant to be determined later) and write
$c_0>0$
is a small constant to be determined later) and write
![]() $M \sim \mathcal {M}_n(\nu )$
for the
$M \sim \mathcal {M}_n(\nu )$
for the
![]() $n\times n$
random matrix
$n\times n$
random matrix
 $$ \begin{align} M = \begin{bmatrix} \mathbf{0 }_{[d] \times [d]} & H_1^T \\ H_1 & \mathbf{0}_{[d+1,n] \times [d+1,n]} \end{bmatrix}\,, \end{align} $$
$$ \begin{align} M = \begin{bmatrix} \mathbf{0 }_{[d] \times [d]} & H_1^T \\ H_1 & \mathbf{0}_{[d+1,n] \times [d+1,n]} \end{bmatrix}\,, \end{align} $$
where
![]() $H_1$
is a
$H_1$
is a
![]() $(n-d) \times d$
random matrix whose entries are i.i.d. copies of
$(n-d) \times d$
random matrix whose entries are i.i.d. copies of
![]() $\tilde {\zeta } Z_\nu $
.
$\tilde {\zeta } Z_\nu $
.
In particular, the matrix M will be useful for analyzing events of the form
![]() $\|Av\|_2 \leqslant \varepsilon n^{1/2} $
, when
$\|Av\|_2 \leqslant \varepsilon n^{1/2} $
, when
![]() $v \in \mathcal {I}([d])$
.
$v \in \mathcal {I}([d])$
.
We now use the definition of
![]() $\mathcal {M}_n(\nu )$
to define another notion of “structure” for vectors
$\mathcal {M}_n(\nu )$
to define another notion of “structure” for vectors
![]() $v \in {\mathbb {S}}^{n-1}$
. This is a very different measure of “structure” from that provided by the LCD, which we saw above. For
$v \in {\mathbb {S}}^{n-1}$
. This is a very different measure of “structure” from that provided by the LCD, which we saw above. For
![]() $L> 0$
and
$L> 0$
and
![]() $v \in \mathbb {R}^n$
, define the threshold of v as
$v \in \mathbb {R}^n$
, define the threshold of v as
One can think of this
![]() $\mathcal {T}_L(v)$
as the “scale” at which the structure of v (relative to M) starts to emerge. So “large threshold” means “more structured.”
$\mathcal {T}_L(v)$
as the “scale” at which the structure of v (relative to M) starts to emerge. So “large threshold” means “more structured.”
III Proof of Theorem I.2
Here, we recall some key notions from [Reference Campos, Jenssen, Michelen and Sahasrabudhe4], state analogous lemmas, and prove Theorem I.2 assuming these lemmas.
III.1 Efficient nets
Our goal is to obtain an exponential bound on the quantity
defined at (4.10), where
In the course of the proof, we will choose
![]() $\alpha ,\gamma ,\mu $
to be sufficiently small.
$\alpha ,\gamma ,\mu $
to be sufficiently small.
We cover
![]() $\Sigma \subseteq {\mathbb {S}}^{n-1}$
with two regions which will be dealt with in very different ways. First, we define
$\Sigma \subseteq {\mathbb {S}}^{n-1}$
with two regions which will be dealt with in very different ways. First, we define
This will be the trickier region and will depend on the net construction from [Reference Campos, Jenssen, Michelen and Sahasrabudhe4]. We also need to take care of the region
which we take care of using the nets constructed by Rudelson and Vershynin in [Reference Rudelson and Vershynin31]. We recall that
![]() $\mathcal {T}_L$
is defined at (II.7).
$\mathcal {T}_L$
is defined at (II.7).
We also note that since the event
![]() $\mathcal {K} := \{ \|A\|_{\text {op}} \geqslant 4n^{1/2} \}$
fails with probability
$\mathcal {K} := \{ \|A\|_{\text {op}} \geqslant 4n^{1/2} \}$
fails with probability
![]() $2e^{-cn}$
(Fact II.3) and we only need to deal with incompressible vectors
$2e^{-cn}$
(Fact II.3) and we only need to deal with incompressible vectors
![]() $v \in \mathcal {I}$
(by Lemma II.6), it is enough to show
$v \in \mathcal {I}$
(by Lemma II.6), it is enough to show
and the same with
![]() $S'$
replacing S. We recall that we define
$S'$
replacing S. We recall that we define
![]() $\mathbb {P}^{\mathcal {K}}(\mathcal {E}) := \mathbb {P}(\mathcal {K} \cap \mathcal {E})$
for every event
$\mathbb {P}^{\mathcal {K}}(\mathcal {E}) := \mathbb {P}(\mathcal {K} \cap \mathcal {E})$
for every event
![]() $\mathcal {E}$
. To deal with the above probability, we will construct nets to approximate vectors in
$\mathcal {E}$
. To deal with the above probability, we will construct nets to approximate vectors in
![]() $\mathcal {I}\cap S$
and
$\mathcal {I}\cap S$
and
![]() $\mathcal {I}\cap S'$
. To define the nets used, we recall a few definitions from [Reference Campos, Jenssen, Michelen and Sahasrabudhe4]. For a random variable
$\mathcal {I}\cap S'$
. To define the nets used, we recall a few definitions from [Reference Campos, Jenssen, Michelen and Sahasrabudhe4]. For a random variable
![]() $Y \in \mathbb {R}^d$
and
$Y \in \mathbb {R}^d$
and
![]() $\varepsilon>0$
, we define the Lévy concentration of Y by
$\varepsilon>0$
, we define the Lévy concentration of Y by
Now, for
![]() $v\in \mathbb {R}^n$
,
$v\in \mathbb {R}^n$
,
![]() $\varepsilon>0$
, define
$\varepsilon>0$
, define
Slightly relaxing the requirements of
![]() $\mathcal {I}$
, we define
$\mathcal {I}$
, we define
Define the (trivial) net
III.1.1 Definition of net for
 $v \in S$
$v \in S$
To deal with vectors in S, for
![]() $\varepsilon \geqslant \exp (-2c_{\Sigma } n)$
, define
$\varepsilon \geqslant \exp (-2c_{\Sigma } n)$
, define
If
![]() $v\in \Sigma _\varepsilon $
, for some
$v\in \Sigma _\varepsilon $
, for some
![]() $\varepsilon \geqslant \exp (-2c_{\Sigma } n)$
, then the proof will be basically the same as in [Reference Campos, Jenssen, Michelen and Sahasrabudhe4]. As such, we approximate
$\varepsilon \geqslant \exp (-2c_{\Sigma } n)$
, then the proof will be basically the same as in [Reference Campos, Jenssen, Michelen and Sahasrabudhe4]. As such, we approximate
![]() $\Sigma _\varepsilon $
by
$\Sigma _\varepsilon $
by
![]() $\mathcal {N}_\varepsilon $
, where we define
$\mathcal {N}_\varepsilon $
, where we define
and show that
![]() $\mathcal {N}_\varepsilon $
is appropriately small.
$\mathcal {N}_\varepsilon $
is appropriately small.
First, the following lemma allows us to approximate
![]() $\Sigma _\varepsilon $
by
$\Sigma _\varepsilon $
by
![]() $\mathcal {N}_\varepsilon $
.
$\mathcal {N}_\varepsilon $
.
Lemma III.1. Let
![]() $\varepsilon \in (\exp (-2c_{\Sigma }n),{\kappa }_0/8)$
. For each
$\varepsilon \in (\exp (-2c_{\Sigma }n),{\kappa }_0/8)$
. For each
![]() $v \in \Sigma _{\varepsilon }$
, then there is
$v \in \Sigma _{\varepsilon }$
, then there is
![]() $u \in \mathcal {N}_{\varepsilon }$
, such that
$u \in \mathcal {N}_{\varepsilon }$
, such that
![]() $\|u-v\|_{\infty } \leqslant 4\varepsilon n^{-1/2}$
.
$\|u-v\|_{\infty } \leqslant 4\varepsilon n^{-1/2}$
.
This lemma is analogous to Lemma 8.2 in [Reference Campos, Jenssen, Michelen and Sahasrabudhe4], and we postpone its proof to Section IX. The main difficulty faced in [Reference Campos, Jenssen, Michelen and Sahasrabudhe4] is to prove an appropriate bound on
![]() $|\mathcal {N}_{\varepsilon }|$
. In our case, we have an analogous bound.
$|\mathcal {N}_{\varepsilon }|$
. In our case, we have an analogous bound.
Theorem III.2. For
![]() $L\geqslant 2$
and
$L\geqslant 2$
and
![]() $0 < c_0 \leqslant 2^{-50}B^{-4}$
, let
$0 < c_0 \leqslant 2^{-50}B^{-4}$
, let
![]() $n \geqslant L^{64/c_0^2}$
,
$n \geqslant L^{64/c_0^2}$
,
![]() $d \in [c_0^2n/4, c_0^2 n] $
, and
$d \in [c_0^2n/4, c_0^2 n] $
, and
![]() $\varepsilon>0$
be so that
$\varepsilon>0$
be so that
![]() $\log \varepsilon ^{-1} \leqslant n L^{-32/c_0^2} $
. Then
$\log \varepsilon ^{-1} \leqslant n L^{-32/c_0^2} $
. Then
 $$ \begin{align*} |\mathcal{N}_{\varepsilon}|\leqslant \left(\frac{C}{c_0^6L^2\varepsilon}\right)^{n}, \end{align*} $$
$$ \begin{align*} |\mathcal{N}_{\varepsilon}|\leqslant \left(\frac{C}{c_0^6L^2\varepsilon}\right)^{n}, \end{align*} $$
where
![]() $C>0$
is an absolute constant.
$C>0$
is an absolute constant.
The proof of Theorem III.2 will follow mostly from Lemma IV.3, with the rest of the deduction following exactly the same path as in [Reference Campos, Jenssen, Michelen and Sahasrabudhe4], which we present in Sections VII and VIII.
III.1.2 Definition of net for
 $v \in S'$
$v \in S'$
We now need to tackle the vectors in
![]() $S'$
; that is, those with
$S'$
; that is, those with
Here, we construct the nets using only the second condition using a construction of Rudelson and Vershynin [Reference Rudelson and Vershynin31]. Then the condition
![]() $\mathcal {T}_L(v)\leqslant \exp (-2c_{\Sigma } n)$
will come in when we union bound over nets. With this in mind, let
$\mathcal {T}_L(v)\leqslant \exp (-2c_{\Sigma } n)$
will come in when we union bound over nets. With this in mind, let
We will approximate
![]() $v\in \Sigma ^{\prime }_\varepsilon $
by the net
$v\in \Sigma ^{\prime }_\varepsilon $
by the net
![]() $G_\varepsilon $
, where we define
$G_\varepsilon $
, where we define
 $$ \begin{align} G_{\varepsilon}:=\bigcup_{|I|\geqslant (1-2\mu) n}\left\{\frac{p}{\|p\|_2}:~p\in \left(\mathbb{Z}^I\oplus \sqrt{\alpha} \mathbb{Z}^{I^c}\right)\cap B_n(0, \varepsilon^{-1})\setminus\{0\}\right\}. \end{align} $$
$$ \begin{align} G_{\varepsilon}:=\bigcup_{|I|\geqslant (1-2\mu) n}\left\{\frac{p}{\|p\|_2}:~p\in \left(\mathbb{Z}^I\oplus \sqrt{\alpha} \mathbb{Z}^{I^c}\right)\cap B_n(0, \varepsilon^{-1})\setminus\{0\}\right\}. \end{align} $$
The following two lemmas tell us that
![]() $G_{\varepsilon }$
is a good
$G_{\varepsilon }$
is a good
![]() $\varepsilon \sqrt {\alpha n}$
-net for
$\varepsilon \sqrt {\alpha n}$
-net for
![]() $\Sigma ^{\prime }_{\varepsilon }$
. Here, this
$\Sigma ^{\prime }_{\varepsilon }$
. Here, this
![]() $\sqrt {\alpha }$
is the “win” over trivial nets.
$\sqrt {\alpha }$
is the “win” over trivial nets.
Lemma III.3. Let
![]() $\varepsilon>0$
satisfy
$\varepsilon>0$
satisfy
![]() $\varepsilon \leqslant \gamma (\alpha n)^{-1/2}/4$
. If
$\varepsilon \leqslant \gamma (\alpha n)^{-1/2}/4$
. If
![]() $v \in \Sigma ^{\prime }_{\varepsilon }$
, then there exists
$v \in \Sigma ^{\prime }_{\varepsilon }$
, then there exists
![]() $u\in G_{\varepsilon }$
, such that
$u\in G_{\varepsilon }$
, such that
![]() $\|u-v\|_{2} \leqslant 16 \varepsilon \sqrt {\alpha n}$
.
$\|u-v\|_{2} \leqslant 16 \varepsilon \sqrt {\alpha n}$
.
Proof. Set
![]() $D=\min _{|I|\geqslant (1-2\mu ) n}D_{\alpha ,\gamma }(v_I)$
, and let I be a set attaining the minimum. By definition of
$D=\min _{|I|\geqslant (1-2\mu ) n}D_{\alpha ,\gamma }(v_I)$
, and let I be a set attaining the minimum. By definition of
![]() $D_{\alpha ,\gamma }$
, there is
$D_{\alpha ,\gamma }$
, there is
![]() $p_I \in \mathbb {Z}^I \cap B_n(0, \varepsilon ^{-1}) $
so that
$p_I \in \mathbb {Z}^I \cap B_n(0, \varepsilon ^{-1}) $
so that
and thus
![]() $p_I \not = 0 $
. We now may greedily choose
$p_I \not = 0 $
. We now may greedily choose
![]() $p_{I^c} \in \sqrt {\alpha } \mathbb {Z}^{I^c} \cap B_n(0, \varepsilon ^{-1})$
so that
$p_{I^c} \in \sqrt {\alpha } \mathbb {Z}^{I^c} \cap B_n(0, \varepsilon ^{-1})$
so that
Thus, if we set
![]() $p = p_I \oplus p_{I^c}$
, by the triangle inequality, we have
$p = p_I \oplus p_{I^c}$
, by the triangle inequality, we have
 $$\begin{align*}\left\|v-\frac{p}{\|p\|_2}\right\|_2\leqslant \frac{1}{D}(\|D v-p\|_2+|D-\|p\|_2|)\leqslant 4D^{-1}\sqrt{\alpha n}\leqslant 16\varepsilon \sqrt{\alpha n}, \end{align*}$$
$$\begin{align*}\left\|v-\frac{p}{\|p\|_2}\right\|_2\leqslant \frac{1}{D}(\|D v-p\|_2+|D-\|p\|_2|)\leqslant 4D^{-1}\sqrt{\alpha n}\leqslant 16\varepsilon \sqrt{\alpha n}, \end{align*}$$
as desired.
We also note that this net is sufficiently small for our purposes (see [Reference Rudelson and Vershynin31]).
Fact III.4. For
![]() $\alpha , \mu \in (0,1)$
,
$\alpha , \mu \in (0,1)$
,
![]() $K\geqslant 1$
and
$K\geqslant 1$
and
![]() $\varepsilon \leqslant Kn^{-1/2}$
, we have
$\varepsilon \leqslant Kn^{-1/2}$
, we have
 $$\begin{align*}|G_\varepsilon|\leqslant \left(\frac{32K}{\alpha^{2\mu}\varepsilon\sqrt{n}}\right)^n\, ,\end{align*}$$
$$\begin{align*}|G_\varepsilon|\leqslant \left(\frac{32K}{\alpha^{2\mu}\varepsilon\sqrt{n}}\right)^n\, ,\end{align*}$$
where
![]() $G_\varepsilon $
is as defined at (III.5).
$G_\varepsilon $
is as defined at (III.5).
The following simple corollary tells us that we can modify
![]() $G_{\varepsilon }$
to build a net
$G_{\varepsilon }$
to build a net
![]() $G^{\prime }_{\varepsilon } \subseteq \Sigma _{\varepsilon }$
, at the cost of a factor of
$G^{\prime }_{\varepsilon } \subseteq \Sigma _{\varepsilon }$
, at the cost of a factor of
![]() $2$
in the accuracy of the next. That is, it is a
$2$
in the accuracy of the next. That is, it is a
![]() $32\varepsilon \sqrt {\alpha n}$
-net rather than a
$32\varepsilon \sqrt {\alpha n}$
-net rather than a
![]() $16\varepsilon \sqrt {\alpha n}$
net.
$16\varepsilon \sqrt {\alpha n}$
net.
Corollary III.5. For
![]() $\alpha , \mu \in (0,1)$
,
$\alpha , \mu \in (0,1)$
,
![]() $K\geqslant 1$
and
$K\geqslant 1$
and
![]() $\varepsilon \leqslant Kn^{-1/2}$
there is a
$\varepsilon \leqslant Kn^{-1/2}$
there is a
![]() $32 \varepsilon \sqrt {\alpha n}$
-net
$32 \varepsilon \sqrt {\alpha n}$
-net
![]() $G^{\prime }_\varepsilon $
for
$G^{\prime }_\varepsilon $
for
![]() $\Sigma ^{\prime }_\varepsilon $
with
$\Sigma ^{\prime }_\varepsilon $
with
![]() $G^{\prime }_\varepsilon \subset \Sigma ^{\prime }_\varepsilon $
and
$G^{\prime }_\varepsilon \subset \Sigma ^{\prime }_\varepsilon $
and
 $$\begin{align*}|G^{\prime}_\varepsilon|\leqslant \left(\frac{32K}{\alpha^{2\mu}\varepsilon\sqrt{n}}\right)^n.\end{align*}$$
$$\begin{align*}|G^{\prime}_\varepsilon|\leqslant \left(\frac{32K}{\alpha^{2\mu}\varepsilon\sqrt{n}}\right)^n.\end{align*}$$
This follows from a standard argument.
III.2 Proof of Theorem I.2
We need the following easy observation to make sure we can use Corollary III.5.
Fact III.6. Let
![]() $v \in \mathcal {I}$
,
$v \in \mathcal {I}$
,
![]() $\mu <d/4n$
, and
$\mu <d/4n$
, and
![]() $\gamma <\kappa _0 \sqrt {d/2n}$
, then
$\gamma <\kappa _0 \sqrt {d/2n}$
, then
![]() $ \hat {D}_{\alpha ,\gamma ,\mu }(v)\geqslant (2\kappa _1)^{-1} \sqrt {n} $
.
$ \hat {D}_{\alpha ,\gamma ,\mu }(v)\geqslant (2\kappa _1)^{-1} \sqrt {n} $
.
Proof. Since
![]() $v\in \mathcal {I}$
, there is
$v\in \mathcal {I}$
, there is
![]() $D\subset [n]$
, such that
$D\subset [n]$
, such that
![]() $|D|=d$
and
$|D|=d$
and
![]() $\kappa _0 n^{-1/2}\leqslant |v_i| \leqslant \kappa _1 n^{-1/2}$
for all
$\kappa _0 n^{-1/2}\leqslant |v_i| \leqslant \kappa _1 n^{-1/2}$
for all
![]() $i\in D$
. Now, write
$i\in D$
. Now, write
![]() $\hat {D}(v) = \min _{|I|\geqslant (1-2\mu ) n}D_{\alpha ,\gamma }(v_I)$
, and let I be a set attaining the minimum. Since
$\hat {D}(v) = \min _{|I|\geqslant (1-2\mu ) n}D_{\alpha ,\gamma }(v_I)$
, and let I be a set attaining the minimum. Since
![]() $|I|\geqslant (1-2\mu )n\geqslant n-d/2$
, we have
$|I|\geqslant (1-2\mu )n\geqslant n-d/2$
, we have
![]() $|I\cap D|\geqslant d/2$
. So put
$|I\cap D|\geqslant d/2$
. So put
![]() $D' := I\cap D$
, and note that for all
$D' := I\cap D$
, and note that for all
![]() $t\leqslant (2\kappa _1)^{-1}\sqrt {n}$
, we have
$t\leqslant (2\kappa _1)^{-1}\sqrt {n}$
, we have
Therefore,
![]() $D_{\alpha ,\gamma }(v_I)\geqslant (2\kappa _1)^{-1}\sqrt {n}$
, by definition.
$D_{\alpha ,\gamma }(v_I)\geqslant (2\kappa _1)^{-1}\sqrt {n}$
, by definition.
When union bounding over the elements of our net, we will also want to use the following lemma to make sure
![]() $\mathcal {L}(Av,\varepsilon )$
is small whenever
$\mathcal {L}(Av,\varepsilon )$
is small whenever
![]() $\mathcal {T}_L(v)\leqslant \varepsilon $
.
$\mathcal {T}_L(v)\leqslant \varepsilon $
.
Lemma III.7. Let
![]() $\nu \leqslant 2^{-8}$
. For
$\nu \leqslant 2^{-8}$
. For
![]() $v \in \mathbb {R}^n$
and
$v \in \mathbb {R}^n$
and
![]() $t \geqslant \mathcal {T}_{L}(v)$
, we have
$t \geqslant \mathcal {T}_{L}(v)$
, we have
We prove this lemma in Section V using a fairly straightforward argument on the Fourier side. We now prove our main theorem, Theorem I.2.
Proof of Theorem I.2.
We pick up from (III.1) and look to show that
and the same with
![]() $S'$
in place of S. We do this in three steps.
$S'$
in place of S. We do this in three steps.
We first pause to describe how we choose the constants. We let
![]() $c_0>0$
to be sufficiently small so that Theorem III.2 holds, and we let
$c_0>0$
to be sufficiently small so that Theorem III.2 holds, and we let
![]() $d := c_0^2n$
. The parameters
$d := c_0^2n$
. The parameters
![]() $\mu , \gamma $
will be chosen small compared to
$\mu , \gamma $
will be chosen small compared to
![]() $d/n$
and
$d/n$
and
![]() ${\kappa }_0$
so that Fact III.6 holds. L will be chosen to be large enough so that
${\kappa }_0$
so that Fact III.6 holds. L will be chosen to be large enough so that
![]() $L>1/\kappa _0$
and so that it is larger than some absolute constants that appear in the proof. We will choose
$L>1/\kappa _0$
and so that it is larger than some absolute constants that appear in the proof. We will choose
![]() $\alpha>0$
to be small compared to
$\alpha>0$
to be small compared to
![]() $1/L$
and
$1/L$
and
![]() $1/{\kappa }_0$
, and we will choose
$1/{\kappa }_0$
, and we will choose
![]() $c_{\Sigma }$
small compared to
$c_{\Sigma }$
small compared to
![]() $1/L$
.
$1/L$
.
Step 1: Reduction to
![]() $\Sigma _\varepsilon $
and
$\Sigma _\varepsilon $
and
![]() $\Sigma _\varepsilon ^{\prime }$
. Using that
$\Sigma _\varepsilon ^{\prime }$
. Using that
![]() $\mathcal {I} = \bigcup _{D} \mathcal {I}(D),$
we union bound over all choices of D. By symmetry of the coordinates, we have
$\mathcal {I} = \bigcup _{D} \mathcal {I}(D),$
we union bound over all choices of D. By symmetry of the coordinates, we have
Thus, it is enough to show that the supremum at (III.7) is at most
![]() $4^{-n}$
, and the same with S replaced by
$4^{-n}$
, and the same with S replaced by
![]() $S'$
.
$S'$
.
Now, let
![]() $\mathcal {W}=\left (2^{-n}\mathbb {Z} \right )\cap [-4\sqrt {n},+4\sqrt {n}] $
and notice that for all
$\mathcal {W}=\left (2^{-n}\mathbb {Z} \right )\cap [-4\sqrt {n},+4\sqrt {n}] $
and notice that for all
![]() $s, t\in [-4\sqrt {n},+4\sqrt {n}]$
, there is
$s, t\in [-4\sqrt {n},+4\sqrt {n}]$
, there is
![]() $s', t'\in \mathcal {W}$
with
$s', t'\in \mathcal {W}$
with
![]() $|s-s'|\leqslant 2^{-n}$
and
$|s-s'|\leqslant 2^{-n}$
and
![]() $|t-t'|\leqslant 2^{-n}$
. So, union bounding over all
$|t-t'|\leqslant 2^{-n}$
. So, union bounding over all
![]() $(s',t')$
, the supremum term in (III.7) is at most
$(s',t')$
, the supremum term in (III.7) is at most
and the same with S replaced with
![]() $S'$
.
$S'$
.
We now need to treat S and
![]() $S'$
a little differently. Starting with S, we let
$S'$
a little differently. Starting with S, we let
![]() $\eta :=\exp (-2c_{\Sigma } n)$
, and note that for
$\eta :=\exp (-2c_{\Sigma } n)$
, and note that for
![]() $v \in S$
, we have, by definition, that
$v \in S$
, we have, by definition, that
where we will guarantee the last inequality holds by our choice of L later.
Now, recalling the definition of
![]() $\Sigma _{\varepsilon } := \Sigma _{\varepsilon }([d])$
at (III.4), we may write
$\Sigma _{\varepsilon } := \Sigma _{\varepsilon }([d])$
at (III.4), we may write
 $$\begin{align*}\mathcal{I}([d]) \cap S \subseteq \bigcup_{j=0}^n \left\{v\in \mathcal{I} : \mathcal{T}_L(v)\in [2^{j}\eta,2^{j+1}\eta] \right\}\, = \bigcup_{j=0}^{ j_0} \Sigma_{2^j\eta}\, ,\end{align*}$$
$$\begin{align*}\mathcal{I}([d]) \cap S \subseteq \bigcup_{j=0}^n \left\{v\in \mathcal{I} : \mathcal{T}_L(v)\in [2^{j}\eta,2^{j+1}\eta] \right\}\, = \bigcup_{j=0}^{ j_0} \Sigma_{2^j\eta}\, ,\end{align*}$$
where
![]() $j_0$
is the largest integer, such that
$j_0$
is the largest integer, such that
![]() $2^{j_0}\eta \leqslant \kappa _0/2$
. Thus, by the union bound, it is enough to show
$2^{j_0}\eta \leqslant \kappa _0/2$
. Thus, by the union bound, it is enough to show
for all
![]() $\varepsilon \in [\eta ,{\kappa }_0/4]$
.
$\varepsilon \in [\eta ,{\kappa }_0/4]$
.
We now organize
![]() $S'$
in a similar way, relative to the sets
$S'$
in a similar way, relative to the sets
![]() $\Sigma _\varepsilon '$
. For this, notice that for
$\Sigma _\varepsilon '$
. For this, notice that for
![]() $v \in \mathcal {I}([d]) \cap S'$
, we have
$v \in \mathcal {I}([d]) \cap S'$
, we have
by Fact III.6. So, if we recall the definition
then
 $$\begin{align*}\mathcal{I}([d]) \cap S' \subseteq \bigcup_{j=-1}^{j_1} \Sigma^{\prime}_{2^j\sqrt{\eta}}\, ,\end{align*}$$
$$\begin{align*}\mathcal{I}([d]) \cap S' \subseteq \bigcup_{j=-1}^{j_1} \Sigma^{\prime}_{2^j\sqrt{\eta}}\, ,\end{align*}$$
where
![]() $j_1$
is the least integer, such that
$j_1$
is the least integer, such that
![]() $2^{j_1}\sqrt {\eta }\geqslant \kappa _1/(2\sqrt {n})$
. Union bounding over j shows that it is sufficient to show
$2^{j_1}\sqrt {\eta }\geqslant \kappa _1/(2\sqrt {n})$
. Union bounding over j shows that it is sufficient to show
for all
![]() $\varepsilon \in [\sqrt {\eta }, {\kappa }_1/\sqrt {n}]$
.
$\varepsilon \in [\sqrt {\eta }, {\kappa }_1/\sqrt {n}]$
.
Step 2: A Bound on
![]() $Q_\varepsilon $
: Take
$Q_\varepsilon $
: Take
![]() $w\in \mathbb {R}^n$
and
$w\in \mathbb {R}^n$
and
![]() $|s|\leqslant 4\sqrt {n}$
; we will bound the probability uniformly over w and s. Since
$|s|\leqslant 4\sqrt {n}$
; we will bound the probability uniformly over w and s. Since
![]() $\exp (-2c_{\Sigma } n)<\varepsilon < {\kappa }_0/8$
, for
$\exp (-2c_{\Sigma } n)<\varepsilon < {\kappa }_0/8$
, for
![]() $v \in \Sigma _{\varepsilon }$
, we apply Lemma III.1, to find a
$v \in \Sigma _{\varepsilon }$
, we apply Lemma III.1, to find a
![]() $u \in \mathcal {N}_{\varepsilon } = \mathcal {N}_{\varepsilon }([d])$
so that
$u \in \mathcal {N}_{\varepsilon } = \mathcal {N}_{\varepsilon }([d])$
so that
![]() $\|v - u\|_2 \leqslant 4\varepsilon $
. So if
$\|v - u\|_2 \leqslant 4\varepsilon $
. So if
![]() $\| A \|_{op}\leqslant 4\sqrt {n}$
, we see that
$\| A \|_{op}\leqslant 4\sqrt {n}$
, we see that
 $$ \begin{align*} \|Au-su -w\|_2 &\leqslant \|Av-sv -w\|_2 + \|A(v-u)\|_2+|s|\|v-u\|_2 \\ &\leqslant \|Av -sv -w\|_2 + 8\sqrt{n}\|(v-u)\|_2 \\ & \leqslant 33\varepsilon\sqrt{n} ,\end{align*} $$
$$ \begin{align*} \|Au-su -w\|_2 &\leqslant \|Av-sv -w\|_2 + \|A(v-u)\|_2+|s|\|v-u\|_2 \\ &\leqslant \|Av -sv -w\|_2 + 8\sqrt{n}\|(v-u)\|_2 \\ & \leqslant 33\varepsilon\sqrt{n} ,\end{align*} $$
and thus
So, by union bounding over our net
![]() $\mathcal {N}_{\varepsilon }$
, we see that
$\mathcal {N}_{\varepsilon }$
, we see that
 $$ \begin{align*} Q_{\varepsilon} \leqslant \mathbb{P}_A^{\mathcal{K}}\left(\exists v \in \mathcal{N}_{\varepsilon} : \|Av-sv-w\|\leqslant 33\varepsilon\sqrt{n} \right) &\leqslant \sum_{u \in \mathcal{N}_{\varepsilon}} \mathbb{P}_A^{\mathcal{K}}( \|Au - s'u-w\|_2 \leqslant 33\varepsilon\sqrt{n}) \\ &\leqslant \sum_{u \in \mathcal{N}_{\varepsilon}} \mathcal{L}_{A,op}\left(u, 33\varepsilon \sqrt{n} \right), \end{align*} $$
$$ \begin{align*} Q_{\varepsilon} \leqslant \mathbb{P}_A^{\mathcal{K}}\left(\exists v \in \mathcal{N}_{\varepsilon} : \|Av-sv-w\|\leqslant 33\varepsilon\sqrt{n} \right) &\leqslant \sum_{u \in \mathcal{N}_{\varepsilon}} \mathbb{P}_A^{\mathcal{K}}( \|Au - s'u-w\|_2 \leqslant 33\varepsilon\sqrt{n}) \\ &\leqslant \sum_{u \in \mathcal{N}_{\varepsilon}} \mathcal{L}_{A,op}\left(u, 33\varepsilon \sqrt{n} \right), \end{align*} $$
where
![]() $\mathcal {L}_{A,op}$
is defined at (III.3).
$\mathcal {L}_{A,op}$
is defined at (III.3).
Note that for any u, we have that
![]() $\mathcal {L}_{A,op}\left (u, 33\varepsilon \sqrt {n} \right ) \leqslant (67)^n \mathcal {L}_{A,op}(u,\varepsilon \sqrt {n})$
(see, e.g., Fact 6.2 in [Reference Campos, Jenssen, Michelen and Sahasrabudhe4]); as such, for any
$\mathcal {L}_{A,op}\left (u, 33\varepsilon \sqrt {n} \right ) \leqslant (67)^n \mathcal {L}_{A,op}(u,\varepsilon \sqrt {n})$
(see, e.g., Fact 6.2 in [Reference Campos, Jenssen, Michelen and Sahasrabudhe4]); as such, for any
![]() $u \in \mathcal {N}_\varepsilon $
, we have
$u \in \mathcal {N}_\varepsilon $
, we have
![]() $\mathcal {L}_{A,op}\left (u, 33\varepsilon \sqrt {n} \right ) \leqslant (2^{17}L\varepsilon )^n$
. Using this bound gives
$\mathcal {L}_{A,op}\left (u, 33\varepsilon \sqrt {n} \right ) \leqslant (2^{17}L\varepsilon )^n$
. Using this bound gives
 $$\begin{align*}Q_{\varepsilon} \leqslant |\mathcal{N}_{\varepsilon}|(2^{17} L\varepsilon)^n \leqslant \left(\frac{C}{L^2\varepsilon}\right)^n(2^{17} L\varepsilon)^n \leqslant 2^{-4n}, \end{align*}$$
$$\begin{align*}Q_{\varepsilon} \leqslant |\mathcal{N}_{\varepsilon}|(2^{17} L\varepsilon)^n \leqslant \left(\frac{C}{L^2\varepsilon}\right)^n(2^{17} L\varepsilon)^n \leqslant 2^{-4n}, \end{align*}$$
where the penultimate inequality follows from our Theorem III.2 and the last inequality holds for the choice of L large enough relative to the universal constant C and so that (III.8) holds. To see that the application of Theorem III.2 is valid, note that
where the last inequality holds for
![]() $c_{\Sigma }$
small compared to
$c_{\Sigma }$
small compared to
![]() $L^{-1}$
.
$L^{-1}$
.
Step 3: A Bound on
![]() $Q_\varepsilon ^{\prime }$
. To deal with
$Q_\varepsilon ^{\prime }$
. To deal with
![]() $Q^{\prime }_\varepsilon $
, we employ a similar strategy. Fix
$Q^{\prime }_\varepsilon $
, we employ a similar strategy. Fix
![]() $w\in \mathbb {R}^n$
and
$w\in \mathbb {R}^n$
and
![]() $|s|\leqslant 4\sqrt {n}$
. Since we chose
$|s|\leqslant 4\sqrt {n}$
. Since we chose
![]() $\mu ,\gamma $
to be sufficiently small so that Fact III.6 holds, we have that
$\mu ,\gamma $
to be sufficiently small so that Fact III.6 holds, we have that
Thus, we may apply Corollary III.5 with
![]() $K=\kappa _1$
for each
$K=\kappa _1$
for each
![]() $v\in \Sigma ^{\prime }_{\varepsilon }$
to get
$v\in \Sigma ^{\prime }_{\varepsilon }$
to get
![]() $u\in G^{\prime }_\varepsilon \subset \Sigma ^{\prime }_\varepsilon $
, such that
$u\in G^{\prime }_\varepsilon \subset \Sigma ^{\prime }_\varepsilon $
, such that
![]() $\|v-u\|_2\leqslant 32\varepsilon \sqrt {\alpha n}$
. Now, since
$\|v-u\|_2\leqslant 32\varepsilon \sqrt {\alpha n}$
. Now, since
and since
![]() $2^9\varepsilon \sqrt {\alpha n} \geqslant \exp (-2c_{\Sigma } n)\geqslant \mathcal {T}_L(u)$
, by Lemma III.7, we have
$2^9\varepsilon \sqrt {\alpha n} \geqslant \exp (-2c_{\Sigma } n)\geqslant \mathcal {T}_L(u)$
, by Lemma III.7, we have
 $$\begin{align*}Q^{\prime}_\varepsilon\leqslant \left(\frac{32\kappa_1}{\alpha^{\mu} \varepsilon\sqrt{n}}\right)^n\sup_{u\in G^{\prime}_\varepsilon}\mathcal{L}(Au,2^9\varepsilon \sqrt{\alpha} n)\leqslant (2^{20}L\kappa_1\alpha^{1/4})^n\leqslant 2^{-4n},\end{align*}$$
$$\begin{align*}Q^{\prime}_\varepsilon\leqslant \left(\frac{32\kappa_1}{\alpha^{\mu} \varepsilon\sqrt{n}}\right)^n\sup_{u\in G^{\prime}_\varepsilon}\mathcal{L}(Au,2^9\varepsilon \sqrt{\alpha} n)\leqslant (2^{20}L\kappa_1\alpha^{1/4})^n\leqslant 2^{-4n},\end{align*}$$
assuming that
![]() $\alpha $
is chosen to be sufficiently small relative to
$\alpha $
is chosen to be sufficiently small relative to
![]() $L\kappa _1$
. This completes the proof of Theorem I.2.
$L\kappa _1$
. This completes the proof of Theorem I.2.
IV Fourier preparations for Theorem I.3
IV.1 Concentration, level sets, and Esseen-type inequalities
One of the main differences between this work and [Reference Campos, Jenssen, Michelen and Sahasrabudhe4] is the notion of a “level set” of the Fourier transform, an change that requires us to make a fair number of small adjustments throughout. Here, we set up this definition along with a few related definitions.
For a random variable
![]() $Y \in \mathbb {R}^d$
and
$Y \in \mathbb {R}^d$
and
![]() $\varepsilon>0$
, we recall that Lévy concentration of Y was defined at (III.2) by
$\varepsilon>0$
, we recall that Lévy concentration of Y was defined at (III.2) by
Our goal is to compare the concentration of certain random vectors to the gaussian measure of associated (sub-)level sets. Given a
![]() $2d \times \ell $
matrix W, define the W-level set for
$2d \times \ell $
matrix W, define the W-level set for
![]() $t \geqslant 0$
to be
$t \geqslant 0$
to be
Let
![]() $g = g_d$
denote the gaussian random variable in dimension d with mean
$g = g_d$
denote the gaussian random variable in dimension d with mean
![]() $0$
and covariance matrix
$0$
and covariance matrix
![]() $(2\pi )^{-1} I_{d \times d}$
. Define
$(2\pi )^{-1} I_{d \times d}$
. Define
![]() $\gamma _d$
to be the corresponding measure, that is
$\gamma _d$
to be the corresponding measure, that is
![]() $\gamma _d(S) = \mathbb {P}_g(g \in S)$
for every Borel set
$\gamma _d(S) = \mathbb {P}_g(g \in S)$
for every Borel set
![]() $S \subset \mathbb {R}^d$
. We first upper bound the concentration via an Esseen-like inequality.
$S \subset \mathbb {R}^d$
. We first upper bound the concentration via an Esseen-like inequality.
Lemma IV.1. Let
![]() $\beta> 0, \nu \in (0,1/4)$
, let W be a
$\beta> 0, \nu \in (0,1/4)$
, let W be a
![]() $2d \times \ell $
matrix and
$2d \times \ell $
matrix and
![]() $\tau \sim \Phi _\nu (2d;\zeta )$
. Then there is an
$\tau \sim \Phi _\nu (2d;\zeta )$
. Then there is an
![]() $m> 0$
so that
$m> 0$
so that
Proof. For
![]() $w\in \mathbb {R}^\ell $
, apply Markov’s inequality to obtain
$w\in \mathbb {R}^\ell $
, apply Markov’s inequality to obtain
 $$ \begin{align*} \mathbb{P}_\tau\big( \|W^T \tau - w \|_2 \leqslant \beta \sqrt{\ell} \big) \leqslant \exp\left(\frac{\pi}{2} \beta^2 \ell \right) \mathbb{E}_\tau \exp\left(- \frac{\pi \|W^T \tau - w\|_2^2 }{2}\right)\,. \end{align*} $$
$$ \begin{align*} \mathbb{P}_\tau\big( \|W^T \tau - w \|_2 \leqslant \beta \sqrt{\ell} \big) \leqslant \exp\left(\frac{\pi}{2} \beta^2 \ell \right) \mathbb{E}_\tau \exp\left(- \frac{\pi \|W^T \tau - w\|_2^2 }{2}\right)\,. \end{align*} $$
Using the Fourier transform of a gaussian, we compute
 $$ \begin{align} \mathbb{E}_{\tau} \exp\left(-\frac{ \pi \| W^T \tau - w\|_2^2}{2}\right) = \mathbb{E}_{g}\, e^{-2\pi i\langle w, g\rangle} \mathbb{E}_\tau e^{ 2\pi i g^T W^T \tau }. \end{align} $$
$$ \begin{align} \mathbb{E}_{\tau} \exp\left(-\frac{ \pi \| W^T \tau - w\|_2^2}{2}\right) = \mathbb{E}_{g}\, e^{-2\pi i\langle w, g\rangle} \mathbb{E}_\tau e^{ 2\pi i g^T W^T \tau }. \end{align} $$
Now, denote the rows of W as
![]() $w_1,\ldots ,w_{2d}$
and write
$w_1,\ldots ,w_{2d}$
and write
 $$\begin{align*}\mathbb{E}_\tau e^{ 2\pi i g^T W^T \tau } = \prod_{i=1}^{2d} \mathbb{E}_{\tau_i} e^{2\pi i \sum \tau_i \langle g, w_i\rangle } = \prod_{i=1}^{2d} \phi_{\tau}( \langle g, w_i\rangle ), \end{align*}$$
$$\begin{align*}\mathbb{E}_\tau e^{ 2\pi i g^T W^T \tau } = \prod_{i=1}^{2d} \mathbb{E}_{\tau_i} e^{2\pi i \sum \tau_i \langle g, w_i\rangle } = \prod_{i=1}^{2d} \phi_{\tau}( \langle g, w_i\rangle ), \end{align*}$$
where
![]() $\phi _{\tau }({\theta })$
is the characteristic function of
$\phi _{\tau }({\theta })$
is the characteristic function of
![]() $\tau $
. Now, apply (II.3) and then (II.2) to see the right-hand side of (IV.2) is
$\tau $
. Now, apply (II.3) and then (II.2) to see the right-hand side of (IV.2) is
We rewrite this as
 $$ \begin{align*} \int_{0}^{1} \mathbb{P}_{g}(\exp(-\nu p \mathbb{E}_{\bar{\zeta}}\|\bar{\zeta} W g\|_{\mathbb{T}}^2)\geqslant t)\, dt &= \nu p\int_{0}^{\infty} \mathbb{P}_{g}(\mathbb{E}_{\bar{\zeta}}\|\bar{\zeta} W g\|_{\mathbb{T}}^2\leqslant u) e^{-\nu p u}\, du \\ &= \nu p\int_{0}^{\infty} \gamma_{\ell}(S_W(u)) e^{-\nu p u}\, du \, , \end{align*} $$
$$ \begin{align*} \int_{0}^{1} \mathbb{P}_{g}(\exp(-\nu p \mathbb{E}_{\bar{\zeta}}\|\bar{\zeta} W g\|_{\mathbb{T}}^2)\geqslant t)\, dt &= \nu p\int_{0}^{\infty} \mathbb{P}_{g}(\mathbb{E}_{\bar{\zeta}}\|\bar{\zeta} W g\|_{\mathbb{T}}^2\leqslant u) e^{-\nu p u}\, du \\ &= \nu p\int_{0}^{\infty} \gamma_{\ell}(S_W(u)) e^{-\nu p u}\, du \, , \end{align*} $$
where for the first equality, we made the change of variable
![]() $t= e^{-\nu p u}$
. Choosing m to maximize
$t= e^{-\nu p u}$
. Choosing m to maximize
![]() $\gamma _{\ell }(S_W(u)) e^{-\nu p u/2}$
as a function of u yields
$\gamma _{\ell }(S_W(u)) e^{-\nu p u/2}$
as a function of u yields
Putting everything together, we obtain
We also prove a comparable lower bound.
Lemma IV.2. Let
![]() $\beta> 0$
,
$\beta> 0$
,
![]() $\nu \in (0,1/4)$
, let W be a
$\nu \in (0,1/4)$
, let W be a
![]() $2d \times \ell $
matrix, and let
$2d \times \ell $
matrix, and let
![]() $\tau \sim \Xi _\nu (2d;\zeta )$
. Then for all
$\tau \sim \Xi _\nu (2d;\zeta )$
. Then for all
![]() $t \geqslant 0$
, we have
$t \geqslant 0$
, we have
Proof. Set
![]() $X = \|W^T\tau \|_2$
, and write
$X = \|W^T\tau \|_2$
, and write
Bounding
![]() $\exp (-\pi \beta ^2\ell /2)\leqslant \exp (-\beta ^2\ell )$
implies
$\exp (-\pi \beta ^2\ell /2)\leqslant \exp (-\beta ^2\ell )$
implies
 $$ \begin{align*} \mathbb{E}_\tau \exp\left(\frac{-\pi \|W^T \tau\|_2^2}{2}\right) \leqslant \mathbb{P}_\tau(\|W^T \tau\|_2\leqslant \beta\sqrt{\ell}) + e^{-\beta^2\ell}. \end{align*} $$
$$ \begin{align*} \mathbb{E}_\tau \exp\left(\frac{-\pi \|W^T \tau\|_2^2}{2}\right) \leqslant \mathbb{P}_\tau(\|W^T \tau\|_2\leqslant \beta\sqrt{\ell}) + e^{-\beta^2\ell}. \end{align*} $$
As in the proof of Lemma IV.1 above, use the Fourier transform of the gaussian and (II.2) to lower bound
 $$ \begin{align*} \mathbb{E}_\tau \exp\left(-\frac{ \pi\|W^T \tau\|_2^2}{2}\right) \geqslant \mathbb{E}_{g}[\exp(-32\nu p\mathbb{E}_{\bar{\zeta}}\|\bar{\zeta} W g\|_{\mathbb{T}}^2)]\,. \end{align*} $$
$$ \begin{align*} \mathbb{E}_\tau \exp\left(-\frac{ \pi\|W^T \tau\|_2^2}{2}\right) \geqslant \mathbb{E}_{g}[\exp(-32\nu p\mathbb{E}_{\bar{\zeta}}\|\bar{\zeta} W g\|_{\mathbb{T}}^2)]\,. \end{align*} $$
Similar to the proof of Lemma IV.1, write
where we have used that
![]() $\gamma _{\ell }(S_W(b)) \geqslant \gamma _{\ell }(S_W(a))$
for all
$\gamma _{\ell }(S_W(b)) \geqslant \gamma _{\ell }(S_W(a))$
for all
![]() $b \geqslant a$
. This completes the proof of Lemma IV.2.
$b \geqslant a$
. This completes the proof of Lemma IV.2.
IV.2 Inverse Littlewood-Offord for conditioned random walks
First, we need a generalization of our important Lemma 3.1 from [Reference Campos, Jenssen, Michelen and Sahasrabudhe4]. Given a
![]() $2d \times \ell $
matrix W and a vector
$2d \times \ell $
matrix W and a vector
![]() $Y\in \mathbb {R}^d$
, we define the Y-augmented matrix
$Y\in \mathbb {R}^d$
, we define the Y-augmented matrix
![]() $W_Y$
as
$W_Y$
as
 $$ \begin{align} W_Y = \begin{bmatrix} \, \, \, W \, \, \, , \begin{bmatrix} \mathbf{0}_d \\ Y \end{bmatrix} , \begin{bmatrix} Y \\ \mathbf{0}_d \end{bmatrix} \end{bmatrix}. \end{align} $$
$$ \begin{align} W_Y = \begin{bmatrix} \, \, \, W \, \, \, , \begin{bmatrix} \mathbf{0}_d \\ Y \end{bmatrix} , \begin{bmatrix} Y \\ \mathbf{0}_d \end{bmatrix} \end{bmatrix}. \end{align} $$
When possible, we are explicit with the many necessary constants and “pin” several to a constant
![]() $c_0$
, which we treat as a parameter to be taken sufficiently small. We also recall the definition of “least common denominator”
$c_0$
, which we treat as a parameter to be taken sufficiently small. We also recall the definition of “least common denominator”
![]() $D_{\alpha ,\gamma }$
from (I.1)
$D_{\alpha ,\gamma }$
from (I.1)
The following is our generalization of Lemma 3.1 from [Reference Campos, Jenssen, Michelen and Sahasrabudhe4].
Lemma IV.3. For any
![]() $0<\nu \leqslant 2^{-15}$
,
$0<\nu \leqslant 2^{-15}$
,
![]() $c_0\leqslant 2^{-35}B^{-4}\nu $
,
$c_0\leqslant 2^{-35}B^{-4}\nu $
,
![]() $d \in \mathbb {N}$
,
$d \in \mathbb {N}$
,
![]() $\alpha \in (0,1)$
, and
$\alpha \in (0,1)$
, and
![]() $\gamma \in (0,1)$
, let
$\gamma \in (0,1)$
, let
![]() $k\leqslant 2^{-32}B^{-4}\nu \alpha d$
and
$k\leqslant 2^{-32}B^{-4}\nu \alpha d$
and
![]() $t \geqslant \exp \left (-2^{-32}B^{-4}\nu \alpha d\right )$
. Let
$t \geqslant \exp \left (-2^{-32}B^{-4}\nu \alpha d\right )$
. Let
![]() $Y \in \mathbb {R}^d$
satisfy
$Y \in \mathbb {R}^d$
satisfy
![]() $\| Y \|_2 \geqslant 2^{-10} c_0 \gamma ^{-1}t^{-1}$
, let W be a
$\| Y \|_2 \geqslant 2^{-10} c_0 \gamma ^{-1}t^{-1}$
, let W be a
![]() $2d \times k$
matrix with
$2d \times k$
matrix with
![]() $\|W\| \leqslant 2$
,
$\|W\| \leqslant 2$
,
![]() $\|W\|_{\mathrm {HS}}\geqslant \sqrt {k}/2$
, and let
$\|W\|_{\mathrm {HS}}\geqslant \sqrt {k}/2$
, and let
![]() $\tau \sim \Phi _\nu (2d;\zeta )$
.
$\tau \sim \Phi _\nu (2d;\zeta )$
.
If
![]() $D_{\alpha ,\gamma }(Y)> 2^{10} B^2$
, then
$D_{\alpha ,\gamma }(Y)> 2^{10} B^2$
, then
where
![]() $R = 2^{35} B^2 \nu ^{-1/2} c_0^{-2}$
.
$R = 2^{35} B^2 \nu ^{-1/2} c_0^{-2}$
.
We present the proof of Lemma IV.3 in Section VI, and deduce our standalone “inverse Littlewood-Offord theorem” Theorem I.3 here:
Proof of Theorem I.3.
Let
![]() $c_0= 2^{-35}B^{-4}\gamma ^2\nu $
. First, note that
$c_0= 2^{-35}B^{-4}\gamma ^2\nu $
. First, note that
 $$\begin{align*}\mathbb{P}\left( |\langle v, \tau\rangle|\leqslant t \text{ and } \sum_{i=1}^k \langle w_i, \tau\rangle^2\leqslant c_0 k\right)^2 \leqslant \mathbb{P}\left( |\langle v, \tau\rangle|\leqslant t\, , |\langle v, \tau'\rangle|\leqslant t \text{ and } \sum_{i=1}^k \langle w_i, \tau\rangle^2\leqslant c_0 k\right), \end{align*}$$
$$\begin{align*}\mathbb{P}\left( |\langle v, \tau\rangle|\leqslant t \text{ and } \sum_{i=1}^k \langle w_i, \tau\rangle^2\leqslant c_0 k\right)^2 \leqslant \mathbb{P}\left( |\langle v, \tau\rangle|\leqslant t\, , |\langle v, \tau'\rangle|\leqslant t \text{ and } \sum_{i=1}^k \langle w_i, \tau\rangle^2\leqslant c_0 k\right), \end{align*}$$
where
![]() $\tau ,\tau ' \sim \Phi _\nu (d;\zeta )$
are independent. We now look to bound the probability on the right-hand side using Lemma IV.3.
$\tau ,\tau ' \sim \Phi _\nu (d;\zeta )$
are independent. We now look to bound the probability on the right-hand side using Lemma IV.3.
Let W be the
![]() $2d \times k$
matrix
$2d \times k$
matrix
 $$\begin{align*}W=\begin{bmatrix} \, w_1 \, \ldots \, w_k\\ \, \mathbf{{0}_d }\, \ldots \, \mathbf{{0}_d}\, \end{bmatrix}\end{align*}$$
$$\begin{align*}W=\begin{bmatrix} \, w_1 \, \ldots \, w_k\\ \, \mathbf{{0}_d }\, \ldots \, \mathbf{{0}_d}\, \end{bmatrix}\end{align*}$$
and
![]() $Y= \sqrt {c_0/2} vt^{-1}$
. Note that if
$Y= \sqrt {c_0/2} vt^{-1}$
. Note that if
![]() $|\langle v, \tau \rangle |\leqslant t$
,
$|\langle v, \tau \rangle |\leqslant t$
,
![]() $|\langle v, \tau '\rangle |\leqslant t$
and
$|\langle v, \tau '\rangle |\leqslant t$
and
![]() $\sum _{i=1}^k \langle w_i, \tau \rangle ^2 \leqslant c_0 k$
, then
$\sum _{i=1}^k \langle w_i, \tau \rangle ^2 \leqslant c_0 k$
, then
![]() $\|W^T_Y (\tau ,\tau ')\|_2\leqslant c_0^{1/2} \sqrt {k+1}$
. Therefore
$\|W^T_Y (\tau ,\tau ')\|_2\leqslant c_0^{1/2} \sqrt {k+1}$
. Therefore
 $$\begin{align*}\mathbb{P}\left( |\langle v, \tau\rangle|\leqslant t\, , |\langle v, \tau'\rangle|\leqslant t \text{ and } \sum_{i=1}^k \langle w_i, \tau\rangle^2\leqslant c_0 k\right)\leqslant \mathcal{L} \left( W^T_Y (\tau,\tau'), c_0^{1/2} \sqrt{k+1} \right).\end{align*}$$
$$\begin{align*}\mathbb{P}\left( |\langle v, \tau\rangle|\leqslant t\, , |\langle v, \tau'\rangle|\leqslant t \text{ and } \sum_{i=1}^k \langle w_i, \tau\rangle^2\leqslant c_0 k\right)\leqslant \mathcal{L} \left( W^T_Y (\tau,\tau'), c_0^{1/2} \sqrt{k+1} \right).\end{align*}$$
Now,
![]() $\|Y\|_2=\sqrt {c_0/2}t^{-1}>2^{-10}c_0\gamma ^{-1}t^{-1}$
,
$\|Y\|_2=\sqrt {c_0/2}t^{-1}>2^{-10}c_0\gamma ^{-1}t^{-1}$
,
![]() $\|W\|=1$
,
$\|W\|=1$
,
![]() $\|W\|_{\mathrm {HS}}=\sqrt {k}$
, and
$\|W\|_{\mathrm {HS}}=\sqrt {k}$
, and
We may therefore apply Lemma IV.3 to bound
The result follows.
V Fourier replacement
The goal of this section is to prove Lemma III.7, which relates the “zeroed out and lazy” matrix M, defined at (II.6), to our original matrix A. We will need a few inequalities on the Fourier side first.
Lemma V.1. For every
![]() $t \in \mathbb {R}$
and
$t \in \mathbb {R}$
and
![]() $\nu \leqslant 1/4$
, we have
$\nu \leqslant 1/4$
, we have
Proof. Note
![]() $|\phi _\zeta (t)|^2 = \mathbb {E}_{\tilde {\zeta }} \cos (2\pi t\tilde {\zeta })$
. Use the elementary inequality
$|\phi _\zeta (t)|^2 = \mathbb {E}_{\tilde {\zeta }} \cos (2\pi t\tilde {\zeta })$
. Use the elementary inequality
and that
![]() $\sqrt {1-x}\leqslant 1-x/2$
to bound
$\sqrt {1-x}\leqslant 1-x/2$
to bound
We also need a bound on a gaussian-type moment for
![]() $\|Mv\|_2$
. On a somewhat technical point, we notice that
$\|Mv\|_2$
. On a somewhat technical point, we notice that
![]() $\mathcal {T}_L(v) \geqslant 2^n$
, since the definition of
$\mathcal {T}_L(v) \geqslant 2^n$
, since the definition of
![]() $\mathcal {T}_L$
(II.7) depends on the definition of M at (II.6), which trivially satisfies
$\mathcal {T}_L$
(II.7) depends on the definition of M at (II.6), which trivially satisfies
for all v and
![]() $\nu < 1/2$
.
$\nu < 1/2$
.
Fact V.2. For
![]() $v \in \mathbb {R}^n$
, and
$v \in \mathbb {R}^n$
, and
![]() $t \geqslant \mathcal {T}_L(v)$
, we have
$t \geqslant \mathcal {T}_L(v)$
, we have
Proof. Bound
Since
![]() $t \geqslant \mathcal {T}_L(v)$
, we have
$t \geqslant \mathcal {T}_L(v)$
, we have
![]() $\mathbb {P}(\|Mv \|_2 \leqslant s\sqrt {n}) \leqslant (4Ls)^n$
for all
$\mathbb {P}(\|Mv \|_2 \leqslant s\sqrt {n}) \leqslant (4Ls)^n$
for all
![]() $s\geqslant t$
. Thus, we may bound
$s\geqslant t$
. Thus, we may bound
 $$ \begin{align*} \sqrt{n}\int_{t}^\infty \exp\left(- \frac{s^2 n }{t^2}\right)\mathbb{P}(\|M v \|_2 \leqslant s \sqrt{n})\,ds \leqslant \sqrt{n}(8Lt)^n \int_t^\infty \exp\left(- \frac{s^2 n }{t^2}\right)(s/t)^n \,ds\,. \end{align*} $$
$$ \begin{align*} \sqrt{n}\int_{t}^\infty \exp\left(- \frac{s^2 n }{t^2}\right)\mathbb{P}(\|M v \|_2 \leqslant s \sqrt{n})\,ds \leqslant \sqrt{n}(8Lt)^n \int_t^\infty \exp\left(- \frac{s^2 n }{t^2}\right)(s/t)^n \,ds\,. \end{align*} $$
Changing variables
![]() $u=s/t$
, we may bound the right-hand side by
$u=s/t$
, we may bound the right-hand side by
as desired. Note, here, that we used that
![]() $t \geqslant 2^{-n}$
.
$t \geqslant 2^{-n}$
.
For
![]() $v,x \in \mathbb {R}^n$
and
$v,x \in \mathbb {R}^n$
and
![]() $\nu \in (0,1/4)$
, define the characteristic functions of
$\nu \in (0,1/4)$
, define the characteristic functions of
![]() $Av$
and
$Av$
and
![]() $Mv$
, respectively,
$Mv$
, respectively,
![]() $\psi _v$
and
$\psi _v$
and
![]() $\chi _{v,\nu }$
, by
$\chi _{v,\nu }$
, by
 $$ \begin{align*}\psi_v(x) := \mathbb{E}_A\, e^{2\pi i \langle Av,x\rangle} = \left( \prod_{k = 1}^n \phi_\zeta(v_k x_k ) \right)\left(\prod_{j < k} \phi_\zeta( x_j v_k + x_k v_j) \right)\end{align*} $$
$$ \begin{align*}\psi_v(x) := \mathbb{E}_A\, e^{2\pi i \langle Av,x\rangle} = \left( \prod_{k = 1}^n \phi_\zeta(v_k x_k ) \right)\left(\prod_{j < k} \phi_\zeta( x_j v_k + x_k v_j) \right)\end{align*} $$
and
 $$ \begin{align*}\chi_{v}(x) := \mathbb{E}_M\, e^{2\pi i \langle M v,x\rangle} = \prod_{j = 1}^d \prod_{k = d+1}^n \phi_{\tilde{\zeta} Z_\nu}( x_j v_k + x_k v_j)\,.\end{align*} $$
$$ \begin{align*}\chi_{v}(x) := \mathbb{E}_M\, e^{2\pi i \langle M v,x\rangle} = \prod_{j = 1}^d \prod_{k = d+1}^n \phi_{\tilde{\zeta} Z_\nu}( x_j v_k + x_k v_j)\,.\end{align*} $$
Our “replacement” now goes through.
Proof of Lemma III.7.
By Markov, we have
Then use Fourier inversion to write
Now, apply the triangle inequality, Lemma V.1 and the nonnegativity of
![]() $\chi _{v}$
yield that the right-hand side of (V.3) is
$\chi _{v}$
yield that the right-hand side of (V.3) is
Now, use Fact V.2 along with the assumption
![]() $t \geqslant \mathcal {T}_L(v)$
to bound
$t \geqslant \mathcal {T}_L(v)$
to bound
as desired.
VI Proof of Lemma IV.3
In this section, we prove the crucial Lemma IV.3. Fortunately, much of the geometry needed to prove this theorem can be pulled from the proof of the
![]() $\{-1,0, 1\}$
-case in [Reference Campos, Jenssen, Michelen and Sahasrabudhe4], and so the deduction of the theorem becomes relatively straightforward.
$\{-1,0, 1\}$
-case in [Reference Campos, Jenssen, Michelen and Sahasrabudhe4], and so the deduction of the theorem becomes relatively straightforward.
VI.1 Properties of gaussian space and level sets
For
![]() $r, s> 0$
and
$r, s> 0$
and
![]() $k \in \mathbb {N}$
, define the cylinder
$k \in \mathbb {N}$
, define the cylinder
![]() $\Gamma _{r,s}$
by
$\Gamma _{r,s}$
by
For a measurable set
![]() $S \subset \mathbb {R}^{k+2}$
and
$S \subset \mathbb {R}^{k+2}$
and
![]() $y \in \mathbb {R}^{k+2}$
, define the set
$y \in \mathbb {R}^{k+2}$
, define the set
Recall that
![]() $\gamma _k$
is the k-dimensional gaussian measure defined by
$\gamma _k$
is the k-dimensional gaussian measure defined by
![]() $\gamma _k(S) = \mathbb {P}(g \in S)$
, where
$\gamma _k(S) = \mathbb {P}(g \in S)$
, where
![]() $g \sim \mathcal {N}(0, (2\pi )^{-1} I_{k})$
, and where
$g \sim \mathcal {N}(0, (2\pi )^{-1} I_{k})$
, and where
![]() $I_k$
denotes the
$I_k$
denotes the
![]() $k \times k$
identity matrix. The following is a key geometric lemma from [Reference Campos, Jenssen, Michelen and Sahasrabudhe4].
$k \times k$
identity matrix. The following is a key geometric lemma from [Reference Campos, Jenssen, Michelen and Sahasrabudhe4].
Lemma VI.1. Let
![]() $S \subset \mathbb {R}^{k+2}$
and
$S \subset \mathbb {R}^{k+2}$
and
![]() $s> 0$
satisfy
$s> 0$
satisfy
Then there is an
![]() $x \in S$
so that
$x \in S$
so that
This geometric lemma will be of crucial importance for identifying the LCD. Indeed, we will take S to be a representative level set, on the Fourier side, for the probability implicit on the left-hand side of Lemma IV.3. The following basic fact will help explain the use of the difference appearing in Lemma VI.1.
Fact VI.2. For any
![]() $2d \times \ell $
matrix W and
$2d \times \ell $
matrix W and
![]() $m> 0$
, we have
$m> 0$
, we have
Proof. For any
![]() $x,y\in S_W(m)$
, we have
$x,y\in S_W(m)$
, we have
![]() $\mathbb {E}_{\bar {\zeta }}\|\bar {\zeta } W x\|_{\mathbb {T}}^2, \mathbb {E}_{\bar {\zeta }}\|\bar {\zeta } W y\|_{\mathbb {T}}^2\leqslant m\, $
. The triangle inequality implies
$\mathbb {E}_{\bar {\zeta }}\|\bar {\zeta } W x\|_{\mathbb {T}}^2, \mathbb {E}_{\bar {\zeta }}\|\bar {\zeta } W y\|_{\mathbb {T}}^2\leqslant m\, $
. The triangle inequality implies
Taking
![]() $\mathbb {E}_{\bar {\zeta }}$
on both sides completes the fact.
$\mathbb {E}_{\bar {\zeta }}$
on both sides completes the fact.
VI.2 Proof of Lemma IV.3
The following is our main step toward Lemma IV.3.
Lemma VI.3. For
![]() $d \in \mathbb {N}$
,
$d \in \mathbb {N}$
,
![]() $\gamma ,\alpha \in (0,1)$
and
$\gamma ,\alpha \in (0,1)$
and
![]() $0<\nu \leqslant 2^{-15}$
, let
$0<\nu \leqslant 2^{-15}$
, let
![]() $k\leqslant 2^{-17}B^{-4}\nu \alpha d $
and
$k\leqslant 2^{-17}B^{-4}\nu \alpha d $
and
![]() $t \geqslant \exp (-2^{-17}B^{-4}\nu \alpha d)$
. For
$t \geqslant \exp (-2^{-17}B^{-4}\nu \alpha d)$
. For
![]() $c_0 \in (0,2^{-50}B^{-4})$
, let
$c_0 \in (0,2^{-50}B^{-4})$
, let
![]() $Y \in \mathbb {R}^d$
satisfy
$Y \in \mathbb {R}^d$
satisfy
![]() $\|Y \| \geqslant 2^{-10} c_0 \gamma ^{-1} / t$
and let W be a
$\|Y \| \geqslant 2^{-10} c_0 \gamma ^{-1} / t$
and let W be a
![]() $2d \times k$
matrix with
$2d \times k$
matrix with
![]() $\|W\| \leqslant 2$
.
$\|W\| \leqslant 2$
.
Let
![]() $\tau \sim \Xi _\nu (2d;\zeta )$
and
$\tau \sim \Xi _\nu (2d;\zeta )$
and
![]() $\tau ' \sim \Xi _\nu (2d;\zeta )$
with
$\tau ' \sim \Xi _\nu (2d;\zeta )$
with
![]() $\nu = 2^{-7}\nu $
, and let
$\nu = 2^{-7}\nu $
, and let
![]() $\beta \in [c_0/2^{10},\sqrt {c_0}]$
and
$\beta \in [c_0/2^{10},\sqrt {c_0}]$
and
![]() $\beta ' \in (0,1/2) $
. If
$\beta ' \in (0,1/2) $
. If
then
![]() $D_{\alpha ,\gamma }(Y)\leqslant 2^{10}B^2$
. Here, we have set
$D_{\alpha ,\gamma }(Y)\leqslant 2^{10}B^2$
. Here, we have set
![]() $R = 2^{35}\nu ^{-1/2} B^2 /c_0^2$
.
$R = 2^{35}\nu ^{-1/2} B^2 /c_0^2$
.
Proof. By Lemma IV.1, we may find an m for which the level set
![]() $S = S_{W_Y}(m)$
satisfies
$S = S_{W_Y}(m)$
satisfies
Combining (VI.4) with the assumption (VI.3) provides a lower bound of
Now, preparing for an application of Lemma VI.1, define
Recalling the definition of our cylinders from (VI.1), we state the following claim:
Claim VI.4. There exists
![]() $x \in S \subseteq \mathbb {R}^{k+2}$
so that
$x \in S \subseteq \mathbb {R}^{k+2}$
so that
Proof of Claim VI.4.
We will use Lemma VI.1 with
![]() $s = s_0$
, and so we check the hypotheses. We first observe that for any
$s = s_0$
, and so we check the hypotheses. We first observe that for any
![]() $y, a, b$
, if
$y, a, b$
, if
![]() ${\theta }_{[k]},{\theta }^{\prime }_{[k]} \in F_y(S;a,b)$
, then we have
${\theta }_{[k]},{\theta }^{\prime }_{[k]} \in F_y(S;a,b)$
, then we have
by Fact VI.2. This shows that for any
![]() $y, a, b$
, we have
$y, a, b$
, we have
where the equality holds by definition of
![]() $W_Y$
and the level set
$W_Y$
and the level set
![]() $S_{W_Y}$
. Thus, we may apply Lemma IV.2 to obtain
$S_{W_Y}$
. Thus, we may apply Lemma IV.2 to obtain
Combining lines (VI.5), (VI.8), and (VI.9), we note that in order to apply Lemma VI.1, it is sufficient to check
 $$ \begin{align} 8s_0^2 e^{-k/8} &+ 32 s_0^2 e^{32 \nu p m}\left(\mathbb{P}(\|W^T \tau'\|_2\leqslant \beta'\sqrt{k})+\exp(- \beta^{\prime 2} k)\right)^{1/4} \nonumber \\ &\qquad < \frac{1}{4} e^{\nu p m/2 + 2 \beta^2 k}\left( R t\right)^2 \left(\mathbb{P}(\|W^T \tau'\|_2\leqslant \beta'\sqrt{k}) + \exp(-\beta^{\prime 2} k) \right)^{1/4}\,. \end{align} $$
$$ \begin{align} 8s_0^2 e^{-k/8} &+ 32 s_0^2 e^{32 \nu p m}\left(\mathbb{P}(\|W^T \tau'\|_2\leqslant \beta'\sqrt{k})+\exp(- \beta^{\prime 2} k)\right)^{1/4} \nonumber \\ &\qquad < \frac{1}{4} e^{\nu p m/2 + 2 \beta^2 k}\left( R t\right)^2 \left(\mathbb{P}(\|W^T \tau'\|_2\leqslant \beta'\sqrt{k}) + \exp(-\beta^{\prime 2} k) \right)^{1/4}\,. \end{align} $$
We will show that each term on the left-hand side of (VI.10) is at most half of the right-hand side. Bound
since
![]() $R= 2^{35}B^2\nu ^{-1/2}c_0^{-2}$
. By Lemma II.1, we have that
$R= 2^{35}B^2\nu ^{-1/2}c_0^{-2}$
. By Lemma II.1, we have that
![]() $p\geqslant 2^{-7}B^{-4}$
and so we may bound
$p\geqslant 2^{-7}B^{-4}$
and so we may bound
Similarly, use (VI.11),
![]() $c_0\leqslant \beta $
and
$c_0\leqslant \beta $
and
![]() $\nu = 2^{-7}\nu $
to bound
$\nu = 2^{-7}\nu $
to bound
thus showing (VI.10). Applying Lemma VI.1 completes the claim.
The following basic consequence of Claim VI.4 will bring us closer to the construction of our LCD:
Claim VI.5. We have that
![]() $S_{W_Y}(4m) \cap (\Gamma _{2r_0,16} \setminus \Gamma _{2r_0,s_0}) \neq \emptyset \,$
.
$S_{W_Y}(4m) \cap (\Gamma _{2r_0,16} \setminus \Gamma _{2r_0,s_0}) \neq \emptyset \,$
.
Proof of Claim VI.5.
Claim VI.4 shows that there exists
![]() $x,y \in S = S_{W_Y}(m)$
so that
$x,y \in S = S_{W_Y}(m)$
so that
![]() $y \in ( \Gamma _{2r_0,16} \setminus \Gamma _{2r_0,s_0} + x \big ) $
. Now define
$y \in ( \Gamma _{2r_0,16} \setminus \Gamma _{2r_0,s_0} + x \big ) $
. Now define
![]() $\phi := y-x$
, and note that
$\phi := y-x$
, and note that
![]() $\phi \in S_{W_Y}(4m) \cap (\Gamma _{2r_0,16} \setminus \Gamma _{2r_0,s_0})$
due to Fact VI.2.
$\phi \in S_{W_Y}(4m) \cap (\Gamma _{2r_0,16} \setminus \Gamma _{2r_0,s_0})$
due to Fact VI.2.
We now complete the proof of Lemma VI.3 by showing that an element of the nonempty intersection above provides an LCD.
Claim VI.6. If
![]() $\phi \in S_{W_Y}(4m) \cap (\Gamma _{2r_0,16} \setminus \Gamma _{2r_0,s_0})$
, then there is a
$\phi \in S_{W_Y}(4m) \cap (\Gamma _{2r_0,16} \setminus \Gamma _{2r_0,s_0})$
, then there is a
![]() $\bar {\zeta }_0 \in (1,16 B^2)$
and
$\bar {\zeta }_0 \in (1,16 B^2)$
and
![]() $i \in \{k+1,k+2\}$
so that
$i \in \{k+1,k+2\}$
so that
Proof of Claim VI.6.
Note that since
![]() $\phi \in S_{W_Y}(4m)$
, we have
$\phi \in S_{W_Y}(4m)$
, we have
Thus, there is some instance
![]() $\bar {\zeta }_0 \in (1,16 B^2)$
of
$\bar {\zeta }_0 \in (1,16 B^2)$
of
![]() $\bar {\zeta }$
so that
$\bar {\zeta }$
so that
For simplicity, define
![]() $\psi =: \bar {\zeta }_0 \phi $
.
$\psi =: \bar {\zeta }_0 \phi $
.
By (VI.12), there is a
![]() $z \in \mathbb {Z}^{2d}$
so that
$z \in \mathbb {Z}^{2d}$
so that
![]() $W_Y \psi \in B_{2d}(z,2\sqrt {m})$
. Expand
$W_Y \psi \in B_{2d}(z,2\sqrt {m})$
. Expand
 $$ \begin{align*} W_Y\psi = W\psi_{[k]} + \psi_{k+1} \begin{bmatrix} Y \\ \mathbf{0}_d \end{bmatrix} + \psi_{k+2} \begin{bmatrix} \mathbf{0}_d \\ Y \end{bmatrix}\,, \end{align*} $$
$$ \begin{align*} W_Y\psi = W\psi_{[k]} + \psi_{k+1} \begin{bmatrix} Y \\ \mathbf{0}_d \end{bmatrix} + \psi_{k+2} \begin{bmatrix} \mathbf{0}_d \\ Y \end{bmatrix}\,, \end{align*} $$
and note that
 $$ \begin{align} \psi_{k+1} \begin{bmatrix} Y \\ \mathbf{{0}}_d \end{bmatrix} + \psi_{k+2} \begin{bmatrix} \mathbf{{0}}_d \\ Y \end{bmatrix} \in B_{2d}(z,2\sqrt{m}) - W \psi_{[k]} \subseteq B_{2d}(z, 2\sqrt{m} + 2^6 B^2\sqrt{k})\,, \end{align} $$
$$ \begin{align} \psi_{k+1} \begin{bmatrix} Y \\ \mathbf{{0}}_d \end{bmatrix} + \psi_{k+2} \begin{bmatrix} \mathbf{{0}}_d \\ Y \end{bmatrix} \in B_{2d}(z,2\sqrt{m}) - W \psi_{[k]} \subseteq B_{2d}(z, 2\sqrt{m} + 2^6 B^2\sqrt{k})\,, \end{align} $$
where the last inclusion holds because
since
![]() $\phi \in \Gamma _{2r_0,16}$
,
$\phi \in \Gamma _{2r_0,16}$
,
![]() $|\bar {\zeta }_0| \leqslant 16 B^2$
, and
$|\bar {\zeta }_0| \leqslant 16 B^2$
, and
![]() $\|W\|_{op} \leqslant 2$
.
$\|W\|_{op} \leqslant 2$
.
Since
![]() $\phi \not \in \Gamma _{2r_0,s_0}$
and
$\phi \not \in \Gamma _{2r_0,s_0}$
and
![]() $\bar {\zeta }_0> 1$
, we have
$\bar {\zeta }_0> 1$
, we have
![]() $\max \{|\psi _{k+1}|,|\psi _{k+2}|\}> s_0$
, and so we assume, without loss, that
$\max \{|\psi _{k+1}|,|\psi _{k+2}|\}> s_0$
, and so we assume, without loss, that
![]() $|\psi _{k+1}|>s_0$
. Projecting (VI.13) onto the first d coordinates yields
$|\psi _{k+1}|>s_0$
. Projecting (VI.13) onto the first d coordinates yields
Now, we show that
![]() $\|\psi _{k+1} Y\|_{\mathbb {T}} < \gamma \psi _{k+1}\| Y\|_2$
. Indeed,
$\|\psi _{k+1} Y\|_{\mathbb {T}} < \gamma \psi _{k+1}\| Y\|_2$
. Indeed,
 $$ \begin{align} \psi_{k+1}\| Y\|_2\gamma \geqslant s_0 \|Y\|_2\gamma> \bigg(\frac{2^{15}(\sqrt{m} + 8B^2 \sqrt{k})t}{c_0}\bigg)\bigg(2^{-10}\frac{c_0}{t}\bigg) \geqslant (2\sqrt{m} + 2^6 B^2 \sqrt{k}), \end{align} $$
$$ \begin{align} \psi_{k+1}\| Y\|_2\gamma \geqslant s_0 \|Y\|_2\gamma> \bigg(\frac{2^{15}(\sqrt{m} + 8B^2 \sqrt{k})t}{c_0}\bigg)\bigg(2^{-10}\frac{c_0}{t}\bigg) \geqslant (2\sqrt{m} + 2^6 B^2 \sqrt{k}), \end{align} $$
where we used the definition of
![]() $s_0$
and that
$s_0$
and that
![]() $\|Y\|_2> 2^{-10}c_0 \gamma ^{-1}/t$
.
$\|Y\|_2> 2^{-10}c_0 \gamma ^{-1}/t$
.
We now need to show
Note that since
![]() $k \leqslant 2^{-32} \alpha d / B^4$
, we have
$k \leqslant 2^{-32} \alpha d / B^4$
, we have
![]() $2^8 B^2 \sqrt {k} \leqslant \sqrt {\alpha d}/2$
. We claim that
$2^8 B^2 \sqrt {k} \leqslant \sqrt {\alpha d}/2$
. We claim that
![]() $m \leqslant 2^{-4}\alpha d$
. To show this, apply the lower bound (VI.5) and
$m \leqslant 2^{-4}\alpha d$
. To show this, apply the lower bound (VI.5) and
![]() $\gamma _{k+2}(S) \leqslant 1$
to see
$\gamma _{k+2}(S) \leqslant 1$
to see
where we have used
![]() $k \leqslant 2^{-17} \nu \alpha d / B^4$
and
$k \leqslant 2^{-17} \nu \alpha d / B^4$
and
![]() $t \geqslant e^{-2^{-17} \nu \alpha d / B^4}$
. Therefore,
$t \geqslant e^{-2^{-17} \nu \alpha d / B^4}$
. Therefore,
![]() $m \leqslant 2^{-4}\alpha d$
, that is
$m \leqslant 2^{-4}\alpha d$
, that is
![]() $2\sqrt {m} \leqslant \sqrt {\alpha d}/2$
. Combining this with (VI.14) and (VI.15), we see
$2\sqrt {m} \leqslant \sqrt {\alpha d}/2$
. Combining this with (VI.14) and (VI.15), we see
as desired. This completes the proof of the Claim VI.6.
Let
![]() $\phi $
,
$\phi $
,
![]() $\bar {\zeta }_0$
, and
$\bar {\zeta }_0$
, and
![]() $i \in \{k+1,k+2\}$
be as guaranteed by Claim VI.6. Then
$i \in \{k+1,k+2\}$
be as guaranteed by Claim VI.6. Then
![]() $\bar {\zeta }_0\phi _i \leqslant 2^{10} B^2 $
, and
$\bar {\zeta }_0\phi _i \leqslant 2^{10} B^2 $
, and
and so
![]() $D_{\alpha ,\gamma }(Y)\leqslant 2^{10}B^2$
, thus completing the proof of Lemma VI.3.
$D_{\alpha ,\gamma }(Y)\leqslant 2^{10}B^2$
, thus completing the proof of Lemma VI.3.
VI.3 Proof of Lemma IV.3
In order to bridge the gap between Lemmas VI.3 and IV.3, we need an anticoncentration lemma for
![]() $\| W \sigma \|_2$
when
$\| W \sigma \|_2$
when
![]() $\sigma $
is random and W is fixed. We will use the following bound, which is a version of the Hanson-Wright inequality [Reference Hanson and Wright18, Reference Rudelson and Vershynin33].
$\sigma $
is random and W is fixed. We will use the following bound, which is a version of the Hanson-Wright inequality [Reference Hanson and Wright18, Reference Rudelson and Vershynin33].
Lemma VI.7. Let
![]() $\nu \in (0,1)$
and
$\nu \in (0,1)$
and
![]() $\beta '\in (0,2^{-7}B^{-2}\sqrt {\nu })$
. Let W be a
$\beta '\in (0,2^{-7}B^{-2}\sqrt {\nu })$
. Let W be a
![]() $2d \times k$
matrix satisfying
$2d \times k$
matrix satisfying
![]() $\|W \|_{\mathrm {HS}} \geqslant \sqrt {k}/2$
and
$\|W \|_{\mathrm {HS}} \geqslant \sqrt {k}/2$
and
![]() $\| W \| \leqslant 2$
and
$\| W \| \leqslant 2$
and
![]() $\tau '\sim \Xi _\nu (2d; \zeta )$
. Then
$\tau '\sim \Xi _\nu (2d; \zeta )$
. Then
We derive Lemma VI.7 from Talagrand’s inequality in Section X, (see [Reference Rudelson and Vershynin33] or [Reference Hanson and Wright18] for more context). From here, we are ready to prove Lemma IV.3.
Proof of Lemma IV.3.
Recalling that
![]() $c_0\leqslant 2^{-35} B^{-4}\nu $
, and that our given W satisfies
$c_0\leqslant 2^{-35} B^{-4}\nu $
, and that our given W satisfies
![]() $\|W\|_{\mathrm {HS}}\geqslant \sqrt {k}/2$
and
$\|W\|_{\mathrm {HS}}\geqslant \sqrt {k}/2$
and
![]() $\|W\|\leqslant 2$
, we apply Lemma VI.7, with
$\|W\|\leqslant 2$
, we apply Lemma VI.7, with
![]() $\beta '=2^{6}\sqrt {c_0}$
and the
$\beta '=2^{6}\sqrt {c_0}$
and the
![]() $\nu $
-lazy random vector
$\nu $
-lazy random vector
![]() $\tau '\sim \Xi _\nu (2d;\zeta )$
, where
$\tau '\sim \Xi _\nu (2d;\zeta )$
, where
![]() $\nu = 2^{-7}\nu $
, to see
$\nu = 2^{-7}\nu $
, to see
We now consider the right-hand side of (VI.3) in Lemma VI.3: if
![]() $\beta \leqslant \sqrt {c_0}$
, we have
$\beta \leqslant \sqrt {c_0}$
, we have
 $$ \begin{align*} e^{4\beta^2 k}\left(\mathbb{P}(\|W^T\tau'\|_2 \leqslant \beta' \sqrt{k})+\exp(-\beta^{\prime 2} k)\right)^{1/4} &\leqslant \exp\left(4 c_0 k-8 c_0 k\right)+\exp\left(4 c_0 k-16 c_0 k\right)\\ &\leqslant 2\exp(-c_0 k)\,. \end{align*} $$
$$ \begin{align*} e^{4\beta^2 k}\left(\mathbb{P}(\|W^T\tau'\|_2 \leqslant \beta' \sqrt{k})+\exp(-\beta^{\prime 2} k)\right)^{1/4} &\leqslant \exp\left(4 c_0 k-8 c_0 k\right)+\exp\left(4 c_0 k-16 c_0 k\right)\\ &\leqslant 2\exp(-c_0 k)\,. \end{align*} $$
We now note that the hypotheses in Lemma IV.3 align with the hypotheses in Lemma VI.3 with respect to the selection of
![]() $\beta , \alpha , t, R, Y, W$
; if we additionally assume
$\beta , \alpha , t, R, Y, W$
; if we additionally assume
![]() $D_{\alpha ,\gamma }(Y)> 2^{10}B^2$
, we may apply the contrapositive of Lemma VI.3 to obtain
$D_{\alpha ,\gamma }(Y)> 2^{10}B^2$
, we may apply the contrapositive of Lemma VI.3 to obtain
 $$ \begin{align*} \mathcal{L}\left(W_Y^T \tau , \beta \sqrt{k+1} \right) &\leqslant(2^{35} B^{2}\nu^{-1/2} c_0^{-2} t/2)^{2} e^{4 \beta^2 k} \left(\mathbb{P}(\| W^T \tau' \|_2 \leqslant 2 \beta' \sqrt{k}) + e^{- \beta^{\prime 2} k} \right)^{1/4}\\ &\leqslant (Rt)^2 \exp(-c_0k) \,, \end{align*} $$
$$ \begin{align*} \mathcal{L}\left(W_Y^T \tau , \beta \sqrt{k+1} \right) &\leqslant(2^{35} B^{2}\nu^{-1/2} c_0^{-2} t/2)^{2} e^{4 \beta^2 k} \left(\mathbb{P}(\| W^T \tau' \|_2 \leqslant 2 \beta' \sqrt{k}) + e^{- \beta^{\prime 2} k} \right)^{1/4}\\ &\leqslant (Rt)^2 \exp(-c_0k) \,, \end{align*} $$
as desired.
VII Inverse Littlewood-Offord for conditioned matrix walks
In this section, we prove an inverse Littlewood-Offord theorem for matrices conditioned on their robust rank. Everything in this section will be analogous to Section 6 of [Reference Campos, Jenssen, Michelen and Sahasrabudhe4].
Theorem VII.1. For
![]() $n \in \mathbb {N}$
and
$n \in \mathbb {N}$
and
![]() $0 < c_0 \leqslant 2^{-50}B^{-4}$
, let
$0 < c_0 \leqslant 2^{-50}B^{-4}$
, let
![]() $d \leqslant c_0^2 n$
, and for
$d \leqslant c_0^2 n$
, and for
![]() $\alpha ,\gamma \in (0,1)$
, let
$\alpha ,\gamma \in (0,1)$
, let
![]() $0\leqslant k\leqslant 2^{-32}B^{-4}\alpha d$
and
$0\leqslant k\leqslant 2^{-32}B^{-4}\alpha d$
and
![]() $N\leqslant \exp (2^{-32}B^{-4}\alpha d)$
. Let
$N\leqslant \exp (2^{-32}B^{-4}\alpha d)$
. Let
![]() $X \in \mathbb {R}^d$
satisfy
$X \in \mathbb {R}^d$
satisfy
![]() $\|X\|_2 \geqslant c_02^{-10} \gamma ^{-1}n^{1/2} N$
, and let H be a random
$\|X\|_2 \geqslant c_02^{-10} \gamma ^{-1}n^{1/2} N$
, and let H be a random
![]() $(n-d)\times 2d$
matrix with i.i.d. rows sampled from
$(n-d)\times 2d$
matrix with i.i.d. rows sampled from
![]() $\Phi _\nu (2d;\zeta )$
with
$\Phi _\nu (2d;\zeta )$
with
![]() $\nu = 2^{-15}$
. If
$\nu = 2^{-15}$
. If
![]() $D_{\alpha ,\gamma }(r_n \cdot X)> 2^{10}B^2$
, then
$D_{\alpha ,\gamma }(r_n \cdot X)> 2^{10}B^2$
, then
 $$ \begin{align} \mathbb{P}_H\left(\sigma_{2d-k+1}(H)\leqslant c_02^{-4}\sqrt{n} \text{ and } \|H_1X\|_2,\|H_2 X\|_2\leqslant n\right)\leqslant e^{-c_0nk/3}\left(\frac{R}{N}\right)^{2n-2d}\, , \end{align} $$
$$ \begin{align} \mathbb{P}_H\left(\sigma_{2d-k+1}(H)\leqslant c_02^{-4}\sqrt{n} \text{ and } \|H_1X\|_2,\|H_2 X\|_2\leqslant n\right)\leqslant e^{-c_0nk/3}\left(\frac{R}{N}\right)^{2n-2d}\, , \end{align} $$
where we have set
![]() $H_1 := H_{[n-d]\times [d]}$
,
$H_1 := H_{[n-d]\times [d]}$
,
![]() $H_2 := H_{[n-d] \times [d+1,2d]}$
,
$H_2 := H_{[n-d] \times [d+1,2d]}$
,
![]() $r_n := \frac {c_0}{32\sqrt {n}}$
and
$r_n := \frac {c_0}{32\sqrt {n}}$
and
![]() $R := 2^{43}B^2 c_0^{-3}$
.
$R := 2^{43}B^2 c_0^{-3}$
.
VII.1 Tensorization and random rounding step
We import the following tensorization lemma from [Reference Campos, Jenssen, Michelen and Sahasrabudhe4].
Lemma VII.2. For
![]() $d < n$
and
$d < n$
and
![]() $k \geqslant 0$
, let W be a
$k \geqslant 0$
, let W be a
![]() $2d \times (k+2)$
matrix and let H be a
$2d \times (k+2)$
matrix and let H be a
![]() $(n-d)\times 2d$
random matrix with i.i.d. rows. Let
$(n-d)\times 2d$
random matrix with i.i.d. rows. Let
![]() $\tau \in \mathbb {R}^{2d}$
be a random vector with the same distribution as the rows of H. If
$\tau \in \mathbb {R}^{2d}$
be a random vector with the same distribution as the rows of H. If
![]() $\beta \in (0,1/8)$
, then
$\beta \in (0,1/8)$
, then
Similarly, we use net for the singular vectors of H, constructed in [Reference Campos, Jenssen, Michelen and Sahasrabudhe4]. Let
![]() $\mathcal {U}_{2d,k} \subset \mathbb {R}^{[2d] \times [k]}$
be the set of
$\mathcal {U}_{2d,k} \subset \mathbb {R}^{[2d] \times [k]}$
be the set of
![]() $2d \times k$
matrices with orthonormal columns.
$2d \times k$
matrices with orthonormal columns.
Lemma VII.3. For
![]() $k \leqslant d$
and
$k \leqslant d$
and
![]() $\delta \in (0,1/2)$
, there exists
$\delta \in (0,1/2)$
, there exists
![]() $\mathcal {W} = \mathcal {W}_{2d,k} \subset \mathbb {R}^{[2d]\times [k]}$
with
$\mathcal {W} = \mathcal {W}_{2d,k} \subset \mathbb {R}^{[2d]\times [k]}$
with
![]() $|\mathcal {W}| \leqslant (2^6/\delta )^{2dk}$
so that for any
$|\mathcal {W}| \leqslant (2^6/\delta )^{2dk}$
so that for any
![]() $U\in \mathcal {U}_{2d,k}$
, any
$U\in \mathcal {U}_{2d,k}$
, any
![]() $r \in \mathbb {N}$
, and
$r \in \mathbb {N}$
, and
![]() $r \times 2d$
matrix A, there exists
$r \times 2d$
matrix A, there exists
![]() $W\in \mathcal {W}$
so that
$W\in \mathcal {W}$
so that
-
1.
 $\|A(W-U)\|_{\mathrm {HS}}\leqslant \delta (k/2d)^{1/2} \|A\|_{\mathrm {HS}} $
,
$\|A(W-U)\|_{\mathrm {HS}}\leqslant \delta (k/2d)^{1/2} \|A\|_{\mathrm {HS}} $
, -
2.
 $\|W-U\|_{\mathrm {HS}}\leqslant \delta \sqrt {k}$
, and
$\|W-U\|_{\mathrm {HS}}\leqslant \delta \sqrt {k}$
, and -
3.
 $\|W-U\|_{op} \leqslant 8\delta .$
$\|W-U\|_{op} \leqslant 8\delta .$
VII.2 Proof of Theorem VII.1
We also use the following standard fact from linear algebra.
Fact VII.4. For
![]() $3d < n$
, let H be a
$3d < n$
, let H be a
![]() $(n-d) \times 2d$
matrix. If
$(n-d) \times 2d$
matrix. If
![]() $\sigma _{2d-k+1}(H) \leqslant x$
, then there exist k orthogonal unit vectors
$\sigma _{2d-k+1}(H) \leqslant x$
, then there exist k orthogonal unit vectors
![]() $w_1,\ldots ,w_k \in \mathbb {R}^{2d}$
so that
$w_1,\ldots ,w_k \in \mathbb {R}^{2d}$
so that
![]() $\|Hw_i\|_2 \leqslant x$
. In particular, there exists
$\|Hw_i\|_2 \leqslant x$
. In particular, there exists
![]() $W \in \mathcal {U}_{2d,k}$
so that
$W \in \mathcal {U}_{2d,k}$
so that
![]() $\|HW\|_{\mathrm {HS}} \leqslant x\sqrt {k}$
.
$\|HW\|_{\mathrm {HS}} \leqslant x\sqrt {k}$
.
We will also need a bound on
![]() $\|H\|_{\mathrm {HS}}$
:
$\|H\|_{\mathrm {HS}}$
:
Fact VII.5. Let H be the random
![]() $(n - d) \times (2d)$
matrix whose rows are i.i.d. samples of
$(n - d) \times (2d)$
matrix whose rows are i.i.d. samples of
![]() $\Phi _\nu (2d; \zeta )$
. Then
$\Phi _\nu (2d; \zeta )$
. Then
We are now ready to prove Theorem VII.1.
Proof of Theorem VII.1.
Let
![]() $Y := \frac {c_0}{32\sqrt {n}}\cdot X$
. We may upper bound the left-hand side of (VII.1) by Fact VII.4
$Y := \frac {c_0}{32\sqrt {n}}\cdot X$
. We may upper bound the left-hand side of (VII.1) by Fact VII.4
 $$ \begin{align*} \mathbb{P}(&\sigma_{2d-k+1}(H)\leqslant c_02^{-4}\sqrt{n} \text{ and } \|H_1 X\|_2,\|H_2 X\|_2\leqslant n) \\ &\qquad \leqslant \mathbb{P}(\exists U\in \mathcal{U}_{2d,k}: \|H U_Y\|_{\mathrm{HS}} \leqslant c_0\sqrt{n (k+1)}/8). \end{align*} $$
$$ \begin{align*} \mathbb{P}(&\sigma_{2d-k+1}(H)\leqslant c_02^{-4}\sqrt{n} \text{ and } \|H_1 X\|_2,\|H_2 X\|_2\leqslant n) \\ &\qquad \leqslant \mathbb{P}(\exists U\in \mathcal{U}_{2d,k}: \|H U_Y\|_{\mathrm{HS}} \leqslant c_0\sqrt{n (k+1)}/8). \end{align*} $$
Set
![]() $\delta := c_0/16$
, and let
$\delta := c_0/16$
, and let
![]() $\mathcal {W}$
be as in Lemma VII.3.
$\mathcal {W}$
be as in Lemma VII.3.
For each fixed H, if we have
![]() $\|H\|_{\mathrm {HS}}\leqslant 2\sqrt { d (n-d)}$
and there is some
$\|H\|_{\mathrm {HS}}\leqslant 2\sqrt { d (n-d)}$
and there is some
![]() $U \in \mathcal {U}_{2d,k}$
so that
$U \in \mathcal {U}_{2d,k}$
so that
![]() $\|HU_Y\|_{\mathrm {HS}} \leqslant c_0\sqrt {n (k+1)}/8$
, we may apply Lemma VII.3 to find
$\|HU_Y\|_{\mathrm {HS}} \leqslant c_0\sqrt {n (k+1)}/8$
, we may apply Lemma VII.3 to find
![]() $W \in \mathcal {W}$
so that
$W \in \mathcal {W}$
so that
which is at most
![]() $c_0\sqrt {n(k+1)}/4$
. This shows the bound
$c_0\sqrt {n(k+1)}/4$
. This shows the bound
Conditioning on the event that
![]() $\| H \|_{\mathrm {HS}} \leqslant 2\sqrt {d(n-d)}$
, applying Fact VII.5, and union bounding over
$\| H \|_{\mathrm {HS}} \leqslant 2\sqrt {d(n-d)}$
, applying Fact VII.5, and union bounding over
![]() $\mathcal {W}$
show that the right-hand side of the above is at most
$\mathcal {W}$
show that the right-hand side of the above is at most
Bound
where the last inequality holds since
![]() $d\leqslant c_0^2 n$
. Thus
$d\leqslant c_0^2 n$
. Thus
For each
![]() $W \in \mathcal {W}$
, apply Lemma VII.2 with
$W \in \mathcal {W}$
, apply Lemma VII.2 with
![]() $\beta :=\sqrt {c_0/3}$
(noting that
$\beta :=\sqrt {c_0/3}$
(noting that
![]() $\sqrt {n-d}/3\geqslant \sqrt {n}/4$
) to obtain
$\sqrt {n-d}/3\geqslant \sqrt {n}/4$
) to obtain
Preparing to apply Lemma IV.3, define
![]() $t := (c_0 N/32)^{-1} \geqslant \exp (- 2^{-32}B^{-4}\alpha d)$
and
$t := (c_0 N/32)^{-1} \geqslant \exp (- 2^{-32}B^{-4}\alpha d)$
and
![]() $R_0 := 2^{-8}c_0 R = 2^{-8}c_0(2^{43}B^2c_0^{-3}) = 2^{35}B^2c_0^{-2}$
so that we have
$R_0 := 2^{-8}c_0 R = 2^{-8}c_0(2^{43}B^2c_0^{-3}) = 2^{35}B^2c_0^{-2}$
so that we have
Since
![]() $W \in \mathcal {W}$
, we have
$W \in \mathcal {W}$
, we have
![]() $\|W\|_{op}\leqslant 2$
and
$\|W\|_{op}\leqslant 2$
and
![]() $\|W\|_{\mathrm {HS}} \geqslant \sqrt {k}/2$
. We also note the bounds
$\|W\|_{\mathrm {HS}} \geqslant \sqrt {k}/2$
. We also note the bounds
![]() $k \leqslant 2^{-32}B^{-4}\alpha d$
,
$k \leqslant 2^{-32}B^{-4}\alpha d$
,
![]() $ D_{\alpha ,\gamma }(\frac {c_0}{32\sqrt {n}} X) = D_{\alpha ,\gamma }(Y)> 2^{10}B^2$
. Thus, we may apply Lemma IV.3 to see that
$ D_{\alpha ,\gamma }(\frac {c_0}{32\sqrt {n}} X) = D_{\alpha ,\gamma }(Y)> 2^{10}B^2$
. Thus, we may apply Lemma IV.3 to see that
 $$ \begin{align*} \mathcal{L}\big( W_Y^T \tau, c_0^{1/2} \sqrt{k+1} \big)\leqslant (R_0t)^2e^{-c_0k}\leqslant \left(\frac{R}{8N}\right)^2e^{-c_0k}\,. \end{align*} $$
$$ \begin{align*} \mathcal{L}\big( W_Y^T \tau, c_0^{1/2} \sqrt{k+1} \big)\leqslant (R_0t)^2e^{-c_0k}\leqslant \left(\frac{R}{8N}\right)^2e^{-c_0k}\,. \end{align*} $$
Substituting this bound into (VII.3) gives
 $$ \begin{align*} \max_{W \in \mathcal{W} }\, \mathbb{P}_H(\|H W_Y\|_2\leqslant c_0 \sqrt{n (k+1)}/4 )\leqslant \frac{1}{2}\left(\frac{R}{N}\right)^{2n-2d}e^{-c_0 k(n-d)/3}\,. \end{align*} $$
$$ \begin{align*} \max_{W \in \mathcal{W} }\, \mathbb{P}_H(\|H W_Y\|_2\leqslant c_0 \sqrt{n (k+1)}/4 )\leqslant \frac{1}{2}\left(\frac{R}{N}\right)^{2n-2d}e^{-c_0 k(n-d)/3}\,. \end{align*} $$
Combining with the previous bounds and noting
 $$ \begin{align*}2\exp\left(-2^{-21}B^{-4}nd\right)\leqslant\frac{1}{2}\left(\frac{R}{N}\right)^{2n-2d}e^{-c_0 k(n-d)/3}\end{align*} $$
$$ \begin{align*}2\exp\left(-2^{-21}B^{-4}nd\right)\leqslant\frac{1}{2}\left(\frac{R}{N}\right)^{2n-2d}e^{-c_0 k(n-d)/3}\end{align*} $$
show
 $$ \begin{align*} \mathbb{P}(\sigma_{2d-k+1}(H)\leqslant c_0\sqrt{n}/16 \text{ and } \|H_1 X\|_2,\|H_2 X\|_2\leqslant n)\leqslant \left(\frac{R}{ N}\right)^{2n-2d}e^{-c_0 k(n-d)/3}\,. \end{align*} $$
$$ \begin{align*} \mathbb{P}(\sigma_{2d-k+1}(H)\leqslant c_0\sqrt{n}/16 \text{ and } \|H_1 X\|_2,\|H_2 X\|_2\leqslant n)\leqslant \left(\frac{R}{ N}\right)^{2n-2d}e^{-c_0 k(n-d)/3}\,. \end{align*} $$
This completes the proof of Theorem VII.1.
VIII Nets for structured vectors: Size of the net
The goal of this subsection is to prove Theorem III.2. We follow the same path as Section 7 of [Reference Campos, Jenssen, Michelen and Sahasrabudhe4]. As such, we work with the intersection of
![]() $\mathcal {N}_{\varepsilon }$
with a selection of “boxes” which cover a rescaling of the trivial net
$\mathcal {N}_{\varepsilon }$
with a selection of “boxes” which cover a rescaling of the trivial net
![]() $\Lambda _{\varepsilon }$
. We recall the definition of the relevant boxes from [Reference Campos, Jenssen, Michelen and Sahasrabudhe4].
$\Lambda _{\varepsilon }$
. We recall the definition of the relevant boxes from [Reference Campos, Jenssen, Michelen and Sahasrabudhe4].
Definition VIII.1. Define a
![]() $(N,\kappa ,d)$
-box to be a set of the form
$(N,\kappa ,d)$
-box to be a set of the form
![]() $\mathcal {B}=B_1 \times \ldots \times B_n\subset \mathbb Z^n$
, where
$\mathcal {B}=B_1 \times \ldots \times B_n\subset \mathbb Z^n$
, where
![]() $|B_i|\geqslant N$
for all
$|B_i|\geqslant N$
for all
![]() $i\geqslant 1$
;
$i\geqslant 1$
;
![]() $B_i = [-\kappa N,-N]\cup [N, \kappa N]$
, for
$B_i = [-\kappa N,-N]\cup [N, \kappa N]$
, for
![]() $i \in [d]$
; and
$i \in [d]$
; and
![]() $|\mathcal {B}|\leqslant (\kappa N)^n$
.
$|\mathcal {B}|\leqslant (\kappa N)^n$
.
We now interpret these boxes probabilistically and seek to understand the probability that we have
 $$\begin{align*}\mathbb{P}_M(\|MX\|_2\leqslant n)\geqslant \left(\frac{L}{N}\right)^n, \end{align*}$$
$$\begin{align*}\mathbb{P}_M(\|MX\|_2\leqslant n)\geqslant \left(\frac{L}{N}\right)^n, \end{align*}$$
where X is chosen uniformly at random from
![]() $\mathcal {B}$
. Theorem III.2 will follow quickly from the following “box” version:
$\mathcal {B}$
. Theorem III.2 will follow quickly from the following “box” version:
Lemma VIII.2. For
![]() $L \geqslant 2$
and
$L \geqslant 2$
and
![]() $0 < c_0 \leqslant 2^{-50}B^{-4}$
, let
$0 < c_0 \leqslant 2^{-50}B^{-4}$
, let
![]() $n> L^{64/c_0^2}$
and let
$n> L^{64/c_0^2}$
and let
![]() $\frac {1}{4}c_0^2n\leqslant d\leqslant c_0^2 n$
. For
$\frac {1}{4}c_0^2n\leqslant d\leqslant c_0^2 n$
. For
![]() $N \geqslant 2$
, satisfying
$N \geqslant 2$
, satisfying
![]() $N \leqslant \exp (c_0 L^{-8n/d} d)$
, and
$N \leqslant \exp (c_0 L^{-8n/d} d)$
, and
![]() ${\kappa } \geqslant 2$
, let
${\kappa } \geqslant 2$
, let
![]() $\mathcal {B}$
be a
$\mathcal {B}$
be a
![]() $(N,\kappa ,d)$
-box. If X is chosen uniformly at random from
$(N,\kappa ,d)$
-box. If X is chosen uniformly at random from
![]() $\mathcal {B}$
, then
$\mathcal {B}$
, then
 $$ \begin{align*}\mathbb{P}_X\left(\mathbb{P}_M(\|MX\|_2\leqslant n)\geqslant \left(\frac{L}{N}\right)^n\right)\leqslant \left(\frac{R}{L}\right)^{2n}, \end{align*} $$
$$ \begin{align*}\mathbb{P}_X\left(\mathbb{P}_M(\|MX\|_2\leqslant n)\geqslant \left(\frac{L}{N}\right)^n\right)\leqslant \left(\frac{R}{L}\right)^{2n}, \end{align*} $$
where
![]() $R := C c_0^{-3}$
and
$R := C c_0^{-3}$
and
![]() $C>0$
is an absolute constant.
$C>0$
is an absolute constant.
VIII.1 Counting with the LCD and anticoncentration for linear projections of random vectors
We first show that if we choose
![]() $X \in \mathcal {B}$
uniformly at random, then it typically has a large LCD.
$X \in \mathcal {B}$
uniformly at random, then it typically has a large LCD.
Lemma VIII.3. For
![]() $\alpha \in (0,1), K \geqslant 1$
, and
$\alpha \in (0,1), K \geqslant 1$
, and
![]() ${\kappa } \geqslant 2$
, let
${\kappa } \geqslant 2$
, let
![]() $n \geqslant d\geqslant K^2/\alpha $
and let
$n \geqslant d\geqslant K^2/\alpha $
and let
![]() $N \geqslant 2$
be so that
$N \geqslant 2$
be so that
![]() $ K N < 2^d $
. Let
$ K N < 2^d $
. Let
![]() $\mathcal {B}=\left ([-{\kappa } N,-N]\cup [N,{\kappa } N]\right )^d$
, and let X be chosen uniformly at random from
$\mathcal {B}=\left ([-{\kappa } N,-N]\cup [N,{\kappa } N]\right )^d$
, and let X be chosen uniformly at random from
![]() $\mathcal {B}$
. Then
$\mathcal {B}$
. Then
where we have set
![]() $r_n := c_02^{-5} n^{-1/2}$
.
$r_n := c_02^{-5} n^{-1/2}$
.
Proof. Writing
![]() $\phi = \psi r_n$
, note that
$\phi = \psi r_n$
, note that
We note that any such
![]() $\phi $
must have
$\phi $
must have
![]() $|\phi | \geqslant (2 \kappa N)^{-1}$
, since if we had
$|\phi | \geqslant (2 \kappa N)^{-1}$
, since if we had
![]() $\phi < (2 \kappa N)^{-1}$
, then each coordinate of
$\phi < (2 \kappa N)^{-1}$
, then each coordinate of
![]() $\phi X$
would lie in
$\phi X$
would lie in
![]() $(-1/2,1/2)$
, implying
$(-1/2,1/2)$
, implying
![]() $\|\phi X\|_{\mathbb {T}} = \phi \| X\|_2$
, that is
$\|\phi X\|_{\mathbb {T}} = \phi \| X\|_2$
, that is
![]() $\|\phi X \|_{\mathbb {T}}> \gamma \phi \|X \|_2$
. The proof of Lemma 7.4 in [Reference Campos, Jenssen, Michelen and Sahasrabudhe4] shows that
$\|\phi X \|_{\mathbb {T}}> \gamma \phi \|X \|_2$
. The proof of Lemma 7.4 in [Reference Campos, Jenssen, Michelen and Sahasrabudhe4] shows that
completing the Lemma.
We also import from [Reference Campos, Jenssen, Michelen and Sahasrabudhe4, Lemma 7.5] a result showing anticoncentration for random vectors
![]() $AX$
, where A is a fixed matrix and X is a random vector with independent entries. As noted in [Reference Campos, Jenssen, Michelen and Sahasrabudhe4], this is essentially a rephrasing of Corollary 1.4 and Remark 2.3 in Rudelson and Vershynin’s paper [Reference Rudelson and Vershynin34]:
$AX$
, where A is a fixed matrix and X is a random vector with independent entries. As noted in [Reference Campos, Jenssen, Michelen and Sahasrabudhe4], this is essentially a rephrasing of Corollary 1.4 and Remark 2.3 in Rudelson and Vershynin’s paper [Reference Rudelson and Vershynin34]:
Lemma VIII.4. Let
![]() $N \in \mathbb {N}$
,
$N \in \mathbb {N}$
,
![]() $n,d,k \in \mathbb {N}$
be such that
$n,d,k \in \mathbb {N}$
be such that
![]() $n-d \geqslant 2d> 2k$
, H be a
$n-d \geqslant 2d> 2k$
, H be a
![]() $2d \times (n-d)$
matrix with
$2d \times (n-d)$
matrix with
![]() $\sigma _{2d-k}(H)\geqslant c_0\sqrt {n}/16$
and
$\sigma _{2d-k}(H)\geqslant c_0\sqrt {n}/16$
and
![]() $B_1,\ldots , B_{n-d}\subset \mathbb {Z}$
with
$B_1,\ldots , B_{n-d}\subset \mathbb {Z}$
with
![]() $|B_i|\geqslant N$
. If X is taken uniformly at random from
$|B_i|\geqslant N$
. If X is taken uniformly at random from
![]() $\mathcal {B}:=B_1\times \ldots \times B_{n-d}$
, then
$\mathcal {B}:=B_1\times \ldots \times B_{n-d}$
, then
 $$\begin{align*}\mathbb{P}_X(\|HX\|_2\leqslant n)\leqslant \left(\frac{Cn}{dc_0 N}\right)^{2d-k},\end{align*}$$
$$\begin{align*}\mathbb{P}_X(\|HX\|_2\leqslant n)\leqslant \left(\frac{Cn}{dc_0 N}\right)^{2d-k},\end{align*}$$
where
![]() $C>0$
is an absolute constant.
$C>0$
is an absolute constant.
VIII.2 Proof of Theorem VIII.2
Recall that the matrix M is defined as
 $$ \begin{align*} M = \begin{bmatrix} \mathbf{0 }_{[d]\times [d]} & H^T_1 \\ H_1 & \mathbf{0}_{[n-d] \times [n-d]} \end{bmatrix} ,\end{align*} $$
$$ \begin{align*} M = \begin{bmatrix} \mathbf{0 }_{[d]\times [d]} & H^T_1 \\ H_1 & \mathbf{0}_{[n-d] \times [n-d]} \end{bmatrix} ,\end{align*} $$
where
![]() $H_1$
is a
$H_1$
is a
![]() $(n-d) \times d$
random matrix with whose entries are i.i.d. copies of
$(n-d) \times d$
random matrix with whose entries are i.i.d. copies of
![]() $\tilde {\zeta } Z_\nu $
. Let
$\tilde {\zeta } Z_\nu $
. Let
![]() $H_2$
be an independent copy of
$H_2$
be an independent copy of
![]() $H_1$
, and define H to be the
$H_1$
, and define H to be the
![]() $ (n-d) \times 2d $
matrix
$ (n-d) \times 2d $
matrix
For a vector
![]() $X \in \mathbb {R}^n$
, we define the events
$X \in \mathbb {R}^n$
, we define the events
![]() $\mathcal {A}_1 = \mathcal {A}_1(X)$
and
$\mathcal {A}_1 = \mathcal {A}_1(X)$
and
![]() $\mathcal {A}_2 = \mathcal {A}_2(X)$
by
$\mathcal {A}_2 = \mathcal {A}_2(X)$
by
 $$ \begin{align*} \mathcal{A}_1 &:= \left\{ H : \|H_1 X_{[d]}\|_2\leqslant n \text{ and } \|H_{2} X_{[d]}\|_2\leqslant n \right\} \\ \mathcal{A}_2 &:= \left\{ H : \|H^T X_{[d+1,n]}\|_2\leqslant 2n \right\}\,. \end{align*} $$
$$ \begin{align*} \mathcal{A}_1 &:= \left\{ H : \|H_1 X_{[d]}\|_2\leqslant n \text{ and } \|H_{2} X_{[d]}\|_2\leqslant n \right\} \\ \mathcal{A}_2 &:= \left\{ H : \|H^T X_{[d+1,n]}\|_2\leqslant 2n \right\}\,. \end{align*} $$
We now note a simple bound on
![]() $\mathbb {P}_M(\|MX\|_2 \leqslant n)$
in terms of
$\mathbb {P}_M(\|MX\|_2 \leqslant n)$
in terms of
![]() $\mathcal {A}_1$
and
$\mathcal {A}_1$
and
![]() $\mathcal {A}_2$
.
$\mathcal {A}_2$
.
Fact VIII.5. For
![]() $X \in \mathbb {R}^n$
, let
$X \in \mathbb {R}^n$
, let
![]() $\mathcal {A}_1 =\mathcal {A}_1(X)$
,
$\mathcal {A}_1 =\mathcal {A}_1(X)$
,
![]() $\mathcal {A}_2 = \mathcal {A}_2(X)$
be as above. We have
$\mathcal {A}_2 = \mathcal {A}_2(X)$
be as above. We have
This fact is a straightforward consequence of Fubini’s theorem, the details of which are in [Reference Campos, Jenssen, Michelen and Sahasrabudhe4, Fact 7.7]. We shall also need the “robust” notion of the rank of the matrix H used in [Reference Campos, Jenssen, Michelen and Sahasrabudhe4]: for
![]() $k = 0,\ldots ,2k$
, define
$k = 0,\ldots ,2k$
, define
![]() $\mathcal {E}_k$
to be the event
$\mathcal {E}_k$
to be the event
and note that always at least one of the events
![]() $\mathcal {E}_0,\ldots ,\mathcal {E}_{2d}$
holds.
$\mathcal {E}_0,\ldots ,\mathcal {E}_{2d}$
holds.
We now define
and for a given box
![]() $\mathcal {B}$
, we define the set of typical vectors
$\mathcal {B}$
, we define the set of typical vectors
![]() $T(\mathcal {B}) \subseteq \mathcal {B}$
by
$T(\mathcal {B}) \subseteq \mathcal {B}$
by
Now, set
![]() $K:=2^{10}B^2$
and note the following implication of Lemma VIII.3: if X is chosen uniformly from
$K:=2^{10}B^2$
and note the following implication of Lemma VIII.3: if X is chosen uniformly from
![]() $\mathcal {B}$
and
$\mathcal {B}$
and
![]() $n \geqslant L^{64/c_0^2}\geqslant 2^{10}B^2/\alpha $
, then we have that
$n \geqslant L^{64/c_0^2}\geqslant 2^{10}B^2/\alpha $
, then we have that
 $$ \begin{align} \mathbb{P}_X(X\not \in T)=\mathbb{P}_X(D_{\alpha}(c_0 X_{[d]}/(32\sqrt{n})) \leqslant 2^{10}B^2)\leqslant \left(2^{33}L^{-8n/d}\right)^{d/4}\leqslant \left(\frac{2}{L}\right)^{2n}. \end{align} $$
$$ \begin{align} \mathbb{P}_X(X\not \in T)=\mathbb{P}_X(D_{\alpha}(c_0 X_{[d]}/(32\sqrt{n})) \leqslant 2^{10}B^2)\leqslant \left(2^{33}L^{-8n/d}\right)^{d/4}\leqslant \left(\frac{2}{L}\right)^{2n}. \end{align} $$
Proof of Lemma VIII.2.
Let M,
![]() $H_1,H_2$
, H,
$H_1,H_2$
, H,
![]() $\mathcal {A}_1,\mathcal {A}_2$
,
$\mathcal {A}_1,\mathcal {A}_2$
,
![]() $\mathcal {E}_k$
,
$\mathcal {E}_k$
,
![]() $\alpha $
, and
$\alpha $
, and
![]() $T := T(\mathcal {B})$
be as above. Define
$T := T(\mathcal {B})$
be as above. Define
and bound
For each X, define
and apply (VIII.3) to bound
where the last inequality follows from Markov’s inequality. Thus, in order to prove Lemma VIII.2, it is enough to prove
![]() $\mathbb {E}_X\, f(X)^2 \leqslant 2(R/N)^{2n}$
.
$\mathbb {E}_X\, f(X)^2 \leqslant 2(R/N)^{2n}$
.
Apply Fact VIII.5 to write
 $$ \begin{align} \mathbb{P}_M(\|M X \|_2 \leqslant n)^2 \leqslant \mathbb{P}_H(\mathcal{A}_1 \cap \mathcal{A}_2) = \sum_{k=0}^d \mathbb{P}_H( \mathcal{A}_2 | \mathcal{A}_1 \cap \mathcal{E}_k)\mathbb{P}_H(\mathcal{A}_1 \cap \mathcal{E}_k) \end{align} $$
$$ \begin{align} \mathbb{P}_M(\|M X \|_2 \leqslant n)^2 \leqslant \mathbb{P}_H(\mathcal{A}_1 \cap \mathcal{A}_2) = \sum_{k=0}^d \mathbb{P}_H( \mathcal{A}_2 | \mathcal{A}_1 \cap \mathcal{E}_k)\mathbb{P}_H(\mathcal{A}_1 \cap \mathcal{E}_k) \end{align} $$
and so
 $$ \begin{align} f(X)^2 \leqslant \sum_{k=0}^d \mathbb{P}_H( \mathcal{A}_2 | \mathcal{A}_1 \cap \mathcal{E}_k)\mathbb{P}_H(\mathcal{A}_1 \cap \mathcal{E}_k){\mathbf{1}}( X \in T). \end{align} $$
$$ \begin{align} f(X)^2 \leqslant \sum_{k=0}^d \mathbb{P}_H( \mathcal{A}_2 | \mathcal{A}_1 \cap \mathcal{E}_k)\mathbb{P}_H(\mathcal{A}_1 \cap \mathcal{E}_k){\mathbf{1}}( X \in T). \end{align} $$
We will now apply Theorem VII.1 to upper bound
![]() $\mathbb {P}_H(\mathcal {A}_1 \cap \mathcal {E}_k)$
for
$\mathbb {P}_H(\mathcal {A}_1 \cap \mathcal {E}_k)$
for
![]() $X \in T$
. For this, note that
$X \in T$
. For this, note that
![]() $d\leqslant c_0^2 n$
,
$d\leqslant c_0^2 n$
,
![]() $N\leqslant \exp (c_0L^{-8n/d}d)\leqslant \exp (2^{-32}B^{-4}\alpha n)$
and set
$N\leqslant \exp (c_0L^{-8n/d}d)\leqslant \exp (2^{-32}B^{-4}\alpha n)$
and set
![]() $R_0 := 2^{43}B^2c_0^{-3}$
. Also note that by the definition of a
$R_0 := 2^{43}B^2c_0^{-3}$
. Also note that by the definition of a
![]() $(N,\kappa ,d)$
-box and the fact that
$(N,\kappa ,d)$
-box and the fact that
![]() $d\geqslant \frac {1}{4}c_0^2 n$
, we have that
$d\geqslant \frac {1}{4}c_0^2 n$
, we have that
![]() $\|X_{[d]}\|_2 \geqslant d^{1/2}N \geqslant c_02^{-10}\sqrt {n}N$
. Now, set
$\|X_{[d]}\|_2 \geqslant d^{1/2}N \geqslant c_02^{-10}\sqrt {n}N$
. Now, set
![]() $\alpha ':=2^{-32}B^{-4}\alpha $
and apply Theorem VII.1 to see that for
$\alpha ':=2^{-32}B^{-4}\alpha $
and apply Theorem VII.1 to see that for
![]() $X \in T$
and
$X \in T$
and
![]() $0\leqslant k \leqslant \alpha ' d$
, we have
$0\leqslant k \leqslant \alpha ' d$
, we have
 $$ \begin{align*} \mathbb{P}_H(\mathcal{A}_1 \cap \mathcal{E}_k ) \leqslant e^{-c_0 n k/3}\left(\frac{R_0}{N} \right)^{2n-2d}\,. \end{align*} $$
$$ \begin{align*} \mathbb{P}_H(\mathcal{A}_1 \cap \mathcal{E}_k ) \leqslant e^{-c_0 n k/3}\left(\frac{R_0}{N} \right)^{2n-2d}\,. \end{align*} $$
Additionally, by Theorem VII.1, we may bound the tail sum:
Thus, for all
![]() $X \in \mathcal {B}$
, the previous two equations bound
$X \in \mathcal {B}$
, the previous two equations bound
 $$ \begin{align} f(X)^2 \leqslant \sum_{k = 0}^{\alpha' d} \mathbb{P}_H(\mathcal{A}_2 \,|\, \mathcal{A}_1 \cap \mathcal{E}_k)e^{-c_0 n k/3}\left(\frac{R_0}{N}\right)^{2n-2d} + e^{-c_0 \alpha' dn/3}\,. \end{align} $$
$$ \begin{align} f(X)^2 \leqslant \sum_{k = 0}^{\alpha' d} \mathbb{P}_H(\mathcal{A}_2 \,|\, \mathcal{A}_1 \cap \mathcal{E}_k)e^{-c_0 n k/3}\left(\frac{R_0}{N}\right)^{2n-2d} + e^{-c_0 \alpha' dn/3}\,. \end{align} $$
Seeking to bound the right-hand side of (VIII.7), define
![]() $g_k(X) := \mathbb {P}_H(\mathcal {A}_2 \,|\,\mathcal {A}_1 \cap \mathcal {E}_k)$
. Write
$g_k(X) := \mathbb {P}_H(\mathcal {A}_2 \,|\,\mathcal {A}_1 \cap \mathcal {E}_k)$
. Write
Let
![]() $k \leqslant \alpha 'd$
. Note that each
$k \leqslant \alpha 'd$
. Note that each
![]() $H \in \mathcal {A}_1 \cap \mathcal {E}_k$
has
$H \in \mathcal {A}_1 \cap \mathcal {E}_k$
has
![]() $\sigma _{2d-k}(H) \geqslant c_0 \sqrt {n}/16$
, and thus we may apply Lemma VIII.4 to bound
$\sigma _{2d-k}(H) \geqslant c_0 \sqrt {n}/16$
, and thus we may apply Lemma VIII.4 to bound
 $$ \begin{align*} \mathbb{E}_{X_{[d+1,n]}}\, {\mathbf{1}}[\mathcal{A}_2] = \mathbb{P}_{X_{[d+1,n]}}( \|H^T X_{[d+1,n]} \|_2 \leqslant n ) \leqslant \left(\frac{C'n}{c_0 d N}\right)^{2d - k} \leqslant \left(\frac{4C'}{c_0^3 N}\right)^{2d - k} \end{align*} $$
$$ \begin{align*} \mathbb{E}_{X_{[d+1,n]}}\, {\mathbf{1}}[\mathcal{A}_2] = \mathbb{P}_{X_{[d+1,n]}}( \|H^T X_{[d+1,n]} \|_2 \leqslant n ) \leqslant \left(\frac{C'n}{c_0 d N}\right)^{2d - k} \leqslant \left(\frac{4C'}{c_0^3 N}\right)^{2d - k} \end{align*} $$
for an absolute constant
![]() $C'>0$
, where we used that
$C'>0$
, where we used that
![]() $d\geqslant \frac {1}{4}c_0^2 n$
. Thus, for each
$d\geqslant \frac {1}{4}c_0^2 n$
. Thus, for each
![]() $0\leqslant k \leqslant \alpha ' d$
, if we define
$0\leqslant k \leqslant \alpha ' d$
, if we define
![]() $R := \max \{ 8C' c_0^{-3}, 2R_0\} $
, then we have
$R := \max \{ 8C' c_0^{-3}, 2R_0\} $
, then we have
 $$ \begin{align} \mathbb{E}_X[ g_k(X) ] \leqslant \left(\frac{R}{2N}\right)^{2d - k}\,. \end{align} $$
$$ \begin{align} \mathbb{E}_X[ g_k(X) ] \leqslant \left(\frac{R}{2N}\right)^{2d - k}\,. \end{align} $$
Applying
![]() $\mathbb {E}_X$
to (VIII.7) using (VIII.8) shows
$\mathbb {E}_X$
to (VIII.7) using (VIII.8) shows
 $$ \begin{align*} \mathbb{E}_X f(X)^2 \leqslant \left(\frac{R}{2N}\right)^{2n} \sum_{k=0}^{\alpha' d} \left(\frac{2N}{R}\right)^k e^{-c_0nk/3} + e^{-c_0 \alpha' dn/3}\,. \end{align*} $$
$$ \begin{align*} \mathbb{E}_X f(X)^2 \leqslant \left(\frac{R}{2N}\right)^{2n} \sum_{k=0}^{\alpha' d} \left(\frac{2N}{R}\right)^k e^{-c_0nk/3} + e^{-c_0 \alpha' dn/3}\,. \end{align*} $$
Using that
![]() $N\leqslant e^{c_0L^{-8n/d} d}= e^{c_0\alpha ' d/8}$
and
$N\leqslant e^{c_0L^{-8n/d} d}= e^{c_0\alpha ' d/8}$
and
![]() $N \leqslant e^{c_0 n /3}$
bounds
$N \leqslant e^{c_0 n /3}$
bounds
 $$ \begin{align} \mathbb{E}_X\, f(X)^2 \leqslant 2 \left(\frac{R}{2N}\right)^{2n}. \end{align} $$
$$ \begin{align} \mathbb{E}_X\, f(X)^2 \leqslant 2 \left(\frac{R}{2N}\right)^{2n}. \end{align} $$
Combining (VIII.9) with (VIII.4) completes the proof of Lemma VIII.2.
VIII.3 Proof of Theorem III.2
The main work of proving Theorem III.2 is now complete with the proof of Lemma VIII.2. In order to complete it, we need to cover the sphere with a suitable set of boxes. Recall the definitions from Section III.1:
and
and that the constants
![]() ${\kappa }_0,{\kappa }_1$
satisfy
${\kappa }_0,{\kappa }_1$
satisfy
![]() $0 < {\kappa }_0 < 1 < {\kappa }_1$
and are defined in Section II.3.
$0 < {\kappa }_0 < 1 < {\kappa }_1$
and are defined in Section II.3.
We import the following simple covering lemma from [Reference Campos, Jenssen, Michelen and Sahasrabudhe4, Lemma 7.8]
Lemma VIII.6. For all
![]() $\varepsilon \in [0,1]$
,
$\varepsilon \in [0,1]$
,
![]() ${\kappa } \geqslant \max \{{\kappa }_1/{\kappa }_0,2^8 \kappa _0^{-4} \}$
, there exists a family
${\kappa } \geqslant \max \{{\kappa }_1/{\kappa }_0,2^8 \kappa _0^{-4} \}$
, there exists a family
![]() $\mathcal {F} $
of
$\mathcal {F} $
of
![]() $(N,{\kappa },d)$
-boxes with
$(N,{\kappa },d)$
-boxes with
![]() $|\mathcal {F}| \leqslant {\kappa }^n$
so that
$|\mathcal {F}| \leqslant {\kappa }^n$
so that
where
![]() $N = {\kappa }_{0}/(4\varepsilon )$
.
$N = {\kappa }_{0}/(4\varepsilon )$
.
Combining Lemma VIII.6 with Lemma VIII.2 will imply Theorem III.2.
Proof of Theorem III.2.
Apply Lemma VIII.6 with
![]() $\kappa = \max \{{\kappa }_1/{\kappa }_0,2^8 \kappa _0^{-4} \}$
and use the fact that
$\kappa = \max \{{\kappa }_1/{\kappa }_0,2^8 \kappa _0^{-4} \}$
and use the fact that
![]() $\mathcal {N}_{\varepsilon } \subseteq \Lambda _{\varepsilon }$
to write
$\mathcal {N}_{\varepsilon } \subseteq \Lambda _{\varepsilon }$
to write
and so
Rescaling by
![]() $\sqrt {n}/(4\varepsilon )$
and applying Lemma VIII.2 bound
$\sqrt {n}/(4\varepsilon )$
and applying Lemma VIII.2 bound
 $$ \begin{align*} | (4\varepsilon n^{-1/2} \cdot \mathcal B ) \cap \mathcal N_{\varepsilon}| \leqslant \left| \left\{ X \in \mathcal{B} : \mathbb{P}_M(\|MX\|_2\leqslant n) \geqslant (L\varepsilon)^n \right\} \right| \leqslant \left(\frac{R}{L} \right)^{2n} |\mathcal{B}|. \end{align*} $$
$$ \begin{align*} | (4\varepsilon n^{-1/2} \cdot \mathcal B ) \cap \mathcal N_{\varepsilon}| \leqslant \left| \left\{ X \in \mathcal{B} : \mathbb{P}_M(\|MX\|_2\leqslant n) \geqslant (L\varepsilon)^n \right\} \right| \leqslant \left(\frac{R}{L} \right)^{2n} |\mathcal{B}|. \end{align*} $$
To see that the application of Lemma VIII.2 is justified, note that
![]() $0 < c_0 \leqslant 2^{-50}B^{-4}$
,
$0 < c_0 \leqslant 2^{-50}B^{-4}$
,
![]() $c_0^2 n/2 \leqslant d \leqslant c_0^2 n$
,
$c_0^2 n/2 \leqslant d \leqslant c_0^2 n$
,
![]() ${\kappa } \geqslant 2$
, and
${\kappa } \geqslant 2$
, and
![]() $\log 1/\varepsilon \leqslant n/L^{64/c_0^2}$
and so
$\log 1/\varepsilon \leqslant n/L^{64/c_0^2}$
and so
as required by Lemma VIII.2, since
![]() ${\kappa }_0<1$
,
${\kappa }_0<1$
,
![]() $d\geqslant L^{-1/c_0^2}n$
,
$d\geqslant L^{-1/c_0^2}n$
,
![]() $c_0\geqslant L^{-1/c_0^2}$
, and
$c_0\geqslant L^{-1/c_0^2}$
, and
![]() $8n/d\leqslant 16/c_0^2$
. Using that
$8n/d\leqslant 16/c_0^2$
. Using that
![]() $|\mathcal {F}| \leqslant {\kappa }^{n}$
and
$|\mathcal {F}| \leqslant {\kappa }^{n}$
and
![]() $|\mathcal {B}| \leqslant ({\kappa } N)^n$
for each
$|\mathcal {B}| \leqslant ({\kappa } N)^n$
for each
![]() $\mathcal {B} \in \mathcal {F}$
bound
$\mathcal {B} \in \mathcal {F}$
bound
 $$ \begin{align*} |\mathcal{N}_{\varepsilon}| \leqslant {\kappa}^{n} \left(\frac{R}{L} \right)^{2n} |\mathcal B| \leqslant {\kappa}^{n}\left(\frac{R}{L} \right)^{2n} ({\kappa} N)^n \leqslant \left(\frac{C}{c_0^6L^2\varepsilon}\right)^{n}, \end{align*} $$
$$ \begin{align*} |\mathcal{N}_{\varepsilon}| \leqslant {\kappa}^{n} \left(\frac{R}{L} \right)^{2n} |\mathcal B| \leqslant {\kappa}^{n}\left(\frac{R}{L} \right)^{2n} ({\kappa} N)^n \leqslant \left(\frac{C}{c_0^6L^2\varepsilon}\right)^{n}, \end{align*} $$
where we set
![]() $C:=\kappa ^2 R^2c_0^{6}$
. This completes the proof of Theorem III.2.
$C:=\kappa ^2 R^2c_0^{6}$
. This completes the proof of Theorem III.2.
IX Nets for structured vectors: Approximating with the net
In this section, we prove Lemma III.1, which tells us that
![]() $\mathcal {N}_{\varepsilon }$
is a net for
$\mathcal {N}_{\varepsilon }$
is a net for
![]() $\Sigma _{\varepsilon }$
. The proof uses the random rounding technique developed by Livshyts [Reference Livshyts21] in the same way as in [Reference Campos, Jenssen, Michelen and Sahasrabudhe4].
$\Sigma _{\varepsilon }$
. The proof uses the random rounding technique developed by Livshyts [Reference Livshyts21] in the same way as in [Reference Campos, Jenssen, Michelen and Sahasrabudhe4].
Proof of Lemma III.1.
Given
![]() $v \in \Sigma _{\varepsilon }$
, we define a random variable
$v \in \Sigma _{\varepsilon }$
, we define a random variable
![]() $r = (r_1,\ldots ,r_n)$
, where the
$r = (r_1,\ldots ,r_n)$
, where the
![]() $r_i$
are independent and satisfy
$r_i$
are independent and satisfy
![]() $\mathbb {E}\,r_i = 0 $
as well as the deterministic properties
$\mathbb {E}\,r_i = 0 $
as well as the deterministic properties
![]() $|r_i| \leqslant 4\varepsilon n^{-1/2}$
and
$|r_i| \leqslant 4\varepsilon n^{-1/2}$
and
![]() $v - r\in 4 \varepsilon n^{-1/2} \mathbb {Z}^n$
. We then define the random variable
$v - r\in 4 \varepsilon n^{-1/2} \mathbb {Z}^n$
. We then define the random variable
![]() $u := v - r$
. We will show that with positive probability that
$u := v - r$
. We will show that with positive probability that
![]() $u\in \mathcal {N}_{\varepsilon }$
.
$u\in \mathcal {N}_{\varepsilon }$
.
By definition,
![]() $\|r\|_{\infty } = \|u - v\|_{\infty } \leqslant 4\varepsilon n^{-1/2}$
for all u. Also,
$\|r\|_{\infty } = \|u - v\|_{\infty } \leqslant 4\varepsilon n^{-1/2}$
for all u. Also,
![]() $u \in \mathcal {I}'([d])$
for all u, since
$u \in \mathcal {I}'([d])$
for all u, since
![]() $v \in \mathcal {I}([d])$
and
$v \in \mathcal {I}([d])$
and
![]() $\|u-v\|_{\infty } \leqslant 4\varepsilon /\sqrt {n} \leqslant {\kappa }_0/(2\sqrt {n})$
. Thus, from the definition of
$\|u-v\|_{\infty } \leqslant 4\varepsilon /\sqrt {n} \leqslant {\kappa }_0/(2\sqrt {n})$
. Thus, from the definition of
![]() $\mathcal {N}_{\varepsilon }$
, we need only show that with positive probability u satisfies
$\mathcal {N}_{\varepsilon }$
, we need only show that with positive probability u satisfies
We first show that all u satisfy the upper bound at (IX.1). To see this, recall
![]() $\mathcal {K} = \{\|A\|_{\text {op}}\leqslant 4\sqrt {n} \}$
and let
$\mathcal {K} = \{\|A\|_{\text {op}}\leqslant 4\sqrt {n} \}$
and let
![]() $w(u) \in \mathbb {R}^n$
be such that
$w(u) \in \mathbb {R}^n$
be such that
 $$ \begin{align*} \mathcal{L}_{A,op}(u,\varepsilon \sqrt{n}) &= \mathbb{P}^{\mathcal{K}}\left( \|Av - Ar - w(u)\| \leqslant \varepsilon \sqrt{n} \right) \\ &\leqslant \mathbb{P}^{\mathcal{K}}\left( \|Av - w(u)\| \leqslant 17\varepsilon \sqrt{n} \right) \\ &\leqslant \mathcal{L}_{A,op}(v,17\varepsilon\sqrt{n} ) \leqslant \mathcal{L}(Av, 17\varepsilon\sqrt{n}). \end{align*} $$
$$ \begin{align*} \mathcal{L}_{A,op}(u,\varepsilon \sqrt{n}) &= \mathbb{P}^{\mathcal{K}}\left( \|Av - Ar - w(u)\| \leqslant \varepsilon \sqrt{n} \right) \\ &\leqslant \mathbb{P}^{\mathcal{K}}\left( \|Av - w(u)\| \leqslant 17\varepsilon \sqrt{n} \right) \\ &\leqslant \mathcal{L}_{A,op}(v,17\varepsilon\sqrt{n} ) \leqslant \mathcal{L}(Av, 17\varepsilon\sqrt{n}). \end{align*} $$
Since
![]() $v \in \Sigma _{\varepsilon }$
, Lemma III.7 bounds
$v \in \Sigma _{\varepsilon }$
, Lemma III.7 bounds
We now show that
where the last inequality holds by the fact
![]() $v \in \Sigma _{\varepsilon }$
. From (IX.3), it then follows that there is some
$v \in \Sigma _{\varepsilon }$
. From (IX.3), it then follows that there is some
![]() $u \in \Lambda _{\varepsilon }$
satisfying (IX.1). To prove the first inequality in (IX.1), define the event
$u \in \Lambda _{\varepsilon }$
satisfying (IX.1). To prove the first inequality in (IX.1), define the event
and note that for all u, we have
Since by the Bernstein inequality,
![]() $\mathbb {P}(\|M\|_{\mathrm {HS}}^2\geqslant n^2/16)\leqslant 2\exp (-cn^2)$
and the fact that
$\mathbb {P}(\|M\|_{\mathrm {HS}}^2\geqslant n^2/16)\leqslant 2\exp (-cn^2)$
and the fact that
we have
assuming that
![]() $c_{\Sigma }$
is chosen appropriately small compared to this absolute constant. Thus
$c_{\Sigma }$
is chosen appropriately small compared to this absolute constant. Thus
 $$ \begin{align*} \mathbb{P}_M(\|Mu\|_2\leqslant 4\varepsilon\sqrt{n}) &\geqslant \mathbb{P}_M( \|Mr\|_2 \leqslant 2\varepsilon \sqrt{n} \, \big| \mathcal{E} ) \mathbb{P}( \mathcal{E} ) \\ &\geqslant \left(1 - \mathbb{P}_M( \|Mr\|_2> 2\varepsilon \sqrt{n}\, \big| \mathcal{E} )\right)(1/2)(2L\varepsilon)^n \,. \end{align*} $$
$$ \begin{align*} \mathbb{P}_M(\|Mu\|_2\leqslant 4\varepsilon\sqrt{n}) &\geqslant \mathbb{P}_M( \|Mr\|_2 \leqslant 2\varepsilon \sqrt{n} \, \big| \mathcal{E} ) \mathbb{P}( \mathcal{E} ) \\ &\geqslant \left(1 - \mathbb{P}_M( \|Mr\|_2> 2\varepsilon \sqrt{n}\, \big| \mathcal{E} )\right)(1/2)(2L\varepsilon)^n \,. \end{align*} $$
Taking expectations gives
Exchanging the expectations and rearranging, we see that it is enough to show
We will show that
![]() $\mathbb {P}_r( \|Mr\|_2> 2\varepsilon \sqrt {n}) \leqslant 1/4$
for all
$\mathbb {P}_r( \|Mr\|_2> 2\varepsilon \sqrt {n}) \leqslant 1/4$
for all
![]() $M \in \mathcal {E}$
, by Markov’s inequality. Note that
$M \in \mathcal {E}$
, by Markov’s inequality. Note that
where for the second equality, we have used that the
![]() $r_i$
are mutually independent and
$r_i$
are mutually independent and
![]() $\mathbb {E}\, r_i = 0$
; for the third inequality, we used
$\mathbb {E}\, r_i = 0$
; for the third inequality, we used
![]() $\|r\|_\infty \leqslant 4\varepsilon /\sqrt {n}$
; and for the final inequality, we used
$\|r\|_\infty \leqslant 4\varepsilon /\sqrt {n}$
; and for the final inequality, we used
![]() $\|M\|_{\mathrm {HS}}\leqslant n/4$
. Thus, by Markov’s inequality gives
$\|M\|_{\mathrm {HS}}\leqslant n/4$
. Thus, by Markov’s inequality gives
Putting (IX.5) together with (IX.4) proves (IX.3), completing the proof of (IX.1).
X Proof of Lemma VI.7
We will derive Lemma VI.7 from Talagrand’s inequality:
Theorem X.1 (Talagrand’s inequality).
Let
![]() $F:\mathbb {R}^n \rightarrow \mathbb {R}$
be a convex
$F:\mathbb {R}^n \rightarrow \mathbb {R}$
be a convex
![]() $1$
-Lipschitz function and
$1$
-Lipschitz function and
![]() $\sigma = (\sigma _1,\ldots ,\sigma _n)$
, where the
$\sigma = (\sigma _1,\ldots ,\sigma _n)$
, where the
![]() $\sigma _i$
are i.i.d. random variables, such that
$\sigma _i$
are i.i.d. random variables, such that
![]() $|\sigma _i|\leqslant 1$
. Then for any
$|\sigma _i|\leqslant 1$
. Then for any
![]() $t \geqslant 0$
, we have
$t \geqslant 0$
, we have
where
![]() $m_F$
is the median of
$m_F$
is the median of
![]() $F(\sigma )$
.
$F(\sigma )$
.
Proof of Lemma VI.7.
Note the theorem is trivial if
![]() $k \leqslant 2^{20} B^{4}/\nu $
, so assume that
$k \leqslant 2^{20} B^{4}/\nu $
, so assume that
![]() $k> 2^{20} B^{4}/\nu $
. Set
$k> 2^{20} B^{4}/\nu $
. Set
![]() $\sigma =2^{-4}B^{-2}\tau '$
, define
$\sigma =2^{-4}B^{-2}\tau '$
, define
and note that F is convex and
![]() $1$
-Lipschitz. Since
$1$
-Lipschitz. Since
![]() $|\sigma _i|\leqslant 2^{-4}B^{-2}|\tau _i|\leqslant 1$
and the
$|\sigma _i|\leqslant 2^{-4}B^{-2}|\tau _i|\leqslant 1$
and the
![]() $\sigma _i$
are i.i.d., Theorem X.1 tells us that
$\sigma _i$
are i.i.d., Theorem X.1 tells us that
![]() $F(\sigma )$
is concentrated about the median
$F(\sigma )$
is concentrated about the median
![]() $m_F$
and so we only need to estimate
$m_F$
and so we only need to estimate
![]() $m_F$
. For this, write
$m_F$
. For this, write
and
where for the final inequality, we used that
![]() $\mathbb {E}\, \sigma _i^4\leqslant \mathbb {E}\, \sigma _i^2$
, since
$\mathbb {E}\, \sigma _i^4\leqslant \mathbb {E}\, \sigma _i^2$
, since
![]() $|\sigma _i|\leqslant 1$
. For
$|\sigma _i|\leqslant 1$
. For
![]() $t>0$
, Markov’s inequality bounds
$t>0$
, Markov’s inequality bounds
Setting
![]() $t = \mathbb {E}\, \sigma _i^2\|W\|_{\mathrm {HS}}^2/2$
gives
$t = \mathbb {E}\, \sigma _i^2\|W\|_{\mathrm {HS}}^2/2$
gives
since
![]() $\mathbb {E} \sigma _i^2= 2^{-8}B^{-4}\mathbb {E} \tau _i^{\prime 2}\geqslant 2^{-8}B^{-4} \nu $
and
$\mathbb {E} \sigma _i^2= 2^{-8}B^{-4}\mathbb {E} \tau _i^{\prime 2}\geqslant 2^{-8}B^{-4} \nu $
and
![]() $\|W\|_{\mathrm {HS}}^2\geqslant k/4>2^{11}\nu ^{-1}B^{4}$
(by assumption). It follows that
$\|W\|_{\mathrm {HS}}^2\geqslant k/4>2^{11}\nu ^{-1}B^{4}$
(by assumption). It follows that
since
![]() $\|W\|_{\mathrm {HS}}\geqslant \sqrt {k}/2$
. Now, we may apply Talagrand’s inequality (Theorem X.1) with
$\|W\|_{\mathrm {HS}}\geqslant \sqrt {k}/2$
. Now, we may apply Talagrand’s inequality (Theorem X.1) with
![]() $t=m_F-\beta ' \sqrt {k}\|W\|^{-1}$
to obtain
$t=m_F-\beta ' \sqrt {k}\|W\|^{-1}$
to obtain
as desired.
XI Proof of Theorem 1.4
Here, we deduce Theorem 1.4, which shows negative correlation between a small ball and large deviation event. The proof is similar in theme to those in Section 5 but is, in fact, quite a bit simpler due to the fact we are working with a linear form rather than a quadratic form.
Proof of Theorem 1.4.
We first write
where
![]() ${\lambda } \geqslant 0$
will be optimized later. Now, apply Esseen’s inequality in a similar way to Lemma 5.1 to bound
${\lambda } \geqslant 0$
will be optimized later. Now, apply Esseen’s inequality in a similar way to Lemma 5.1 to bound
 $$ \begin{align} \mathbb{E}\left[{\mathbf{1}}\{|\langle X, v \rangle| \leqslant \varepsilon\} e^{\lambda \langle X, u \rangle - \lambda t} \right] \lesssim \varepsilon e^{-\lambda t} \int_{-1/\varepsilon}^{1/\varepsilon} \left|\mathbb{E} e^{2\pi i \theta \langle X,v\rangle + \lambda \langle X, u\rangle} \right|\,d\theta\,. \end{align} $$
$$ \begin{align} \mathbb{E}\left[{\mathbf{1}}\{|\langle X, v \rangle| \leqslant \varepsilon\} e^{\lambda \langle X, u \rangle - \lambda t} \right] \lesssim \varepsilon e^{-\lambda t} \int_{-1/\varepsilon}^{1/\varepsilon} \left|\mathbb{E} e^{2\pi i \theta \langle X,v\rangle + \lambda \langle X, u\rangle} \right|\,d\theta\,. \end{align} $$
Applying Lemma 5.5 bounds
 $$ \begin{align} \left|\mathbb{E} e^{2\pi i \theta \langle X,v\rangle + \lambda \langle X, u\rangle} \right| \lesssim \exp\left(-c \min_{r \in [1,c^{-1}]} \| \theta r v\|_{\mathbb{T}}^2 + c^{-1}\lambda^2 \right) + e^{-c\alpha n}\,. \end{align} $$
$$ \begin{align} \left|\mathbb{E} e^{2\pi i \theta \langle X,v\rangle + \lambda \langle X, u\rangle} \right| \lesssim \exp\left(-c \min_{r \in [1,c^{-1}]} \| \theta r v\|_{\mathbb{T}}^2 + c^{-1}\lambda^2 \right) + e^{-c\alpha n}\,. \end{align} $$
Combining the lines (XI.1),(XI.2), and (XI.3) and choosing C large enough give the bound
 $$ \begin{align*}\mathbb{P}(|\langle X, v \rangle| \leqslant \varepsilon \text{ and } \langle X,u \rangle> t) &\lesssim \varepsilon e^{-\lambda t + c^{-1}\lambda^2} \int_{-1/\varepsilon}^{1/\varepsilon} \left(e^{- c\gamma^2 \theta^2} + e^{-c\alpha n}\right)\,d\theta \\ &\lesssim \varepsilon e^{-\lambda t + c^{-1}\lambda^2} \gamma^{-1} + e^{-c\alpha n - \lambda t + c^{-1}\lambda^2}\,. \end{align*} $$
$$ \begin{align*}\mathbb{P}(|\langle X, v \rangle| \leqslant \varepsilon \text{ and } \langle X,u \rangle> t) &\lesssim \varepsilon e^{-\lambda t + c^{-1}\lambda^2} \int_{-1/\varepsilon}^{1/\varepsilon} \left(e^{- c\gamma^2 \theta^2} + e^{-c\alpha n}\right)\,d\theta \\ &\lesssim \varepsilon e^{-\lambda t + c^{-1}\lambda^2} \gamma^{-1} + e^{-c\alpha n - \lambda t + c^{-1}\lambda^2}\,. \end{align*} $$
Choosing
![]() $\lambda = ct/2$
completes the proof.
$\lambda = ct/2$
completes the proof.
XII Proof of Lemma 3.2
We deduce the second part of Lemma 3.2 from the following special case of a proposition of Vershynin [Reference Vershynin46, Proposition 4.2].
Proposition XII.1. For
![]() $B>0$
, let
$B>0$
, let
![]() $\zeta \in \Gamma _B$
, let
$\zeta \in \Gamma _B$
, let
![]() $A_n \sim \mathrm {Sym\,}_{n}(\zeta )$
, and let
$A_n \sim \mathrm {Sym\,}_{n}(\zeta )$
, and let
![]() $K \geqslant 1$
. Then there exist
$K \geqslant 1$
. Then there exist
![]() $\rho ,\delta ,c>0$
depending only on
$\rho ,\delta ,c>0$
depending only on
![]() $K, B$
so that for every
$K, B$
so that for every
![]() ${\lambda } \in \mathbb {R}$
and
${\lambda } \in \mathbb {R}$
and
![]() $w\in \mathbb {R}^n$
, we have
$w\in \mathbb {R}^n$
, we have
Proof of Lemma 3.2.
To get the first conclusion of Lemma 3.2, we may assume without loss of generality that
![]() $u\in {\mathbb {S}}^{n-1}$
. So first let
$u\in {\mathbb {S}}^{n-1}$
. So first let
![]() $\mathcal {N}$
be a
$\mathcal {N}$
be a
![]() $c\sqrt {n}$
-net for
$c\sqrt {n}$
-net for
![]() $[-4\sqrt {n},4\sqrt {n}]$
, with
$[-4\sqrt {n},4\sqrt {n}]$
, with
![]() $|\mathcal {N}|\leqslant 8/c$
. Note that
$|\mathcal {N}|\leqslant 8/c$
. Note that
![]() $\mathbb {P}(\|A_n\|_{op}> 4 \sqrt {n})\lesssim e^{-\Omega (n)}$
so if
$\mathbb {P}(\|A_n\|_{op}> 4 \sqrt {n})\lesssim e^{-\Omega (n)}$
so if
![]() $A_nx=tu$
, then we may assume
$A_nx=tu$
, then we may assume
![]() $t\in [-4\sqrt {n},4\sqrt {n}]$
. So
$t\in [-4\sqrt {n},4\sqrt {n}]$
. So
 $$ \begin{align*} \mathbb{P}\big(\exists~x \in \mathrm{Comp\,}(\delta,\rho), \exists t \in [-4\sqrt{n},4\sqrt{n}]& : A_n x= tu \big)\\ \leqslant \sum_{t_0 \in \mathcal{N}}\mathbb{P}&\left(\exists~x \in \mathrm{Comp\,}(\delta,\rho) : \|A_n x-t_0 u\|_2\leqslant c\sqrt{n} \right), \end{align*} $$
$$ \begin{align*} \mathbb{P}\big(\exists~x \in \mathrm{Comp\,}(\delta,\rho), \exists t \in [-4\sqrt{n},4\sqrt{n}]& : A_n x= tu \big)\\ \leqslant \sum_{t_0 \in \mathcal{N}}\mathbb{P}&\left(\exists~x \in \mathrm{Comp\,}(\delta,\rho) : \|A_n x-t_0 u\|_2\leqslant c\sqrt{n} \right), \end{align*} $$
since for each
![]() $t\in [-4\sqrt {n},4\sqrt {n}]$
there’s
$t\in [-4\sqrt {n},4\sqrt {n}]$
there’s
![]() $t_0\in \mathcal {N}$
, such that if
$t_0\in \mathcal {N}$
, such that if
![]() $A_n x=tu$
, then
$A_n x=tu$
, then
![]() $\|A_n x-t_0 u\|_2\leqslant c\sqrt {n}$
. Now to bound each term in the sum, take
$\|A_n x-t_0 u\|_2\leqslant c\sqrt {n}$
. Now to bound each term in the sum, take
![]() $\lambda = 0$
,
$\lambda = 0$
,
![]() $K=4$
,
$K=4$
,
![]() $w=t_0u$
in Proposition XII.1 and notice we may assume
$w=t_0u$
in Proposition XII.1 and notice we may assume
![]() $\|A_n\|_{op}\leqslant 4\sqrt {n}$
again. For the second conclusion, it is sufficient to show
$\|A_n\|_{op}\leqslant 4\sqrt {n}$
again. For the second conclusion, it is sufficient to show
 $$ \begin{align} \begin{aligned} \mathbb{P}\big(\exists~x \in \mathrm{Comp\,}(\delta,\rho), \exists t \in [-4\sqrt{n},4\sqrt{n}] : \|(A_n - tI) x\|_2 &= 0 \text{ and }\|A_n-tI\|_{op} \leqslant 8\sqrt{n}\big)\\ &\qquad\qquad\quad\lesssim e^{-\Omega(n)} \, , \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \mathbb{P}\big(\exists~x \in \mathrm{Comp\,}(\delta,\rho), \exists t \in [-4\sqrt{n},4\sqrt{n}] : \|(A_n - tI) x\|_2 &= 0 \text{ and }\|A_n-tI\|_{op} \leqslant 8\sqrt{n}\big)\\ &\qquad\qquad\quad\lesssim e^{-\Omega(n)} \, , \end{aligned} \end{align} $$
since we have
![]() $\mathbb {P}(\|A_n\|_{op} \geqslant 4\sqrt {n}) \lesssim e^{-\Omega (n)}$
, by (4.11), so we may assume that all eigenvalues of
$\mathbb {P}(\|A_n\|_{op} \geqslant 4\sqrt {n}) \lesssim e^{-\Omega (n)}$
, by (4.11), so we may assume that all eigenvalues of
![]() $A_n$
lie in
$A_n$
lie in
![]() $[-4\sqrt {n},4\sqrt {n}]$
and
$[-4\sqrt {n},4\sqrt {n}]$
and
![]() $\|A_n-tI\|_{op}\leqslant |t|+\|A_n\|_{op}\leqslant 8\sqrt {n}$
, for all
$\|A_n-tI\|_{op}\leqslant |t|+\|A_n\|_{op}\leqslant 8\sqrt {n}$
, for all
![]() $t\in [-4\sqrt {n},4\sqrt {n}]$
.
$t\in [-4\sqrt {n},4\sqrt {n}]$
.
For this, we apply Proposition XII.1 with
![]() $K = 8$
to obtain
$K = 8$
to obtain
![]() $\rho ,\delta ,c$
. Again, let
$\rho ,\delta ,c$
. Again, let
![]() $\mathcal {N}$
be a
$\mathcal {N}$
be a
![]() $c\sqrt {n}$
-net for the interval
$c\sqrt {n}$
-net for the interval
![]() $[-4\sqrt {n},4\sqrt {n}]$
with
$[-4\sqrt {n},4\sqrt {n}]$
with
![]() $|\mathcal {N}| \leqslant 8/c$
. So, if
$|\mathcal {N}| \leqslant 8/c$
. So, if
![]() $t \in [-4\sqrt {n},4\sqrt {n}]$
satisfies
$t \in [-4\sqrt {n},4\sqrt {n}]$
satisfies
![]() $A_nx = tx$
for some
$A_nx = tx$
for some
![]() $x \in {\mathbb {S}}^{n-1}$
, then there is a
$x \in {\mathbb {S}}^{n-1}$
, then there is a
![]() $t_0 \in \mathcal {N}$
with
$t_0 \in \mathcal {N}$
with
![]() $|t - t_0| \leqslant c\sqrt {n}$
and
$|t - t_0| \leqslant c\sqrt {n}$
and
Thus, the left-hand side of (XII.1) s at most
where the last line follows from Proposition XII.1.
Acknowledgments
The authors thank Rob Morris for comments on the presentation of this paper. The authors also thank the anonymous referees for many useful comments and a simplification to the proof of Corollary 8.2. Marcelo Campos is partially supported by Conselho Nacional de Desenvolvimento Científico e Tecnológico. Matthew Jenssen is supported by a UK Research and Innovation Future Leaders Fellowship MR/W007320/1. Marcus Michelen is supported in part by National Science Foundation grants Division of Mathematical Sciences (DMS)-2137623 and DMS-2246624.
Competing interest
The authors have no competing interest to declare.