Hostname: page-component-7dd5485656-s6l46 Total loading time: 0 Render date: 2025-10-30T17:53:32.688Z Has data issue: false hasContentIssue false
  • English
  • Français

EQUIVARIANT 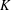$K$ -THEORY OF GRASSMANNIANS

Part of: Special varieties Algebraic combinatorics

Published online by Cambridge University Press:  27 June 2017

OLIVER PECHENIK  and
ALEXANDER YONG
OLIVER PECHENIK
Affiliation:
Department of Mathematics, Rutgers University, Piscataway, NJ 08854, USA; oliver.pechenik@rutgers.edu
ALEXANDER YONG
Affiliation:
Department of Mathematics, University of Illinois at Urbana-Champaign, Urbana, IL 61801, USA; ayong@uiuc.edu

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We address a unification of the Schubert calculus problems solved by Buch [A Littlewood–Richardson rule for the 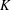$K$ -theory of Grassmannians, Acta Math. 189 (2002), 37–78] and Knutson and Tao [Puzzles and (equivariant) cohomology of Grassmannians, Duke Math. J.119(2) (2003), 221–260]. That is, we prove a combinatorial rule for the structure coefficients in the torus-equivariant 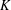$K$ -theory of Grassmannians with respect to the basis of Schubert structure sheaves. This rule is positive in the sense of Anderson et al. [Positivity and Kleiman transversality in equivariant 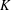$K$ -theory of homogeneous spaces, J. Eur. Math. Soc.13 (2011), 57–84] and in a stronger form. Our work is based on the combinatorics of genomic tableaux and a generalization of Schützenberger’s [Combinatoire et représentation du groupe symétrique, in Actes Table Ronde CNRS, Univ. Louis-Pasteur Strasbourg, Strasbourg, 1976, Lecture Notes in Mathematics, 579 (Springer, Berlin, 1977), 59–113] jeu de taquin. Using our rule, we deduce the two other combinatorial rules for these coefficients. The first is a conjecture of Thomas and Yong [Equivariant Schubert calculus and jeu de taquin, Ann. Inst. Fourier (Grenoble) (2013), to appear]. The second (found in a sequel to this paper) is a puzzle rule, resolving a conjecture of Knutson and Vakil from 2005.

MSC classification

Primary: 14M15: Grassmannians, Schubert varieties, flag manifolds
Secondary: 05E05: Symmetric functions and generalizations 05E15: Combinatorial aspects of groups and algebras

Information

Type
Research Article
Information
Forum of Mathematics, Pi , Volume 5 , 2017 , e3
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2017

References

Anderson, D., Griffeth, S. and Miller, E., ‘Positivity and Kleiman transversality in equivariant K-theory of homogeneous spaces’, J. Eur. Math. Soc. (JEMS) 13 (2011), 57–84.Google Scholar
Brion, M., ‘Lectures on the geometry of flag varieties’, inTopics in Cohomological Studies of Algebraic Varieties, Trends in Mathematics (Birkhäuser, Basel, 2005), 33–85.Google Scholar
Buch, A., ‘A Littlewood–Richardson rule for the K-theory of Grassmannians’, Acta Math. 189 (2002), 37–78.Google Scholar
Buch, A., ‘Mutations of puzzles and equivariant cohomology of two-step flag varieties’, Ann. of Math. (2) 182 (2015), 173–220.Google Scholar
Buch, A., Kresch, A., Purbhoo, K. and Tamvakis, H., ‘The puzzle conjecture for the cohomology of two-step flag manifolds’, J. Algebraic Combin. 44 (2016), 973–1007.Google Scholar
Buch, A., Kresch, A. and Tamvakis, H., ‘Gromov–Witten invariants on Grassmannians’, J. Amer. Math. Soc. 16 (2003), 901–915.Google Scholar
Buch, A. and Mihalcea, L., ‘Quantum K-theory of Grassmannians’, Duke Math. J. 156(3) (2011), 501–538.Google Scholar
Coşkun, I., ‘A Littlewood–Richardson rule for two-step flag varieties’, Invent. Math. 176 (2009), 325–395.Google Scholar
Coşkun, I. and Vakil, R., ‘Geometric positivity in the cohomology of homogeneous spaces and generalized Schubert calculus’, inAlgebraic Geometry—Seattle 2005, Proceedings of Symposia in Pure Mathematics, 80 (American Mathematical Society, Providence, RI, 2009), 77–124, Part 1.Google Scholar
Fulton, W. and Lascoux, A., ‘A Pieri formula in the Grothendieck ring of a flag bundle’, Duke Math. J. 76(3) (1994), 711–729.Google Scholar
Gillespie, M. and Levinson, J., ‘Monodromy and K-theory of Schubert curves via generalized jeu de taquin’, J. Algebraic Combin. 45 (2017), 191–243.Google Scholar
Graham, W., ‘Positivity in equivariant Schubert calculus’, Duke Math. J. 109(3) (2001), 599–614.Google Scholar
Graham, W. and Kumar, S., ‘On positivity in T-equivariant K-theory of flag varieties’, Int. Math. Res. Not. (2008), Art. ID rnn093, 43 pages.Google Scholar
Haglund, J., Luoto, K., Mason, S. and van Willigenburg, S., ‘Refinements of the Littlewood–Richardson rule’, Trans. Amer. Math. Soc. 363 (2011), 1665–1686.Google Scholar
Knutson, A., ‘Puzzles, positroid varieties, and equivariant $K$ -theory of Grassmannians’, Preprint, 2010, arXiv:1008.4302.Google Scholar
Knutson, A., Miller, E. and Yong, A., ‘Gröbner geometry of vertex decompositions and of flagged tableaux’, J. Reine Angew. Math. 630 (2009), 1–31.Google Scholar
Knutson, A. and Tao, T., ‘Puzzles and (equivariant) cohomology of Grassmannians’, Duke Math. J. 119(2) (2003), 221–260.Google Scholar
Kostant, B. and Kumar, S., ‘ T-equivariant K-theory of generalized flag varieties’, J. Differential Geom. 32 (1990), 549–603.Google Scholar
Kreiman, V., ‘Schubert classes in the equivariant $K$ -theory and equivariant cohomology of the Grassmannian’, Preprint, 2005, arXiv:math/0512204.Google Scholar
Lascoux, A. and Schützenberger, M.-P., ‘Structure de Hopf de l’anneau de cohomologie et de l’anneau de Grothendieck d’une variété de drapeaux’, C. R. Acad. Sci. Paris 295 (1982), 629–633.Google Scholar
Lenart, C. and Postnikov, A., ‘Affine Weyl groups in K-theory and representation theory’, Int. Math. Res. Not. IMRN (12) (2007), Art. ID rnm038, 65 pp.Google Scholar
Littlewood, D. E. and Richardson, A. R., ‘Group characters and algebra’, Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 233(721–730) (1934), 99–141.Google Scholar
Molev, A. and Sagan, B., ‘A Littlewood–Richardson rule for factorial Schur functions’, Trans. Amer. Math. Soc. 351(11) (1999), 4429–4443.Google Scholar
Pechenik, O. and Yong, A., ‘Genomic tableaux and combinatorial K-theory’, Discrete Math. Theor. Comput. Sci. Proc. FPSAC‘15 (2015), 37–48. FPSAC 2015, Daejeon, Korea.Google Scholar
Pechenik, O. and Yong, A., ‘Equivariant K-theory of Grassmannians II: The Knutson–Vakil conjecture’, Compos. Math. 153 (2017), 667–677.Google Scholar
Pechenik, O. and Yong, A., ‘Genomic tableaux’, J. Algebraic Combin. 45 (2017), 649–685.Google Scholar
Ross, C. and Yong, A., ‘Combinatorial rules for three bases of polynomials’, Sém. Lothar. Combin. 74 (2015), Art. B74a.Google Scholar
Schützenberger, M.-P., ‘Combinatoire et représentation du groupe symétrique’, inActes Table Ronde CNRS, Univ. Louis-Pasteur Strasbourg, Strasbourg, 1976, Lecture Notes in Mathematics, 579 (Springer, Berlin, 1977), 59–113.Google Scholar
Thomas, H. and Yong, A., ‘A jeu de taquin theory for increasing tableaux, with applications to K-theoretic Schubert calculus’, Algebra Number Theory 3(2) (2009), 121–148.Google Scholar
Thomas, H. and Yong, A., ‘Equivariant Schubert calculus and jeu de taquin’, Ann. Inst. Fourier (Grenoble) (2013), to appear.Google Scholar
Wheeler, M. and Zinn-Justin, P., ‘Littlewood–Richardson coefficients for Grothendieck polynomials from integrability’, Preprint, 2016, arXiv:1607.02396.Google Scholar
Willems, M., ‘ K-théorie équivariante des tours de Bott. Application à la structure multiplicative de la K-théorie équivariante des variétés de drapeaux’, Duke Math. J. 132(2) (2006), 271–309.Google Scholar
Woo, A. and Yong, A., ‘A Gröbner basis for Kazhdan–Lusztig ideals’, Amer. J. Math. 134 (2012), 1089–1137.Google Scholar