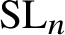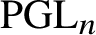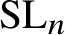0.1 Overview
Throughout, we work over the complex numbers ![]() ${\mathbb {C}}$. Let C be a nonsingular projective curve of genus
${\mathbb {C}}$. Let C be a nonsingular projective curve of genus ![]() $g \geq 2$. Let
$g \geq 2$. Let ![]() $n,d$ be integers with
$n,d$ be integers with ![]() $n>0$ and
$n>0$ and ![]() $\mathrm {gcd}(n,d) = 1$.
$\mathrm {gcd}(n,d) = 1$.
The cohomology of the moduli space  $\widetilde {{\mathcal N}}_{n,d}$ of rank n, degree d stable vector bundles on C has been studied intensively for decades. By [Reference Atiyah and Bott1, Reference Beauville2], the cohomology
$\widetilde {{\mathcal N}}_{n,d}$ of rank n, degree d stable vector bundles on C has been studied intensively for decades. By [Reference Atiyah and Bott1, Reference Beauville2], the cohomology  $H^*\left (\widetilde {{\mathcal N}}_{n,d}, {\mathbb {C}}\right )$ is generated by the tautological classes – the Künneth factors of the Chern characters of a universal family. Relations between the tautological classes were explored in [Reference Earl and Kirwan14, Reference Kirwan27].
$H^*\left (\widetilde {{\mathcal N}}_{n,d}, {\mathbb {C}}\right )$ is generated by the tautological classes – the Künneth factors of the Chern characters of a universal family. Relations between the tautological classes were explored in [Reference Earl and Kirwan14, Reference Kirwan27].
A natural moduli space closely related to  $\widetilde {{\mathcal N}}_{n,d}$ is the moduli of stable
$\widetilde {{\mathcal N}}_{n,d}$ is the moduli of stable ![]() $\mathrm {SL}_n$-bundles
$\mathrm {SL}_n$-bundles
 $$ \begin{align*} {\mathcal N}_{n,L} \subset \widetilde{{\mathcal N}}_{n,d}, \end{align*} $$
$$ \begin{align*} {\mathcal N}_{n,L} \subset \widetilde{{\mathcal N}}_{n,d}, \end{align*} $$which parameterises rank n stable vector bundles with fixed determinant ![]() $L\in \mathrm {Pic}^d(C)$. The finite abelian group
$L\in \mathrm {Pic}^d(C)$. The finite abelian group
acts on ![]() ${\mathcal N}_{n,L}$ via the tensor product, which induces a
${\mathcal N}_{n,L}$ via the tensor product, which induces a ![]() $\Gamma $-action on the cohomology
$\Gamma $-action on the cohomology ![]() $H^*\left ({\mathcal N}_{n,L}, {\mathbb {C}}\right )$. The
$H^*\left ({\mathcal N}_{n,L}, {\mathbb {C}}\right )$. The ![]() $\Gamma $-invariant part
$\Gamma $-invariant part  $H^*\left ({\mathcal N}_{n,L}, {\mathbb {C}}\right )^{\Gamma }$ recovers the cohomology of the quotient
$H^*\left ({\mathcal N}_{n,L}, {\mathbb {C}}\right )^{\Gamma }$ recovers the cohomology of the quotient ![]() ${\mathcal N}_{n,L}/\Gamma $, which can be viewed as the moduli space of stable
${\mathcal N}_{n,L}/\Gamma $, which can be viewed as the moduli space of stable ![]() $\mathrm {PGL}_n$-bundles. The tautological classes associated with a universal family generate the
$\mathrm {PGL}_n$-bundles. The tautological classes associated with a universal family generate the ![]() $\Gamma $-invariant cohomology
$\Gamma $-invariant cohomology  $H^*\left ({\mathcal N}_{n,L}, {\mathbb {C}}\right )^{\Gamma }$.
$H^*\left ({\mathcal N}_{n,L}, {\mathbb {C}}\right )^{\Gamma }$.
The following theorem by Harder and Narasimhan [Reference Harder and Narasimhan19] shows that every class in ![]() $H^*\left ({\mathcal N}_{n,L}, {\mathbb {C}}\right )$ is
$H^*\left ({\mathcal N}_{n,L}, {\mathbb {C}}\right )$ is ![]() $\Gamma $-invariant:
$\Gamma $-invariant:
Theorem 0.1 Harder and Narasimhan [Reference Harder and Narasimhan19]
The ![]() $\Gamma $-action on
$\Gamma $-action on ![]() $H^*\left ({\mathcal N}_{n,L}, {\mathbb {C}}\right )$ is trivial.
$H^*\left ({\mathcal N}_{n,L}, {\mathbb {C}}\right )$ is trivial.
As a consequence of Theorem 0.1, we obtain immediately that the tautological classes generate the total cohomology ![]() $H^*\left ({\mathcal N}_{n,L}, {\mathbb {C}}\right )$.
$H^*\left ({\mathcal N}_{n,L}, {\mathbb {C}}\right )$.
The purpose of this paper is to study the ![]() $\Gamma $-action on the cohomology of the moduli space of stable
$\Gamma $-action on the cohomology of the moduli space of stable ![]() $\mathrm {SL}_n$-Higgs bundles from the viewpoint of the Hausel–Thaddeus conjecture [Reference Hausel and Thaddeus22]. We denote by
$\mathrm {SL}_n$-Higgs bundles from the viewpoint of the Hausel–Thaddeus conjecture [Reference Hausel and Thaddeus22]. We denote by ![]() ${\mathcal M}_{n,L}$ the (coarse) moduli space parameterising stable Higgs bundles
${\mathcal M}_{n,L}$ the (coarse) moduli space parameterising stable Higgs bundles
on the curve C. It is a nonsingular quasi-projective variety admitting a natural hyper-Kähler structure [Reference Hitchin25, Reference Nitsure34]. As in the case of vector bundles, the group ![]() $\Gamma $ acts on
$\Gamma $ acts on ![]() ${\mathcal M}_{n,L}$ via the tensor product
${\mathcal M}_{n,L}$ via the tensor product
The induced ![]() $\Gamma $-action on
$\Gamma $-action on ![]() $H^*\left ({\mathcal M}_{n,L}, {\mathbb {C}}\right )$ yields the following canonical decomposition:
$H^*\left ({\mathcal M}_{n,L}, {\mathbb {C}}\right )$ yields the following canonical decomposition:
 $$ \begin{align} H^*\left({\mathcal M}_{n,L}, {\mathbb{C}}\right) = H^*\left({\mathcal M}_{n,L}/\Gamma, {\mathbb{C}}\right) \oplus \bigoplus_{\kappa \neq 0} H^*\left({\mathcal M}_{n,L}, {\mathbb{C}}\right)_{\kappa}, \end{align} $$
$$ \begin{align} H^*\left({\mathcal M}_{n,L}, {\mathbb{C}}\right) = H^*\left({\mathcal M}_{n,L}/\Gamma, {\mathbb{C}}\right) \oplus \bigoplus_{\kappa \neq 0} H^*\left({\mathcal M}_{n,L}, {\mathbb{C}}\right)_{\kappa}, \end{align} $$where ![]() $\kappa \in \hat {\Gamma }= \mathrm {Hom}(\Gamma , {\mathbb {C}}^*)$ runs through all nontrivial characters of
$\kappa \in \hat {\Gamma }= \mathrm {Hom}(\Gamma , {\mathbb {C}}^*)$ runs through all nontrivial characters of ![]() $\Gamma $ and
$\Gamma $ and  $H^*\left ({\mathcal M}_{n,L}, {\mathbb {C}}\right )_{\kappa }$ denotes the
$H^*\left ({\mathcal M}_{n,L}, {\mathbb {C}}\right )_{\kappa }$ denotes the ![]() $\kappa $-isotypic component. By [Reference Markman30] (and [Reference de Cataldo, Maulik and Shen9, (70)]), the tautological classes associated with a universal family of
$\kappa $-isotypic component. By [Reference Markman30] (and [Reference de Cataldo, Maulik and Shen9, (70)]), the tautological classes associated with a universal family of ![]() ${\mathcal M}_{n,L}$ generate the
${\mathcal M}_{n,L}$ generate the ![]() $\Gamma $-invariant cohomology
$\Gamma $-invariant cohomology
 $$ \begin{align*} H^*\left({\mathcal M}_{n,L}/\Gamma, {\mathbb{C}}\right) = H^*\left({\mathcal M}_{n,L}, {\mathbb{C}}\right)^{\Gamma}. \end{align*} $$
$$ \begin{align*} H^*\left({\mathcal M}_{n,L}/\Gamma, {\mathbb{C}}\right) = H^*\left({\mathcal M}_{n,L}, {\mathbb{C}}\right)^{\Gamma}. \end{align*} $$However, contrary to Theorem 0.1, the ![]() $\Gamma $-variant part of equation (1) is nontrivial and carries a rich structure, predicted by topological mirror symmetry [Reference Hausel and Thaddeus22].
$\Gamma $-variant part of equation (1) is nontrivial and carries a rich structure, predicted by topological mirror symmetry [Reference Hausel and Thaddeus22].
In this paper, we focus on the structure of  $H^*\left ({\mathcal M}_{n,L}, {\mathbb {C}}\right )_{\kappa }$ for
$H^*\left ({\mathcal M}_{n,L}, {\mathbb {C}}\right )_{\kappa }$ for ![]() $\kappa \neq 0$. We introduce natural operators which determine
$\kappa \neq 0$. We introduce natural operators which determine  $H^*\left ({\mathcal M}_{n,L}, {\mathbb {C}}\right )_{\kappa }$ in terms of the cohomology of the moduli space of stable
$H^*\left ({\mathcal M}_{n,L}, {\mathbb {C}}\right )_{\kappa }$ in terms of the cohomology of the moduli space of stable ![]() $\mathrm {GL}_r$-Higgs bundles on a certain curve for some
$\mathrm {GL}_r$-Higgs bundles on a certain curve for some ![]() $r\leq n$. These operators respect the perverse and Hodge filtrations, and upon specialisation to Hodge polynomials, they recover the Hausel–Thaddeus conjecture [Reference Hausel and Thaddeus22]. In particular, this gives a new proof using perverse sheaves of the topological mirror symmetry conjecture of Hausel and Thaddeus, which was recently proven using p-adic integration [Reference Groechenig, Wyss and Ziegler17].
$r\leq n$. These operators respect the perverse and Hodge filtrations, and upon specialisation to Hodge polynomials, they recover the Hausel–Thaddeus conjecture [Reference Hausel and Thaddeus22]. In particular, this gives a new proof using perverse sheaves of the topological mirror symmetry conjecture of Hausel and Thaddeus, which was recently proven using p-adic integration [Reference Groechenig, Wyss and Ziegler17].
0.2 Hitchin fibrations
The moduli space ![]() ${\mathcal M}_{n,L}$ carries a Lagrangian fibration
${\mathcal M}_{n,L}$ carries a Lagrangian fibration
 $$ \begin{align} h: {\mathcal M}_{n,L} \rightarrow {\mathcal A} = \bigoplus_{i\geq 2} H^0\left(C, {\Omega_{C}^{\otimes i}}\right), \end{align} $$
$$ \begin{align} h: {\mathcal M}_{n,L} \rightarrow {\mathcal A} = \bigoplus_{i\geq 2} H^0\left(C, {\Omega_{C}^{\otimes i}}\right), \end{align} $$given by Hitchin’s integrable system, which is now referred to as the Hitchin fibration. The ![]() $\Gamma $-action on
$\Gamma $-action on ![]() ${\mathcal M}_{n,L}$ is fibrewise with respect to equation (2). There are two types of moduli spaces closely related to the cohomological study of
${\mathcal M}_{n,L}$ is fibrewise with respect to equation (2). There are two types of moduli spaces closely related to the cohomological study of ![]() ${\mathcal M}_{n,L}$, from the perspectives of mirror symmetry [Reference Hausel and Thaddeus22] and representation theory [Reference Ngô32, Reference Ngô33].
${\mathcal M}_{n,L}$, from the perspectives of mirror symmetry [Reference Hausel and Thaddeus22] and representation theory [Reference Ngô32, Reference Ngô33].
The moduli spaces of the first type are the fixed loci of an element ![]() $\gamma \in \Gamma $. For any
$\gamma \in \Gamma $. For any ![]() $\gamma \in \Gamma $, we denote by
$\gamma \in \Gamma $, we denote by ![]() ${\mathcal M}_{\gamma } \subset {\mathcal M}_{n,L}$ the
${\mathcal M}_{\gamma } \subset {\mathcal M}_{n,L}$ the ![]() $\gamma $-fixed subvariety, which maps to the Hitchin base via
$\gamma $-fixed subvariety, which maps to the Hitchin base via

The ![]() $\Gamma $-action on
$\Gamma $-action on ![]() ${\mathcal M}_{n,L}$ induces a
${\mathcal M}_{n,L}$ induces a ![]() $\Gamma $-action on
$\Gamma $-action on ![]() ${\mathcal M}_{\gamma }$.
${\mathcal M}_{\gamma }$.
Moduli spaces of the second type are associated with a cyclic Galois cover ![]() $\pi : C' \to C$ of the original curve given by
$\pi : C' \to C$ of the original curve given by ![]() $\gamma \in \Gamma $. We assume
$\gamma \in \Gamma $. We assume ![]() $\mathrm {deg}(\pi ) = \mathrm {ord}(\gamma ) = m$ and
$\mathrm {deg}(\pi ) = \mathrm {ord}(\gamma ) = m$ and ![]() $n=mr$. Let
$n=mr$. Let ![]() ${\mathcal M}_{r,L}(\pi )$ be the moduli space parameterising rank r stable Higgs bundles
${\mathcal M}_{r,L}(\pi )$ be the moduli space parameterising rank r stable Higgs bundles ![]() $({\mathcal E}, \theta )$ on
$({\mathcal E}, \theta )$ on ![]() $C'$ such that
$C'$ such that
It admits a Hitchin fibration
with a fibrewise ![]() $\Gamma $-action; see Section 1 for more details on these moduli spaces. From the viewpoint of representation theory, the moduli spaces
$\Gamma $-action; see Section 1 for more details on these moduli spaces. From the viewpoint of representation theory, the moduli spaces ![]() ${\mathcal M}_{r,L}(\pi )$ are related to the study of the corresponding endoscopic groups for
${\mathcal M}_{r,L}(\pi )$ are related to the study of the corresponding endoscopic groups for ![]() $\mathrm {SL}_n$ over C [Reference Ngô33]. They are nonsingular but disconnected. The Galois group
$\mathrm {SL}_n$ over C [Reference Ngô33]. They are nonsingular but disconnected. The Galois group
acts on both the source ![]() ${\mathcal M}_{r,L}(\pi )$ and the target
${\mathcal M}_{r,L}(\pi )$ and the target ![]() ${\mathcal A}(\pi )$, whose quotients recover
${\mathcal A}(\pi )$, whose quotients recover ![]() ${\mathcal M}_{\gamma }$ and
${\mathcal M}_{\gamma }$ and ![]() ${\mathcal A}_{\gamma }$, respectively. We denote by
${\mathcal A}_{\gamma }$, respectively. We denote by
the quotient map of the base ![]() ${\mathcal A}(\pi )$. We also consider the largest open subset
${\mathcal A}(\pi )$. We also consider the largest open subset ![]() ${\mathcal A}(\pi )^* \subset {\mathcal A}(\pi )$ upon which the
${\mathcal A}(\pi )^* \subset {\mathcal A}(\pi )$ upon which the ![]() $G_{\pi }$-action is free, and set
$G_{\pi }$-action is free, and set ![]() $A_{\gamma }^* := {\mathcal A}(\pi )^*/G_{\pi } \subset A_{\gamma }$.
$A_{\gamma }^* := {\mathcal A}(\pi )^*/G_{\pi } \subset A_{\gamma }$.
0.3 Endoscopic decompositions
In order to understand the decomposition (1) sheaf-theoretically, we consider the canonical decompositions of the direct image complexes
 $$ \begin{align*} \mathrm{Rh}_* {\underline{{\mathbb{C}}}} \in D_c^b({\mathcal A}), \quad {\mathrm{Rh}_{\gamma}}_* {\underline{{\mathbb{C}}}} \in D_c^b\left({\mathcal A}_{\gamma}\right), \quad {\mathrm{Rh}_{\pi}}_* {\underline{{\mathbb{C}}}} \in D_c^b({\mathcal A}(\pi)), \end{align*} $$
$$ \begin{align*} \mathrm{Rh}_* {\underline{{\mathbb{C}}}} \in D_c^b({\mathcal A}), \quad {\mathrm{Rh}_{\gamma}}_* {\underline{{\mathbb{C}}}} \in D_c^b\left({\mathcal A}_{\gamma}\right), \quad {\mathrm{Rh}_{\pi}}_* {\underline{{\mathbb{C}}}} \in D_c^b({\mathcal A}(\pi)), \end{align*} $$into eigen-subcomplexes with respect to the ![]() $\Gamma $-actions. We first clarify some notation before stating the main theorems. Throughout, we use
$\Gamma $-actions. We first clarify some notation before stating the main theorems. Throughout, we use ![]() $D^b_c(-)$ to denote the bounded derived category of constructible sheaves. We say that
$D^b_c(-)$ to denote the bounded derived category of constructible sheaves. We say that ![]() ${\mathcal K} \xrightarrow {\simeq } {\mathcal K}'$ is an isomorphism for two objects in a derived category if it is a quasi-isomorphism between the complexes
${\mathcal K} \xrightarrow {\simeq } {\mathcal K}'$ is an isomorphism for two objects in a derived category if it is a quasi-isomorphism between the complexes ![]() ${\mathcal K}$ and
${\mathcal K}$ and ![]() ${\mathcal K}'$. Given a complex with a
${\mathcal K}'$. Given a complex with a ![]() $\Gamma $-action and a character
$\Gamma $-action and a character ![]() $\kappa \in \hat {\Gamma }$, we denote by
$\kappa \in \hat {\Gamma }$, we denote by ![]() $(-)_{\kappa }$ the
$(-)_{\kappa }$ the ![]() $\kappa $-isotypic component. We call
$\kappa $-isotypic component. We call ![]() $(-)_{\mathrm {st}} = (-)_{0\in \hat {\Gamma }}$ its stable part, which is the subcomplex fixed by the
$(-)_{\mathrm {st}} = (-)_{0\in \hat {\Gamma }}$ its stable part, which is the subcomplex fixed by the ![]() $\Gamma $-action. The Weil pairing identifies canonically the group
$\Gamma $-action. The Weil pairing identifies canonically the group ![]() $\Gamma $ and its dual,
$\Gamma $ and its dual,
(see Section 1.3).
Our first result is the following theorem, which relates the stable part of the endoscopic cohomology with the pullback of the ![]() $\kappa $-isotypic contribution for
$\kappa $-isotypic contribution for ![]() $\mathrm {SL}_n$. This extends the endoscopic decomposition of [Reference Yun39] in the case of
$\mathrm {SL}_n$. This extends the endoscopic decomposition of [Reference Yun39] in the case of ![]() $\mathrm {SL}_n$ from the elliptic locus to a much larger open subset on the Hitchin base.
$\mathrm {SL}_n$ from the elliptic locus to a much larger open subset on the Hitchin base.
Theorem 0.2 Theorem 3.1
Let ![]() $\kappa \in \hat {\Gamma }$ and
$\kappa \in \hat {\Gamma }$ and ![]() $\gamma \in \Gamma $ be identified by equation (3), let
$\gamma \in \Gamma $ be identified by equation (3), let ![]() $\pi :C'\to C$ be the cyclic Galois cover associated with
$\pi :C'\to C$ be the cyclic Galois cover associated with ![]() $\gamma $ and let
$\gamma $ and let ![]() $d_{\gamma } = \mathrm {codim}_{{\mathcal A}}\left ({\mathcal A}_{\gamma }\right )$. There are isomorphisms in
$d_{\gamma } = \mathrm {codim}_{{\mathcal A}}\left ({\mathcal A}_{\gamma }\right )$. There are isomorphisms in ![]() $D^b_c({\mathcal A}(\pi )^*)$ which are canonical up to scaling (see Definition 2.9):
$D^b_c({\mathcal A}(\pi )^*)$ which are canonical up to scaling (see Definition 2.9):
 $$ \begin{align} q_{\mathcal A}^* \left( \mathrm{Rh}_{*} {\underline{{\mathbb{C}}}} \right)_{\kappa}\Big\rvert_{{\mathcal A}(\pi)^*} \xrightarrow{\simeq} \left( {\mathrm{Rh}_{\pi}}_* {\underline{{\mathbb{C}}}} \right)_{\kappa}\Big\rvert_{{\mathcal A}(\pi)^*}\left[-2d_{\gamma}\right] \xrightarrow{\simeq} \left({\mathrm{Rh}_{\pi}}_*{\underline{{\mathbb{C}}}}\right)_{\mathrm{st}}\Big\rvert_{{\mathcal A}(\pi)^*}\left[-2d_{\gamma}\right], \end{align} $$
$$ \begin{align} q_{\mathcal A}^* \left( \mathrm{Rh}_{*} {\underline{{\mathbb{C}}}} \right)_{\kappa}\Big\rvert_{{\mathcal A}(\pi)^*} \xrightarrow{\simeq} \left( {\mathrm{Rh}_{\pi}}_* {\underline{{\mathbb{C}}}} \right)_{\kappa}\Big\rvert_{{\mathcal A}(\pi)^*}\left[-2d_{\gamma}\right] \xrightarrow{\simeq} \left({\mathrm{Rh}_{\pi}}_*{\underline{{\mathbb{C}}}}\right)_{\mathrm{st}}\Big\rvert_{{\mathcal A}(\pi)^*}\left[-2d_{\gamma}\right], \end{align} $$with the first isomorphism ![]() $G_{\pi }$-equivariant.
$G_{\pi }$-equivariant.
In formula (4), the ![]() $G_{\pi }$-equivariant structure for the first term is given by the pullback map along the
$G_{\pi }$-equivariant structure for the first term is given by the pullback map along the ![]() $G_{\pi }$-quotient
$G_{\pi }$-quotient ![]() $q_{\mathcal A}: {\mathcal A}(\pi )^* \to {\mathcal A}_{\gamma }^*$. The
$q_{\mathcal A}: {\mathcal A}(\pi )^* \to {\mathcal A}_{\gamma }^*$. The ![]() $G_{\pi }$-equivariant structure for the second term is induced by the
$G_{\pi }$-equivariant structure for the second term is induced by the ![]() $G_{\pi }$-action on
$G_{\pi }$-action on ![]() ${\mathcal M}_{r,L}(\pi )$.
${\mathcal M}_{r,L}(\pi )$.
The following theorem is a further extension of Theorem 0.2, which provides a complete description of the ![]() $\kappa $-isotypic component of
$\kappa $-isotypic component of ![]() $\mathrm {Rh}_* {\underline {{\mathbb {C}}}}$ in terms of the
$\mathrm {Rh}_* {\underline {{\mathbb {C}}}}$ in terms of the ![]() $\gamma $-fixed subvariety
$\gamma $-fixed subvariety ![]() ${\mathcal M}_{\gamma } \subset {\mathcal M}_{n,L}$:
${\mathcal M}_{\gamma } \subset {\mathcal M}_{n,L}$:
Theorem 0.3 Theorem 3.2
Let ![]() $\kappa \in \hat {\Gamma }$ and
$\kappa \in \hat {\Gamma }$ and ![]() $\gamma \in \Gamma $ be identified by equation (3) and let
$\gamma \in \Gamma $ be identified by equation (3) and let ![]() $d_{\gamma } = \mathrm {codim}_{{\mathcal A}}\left ({\mathcal A}_{\gamma }\right )$. We have an isomorphism
$d_{\gamma } = \mathrm {codim}_{{\mathcal A}}\left ({\mathcal A}_{\gamma }\right )$. We have an isomorphism
 $$ \begin{align} c_{\kappa}: \left(\mathrm{Rh}_* {\underline{{\mathbb{C}}}}\right)_{\kappa} \xrightarrow{\simeq} {i_{\gamma}}_*\left({\mathrm{Rh}_{\gamma}}_* {\underline{{\mathbb{C}}}}\right)_{\kappa} \left[-2d_{\gamma}\right] \in D_c^b({\mathcal A}), \end{align} $$
$$ \begin{align} c_{\kappa}: \left(\mathrm{Rh}_* {\underline{{\mathbb{C}}}}\right)_{\kappa} \xrightarrow{\simeq} {i_{\gamma}}_*\left({\mathrm{Rh}_{\gamma}}_* {\underline{{\mathbb{C}}}}\right)_{\kappa} \left[-2d_{\gamma}\right] \in D_c^b({\mathcal A}), \end{align} $$which is canonical up to scaling.
The construction of the operator
 $$ \begin{align*} c_{\kappa}: \left(\mathrm{Rh}_* {\underline{{\mathbb{C}}}}\right)_{\kappa} \xrightarrow{\simeq} {i_{\gamma}}_*\left({\mathrm{Rh}_{\gamma}}_* {\underline{{\mathbb{C}}}}\right)_{\kappa} \left[-2d_{\gamma}\right] \in D_c^b({\mathcal A}) \end{align*} $$
$$ \begin{align*} c_{\kappa}: \left(\mathrm{Rh}_* {\underline{{\mathbb{C}}}}\right)_{\kappa} \xrightarrow{\simeq} {i_{\gamma}}_*\left({\mathrm{Rh}_{\gamma}}_* {\underline{{\mathbb{C}}}}\right)_{\kappa} \left[-2d_{\gamma}\right] \in D_c^b({\mathcal A}) \end{align*} $$realising the isomorphism of Theorem 0.3 is the main theme of this paper. It is of a geometric nature, given by a combination of algebraic correspondences and vanishing cycle functors. Since it induces a correspondence between the ![]() $\kappa $-part of the cohomology of an
$\kappa $-part of the cohomology of an ![]() $\mathrm {SL}_n$-Hitchin fibre and the
$\mathrm {SL}_n$-Hitchin fibre and the ![]() $\kappa $-part of the cohomology of the corresponding endoscopic Hitchin fibre, we call Theorems 0.2 and 0.3 the endoscopic decomposition associated with
$\kappa $-part of the cohomology of the corresponding endoscopic Hitchin fibre, we call Theorems 0.2 and 0.3 the endoscopic decomposition associated with ![]() $\mathrm {SL}_n$ and the character
$\mathrm {SL}_n$ and the character ![]() $\kappa $. A major difference between Theorem 0.3 and the work of Ngô [Reference Ngô33] and Yun [Reference Yun39] is that they mainly work with D-twisted Hitchin fibrations with
$\kappa $. A major difference between Theorem 0.3 and the work of Ngô [Reference Ngô33] and Yun [Reference Yun39] is that they mainly work with D-twisted Hitchin fibrations with ![]() $\mathrm {deg}(D)>2g-2$ or with just the elliptic locus of the
$\mathrm {deg}(D)>2g-2$ or with just the elliptic locus of the ![]() $K_C$-twisted Hitchin fibration, whereas we are interested in entire space in the latter setting. The structure of the supports of the direct image complexes is much more complicated in the
$K_C$-twisted Hitchin fibration, whereas we are interested in entire space in the latter setting. The structure of the supports of the direct image complexes is much more complicated in the ![]() $K_C$-case over the total Hitchin base; see [Reference de Cataldo, Heinloth and Migliorini8].
$K_C$-case over the total Hitchin base; see [Reference de Cataldo, Heinloth and Migliorini8].
In the following, we give some applications of Theorem 0.3.
0.4 Structure of the cohomology of  ${\mathcal M}_{n,L}$
${\mathcal M}_{n,L}$
Let ![]() $\kappa \in \hat {\Gamma }$ and
$\kappa \in \hat {\Gamma }$ and ![]() $\gamma \in \Gamma $ be identified by equation (3). Let
$\gamma \in \Gamma $ be identified by equation (3). Let ![]() $\pi : C' \to C$ be the degree m cyclic Galois cover associated with
$\pi : C' \to C$ be the degree m cyclic Galois cover associated with ![]() $\gamma $. Assume
$\gamma $. Assume ![]() $n=mr$. We denote by
$n=mr$. We denote by  $\widetilde {{\mathcal M}}^{\prime }_{r,d}$ the moduli space of stable (
$\widetilde {{\mathcal M}}^{\prime }_{r,d}$ the moduli space of stable (![]() $\mathrm {GL}_r$-)Higgs bundles
$\mathrm {GL}_r$-)Higgs bundles
on the curve ![]() $C'$.
$C'$.
Recall decomposition (1). The following theorem is a structural result for  $H^*\left ({\mathcal M}_{n,L}, {\mathbb {C}}\right )_{\kappa }$:
$H^*\left ({\mathcal M}_{n,L}, {\mathbb {C}}\right )_{\kappa }$:
Theorem 0.4 Theorem 5.4
The operator (5) induces a surjective morphism
 $$ \begin{align*} \mathfrak{p}_{\kappa}: H^{i}\left(\widetilde{{\mathcal M}}^{\prime}_{r,d}, {\mathbb{C}}\right) \twoheadrightarrow H^{i+2d_{\gamma}}\left({\mathcal M}_{n,L}, {\mathbb{C}}\right)_{\kappa}. \end{align*} $$
$$ \begin{align*} \mathfrak{p}_{\kappa}: H^{i}\left(\widetilde{{\mathcal M}}^{\prime}_{r,d}, {\mathbb{C}}\right) \twoheadrightarrow H^{i+2d_{\gamma}}\left({\mathcal M}_{n,L}, {\mathbb{C}}\right)_{\kappa}. \end{align*} $$ Moreover, let  $P_kH^*\left (\widetilde {{\mathcal M}}^{\prime }_{r,d}, {\mathbb {C}}\right )$ and
$P_kH^*\left (\widetilde {{\mathcal M}}^{\prime }_{r,d}, {\mathbb {C}}\right )$ and  $P_kH^{*}\left ({\mathcal M}_{n,L}, {\mathbb {C}}\right )_{\kappa }$ be the perverse filtrations defined via the Hitchin fibrations; then
$P_kH^{*}\left ({\mathcal M}_{n,L}, {\mathbb {C}}\right )_{\kappa }$ be the perverse filtrations defined via the Hitchin fibrations; then
 $$ \begin{align*} \mathfrak{p}_{\kappa} \left( P_k H^i\left(\widetilde{{\mathcal M}}^{\prime}_{r,d}, {\mathbb{C}}\right)\right) = P_{k+d_{\gamma}}H^{i+2d_{\gamma}}\left( {\mathcal M}_{n,L}, {\mathbb{C}}\right)_{\kappa}. \end{align*} $$
$$ \begin{align*} \mathfrak{p}_{\kappa} \left( P_k H^i\left(\widetilde{{\mathcal M}}^{\prime}_{r,d}, {\mathbb{C}}\right)\right) = P_{k+d_{\gamma}}H^{i+2d_{\gamma}}\left( {\mathcal M}_{n,L}, {\mathbb{C}}\right)_{\kappa}. \end{align*} $$We refer to [Reference de Cataldo and Migliorini11, Reference de Cataldo, Hausel and Migliorini7] for perverse filtrations; see also Section 5.1 for a brief review.
If ![]() $\kappa =0$, we have
$\kappa =0$, we have ![]() $\pi = \mathrm {id}: C \xrightarrow {\simeq } C$. The operator
$\pi = \mathrm {id}: C \xrightarrow {\simeq } C$. The operator ![]() $\mathfrak {p}_{\kappa =0}$ in this special case recovers the restriction map
$\mathfrak {p}_{\kappa =0}$ in this special case recovers the restriction map
 $$ \begin{align*} j^*: H^{i}\left(\widetilde{{\mathcal M}}_{n,d}, {\mathbb{C}}\right) \twoheadrightarrow H^{i}\left({\mathcal M}_{n,L}, {\mathbb{C}}\right)^{\Gamma} \end{align*} $$
$$ \begin{align*} j^*: H^{i}\left(\widetilde{{\mathcal M}}_{n,d}, {\mathbb{C}}\right) \twoheadrightarrow H^{i}\left({\mathcal M}_{n,L}, {\mathbb{C}}\right)^{\Gamma} \end{align*} $$associated with the embedding  $j: {\mathcal M}_{n,L} \hookrightarrow \widetilde {{\mathcal M}}_{n,d}=\widetilde {{\mathcal M}}^{\prime }_{r,d}$.
$j: {\mathcal M}_{n,L} \hookrightarrow \widetilde {{\mathcal M}}_{n,d}=\widetilde {{\mathcal M}}^{\prime }_{r,d}$.
By Markman’s theorem [Reference Markman30], the cohomology  $H^*\left (\widetilde {{\mathcal M}}^{\prime }_{r,d}, {\mathbb {C}}\right )$ is generated by the tautological classes associated with a universal family on
$H^*\left (\widetilde {{\mathcal M}}^{\prime }_{r,d}, {\mathbb {C}}\right )$ is generated by the tautological classes associated with a universal family on  $\widetilde {{\mathcal M}}^{\prime }_{r,d}$. Hence Theorem 0.4 shows that each isotypic component
$\widetilde {{\mathcal M}}^{\prime }_{r,d}$. Hence Theorem 0.4 shows that each isotypic component  $H^{*}\left ( {\mathcal M}_{n,L}, {\mathbb {C}}\right )_{\kappa }$ for
$H^{*}\left ( {\mathcal M}_{n,L}, {\mathbb {C}}\right )_{\kappa }$ for ![]() $\kappa \neq 0$ is governed by the tautological classes of a different moduli space of Higgs bundles through the operator
$\kappa \neq 0$ is governed by the tautological classes of a different moduli space of Higgs bundles through the operator ![]() $\mathfrak {p}_{\kappa }$. More discussions concerning Theorem 0.4 and the P=W conjecture [Reference de Cataldo, Hausel and Migliorini7] are given in Section 5.
$\mathfrak {p}_{\kappa }$. More discussions concerning Theorem 0.4 and the P=W conjecture [Reference de Cataldo, Hausel and Migliorini7] are given in Section 5.
0.5 The Hausel–Thaddeus conjecture
In [Reference Hausel and Thaddeus22], Hausel and Thaddeus showed that the moduli spaces of stable ![]() $\mathrm {SL}_n$- and
$\mathrm {SL}_n$- and ![]() $\mathrm {PGL}_n$-Higgs bundles are mirror partners in the sense of the Strominger–Yau–Zaslow mirror symmetry. As a consequence, these two moduli spaces should have identical Hodge numbers.
$\mathrm {PGL}_n$-Higgs bundles are mirror partners in the sense of the Strominger–Yau–Zaslow mirror symmetry. As a consequence, these two moduli spaces should have identical Hodge numbers.
As explained in [Reference Hausel and Thaddeus22], the moduli space of degree d stable ![]() $\mathrm {PGL}_n$-Higgs bundles can be realised as the quotient
$\mathrm {PGL}_n$-Higgs bundles can be realised as the quotient ![]() ${\mathcal M}_{n,L}/\Gamma $, which is naturally a Deligne–Mumford stack. Therefore, Hausel and Thaddeus conjectured that for any two line bundles
${\mathcal M}_{n,L}/\Gamma $, which is naturally a Deligne–Mumford stack. Therefore, Hausel and Thaddeus conjectured that for any two line bundles ![]() $L,L'$ with
$L,L'$ with
the Hodge numbers of ![]() ${\mathcal M}_{n,L}$ are the same as the stringy Hodge numbers of the stack
${\mathcal M}_{n,L}$ are the same as the stringy Hodge numbers of the stack  $\left [{\mathcal M}_{n,L'}/\Gamma \right ]$ (twisted by a certain gerbe
$\left [{\mathcal M}_{n,L'}/\Gamma \right ]$ (twisted by a certain gerbe ![]() $\alpha $):
$\alpha $):
 $$ \begin{align} h^{i,j}\left({\mathcal M}_{n,L}\right) = h_{\mathrm{st}}^{i,j}\left(\left[{\mathcal M}_{n,L'}/\Gamma\right], \alpha\right) \end{align} $$
$$ \begin{align} h^{i,j}\left({\mathcal M}_{n,L}\right) = h_{\mathrm{st}}^{i,j}\left(\left[{\mathcal M}_{n,L'}/\Gamma\right], \alpha\right) \end{align} $$(see [Reference Hausel and Thaddeus22, Section 4] for precise definitions of the gerbe ![]() $\alpha $ and the stringy Hodge numbers). Later, Hausel further conjectured a refinement of equation (6): the Hodge numbers of
$\alpha $ and the stringy Hodge numbers). Later, Hausel further conjectured a refinement of equation (6): the Hodge numbers of  $H^*\left ({\mathcal M}_{n,L}, {\mathbb {C}}\right )_{\kappa }$ coincide with the Hodge numbers of the gerby sector
$H^*\left ({\mathcal M}_{n,L}, {\mathbb {C}}\right )_{\kappa }$ coincide with the Hodge numbers of the gerby sector  $\left [\left ({\mathcal M}_{n,L'}\right )_{\gamma }/\Gamma \right ]$. Here
$\left [\left ({\mathcal M}_{n,L'}\right )_{\gamma }/\Gamma \right ]$. Here  $\left ({\mathcal M}_{n,L'}\right )_{\gamma } \subset {\mathcal M}_{n,L'}$ is the
$\left ({\mathcal M}_{n,L'}\right )_{\gamma } \subset {\mathcal M}_{n,L'}$ is the ![]() $\gamma $-fixed subvariety, and
$\gamma $-fixed subvariety, and ![]() $\kappa $ and
$\kappa $ and ![]() $\gamma $ are matched via equation (3). We refer to [Reference Hausel20, Conjecture 4.5] concerning Hodge numbers and [Reference Hausel20, Conjecture 5.9] for a further refinement involving perverse filtrations.
$\gamma $ are matched via equation (3). We refer to [Reference Hausel20, Conjecture 4.5] concerning Hodge numbers and [Reference Hausel20, Conjecture 5.9] for a further refinement involving perverse filtrations.
The following theorem is a direct consequence of Theorem 0.3 which proves the Hausel–Thaddeus conjecture and a refinement of it; see [Reference Loeser and Wyss29] for an explanation of how the right-hand side is equivalent to the gerby description just given:
Theorem 0.5. Assume that e is a multiplicative inverse of ![]() $d'$ modulo n. Let
$d'$ modulo n. Let ![]() $\gamma $ and
$\gamma $ and ![]() $\kappa $ be matched via equation (3). The following identity holds in the Grothendieck group of complex Hodge structures
$\kappa $ be matched via equation (3). The following identity holds in the Grothendieck group of complex Hodge structures ![]() $K_0(\mathrm {HS})$:
$K_0(\mathrm {HS})$:
 $$ \begin{align} \left[P_kH^i\left({\mathcal M}_{n,L}, {\mathbb{C}}\right)_{\kappa}\right] = \left[P_{k-d_{\gamma}}H^{i-2d_{\gamma}}\left(\left({\mathcal M}_{n,L'}\right)_{\gamma}, {\mathbb{C}}\right)_{de\kappa}\left(-d_{\gamma}\right)\right]. \end{align} $$
$$ \begin{align} \left[P_kH^i\left({\mathcal M}_{n,L}, {\mathbb{C}}\right)_{\kappa}\right] = \left[P_{k-d_{\gamma}}H^{i-2d_{\gamma}}\left(\left({\mathcal M}_{n,L'}\right)_{\gamma}, {\mathbb{C}}\right)_{de\kappa}\left(-d_{\gamma}\right)\right]. \end{align} $$Here ![]() $(\bullet )$ stands for the Tate twist,Footnote 1 and each piece of the perverse filtrations admits a natural Hodge structure by the theory of mixed Hodge modules. In particular, for any
$(\bullet )$ stands for the Tate twist,Footnote 1 and each piece of the perverse filtrations admits a natural Hodge structure by the theory of mixed Hodge modules. In particular, for any ![]() $q\in {\mathbb {Z}}$ coprime to n, we have
$q\in {\mathbb {Z}}$ coprime to n, we have
 $$ \begin{align} \left[P_kH^i\left({\mathcal M}_{n,L}, {\mathbb{C}}\right)\right] = \sum_{\gamma\in \Gamma} \left[P_{k-d_{\gamma}}H^{i-2d_{\gamma}}\left(\left({\mathcal M}_{n,L'}\right)_{\gamma}, {\mathbb{C}}\right)_{q\kappa}\left(-d_{\gamma}\right)\right] \in K_0(\mathrm{HS}). \end{align} $$
$$ \begin{align} \left[P_kH^i\left({\mathcal M}_{n,L}, {\mathbb{C}}\right)\right] = \sum_{\gamma\in \Gamma} \left[P_{k-d_{\gamma}}H^{i-2d_{\gamma}}\left(\left({\mathcal M}_{n,L'}\right)_{\gamma}, {\mathbb{C}}\right)_{q\kappa}\left(-d_{\gamma}\right)\right] \in K_0(\mathrm{HS}). \end{align} $$Remark 0.6. By the last paragraph of [Reference Hausel and Thaddeus22, Proof of Proposition 8.2], the shift
 $$ \begin{align*} d_{\gamma} = \mathrm{codim}_{{\mathcal A}}\left({\mathcal A}_{\gamma}\right) = \frac{1}{2} \mathrm{codim}_{{\mathcal M}_{n,L}}\left({\mathcal M}_{\gamma}\right) \end{align*} $$
$$ \begin{align*} d_{\gamma} = \mathrm{codim}_{{\mathcal A}}\left({\mathcal A}_{\gamma}\right) = \frac{1}{2} \mathrm{codim}_{{\mathcal M}_{n,L}}\left({\mathcal M}_{\gamma}\right) \end{align*} $$in equation (7) coincides with the ‘fermionic shift’ ![]() $F(\gamma )$ in the formulation of Hausel and Thaddeus.
$F(\gamma )$ in the formulation of Hausel and Thaddeus.
A refined version of the Hausel–Thaddeus conjecture was previously proven by Gröchenig, Wyss and Ziegler [Reference Groechenig, Wyss and Ziegler17, Theorem 7.24] by p-adic integration, and was generalised by Loeser and Wyss [Reference Loeser and Wyss29, Remark 5.3.4] by motivic integration. Note that our refined version in equation (7) is slightly different from the versions of [Reference Groechenig, Wyss and Ziegler17, Reference Loeser and Wyss29], since the right-hand side of equation (7) depends on the degree of L, whereas the corresponding term in [Reference Groechenig, Wyss and Ziegler17, Reference Loeser and Wyss29] is independent of this degree. Instead, our refined version is closer to the conjectures formulated by Hausel [Reference Hausel20, Conjectures 4.5 and 5.9]. Motivated by the Hausel–Thaddeus conjecture, connections between the moduli of Higgs bundles and the ![]() $\gamma $-fixed locus with
$\gamma $-fixed locus with ![]() $\gamma \in \Gamma $ were discussed in [Reference Franco, Gothen, Oliveira and Peón-Netao15] via the Fourier–Mukai transform.
$\gamma \in \Gamma $ were discussed in [Reference Franco, Gothen, Oliveira and Peón-Netao15] via the Fourier–Mukai transform.
0.6 Idea of the proof
Our approach proceeds in two steps. We first show analogus of Theorems 0.2 and 0.3 for the moduli space  ${\mathcal M}^D_{n,L}$ of D-twisted
${\mathcal M}^D_{n,L}$ of D-twisted ![]() $\mathrm {SL}_n$-Higgs bundles with
$\mathrm {SL}_n$-Higgs bundles with ![]() $\mathrm {deg} (D)> 2g-2$ (see Section 1 for precise definitions). As mentioned earlier, one expects this case to be simpler than the original setting, due to work of Chaudouard and Laumon [Reference Chaudouard and Laumon5] and of de Cataldo [Reference de Cataldo6], which determines the supports appearing in the decomposition theorem for the twisted Hitchin map. After proving the corresponding support theorem for endoscopic moduli, we study the endoscopic decomposition of Ngô [Reference Ngô33] and Yun [Reference Yun39] over the elliptic locus and extend it over the full twisted Hitchin base.
$\mathrm {deg} (D)> 2g-2$ (see Section 1 for precise definitions). As mentioned earlier, one expects this case to be simpler than the original setting, due to work of Chaudouard and Laumon [Reference Chaudouard and Laumon5] and of de Cataldo [Reference de Cataldo6], which determines the supports appearing in the decomposition theorem for the twisted Hitchin map. After proving the corresponding support theorem for endoscopic moduli, we study the endoscopic decomposition of Ngô [Reference Ngô33] and Yun [Reference Yun39] over the elliptic locus and extend it over the full twisted Hitchin base.
Unfortunately, this approach is not sufficient when ![]() $D = K_C$, since the supports of the Hitchin map remain mysterious [Reference de Cataldo, Heinloth and Migliorini8]. Moreover, although
$D = K_C$, since the supports of the Hitchin map remain mysterious [Reference de Cataldo, Heinloth and Migliorini8]. Moreover, although ![]() ${\mathcal M}_{n,L}$ embeds inside
${\mathcal M}_{n,L}$ embeds inside  ${\mathcal M}^D_{n,L}$ for a certain effective divisor D with
${\mathcal M}^D_{n,L}$ for a certain effective divisor D with ![]() $\mathrm {deg}(D)>2g-2$, we cannot simply pull back formula (5).
$\mathrm {deg}(D)>2g-2$, we cannot simply pull back formula (5).
Instead, we realise ![]() ${\mathcal M}_{n,L}$ as the critical locus of a regular function
${\mathcal M}_{n,L}$ as the critical locus of a regular function
 $$ \begin{align} \mu_{\pi,{\mathcal M}}: {\mathcal M}^D_{n,L} \to {\mathbb{A}}^1 \end{align} $$
$$ \begin{align} \mu_{\pi,{\mathcal M}}: {\mathcal M}^D_{n,L} \to {\mathbb{A}}^1 \end{align} $$(see Theorem 4.5). This allows us to express the cohomology of ![]() ${\mathcal M}_{n,L}$ as the vanishing cohomology of this function. In addition, since the function
${\mathcal M}_{n,L}$ as the vanishing cohomology of this function. In addition, since the function ![]() $\mu _{\pi ,{\mathcal M}}$ factors through the Hitchin base, we can use the vanishing cycles functor to relate the decomposition theorem for
$\mu _{\pi ,{\mathcal M}}$ factors through the Hitchin base, we can use the vanishing cycles functor to relate the decomposition theorem for ![]() ${\mathcal M}_{n,L}$ in terms of that for
${\mathcal M}_{n,L}$ in terms of that for  ${\mathcal M}^D_{n,L}$. By applying this technique to the twisted version of formula (5), we obtain the full result.
${\mathcal M}^D_{n,L}$. By applying this technique to the twisted version of formula (5), we obtain the full result.
0.7 Relation to other work
As discussed in Section 0.5, the Hausel–Thaddeus conjecture and its refinements have been proven by Gröchenig, Wyss and Ziegler [Reference Groechenig, Wyss and Ziegler17] via p-adic integration. Using a similar approach, they have also given a new proof of Ngô’s geometric stabilisation theorem [Reference Groechenig, Wyss and Ziegler18], which plays a crucial role in Ngô’s proof of the fundamental lemma of the Langlands program [Reference Ngô33]. Our approach goes in the inverse direction – we prove the Hausel–Thaddeus conjecture by extending Ngô’s method [Reference Ngô33, Reference Yun39] in the proof the geometric stabilisation theorem via perverse sheaves and the support theorems. This carries out Hausel’s proposal in [Reference Hausel20, Section 5.4]. A benefit of the sheaf-theoretic approach is that it allows us to construct concrete geometric operators which realise the Hausel–Thaddeus conjecture (Theorems 0.2 and 0.3) and provide a better understanding of  $H^*\left ({\mathcal M}_{n,L}, {\mathbb {C}}\right )_{\kappa }$ for each nontrivial
$H^*\left ({\mathcal M}_{n,L}, {\mathbb {C}}\right )_{\kappa }$ for each nontrivial ![]() $\kappa $.
$\kappa $.
In the case of D-twisted Higgs bundles, our result (Theorem 3.2) removes a technical condition of [Reference Groechenig, Wyss and Ziegler17, Theorems 7.21] on the parity of ![]() $\mathrm {deg}(D)$.
$\mathrm {deg}(D)$.
1 Hitchin-type moduli spaces
Throughout, we work over the complex numbers ![]() ${\mathbb {C}}$. In this section, we fix the curve C of genus
${\mathbb {C}}$. In this section, we fix the curve C of genus ![]() $g \geq 2$, the rank n and the line bundle
$g \geq 2$, the rank n and the line bundle ![]() $L \in \mathrm {Pic}^d(C)$, which serves as the determinant of the Higgs bundles as in Section 0.1. We study several Hitchin-type moduli spaces relevant to Theorems 0.2 and 0.3.
$L \in \mathrm {Pic}^d(C)$, which serves as the determinant of the Higgs bundles as in Section 0.1. We study several Hitchin-type moduli spaces relevant to Theorems 0.2 and 0.3.
1.1 D-Higgs bundles
For our purpose, it is important to consider generalised Higgs bundles ![]() $({\mathcal E}, \theta )$ with the Higgs field
$({\mathcal E}, \theta )$ with the Higgs field ![]() $\theta $ twisted by a divisor D that is not necessarily the canonical divisor
$\theta $ twisted by a divisor D that is not necessarily the canonical divisor ![]() $K_C$. This flexibility also plays a crucial role in the proof of the fundamental lemma [Reference Ngô32, Reference Ngô33].
$K_C$. This flexibility also plays a crucial role in the proof of the fundamental lemma [Reference Ngô32, Reference Ngô33].
Let D be either an effective divisor of degree ![]() $\mathrm {deg}(D)> 2g-2$ or
$\mathrm {deg}(D)> 2g-2$ or ![]() $D= K_C$. A D-Higgs bundle is a pair
$D= K_C$. A D-Higgs bundle is a pair ![]() $({\mathcal E}, \theta )$, where
$({\mathcal E}, \theta )$, where ![]() ${\mathcal E}$ is a vector bundle and
${\mathcal E}$ is a vector bundle and ![]() $\theta $ is a D-twisted Higgs field
$\theta $ is a D-twisted Higgs field
We denote by ![]() $\mathrm {char}(\theta )$ the tuple of the coefficients for the characteristic polynomial associated with
$\mathrm {char}(\theta )$ the tuple of the coefficients for the characteristic polynomial associated with ![]() $({\mathcal E}, \theta )$:
$({\mathcal E}, \theta )$:
 $$ \begin{align*} \mathrm{char}(\theta) = (a_1, \dots, a_n), \quad a_i =\mathrm{trace}\left(\wedge^i \theta\right) \in H^0(C, {\mathcal O}_C(iD)). \end{align*} $$
$$ \begin{align*} \mathrm{char}(\theta) = (a_1, \dots, a_n), \quad a_i =\mathrm{trace}\left(\wedge^i \theta\right) \in H^0(C, {\mathcal O}_C(iD)). \end{align*} $$ Parallel to the case of ![]() $K_C$-Higgs bundles, the stability condition for D-Higgs bundles is with respect to the slope
$K_C$-Higgs bundles, the stability condition for D-Higgs bundles is with respect to the slope ![]() $\mu ({\mathcal E}) = \mathrm {deg}({\mathcal E})/\mathrm {rank}({\mathcal E})$. By [Reference Nitsure34], there is a nonsingular quasi-projective moduli space
$\mu ({\mathcal E}) = \mathrm {deg}({\mathcal E})/\mathrm {rank}({\mathcal E})$. By [Reference Nitsure34], there is a nonsingular quasi-projective moduli space  $\widetilde {{\mathcal M}}_{n,d}^D$ parameterising stable D-Higgs bundles of rank n and degree d, with the Hitchin map
$\widetilde {{\mathcal M}}_{n,d}^D$ parameterising stable D-Higgs bundles of rank n and degree d, with the Hitchin map
 $$ \begin{align} \widetilde{h}^D : \widetilde{{\mathcal M}}_{n,d}^D \rightarrow \widetilde{{\mathcal A}}^D = \oplus_{i=1}^n H^0(C, {\mathcal O}_C(iD)), \quad ({\mathcal E}, \theta) \mapsto \mathrm{char}(\theta), \end{align} $$
$$ \begin{align} \widetilde{h}^D : \widetilde{{\mathcal M}}_{n,d}^D \rightarrow \widetilde{{\mathcal A}}^D = \oplus_{i=1}^n H^0(C, {\mathcal O}_C(iD)), \quad ({\mathcal E}, \theta) \mapsto \mathrm{char}(\theta), \end{align} $$which is proper and surjective.
The moduli space of stable ![]() $\mathrm {SL}_n\ D$-Higgs bundles is defined to be the subvariety
$\mathrm {SL}_n\ D$-Higgs bundles is defined to be the subvariety
 $$ \begin{align} {\mathcal M}^D_{n,L} = \left\{({\mathcal E}, \theta) \in \widetilde{{\mathcal M}}_{n,d}^D; \ \mathrm{det}({\mathcal E}) \simeq L, \ \mathrm{trace}(\theta) = 0 \right\} \subset \widetilde{{\mathcal M}}_{n,d}^D. \end{align} $$
$$ \begin{align} {\mathcal M}^D_{n,L} = \left\{({\mathcal E}, \theta) \in \widetilde{{\mathcal M}}_{n,d}^D; \ \mathrm{det}({\mathcal E}) \simeq L, \ \mathrm{trace}(\theta) = 0 \right\} \subset \widetilde{{\mathcal M}}_{n,d}^D. \end{align} $$It is nonsingular and irreducible by [Reference de Cataldo6, Section 2.1], which has a Hitchin map induced from the Hitchin map of the ambient space (10),
 $$ \begin{align} h^D: {\mathcal M}^D_{n,L} \rightarrow {\mathcal A}^D = \oplus_{i=2}^n H^0(C, {\mathcal O}_C(iD)). \end{align} $$
$$ \begin{align} h^D: {\mathcal M}^D_{n,L} \rightarrow {\mathcal A}^D = \oplus_{i=2}^n H^0(C, {\mathcal O}_C(iD)). \end{align} $$It is clear that the variety  ${\mathcal M}^D_{n,L}$ is the fibre over the closed point
${\mathcal M}^D_{n,L}$ is the fibre over the closed point ![]() $(L,0)$ of the smooth map
$(L,0)$ of the smooth map
 $$ \begin{align} q: \widetilde{{\mathcal M}}_{r,d}^{D} \rightarrow \widetilde{{\mathcal M}}_{1,d}^{D} =\mathrm{Pic}^d(C) \times H^0(C, {\mathcal O}_C(D)), \quad ({\mathcal E}, \theta) \mapsto (\mathrm{det}({\mathcal E}), \mathrm{trace}(\theta)). \end{align} $$
$$ \begin{align} q: \widetilde{{\mathcal M}}_{r,d}^{D} \rightarrow \widetilde{{\mathcal M}}_{1,d}^{D} =\mathrm{Pic}^d(C) \times H^0(C, {\mathcal O}_C(D)), \quad ({\mathcal E}, \theta) \mapsto (\mathrm{det}({\mathcal E}), \mathrm{trace}(\theta)). \end{align} $$ A major difference between the cases ![]() $D = K_C$ and
$D = K_C$ and ![]() $\mathrm {deg}(D)>2g-2$ is that the Hitchin fibration for either
$\mathrm {deg}(D)>2g-2$ is that the Hitchin fibration for either ![]() $\mathrm {GL}_n$ or
$\mathrm {GL}_n$ or ![]() $\mathrm {SL}_n$ is Lagrangian with respect to the canonical hyper-Kähler structure for
$\mathrm {SL}_n$ is Lagrangian with respect to the canonical hyper-Kähler structure for ![]() $D = K_C$, but the dimension of the Hitchin base is always larger than the dimension of a fibre in the case of
$D = K_C$, but the dimension of the Hitchin base is always larger than the dimension of a fibre in the case of ![]() $\mathrm {deg}(D)>2g-2$. In view of the support theorems (Section 2.2), such a difference will substantially influence the study of the topology of Hitchin fibrations.
$\mathrm {deg}(D)>2g-2$. In view of the support theorems (Section 2.2), such a difference will substantially influence the study of the topology of Hitchin fibrations.
From now on, all D-Higgs bundles will be uniformly called Higgs bundles for convenience.
1.2 Relative Hitchin moduli spaces
In this section, we study the relative Hitchin moduli space associated with a Galois cover ![]() $\pi : C' \to C$. This parameterises stable Higgs bundles with respect to the endoscopic group of
$\pi : C' \to C$. This parameterises stable Higgs bundles with respect to the endoscopic group of ![]() $\mathrm {SL}_n$ over C attached to a character
$\mathrm {SL}_n$ over C attached to a character ![]() $\kappa \in \hat {\Gamma }$ [Reference Ngô32, Reference Ngô33].
$\kappa \in \hat {\Gamma }$ [Reference Ngô32, Reference Ngô33].
Let ![]() $C'$ be a nonsingular curve with a cyclic Galois cover
$C'$ be a nonsingular curve with a cyclic Galois cover
whose Galois group is ![]() $G_{\pi } \cong \mathbb {Z}/m{\mathbb {Z}}$. We denote the divisor
$G_{\pi } \cong \mathbb {Z}/m{\mathbb {Z}}$. We denote the divisor ![]() $\pi ^*D$ by
$\pi ^*D$ by ![]() $D'$. For an element
$D'$. For an element ![]() $\sigma \in H^0(C', {\mathcal O}_{C'}(D'))$, the push-forward along
$\sigma \in H^0(C', {\mathcal O}_{C'}(D'))$, the push-forward along ![]() $\pi $ gives an element
$\pi $ gives an element
The trace of ![]() $\pi _*\sigma $ recovers its projection to the direct summand component:
$\pi _*\sigma $ recovers its projection to the direct summand component:
The moduli space  $\widetilde {{\mathcal M}}_{r,d}^{D'}(C')$ of rank r, degree d stable Higgs bundles on
$\widetilde {{\mathcal M}}_{r,d}^{D'}(C')$ of rank r, degree d stable Higgs bundles on ![]() $C'$ admits a map
$C'$ admits a map
 $$ \begin{align} q_{\pi}: \widetilde{{\mathcal M}}_{r,d}^{D'}(C') \rightarrow \widetilde{{\mathcal M}}_{1,d}^{D}(C), \end{align} $$
$$ \begin{align} q_{\pi}: \widetilde{{\mathcal M}}_{r,d}^{D'}(C') \rightarrow \widetilde{{\mathcal M}}_{1,d}^{D}(C), \end{align} $$which is the composition of equation (13) for the curve ![]() $C'$ and the push-forward
$C'$ and the push-forward
 $$ \begin{align} \pi_*: \widetilde{{\mathcal M}}_{1,d}^{D'}(C') \rightarrow \widetilde{{\mathcal M}}_{1,d}^D(C), \quad ({\mathcal L}, \sigma) \mapsto (\mathrm{det}(\pi_*{\mathcal L}), \mathrm{trace}(\pi_{\ast} \sigma)).^{2} \end{align} $$
$$ \begin{align} \pi_*: \widetilde{{\mathcal M}}_{1,d}^{D'}(C') \rightarrow \widetilde{{\mathcal M}}_{1,d}^D(C), \quad ({\mathcal L}, \sigma) \mapsto (\mathrm{det}(\pi_*{\mathcal L}), \mathrm{trace}(\pi_{\ast} \sigma)).^{2} \end{align} $$SinceFootnote 2 both formulas (13) and (15) are smooth, the composition ![]() $q_{\pi }$ is also smooth.
$q_{\pi }$ is also smooth.
We define the relative Hitchin moduli space of rank r and degree d associated with ![]() $\pi $ as the subvariety of
$\pi $ as the subvariety of  $\widetilde {{\mathcal M}}_{r,d}^{D'}(C')$ given as a fibre of formula (14):
$\widetilde {{\mathcal M}}_{r,d}^{D'}(C')$ given as a fibre of formula (14):
 $$ \begin{align*} {\mathcal M}_{r,L}^D(\pi) = q_{\pi} ^{-1}(L,0) \subset \widetilde{{\mathcal M}}_{r,d}^{D'}(C'). \end{align*} $$
$$ \begin{align*} {\mathcal M}_{r,L}^D(\pi) = q_{\pi} ^{-1}(L,0) \subset \widetilde{{\mathcal M}}_{r,d}^{D'}(C'). \end{align*} $$The variety  ${\mathcal M}_{r,L}^D(\pi )$, which recovers the
${\mathcal M}_{r,L}^D(\pi )$, which recovers the ![]() $\mathrm {SL}_n$-Hitchin moduli space (11) when
$\mathrm {SL}_n$-Hitchin moduli space (11) when ![]() $\pi = \mathrm {id}$, is nonsingular due to the smoothness of
$\pi = \mathrm {id}$, is nonsingular due to the smoothness of ![]() $q_{\pi }$.
$q_{\pi }$.
Next we describe the Hitchin fibration associated with  ${\mathcal M}_{r,L}^D(\pi )$ which generalises equation (12). Recall from equation (10) the
${\mathcal M}_{r,L}^D(\pi )$ which generalises equation (12). Recall from equation (10) the ![]() $\mathrm {GL}_r$-Hitchin fibration
$\mathrm {GL}_r$-Hitchin fibration  $h^{D'}: \widetilde {{\mathcal M}}_{r,d}^{D'}(C') \to \widetilde {{\mathcal A}}^{D'}(C')$ associated with the curve
$h^{D'}: \widetilde {{\mathcal M}}_{r,d}^{D'}(C') \to \widetilde {{\mathcal A}}^{D'}(C')$ associated with the curve ![]() $C'$. The restriction of
$C'$. The restriction of ![]() $h^{D'}$ to
$h^{D'}$ to  ${\mathcal M}_{r,L}^D(\pi )$ induces the Hitchin map
${\mathcal M}_{r,L}^D(\pi )$ induces the Hitchin map
 $$ \begin{align} h_{\pi}^D: {\mathcal M}_{r,L}^D(\pi) \to {\mathcal A}^D(\pi), \end{align} $$
$$ \begin{align} h_{\pi}^D: {\mathcal M}_{r,L}^D(\pi) \to {\mathcal A}^D(\pi), \end{align} $$which fits into the commutative diagram

The Hitchin base ![]() ${\mathcal A}^D(\pi )$ can be concretely described as
${\mathcal A}^D(\pi )$ can be concretely described as
 $$ \begin{align} {\mathcal A}^D(\pi) = H^0(C', {\mathcal O}_{C'}(D'))_{\mathrm{var}} \oplus \left(\oplus_{i=2}^r H^0(C', {\mathcal O}_{C'}(iD'))\right), \end{align} $$
$$ \begin{align} {\mathcal A}^D(\pi) = H^0(C', {\mathcal O}_{C'}(D'))_{\mathrm{var}} \oplus \left(\oplus_{i=2}^r H^0(C', {\mathcal O}_{C'}(iD'))\right), \end{align} $$where ![]() $H^0(C', {\mathcal O}_{C'}(D'))_{\mathrm {var}}$ is the variant part with respect to the natural Galois group
$H^0(C', {\mathcal O}_{C'}(D'))_{\mathrm {var}}$ is the variant part with respect to the natural Galois group ![]() $G_{\pi }$-action induced by the
$G_{\pi }$-action induced by the ![]() $G_{\pi }$-action on
$G_{\pi }$-action on ![]() $C'$ [Reference Hausel and Pauly21, Section 5]. Since the line bundles
$C'$ [Reference Hausel and Pauly21, Section 5]. Since the line bundles ![]() ${\mathcal O}_{C'}(iD')$ have canonical
${\mathcal O}_{C'}(iD')$ have canonical ![]() $G_{\pi }$-linearisations, there is a natural
$G_{\pi }$-linearisations, there is a natural ![]() $G_{\pi }$-action on the Hitchin base (18).
$G_{\pi }$-action on the Hitchin base (18).
Proposition 1.1. We have the following properties:
(a) The moduli space
 ${\mathcal M}_{r,L}^D(\pi )$ is a disjoint union of m nonsingular isomorphic components: (19)
${\mathcal M}_{r,L}^D(\pi )$ is a disjoint union of m nonsingular isomorphic components: (19) $$ \begin{align} {\mathcal M}_{r,L}^D(\pi) = \bigsqcup_{i=1}^m M_i. \end{align} $$
$$ \begin{align} {\mathcal M}_{r,L}^D(\pi) = \bigsqcup_{i=1}^m M_i. \end{align} $$(b) The restrictions of
 $h_{\pi }^D$ to all components
$h_{\pi }^D$ to all components  $h_i: M_i \to {\mathcal A}^D(\pi )$ are
$h_i: M_i \to {\mathcal A}^D(\pi )$ are  ${\mathcal A}^D(\pi )$-isomorphic. More precisely, for each pair
${\mathcal A}^D(\pi )$-isomorphic. More precisely, for each pair  $1 \leq i,j \leq m$, there exists an isomorphism
$1 \leq i,j \leq m$, there exists an isomorphism  $\phi _{ij}: M_i \xrightarrow {\simeq } M_j$ induced by tensoring with a line bundle
$\phi _{ij}: M_i \xrightarrow {\simeq } M_j$ induced by tensoring with a line bundle  ${\mathcal L}_{ij} \in \Gamma $ satisfying the commutative diagram(20)
${\mathcal L}_{ij} \in \Gamma $ satisfying the commutative diagram(20)
Proof. Recall that  ${\mathcal M}_{r,L}^D(\pi )$ is the fibre of
${\mathcal M}_{r,L}^D(\pi )$ is the fibre of
(see formula (14)) over the point  $(L,0) \in \widetilde {{\mathcal M}}_{1,d}^{D}(C)$. The map q is surjective and smooth, and its fibres are isomorphic to the moduli of stable
$(L,0) \in \widetilde {{\mathcal M}}_{1,d}^{D}(C)$. The map q is surjective and smooth, and its fibres are isomorphic to the moduli of stable ![]() $\mathrm {SL}_r$-Higgs bundles of degree d on the curve
$\mathrm {SL}_r$-Higgs bundles of degree d on the curve ![]() $C'$. In particular, each fibre of q is nonsingular and irreducible.
$C'$. In particular, each fibre of q is nonsingular and irreducible.
The morphism ![]() $\pi _*$ given in formula (15) respects the product structures
$\pi _*$ given in formula (15) respects the product structures
where the morphism between the second factors form a trivial affine bundle. For the first factors, a fibre of ![]() $\pi _*: \mathrm {Pic}^d(C') \rightarrow \mathrm {Pic}^d(C)$ is isomorphic to the degree d Prym variety associated with the Galois cover
$\pi _*: \mathrm {Pic}^d(C') \rightarrow \mathrm {Pic}^d(C)$ is isomorphic to the degree d Prym variety associated with the Galois cover ![]() $\pi : C' \to C$, which is the disjoint union of m isomorphic abelian varieties [Reference Hausel and Thaddeus22, Section 7]. Hence the moduli space
$\pi : C' \to C$, which is the disjoint union of m isomorphic abelian varieties [Reference Hausel and Thaddeus22, Section 7]. Hence the moduli space  ${\mathcal M}_{r,L}^D(\pi )$ has m nonsingular connected components.
${\mathcal M}_{r,L}^D(\pi )$ has m nonsingular connected components.
Assume ![]() $n = mr$. Tensoring with a line bundle
$n = mr$. Tensoring with a line bundle ![]() ${\mathcal L} \in \Gamma = \mathrm {Pic}^0(C)[n]$ induces an
${\mathcal L} \in \Gamma = \mathrm {Pic}^0(C)[n]$ induces an ![]() ${\mathcal A}^D(\pi )$-automorphism
${\mathcal A}^D(\pi )$-automorphism
 $$ \begin{align} \phi_{\mathcal L}: {\mathcal M}_{r,L}^D(\pi) \xrightarrow{\simeq} {\mathcal M}_{r,L}^D(\pi), \quad \phi_{\mathcal L} ({\mathcal E}, \theta) = ({\mathcal L}\otimes {\mathcal E} , \theta). \end{align} $$
$$ \begin{align} \phi_{\mathcal L}: {\mathcal M}_{r,L}^D(\pi) \xrightarrow{\simeq} {\mathcal M}_{r,L}^D(\pi), \quad \phi_{\mathcal L} ({\mathcal E}, \theta) = ({\mathcal L}\otimes {\mathcal E} , \theta). \end{align} $$Moreover, for a general point ![]() $a \in {\mathcal A}^D(\pi )$ corresponding to a degree
$a \in {\mathcal A}^D(\pi )$ corresponding to a degree ![]() $n=rm$ spectral cover
$n=rm$ spectral cover
 $$ \begin{align*} g_a: C^{\prime}_a \to C' \xrightarrow{\pi} C, \end{align*} $$
$$ \begin{align*} g_a: C^{\prime}_a \to C' \xrightarrow{\pi} C, \end{align*} $$the fibre  ${\left (h_{\pi }^D\right )}^{-1}(a)$ is identical to a fibre of the morphism
${\left (h_{\pi }^D\right )}^{-1}(a)$ is identical to a fibre of the morphism
 $$ \begin{align*} {g_a}_*: \mathrm{Pic}^d\left(C^{\prime}_a\right) \rightarrow \mathrm{Pic}^d(C), \quad {\mathcal L} \mapsto \mathrm{det}\left({g_a}_* {\mathcal L}\right), \end{align*} $$
$$ \begin{align*} {g_a}_*: \mathrm{Pic}^d\left(C^{\prime}_a\right) \rightarrow \mathrm{Pic}^d(C), \quad {\mathcal L} \mapsto \mathrm{det}\left({g_a}_* {\mathcal L}\right), \end{align*} $$where ![]() $\Gamma $ acts transitively on the set of its connected components (compare [Reference Hausel and Pauly21, Lemmas 2.1 and 2,2]). This ensures that
$\Gamma $ acts transitively on the set of its connected components (compare [Reference Hausel and Pauly21, Lemmas 2.1 and 2,2]). This ensures that ![]() $\Gamma $ acts transitively on
$\Gamma $ acts transitively on ![]() $\{M_i\}_{1\leq i\leq m}$. In particular, for any pair
$\{M_i\}_{1\leq i\leq m}$. In particular, for any pair ![]() $1\leq i,j \leq m$, there exists a line bundle
$1\leq i,j \leq m$, there exists a line bundle ![]() ${\mathcal L}_{ij}\in \Gamma $ such that the isomorphism
${\mathcal L}_{ij}\in \Gamma $ such that the isomorphism ![]() $\phi _{ij} = \phi _{{\mathcal L}_{ij}}$ given in formula (22) satisfies the commutative diagram (20). Thus (a) and (b) are proved.
$\phi _{ij} = \phi _{{\mathcal L}_{ij}}$ given in formula (22) satisfies the commutative diagram (20). Thus (a) and (b) are proved.
1.3 Weil pairing and cyclic covers
Recall from Section 0.1 that the group ![]() $\Gamma = \mathrm {Pic}^0(C)[n]$ acts on the
$\Gamma = \mathrm {Pic}^0(C)[n]$ acts on the ![]() $\mathrm {SL}_n$-moduli space
$\mathrm {SL}_n$-moduli space  ${\mathcal M}^D_{n,L}$ via the tensor product. For
${\mathcal M}^D_{n,L}$ via the tensor product. For ![]() $\gamma \in \Gamma $, the
$\gamma \in \Gamma $, the ![]() $\gamma $-fixed subvariety
$\gamma $-fixed subvariety  ${\mathcal M}^D_{\gamma } \subset {\mathcal M}^D_{n,L}$ carries an induced Hitchin map
${\mathcal M}^D_{\gamma } \subset {\mathcal M}^D_{n,L}$ carries an induced Hitchin map

As indicated by Theorem 0.3, the cohomology of  ${\mathcal M}^D_{\gamma }$ is related to a
${\mathcal M}^D_{\gamma }$ is related to a ![]() $\kappa $-isotypic component of the cohomology of
$\kappa $-isotypic component of the cohomology of  ${\mathcal M}^D_{n,L}$ with respect to the
${\mathcal M}^D_{n,L}$ with respect to the ![]() $\Gamma $-action.
$\Gamma $-action.
In order to describe this connection, we need a correspondence (3) between an element ![]() $\gamma \in \Gamma $ and a character
$\gamma \in \Gamma $ and a character ![]() $\kappa \in \hat {\Gamma }$, which we review in the following.
$\kappa \in \hat {\Gamma }$, which we review in the following.
Let ![]() $\mu _n \subset {\mathbb {C}}^*$ denote the finite group of the nth roots of unity. We have the Weil pairing on the group of n-torsion points of
$\mu _n \subset {\mathbb {C}}^*$ denote the finite group of the nth roots of unity. We have the Weil pairing on the group of n-torsion points of ![]() $\mathrm {Pic}^0(C)$,
$\mathrm {Pic}^0(C)$,
Under the identification
the Weil pairing coincides with the intersection pairing on ![]() $H_1(C, {\mathbb {Z}}/n{\mathbb {Z}})$. In particular, it is nondegenerate, which induces a character
$H_1(C, {\mathbb {Z}}/n{\mathbb {Z}})$. In particular, it is nondegenerate, which induces a character
for each ![]() $\gamma \in \Gamma $. This gives the identification (3).
$\gamma \in \Gamma $. This gives the identification (3).
We also note that an element ![]() $\gamma \in \Gamma $ naturally corresponds to a cyclic Galois cover of C whose degree is the order of
$\gamma \in \Gamma $ naturally corresponds to a cyclic Galois cover of C whose degree is the order of ![]() $\gamma \in \Gamma $. In fact, for fixed
$\gamma \in \Gamma $. In fact, for fixed ![]() $\gamma \in \Gamma $, we denote by
$\gamma \in \Gamma $, we denote by ![]() $L_{\gamma }$ the n-torsion line bundle associated with
$L_{\gamma }$ the n-torsion line bundle associated with ![]() $\gamma $, and let m be its order which divides n. Taking the mth roots of unity fibrewise inside the total space of
$\gamma $, and let m be its order which divides n. Taking the mth roots of unity fibrewise inside the total space of ![]() $L_{\gamma }$ with respect to the zero section C, we obtain a cyclic Galois cover
$L_{\gamma }$ with respect to the zero section C, we obtain a cyclic Galois cover
with the Galois group ![]() $G_{\pi } \simeq \mathbb {Z}/m{\mathbb {Z}}$. Conversely, every degree m étale cyclic Galois cover arises this way.
$G_{\pi } \simeq \mathbb {Z}/m{\mathbb {Z}}$. Conversely, every degree m étale cyclic Galois cover arises this way.
1.4 Characters
In this section we give a concrete description of the character ![]() $\kappa $ in terms of the Prym variety associated with the corresponding Galois cover
$\kappa $ in terms of the Prym variety associated with the corresponding Galois cover ![]() $\pi : C' \to C$.
$\pi : C' \to C$.
As before, we assume that ![]() $\pi :C' \to C$ is a degree m cyclic Galois cover associated with
$\pi :C' \to C$ is a degree m cyclic Galois cover associated with ![]() $\kappa \in \hat {\Gamma }$ as in Section 1.3, and we assume that
$\kappa \in \hat {\Gamma }$ as in Section 1.3, and we assume that ![]() $n = mr$. The character
$n = mr$. The character ![]() $\kappa \in \hat {\Gamma }$ matches with
$\kappa \in \hat {\Gamma }$ matches with ![]() $\gamma \in \Gamma $ via equation (3). We consider the Prym variety
$\gamma \in \Gamma $ via equation (3). We consider the Prym variety
 $$ \begin{align} \mathrm{Prym}(C'/C) = \mathrm{Ker}\left( \mathrm{det}(\pi_*-): \mathrm{Pic}^0(C') \to \mathrm{Pic}^0(C) \right) \end{align} $$
$$ \begin{align} \mathrm{Prym}(C'/C) = \mathrm{Ker}\left( \mathrm{det}(\pi_*-): \mathrm{Pic}^0(C') \to \mathrm{Pic}^0(C) \right) \end{align} $$with the component group
For an n-torsion line bundle ![]() ${\mathcal L} \in \Gamma $, the projection formula yields
${\mathcal L} \in \Gamma $, the projection formula yields
In particular, the line bundle ![]() $\pi ^*{\mathcal L}^{\otimes r}\in \mathrm {Pic}^0(C')$ represents a point in
$\pi ^*{\mathcal L}^{\otimes r}\in \mathrm {Pic}^0(C')$ represents a point in ![]() $\mathrm {Prym}(C'/C))$, which yields a natural group homomorphism
$\mathrm {Prym}(C'/C))$, which yields a natural group homomorphism
 $$ \begin{align} \Gamma \rightarrow \pi_0(\mathrm{Prym}(C'/C)), \quad {\mathcal L} \mapsto \left[\pi^*{\mathcal L}^{\otimes r}\right] \in \pi_0(\mathrm{Prym}(C'/C)). \end{align} $$
$$ \begin{align} \Gamma \rightarrow \pi_0(\mathrm{Prym}(C'/C)), \quad {\mathcal L} \mapsto \left[\pi^*{\mathcal L}^{\otimes r}\right] \in \pi_0(\mathrm{Prym}(C'/C)). \end{align} $$The morphism (24) admits a factorisation
 $$ \begin{align*} \Gamma =\mathrm{Pic}^0(C)[n] \xrightarrow{[r]} \mathrm{Pic}^0(C)[m] \rightarrow \pi_0(\mathrm{Prym}(C'/C)). \end{align*} $$
$$ \begin{align*} \Gamma =\mathrm{Pic}^0(C)[n] \xrightarrow{[r]} \mathrm{Pic}^0(C)[m] \rightarrow \pi_0(\mathrm{Prym}(C'/C)). \end{align*} $$The first map is multiplication by r, which is clearly surjective. The second map sends ![]() ${\mathcal L} \in \mathrm {Pic}^0(C)[m]$ to the equivalent class of the line bundle
${\mathcal L} \in \mathrm {Pic}^0(C)[m]$ to the equivalent class of the line bundle ![]() $\pi ^*{\mathcal L} \in \mathrm {Prym}(C'/C)$, and its surjectivity is given by the proof of [Reference Hausel and Pauly21, Theorem 1.1 (2)]. Hence formula (24) is surjective.
$\pi ^*{\mathcal L} \in \mathrm {Prym}(C'/C)$, and its surjectivity is given by the proof of [Reference Hausel and Pauly21, Theorem 1.1 (2)]. Hence formula (24) is surjective.
Recall that ![]() $\gamma \in \Gamma $ is of order m, so
$\gamma \in \Gamma $ is of order m, so
The following lemma is obtained by viewing the Weil pairing on ![]() $\mathrm {Pic}^0(C)[i]$ for any
$\mathrm {Pic}^0(C)[i]$ for any ![]() $i \in {\mathbb {N}}$, via Poincaré duality, as the intersection pairing
$i \in {\mathbb {N}}$, via Poincaré duality, as the intersection pairing
Lemma 1.2. Assume ![]() $\gamma ' \in \Gamma $. We let
$\gamma ' \in \Gamma $. We let ![]() $\langle ~, ~\rangle _{\mathrm {Pic}^0(C)[m]}$ denote the Weil pairing on
$\langle ~, ~\rangle _{\mathrm {Pic}^0(C)[m]}$ denote the Weil pairing on ![]() $\mathrm {Pic}^0(C)[m]$, and we view
$\mathrm {Pic}^0(C)[m]$, and we view ![]() $r\gamma '$ naturally as an element in
$r\gamma '$ naturally as an element in ![]() $\mathrm {Pic}^0(C)[m]$. We have
$\mathrm {Pic}^0(C)[m]$. We have
 $$ \begin{align*} \langle \gamma, \gamma'\rangle_{\Gamma} = \langle \gamma, r\gamma'\rangle_{\mathrm{Pic}^0(C)[m]}. \end{align*} $$
$$ \begin{align*} \langle \gamma, \gamma'\rangle_{\Gamma} = \langle \gamma, r\gamma'\rangle_{\mathrm{Pic}^0(C)[m]}. \end{align*} $$Proposition 1.3. The character ![]() $\kappa \in \hat {\Gamma }$ (corresponding to
$\kappa \in \hat {\Gamma }$ (corresponding to ![]() $\pi :C' \to C$) factors through a character of
$\pi :C' \to C$) factors through a character of ![]() $\pi _0(\mathrm {Prym}(C'/C))$ of order m via the morphism (24):
$\pi _0(\mathrm {Prym}(C'/C))$ of order m via the morphism (24):
Proof. Recall from Section 1.3 that the character ![]() $\kappa $ is given by the Weil pairing
$\kappa $ is given by the Weil pairing ![]() $\langle \gamma , ~\rangle _{\Gamma }$, where
$\langle \gamma , ~\rangle _{\Gamma }$, where ![]() $\gamma \in \Gamma $ corresponds to
$\gamma \in \Gamma $ corresponds to ![]() $\pi $. We have that
$\pi $. We have that ![]() $\gamma $ is of order m – that is,
$\gamma $ is of order m – that is,
Therefore Lemma 1.2 implies for any element ![]() $\gamma ' \in \Gamma $ that
$\gamma ' \in \Gamma $ that
 $$ \begin{align} \kappa(\gamma') = \langle \gamma, \gamma'\rangle_{\Gamma} = \langle \gamma, r\gamma'\rangle_{\mathrm{Pic}^0(C)[m]}. \end{align} $$
$$ \begin{align} \kappa(\gamma') = \langle \gamma, \gamma'\rangle_{\Gamma} = \langle \gamma, r\gamma'\rangle_{\mathrm{Pic}^0(C)[m]}. \end{align} $$We consider the subgroup
 $$ \begin{align*} K = \mathrm{Ker}\left\{ \pi^*: \mathrm{Pic}^0(C) \to \mathrm{Pic}^0(C') \right\} \subset \mathrm{Pic}^0(C). \end{align*} $$
$$ \begin{align*} K = \mathrm{Ker}\left\{ \pi^*: \mathrm{Pic}^0(C) \to \mathrm{Pic}^0(C') \right\} \subset \mathrm{Pic}^0(C). \end{align*} $$It is the cyclic finite subgroup ![]() $\langle \gamma \rangle $ of
$\langle \gamma \rangle $ of ![]() $\mathrm {Pic}^0(C)$ generated by
$\mathrm {Pic}^0(C)$ generated by ![]() $\gamma $. Since
$\gamma $. Since ![]() $\gamma $ is of order m, we have
$\gamma $ is of order m, we have ![]() $K \subset \mathrm {Pic}^0(C)[m]$. By the proof of [Reference Hausel and Pauly21, Theorem 1.1 (1)], there is a canonical isomorphism
$K \subset \mathrm {Pic}^0(C)[m]$. By the proof of [Reference Hausel and Pauly21, Theorem 1.1 (1)], there is a canonical isomorphism
which, for any ![]() ${\mathcal L}\in \mathrm {Pic}^0(C)[m]$, identifies
${\mathcal L}\in \mathrm {Pic}^0(C)[m]$, identifies ![]() $[\pi ^*{\mathcal L}]\in \pi _0(\mathrm {Prym}(C'/C))$ with the character of K sending the generator
$[\pi ^*{\mathcal L}]\in \pi _0(\mathrm {Prym}(C'/C))$ with the character of K sending the generator ![]() $\gamma \in K$ to
$\gamma \in K$ to
 $$ \begin{align*} \langle \gamma, {\mathcal L}\rangle_{\mathrm{Pic}^0(C)[m]} \in \mu_m \subset {\mathbb{C}}^*. \end{align*} $$
$$ \begin{align*} \langle \gamma, {\mathcal L}\rangle_{\mathrm{Pic}^0(C)[m]} \in \mu_m \subset {\mathbb{C}}^*. \end{align*} $$Comparing with equation (25), this implies that ![]() $\kappa : \Gamma \to {\mathbb {C}}^*$ is the composition of formula (24) and the order m character of
$\kappa : \Gamma \to {\mathbb {C}}^*$ is the composition of formula (24) and the order m character of ![]() $\pi _0(\mathrm {Prym}(C'/C))$ given by
$\pi _0(\mathrm {Prym}(C'/C))$ given by
Here we dualise equation (26) in the last identity. This completes the proof.
Since ![]() ${\pi _0(\mathrm {Prym}(C'/C))}\cong {\mathbb {Z}}/m{\mathbb {Z}}$, its character group is also cyclic. We obtain the following corollary of Proposition 1.3:
${\pi _0(\mathrm {Prym}(C'/C))}\cong {\mathbb {Z}}/m{\mathbb {Z}}$, its character group is also cyclic. We obtain the following corollary of Proposition 1.3:
Corollary 1.4. A character ![]() $\rho : \Gamma \to {\mathbb {C}}^*$ lies in the cyclic subgroup
$\rho : \Gamma \to {\mathbb {C}}^*$ lies in the cyclic subgroup ![]() $\langle \kappa \rangle \subset \hat {\Gamma }$ if and only if
$\langle \kappa \rangle \subset \hat {\Gamma }$ if and only if ![]() $\rho $ is induced by a character of
$\rho $ is induced by a character of ![]() $\pi _0(\mathrm {Prym}(C'/C))$ factoring through formula (24).
$\pi _0(\mathrm {Prym}(C'/C))$ factoring through formula (24).
Now we consider the kernel of the morphism (24), which we denote by
The subgroup ![]() $\Omega $ acts on the moduli space
$\Omega $ acts on the moduli space  ${\mathcal M}^D_{r,L}(\pi )$ via the tensor product.
${\mathcal M}^D_{r,L}(\pi )$ via the tensor product.
Lemma 1.5. The ![]() $\Omega $-action on
$\Omega $-action on  ${\mathcal M}^D_{r,L}(\pi )$ preserves each connected component
${\mathcal M}^D_{r,L}(\pi )$ preserves each connected component ![]() $M_i$ of equation (19).
$M_i$ of equation (19).
Proof. Recall that  ${\mathcal M}_{r,L}^D(\pi )$ is a fibre of
${\mathcal M}_{r,L}^D(\pi )$ is a fibre of
 $$ \begin{align*} q_{\pi} = (\pi_*) \circ q: \widetilde{{\mathcal M}}_{r,d}^{D'}(C') \xrightarrow{q} \widetilde{{\mathcal M}}_{1,d}^{D'}(C') \xrightarrow{\pi_*} \widetilde{{\mathcal M}}_{1,d}^{D}(C). \end{align*} $$
$$ \begin{align*} q_{\pi} = (\pi_*) \circ q: \widetilde{{\mathcal M}}_{r,d}^{D'}(C') \xrightarrow{q} \widetilde{{\mathcal M}}_{1,d}^{D'}(C') \xrightarrow{\pi_*} \widetilde{{\mathcal M}}_{1,d}^{D}(C). \end{align*} $$The fibres of the first map are connected. The second map respects the product structure (21). Both the maps q and ![]() $\pi _*$ are
$\pi _*$ are ![]() $\Gamma $-equivariant. Hence the m connected components of equation (19) match the connected components of the degree d Prym variety
$\Gamma $-equivariant. Hence the m connected components of equation (19) match the connected components of the degree d Prym variety
Since ![]() $\mathrm {Prym}^d(C'/C)$ is a torsor of
$\mathrm {Prym}^d(C'/C)$ is a torsor of ![]() $\mathrm {Prym}(C'/C)$ (defined in equation (23)), and by definition the group
$\mathrm {Prym}(C'/C)$ (defined in equation (23)), and by definition the group ![]() $\Omega $ acts trivially on the component group
$\Omega $ acts trivially on the component group ![]() $\pi _0(\mathrm {Prym}(C'/C))$, we obtain that the action of
$\pi _0(\mathrm {Prym}(C'/C))$, we obtain that the action of ![]() $\Omega $ preserves each connected component of
$\Omega $ preserves each connected component of ![]() $\mathrm {Prym}^d(C'/C)$. The proposition then follows from the fact that the restriction of q to
$\mathrm {Prym}^d(C'/C)$. The proposition then follows from the fact that the restriction of q to  ${\mathcal M}^D_{r,d}(\pi )$,
${\mathcal M}^D_{r,d}(\pi )$,
 $$ \begin{align*}q|_{\left(\pi_*\right)^{-1}\left(L,0\right)}: {\mathcal M}^D_{r,L}(\pi) \to (\pi_*)^{-1}(L,0) = \mathrm{Prym}^d(C'/C)\times H^0(C', {\mathcal O}_{C'}(D'))_{\mathrm{var}}, \end{align*} $$
$$ \begin{align*}q|_{\left(\pi_*\right)^{-1}\left(L,0\right)}: {\mathcal M}^D_{r,L}(\pi) \to (\pi_*)^{-1}(L,0) = \mathrm{Prym}^d(C'/C)\times H^0(C', {\mathcal O}_{C'}(D'))_{\mathrm{var}}, \end{align*} $$is ![]() $\Omega $-equivariant.
$\Omega $-equivariant.
1.5 Endoscopic moduli spaces and  $\gamma $-fixed loci
$\gamma $-fixed loci
In this section, we connect the ![]() $\gamma $-fixed subvariety
$\gamma $-fixed subvariety  ${\mathcal M}^D_{\gamma }$ to the relative Hitchin moduli spaces introduced in Section 1.2.
${\mathcal M}^D_{\gamma }$ to the relative Hitchin moduli spaces introduced in Section 1.2.
We fix ![]() $\gamma \in \Gamma $ of order m. Let
$\gamma \in \Gamma $ of order m. Let ![]() $\pi : C' \rightarrow C$ be the cyclic Galois cover with the Galois group
$\pi : C' \rightarrow C$ be the cyclic Galois cover with the Galois group ![]() $G_{\pi } \simeq \mathbb {Z}/m{\mathbb {Z}}$ corresponding to
$G_{\pi } \simeq \mathbb {Z}/m{\mathbb {Z}}$ corresponding to ![]() $\gamma $, as in Section 1.3. Assume
$\gamma $, as in Section 1.3. Assume ![]() $n=mr$. We consider the relative Hitchin moduli space
$n=mr$. We consider the relative Hitchin moduli space  ${\mathcal M}^D_{r,L}(\pi )$ with the Hitchin fibration
${\mathcal M}^D_{r,L}(\pi )$ with the Hitchin fibration
 $$ \begin{align} h_{\pi}^D:{\mathcal M}^D_{r,L}(\pi) \rightarrow {\mathcal A}^D(\pi). \end{align} $$
$$ \begin{align} h_{\pi}^D:{\mathcal M}^D_{r,L}(\pi) \rightarrow {\mathcal A}^D(\pi). \end{align} $$ By [Reference Hausel and Thaddeus22, Proposition 7.1], the Galois group ![]() $G_{\pi }$ acts freely on the relative moduli space
$G_{\pi }$ acts freely on the relative moduli space  ${\mathcal M}^D_{r,L}(\pi )$ whose quotient recovers the
${\mathcal M}^D_{r,L}(\pi )$ whose quotient recovers the ![]() $\gamma $-fixed subvariety
$\gamma $-fixed subvariety  ${\mathcal M}^D_{\gamma }$. The group
${\mathcal M}^D_{\gamma }$. The group ![]() $G_{\pi }$ also acts on the base
$G_{\pi }$ also acts on the base ![]() ${\mathcal A}^D(\pi )$ with the Hitchin map (28)
${\mathcal A}^D(\pi )$ with the Hitchin map (28) ![]() $G_{\pi }$-equivariant. In summary, we have the following commutative diagram:
$G_{\pi }$-equivariant. In summary, we have the following commutative diagram:

where ![]() $q_{\mathcal M}$ and
$q_{\mathcal M}$ and ![]() $q_{\mathcal A}$ are the quotient maps with respect to the natural actions of the Galois group
$q_{\mathcal A}$ are the quotient maps with respect to the natural actions of the Galois group ![]() $G_{\pi }$. Let
$G_{\pi }$. Let ![]() ${\mathcal A}^D(\pi )^*$ be the largest open subset of
${\mathcal A}^D(\pi )^*$ be the largest open subset of ![]() ${\mathcal A}^D(\pi )$ upon which the
${\mathcal A}^D(\pi )$ upon which the ![]() $G_{\pi }$-action is free. Then the left diagram is Cartesian after restricting to
$G_{\pi }$-action is free. Then the left diagram is Cartesian after restricting to
 $$ \begin{align*} {\mathcal A}^D(\pi)^* \xrightarrow{~~~q_{\mathcal A}~~~} {{\mathcal A}_{\gamma}^{D}}^*:= {\mathcal A}^D(\pi)^*/G_{\pi}. \end{align*} $$
$$ \begin{align*} {\mathcal A}^D(\pi)^* \xrightarrow{~~~q_{\mathcal A}~~~} {{\mathcal A}_{\gamma}^{D}}^*:= {\mathcal A}^D(\pi)^*/G_{\pi}. \end{align*} $$Remark 1.6. We see from the description (equation (18)) that ![]() ${\mathcal A}^D(\pi )^*$ is nonempty. In fact, it suffices to find vectors in the affine space
${\mathcal A}^D(\pi )^*$ is nonempty. In fact, it suffices to find vectors in the affine space ![]() ${\mathcal A}^D(\pi )$ that are not fixed by any nontrivial element of the cyclic group
${\mathcal A}^D(\pi )$ that are not fixed by any nontrivial element of the cyclic group ![]() $G_{\pi }$. We consider the push-forward of the structure sheaf
$G_{\pi }$. We consider the push-forward of the structure sheaf ![]() ${\mathcal O}_{C'}$ along the Galois cover
${\mathcal O}_{C'}$ along the Galois cover ![]() $\pi : C' \to C$, which admits a splitting
$\pi : C' \to C$, which admits a splitting ![]() $\pi _* {\mathcal O}_{C'} = \oplus _\chi L_\chi $, where
$\pi _* {\mathcal O}_{C'} = \oplus _\chi L_\chi $, where ![]() $\chi $ runs through all characters of
$\chi $ runs through all characters of ![]() $G_{\pi }$ and
$G_{\pi }$ and ![]() $L_\chi $ is a degree
$L_\chi $ is a degree ![]() $0$ line bundle corresponding to
$0$ line bundle corresponding to ![]() $\chi $. The projection formula yields
$\chi $. The projection formula yields
 $$ \begin{align*} \pi_* {\mathcal O}_{C'}(iD') = \pi_* \pi^* {\mathcal O}_C(iD) = \bigoplus_{\chi} {\mathcal O}_C(iD)\otimes L_\chi,\quad \forall \ i \geq 1. \end{align*} $$
$$ \begin{align*} \pi_* {\mathcal O}_{C'}(iD') = \pi_* \pi^* {\mathcal O}_C(iD) = \bigoplus_{\chi} {\mathcal O}_C(iD)\otimes L_\chi,\quad \forall \ i \geq 1. \end{align*} $$In particular, for any character ![]() $\chi $ of
$\chi $ of ![]() $G_{\pi }$, we have
$G_{\pi }$, we have
 $$ \begin{align} H^0(C',{\mathcal O}_{C'}(iD'))_\chi=H^0(C, {\mathcal O}_{C}(iD)\otimes L_\chi) \neq 0, \end{align} $$
$$ \begin{align} H^0(C',{\mathcal O}_{C'}(iD'))_\chi=H^0(C, {\mathcal O}_{C}(iD)\otimes L_\chi) \neq 0, \end{align} $$where we used the Riemann–Roch formula. The nonemptiness of ![]() ${\mathcal A}^D(\pi )^*$ follows from equations (30) and (18).
${\mathcal A}^D(\pi )^*$ follows from equations (30) and (18).
Lemma 1.7. The direct image complex
 $$ \begin{align*} {\mathrm{Rh}^{\text{D}}_{\pi}}_* {\underline{{\mathbb{C}}}} \in D^b_c\left({\mathcal A}^D(\pi)\right) \end{align*} $$
$$ \begin{align*} {\mathrm{Rh}^{\text{D}}_{\pi}}_* {\underline{{\mathbb{C}}}} \in D^b_c\left({\mathcal A}^D(\pi)\right) \end{align*} $$is ![]() $G_{\pi }$-equivariant, and we have a canonical isomorphism
$G_{\pi }$-equivariant, and we have a canonical isomorphism
 $$ \begin{align*} \left( {q_{\mathcal A}}_* {\mathrm{Rh}^D_{\pi}}_* {\underline{{\mathbb{C}}}} \right)^{G_{\pi}} \xrightarrow{\simeq} {\mathrm{Rh}^D_{\gamma}}_* {\underline{{\mathbb{C}}}} \in D^b_c\left({\mathcal A}^D_{\gamma}\right). \end{align*} $$
$$ \begin{align*} \left( {q_{\mathcal A}}_* {\mathrm{Rh}^D_{\pi}}_* {\underline{{\mathbb{C}}}} \right)^{G_{\pi}} \xrightarrow{\simeq} {\mathrm{Rh}^D_{\gamma}}_* {\underline{{\mathbb{C}}}} \in D^b_c\left({\mathcal A}^D_{\gamma}\right). \end{align*} $$Proof. Since the trivial local system on  ${\mathcal M}^D_{r,L}(\pi )$ is
${\mathcal M}^D_{r,L}(\pi )$ is ![]() $G_{\pi }$-equivariant, the push-forward
$G_{\pi }$-equivariant, the push-forward ![]() ${q_{\mathcal M}}_* {\underline {{\mathbb {C}}}}$ along the quotient map
${q_{\mathcal M}}_* {\underline {{\mathbb {C}}}}$ along the quotient map ![]() $q_{\mathcal M}$ admits a natural
$q_{\mathcal M}$ admits a natural ![]() $G_{\pi }$-action with a canonical isomorphism
$G_{\pi }$-action with a canonical isomorphism
 $$ \begin{align} \left( {q_{\mathcal M}}_* {\underline{{\mathbb{C}}}} \right)^{G_{\pi}} \xrightarrow{\simeq} {\underline{{\mathbb{C}}}} \in D^b_c\left({\mathcal M}^D_{\gamma}\right). \end{align} $$
$$ \begin{align} \left( {q_{\mathcal M}}_* {\underline{{\mathbb{C}}}} \right)^{G_{\pi}} \xrightarrow{\simeq} {\underline{{\mathbb{C}}}} \in D^b_c\left({\mathcal M}^D_{\gamma}\right). \end{align} $$The map ![]() $h^D_{\pi }$ is
$h^D_{\pi }$ is ![]() $G_{\pi }$-equivalent, and therefore we obtain in
$G_{\pi }$-equivalent, and therefore we obtain in  $D^b_c\left ({\mathcal A}^D_{\gamma }\right )$ that
$D^b_c\left ({\mathcal A}^D_{\gamma }\right )$ that
 $$ \begin{align*} \left({q_{\mathcal A}}_* {\mathrm{Rh}^{\text{D}}_{\pi}}_* {\underline{{\mathbb{C}}}} \right)^{G_{\pi}} =\left({\mathrm{Rh}^{\text{D}}_{\gamma}}_* {q_{\mathcal M}}_* {\underline{{\mathbb{C}}}} \right)^{G_{\pi}} = {\mathrm{Rh}^{\text{D}}_{\gamma}}_*\left( {q_{\mathcal M}}_* {\underline{{\mathbb{C}}}} \right)^{G_{\pi}} \xrightarrow{\simeq} {\mathrm{Rh}^{\text{D}}_{\gamma}}_*{\underline{{\mathbb{C}}}}, \end{align*} $$
$$ \begin{align*} \left({q_{\mathcal A}}_* {\mathrm{Rh}^{\text{D}}_{\pi}}_* {\underline{{\mathbb{C}}}} \right)^{G_{\pi}} =\left({\mathrm{Rh}^{\text{D}}_{\gamma}}_* {q_{\mathcal M}}_* {\underline{{\mathbb{C}}}} \right)^{G_{\pi}} = {\mathrm{Rh}^{\text{D}}_{\gamma}}_*\left( {q_{\mathcal M}}_* {\underline{{\mathbb{C}}}} \right)^{G_{\pi}} \xrightarrow{\simeq} {\mathrm{Rh}^{\text{D}}_{\gamma}}_*{\underline{{\mathbb{C}}}}, \end{align*} $$where the last isomorphism is induced by formula (31).
2 Support theorems for Hitchin moduli spaces
2.1 Supports
Let ![]() $f: X\to Y$ be a proper morphism between nonsingular quasi-projective varieties. The decomposition theorem of Bernstein, Beilinson, Deligne and Gabber [Reference Beĭlinson, Bernstein and Deligne3] implies that the direct image complex
$f: X\to Y$ be a proper morphism between nonsingular quasi-projective varieties. The decomposition theorem of Bernstein, Beilinson, Deligne and Gabber [Reference Beĭlinson, Bernstein and Deligne3] implies that the direct image complex ![]() $\mathrm {Rf}_{\ast } {\underline {{\mathbb {C}}}}$ is (noncanonically) isomorphic to a direct sum of shifted simple perverse sheaves:
$\mathrm {Rf}_{\ast } {\underline {{\mathbb {C}}}}$ is (noncanonically) isomorphic to a direct sum of shifted simple perverse sheaves:
 $$ \begin{align} \mathrm{Rf}_* {\underline{{\mathbb{C}}}} \simeq \bigoplus_{Z_i} \mathrm{IC}_{Z_i}(L_i)[d_i] \in D^b_c(Y), \end{align} $$
$$ \begin{align} \mathrm{Rf}_* {\underline{{\mathbb{C}}}} \simeq \bigoplus_{Z_i} \mathrm{IC}_{Z_i}(L_i)[d_i] \in D^b_c(Y), \end{align} $$where ![]() $d_i \in {\mathbb {Z}}$,
$d_i \in {\mathbb {Z}}$, ![]() $Z_i \subset Y$ is an irreducible subvariety and
$Z_i \subset Y$ is an irreducible subvariety and ![]() $L_i$ is a local system on an open subset
$L_i$ is a local system on an open subset ![]() $U_i$ of
$U_i$ of ![]() $Z_i$. Every
$Z_i$. Every ![]() $Z_i$ here is called a support of
$Z_i$ here is called a support of ![]() $f: X\to Y$. We say that a direct summand
$f: X\to Y$. We say that a direct summand ![]() ${\mathcal F}$ of the object
${\mathcal F}$ of the object
has full support if each perverse constituent ![]() $ \mathrm {IC}_{Z_i}(L_i)[d_i]$ of
$ \mathrm {IC}_{Z_i}(L_i)[d_i]$ of ![]() ${\mathcal F}$ has support
${\mathcal F}$ has support ![]() $Z_i = Y$.
$Z_i = Y$.
In this section, we analyse the supports of various Hitchin fibrations introduced in Section 1 when ![]() $\mathrm {deg}(D)>2g-2$.
$\mathrm {deg}(D)>2g-2$.
2.2 Support theorems
For the Hitchin fibration ![]() $h^D$ (resp.,
$h^D$ (resp., ![]() $h^D_{\pi }$), we define the elliptic locus of the Hitchin bases
$h^D_{\pi }$), we define the elliptic locus of the Hitchin bases ![]() ${\mathcal A}^D$ (resp.,
${\mathcal A}^D$ (resp., ![]() ${\mathcal A}^D(\pi )$), denoted by
${\mathcal A}^D(\pi )$), denoted by ![]() ${\mathcal A}^{D,\mathrm {ell}}$ (resp.,
${\mathcal A}^{D,\mathrm {ell}}$ (resp., ![]() ${\mathcal A}^{D,\mathrm {ell}}(\pi ))$, to be the open subset consisting of integral spectral curves.
${\mathcal A}^{D,\mathrm {ell}}(\pi ))$, to be the open subset consisting of integral spectral curves.
Following the methods of Ngô [Reference Ngô33] and Chaudouard and Laumon [Reference Chaudouard and Laumon5], de Cataldo showed in [Reference de Cataldo6] that all the supports for the ![]() $\mathrm {SL}_n$-Hitchin fibration (12) are governed by the elliptic locus
$\mathrm {SL}_n$-Hitchin fibration (12) are governed by the elliptic locus ![]() ${\mathcal A}^{D,\mathrm {ell}} \subset {\mathcal A}^D$ when
${\mathcal A}^{D,\mathrm {ell}} \subset {\mathcal A}^D$ when ![]() $\mathrm {deg}(D)>2g-2$.
$\mathrm {deg}(D)>2g-2$.
Theorem 2.1 [Reference de Cataldo6, Theorem 1.0.2]
Let D be an effective divisor on C of degree ![]() $\mathrm {deg}(D)>2g-2$. Then the generic points of the supports of
$\mathrm {deg}(D)>2g-2$. Then the generic points of the supports of
 $$ \begin{align*} h^D: {\mathcal M}^D_{n,L} \to {\mathcal A}^D \end{align*} $$
$$ \begin{align*} h^D: {\mathcal M}^D_{n,L} \to {\mathcal A}^D \end{align*} $$are contained in ![]() ${\mathcal A}^{D,\mathrm {ell}} \subset {\mathcal A}^D$.
${\mathcal A}^{D,\mathrm {ell}} \subset {\mathcal A}^D$.
Now we consider the ![]() $\Gamma $-action on the moduli space
$\Gamma $-action on the moduli space  ${\mathcal M}^D_{n,L}$. This action is fibrewise with respect to the Hitchin map
${\mathcal M}^D_{n,L}$. This action is fibrewise with respect to the Hitchin map ![]() $h^D$, which induces a canonical decomposition of the direct image complex
$h^D$, which induces a canonical decomposition of the direct image complex
 $$ \begin{align} \mathrm{Rh}^{\text{D}}_{*} {\underline{{\mathbb{C}}}} = \bigoplus_{\kappa \in \hat{\Gamma}} \left(\mathrm{Rh}^{\text{D}}_{*} {\underline{{\mathbb{C}}}} \right)_{\kappa} \in D^b_c\left({\mathcal A}^D\right) \end{align} $$
$$ \begin{align} \mathrm{Rh}^{\text{D}}_{*} {\underline{{\mathbb{C}}}} = \bigoplus_{\kappa \in \hat{\Gamma}} \left(\mathrm{Rh}^{\text{D}}_{*} {\underline{{\mathbb{C}}}} \right)_{\kappa} \in D^b_c\left({\mathcal A}^D\right) \end{align} $$(see [Reference Laumon and Ngô28, Lemma 3.2.5]). We define the stable part  $\left (\mathrm {Rh}^{\text {D}}_{*} {\underline {{\mathbb {C}}}} \right )_{\mathrm {st}}$ as the component in equation (33) corresponding to the trivial character
$\left (\mathrm {Rh}^{\text {D}}_{*} {\underline {{\mathbb {C}}}} \right )_{\mathrm {st}}$ as the component in equation (33) corresponding to the trivial character ![]() $\kappa = 0 \in \hat {\Gamma }$.
$\kappa = 0 \in \hat {\Gamma }$.
Combining Theorem 2.1 with Ngô’s support theorems over the elliptic loci [Reference Ngô33, Theorems 7.8.3 and 7.8.5], we obtain the following complete description of the supports for every ![]() $\kappa $-part of equation (33):
$\kappa $-part of equation (33):
Corollary 2.2. The only support of  $\left (\mathrm {Rh}^{\mathrm {D}}_{*} {\underline {{\mathbb {C}}}}\right )_{\kappa }$ is
$\left (\mathrm {Rh}^{\mathrm {D}}_{*} {\underline {{\mathbb {C}}}}\right )_{\kappa }$ is  ${\mathcal A}^D_{\gamma }$, where
${\mathcal A}^D_{\gamma }$, where ![]() $\gamma $ corresponds to
$\gamma $ corresponds to ![]() $\kappa $ via equation (3).
$\kappa $ via equation (3).
The trivial character ![]() $0 \in \hat {\Gamma }$ corresponds to
$0 \in \hat {\Gamma }$ corresponds to ![]() $0 \in \Gamma $, and
$0 \in \Gamma $, and  ${\mathcal A}^D_{0} = {\mathcal A}^D$. Hence as a special case of Corollary 2.2, the stable part
${\mathcal A}^D_{0} = {\mathcal A}^D$. Hence as a special case of Corollary 2.2, the stable part  $\left (\mathrm {Rh}^{\text {D}}_{*} {\mathbb {C}} \right )_{\mathrm {st}}$ has full support
$\left (\mathrm {Rh}^{\text {D}}_{*} {\mathbb {C}} \right )_{\mathrm {st}}$ has full support ![]() ${\mathcal A}^D$.
${\mathcal A}^D$.
We fix a character ![]() $\kappa \in \hat {\Gamma }$ of order m. Let
$\kappa \in \hat {\Gamma }$ of order m. Let ![]() $\pi : C' \to C$ be the cyclic Galois cover associated with
$\pi : C' \to C$ be the cyclic Galois cover associated with ![]() $\kappa $, as in Section 1.3. Assume
$\kappa $, as in Section 1.3. Assume ![]() $n = mr$. By the projection formula, we have
$n = mr$. By the projection formula, we have
for ![]() ${\mathcal L} \in \Gamma =\mathrm {Pic}^0(C)[n]$ and
${\mathcal L} \in \Gamma =\mathrm {Pic}^0(C)[n]$ and ![]() ${\mathcal E}$ a rank r vector bundle on
${\mathcal E}$ a rank r vector bundle on ![]() $C'$. Therefore, the group
$C'$. Therefore, the group ![]() $\Gamma $ acts on the moduli space
$\Gamma $ acts on the moduli space  ${\mathcal M}^D_{r,L}(\pi )$ via the tensor product:
${\mathcal M}^D_{r,L}(\pi )$ via the tensor product:
We have a similar ![]() $\kappa $-decomposition to equation (33) for the Hitchin fibration (16) associated with
$\kappa $-decomposition to equation (33) for the Hitchin fibration (16) associated with  ${\mathcal M}^D_{r,L}(\pi )$:
${\mathcal M}^D_{r,L}(\pi )$:
 $$ \begin{align*} {\mathrm{Rh}_{\pi}^{\text{D}}}_* {\underline{{\mathbb{C}}}} = \bigoplus_{\kappa \in \hat{\Gamma}} \left({\mathrm{Rh}_{\pi}^{\text{D}}}_* {\underline{{\mathbb{C}}}} \right)_{\kappa} \in D^b_c\left({\mathcal A}^D(\pi)\right). \end{align*} $$
$$ \begin{align*} {\mathrm{Rh}_{\pi}^{\text{D}}}_* {\underline{{\mathbb{C}}}} = \bigoplus_{\kappa \in \hat{\Gamma}} \left({\mathrm{Rh}_{\pi}^{\text{D}}}_* {\underline{{\mathbb{C}}}} \right)_{\kappa} \in D^b_c\left({\mathcal A}^D(\pi)\right). \end{align*} $$ The main result of this section is to prove a support theorem for the Hitchin map (16) associated with ![]() $\pi : C' \to C$:
$\pi : C' \to C$:
Theorem 2.3. Let D be an effective divisor on C of degree ![]() $\mathrm {deg}(D)>2g-2$. Assume that the degree m Galois cover
$\mathrm {deg}(D)>2g-2$. Assume that the degree m Galois cover ![]() $\pi :C' \to C$ is associated with
$\pi :C' \to C$ is associated with ![]() $\kappa \in \hat {\Gamma }$ via equation (3). Assume
$\kappa \in \hat {\Gamma }$ via equation (3). Assume ![]() $n = mr$. Then we have the following concerning the supports of the Hitchin map
$n = mr$. Then we have the following concerning the supports of the Hitchin map  $h_{\pi }^D: {\mathcal M}_{r,L}^D(\pi ) \to {\mathcal A}^D(\pi )$:
$h_{\pi }^D: {\mathcal M}_{r,L}^D(\pi ) \to {\mathcal A}^D(\pi )$:
(a) The generic points of the supports of
 ${\mathrm {Rh}^{\text {D}}_{\pi }}_* {\underline {{\mathbb {C}}}}$ are contained in the elliptic locus
${\mathrm {Rh}^{\text {D}}_{\pi }}_* {\underline {{\mathbb {C}}}}$ are contained in the elliptic locus  ${\mathcal A}^{D,\mathrm {ell}}(\pi )$.
${\mathcal A}^{D,\mathrm {ell}}(\pi )$.(b) The stable part
 $\left ( {\mathrm {Rh}_{\pi }^{\text {D}}}_* {\mathbb {C}} \right )_{\mathrm {st}}$ has full support
$\left ( {\mathrm {Rh}_{\pi }^{\text {D}}}_* {\mathbb {C}} \right )_{\mathrm {st}}$ has full support  ${\mathcal A}^D(\pi )$.
${\mathcal A}^D(\pi )$.
The validity of the support theorems (Theorems 2.1 and 2.3) is the main ingredient in the proof of the endoscopic decomposition in the twisted case of ![]() $\mathrm {deg}(D)>2g-2$ when
$\mathrm {deg}(D)>2g-2$ when ![]() $\mathrm {deg}(D)$ is even (see the proof of Theorem 3.3).
$\mathrm {deg}(D)$ is even (see the proof of Theorem 3.3).
2.3 Weak abelian fibrations
We recall the notion of weak abelian fibration introduced in [Reference Ngô33], which is modelled on the properties of Hitchin fibrations.
We follow closely the exposition of [Reference de Cataldo6, Section 2.6]. Let A be an irreducible nonsingular variety. Assume that
are morphisms of the same relative dimensions ![]() $\mathrm {dim}(h) = \mathrm {dim}(g)$ satisfying the following properties:
$\mathrm {dim}(h) = \mathrm {dim}(g)$ satisfying the following properties:
(a) The map
 $g: P\to A$ is a smooth commutative group scheme with connected fibres.
$g: P\to A$ is a smooth commutative group scheme with connected fibres.(b) The map h is proper and M is nonsingular.
(c) The group scheme P acts on M fibrewise with affine stabilisers for every geometric point of M.
We call a triple ![]() $(M,A,P)$ a weak abelian fibration if the Tate module
$(M,A,P)$ a weak abelian fibration if the Tate module
 $$ \begin{align*} T_{\overline{{\mathbb{Q}}}_l}(P) = \mathrm{R}^{\text{2d}_{\text{g}} - 1}\text{g}_!\overline{{\mathbb{Q}}}_l\left(d_g\right) \end{align*} $$
$$ \begin{align*} T_{\overline{{\mathbb{Q}}}_l}(P) = \mathrm{R}^{\text{2d}_{\text{g}} - 1}\text{g}_!\overline{{\mathbb{Q}}}_l\left(d_g\right) \end{align*} $$as an l-adic sheaf is polarisable [Reference de Cataldo6, Section 2.6].
Over a closed point ![]() $a \in A$, we consider the Chevalley decomposition for the restricted group scheme
$a \in A$, we consider the Chevalley decomposition for the restricted group scheme ![]() $P_a$,
$P_a$,
 $$ \begin{align*} 0 \to P_a^{\mathrm{aff}} \to P_a \to P_a^{\mathrm{ab}} \to 0, \end{align*} $$
$$ \begin{align*} 0 \to P_a^{\mathrm{aff}} \to P_a \to P_a^{\mathrm{ab}} \to 0, \end{align*} $$where ![]() $P_a^{\mathrm {aff}}$ is the maximal connected affine linear subgroup of
$P_a^{\mathrm {aff}}$ is the maximal connected affine linear subgroup of ![]() $P_a$ and
$P_a$ and ![]() $P_a^{\mathrm {ab}}$ is an abelian variety.
$P_a^{\mathrm {ab}}$ is an abelian variety.
We recall in the following the support inequality of Ngô [Reference Ngô33]:
Theorem 2.4 [Reference Ngô33, Theorem 7.2.2]
Let ![]() $(M,A,P)$ be a weak abelian fibration. Assume the irreducible subvariety
$(M,A,P)$ be a weak abelian fibration. Assume the irreducible subvariety ![]() $Z \subset A$ is a support of
$Z \subset A$ is a support of ![]() $h: M \to A$; then
$h: M \to A$; then
 $$ \begin{align} \mathrm{dim}(h) -\mathrm{dim}(A) +\mathrm{dim}(Z) \geq d_Z^{\mathrm{ab}}(P). \end{align} $$
$$ \begin{align} \mathrm{dim}(h) -\mathrm{dim}(A) +\mathrm{dim}(Z) \geq d_Z^{\mathrm{ab}}(P). \end{align} $$Here  $d_Z^{\mathrm {ab}}(P)=\mathrm {dim} \left (P_a^{\mathrm {ab}}\right )$, with
$d_Z^{\mathrm {ab}}(P)=\mathrm {dim} \left (P_a^{\mathrm {ab}}\right )$, with ![]() $a \in Z$ a general point.
$a \in Z$ a general point.
2.4 Hitchin fibrations
Following [Reference Chaudouard and Laumon5, Reference de Cataldo6], we show that the Hitchin fibration
 $$ \begin{align} h_{\pi}^D: {\mathcal M}_{r,L}^D(\pi) \to {\mathcal A}^D(\pi) \end{align} $$
$$ \begin{align} h_{\pi}^D: {\mathcal M}_{r,L}^D(\pi) \to {\mathcal A}^D(\pi) \end{align} $$associated with ![]() $\pi : C' \to C$ admits the structure of a weak abelian fibration.
$\pi : C' \to C$ admits the structure of a weak abelian fibration.
Recall commutative diagram (17). The ![]() $\mathrm {GL}_r$-Hitchin base
$\mathrm {GL}_r$-Hitchin base  $\widetilde {{\mathcal A}}^{D'}(C')$ parameterises spectral curves in the total space
$\widetilde {{\mathcal A}}^{D'}(C')$ parameterises spectral curves in the total space ![]() $V(D')$ of the line bundle
$V(D')$ of the line bundle ![]() ${\mathcal O}_{C'}(D')$. We assume that
${\mathcal O}_{C'}(D')$. We assume that
 $$ \begin{align} {\mathcal C} \to \widetilde{{\mathcal A}}^{D'}(C') \end{align} $$
$$ \begin{align} {\mathcal C} \to \widetilde{{\mathcal A}}^{D'}(C') \end{align} $$is the universal spectral curve. Let  $g_{\mathcal C}: \mathrm {Pic}^0_{\mathcal C} \to \widetilde {{\mathcal A}}^{D'}(C')$ be the relative degree
$g_{\mathcal C}: \mathrm {Pic}^0_{\mathcal C} \to \widetilde {{\mathcal A}}^{D'}(C')$ be the relative degree ![]() $0$ Picard scheme associated with formula (36), which acts on
$0$ Picard scheme associated with formula (36), which acts on  $\widetilde {{\mathcal M}}^{D'}_{r,d}(C')$ via the tensor product. The following result is obtained in [Reference Chaudouard and Laumon5]; see also [Reference de Cataldo6, Section 3] for a detailed review:
$\widetilde {{\mathcal M}}^{D'}_{r,d}(C')$ via the tensor product. The following result is obtained in [Reference Chaudouard and Laumon5]; see also [Reference de Cataldo6, Section 3] for a detailed review:
Proposition 2.5 [Reference Chaudouard and Laumon5]
The triple
 $$ \begin{align} \left(\widetilde{{\mathcal M}}^{D'}_{r,d}(C'), \widetilde{{\mathcal A}}^{D'}(C'), \mathrm{Pic}^0_{\mathcal C} \right), \quad \widetilde{h}^{D'}:\widetilde{{\mathcal M}}^{D'}_{r,d}(C') \rightarrow \widetilde{{\mathcal A}}^{D'}(C'), \quad g_{\mathcal C}: \mathrm{Pic}^0_{\mathcal C} \to \widetilde{{\mathcal A}}^{D'}(C') \end{align} $$
$$ \begin{align} \left(\widetilde{{\mathcal M}}^{D'}_{r,d}(C'), \widetilde{{\mathcal A}}^{D'}(C'), \mathrm{Pic}^0_{\mathcal C} \right), \quad \widetilde{h}^{D'}:\widetilde{{\mathcal M}}^{D'}_{r,d}(C') \rightarrow \widetilde{{\mathcal A}}^{D'}(C'), \quad g_{\mathcal C}: \mathrm{Pic}^0_{\mathcal C} \to \widetilde{{\mathcal A}}^{D'}(C') \end{align} $$is a weak abelian fibration.
In order to study formula (35), we ‘fix the determinant’ after pushing forward along ![]() $\pi : C' \to C$. Since the relative Hitchin moduli space
$\pi : C' \to C$. Since the relative Hitchin moduli space  ${\mathcal M}_{r,L}^D(\pi )$ is a closed fibre of formula (14), we consider the morphism of
${\mathcal M}_{r,L}^D(\pi )$ is a closed fibre of formula (14), we consider the morphism of ![]() ${\mathcal A}^D(\pi )$-group schemes
${\mathcal A}^D(\pi )$-group schemes
 $$ \begin{align*} N_{\pi}: \mathrm{Pic}^0_{\mathcal C} \times_{\widetilde{{\mathcal A}}^{D'}\left(C'\right)}{\mathcal A}^D(\pi) \to \mathrm{Pic}^0(C)\times {\mathcal A}^D(\pi), \end{align*} $$
$$ \begin{align*} N_{\pi}: \mathrm{Pic}^0_{\mathcal C} \times_{\widetilde{{\mathcal A}}^{D'}\left(C'\right)}{\mathcal A}^D(\pi) \to \mathrm{Pic}^0(C)\times {\mathcal A}^D(\pi), \end{align*} $$given by composition of the ![]() ${\mathcal A}^D(\pi )$-morphisms
${\mathcal A}^D(\pi )$-morphisms
 $$ \begin{align*} \mathrm{Pic}^0_{\mathcal C} \times_{\widetilde{{\mathcal A}}^{D'}\left(C'\right)}A^D(\pi) \to \mathrm{Pic}^0(C') \times {\mathcal A}^D(\pi) \rightarrow \mathrm{Pic}^0(C) \times {\mathcal A}^D(\pi). \end{align*} $$
$$ \begin{align*} \mathrm{Pic}^0_{\mathcal C} \times_{\widetilde{{\mathcal A}}^{D'}\left(C'\right)}A^D(\pi) \to \mathrm{Pic}^0(C') \times {\mathcal A}^D(\pi) \rightarrow \mathrm{Pic}^0(C) \times {\mathcal A}^D(\pi). \end{align*} $$Here the first map is the restriction of the norm map ![]() $N_p$ ([Reference de Cataldo6, (42)]) to
$N_p$ ([Reference de Cataldo6, (42)]) to ![]() $A^D(\pi )$, and the second map is
$A^D(\pi )$, and the second map is
By the discussion of [Reference de Cataldo6, Section 4.1], the map ![]() $N_{\pi }$ is smooth. We let
$N_{\pi }$ is smooth. We let
be the kernel of ![]() $N_{\pi }$, and we let the group scheme
$N_{\pi }$, and we let the group scheme ![]() $g^0_{\pi }: P^0 \to {\mathcal A}^D(\pi )$ be the identity component of P. The nonsingular group schemes P and
$g^0_{\pi }: P^0 \to {\mathcal A}^D(\pi )$ be the identity component of P. The nonsingular group schemes P and ![]() $P^0$ act on
$P^0$ act on  ${\mathcal M}^D_{r,L}(\pi )$ induced by the
${\mathcal M}^D_{r,L}(\pi )$ induced by the  $\mathrm {Pic}^0_{\mathcal C}$-action on
$\mathrm {Pic}^0_{\mathcal C}$-action on  $\widetilde {{\mathcal M}}^{D'}_{r,d}(C')$.
$\widetilde {{\mathcal M}}^{D'}_{r,d}(C')$.
Proposition 2.6. The triple
 $$ \begin{align} \left( {\mathcal M}^D_{r,L}(\pi), A^D(\pi), P^0 \right), \quad h_{\pi}^D: {\mathcal M}^D_{r,L}(\pi)\to A^D(\pi), \quad g^0_{\pi}: P^0 \to A^D(\pi) \end{align} $$
$$ \begin{align} \left( {\mathcal M}^D_{r,L}(\pi), A^D(\pi), P^0 \right), \quad h_{\pi}^D: {\mathcal M}^D_{r,L}(\pi)\to A^D(\pi), \quad g^0_{\pi}: P^0 \to A^D(\pi) \end{align} $$is a weak abelian fibration.
Proof. The weak abelian fibration structure for formula (39) is essentially inherited from that for formula (37). The proof is parallel to [Reference de Cataldo6, Section 4]. Here we summarise some necessary minor modifications.
It is clear that Section 2.3(a) and (c) follow from the construction. We need to verify (b), and show that the Tate module associated with ![]() $g_{\pi }: P \to {\mathcal A}^D(\pi )$ is polarisable.
$g_{\pi }: P \to {\mathcal A}^D(\pi )$ is polarisable.
(i) Affine stabilisers. For a closed point in ${\mathcal M}^D_{r,L}(\pi ) \subset \widetilde {{\mathcal M}}^{D'}_{r,d}(C')$, its stabiliser with respect to the
${\mathcal M}^D_{r,L}(\pi ) \subset \widetilde {{\mathcal M}}^{D'}_{r,d}(C')$, its stabiliser with respect to the ![]() $P^0$-action on
$P^0$-action on  ${\mathcal M}^D_{r,L}(\pi )$ is a subgroup of the corresponding stabiliser with respect the
${\mathcal M}^D_{r,L}(\pi )$ is a subgroup of the corresponding stabiliser with respect the  $\mathrm {Pic}^0_{\mathcal C}$-action on
$\mathrm {Pic}^0_{\mathcal C}$-action on  $\widetilde {{\mathcal M}}^{D'}_{r,d}(C')$, whose affineness follows from the fact that formula (37) is a weak abelian fibration.
$\widetilde {{\mathcal M}}^{D'}_{r,d}(C')$, whose affineness follows from the fact that formula (37) is a weak abelian fibration.
(ii) Polarisability of the Tate module. This follows from the proof of [Reference de Cataldo6, Theorem 4.7.2]. In fact, for a closed point ![]() $a\in {\mathcal A}^D(\pi )$, the Tate module of the abelian part
$a\in {\mathcal A}^D(\pi )$, the Tate module of the abelian part ![]() $P^{\mathrm {ab}}_a$ is an orthogonal direct summand component of
$P^{\mathrm {ab}}_a$ is an orthogonal direct summand component of  $T_{\overline {{\mathbb {Q}}}_l}\left (\mathrm {Pic}^{0,\mathrm {ab}}_{{\mathcal C},a}\right )$ with respect to the nondegenerate Tate–Weil pairing on
$T_{\overline {{\mathbb {Q}}}_l}\left (\mathrm {Pic}^{0,\mathrm {ab}}_{{\mathcal C},a}\right )$ with respect to the nondegenerate Tate–Weil pairing on  $T_{\overline {{\mathbb {Q}}}_l}\left (\mathrm {Pic}^{0,\mathrm {ab}}_{{\mathcal C},a}\right )$. Hence the restriction of the Tate–Weil pairing on
$T_{\overline {{\mathbb {Q}}}_l}\left (\mathrm {Pic}^{0,\mathrm {ab}}_{{\mathcal C},a}\right )$. Hence the restriction of the Tate–Weil pairing on  $T_{\overline {{\mathbb {Q}}}_l}\left (\mathrm {Pic}^{0,\mathrm {ab}}_{{\mathcal C},a}\right )$ to
$T_{\overline {{\mathbb {Q}}}_l}\left (\mathrm {Pic}^{0,\mathrm {ab}}_{{\mathcal C},a}\right )$ to  $T_{\overline {{\mathbb {Q}}}_l}\left (P^{\mathrm {ab}}_a\right )$ is nondegenerate.
$T_{\overline {{\mathbb {Q}}}_l}\left (P^{\mathrm {ab}}_a\right )$ is nondegenerate.
By [Reference Chaudouard and Laumon5, Section 9] (see also [Reference de Cataldo6, Section 5.2]), the ![]() $\mathrm {GL}_r$-Hitchin base admits a stratification
$\mathrm {GL}_r$-Hitchin base admits a stratification
 $$ \begin{align*} \widetilde{{\mathcal A}}^{D'}(C') = \bigsqcup_{\underline{m}, \underline{n}}\widetilde{{\mathcal A}}_{\underline{m}, \underline{n}}, \end{align*} $$
$$ \begin{align*} \widetilde{{\mathcal A}}^{D'}(C') = \bigsqcup_{\underline{m}, \underline{n}}\widetilde{{\mathcal A}}_{\underline{m}, \underline{n}}, \end{align*} $$with ![]() $\underline {m} = (m_1, m_2, \dots , m_s)$,
$\underline {m} = (m_1, m_2, \dots , m_s)$, ![]() $\underline {n}=(n_1, n_2, \dots , n_s)$ satisfying
$\underline {n}=(n_1, n_2, \dots , n_s)$ satisfying
(a)
 $n_i \geq n_{i+1}$ for any i;
$n_i \geq n_{i+1}$ for any i;(b)
 $m_i \geq m_{i+1}$ whenever
$m_i \geq m_{i+1}$ whenever  $n_i = n_{i+1}$;
$n_i = n_{i+1}$;(c)
 $\sum _{i=1}^s m_in_i = r$.
$\sum _{i=1}^s m_in_i = r$.
Each  $\widetilde {{\mathcal A}}_{\underline {m}, \underline {n}}$ is a locally closed subset formed by spectral curves of the topological type
$\widetilde {{\mathcal A}}_{\underline {m}, \underline {n}}$ is a locally closed subset formed by spectral curves of the topological type ![]() $(\underline {m}, \underline {n})$:
$(\underline {m}, \underline {n})$:
 $$ \begin{align} \widetilde{{\mathcal A}}_{\underline{m}, \underline{n}} = \left\{ E \subset V(D'): E = \sum_i m_iE_i, \ E_i \subset V(D')\right\}, \end{align} $$
$$ \begin{align} \widetilde{{\mathcal A}}_{\underline{m}, \underline{n}} = \left\{ E \subset V(D'): E = \sum_i m_iE_i, \ E_i \subset V(D')\right\}, \end{align} $$where ![]() $V(D')$ is the total space of
$V(D')$ is the total space of ![]() ${\mathcal O}_{C'}(D')$ and
${\mathcal O}_{C'}(D')$ and ![]() $E_i$ is an integral spectral curve of degree
$E_i$ is an integral spectral curve of degree ![]() $n_i$ over
$n_i$ over ![]() $C'$. The stratification (40) induces a stratification on
$C'$. The stratification (40) induces a stratification on ![]() ${\mathcal A}^D(\pi ) \subset {\mathcal A}^{D'}(C')$,
${\mathcal A}^D(\pi ) \subset {\mathcal A}^{D'}(C')$,
 $$ \begin{align*} {\mathcal A}^D(\pi) = \bigsqcup_{\underline{m}, \underline{n}}{{\mathcal A}}(\pi)_{\underline{m}, \underline{n}}, \quad {{\mathcal A}}(\pi)_{\underline{m}, \underline{n}} = {\mathcal A}^D(\pi) \cap \widetilde{{\mathcal A}}_{\underline{m}, \underline{n}}. \end{align*} $$
$$ \begin{align*} {\mathcal A}^D(\pi) = \bigsqcup_{\underline{m}, \underline{n}}{{\mathcal A}}(\pi)_{\underline{m}, \underline{n}}, \quad {{\mathcal A}}(\pi)_{\underline{m}, \underline{n}} = {\mathcal A}^D(\pi) \cap \widetilde{{\mathcal A}}_{\underline{m}, \underline{n}}. \end{align*} $$We have the following multivariable inequality:
Proposition 2.7 compare [Reference de Cataldo6, Corollary 5.4.4]
Let ![]() $Z \subset {\mathcal A}^D(\pi )$ be an irreducible subvariety whose general points are of the type
$Z \subset {\mathcal A}^D(\pi )$ be an irreducible subvariety whose general points are of the type ![]() $(\underline {m}, \underline {n})$. Then we have
$(\underline {m}, \underline {n})$. Then we have
 $$ \begin{align} d^{\mathrm{ab}}_Z\left(\mathrm{Pic}^0_{\mathcal C}\right) \geq \sum_i \left( {d_{\widetilde{h}^{D'}_{n_i}\left(C'\right)}}- d_{\widetilde{{\mathcal A}}^{D'}_{n_i}\left(C'\right)} \right) + \mathrm{dim}(Z)+ \left(\mathrm{deg}(D)-g+1\right). \end{align} $$
$$ \begin{align} d^{\mathrm{ab}}_Z\left(\mathrm{Pic}^0_{\mathcal C}\right) \geq \sum_i \left( {d_{\widetilde{h}^{D'}_{n_i}\left(C'\right)}}- d_{\widetilde{{\mathcal A}}^{D'}_{n_i}\left(C'\right)} \right) + \mathrm{dim}(Z)+ \left(\mathrm{deg}(D)-g+1\right). \end{align} $$Here  ${d_{\widetilde {h}^{D'}_{n_i}\left (C'\right )}}$ and
${d_{\widetilde {h}^{D'}_{n_i}\left (C'\right )}}$ and  $d_{\widetilde {{\mathcal A}}^{D'}_{n_i}\left (C'\right )}$ are the dimensions of a fibre and the base, respectively, of the
$d_{\widetilde {{\mathcal A}}^{D'}_{n_i}\left (C'\right )}$ are the dimensions of a fibre and the base, respectively, of the ![]() $\mathrm {GL}_{n_i}$-Hitchin fibration (10) associated with the curve
$\mathrm {GL}_{n_i}$-Hitchin fibration (10) associated with the curve ![]() $C'$ and the divisor
$C'$ and the divisor ![]() $D'=\pi ^*D$, and
$D'=\pi ^*D$, and
 $$ \begin{align*} d^{\mathrm{ab}}_Z\left(\mathrm{Pic}^0_{\mathcal C}\right) = \mathrm{dim}\left(\left(\mathrm{Pic}^{0}_{{\mathcal C},a}\right)^{\mathrm{ab}}\right), \end{align*} $$
$$ \begin{align*} d^{\mathrm{ab}}_Z\left(\mathrm{Pic}^0_{\mathcal C}\right) = \mathrm{dim}\left(\left(\mathrm{Pic}^{0}_{{\mathcal C},a}\right)^{\mathrm{ab}}\right), \end{align*} $$with ![]() $a \in Z$ a general point.
$a \in Z$ a general point.
Proof. When ![]() $\pi =\mathrm {id}$, the subspace
$\pi =\mathrm {id}$, the subspace
 $$ \begin{align} {\mathcal A}^D(\mathrm{id}) = \left\{\mathrm{char}(\theta) \in \widetilde{{\mathcal A}}^D: \mathrm{trace}(\theta)=0\right\} \subset \widetilde{{\mathcal A}}^D \end{align} $$
$$ \begin{align} {\mathcal A}^D(\mathrm{id}) = \left\{\mathrm{char}(\theta) \in \widetilde{{\mathcal A}}^D: \mathrm{trace}(\theta)=0\right\} \subset \widetilde{{\mathcal A}}^D \end{align} $$coincides with the ![]() $\mathrm {SL}_n$-Hitchin base, and the inequality (41) is the
$\mathrm {SL}_n$-Hitchin base, and the inequality (41) is the ![]() $\delta $-inequality for
$\delta $-inequality for ![]() $\mathrm {SL}_n$ proven in [Reference de Cataldo6, Corollary 5.4.4 (76)]. As explained in the last paragraph of [Reference de Cataldo6, Proof of Corollary 5.4.4], the main ingredient in the proof of enhancing the
$\mathrm {SL}_n$ proven in [Reference de Cataldo6, Corollary 5.4.4 (76)]. As explained in the last paragraph of [Reference de Cataldo6, Proof of Corollary 5.4.4], the main ingredient in the proof of enhancing the ![]() $\delta $-inequality for
$\delta $-inequality for ![]() $\mathrm {GL}_n$ to that for
$\mathrm {GL}_n$ to that for ![]() $\mathrm {SL}_n$ is [Reference de Cataldo6, Theorem 5.4.2], which asserts that the restriction of the
$\mathrm {SL}_n$ is [Reference de Cataldo6, Theorem 5.4.2], which asserts that the restriction of the ![]() $\delta $-regular weak abelian fibrations to their elliptic loci in the sub-Hitchin base (42) remains
$\delta $-regular weak abelian fibrations to their elliptic loci in the sub-Hitchin base (42) remains ![]() $\delta $-regular. This follows from the product structure [Reference de Cataldo6, (74)] for the group schemes associated with the spectral curves, which says that the variations of the group schemes associated with the spectral curves are trivial along the
$\delta $-regular. This follows from the product structure [Reference de Cataldo6, (74)] for the group schemes associated with the spectral curves, which says that the variations of the group schemes associated with the spectral curves are trivial along the ![]() $H^0(C, {\mathcal O}_C(D))$-direction.
$H^0(C, {\mathcal O}_C(D))$-direction.
Now for a general ![]() $\pi : C' \to C$ with
$\pi : C' \to C$ with ![]() $D' =\pi ^*D'$ as we consider here, we have the canonical decomposition for the Hitchin base
$D' =\pi ^*D'$ as we consider here, we have the canonical decomposition for the Hitchin base
 $$ \begin{align} {\mathcal A}^D(\pi) \oplus H = \widetilde{{\mathcal A}}^{D'}, \end{align} $$
$$ \begin{align} {\mathcal A}^D(\pi) \oplus H = \widetilde{{\mathcal A}}^{D'}, \end{align} $$with ![]() $H = H^0(C, {\mathcal O}_C(D))$ a direct summand component of
$H = H^0(C, {\mathcal O}_C(D))$ a direct summand component of ![]() $H^0(C', {\mathcal O}_{C'}(D'))$. Applying the product structure [Reference de Cataldo6, (74)] to the curve
$H^0(C', {\mathcal O}_{C'}(D'))$. Applying the product structure [Reference de Cataldo6, (74)] to the curve ![]() $C'$ and the divisor
$C'$ and the divisor ![]() $D'$, we obtain an analogous product structure for equation (43), that the variations of the group schemes associated with the spectral curves are trivial along the H-direction. Hence formula (41) holds in the relative case
$D'$, we obtain an analogous product structure for equation (43), that the variations of the group schemes associated with the spectral curves are trivial along the H-direction. Hence formula (41) holds in the relative case ![]() $\pi : C' \to C$, by the same reason as for
$\pi : C' \to C$, by the same reason as for ![]() $\mathrm {SL}_n$.
$\mathrm {SL}_n$.
2.5 Proof of Theorem 2.3(a)
The proof of Theorem 2.3(a) is parallel to the proofs of the main theorems in [Reference Chaudouard and Laumon5, Reference de Cataldo6], which we provide in the following for the reader’s convenience. The crucial ingredient is to combine Ngô’s support inequality (34) and the multivariable inequality (41).
We assume ![]() $Z \subset {\mathcal A}^D(\pi )$ is an irreducible support of formula (35) whose general points have types
$Z \subset {\mathcal A}^D(\pi )$ is an irreducible support of formula (35) whose general points have types ![]() $(\underline {m}, \underline {n})$. By Theorem 2.4 and Propositions 2.6 and 2.7, we have
$(\underline {m}, \underline {n})$. By Theorem 2.4 and Propositions 2.6 and 2.7, we have
 $$ \begin{align*} &\mathrm{dim}\left({h^D_{\pi}}\right) - \mathrm{dim}\left({A^D(\pi)}\right)+ \mathrm{dim}(Z) \geq d^{\mathrm{ab}}_Z \left(\mathrm{Pic}^0_{\mathcal C}\right) - g \\ &\quad \ \geq \sum_i \left( {d_{\widetilde{h}^{D'}_{n_i}(C')}}- d_{\widetilde{{\mathcal A}}^{D'}_{n_i}(C')} \right) + \mathrm{dim}(Z) +(\mathrm{deg}(D)-g+1)-g, \end{align*} $$
$$ \begin{align*} &\mathrm{dim}\left({h^D_{\pi}}\right) - \mathrm{dim}\left({A^D(\pi)}\right)+ \mathrm{dim}(Z) \geq d^{\mathrm{ab}}_Z \left(\mathrm{Pic}^0_{\mathcal C}\right) - g \\ &\quad \ \geq \sum_i \left( {d_{\widetilde{h}^{D'}_{n_i}(C')}}- d_{\widetilde{{\mathcal A}}^{D'}_{n_i}(C')} \right) + \mathrm{dim}(Z) +(\mathrm{deg}(D)-g+1)-g, \end{align*} $$where we use  $d^{\mathrm {ab}}\left (P^0_a\right ) = d^{\mathrm {ab}}\left (\mathrm {Pic}^0_{{\mathcal C},a}\right )-g$. Hence
$d^{\mathrm {ab}}\left (P^0_a\right ) = d^{\mathrm {ab}}\left (\mathrm {Pic}^0_{{\mathcal C},a}\right )-g$. Hence
 $$ \begin{align} \mathrm{dim}\left({h^D_{\pi}}\right) - \mathrm{dim}\left({{\mathcal A}^D(\pi)}\right) \geq \sum_{i=1}^s \left( {d_{\widetilde{h}^{D'}_{n_i}(C')}}- d_{\widetilde{{\mathcal A}}^{D'}_{n_i}(C')} \right)+(\mathrm{deg}(D)-2g+1). \end{align} $$
$$ \begin{align} \mathrm{dim}\left({h^D_{\pi}}\right) - \mathrm{dim}\left({{\mathcal A}^D(\pi)}\right) \geq \sum_{i=1}^s \left( {d_{\widetilde{h}^{D'}_{n_i}(C')}}- d_{\widetilde{{\mathcal A}}^{D'}_{n_i}(C')} \right)+(\mathrm{deg}(D)-2g+1). \end{align} $$Here we recall that s is the number of irreducible components of the spectral curve. We now apply the dimension formulas for ![]() $\mathrm {GL}_*$-Hitchin fibrations [Reference de Cataldo6, Section 6.1] to compute both sides of formula (44). The left-hand side is equal to
$\mathrm {GL}_*$-Hitchin fibrations [Reference de Cataldo6, Section 6.1] to compute both sides of formula (44). The left-hand side is equal to
 $$ \begin{align*} &\left({d_{\widetilde{h}^{D'}_{r}(C')}}- d_{\widetilde{{\mathcal A}}^{D'}_{r}(C')} \right) + \left( \mathrm{dim}H^0(C, {\mathcal O}_C(D))-g\right)\\ &\quad \quad \ = \left(-r\mathrm{deg}(D') + 2r(g'-1)+1\right) +\left(\mathrm{deg}(D)-2g+1\right), \end{align*} $$
$$ \begin{align*} &\left({d_{\widetilde{h}^{D'}_{r}(C')}}- d_{\widetilde{{\mathcal A}}^{D'}_{r}(C')} \right) + \left( \mathrm{dim}H^0(C, {\mathcal O}_C(D))-g\right)\\ &\quad \quad \ = \left(-r\mathrm{deg}(D') + 2r(g'-1)+1\right) +\left(\mathrm{deg}(D)-2g+1\right), \end{align*} $$where ![]() $g'$ is the genus of
$g'$ is the genus of ![]() $C'$ and we used the last formula of [Reference de Cataldo6, (77)]. Similarly, the right-hand side is equal to
$C'$ and we used the last formula of [Reference de Cataldo6, (77)]. Similarly, the right-hand side is equal to
 $$ \begin{align*} &\sum_{i=1}^s\left(-n_i\mathrm{deg}(D') + 2n_i(g'-1)+1\right) +\left(\mathrm{deg}(D)-2g+1\right) \\ &\quad\quad \ = \left( \left(-\sum_{i=1}^sn_i\right)\left((\mathrm{deg}(D')-2(g'-1)\right)+s \right) +\left(\mathrm{deg}(D)-2g+1\right). \end{align*} $$
$$ \begin{align*} &\sum_{i=1}^s\left(-n_i\mathrm{deg}(D') + 2n_i(g'-1)+1\right) +\left(\mathrm{deg}(D)-2g+1\right) \\ &\quad\quad \ = \left( \left(-\sum_{i=1}^sn_i\right)\left((\mathrm{deg}(D')-2(g'-1)\right)+s \right) +\left(\mathrm{deg}(D)-2g+1\right). \end{align*} $$In particular, formula (44) implies that
 $$ \begin{align} 1-s \geq \left(r-\sum_in_i \right)\left(\mathrm{deg}(D')-(2g'-2)\right). \end{align} $$
$$ \begin{align} 1-s \geq \left(r-\sum_in_i \right)\left(\mathrm{deg}(D')-(2g'-2)\right). \end{align} $$Since
by the assumption on D, inequality (45) forces ![]() $s=1$ and
$s=1$ and ![]() $m_1=1$. This implies that the generic point of Z lies in
$m_1=1$. This implies that the generic point of Z lies in ![]() ${\mathcal A}^{D,\mathrm {ell}}(\pi )$, which completes the proof of Theorem 2.3(a).
${\mathcal A}^{D,\mathrm {ell}}(\pi )$, which completes the proof of Theorem 2.3(a).
2.6 Proof of Theorem 2.3(b)
Due to Theorem 2.3(a), it suffices to prove (b) over the elliptic locus with respect to the restricted Hitchin map
 $$ \begin{align} h^{\mathrm{ell}}_{\pi} = h_{\pi}^D\Big\rvert_{{\mathcal A}^{D,\mathrm{ell}}(\pi)}: {\mathcal M}^{D,\mathrm{ell}}_{r,L}(\pi) \to {\mathcal A}^{D,\mathrm{ell}}(\pi). \end{align} $$
$$ \begin{align} h^{\mathrm{ell}}_{\pi} = h_{\pi}^D\Big\rvert_{{\mathcal A}^{D,\mathrm{ell}}(\pi)}: {\mathcal M}^{D,\mathrm{ell}}_{r,L}(\pi) \to {\mathcal A}^{D,\mathrm{ell}}(\pi). \end{align} $$Recall the group scheme (38) of the relative Prym variety. By the support theorem [Reference Ngô33, Propositions 7.2.2 and 7.2.3], we only need to show that the constructible sheaf of the top degree cohomology
 $$ \begin{align} \left(\mathrm{R}^{\text{2d}_{\text{h}_{\pi}^{\text{D}}}} {\text{h}^{\mathrm{ell}}_{\pi}}_* {\underline{{\mathbb{C}}}}\right)_{\mathrm{st}},\quad d_{h_{\pi}^D} = \mathrm{dim}\left(h_{\pi}^D\right), \end{align} $$
$$ \begin{align} \left(\mathrm{R}^{\text{2d}_{\text{h}_{\pi}^{\text{D}}}} {\text{h}^{\mathrm{ell}}_{\pi}}_* {\underline{{\mathbb{C}}}}\right)_{\mathrm{st}},\quad d_{h_{\pi}^D} = \mathrm{dim}\left(h_{\pi}^D\right), \end{align} $$is the trivial local system on the elliptic locus ![]() ${\mathcal A}^{D,\mathrm {ell}}(\pi )$.
${\mathcal A}^{D,\mathrm {ell}}(\pi )$.
It is clear that formula (47) contains the trivial local system given by the sum of point classes for all irreducible components of the fibres of equation (46). Hence it suffices to prove that the stable part of the degree ![]() $2d_{h_{\pi }^D}$ cohomology group is
$2d_{h_{\pi }^D}$ cohomology group is ![]() $1$-dimensional for each fibre of equation (46).
$1$-dimensional for each fibre of equation (46).
Assume ![]() $a \in {\mathcal A}^{D,\mathrm {ell}}(\pi )$. Let
$a \in {\mathcal A}^{D,\mathrm {ell}}(\pi )$. Let ![]() $C^{\prime }_a$ be the corresponding integral spectral curve with the spectral cover
$C^{\prime }_a$ be the corresponding integral spectral curve with the spectral cover
 $$ \begin{align} C^{\prime}_a \xrightarrow{p_a} C' \xrightarrow{\pi} C. \end{align} $$
$$ \begin{align} C^{\prime}_a \xrightarrow{p_a} C' \xrightarrow{\pi} C. \end{align} $$The Hitchin fibre  ${\mathcal M}^{D}_{r,d}(\pi )_a$ contains a Zariski dense open subset
${\mathcal M}^{D}_{r,d}(\pi )_a$ contains a Zariski dense open subset
 $$ \begin{align*} {\mathcal M}^{\mathrm{reg}}_a \subset {\mathcal M}^{D}_{r,L}(\pi)_a \end{align*} $$
$$ \begin{align*} {\mathcal M}^{\mathrm{reg}}_a \subset {\mathcal M}^{D}_{r,L}(\pi)_a \end{align*} $$parameterising line bundles on the spectral curve ![]() $C^{\prime }_a$, which is a torsor of the group scheme
$C^{\prime }_a$, which is a torsor of the group scheme ![]() $P_a$. Hence
$P_a$. Hence  ${\mathcal M}^{D}_{r,L}(\pi )_a$ has
${\mathcal M}^{D}_{r,L}(\pi )_a$ has ![]() $\lvert \pi _0(P_a)\rvert $ irreducible components.
$\lvert \pi _0(P_a)\rvert $ irreducible components.
We fix a base point in ![]() $x\in {\mathcal M}_a^{\mathrm {reg}}$. Since
$x\in {\mathcal M}_a^{\mathrm {reg}}$. Since ![]() ${\mathcal M}_a^{\mathrm {reg}}$ is a torsor of the group scheme
${\mathcal M}_a^{\mathrm {reg}}$ is a torsor of the group scheme ![]() $P_a$, the base point x trivialises the torsor, and therefore the
$P_a$, the base point x trivialises the torsor, and therefore the ![]() $\pi _0(P_a)$-action on x yields an isomorphism
$\pi _0(P_a)$-action on x yields an isomorphism
 $$ \begin{align*} [x]: \pi_0\left({\mathcal M}^{\mathrm{reg}}_a\right) \xrightarrow{\simeq} \pi_0(P_a), \end{align*} $$
$$ \begin{align*} [x]: \pi_0\left({\mathcal M}^{\mathrm{reg}}_a\right) \xrightarrow{\simeq} \pi_0(P_a), \end{align*} $$which further induces
 $$ \begin{align} H^{2d_{h_{\pi}^D}}\left({\mathcal M}^{D}_{r,L}(\pi)_a, {\mathbb{C}} \right) = \bigoplus_{v\in \pi_0\left(P_a\right)} {\mathbb{C}} v. \end{align} $$
$$ \begin{align} H^{2d_{h_{\pi}^D}}\left({\mathcal M}^{D}_{r,L}(\pi)_a, {\mathbb{C}} \right) = \bigoplus_{v\in \pi_0\left(P_a\right)} {\mathbb{C}} v. \end{align} $$The action of ![]() $P_a$ on the cohomology
$P_a$ on the cohomology  $H^*\left ({\mathcal M}^{D}_{r,L}(\pi )_a, {\mathbb {C}} \right )$ factors through the group
$H^*\left ({\mathcal M}^{D}_{r,L}(\pi )_a, {\mathbb {C}} \right )$ factors through the group ![]() $\pi _0(P_a)$ of connected components, which acts naturally on the right-hand side of equation (49). In particular, the action of the discrete subgroup
$\pi _0(P_a)$ of connected components, which acts naturally on the right-hand side of equation (49). In particular, the action of the discrete subgroup ![]() $\Gamma \subset P_a$ on equation (49) factors through the natural action of
$\Gamma \subset P_a$ on equation (49) factors through the natural action of ![]() $\pi _0(P_a)$. By the proof of [Reference Hausel and Pauly21, Theorem 1.1 (2)], the morphism
$\pi _0(P_a)$. By the proof of [Reference Hausel and Pauly21, Theorem 1.1 (2)], the morphism
induced by the pullback ![]() $p_a^*\circ \pi ^*$ along formula (48) is a surjection. Therefore we obtain
$p_a^*\circ \pi ^*$ along formula (48) is a surjection. Therefore we obtain
 $$ \begin{align*} H^{2d_{h_{\pi}^D}}\left({\mathcal M}^{D}_{r,L}(\pi)_a, {\mathbb{C}} \right)_{\mathrm{st}} = H^{2d_{h_{\pi}^D}}\left({\mathcal M}^{D}_{r,L}(\pi)_a, {\mathbb{C}} \right)^{\Gamma} \subseteq H^{2d_{h_{\pi}^D}}\left({\mathcal M}^{D}_{r,L}(\pi)_a, {\mathbb{C}} \right)^{\pi_0\left(P_a\right)} = {\mathbb{C}}, \end{align*} $$
$$ \begin{align*} H^{2d_{h_{\pi}^D}}\left({\mathcal M}^{D}_{r,L}(\pi)_a, {\mathbb{C}} \right)_{\mathrm{st}} = H^{2d_{h_{\pi}^D}}\left({\mathcal M}^{D}_{r,L}(\pi)_a, {\mathbb{C}} \right)^{\Gamma} \subseteq H^{2d_{h_{\pi}^D}}\left({\mathcal M}^{D}_{r,L}(\pi)_a, {\mathbb{C}} \right)^{\pi_0\left(P_a\right)} = {\mathbb{C}}, \end{align*} $$where the last equality is given by the ![]() $\pi _0(P_a)$-equivariant isomorphism (49). This implies
$\pi _0(P_a)$-equivariant isomorphism (49). This implies
 $$ \begin{align} \left(\mathrm{R}^{\text{2d}_{\text{h}_{\pi}^{\text{D}}}} {\text{h}^{\mathrm{ell}}_{\pi}}_* {\underline{{\mathbb{C}}}}\right)_{\mathrm{st}} = {\underline{{\mathbb{C}}}} \end{align} $$
$$ \begin{align} \left(\mathrm{R}^{\text{2d}_{\text{h}_{\pi}^{\text{D}}}} {\text{h}^{\mathrm{ell}}_{\pi}}_* {\underline{{\mathbb{C}}}}\right)_{\mathrm{st}} = {\underline{{\mathbb{C}}}} \end{align} $$and completes the proof of Theorem 2.3(b).
Remark 2.8. The vector space
 $$ \begin{align*} H^{2d_{h_{\pi}^D}}\left({\mathcal M}^{D}_{r,L}(\pi)_a, {\mathbb{C}} \right)_{\mathrm{st}} = H^{2d_{h_{\pi}^D}}\left({\mathcal M}^{D}_{r,L}(\pi)_a, {\mathbb{C}} \right)^{\Gamma} \end{align*} $$
$$ \begin{align*} H^{2d_{h_{\pi}^D}}\left({\mathcal M}^{D}_{r,L}(\pi)_a, {\mathbb{C}} \right)_{\mathrm{st}} = H^{2d_{h_{\pi}^D}}\left({\mathcal M}^{D}_{r,L}(\pi)_a, {\mathbb{C}} \right)^{\Gamma} \end{align*} $$may fail to be ![]() $1$-dimensional when
$1$-dimensional when ![]() $a \in {\mathcal A}^D(\pi ) \setminus {\mathcal A}^{D,\mathrm {ell}}(\pi )$. In particular, the constructible sheaf
$a \in {\mathcal A}^D(\pi ) \setminus {\mathcal A}^{D,\mathrm {ell}}(\pi )$. In particular, the constructible sheaf  $\left (\mathrm {R}^{\text {2d}_{\text {h}_{\pi }^{\text {D}}}} {\text {h}^{\text {D}_{\pi }}}_* {\underline {{\mathbb {C}}}}\right )_{\mathrm {st}}$ is not a rank
$\left (\mathrm {R}^{\text {2d}_{\text {h}_{\pi }^{\text {D}}}} {\text {h}^{\text {D}_{\pi }}}_* {\underline {{\mathbb {C}}}}\right )_{\mathrm {st}}$ is not a rank ![]() $1$ local system over the total Hitchin base
$1$ local system over the total Hitchin base ![]() ${\mathcal A}^D(\pi )$. Hence the proof of Theorem 2.3(b) relies heavily on the support theorem – Theorem 2.3(a).
${\mathcal A}^D(\pi )$. Hence the proof of Theorem 2.3(b) relies heavily on the support theorem – Theorem 2.3(a).
2.7 Transfer from the  $\kappa $-part to the stable part
$\kappa $-part to the stable part
In this section, we assume that D is an effective divisor of degree ![]() $\mathrm {deg}(D)>2g-2$ or
$\mathrm {deg}(D)>2g-2$ or ![]() $D= K_C$. Our main purpose is to prove Proposition 2.10, which allows us to transfer naturally from the
$D= K_C$. Our main purpose is to prove Proposition 2.10, which allows us to transfer naturally from the ![]() $\kappa $-part to the stable part of the complex
$\kappa $-part to the stable part of the complex ![]() ${\mathrm {Rh}_{\pi }^{\text {D}}}_* {\underline {{\mathbb {C}}}}$. This extends [Reference Yun39, Proposition 2.3.2] to the total Hitchin base for certain endoscopic Hitchin moduli spaces associated with
${\mathrm {Rh}_{\pi }^{\text {D}}}_* {\underline {{\mathbb {C}}}}$. This extends [Reference Yun39, Proposition 2.3.2] to the total Hitchin base for certain endoscopic Hitchin moduli spaces associated with ![]() $\mathrm {SL}_n$. We note that this transfer does not rely on the support theorem.
$\mathrm {SL}_n$. We note that this transfer does not rely on the support theorem.
Recall the decomposition (19) of Proposition 1.1(a). By Lemma 1.5, the group ![]() $\Omega $ (introduced in formula (27)) acts on each direct image complex
$\Omega $ (introduced in formula (27)) acts on each direct image complex ![]() ${\mathrm {Rh}_{i}}_* {\underline {{\mathbb {C}}}}$, and we consider its
${\mathrm {Rh}_{i}}_* {\underline {{\mathbb {C}}}}$, and we consider its ![]() $\Omega $-invariant part
$\Omega $-invariant part
 $$ \begin{align*} \left({\mathrm{Rh}_i}_* {\underline{{\mathbb{C}}}}\right)^{\Omega} \in D_c^b\left({\mathcal A}^D(\pi)\right). \end{align*} $$
$$ \begin{align*} \left({\mathrm{Rh}_i}_* {\underline{{\mathbb{C}}}}\right)^{\Omega} \in D_c^b\left({\mathcal A}^D(\pi)\right). \end{align*} $$For any pair ![]() $1 \leq i,j \leq m$, the isomorphism of Proposition 1.1(b),
$1 \leq i,j \leq m$, the isomorphism of Proposition 1.1(b),
 $$ \begin{align*} \phi_{ij} = \phi_{{\mathcal L}_{ij}}: M_i \xrightarrow{\simeq} M_j, \quad ({\mathcal E}, \phi) \mapsto \left({\mathcal E} \otimes {\mathcal L}_{ij}, \theta\right) \end{align*} $$
$$ \begin{align*} \phi_{ij} = \phi_{{\mathcal L}_{ij}}: M_i \xrightarrow{\simeq} M_j, \quad ({\mathcal E}, \phi) \mapsto \left({\mathcal E} \otimes {\mathcal L}_{ij}, \theta\right) \end{align*} $$induced by a line bundle ![]() ${\mathcal L}_{ij} \in \Gamma $, yields an isomorphism
${\mathcal L}_{ij} \in \Gamma $, yields an isomorphism
 $$ \begin{align*} \phi_{ij}^*: {\mathrm{Rh}_j}_* {\underline{{\mathbb{C}}}} \xrightarrow{\simeq} {\mathrm{Rh}_i}_* {\underline{{\mathbb{C}}}}. \end{align*} $$
$$ \begin{align*} \phi_{ij}^*: {\mathrm{Rh}_j}_* {\underline{{\mathbb{C}}}} \xrightarrow{\simeq} {\mathrm{Rh}_i}_* {\underline{{\mathbb{C}}}}. \end{align*} $$It preserves the ![]() $\Omega $-invariant parts:
$\Omega $-invariant parts:
 $$ \begin{align} \phi_{ij}^*: \left({\mathrm{Rh}_j}_* {\underline{{\mathbb{C}}}}\right)^{\Omega} \xrightarrow{\simeq} \left({\mathrm{Rh}_i}_* {\underline{{\mathbb{C}}}}\right)^{\Omega}. \end{align} $$
$$ \begin{align} \phi_{ij}^*: \left({\mathrm{Rh}_j}_* {\underline{{\mathbb{C}}}}\right)^{\Omega} \xrightarrow{\simeq} \left({\mathrm{Rh}_i}_* {\underline{{\mathbb{C}}}}\right)^{\Omega}. \end{align} $$We note that the isomorphism (51) depends only on the class of the line bundle ![]() ${\mathcal L}_{ij} \in \Gamma $ in the quotient group
${\mathcal L}_{ij} \in \Gamma $ in the quotient group
Hence the ![]() $\Gamma $-action on
$\Gamma $-action on  $\bigoplus _{j=1}^m \left ({\mathrm {Rh}_j}_* {\underline {{\mathbb {C}}}}\right )^{\Omega }$ passes through
$\bigoplus _{j=1}^m \left ({\mathrm {Rh}_j}_* {\underline {{\mathbb {C}}}}\right )^{\Omega }$ passes through ![]() $\pi _0(\mathrm {Prym}(C'/C))$. Since the group
$\pi _0(\mathrm {Prym}(C'/C))$. Since the group ![]() $\Omega $ preserves each component
$\Omega $ preserves each component ![]() $M_i$, it follows from Proposition 1.1(b) that the elements of the cyclic group
$M_i$, it follows from Proposition 1.1(b) that the elements of the cyclic group ![]() $\pi _0(\mathrm {Prym}(C'/C)) = \Gamma /\Omega $ act transitively on the set
$\pi _0(\mathrm {Prym}(C'/C)) = \Gamma /\Omega $ act transitively on the set ![]() $\{M_i\}_{i=1}^m$. We may view
$\{M_i\}_{i=1}^m$. We may view ![]() $\pi _0(\mathrm {Prym}(C'/C))$ as the group of connected components of
$\pi _0(\mathrm {Prym}(C'/C))$ as the group of connected components of  ${\mathcal M}^D_{r,L}(\pi )$. For any fixed
${\mathcal M}^D_{r,L}(\pi )$. For any fixed ![]() $1\leq i_0 \leq m$, the isomorphism (51) yields a canonical
$1\leq i_0 \leq m$, the isomorphism (51) yields a canonical ![]() $\pi _0(\mathrm {Prym}(C'/C))$-equivariant isomorphism
$\pi _0(\mathrm {Prym}(C'/C))$-equivariant isomorphism
 $$ \begin{align} \bigoplus_{j=1}^m \left({\mathrm{Rh}_j}_* {\underline{{\mathbb{C}}}}\right)^{\Omega} = \left({\mathrm{Rh}_{i_0}}_*{\underline{{\mathbb{C}}}}\right)^{\Omega} \otimes \left(\bigoplus_{v\in \pi_0\left(\mathrm{Prym}\left(C'/C\right)\right)} {\mathbb{C}} v \right), \end{align} $$
$$ \begin{align} \bigoplus_{j=1}^m \left({\mathrm{Rh}_j}_* {\underline{{\mathbb{C}}}}\right)^{\Omega} = \left({\mathrm{Rh}_{i_0}}_*{\underline{{\mathbb{C}}}}\right)^{\Omega} \otimes \left(\bigoplus_{v\in \pi_0\left(\mathrm{Prym}\left(C'/C\right)\right)} {\mathbb{C}} v \right), \end{align} $$where the action on the right-hand side is the natural one.
Before stating Proposition 2.10, we introduce the following definition for convenience:
Definition 2.9. Let X be an algebraic variety, and let ![]() ${\mathcal F}_1, {\mathcal F}_2 \in D^b_c(X)$ be two objects. We say that two morphisms
${\mathcal F}_1, {\mathcal F}_2 \in D^b_c(X)$ be two objects. We say that two morphisms
are equivalent up to scaling if there exists ![]() $\lambda \in {\mathbb {C}}^*$ such that
$\lambda \in {\mathbb {C}}^*$ such that ![]() $f_1 = \lambda f_2$. We say that there is an isomorphism between two objects
$f_1 = \lambda f_2$. We say that there is an isomorphism between two objects ![]() ${\mathcal F}_1$ and
${\mathcal F}_1$ and ![]() ${\mathcal F}_2$,
${\mathcal F}_2$,
which is canonical up to scaling if our construction induces a set of isomorphisms  $f_i: {\mathcal F}_1 \xrightarrow {\simeq } {\mathcal F}_2$ which are all equivalent up to scaling.
$f_i: {\mathcal F}_1 \xrightarrow {\simeq } {\mathcal F}_2$ which are all equivalent up to scaling.
Proposition 2.10. Let D be an effective divisor on C of degree ![]() $\mathrm {deg}(D)>2g-2$ or
$\mathrm {deg}(D)>2g-2$ or ![]() $D= K_C$. Assume that
$D= K_C$. Assume that ![]() $\pi :C' \to C$ is the degree m Galois cover associated with
$\pi :C' \to C$ is the degree m Galois cover associated with ![]() $\gamma \in \Gamma $, which corresponds to the character
$\gamma \in \Gamma $, which corresponds to the character ![]() $\kappa \in \hat {\Gamma }$ via equation (3). Assume
$\kappa \in \hat {\Gamma }$ via equation (3). Assume ![]() $n = mr$. Then for any two elements
$n = mr$. Then for any two elements ![]() $\kappa _1, \kappa _2$ in the cyclic group
$\kappa _1, \kappa _2$ in the cyclic group ![]() $\langle \kappa \rangle \subset \hat {\Gamma }$ generated by
$\langle \kappa \rangle \subset \hat {\Gamma }$ generated by ![]() $\kappa $, there is an isomorphism for the corresponding isotypic components,
$\kappa $, there is an isomorphism for the corresponding isotypic components,
 $$ \begin{align} \left({ \mathrm{Rh}_{\pi}^{\text{D}}}_* {\underline{{\mathbb{C}}}} \right)_{\kappa_1} = \left( {\mathrm{Rh}_{\pi}^{\text{D}}}_* {\underline{{\mathbb{C}}}} \right)_{\kappa_2}, \end{align} $$
$$ \begin{align} \left({ \mathrm{Rh}_{\pi}^{\text{D}}}_* {\underline{{\mathbb{C}}}} \right)_{\kappa_1} = \left( {\mathrm{Rh}_{\pi}^{\text{D}}}_* {\underline{{\mathbb{C}}}} \right)_{\kappa_2}, \end{align} $$which is canonical up to scaling. In particular, equation (53) induces an isomorphism which is canonical up to scaling:
 $$ \begin{align*} \left( {\mathrm{Rh}_{\pi}^{\text{D}}}_* {\underline{{\mathbb{C}}}} \right)_{\kappa} = \left( {\mathrm{Rh}_{\pi}^{\text{D}}}_* {\underline{{\mathbb{C}}}} \right)_{\mathrm{st}}. \end{align*} $$
$$ \begin{align*} \left( {\mathrm{Rh}_{\pi}^{\text{D}}}_* {\underline{{\mathbb{C}}}} \right)_{\kappa} = \left( {\mathrm{Rh}_{\pi}^{\text{D}}}_* {\underline{{\mathbb{C}}}} \right)_{\mathrm{st}}. \end{align*} $$Proof. We consider the ![]() $\Omega $-invariant part
$\Omega $-invariant part
 $$ \begin{align} \left( {\mathrm{Rh}_{\pi}^{\text{D}}}_* {\underline{{\mathbb{C}}}} \right)^{\Omega} \in D_c^b\left({\mathcal A}^D(\pi)\right) \end{align} $$
$$ \begin{align} \left( {\mathrm{Rh}_{\pi}^{\text{D}}}_* {\underline{{\mathbb{C}}}} \right)^{\Omega} \in D_c^b\left({\mathcal A}^D(\pi)\right) \end{align} $$of the direct image complex ![]() ${\mathrm {Rh}_{\pi }^{\text {D}}}_* {\mathbb {C}}$. On one hand, the group
${\mathrm {Rh}_{\pi }^{\text {D}}}_* {\mathbb {C}}$. On one hand, the group ![]() $\Omega $ acts on each complex
$\Omega $ acts on each complex ![]() ${\mathrm {Rh}_i}_* {\mathbb {C}}$, and we have
${\mathrm {Rh}_i}_* {\mathbb {C}}$, and we have
 $$ \begin{align} \left( {\mathrm{Rh}_{\pi}^{\text{D}}}_* {\underline{{\mathbb{C}}}} \right)^{\Omega} = \bigoplus_{j=1}^m \left({\mathrm{Rh}_j}_* {\underline{{\mathbb{C}}}}\right)^{\Omega}. \end{align} $$
$$ \begin{align} \left( {\mathrm{Rh}_{\pi}^{\text{D}}}_* {\underline{{\mathbb{C}}}} \right)^{\Omega} = \bigoplus_{j=1}^m \left({\mathrm{Rh}_j}_* {\underline{{\mathbb{C}}}}\right)^{\Omega}. \end{align} $$On the other hand, by Corollary 1.4, an isotypic component  $\left ( {\mathrm {Rh}_{\pi }^{\text {D}}}_* {\underline {{\mathbb {C}}}} \right )_{\kappa '}$ contributes to formula (54) if and only if
$\left ( {\mathrm {Rh}_{\pi }^{\text {D}}}_* {\underline {{\mathbb {C}}}} \right )_{\kappa '}$ contributes to formula (54) if and only if ![]() $\kappa '$ lies in
$\kappa '$ lies in ![]() $\langle \kappa \rangle $. Hence
$\langle \kappa \rangle $. Hence
 $$ \begin{align} \left( {\mathrm{Rh}_{\pi}^{\text{D}}}_* {\underline{{\mathbb{C}}}} \right)^{\Omega} = \bigoplus_{\kappa' \in \langle \kappa \rangle} \left( {\mathrm{Rh}_{\pi}^{\text{D}}}_* {\underline{{\mathbb{C}}}} \right)_{\kappa'}. \end{align} $$
$$ \begin{align} \left( {\mathrm{Rh}_{\pi}^{\text{D}}}_* {\underline{{\mathbb{C}}}} \right)^{\Omega} = \bigoplus_{\kappa' \in \langle \kappa \rangle} \left( {\mathrm{Rh}_{\pi}^{\text{D}}}_* {\underline{{\mathbb{C}}}} \right)_{\kappa'}. \end{align} $$Combining equations (52), (55) and (56), we obtain a natural ![]() $\pi _0(\mathrm {Prym}(C'/C))$-equivariant isomorphism
$\pi _0(\mathrm {Prym}(C'/C))$-equivariant isomorphism
 $$ \begin{align*} \bigoplus_{\kappa' \in \langle \kappa \rangle} \left( {\mathrm{Rh}_{\pi}^{\text{D}}}_* {\underline{{\mathbb{C}}}} \right)_{\kappa'} = \left({\mathrm{Rh}_{i_0}}_*{\underline{{\mathbb{C}}}}\right)^{\Omega} \otimes \left(\bigoplus_{v\in \pi_0(\mathrm{Prym}(C'/C))} {\mathbb{C}} v \right). \end{align*} $$
$$ \begin{align*} \bigoplus_{\kappa' \in \langle \kappa \rangle} \left( {\mathrm{Rh}_{\pi}^{\text{D}}}_* {\underline{{\mathbb{C}}}} \right)_{\kappa'} = \left({\mathrm{Rh}_{i_0}}_*{\underline{{\mathbb{C}}}}\right)^{\Omega} \otimes \left(\bigoplus_{v\in \pi_0(\mathrm{Prym}(C'/C))} {\mathbb{C}} v \right). \end{align*} $$In particular, if we take the ![]() $\kappa '$-parts on both sides, since the
$\kappa '$-parts on both sides, since the ![]() $\kappa '$-part of the regular representation is
$\kappa '$-part of the regular representation is ![]() $1$-dimensional, this yields a natural isomorphism up to scaling
$1$-dimensional, this yields a natural isomorphism up to scaling
 $$ \begin{align} f_{i_0,\kappa'}: \left( {\mathrm{Rh}_{\pi}^{\text{D}}}_* {\underline{{\mathbb{C}}}} \right)_{\kappa'} \xrightarrow{\simeq} \left({\mathrm{Rh}_{i_0}}_*{\underline{{\mathbb{C}}}}\right)^{\Omega}. \end{align} $$
$$ \begin{align} f_{i_0,\kappa'}: \left( {\mathrm{Rh}_{\pi}^{\text{D}}}_* {\underline{{\mathbb{C}}}} \right)_{\kappa'} \xrightarrow{\simeq} \left({\mathrm{Rh}_{i_0}}_*{\underline{{\mathbb{C}}}}\right)^{\Omega}. \end{align} $$This gives isomorphism (53) up to scaling, which a priori still depends on the choice of ![]() $1\leq i_0 \leq m$.
$1\leq i_0 \leq m$.
Different choices of ![]() $i_0$ influence the isomorphism (53) via the action of an element
$i_0$ influence the isomorphism (53) via the action of an element
on both objects of formula (57). After isolating the ![]() $\kappa '$-isotypic component, we conclude that this changes the isomorphism (53) by only a possible scalar ambiguity.
$\kappa '$-isotypic component, we conclude that this changes the isomorphism (53) by only a possible scalar ambiguity.
2.8 Changing the degree
Assume ![]() $\mathrm {deg}(D)>2g-2$. As another application of Ngô’s support theorem, we analyse the
$\mathrm {deg}(D)>2g-2$. As another application of Ngô’s support theorem, we analyse the ![]() $G_{\pi }$-equivariant complex
$G_{\pi }$-equivariant complex
 $$ \begin{align} \left({\mathrm{Rh}_{\pi}^{\text{D}}}_* {\underline{{\mathbb{C}}}} \right)_{\kappa} \in D_c^b\left({\mathcal A}^D(\pi)\right) \end{align} $$
$$ \begin{align} \left({\mathrm{Rh}_{\pi}^{\text{D}}}_* {\underline{{\mathbb{C}}}} \right)_{\kappa} \in D_c^b\left({\mathcal A}^D(\pi)\right) \end{align} $$when the degree of the line bundle ![]() $L \in \mathrm {Pic}^d(C)$ is changed.
$L \in \mathrm {Pic}^d(C)$ is changed.
Due to Theorem 2.3(b) and Proposition 2.10, the object (58) has full support ![]() ${\mathcal A}^D(\pi )$, and hence is completely determined by its restriction to the open subset
${\mathcal A}^D(\pi )$, and hence is completely determined by its restriction to the open subset ![]() $U^{\mathrm {sm}} \subset {\mathcal A}^D(\pi )$ where the spectral curves are nonsingular.
$U^{\mathrm {sm}} \subset {\mathcal A}^D(\pi )$ where the spectral curves are nonsingular.
Ngô’s analysis of supports for direct image complexes [Reference Ngô33, Section 7] works for each ![]() $\kappa $-part (see [Reference Ngô33, Proposition 7.2.3]). In particular, as a corollary of ‘freeness’ [Reference Ngô33, Proposition 7.4.10], the isomorphism class of the restriction of formula (58) to
$\kappa $-part (see [Reference Ngô33, Proposition 7.2.3]). In particular, as a corollary of ‘freeness’ [Reference Ngô33, Proposition 7.4.10], the isomorphism class of the restriction of formula (58) to ![]() $U^{\mathrm {sm}}$ is determined by the group scheme
$U^{\mathrm {sm}}$ is determined by the group scheme ![]() $P^0\rvert _{U^{\mathrm {sm}}}$ of formula (39) and the constructible sheaf
$P^0\rvert _{U^{\mathrm {sm}}}$ of formula (39) and the constructible sheaf
 $$ \begin{align} \left(\mathrm{R}^{\text{2d}_{\text{h}_{\pi}^{\text{D}}}} {\text{h}^{\text{D}}_{\pi}}_* {\underline{{\mathbb{C}}}}\right)_{\kappa}\Big\rvert_{U^{\mathrm{sm}}} \in \mathrm{Sh}_c(U^{\mathrm{sm}}), \end{align} $$
$$ \begin{align} \left(\mathrm{R}^{\text{2d}_{\text{h}_{\pi}^{\text{D}}}} {\text{h}^{\text{D}}_{\pi}}_* {\underline{{\mathbb{C}}}}\right)_{\kappa}\Big\rvert_{U^{\mathrm{sm}}} \in \mathrm{Sh}_c(U^{\mathrm{sm}}), \end{align} $$which are both equipped with the ![]() $G_{\pi }$-actions. See [Reference de Cataldo, Rapagnetta and Saccà12, Appendix] for a precise form expressing formula (58) in terms of the direct image complex associated with
$G_{\pi }$-actions. See [Reference de Cataldo, Rapagnetta and Saccà12, Appendix] for a precise form expressing formula (58) in terms of the direct image complex associated with
 $$ \begin{align*} g^0_{\pi}\Big\rvert_{U^{\mathrm{sm}}}: P^0\rvert_{U^{\mathrm{sm}}} \rightarrow U^{\mathrm{sm}} \end{align*} $$
$$ \begin{align*} g^0_{\pi}\Big\rvert_{U^{\mathrm{sm}}}: P^0\rvert_{U^{\mathrm{sm}}} \rightarrow U^{\mathrm{sm}} \end{align*} $$and formula (59).
The following proposition will be used only in Section 5.5:
Proposition 2.11. Assume ![]() $\mathrm {deg}(D)>2g-2$. Let q be an integer coprime to n. We have an isomorphism of the
$\mathrm {deg}(D)>2g-2$. Let q be an integer coprime to n. We have an isomorphism of the ![]() $G_{\pi }$-equivariant objects
$G_{\pi }$-equivariant objects
 $$ \begin{align} \left({\mathrm{Rh}_{\pi,\text{L}}^{\text{D}}}_* {\underline{{\mathbb{C}}}} \right)_{q\kappa} \simeq \left({\mathrm{Rh}_{\pi,\text{L}^{\otimes \text{q}}}^{\text{D}}}_* {\underline{{\mathbb{C}}}} \right)_{\kappa} \in D_c^b\left({\mathcal A}^D(\pi)\right). \end{align} $$
$$ \begin{align} \left({\mathrm{Rh}_{\pi,\text{L}}^{\text{D}}}_* {\underline{{\mathbb{C}}}} \right)_{q\kappa} \simeq \left({\mathrm{Rh}_{\pi,\text{L}^{\otimes \text{q}}}^{\text{D}}}_* {\underline{{\mathbb{C}}}} \right)_{\kappa} \in D_c^b\left({\mathcal A}^D(\pi)\right). \end{align} $$Here  $h_{\pi ,L^{\otimes q}}^D: {\mathcal M}^D_{r,L^{\otimes q}}(\pi ) \to {\mathcal A}^D(\pi ) $ stands for the Hitchin fibration associated with the line bundle
$h_{\pi ,L^{\otimes q}}^D: {\mathcal M}^D_{r,L^{\otimes q}}(\pi ) \to {\mathcal A}^D(\pi ) $ stands for the Hitchin fibration associated with the line bundle ![]() $L^{\otimes q}$.
$L^{\otimes q}$.
Proof. For notational convenience, we use e to denote ![]() $2d_{h_{\pi }^D}$. After restricting to
$2d_{h_{\pi }^D}$. After restricting to ![]() $U^{\mathrm {sm}}$ we have
$U^{\mathrm {sm}}$ we have
 $$ \begin{align} \left(\mathrm{R}^{\text{e}} {\text{h}_{\pi,\text{L}^{\otimes \text{q}}}^{\text{D}}}_* {\underline{{\mathbb{C}}}} \right)_{\kappa'} \simeq {\underline{{\mathbb{C}}}}, \quad \forall \ \kappa' \in \langle \kappa \rangle, \end{align} $$
$$ \begin{align} \left(\mathrm{R}^{\text{e}} {\text{h}_{\pi,\text{L}^{\otimes \text{q}}}^{\text{D}}}_* {\underline{{\mathbb{C}}}} \right)_{\kappa'} \simeq {\underline{{\mathbb{C}}}}, \quad \forall \ \kappa' \in \langle \kappa \rangle, \end{align} $$by Proposition 2.10 and equation (50). We need to analyse the ![]() $G_{\pi }$-equivariant structure on the rank
$G_{\pi }$-equivariant structure on the rank ![]() $1$ trivial local systems (61).
$1$ trivial local systems (61).
Now we consider the constructible sheaf
 $$ \begin{align} \mathrm{R}^{\text{e}} {\text{h}_{\pi,\text{L}^{\otimes \text{q}}}^{\text{D}}}_* {\underline{{\mathbb{C}}}} \Big{|}_{U^{\mathrm{sm}}} \in \mathrm{Sh}_c(U^{\mathrm{sm}}) \end{align} $$
$$ \begin{align} \mathrm{R}^{\text{e}} {\text{h}_{\pi,\text{L}^{\otimes \text{q}}}^{\text{D}}}_* {\underline{{\mathbb{C}}}} \Big{|}_{U^{\mathrm{sm}}} \in \mathrm{Sh}_c(U^{\mathrm{sm}}) \end{align} $$with the ![]() $G_{\pi }$-equivariant structure.
$G_{\pi }$-equivariant structure.
By Proposition 1.1(b), the sheaf (62) is a trivial local system of rank m (corresponding to the m connected components of  ${\mathcal M}^D_{r,L^{\otimes q}}(\pi )$). We may view it as an m-dimensional vector space
${\mathcal M}^D_{r,L^{\otimes q}}(\pi )$). We may view it as an m-dimensional vector space ![]() $V_q \simeq {\mathbb {C}}^m$ on which the cyclic groups
$V_q \simeq {\mathbb {C}}^m$ on which the cyclic groups ![]() $G_{\pi }$ and
$G_{\pi }$ and ![]() $\Gamma $ act. Therefore, to prove formula (60) we only need to show that the isotypic component
$\Gamma $ act. Therefore, to prove formula (60) we only need to show that the isotypic component  $\left (V_q\right )_{\kappa }$ is
$\left (V_q\right )_{\kappa }$ is ![]() $G_{\pi }$-equivariantly isomorphic to
$G_{\pi }$-equivariantly isomorphic to ![]() $(V_1)_{q\kappa }$.
$(V_1)_{q\kappa }$.
Recall the degree ![]() $dq$ Prym variety
$dq$ Prym variety ![]() $\mathrm {Prym}^{dq}(C'/C)$ associated with the line bundle
$\mathrm {Prym}^{dq}(C'/C)$ associated with the line bundle ![]() $L^{\otimes q}$, whose m connected components are identified with the m connected components of
$L^{\otimes q}$, whose m connected components are identified with the m connected components of  ${\mathcal M}^D_{r,L^{\otimes q}}(\pi )$. To connect
${\mathcal M}^D_{r,L^{\otimes q}}(\pi )$. To connect ![]() $V_q$ and
$V_q$ and ![]() $V_1$, we consider the ‘multiplication by q’ map
$V_1$, we consider the ‘multiplication by q’ map
 $$ \begin{align} \mathrm{mult}_q: \mathrm{Prym}^{d}(C'/C) \to \mathrm{Prym}^{dq}(C'/C), \quad {\mathcal L} \mapsto {\mathcal L}^{\otimes q}, \end{align} $$
$$ \begin{align} \mathrm{mult}_q: \mathrm{Prym}^{d}(C'/C) \to \mathrm{Prym}^{dq}(C'/C), \quad {\mathcal L} \mapsto {\mathcal L}^{\otimes q}, \end{align} $$which is clearly ![]() $G_{\pi }$-equivariant.
$G_{\pi }$-equivariant.
We note that ![]() $\mathrm {mult}_q$ induces an identification of the m connected components for the Prym varieties on both sides of formula (63). In fact, choosing base points
$\mathrm {mult}_q$ induces an identification of the m connected components for the Prym varieties on both sides of formula (63). In fact, choosing base points ![]() $x \in \mathrm {Prym}^{q}(C'/C)$ and
$x \in \mathrm {Prym}^{q}(C'/C)$ and ![]() $qx \in \mathrm {Prym}^{dq}(C'/C)$ trivialises both
$qx \in \mathrm {Prym}^{dq}(C'/C)$ trivialises both ![]() $\mathrm {Prym}(C'/C)$-torsors, and the map
$\mathrm {Prym}(C'/C)$-torsors, and the map ![]() $\mathrm {mult}_q$ induces a ‘multiplication by q’ map on the cyclic group
$\mathrm {mult}_q$ induces a ‘multiplication by q’ map on the cyclic group ![]() $\pi _0(\mathrm {Prym}(C'/C))\simeq {\mathbb {Z}}/m{\mathbb {Z}}$. The claim follows from the fact that
$\pi _0(\mathrm {Prym}(C'/C))\simeq {\mathbb {Z}}/m{\mathbb {Z}}$. The claim follows from the fact that ![]() $\mathrm {gcd}(m,q)=1$.
$\mathrm {gcd}(m,q)=1$.
In conclusion, formula (63) induces a ![]() $G_{\pi }$-equivariant isomorphism
$G_{\pi }$-equivariant isomorphism
 $$ \begin{align*} \left[\mathrm{mult}_q\right]: V_1 \xrightarrow{\simeq} V_q \end{align*} $$
$$ \begin{align*} \left[\mathrm{mult}_q\right]: V_1 \xrightarrow{\simeq} V_q \end{align*} $$whose ![]() $\Gamma $-action on the right-hand side is given by the
$\Gamma $-action on the right-hand side is given by the ![]() $\Gamma $-action on the left-hand side composed with the ‘multiplication by q’
$\Gamma $-action on the left-hand side composed with the ‘multiplication by q’ ![]() $\Gamma \xrightarrow {\cdot q} \Gamma $. In particular, we have a
$\Gamma \xrightarrow {\cdot q} \Gamma $. In particular, we have a ![]() $G_{\pi }$-equivariant isomorphism between
$G_{\pi }$-equivariant isomorphism between  $\left (V_q\right )_{\kappa }$ and
$\left (V_q\right )_{\kappa }$ and ![]() $(V_1)_{q\kappa }$. This completes the proof of the proposition.
$(V_1)_{q\kappa }$. This completes the proof of the proposition.
The constraint ![]() $\mathrm {deg}(D)> 2g-2$ will be removed by Remark 4.9, despite the fact that we no longer have full supports in that case.
$\mathrm {deg}(D)> 2g-2$ will be removed by Remark 4.9, despite the fact that we no longer have full supports in that case.
3 Endoscopic decompositions
3.1 Overview: Main results
In Sections 3 and 4, we establish a generalised version of Theorem 0.3 for any effective divisor D with ![]() $\mathrm {deg}(D)>2g-2$ or
$\mathrm {deg}(D)>2g-2$ or ![]() $D = K_C$.
$D = K_C$.
Let D be as before, and let ![]() $\pi : C' \to C$ be a degree m cyclic Galois cover with
$\pi : C' \to C$ be a degree m cyclic Galois cover with ![]() $n=mr$. Recall the Hitchin fibrations
$n=mr$. Recall the Hitchin fibrations
 $$ \begin{align*} h^D: {\mathcal M}^D_{n,L} \to {\mathcal A}^D, \quad h_{\pi}^D: {\mathcal M}^D_{r,L}(\pi) \rightarrow {\mathcal A}^D(\pi), \end{align*} $$
$$ \begin{align*} h^D: {\mathcal M}^D_{n,L} \to {\mathcal A}^D, \quad h_{\pi}^D: {\mathcal M}^D_{r,L}(\pi) \rightarrow {\mathcal A}^D(\pi), \end{align*} $$the fibrewise ![]() $\Gamma $-actions and the corresponding
$\Gamma $-actions and the corresponding ![]() $\kappa $-decompositions. The Galois group
$\kappa $-decompositions. The Galois group ![]() $G_{\pi }$ acts naturally on
$G_{\pi }$ acts naturally on  ${\mathcal M}^D_{r,d}(\pi )$ and
${\mathcal M}^D_{r,d}(\pi )$ and ![]() ${\mathcal A}^D(\pi )$ such that the Hitchin map
${\mathcal A}^D(\pi )$ such that the Hitchin map ![]() $h_{\pi }^D$ is
$h_{\pi }^D$ is ![]() $G_{\pi }$-equivariant (see Section 1.5). By Lemma 1.7, the direct image complex
$G_{\pi }$-equivariant (see Section 1.5). By Lemma 1.7, the direct image complex ![]() ${\mathrm {Rh}_{\pi }^{\text {D}}}_*{\mathbb {C}}$ is
${\mathrm {Rh}_{\pi }^{\text {D}}}_*{\mathbb {C}}$ is ![]() $G_{\pi }$-equivariant, and so is each
$G_{\pi }$-equivariant, and so is each ![]() $\kappa $-isotypic part
$\kappa $-isotypic part
 $$ \begin{align*} \left({\mathrm{Rh}_{\pi}^{\text{D}}}_*{\underline{{\mathbb{C}}}}\right)_{\kappa} \in D^b_c({\mathcal A}^D(\pi)), \end{align*} $$
$$ \begin{align*} \left({\mathrm{Rh}_{\pi}^{\text{D}}}_*{\underline{{\mathbb{C}}}}\right)_{\kappa} \in D^b_c({\mathcal A}^D(\pi)), \end{align*} $$due to the commutativity of the ![]() $\Gamma $- and the
$\Gamma $- and the ![]() $G_{\pi }$-actions. We also note that
$G_{\pi }$-actions. We also note that
 $$ \begin{align*} q_{\mathcal A}^* \left( \mathrm{Rh}^{\text{D}}_{*} {\underline{{\mathbb{C}}}} \right)_{\kappa}\in D^b_c\left({\mathcal A}^D(\pi)\right) \end{align*} $$
$$ \begin{align*} q_{\mathcal A}^* \left( \mathrm{Rh}^{\text{D}}_{*} {\underline{{\mathbb{C}}}} \right)_{\kappa}\in D^b_c\left({\mathcal A}^D(\pi)\right) \end{align*} $$is naturally ![]() $G_{\pi }$-equivariant, induced by the pullback map from the
$G_{\pi }$-equivariant, induced by the pullback map from the ![]() $G_{\pi }$-quotient
$G_{\pi }$-quotient
 $$ \begin{align*} q_{\mathcal A}: {\mathcal A}^D(\pi) \rightarrow {{\mathcal A}^D_{\gamma}}. \end{align*} $$
$$ \begin{align*} q_{\mathcal A}: {\mathcal A}^D(\pi) \rightarrow {{\mathcal A}^D_{\gamma}}. \end{align*} $$Recall the open subsets ![]() ${\mathcal A}^D(\pi )^*$ and
${\mathcal A}^D(\pi )^*$ and  ${{\mathcal A}^D_{\gamma }}^*$ for the Hitchin bases and the free
${{\mathcal A}^D_{\gamma }}^*$ for the Hitchin bases and the free ![]() $G_{\pi }$-quotient map between them from Section 1.5.
$G_{\pi }$-quotient map between them from Section 1.5.
The following theorem is a generalisation of Theorem 0.2:
Theorem 3.1. Let ![]() $\kappa \in \hat {\Gamma }$ and
$\kappa \in \hat {\Gamma }$ and ![]() $\gamma \in \Gamma $ be identified by equation (3), let
$\gamma \in \Gamma $ be identified by equation (3), let ![]() $\pi :C'\to C$ be the Galois cover associated with
$\pi :C'\to C$ be the Galois cover associated with ![]() $\gamma $ and let
$\gamma $ and let  $d^D_{\gamma } = \mathrm {codim}_{{\mathcal A}^D}\left ({\mathcal A}^D_{\gamma }\right )$. There are isomorphisms in
$d^D_{\gamma } = \mathrm {codim}_{{\mathcal A}^D}\left ({\mathcal A}^D_{\gamma }\right )$. There are isomorphisms in  $D^b_c\left ({\mathcal A}^D(\pi )^*\right )$ which are canonical up to scaling:
$D^b_c\left ({\mathcal A}^D(\pi )^*\right )$ which are canonical up to scaling:
 $$ \begin{align} q_{\mathcal A}^* \left( \mathrm{Rh}^{\text{D}}_{*} {\underline{{\mathbb{C}}}} \right)_{\kappa}\Big\rvert_{{\mathcal A}^D(\pi)^*} \xrightarrow{\simeq} \left( {\mathrm{Rh}_{\pi}^{\text{D}}}_* {\underline{{\mathbb{C}}}} \right)_{\kappa}\Big\rvert_{{\mathcal A}^D(\pi)^*}\left[-2d^D_{\gamma}\right] \xrightarrow{\simeq} \left({\mathrm{Rh}_{\pi}^{\text{D}}}_*{\underline{{\mathbb{C}}}}\right)_{\mathrm{st}}\Big\rvert_{{\mathcal A}^D(\pi)^*} \left[-2d^D_{\gamma}\right], \end{align} $$
$$ \begin{align} q_{\mathcal A}^* \left( \mathrm{Rh}^{\text{D}}_{*} {\underline{{\mathbb{C}}}} \right)_{\kappa}\Big\rvert_{{\mathcal A}^D(\pi)^*} \xrightarrow{\simeq} \left( {\mathrm{Rh}_{\pi}^{\text{D}}}_* {\underline{{\mathbb{C}}}} \right)_{\kappa}\Big\rvert_{{\mathcal A}^D(\pi)^*}\left[-2d^D_{\gamma}\right] \xrightarrow{\simeq} \left({\mathrm{Rh}_{\pi}^{\text{D}}}_*{\underline{{\mathbb{C}}}}\right)_{\mathrm{st}}\Big\rvert_{{\mathcal A}^D(\pi)^*} \left[-2d^D_{\gamma}\right], \end{align} $$with the first isomorphism ![]() $G_{\pi }$-equivariant.
$G_{\pi }$-equivariant.
The second isomorphism of formula (64) is obtained immediately from Proposition 2.10, which actually holds over the total space ![]() ${\mathcal A}^D(\pi )$:
${\mathcal A}^D(\pi )$:
 $$ \begin{align*} \left( {\mathrm{Rh}_{\pi}^{\text{D}}}_* {\underline{{\mathbb{C}}}} \right)_{\kappa}\left[-2d^D_{\gamma}\right] \xrightarrow{\simeq} \left({\mathrm{Rh}_{\pi}^{\text{D}}}_*{\underline{{\mathbb{C}}}}\right)_{\mathrm{st}}\left[-2d^D_{\gamma}\right]. \end{align*} $$
$$ \begin{align*} \left( {\mathrm{Rh}_{\pi}^{\text{D}}}_* {\underline{{\mathbb{C}}}} \right)_{\kappa}\left[-2d^D_{\gamma}\right] \xrightarrow{\simeq} \left({\mathrm{Rh}_{\pi}^{\text{D}}}_*{\underline{{\mathbb{C}}}}\right)_{\mathrm{st}}\left[-2d^D_{\gamma}\right]. \end{align*} $$The following theorem is a sheaf-theoretic enhancement of the Hausel–Thaddeus conjecture:
Theorem 3.2. Let  $i^D_{\gamma }: {\mathcal A}^D_{\gamma } \hookrightarrow {\mathcal A}^D$ be the closed embedding. With the same notation as in Theorem 3.1, there is an isomorphism which is canonical up to scaling:
$i^D_{\gamma }: {\mathcal A}^D_{\gamma } \hookrightarrow {\mathcal A}^D$ be the closed embedding. With the same notation as in Theorem 3.1, there is an isomorphism which is canonical up to scaling:
 $$ \begin{align} c^D_{\kappa}: \left(\mathrm{Rh}^{\text{D}}_{*} {\underline{{\mathbb{C}}}}\right)_{\kappa} \xrightarrow{\simeq} {i^D_{\gamma}}_*\left({\mathrm{Rh}^{\text{D}}_{\gamma}}_* {\underline{{\mathbb{C}}}}\right)_{\kappa} \left[-2d^D_{\gamma}\right] \in D_c^b\left({\mathcal A}^D\right). \end{align} $$
$$ \begin{align} c^D_{\kappa}: \left(\mathrm{Rh}^{\text{D}}_{*} {\underline{{\mathbb{C}}}}\right)_{\kappa} \xrightarrow{\simeq} {i^D_{\gamma}}_*\left({\mathrm{Rh}^{\text{D}}_{\gamma}}_* {\underline{{\mathbb{C}}}}\right)_{\kappa} \left[-2d^D_{\gamma}\right] \in D_c^b\left({\mathcal A}^D\right). \end{align} $$ We first observe that formula (65) induces the first isomorphism of formula (64). So Theorem 3.1 is recovered by Theorem 3.2. In fact, we restrict ![]() $c^D_{\kappa }$ to the open subset
$c^D_{\kappa }$ to the open subset  ${{\mathcal A}_{\gamma }^D}^* \subset {\mathcal A}_{\gamma }^D$ and pull it back along the free
${{\mathcal A}_{\gamma }^D}^* \subset {\mathcal A}_{\gamma }^D$ and pull it back along the free ![]() $G_{\pi }$-quotient map
$G_{\pi }$-quotient map
 $$ \begin{align} q_{\mathcal A}: {\mathcal A}^D(\pi)^* \to {{\mathcal A}^D_{\gamma}}^*. \end{align} $$
$$ \begin{align} q_{\mathcal A}: {\mathcal A}^D(\pi)^* \to {{\mathcal A}^D_{\gamma}}^*. \end{align} $$Since the left diagram in diagram (29) is Cartesian restricting to formula (66), we recover the first map of formula (64) via proper base change.
Theorems 3.1 and 3.2 recover Theorems 0.2 and 0.3 when ![]() $D = K_C$. When
$D = K_C$. When ![]() $\mathrm {deg}(D)>2g-2$, Theorem 3.2 provides a concrete description of the contribution of each support
$\mathrm {deg}(D)>2g-2$, Theorem 3.2 provides a concrete description of the contribution of each support  ${\mathcal A}^D_{\gamma }$ to
${\mathcal A}^D_{\gamma }$ to
 $$ \begin{align*} \mathrm{Rh}^{\text{D}}_{*} {\underline{{\mathbb{C}}}} \in D_c^b\left({\mathcal A}^D\right). \end{align*} $$
$$ \begin{align*} \mathrm{Rh}^{\text{D}}_{*} {\underline{{\mathbb{C}}}} \in D_c^b\left({\mathcal A}^D\right). \end{align*} $$This enhances the main theorem of de Cataldo [Reference de Cataldo6].
As already discussed, to prove Theorems 3.1 and 3.2, we only need to construct ![]() $G_{\pi }$-equivariant isomorphisms
$G_{\pi }$-equivariant isomorphisms
 $$ \begin{align*} c^D_{\kappa}: \left(\mathrm{Rh}^{\text{D}}_{*} {\underline{{\mathbb{C}}}}\right)_{\kappa} \xrightarrow{\simeq} {i^D_{\gamma}}_*\left({\mathrm{Rh}^{\text{D}}_{\gamma}}_* {\underline{{\mathbb{C}}}}\right)_{\kappa} \left[-2d^D_{\gamma}\right] \in D_c^b\left({\mathcal A}^D\right), \end{align*} $$
$$ \begin{align*} c^D_{\kappa}: \left(\mathrm{Rh}^{\text{D}}_{*} {\underline{{\mathbb{C}}}}\right)_{\kappa} \xrightarrow{\simeq} {i^D_{\gamma}}_*\left({\mathrm{Rh}^{\text{D}}_{\gamma}}_* {\underline{{\mathbb{C}}}}\right)_{\kappa} \left[-2d^D_{\gamma}\right] \in D_c^b\left({\mathcal A}^D\right), \end{align*} $$which we treat in this section for the following special cases.
In Section 4, we reduce the other cases of Theorem 3.2 – including possibly the most interesting case, ![]() $D=K_C$ – to Theorem 3.3.
$D=K_C$ – to Theorem 3.3.
3.2 Spectral curves and line bundles
Recall the universal spectral curve (36) for ![]() $\mathrm {GL}_r$-Higgs bundles over the curve
$\mathrm {GL}_r$-Higgs bundles over the curve ![]() $C'$. We denote its restriction to the subspace
$C'$. We denote its restriction to the subspace  ${\mathcal A}^D(\pi ) \subset \widetilde {{\mathcal A}}^{D'}(C')$ by
${\mathcal A}^D(\pi ) \subset \widetilde {{\mathcal A}}^{D'}(C')$ by
This is ![]() $G_{\pi }$-equivariant with respect to the natural Galois group
$G_{\pi }$-equivariant with respect to the natural Galois group ![]() $G_{\pi }$ actions on both the base
$G_{\pi }$ actions on both the base ![]() ${\mathcal A}^{D}(\pi )$ and the universal curve
${\mathcal A}^{D}(\pi )$ and the universal curve ![]() ${\mathcal C}_{\pi }$.
${\mathcal C}_{\pi }$.
We consider the largest Zariski open subset
such thatFootnote 3
(a) the action of
 $G_{\pi }$ is free on
$G_{\pi }$ is free on  ${\mathcal A}^{\heartsuit }(\pi )$ and
${\mathcal A}^{\heartsuit }(\pi )$ and(b) the restriction
(68)of the spectral curves (67) is smooth. $$ \begin{align} {\mathcal C}^{\heartsuit}_{\pi} \rightarrow {\mathcal A}^{\heartsuit}(\pi) \end{align} $$
$$ \begin{align} {\mathcal C}^{\heartsuit}_{\pi} \rightarrow {\mathcal A}^{\heartsuit}(\pi) \end{align} $$
Taking the ![]() $G_{\pi }$-quotients, the family (68) descends to a family of nonsingular curves
$G_{\pi }$-quotients, the family (68) descends to a family of nonsingular curves
 $$ \begin{align} {\mathcal C}^{\heartsuit}_{\gamma} \rightarrow {\mathcal A}^{\heartsuit}_{\gamma}, \end{align} $$
$$ \begin{align} {\mathcal C}^{\heartsuit}_{\gamma} \rightarrow {\mathcal A}^{\heartsuit}_{\gamma}, \end{align} $$where  ${\mathcal A}^{\heartsuit }_{\gamma } = {\mathcal A}^{\heartsuit }(\pi )/G_{\pi }$ is an open dense subset of
${\mathcal A}^{\heartsuit }_{\gamma } = {\mathcal A}^{\heartsuit }(\pi )/G_{\pi }$ is an open dense subset of  ${\mathcal A}^D_{\gamma } = {\mathcal A}^D(\pi )/G_{\pi }$. We denote by
${\mathcal A}^D_{\gamma } = {\mathcal A}^D(\pi )/G_{\pi }$. We denote by
 $$ \begin{align} {\mathcal C}^{\circ}_{\gamma} \rightarrow {\mathcal A}^{\heartsuit}_{\gamma} \end{align} $$
$$ \begin{align} {\mathcal C}^{\circ}_{\gamma} \rightarrow {\mathcal A}^{\heartsuit}_{\gamma} \end{align} $$the restriction of the universal ![]() $\mathrm {SL}_n$-spectral curves over
$\mathrm {SL}_n$-spectral curves over ![]() ${\mathcal A}^D$ to
${\mathcal A}^D$ to  ${\mathcal A}^{\heartsuit }_{\gamma }$. The families (69) and (70) are connected by the following lemma:
${\mathcal A}^{\heartsuit }_{\gamma }$. The families (69) and (70) are connected by the following lemma:
Lemma 3.4. There is a natural  ${\mathcal A}^{\heartsuit }_{\gamma }$-morphism
${\mathcal A}^{\heartsuit }_{\gamma }$-morphism

whose restriction to each closed fibre
 $$ \begin{align*} u_{a}: {\mathcal C}^{\heartsuit}_{\gamma,a} \rightarrow {\mathcal C}^{\circ}_{\gamma,a}, \quad a\in {\mathcal A}^{\heartsuit}_{\gamma}, \end{align*} $$
$$ \begin{align*} u_{a}: {\mathcal C}^{\heartsuit}_{\gamma,a} \rightarrow {\mathcal C}^{\circ}_{\gamma,a}, \quad a\in {\mathcal A}^{\heartsuit}_{\gamma}, \end{align*} $$is a normalisation of curves.
Proof. We first recall the construction in [Reference Hausel and Pauly21, Section 5.1] that, for a given degree r spectral curve ![]() $C^{\prime }_{\alpha } \rightarrow C'$ lying in
$C^{\prime }_{\alpha } \rightarrow C'$ lying in ![]() $V(D')$, there is a natural birational morphism
$V(D')$, there is a natural birational morphism
with ![]() $C_{\alpha }$ a degree n spectral curve over C lying in the total space
$C_{\alpha }$ a degree n spectral curve over C lying in the total space ![]() $V(D)$. In fact, given
$V(D)$. In fact, given ![]() $C^{\prime }_{\alpha } \to C'$, let
$C^{\prime }_{\alpha } \to C'$, let
be another degree r spectral cover over ![]() $C'$ obtained as the pullback of
$C'$ obtained as the pullback of ![]() $C^{\prime }_{\alpha } \rightarrow C'$ along the Galois automorphism
$C^{\prime }_{\alpha } \rightarrow C'$ along the Galois automorphism
 $$ \begin{align*} g: C' \xrightarrow{\simeq} C', \quad g\in G_{\pi}. \end{align*} $$
$$ \begin{align*} g: C' \xrightarrow{\simeq} C', \quad g\in G_{\pi}. \end{align*} $$The ![]() $G_{\pi }$-invariant curve
$G_{\pi }$-invariant curve
 $$ \begin{align*} \widetilde{C}^{\prime}_{\alpha} = \bigcup_{g\in G_{\pi}} g^* C^{\prime}_{\alpha} \end{align*} $$
$$ \begin{align*} \widetilde{C}^{\prime}_{\alpha} = \bigcup_{g\in G_{\pi}} g^* C^{\prime}_{\alpha} \end{align*} $$is a degree ![]() $n(=mr)$ spectral cover over
$n(=mr)$ spectral cover over ![]() $C'$, which descends to a degree n spectral cover
$C'$, which descends to a degree n spectral cover ![]() $C_{\alpha } \to C$ via taking the
$C_{\alpha } \to C$ via taking the ![]() $G_{\pi }$-quotient. Moreover, we see from the construction of
$G_{\pi }$-quotient. Moreover, we see from the construction of ![]() $\Phi _{\Gamma }$ in [Reference Hausel and Pauly21, Section 5.1] that the point
$\Phi _{\Gamma }$ in [Reference Hausel and Pauly21, Section 5.1] that the point  $\left [C^{\prime }_{\alpha }\right ] \in {\mathcal A}^{\heartsuit }(\pi )$ maps to
$\left [C^{\prime }_{\alpha }\right ] \in {\mathcal A}^{\heartsuit }(\pi )$ maps to  $[C_{\alpha }] \in {\mathcal A}^{\heartsuit }_{\gamma }$ via the natural quotient map
$[C_{\alpha }] \in {\mathcal A}^{\heartsuit }_{\gamma }$ via the natural quotient map  $q^D_{\mathcal A}: {\mathcal A}^{\heartsuit }(\pi ) \to {\mathcal A}^{\heartsuit }_{\gamma }$. The composition
$q^D_{\mathcal A}: {\mathcal A}^{\heartsuit }(\pi ) \to {\mathcal A}^{\heartsuit }_{\gamma }$. The composition
 $$ \begin{align*} C^{\prime}_{\alpha} \hookrightarrow \widetilde{C}^{\prime}_{\alpha} \rightarrow C_{\alpha} \end{align*} $$
$$ \begin{align*} C^{\prime}_{\alpha} \hookrightarrow \widetilde{C}^{\prime}_{\alpha} \rightarrow C_{\alpha} \end{align*} $$is birational, hence it is a normalisation by the smoothness of ![]() $C^{\prime }_{\alpha }$.
$C^{\prime }_{\alpha }$.
This construction works for families of spectral curves over the Hitchin bases. Hence we obtain a commutative diagram

where the left vertical morphism is ![]() $G_{\pi }$-equivariant and the horizontal morphisms are
$G_{\pi }$-equivariant and the horizontal morphisms are ![]() $G_{\pi }$-quotient maps. The lemma follows from descending the left vertical arrow.
$G_{\pi }$-quotient maps. The lemma follows from descending the left vertical arrow.
For a closed point  $a \in {\mathcal A}^{\heartsuit }_{\gamma }$, we denote the corresponding spectral curves over
$a \in {\mathcal A}^{\heartsuit }_{\gamma }$, we denote the corresponding spectral curves over ![]() $C'$ and C by
$C'$ and C by ![]() $C^{\prime }_a$ and
$C^{\prime }_a$ and ![]() $C_a$, respectively, with the morphism
$C_a$, respectively, with the morphism
given by Lemma 3.4. We consider the commutative diagram

Here ![]() $s_a: C_a \to C$ is the spectral cover over C, and
$s_a: C_a \to C$ is the spectral cover over C, and ![]() $s^{\prime }_a: C^{\prime }_a \to C$ is the composition of the spectral cover
$s^{\prime }_a: C^{\prime }_a \to C$ is the composition of the spectral cover ![]() $C^{\prime }_a \to C'$ and the cyclic Galois cover
$C^{\prime }_a \to C'$ and the cyclic Galois cover ![]() $\pi :C' \to C$. Both
$\pi :C' \to C$. Both ![]() $s^{\prime }_a$ and
$s^{\prime }_a$ and ![]() $s_a$ are finite of degree n.
$s_a$ are finite of degree n.
We also consider the line bundles
The line bundle ![]() $\omega _{\pi ,a}$ is defined for every spectral curve over
$\omega _{\pi ,a}$ is defined for every spectral curve over ![]() ${\mathcal A}^D(\pi )$, which gives a family of line bundles over the affine space
${\mathcal A}^D(\pi )$, which gives a family of line bundles over the affine space ![]() ${\mathcal A}^D(\pi )$. Hence it is constant over
${\mathcal A}^D(\pi )$. Hence it is constant over ![]() ${\mathcal A}^D(\pi )$ and does not depend on the choice of the spectral curve. Similarly, the line bundle
${\mathcal A}^D(\pi )$ and does not depend on the choice of the spectral curve. Similarly, the line bundle ![]() $\omega _a$ is also independent of the spectral curve over C. So we may write
$\omega _a$ is also independent of the spectral curve over C. So we may write
The following lemma is obtained via a direct calculation:
Lemma 3.5. We have
 $$ \begin{align*} \mathrm{deg}(\omega_{\pi}) =n(1-r)\frac{\mathrm{deg}(D)}{2}, \quad \mathrm{deg}(\omega) = n(1-n)\frac{\mathrm{deg}(D)}{2}. \end{align*} $$
$$ \begin{align*} \mathrm{deg}(\omega_{\pi}) =n(1-r)\frac{\mathrm{deg}(D)}{2}, \quad \mathrm{deg}(\omega) = n(1-n)\frac{\mathrm{deg}(D)}{2}. \end{align*} $$In particular, if ![]() $\mathrm {deg}(D)$ is even, both line bundles
$\mathrm {deg}(D)$ is even, both line bundles ![]() $\omega _{\pi }$ and
$\omega _{\pi }$ and ![]() $\omega $ have degrees divisible by n.
$\omega $ have degrees divisible by n.
Proof. Since the second equality is a special case of the first one, we only prove the degree formula for ![]() $\mathrm {deg}(\omega _{\pi })$.
$\mathrm {deg}(\omega _{\pi })$.
By the discussion before Lemma 3.5, the line bundle ![]() $\omega _{\pi }$ does not depend on the choice of the spectral curve. Let
$\omega _{\pi }$ does not depend on the choice of the spectral curve. Let
 $$ \begin{align*} s^{\prime}_a: C^{\prime}_a \to C' \xrightarrow{\pi} C \end{align*} $$
$$ \begin{align*} s^{\prime}_a: C^{\prime}_a \to C' \xrightarrow{\pi} C \end{align*} $$be the spectral cover where ![]() $C^{\prime }_a$ is a nonsingular curve lying in
$C^{\prime }_a$ is a nonsingular curve lying in ![]() $V(D')$ of genus
$V(D')$ of genus
 $$ \begin{align*} g\left(C^{\prime}_a\right) = r(r-1) \frac{\mathrm{deg}(D')}{2}+r\left(g(C')-1\right)+1 \end{align*} $$
$$ \begin{align*} g\left(C^{\prime}_a\right) = r(r-1) \frac{\mathrm{deg}(D')}{2}+r\left(g(C')-1\right)+1 \end{align*} $$(see the formula for ![]() $d_{h_n}$ in [Reference de Cataldo6, Section 6.1]). Then applying the Riemann–Roch formula to
$d_{h_n}$ in [Reference de Cataldo6, Section 6.1]). Then applying the Riemann–Roch formula to ![]() $\chi \left (C^{\prime }_a, {\mathcal O}_{C^{\prime }_a}\right ) = \chi (C, \omega _{\pi })$, we obtain
$\chi \left (C^{\prime }_a, {\mathcal O}_{C^{\prime }_a}\right ) = \chi (C, \omega _{\pi })$, we obtain
which implies the lemma.
The following lemma concerns pushing forward a line bundle ![]() ${\mathcal N} \in \mathrm {Pic}(C_a)$ and its pullback
${\mathcal N} \in \mathrm {Pic}(C_a)$ and its pullback
to the curve ![]() $C_a'$:
$C_a'$:
Lemma 3.6. With the same notation as in diagram (72), we have
 $$ \begin{align*} \mathrm{det}\left({s_a}_* {\mathcal N}\right) = \mathrm{det}\left({s^{\prime}_a}_*u_a^*{\mathcal N}\right)\otimes \omega \otimes \omega_{\pi}^{-1}. \end{align*} $$
$$ \begin{align*} \mathrm{det}\left({s_a}_* {\mathcal N}\right) = \mathrm{det}\left({s^{\prime}_a}_*u_a^*{\mathcal N}\right)\otimes \omega \otimes \omega_{\pi}^{-1}. \end{align*} $$Proof. Recall the norm maps
from [Reference Hausel and Pauly21, Section 3]. By [Reference Hausel and Pauly21, Lemma 3.4], we have
Then [Reference Hausel and Pauly21, Corollary 3.12] implies that
 $$ \begin{align*} \mathrm{det}\left({s_a}_*{\mathcal N}\,\right) \otimes \omega^{-1} = \mathrm{Nm}({\mathcal N}\,) = \mathrm{Nm}\left(u_a^*{\mathcal N}\,\right) = \mathrm{det}\left({s^{\prime}_a}_*u_a^*{\mathcal N}\,\right)\otimes \omega_{\pi}^{-1}. \end{align*} $$
$$ \begin{align*} \mathrm{det}\left({s_a}_*{\mathcal N}\,\right) \otimes \omega^{-1} = \mathrm{Nm}({\mathcal N}\,) = \mathrm{Nm}\left(u_a^*{\mathcal N}\,\right) = \mathrm{det}\left({s^{\prime}_a}_*u_a^*{\mathcal N}\,\right)\otimes \omega_{\pi}^{-1}. \end{align*} $$ For ![]() $n\geq 1$ and
$n\geq 1$ and ![]() $L \in \mathrm {Pic}(C)$, we consider the regular parts
$L \in \mathrm {Pic}(C)$, we consider the regular parts
 $$ \begin{align*} {\mathcal M}^{D,\mathrm{reg}}_{n,L} \subset {\mathcal M}^D_{n,L}, \quad {\mathcal M}^{D, \mathrm{reg}}_{r,L}(\pi) \subset {\mathcal M}^{D}_{r,L}(\pi), \end{align*} $$
$$ \begin{align*} {\mathcal M}^{D,\mathrm{reg}}_{n,L} \subset {\mathcal M}^D_{n,L}, \quad {\mathcal M}^{D, \mathrm{reg}}_{r,L}(\pi) \subset {\mathcal M}^{D}_{r,L}(\pi), \end{align*} $$which are open subvarieties parameterising Higgs bundles obtained as the push-forward of line bundles supported on the spectral curves. We define the line bundle
 $$ \begin{align} L' = L \otimes \omega \otimes \omega_{\pi}^{-1} \in \mathrm{Pic}(C). \end{align} $$
$$ \begin{align} L' = L \otimes \omega \otimes \omega_{\pi}^{-1} \in \mathrm{Pic}(C). \end{align} $$The following is a corollary of Lemma 3.6:
Corollary 3.7. The pullback ![]() $u^*_{\mathcal C}$ of diagram (71) induces a
$u^*_{\mathcal C}$ of diagram (71) induces a ![]() $G_{\pi }$-equivariant morphism of the regular parts
$G_{\pi }$-equivariant morphism of the regular parts
 $$ \begin{align*} g_u: {\mathcal M}^{D,\mathrm{reg}}_{n,L}\times_{{\mathcal A}^D} {\mathcal A}^{\heartsuit}(\pi) \rightarrow {\mathcal M}^{D, \mathrm{reg}}_{r,L'}(\pi)\times_{{\mathcal A}^D(\pi)}{\mathcal A}^{\heartsuit}(\pi), \end{align*} $$
$$ \begin{align*} g_u: {\mathcal M}^{D,\mathrm{reg}}_{n,L}\times_{{\mathcal A}^D} {\mathcal A}^{\heartsuit}(\pi) \rightarrow {\mathcal M}^{D, \mathrm{reg}}_{r,L'}(\pi)\times_{{\mathcal A}^D(\pi)}{\mathcal A}^{\heartsuit}(\pi), \end{align*} $$where ![]() $L'$ is given by equation (73). The morphism
$L'$ is given by equation (73). The morphism ![]() ${\mathcal A}^{\heartsuit }(\pi ) \rightarrow {\mathcal A}^D$ used in the base change of the left-hand side is the composition
${\mathcal A}^{\heartsuit }(\pi ) \rightarrow {\mathcal A}^D$ used in the base change of the left-hand side is the composition
 $$ \begin{align*} {\mathcal A}^{\heartsuit}(\pi) \xrightarrow{q_{\mathcal A}} {\mathcal A}^{\heartsuit}_{\gamma} \hookrightarrow {\mathcal A}^D. \end{align*} $$
$$ \begin{align*} {\mathcal A}^{\heartsuit}(\pi) \xrightarrow{q_{\mathcal A}} {\mathcal A}^{\heartsuit}_{\gamma} \hookrightarrow {\mathcal A}^D. \end{align*} $$Remark 3.8. Since ![]() $\mathrm {gcd}(n, \mathrm {deg}(L)) = 1$ and
$\mathrm {gcd}(n, \mathrm {deg}(L)) = 1$ and
Lemma 3.5 implies that
when ![]() $\mathrm {deg}(D)$ is even.
$\mathrm {deg}(D)$ is even.
Finally, we note that both varieties  ${\mathcal M}^{D,\mathrm {reg}}_{n,L}$ and
${\mathcal M}^{D,\mathrm {reg}}_{n,L}$ and  ${\mathcal M}^{D, \mathrm {reg}}_{r,L'}(\pi )$ admit
${\mathcal M}^{D, \mathrm {reg}}_{r,L'}(\pi )$ admit ![]() $\Gamma $-actions induced by the tensor product with n-torsion line bundles. The
$\Gamma $-actions induced by the tensor product with n-torsion line bundles. The ![]() $\Gamma $-actions are clearly fibrewise with respect to the Hitchin maps
$\Gamma $-actions are clearly fibrewise with respect to the Hitchin maps
 $$ \begin{align} {\mathcal M}^{D,\mathrm{reg}}_{n,L} \to {\mathcal A}^D, \quad {\mathcal M}^{D, \mathrm{reg}}_{r,L'}(\pi) \to {\mathcal A}^D(\pi). \end{align} $$
$$ \begin{align} {\mathcal M}^{D,\mathrm{reg}}_{n,L} \to {\mathcal A}^D, \quad {\mathcal M}^{D, \mathrm{reg}}_{r,L'}(\pi) \to {\mathcal A}^D(\pi). \end{align} $$Since the pullback ![]() $u_a^*: \mathrm {Pic}(C_a) \to \mathrm {Pic}\left (C_a'\right )$ induced by diagram (72) is compatible with the
$u_a^*: \mathrm {Pic}(C_a) \to \mathrm {Pic}\left (C_a'\right )$ induced by diagram (72) is compatible with the ![]() $\Gamma $-action on both sides, we conclude the following lemma:
$\Gamma $-action on both sides, we conclude the following lemma:
Lemma 3.9. The morphism ![]() $g_u$ given in Corollary 3.7 is
$g_u$ given in Corollary 3.7 is ![]() $\Gamma $-equivariant.
$\Gamma $-equivariant.
3.3 Proof of Theorem 3.3, step 1: Cohomological correspondences
Through Section 3.5, we assume that D is an effective divisor with ![]() $\mathrm {deg}(D)$ even and
$\mathrm {deg}(D)$ even and ![]() $\mathrm {deg}(D)>2g-2$. Our first step in the proof of Theorem 3.3 is to construct a correspondence between the direct image complexes associated with the two Hitchin maps attached to formula (74). Then we show that this correspondence induces an isomorphism for the
$\mathrm {deg}(D)>2g-2$. Our first step in the proof of Theorem 3.3 is to construct a correspondence between the direct image complexes associated with the two Hitchin maps attached to formula (74). Then we show that this correspondence induces an isomorphism for the ![]() $\kappa $-parts following Ngô and Yun ([Reference Yun39, Appendix A]).
$\kappa $-parts following Ngô and Yun ([Reference Yun39, Appendix A]).
We consider the graph of ![]() $g_u$ in Corollary 3.7, which gives a subvariety
$g_u$ in Corollary 3.7, which gives a subvariety
 $$ \begin{align*} \mathrm{Graph}(g_u) \subset \left({\mathcal M}^{D, \mathrm{reg}}_{r,L'}(\pi)\times_{{\mathcal A}^D(\pi)}{\mathcal A}^{\heartsuit}(\pi)\right)\times _{{\mathcal A}^{\heartsuit}(\pi)} \left({\mathcal M}^{D,\mathrm{reg}}_{n,L}\times_{{\mathcal A}^D} {\mathcal A}^{\heartsuit}(\pi)\right). \end{align*} $$
$$ \begin{align*} \mathrm{Graph}(g_u) \subset \left({\mathcal M}^{D, \mathrm{reg}}_{r,L'}(\pi)\times_{{\mathcal A}^D(\pi)}{\mathcal A}^{\heartsuit}(\pi)\right)\times _{{\mathcal A}^{\heartsuit}(\pi)} \left({\mathcal M}^{D,\mathrm{reg}}_{n,L}\times_{{\mathcal A}^D} {\mathcal A}^{\heartsuit}(\pi)\right). \end{align*} $$Taking its Zariski closure, we obtain a closed subvariety
 $$ \begin{align*} \Sigma = \overline{\mathrm{Graph}(g_u)} \subset {\mathcal M}^D_{r,L'}(\pi) \times_{{\mathcal A}^D(\pi)} \left( {\mathcal M}^D_{n,L} \times_{{\mathcal A}^D} {\mathcal A}^D(\pi) \right), \end{align*} $$
$$ \begin{align*} \Sigma = \overline{\mathrm{Graph}(g_u)} \subset {\mathcal M}^D_{r,L'}(\pi) \times_{{\mathcal A}^D(\pi)} \left( {\mathcal M}^D_{n,L} \times_{{\mathcal A}^D} {\mathcal A}^D(\pi) \right), \end{align*} $$which fits into the commutative diagram

Here we use  $h^D_{\pi ,L'}$ to denote the Hitchin fibration
$h^D_{\pi ,L'}$ to denote the Hitchin fibration
 $$ \begin{align*} h^D_{\pi,L'} := h^D_{\pi}: {\mathcal M}^D_{r,L'}(\pi) \to {\mathcal A}^D(\pi), \end{align*} $$
$$ \begin{align*} h^D_{\pi,L'} := h^D_{\pi}: {\mathcal M}^D_{r,L'}(\pi) \to {\mathcal A}^D(\pi), \end{align*} $$indicating its dependence on the line bundle ![]() $L'$. All the morphisms in the diagram are proper.
$L'$. All the morphisms in the diagram are proper.
By Corollary 3.7 and Lemma 3.9, the morphism ![]() $g_u$ is equivariant under the actions of
$g_u$ is equivariant under the actions of ![]() $G_{\pi }$ and
$G_{\pi }$ and ![]() $\Gamma $. Hence, as the Zariski closure of the graph of
$\Gamma $. Hence, as the Zariski closure of the graph of ![]() $g_u$, the subvariety
$g_u$, the subvariety ![]() $\Sigma $ is invariant under the natural actions of
$\Sigma $ is invariant under the natural actions of ![]() $G_{\pi }$ and
$G_{\pi }$ and ![]() $\Gamma $ on the ambient space
$\Gamma $ on the ambient space  ${\mathcal M}^D_{r,L'}(\pi ) \times _{{\mathcal A}^D(\pi )} \left ( {\mathcal M}^D_{n,L} \times _{{\mathcal A}^D} {\mathcal A}^D(\pi ) \right )$. Since the projections
${\mathcal M}^D_{r,L'}(\pi ) \times _{{\mathcal A}^D(\pi )} \left ( {\mathcal M}^D_{n,L} \times _{{\mathcal A}^D} {\mathcal A}^D(\pi ) \right )$. Since the projections
 $$ \begin{align*} \begin{split} {\mathcal M}^D_{r,L'}(\pi) \times_{{\mathcal A}^D(\pi)} \left( {\mathcal M}^D_{n,L} \times_{{\mathcal A}^D} {\mathcal A}^D(\pi) \right) & \to {\mathcal M}^D_{r,L'}, \\ {\mathcal M}^D_{r,L'}(\pi) \times_{{\mathcal A}^D(\pi)} \left( {\mathcal M}^D_{n,L} \times_{{\mathcal A}^D} {\mathcal A}^D(\pi) \right) & \to {\mathcal M}^D_{n,L} \times_{{\mathcal A}^D} {\mathcal A}^D(\pi), \end{split} \end{align*} $$
$$ \begin{align*} \begin{split} {\mathcal M}^D_{r,L'}(\pi) \times_{{\mathcal A}^D(\pi)} \left( {\mathcal M}^D_{n,L} \times_{{\mathcal A}^D} {\mathcal A}^D(\pi) \right) & \to {\mathcal M}^D_{r,L'}, \\ {\mathcal M}^D_{r,L'}(\pi) \times_{{\mathcal A}^D(\pi)} \left( {\mathcal M}^D_{n,L} \times_{{\mathcal A}^D} {\mathcal A}^D(\pi) \right) & \to {\mathcal M}^D_{n,L} \times_{{\mathcal A}^D} {\mathcal A}^D(\pi), \end{split} \end{align*} $$to both factors are ![]() $G_{\pi }$- and
$G_{\pi }$- and ![]() $\Gamma $-equivariant, the projections from the invariant subvariety
$\Gamma $-equivariant, the projections from the invariant subvariety ![]() $\Sigma $ to both factors are also
$\Sigma $ to both factors are also ![]() $G_{\pi }$- and
$G_{\pi }$- and ![]() $\Gamma $-equivariant.
$\Gamma $-equivariant.
Theorem 3.10. The correspondence (75) induces a morphism
 $$ \begin{align} [\Sigma]_\#: q_{\mathcal A}^* \left( \mathrm{Rh}^{\text{D}}_{*} {\underline{{\mathbb{C}}}}\right) \rightarrow {\mathrm{Rh}_{\pi,\text{L}'}^{\text{D}}}_*{\underline{{\mathbb{C}}}} \left[-2d^D_{\gamma}\right], \end{align} $$
$$ \begin{align} [\Sigma]_\#: q_{\mathcal A}^* \left( \mathrm{Rh}^{\text{D}}_{*} {\underline{{\mathbb{C}}}}\right) \rightarrow {\mathrm{Rh}_{\pi,\text{L}'}^{\text{D}}}_*{\underline{{\mathbb{C}}}} \left[-2d^D_{\gamma}\right], \end{align} $$which is equivariant under the natural actions of ![]() $G_{\pi }$ and
$G_{\pi }$ and ![]() $\Gamma $. Assume that the element
$\Gamma $. Assume that the element ![]() $\gamma \in \Gamma $ inducing the Galois cover
$\gamma \in \Gamma $ inducing the Galois cover ![]() $\pi : C' \to C$ matches with
$\pi : C' \to C$ matches with ![]() $\kappa $ via equation (3). Then the
$\kappa $ via equation (3). Then the ![]() $G_{\pi }$-equivariant morphism for the
$G_{\pi }$-equivariant morphism for the ![]() $\kappa $-parts
$\kappa $-parts
 $$ \begin{align} [\Sigma]_{\#,\kappa}: q_{\mathcal A}^* \left( \mathrm{Rh}^{\text{D}}_{*} {\underline{{\mathbb{C}}}}\right)_{\kappa} \to \left({\mathrm{Rh}_{\pi,\text{L}'}^{\text{D}}}_*{\underline{{\mathbb{C}}}}\right)_{\kappa} \left[-2d^D_{\gamma}\right] \end{align} $$
$$ \begin{align} [\Sigma]_{\#,\kappa}: q_{\mathcal A}^* \left( \mathrm{Rh}^{\text{D}}_{*} {\underline{{\mathbb{C}}}}\right)_{\kappa} \to \left({\mathrm{Rh}_{\pi,\text{L}'}^{\text{D}}}_*{\underline{{\mathbb{C}}}}\right)_{\kappa} \left[-2d^D_{\gamma}\right] \end{align} $$induced by formula (76) is an isomorphism after restricting to ![]() ${\mathcal A}^D(\pi )^*$:
${\mathcal A}^D(\pi )^*$:
 $$ \begin{align} [\Sigma]_{\#,\kappa}\Big\rvert_{{\mathcal A}^D(\pi)^*}: q_{\mathcal A}^* \left( \mathrm{Rh}^{\text{D}}_{*} {\underline{{\mathbb{C}}}}\right)_{\kappa}\Big\rvert_{{\mathcal A}^D(\pi)^*} \xrightarrow{\simeq} \left({\mathrm{Rh}_{\pi,\text{L}'}^{\text{D}}}_*{\underline{{\mathbb{C}}}}\right)_{\kappa}\Big\rvert_{{\mathcal A}^D(\pi)^*} \left[-2d^D_{\gamma}\right]. \end{align} $$
$$ \begin{align} [\Sigma]_{\#,\kappa}\Big\rvert_{{\mathcal A}^D(\pi)^*}: q_{\mathcal A}^* \left( \mathrm{Rh}^{\text{D}}_{*} {\underline{{\mathbb{C}}}}\right)_{\kappa}\Big\rvert_{{\mathcal A}^D(\pi)^*} \xrightarrow{\simeq} \left({\mathrm{Rh}_{\pi,\text{L}'}^{\text{D}}}_*{\underline{{\mathbb{C}}}}\right)_{\kappa}\Big\rvert_{{\mathcal A}^D(\pi)^*} \left[-2d^D_{\gamma}\right]. \end{align} $$Proof. The first part follows from the general theory of cohomological correspondences. We refer to [Reference Yun38, Appendix A] as a reference; see also the paragraph before [Reference Yun39, Proposition 3.3.1]. In particular, since the variety ![]() $\Sigma $ is invariant under the
$\Sigma $ is invariant under the ![]() $G_{\pi }$- and
$G_{\pi }$- and ![]() $\Gamma $-actions, and both projections from
$\Gamma $-actions, and both projections from ![]() $\Sigma $ to
$\Sigma $ to  ${\mathcal M}^D_{n,L}\times _{{\mathcal A}^D}{\mathcal A}^D(\pi )$ and
${\mathcal M}^D_{n,L}\times _{{\mathcal A}^D}{\mathcal A}^D(\pi )$ and  ${\mathcal M}^D_{r,L'}(\pi )$ are
${\mathcal M}^D_{r,L'}(\pi )$ are ![]() $G_{\pi }$- and
$G_{\pi }$- and ![]() $\Gamma $-equivariant, we conclude that the cohomological correspondence (76) is also
$\Gamma $-equivariant, we conclude that the cohomological correspondence (76) is also ![]() $G_{\pi }$- and
$G_{\pi }$- and ![]() $\Gamma $-equivariant.
$\Gamma $-equivariant.
Now we restrict ![]() $[\Sigma ]_{\#,\kappa }$ to the open subset
$[\Sigma ]_{\#,\kappa }$ to the open subset ![]() ${\mathcal A}^D(\pi )^*$ and show that it is an isomorphism. It suffices to prove that the restriction of
${\mathcal A}^D(\pi )^*$ and show that it is an isomorphism. It suffices to prove that the restriction of ![]() $[\Sigma ]_{\#,\kappa }$ induces an isomorphism on every perverse cohomology – that is,
$[\Sigma ]_{\#,\kappa }$ induces an isomorphism on every perverse cohomology – that is,
 $$ \begin{align} {}^p{\mathcal H}^i\left([\Sigma]_{\#,\kappa}\right)\Big\rvert_{{\mathcal A}^D(\pi)^*}: q_{\mathcal A}^* {{}^p{\mathcal H}^i}\left( \mathrm{Rh}^{\text{D}}_{*} {\underline{{\mathbb{C}}}}\right)_{\kappa} \Big\rvert_{{\mathcal A}^D(\pi)^*} \xrightarrow{\simeq} {{}^p{\mathcal H}^{i-2d^D_{\gamma}}}\left({\mathrm{Rh}_{\pi,\text{L}'}^{\text{D}}}_*{\underline{{\mathbb{C}}}}\right)_{\kappa} \Big\rvert_{{\mathcal A}^D(\pi)^*}. \end{align} $$
$$ \begin{align} {}^p{\mathcal H}^i\left([\Sigma]_{\#,\kappa}\right)\Big\rvert_{{\mathcal A}^D(\pi)^*}: q_{\mathcal A}^* {{}^p{\mathcal H}^i}\left( \mathrm{Rh}^{\text{D}}_{*} {\underline{{\mathbb{C}}}}\right)_{\kappa} \Big\rvert_{{\mathcal A}^D(\pi)^*} \xrightarrow{\simeq} {{}^p{\mathcal H}^{i-2d^D_{\gamma}}}\left({\mathrm{Rh}_{\pi,\text{L}'}^{\text{D}}}_*{\underline{{\mathbb{C}}}}\right)_{\kappa} \Big\rvert_{{\mathcal A}^D(\pi)^*}. \end{align} $$Here we used the fact that ![]() $q_{\mathcal A}$ is étale restricting to
$q_{\mathcal A}$ is étale restricting to ![]() ${\mathcal A}^D(\pi )^*$. By Corollary 2.2, the left-hand side has
${\mathcal A}^D(\pi )^*$. By Corollary 2.2, the left-hand side has ![]() ${\mathcal A}^D(\pi )^*$ as the only support. Theorem 2.3(b) and Proposition 2.10 yield that the right-hand side also has
${\mathcal A}^D(\pi )^*$ as the only support. Theorem 2.3(b) and Proposition 2.10 yield that the right-hand side also has ![]() ${\mathcal A}^D(\pi )^*$ as the only support. Therefore, both sides are intermediate extensions of certain local systems defined on an open subset of
${\mathcal A}^D(\pi )^*$ as the only support. Therefore, both sides are intermediate extensions of certain local systems defined on an open subset of ![]() ${\mathcal A}^D(\pi )$. As a consequence, in order to prove formula (79), we only need to show that
${\mathcal A}^D(\pi )$. As a consequence, in order to prove formula (79), we only need to show that
 $$ \begin{align*} {}^p{\mathcal H}^i\left([\Sigma]_{\#,\kappa}\right)\Big\rvert_U: q_{\mathcal A}^* {{}^p{\mathcal H}^i}\left( \mathrm{Rh}^{\text{D}}_{*} {\underline{{\mathbb{C}}}}\right)_{\kappa} \Big\rvert_U \xrightarrow{\simeq} {{}^p{\mathcal H}^{i-2d^D_{\gamma}}}\left({\mathrm{Rh}_{\pi,\text{L}'}^{\text{D}}}_*{\underline{{\mathbb{C}}}}\right)_{\kappa}\Big\rvert_U, \end{align*} $$
$$ \begin{align*} {}^p{\mathcal H}^i\left([\Sigma]_{\#,\kappa}\right)\Big\rvert_U: q_{\mathcal A}^* {{}^p{\mathcal H}^i}\left( \mathrm{Rh}^{\text{D}}_{*} {\underline{{\mathbb{C}}}}\right)_{\kappa} \Big\rvert_U \xrightarrow{\simeq} {{}^p{\mathcal H}^{i-2d^D_{\gamma}}}\left({\mathrm{Rh}_{\pi,\text{L}'}^{\text{D}}}_*{\underline{{\mathbb{C}}}}\right)_{\kappa}\Big\rvert_U, \end{align*} $$with ![]() $U \subset {\mathcal A}^D(\pi )^*$ a Zariski open subset. This reduces the proof to showing that, for a general point
$U \subset {\mathcal A}^D(\pi )^*$ a Zariski open subset. This reduces the proof to showing that, for a general point ![]() $a \in {\mathcal A}^D(\pi )^*$, the correspondence between the Hitchin fibres
$a \in {\mathcal A}^D(\pi )^*$, the correspondence between the Hitchin fibres
 $$ \begin{align} [\Sigma_a]: H^i\left(\left({\mathcal M}^D_{n,L}\right)_a, {\mathbb{C}}\right) \rightarrow H^{i-2d^D_{\gamma}}\left({\mathcal M}^D_{r,L'}(\pi)_a, {\mathbb{C}}\right) \end{align} $$
$$ \begin{align} [\Sigma_a]: H^i\left(\left({\mathcal M}^D_{n,L}\right)_a, {\mathbb{C}}\right) \rightarrow H^{i-2d^D_{\gamma}}\left({\mathcal M}^D_{r,L'}(\pi)_a, {\mathbb{C}}\right) \end{align} $$induced by the fundamental class of ![]() $\Sigma _a$ is an isomorphism between the
$\Sigma _a$ is an isomorphism between the ![]() $\kappa $-parts. Here
$\kappa $-parts. Here ![]() $\Sigma _a$ is the restriction of
$\Sigma _a$ is the restriction of ![]() $\Sigma $ over a. Let a be a general point lying in the open subset
$\Sigma $ over a. Let a be a general point lying in the open subset ![]() ${\mathcal A}^{\heartsuit }(\pi )\subset {\mathcal A}^D(\pi )$. The pullback of the diagram (71) along
${\mathcal A}^{\heartsuit }(\pi )\subset {\mathcal A}^D(\pi )$. The pullback of the diagram (71) along  $\{a\} \rightarrow {\mathcal A}^{\heartsuit }_{\gamma }$ is a normalisation
$\{a\} \rightarrow {\mathcal A}^{\heartsuit }_{\gamma }$ is a normalisation
of curves where ![]() $C_a$ has at worst nodal singularities. In this case, the description of the correspondence (80) is concretely given in [Reference Yun39, Appendix A], and the isomorphism of the
$C_a$ has at worst nodal singularities. In this case, the description of the correspondence (80) is concretely given in [Reference Yun39, Appendix A], and the isomorphism of the ![]() $\kappa $-parts follows from a direct calculation [Reference Yun39, Lemma 3.4.1].Footnote 4 This completes the proof.
$\kappa $-parts follows from a direct calculation [Reference Yun39, Lemma 3.4.1].Footnote 4 This completes the proof.
Corollary 3.11. With the same assumption as in Theorem 3.10, the ![]() $G_{\pi }$-equivariant isomorphism (78) induces an isomorphism
$G_{\pi }$-equivariant isomorphism (78) induces an isomorphism
 $$ \begin{align*} [\Sigma]^{G_{\pi}}_{\#,\kappa}: \left(\mathrm{Rh}^{\text{D}}_{*} {\underline{{\mathbb{C}}}}\right)_{\kappa} \xrightarrow{\simeq} {i^D_{\gamma}}_*\left({\mathrm{Rh}^{\text{D}}_{\gamma,L'}}_* {\underline{{\mathbb{C}}}}\right)_{\kappa} \left[-2d^D_{\gamma}\right] \in D^b_c\left({\mathcal A}^D\right). \end{align*} $$
$$ \begin{align*} [\Sigma]^{G_{\pi}}_{\#,\kappa}: \left(\mathrm{Rh}^{\text{D}}_{*} {\underline{{\mathbb{C}}}}\right)_{\kappa} \xrightarrow{\simeq} {i^D_{\gamma}}_*\left({\mathrm{Rh}^{\text{D}}_{\gamma,L'}}_* {\underline{{\mathbb{C}}}}\right)_{\kappa} \left[-2d^D_{\gamma}\right] \in D^b_c\left({\mathcal A}^D\right). \end{align*} $$Proof. We push forward the morphism (77) along the ![]() $G_{\pi }$-quotient map
$G_{\pi }$-quotient map  $q_{\mathcal A}: {\mathcal A}^D(\pi ) \to {\mathcal A}^D_{\gamma }$ and take the
$q_{\mathcal A}: {\mathcal A}^D(\pi ) \to {\mathcal A}^D_{\gamma }$ and take the ![]() $G_{\pi }$-invariant parts on both sides. This gives a morphism
$G_{\pi }$-invariant parts on both sides. This gives a morphism
 $$ \begin{align*} [\Sigma]^{G_{\pi}}_{\#,\kappa}: \left(\mathrm{Rh}^{\text{D}}_{*} {\underline{{\mathbb{C}}}}\right)_{\kappa} \to {i^D_{\gamma}}_*\left( {\mathrm{Rh}^{\text{D}}_{\gamma,L'}}_* {\underline{{\mathbb{C}}}}\right)_{\kappa} \left[-2d^D_{\gamma}\right], \end{align*} $$
$$ \begin{align*} [\Sigma]^{G_{\pi}}_{\#,\kappa}: \left(\mathrm{Rh}^{\text{D}}_{*} {\underline{{\mathbb{C}}}}\right)_{\kappa} \to {i^D_{\gamma}}_*\left( {\mathrm{Rh}^{\text{D}}_{\gamma,L'}}_* {\underline{{\mathbb{C}}}}\right)_{\kappa} \left[-2d^D_{\gamma}\right], \end{align*} $$where both sides are semisimple with  ${\mathcal A}^D_{\gamma }$ the only support, by Corollary 2.2, Theorem 2.3(b) and Proposition 2.10. Hence, similar to the proof of Theorem 3.10, it suffices to check that it is an isomorphism restricting to
${\mathcal A}^D_{\gamma }$ the only support, by Corollary 2.2, Theorem 2.3(b) and Proposition 2.10. Hence, similar to the proof of Theorem 3.10, it suffices to check that it is an isomorphism restricting to  ${{\mathcal A}^D_{\gamma }}^*$ which is equivalent to formula (78).
${{\mathcal A}^D_{\gamma }}^*$ which is equivalent to formula (78).
Remark 3.12. We cannot conclude that formula (77) is an isomorphism over the total space ![]() ${\mathcal A}^D(\pi )$ from the isomorphism (78), for the following reason. For a nonsmooth finite morphism
${\mathcal A}^D(\pi )$ from the isomorphism (78), for the following reason. For a nonsmooth finite morphism ![]() $f: X \to Y$ and a semisimple perverse sheaf
$f: X \to Y$ and a semisimple perverse sheaf ![]() ${\mathcal K}$ on Y, the pullback
${\mathcal K}$ on Y, the pullback ![]() $f^*{\mathcal K}$ may fail to be semisimple. A typical example is the case where
$f^*{\mathcal K}$ may fail to be semisimple. A typical example is the case where
and ![]() ${\mathcal K}$ is the intermediate extension of a
${\mathcal K}$ is the intermediate extension of a ![]() $2$-torsion rank
$2$-torsion rank ![]() $1$ local system on
$1$ local system on ![]() ${\mathbb {C}}^* \subset {\mathbb {A}}^1$. The object
${\mathbb {C}}^* \subset {\mathbb {A}}^1$. The object ![]() $f^*{\mathcal K}$ is not determined by its restriction to the open subset
$f^*{\mathcal K}$ is not determined by its restriction to the open subset ![]() ${\mathbb {C}}^*$. In particular, although the restriction of the natural morphism
${\mathbb {C}}^*$. In particular, although the restriction of the natural morphism ![]() $f^*{\mathcal K}\to \underline {{\mathbb {C}}}$ to
$f^*{\mathcal K}\to \underline {{\mathbb {C}}}$ to ![]() ${\mathbb {C}}^*$ is an isomorphism, the morphism
${\mathbb {C}}^*$ is an isomorphism, the morphism ![]() $f^*{\mathcal K} \to \underline {{\mathbb {C}}}$ itself fails to be an isomorphism on
$f^*{\mathcal K} \to \underline {{\mathbb {C}}}$ itself fails to be an isomorphism on ![]() ${\mathbb {A}}^1$. The issue here is caused by the fact that f is not étale at
${\mathbb {A}}^1$. The issue here is caused by the fact that f is not étale at ![]() $0\in {\mathbb {A}}^1$.
$0\in {\mathbb {A}}^1$.
3.4 Proof of Theorem 3.3, step 2: Changing from  $L'$ to L
$L'$ to L
By Lemma 3.5, we have
Hence there exists a line bundle
 $$ \begin{align} {\mathcal N}_0 \in \mathrm{Pic}^k(C), \quad k = \frac{\mathrm{deg}(L') - \mathrm{deg}(L)}{n} \in {\mathbb{Z}}, \end{align} $$
$$ \begin{align} {\mathcal N}_0 \in \mathrm{Pic}^k(C), \quad k = \frac{\mathrm{deg}(L') - \mathrm{deg}(L)}{n} \in {\mathbb{Z}}, \end{align} $$such that  $L' = L \otimes {\mathcal N}_0^{\otimes n}$. The line bundle
$L' = L \otimes {\mathcal N}_0^{\otimes n}$. The line bundle ![]() ${\mathcal N}_0$ induces an
${\mathcal N}_0$ induces an ![]() ${\mathcal A}^D(\pi )$-isomorphism between the relative Hitchin moduli spaces,
${\mathcal A}^D(\pi )$-isomorphism between the relative Hitchin moduli spaces,

via the tensor product ![]() $\phi _{{\mathcal N}_0}({\mathcal E}, \theta ) = ({\mathcal E} \otimes {\mathcal N}_0, \theta )$. It is clear that
$\phi _{{\mathcal N}_0}({\mathcal E}, \theta ) = ({\mathcal E} \otimes {\mathcal N}_0, \theta )$. It is clear that ![]() $\phi _{{\mathcal N}_0}$ is
$\phi _{{\mathcal N}_0}$ is ![]() $G_{\pi }$- and
$G_{\pi }$- and ![]() $\Gamma $-equivariant.
$\Gamma $-equivariant.
Proposition 3.13. There is a ![]() $G_{\pi }$-equivariant isomorphism
$G_{\pi }$-equivariant isomorphism
 $$ \begin{align} \left({\mathrm{Rh}_{\pi,\text{L}'}^{\text{D}}}_*{\underline{{\mathbb{C}}}}\right)_{\kappa} = \left({\mathrm{Rh}_{\pi,\text{L}}^{\text{D}}}_*{\underline{{\mathbb{C}}}}\right)_{\kappa} \in D^b_c\left({\mathcal A}^D(\pi)\right) \end{align} $$
$$ \begin{align} \left({\mathrm{Rh}_{\pi,\text{L}'}^{\text{D}}}_*{\underline{{\mathbb{C}}}}\right)_{\kappa} = \left({\mathrm{Rh}_{\pi,\text{L}}^{\text{D}}}_*{\underline{{\mathbb{C}}}}\right)_{\kappa} \in D^b_c\left({\mathcal A}^D(\pi)\right) \end{align} $$induced by diagram (83). Up to scaling, it is independent of the choice of line bundle (82). In particular, equation (84) induces
 $$ \begin{align*} \left({\mathrm{Rh}_{\gamma,\text{L}'}^{\text{D}}}_*{\underline{{\mathbb{C}}}}\right)_{\kappa} = \left({\mathrm{Rh}_{\gamma,\text{L}}^{\text{D}}}_*{\underline{{\mathbb{C}}}}\right)_{\kappa} \in D^b_c\left({\mathcal A}_{\gamma}^D\right). \end{align*} $$
$$ \begin{align*} \left({\mathrm{Rh}_{\gamma,\text{L}'}^{\text{D}}}_*{\underline{{\mathbb{C}}}}\right)_{\kappa} = \left({\mathrm{Rh}_{\gamma,\text{L}}^{\text{D}}}_*{\underline{{\mathbb{C}}}}\right)_{\kappa} \in D^b_c\left({\mathcal A}_{\gamma}^D\right). \end{align*} $$Proof. The pullback along ![]() $\phi _{{\mathcal N}_0}$ in the diagram (83) induces a
$\phi _{{\mathcal N}_0}$ in the diagram (83) induces a ![]() $G_{\pi }$- and
$G_{\pi }$- and ![]() $\Gamma $- equivariant isomorphism
$\Gamma $- equivariant isomorphism
 $$ \begin{align} {\mathrm{Rh}_{\pi,\text{L}'}^{\text{D}}}_*{\underline{{\mathbb{C}}}} = {\mathrm{Rh}_{\pi,\text{L}}^{\text{D}}}_*{\underline{{\mathbb{C}}}}, \end{align} $$
$$ \begin{align} {\mathrm{Rh}_{\pi,\text{L}'}^{\text{D}}}_*{\underline{{\mathbb{C}}}} = {\mathrm{Rh}_{\pi,\text{L}}^{\text{D}}}_*{\underline{{\mathbb{C}}}}, \end{align} $$which gives our desired isomorphism. For another choice ![]() ${\mathcal N}^{\prime }_0$ of the line bundle (82), we have
${\mathcal N}^{\prime }_0$ of the line bundle (82), we have
 $$ \begin{align*} {\mathcal N}_0^{-1}\otimes {\mathcal N}^{\prime}_0 \in \Gamma. \end{align*} $$
$$ \begin{align*} {\mathcal N}_0^{-1}\otimes {\mathcal N}^{\prime}_0 \in \Gamma. \end{align*} $$Hence the difference of the isomorphisms ![]() $\phi ^*_{{\mathcal N}_0}$ and
$\phi ^*_{{\mathcal N}_0}$ and  $\phi ^*_{{\mathcal N}^{\prime }_0}$ is induced by an automorphism of
$\phi ^*_{{\mathcal N}^{\prime }_0}$ is induced by an automorphism of  ${\mathcal M}^D_{r,L}$ given by an element
${\mathcal M}^D_{r,L}$ given by an element ![]() $g\in \Gamma $. In particular, our choice of isomorphism is affected only by scaling.
$g\in \Gamma $. In particular, our choice of isomorphism is affected only by scaling.
The last claim follows from Lemma 1.7.
3.5 Completing the proof of Theorem 3.3
Theorem 3.3 follows from Corollary 3.11 and Proposition 3.13.
More precisely, we construct an isomorphism
 $$ \begin{align*} c^D_{\kappa}: \left(\mathrm{Rh}^{\text{D}}_{*} {\underline{{\mathbb{C}}}}\right)_{\kappa} \xrightarrow{\simeq} {i^D_{\gamma}}_*\left({\mathrm{Rh}^{\text{D}}_{\gamma}}_* {\underline{{\mathbb{C}}}}\right)_{\kappa} \left[-2d^D_{\gamma}\right] \in D_c^b\left({\mathcal A}^D\right) \end{align*} $$
$$ \begin{align*} c^D_{\kappa}: \left(\mathrm{Rh}^{\text{D}}_{*} {\underline{{\mathbb{C}}}}\right)_{\kappa} \xrightarrow{\simeq} {i^D_{\gamma}}_*\left({\mathrm{Rh}^{\text{D}}_{\gamma}}_* {\underline{{\mathbb{C}}}}\right)_{\kappa} \left[-2d^D_{\gamma}\right] \in D_c^b\left({\mathcal A}^D\right) \end{align*} $$which is canonical up to scaling as the composition
 $$ \begin{align*} \left( \mathrm{Rh}^{\text{D}}_{*} {\underline{{\mathbb{C}}}}\right)_{\kappa} \xrightarrow[\simeq]{~~[\Sigma]^{G_{\pi}}_{\#,\kappa}~~} {i^D_{\gamma}}_*\left({\mathrm{Rh}_{\gamma,\text{L}'}^{\text{D}}}_*{\underline{{\mathbb{C}}}}\right)_{\kappa} \left[-2d^D_{\gamma}\right] \xrightarrow[\simeq]{\text{Prop.~3.13}} {i^D_{\gamma}}_*\left({\mathrm{Rh}_{\gamma,\text{L}}^{\text{D}}}_*{\underline{{\mathbb{C}}}}\right)_{\kappa} \left[-2d^D_{\gamma}\right]. \end{align*} $$
$$ \begin{align*} \left( \mathrm{Rh}^{\text{D}}_{*} {\underline{{\mathbb{C}}}}\right)_{\kappa} \xrightarrow[\simeq]{~~[\Sigma]^{G_{\pi}}_{\#,\kappa}~~} {i^D_{\gamma}}_*\left({\mathrm{Rh}_{\gamma,\text{L}'}^{\text{D}}}_*{\underline{{\mathbb{C}}}}\right)_{\kappa} \left[-2d^D_{\gamma}\right] \xrightarrow[\simeq]{\text{Prop.~3.13}} {i^D_{\gamma}}_*\left({\mathrm{Rh}_{\gamma,\text{L}}^{\text{D}}}_*{\underline{{\mathbb{C}}}}\right)_{\kappa} \left[-2d^D_{\gamma}\right]. \end{align*} $$Here the first isomorphism  $[\Sigma ]^{G_{\pi }}_{\#,\kappa }$ is given by Corollary 3.11, and the second isomorphism is given by Proposition 3.13. This completes the proof of Theorem 3.3.
$[\Sigma ]^{G_{\pi }}_{\#,\kappa }$ is given by Corollary 3.11, and the second isomorphism is given by Proposition 3.13. This completes the proof of Theorem 3.3.
4 Vanishing cycles and Hitchin moduli spaces
4.1 Overview
In this section we follow the same notation as in Section 3. We complete the proof of Theorem 3.2 (and therefore of Theorem 3.1, as explained in the text after Theorem 3.2) by constructing an operator
 $$ \begin{align*} c^D_{\kappa}: \left(\mathrm{Rh}^{\text{D}}_{*} {\underline{{\mathbb{C}}}}\right)_{\kappa} \xrightarrow{\simeq} {i^D_{\gamma}}_*\left({\mathrm{Rh}^{\text{D}}_{\gamma}}_* {\underline{{\mathbb{C}}}}\right)_{\kappa} \left[-2d^D_{\gamma}\right] \in D_c^b\left({\mathcal A}^D\right), \end{align*} $$
$$ \begin{align*} c^D_{\kappa}: \left(\mathrm{Rh}^{\text{D}}_{*} {\underline{{\mathbb{C}}}}\right)_{\kappa} \xrightarrow{\simeq} {i^D_{\gamma}}_*\left({\mathrm{Rh}^{\text{D}}_{\gamma}}_* {\underline{{\mathbb{C}}}}\right)_{\kappa} \left[-2d^D_{\gamma}\right] \in D_c^b\left({\mathcal A}^D\right), \end{align*} $$which is constructed up to scaling for any effective divisor D with ![]() $\mathrm {deg}(D)>2g-2$ or
$\mathrm {deg}(D)>2g-2$ or ![]() $D= K_C$. Our main tool is Theorem 4.5, where we apply a vanishing cycle functor to connect the moduli of D-Higgs bundles to the moduli of
$D= K_C$. Our main tool is Theorem 4.5, where we apply a vanishing cycle functor to connect the moduli of D-Higgs bundles to the moduli of ![]() $(D+p)$-Higgs bundles, with
$(D+p)$-Higgs bundles, with ![]() $p\in C$ a closed point. This reduces the general cases of Theorem 3.2 to the special cases already treated in Theorem 3.3.
$p\in C$ a closed point. This reduces the general cases of Theorem 3.2 to the special cases already treated in Theorem 3.3.
In this section, it is convenient to work with the moduli stacks of stable ![]() $\mathrm {SL}_n$-Higgs bundles and relative stable Higgs bundles associated with
$\mathrm {SL}_n$-Higgs bundles and relative stable Higgs bundles associated with ![]() $\pi : C' \to C$. As these are nonsingular Deligne–Mumford stacks, gerbes over the coarse moduli spaces, this has no effect on the direct image complexes (64). Therefore, throughout this section, we still use the notation
$\pi : C' \to C$. As these are nonsingular Deligne–Mumford stacks, gerbes over the coarse moduli spaces, this has no effect on the direct image complexes (64). Therefore, throughout this section, we still use the notation  ${\mathcal M}^D_{n,L}$ and
${\mathcal M}^D_{n,L}$ and  ${\mathcal M}^D_{r,L}(\pi )$ to denote the corresponding moduli stacks for stable Higgs bundles and relative stable Higgs bundles.
${\mathcal M}^D_{r,L}(\pi )$ to denote the corresponding moduli stacks for stable Higgs bundles and relative stable Higgs bundles.
4.2 Restrictions of Higgs bundles to a point
Let p be an abstract reduced point ![]() $\mathrm {Spec}({\mathbb {C}})$. Any rank n vector bundle on p is an n-dimensional vector space. Hence the category of
$\mathrm {Spec}({\mathbb {C}})$. Any rank n vector bundle on p is an n-dimensional vector space. Hence the category of ![]() $\mathrm {SL}_n$-Higgs bundles on p can be thought of as the category of matrices in
$\mathrm {SL}_n$-Higgs bundles on p can be thought of as the category of matrices in ![]() $\mathfrak {sl}_n$ up to
$\mathfrak {sl}_n$ up to ![]() $\mathrm {SL}_n$-conjugation, whose moduli stack is given by the quotient
$\mathrm {SL}_n$-conjugation, whose moduli stack is given by the quotient
Here ![]() $\mathrm {SL}_n$ acts on
$\mathrm {SL}_n$ acts on ![]() $\mathfrak {sl}_n$ via conjugation. The Hitchin fibration associated with
$\mathfrak {sl}_n$ via conjugation. The Hitchin fibration associated with ![]() ${\mathcal M}_{n,p}$ is
${\mathcal M}_{n,p}$ is
where ![]() ${\mathcal A}_p = \mathfrak {sl}_n\mathbin {/\mkern -6mu/}\mathrm {SL}_n$ is the affine
${\mathcal A}_p = \mathfrak {sl}_n\mathbin {/\mkern -6mu/}\mathrm {SL}_n$ is the affine ![]() $\mathrm {GIT}$-quotient parameterising all characteristic polynomials
$\mathrm {GIT}$-quotient parameterising all characteristic polynomials
 $$ \begin{align*} (a_2, a_3, \dots, a_n) \in {\mathcal A}_p, \quad a_i = \mathrm{trace}\left(\wedge^i \theta_p\right), \end{align*} $$
$$ \begin{align*} (a_2, a_3, \dots, a_n) \in {\mathcal A}_p, \quad a_i = \mathrm{trace}\left(\wedge^i \theta_p\right), \end{align*} $$of the traceless endomorphism ![]() $\theta _p \in \mathrm {End}({\mathbb {A}}^n)_0$ associated with a matrix in
$\theta _p \in \mathrm {End}({\mathbb {A}}^n)_0$ associated with a matrix in ![]() ${\mathcal M}_{n,p}$. We refer to [Reference Ngô33, Section 2.2] for more details concerning the stack
${\mathcal M}_{n,p}$. We refer to [Reference Ngô33, Section 2.2] for more details concerning the stack ![]() ${\mathcal M}_{n,p}$ and the morphism
${\mathcal M}_{n,p}$ and the morphism ![]() $h_p$.
$h_p$.
Now we consider p as a closed point on the curve C. We fix a trivialisation
 $$ \begin{align} {\mathcal O}_C(D)_p \xrightarrow{\simeq} {\mathbb{C}}. \end{align} $$
$$ \begin{align} {\mathcal O}_C(D)_p \xrightarrow{\simeq} {\mathbb{C}}. \end{align} $$Then the restriction map with respect to the closed embedding
induces the following commutative diagram:

where the trivialisation (86) induces an evaluation (at p) map ![]() $\mathrm {ev}_p$:
$\mathrm {ev}_p$:
To generalise the diagram (87) for the relative moduli space  ${\mathcal M}^D_{r,L}(\pi )$ with
${\mathcal M}^D_{r,L}(\pi )$ with ![]() $n=mr$, we consider the Lie group
$n=mr$, we consider the Lie group
 $$ \begin{align*} H_{\pi} = \left\{(g_1, g_2, \dots, g_m) \in \mathrm{GL}_r^{\times m}: \prod_{i} \mathrm{det}(g_i) = 1\right\} \subset \mathrm{GL}_r^{\times m}, \end{align*} $$
$$ \begin{align*} H_{\pi} = \left\{(g_1, g_2, \dots, g_m) \in \mathrm{GL}_r^{\times m}: \prod_{i} \mathrm{det}(g_i) = 1\right\} \subset \mathrm{GL}_r^{\times m}, \end{align*} $$which is naturally a subgroup of ![]() $\mathrm {SL}_n$ with Lie algebra
$\mathrm {SL}_n$ with Lie algebra
 $$ \begin{align*} \mathfrak{h}_{\pi} = \left\{(g_1, g_2, \dots, g_m) \in \mathfrak{gl}_r^{\times m}: \sum_{i} \mathrm{trace}(g_i) = 0\right\}. \end{align*} $$
$$ \begin{align*} \mathfrak{h}_{\pi} = \left\{(g_1, g_2, \dots, g_m) \in \mathfrak{gl}_r^{\times m}: \sum_{i} \mathrm{trace}(g_i) = 0\right\}. \end{align*} $$The quotient stack
is the moduli of ![]() $\mathrm {SL}_n$-Higgs bundles on the point p obtained as the push-forward of rank r Higgs bundles on m distinct reduced points
$\mathrm {SL}_n$-Higgs bundles on the point p obtained as the push-forward of rank r Higgs bundles on m distinct reduced points ![]() $\sqcup _{i=1}^m p_i$ along the projection
$\sqcup _{i=1}^m p_i$ along the projection
Similar to diagram (87), we have the following diagram given by the restriction to ![]() $p \in C$:
$p \in C$:

Here for a Higgs bundle  $({\mathcal E}, \theta ) \in {\mathcal M}^D_{r,L}$ on
$({\mathcal E}, \theta ) \in {\mathcal M}^D_{r,L}$ on ![]() $C'$, again formula (86) induces an evaluation map:
$C'$, again formula (86) induces an evaluation map:
and the ‘Hitchin map over a point’ ![]() $h_p$ is the natural projection
$h_p$ is the natural projection
Diagram (88) recovers diagram (87) when ![]() $C' = C$ and
$C' = C$ and ![]() $\pi : C' \to C$ is the identity.
$\pi : C' \to C$ is the identity.
Proposition 4.1. Assume that D is a divisor on C satisfying either
(a)
 $D-p = K_C$ or
$D-p = K_C$ or(b)
 $D-p$ is effective and
$D-p$ is effective and  $\mathrm {deg}(D-p)> 2g-2$.
$\mathrm {deg}(D-p)> 2g-2$.
Then the evaluation map  $\mathrm {ev}_p: {\mathcal M}^D_{r,L}(\pi ) \to {\mathcal M}_{r,p}(\pi )$ in diagram (88) is smooth.
$\mathrm {ev}_p: {\mathcal M}^D_{r,L}(\pi ) \to {\mathcal M}_{r,p}(\pi )$ in diagram (88) is smooth.
Proof. We first review the deformation theory of  ${\mathcal M}^D_{r,L}(\pi )$ following [Reference Biswas and Ramanan4] and [Reference Ngô33, Section 4.14]. The deformation theory of a rank r Higgs bundle
${\mathcal M}^D_{r,L}(\pi )$ following [Reference Biswas and Ramanan4] and [Reference Ngô33, Section 4.14]. The deformation theory of a rank r Higgs bundle ![]() $({\mathcal E}, \theta )$ on
$({\mathcal E}, \theta )$ on ![]() $C'$ is governed by the tangent complex
$C'$ is governed by the tangent complex
 $$ \begin{align} \left[{\mathcal E}{nd}({\mathcal E}) \xrightarrow{\mathrm{ad}(\theta)} {\mathcal E}{nd}({\mathcal E})\otimes {\mathcal O}_{C'}(D')\right] \end{align} $$
$$ \begin{align} \left[{\mathcal E}{nd}({\mathcal E}) \xrightarrow{\mathrm{ad}(\theta)} {\mathcal E}{nd}({\mathcal E})\otimes {\mathcal O}_{C'}(D')\right] \end{align} $$lying in degrees ![]() $-1$ and
$-1$ and ![]() $0$. Since now we only consider rank r Higgs bundles
$0$. Since now we only consider rank r Higgs bundles ![]() $({\mathcal E}, \theta )$ on
$({\mathcal E}, \theta )$ on ![]() $C'$ with the fixed determinant and trace after pushing forward to C, to govern the deformation theory of
$C'$ with the fixed determinant and trace after pushing forward to C, to govern the deformation theory of  ${\mathcal M}^D_{r,L}(\pi )$ we need to remove the traces of
${\mathcal M}^D_{r,L}(\pi )$ we need to remove the traces of ![]() ${\mathcal E}{nd}({\mathcal E})$ after pushing forward the complex (89) to C. Hence the deformation theory of
${\mathcal E}{nd}({\mathcal E})$ after pushing forward the complex (89) to C. Hence the deformation theory of  ${\mathcal M}^D_{r,L}(\pi )$ is governed by
${\mathcal M}^D_{r,L}(\pi )$ is governed by
 $$ \begin{align} C^{\bullet}({\mathcal E},\theta,D) = \left[(\pi_*{\mathcal E}{nd}({\mathcal E}))_0 \xrightarrow{\pi_*\mathrm{ad}(\theta)} (\pi_*{\mathcal E}{nd}({\mathcal E}))_0\otimes {\mathcal O}_C(D)\right], \quad ({\mathcal E},\theta)\in {\mathcal M}^D_{r,L}(\pi), \end{align} $$
$$ \begin{align} C^{\bullet}({\mathcal E},\theta,D) = \left[(\pi_*{\mathcal E}{nd}({\mathcal E}))_0 \xrightarrow{\pi_*\mathrm{ad}(\theta)} (\pi_*{\mathcal E}{nd}({\mathcal E}))_0\otimes {\mathcal O}_C(D)\right], \quad ({\mathcal E},\theta)\in {\mathcal M}^D_{r,L}(\pi), \end{align} $$where ![]() $(\pi _*{\mathcal E}{nd}({\mathcal E}))_0$ denotes the kernel with respect to the trace
$(\pi _*{\mathcal E}{nd}({\mathcal E}))_0$ denotes the kernel with respect to the trace
 $$ \begin{align*} \mathrm{tr}_C: \pi_* {\mathcal E}{nd}({\mathcal E}) \xrightarrow{\pi_*\mathrm{tr}_{C'}} \pi_*{\mathcal O}_{C'} \to {\mathcal O}_C \end{align*} $$
$$ \begin{align*} \mathrm{tr}_C: \pi_* {\mathcal E}{nd}({\mathcal E}) \xrightarrow{\pi_*\mathrm{tr}_{C'}} \pi_*{\mathcal O}_{C'} \to {\mathcal O}_C \end{align*} $$on C. The complex (90) is the tangent complex of  ${\mathcal M}^D_{r,L}(\pi )$. The automorphism space, the tangent space and the obstruction space, respectively, are thus given by the cohomology groups
${\mathcal M}^D_{r,L}(\pi )$. The automorphism space, the tangent space and the obstruction space, respectively, are thus given by the cohomology groups
Since the evaluation map ![]() $\mathrm {ev}_p$ is induced by the restriction to the point p via
$\mathrm {ev}_p$ is induced by the restriction to the point p via ![]() $i_p: \{p\}\hookrightarrow C$, the tangent map of
$i_p: \{p\}\hookrightarrow C$, the tangent map of ![]() $\mathrm {ev}_p$ is
$\mathrm {ev}_p$ is
 $$ \begin{align} \mathrm{Tan}_{\mathrm{ev}_p}: H^1(C, C^{\bullet}({\mathcal E},\theta,D)) \rightarrow H^1\left(p, i_p^*C^{\bullet}({\mathcal E},\theta,D)\right), \end{align} $$
$$ \begin{align} \mathrm{Tan}_{\mathrm{ev}_p}: H^1(C, C^{\bullet}({\mathcal E},\theta,D)) \rightarrow H^1\left(p, i_p^*C^{\bullet}({\mathcal E},\theta,D)\right), \end{align} $$induced by the restriction morphism between the tangent complexes. Here  $i_p^*C^{\bullet }({\mathcal E},\theta ,D) = \left [\mathfrak {h}_{\pi } \xrightarrow {\mathrm {ad}} \mathfrak {h}_{\pi }\right ]$ recovers the tangent complex of
$i_p^*C^{\bullet }({\mathcal E},\theta ,D) = \left [\mathfrak {h}_{\pi } \xrightarrow {\mathrm {ad}} \mathfrak {h}_{\pi }\right ]$ recovers the tangent complex of ![]() ${\mathcal M}_{r,p}(\pi )$; see [Reference de Cataldo, Heinloth and Migliorini8, Appendix 8.2]. To prove the smoothness of
${\mathcal M}_{r,p}(\pi )$; see [Reference de Cataldo, Heinloth and Migliorini8, Appendix 8.2]. To prove the smoothness of ![]() $\mathrm {ev}_p$, we show in the following that formula (91) is surjective.
$\mathrm {ev}_p$, we show in the following that formula (91) is surjective.
The restriction map between the tangent complexes
fits into the exact triangle
 $$ \begin{align} E^{\bullet} \to C^{\bullet}({\mathcal E},\theta,D) \to {i_p}_*i_p^*C^{\bullet}({\mathcal E},\theta,D) \xrightarrow {+1}, \end{align} $$
$$ \begin{align} E^{\bullet} \to C^{\bullet}({\mathcal E},\theta,D) \to {i_p}_*i_p^*C^{\bullet}({\mathcal E},\theta,D) \xrightarrow {+1}, \end{align} $$where ![]() $E^{\bullet }$ is given by
$E^{\bullet }$ is given by
 $$ \begin{align*} E^{\bullet} =C^{\bullet}({\mathcal E},\theta,D)\otimes {\mathcal O}_C(-p) = \left[(\pi_*{\mathcal E}{nd}({\mathcal E}))_0\otimes {\mathcal O}_C(-p) \xrightarrow{\pi_*\mathrm{ad}(\theta)} (\pi_*{\mathcal E}{nd}({\mathcal E}))_0\otimes {\mathcal O}_C\left(D-p\right)\right]. \end{align*} $$
$$ \begin{align*} E^{\bullet} =C^{\bullet}({\mathcal E},\theta,D)\otimes {\mathcal O}_C(-p) = \left[(\pi_*{\mathcal E}{nd}({\mathcal E}))_0\otimes {\mathcal O}_C(-p) \xrightarrow{\pi_*\mathrm{ad}(\theta)} (\pi_*{\mathcal E}{nd}({\mathcal E}))_0\otimes {\mathcal O}_C\left(D-p\right)\right]. \end{align*} $$The long exact sequence associated with formula (92) contains
 $$ \begin{align*} H^1(C, C^{\bullet}({\mathcal E},\theta,D)) \xrightarrow{\mathrm{Tan}_{\mathrm{ev}_p}} H^1\left(C,{i_p}_* i_p^*C^{\bullet}({\mathcal E},\theta,D)\right) \rightarrow H^2(C, E^{\bullet}). \end{align*} $$
$$ \begin{align*} H^1(C, C^{\bullet}({\mathcal E},\theta,D)) \xrightarrow{\mathrm{Tan}_{\mathrm{ev}_p}} H^1\left(C,{i_p}_* i_p^*C^{\bullet}({\mathcal E},\theta,D)\right) \rightarrow H^2(C, E^{\bullet}). \end{align*} $$Hence, in view of the Serre duality, it suffices to show the vanishing of
 $$ \begin{align} H^2(C, E^{\bullet})^{\vee} = H^0\left(C, (E^{\bullet})^{\vee} \otimes \Omega_C\right), \end{align} $$
$$ \begin{align} H^2(C, E^{\bullet})^{\vee} = H^0\left(C, (E^{\bullet})^{\vee} \otimes \Omega_C\right), \end{align} $$where
 $$ \begin{align*} (E^{\bullet})^{\vee} \otimes \Omega_C = \left[(\pi_*{\mathcal E}{nd}({\mathcal E}))_0\otimes {\mathcal O}_C(p-D+K_C) \xrightarrow{-\mathrm{ad}(\pi_*\theta)} (\pi_*{\mathcal E}{nd}({\mathcal E})_0\otimes {\mathcal O}_C\left(p+K_C\right)\right]. \end{align*} $$
$$ \begin{align*} (E^{\bullet})^{\vee} \otimes \Omega_C = \left[(\pi_*{\mathcal E}{nd}({\mathcal E}))_0\otimes {\mathcal O}_C(p-D+K_C) \xrightarrow{-\mathrm{ad}(\pi_*\theta)} (\pi_*{\mathcal E}{nd}({\mathcal E})_0\otimes {\mathcal O}_C\left(p+K_C\right)\right]. \end{align*} $$ To calculate equation (93), we consider the hypercohomology group  $H^0\left (C, \left (\widetilde {E}^{\bullet }\right )^{\vee } \otimes \Omega _C\right )$ with
$H^0\left (C, \left (\widetilde {E}^{\bullet }\right )^{\vee } \otimes \Omega _C\right )$ with
 $$ \begin{align*} \widetilde{E}^{\bullet} = \left[(\pi_*{\mathcal E}{nd}({\mathcal E}))\otimes {\mathcal O}_C(-p) \xrightarrow{\pi_*\mathrm{ad}(\theta)} (\pi_*{\mathcal E}{nd}({\mathcal E}))\otimes {\mathcal O}_C(D-p)\right]. \end{align*} $$
$$ \begin{align*} \widetilde{E}^{\bullet} = \left[(\pi_*{\mathcal E}{nd}({\mathcal E}))\otimes {\mathcal O}_C(-p) \xrightarrow{\pi_*\mathrm{ad}(\theta)} (\pi_*{\mathcal E}{nd}({\mathcal E}))\otimes {\mathcal O}_C(D-p)\right]. \end{align*} $$It is clear that  $H^0\left (C, \left (\widetilde {E}^{\bullet }\right )^{\vee } \otimes \Omega _C\right )$ contains equation (93) as a direct sum component, and the complement is contributed by the trace parts on C. The hypercohomology group
$H^0\left (C, \left (\widetilde {E}^{\bullet }\right )^{\vee } \otimes \Omega _C\right )$ contains equation (93) as a direct sum component, and the complement is contributed by the trace parts on C. The hypercohomology group  $H^0\left (C, \left (\widetilde {E}^{\bullet }\right )^{\vee } \otimes \Omega _C\right )$ can be written as
$H^0\left (C, \left (\widetilde {E}^{\bullet }\right )^{\vee } \otimes \Omega _C\right )$ can be written as
 $$ \begin{align} H^0\left(C', \left[{\mathcal E}{nd}({\mathcal E})\otimes \pi^*{\mathcal O}_C(p-D+K_C) \xrightarrow{-\mathrm{ad}(\theta)} {\mathcal E}{nd}({\mathcal E})\otimes \pi^*{\mathcal O}_C(p+K_C)\right] \right) \end{align} $$
$$ \begin{align} H^0\left(C', \left[{\mathcal E}{nd}({\mathcal E})\otimes \pi^*{\mathcal O}_C(p-D+K_C) \xrightarrow{-\mathrm{ad}(\theta)} {\mathcal E}{nd}({\mathcal E})\otimes \pi^*{\mathcal O}_C(p+K_C)\right] \right) \end{align} $$via the projection formula associated with ![]() $\pi : C' \to C$. By [Reference Gothen and King16, Theorem 5.1] (see also the calculation of [Reference Groechenig, Wyss and Ziegler17, Lemma 7.3]), formula (94) can be interpreted as the group of homomorphisms of stable Higgs bundles
$\pi : C' \to C$. By [Reference Gothen and King16, Theorem 5.1] (see also the calculation of [Reference Groechenig, Wyss and Ziegler17, Lemma 7.3]), formula (94) can be interpreted as the group of homomorphisms of stable Higgs bundles
In case (a), these two stable Higgs bundles coincide, so the ![]() $\mathrm {Hom}$ space (95) is
$\mathrm {Hom}$ space (95) is ![]() $1$-dimensional, given by the identity map. Hence we have the vanishing of equation (93) by the removal of the
$1$-dimensional, given by the identity map. Hence we have the vanishing of equation (93) by the removal of the ![]() $1$-dimensional trace parts on C from formula (95). In case (b), we have
$1$-dimensional trace parts on C from formula (95). In case (b), we have
Hence formula (95) vanishes due to the stability condition, which further implies the vanishing of equation (93).
Assume that the divisor D satisfies Proposition 4.1(a) and (b). The moduli of stable ![]() $(D-p)$-Higgs bundles admits a natural closed embedding into the moduli of D-Higgs bundles. More precisely, let
$(D-p)$-Higgs bundles admits a natural closed embedding into the moduli of D-Higgs bundles. More precisely, let ![]() $({\mathcal E}, \theta )$ be a stable
$({\mathcal E}, \theta )$ be a stable ![]() $(D-p)$-Higgs bundle on C; then we may view it naturally as a D-Higgs bundle
$(D-p)$-Higgs bundle on C; then we may view it naturally as a D-Higgs bundle ![]() $({\mathcal E}, \theta ')$ by setting the new Higgs field as the composition
$({\mathcal E}, \theta ')$ by setting the new Higgs field as the composition
 $$ \begin{align*} \theta': {\mathcal E} \xrightarrow{\theta} {\mathcal E}\otimes {\mathcal O}_C(D-p) \rightarrow {\mathcal E} \otimes{\mathcal O}_C(D), \end{align*} $$
$$ \begin{align*} \theta': {\mathcal E} \xrightarrow{\theta} {\mathcal E}\otimes {\mathcal O}_C(D-p) \rightarrow {\mathcal E} \otimes{\mathcal O}_C(D), \end{align*} $$where the second map is induced by ![]() ${\mathcal O}_C(-p) \hookrightarrow {\mathcal O}_C$. By definition, the (slope-)stability conditions of
${\mathcal O}_C(-p) \hookrightarrow {\mathcal O}_C$. By definition, the (slope-)stability conditions of ![]() $({\mathcal E}, \theta )$ and
$({\mathcal E}, \theta )$ and ![]() $({\mathcal E}, \theta ')$ coincide. Hence we obtain a closed embedding
$({\mathcal E}, \theta ')$ coincide. Hence we obtain a closed embedding
 $$ \begin{align} {\mathcal M}^{D-p}_{n,L} \hookrightarrow {\mathcal M}^D_{n,L}, \quad ({\mathcal E},\theta) \mapsto ({\mathcal E}, \theta'). \end{align} $$
$$ \begin{align} {\mathcal M}^{D-p}_{n,L} \hookrightarrow {\mathcal M}^D_{n,L}, \quad ({\mathcal E},\theta) \mapsto ({\mathcal E}, \theta'). \end{align} $$Similarly, we also have the relative version with respect to ![]() $\pi : C' \to C$:
$\pi : C' \to C$:
 $$ \begin{align} {\mathcal M}^{D-p}_{r,L}(\pi) \hookrightarrow {\mathcal M}^D_{r,L}(\pi), \quad ({\mathcal E},\theta)\mapsto ({\mathcal E}, \theta'), \end{align} $$
$$ \begin{align} {\mathcal M}^{D-p}_{r,L}(\pi) \hookrightarrow {\mathcal M}^D_{r,L}(\pi), \quad ({\mathcal E},\theta)\mapsto ({\mathcal E}, \theta'), \end{align} $$where ![]() $\theta ': {\mathcal E} \to {\mathcal E}\otimes \pi ^*{\mathcal O}_{C}(D)$ is given by the composition
$\theta ': {\mathcal E} \to {\mathcal E}\otimes \pi ^*{\mathcal O}_{C}(D)$ is given by the composition
 $$ \begin{align*} \theta': {\mathcal E}\xrightarrow{\theta} {\mathcal E} \otimes \pi^*{\mathcal O}_C(D-p) \to {\mathcal E} \otimes \pi^*{\mathcal O}_C(D). \end{align*} $$
$$ \begin{align*} \theta': {\mathcal E}\xrightarrow{\theta} {\mathcal E} \otimes \pi^*{\mathcal O}_C(D-p) \to {\mathcal E} \otimes \pi^*{\mathcal O}_C(D). \end{align*} $$As before, the relative case (97) recovers formula (96) by setting ![]() $\pi = \mathrm {id}$.
$\pi = \mathrm {id}$.
A Higgs bundle in  ${\mathcal M}^D_{r,L}(\pi )$ which sits inside
${\mathcal M}^D_{r,L}(\pi )$ which sits inside  ${\mathcal M}^{D-p}_{r,L}(\pi )$ can be characterised by the vanishing of the restricted Higgs field over the point p. Therefore it is natural to use the evaluation map
${\mathcal M}^{D-p}_{r,L}(\pi )$ can be characterised by the vanishing of the restricted Higgs field over the point p. Therefore it is natural to use the evaluation map ![]() $\mathrm {ev}_p$ to describe formulas (96) and (97) as in the following lemma:
$\mathrm {ev}_p$ to describe formulas (96) and (97) as in the following lemma:
Lemma 4.2. Assume that the divisor D satisfies Proposition 4.1(a) and (b). We denote by
the closed substack corresponding to the ![]() $0$ matrix. Then the closed embedding (97) is realised as a closed fibre of
$0$ matrix. Then the closed embedding (97) is realised as a closed fibre of ![]() $\mathrm {ev}_p$ over
$\mathrm {ev}_p$ over ![]() $0_H$.
$0_H$.
4.3 Functions and critical loci
We consider the quotient map
sending a matrix to the coefficients
 $$ \begin{align*} (a_2, a_3, \dots, a_n)\in \mathfrak{sl}_n\mathbin{/\mkern-6mu/} \mathrm{SL}_n = \mathrm{Spec}\left({\mathbb{C}}[\mathfrak{sl}_n]^{\mathrm{SL}_n}\right), \quad \mathrm{deg}(a_i) = i, \end{align*} $$
$$ \begin{align*} (a_2, a_3, \dots, a_n)\in \mathfrak{sl}_n\mathbin{/\mkern-6mu/} \mathrm{SL}_n = \mathrm{Spec}\left({\mathbb{C}}[\mathfrak{sl}_n]^{\mathrm{SL}_n}\right), \quad \mathrm{deg}(a_i) = i, \end{align*} $$of its characteristic polynomial. The term ![]() $a_i$ defines a degree i polynomial function on the Lie algebra
$a_i$ defines a degree i polynomial function on the Lie algebra ![]() $\mathfrak {sl}_n$. We define the quadratic function on the Lie algebra
$\mathfrak {sl}_n$. We define the quadratic function on the Lie algebra ![]() $\mathfrak {sl}_n$ given by
$\mathfrak {sl}_n$ given by ![]() $a_2$ as
$a_2$ as
which induces a function ![]() $\mu _{\pi }: \mathfrak {h}_{\pi } \to {\mathbb {A}}^1$ via the composition
$\mu _{\pi }: \mathfrak {h}_{\pi } \to {\mathbb {A}}^1$ via the composition
 $$ \begin{align} \mu_{\pi} : \mathfrak{h}_{\pi} \hookrightarrow \mathfrak{sl}_n \xrightarrow{\mu} {\mathbb{A}}^1. \end{align} $$
$$ \begin{align} \mu_{\pi} : \mathfrak{h}_{\pi} \hookrightarrow \mathfrak{sl}_n \xrightarrow{\mu} {\mathbb{A}}^1. \end{align} $$By definition, the functions ![]() $\mu $ and
$\mu $ and ![]() $\mu _{\pi }$ are invariant under the conjugation actions by the Lie groups
$\mu _{\pi }$ are invariant under the conjugation actions by the Lie groups ![]() $\mathrm {SL}_n$ and
$\mathrm {SL}_n$ and ![]() $H_{\pi }$, respectively.
$H_{\pi }$, respectively.
Since any matrix ![]() $g \in \mathfrak {h}_{\pi } \subset \mathfrak {sl}_n$ satisfies
$g \in \mathfrak {h}_{\pi } \subset \mathfrak {sl}_n$ satisfies ![]() $\mathrm {trace}(g) = 0$, the quadratic function
$\mathrm {trace}(g) = 0$, the quadratic function ![]() $\mu _{\pi }$ (up to scaling) can be written as
$\mu _{\pi }$ (up to scaling) can be written as
 $$ \begin{align} g \mapsto \mathrm{trace}\left(g^2\right). \end{align} $$
$$ \begin{align} g \mapsto \mathrm{trace}\left(g^2\right). \end{align} $$For the semisimple Lie algebra ![]() $\mathfrak {sl}_n$, formula (100) is the Killing form, which is clearly nondegenerate. In the following we prove the nondegeneracy for general
$\mathfrak {sl}_n$, formula (100) is the Killing form, which is clearly nondegenerate. In the following we prove the nondegeneracy for general ![]() $\mathfrak {h}_{\pi }$:
$\mathfrak {h}_{\pi }$:
Lemma 4.3. The critical locus of the quadratic function ![]() $\mu _{\pi }$ is the isolated reduced point
$\mu _{\pi }$ is the isolated reduced point ![]() $0 \in \mathfrak {h}_{\pi }$ – that is,
$0 \in \mathfrak {h}_{\pi }$ – that is,
Consequently, the perverse sheaf of vanishing cycles ![]() $\varphi _{\mu _{\pi }}(\underline {{\mathbb {C}}}[\mathrm {dim}({\mathfrak {h}_{\pi }}])$ [Reference Dimca13, Theorem 5.2.21] is the skyscraper sheaf supported on the closed point
$\varphi _{\mu _{\pi }}(\underline {{\mathbb {C}}}[\mathrm {dim}({\mathfrak {h}_{\pi }}])$ [Reference Dimca13, Theorem 5.2.21] is the skyscraper sheaf supported on the closed point ![]() $0 \in \mathfrak {h}_{\pi }$.
$0 \in \mathfrak {h}_{\pi }$.
Proof. To prove the first part of the lemma, it suffices to show that the quadratic form (100) on ![]() $\mathfrak {h}_{\pi }$ is nondegenerate.
$\mathfrak {h}_{\pi }$ is nondegenerate.
We consider the decomposition
where ![]() $\mathfrak {c} \subset \mathfrak {h}_{\pi }$ is the Cartan subalgebra of trace-free diagonal matrices and
$\mathfrak {c} \subset \mathfrak {h}_{\pi }$ is the Cartan subalgebra of trace-free diagonal matrices and ![]() $\mathfrak {h}^{\prime }_{\pi }$ consists of the matrices in
$\mathfrak {h}^{\prime }_{\pi }$ consists of the matrices in ![]() $\mathfrak {h}_{\pi }$ such that the entries of the diagonals vanish. For a matrix
$\mathfrak {h}_{\pi }$ such that the entries of the diagonals vanish. For a matrix ![]() $g\in \mathfrak {h}_{\pi }$ with the decomposition
$g\in \mathfrak {h}_{\pi }$ with the decomposition
a direct calculation yields ![]() $\mathrm {trace}(g'c)=0$. Therefore we have
$\mathrm {trace}(g'c)=0$. Therefore we have
 $$ \begin{align*} \mathrm{trace}\left(g^2\right) = \mathrm{trace}\left({g'}^2\right) + \mathrm{trace}\left(c^2\right). \end{align*} $$
$$ \begin{align*} \mathrm{trace}\left(g^2\right) = \mathrm{trace}\left({g'}^2\right) + \mathrm{trace}\left(c^2\right). \end{align*} $$So it suffices to show that the quadratic forms (100) are nondegenerate for both ![]() $\mathfrak {h}^{\prime }_{\pi }$ and
$\mathfrak {h}^{\prime }_{\pi }$ and ![]() $\mathfrak {c}$.
$\mathfrak {c}$.
We notice that the Cartan subalgebra ![]() $\mathfrak {c}$ of
$\mathfrak {c}$ of ![]() $\mathfrak {h}_{\pi }$ is the same as that of
$\mathfrak {h}_{\pi }$ is the same as that of ![]() $\mathfrak {sl}_n$. Also, equipped with the quadratic forms (100),
$\mathfrak {sl}_n$. Also, equipped with the quadratic forms (100), ![]() $\mathfrak {h}^{\prime }_{\pi }$ is a direct summand component of the Lie algebra
$\mathfrak {h}^{\prime }_{\pi }$ is a direct summand component of the Lie algebra ![]() $\mathfrak {sl}_r^{\times m}$ via the decomposition (101) for
$\mathfrak {sl}_r^{\times m}$ via the decomposition (101) for ![]() $\mathfrak {sl}_r^{\times m}$. Since both
$\mathfrak {sl}_r^{\times m}$. Since both ![]() $\mathfrak {h}_{\pi }'$ and
$\mathfrak {h}_{\pi }'$ and ![]() $\mathfrak {c}$ are direct summand components of semisimple Lie algebras where the Killing forms (100) are nondegenerate, we conclude the nondegeneracy of formula (100) for
$\mathfrak {c}$ are direct summand components of semisimple Lie algebras where the Killing forms (100) are nondegenerate, we conclude the nondegeneracy of formula (100) for ![]() $\mathfrak {h}^{\prime }_{\pi }$ and
$\mathfrak {h}^{\prime }_{\pi }$ and ![]() $\mathfrak {c}$, which further implies the nondegeneracy of
$\mathfrak {c}$, which further implies the nondegeneracy of ![]() $\mathfrak {h}_{\pi }$ through equation (101).
$\mathfrak {h}_{\pi }$ through equation (101).
This completes the proof of the first part of the lemma and reduces the second part to the case
 $$ \begin{align*} \mu_{\pi}: {\mathbb{A}}^N \to {\mathbb{A}}^1, \quad (z_1, \dots, z_N) \mapsto \sum_{i=1}^N z_i^2. \end{align*} $$
$$ \begin{align*} \mu_{\pi}: {\mathbb{A}}^N \to {\mathbb{A}}^1, \quad (z_1, \dots, z_N) \mapsto \sum_{i=1}^N z_i^2. \end{align*} $$In this case, the Milnor fibre is a sphere [Reference Milnor31] whose reduced homology computes the vanishing cycle [Reference Dimca13, Proposition 4.2.2].
The ![]() $H_{\pi }$-invariant function (99) induces the functions
$H_{\pi }$-invariant function (99) induces the functions
which form the commutative diagram

The pullback of diagram (102) along diagram (88) yields the functions
 $$ \begin{align} \mu_{\pi,{\mathcal M}}: {\mathcal M}^D_{r,L}(\pi) \to {\mathbb{A}}^1,\quad \mu_{\pi,{\mathcal A}}: {\mathcal A}^D(\pi) \to {\mathbb{A}}^1, \end{align} $$
$$ \begin{align} \mu_{\pi,{\mathcal M}}: {\mathcal M}^D_{r,L}(\pi) \to {\mathbb{A}}^1,\quad \mu_{\pi,{\mathcal A}}: {\mathcal A}^D(\pi) \to {\mathbb{A}}^1, \end{align} $$fitting into the commuatative diagram

Before stating and proving the main theorem (Theorem 4.5) of this section, we note the following standard facts:
Lemma 4.4. Let ![]() $f: V\to {\mathbb {A}}^1$ be a regular function.
$f: V\to {\mathbb {A}}^1$ be a regular function.
(a) Assume that V admits an action of a finite group G which is fibrewise with respect to f. Then the nearby and vanishing cycle functors
 $\Phi _f, \varphi _f$ are G-equivariant.
$\Phi _f, \varphi _f$ are G-equivariant.(b) Assume
 ${\mathcal F} \in D^b_c(V)$ and that
${\mathcal F} \in D^b_c(V)$ and that  $g = \lambda \cdot \mathrm {id} \in \mathrm {End}({\mathcal F})$ is a scaling automorphism of
$g = \lambda \cdot \mathrm {id} \in \mathrm {End}({\mathcal F})$ is a scaling automorphism of  ${\mathcal F}$ with
${\mathcal F}$ with  $\lambda \in {\mathbb {C}}^*$. Then applying the nearby or vanishing cycle functor to g yields also a scaling endomorphism:
$\lambda \in {\mathbb {C}}^*$. Then applying the nearby or vanishing cycle functor to g yields also a scaling endomorphism:  $$ \begin{align*} \Phi_f(g) = \lambda\cdot \mathrm{id}: \Phi_f{\mathcal F} \xrightarrow{\simeq} \Phi_f{\mathcal F}, \quad \varphi_f(g) = \lambda\cdot \mathrm{id}: \varphi_f{\mathcal F} \xrightarrow{\simeq} \varphi_f{\mathcal F}. \end{align*} $$
$$ \begin{align*} \Phi_f(g) = \lambda\cdot \mathrm{id}: \Phi_f{\mathcal F} \xrightarrow{\simeq} \Phi_f{\mathcal F}, \quad \varphi_f(g) = \lambda\cdot \mathrm{id}: \varphi_f{\mathcal F} \xrightarrow{\simeq} \varphi_f{\mathcal F}. \end{align*} $$(c) Assume that
 $g: W \to V$ is smooth with
$g: W \to V$ is smooth with  $f' = f\circ g: W \to {\mathbb {A}}^1$ the composition; then we have the smooth pullback formula for vanishing cycles:
$f' = f\circ g: W \to {\mathbb {A}}^1$ the composition; then we have the smooth pullback formula for vanishing cycles:  $$ \begin{align*} g^* \circ \varphi_f = \varphi_{f'}\circ g^*: D^b_c(V) \to D_c^b\left({f^{\prime}}^{-1}\left(0_{{\mathbb{A}}^1}\right)\right). \end{align*} $$
$$ \begin{align*} g^* \circ \varphi_f = \varphi_{f'}\circ g^*: D^b_c(V) \to D_c^b\left({f^{\prime}}^{-1}\left(0_{{\mathbb{A}}^1}\right)\right). \end{align*} $$
Parts (a) and (c) follow directly from the definition of these functors [Reference Illusie, Deligne, Gabber, Laumon and Orgogozo26, (1.1.5)]; part (b) holds more generally for any ![]() ${\mathbb {C}}$-linear exact functor between triangulated categories.
${\mathbb {C}}$-linear exact functor between triangulated categories.
Theorem 4.5. Assume that the divisor D satisfies Proposition 4.1(a) and (b).
(a) The closed embedding (97) can be realised as the critical locus of the function
 $\mu _{\pi ,{\mathcal M}}: {\mathcal M}^D_{r,L}(\pi ) \to {\mathbb {A}}^1$ – that is, we have
$\mu _{\pi ,{\mathcal M}}: {\mathcal M}^D_{r,L}(\pi ) \to {\mathbb {A}}^1$ – that is, we have  $$ \begin{align*} {\mathcal M}^{D-p}_{r,L}(\pi) = \mathrm{Crit}\left(\mu_{\pi,{\mathcal M}}\right)\hookrightarrow {\mathcal M}^{D}_{r,L}(\pi). \end{align*} $$
$$ \begin{align*} {\mathcal M}^{D-p}_{r,L}(\pi) = \mathrm{Crit}\left(\mu_{\pi,{\mathcal M}}\right)\hookrightarrow {\mathcal M}^{D}_{r,L}(\pi). \end{align*} $$(b) We have a natural isomorphism
(105)Here the first and the second $$ \begin{align} \varphi_{\mu_{\pi,{\mathcal M}}} \underline{{\mathbb{C}}} = \underline{{\mathbb{C}}}[-r_0]. \end{align} $$
$$ \begin{align} \varphi_{\mu_{\pi,{\mathcal M}}} \underline{{\mathbb{C}}} = \underline{{\mathbb{C}}}[-r_0]. \end{align} $$ $\underline {{\mathbb {C}}}$ stand for the trivial local systems on
$\underline {{\mathbb {C}}}$ stand for the trivial local systems on  ${\mathcal M}^D_{r,L}(\pi )$ and
${\mathcal M}^D_{r,L}(\pi )$ and  ${\mathcal M}^{D-p}_{r,L}(\pi )$, respectively, and
${\mathcal M}^{D-p}_{r,L}(\pi )$, respectively, and  $r_0$ is the codimension of formula (97).
$r_0$ is the codimension of formula (97).(c) For any character
 $\kappa \in \hat {\Gamma }$, the isomorphism (105) induces a natural isomorphism where
$\kappa \in \hat {\Gamma }$, the isomorphism (105) induces a natural isomorphism where $$ \begin{align*} \varphi_{\mu_{\pi,{\mathcal A}}}\left({\mathrm{Rh}^{\text{D}}_{\pi}}_* {\underline{{\mathbb{C}}}} \right)_{\kappa} = \left({\mathrm{Rh}^{\text{D}-\text{p}}_{\pi}}_* {\underline{{\mathbb{C}}}} \right)_{\kappa} [-r_0], \end{align*} $$
$$ \begin{align*} \varphi_{\mu_{\pi,{\mathcal A}}}\left({\mathrm{Rh}^{\text{D}}_{\pi}}_* {\underline{{\mathbb{C}}}} \right)_{\kappa} = \left({\mathrm{Rh}^{\text{D}-\text{p}}_{\pi}}_* {\underline{{\mathbb{C}}}} \right)_{\kappa} [-r_0], \end{align*} $$ $\mu _{\pi ,{\mathcal A}}$ is given in diagram (104) and
$\mu _{\pi ,{\mathcal A}}$ is given in diagram (104) and  $r_0$ is the same as in (b).
$r_0$ is the same as in (b).
Proof. By definition, the function  $\mu _{\pi ,{\mathcal M}}: {\mathcal M}^D_{r,L}(\pi ) \to {\mathbb {A}}^1$ is the composition
$\mu _{\pi ,{\mathcal M}}: {\mathcal M}^D_{r,L}(\pi ) \to {\mathbb {A}}^1$ is the composition
 $$ \begin{align*} {\mathcal M}^D_{r,L}(\pi) \xrightarrow{\mathrm{ev}_p} {\mathcal M}_{r,p}(\pi) \xrightarrow{\mu_1} {\mathbb{A}}^1, \end{align*} $$
$$ \begin{align*} {\mathcal M}^D_{r,L}(\pi) \xrightarrow{\mathrm{ev}_p} {\mathcal M}_{r,p}(\pi) \xrightarrow{\mu_1} {\mathbb{A}}^1, \end{align*} $$where the first morphism is smooth. Hence we have
 $$ \begin{align*} \mathrm{Crit}\left(\mu_{\pi,{\mathcal M}}\right) =\mathrm{Crit}\left(\mu_1\circ \mathrm{ev}_p\right) = \mathrm{ev}_p^{-1}\mathrm{Crit}(\mu_{1}) = \mathrm{ev}_p^{-1}(0_H). \end{align*} $$
$$ \begin{align*} \mathrm{Crit}\left(\mu_{\pi,{\mathcal M}}\right) =\mathrm{Crit}\left(\mu_1\circ \mathrm{ev}_p\right) = \mathrm{ev}_p^{-1}\mathrm{Crit}(\mu_{1}) = \mathrm{ev}_p^{-1}(0_H). \end{align*} $$Here the last identity follows from Lemma 4.3. This implies (a) by Lemma 4.2.
Now we prove (b). The smooth pullback of vanishing cycles (Lemma 4.4(c)) yields the canonical equivalence of the functors
Since the vanishing cycle complex
 $$ \begin{align} \varphi_{\mu_1} {\underline{{\mathbb{C}}}} \in \mathrm{D}^b_c\left([\mathfrak{h}_{\pi}/H_{\pi}]\right) \end{align} $$
$$ \begin{align} \varphi_{\mu_1} {\underline{{\mathbb{C}}}} \in \mathrm{D}^b_c\left([\mathfrak{h}_{\pi}/H_{\pi}]\right) \end{align} $$is the ![]() $H_{\pi }$-equivariant vanishing cycle complex
$H_{\pi }$-equivariant vanishing cycle complex ![]() $\varphi _{\mu _{\pi }}{\underline {{\mathbb {C}}}}$ on
$\varphi _{\mu _{\pi }}{\underline {{\mathbb {C}}}}$ on ![]() $\mathfrak {h}_{\pi }$, we see from Lemma 4.3 that formula (107) is the shifted skyscraper sheaf supported at
$\mathfrak {h}_{\pi }$, we see from Lemma 4.3 that formula (107) is the shifted skyscraper sheaf supported at ![]() $0_H$ with the trivial
$0_H$ with the trivial ![]() $H_{\pi }$-action. Hence, applying equation (106) to the trivial local system
$H_{\pi }$-action. Hence, applying equation (106) to the trivial local system ![]() ${\underline {{\mathbb {C}}}}$, we deduce that the vanishing cycle complex
${\underline {{\mathbb {C}}}}$, we deduce that the vanishing cycle complex ![]() $\varphi _{\mu _{\pi ,{\mathcal M}}} {\underline {{\mathbb {C}}}}$ is canonically isomorphic to
$\varphi _{\mu _{\pi ,{\mathcal M}}} {\underline {{\mathbb {C}}}}$ is canonically isomorphic to ![]() ${\underline {{\mathbb {C}}}}$ on
${\underline {{\mathbb {C}}}}$ on  ${\mathcal M}^D_{r,L}(\pi )$ with a shift. Since the functor
${\mathcal M}^D_{r,L}(\pi )$ with a shift. Since the functor ![]() $\varphi _{\mu _{\pi ,{\mathcal M}}}$ preserves the perverse t-structures, equation (105) is concluded.
$\varphi _{\mu _{\pi ,{\mathcal M}}}$ preserves the perverse t-structures, equation (105) is concluded.
For (c), the proper base change of vanishing cycles [Reference Dimca13, Proposition 4.2.11] implies the canonical equivalence of the functors
 $$ \begin{align*} {\mathrm{Rh}^{\text{D}}_{\pi}}_* \circ \varphi_{\mu_{\pi,{\mathcal M}}} = \varphi_{\mu_{\pi,{\mathcal A}}} \circ {\mathrm{Rh}^{\text{D}}_{\pi}}_*. \end{align*} $$
$$ \begin{align*} {\mathrm{Rh}^{\text{D}}_{\pi}}_* \circ \varphi_{\mu_{\pi,{\mathcal M}}} = \varphi_{\mu_{\pi,{\mathcal A}}} \circ {\mathrm{Rh}^{\text{D}}_{\pi}}_*. \end{align*} $$As a consequence, we obtain
 $$ \begin{align} \varphi_{\mu_{\pi,{\mathcal A}}}\left({\mathrm{Rh}^{\text{D}}_{\pi}}_* {\underline{{\mathbb{C}}}} \right) = {\mathrm{Rh}^{\text{D}-\text{p}}_{\pi}}_* {\underline{{\mathbb{C}}}} [-r_0] \end{align} $$
$$ \begin{align} \varphi_{\mu_{\pi,{\mathcal A}}}\left({\mathrm{Rh}^{\text{D}}_{\pi}}_* {\underline{{\mathbb{C}}}} \right) = {\mathrm{Rh}^{\text{D}-\text{p}}_{\pi}}_* {\underline{{\mathbb{C}}}} [-r_0] \end{align} $$by applying the push-forward functor ![]() ${\mathrm {Rh}^{\text {D}}_{\pi }}_*$ to equation (105) and the fact that
${\mathrm {Rh}^{\text {D}}_{\pi }}_*$ to equation (105) and the fact that ![]() $h^D_{\pi }$ coincides with
$h^D_{\pi }$ coincides with  $h^{D-p}_{\pi }$ restricting to
$h^{D-p}_{\pi }$ restricting to  ${\mathcal M}^{D-p}_{r,L}$. Because the regular function
${\mathcal M}^{D-p}_{r,L}$. Because the regular function
 $$ \begin{align*} \mu_{\pi,{\mathcal M}}: {\mathcal M}^D_{r,L}(\pi) \to {\mathbb{A}}^1 \end{align*} $$
$$ \begin{align*} \mu_{\pi,{\mathcal M}}: {\mathcal M}^D_{r,L}(\pi) \to {\mathbb{A}}^1 \end{align*} $$passes through the Hitchin base ![]() ${\mathcal A}^D(\pi )$, it admits a fibrewise
${\mathcal A}^D(\pi )$, it admits a fibrewise ![]() $\Gamma $-action. By Lemma 4.4(a), the vanishing cycle functor
$\Gamma $-action. By Lemma 4.4(a), the vanishing cycle functor ![]() $\varphi _{\mu _{\pi ,{\mathcal M}}}$ is
$\varphi _{\mu _{\pi ,{\mathcal M}}}$ is ![]() $\Gamma $-equivariant. Hence the isomorphism (105) is compatible with the
$\Gamma $-equivariant. Hence the isomorphism (105) is compatible with the ![]() $\Gamma $-equivariant structures on the shifted trivial local systems on
$\Gamma $-equivariant structures on the shifted trivial local systems on  ${\mathcal M}^D_{r,L}(\pi )$ and
${\mathcal M}^D_{r,L}(\pi )$ and  ${\mathcal M}^{D-p}_{r,L}(\pi )$. After pushing forward, we see that equation (108) matches for any
${\mathcal M}^{D-p}_{r,L}(\pi )$. After pushing forward, we see that equation (108) matches for any ![]() $\kappa $-isotypic components with respect to the
$\kappa $-isotypic components with respect to the ![]() $\Gamma $-action. This completes the proof of (c).
$\Gamma $-action. This completes the proof of (c).
The value of the function ![]() $\mu _{\pi ,{\mathcal A}}: {\mathcal A}^D(\pi ) \rightarrow {\mathbb {A}}^1$ is constant along each orbit of the Galois group
$\mu _{\pi ,{\mathcal A}}: {\mathcal A}^D(\pi ) \rightarrow {\mathbb {A}}^1$ is constant along each orbit of the Galois group ![]() $G_{\pi }$-action on
$G_{\pi }$-action on ![]() ${\mathcal A}^D(\pi )$. Hence
${\mathcal A}^D(\pi )$. Hence ![]() $\mu _{\pi ,{\mathcal A}}$ induces a regular function on the
$\mu _{\pi ,{\mathcal A}}$ induces a regular function on the ![]() $G_{\pi }$-quotient of
$G_{\pi }$-quotient of ![]() ${\mathcal A}^{D}(\pi )$,
${\mathcal A}^{D}(\pi )$,
 $$ \begin{align} \mu_{\gamma,{\mathcal A}}: {\mathcal A}^D_{\gamma} \to {\mathbb{A}}^1, \end{align} $$
$$ \begin{align} \mu_{\gamma,{\mathcal A}}: {\mathcal A}^D_{\gamma} \to {\mathbb{A}}^1, \end{align} $$where the element ![]() $\gamma \in \Gamma $ corresponds to
$\gamma \in \Gamma $ corresponds to ![]() $\pi : C' \to C$. Alternatively, formula (109) is the restriction of the function on the
$\pi : C' \to C$. Alternatively, formula (109) is the restriction of the function on the ![]() $\mathrm {SL}_n$-Hitchin base
$\mathrm {SL}_n$-Hitchin base
 $$ \begin{align*} \mu_{\pi=\mathrm{id},{\mathcal A}}: {\mathcal A}^D \to {\mathbb{A}}^1 \end{align*} $$
$$ \begin{align*} \mu_{\pi=\mathrm{id},{\mathcal A}}: {\mathcal A}^D \to {\mathbb{A}}^1 \end{align*} $$to the closed subvariety  $i^D_{\gamma }: {\mathcal A}^D_{\gamma } \hookrightarrow {\mathcal A}^D$.
$i^D_{\gamma }: {\mathcal A}^D_{\gamma } \hookrightarrow {\mathcal A}^D$.
Recall the notation from diagram (29). We have the following corollary of Theorem 4.5:
Corollary 4.6. Theorem 4.5(c) induces for any character ![]() $\kappa \in \hat {\Gamma }$ a natural isomorphism
$\kappa \in \hat {\Gamma }$ a natural isomorphism
 $$ \begin{align*} \varphi_{\mu_{\gamma,{\mathcal A}}} \left({\mathrm{Rh}^{\text{D}}_{\gamma}}_* {\underline{{\mathbb{C}}}} \right)_{\kappa} = \left({\mathrm{Rh}^{\text{D}-\text{p}}_{\gamma}}_* {\underline{{\mathbb{C}}}} \right)_{\kappa} [-r_0]. \end{align*} $$
$$ \begin{align*} \varphi_{\mu_{\gamma,{\mathcal A}}} \left({\mathrm{Rh}^{\text{D}}_{\gamma}}_* {\underline{{\mathbb{C}}}} \right)_{\kappa} = \left({\mathrm{Rh}^{\text{D}-\text{p}}_{\gamma}}_* {\underline{{\mathbb{C}}}} \right)_{\kappa} [-r_0]. \end{align*} $$Here ![]() $r_0$ is the same as in Theorem 4.5(b) and (c).
$r_0$ is the same as in Theorem 4.5(b) and (c).
Proof. We consider the quotient map  $q_{\mathcal A}: {\mathcal A}^D(\pi ) \to {\mathcal A}^D_{\gamma }$. By the proper base change [Reference Dimca13, Proposition 4.2.11], we have
$q_{\mathcal A}: {\mathcal A}^D(\pi ) \to {\mathcal A}^D_{\gamma }$. By the proper base change [Reference Dimca13, Proposition 4.2.11], we have
 $$ \begin{align} \varphi_{\mu_{\gamma,{\mathcal A}}} \left({q_{\mathcal A}}_* {\mathrm{Rh}^{\text{D}}_{\pi}}_* {\underline{{\mathbb{C}}}} \right) = {q_{\mathcal A}}_* \varphi_{\mu_{\pi,{\mathcal A}}} \left({\mathrm{Rh}^{\text{D}}_{\pi}}_* {\underline{{\mathbb{C}}}} \right). \end{align} $$
$$ \begin{align} \varphi_{\mu_{\gamma,{\mathcal A}}} \left({q_{\mathcal A}}_* {\mathrm{Rh}^{\text{D}}_{\pi}}_* {\underline{{\mathbb{C}}}} \right) = {q_{\mathcal A}}_* \varphi_{\mu_{\pi,{\mathcal A}}} \left({\mathrm{Rh}^{\text{D}}_{\pi}}_* {\underline{{\mathbb{C}}}} \right). \end{align} $$Similar to the proof of Theorem 4.5(c), the identity (110) is compatible with the ![]() $G_{\pi }$- and
$G_{\pi }$- and ![]() $\Gamma $-actions on both sides. By taking the
$\Gamma $-actions on both sides. By taking the ![]() $G_{\pi }$-invariant and the
$G_{\pi }$-invariant and the ![]() $\kappa $-isotypic parts, we obtain
$\kappa $-isotypic parts, we obtain
 $$ \begin{align*} \varphi_{\mu_{\gamma,{\mathcal A}}} \left(\left({q_{\mathcal A}}_*{\mathrm{Rh}^{\text{D}}_{\pi}}_* {\underline{{\mathbb{C}}}}\right)^{G_{\pi}}\right)_{\kappa} = \left({q_{\mathcal A}}_* \varphi_{\mu_{\pi,{\mathcal A}}} \left({\mathrm{Rh}^{\text{D}}_{\pi}}_* {\underline{{\mathbb{C}}}}\right)_{\kappa} \right)^{G_{\pi}} = \left({q_{\mathcal A}}_* {\mathrm{Rh}^{\text{D}-\text{p}}_{\pi}}_* {\underline{{\mathbb{C}}}} \right)_{\kappa}^{G_{\pi}}[-r_0], \end{align*} $$
$$ \begin{align*} \varphi_{\mu_{\gamma,{\mathcal A}}} \left(\left({q_{\mathcal A}}_*{\mathrm{Rh}^{\text{D}}_{\pi}}_* {\underline{{\mathbb{C}}}}\right)^{G_{\pi}}\right)_{\kappa} = \left({q_{\mathcal A}}_* \varphi_{\mu_{\pi,{\mathcal A}}} \left({\mathrm{Rh}^{\text{D}}_{\pi}}_* {\underline{{\mathbb{C}}}}\right)_{\kappa} \right)^{G_{\pi}} = \left({q_{\mathcal A}}_* {\mathrm{Rh}^{\text{D}-\text{p}}_{\pi}}_* {\underline{{\mathbb{C}}}} \right)_{\kappa}^{G_{\pi}}[-r_0], \end{align*} $$where we use Theorem 4.5(c) in the last identity. Hence Lemma 1.7 implies that
 $$ \begin{align*} \varphi_{\mu_{\gamma,{\mathcal A}}} \left({\mathrm{Rh}^{\text{D}}_{\gamma}}_* {\underline{{\mathbb{C}}}} \right)_{\kappa} = \left({\mathrm{Rh}^{\text{D}-\text{p}}_{\gamma}}_* {\underline{{\mathbb{C}}}} \right)_{\kappa} [-r_0]. \end{align*} $$
$$ \begin{align*} \varphi_{\mu_{\gamma,{\mathcal A}}} \left({\mathrm{Rh}^{\text{D}}_{\gamma}}_* {\underline{{\mathbb{C}}}} \right)_{\kappa} = \left({\mathrm{Rh}^{\text{D}-\text{p}}_{\gamma}}_* {\underline{{\mathbb{C}}}} \right)_{\kappa} [-r_0]. \end{align*} $$Remark 4.7. A different choice of trivialisation (86) affects the functions (103), and therefore the vanishing cycle sheaves, by a scalar ![]() $\lambda \in {\mathbb {C}}^*$. Since all the isomorphisms in our main theorems are constructed only up to scaling, choices of trivialisation (86) do not matter for our purpose.
$\lambda \in {\mathbb {C}}^*$. Since all the isomorphisms in our main theorems are constructed only up to scaling, choices of trivialisation (86) do not matter for our purpose.
4.4 Proof of Theorem 3.2
In this section, we prove Theorem 3.2 by constructing the operator
 $$ \begin{align} c^D_{\kappa}: \left(\mathrm{Rh}^{\text{D}}_{*} {\underline{{\mathbb{C}}}}\right)_{\kappa} \xrightarrow{\simeq} {i^D_{\gamma}}_*\left({\mathrm{Rh}^{\text{D}}_{\gamma}}_* {\underline{{\mathbb{C}}}}\right)_{\kappa} \left[-2d^D_{\gamma}\right]. \end{align} $$
$$ \begin{align} c^D_{\kappa}: \left(\mathrm{Rh}^{\text{D}}_{*} {\underline{{\mathbb{C}}}}\right)_{\kappa} \xrightarrow{\simeq} {i^D_{\gamma}}_*\left({\mathrm{Rh}^{\text{D}}_{\gamma}}_* {\underline{{\mathbb{C}}}}\right)_{\kappa} \left[-2d^D_{\gamma}\right]. \end{align} $$This recovers the ![]() $G_{\pi }$-equivariant operator
$G_{\pi }$-equivariant operator
 $$ \begin{align*} q_{\mathcal A}^*\left(c^D_{\kappa}\right): q_{\mathcal A}^* \left( \mathrm{Rh}^{\text{D}}_{*} {\underline{{\mathbb{C}}}} \right)_{\kappa} \Big\rvert_{{\mathcal A}^D(\pi)^*} \xrightarrow{~~\simeq~~} \left( {\mathrm{Rh}_{\pi}^{\text{D}}}_* {\underline{{\mathbb{C}}}} \right)_{\kappa}\Big\rvert_{{\mathcal A}^D(\pi)^*}\left[-2d^D_{\gamma}\right] \end{align*} $$
$$ \begin{align*} q_{\mathcal A}^*\left(c^D_{\kappa}\right): q_{\mathcal A}^* \left( \mathrm{Rh}^{\text{D}}_{*} {\underline{{\mathbb{C}}}} \right)_{\kappa} \Big\rvert_{{\mathcal A}^D(\pi)^*} \xrightarrow{~~\simeq~~} \left( {\mathrm{Rh}_{\pi}^{\text{D}}}_* {\underline{{\mathbb{C}}}} \right)_{\kappa}\Big\rvert_{{\mathcal A}^D(\pi)^*}\left[-2d^D_{\gamma}\right] \end{align*} $$for Theorem 3.1, as explained in Section 3.1.
We construct the operator (111) in the following three cases:
Case 1. The effective divisor D satisfies the conditions that
 $\mathrm {deg}(D)$ is even and greater than
$\mathrm {deg}(D)$ is even and greater than  $2g-2$. This is Theorem 3.3, already proven in Section 3, where the operator comes from Ngô’s endoscopic correspondence and the support theorems.
$2g-2$. This is Theorem 3.3, already proven in Section 3, where the operator comes from Ngô’s endoscopic correspondence and the support theorems.Case 2. The effective divisor D satisfies the conditions that
 $\mathrm {deg}(D)$ is odd and greater than
$\mathrm {deg}(D)$ is odd and greater than  $2g-2$. In this case, the support theorems still hold, but the isomorphism of Proposition 3.13 is missed due to parity reasons (see Remark 3.14). We apply Theorem 4.5 to reduce this case to case 1 as follows:
$2g-2$. In this case, the support theorems still hold, but the isomorphism of Proposition 3.13 is missed due to parity reasons (see Remark 3.14). We apply Theorem 4.5 to reduce this case to case 1 as follows:Let p be a closed point of C. Then the effective divisor
satisfies the assumption of case 1. Hence we have an isomorphism $$ \begin{align*} D_p = D+p \end{align*} $$(112)which is canonical up to scaling, constructed from Ngô’s endoscopic correspondence. Applying to formula (112) the vanishing cycle functor
$$ \begin{align*} D_p = D+p \end{align*} $$(112)which is canonical up to scaling, constructed from Ngô’s endoscopic correspondence. Applying to formula (112) the vanishing cycle functor $$ \begin{align} c^{D_p}_{\kappa}: \left(\mathrm{Rh}^{\text{D}_{\text{p}}}_{*} {\underline{{\mathbb{C}}}}\right)_{\kappa} \xrightarrow{\simeq} {i^{D_p}_{\gamma}}_*\left({\mathrm{Rh}^{\text{D}_{\text{p}}}_{\gamma}}_* {\underline{{\mathbb{C}}}}\right)_{\kappa} \left[-2d^{D_p}_{\gamma}\right] \in D^b_c\left({\mathcal A}^{D_p}\right), \end{align} $$
$$ \begin{align} c^{D_p}_{\kappa}: \left(\mathrm{Rh}^{\text{D}_{\text{p}}}_{*} {\underline{{\mathbb{C}}}}\right)_{\kappa} \xrightarrow{\simeq} {i^{D_p}_{\gamma}}_*\left({\mathrm{Rh}^{\text{D}_{\text{p}}}_{\gamma}}_* {\underline{{\mathbb{C}}}}\right)_{\kappa} \left[-2d^{D_p}_{\gamma}\right] \in D^b_c\left({\mathcal A}^{D_p}\right), \end{align} $$ $\varphi _{\mu _{{\mathcal A}}}$ associated with the function we obtain
$\varphi _{\mu _{{\mathcal A}}}$ associated with the function we obtain $$ \begin{align*} \mu_{\mathcal A} :=\mu_{\mathrm{id},{\mathcal A}}: {\mathcal A}^{D_p} \to {\mathbb{A}}^1, \end{align*} $$(113)Since formula (112) is canonical up to scaling, so is formula (113), by Lemma 4.4(b). In fact, the operator (113) gives the desired operator
$$ \begin{align*} \mu_{\mathcal A} :=\mu_{\mathrm{id},{\mathcal A}}: {\mathcal A}^{D_p} \to {\mathbb{A}}^1, \end{align*} $$(113)Since formula (112) is canonical up to scaling, so is formula (113), by Lemma 4.4(b). In fact, the operator (113) gives the desired operator $$ \begin{align} \varphi_p\left(c^{D_p}_{\kappa}\right):= \varphi_{\mu_{\mathcal A}}\left(c^{D_p}_{\kappa}\right): \varphi_{\mu_{{\mathcal A}}}\left(\mathrm{Rh}^{\text{D}_{\text{p}}}_{*} {\underline{{\mathbb{C}}}}\right)_{\kappa} \xrightarrow{\simeq} \varphi_{\mu_{{\mathcal A}}}\left({i^{D_p}_{\gamma}}_*\left({\mathrm{Rh}^{\text{D}_{\text{p}}}_{\gamma}}_* {\underline{{\mathbb{C}}}}\right)_{\kappa} \right) \left[-2d^{D_p}_{\gamma}\right]. \end{align} $$
$$ \begin{align} \varphi_p\left(c^{D_p}_{\kappa}\right):= \varphi_{\mu_{\mathcal A}}\left(c^{D_p}_{\kappa}\right): \varphi_{\mu_{{\mathcal A}}}\left(\mathrm{Rh}^{\text{D}_{\text{p}}}_{*} {\underline{{\mathbb{C}}}}\right)_{\kappa} \xrightarrow{\simeq} \varphi_{\mu_{{\mathcal A}}}\left({i^{D_p}_{\gamma}}_*\left({\mathrm{Rh}^{\text{D}_{\text{p}}}_{\gamma}}_* {\underline{{\mathbb{C}}}}\right)_{\kappa} \right) \left[-2d^{D_p}_{\gamma}\right]. \end{align} $$ $c^{D}_{\kappa }$. To justify this, we calculate both sides of it.For the left-hand side, Theorem 4.5(c) applied to the special case
$c^{D}_{\kappa }$. To justify this, we calculate both sides of it.For the left-hand side, Theorem 4.5(c) applied to the special case  $\pi = \mathrm {id}$ yields
$\pi = \mathrm {id}$ yields  $$ \begin{align*} \varphi_{\mu_{{\mathcal A}}}\left(\mathrm{Rh}^{\text{D}_{\text{p}}}_{*} {\underline{{\mathbb{C}}}}\right)_{\kappa} = \left(\mathrm{Rh}^{\text{D}}_{*} {\underline{{\mathbb{C}}}}\right)_{\kappa}[-r_1], \quad r_1 = \mathrm{codim}_{{\mathcal M}^{D_p}_{n,L}} \left({\mathcal M}^D_{n,L}\right). \end{align*} $$
$$ \begin{align*} \varphi_{\mu_{{\mathcal A}}}\left(\mathrm{Rh}^{\text{D}_{\text{p}}}_{*} {\underline{{\mathbb{C}}}}\right)_{\kappa} = \left(\mathrm{Rh}^{\text{D}}_{*} {\underline{{\mathbb{C}}}}\right)_{\kappa}[-r_1], \quad r_1 = \mathrm{codim}_{{\mathcal M}^{D_p}_{n,L}} \left({\mathcal M}^D_{n,L}\right). \end{align*} $$For the right-hand side, we have by the proper base change ([Reference Dimca13, Proposition 4.2.11]) and Corollary 4.6 that
where $$ \begin{align*} \varphi_{\mu_{{\mathcal A}}}\left({i^{D_p}_{\gamma}}_*\left({\mathrm{Rh}^{\text{D}_{\text{p}}}_{\gamma}}_* {\underline{{\mathbb{C}}}}\right)_{\kappa} \right) & = {i^{D_p}_{\gamma}}_*\varphi_{\mu_{\gamma,{\mathcal A}}}\left({\mathrm{Rh}^{\text{D}_{\text{p}}}_{\gamma}}_* {\underline{{\mathbb{C}}}}\right)_{\kappa} \\ &= {i^{D}_{\gamma}}_*\left({\mathrm{Rh}^{\text{D}}_{\gamma}}_* {\underline{{\mathbb{C}}}} \right)_{\kappa} [-r_2], \end{align*} $$In conclusion, formula (113) gives an isomorphism
$$ \begin{align*} \varphi_{\mu_{{\mathcal A}}}\left({i^{D_p}_{\gamma}}_*\left({\mathrm{Rh}^{\text{D}_{\text{p}}}_{\gamma}}_* {\underline{{\mathbb{C}}}}\right)_{\kappa} \right) & = {i^{D_p}_{\gamma}}_*\varphi_{\mu_{\gamma,{\mathcal A}}}\left({\mathrm{Rh}^{\text{D}_{\text{p}}}_{\gamma}}_* {\underline{{\mathbb{C}}}}\right)_{\kappa} \\ &= {i^{D}_{\gamma}}_*\left({\mathrm{Rh}^{\text{D}}_{\gamma}}_* {\underline{{\mathbb{C}}}} \right)_{\kappa} [-r_2], \end{align*} $$In conclusion, formula (113) gives an isomorphism $$ \begin{align*} r_2 = \mathrm{codim}_{{\mathcal M}^{D_p}_{r,L}(\pi)}\left({\mathcal M}^D_{r,L}(\pi)\right). \end{align*} $$By the dimension formulas in [Reference de Cataldo6, Section 6.1], we have
$$ \begin{align*} r_2 = \mathrm{codim}_{{\mathcal M}^{D_p}_{r,L}(\pi)}\left({\mathcal M}^D_{r,L}(\pi)\right). \end{align*} $$By the dimension formulas in [Reference de Cataldo6, Section 6.1], we have $$ \begin{align*} \varphi_p\left(c^{D_p}_{\kappa}\right): \left(\mathrm{Rh}^{\text{D}}_{*} {\underline{{\mathbb{C}}}}\right)_{\kappa} \xrightarrow{\simeq} {i_{\gamma}}_*\left({\mathrm{Rh}^{\text{D}}_{\gamma}}_* {\underline{{\mathbb{C}}}}\right)_{\kappa} \left[-2d^{D_p}_{\gamma}+r_1-r_2\right]. \end{align*} $$Hence
$$ \begin{align*} \varphi_p\left(c^{D_p}_{\kappa}\right): \left(\mathrm{Rh}^{\text{D}}_{*} {\underline{{\mathbb{C}}}}\right)_{\kappa} \xrightarrow{\simeq} {i_{\gamma}}_*\left({\mathrm{Rh}^{\text{D}}_{\gamma}}_* {\underline{{\mathbb{C}}}}\right)_{\kappa} \left[-2d^{D_p}_{\gamma}+r_1-r_2\right]. \end{align*} $$Hence $$ \begin{align*} r_1 -r_2 & = \left(\mathrm{dim}\left({\mathcal M}^{D_p}_{n,L}\right) - \mathrm{dim}\left({\mathcal M}^{D}_{n,L}\right)\right) - \left(\mathrm{dim}\left({\mathcal M}^{D_p}_{r,L}(\pi)\right) - \mathrm{dim}\left({\mathcal M}^{D}_{r,L}(\pi)\right)\right)\\ & =2d^{D_p}_{\gamma} - 2d^{D}_{\gamma}. \end{align*} $$
$$ \begin{align*} r_1 -r_2 & = \left(\mathrm{dim}\left({\mathcal M}^{D_p}_{n,L}\right) - \mathrm{dim}\left({\mathcal M}^{D}_{n,L}\right)\right) - \left(\mathrm{dim}\left({\mathcal M}^{D_p}_{r,L}(\pi)\right) - \mathrm{dim}\left({\mathcal M}^{D}_{r,L}(\pi)\right)\right)\\ & =2d^{D_p}_{\gamma} - 2d^{D}_{\gamma}. \end{align*} $$ $-2d^{D_p}_{\gamma }+r_1-r_2 = - 2d^{D}_{\gamma }$, and the operator (114)induces an isomorphism (111), as desired.
$-2d^{D_p}_{\gamma }+r_1-r_2 = - 2d^{D}_{\gamma }$, and the operator (114)induces an isomorphism (111), as desired. $$ \begin{align} c^D_{\kappa} = \varphi_p\left(c^{D_p}_{\kappa}\right) \end{align} $$
$$ \begin{align} c^D_{\kappa} = \varphi_p\left(c^{D_p}_{\kappa}\right) \end{align} $$Case 3. We now treat the last case,
 $D = K_C$. In this case the support theorems fail for the Hitchin fibrations (compare [Reference de Cataldo, Heinloth and Migliorini8]). However, we are able to construct the operator (111) following the same strategy as in case 2.
$D = K_C$. In this case the support theorems fail for the Hitchin fibrations (compare [Reference de Cataldo, Heinloth and Migliorini8]). However, we are able to construct the operator (111) following the same strategy as in case 2.Let
 $p,q$ be two closed points on the curve C. Then the divisor satisfies the assumption of case 1, and we have
$p,q$ be two closed points on the curve C. Then the divisor satisfies the assumption of case 1, and we have $$ \begin{align*} K_{p,q}=K_C+p+q \end{align*} $$Similar to equation (114), we define
$$ \begin{align*} K_{p,q}=K_C+p+q \end{align*} $$Similar to equation (114), we define $$ \begin{align*} c^{K_{p,q}}_{\kappa}: \left(\mathrm{Rh}^{\text{K}_{\text{p,q}}}_{*} {\underline{{\mathbb{C}}}}\right)_{\kappa} \xrightarrow{\simeq} {i^{K_{p,q}}_{\gamma}}_*\left({\mathrm{Rh}^{\text{K}_{\text{p,q}}}_{\gamma}}_* {\underline{{\mathbb{C}}}}\right)_{\kappa} \left[-2d^{K_{p,q}}_{\gamma}\right]. \end{align*} $$(115)which gives the desired isomorphism (111) for
$$ \begin{align*} c^{K_{p,q}}_{\kappa}: \left(\mathrm{Rh}^{\text{K}_{\text{p,q}}}_{*} {\underline{{\mathbb{C}}}}\right)_{\kappa} \xrightarrow{\simeq} {i^{K_{p,q}}_{\gamma}}_*\left({\mathrm{Rh}^{\text{K}_{\text{p,q}}}_{\gamma}}_* {\underline{{\mathbb{C}}}}\right)_{\kappa} \left[-2d^{K_{p,q}}_{\gamma}\right]. \end{align*} $$(115)which gives the desired isomorphism (111) for $$ \begin{align} c^{K_C}_{\kappa} := \varphi_q\left(\varphi_p\left( c^{K_{p,q}}_{\kappa}\right)\right), \end{align} $$
$$ \begin{align} c^{K_C}_{\kappa} := \varphi_q\left(\varphi_p\left( c^{K_{p,q}}_{\kappa}\right)\right), \end{align} $$ $D = K_C$.
$D = K_C$.
We have completed the construction of formula (111), which proves Theorems 3.1 and 3.2. In cases 2 and 3, the construction of the operator ![]() $c^D_{\kappa }$ a priori depends on the choice of the closed points p and q. We finish this section by showing in the following proposition that
$c^D_{\kappa }$ a priori depends on the choice of the closed points p and q. We finish this section by showing in the following proposition that ![]() $c^D_{\kappa }$ in case 2 or 3 is in fact independent of the choice of points:
$c^D_{\kappa }$ in case 2 or 3 is in fact independent of the choice of points:
Proposition 4.8. The operators (114) and (115) do not depend on the choice of ![]() $p \in C$ and
$p \in C$ and ![]() $p,q\in C$ respectively.
$p,q\in C$ respectively.
Proof. We prove independence for the operator (114). By varying the point p, we have a family of Hitchin fibrations
 $$ \begin{align*} h^{D_p}: {\mathcal M}^{D_p}_{n,L} \to {\mathcal A}^{D_p} \end{align*} $$
$$ \begin{align*} h^{D_p}: {\mathcal M}^{D_p}_{n,L} \to {\mathcal A}^{D_p} \end{align*} $$over a base T. The construction of the correspondence (112) works relatively over the base, which gives a family of operators  $c^{D_p}_{\kappa }$. By applying the vanishing cycle functor relatively over T, we obtain a family of operators
$c^{D_p}_{\kappa }$. By applying the vanishing cycle functor relatively over T, we obtain a family of operators  $\phi _p\left (c^{D_p}_{\kappa }\right )$ which form a section of the trivial local system
$\phi _p\left (c^{D_p}_{\kappa }\right )$ which form a section of the trivial local system
on T. Here
 $$ \begin{align*} {\mathcal F}_1 = \left(\mathrm{Rh}^{\text{D}}_{*} {\underline{{\mathbb{C}}}}\right)_{\kappa} \text{ and } {\mathcal F}_2 = {i_{\gamma}}_*\left({\mathrm{Rh}^{\text{D}}_{\gamma}}_* {\underline{{\mathbb{C}}}}\right)_{\kappa} \left[-2d^{D}\right] \end{align*} $$
$$ \begin{align*} {\mathcal F}_1 = \left(\mathrm{Rh}^{\text{D}}_{*} {\underline{{\mathbb{C}}}}\right)_{\kappa} \text{ and } {\mathcal F}_2 = {i_{\gamma}}_*\left({\mathrm{Rh}^{\text{D}}_{\gamma}}_* {\underline{{\mathbb{C}}}}\right)_{\kappa} \left[-2d^{D}\right] \end{align*} $$are independent of the point p. Hence  $\phi _p\left (c^{D_p}_{\kappa }\right )$ is constant over T.
$\phi _p\left (c^{D_p}_{\kappa }\right )$ is constant over T.
An identical argument works for formula (115), which we omit.
Remark 4.9. Applying the vanishing cycle functors as in cases 2 and 3, we obtain that Proposition 2.11 also holds for ![]() $D= K_C$.
$D= K_C$.
5 The P=W conjecture and the Hausel–Thaddeus conjecture
Throughout this section, we assume that the curve C has genus ![]() $g \geq 2$. We assume that D is an effective divisor of degree
$g \geq 2$. We assume that D is an effective divisor of degree ![]() $\mathrm {deg}(D)>2g-2$ or
$\mathrm {deg}(D)>2g-2$ or ![]() $D = {K}_C$. For a cyclic Galois cover
$D = {K}_C$. For a cyclic Galois cover ![]() $\pi : C' \to C$, we denote by
$\pi : C' \to C$, we denote by ![]() $D'$ the divisor
$D'$ the divisor ![]() $\pi ^*D$ on
$\pi ^*D$ on ![]() $C'$.
$C'$.
We discuss some applications of Theorems 3.1 and 3.2.
5.1 Perverse filtrations
We briefly recall the definition of perverse filtrations [Reference de Cataldo and Migliorini11, Reference de Cataldo, Hausel and Migliorini7].
Let ![]() $f: X \rightarrow Y$ be a proper morphism, with X a nonsingular algebraic variety. The perverse t-structure on the constructible derived category
$f: X \rightarrow Y$ be a proper morphism, with X a nonsingular algebraic variety. The perverse t-structure on the constructible derived category ![]() $D_c^b(Y)$ induces an increasing filtration on the cohomology
$D_c^b(Y)$ induces an increasing filtration on the cohomology ![]() $H^*(X, {\mathbb {C}})$,
$H^*(X, {\mathbb {C}})$,
called the perverse filtration associated with f.
The perverse filtration (116) can be described via the decomposition theorem [Reference Beĭlinson, Bernstein and Deligne3]. In fact, applying the decomposition theorem to the map ![]() $f: X \to Y$, we obtain an isomorphism
$f: X \to Y$, we obtain an isomorphism
 $$ \begin{align*} \mathrm{Rf}_*{\underline{{\mathbb{C}}}}[\dim(X)-l]\simeq \bigoplus_{i=0}^{2l}\mathcal{P}_i[-i] \in D^b_c(Y), \end{align*} $$
$$ \begin{align*} \mathrm{Rf}_*{\underline{{\mathbb{C}}}}[\dim(X)-l]\simeq \bigoplus_{i=0}^{2l}\mathcal{P}_i[-i] \in D^b_c(Y), \end{align*} $$with ![]() $\mathcal {P}_i$ a perverse sheaf on Y and l the defect of semismallness:
$\mathcal {P}_i$ a perverse sheaf on Y and l the defect of semismallness:
The kth piece of the perverse filtration is
 $$ \begin{align*} P_kH^j(X,{\mathbb{Q}})=\mathrm{Im}\left\{H^{j-(\dim(X) - l)}\left(Y, \bigoplus_{i=0}^k\mathcal{P}_i[-i]\right)\to H^j(X,{\mathbb{Q}})\right\}. \end{align*} $$
$$ \begin{align*} P_kH^j(X,{\mathbb{Q}})=\mathrm{Im}\left\{H^{j-(\dim(X) - l)}\left(Y, \bigoplus_{i=0}^k\mathcal{P}_i[-i]\right)\to H^j(X,{\mathbb{Q}})\right\}. \end{align*} $$5.2 The P=W conjecture
Perverse filtrations appear naturally in studying the topology of Hitchin fibrations. For notational convenience, we let
be the Hitchin fibration with ![]() ${\mathcal M} = {\mathcal M}_{n,L}$ or
${\mathcal M} = {\mathcal M}_{n,L}$ or  $\widetilde {{\mathcal M}}_{n,d}$.Footnote 5 We denote by
$\widetilde {{\mathcal M}}_{n,d}$.Footnote 5 We denote by ![]() ${\mathcal M}^{B}$ the Betti moduli space associated with
${\mathcal M}^{B}$ the Betti moduli space associated with ![]() ${\mathcal M}$. There is a diffeomorphism
${\mathcal M}$. There is a diffeomorphism ![]() ${\mathcal M} \cong {\mathcal M}^{B}$ induced by nonabelian Hodge theory [Reference Simpson36, Reference Simpson37, Reference Hausel and Thaddeus23] which identifies the cohomology
${\mathcal M} \cong {\mathcal M}^{B}$ induced by nonabelian Hodge theory [Reference Simpson36, Reference Simpson37, Reference Hausel and Thaddeus23] which identifies the cohomology
 $$ \begin{align} H^*({\mathcal M}, {\mathbb{C}}) = H^*\left({\mathcal M}^{B}, {\mathbb{C}}\right). \end{align} $$
$$ \begin{align} H^*({\mathcal M}, {\mathbb{C}}) = H^*\left({\mathcal M}^{B}, {\mathbb{C}}\right). \end{align} $$A central question concerning the cohomological aspect of nonabelian Hodge theory is the P=W conjecture formulated by de Cataldo, Hausel and Migliorini [Reference de Cataldo, Hausel and Migliorini7], connecting the perverse filtration associated with the Hitchin fibration h to the weight filtration
 $$ \begin{align*} W_{0}H^*\left({\mathcal M}^{B}, {\mathbb{C}}\right) \subset W_{1}H^*\left({\mathcal M}^{B}, {\mathbb{C}}\right) \subset \cdots \subset W_kH^*\left({\mathcal M}^{B}, {\mathbb{C}}\right) \subset \cdots \subset H^*\left({\mathcal M}^{\mathrm{B}}, {\mathbb{C}}\right) \end{align*} $$
$$ \begin{align*} W_{0}H^*\left({\mathcal M}^{B}, {\mathbb{C}}\right) \subset W_{1}H^*\left({\mathcal M}^{B}, {\mathbb{C}}\right) \subset \cdots \subset W_kH^*\left({\mathcal M}^{B}, {\mathbb{C}}\right) \subset \cdots \subset H^*\left({\mathcal M}^{\mathrm{B}}, {\mathbb{C}}\right) \end{align*} $$associated with the mixed Hodge structure on ![]() ${\mathcal M}^{\mathrm {B}}$.
${\mathcal M}^{\mathrm {B}}$.
Conjecture 5.1 P=W [Reference de Cataldo, Hausel and Migliorini7]
Under the nonabelian Hodge correspondence (117), we have
 $$ \begin{align*} P_kH^i({\mathcal M}, {\mathbb{C}}) = W_{2k}H^i\left({\mathcal M}^B, {\mathbb{C}}\right). \end{align*} $$
$$ \begin{align*} P_kH^i({\mathcal M}, {\mathbb{C}}) = W_{2k}H^i\left({\mathcal M}^B, {\mathbb{C}}\right). \end{align*} $$ For the ![]() $\mathrm {GL}_n$ case, the P=W conjecture was proven for
$\mathrm {GL}_n$ case, the P=W conjecture was proven for ![]() $n=2$ in [Reference de Cataldo, Hausel and Migliorini7], and recently for
$n=2$ in [Reference de Cataldo, Hausel and Migliorini7], and recently for ![]() $g=2$ [Reference de Cataldo, Maulik and Shen9]. Furthermore, [Reference de Cataldo, Maulik and Shen9] reduces the full P=W conjecture to the multiplicativity of the perverse filtration (see [Reference de Cataldo, Maulik and Shen9, Introduction] for the precise statement). In either situation, the way to attack the P=W conjecture is to analyse the location of the tautological classes in both the perverse and the weight filtrations.
$g=2$ [Reference de Cataldo, Maulik and Shen9]. Furthermore, [Reference de Cataldo, Maulik and Shen9] reduces the full P=W conjecture to the multiplicativity of the perverse filtration (see [Reference de Cataldo, Maulik and Shen9, Introduction] for the precise statement). In either situation, the way to attack the P=W conjecture is to analyse the location of the tautological classes in both the perverse and the weight filtrations.
The case of ![]() $\mathrm {SL}_n$ is more complicated, due to the lack of tautological classes accessing the
$\mathrm {SL}_n$ is more complicated, due to the lack of tautological classes accessing the ![]() $\Gamma $-variant cohomology. When n is a prime number, the shapes of the perverse and weight filtrations on the
$\Gamma $-variant cohomology. When n is a prime number, the shapes of the perverse and weight filtrations on the ![]() $\Gamma $-variant parts are of simpler forms, and therefore the P=W conjecture has been verified for the
$\Gamma $-variant parts are of simpler forms, and therefore the P=W conjecture has been verified for the ![]() $\Gamma $-variant cohomology via direct calculations; see [Reference de Cataldo, Hausel and Migliorini7] for
$\Gamma $-variant cohomology via direct calculations; see [Reference de Cataldo, Hausel and Migliorini7] for ![]() $n=2$ and [Reference de Cataldo, Maulik and Shen10] for any prime number n.
$n=2$ and [Reference de Cataldo, Maulik and Shen10] for any prime number n.
When n is not a prime number, numerical evidence from the Hausel–Thaddeus conjecture suggests that the P=W conjecture for ![]() $\mathrm {SL}_n$ should rely on the P=W conjecture for a sequence of moduli spaces of stable
$\mathrm {SL}_n$ should rely on the P=W conjecture for a sequence of moduli spaces of stable ![]() $\mathrm {GL}_*$-Higgs bundles on different curves with different ranks. In particular, we expect that the P=W conjecture for
$\mathrm {GL}_*$-Higgs bundles on different curves with different ranks. In particular, we expect that the P=W conjecture for ![]() $\mathrm {SL}_n$ can be eventually reduced to the P=W conjecture for
$\mathrm {SL}_n$ can be eventually reduced to the P=W conjecture for ![]() $\mathrm {GL}_r$.
$\mathrm {GL}_r$.
As a first step in this direction, we will introduce the operator (125) connecting  $H^*\left ({\mathcal M}_{n,L}, {\mathbb {C}}\right )_{\kappa }$ and the cohomology of the moduli space of stable
$H^*\left ({\mathcal M}_{n,L}, {\mathbb {C}}\right )_{\kappa }$ and the cohomology of the moduli space of stable ![]() $\mathrm {GL}_r$-Higgs bundles on another curve
$\mathrm {GL}_r$-Higgs bundles on another curve ![]() $C'$, where r and
$C'$, where r and ![]() $C'$ are determined by
$C'$ are determined by ![]() $\kappa \in \hat {\Gamma }$. Then we prove Theorem 5.4 on the compatibility of the perverse filtrations.
$\kappa \in \hat {\Gamma }$. Then we prove Theorem 5.4 on the compatibility of the perverse filtrations.
5.3 The stable cohomology
Let ![]() $\pi : C'\to C$ be a cyclic Galois cover of degree m. Let
$\pi : C'\to C$ be a cyclic Galois cover of degree m. Let ![]() $L \in \mathrm {Pic}^d(C)$ be a fixed line bundle with
$L \in \mathrm {Pic}^d(C)$ be a fixed line bundle with ![]() $\mathrm {gcd}(n,d)=1$. We allow D to be any effective divisor with
$\mathrm {gcd}(n,d)=1$. We allow D to be any effective divisor with ![]() $\mathrm {deg}(D)>2g-2$ or
$\mathrm {deg}(D)>2g-2$ or ![]() $D= K_C$.
$D= K_C$.
We recall the moduli spaces  $\widetilde {{\mathcal M}}_{r,d}^{D'}(C')$ and
$\widetilde {{\mathcal M}}_{r,d}^{D'}(C')$ and  ${\mathcal M}_{r,L}^{D}(\pi )$ as well as their respective Hitchin fibrations (10) and (16). The group scheme
${\mathcal M}_{r,L}^{D}(\pi )$ as well as their respective Hitchin fibrations (10) and (16). The group scheme
 $$ \begin{align*} \widetilde{{\mathcal M}}^D_{1,0}(C) = \mathrm{Pic}^0(C)\times H^0(C, {\mathcal O}_C(D)) \end{align*} $$
$$ \begin{align*} \widetilde{{\mathcal M}}^D_{1,0}(C) = \mathrm{Pic}^0(C)\times H^0(C, {\mathcal O}_C(D)) \end{align*} $$acts on the moduli space  $\widetilde {{\mathcal M}}_{r,d}^{D'}(C')$ inducing
$\widetilde {{\mathcal M}}_{r,d}^{D'}(C')$ inducing
 $$ \begin{align} \widetilde{q}: \widetilde{{\mathcal M}}^D_{1,0}(C) \times {\mathcal M}_{r,L}^{D}(\pi) \to \widetilde{{\mathcal M}}_{r,d}^{D'}(C'), \quad \left( ({\mathcal E}_1, \theta_1), ({\mathcal E}_r, \theta_r) \right) \mapsto (\pi^*{\mathcal E}_1 \otimes {\mathcal E}_r, \pi^*\theta_1+ \theta_r). \end{align} $$
$$ \begin{align} \widetilde{q}: \widetilde{{\mathcal M}}^D_{1,0}(C) \times {\mathcal M}_{r,L}^{D}(\pi) \to \widetilde{{\mathcal M}}_{r,d}^{D'}(C'), \quad \left( ({\mathcal E}_1, \theta_1), ({\mathcal E}_r, \theta_r) \right) \mapsto (\pi^*{\mathcal E}_1 \otimes {\mathcal E}_r, \pi^*\theta_1+ \theta_r). \end{align} $$Here ![]() $\theta _1 \in H^0(C, {\mathcal O}_C(D))$ and its pullback give a section
$\theta _1 \in H^0(C, {\mathcal O}_C(D))$ and its pullback give a section ![]() $\pi ^*\theta _1 \in H^0(C', {\mathcal O}_{C'}(D'))$. The finite group
$\pi ^*\theta _1 \in H^0(C', {\mathcal O}_{C'}(D'))$. The finite group ![]() $\Gamma $ acts on the left-hand side of formula (118) diagonally:
$\Gamma $ acts on the left-hand side of formula (118) diagonally:
 $$ \begin{align*} {\mathcal L} \cdot \left( ({\mathcal E}_1, \theta_1), ({\mathcal E}_r, \theta_r) \right) = \left(\left({\mathcal E}_1 \otimes {\mathcal L}^{-1}, \theta_1\right), ({\mathcal E}_r \otimes {\mathcal L}, \theta_r)\right), \quad {\mathcal L} \in \Gamma. \end{align*} $$
$$ \begin{align*} {\mathcal L} \cdot \left( ({\mathcal E}_1, \theta_1), ({\mathcal E}_r, \theta_r) \right) = \left(\left({\mathcal E}_1 \otimes {\mathcal L}^{-1}, \theta_1\right), ({\mathcal E}_r \otimes {\mathcal L}, \theta_r)\right), \quad {\mathcal L} \in \Gamma. \end{align*} $$The morphism (118) factors through this ![]() $\Gamma $-quotient, and its fibres are given by
$\Gamma $-quotient, and its fibres are given by ![]() $\Gamma $-orbits. For dimension reasons, the right-hand side of formula (118) coincides with the
$\Gamma $-orbits. For dimension reasons, the right-hand side of formula (118) coincides with the ![]() $\Gamma $-quotient of the left-hand side. We have the following canonical isomorphisms of the cohomology:
$\Gamma $-quotient of the left-hand side. We have the following canonical isomorphisms of the cohomology:
 $$ \begin{align} H^*\left(\widetilde{{\mathcal M}}_{r,d}^{D'}(C'), {\mathbb{C}}\right) & \xrightarrow{\simeq} H^*\left(\widetilde{{\mathcal M}}^D_{1,0}(C) \times {\mathcal M}_{r,L}^{D}(\pi) , {\mathbb{C}}\right)^{\Gamma} \notag \\ & = \left(H^*\left(\widetilde{{\mathcal M}}^D_{1,0}(C), {\mathbb{C}}\right) \otimes H^*\left( {\mathcal M}_{r,L}^{D}(\pi) , {\mathbb{C}}\right) \right)^{\Gamma}\\ & = H^*\left(\widetilde{{\mathcal M}}^D_{1,0}(C), {\mathbb{C}}\right) \otimes H^*\left( {\mathcal M}_{r,L}^{D}(\pi) , {\mathbb{C}}\right)^{\Gamma},\notag \end{align} $$
$$ \begin{align} H^*\left(\widetilde{{\mathcal M}}_{r,d}^{D'}(C'), {\mathbb{C}}\right) & \xrightarrow{\simeq} H^*\left(\widetilde{{\mathcal M}}^D_{1,0}(C) \times {\mathcal M}_{r,L}^{D}(\pi) , {\mathbb{C}}\right)^{\Gamma} \notag \\ & = \left(H^*\left(\widetilde{{\mathcal M}}^D_{1,0}(C), {\mathbb{C}}\right) \otimes H^*\left( {\mathcal M}_{r,L}^{D}(\pi) , {\mathbb{C}}\right) \right)^{\Gamma}\\ & = H^*\left(\widetilde{{\mathcal M}}^D_{1,0}(C), {\mathbb{C}}\right) \otimes H^*\left( {\mathcal M}_{r,L}^{D}(\pi) , {\mathbb{C}}\right)^{\Gamma},\notag \end{align} $$where the first isomorphism is induced by the ![]() $\Gamma $-quotient map
$\Gamma $-quotient map ![]() $\widetilde {q}^*$, the second identity is the Künneth decomposition and the last identity follows from the triviality of the
$\widetilde {q}^*$, the second identity is the Künneth decomposition and the last identity follows from the triviality of the ![]() $\Gamma $-action on
$\Gamma $-action on  $H^*\left (\widetilde {{\mathcal M}}^D_{1,0}(C), {\mathbb {C}}\right )$.
$H^*\left (\widetilde {{\mathcal M}}^D_{1,0}(C), {\mathbb {C}}\right )$.
For any Hitchin-type moduli space  $\widetilde {{\mathcal M}}^D_{n,d}$,
$\widetilde {{\mathcal M}}^D_{n,d}$,  ${\mathcal M}^D_{n,L}$ or
${\mathcal M}^D_{n,L}$ or  ${\mathcal M}^D_{r,L}(\pi )$, we consider the perverse filtrations on the cohomology defined via the corresponding Hitchin fibration (10), (12) or (16). The following proposition provides a description of the perverse filtration on the stable part of
${\mathcal M}^D_{r,L}(\pi )$, we consider the perverse filtrations on the cohomology defined via the corresponding Hitchin fibration (10), (12) or (16). The following proposition provides a description of the perverse filtration on the stable part of  $H^*\left ( {\mathcal M}_{r,L}^{D}(\pi ) , {\mathbb {C}}\right )$:
$H^*\left ( {\mathcal M}_{r,L}^{D}(\pi ) , {\mathbb {C}}\right )$:
Proposition 5.2. The quotient map (118) induces a canonical isomorphism
 $$ \begin{align} H^*\left(\widetilde{{\mathcal M}}_{r,d}^{D'}(C'), {\mathbb{C}}\right) = H^*\left(\widetilde{{\mathcal M}}^D_{1,0}(C), {\mathbb{C}}\right) \otimes H^*\left( {\mathcal M}_{r,L}^{D}(\pi) , {\mathbb{C}}\right)_{\mathrm{st}} \end{align} $$
$$ \begin{align} H^*\left(\widetilde{{\mathcal M}}_{r,d}^{D'}(C'), {\mathbb{C}}\right) = H^*\left(\widetilde{{\mathcal M}}^D_{1,0}(C), {\mathbb{C}}\right) \otimes H^*\left( {\mathcal M}_{r,L}^{D}(\pi) , {\mathbb{C}}\right)_{\mathrm{st}} \end{align} $$satisfying
 $$ \begin{align} P_kH^*\left(\widetilde{{\mathcal M}}_{r,d}^{D'}(C'), {\mathbb{C}}\right) = \bigoplus_{i+j = k} H^i\left(\widetilde{{\mathcal M}}^D_{1,0}(C), {\mathbb{C}}\right) \otimes P_jH^*\left( {\mathcal M}_{r,L}^{D}(\pi) , {\mathbb{C}}\right)_{\mathrm{st}}. \end{align} $$
$$ \begin{align} P_kH^*\left(\widetilde{{\mathcal M}}_{r,d}^{D'}(C'), {\mathbb{C}}\right) = \bigoplus_{i+j = k} H^i\left(\widetilde{{\mathcal M}}^D_{1,0}(C), {\mathbb{C}}\right) \otimes P_jH^*\left( {\mathcal M}_{r,L}^{D}(\pi) , {\mathbb{C}}\right)_{\mathrm{st}}. \end{align} $$Here the stable part ![]() $(-)_{\mathrm {st}}$ denotes the
$(-)_{\mathrm {st}}$ denotes the ![]() $\Gamma $-invariant part of the cohomology.
$\Gamma $-invariant part of the cohomology.
Proof. The first isomorphism is induced by formula (119). It suffices to show the compatibility (121) of the perverse filtrations.
We notice that the quotient map (118) is compatible with the Hitchin fibrations, and we have the commutative diagram

where the bottom arrow is a canonical identification. The pullback morphism ![]() $\widetilde {q}^*$ for the cohomology is induced sheaf-theoretically by the canonical morphism
$\widetilde {q}^*$ for the cohomology is induced sheaf-theoretically by the canonical morphism
where the first and the second ![]() ${\underline {{\mathbb {C}}}}$, respectively, denote the trivial local systems on the target and the source of
${\underline {{\mathbb {C}}}}$, respectively, denote the trivial local systems on the target and the source of ![]() $\widetilde {q}$. By applying the perverse truncation functor to the push-forward of formula (122) along
$\widetilde {q}$. By applying the perverse truncation functor to the push-forward of formula (122) along ![]() $\widetilde {h}^{D'}$, we find that the first map of formula (119) satisfies
$\widetilde {h}^{D'}$, we find that the first map of formula (119) satisfies
 $$ \begin{align} P_kH^*\left(\widetilde{{\mathcal M}}_{r,d}^{D'}(C'), {\mathbb{C}}\right) \xrightarrow{\simeq} P_kH^*\left(\widetilde{{\mathcal M}}^D_{1,0}(C) \times {\mathcal M}_{r,L}^{D}(\pi) , {\mathbb{C}}\right)^{\Gamma}. \end{align} $$
$$ \begin{align} P_kH^*\left(\widetilde{{\mathcal M}}_{r,d}^{D'}(C'), {\mathbb{C}}\right) \xrightarrow{\simeq} P_kH^*\left(\widetilde{{\mathcal M}}^D_{1,0}(C) \times {\mathcal M}_{r,L}^{D}(\pi) , {\mathbb{C}}\right)^{\Gamma}. \end{align} $$We conclude equation (121) from formula (123), the Künneth decomposition and the fact that the perverse filtration on
 $$ \begin{align*} H^*\left(\widetilde{{\mathcal M}}^D_{1,0}(C), {\mathbb{C}}\right) = H^*\left(\mathrm{Pic}^0(C), {\mathbb{C}}\right) \end{align*} $$
$$ \begin{align*} H^*\left(\widetilde{{\mathcal M}}^D_{1,0}(C), {\mathbb{C}}\right) = H^*\left(\mathrm{Pic}^0(C), {\mathbb{C}}\right) \end{align*} $$coincides with the cohomological filtration ![]() $H^{*\leq k}$.
$H^{*\leq k}$.
As a consequence of Proposition 5.2, we obtain a canonical operator given by the projection
 $$ \begin{align} \mathfrak{p_1}: H^i\left(\widetilde{{\mathcal M}}_{r,d}^{D'}(C'), {\mathbb{C}}\right) \rightarrow H^i\left( {\mathcal M}_{r,L}^{D}(\pi) , {\mathbb{C}}\right)_{\mathrm{st}}, \quad \ \forall i\geq 0, \end{align} $$
$$ \begin{align} \mathfrak{p_1}: H^i\left(\widetilde{{\mathcal M}}_{r,d}^{D'}(C'), {\mathbb{C}}\right) \rightarrow H^i\left( {\mathcal M}_{r,L}^{D}(\pi) , {\mathbb{C}}\right)_{\mathrm{st}}, \quad \ \forall i\geq 0, \end{align} $$sending a class in  $H^i\left (\widetilde {{\mathcal M}}_{r,d}^{D'}(C'), {\mathbb {C}}\right )$ to its projection to the direct summand component
$H^i\left (\widetilde {{\mathcal M}}_{r,d}^{D'}(C'), {\mathbb {C}}\right )$ to its projection to the direct summand component
 $$ \begin{align*} H^0\left(\widetilde{{\mathcal M}}^D_{1,0}(C), {\mathbb{C}}\right) \otimes H^i\left( {\mathcal M}_{r,L}^{D}(\pi) , {\mathbb{C}}\right)_{\mathrm{st}} = H^i\left( {\mathcal M}_{r,L}^{D}(\pi) , {\mathbb{C}}\right)_{\mathrm{st}} \end{align*} $$
$$ \begin{align*} H^0\left(\widetilde{{\mathcal M}}^D_{1,0}(C), {\mathbb{C}}\right) \otimes H^i\left( {\mathcal M}_{r,L}^{D}(\pi) , {\mathbb{C}}\right)_{\mathrm{st}} = H^i\left( {\mathcal M}_{r,L}^{D}(\pi) , {\mathbb{C}}\right)_{\mathrm{st}} \end{align*} $$with respect to the decomposition (120). This identity is induced by the fundamental class  $1\in H^0\left (\widetilde {{\mathcal M}}^D_{1,0}(C), {\mathbb {C}}\right )$.
$1\in H^0\left (\widetilde {{\mathcal M}}^D_{1,0}(C), {\mathbb {C}}\right )$.
Corollary 5.3. The operator (124) respects the perverse filtrations:
 $$ \begin{align*} \mathfrak{p_1}\left( P_k H^i\left(\widetilde{{\mathcal M}}_{r,d}^{D'}(C'), {\mathbb{C}}\right)\right) = P_kH^i\left( {\mathcal M}_{r,L}^{D}(\pi) , {\mathbb{C}}\right)_{\mathrm{st}}. \end{align*} $$
$$ \begin{align*} \mathfrak{p_1}\left( P_k H^i\left(\widetilde{{\mathcal M}}_{r,d}^{D'}(C'), {\mathbb{C}}\right)\right) = P_kH^i\left( {\mathcal M}_{r,L}^{D}(\pi) , {\mathbb{C}}\right)_{\mathrm{st}}. \end{align*} $$Proof. Since the fundamental class  $1\in H^0\left (\widetilde {{\mathcal M}}^D_{1,0}(C), {\mathbb {C}}\right )$ lies in
$1\in H^0\left (\widetilde {{\mathcal M}}^D_{1,0}(C), {\mathbb {C}}\right )$ lies in  $P_0H^0\left (\widetilde {{\mathcal M}}^D_{1,0}(C), {\mathbb {C}}\right )$, the corollary follows from equation (121).
$P_0H^0\left (\widetilde {{\mathcal M}}^D_{1,0}(C), {\mathbb {C}}\right )$, the corollary follows from equation (121).
5.4 Operators
Let ![]() $\pi : C' \to C$ be the cyclic Galois cover given by
$\pi : C' \to C$ be the cyclic Galois cover given by ![]() $\gamma \in \Gamma $, which corresponds to
$\gamma \in \Gamma $, which corresponds to ![]() $\kappa \in \hat {\Gamma }$ via equation (3). We define the operator
$\kappa \in \hat {\Gamma }$ via equation (3). We define the operator
 $$ \begin{align} \mathfrak{p}_{\kappa}: H^{i-2d^D_{\gamma}}\left(\widetilde{{\mathcal M}}_{r,d}^{D'}(C'), {\mathbb{C}}\right) \twoheadrightarrow H^{i}\left({\mathcal M}^D_{n,L}, {\mathbb{C}}\right)_{\kappa} \end{align} $$
$$ \begin{align} \mathfrak{p}_{\kappa}: H^{i-2d^D_{\gamma}}\left(\widetilde{{\mathcal M}}_{r,d}^{D'}(C'), {\mathbb{C}}\right) \twoheadrightarrow H^{i}\left({\mathcal M}^D_{n,L}, {\mathbb{C}}\right)_{\kappa} \end{align} $$as the following composition:
 $$ \begin{align} H^*\left(\widetilde{{\mathcal M}}_{r,d}^{D'}(C'),{\mathbb{C}}\right) & \xrightarrow{\mathfrak{p}_1} H^*\left( {\mathcal M}_{r,L}^{D}(\pi) , {\mathbb{C}}\right)_{\mathrm{st}} = H^*\left( {\mathcal M}_{r,L}^{D}(\pi) , {\mathbb{C}}\right)_{\kappa} \notag \\ \xrightarrow{\mathrm{proj.}} H^*\left( {\mathcal M}_{r,L}^{D}(\pi) , {\mathbb{C}}\right)^{G_{\pi}}_{\kappa} & = H^*\left( {\mathcal M}_{\gamma}^{D} , {\mathbb{C}}\right)_{\kappa} \xrightarrow[\simeq]{\text{Thm.~3.2}} H^{*+2d^D_{\gamma}}\left({\mathcal M}^D_{n,L}, {\mathbb{C}}\right)_{\kappa}. \end{align} $$
$$ \begin{align} H^*\left(\widetilde{{\mathcal M}}_{r,d}^{D'}(C'),{\mathbb{C}}\right) & \xrightarrow{\mathfrak{p}_1} H^*\left( {\mathcal M}_{r,L}^{D}(\pi) , {\mathbb{C}}\right)_{\mathrm{st}} = H^*\left( {\mathcal M}_{r,L}^{D}(\pi) , {\mathbb{C}}\right)_{\kappa} \notag \\ \xrightarrow{\mathrm{proj.}} H^*\left( {\mathcal M}_{r,L}^{D}(\pi) , {\mathbb{C}}\right)^{G_{\pi}}_{\kappa} & = H^*\left( {\mathcal M}_{\gamma}^{D} , {\mathbb{C}}\right)_{\kappa} \xrightarrow[\simeq]{\text{Thm.~3.2}} H^{*+2d^D_{\gamma}}\left({\mathcal M}^D_{n,L}, {\mathbb{C}}\right)_{\kappa}. \end{align} $$Here the first morphism is formula (124), the second isomorphism is given by Proposition 2.10, the third morphism is the projection to the ![]() $G_{\pi }$-invariant part, the fourth isomorphism is given by Lemma 1.7 and the last isomorphism follows from Theorem 3.2. Hence we obtain that formula (125) is surjective and canonically defined up to scaling.
$G_{\pi }$-invariant part, the fourth isomorphism is given by Lemma 1.7 and the last isomorphism follows from Theorem 3.2. Hence we obtain that formula (125) is surjective and canonically defined up to scaling.
Theorem 5.4. We have
 $$ \begin{align*} \mathfrak{p}_{\kappa} \left( P_k H^i\left(\widetilde{{\mathcal M}}_{r,d}^{D'}(C'), {\mathbb{C}}\right)\right) = P_{k+d^D_{\gamma}}H^{i+2d^D_{\gamma}}\left( {\mathcal M}_{n,L}^{D}, {\mathbb{C}}\right)_{\kappa}. \end{align*} $$
$$ \begin{align*} \mathfrak{p}_{\kappa} \left( P_k H^i\left(\widetilde{{\mathcal M}}_{r,d}^{D'}(C'), {\mathbb{C}}\right)\right) = P_{k+d^D_{\gamma}}H^{i+2d^D_{\gamma}}\left( {\mathcal M}_{n,L}^{D}, {\mathbb{C}}\right)_{\kappa}. \end{align*} $$Proof. By Corollary 5.3, the morphism ![]() $\mathfrak {p}_1$ preserves the perverse filtrations. All the other morphisms in formula (126) except the last one are deduced from sheaf-theoretic morphisms which clearly preserve the perverse filtrations. Hence we have
$\mathfrak {p}_1$ preserves the perverse filtrations. All the other morphisms in formula (126) except the last one are deduced from sheaf-theoretic morphisms which clearly preserve the perverse filtrations. Hence we have
 $$ \begin{align*} P_kH^i\left(\widetilde{{\mathcal M}}_{r,d}^{D'}(C'), {\mathbb{C}}\right) \twoheadrightarrow P_k H^i\left({\mathcal M}^D_{\gamma}, {\mathbb{C}}\right)_{\kappa}. \end{align*} $$
$$ \begin{align*} P_kH^i\left(\widetilde{{\mathcal M}}_{r,d}^{D'}(C'), {\mathbb{C}}\right) \twoheadrightarrow P_k H^i\left({\mathcal M}^D_{\gamma}, {\mathbb{C}}\right)_{\kappa}. \end{align*} $$The last morphism of formula (126) is given by the sheaf-theoretic isomorphism (65). Taking account of the shift, we have
 $$ \begin{align*} P_k H^i\left({\mathcal M}^D_{\gamma}, {\mathbb{C}}\right)_{\kappa} \xrightarrow{\simeq} P_{k+d^D_{\gamma}}H^{i+2d^D_{\gamma}}\left( {\mathcal M}_{r,L}^{D}(\pi) , {\mathbb{C}}\right)_{\kappa}.\end{align*} $$
$$ \begin{align*} P_k H^i\left({\mathcal M}^D_{\gamma}, {\mathbb{C}}\right)_{\kappa} \xrightarrow{\simeq} P_{k+d^D_{\gamma}}H^{i+2d^D_{\gamma}}\left( {\mathcal M}_{r,L}^{D}(\pi) , {\mathbb{C}}\right)_{\kappa}.\end{align*} $$ Now we consider the special case ![]() $D = K_C$. Passing through the isomorphisms (117) induced by the nonabelian Hodge theory, we obtain an operator for the corresponding Betti moduli spaces
$D = K_C$. Passing through the isomorphisms (117) induced by the nonabelian Hodge theory, we obtain an operator for the corresponding Betti moduli spaces
 $$ \begin{align*} \mathfrak{p}^B_{\kappa}: H^{i-2d_{\gamma}}\left(\widetilde{{\mathcal M}}_{r,d}^{B}(C'), {\mathbb{C}}\right) \twoheadrightarrow H^{i}\left({\mathcal M}^B_{n,L}, {\mathbb{C}}\right)_{\kappa}. \end{align*} $$
$$ \begin{align*} \mathfrak{p}^B_{\kappa}: H^{i-2d_{\gamma}}\left(\widetilde{{\mathcal M}}_{r,d}^{B}(C'), {\mathbb{C}}\right) \twoheadrightarrow H^{i}\left({\mathcal M}^B_{n,L}, {\mathbb{C}}\right)_{\kappa}. \end{align*} $$Here  $\widetilde {{\mathcal M}}_{r,d}^{B}(C')$ is the Betti moduli space associated with the curve
$\widetilde {{\mathcal M}}_{r,d}^{B}(C')$ is the Betti moduli space associated with the curve ![]() $C'$, the group
$C'$, the group ![]() $\mathrm {GL}_r$ and the degree d, and
$\mathrm {GL}_r$ and the degree d, and  ${\mathcal M}^B_{n,L}$ stands for the Betti moduli space associated with the curve C, the group
${\mathcal M}^B_{n,L}$ stands for the Betti moduli space associated with the curve C, the group ![]() $\mathrm {SL}_n$ and the line bundle L. We refer to [Reference Hausel and Thaddeus23] for more details on these moduli spaces.
$\mathrm {SL}_n$ and the line bundle L. We refer to [Reference Hausel and Thaddeus23] for more details on these moduli spaces.
Question 5.5. Is it true that
 $$ \begin{align*} \mathfrak{p}^B_{\kappa} \left( W_{2k} H^i\left(\widetilde{{\mathcal M}}_{r,d}^{B}(C'), {\mathbb{C}}\right)\right) = W_{2k+2d_{\gamma}}H^{i+2d_{\gamma}}\left( {\mathcal M}_{n,L}^{B}, {\mathbb{C}}\right)_{\kappa}? \end{align*} $$
$$ \begin{align*} \mathfrak{p}^B_{\kappa} \left( W_{2k} H^i\left(\widetilde{{\mathcal M}}_{r,d}^{B}(C'), {\mathbb{C}}\right)\right) = W_{2k+2d_{\gamma}}H^{i+2d_{\gamma}}\left( {\mathcal M}_{n,L}^{B}, {\mathbb{C}}\right)_{\kappa}? \end{align*} $$ If Question 5.5 has an affirmative answer, then Theorem 5.4 implies that if the P=W conjecture holds for ![]() $\mathrm {GL}_r$ for any r dividing n, then the P=W conjecture holds for
$\mathrm {GL}_r$ for any r dividing n, then the P=W conjecture holds for ![]() $\mathrm {SL}_n$. However, the construction of the operator
$\mathrm {SL}_n$. However, the construction of the operator ![]() $\mathfrak {p}_{\kappa }$ relies heavily on the topology of Hitchin fibrations, which is mysterious on the Betti side. A better understanding of the operator
$\mathfrak {p}_{\kappa }$ relies heavily on the topology of Hitchin fibrations, which is mysterious on the Betti side. A better understanding of the operator ![]() $\mathfrak {p}_{\kappa }$ may be needed.
$\mathfrak {p}_{\kappa }$ may be needed.
5.5 The Hausel–Thaddeus conjecture
We explain in this final section that Theorem 3.2 implies Theorem 0.5. Here for Higgs bundles, we again work with any effective divisor D with ![]() $\mathrm {deg}(D)>2g-2$ or
$\mathrm {deg}(D)>2g-2$ or ![]() $D= K_C$.
$D= K_C$.
Proof of Theorem 0.5. We first note that for two line bundles ![]() $L_1$ and
$L_1$ and ![]() $L_2$ with
$L_2$ with ![]() $L_1 = L_2 \otimes N^{\otimes n}$, there is a natural identification of the moduli spaces
$L_1 = L_2 \otimes N^{\otimes n}$, there is a natural identification of the moduli spaces
 $$ \begin{align} {\mathcal M}^D_{n, L_1} \xrightarrow{\simeq} {\mathcal M}^D_{n, L_2}, \quad ({\mathcal E}, \theta) \mapsto ({\mathcal E}\otimes N, \theta), \end{align} $$
$$ \begin{align} {\mathcal M}^D_{n, L_1} \xrightarrow{\simeq} {\mathcal M}^D_{n, L_2}, \quad ({\mathcal E}, \theta) \mapsto ({\mathcal E}\otimes N, \theta), \end{align} $$compatible with the Hitchin fibrations. Hence we obtain
 $$ \begin{align} \left[P_kH^i\left({\mathcal M}^D_{n,L}, {\mathbb{C}}\right)_{\kappa}\right] & = \left[P_kH^i\left({\mathcal M}^D_{n,{L^{\prime}}^{\otimes de}}, {\mathbb{C}}\right)_{\kappa}\right]\notag \\& = \left[P_{k-d^D_{\gamma}}H^{i-2d^D_{\gamma}}\left(\left({\mathcal M}^D_{n,{L^{\prime}}^{\otimes de}}\right)_{\gamma}, {\mathbb{C}}\right)_{\kappa}\right] \\& = \left[P_{k-d^D_{\gamma}}H^{i-2d^D_{\gamma}}\left(\left({\mathcal M}^D_{n,L'}\right)_{\gamma}, {\mathbb{C}}\right)_{de\kappa}\right] \notag \end{align} $$
$$ \begin{align} \left[P_kH^i\left({\mathcal M}^D_{n,L}, {\mathbb{C}}\right)_{\kappa}\right] & = \left[P_kH^i\left({\mathcal M}^D_{n,{L^{\prime}}^{\otimes de}}, {\mathbb{C}}\right)_{\kappa}\right]\notag \\& = \left[P_{k-d^D_{\gamma}}H^{i-2d^D_{\gamma}}\left(\left({\mathcal M}^D_{n,{L^{\prime}}^{\otimes de}}\right)_{\gamma}, {\mathbb{C}}\right)_{\kappa}\right] \\& = \left[P_{k-d^D_{\gamma}}H^{i-2d^D_{\gamma}}\left(\left({\mathcal M}^D_{n,L'}\right)_{\gamma}, {\mathbb{C}}\right)_{de\kappa}\right] \notag \end{align} $$in the Grothendieck group ![]() $K_0(\mathrm {Vect})$ of
$K_0(\mathrm {Vect})$ of ![]() ${\mathbb {C}}$-vector spaces. Here the first identity is induced by formula (127), since
${\mathbb {C}}$-vector spaces. Here the first identity is induced by formula (127), since  $\mathrm {deg}(L) = \mathrm {deg}\left ({L^{\prime }}^{\otimes de}\right )\mod n$; the second identity follows from formula (65); and the third identity is given by Remark 4.9 and Proposition 2.11.
$\mathrm {deg}(L) = \mathrm {deg}\left ({L^{\prime }}^{\otimes de}\right )\mod n$; the second identity follows from formula (65); and the third identity is given by Remark 4.9 and Proposition 2.11.
This proves the Betti-number version of the refined Hausel–Thaddeus conjecture (7). To get the enhanced version concerning Hodge structures, we follow [Reference de Cataldo, Rapagnetta and Saccà12, Section 2.1] to work with the category of mixed Hodge modules [Reference Saito35], which refines the category of perverse sheaves. Identical arguments show that Theorems 3.1 and 3.2 actually hold in the derived category of mixed Hodge modules, which gives the enhanced version of equation (128) in ![]() $K_0(\mathrm {HS})$. This completes the proof of equation (7).
$K_0(\mathrm {HS})$. This completes the proof of equation (7).
Finally, we note that equation (7) implies equation (8). This follows from taking the summation over all ![]() $\gamma \in \Gamma $ and the natural identification of the fixed loci
$\gamma \in \Gamma $ and the natural identification of the fixed loci
 $$ \begin{align*} \left({\mathcal M}^D_{n,L'}\right)_{\gamma} = \left({\mathcal M}^D_{n,L'}\right)_{q\gamma} \end{align*} $$
$$ \begin{align*} \left({\mathcal M}^D_{n,L'}\right)_{\gamma} = \left({\mathcal M}^D_{n,L'}\right)_{q\gamma} \end{align*} $$for any ![]() $q \in {\mathbb {Z}}$ coprime to n.
$q \in {\mathbb {Z}}$ coprime to n.
Acknowledgements
We are grateful to Mark Andrea de Cataldo, Michael Gröchenig and Zhiwei Yun for helpful discussions. We also thank the anonymous referee for careful reading and numerous useful suggestions. The first author would like to thank Chris and Martin Kratt for providing logistical support. The second author was supported by NSF DMS-2000726 and DMS-2134315.
Conflict of Interest:
None.