Article contents
Projective Reeds-Shepp car on S 2 with quadratic cost
Published online by Cambridge University Press: 19 December 2008
Abstract
Fix two points $x,\bar{x}\in S^2$  and two directions (without orientation) $\eta,\bar\eta$
and two directions (without orientation) $\eta,\bar\eta$ 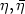 of the velocities in these points. In this paper we are interested to the problem of minimizing the cost
of the velocities in these points. In this paper we are interested to the problem of minimizing the cost
$J[\gamma]=\int_0^T \left({\g}_{\gamma(t)}(\dot\gamma(t),\dot\gamma(t))+K^2_{\gamma(t)}{\g}_{\gamma(t)}(\dot\gamma(t),\dot\gamma(t)) \right) ~{\rm d}t$ 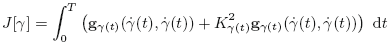
along all smooth curves starting from x with direction η and ending in $\bar{x}$ 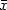 with direction $\bar\eta$
with direction $\bar\eta$ 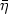 . Here g is the standard Riemannian metric on S 2 and $K_\gamma$
. Here g is the standard Riemannian metric on S 2 and $K_\gamma$ 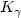 is the corresponding geodesic curvature.The interest of this problem comes from mechanics and geometry of vision. It can be formulated as a sub-Riemannian problem on the lens space L(4,1).We compute the global solution for this problem: an interesting feature is that some optimal geodesics present cusps. The cut locus is a stratification with non trivial topology.
is the corresponding geodesic curvature.The interest of this problem comes from mechanics and geometry of vision. It can be formulated as a sub-Riemannian problem on the lens space L(4,1).We compute the global solution for this problem: an interesting feature is that some optimal geodesics present cusps. The cut locus is a stratification with non trivial topology.
Information
- Type
- Research Article
- Information
- ESAIM: Control, Optimisation and Calculus of Variations , Volume 16 , Issue 2 , April 2010 , pp. 275 - 297
- Copyright
- © EDP Sciences, SMAI, 2008
References
- 7
- Cited by

