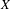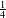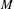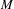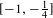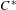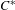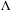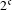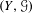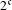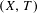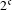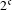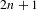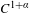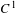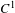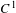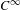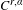Contents
Original Article
Embeddings of interval exchange transformations into planar piecewise isometries
- Part of:
-
- Published online by Cambridge University Press:
- 23 October 2018, pp. 1153-1179
-
- Article
- Export citation
Spectral gap property and strong ergodicity for groups of affine transformations of solenoids
- Part of:
-
- Published online by Cambridge University Press:
- 11 October 2018, pp. 1180-1193
-
- Article
- Export citation
Hyperbolic rank rigidity for manifolds of
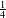 $\frac{1}{4}$-pinched negative curvature
$\frac{1}{4}$-pinched negative curvature
- Part of:
-
- Published online by Cambridge University Press:
- 08 October 2018, pp. 1194-1216
-
- Article
- Export citation
Equidistribution of divergent orbits of the diagonal group in the space of lattices
- Part of:
-
- Published online by Cambridge University Press:
- 25 September 2018, pp. 1217-1237
-
- Article
- Export citation
Monic representations of finite higher-rank graphs
- Part of:
-
- Published online by Cambridge University Press:
- 06 September 2018, pp. 1238-1267
-
- Article
- Export citation
A metric minimal PI cascade with
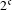 $2^{\mathfrak{c}}$minimal ideals
$2^{\mathfrak{c}}$minimal ideals
- Part of:
-
- Published online by Cambridge University Press:
- 14 September 2018, pp. 1268-1281
-
- Article
- Export citation
Rigidity, universality, and hyperbolicity of renormalization for critical circle maps with non-integer exponents
- Part of:
-
- Published online by Cambridge University Press:
- 25 September 2018, pp. 1282-1334
-
- Article
- Export citation
The
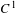 $C^{1}$ property of convex carrying simplices for competitive maps
$C^{1}$ property of convex carrying simplices for competitive maps
- Part of:
-
- Published online by Cambridge University Press:
- 17 October 2018, pp. 1335-1350
-
- Article
- Export citation
Amenability and unique ergodicity of automorphism groups of countable homogeneous directed graphs
- Part of:
-
- Published online by Cambridge University Press:
- 17 October 2018, pp. 1351-1401
-
- Article
- Export citation
On the conservative pasting lemma
- Part of:
-
- Published online by Cambridge University Press:
- 17 October 2018, pp. 1402-1440
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
ETS volume 40 Issue 5 Cover and Front matter
-
- Published online by Cambridge University Press:
- 06 April 2020, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (OBC, IBC) and matter
ETS volume 40 Issue 5 Cover and Back matter
-
- Published online by Cambridge University Press:
- 06 April 2020, pp. b1-b2
-
- Article
-
- You have access
- Export citation