Hostname: page-component-7dd5485656-wjfd9 Total loading time: 0 Render date: 2025-10-26T12:45:17.607Z Has data issue: false hasContentIssue false
  • English
  • Français

Shy shadows of infinite-dimensional partially hyperbolic invariant sets

Published online by Cambridge University Press:  25 September 2017

DANIEL SMANIA
DANIEL SMANIA*
Affiliation:
Departamento de Matemática, ICMC/USP – São Carlos, Caixa Postal 668, São Carlos-SP, CEP 13560-970, Brazil email smania@icmc.usp.br
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 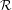${\mathcal{R}}$ be a strongly compact 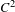$C^{2}$ map defined in an open subset of an infinite-dimensional Banach space such that the image of its derivative 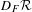$D_{F}{\mathcal{R}}$ is dense for every $F$. Let 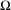$\unicode[STIX]{x1D6FA}$ be a compact, forward invariant and partially hyperbolic set of 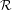${\mathcal{R}}$ such that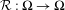${\mathcal{R}}:\unicode[STIX]{x1D6FA}\rightarrow \unicode[STIX]{x1D6FA}$ is onto. The $\unicode[STIX]{x1D6FF}$-shadow 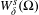$W_{\unicode[STIX]{x1D6FF}}^{s}(\unicode[STIX]{x1D6FA})$ of 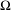$\unicode[STIX]{x1D6FA}$ is the union of the sets

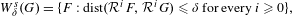$$\begin{eqnarray}W_{\unicode[STIX]{x1D6FF}}^{s}(G)=\{F:\operatorname{dist}({\mathcal{R}}^{i}F,{\mathcal{R}}^{i}G)\leq \unicode[STIX]{x1D6FF}\text{for every }i\geq 0\},\end{eqnarray}$$
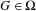where $G\in \unicode[STIX]{x1D6FA}$. Suppose that 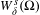$W_{\unicode[STIX]{x1D6FF}}^{s}(\unicode[STIX]{x1D6FA})$ has transversal empty interior, that is, for every 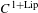$C^{1+\text{Lip}}$$n$-dimensional manifold 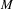$M$ transversal to the distribution of dominated directions of 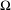$\unicode[STIX]{x1D6FA}$ and sufficiently close to 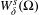$W_{\unicode[STIX]{x1D6FF}}^{s}(\unicode[STIX]{x1D6FA})$ we have that 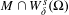$M\cap W_{\unicode[STIX]{x1D6FF}}^{s}(\unicode[STIX]{x1D6FA})$ has empty interior in 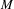$M$. Here $n$ is the finite dimension of the strong unstable direction. We show that if 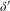$\unicode[STIX]{x1D6FF}^{\prime }$ is small enough then
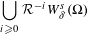$$\begin{eqnarray}\mathop{\bigcup }_{i\geq 0}{\mathcal{R}}^{-i}W_{\unicode[STIX]{x1D6FF}^{\prime }}^{s}(\unicode[STIX]{x1D6FA})\end{eqnarray}$$
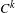 intercepts a $C^{k}$-generic finite-dimensional curve inside the Banach space in a set of parameters with zero Lebesgue measure for every 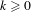$k\geq 0$. This extends to infinite-dimensional dynamical systems previous studies on the Lebesgue measure of stable laminations of invariants sets.

Information

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 39 , Issue 5 , May 2019 , pp. 1361 - 1400
Copyright
© Cambridge University Press, 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Alves, J. F. and Pinheiro, V.. Topological structure of (partially) hyperbolic sets with positive volume. Trans. Amer. Math. Soc. 360(10) (2008), 5551–5569.Google Scholar
Avila, A., Lyubich, M. and de Melo, W.. Regular or stochastic dynamics in real analytic families of unimodal maps. Invent. Math. 154(3) (2003), 451–550.Google Scholar
Avila, A. and Moreira, C. G.. Statistical properties of unimodal maps: smooth families with negative Schwarzian derivative. Geometric Methods in Dynamics. I . Astérisque 286 (2003), 81–118.Google Scholar
Bochnak, J. and Siciak, J.. Analytic functions in topological vector spaces. Studia Math. 39 (1971), 77–112.Google Scholar
Bowen, R.. Equilibrium States and the Ergodic Theory of Anosov Diffeomorphisms (Lecture Notes in Mathematics, 470) . Revised edn. Springer, Berlin, 2008, with a preface by D. Ruelle, edited by J.-R. Chazottes.Google Scholar
Bowen, R. and Ruelle, D.. The ergodic theory of Axiom A flows. Invent. Math. 29(3) (1975), 181–202.Google Scholar
Christensen, J. P. R.. On sets of Haar measure zero in abelian Polish groups Proc. Int. Symp. Partial Differential Equations and the Geometry of Normed Linear Spaces (Jerusalem, 1972) . Israel J. Math. 13 (1972), 255–260.Google Scholar
Csörnyei, M.. Aronszajn null and Gaussian null sets coincide. Israel J. Math. 111 (1999), 191–201.Google Scholar
de Faria, E., de Melo, W. and Pinto, A.. Global hyperbolicity of renormalization for C r unimodal mappings. Ann. of Math. (2) 164(3) (2006), 731–824.Google Scholar
Hunt, B. and Kaloshin, V.. Prevalence. Handbook of Dynamical Systems. Vol. 3. Eds. Broer, H., Takens, F. and Hasselblatt, B.. Elsevier/North-Holland, Amsterdam, 2010, pp. 43–87.Google Scholar
Hunt, B. R., Sauer, T. and Yorke, J. A.. Prevalence: a translation-invariant ‘almost every’ on infinite-dimensional spaces. Bull. Amer. Math. Soc. (N.S.) 27(2) (1992), 217–238.Google Scholar
Kaloshin, V. Y.. Some prevalent properties of smooth dynamical systems. Tr. Mat. Inst. Steklova 213 (1997), 123–151. (Differ. Uravn. s Veshchestv. i Kompleks. Vrem.).Google Scholar
Kirwan, P.. Complexification of multilinear mappings and polynomials. Math. Nachr. 231 (2001), 39–68.Google Scholar
Kolmogorov, A. N.. Théorie générale des systèmes dynamiques et mécanique classique. Proc. Int. Congr. Mathematicians, Amsterdam, 1954. Vol. 1. Eds. Noordhoff, E. P. and Groningen, N. V.. North-Holland, Amsterdam, 1957, pp. 315–333.Google Scholar
Lian, Z. and Young, L.-S.. Lyapunov exponents, periodic orbits and horseshoes for mappings of Hilbert spaces. Ann. Henri Poincaré 12(6) (2011), 1081–1108.Google Scholar
Lian, Z. and Young, L.-S.. Lyapunov exponents, periodic orbits, and horseshoes for semiflows on Hilbert spaces. J. Amer. Math. Soc. 25(3) (2012), 637–665.Google Scholar
Lian, Z., Young, L.-S. and Zeng, C.. Absolute continuity of stable foliations for systems on Banach spaces. J. Differential Equations 254(1) (2013), 283–308.Google Scholar
Lindenstrauss, J. and Preiss, D.. On Fréchet differentiability of Lipschitz maps between Banach spaces. Ann. of Math. (2) 157(1) (2003), 257–288.Google Scholar
Lindenstrauss, J., Preiss, D. and Tišer, J.. Fréchet Differentiability of Lipschitz Functions and Porous Sets in Banach Spaces (Annals of Mathematics Studies, 179) . Princeton University Press, Princeton, NJ, 2012.Google Scholar
Lyubich, M.. Feigenbaum–Coullet–Tresser universality and Milnor’s hairiness conjecture. Ann. of Math. (2) 149(2) (1999), 319–420.Google Scholar
Mañé, R.. Lyapounov exponents and stable manifolds for compact transformations. Geometric Dynamics (Rio de Janeiro, 1981) (Lecture Notes in Mathematics, 1007) . Springer, Berlin, 1983, pp. 522–577.Google Scholar
Muñoz, G. A., Sarantopoulos, Y. and Tonge, A.. Complexifications of real Banach spaces, polynomials and multilinear maps. Studia Math. 134(1) (1999), 1–33.Google Scholar
Palis, J.. On Morse–Smale dynamical systems. Topology 8 (1968), 385–404.Google Scholar
Palis, J.. A global perspective for non-conservative dynamics. Ann. Inst. H. Poincaré Anal. Non Linéaire 22(4) (2005), 485–507.Google Scholar
Palis, J.. Open questions leading to a global perspective in dynamics. Nonlinearity 21(4) (2008), T37–T43.Google Scholar
Palis, J. Jr. and de Melo, W.. Geometric Theory of Dynamical Systems: An Introduction. Springer, New York, 1982, translated from the Portuguese by A. K. Manning.Google Scholar
Smania, D.. Phase space universality for multimodal maps. Bull. Braz. Math. Soc. (N.S.) 36(2) (2005), 225–274.Google Scholar
Smania, D.. Solenoidal attractors with bounded combinatorics are shy. Submitted Preprint, 2016, p. 61,arXiv:1603.06300.Google Scholar