Article contents
Errata to ‘Hausdorff dimension for horseshoes’
Published online by Cambridge University Press: 19 September 2008
Extract
In our paper ‘Hausdorff dimension for horseshoes’ (H. McCluskey and A. Manning, Ergod. Th. & Dynam. Sys. (1983) 3, 251–260), § 3 entitled ‘Continuity across a bifurcation’ should be deleted since the proof of theorem 3 there is wrong.
The mistake is that 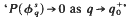 does not in fact imply that δs → 1. This is because, for q = q0, the function
does not in fact imply that δs → 1. This is because, for q = q0, the function 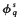 is is only non-positive rather than negative and so
is is only non-positive rather than negative and so 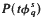 is not strictly decreasing function of t.(Thus the pressure curve in figure 3 may, for q = q0, have become horizontal before t = l.) A similar mistake occurs in the second half of the same proof. Thus the claim of theorem 3 that the Hausdorff dimension of the basic set changes continuously in the bifurcation from Anosov to DA remains unproved. The rest of the paper is not affected.
is not strictly decreasing function of t.(Thus the pressure curve in figure 3 may, for q = q0, have become horizontal before t = l.) A similar mistake occurs in the second half of the same proof. Thus the claim of theorem 3 that the Hausdorff dimension of the basic set changes continuously in the bifurcation from Anosov to DA remains unproved. The rest of the paper is not affected.
Information
- Type
- Errata
- Information
- Copyright
- Copyright © Cambridge University Press 1985
- 6
- Cited by

