Hostname: page-component-7dd5485656-frp75 Total loading time: 0 Render date: 2025-10-29T15:07:05.166Z Has data issue: false hasContentIssue false
  • English
  • Français

Statistical determinism in non-Lipschitz dynamical systems

Part of: Dynamical systems with hyperbolic behavior Equations and systems with randomness Random dynamical systems

Published online by Cambridge University Press:  11 October 2023

THEODORE D. DRIVAS Open the ORCID record for THEODORE D. DRIVAS [Opens in a new window] ,
ALEXEI A. MAILYBAEV Open the ORCID record for ALEXEI A. MAILYBAEV [Opens in a new window]  and
ARTEM RAIBEKAS
THEODORE D. DRIVAS
Affiliation:
Department of Mathematics, Stony Brook University, Stony Brook, NY 11794, USA (e-mail: tdrivas@math.stonybrook.edu)
ALEXEI A. MAILYBAEV*
Affiliation:
Instituto de Matemática Pura e Aplicada, Rio de Janeiro, Brazil
ARTEM RAIBEKAS
Affiliation:
Instituto de Matemática e Estatística, Universidade Federal Fluminense, Niterói, Brazil (e-mail: artemr@id.uff.br)
*
e-mail: alexei@impa.br
Get access Rights & Permissions [Opens in a new window]

Abstract

We study a class of ordinary differential equations with a non-Lipschitz point singularity that admits non-unique solutions through this point. As a selection criterion, we introduce stochastic regularizations depending on a parameter $\nu $: the regularized dynamics is globally defined for each $\nu> 0$, and the original singular system is recovered in the limit of vanishing 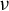$\nu $. We prove that this limit yields a unique statistical solution independent of regularization when the deterministic system possesses a chaotic attractor having a physical measure with the convergence to equilibrium property. In this case, solutions become spontaneously stochastic after passing through the singularity: they are selected randomly with an intrinsic probability distribution.

Keywords

singular dynamical systemsnon-Lipschitz differential equationsspontaneous stochasticity

MSC classification

Primary: 34F05: Equations and systems with randomness
Secondary: 37H05: Foundations, general theory of cocycles, algebraic ergodic theory 37D45: Strange attractors, chaotic dynamics

Information

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 44 , Issue 7 , July 2024 , pp. 1856 - 1884
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Araújo, V. and Melbourne, I.. Exponential decay of correlations for nonuniformly hyperbolic flows with a ${C}^{1+\alpha }$ stable foliation, including the classical Lorenz attractor. Ann. Henri Poincaré 17 (2016), 2975–3004.CrossRefGoogle Scholar
Araujo, V. and Melbourne, I.. Mixing properties and statistical limit theorems for singular hyperbolic flows without a smooth stable foliation. Adv. Math. 349 (2019), 212–245.CrossRefGoogle Scholar
Araújo, V. and Pacifico, M. J.. Three-Dimensional Flows (A Series of Modern Surveys in Mathematics, 53). Springer, Heidelberg, 2010.CrossRefGoogle Scholar
Araujo, V., Pacifico, M. J., Pujals, E. and Viana, M.. Singular-hyperbolic attractors are chaotic. Trans. Amer. Math. Soc. 361 (2009), 2431–2485.CrossRefGoogle Scholar
Araujo, V. and Trindade, E.. Robust exponential mixing and convergence to equilibrium for singular hyperbolic attracting sets. J. Dynam. Differential Equations 35 (2023), 2487–2536.CrossRefGoogle Scholar
Attanasio, S. and Flandoli, F.. Zero-noise solutions of linear transport equations without uniqueness: an example. C. R. Math. 347 (2009), 753–756.CrossRefGoogle Scholar
Bafico, R. and Baldi, P.. Small random perturbations of Peano phenomena. Stochastics 6 (1982), 279–292.CrossRefGoogle Scholar
Bernard, D., Gawedzki, K. and Kupiainen, A.. Slow modes in passive advection. J. Stat. Phys. 90 (1998), 519–569.CrossRefGoogle Scholar
Biferale, L., Boffetta, G., Mailybaev, A. A. and Scagliarini, A.. Rayleigh–Taylor turbulence with singular nonuniform initial conditions. Phys. Rev. Fluids 3 (2018), 092601.CrossRefGoogle Scholar
Bonatti, C., Díaz, L. and Viana, M.. Dynamics Beyond Uniform Hyperbolicity: A Global Geometric and Probabilistic Perspective (Encyclopaedia of Mathematical Sciences, 102). Springer Science & Business Media, Berlin–Heidelberg, 2006.Google Scholar
Bowen, R. and Ruelle, D.. The ergodic theory of Axiom A flows. Invent. Math. 29 (1975), 181–202.CrossRefGoogle Scholar
Campolina, C. S. and Mailybaev, A. A.. Chaotic blowup in the 3D incompressible Euler equations on a logarithmic lattice. Phys. Rev. Lett. 121 (2018), 064501.CrossRefGoogle ScholarPubMed
Ciampa, G., Crippa, G. and Spirito, S.. On smooth approximations of rough vector fields and the selection of flows. Preprint, 2019, arXiv:1902.00710.Google Scholar
Ciampa, G., Crippa, G. and Spirito, S.. Smooth approximation is not a selection principle for the transport equation with rough vector field. Calc. Var. Partial Differential Equations 59 (2020), 13.CrossRefGoogle Scholar
Cornfeld, I. P., Fomin, S. V. and Sinai, Y. G.. Ergodic Theory. Springer, New York, 2012.Google Scholar
Dallaston, M. C., Fontelos, M. A., Tseluiko, D. and Kalliadasis, S.. Discrete self-similarity in interfacial hydrodynamics and the formation of iterated structures. Phys. Rev. Lett. 120 (2018), 034505.CrossRefGoogle ScholarPubMed
Diacu, F.. Singularities of the N-Body Problem: An Introduction to Celestial Mechanics. Publications CRM, Université de Montréal, Montréal, 1992.Google Scholar
DiPerna, R. J. and Lions, P.-L.. Ordinary differential equations, transport theory and Sobolev spaces. Invent. Math. 98 (1989), 511–547.CrossRefGoogle Scholar
Drivas, T. D. and Eyink, G. L.. A Lagrangian fluctuation–dissipation relation for scalar turbulence. Part I. Flows with no bounding walls. J. Fluid Mech. 829 (2017), 153–189.CrossRefGoogle Scholar
Drivas, T. D. and Mailybaev, A. A.. ‘Life after death’ in ordinary differential equations with a non-Lipschitz singularity. Nonlinearity 34 (2021), 2296–2326.CrossRefGoogle Scholar
Eggers, J. and Fontelos, M. A.. Singularities: Formation, Structure, and Propagation. Cambridge University Press, Cambridge, 2015.CrossRefGoogle Scholar
Eijnden, W. E. V. and Eijnden, E. V.. Generalized flows, intrinsic stochasticity, and turbulent transport. Proc. Natl. Acad. Sci. USA 97 (2000), 8200–8205.CrossRefGoogle Scholar
Eyink, G. L.. Turbulence noise. J. Stat. Phys. 83 (1996), 955–1019.CrossRefGoogle Scholar
Eyink, G. L. and Drivas, T. D.. Quantum spontaneous stochasticity. Preprint, 2015, arXiv:1509.04941.Google Scholar
Eyink, G. L. and Drivas, T. D.. Spontaneous stochasticity and anomalous dissipation for Burgers equation. J. Stat. Phys. 158 (2015), 386–432.CrossRefGoogle Scholar
Flandoli, F.. Topics on Regularization by Noise (Lecture Notes). University of Pisa, 2013, http://users.dma.unipi.it/~flandoli/Berlino_Lectures_Flandoli.pdf.Google Scholar
Frisch, U.. Turbulence: The Legacy of A. N. Kolmogorov. Cambridge University Press, Cambridge, 1995.CrossRefGoogle Scholar
Hirsch, M. W., Pugh, C. C. and Shub, M.. Invariant Manifolds (Lecture Notes in Mathematics, 583). Springer-Verlag, Berlin–New York, 1977.CrossRefGoogle Scholar
Kocarev, L. and Parlitz, U.. Generalized synchronization, predictability, and equivalence of unidirectionally coupled dynamical systems. Phys. Rev. Lett. 76 (1996), 1816.CrossRefGoogle ScholarPubMed
Kupiainen, A.. Nondeterministic dynamics and turbulent transport. International Conference on Theoretical Physics. Eds. Iagolnitzer, D., Rivasseau, V. and Zinn-Justin, J.. Springer, Basel, 2003, pp. 713–726.CrossRefGoogle Scholar
Le Jan, Y. and Raimond, O.. Integration of rownian vector fields. Ann. Probab. 30 (2002), 826–873.CrossRefGoogle Scholar
Le Jan, Y. and Raimond, O.. Flows, coalescence and noise. Ann. Probab. 32 (2004), 1247–1315.CrossRefGoogle Scholar
Leith, C. and Kraichnan, R.. Predictability of turbulent flows. J. Atmos. Sci. 29 (1972), 1041–1058.2.0.CO;2>CrossRefGoogle Scholar
Lorenz, E. N.. The predictability of a flow which possesses many scales of motion. Tellus 21 (1969), 289–307.CrossRefGoogle Scholar
Mailybaev, A. A.. Spontaneous stochasticity of velocity in turbulence models. Multiscale Model. Simul. 14 (2016), 96–112.CrossRefGoogle Scholar
Mailybaev, A. A.. Spontaneously stochastic solutions in one-dimensional inviscid systems. Nonlinearity 29 (2016), 2238–2252.CrossRefGoogle Scholar
Mailybaev, A. A.. Toward analytic theory of the Rayleigh–Taylor instability: lessons from a toy model. Nonlinearity 30 (2017), 2466–2484.CrossRefGoogle Scholar
Mailybaev, A. A. and Raibekas, A.. Spontaneous stochasticity and renormalization group in discrete multi-scale dynamics. Comm. Math. Phys. 401 (2023), 2643–2671.CrossRefGoogle Scholar
Mailybaev, A. A. and Raibekas, A.. Spontaneously stochastic Arnold’s cat. Arnold Math. J. 9 (2023), 339–357.CrossRefGoogle Scholar
McGehee, R.. Triple collision in the collinear three-body problem. Invent. Math. 27 (1974), 191–227.CrossRefGoogle Scholar
Newton, P. K.. The N-Vortex Problem: Analytical Techniques. Springer, New York, 2013.Google Scholar
Robinson, C.. Dynamical Systems: Stability, Symbolic Dynamics, and Chaos. Taylor and Francis, London, 1999.Google Scholar
Ruelle, D.. Microscopic fluctuations and turbulence. Phys. Lett. A 72 (1979), 81–82.CrossRefGoogle Scholar
Shub, M.. Global Stability of Dynamical Systems. Springer-Verlag, New York, 1987; with the collaboration of A. Fathi and R.Langevin, translated from the French by J. Christy.CrossRefGoogle Scholar
Thalabard, S., Bec, J. and Mailybaev, A. A.. From the butterfly effect to spontaneous stochasticity in singular shear flows. Comm. Phys. 3 (2020), 122.CrossRefGoogle Scholar
Trevisan, D.. Zero noise limits using local times. Electron. Commun. Probab. 18 (2013), 1–7.CrossRefGoogle Scholar
Wiggins, S.. Normally Hyperbolic Invariant Manifolds in Dynamical Systems (Applied Mathematical Sciences, 105). Springer-Verlag, New York, 1994.CrossRefGoogle Scholar
Young, L.. What are SRB measures, and which dynamical systems have them?. J. Stat. Phys. 108 (2002), 733–754.CrossRefGoogle Scholar

Drivas et al. supplementary material

Drivas et al. supplementary material

Download Drivas et al. supplementary material(Video)
Video 2.6 MB