Hostname: page-component-7dd5485656-npwhs Total loading time: 0 Render date: 2025-10-29T12:25:53.015Z Has data issue: false hasContentIssue false
  • English
  • Français

On the selection of subaction and measure for a subclass of potentials defined by P. Walters

Published online by Cambridge University Press:  04 July 2012

A. T. BARAVIERA ,
A. O. LOPES  and
J. K. MENGUE
A. T. BARAVIERA
Affiliation:
Instituto de Matemática, Universidade Federal do Rio Grande do Sul, Avenida Bento Gonçalves 9500, Porto Alegre, RS, Brazil (email: baravi@mat.ufrgs.br, arturoscar.lopes@gmail.com, jairokras@gmail.com)
A. O. LOPES
Affiliation:
Instituto de Matemática, Universidade Federal do Rio Grande do Sul, Avenida Bento Gonçalves 9500, Porto Alegre, RS, Brazil (email: baravi@mat.ufrgs.br, arturoscar.lopes@gmail.com, jairokras@gmail.com)
J. K. MENGUE
Affiliation:
Instituto de Matemática, Universidade Federal do Rio Grande do Sul, Avenida Bento Gonçalves 9500, Porto Alegre, RS, Brazil (email: baravi@mat.ufrgs.br, arturoscar.lopes@gmail.com, jairokras@gmail.com)
Get access Rights & Permissions [Opens in a new window]

Abstract

Suppose 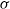$\sigma $ is the shift acting on Bernoulli space 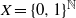$X=\{0,1\}^{\mathbb {N}}$, and consider a fixed function 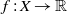$f:X \to \mathbb {R}$ satisfying the Walters conditions (defined in [P. Walters. A natural space of functions for the Ruelle operator theorem. Ergod. Th. & Dynam. Sys.27 (2007), 1323–1348]). For each real value 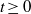$t\geq 0$ we consider the Ruelle operator 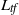$L_{\mathit {tf}}$. We are interested in the main eigenfunction 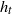$h_t$ of 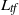$L_{\mathit {tf}}$ and the main eigenmeasure 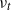$\nu _t$ for the dual operator 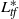$L_{\mathit {tf}}^*$, which we consider normalized in such a way that 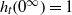$h_t(0^\infty )=1$ and 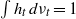$\int h_t \,d\nu _t=1$ for all 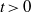$t\gt 0$. We denote by 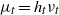$\mu _t= h_t \nu _t$ the Gibbs state for the potential 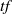$\mathit {tf}$. By the selection of a subaction 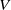$V$, when the temperature goes to zero (or 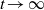$t\to \infty $), we mean the existence of the limit

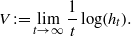\[ V:=\lim _{t\to \infty }\frac {1}{t}\log (h_{t}). \]
By the selection of a measure $\mu $, when the temperature goes to zero (or 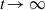$t\to \infty $), we mean the existence of the limit (in the weak* sense)
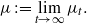\[\mu :=\lim _{t\to \infty } \mu _t.\]
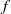 We present a large family of non-trivial examples of $f$ where the selection of a measure exists. These 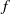$f$ belong to a sub-class of potentials introduced by Walters. In this case, explicit expressions for the selected 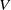$V$can be obtained for a certain large family of parameters.

Information

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 33 , Issue 5 , October 2013 , pp. 1338 - 1362
Copyright
Copyright © 2012 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

[1]Baraviera, A., Leplaideur, R. and Lopes, A. O.. Selection of ground states in the zero-temperature limit for a one-parameter family of potentials. SIAM J. Appl. Dyn. Syst. 11(1) (2012), 243–260.Google Scholar
[2]Baraviera, A., Lopes, A. O. and Thieullen, Ph.. A large deviation principle for Gibbs states of Holder potentials: the zero temperature case. Stoch. Dyn. (6) (2006), 77–96.Google Scholar
[3]Baraviera, A. T., Cioletti, L. M., Lopes, A. O., Mohr, J. and Souza, R. R.. On the general $\mathit {XY}$ model: positive and zero temperature, selection and non-selection. Rev. Modern Phys. 23(10) (2011), 1063–1113.Google Scholar
[4]Bousch, T.. Le poisson n’a pas d’arêtes. Ann. Inst. Henri Poincaré Probab. Stat. 36 (2000), 489–508.CrossRefGoogle Scholar
[5]Bousch, T.. La condition de Walters. Ann. Sci. Éc. Norm. Supér. (4) 34 (2001), 287–311.Google Scholar
[6]Brémont, J.. Gibbs measures at temperature zero. Nonlinearity 16(2) (2003), 419–426.CrossRefGoogle Scholar
[7]Chazottes, J. R. and Hochman, M.. On the zero-temperature limit of Gibbs states. Comm. Math. Phys. 297(1) (2010), 265–281.Google Scholar
[8]Chazottes, J. R., Gambaudo, J. M. and Ugalde, E.. Zero-temperature limit of one dimensional Gibbs states via renormalization: the case of locally constant potentials. Ergod. Th. & Dynam. Sys. 31(4) (2011), 1109–1161.Google Scholar
[9]Conze, J. P. and Guivarc’h, Y.. Croissance des sommes ergodiques et principe variationnel. Preprint, circa 1993.Google Scholar
[10]Contreras, G., Lopes, A. O. and Thieullen, Ph.. Lyapunov minimizing measures for expanding maps of the circle. Ergod. Th. & Dynam. Sys. 21 (2001), 1379–1409.Google Scholar
[11]Fisher, A. and Lopes, A. O.. Exact bounds for the polynomial decay of correlation, $1/f$ noise and the CLT for the equilibrium state of a non-Hölder potential. Nonlinearity 14(5) (2001), 1071–1104.Google Scholar
[12]Garibaldi, E. and Lopes, A. O.. On the Aubry–Mather theory for symbolic dynamics. Ergod. Th. & Dynam. Sys. 28 (2008), 791–815.Google Scholar
[13]Hofbauer, F.. Examples for the non-uniqueness of the Gibbs states. Trans. Amer. Math. Soc. 228 (1977), 133–141.Google Scholar
[14]Jenkinson, O.. Ergodic optimization. Discrete Contin. Dyn. Syst. 15 (2006), 197–224.CrossRefGoogle Scholar
[15]Keller, G.. Gibbs States in Ergodic Theory. Cambridge University Press, Cambridge, 1998.Google Scholar
[16]Leplaideur, R.. A dynamical proof for the convergence of Gibbs measures at temperature zero. Nonlinearity 18(6) (2005), 2847–2880.Google Scholar
[17]Leplaideur, R.. Local product structure for Gibbs states. Trans. Amer. Math. Soc. 352(4) (2000), 1889–1912.Google Scholar
[18]Lopes, A. O.. The zeta function, non-differentiability of pressure and the critical exponent of transition. Adv. Math. 101 (1993), 133–167.Google Scholar
[19]Lopes, A. O. and Mengue, J.. Zeta measures and thermodynamic formalism for temperature zero. Bull. Braz. Math. Soc. (N.S.) 41(3) (2010), 449–480.Google Scholar
[20]Mañé, R.. Ergodic Theory and Differentiable Dynamics. Springer, Berlin, 1987.Google Scholar
[21]Mengue, J.. Zeta-medidas e princípio dos grandes desvios. PhD Thesis, Universidade Federal do Rio Grande do Sul, 2010; http://hdl.handle.net/10183/26002.Google Scholar
[22]Morris, I. D.. A sufficient condition for the subordination principle in ergodic optimization. Bull. Lond. Math. Soc. 39(2) (2007), 214–220.Google Scholar
[23]Parry, W. and Pollicott, M.. Zeta functions and the periodic orbit structure of hyperbolic dynamics. Astérisque 187–188 (1990).Google Scholar
[24]van Enter, A. and Ruszel, W.. Chaotic temperature dependence at zero temperature. J. Stat. Phys. 127(3) (2007), 567–573.CrossRefGoogle Scholar
[25]Walters, P.. A natural space of functions for the Ruelle operator theorem. Ergod. Th. & Dynam. Sys. 27 (2007), 1323–1348.CrossRefGoogle Scholar