Hostname: page-component-7dd5485656-7jgsp Total loading time: 0 Render date: 2025-10-31T16:34:21.921Z Has data issue: false hasContentIssue false
  • English
  • Français

Lyapunov exponent of random dynamical systems on the circle

Part of: Random dynamical systems Smooth dynamical systems: general theory Low-dimensional dynamical systems

Published online by Cambridge University Press:  31 May 2021

DOMINIQUE MALICET Open the ORCID record for DOMINIQUE MALICET [Opens in a new window]
DOMINIQUE MALICET*
Affiliation:
Laboratoire d’Analyse et de Mathématiques Appliquées, Université Gustave Eiffel, 5 Boulevard Descartes, 77420 Champs-sur-Marne, France
*
e-mail: mdominique@crans.org
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider products of an independent and identically distributed sequence in a set $\{f_1,\ldots ,f_m\}$ of orientation-preserving diffeomorphisms of the circle. We can naturally associate a Lyapunov exponent 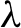$\lambda $. Under few assumptions, it is known that 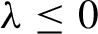$\lambda \leq 0$ and that the equality holds if and only if $f_1,\ldots ,f_m$ are simultaneously conjugated to rotations. In this paper, we state a quantitative version of this fact in the case where $f_1,\ldots ,f_m$ are 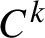$C^k$ perturbations of rotations with rotation numbers $\rho (f_1),\ldots ,\rho (f_m)$ satisfying a simultaneous diophantine condition in the sense of Moser [On commuting circle mappings and simultaneous diophantine approximations. Math. Z. 205(1) (1990), 105–121]: we give a precise estimate of 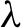$\lambda $ (Taylor expansion) and we prove that there exist a diffeomorphism g and rotations 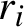$r_i$ such that $\mbox {dist}(gf_ig^{-1},r_i)\ll |\lambda |^{{1}/{2}}$ for 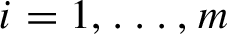$i=1,\ldots , m$. We also state analogous results for random products of $2\times 2$ matrices, without any diophantine condition.

Keywords

random dynamicsone dimensional dynamicsKAM theoryLyapunov exponents

MSC classification

Primary: 37C05: Smooth mappings and diffeomorphisms 37C75: Stability theory 37E10: Maps of the circle 37H15: Multiplicative ergodic theory, Lyapunov exponents

Information

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 42 , Issue 6 , June 2022 , pp. 2080 - 2107
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Arnold, V.. Small divisors I: on mappings of the circle onto itself. Amer. Math. Soc. Transl. Ser. 2 46 (1965), 213–284.Google Scholar
Ávila, A. and Viana, M.. Extremal Lyapunov exponents: an invariance principle and applications. Invent. Math. 181(1) (2010), 115–178.CrossRefGoogle Scholar
Bocker-Neto, C. and Viana, M.. Continuity of Lyapunov exponents for random two-dimensional matrices. Ergod. Th. & Dynam. Sys. 37(5) (2017), 1413–1442.CrossRefGoogle Scholar
Crauel, H.. Extremal exponents of random dynamical systems do not vanish. J. Dynam. Differential Equations 2(3) (1990), 245–291.CrossRefGoogle Scholar
Deroin, B., Kleptsyn, V. and Navas, A.. Sur la dynamique unidimensionnelle en régularité intermédiaire. Acta Math. 199(2) (2007), 199–262.CrossRefGoogle Scholar
Dolgopyat, D. and Krikorian, R.. On simultaneous linearization of diffeomorphisms of the sphere. Duke Math. J. 136(3) (2007), 475–506.CrossRefGoogle Scholar
Furstenberg, H.. Noncommuting random products. Trans. Amer. Math. Soc. 108 (1963), 377–428.CrossRefGoogle Scholar
Furstenberg, H. and Kesten, H.. Products of random matrices. Ann. Math. Stat. 31(2) (1960), 457–469.CrossRefGoogle Scholar
Ledrappier, F.. Positivity of the exponent for stationary sequences of matrices. Lyapunov Exponents . Springer, Berlin, 1986, pp. 56–73.CrossRefGoogle Scholar
Malicet, D.. Random walks on Homeo(S 1). Comm. Math. Phys. 356(3) (2017), 1083–1116.CrossRefGoogle Scholar
Moser, J.. On commuting circle mappings and simultaneous Diophantine approximations. Math. Z. 205(1) (1990), 105–121.CrossRefGoogle Scholar
Pastur, L. and Figotin, A.. Spectra of Random and Almost-Periodic Operators (Grundlehren der mathematischen Wissenschaften, 297). Springer-Verlag, Berlin, 1992.CrossRefGoogle Scholar