Hostname: page-component-7dd5485656-zklqj Total loading time: 0 Render date: 2025-10-31T01:51:19.911Z Has data issue: false hasContentIssue false
  • English
  • Français

Host–Kra theory for 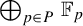$\bigoplus _{p\in P}{\mathbb {F}}_p$-systems and multiple recurrence

Part of: Measure-theoretic ergodic theory Ergodic theory

Published online by Cambridge University Press:  25 October 2021

OR SHALOM
OR SHALOM*
Affiliation:
Einstein Institute of Mathematics, The Hebrew University of Jerusalem, Edmond J. Safra Campus, Jerusalem 91904, Israel
*
e-mail: Or.Shalom@mail.huji.ac.il
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 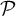$\mathcal {P}$ be an (unbounded) countable multiset of primes (that is, every prime may appear multiple times) and let 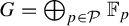$G=\bigoplus _{p\in \mathcal {P}}\mathbb {F}_p$. We develop a Host–Kra structure theory for the universal characteristic factors of an ergodic G-system. More specifically, we generalize the main results of Bergelson, Tao and Ziegler [An inverse theorem for the uniformity seminorms associated with the action of 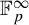$\mathbb {F}_p^\infty $. Geom. Funct. Anal. 19(6) (2010), 1539–1596], who studied these factors in the special case 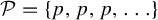$\mathcal {P}=\{p,p,p,\ldots \}$ for some fixed prime p. As an application we deduce a Khintchine-type recurrence theorem in the flavor of Bergelson, Tao and Ziegler [Multiple recurrence and convergence results associated to 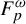$F_p^\omega $-actions. J. Anal. Math. 127 (2015), 329–378] and Bergelson, Host and Kra [Multiple recurrence and nilsequences. Invent. Math. 160(2) (2005), 261–303, with an appendix by I. Ruzsa].

Keywords

characteristic factorsnilsystemscocycles

MSC classification

Primary: 37A30: Ergodic theorems, spectral theory, Markov operators
Secondary: 28D05: Measure-preserving transformations 37A45: Relations with number theory and harmonic analysis

Information

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 43 , Issue 1 , January 2023 , pp. 299 - 360
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

REFERENCES

Abramov, L. M.. Metric automorphisms with quasi-discrete spectrum. Izv. Akad. Nauk SSSR Ser. Mat. 26 (1962), 513–530; Engl. Transl. Amer. Math. Soc. Transl. Ser. 2 39 (1964), 37–56.Google Scholar
Camarena, O. A. and Szegedy, B.. Nilspaces, nilmanifolds and their morphisms. Preprint, 2012, arXiv:1009.3825.Google Scholar
Auslander, L., Green, L. and Hahn, F.. Flows on Homogeneous Spaces (Annals of Mathematics Studies, 53). Princeton University Press, Princeton, NJ, 1963, with the assistance of L. Markus and W. Massey, and an appendix by L. Greenberg.Google Scholar
Becker, H. and Kechris, A. S.. The Descriptive Theory of Polish Groups Actions (London Mathematical Society Lecture Note Series, 232). Cambridge University Press, Cambridge, 1996.Google Scholar
Bergelson, V., Host, B. and Kra, B.. Multiple recurrence and nilsequences. Invent. Math. 160(2) (2005), 261–303, with an Appendix by I. Ruzsa.CrossRefGoogle Scholar
Bergelson, V.. Combinatorial and Diophantine applications of ergodic theory. Handbook of Dynamical Systems. Vol. 1B. Elsevier, Amsterdam, 2006, pp. 745–869, with Appendix A by A. Leibman and Appendix B by A. Quas and M. Wierdl.Google Scholar
Bergelson, V., Tao, T. and Ziegler, T.. An inverse theorem for the uniformity seminorms associated with the action of ${F}_p^{\infty }$ . Geom. Funct. Anal. 19(6) (2010), 1539–1596.CrossRefGoogle Scholar
Bergelson, V., Tao, T. and Ziegler, T.. Multiple recurrence and convergence results associated to ${F}_p^{\omega }$ -actions. J. Anal. Math. 127 (2015), 329–378.Google Scholar
Candela, P., González-Sánchez, D. and Szegedy, B.. On nilspace systems and their morphisms. Ergod. Th. & Dynam. Sys. 40(11) (2020), 3015–3029.CrossRefGoogle Scholar
Candela, P. and Szegedy, B.. Nilspace factors for general uniformity seminorms, cubic exchangeability and limits. Preprint, 2020, arXiv:1803.08758.Google Scholar
Candela, P. and Szegedy, B.. Regularity and inverse theorems for uniformity norms on compact abelian groups and nilmanifolds. Preprint, 2021, arXiv:1902.01098.Google Scholar
Christian, R.. Automatic continuity of group homomorphisms. Bull. Symbolic Logic 15(2) (2009), 184–214.Google Scholar
Conze, J.-P. and Lesigne, E.. Théormes ergodiques pour des mesures diagonales. Bull. Soc. Math. France 112 (1984), 143–175.CrossRefGoogle Scholar
Conze, J.-P. and Lesigne, E.. Sur un théorme ergodique pour des mesures diagonales. C. R. Acad. Sci. Paris Sér. I 306 (1988), 491–493.Google Scholar
Conze, J.-P. and Lesigne, E.. Sur un théorme ergodique pour des mesures diagonales. Probabilités (Publications d’Institute de Recherche Mathématique de Rennes 1987-1). Université de Rennes I, Rennes, 1998, pp. 1–31.Google Scholar
Frantzikinakis, N.. Multiple ergodic averages for three polynomials and applications. Trans. Amer. Math. Soc. 360 (2008), 5435–5475. CrossRefGoogle Scholar
Furstenberg, H.. Ergodic behavior of diagonal measures and a theorem of Szemerédi on arithmetic progression. J. Analyse Math. 31 (1977), 204–256.CrossRefGoogle Scholar
Furstenberg, H.. Nonconventional ergodic averages. The Legacy of John von Neumann (Hempstead, NY, 1988) (Proceedings of Symposia in Pure Mathematics, 50). Eds. J. Glimm, J. Impagliazzo and I. Singer. American Mathematical Society, Providence, RI, 1990, pp. 43–56.CrossRefGoogle Scholar
Furstenberg, H. and Weiss, B.. A mean ergodic theorem for $\frac{1}{N}{\sum}_{n=1}^Nf({T}^n(x))g({T}^{n^2}(x))$ . Convergence in Ergodic Theory and Probability (Columbus, OH, 1993) (Ohio State University Mathematical Research Institute Publications, 5). Ed. Bergelson, V., March, P. and Rosenblatt, J.. De Gruyter, Berlin, 1996, pp. 193–227.CrossRefGoogle Scholar
Glasner, E., Gutman, Y. and Ye, X.. Higher order regionally proximal equivalence relations for general minimal group actions. Adv. Math. 333 (2018), 1004–1041.Google Scholar
Gowers, T.. A new proof of Szemeredi’s theorem. Geom. Funct. Anal. 11 (2001), 465–588.CrossRefGoogle Scholar
Green, B. and Tao, T.. An inverse theorem for the Gowers ${U}^3(G)$ norm. Proc. Edinb. Math. Soc. (2) 51(1) (2008), 73–153.CrossRefGoogle Scholar
Green, B., Tao, T. and Ziegler, T.. An inverse theorem for the Gowers ${U}^{s+1}\left[N\right]$ -norm. Ann. of Math. (2) 176(2) (2012), 1231–1372.CrossRefGoogle Scholar
Gutman, Y. and Lian, Z.. Strictly ergodic distal models and a new approach to the Host–Kra factors. Preprint, 2019, arXiv:1909.11349.Google Scholar
Gutman, Y., Manners, F. and Varjú, P.. The structure theory of nilspaces II: representation as nilmanifolds. Trans. Amer. Math. Soc. 371(7) (2019), 4951–4992.CrossRefGoogle Scholar
Gutman, Y., Manners, F. and Varjú, P.. The structure theory of nilspaces I. J. Anal. Math. 140(1) (2020), 299–369.Google Scholar
Gutman, Y., Manners, F. and Varjú, P.. The structure theory of nilspaces III: inverse limit representations and topological dynamics. Adv. Math. 365 (2020), 107059.Google Scholar
Hofmann, K. H. and Morris, S. A.. The Structure of Compact Groups: A Primer for the Student—A Handbook for the Expert (De Gruyter Studies in Mathematics, 25), 3rd edn. De Gruyter, Berlin, 2013.CrossRefGoogle Scholar
Host, B. and Kra, B.. An odd Furstenberg–Szemerédi theorem and quasi-affine systems. J. Anal. Math. 86 (2002), 183–220.Google Scholar
Host, B. and Kra, B.. Nonconventional ergodic averages and nilmanifolds. Ann. of Math. (2) 161(1) (2005), 397–488.Google Scholar
Host, B. and Kra, B.. Nilpotent Structures in Ergodic Theory (Mathematical Surveys and Monographs, 236). American Mathematical Society, Providence, RI, 2018.CrossRefGoogle Scholar
Iwasawa, K.. On some type of topological groups. Ann. of Math. (2) 50 (1949), 507–558.CrossRefGoogle Scholar
Lesigne, E.. Théorèms ergodiques pour une translation sur une nilvariété. Ergod. Th. & Dynam. Sys. 9(1) (1989), 115–126.CrossRefGoogle Scholar
Moore, C. C. and Schmidt, K.. Coboundaries and homomorphisms for non-singular actions and a problem of H. Helson. Proc. Lond. Math. Soc. 40(3) (1980), 443–475.CrossRefGoogle Scholar
Morris, S. A.. Pontryagin Duality and the Structure of Locally Compact Abelian Groups (London Mathematical Society Lecture Note Series, 29). Cambridge University Press, Cambridge, 1977.CrossRefGoogle Scholar
Neukirch, J., Schmidt, A. and Wingberg, K.. Cohomology of Number Fields (Grundlehren der mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], 323), 2nd edn. Springer, Berlin, 2008.Google Scholar
Parry, W.. Compact abelian group extensions of discrete dynamical systems. Z. Wahrscheinlichkeitstheorie verw. Geb. 13 (1969), 95–113.CrossRefGoogle Scholar
Parry, W.. Ergodic properties of affine transformations and flows on nilmanifolds. Amer. J. Math. 91 (1969), 757–771.Google Scholar
Parry, W.. Dynamical systems on nilmanifolds. Bull. Lond. Math. Soc. 2 (1970), 37–40.Google Scholar
Sepanski, M. R.. Compact Lie groups (Graduate Texts in Mathematics, 235). Springer, New York, 2007.Google Scholar
Szemerédi, E.. On sets of integers containing k elements in arithmetic progression. Acta Arith. 27 (1975), 199–245.CrossRefGoogle Scholar
Tao, T. and Ziegler, T.. The inverse conjecture for the Gowers norm over finite fields via the correspondence principle. Anal. PDE 3(1) (2010), 1–20.Google Scholar
Walsh, N. M.. Norm convergence of nilpotent ergodic averages. Ann. of Math. (2) 175(3) (2012), 1667–1688.CrossRefGoogle Scholar
Ziegler, T.. A non-conventional ergodic theorem for a nilsystem. Ergod. Th. & Dynam. Sys. 25(4) (2005), 1357–1370.CrossRefGoogle Scholar
Ziegler, T.. Universal characteristic factors and Furstenberg averages. J. Amer. Math. Soc. 20(1) (2007), 53–97.CrossRefGoogle Scholar
Zimmer, R.. Extensions of ergodic group actions. Illinois J. Math. 20(3) (1976), 373–409.Google Scholar