Hostname: page-component-7dd5485656-c8zdz Total loading time: 0 Render date: 2025-10-31T00:28:32.221Z Has data issue: false hasContentIssue false
  • English
  • Français

Expansive dynamics on locally compact groups

Part of: Connections with other structures, applications Topological dynamics

Published online by Cambridge University Press:  18 November 2020

BRUCE P. KITCHENS
BRUCE P. KITCHENS*
Affiliation:
Indiana University–Purdue University Indianapolis, Indianapolis, IN 46202, USA
*
e-mail: bkitchen@iupui.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 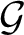$\mathcal {G}$ be a second countable, Hausdorff topological group. If 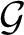$\mathcal {G}$ is locally compact, totally disconnected and T is an expansive automorphism then it is shown that the dynamical system 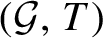$(\mathcal {G}, T)$ is topologically conjugate to the product of a symbolic full-shift on a finite number of symbols, a totally wandering, countable-state Markov shift and a permutation of a countable coset space of 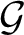$\mathcal {G}$ that fixes the defining subgroup. In particular if the automorphism is transitive then 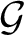$\mathcal {G}$ is compact and 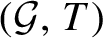$(\mathcal {G}, T)$ is topologically conjugate to a full-shift on a finite number of symbols.

Keywords

automorphismslocally compact groupssymbolic dynamics

MSC classification

Primary: 37B10: Symbolic dynamics
Secondary: 54H11: Topological groups

Information

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 41 , Issue 12 , December 2021 , pp. 3768 - 3779
Check for updates
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Cornulier, Y. and de la Harpe, P.. Metric Geometry of Locally Compact Groups ( European Mathematical Society Tracts in Mathematics , 25). European Mathematical Society, Zurich, 2016.CrossRefGoogle Scholar
Caprace, P.-E. and Monod, N. (Eds.). New Directions in Locally Compact Groups ( London Mathematical Society Lecture Note Series , 447). Cambridge University Press, Cambridge, 2018.CrossRefGoogle Scholar
Handel, M., Kitchens, B. P. and Rudolph, D. J.. Metrics and entropy for non-compact sets. Israel J. Math. 91 (1995), 253–271.CrossRefGoogle Scholar
Kitchens, B. P.. Expansive dynamics on zero-dimensional groups. Ergod. Th. & Dynam. Sys. 7 (1987), 249–261.CrossRefGoogle Scholar
Kitchens, B. P.. Symbolic Dynamics; One sided, Two-sided and Countable State Markov Shifts. Springer, Berlin, 1998.Google Scholar