Hostname: page-component-7dd5485656-g8tfn Total loading time: 0 Render date: 2025-10-30T06:05:04.313Z Has data issue: false hasContentIssue false
  • English
  • Français

Entropy bounds for multi-word perturbations of subshifts

Part of: Topological dynamics

Published online by Cambridge University Press:  27 March 2023

NICK RAMSEY
NICK RAMSEY*
Affiliation:
Department of Mathematical Sciences, DePaul University, 2320 N Kenmore Ave, Chicago, IL 60614, USA
*
e-mail: nramsey@depaul.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Given a subshift 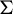$\Sigma $ of finite type and a finite set S of finite words, let 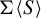$\Sigma \langle S\rangle $ denote the subshift of 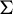$\Sigma $ that avoids S. We establish a general criterion under which we can bound the entropy perturbation 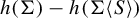$h(\Sigma ) - h(\Sigma \langle S\rangle )$ from above. As an application, we prove that this entropy difference tends to zero with a sequence of such sets 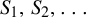$S_1, S_2,\ldots $ under various assumptions on the 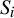$S_i$.

Keywords

symbolic dynamicssubshifts of finite typeentropy

MSC classification

Primary: 37B10: Symbolic dynamics 37B40: Topological entropy

Information

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 44 , Issue 2 , February 2024 , pp. 665 - 673
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Guibas, L. J. and Odlyzko, A. M.. Maximal prefix-synchronized codes. SIAM J. Appl. Math. 35(2) (1978), 401–418.10.1137/0135034CrossRefGoogle Scholar
Guibas, L. J. and Odlyzko, A. M.. String overlaps, pattern matching, and nontransitive games. J. Combin. Theory Ser. A 30(2) (1981), 183–208.10.1016/0097-3165(81)90005-4CrossRefGoogle Scholar
Guibas, L. J. and Odlyzko, A. M.. Periods in strings. J. Combin. Theory Ser. A 30(1) (1981), 19–42.10.1016/0097-3165(81)90038-8CrossRefGoogle Scholar
Lind, D. A.. Perturbations of shifts of finite type. SIAM J. Discrete Math. 2(3) (1989), 350–365.CrossRefGoogle Scholar
Miller, J. S.. Two notes on subshifts. Proc. Amer. Math. Soc. 140(5) (2012), 1617–1622.10.1090/S0002-9939-2011-11000-1CrossRefGoogle Scholar
Parry, W.. Intrinsic Markov chains. Trans. Amer. Math. Soc. 112 (1964), 55–66.CrossRefGoogle Scholar
Pavlov, R.. Perturbations of multidimensional shifts of finite type. Ergod. Th. & Dynam. Sys. 31(2) (2011), 483–526.10.1017/S0143385710000040CrossRefGoogle Scholar
Ramsey, N.. Perturbing subshifts of finite type: two words. Preprint, 2019, arXiv:1902.03352.Google Scholar