Article contents
Symplectomorphism groups and embeddings of balls into rational ruled 4-manifolds
Published online by Cambridge University Press: 01 May 2008
Abstract
Let Mμ0 denote S2×S2 endowed with a split symplectic form 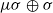 normalized so that μ≥1 and σ(S2)=1. Given a symplectic embedding
normalized so that μ≥1 and σ(S2)=1. Given a symplectic embedding 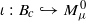 of the standard ball of capacity c∈(0,1) into Mμ0, consider the corresponding symplectic blow-up
of the standard ball of capacity c∈(0,1) into Mμ0, consider the corresponding symplectic blow-up 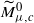 . In this paper, we study the homotopy type of the symplectomorphism group
. In this paper, we study the homotopy type of the symplectomorphism group 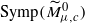 and that of the space
and that of the space  of unparametrized symplectic embeddings of Bc into Mμ0. Writing ℓ for the largest integer strictly smaller than μ, and λ∈(0,1] for the difference μ−ℓ, we show that the symplectomorphism group of a blow-up of ‘small’ capacity c<λ is homotopically equivalent to the stabilizer of a point in Symp(Mμ0), while that of a blow-up of ‘large’ capacity c≥λ is homotopically equivalent to the stabilizer of a point in the symplectomorphism group of a non-trivial bundle
of unparametrized symplectic embeddings of Bc into Mμ0. Writing ℓ for the largest integer strictly smaller than μ, and λ∈(0,1] for the difference μ−ℓ, we show that the symplectomorphism group of a blow-up of ‘small’ capacity c<λ is homotopically equivalent to the stabilizer of a point in Symp(Mμ0), while that of a blow-up of ‘large’ capacity c≥λ is homotopically equivalent to the stabilizer of a point in the symplectomorphism group of a non-trivial bundle 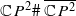 obtained by blowing down
obtained by blowing down 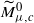 . It follows that, for c<λ, the space
. It follows that, for c<λ, the space 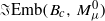 is homotopy equivalent to S2 ×S2, while, for c≥λ, it is not homotopy equivalent to any finite CW-complex. A similar result holds for symplectic ruled manifolds diffeomorphic to
is homotopy equivalent to S2 ×S2, while, for c≥λ, it is not homotopy equivalent to any finite CW-complex. A similar result holds for symplectic ruled manifolds diffeomorphic to 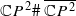 . By contrast, we show that the embedding spaces
. By contrast, we show that the embedding spaces 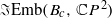 and
and 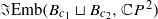 , if non-empty, are always homotopy equivalent to the spaces of ordered configurations
, if non-empty, are always homotopy equivalent to the spaces of ordered configurations 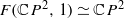 and
and 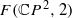 . Our method relies on the theory of pseudo-holomorphic curves in 4 -manifolds, on the computation of Gromov invariants in rational 4 -manifolds, and on the inflation technique of Lalonde and McDuff.
. Our method relies on the theory of pseudo-holomorphic curves in 4 -manifolds, on the computation of Gromov invariants in rational 4 -manifolds, and on the inflation technique of Lalonde and McDuff.
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Foundation Compositio Mathematica 2008
References
This research was funded partly by NSERC grant BP-301203-2004.
- 10
- Cited by

