Hostname: page-component-7dd5485656-glrdx Total loading time: 0 Render date: 2025-10-25T08:42:30.387Z Has data issue: false hasContentIssue false
  • English
  • Français

Goresky–Pardon lifts of Chern classes and associated Tate extensions

Part of: (Co)homology theory Arithmetic problems. Diophantine geometry Singularities

Published online by Cambridge University Press:  03 May 2017

Eduard Looijenga
Eduard Looijenga*
Affiliation:
Yau Mathematical Sciences Center, Tsinghua University Beijing, China Mathematisch Instituut, Universiteit Utrecht, Nederland email eduard@math.tsinghua.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 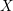$X$ be an irreducible complex-analytic variety, 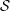${\mathcal{S}}$ a stratification of 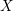$X$ and 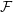${\mathcal{F}}$ a holomorphic vector bundle on the open stratum 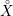${X\unicode[STIX]{x0030A}}$ . We give geometric conditions on 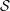${\mathcal{S}}$ and 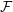${\mathcal{F}}$ that produce a natural lift of the Chern class 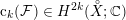$\operatorname{c}_{k}({\mathcal{F}})\in H^{2k}({X\unicode[STIX]{x0030A}};\mathbb{C})$ to 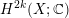$H^{2k}(X;\mathbb{C})$ , which, in the algebraic setting, is of Hodge level 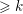${\geqslant}k$ . When applied to the Baily–Borel compactification 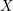$X$ of a locally symmetric variety 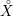${X\unicode[STIX]{x0030A}}$ and an automorphic vector bundle 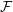${\mathcal{F}}$ on 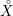${X\unicode[STIX]{x0030A}}$ , this refines a theorem of Goresky–Pardon. In passing we define a class of simplicial resolutions of the Baily–Borel compactification that can be used to define its mixed Hodge structure. We use this to show that the stable cohomology of the Satake ( $=$ Baily–Borel) compactification of 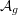${\mathcal{A}}_{g}$ contains nontrivial Tate extensions.

Keywords

Baily–Borel compactificationGoresky–Pardon Chern classTate extension

MSC classification

Primary: 14G35: Modular and Shimura varieties 14F43: Other algebro-geometric (co)homologies (e.g., intersection, equivariant, Lawson, Deligne (co)homologies) 32S35: Mixed Hodge theory of singular varieties

Information

Type
Research Article
Information
Compositio Mathematica , Volume 153 , Issue 7 , July 2017 , pp. 1349 - 1371
Copyright
© The Author 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Ash, A., Mumford, D., Rapoport, M. and Tai, Y.-S., Smooth compactifications of locally symmetric varieties, second edition, with the collaboration of Peter Scholze (Cambridge University Press, Cambridge, 2010).Google Scholar
Ayoub, J. and Zucker, S., Relative Artin motives and the reductive Borel–Serre compactification of a locally symmetric variety , Invent. Math. 188 (2012), 277–427.CrossRefGoogle Scholar
Burgos Gil, J. I., The regulators of Beilinson and Borel, CRM Monograph Series, vol. 15 (American Mathematical Society, Providence, RI, 2002).Google Scholar
Charney, R. and Lee, R., Cohomology of the Satake compactification , Topology 22 (1983), 389–423.Google Scholar
Chen, J. and Looijenga, E., The stable cohomology of the Satake compactification of A g , Geom. Topol., to appear. Preprint (2015), arXiv:1508.05600.Google Scholar
Dupont, J., Hain, R. and Zucker, S., Regulators and characteristic classes of flat bundles , in The arithmetic and geometry of algebraic cycles (Banff, AB, 1998), CRM Proceedings & Lecture Notes, vol. 24 (American Mathematical Society, Providence, RI, 2000), 47–92.Google Scholar
Goresky, M. and Pardon, W., Chern classes of automorphic vector bundles , Invent. Math. 147 (2002), 561–612.Google Scholar
Goresky, M. and Tai, Y.-S., Toroidal and reductive Borel–Serre compactifications of locally symmetric spaces , Amer. J. Math. 121 (1999), 1095–1151.Google Scholar
Hain, R., The rational cohomology ring of the moduli space of abelian 3-folds , Math. Res. Lett. 9 (2002), 473–491.Google Scholar
Mumford, D., Hirzebruch’s proportionality theorem in the noncompact case , Invent. Math. 42 (1977), 239–272.Google Scholar
Nair, A. N., Mixed structures in Shimura varieties and automorphic forms, Preprint (2013), http://www.math.tifr.res.in/∼arvind/.Google Scholar
Nair, A. N., Chern classes of automorphic vector bundles and the reductive Borel–Serre compactification, Preprint (2014), http://www.math.tifr.res.in/∼arvind/.Google Scholar
Verona, A., Le théorème de de Rham pour les préstratifications abstraites , C. R. Acad. Sci. Paris Sér. A–B 273 (1971), A886–A889.Google Scholar
Zucker, S. M., On the reductive Borel–Serre compactification: L p -cohomology of arithmetic groups (for large p) , Amer. J. Math. 123 (2001), 951–984.Google Scholar
Zucker, S. M., On the reductive Borel–Serre compactification. III. Mixed Hodge structures , Asian J. Math. 8 (2004), 881–911.Google Scholar
Zucker, S. M., On the reductive Borel–Serre compactification. II. Excentric quotients and least common modifications , Amer. J. Math. 130 (2008), 859–912.Google Scholar