Hostname: page-component-7dd5485656-zklqj Total loading time: 0 Render date: 2025-10-30T03:16:14.806Z Has data issue: false hasContentIssue false
  • English
  • Français

Gonality of dynatomic curves and strong uniform boundedness of preperiodic points

Part of: Arithmetic algebraic geometry Curves Arithmetic and non-Archimedean dynamical systems

Published online by Cambridge University Press:  17 February 2020

John R. Doyle  and
Bjorn Poonen
John R. Doyle
Affiliation:
Department of Mathematics and Statistics, Louisiana Tech University, Ruston,LA 71272, USA email jdoyle@latech.edu
Bjorn Poonen
Affiliation:
Department of Mathematics, Massachusetts Institute of Technology, Cambridge,MA 02139-4307, USA email poonen@math.mit.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Fix 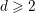$d\geqslant 2$ and a field 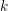$k$ such that 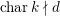$\operatorname{char}k\nmid d$. Assume that 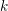$k$ contains the 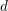$d$th roots of 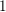$1$. Then the irreducible components of the curves over 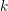$k$ parameterizing preperiodic points of polynomials of the form 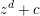$z^{d}+c$ are geometrically irreducible and have gonality tending to 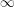$\infty$. This implies the function field analogue of the strong uniform boundedness conjecture for preperiodic points of 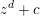$z^{d}+c$. It also has consequences over number fields: it implies strong uniform boundedness for preperiodic points of bounded eventual period, which in turn reduces the full conjecture for preperiodic points to the conjecture for periodic points. Our proofs involve a novel argument specific to finite fields, in addition to more standard tools such as the Castelnuovo–Severi inequality.

Keywords

gonalitydynatomic curvepreperiodic point

MSC classification

Primary: 37P35: Arithmetic properties of periodic points
Secondary: 11G30: Curves of arbitrary genus or genus $ne 1$ over global fields 14H51: Special divisors (gonality, Brill-Noether theory) 37P05: Polynomial and rational maps 37P15: Global ground fields

Information

Type
Research Article
Information
Compositio Mathematica , Volume 156 , Issue 4 , April 2020 , pp. 733 - 743
Copyright
© The Authors 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

The second author was supported in part by National Science Foundation grants DMS-1069236 and DMS-1601946 and Simons Foundation grants #402472 (to Bjorn Poonen) and #550033.

References

Bousch, T., Sur quelques problèmes de dynamique holomorphe, PhD thesis, Université de Paris-Sud, Centre d’Orsay (1992).Google Scholar
Doyle, J. R., Krieger, H., Obus, A., Pries, R., Rubinstein-Salzedo, S. and West, L., Reduction of dynatomic curves, Ergodic Theory Dynam. Systems 39 (2019), 2717–2768; MR 4000512.CrossRefGoogle Scholar
Epstein, A., Integrality and rigidity for postcritically finite polynomials, Bull. Lond. Math. Soc. 44 (2012), 39–46; with an appendix by Epstein and Bjorn Poonen; MR 2881322.CrossRefGoogle Scholar
Flynn, E. V., Poonen, B. and Schaefer, E. F., Cycles of quadratic polynomials and rational points on a genus-2 curve, Duke Math. J. 90 (1997), 435–463; MR 1480542 (98j:11048).CrossRefGoogle Scholar
Frey, G., Curves with infinitely many points of fixed degree, Israel J. Math. 85 (1994), 79–83; MR 1264340.CrossRefGoogle Scholar
Gao, Y., Preperiodic dynatomic curves for z↦z d + c, Fund. Math. 233 (2016), 37–69; MR 3460633.Google Scholar
Hutz, B. and Towsley, A., Misiurewicz points for polynomial maps and transversality, New York J. Math. 21 (2015), 297–319; MR 3358544.Google Scholar
Lau, E. and Schleicher, D., Internal addresses in the Mandelbrot set and irreducibility of polynomials, SUNY Stony Brook Preprint 1994/19, arXiv:math/9411238v1.Google Scholar
Looper, N., Dynamical uniform boundedness and the abc-conjecture. Preprint (2019), arXiv:1901.04385v1.CrossRefGoogle Scholar
Merel, L., Bornes pour la torsion des courbes elliptiques sur les corps de nombres, Invent. Math. 124 (1996), 437–449 (French); MR 1369424 (96i:11057).CrossRefGoogle Scholar
Morton, P., On certain algebraic curves related to polynomial maps, Compos. Math. 103 (1996), 319–350; MR 1414593.Google Scholar
Morton, P., Galois groups of periodic points, J. Algebra 201 (1998), 401–428; MR 1612390.CrossRefGoogle Scholar
Morton, P., Arithmetic properties of periodic points of quadratic maps. II, Acta Arith. 87 (1998), 89–102; MR 1665198.CrossRefGoogle Scholar
Morton, P. and Silverman, J. H., Rational periodic points of rational functions, Int. Math. Res. Not. IMRN 1994 (1994), 97–110; MR 1264933 (95b:11066).CrossRefGoogle Scholar
Nguyen, K. V. and Saito, M.-H., $d$-gonality of modular curves and bounding torsions, Preprint (1996), arXiv:alg-geom/9603024.Google Scholar
Northcott, D. G., Periodic points on an algebraic variety, Ann. of Math. (2) 51 (1950), 167–177; MR 0034607 (11,615c).CrossRefGoogle Scholar
Ogg, A. P., Hyperelliptic modular curves, Bull. Soc. Math. France 102 (1974), 449–462; MR 0364259 (51 #514).CrossRefGoogle Scholar
Poonen, B., Gonality of modular curves in characteristic p, Math. Res. Lett. 14 (2007), 691–701; MR 2335995.CrossRefGoogle Scholar
Schleicher, D., Internal addresses of the Mandelbrot set and Galois groups of polynomials, Arnold Math. J. 3 (2017), 1–35; MR 3646529.CrossRefGoogle Scholar
Stichtenoth, H., Algebraic function fields and codes, Graduate Texts in Mathematics, vol. 254, second edition (Springer, Berlin, 2009); MR 2464941.Google Scholar
Stoll, M., Rational 6-cycles under iteration of quadratic polynomials, LMS J. Comput. Math. 11 (2008), 367–380; MR 2465796.CrossRefGoogle Scholar