Hostname: page-component-7dd5485656-2pp2p Total loading time: 0 Render date: 2025-10-31T05:10:40.427Z Has data issue: false hasContentIssue false
  • English
  • Français

Conformal blocks for Galois covers of algebraic curves

Part of: Groups and algebras in quantum theory Families, fibrations Curves Lie algebras and Lie superalgebras

Published online by Cambridge University Press:  29 August 2023

Jiuzu Hong  and
Shrawan Kumar
Jiuzu Hong
Affiliation:
Department of Mathematics, University of North Carolina at Chapel Hill, Chapel Hill, NC 27599-3250, USA jiuzu@email.unc.edu
Shrawan Kumar
Affiliation:
Department of Mathematics, University of North Carolina at Chapel Hill, Chapel Hill, NC 27599-3250, USA shrawan@email.unc.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the spaces of twisted conformal blocks attached to a 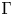$\Gamma$-curve 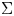$\Sigma$ with marked 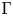$\Gamma$-orbits and an action of 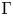$\Gamma$ on a simple Lie algebra 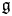$\mathfrak {g}$, where 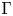$\Gamma$ is a finite group. We prove that if 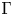$\Gamma$ stabilizes a Borel subalgebra of 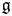$\mathfrak {g}$, then the propagation theorem and factorization theorem hold. We endow a flat projective connection on the sheaf of twisted conformal blocks attached to a smooth family of pointed 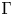$\Gamma$-curves; in particular, it is locally free. We also prove that the sheaf of twisted conformal blocks on the stable compactification of Hurwitz stack is locally free. Let 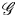$\mathscr {G}$ be the parahoric Bruhat–Tits group scheme on the quotient curve 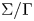$\Sigma /\Gamma$ obtained via the 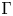$\Gamma$-invariance of Weil restriction associated to 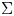$\Sigma$ and the simply connected simple algebraic group 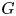$G$ with Lie algebra 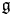$\mathfrak {g}$. We prove that the space of twisted conformal blocks can be identified with the space of generalized theta functions on the moduli stack of quasi-parabolic 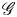$\mathscr {G}$-torsors on 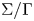$\Sigma /\Gamma$ when the level 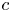$c$ is divisible by 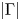$|\Gamma |$ (establishing a conjecture due to Pappas and Rapoport).

Keywords

twisted affine Kac–Moody Lie algebrasconformal blockspropagation of vacuafactorization theoremHurwitz stackflat projective connectionparahoric Bruhat–Tits group schemesmoduli stack of bundles

MSC classification

Primary: 17B67: Kac-Moody (super)algebras; extended affine Lie algebras; toroidal Lie algebras 17B68: Virasoro and related algebras 14H81: Relationships with physics 17B81: Applications to physics 14D21: Applications of vector bundles and moduli spaces in mathematical physics (twistor theory, instantons, quantum field theory)
Secondary: 14H60: Vector bundles on curves and their moduli 81R10: Infinite-dimensional groups and algebras motivated by physics, including Virasoro, Kac-Moody, $W$-algebras and other current algebras and their representations

Information

Type
Research Article
Information
Compositio Mathematica , Volume 159 , Issue 10 , October 2023 , pp. 2191 - 2259
Check for updates
Copyright
© 2023 The Author(s). The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Atiyah, M. F. and Macdonald, I. G., Introduction to commutative algebra (Addison–Wesley, 1969).Google Scholar
Balaji, V. and Seshadri, C. S., Moduli of parahoric $\mathcal {G}$-torsors on a compact Riemann surface, J. Algebraic Geom. 24 (2015), 1–49.CrossRefGoogle Scholar
Beauville, A., Conformal blocks, fusion rules and the Verlinde formula, Israel Math. Conf. Proc. 9 (1996), 75–96.Google Scholar
Beauville, A. and Laszlo, Y., Conformal blocks and generalized theta functions, Comm. Math. Phys. 164 (1994), 385–419.10.1007/BF02101707CrossRefGoogle Scholar
Beilinson, A., Feigin, B. and Mazur, B., Notes on conformal field theory, Preprint (1991), https://www.math.stonybrook.edu/~kirillov/manuscripts/bfmn.pdf.Google Scholar
Bertin, J. and Romagny, M., Champs de Hurwitz, Mémoires de la Société Mathématique de France, Numéro 125–126 (Société Mathématique de France, 2011).Google Scholar
Borel, A. and Tits, J., Homomorphismes “abstraits” de groupes algébriques simples, Ann. of Math. (2) 97 (1973), 499–571.CrossRefGoogle Scholar
Bourbaki, N., Lie groups and Lie algebras, Chap. 7–9 (Springer, 2005).Google Scholar
Cartan, H. and Eilenberg, S., Homological algebra (Princeton University Press, 1956).Google Scholar
Damiolini, C., Conformal blocks attached to twisted groups, Math. Z. 295 (2020), 1643–1681.CrossRefGoogle Scholar
Deshpande, T. and Mukhopadhyay, S., Crossed modular categories and the Verlinde formula for twisted conformal blocks, Camb. J. Math. 11 (2023), 159–297.CrossRefGoogle Scholar
Faltings, G., A proof for the Verlinde formula, J. Algebraic Geom. 3 (1994), 347–374.Google Scholar
Faltings, G., Algebraic loop groups and moduli spaces of bundles, J. Eur. Math. Soc. (JEMS) 5 (2003), 41–68.CrossRefGoogle Scholar
Frenkel, E. and Szczesny, M., Twisted modules over vertex algebras on algebraic curves, Adv. Math. 187 (2004), 195–227.CrossRefGoogle Scholar
Fuchs, J. and Schweigert, C., The action of outer automorphisms on bundles of chiral blocks, Comm. Math. Phys. 206 (1996), 691–736.CrossRefGoogle Scholar
Grothendieck, A., Revêtements Étales et Groupe Fondamental (SGA 1), Lecture Notes in Mathematics, vol. 224 (Springer, 1971).10.1007/BFb0058656CrossRefGoogle Scholar
Grothendieck, A., Éléments de géométrie algébrique: IV. Étude locale des schémas et des morphismes de schémas (Quatrième partie), Publ. Math. Inst. Hautes Études Sci. 32 (1997) 5–361.Google Scholar
Hartshorne, R., Algebraic geometry, Graduate Texts in Mathematics, vol. 52 (Springer, 1977).CrossRefGoogle Scholar
Heinloth, J., Uniformization of $\mathcal {G}$-bundles, Math. Ann. 347 (2010), 499–528.CrossRefGoogle Scholar
Hong, J., Fusion ring revisited, Contemp. Math. 713 (2018), 135–147.CrossRefGoogle Scholar
Hong, J., Conformal blocks, Verlinde formula and diagram automorphisms, Adv. Math. 354 (2019), 106731.CrossRefGoogle Scholar
Hong, J. and Kumar, S., Twisted conformal blocks and their dimension, Preprint (2022), arXiv:2207.09578.Google Scholar
Hotta, R., Takeuchi, K. and Tanisaki, T., D-modules, perverse sheaves, and representation theory, Progress in Mathematics, vol. 236 (Birkhäuser, 2008).10.1007/978-0-8176-4523-6CrossRefGoogle Scholar
Jarvis, T., Kaufmann, R. and Kimura, T., Pointed admissible G-covers and G-equivariant cohomological field theories, Compos. Math. 141 (2005), 926–978.CrossRefGoogle Scholar
Kac, V., Infinite-dimensional Lie algebras, third edition (Cambridge University Press, 1990).CrossRefGoogle Scholar
Kac, V. and Wakimoto, M., Modular and conformal invariance constraints in representation theory of affine algebras, Adv. Math. 70 (1988), 156–236.CrossRefGoogle Scholar
Kumar, S., Kac–Moody groups, their flag varieties and representation theory, Progress in Mathematics, vol. 214 (Birkhäuser, 2002).CrossRefGoogle Scholar
Kumar, S., Conformal blocks, generalized theta functions and the Verlinde formula, New Mathematical Monographs, vol. 42 (Cambridge University Press, 2022).Google Scholar
Kumar, S., Narasimhan, M. S. and Ramanathan, A., Infinite Grassmannians and moduli spaces of $G$-bundles, Math. Ann. 300 (1994), 41–75.CrossRefGoogle Scholar
Kuroki, G. and Takebe, T., Twisted Wess–Zumino–Witten models on elliptic curves, Comm. Math. Phys. 190 (1997), 1–56.CrossRefGoogle Scholar
Laszlo, Y. and Sorger, C., The line bundles on the moduli of parabolic $G$-bundles over curves and their sections, Ann. Sci. Éc. Norm. Supér. (4) 30 (1997), 499–525.CrossRefGoogle Scholar
Looijenga, E., From WZW models to modular functors, in Handbook of moduli, Vol. II, Advanced Lectures in Mathematics, vol. 25 (International Press, Somerville, MA, 2013), 427–466.Google Scholar
Pappas, G. and Rapoport, M., Twisted loop groups and their flag varieties, Adv. Math. 219 (2008), 118–198.10.1016/j.aim.2008.04.006CrossRefGoogle Scholar
Pappas, G. and Rapoport, M., Some questions about $\mathcal {G}$-bundles on curves, in Algebraic and arithmetic structures of moduli spaces (Sapporo 2007), Advanced Studies in Pure Mathematics, vol. 58 (Mathematical Society of Japan, 2010), 159–171.CrossRefGoogle Scholar
Pauly, C., Espaces de modules de fibrés praboliques et blocs conformes, Duke Math. J. 84 (1996), 217–235.CrossRefGoogle Scholar
Sorger, C., La formule de Verlinde, in Séminaire Bourbaki: volume 1994/95, exposés 790-804, Astérisque, vol. 237 (1996), talk no. 794.Google Scholar
Sorger, C., On moduli of $G$-bundles on a curve for exceptional $G$, Ann. Sci. Éc. Norm. Supér (4) 32 (1999), 127–133.10.1016/S0012-9593(99)80011-1CrossRefGoogle Scholar
Spanier, E., Algebraic topology (McGraw-Hill, 1966).Google Scholar
Steinberg, R., Endomorphisms of Linear algebraic groups, Memoirs of the American Mathematical Society, vol. 80 (American Mathematical Society, Providence, RI, 1968).CrossRefGoogle Scholar
Steinberg, R., Lectures on Chevalley groups, University Lecture Series, vol. 66 (American Mathematical Society, Providence, RI, 2016).CrossRefGoogle Scholar
Tsuchiya, A., Ueno, K. and Yamada, Y., Conformal field theory on universal family of stable curves with gauge symmetries, Adv. Stud. Pure Math. 19 (1989), 459–566.CrossRefGoogle Scholar
van Dobben de Bruyn, R., Answer to the question “when a family of curves is an affine morphism” on mathoverflow.net, https://mathoverflow.net/questions/298710/when-a-family-of-curve-is-an-affine-morphism.Google Scholar
Verlinde, E., Fusion rules and modular transformations in 2D conformal field theory, Nucl. Phys. B 300 (1988), 360–376.CrossRefGoogle Scholar
Wakimoto, M., Affine Lie algebras and the Virasoro Algebra I, Jpn. J. Math. 12 (1986), 379–400.CrossRefGoogle Scholar
Zelaci, H., Moduli spaces of anti-invariant vector bundles and twisted conformal blocks, Math. Res. Lett. 26 (2019), 1849–1875.CrossRefGoogle Scholar
Zhu, X., On the coherence conjecture of Pappas and Rapoport, Ann. of Math. (2) 180 (2014), 1–85.CrossRefGoogle Scholar