Hostname: page-component-7dd5485656-2pp2p Total loading time: 0 Render date: 2025-10-30T03:15:59.882Z Has data issue: false hasContentIssue false
  • English
  • Français

Spins of prime ideals and the negative Pell equation 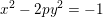$x^{2}-2py^{2}=-1$

Part of: Algebraic number theory: global fields Additive number theory; partitions Multiplicative number theory

Published online by Cambridge University Press:  23 November 2018

P. Koymans  and
D. Z. Milovic
P. Koymans
Affiliation:
Mathematisch Instituut, Universiteit Leiden, Niels Bohrweg 1, 2333 CA Leiden, The Netherlands email p.h.koymans@math.leidenuniv.nl
D. Z. Milovic
Affiliation:
Department of Mathematics, University College London, Gower Street, London WC1E 6BT, UK email djordjo.milovic@ucl.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 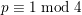$p\equiv 1\hspace{0.2em}{\rm mod}\hspace{0.2em}4$ be a prime number. We use a number field variant of Vinogradov’s method to prove density results about the following four arithmetic invariants: (i) 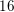$16$-rank of the class group 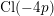$\text{Cl}(-4p)$ of the imaginary quadratic number field 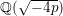$\mathbb{Q}(\sqrt{-4p})$; (ii) 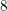$8$-rank of the ordinary class group 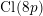$\text{Cl}(8p)$ of the real quadratic field 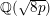$\mathbb{Q}(\sqrt{8p})$; (iii) the solvability of the negative Pell equation 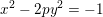$x^{2}-2py^{2}=-1$ over the integers; (iv) 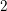$2$-part of the Tate–Šafarevič group 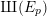$\unicode[STIX]{x0428}(E_{p})$ of the congruent number elliptic curve 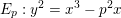$E_{p}:y^{2}=x^{3}-p^{2}x$. Our results are conditional on a standard conjecture about short character sums.

Keywords

class groupsnegative Pell equationsieve theory

MSC classification

Primary: 11R29: Class numbers, class groups, discriminants 11R45: Density theorems 11N45: Asymptotic results on counting functions for algebraic and topological structures 11P21: Lattice points in specified regions

Information

Type
Research Article
Information
Compositio Mathematica , Volume 155 , Issue 1 , January 2019 , pp. 100 - 125
Copyright
© The Authors 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

The second author is supported by ERC grant agreement No. 670239.

References

Bruin, N. and Hemenway, B., On congruent primes and class numbers of imaginary quadratic fields , Acta Arith. 159 (2013), 63–87.Google Scholar
Burgess, D. A., On character sums and primitive roots , Proc. Lond. Math. Soc. (3) 12 (1962), 179–192.Google Scholar
Burgess, D. A., On character sums and L-series. II , Proc. Lond. Math. Soc. (3) 13 (1963), 524–536.Google Scholar
Cohn, H. and Lagarias, J. C., On the existence of fields governing the 2-invariants of the classgroup of Q(√dp) as p varies , Math. Comp. 41 (1983), 711–730.Google Scholar
Cohn, H. and Lagarias, J. C., Is there a density for the set of primes p such that the class number of  Q(√-p) is divisible by 16? , in Topics in classical number theory, Vol. I, II, Colloq. Math. Soc. János Bolyai, vol. 34 (North-Holland, Amsterdam, 1984), 257–280.Google Scholar
Fouvry, É. and Klüners, J., On the 4-rank of class groups of quadratic number fields , Invent. Math. 167 (2007), 455–513.Google Scholar
Fouvry, É. and Klüners, J., On the negative Pell equation , Ann. of Math. (2) 172 (2010), 2035–2104.Google Scholar
Fouvry, É. and Klüners, J., On the Spiegelungssatz for the 4-rank , Algebra Number Theory 4 (2010), 493–508.Google Scholar
Fouvry, É. and Klüners, J., The parity of the period of the continued fraction of √d , Proc. Lond. Math. Soc. (3) 101 (2010), 337–391.Google Scholar
Fouvry, É. and Klüners, J., Weighted distribution of the 4-rank of class groups and applications , Int. Math. Res. Not. IMRN 11 (2011), 3618–3656.Google Scholar
Friedlander, J. B., Iwaniec, H., Mazur, B. and Rubin, K., The spin of prime ideals , Invent. Math. 193 (2013), 697–749.Google Scholar
Friedlander, J. B., Iwaniec, H., Mazur, B. and Rubin, K., Erratum to: The spin of prime ideals , Invent. Math. 202 (2015), 923–925.Google Scholar
Friedlander, J. and Iwaniec, H., The polynomial X 2 + Y 4 captures its primes , Ann. of Math. (2) 148 (1998), 945–1040.Google Scholar
Heath-Brown, D. R., The size of Selmer groups for the congruent number problem , Invent. Math. 111 (1993), 171–195.Google Scholar
Heath-Brown, D. R., The size of Selmer groups for the congruent number problem. II , Invent. Math. 118 (1994), 331–370; with an appendix by P. Monsky.Google Scholar
Kaplan, P., Cycles d’ordre au moins 16 dans le 2-groupe des classes d’idéaux de certains corps quadratiques , Bull. Soc. Math. France Mém. 49–50 (1977), 113–124; utilisation des calculateurs en mathématiques pures (Conf., Limoges, 1975).Google Scholar
Kaplan, P. and Williams, K. S., On the class numbers of  ℚ(√±2p) modulo 16, for p ≡ 1 (mod 8) a prime , Acta Arith. 40 (1981/82), 289–296.Google Scholar
Kaplan, P. and Williams, K. S., On the strict class number of  ℚ(√2p) modulo 16, p ≡ 1 (mod 8) prime , Osaka J. Math. 21 (1984), 23–29.Google Scholar
Kaplan, P., Williams, K. S. and Hardy, K., Divisibilité par 16 du nombre des classes au sens strict des corps quadratiques réels dont le deux-groupe des classes est cyclique , Osaka J. Math. 23 (1986), 479–489.Google Scholar
Koymans, P. and Milovic, D., On the 16-rank of class groups of  ℚ(√-2p) for primes p ≡ 1 mod 4 , Int. Math. Res. Not. IMRN (2018), rny010.Google Scholar
Lang, S., Algebraic number theory, second edition (Springer, New York, 1986).Google Scholar
Leonard, P. A. and Williams, K. S., On the divisibility of the class numbers of  ℚ(√-p) and ℚ(√-2p) by 16 , Canad. Math. Bull. 25 (1982), 200–206.Google Scholar
Milovic, D., The infinitude of  ℚ(√-p) with class number divisible by 16 , Acta Arith. 178 (2017), 201–233.Google Scholar
Milovic, D., On the 16-rank of class groups of  ℚ(√-8p) for p ≡-1 mod 4 , Geom. Funct. Anal. 27 (2017), 973–1016.Google Scholar
Milovic, D., On the 8-rank of narrow class groups of  ℚ(√-4pq), ℚ(√-8pq) and ℚ(√8pq) , Int. J. Number Theory 14 (2018), 2165–2193.Google Scholar
Oriat, B., Sur la divisibilité par 8 et 16 des nombres de classes d’idéaux des corps quadratiques Q (√2p) et Q (√-2) , J. Math. Soc. Japan 30 (1978), 279–285.Google Scholar
Rédei, L., Arithmetischer Beweis des Satzes über die Anzahl der durch vier teilbaren Invarianten der absoluten Klassengruppe im quadratischen Zahlkörper , J. Reine Angew. Math. 171 (1934), 55–60.Google Scholar
Reichardt, H., Zur Struktur der absoluten Idealklassengruppe im quadratischen Zahlkörper , J. Reine Angew. Math. 170 (1934), 75–82.Google Scholar
Scholz, A., Über die Lösbarkeit der Gleichung t 2 - Du 2 = -4 , Math. Z. 39 (1935), 95–111.Google Scholar
Serre, J.-P., Lectures on N X (p), Chapman & Hall/CRC Research Notes in Mathematics, vol. 11 (CRC Press, Boca Raton, FL, 2012).Google Scholar
Smith, A., Governing fields and statistics for 4-Selmer groups and 8-class groups, Preprint (2016), arXiv:1607.07860.Google Scholar
Smith, A., $2^{\infty }$ -Selmer groups, $2^{\infty }$ -class groups, and Goldfeld’s conjecture, Preprint (2017), arXiv:1702.02325.Google Scholar
Stevenhagen, P., Ray class groups and governing fields , in Théorie des nombres, Année 1988/89, Fasc. 1, Publications Mathématiques de la Faculté des Sciences de Besançon (Université de Franche-Comté, Faculté des Sciences, Besançon, 1989).Google Scholar
Stevenhagen, P., Divisibility by 2-powers of certain quadratic class numbers , J. Number Theory 43 (1993), 1–19.Google Scholar
Stevenhagen, P., The number of real quadratic fields having units of negative norm , Experiment. Math. 2 (1993), 121–136.Google Scholar
Vaughan, R.-C., Sommes trigonométriques sur les nombres premiers , C. R. Acad. Sci. Paris Sér. A-B 983 (1977), A981–A983.Google Scholar
Vinogradov, I. M., The method of trigonometrical sums in the theory of numbers , Trav. Inst. Math. Stekloff 23 (1947).Google Scholar
Vinogradov, I. M., The method of trigonometrical sums in the theory of numbers (Dover Publications, Mineola, NY, 2004); translated from the Russian, revised and annotated by K. F. Roth and Anne Davenport, reprint of the 1954 translation.Google Scholar
Widmer, M., Counting primitive points of bounded height , Trans. Am. Math. Soc. 362 (2010), 4793–4829.Google Scholar
Yamamoto, Y., Divisibility by 16 of class number of quadratic fields whose 2-class groups are cyclic , Osaka J. Math. 21 (1984), 1–22.Google Scholar