Rapoport–Zink spaces are deformation spaces for 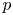$p$-divisible groups with additional structure. At infinite level, they become preperfectoid spaces. Let 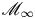${{\mathscr M}}_{\infty }$ be an infinite-level Rapoport–Zink space of EL type, and let ${{\mathscr M}}_{\infty }^{\circ }$ be one connected component of its geometric fiber. We show that 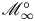${{\mathscr M}}_{\infty }^{\circ }$ contains a dense open subset which is cohomologically smooth in the sense of Scholze. This is the locus of 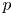$p$-divisible groups which do not have any extra endomorphisms. As a corollary, we find that the cohomologically smooth locus in the infinite-level modular curve 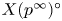$X(p^{\infty })^{\circ }$ is exactly the locus of elliptic curves 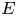$E$ with supersingular reduction, such that the formal group of 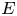$E$ has no extra endomorphisms.