Hostname: page-component-7dd5485656-dk7s8 Total loading time: 0 Render date: 2025-10-29T23:10:00.715Z Has data issue: false hasContentIssue false
  • English
  • Français

A remark on fullness of some group measure space von Neumann algebras

Part of: Abstract harmonic analysis Selfadjoint operator algebras

Published online by Cambridge University Press:  02 November 2016

Narutaka Ozawa
Narutaka Ozawa*
Affiliation:
RIMS, Kyoto University, 606-8502 Kyoto, Japan email narutaka@kurims.kyoto-u.ac.jp
Get access Rights & Permissions [Opens in a new window]

Abstract

Recently Houdayer and Isono have proved, among other things, that every biexact group 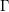$\unicode[STIX]{x1D6E4}$ has the property that for any non-singular strongly ergodic essentially free action 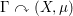$\unicode[STIX]{x1D6E4}\curvearrowright (X,\unicode[STIX]{x1D707})$ on a standard measure space, the group measure space von Neumann algebra 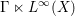$\unicode[STIX]{x1D6E4}\ltimes L^{\infty }(X)$ is full. In this paper, we prove the same property for a wider class of groups, notably including 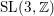$\text{SL}(3,\mathbb{Z})$ . We also prove that for any connected simple Lie group 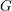$G$ with finite center, any lattice 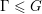$\unicode[STIX]{x1D6E4}\leqslant G$ , and any closed non-amenable subgroup 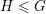$H\leqslant G$ , the non-singular action 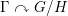$\unicode[STIX]{x1D6E4}\curvearrowright G/H$ is strongly ergodic and the von Neumann factor 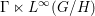$\unicode[STIX]{x1D6E4}\ltimes L^{\infty }(G/H)$ is full.

Keywords

full factorsstrongly ergodic actions

MSC classification

Primary: 46L36: Classification of factors
Secondary: 46L10: General theory of von Neumann algebras 43A07: Means on groups, semigroups, etc.; amenable groups

Information

Type
Research Article
Information
Compositio Mathematica , Volume 152 , Issue 12 , December 2016 , pp. 2493 - 2502
Copyright
© The Author 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Anantharaman-Delaroche, C., Systèmes dynamiques non commutatifs et moyennabilité , Math. Ann. 279 (1987), 297–315.Google Scholar
Ando, H. and Haagerup, U., Ultraproducts of von Neumann algebras , J. Funct. Anal. 266 (2014), 6842–6913.CrossRefGoogle Scholar
Bekka, M. E. B. and Valette, A., Lattices in semi-simple Lie groups, and multipliers of group C∗ -algebras , in Recent advances in operator algebras (Orléans, 1992), Astérisque, vol. 232 (Société Mathématique de France, Paris, 1995), 67–79.Google Scholar
Choda, M., Inner amenability and fullness , Proc. Amer. Math. Soc. 86 (1982), 663–666.Google Scholar
Connes, A., Almost periodic states and factors of type III1 , J. Funct. Anal. 16 (1974), 415–445.Google Scholar
Connes, A., Feldman, J. and Weiss, B., An amenable equivalence relation is generated by a single transformation , Ergod. Th. & Dynam. Sys. 1 (1981), 431–450.CrossRefGoogle Scholar
Connes, A. and Weiss, B., Property T and asymptotically invariant sequences , Israel J. Math. 37 (1980), 209–210.CrossRefGoogle Scholar
Cowling, M., Sur les coefficients des représentations unitaires des groupes de Lie simples , in Analyse harmonique sur les groupes de Lie II, Lecture Notes in Mathematics, vol. 739, eds Eymard, P., Takahashi, R., Faraut, J. and Schiffmann, G. (Springer, Berlin, 1979), 132–178.Google Scholar
Creutz, D. and Peterson, J., Stabilizers of ergodic actions of lattices and commensurators, Trans. Amer. Math. Soc., to appear. Preprint (2013), arXiv:1303.3949.Google Scholar
Houdayer, C. and Isono, Y., Bi-exact groups, strongly ergodic actions and group measure space type III factors with no central sequence , Comm. Math. Phys. 348 (2016), 991–1015, doi:10.1007/s00220-016-2634-7.Google Scholar
Houdayer, C. and Raum, S., Asymptotic structure of free Araki–Woods factors , Math. Ann. 363 (2015), 237–267.Google Scholar
Ioana, A., Strong ergodicity, property (T), and orbit equivalence rigidity for translation actions, J. Reine Angew. Math., to appear. Preprint (2014), arXiv:1406.6628.Google Scholar
Jones, V. F. R. and Schmidt, K., Asymptotically invariant sequences and approximate finiteness , Amer. J. Math. 109 (1987), 91–114.Google Scholar
Moore, C. C., Exponential decay of correlation coefficients for geodesic flows , in Group representations, ergodic theory, operator algebras, and mathematical physics (Berkeley, CA, 1984), Mathematical Sciences Research Institute Publications, vol. 6 (Springer, New York, 1987), 163–181.Google Scholar
Ozawa, N., A Kurosh-type theorem for type $\text{II}_{1}$ factors, Int. Math. Res. Not. IMRN 2006 (2006), doi:10.1155/IMRN/2006/97560.Google Scholar
Ozawa, N., Boundary amenability of relatively hyperbolic groups , Topology Appl. 153 (2006), 2624–2630.CrossRefGoogle Scholar
Pimsner, M. and Popa, S., Entropy and index for subfactors , Ann. Sci. Éc. Norm. Supér. (4) 19 (1986), 57–106.Google Scholar
Popa, S. and Vaes, S., Cocycle and orbit superrigidity for lattices in SL(n, ℝ) acting on homogeneous spaces , in Geometry, rigidity, and group actions (University of Chicago Press, Chicago, 2011), 419–451.Google Scholar
Sako, H., The class S as an ME invariant , Int. Math. Res. Not. IMRN 2009 (2009), 2749–2759.Google Scholar
Schmidt, K., Amenability, Kazhdan’s property T, strong ergodicity and invariant means for ergodic group-actions , Ergod. Th. & Dynam. Sys. 1 (1981), 223–236.Google Scholar
Zimmer, R. J., Hyperfinite factors and amenable ergodic actions , Invent. Math. 41 (1977), 23–31.Google Scholar