Hostname: page-component-7dd5485656-dk7s8 Total loading time: 0 Render date: 2025-10-31T05:15:51.575Z Has data issue: false hasContentIssue false
  • English
  • Français

Monoidal transforms and invariants of singularities in positive characteristic

Part of: Birational geometry

Published online by Cambridge University Press:  19 June 2013

Angélica Benito  and
Orlando E. Villamayor U.
Angélica Benito
Affiliation:
Department of Mathematics, University of Michigan, 530 Church Street, Ann Arbor, MI 48109-1043, USA email abenitos@umich.edu
Orlando E. Villamayor U.
Affiliation:
Dpto. Matemáticas, Universidad Autónoma de Madrid and ICMAT-UAM, Ciudad Universitaria de Cantoblanco, 28049 Madrid, Spain email villamayor@uam.es
Get access Rights & Permissions [Opens in a new window]

Abstract

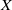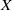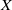The problem of resolution of singularities in positive characteristic can be reformulated as follows: fix a hypersurface $X$, embedded in a smooth scheme, with points of multiplicity at most $n$. Let an $n$-sequence of transformations of $X$ be a finite composition of monoidal transformations with centers included in the $n$-fold points of $X$, and of its successive strict transforms. The open problem (in positive characteristic) is to prove that there is an $n$-sequence such that the final strict transform of 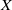$X$ has no points of multiplicity $n$ (no $n$-fold points). In characteristic zero, such an $n$-sequence is defined in two steps. The first consists of the transformation of 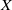$X$ to a hypersurface with $n$-fold points in the so-called monomial case. The second step consists of the elimination of these $n$-fold points (in the monomial case), which is achieved by a simple combinatorial procedure for choices of centers. The invariants treated in this work allow us to present a notion of strong monomial case which parallels that of monomial case in characteristic zero: if a hypersurface is within the strong monomial case we prove that a resolution can be achieved in a combinatorial manner.

Keywords

positive characteristicresolution of singularitiesdifferential operatorsRees algebras

MSC classification

Secondary: 14E15: Global theory and resolution of singularities

Information

Type
Research Article
Information
Compositio Mathematica , Volume 149 , Issue 8 , August 2013 , pp. 1267 - 1311
Copyright
© The Author(s) 2013 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Abhyankar, S., Local uniformization on algebraic surfaces over ground fields of characteristic $p\not = 0$, Ann. of Math. (2) 63 (1956), 256–491.Google Scholar
Abhyankar, S., Ramification theoretic methods in algebraic geometry, Annals of Mathematics Studies, vol. 43 (Princeton University Press, Princeton, NJ, 1959).Google Scholar
Altman, A. and Kleiman, S., Introduction to Grothendieck duality theory, Lecture Notes in Mathematics, vol. 146 (Springer, Berlin, 1970).CrossRefGoogle Scholar
Benito, A., The $\tau $-invariant and elimination, J. Algebra 324 (2010), 1903–1920.Google Scholar
Benito, A. and Villamayor U., O. E., On elimination of variables in the study of singularities in positive characteristic, Preprint (2011), available at http://arxiv.org/abs/1103.3462.Google Scholar
Benito, A. and Villamayor U., O. E., Techniques for the study of singularities with applications to resolution of 2-dimensional schemes, Math. Ann. 353 (2012), 1037–1068.CrossRefGoogle Scholar
Bravo, A. and Villamayor U., O. E., Singularities in positive characteristic, stratification and simplification of the singular locus, Adv. Math. 224 (2010), 1349–1418.Google Scholar
Cossart, V., Sur le polyèdre caractéristique. Thèse d’État, Universitè Paris–Sud, Orsay (1987).Google Scholar
Cossart, V., Jannsen, U. and Saito, S., Canonical embedded and non-embedded resolution of singularities for excellent two-dimensional schemes, Preprint (2009), available at http://arxiv.org/abs/0905.2191v1.Google Scholar
Cossart, V. and Piltant, O., Resolution of singularities of threefolds in positive characteristic I, J. Algebra 320 (2008), 1051–1082.Google Scholar
Cossart, V. and Piltant, O., Resolution of singularities of threefolds in positive characteristic II, J. Algebra 321 (2009), 1836–1976.CrossRefGoogle Scholar
Cutkosky, S. D., Resolution of singularities for 3-folds in positive characteristic, Amer. J. Math. 131 (2009), 59–127.Google Scholar
Cutkosky, S. D., A skeleton key to Abhyankar’s proof of embedded resolution of characteristic $p$ surfaces, Asian J. Math. 15 (2011), 369–416.Google Scholar
Encinas, S. and Villamayor U., O. E., A course on constructive desingularization and equivariance, in Resolution of singularities: A research textbook in tribute to Oscar Zariski, Progress in Mathematics, vol. 181, eds Hauser, H., Lipman, J., Oort, F. and Quirós, A. (Birkhäuser, Basel, 2000), 147–227.Google Scholar
Encinas, S. and Villamayor U., O. E., Rees algebras and resolution of singularities, in Actas del ‘XVI Coloquio Latinoamericano de Algebra’ Colonia del Sacramento, Uruguay, 2005, eds W. F. Santos, G. González-Springer, A. Rittatore and A. Solotar, (Library of the Revista Matemática Iberoamericana, 2007), 1–24.Google Scholar
Giraud, J., Contact maximal en caractéristique positive, Ann. Sci. Éc. Norm. Supér. (4) 8 (1975), 201–234.Google Scholar
Giraud, J., Forme normale d’une fonction sur une surface de caractéristique positive, Bull. Soc. Math. France 111 (1983), 109–124.Google Scholar
Giraud, J., Condition de Jung pour les revêtements radiciels de hauteur 1, in Algebraic geometry Tokyo/Kyoto, 1982, Lecture Notes in Mathematics, vol. 1016 (Springer, Berlin, 1983), 313–333.Google Scholar
Hauser, H., Wild singularities and kangaroo points for the resolution in positive characteristic. Preprint (2009).Google Scholar
Hauser, H., On the problem of resolution of singularities in positive characteristic (Or: A proof we are still waiting for), Bull. Amer. Math. Soc. (N.S.) 47 (2010), 1–30.CrossRefGoogle Scholar
Hauser, H. and Wagner, D., Two new invariants for the resolution of surfaces in positive characteristic. In preparation.Google Scholar
Hironaka, H., Resolution of singularities of an algebraic variety over a field of characteristic zero I, Ann. of Math. (2) 79 (1964), 109–203.Google Scholar
Hironaka, H., Resolution of singularities of an algebraic variety over a field of characteristic zero II, Ann. of Math. (2) 79 (1964), 205–306.Google Scholar
Hironaka, H., Program for resolution of singularities in characteristics $p\gt 0$. Notes from lectures at the Clay Mathematics Institute, September (2008).Google Scholar
Kawanoue, H., Toward resolution of singularities over a field of positive characteristic. I. Foundation; the language of the idealistic filtration, Publ. Res. Inst. Math. Sci. 43 (2007), 819–909.Google Scholar
Kawanoue, H. and Matsuki, K., Toward resolution of singularities over a field of positive characteristic. (The idealistic filtration program), Publ. Res. Inst. Math. Sci. 46 (2010), 359–422.Google Scholar
Kawanoue, H. and Matsuki, K., Resolution of singularities of an idealistic filtration in dimension 3 after Benito–Villamayor. Accepted for publication. Available at arXiv:1205.4556v1.Google Scholar
Lipman, J., Desingularization of two-dimensional schemes, Ann. of Math. (2) 107 (1978), 151–207.Google Scholar
Moh, T. T., On a stability theorem for local uniformization in characteristic $p$, Publ. Res. Inst. Math. Sci. 23 (1987), 965–973.Google Scholar
Moh, T. T., On a Newton polygon approach to the uniformization of singularities in characteristic $p$, in Algebraic Geometry and Singularities: Proceedings of the Conference on Singularities La Rábida, eds Campillo, A. and Narváez, L. (Birkhäuser, 1996).Google Scholar
Piltant, O., On the Jung method in positive characteristic, in Proceedings of the International Conference in Honor of Frédéric Pham, Nice, 2002, Ann. Inst. Fourier (Grenoble) 53 (2003), 1237–1258.Google Scholar
Villamayor U., O. E., Constructiveness of Hironaka’s resolution, Ann. Sci. Éc. Norm. Supér. (4) 22 (1989), 1–32.CrossRefGoogle Scholar
Villamayor U., O. E., Hypersurface singularities in positive characteristic, Adv. Math. 213 (2007), 687–733.Google Scholar
Villamayor U., O. E., Rees algebras on smooth schemes: integral closure and higher differential operators, Rev. Mat. Iberoam. 24 (2008), 213–242.Google Scholar
Villamayor U., O. E., Elimination with applications to singularities in positive characteristic, Publ. Res. Inst. Math. Sci. 44 (2008), 661–697.Google Scholar
Włodarczyk, J., Simple Hironaka resolution in characteristic zero, J. Amer. Math. Soc. 18 (2005), 779–822.Google Scholar
Włodarczyk, J., Program on resolution of singularities in characteristic $p$, Notes from Lectures at RIMS, Kyoto, December (2008).Google Scholar