No CrossRef data available.
Article contents
Colouring random subgraphs
Part of:
Graph theory
Published online by Cambridge University Press: 28 April 2025
Abstract
We study several basic problems about colouring the 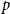 $p$-random subgraph
$p$-random subgraph 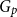 $G_p$ of an arbitrary graph
$G_p$ of an arbitrary graph 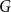 $G$, focusing primarily on the chromatic number and colouring number of
$G$, focusing primarily on the chromatic number and colouring number of 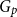 $G_p$. In particular, we show that there exist infinitely many
$G_p$. In particular, we show that there exist infinitely many 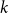 $k$-regular graphs
$k$-regular graphs 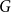 $G$ for which the colouring number (i.e., degeneracy) of
$G$ for which the colouring number (i.e., degeneracy) of 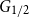 $G_{1/2}$ is at most
$G_{1/2}$ is at most 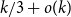 $k/3 + o(k)$ with high probability, thus disproving the natural prediction that such random graphs must have colouring number at least
$k/3 + o(k)$ with high probability, thus disproving the natural prediction that such random graphs must have colouring number at least 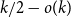 $k/2 - o(k)$.
$k/2 - o(k)$.
MSC classification
Primary:
05C80: Random graphs
Secondary:
05C15: Coloring of graphs and hypergraphs
Information
- Type
- Paper
- Information
- Copyright
- © The Author(s), 2025. Published by Cambridge University Press
References
Alon, N., Krivelevich, M. and Sudakov, B. (1997) Subgraphs with a large cochromatic number. J. Graph Theory 25(4) 295–297.3.0.CO;2-F>CrossRefGoogle Scholar
Alon, N. and Milman, V. D. (1985)
 $\lambda _1,$
isoperimetric inequalities for graphs, and superconcentrators. J. Combin. Theory Ser. B. 38 73–88.CrossRefGoogle Scholar
$\lambda _1,$
isoperimetric inequalities for graphs, and superconcentrators. J. Combin. Theory Ser. B. 38 73–88.CrossRefGoogle Scholar
Alon, N. and Spencer, J. H. (2016) The probabilistic method, Wiley Series in Discrete Mathematics and Optimization. fourth ed. Hoboken, NJ: John Wiley & Sons, Inc.Google Scholar
Balogh, J. and Pittel, B. G. (2007) Bootstrap percolation on the random regular graph. Random Struct. Algor. 30(1–2) 257–286.CrossRefGoogle Scholar
Beveridge, A., Frieze, A. and McDiarmid, C. (1998) Random minimum length spanning trees in regular graphs. Combinatorica 18(3) 311–333.CrossRefGoogle Scholar
Blume, L., Easley, D., Kleinberg, J., Kleinberg, R. and Tardos, É. (2011) Which networks are least susceptible to cascading failures? In 2011 IEEE 52nd Annual Symposium on Foundations of Computer Science—FOCS. 2011, IEEE Computer Soc, Los Alamitos, CA, pp. 393–402.CrossRefGoogle Scholar
Bollobás, B. (1988) The chromatic number of random graphs. Combinatorica 8(1) 49–55.CrossRefGoogle Scholar
Bollobás, B. (1998) Modern graph theory, Graduate Texts in Mathematics, Vol. 184, New York: Springer-Verlag.Google Scholar
Chalupa, J., Leath, P. L. and Reich, G. R. (1979) Bootstrap percolation on a Bethe lattice. J. Phys. C. 12(1) L31–L35.CrossRefGoogle Scholar
Erdős, P. (1969) Problems and results in chromatic graph theory, Proof Techniques in Graph Theory (Proc. Second Ann Arbor Graph Theory Conf., Ann Arbor, Mich., 1968), New York: Academic Press, 27–35.Google Scholar
Erdős, P. (1971) Some unsolved problems in graph theory and combinatorial analysis, Combinatorial Mathematics and its Applications (Proc. Conf., Oxford, 1969), Academic Press, London, pp. 97–109,Google Scholar
Erdős, P. and Hajnal, A. (1966) On chromatic number of graphs and set-systems. Acta Math. Acad. Sci. Hungar. 17(1-2) 61–99.CrossRefGoogle Scholar
Hoory, S., Linial, N. and Wigderson, A. (2006) Expander graphs and their applications. Bull. Amer. Math. Soc. 43(04) 439–561.(N.S.)CrossRefGoogle Scholar
Janson, S., Łuczak, T., Turova, T. and Vallier, T. (2012) Bootstrap percolation on the random graph
 $G_{n,p}$
. Ann. Appl. Probab. 22 1989–2047.CrossRefGoogle Scholar
$G_{n,p}$
. Ann. Appl. Probab. 22 1989–2047.CrossRefGoogle Scholar
Mohar, B. and Wu, H. (2020) Fractional chromatic number of a random subgraph. J. Graph Theory 95(3) 467–472.CrossRefGoogle Scholar
Thomassen, C. (1983) Girth in graphs. J. Combin. Theory Ser. B. 35(2) 129–141.CrossRefGoogle Scholar
Watts, D. J. (2002) A simple model of global cascades on random networks. Proc. Natl. Acad. Sci. 99(9) 5766–5771.USACrossRefGoogle ScholarPubMed


